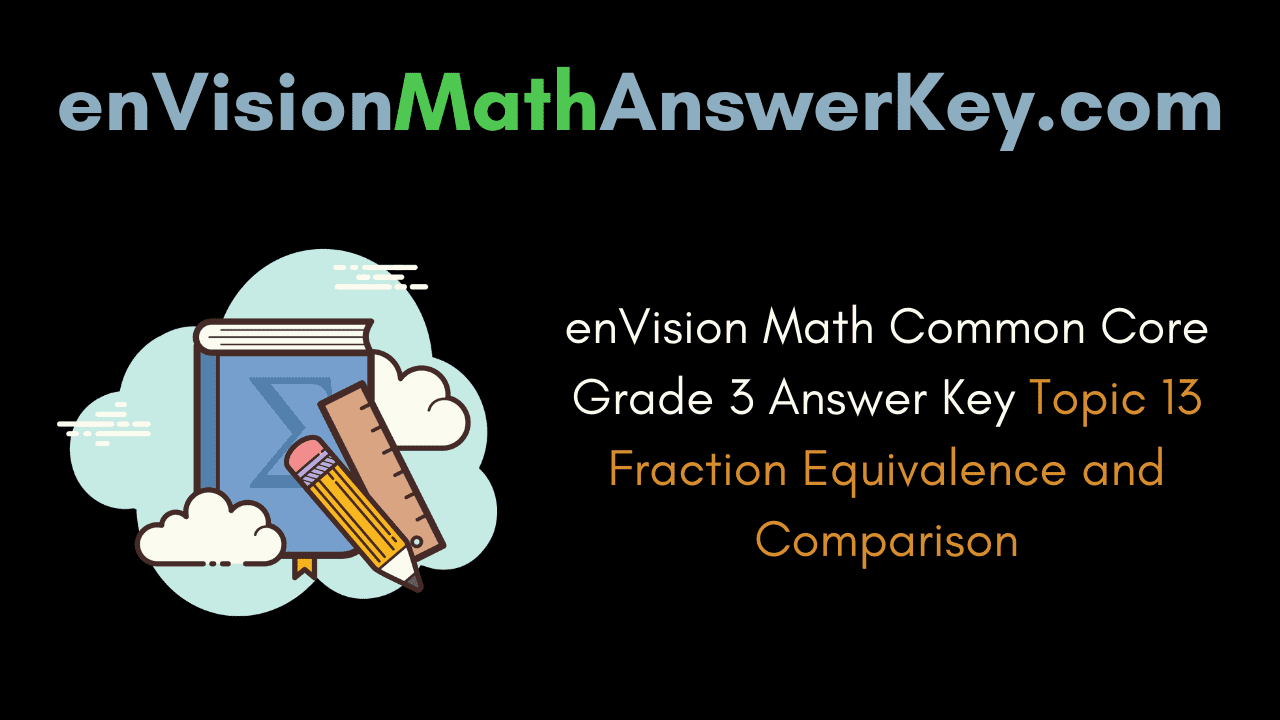Go through the enVision Math Common Core Grade 3 Answer Key Topic 13 Fraction Equivalence and Comparison regularly and improve your accuracy in solving questions.
enVision Math Common Core 3rd Grade Answers Key Topic 13 Fraction Equivalence and Comparison
Essential Question:
What are different ways to compare fractions?

enVision STEM Project: Life Cycles
Do Research A frog egg hatches into a tadpole that lives in water. The tadpole will change and eventually become an adult frog. Use the Internet or another source to gather information about the life cycle of a frog and other animals.
Journal: Write a Report Include what you found. Also in your report:
- Tell about what is in a frog’s habitat to support changes the frog goes through in its life cycle.
- Compare the life cycles of the different animals you studied.
- For the animals you studied, make up and solve problems using fractions. Draw fraction strips to represent the fractions.
Review What You Know
Choose the best term from the box. Write it on the blank.
- <
- >
- numerator
- unit fraction
Vocabulary
Question 1.
The symbol ___________ means is greater than.
Answer:
The symbol > means greater than.
Explanation:
In the above-given question,
given that,
greater than symbol is used to compare numbers.
for example:
3 > 1.
so the symbol > is used for large numbers when compared with small numbers.

Question 2.
The symbol _________ means is less than.
Answer:
The symbol < means less than.
Explanation:
In the above-given question,
given that,
less than a symbol is used to compare numbers.
for example:
1 < 3.
so the symbol < is used for small numbers when compared with large numbers.
Question 3.
A ________ represents one equal part of a whole.
Answer:
The fraction represents one equal part of a whole.
Explanation:
In the above-given question,
given that,
a fraction represents one equal part of a whole.
for example:
3/4.
the whole part is 4.
the 3/4 of the portion is filled.
so the fraction represents one equal part of a whole.
Comparing Whole Numbers
Compare. Write <, >, or =.
Question 4.
48 ![]() 30
30
Answer:
48 > 30.
Explanation:
In the above-given question,
given that,
the two numbers are 48 and 30.
30 is less than 48.
48 is greater than 30.
48 > 30.
![]()
Question 5.
6 ![]() 6
6
Answer:
6 = 6.
Explanation:
In the above-given question,
given that,
the two numbers are 6 and 6.
6 is equal to 6.
6 = 6.
![]()
Question 6.
723 ![]() 732
732
Answer:
723 < 732.
Explanation:
In the above-given question,
given that,
the two numbers are 723 and 732.
723 is less than 732.
732 is greater than 723.
723 < 732.
![]()
Question 7.
152 ![]() 183
183
Answer:
152 < 183.
Explanation:
In the above-given question,
given that,
the two numbers are 152 and 183.
152 is less than 183.
183 is greater than 152.
152 < 183.
![]()
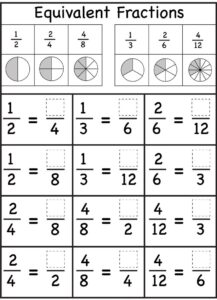
Question 8.
100 ![]() 10
10
Answer:
100 > 10.
Explanation:
In the above-given question,
given that,
the two numbers are 100 and 10.
100 is greater than 10.
10 is less than 100.
100 > 10.
Question 9.
189 ![]() 99
99
Answer:
189 > 99.
Explanation:
In the above-given question,
given that,
the two numbers are 189 and 99.
189 is greater than 99.
99 is less than 189.
189 > 99.
![]()
Question 10.
456 ![]() 456
456
Answer:
456 = 456.
Explanation:
In the above-given question,
given that,
the two numbers are 456 and 456.
456 is equal to 456.
456 = 456.
![]()
Question 11.
123 ![]() 223
223
Answer:
123 < 223.
Explanation:
In the above-given question,
given that,
the two numbers are 123 and 223.
123 is less than 223.
223 is greater than 123.
123 < 223.
![]()
Question 12.
421 ![]() 399
399
Answer:
421 > 399.
Explanation:
In the above-given question,
given that,
the two numbers are 421 and 399.
421 is greater than 399.
399 is less than 421.
421 > 399.
![]()
Question 13.
158 ![]() 185
185
Answer:
158 < 185.
Explanation:
In the above-given question,
given that,
the two numbers are 158 and 185.
158 is less than 185.
185 is greater than 158.
158 < 185.
![]()
Question 14.
117 ![]() 117
117
Answer:
117 = 117.
Explanation:
In the above-given question,
given that,
the two numbers are 117 and 117.
117 is equal to 117.
117 = 117.
![]()
Question 15.
900 ![]() 893
893
Answer:
900 > 893.
Explanation:
In the above-given question,
given that,
the two numbers are 900 and 893.
900 is greater than 893.
893 is less than 900.
900 > 893.

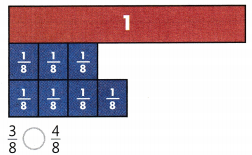
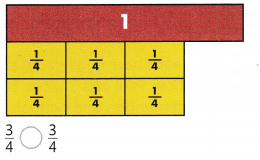
Identifying Fractions
For each shape, write the fraction that is shaded.
Question 16.

Answer:
The fraction is 4/8.
Explanation:
In the above-given question,
given that,
the figure contains 8 boxes.
4 boxes are filled.
4/8 portion of the boxes are filled.
4/8 = 1/2.
so half portion of the boxes is filled.
Question 17.

Answer:
The fraction is 1/6.
Explanation:
In the above-given question,
given that,
there are 6 boxes in the figure.
1 box is filled.
so 1/6 portion is filled.
Question 18.
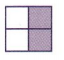
Answer:
The fraction is 2/4.
Explanation:
In the above-given question,
given that,
the figure contains 4 boxes.
2 boxes are filled.
2/4 portion of the boxes are filled.
2/4 = 1/2.
so half portion of the boxes is filled.
Division
Divide.
Question 19.
30 ÷ 5
Answer:
The answer is 6.
Explanation:
In the above-given question,
given that,
the two numbers are 30 and 5.
5 x 6 = 30.
30 / 5 = 6.
Question 20.
72 ÷ 8
Answer:
72 / 8 = 9.
Explanation:
In the above-given question,
given that,
the two numbers are 72 and 8.
8 x 9 = 72.
72 / 8 = 9.
Question 21.
28 ÷ 4
Answer:
28 / 4 = 7.
Explanation:
In the above-given question,
given that,
the two numbers are 28 and 4.
4 x 7 = 28.
28 / 4 = 7.
Question 22.
48 ÷ 6
Answer:
48 / 6 = 8.
Explanation:
In the above-given question,
given that,
the two numbers are 48 and 6.
6 x 8 = 48.
48 / 6 = 8.
Question 23.
81 ÷ 9
Answer:
81 / 9 = 9.
Explanation:
In the above-given question,
given that,
the two numbers are 81 and 9.
9 x 9 = 81.
81 / 9 = 9.
Question 24.
45 ÷ 5
Answer:
45 / 5 = 9.
Explanation:
In the above-given question,
given that,
the two numbers are 45 and 5.
5 x 9 = 45.
45 / 5 = 9.
Question 25.
32 ÷ 8
Answer:
32 / 8 = 4.
Explanation:
In the above-given question,
given that,
the two numbers are 32 and 8.
8 x 4 = 32.
32 / 8 = 4.
Question 26.
42 ÷ 6
Answer:
42 / 6 = 7.
Explanation:
In the above-given question,
given that,
the two numbers are 42 and 6.
6 x 7 = 42.
42 / 6 = 7.
Question 27.
49 ÷ 7
Answer:
49 / 7 = 7.
Explanation:
In the above-given question,
given that,
the two numbers are 49 and 7.
7 x 7 = 49.
49 / 7 = 7.
Question 28.
How can you check if the answer to 40 ÷ 5 is 8?
Answer:
40 / 5 = 8.
Explanation:
In the above-given question,
given that,
the two numbers are 40 and 5.
40 / 5 = 8.
8 x 5 = 40.
Pick a Project
PROJECT 13A
Do you want to ride a horse?
Project: Design a Racetrack for Horses

PROJECT 13B
How deep do you have to dig before you reach water?
Project: Create a Picture of a Well

PROJECT 13C
How many coffee beans does it take to fill up a container?
Project: Plot Fractions on a Number Line

3-ACT MATH PREVIEW
Math Modeling
What’s the Beef?

Lesson 13.1 Equivalent Fractions: Use Models
Solve & Share
Gregor threw a softball of the length of the yard in front of his house. Find as many fractions as you can that name the same part of the length of the yard that Gregor threw the ball. Explain how you decided
I can … find equivalent fractions that name the same part of a whole.

Answer:
1/9, 2/9, 3/9, 4/9.
Explanation:
In the above-given question,
given that,
Gregor threw a softball off the length of the yard in front of his house.
Gregor threw the 1st ball at 1 yard.
1/9.
the length of the yard is 9.
Gregor threw the 2nd ball at 2 yards.
2/9.
Gregor threw the 3rd ball at 3 yards.
3/9.
Gregor threw the 4th ball at 4 yards.
4/9.
so the fractions are 1/9, 2/9, 3/9, and 4/9.
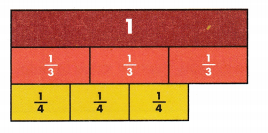
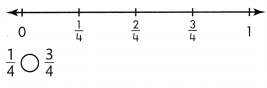
Look Back! How can fraction strips help you tell if a fraction with a denominator of 2, 3, or 6 would name the same part of a whole as \(\frac{3}{4}\)?
Answer:
2/4 and 6/4.
Explanation:
In the above-given question,
given that,
the denominators are 2, 3, and 6.
3/4 and 2/4 = 1/2.
6/4 = 3/2.
Essentials Question
How Can Different Fractions Name the Same Part of a Whole?
Visual Learning Bridge
The Chisholm Trail was used to drive cattle to market. Ross’s herd has walked \(\frac{1}{2}\) the distance to market. What is another way to name \(\frac{1}{2}\)?
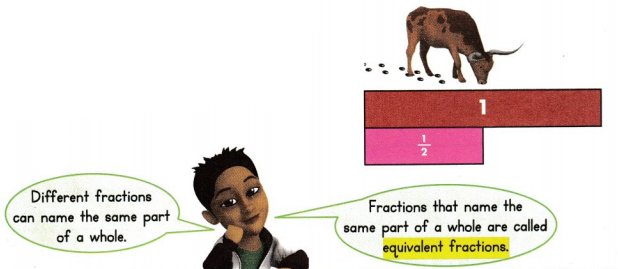
\(\frac{1}{2}\) = \(\frac{}{}\) You can use fraction strips.
The fractions \(\frac{1}{2}\) and \(\frac{2}{4}\) represent the same part of the whole.
Two \(\frac{1}{4}\) strips are equal to \(\frac{1}{2}\), so \(\frac{1}{2}\) = \(\frac{2}{4}\).
Another name for \(\frac{1}{2}\) is \(\frac{2}{4}\).
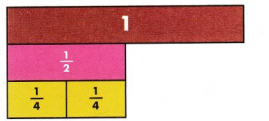
You can find other equivalent fractions. Think about fractions that name the same part of the whole.
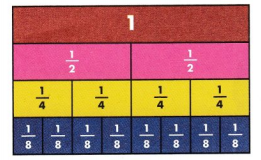
Four \(\frac{1}{8}\) strips are equal to \(\frac{1}{2}\), so \(\frac{1}{2}\) = \(\frac{4}{8}\).
Another name for \(\frac{1}{2}\) is \(\frac{4}{8}\)
Convince Me! Look for Relationships In the examples above, what pattern do you see in the fractions that are equivalent to \(\frac{1}{2}\)? What is another name for \(\frac{1}{2}\) that is not shown above?
Answer:
The other name is 4/8.
Explanation:
In the above-given question,
given that,
Four \(\frac{1}{8}\) strips are equal to \(\frac{1}{2}\).
\(\frac{1}{2}\) = \(\frac{4}{8}\).
\(\frac{1}{2}\) is \(\frac{4}{8}\).
so the other name is 4/8.
Another Example!
You can find an equivalent fraction for \(\frac{4}{6}\) using an area model.
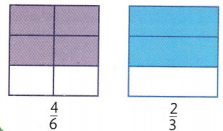
Both area models have the same-sized whole. One is divided into sixths. The other shows thirds. The shaded parts show the same part of a whole. Because \(\frac{4}{6}\) = \(\frac{2}{3}\), another name for \(\frac{4}{6}\) is \(\frac{2}{3}\).
Guided Practice
Do You Understand?
Question 1.
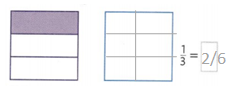
Divide the second area model into sixths. Shade it to show a fraction equivalent to \(\frac{1}{3}\):
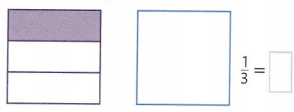
Answer:
1/3 = 2/6.
Explanation:
In the above-given question,
given that,
divide the second area model into sixths.
\(\frac{1}{3}\) = \(\frac{2}{6}\).
\(\frac{1}{3}\) is \(\frac{2}{6}\).
2/6 = 1/3.
Do You Know How?
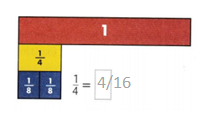
Question 2.
Use the fraction strips to help find an equivalent fraction.

Answer:
1/4 = 4/16.
Explanation:
In the above-given question,
given that,
\(\frac{1}{4}\) = \(\frac{4}{16}\).
\(\frac{4}{16}\) is \(\frac{1}{4}\).
1/4 = 4/16.
Independent Practice
Question 3.
Use the fraction strips to help find an equivalent fraction.
Answer:
1/2 = 4/8.
Explanation:
In the above-given question,
given that,
1/4 + 1/4 = 1/2.
1/2 + 1/2 = 1.
4/8 = 1/2.
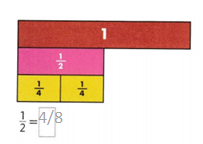
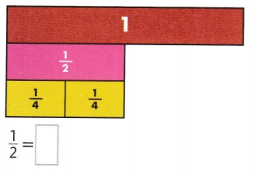
Question 4.
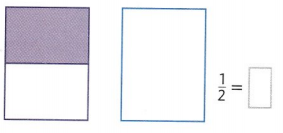
Divide the second area model into eighths. Shade it to show a fraction equivalent to \(\frac{1}{2}\).
Answer:
1/2 = 4/8.
Explanation:
In the above-given question,
given that,
divide the second area model into eights.
\(\frac{1}{2}\) = \(\frac{4}{8}\).
\(\frac{1}{2}\) is \(\frac{4}{8}\).
1/2 = 4/8.

In 5-8, find each equivalent fraction. Use fraction strips or draw area models to help.
Question 5.
\(\frac{3}{4}\) = \(\frac{}{8}\)
Answer:
\(\frac{3}{4}\) = \(\frac{6}{8}\).
Explanation:
In the above-given question,
given that,
divide the 1st area model into fourths.
divide the second area model into eights.
3/4 = 6/8.
6/8 = 3/4.
Question 6.
\(\frac{6}{6}\) = \(\frac{}{8}\)
Answer:
\(\frac{6}{6}\) = \(\frac{1}{8}\).
Explanation:
In the above-given question,
given that,
divide the 1st area model into sixths.
divide the second area model into eights.
6/6 = 1.
1/8 = 6/6.
Question 7.
\(\frac{2}{6}\) = \(\frac{}{3}\)
Answer:
\(\frac{2}{6}\) = \(\frac{1}{3}\).
Explanation:
In the above-given question,
given that,
divide the 1st area model into sixths.
divide the second area model into thirds.
2/6 = 1/3.
1/3 = 2/6.
Question 8.
\(\frac{4}{8}\) = \(\frac{}{2}\)
Answer:
\(\frac{4}{8}\) = \(\frac{1}{2}\).
Explanation:
In the above-given question,
given that,
divide the 1st area model into eigths.
divide the second area model into halfs.
4/8 = 1/2.
1/2 = 4/8.
Problem Solving
In 9 and 10, use the fraction strips at the right.
Question 9.
Marcy used fraction strips to show equivalent fractions. Complete the equation.
\(\frac{}{4}\) = ________
Answer:
\(\frac{1}{4}\) = \(\frac{2}{8}\).
Explanation:
In the above-given question,
given that,
divide the 1st area model into fourths.
divide the second area model into eights.
1/4 = 2/8.
2/8 = 1/4.
Question 10.
Rita says the fraction strips show fractions that are equivalent to \(\frac{1}{2}\). Explain what you could do to the diagram to see if she is correct.
Answer:
\(\frac{2}{4}\) = \(\frac{1}{2}\).
Explanation:
In the above-given question,
given that,
divide the 1st area model into fourths.
divide the second area model into halves.
2/4 = 1/2.
1/2 = 2/4.
Question 11.
Reasoning A band learns 4 to 6 new songs every month. What is a good estimate for the number of songs the band will learn in 8 months? Explain.
Answer:
The number of songs the band will learn in 8 months = 80 songs.
Explanation:
In the above-given question,
given that,
A band learns 4 to 6 new songs every month.
4 + 6 = 10.
10 x 8 = 80.
so the number of songs the band will learn in 8 months = 80 songs.
Question 12.
Three-eighths of a playground is covered by grass. What fraction of the playground is NOT covered by grass?
Answer:
The fraction of the playground is not covered by grass = 5/8.
Explanation:
In the above-given question,
given that,
three-eights of a playground is covered by grass.
8 – 3 = 5.
so the fraction of the playground is not covered by grass = 5/8.
Question 13.
Higher Order Thinking Aiden folded 2 strips of paper into eighths. He shaded a fraction equal to \(\frac{1}{4}\) on the first strip and a fraction equal to \(\frac{3}{4}\) on the second strip. Use eighths to show the fractions Aiden shaded on the pictures to the right. Which fraction of each strip did he shade?
Answer:
The fraction he shaded = 6/8.
Explanation:
In the above-given question,
given that,
Aiden folded 2 strips of paper into eighths.
2/8.
He shaded a fraction equal to \(\frac{1}{4}\) on the first strip.
1/4.
fraction equal to \(\frac{3}{4}\) on the second strip.
3/4.
he shaded the 6/8 portion of each strip.
6/8 = 3/4.
Assessment Practice
Question 14.
Which fractions are equivalent? Select all that apply.

Answer:
1/4 and 2/8.
3/4 and 6/8.
2/4 and 4/8.
Explanation:
In the above-given question,
given that,
there are three equivalent fractions.
the fractions are:
2/8 = 1/4.
6/8 = 3/4.
4/8 = 2/4.
Lesson 13.2 Equivalent Fractions: Use the Number Line
Solve & Share
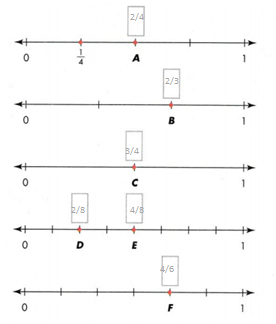
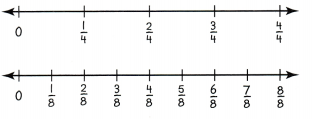
The top number line shows a point at \(\frac{1}{4}\). Write the fraction for each of the points labeled A, B, C, D, E, and F. Which of these fractions show the same distance from 0 as \(\frac{1}{4}\)?
I can … use number lines to represent equivalent fractions.
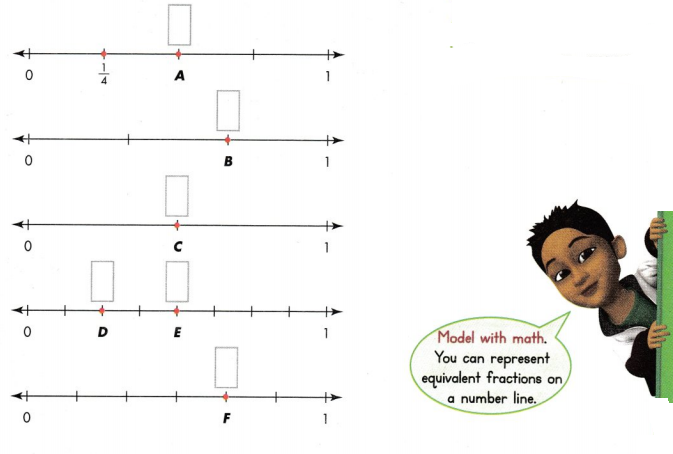
Look Back! How can number lines show that two fractions are equivalent?
Answer:
The fractions are 1/2, 2/4, 3/4, 2/8, 4/8, and 4/6.
Explanation:
In the above-given question,
given that,
The number line A shows the fraction 1/2.
B shows the fraction 2/4.
C shows the fraction 3/4.
D shows the fraction 2/8.
E shows the fraction 4/8.
F shows the fraction 4/6.
2/4 = 1/2.
2/8 = 1/4.
4/8 = 1/2.
4/6 = 2/3.
Essential Question
How Can You Use Number Lines to Find Equivalent Fractions?
Visual Learning Bridge
The Circle W Ranch 1-mile trail has water for cattle at each \(\frac{1}{4}\) mile mark. The Big T Ranch 1-mile trail has water for cattle at the \(\frac{1}{2}\)-mile mark. What fractions name the points on the trails where there is water for cattle at the same distance from the start of each trail?

You can use number lines to find the fractions.
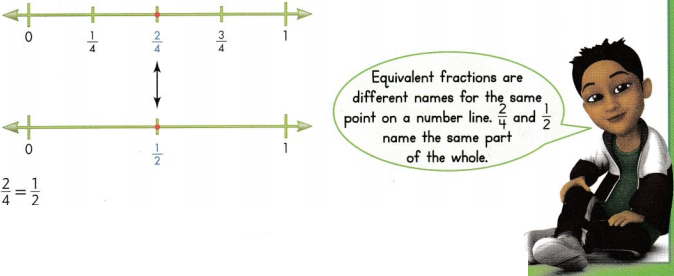
The fractions \(\frac{2}{4}\) and \(\frac{1}{2}\) name the same points on the trails where there is water for cattle. They are at the same distance from the start of the trails.
Convince Me! Model with Math lan paints \(\frac{6}{8}\) of a fence. Anna paints \(\frac{3}{4}\) of another fence of equal size and length. How can you show that lan and Anna have painted the same amount of each fence?
Answer:
Yes, both Anna and Lan have painted the same amount of each fence.
Explanation:
In the above-given question,
given that,
Lan paints \(\frac{6}{8}\) of a fence.
Anna paints \(\frac{3}{4}\) of another fence of equal size and length.
3/4 = 6/8.
2 x 3 = 6.
4 x 2 = 8.
so both Anna and Lan have painted the same amount of each fence.
Guided Practice
Do You Understand?
Question 1.
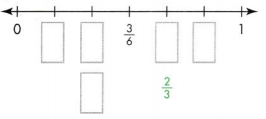
Complete the number line to show that \(\frac{2}{6}\) and \(\frac{1}{3}\) are equivalent fractions.
Answer:
2/6 = 1/3.
Explanation:
In the above-given question,
given that,
the fractions on the number line are:
1/6, 2/6, 3/6, 4/6, and 5/6.
2/6 = 1/3.
4/6 = 2/3.
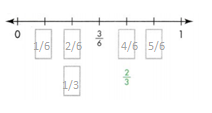
Question 2.
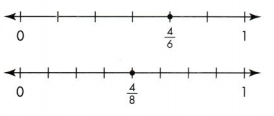
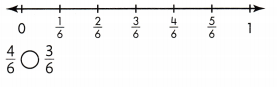
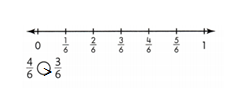
Sheila compares \(\frac{4}{6}\) and \(\frac{4}{8}\) she discovers that the fractions are NOT equivalent. How does Sheila know?
Answer:
Yes, both fractions are not equivalent.
Explanation:
In the above-given question,
given that,
Sheila compares \(\frac{4}{6}\) and \(\frac{4}{8}\).
4/6 = 2/3.
2 x 2 = 4.
2 x 3 = 6.
4/8 = 2/4.
2 x 2 = 4.
4 x 2 = 8.
so 4/6 is not equal to 4/8.
Do You Know How?
In 3 and 4, find the missing equivalent fractions on the number line. Then write the equivalent fractions below.
Question 3.
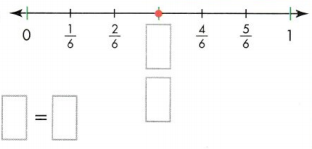
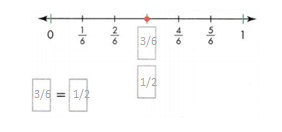
Answer:
The missing equivalent fractions on the number line is 3/6.
Explanation:
In the above-given question,
given that,
the fractions on the number line are:
1/6, 2/6, 3/6, 4/6, 5/6, and 1.
3/6 = 1/2.
so the 3/6 and 1/2 are the equivalent fractions.
Question 4.
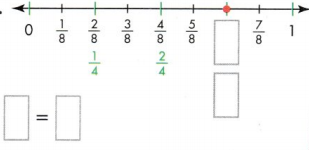
Answer:
6/8 = 3/4.
Explanation:
In the above-given question,
given that,
the fractions on the number line are:
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, and 7/8.
2/8 = 1/4.
4/8 = 1/2.
6/8 = 3/4.
2 x 3 = 6.
2 x 4 = 8.
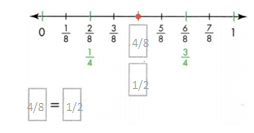
Independent Practice
In 5-8, find the missing equivalent fractions on the number line. Then write the equivalent fractions below.
Question 5.
Answer:
The missing equivalent fractions on the number line are 2/8.
Explanation:
In the above-given question,
given that,
the fractions on the number line are 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, and 7/8.
2/8 = 1/4.
1 x 2 = 2.
4 x 2 = 8.
so the missing equivalent fraction is 2/8 = 1/4.

Question 6.
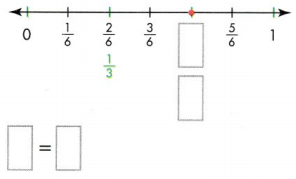
Answer:
The missing equivalent fractions on the number line are 4/6.
Explanation:
In the above-given question,
given that,
the fractions on the number line are 1/6, 2/6, 3/8, and 5/6.
2/6 = 1/3.
1 x 2 = 2.
3 x 2 = 6.
4/6 = 2/3.
2 x 2 = 4.
3 x 2 = 6.
so the missing equivalent fraction is 4/6 = 2/3.

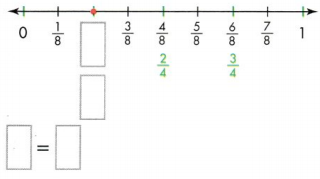
Question 7.

Answer:
The missing equivalent fractions on the number line are 4/8.
Explanation:
In the above-given question,
given that,
the fractions on the number line are 1/8, 2/8, 3/8, 5/8, 6/8, and 7/8.
2/8 = 1/4.
1 x 2 = 2.
4 x 2 = 8.
4/8 = 2/4.
2 x 2 = 4.
4 x 2 = 8.
so the missing equivalent fraction is 4/8 = 2/4.
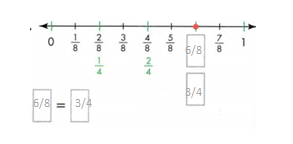
Question 8.
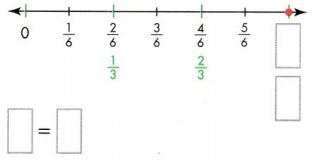
Answer:
The missing equivalent fractions on the number line are 6/6.
Explanation:
In the above-given question,
given that,
the fractions on the number line are 1/6, 2/6, 3/6, 4/6, and 5/6.
2/6 = 1/3.
1 x 2 = 2.
3 x 2 = 6.
4/6 = 2/3.
2 x 2 = 4.
3 x 2 = 6.
6/6 = 1.
1 x 6 = 6.
so the missing equivalent fraction is 6/6 = 1.
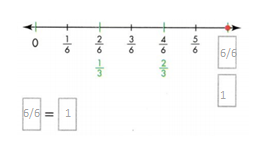
Problem Solving
Question 9.
Number Sense Bradley had 40 slices of pizza to share. How many pizzas did he have? Explain how you solved the problem.

Answer:
The number of pizzas did he have = 5.
Explanation:
In the above-given question,
given that,
Bradley had 40 slices of pizza to share.
each pizza was cut into 8 slices.
40/8 = 5.
5 x 8 = 40.
so the number of pizzas did he have = 5.
Question 10.
Ms. Owen has 15 magazines to share among 5 students for an art project. How many magazines will each student get? Use the bar diagram to write an equation that helps solve the problem.
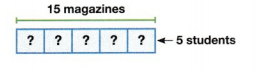
Answer:
The number of magazines will each student get = 3.
Explanation:
In the above-given question,
given that,
Ms. Owen has 15 magazines to share among 5 students for an art project.
15 / 5 = 3.
3 + 3 + 3 + 3 + 3 = 15.
3 x 5 = 15.
so the number of magazines will each student get = 3.
Question 11.
Yonita has 28 different apps on her computer. Casey has 14 music apps and 20 game apps on his computer. How many more apps does Casey have than Yonita? Explain.
Answer:
The number of apps does Casey has more than Yonita = 6.
Explanation:
In the above-given question,
given that,
Yonita has 28 different apps on her computer.
Casey has 14 music apps and 20 game apps on his computer.
14 + 20 = 34.
34 – 28 = 6.
so the number of apps does Casey has more than Yonita = 6.
Question 12.
Construct Arguments How can you tell, just by looking at the fractions, that \(\frac{2}{4}\) and \(\frac{3}{4}\) are NOT equivalent? Construct an argument to explain.
Answer:
Yes, 2/4 and 3/4 are not equivalent fractions.
Explanation:
In the above-given question,
given that,
the fraction 2/4 = 1/2.
1 x 2 = 2.
2 x 2 = 4.
the fraction 3/4 is not an equivalent fraction.
so both the fractions are not equal.
Question 13.
Higher Order Thinking Fiona and Gabe each had the same length of rope. Fiona used \(\frac{2}{3}\) of her rope. Using sixths, what fraction of the length of rope will Gabe need to use to match the amount Fiona used? Draw a number line as part of your answer.
Answer:
The fraction of the rope Gabe used is 4/6.
Explanation:
In the above-given question,
given that,
Fiona and Gabe each had the same length of rope.
Fiona used \(\frac{2}{3}\) of her rope.
4/6 = 2/3.
2 x 2 = 4.
3 x 2 = 6.
so the fraction of rope Gabe used is 4/6.
Assessment Practice
Question 14.
Use the number line to find which fraction is equivalent to \(\frac{3}{6}\).
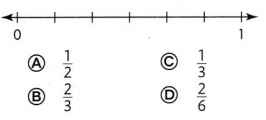
Answer:
Option A is the correct answer.
Explanation:
In the above-given question,
given that,
3/6 = 1/2.
1 x 3 = 3.
3 x 2 = 6.
1/2 = 3/6.
so option A is correct.
Question 15.
Use the number line to find which fraction is equivalent to \(\frac{4}{8}\).
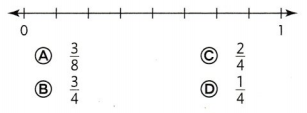
Answer:
Option C is the correct answer.
Explanation:
In the above-given question,
given that,
4/8 = 2/4.
2 x 2 = 4.
4 x 2 = 8.
2/4 = 4/8.
so option C is correct.
Lesson 13.3 Use Models to Compare Fractions: Same Denominator
Solve & Share
Maria and Evan are both jogging a mile. Maria has jogged mile, and Evan has jogged mile. Show how far each has jogged. Use any model you choose. Who jogged farther? How do you know?
I can … compare fractions that refer to the same-sized whole and have the same denominator by comparing their numerators.

Look Back! Suppose Evan had jogged \(\frac{5}{8}\) mile instead of \(\frac{3}{8}\) mile. Now, who has jogged farther? Explain.
Answer:
Evan jogged farther than Maria.
Explanation:
In the above-given question,
given that,
Evan had jogged \(\frac{5}{8}\) mile instead of \(\frac{3}{8}\).
5/8 – 3/8 = 2/8.
so I think maria jogged very little when compared to Evan.
so Evan jogged farther than Maria.
Essential Question
How Can You Compare Fractions with the Same Denominator?
Visual Learning Bridge
Two banners with positive messages are the same size. One banner is \(\frac{4}{6}\) yellow, and the other banner is \(\frac{2}{6}\) yellow. Which is greater, \(\frac{4}{6}\) or \(\frac{2}{6}\)?
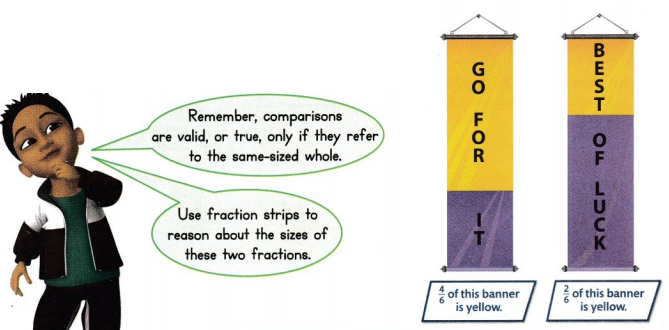
\(\frac{4}{6}\) is 4 of the unit fraction is \(\frac{1}{6}\).
\(\frac{2}{6}\) of the unit fraction \(\frac{1}{6}\).
So, \(\frac{4}{6}\) is greater than \(\frac{2}{6}\).
Record the comparison using symbols or words.
\(\frac{4}{6}\) > \(\frac{2}{6}\)
Four sixths is greater than two sixths.
If two fractions have the same denominator, the fraction with the greater numerator is the greater fraction.
Convince Me! Reasoning Write a number for each numerator to make each comparison true. Use a picture and words to explain how you decided.

Guided Practice
Do You Understand?
Question 1.
Explain how you can use fraction strips to show whether \(\frac{5}{6}\) or \(\frac{3}{6}\) of the same whole is greater.
Answer:
5/6 > 3/6.
Explanation:
In the above-given question,
given that,
the fractions are 5/6 and 3/6.
so 5/6 is greater than 3/6.
3/6 < 5/6.
5/6 > 3/6.
Question 2.
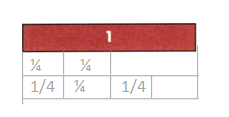
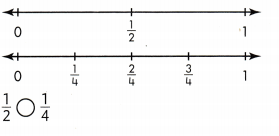
Which is greater, \(\frac{3}{4}\) or \(\frac{2}{4}\)? Draw \(\frac{1}{4}\)-strips to complete the diagram and answer the question.

Answer:
3/4 is greater than 2/4.
Explanation:
In the above-given question,
given that,
3/4 is greater than 2/4.
the whole is 4.
but one time it is divided into 3 parts.
it is divided into 2 parts.
so 3/4 > 2/4.
Do You Know How?
In 3 and 4, compare. Write <, >, or =. Use the fraction strips to help.
Question 3.
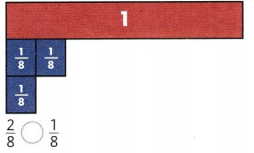
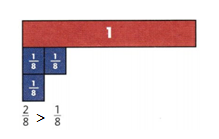
Answer:
2/8 > 1/8.
Explanation:
In the above-given question,
given that,
the fractions are 2/8 and 1/8.
1/8 + 1/8 = 2/8.
2/8 is greater than 1/8.
so 2/8 > 1/8.
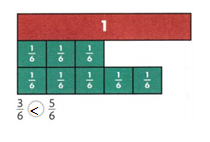
Question 4.
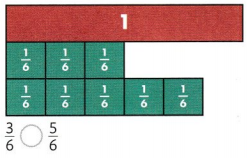
Answer:
3/6 < 5/6.
Explanation:
In the above-given question,
given that,
the fractions are 3/6 and 5/6.
5/6 is divided into 5 parts.
1/6 + 1/6 + 1/6 = 3/6.
so 3/6 < 5/6.
Independent Practice
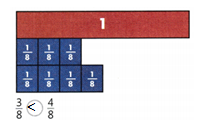
Leveled Practice In 5-14, compare. Write <, >, or =. Use or draw fraction strips to help. The fractions refer to the same whole.
Question 5.
Answer:
3/8 < 4/8.
Explanation:
In the above-given question,
given that,
the two fractions are 3/8 and 4/8.
1/8 + 1/8 + 1/8 = 3/8.
1/8 + 1/8 + 1/8 + 1/8 = 4/8.
so 3/8 < 4/8.
Question 6.
Answer:
3/4 = 3/4.
Explanation:
In the above-given question,
given that,
the two fractions are 3/4 and 3/4.
1/4 + 1/4 + 1/4 = 3/4.
3/4 = 3/4.
so both of them are equal.
Question 7.
\(\frac{6}{8}\) ![]() \(\frac{3}{8}\)
\(\frac{3}{8}\)
Answer:
6/8 > 3/8.
Explanation:
In the above-given question,
given that,
the two fractions are 6/8 and 3/8.
6/8 = 3/4.
2 x 3 = 6.
4 x 2 = 8.
1/8 + 1/8 + 1/8 = 3/8.
6/8 > 3/8.
Question 8.
\(\frac{5}{8}\) ![]() \(\frac{7}{8}\)
\(\frac{7}{8}\)
Answer:
5/8 < 7/8.
Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 7/8.
1/8 + 1/8 + 1/8 + 1/8 + 1/8 = 5/8.
1/8 x 7 = 7/8.
5/8 < 7/8.
Question 9.
\(\frac{1}{2}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
Answer:
1/2 = 1/2.
Explanation:
In the above-given question,
given that,
the two fractions are 1/2 and 1/2.
1/2 x 1 = 1/2.
1/2 x 1 =1/2.
so both of them are equal.
Question 10.
\(\frac{1}{3}\) ![]() \(\frac{2}{3}\)
\(\frac{2}{3}\)
Answer:
1/3 < 2/3.
Explanation:
In the above-given question,
given that,
the two fractions are 1/3 and 2/3.
1/3 x 1 = 1/3.
1/3 + 1/3 = 2/3.
1/3 < 2/3.
Question 11.
\(\frac{6}{6}\) ![]() \(\frac{3}{6}\)
\(\frac{3}{6}\)
Answer:
6/6 > 3/6.
Explanation:
In the above-given question,
given that,
the two fractions are 6/6 and 3/6.
1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 6/6.
1/6 + 1/6 + 1/6 = 3/6.
6/6 > 3/6.
Question 12.
\(\frac{2}{8}\) ![]() \(\frac{3}{8}\)
\(\frac{3}{8}\)
Answer:
2/8 < 3/8.
Explanation:
In the above-given question,
given that,
the two fractions are 2/8 and 3/8.
1/8 + 1/8 = 2/8.
1/8 + 1/8 +1/8 = 3/8.
2/8 < 3/8.
Question 13.
\(\frac{3}{3}\) ![]() \(\frac{1}{3}\)
\(\frac{1}{3}\)
Answer:
3/3 > 1/3.
Explanation:
In the above-given question,
given that,
the two fractions are 3/3 and 1/3.
1/3 + 1/3 + 1/3 = 3/3.
1/3 x 1 = 1/3.
3/3 > 1/3.
Question 14.
\(\frac{1}{4}\) ![]() \(\frac{3}{4}\)
\(\frac{3}{4}\)
Answer:
1/4 < 3/4.
Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 3/4.
1/4 x 1 = 1/4.
1/4 +1/4 + 1/4 = 3/4.
1/4 < 3/4.
Problem Solving
In 15 and 16, use the pictures of the strips that have been partly shaded.
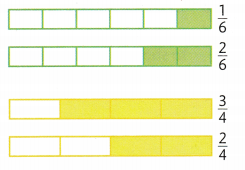
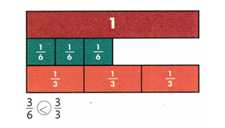
Question 15.
Compare. Write <, >, or =
The green strips show \(\frac{1}{6}\) ![]() \(\frac{2}{6}\)
\(\frac{2}{6}\)
Answer:
1/6 < 2/6.
Explanation:
In the above-given question,
given that,
the two fractions are 1/6 and 2/6.
1/6 x 1 = 1/6.
1/6 +1/6 = 2/6.
1/6 < 2/6.
Question 16.
Do the yellow strips show \(\frac{2}{4}\) > \(\frac{3}{4}\)? Explain.
Answer:
No, 2/4 < 3/4.
Explanation:
In the above-given question,
given that,
the two fractions are 2/4 and 3/4.
1/4 +1/4 = 2/4.
1/4 +1/4 + 1/4 = 3/4.
2/4 < 3/4.
Question 17.
Izzy and Henry have two different pizzas. Izzy ate \(\frac{3}{8}\) of her pizza. Henry ate \(\frac{3}{8}\) of his pizza. Izzy ate more pizza than Henry. How is this possible? Explain.
Answer:
No, it was not possible.
Explanation:
In the above-given question,
given that,
Izzy and Henry have two different pizzas.
Izzy ate \(\frac{3}{8}\) of her pizza.
Henry ate \(\frac{3}{8}\) of his pizza.
3/8 = 1/8 + 1/8 + 1/8.
3/8 x 1 = 3/8.
3/8 = 3/8.
so both of them ate the equal.
Question 18.
Generalize Two fractions are equal. They also have the same denominator. What must be true of the numerators of the fractions? Explain.
Answer:
Yes, the two fractions are equal.
Explanation:
In the above-given question,
given that,
Izzy and Henry have two different pizzas.
Izzy ate \(\frac{3}{8}\) of her pizza.
Henry ate \(\frac{3}{8}\) of his pizza.
3/8 = 1/8 + 1/8 + 1/8.
3/8 x 1 = 3/8.
3/8 = 3/8.
so both of them ate the equal.
Question 19.
Number Sense Mr. Domini had $814 in the bank on Wednesday. On Thursday, he withdrew $250, and on Friday, he withdrew $185. How much money did he have in the bank then?
Answer:
The money he has in the bank = $379.
Explanation:
In the above-given question,
given that,
Mr. Domini had $814 in the bank on Wednesday.
On Thursday, he withdrew $250.
On Friday, he withdrew $185.
250 + 185 = 435.
814 – 435 = 379.
so Mr. Domini had $814 in the bank on Wednesday.
Question 20.
Higher Order Thinking Tom’s parents let him choose whether to play his favorite board game for \(\frac{7}{8}\) hour or for \(\frac{8}{8}\) hour. Explain which amount of time you think Tom should choose and why.
Answer:
Tom should choose 8/8 hour.
Explanation:
In the above-given question,
given that,
Tom’s parents let him choose whether to play his favorite board game for 7/8 hours.
8/8 hour = 1.
7/8 x 1 = 7/8.
1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 = 8/8.
1 = 8/8.
so i think Tom should choose 1 hour.
Assessment Practice
Question 21.
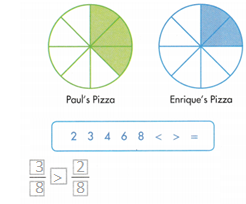
Paul and Enrique each have equal-sized pizzas cut into 8 equal slices. Paul eats 3 slices. Enrique eats 2 slices. Select numbers and symbols from the box to write a comparison for the fraction of pizza Paul and Enrique have each eaten.
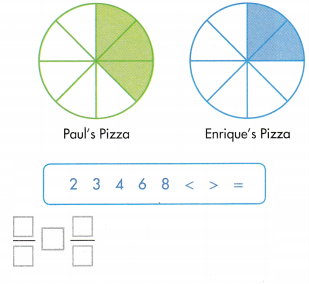
Answer:
Paul eats more slices than Enriques.
Explanation:
In the above-given question,
given that,
Paul and Enrique each have equal-sized pizzas cut into 8 equal slices.
Paul eats 3 slices.
Enrique eats 2 slices.
1/8 + 1/8 + 1/8 = 3/8.
1/8 + 1/8 = 2/8.
so paul eats more slices than Enriques.
Lesson 13.4 Use Models to Compare Fractions: Same Numerator
Solve & Share
Krista, Jamal, and Rafe each had 1 serving of vegetables. Krista ate \(\frac{2}{6}\), Jamal ate \(\frac{2}{3}\), and Rafe ate \(\frac{2}{8}\) of his serving. Arrange the fractions in order from least to greatest to show who ate the least and who ate the greatest amount of vegetables.
I can … compare fractions that refer to the same whole and have the same numerator by comparing their denominators.

Answer:
Rafe, Krista, and Jamal.
Explanation:
In the above-given question,
given that,
Krista, Jamal, and Rafe each had 1 serving of vegetables.
Krista ate \(\frac{2}{6}\), Jamal ate \(\frac{2}{3}\).
Rafe ate \(\frac{2}{8}\) of his serving.
2/6 = 1/6 + 1/6.
2/3 = 1/3 + 1/3.
2/8 = 1/8 + 1/8.
so Rafe ate least when compared to Krista and Jamal.
so the order from least to highest.
Rafe, Krista, and Jamal.
Look Back! Tamika ate \(\frac{2}{2}\) of a serving of vegetables. In order from least to greatest, arrange the fractions of a serving Krista, Jamal, Rafe, and Tamika each ate. Explain your reasoning.
Answer:
Rafe, Krista, Jamal, and Tamika.
Explanation:
In the above-given question,
given that,
Tamika ate \(\frac{2}{2}\) of a serving of vegetables.
2/2 = 1.
so Tamika at more than Rafe, Krista, and Jamal.
Essential Question
How Can You Compare Fractions with the Same Numerator?
Visual Learning Bridge
Claire bought 2 scarves as souvenirs from her visit to a Florida university. The scarves are the same size. One scarf is \(\frac{5}{6}\) orange, and the other scarf is \(\frac{5}{8}\) orange. Which is greater, \(\frac{5}{6}\) or \(\frac{5}{8}\)?

What You Show
Use fraction strips to reason about the size of \(\frac{5}{6}\) a compared to the size of \(\frac{5}{8}\).
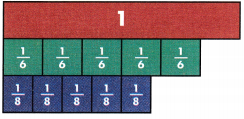
There are 5 sixths. There are 5 eighths. The parts are different sizes.
The greater the denominator, the smaller each part will be.
What You Write
Describe the comparison using symbols or words.
\(\frac{5}{6}\) > \(\frac{5}{8}\)
Five sixths is greater than five eighths.
If two fractions have the same numerator, the fraction with the lesser denominator is the greater fraction.
Convince Me! Critique Reasoning Julia says \(\frac{1}{8}\) is greater than \(\frac{1}{4}\) because 8 is greater than 4. Critique Julia’s reasoning. Is she correct? Explain.
Answer:
Yes, Julia’s reasoning was correct.
Explanation:
In the above-given question,
given that,
Julia says \(\frac{1}{8}\) is greater than \(\frac{1}{4}\).
1/8 = 1 x 1/8.
1/4 = 1 x 1/4.
so Julia’s reasoning was correct.
Guided Practice
Do You Understand?
Question 1.
How can fraction strips help you reason about whether \(\frac{4}{6}\) or \(\frac{4}{8}\) of the same whole is greater?
Answer:
4/6 > 4/8.
Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 4/8.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
4/6 x 1 = 4/6.
4/8 x 1 = 4/8.
so 4/6 > 4/8.
Question 2.
Which is greater, \(\frac{1}{4}\) or \(\frac{1}{6}\)? Draw fraction strips to complete the diagram and answer the question.

Answer:
1/4 > 1/6.
Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 1/6.
1/4 x 1 = 1/4.
1/6 x 1 = 1/6.
1 is divided into 1/4 and 1/6.
1/4 > 1/6.

Do You Know How?
In 3 and 4, compare. Write <, >, or =. Use fraction strips to help.
Question 3.
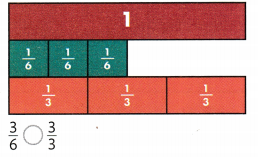
Answer:
3/6 < 3/3.
Explanation:
In the above-given question,
given that,
the two fractions are 3/6 and 3/3.
3/6 = 1/6 + 1/6 + 1/6.
3/3 = 1.
so 3/6 < 3/3.
Question 4.
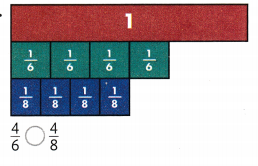
Answer:
4/6 < 4/8.
Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 4/8.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
so 4/6 = 1 x 4/6.
so 4/6 < 4/8.

Independent Practice
Leveled Practice In 5-14, compare. Write <, >, or =. Use or draw fraction strips to help. The fractions refer to the same whole.
Question 5.
Answer:
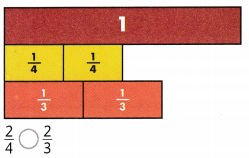
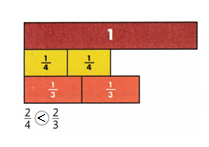
2/4 < 2/3.
Explanation:
In the above-given question,
given that,
the two fractions are 2/4 and 2/3.
2/4 = 1/4 + 1/4.
2/3 = 1/3 + 1/3.
so 2/4 < 2/3.
Question 6.

Answer:
4/4 > 4/6.
Explanation:
In the above-given question,
given that,
the two fractions are 4/4 and 4/6.
4/4 = 1.
1/6 + 1/6 + 1/6 + 1/6 = 4/6.
so 4/4 > 4/6.

Question 7.
\(\frac{2}{3}\) ![]() \(\frac{2}{2}\)
\(\frac{2}{2}\)
Answer:
2/3 > 2/2.
Explanation:
In the above-given question,
given that,
the two fractions are 2/3 and 2/2.
2/2 = 1.
1/3 + 1/3 = 2/3.
so 2/3 > 2/2.
Question 8.
\(\frac{4}{8}\) ![]() \(\frac{4}{8}\)
\(\frac{4}{8}\)
Answer:
4/8 = 4/8.
Explanation:
In the above-given question,
given that,
the two fractions are 4/8 and 4/8.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
4/8 x 1 = 4/8.
so 4/8 = 4/8.
Question 9.
\(\frac{5}{6}\) ![]() \(\frac{5}{8}\)
\(\frac{5}{8}\)
Answer:
5/6 > 5/8.
Explanation:
In the above-given question,
given that,
the two fractions are 5/6 and 5/8.
5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
so 5/6 > 5/8.
Question 10.
\(\frac{1}{4}\) ![]() \(\frac{1}{3}\)
\(\frac{1}{3}\)
Answer:
1/4 > 1/3.
Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 1/3.
1/4 = 1/4 x 1.
1/3 x 1 = 2/3.
so 1/4 > 1/3.
Question 11.
\(\frac{1}{3}\) ![]() \(\frac{1}{6}\)
\(\frac{1}{6}\)
Answer:
1/3 > 1/6.
Explanation:
In the above-given question,
given that,
the two fractions are 1/3 and 1/2.
1/3 = 1 x 1/3.
1/2 x 1 = 1/3.
so 1/3 > 1/6.
Question 12.
\(\frac{4}{6}\) ![]() \(\frac{4}{6}\)
\(\frac{4}{6}\)
Answer:
4/6 = 4/6.
Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 4/6.
4/6 = 1 x 4/6.
1/6 + 1/6 + 1/6 + 1/6 = 4/6.
so 4/6 = 4/6.
Question 13.
\(\frac{1}{8}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
Answer:
1/8 < 1/2.
Explanation:
In the above-given question,
given that,
the two fractions are 1/8 and 1/2.
1/8 = 1 x 1/8.
1/2 x 1 = 1/2.
so 1/8 < 1/2.
Question 14.
\(\frac{2}{6}\) ![]() \(\frac{2}{3}\)
\(\frac{2}{3}\)
Answer:
2/6 < 2/3.
Explanation:
In the above-given question,
given that,
the two fractions are 2/6 and 2/3.
2/6 = 1/6 + 1/6.
1/3 + 1/3 = 2/3.
so 2/6 < 2/3.
Problem Solving
Question 15.
James uses blue and white tiles to make the two designs shown here. James says that the total blue area in the top design is the same as the total blue area in the bottom design. Is he correct? Explain.

Answer:
Yes, James was correct.
Explanation:
In the above-given question,
given that,
James uses blue and white tiles to make the two designs.
James says that the total blue area in the top design is the same as the total blue area in the bottom design.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
1/8 x 4 = 4/8.
so James was correct.
Question 16.
Amy sold 8 large quilts and 1 baby quilt. How much money did she make from selling quilts?

Answer:
The money did she make from selling quilts = $520.
Explanation:
In the above-given question,
given that,
Amy sold 8 large quilts and 1 baby quilt.
60 x 8 = 480.
40 x 1 = 40.
480 + 40 = 520.
so the money did she make from selling quilts = $520.
Question 17.
Be Precise Write two comparison statements about the fractions shown below.
Answer:
3/3 > 3/4.
Explanation:
In the above-given question,
given that,
the two fractions are 3/3 and 3/4.
3/3 = 1/3 + 1/3 + 1/3.
3/4 = 1/4 + 1/4 + 1/4.
so 3/3 > 3/4.
Question 18.
Higher Order Thinking John says that when you compare two fractions with the same numerator, you look at the denominators because the fraction with the greater denominator is greater. Is he correct? Explain, and give an example.
Answer:
Yes, he was correct.
Explanation:
In the above-given question,
given that,
John says that when you compare two fractions with the same numerator,
3/3 and 3/4.
3/3 = 1.
3/4 = 1/4 + 1/4 + 1/4.
1 > 1/4.
so he was correct.
Assessment Practice
Question 19.
These fractions refer to the same whole. Which of these comparisons are correct? Select all that apply.

Answer:
2/4 > 2/3, 1/2 > 1/4, 5/6 = 5/6, and 3/4 > 3/6.
Explanation:
In the above-given question,
given that,
the fractions are 2/4 and 2/3.
2/4 = 1/4 + 1/4.
2/3 = 1/3 + 1/3.
the fractions are 1/2 and 1/4.
1/4 x 1 = 1/4.
1/2 x 1 = 1/2.
the fractions are 3/4 and 3/6.
3/4 = 1/4 + 1/4 + 1/4.
3/6 = 1/6 + 1/6 + 1/6.
so the four fractions are correct.
Lesson 13.5 Compare Fractions: Use Benchmarks
Solve & Share
Mr. Evans wrote \(\frac{2}{8}, \frac{4}{8}, \frac{6}{8}, \frac{1}{8}, \frac{3}{8}, \frac{5}{8}\) on and \(\frac{7}{8}\) on the board. Then he circled the fractions that are closer to 0 than to 1. Which fractions did he circle? Which fractions did he not circle? Explain how you decided.
I can … use what I know about the size of benchmark numbers to compare fractions.

Look Back! Eric says that \(\frac{3}{8}\) is closer to 1 than to 0 because \(\frac{3}{8}\) is greater than \(\frac{1}{8}\). Is he correct? Use benchmark numbers to evaluate Eric’s reasoning and justify your answer.
Answer:
Yes, Eric was correct.
Explanation:
In the above-given question,
given that,
Eric says that 3/8 is closer to 1.
3/8 is greater than 1/8.
3/8 = 1/8 + 1/8 + 1/8.
so 3/8 > 1/8.
so Eric was correct.
Essential Question
How Can Benchmark Numbers Be Used to Compare Fractions?
Visual Learning Bridge
Keri wants to buy of a container of roasted peanuts. Alan wants to buy of a container of roasted peanuts. The containers are the same size. Who will buy more peanuts?

Compare each fraction to the benchmark number \(\frac{1}{2}\). Then see how they relate to each other in size.
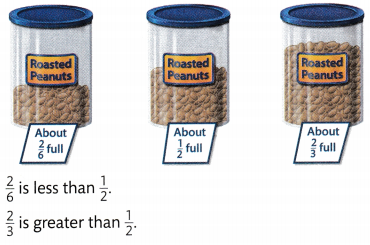
So, \(\frac{2}{6}\) is less than \(\frac{2}{3}\).
\(\frac{2}{6}\) < \(\frac{2}{3}\)
Alan will buy more peanuts than Keri.
Convince Me! Make Sense and Persevere Candice buys \(\frac{2}{8}\) of a container of roasted peanuts. The container is the same size as those used by Keri and Alan. She says \(\frac{2}{8}\) is between \(\frac{1}{2}\) and 1, so she buys more peanuts than Alan. Is Candice correct? Explain.
Answer:
Candice, she was correct.
Explanation:
In the above-given question,
given that,
Candice buys \(\frac{2}{8}\) of a container of roasted peanuts.
The container is the same size as those used by Keri and Alan.
She says \(\frac{2}{8}\) is between \(\frac{1}{2}\) and 1.
2/8 = 1/8 + 1/8.
1/2 x 1 = 1/2.
so Candice was correct.
Guided Practice
Do You Understand?
Question 1.
Tina used benchmark numbers to decide that \(\frac{3}{8}\) is less than \(\frac{7}{8}\). Do you agree? Explain.
Answer:
Yes, 3/8 is less than 7/8.
Explanation:
In the above-given question,
given that,
Tina used benchmark numbers to decide that 3/8 is less than 7/8.
3/8 = 1/8 + 1/8 + 1/8.
7/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
so 3/8 is less than 7/8.
Question 2.
Write two fractions with a denominator of 6 that are closer to 0 than to 1.
Answer:
The two fractions are 3/6 and 4/6.
Explanation:
In the above-given question,
given that,
the two fractions are 3/6 and 4/6
3/6 = 1/6 + 1/6 + 1/6.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
so 3/6 and 4/6 equal to 0 and 1.
Question 3.
Write two fractions with a denominator of 8 that are closer to 1 than to 0.
Answer:
The two fractions are 2/8 and 7/8.
Explanation:
In the above-given question,
given that,
the two fractions with a denominator of 8 that are closer to 1 than to 0.
2/8 = 1/8 + 1/8.
7/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
so the two fractions are 2/8 and 7/8 is equal to 0 and 1.
Do You Know How?
In 4-6, choose from the fractions \(\frac{1}{8}, \frac{1}{4}, \frac{6}{8}\) and \(\frac{3}{4}\). Use fraction strips to help.
Question 4.
Which fractions are closer to 0 than to 1?
Answer:
The two fractions are 3/4 and 1/4.
Explanation:
In the above-given question,
given that,
the fractions are 1/8, 1/4, 6/8, and 3/4.
3/4 = 1/4 + 1/4 + 1/4.
1/4 x 1 = 1/4
so the two fractions are 3/4 and 1/4.
Question 5.
Which fractions are closer to 1 than to 0?
Answer:
The fractions are 6/8 and 3/4.
Explanation:
In the above-given question,
given that,
the fractions are 1/8, 1/4, 6/8, and 3/4.
6/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
3/4 = 1/4 + 1/4 + 1/4.
so the fractions closer to 1 than to 0 are 6/8 and 3/4.
Question 6.
Use the two fractions with a denominator of 8 to write a true statement: < .
Answer:
1/8 < 6/8.
Explanation:
In the above-given question,
given that,
the fractions are 1/8, 1/4, 6/8, and 3/4.
6/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
3/4 = 1/4 + 1/4 + 1/4.
the two fractions with a denominator of 8.
so 1/8 < 6/8.
Independent Practice
In 7 and 8, choose from the fractions, \(\frac{2}{3}, \frac{7}{8}, \frac{1}{4}\), and \(\frac{2}{6}\).
Question 7.
Which of the fractions are closer to 0 than to 1?
Answer:
The fractions are closer to 0 than to 1 are 2/3 and 1/4.
Explanation:
In the above-given question,
given that,
the fractions are 2/3, 7/8, 1/4, and 2/6.
2/3 = 1/3 + 1/3.
1/4 x 1 = 1/4.
so the fractions are closer to 0 than to 1 are 2/3 and 1/4.
Question 8.
Which of the fractions are closer to 1 than to 0?
Answer:
The fractions are closer to 1 than to 0 are 7/8 and 2/6.
Explanation:
In the above-given question,
given that,
the fractions are 2/3, 7/8, 1/4, and 2/6.
7/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
2/6 = 1/6 + 1/6.
so the fractions are closer to 1 than to 0 are 7/8 and 2/6.
In 9-14, use a strategy to compare. Write <, >, or =.

Question 9.
\(\frac{5}{8}\) ![]() \(\frac{7}{8}\)
\(\frac{7}{8}\)
Answer:
5/8 < 7/8.
Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 7/8.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
7/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
so 5/8 < 7/8.
Question 10.
\(\frac{5}{8}\) ![]() \(\frac{2}{8}\)
\(\frac{2}{8}\)
Answer:
5/8 > 2/8.
Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 2/8.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
2/8 = 1/8 + 1/8.
so 5/8 > 2/8.
Question 11.
\(\frac{3}{4}\) ![]() \(\frac{3}{6}\)
\(\frac{3}{6}\)
Answer:
3/4 > 3/6.
Explanation:
In the above-given question,
given that,
the two fractions are 3/4 and 3/6.
3/4 = 1/4 + 1/4 + 1/4.
3/6 = 1/6 + 1/6 + 1/6.
so 3/4 < 3/6.
Question 12.
\(\frac{4}{6}\) ![]() \(\frac{4}{8}\)
\(\frac{4}{8}\)
Answer:
4/6 < 4/8.
Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 4/8.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
so 4/6 < 4/8.
Question 13.
\(\frac{2}{6}\) ![]() \(\frac{2}{4}\)
\(\frac{2}{4}\)
Answer:
2/6 > 2/4.
Explanation:
In the above-given question,
given that,
the two fractions are 2/6 and 2/4.
2/6 = 1/6 + 1/6.
2/4 = 1/4 + 1/4.
so 2/6 > 2/4.
Question 14.
\(\frac{2}{3}\) ![]() \(\frac{1}{3}\)
\(\frac{1}{3}\)
Answer:
2/3 > 1/3.
Explanation:
In the above-given question,
given that,
the two fractions are 2/3 and 1/3.
2/3 = 1/3 + 1/3.
1/3 = 1/3 x 1.
so 2/3 > 1/3.
Problem Solving
In 15-17, use the table at the right.

Question 15.
Which people have walked closer to 1 mile than to 0 miles?
Answer:
Mr. Nunez and Miss Lee have walked closer to 1 mile than to 0 miles.
Explanation:
In the above-given question,
given that,
there are 5 people in the chart.
they are 1/6, 5/6, 1/3, 4/8, and 4/6.
the people closer to 1 mile than to 0 miles are Mr. Nunez and Miss.
the fractions closer to 1 mile is 5/6 and 4/6.
Question 16.
Which people have walked closer to 0 miles than to 1 mile?
Answer:
Mrs. Avery and Miss Chang have walked closer to 0 miles than to 1 mile.
Explanation:
In the above-given question,
given that,
there are 5 people in the chart.
they are 1/6, 5/6, 1/3, 4/8, and 4/6.
the people closer to 0 miles than to 1 mile are Mrs. Avery and Miss chang.
the fractions closer to 0 miles is 1/6 and 1/3.
Question 17.
Who has walked a fraction of a mile that is closer to neither 0 nor 1? Explain.
Answer:
Mr. O’Leary has walked closer to neither 0 nor 1.
Explanation:
In the above-given question,
given that,
there are 5 people in the chart.
they are 1/6, 5/6, 1/3, 4/8, and 4/6.
the people closer to neither 0 nor 1.
the fractions are 4/8.
Question 18.
Rahul compares two wholes that are the same size. He says that \(\frac{2}{6}\) < \(\frac{2}{3}\) because \(\frac{2}{6}\) is less than \(\frac{1}{2}\), and \(\frac{2}{3}\) is greater than \(\frac{1}{2}\). Is he correct? Explain.

Answer:
Yes, he was correct.
Explanation:
In the above-given question,
given that,
Rahul compares two wholes that are the same size.
He says that \(\frac{2}{6}\) < \(\frac{2}{3}\).
\(\frac{2}{6}\) is less than \(\frac{1}{2}\).
2/6 < 2/3.
2/6 < 1/2.
2/3 > 1/2.
so he was correct.
Question 19.
Make Sense and Persevere Manish drives 265 more miles than Janice. Manish drives 642 miles. How many miles does Janice drive?
Answer:
The number of miles does Janice drive =
Explanation:
In the above-given question,
given that,
Manish drives 265 more miles than Janice.
Manish drives 642 miles.
642 – 265 = 377.
so the number of miles does Janice drives = 377.
Question 20.
Algebra Nika has 90 pencils. Forty of them are yellow, 13 are green, 18 are red, and the rest are blue. How many blue pencils does Nika have?
Answer:
The number of blue pencils does Nika have = 47.
Explanation:
In the above-given that,
given that,
Algebra Nika has 90 pencils.
Forty of them are yellow, 13 are green, 18 are red, and the rest are blue.
13 + 18 = 43.
90 – 43 = 47.
so the number of blue pencils does Nika have = 47.
Question 21.
Higher Order Thinking Omar says that \(\frac{2}{6}\) < \(\frac{4}{6}\) because \(\frac{2}{6}\) is between 0 and \(\frac{1}{2}\), and \(\frac{4}{6}\) is between \(\frac{1}{2}\) and 1. Is he correct? Explain.

Answer:
Yes, he was correct.
Explanation:
In the above-given question,
given that,
2/6 < 4/6.
2/6 is between 0 and 1/2.
4/6 is between 1/2 and 1.
0, 2/6, and 1/2.
1/2, 4/6, and 1.
so Omar was correct.
Assessment Practice
Question 22.
Each of the fractions in the comparisons at the right refer to the same whole. Use benchmark fractions to reason about the size of each fraction. Select all the correct comparisons.

Answer:
2/3 < 2/4, 3/6 > 3/8, and 3/8 > 5/8.
Explanation:
In the above-given question,
given that,
the fractions are 2/3 < 2/4, 2/4 < 2/3, 3/8 > 5/8, 1/4 < 2/4, and 3/6 > 3/8.
so the 2/3 < 2/4.
2/3 < 1 and 1/2 > 1.
3/6 > 3/8.
3/8 > 5/8.
so the correct fractions are 2/3 < 2/4, 3/6 > 3/8, and 3/8 > 5/8.
Lesson 13.6 Compare Fractions: Use the Number Line
Solve & Share
Tanya, Riaz, and Ryan each used a bag of flour to make modeling clay. The bags were labeled lb, á lb, and Ź lb. Show these fractions on a number line. How can you use the number line to compare two of these fractions?
I can … compare two fractions by locating them on a number line.

Look Back! If the bags were labeled \(\frac{4}{8}\) lb, \(\frac{3}{8}\) lb, and \(\frac{6}{8}\) lb, how could a number line help you solve this problem?
Answer:
3/8 < 4/8 < 6/8.
Explanation:
In the above-given question,
given that,
if the bags were labeled 4/8 lb, 3/8 lb, and 6/8 lb.
so the fractions from least to greatest are 3/8, 4/8, and 6/8.
3/8 is near to 0.
4/8 is in between 0 and 1.
6/8 is near to 1.
Essentials Question
How Can You Compare Fractions Using the Number Line?
Visual Learning Bridge
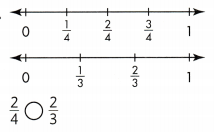
Talia has two different lengths of blue and red ribbon. Does she have more blue ribbon or more red ribbon?

The fractions both refer to 1 yard of ribbon. This is the whole.
You can use a number line to compare \(\frac{1}{3}\) and \(\frac{2}{3}\).
The farther the distance of the fraction from zero on the number line, the greater the fraction.

On the number line, \(\frac{2}{3}\) is farther to the right than \(\frac{1}{3}\).
So, \(\frac{2}{3}\) > \(\frac{1}{3}\).
Talia has more blue ribbon than red ribbon.
Convince Me! Use Structure Talia has an additional length of green ribbon that measures \(\frac{2}{4}\) yard. How can you compare the length of the green ribbon to the lengths of the blue and red ribbons?
Guided Practice
Do You Understand?
Question 1.
When two fractions refer to the same whole, what do you notice when the denominators you are comparing are the same?
Answer:
The denominators are greater than the numerators.
Explanation:
In the above-given question,
given that,
if two fractions are the same.
the denominators are greater than the numerators.
Question 2.
Write a problem that compares two fractions with different numerators.
Answer:
1/3 > 2/3.
Explanation:
In the above-given question,
given that,
the two different fractions are 1/3 and 2/5.
1/3 x 1 = 1/3.
2/3 = 1/3 + 1/3.
so 1/3 > 2/3.
Do You Know How?
In 3-5, compare fractions using <, >, or =. Use the number lines to help.
Question 3.
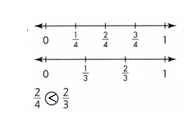
Answer:
2/4 < 2/3.
Explanation:
In the above-given question,
given that,
the two fractions are 2/4 and 2/3.
2/4 = 1/4 + 1/4.
2/3 = 1/3 + 1/3.
2/4 is the half portion in the number line.
so 2/4 > 2/3.
Question 4.
Answer:
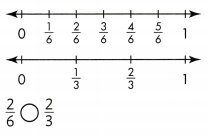
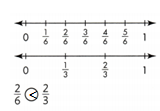
2/6 < 2/3.
Explanation:
In the above-given question,
given that,
the two fractions are 2/6 and 2/3.
2/6 = 1/6 + 1/6.
2/3 = 1/3 + 1/3.
2/6 is below the half portion in the number line.
so 2/6 < 2/3.
Question 5.
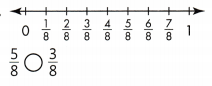
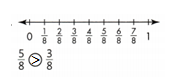
Answer:
5/8 > 3/8.
Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 3/8.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
3/8 = 1/8 + 1/8 + 1/8.
3/8 is the half portion in the number line.
so 5/8 > 3/8.
Independent Practice
In 6-9, use the number lines to compare the fractions. Write >, <, or =.
Question 6.
Answer:
1/4 > 3/4.
Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 3/4.
1/4 = 1/4 x 1.
3/4 = 1/4 + 1/4 + 1/4.
1/4 is nearest to 0.
so 1/4 > 3/4.

Question 7.
Answer:
4/6 < 3/6.
Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 3/6.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
3/6 = 1/6 + 1/6 + 1/6.
so 4/6 < 3/6.
Question 8.
Answer:
1/2 > 1/4.
Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 1/2.
1/2 = 1/2 x 1.
1/4 = 1/4 x 1
1/4 is nearest to 0.
so 1/2 > 1/4.
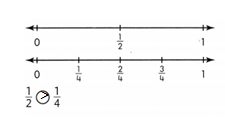
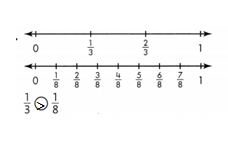
Question 9.
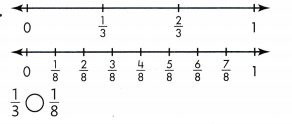
Answer:
1/3 > 1/8.
Explanation:
In the above-given question,
given that,
the two fractions are 1/3 and 1/8.
1/3 = 1/3 x 1.
1/8 = 1/8 x 1.
1/8 is nearest to 0.
so 1/3 > 1/8.
Problem Solving
Question 10.
Number Sense Randy wants to save $39. The table shows how much money he has saved. Explain how you can use estimation to decide if he has saved enough money.

Answer:
Yes, he has saved enough money.
Explanation:
In the above-given question,
given that,
Randy wants to save $39.
in march month he saved $14.
in April he saved $11.
in May he saved $22.
14 + 11 + 22 = 47.
so he has saved enough money.
Question 11.
Scott ate \(\frac{2}{8}\) of a fruit bar. Anne ate \(\frac{4}{8}\) of a same-sized fruit bar. Can you tell who ate more of a fruit bar, Scott or Anne? Explain.
Answer:
Anne ate more of a fruit bar.
Explanation:
In the above-given question,
given that,
Scott ate \(\frac{2}{8}\) of a fruit bar.
Anne ate \(\frac{4}{8}\) of a same-sized fruit bar.
2/8 = 1/8 + 1/8.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
4 > 2.
so the whole is 8.
so Anne ate more of a fruit bar.
Question 12.
Be Precise Matt and Adara have identical pieces of cardboard for an art project. Matt uses \(\frac{2}{3}\) of his piece. Adara uses \(\frac{2}{6}\) of her piece. Who uses more, Matt or Adara? Draw two number lines to help explain your answer.
Answer:
Matt uses more cardboard.
Explanation:
In the above-given question,
given that,
Matt and Adara have identical pieces of cardboard for an art project.
matt uses 2/3 of his piece.
Adara uses 2/6 of her piece.
2/3 = 1/3 + 1/3.
2/6 = 1/6 + 1/6.
in 1st 3 is the whole part.
2 is near to 3.
so matt uses more cardboard.
Question 13.
Higher Order Thinking Some friends shared a pizza. Nicole ate \(\frac{2}{8}\) of the pizza. Chris ate \(\frac{1}{8}\) more than Johan. Mike ate \(\frac{1}{8}\) of the pizza. Johan ate more than Mike. Who ate the most pizza?
Answer:
Chris ate more pizza.
Explanation:
In the above-given question,
given that,
Some friends shared a pizza.
Nicole ate \(\frac{2}{8}\) of the pizza.
Chris ate \(\frac{1}{8}\) more than Johan.
Mike ate \(\frac{1}{8}\) of the pizza.
1/8 + 1 = 2/8.
2/8 + 1 = 3/8.
so Chris ate more pizza.
Question 14.
Inez has 2 rows of plants. There are 8 plants in each row. Each plant has 3 flowers. How many flowers are there in all?
Answer:
The number of flowers is there = 48.
Explanation:
In the above-given question,
given that,
Inez has 2 rows of plants.
there are 8 plants in each row.
each plant has 3 flowers.
8 x 2 =16.
16 x 3 = 48.
so the number of flowers is there = 48.
Assessment Practice
Question 15.
Daniel walked \(\frac{3}{4}\) of a mile. Theo walked \(\frac{3}{8}\) of a mile. Use the number lines to show 0 the fraction of a mile Daniel and Theo each walked. Then select all the correct statements that describe the fractions.

☐ \(\frac{3}{4}\) is equivalent to \(\frac{3}{8}\) because the fractions mark the same point.
☐ \(\frac{3}{4}\) is greater than \(\frac{3}{8}\) because it is farther from zero.
☐ \(\frac{3}{4}\) is less than \(\frac{3}{8}\) because it is farther from zero.
☐ \(\frac{3}{8}\) is less than \(\frac{3}{4}\) because it is closer to zero.
☐ \(\frac{3}{8}\) is greater than \(\frac{3}{4}\) because it is closer to zero.
Answer:
Option B is the correct answer.
Explanation:
In the above-given question,
given that,
Daniel walked \(\frac{3}{4}\) of a mile.
Theo walked \(\frac{3}{8}\) of a mile.
in the 1st line, the 3 is farther from the 0.
so 3/4 > 3/8.
so option B is the correct answer.
Lesson 13.7 Whole Numbers and Fractions
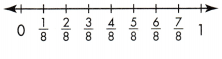
Solve & Share
Jamie’s family ate 12 pieces of apple pie during the week. Each piece was \(\frac{1}{6}\) of a whole pie. How many whole pies did Jamie’s family eat? What fraction of a pie was left over? Explain how you decided.
I can … use representations to find fraction names for whole numbers.
Look Back! Jamie cuts another pie into smaller pieces. Each piece of pie is \(\frac{1}{8}\) of the whole. Jamie gives away 8 pieces. Does Jamie have any pie left over? Explain how you know.
Answer:
Jamie does not have left any pie.
Explanation:
In the above-given question,
given that,
Jamie cuts another pie into smaller pieces.
Each piece of pie is \(\frac{1}{8}\) of the whole.
Jamie gives away 8 pieces.
8 – 8 = 0.
so Jamie does not have left any pie.
Essential Question
How Can You Use Fraction Names to Represent Whole Numbers?
Visual Learning Bridge
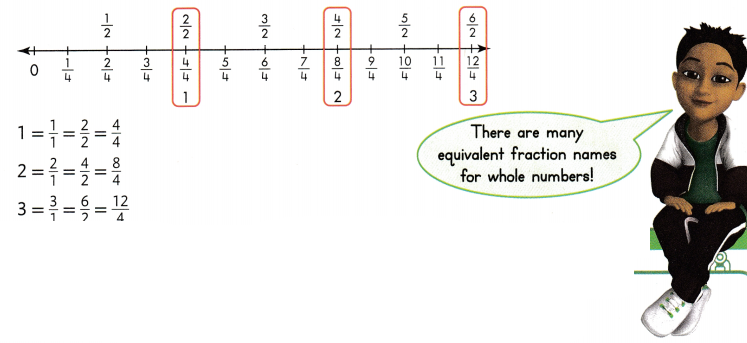
What are some equivalent fraction names for 1, 2, and 3?
You can write a whole number as a fraction by writing the whole number as the numerator and
![]()
The number line shows 3 wholes. Each whole is divided into 1 equal part.
1 whole divided into 1 equal part can be written as \(\frac{1}{1}\).
2 wholes each divided into 1 equal part can be written as \(\frac{2}{1}\).
3 wholes each divided into 1 equal part can be written as \(\frac{1}{1}\)
1 = \(\frac{1}{2}\)
2 = \(\frac{2}{1}\)
3 = \(\frac{3}{1}\)
You can find other equivalent fraction names for whole numbers.
Convince Me! Reasoning What equivalent fraction names can you write for 4 using denominators of 1, 2, or 4?
Another Example!
You can use fractions to name whole numbers.

Twelve \(\frac{1}{3}\) fraction strips equal 4 whole fraction strips.
All whole numbers have fraction names. You can write 4 = \(\frac{12}{3}\).
You also know 4 = \(\frac{4}{1}\), so you can write 4 = \(\frac{4}{1}\) = \(\frac{12}{3}\).
Guided Practice
Do You Understand?
Question 1.
Explain how you know that \(\frac{4}{1}\) = 4.
Answer:
4/1 = 4.
Explanation:
In the above-given question,
given that,
12/3 = 4/1.
3 x 1 = 3.
3 x 4 = 12.
so 4/1 = 4.
Do You Know How?
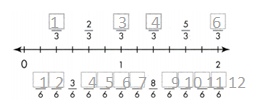
Question 2.
Complete the number line.

Answer:
The missing numbers in upside are 1/3, 3/3, 4/3, and 6/3.
the missing numbers on the downside are 1/6, 2/6, 4/6, 5/6, 6/6, 7/6, 9/6, 10/6, 11/6, and 12/6.
Explanation:
In the above-given question,
given that,
the number line is 1/3, 2/3, 3/3, 4/3, 5/3, 6/3.
2/6 = 1/3.
1 x 2 = 2.
3 x 2 = 6.
6/6 = 1.
9/6 = 3/2.
3 x 3 = 9.
3 x 2 = 6.
so the missing numbers are 1/3, 3/3, 4/3, and 6/3.
1/6, 2/6, 4/6, 5/6, 6/6, 7/6, 9/6, 10/6, 11/6, and 12/6.
Question 3.
Look at the number line. Write two equivalent fractions for each whole number.
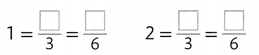
Answer:
1 = 3/3 = 6/6.
2 = 6/3 = 12/6.
Explanation:
In the above-given question,
given that,
the two numbers are 1 and 2.
1 = 3/3.
6 / 6 = 1.
6/3 = 2.
12 / 6 = 2.
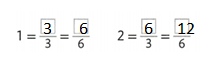
Independent Practice
In 4-7, write two equivalent fractions for each whole number. You can draw number lines to help.
Question 4.
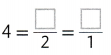
Answer:
4 = 8/2 = 4/1.
Explanation:
In the above-given question,
given that,
the number is 4.
8/2 = 4.
2 x 1 = 2.
2 x 4 = 8.
4 / 1 = 4.
so the missing numbers are 8 and 4.
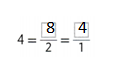
Question 5.
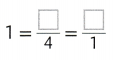
Answer:
1 = 4/4 = 1/1.
Explanation:
In the above-given question,
given that,
the number is 1.
4/4 = 1.
4 x 1 = 4.
1 x 4 = 4.
1 / 1 = 1.
so the missing numbers are 4 and 1.
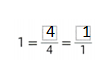
Question 6.
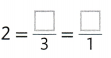
Answer:
2 = 6/3 = 2/1.
Explanation:
In the above-given question,
given that,
the number is 2.
6/3 = 2.
3 x 1 = 3.
3 x 2 = 6.
2 / 1 = 2.
so the missing numbers are 6 and 1.
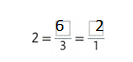
Question 7.
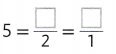
Answer:
5 = 10/2 = 5/1.
Explanation:
In the above-given question,
given that,
the number is 5.
10/2 = 5.
2 x 1 = 2.
2 x 5 = 10.
5 / 1 = 5.
so the missing numbers are 10 and 5.
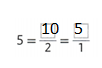
In 8-11, for each pair of fractions, write the equivalent whole number.
Question 8.
\(\frac{6}{2}\) = \(\frac{3}{1}\) =
Answer:
\(\frac{6}{2}\) = \(\frac{3}{1}\) = 3.
Explanation:
In the above-given question,
given that,
for each pair of fractions, write the equivalent whole number.
6/2 = 3.
3/1 = 3.
so \(\frac{6}{2}\) = \(\frac{3}{1}\) = 3.
Question 9.
\(\frac{3}{3}\) = \(\frac{6}{6}\) =
Answer:
\(\frac{3}{3}\) = \(\frac{6}{6}\) = 1.
Explanation:
In the above-given question,
given that,
for each pair of fractions, write the equivalent whole number.
3/3 = 1.
6/6 = 1.
so \(\frac{3}{3}\) = \(\frac{6}{6}\) = 1.
Question 10.
\(\frac{8}{4}\) = \(\frac{6}{3}\) =
Answer:
\(\frac{8}{4}\) = \(\frac{6}{3}\) = 2.
Explanation:
In the above-given question,
given that,
for each pair of fractions, write the equivalent whole number.
8/4 = 2.
6/3 = 2.
so \(\frac{8}{4}\) = \(\frac{6}{3}\) = 2.
Question 11.
\(\frac{9}{3}\) = \(\frac{12}{4}\) =
Answer:
\(\frac{9}{3}\) = \(\frac{12}{4}\) = 3.
Explanation:
In the above-given question,
given that,
for each pair of fractions, write the equivalent whole number.
9/3 = 3.
12/4 = 3.
so \(\frac{9}{3}\) = \(\frac{12}{4}\) = 3.
Problem Solving
Question 12.
Henry needs to fix or replace his refrigerator. It will cost $376 to fix it. How much more will it cost to buy a new refrigerator than to fix the current one?

Answer:
The more it costs to buy a new refrigerator = $593.
Explanation:
In the above-given question,
given that,
Henry needs to fix or replace his refrigerator.
It will cost $376 to fix.
the new refrigerator cost is $969.
969 – 376 = 593.
so more it costs to buy a new refrigerator = $593.
Question 13.
Declan says, “To write an equivalent fraction name for 5, I can write 5 as the denominator and 1 as the numerator.” Do you agree with Declan? Explain.
Answer:
No, Declan was wrong.
Explanation:
In the above-given question,
given that,
To write an equivalent fraction name for 5, I can write 5 as the denominator and 1 as the numerator.
5/1 = 5.
so Declan was wrong.
Question 14.
Look for Relationships Describe a pattern in fractions equivalent to 1 whole.
Answer:
Question 15.
enVision® STEM There are four stages in a butterfly’s life cycle: egg, caterpillar, chrysalis, and butterfly. Dan makes one whole poster for each stage. Use a fraction to show the number of whole posters Dan makes.
Answer:
Dan makes the fractions 1/4, 2/4, 3/4, and 4/4.
Explanation:
In the above-given question,
given that,
There are four stages in a butterfly’s life cycle: egg, caterpillar, chrysalis, and butterfly.
1st stage is egg = 1/4.
2nd stage is caterpillar = 2/4.
3rd stage is chrysalis = 3/4.
4th stage is butterfly = 4/4.
so the fractions are 1/4, 2/4, 3/4, and 4/4.
Question 16.
Karen bought 4 movie tickets for $9 each. She has $12 left over. How much money did Karen have to start? Explain.
Answer:
The money Karen has to start = $48.
Explanation:
In the above-given question,
given that,
Karen bought 4 movie tickets for $9 each. She has $12 left over
4 x 9 = 36.
36 + 12 = 48.
so the money Karen has to start = $48.
Question 17.
Higher Order Thinking Peggy has 4 whole sandwiches. She cuts each whole into halves. Then Peggy gives away 1 whole sandwich. Show the number of sandwiches Peggy has left as a fraction.
Each sandwich is cut into equal parts.
Answer:
The number of sandwiches Peggy has left as a fraction = 6/8.
Explanation:
In the above-given question,
given that,
Peggy has 4 whole sandwiches.
She cuts each whole into halves.
4 x 2 = 8.
Then Peggy gives away 1 whole sandwich.
8 – 2 = 6.
so the number of sandwiches Peggy has left as a fraction = 6/8.
Assessment Practice
Question 18.
Complete the equations. Match the fractions with their equivalent whole numbers.
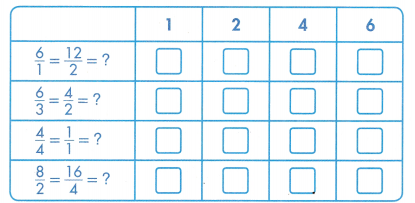
Answer:
6/1 = 12/2 = 6.
6/3 = 4/2 = 2.
4/4 = 1/1 = 1.
8/2 = 16/4 = 4.
Explanation:
In the above-given question,
given that,
the numbers are 1, 2, 4, and 6.
6/1 = 12/2 = 6.
6/3 = 4/2 = 2.
4/4 = 1/1 = 1.
8/2 = 16/4 = 4.
Lesson 13.8 Problem Solving
Construct Arguments
Solve & Share
Lindsey and Matt are running in a 1-mile race. They have both run the same distance so far. Write a fraction that shows how far Lindsey could have run. Write a different fraction that shows how far Matt could have run. Construct a math argument to support your answer.
I can … construct math arguments using what I know about fractions.

Thinking Habits
Be a good thinker! These questions can help you.
- How can I use numbers, objects, drawings, or actions to justify my argument?
- Am I using numbers and symbols correctly?
- Is my explanation clear and complete?

Look Back! Construct Arguments Are the two fractions you wrote equivalent? Construct a math argument using pictures, words, and numbers to support your answer.
Essential Question
How Can You Construct Arguments?
Visual Learning Bridge
Clara and Ana are making rugs. The rugs will be the same size. Clara has finished of her rug. Ana has finished of her rug. Who has finished more of her rug? Conjecture: Clara has finished a greater portion of her rug than Ana.
A conjecture is a statement that you think is true. It needs to be proved.
How can I explain why my conjecture is correct?
I need to construct an argument to justify my conjecture.
How can I construct an argument?
I can
- use numbers, objects, drawings, or actions correctly to explain my thinking.
- make sure my explanation is simple, complete, and easy to understand.
Here’s my thinking…
I will use drawings and numbers to explain my thinking.
The number lines represent the same whole. One is divided into fourths. One is divided into eighths.
The number lines show that 3 of the fourths is greater than 3 of the eighths.
So, \(\frac{3}{4}\) > \(\frac{3}{8}\). The conjecture is correct.
Convince Me! Construct Arguments Use numbers to construct another math argument to justify the conjecture above. Think about how you can look at the numerator and the denominator.
Guided Practice
Construct Arguments Paul and Anna were eating burritos. The burritos were the same size. Paul ate \(\frac{2}{6}\) of a burrito. Anna ate \(\frac{2}{3}\) of a burrito. Conjecture: Paul and Anna ate the same amount.
Question 1.
Draw a diagram to help justify the conjecture.

Answer:
No, Paul and Anna were correct.
Explanation:
In the above-given question,
given that,
Paul and Anna were eating burritos.
The burritos were the same size.
Paul ate \(\frac{2}{6}\) of a burrito.
Anna ate \(\frac{2}{3}\) of a burrito.
paul ate 2 of the sixths is less than the 2 of the thirds.
2/6 = 1/6 + 1/6.
2/3 = 1/3 + 1/3.
yes, the conjecture is not correct.
Question 2.
Is the conjecture correct? Construct an argument to justify your answer.
Answer:
No, the conjecture was not correct.
Explanation:
In the above-given question,
given that,
Paul and Anna were eating burritos.
The burritos were the same size.
Paul ate \(\frac{2}{6}\) of a burrito.
Anna ate \(\frac{2}{3}\) of a burrito.
paul ate 2 of the sixths is less than the 2 of the thirds.
2/6 = 1/6 + 1/6.
2/3 = 1/3 + 1/3.
yes, the conjecture is not correct.
Independent Practice
Construct Arguments Reyna has a blue ribbon that is 1 yard long and a red ribbon that is 2 yards long. She uses \(\frac{2}{4}\) of the red ribbon and \(\frac{2}{4}\) of the blue ribbon.
Conjecture: Reyna uses the same amount of red and blue ribbon.
Question 3.
Draw a diagram to help justify the conjecture.
Answer:
Yes, the conjecture was correct.
Explanation:
In the above-given question,
given that,
Reyna has a blue ribbon that is 1 yard long and a red ribbon that is 2 yards long.
She uses \(\frac{2}{4}\) of the red ribbon and \(\frac{2}{4}\) of the blue ribbon.
2/4 = 1/4 + 1/4.
2/4 = 1/4 + 1/4.
yes, the conjecture is correct.

Question 4.
Is the conjecture correct? Construct an argument to justify your answer.
Answer:
Yes, the conjecture is correct.
Explanation:
In the above-given question,
given that,
Reyna has a blue ribbon that is 1 yard long and a red ribbon that is 2 yards long.
She uses \(\frac{2}{4}\) of the red ribbon and \(\frac{2}{4}\) of the blue ribbon.
2/4 = 1/4 + 1/4.
2/4 = 1/4 + 1/4.
yes, the conjecture is correct.
Question 5.
Explain another way you could justify the conjecture.
Answer:
Problem Solving
Performance Task School Fair Twenty-one students worked at the school fair. Mrs. Gold’s students worked at a class booth. The table shows the fraction of 1 hour that her students worked. Mrs. Gold wants to know the order of the work times for the students from least to greatest.

Question 6.
Make Sense and Persevere What comparisons do you need to make to find out who worked the least?
Answer:
The student who worked least is Pedro.
Explanation:
In the above-given question,
given that,
School Fair Twenty-one students worked at the school fair.
Gold’s students worked at a class booth.
The table shows the fraction of 1 hour that her students worked.
Tim worked 4 hours.
Cathy worked 2/4 hours.
Jose worked 2/6 hours.
Pedro worked 3/4 hours.
3/4 < 2/4 < 2/6.
so the student who worked least is Pedro.
Question 7.
Be Precise What is the whole for each student’s time? Do all the fractions refer to the same whole?
Answer:
The same whole is 4.
Explanation:
In the above-given question,
given that,
School Fair Twenty-one students worked at the school fair.
Gold’s students worked at a class booth.
The table shows the fraction of 1 hour that her students worked.
Tim worked 4 hours.
Cathy worked 2/4 hours.
Jose worked 2/6 hours.
Pedro worked 3/4 hours.
3/4 < 2/4 < 2/6.
so the students who worked least is Pedro.
Question 8.
Use Appropriate Tools What tool could you use to solve this problem? Explain how you would use this tool.

Answer:
Question 9.
Construct Arguments What is the order of the work times from least to greatest? Construct a math argument to justify your answer.
Answer:
The student who worked the least is Pedro.
Explanation:
In the above-given question,
given that,
School Fair Twenty-one students worked at the school fair.
Gold’s students worked at a class booth.
The table shows the fraction of 1 hour that her students worked.
Tim worked 4 hours.
Cathy worked 2/4 hours.
Jose worked 2/6 hours.
Pedro worked 3/4 hours.
3/4 < 2/4 < 2/6.
so the student who worked least is Pedro.
Topic 13 Fluency Practice Activity
Find a Match
Work with a partner. Point to a clue. Read the clue.
Look below the clues to find a match. Write the clue letter in the box next to the match.
Find a match for every clue.
I can … multiply and divide within 100.
Clues
A. ls equal to 3 × 3
B. is equal to 4 × 4
C. is equal to 9 × 4
D. is equal to 0 ÷ 10
E. is equal to 35 ÷ 5
F. is equal to 12 ÷ 4
G. is equal to 5 × 4
H. is equal to 3 × 8
I. Is equal to 2 × 5
J. Is equal to 3 × 10
K. is equal to 9 × 2
L. is equal to 2 × 4
Answer:
6 x 6 = 36, 40 / 4 = 10, 0 x 9 = 0, 3 x 6 = 18, 32 / 4 = 8, 10 x 2 = 20, 5 x 6 = 30, 7 / 21 = 3, 8 x 2 = 16, and 6 x 4 = 24.
Explanation:
In the above-given question,
given that,
A is not equal to 9.
B is equal to 16.
C is equal to 36.
D is equal to 0.
E is equal to 35 / 5 = 7.
F is equal to 3.
G is equal to 20.
H is equal to 24.
I is equal to 10.
J is equal to 30.
K is equal to 18.
L is equal to 8.
Topic 13 Vocabulary Review
Word List
- denominator
- equivalent fractions
- fraction
- number line
- numerator
- unit fraction
Understand Vocabulary
Write T for true or F for false.
Question 1.
______ \(\frac{1}{6}\) and \(\frac{2}{6}\) have the same numerator.
Answer:
True.
Explanation:
In the above-given question,
given that,
the fractions are 1/6 and 2/6.
2/6 = 1/3.
2 x 1 = 2.
2 x 3 = 6.
so both the fractions have the same numerator.
Question 2.
________ \(\frac{1}{2}\) and \(\frac{4}{8}\) are equivalent fractions.
Answer:
True.
Explanation:
In the above-given question,
given that,
the fractions are 1/2 and 4/8.
4/8 = 1/2.
4 x 1 = 4.
4 x 2 = 8.
so both the fractions are equivalent fractions.
Question 3.
_______ \(\frac{3}{8}\) is a unit fraction.
Answer:
True.
Explanation:
In the above-given question,
given that,
the fraction is 3/8.
3/8 = 1/8 + 1/8 + 1/8.
so 3/8 is a unit fraction.
Question 4.
_________ A whole number can be written as a fraction.
Answer:
True.
Explanation:
In the above-given question,
given that,
A whole number can be written as a fraction.
2 / 2 = 1.
so the whole number can be written as a fraction.
Question 5.
________ The denominators in \(\frac{1}{3}\) and \(\frac{2}{3}\) in are the same.
Answer:
True.
Explanation:
In the above-given question,
given that,
the fractions are 1/3 and 2/3.
2/3 = 1/3 + 1/3.
in both the fractions, the numerator, and denominator are the same.
so both the fractions have the same denominators.
Question 6.
_______ A number line always shows fractions.
Answer:
A unit fraction is a number line that always shows fractions.
Explanation:
In the above-given question,
given that,
3/8 is a unit fraction.
3 is the numerator and 8 is a denominator.
so the unit fraction is a number line that always shows fractions.
For each of these terms, give an example and a non-example.

Answer:
1/2 is a fraction.
3/8 is a unit fraction.
1/2 = 2/4 are equivalent fractions.
Explanation:
In the above-given question,
given that,
the terms are fraction, unit fraction, and equivalent fractions.
1/2 is a fraction.
3/8 is a unit fraction.
1/2 = 2/4 are equivalent fractions.

Use Vocabulary in Writing
Question 10.
Use at least 2 terms from the Word List to explain how to compare \(\frac{1}{2}\) and \(\frac{1}{3}\).
Answer:
The two terms have different denominators.
Explanation:
In the above-given question,
given that,
the two fractions are 1/2 and 1/3.
1/2 = 2/4.
1/3 = 2/6.
so both the fractions have different denominators.
Topic 13 Reteaching
Set A pages 485-488
Two fractions are equivalent if they name the same part of a whole.
What is one fraction that is equivalent to \(\frac{6}{8}\)?
You can use fraction strips to find equivalent fractions.
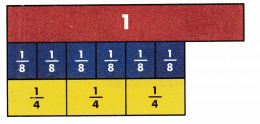
\(\frac{6}{8}\) = \(\frac{3}{4}\)
You also can use area models to see that a I are equivalent fractions. The shaded fractions both show the same part of the whole.

Remember to check that both sets of strips are the same length
In 1 and 2, find an equivalent fraction. Use fraction strips and models to help.
Question 1.
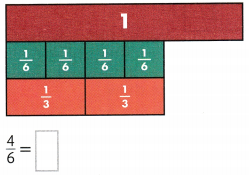
Answer:
4/6 = 2/3.
Explanation:
In the above-given question,
given that,
the fraction is 4/6.
4/6 = 2/3.
2 x 2 = 4.
2 x 3 = 6.
so the equivalent fraction is 2/3.
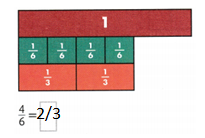
Question 2.
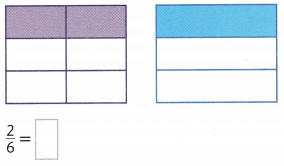
Answer:
2/6 = 1/3.
Explanation:
In the above-given question,
given that,
the fraction is 2/6.
2/6 = 1/3.
1 x 2 = 2.
2 x 3 = 6.
so the equivalent fraction is 1/3.
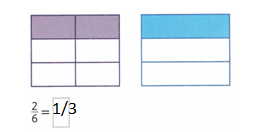
Set B pages 489-492
Riley says the library is \(\frac{2}{8}\) of a mile from their house. Sydney says it is \(\frac{1}{4}\) of a mile.
Use the number lines to find who is correct.

The fractions \(\frac{2}{8}\) and \(\frac{1}{4}\) are equivalent. They are the same distance from 0 on a number line. Riley and Sydney are both correct.
Remember that equivalent fractions have different names, but they represent the same point on a number line.
In 1 and 2, write two fractions that name the same location on the number line.
Question 1.
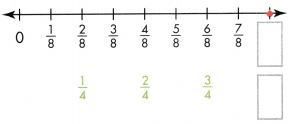
Answer:
The two fractions that name the same location on the number line = 1.
Explanation:
In the above-given question,
given that,
the fractions are 8/8 and 4/4.
8/8 = 1.
4/4 = 1.
so the two fractions that name the same location on the number line = 1.

Question 2.
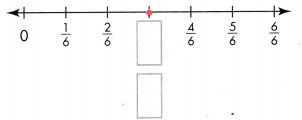
Answer:
The two fractions that name the same location on the number line = 3/6 and 1/2.
Explanation:
In the above-given question,
given that,
the fractions are 3/6 and 1/2.
3/6 = 1/2.
3 x 1 = 3.
3 x 2 = 6.
so the two fractions that name the same location on the number line = 3/6 and 1/2.
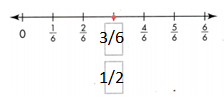
Set C pages 493-496
You can use fraction strips to compare fractions with the same denominator.
Compare \(\frac{3}{4}\) to \(\frac{2}{4}\).
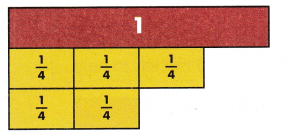
The denominator of each fraction is 4.
Three \(\frac{1}{4}\) fraction strips show \(\frac{3}{4}\).
Two \(\frac{1}{4}\) fraction strips show \(\frac{2}{4}\).
The fraction strips showing \(\frac{3}{4}\) have 1 more unit fraction than the strips showing \(\frac{2}{4}\).
So \(\frac{3}{4}\) > \(\frac{2}{4}\).
Remember that if fractions have the same denominator, the greater fraction has a greater numerator.
In 1-3, compare. Write <, >, or =. Use fraction strips to help.
Question 1.
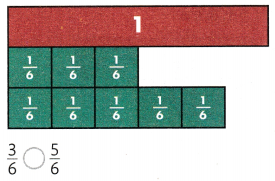
Answer:
3/6 < 5/6.
Explanation:
In the above-given question,
given that,
the two fractions are 3/6 and 5/6.
3/6 = 1/6 + 1/6 + 1/6.
5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6.
3/6 < 5/6.

Question 2.
\(\frac{4}{6}\) ![]() \(\frac{5}{6}\)
\(\frac{5}{6}\)
Answer:
4/6 < 5/6.
Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 5/6.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6.
4/6 < 5/6.
Question 3.
\(\frac{5}{8}\) ![]() \(\frac{3}{8}\)
\(\frac{3}{8}\)
Answer:
5/8 > 3/8.
Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 3/8.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
3/8 = 1/8 + 1/8 + 1/8.
5/8 > 3/8.
Set D pages 497-500
You can use fraction strips to compare fractions with the same numerator.
Compare \(\frac{1}{6}\) to \(\frac{1}{2}\).
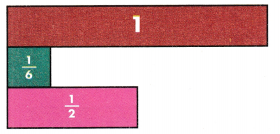
The numerator of each fraction is 1.
The \(\frac{1}{6}\) fraction strip is less than the \(\frac{1}{2}\) strip.
So \(\frac{1}{6}\) < \(\frac{1}{2}\)
You can use reasoning to understand. Think about dividing a whole into 6 pieces and dividing it into 2 pieces. One of 6 pieces is less than 1 of 2 pieces.
Remember that if fractions have the same numerator, the greater fraction has a lesser denominator.
In 1-3, compare. Write <, >, or=. Use fraction strips to help.
Question 1.
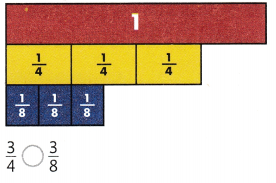
Answer:
3/4 < 3/8.
Explanation:
In the above-given question,
given that,
the two fractions are 3/4 and 3/8.
3/4 = 1/4 + 1/4 + 1/4.
3/8 = 1/8 + 1/8 + 1/8.
3/4 < 3/8.
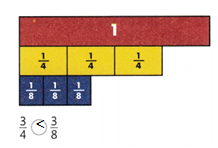
Question 2.
\(\frac{5}{6}\) ![]() \(\frac{5}{8}\)
\(\frac{5}{8}\)
Answer:
5/6 < 5/8.
Explanation:
In the above-given question,
given that,
the two fractions are 5/6 and 5/8.
5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
5/6 < 5/8.
Question 3.
\(\frac{1}{3}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
Answer:
1/3 > 1/2.
Explanation:
In the above-given question,
given that,
the two fractions are 1/3 and 1/2.
1/3 = 2/6.
2/6 = 1/6 + 1/6.
1/3 > 1/2.
Set E pages 501-504
You can compare fractions using benchmark numbers such as 0, \(\frac{1}{2}\), and 1.
Chris and Mary are painting pictures. The pictures are the same size. Chris painted \(\frac{3}{4}\) of his picture. Mary painted her picture. Who painted the greater amount?
\(\frac{3}{4}\) is greater than \(\frac{1}{2}\).
\(\frac{3}{8}\) is less than \(\frac{1}{2}\).
Chris painted the greater amount.
Remember that you can compare each fraction to a benchmark number to see how they relate to each other.
In 1 and 2, use benchmark numbers to help solve.
Question 1.
Mike had \(\frac{2}{6}\) of a candy bar. Sally had \(\frac{4}{6}\) of a candy bar. Whose fraction of a candy bar was closer to 1? Closer to 0?
Answer:
Sally was closer to 1.
Explanation:
In the above-given question,
given that,
Mike had \(\frac{2}{6}\) of a candy bar.
Sally had \(\frac{4}{6}\) of a candy bar.
2/6 = 1/3.
4/6 = 2/3.
2/3 is closer to 1.
so sally was closer to 1.
Question 2.
Paul compared two bags of rice. One weighs \(\frac{4}{6}\) pound, and the other weighs \(\frac{4}{8}\) pound. Which bag is heavier?
Answer:
The 4/6 pounds bag is heavier.
Explanation:
In the above-given question,
given that,
Paul compared two bags of rice.
One weighs 4/6 pound.
the other weighs 4/8 pound.
4/6 = 2/3.
4/8 = 2/4.
so the 4/6 pounds bag is heavier.
Set F pages 505-508
You can use a number line to compare fractions.
Which is greater, \(\frac{3}{6}\) or \(\frac{4}{6}\)?
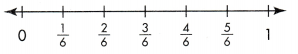
\(\frac{4}{6}\) is farther from zero than \(\frac{3}{6}\), so \(\frac{4}{6}\) is greater.
You also can compare two fractions with the same numerator by drawing two number lines.
Which is greater, \(\frac{2}{4}\) or \(\frac{2}{3}\)?
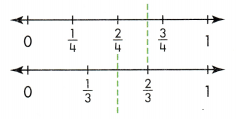
\(\frac{2}{3}\) is farther from zero than \(\frac{2}{4}\), so \(\frac{2}{3}\) is greater.
Remember to draw two number lines that are equal in length when comparing fractions with different denominators.
In 1 and 2, compare. Write <, >, or=. Use number lines to help.
Question 1.
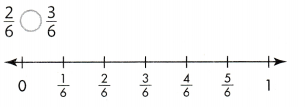
Answer:
2/6 < 3/6.
Explanation:
In the above-given question,
given that,
the two fractions are 2/6 and 3/6.
2/6 = 1/3.
2/6 = 1/6 + 1/6.
3/6 = 1/2.
3/6 = 1/6 + 1/6 + 1/6.
so 2/6 < 3/6.

Question 2.
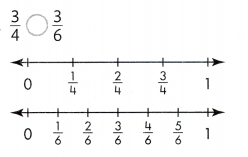
Answer:
3/4 > 3/6.
Explanation:
In the above-given question,
given that,
the two fractions are 3/4 and 3/6.
3/4 = 1/4 + 1/4 + 1/4.
3/6 = 1/6 + 1/6 + 1/6.
3/6 = 1/2.
so 3/4 > 3/6.
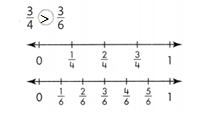
Set G pages 509-512
How many thirds are in 2 wholes?
You can use a number line or fraction strips to find a fraction name for 2 using thirds.
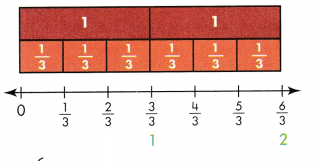
2 = \(\frac{6}{3}\)
The whole number 2 can also be written as the fraction \(\frac{6}{3}\).
Remember that when you write whole numbers as fractions, the numerator can be greater than the denominator.
In 1-4, write an equivalent fraction for each whole number.
Question 1.
3
Answer:
The equivalent fraction is 12/4.
Explanation:
In the above-given question,
given that,
the whole number is 3.
12/4 = 3.
3 x 4 = 12.
3 x 1 = 3.
so the equivalent fraction is 12/4.
Question 2.
2
Answer:
The equivalent fraction is 4/2.
Explanation:
In the above-given question,
given that,
the whole number is 2.
4/2 = 2/1.
2 x 2 = 4.
2 x 1 = 2.
so the equivalent fraction is 4/2.
Question 3.
5
Answer:
The equivalent fraction is 15/3.
Explanation:
In the above-given question,
given that,
the whole number is 5.
15/3 = 5.
3 x 1 = 3.
3 x 5 = 15.
so the equivalent fraction is 15/3.
Question 4.
1
Answer:
The equivalent fraction is 3/3.
Explanation:
In the above-given question,
given that,
the whole number is 1.
3/3 = 1.
so the equivalent fraction is 3/3.
In 5-8, write the equivalent whole number for each fraction.
Question 5.
\(\frac{6}{3}\)
Answer:
The equivalent whole number is 2.
Explanation:
In the above-given question,
given that,
The fraction is 6/3.
6/3 = 2.
3 x 1 = 3.
3 x 2 = 6.
so the equivalent whole number is 2.
Question 6.
\(\frac{10}{2}\)
Answer:
The equivalent whole number is 5.
Explanation:
In the above-given question,
given that,
The fraction is 10/2.
10/2 = 5.
2 x 1 = 2.
2 x 5 = 10.
so the equivalent whole number is 5.
Question 7.
\(\frac{14}{2}\)
Answer:
The equivalent whole number is 7.
Explanation:
In the above-given question,
given that,
The fraction is 14/2.
14/2 = 7.
2 x 1 = 2.
7 x 2 = 14.
so the equivalent whole number is 7.
Question 8.
\(\frac{8}{8}\)
Answer:
The equivalent whole number is 1.
Explanation:
In the above-given question,
given that,
The fraction is 8/8.
8/8 = 1.
8 x 1 = 8.
1 x 8 = 8.
so the equivalent whole number is 1.
Set H pages 513-516
Think about these questions to help construct arguments.
Thinking Habits
- How can I use numbers, objects, drawings, or actions to justify my argument?
- Am I using numbers and symbols correctly?
- Is my explanation clear and complete?

Remember that when you construct an argument, you explain why your work is correct.
Odell and Tamra paint two walls with the same dimensions. Odell paints \(\frac{1}{6}\) of a wall. Tamra paints \(\frac{1}{3}\) of the other wall. Conjecture: Odell paints less than Tamra.
Question 1.
Draw a diagram to justify the conjecture.
Answer:
Yes, Odell paints less than Tamra.
Explanation:
In the above-given question,
given that,
Odell and Tamra paint two walls with the same dimensions.
Odell paints \(\frac{1}{6}\) of a wall.
Tamra paints \(\frac{1}{3}\) of the other wall.
1/6 < 1/3.
so Odell paints less than Tamra.
Question 2.
Use the diagram to justify the conjecture.
Answer:
Topic 13 Assessment Practice
Question 1.
Two friends are working on a project. So far, Cindy has done \(\frac{4}{8}\) of the project, and Kim has done \(\frac{3}{8}\) of the project. Who has done more of the project? Explain.
Answer:
Cindy has done more of the project.
Explanation:
In the above-given question,
given that,
Two friends are working on a project.
Cindy has done \(\frac{4}{8}\) of the project.
Kim has done \(\frac{3}{8}\) of the project.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
3/8 = 1/8 + 1/8 + 1/8.
so Cindy has done more of the project.
Question 2.
Serena can compare \(\frac{3}{4}\) and \(\frac{3}{6}\) without using fraction strips. She says that a whole divided into 4 equal parts will have larger parts than the same whole divided into 6 equal parts. Three larger parts must be more than three smaller parts, so \(\frac{3}{4}\) is greater than \(\frac{3}{6}\). Is Serena correct? If not, explain Serena’s error. Then, write the correct comparison using symbols.
Answer:
Yes, Serena is correct.
Explanation:
In the above-given question,
given that,
Serena can compare 3/4 and 3/6 without using fraction strips.
3/4 = 1/4 + 1/4 + 1/4.
3/6 = 1/2.
3 x 1 = 3.
3 x 2 = 6.
so Serena is correct.
Question 3.
Jill finished reading \(\frac{2}{3}\) of a book for a summer reading project. Owen read \(\frac{2}{8}\) of the same book. Use the number lines to compare how much Jill and Owen each read. Who reads more of the book?
Answer:
The missing fractions are 1/3 and 2/3.
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, and 7/8.
Explanation:
In the above-given question,
given that,
Jill finished reading \(\frac{2}{3}\) of a book for a summer reading project
Owen read \(\frac{2}{8}\) of the same book.
2/8 = 1/4.
2 x 1 = 2.
4 x 2 = 8.
so Jill read more of the book.

Question 4.
A small cake is cut into 4 equal pieces. What fraction represents the entire cake? Explain.
Answer:
The fraction 4/4 represents the entire cake.
Explanation:
In the above-given question,
given that,
A small cake is cut into 4 equal pieces.
4 / 4 = 1.
so the fraction 4/4 represents the entire cake.
Question 5.
Mark and Sidney each have a piece of wood that is the same size. Mark paints \(\frac{2}{8}\) of his piece of wood. Sidney paints \(\frac{5}{8}\) of her piece of wood. Who painted a fraction that is closer to 1 than to 0? Explain how you found your answer. Then tell who painted less of his or her piece of wood.
Answer:
Sidney is closer to 1 than to 0.
Explanation:
In the above-given question,
given that,
Mark and Sidney each have a piece of wood that is the same size.
Mark paints \(\frac{2}{8}\) of his piece of wood.
Sidney paints \(\frac{5}{8}\) of her piece of wood.
2/8 is near to 0.
5/8 is closer to 1.
so Sidney is closer to 1 than to 0.
Question 6.
Greg colored the fraction model below.
A. Which fractions name the purple part of the model? Select all that apply.
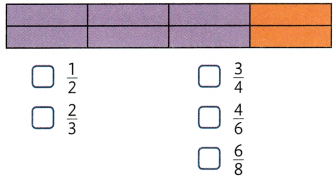
Answer:
The fraction 6/8 names the purple part of the model.
Explanation:
In the above-given question,
given that,
the fractions are 1/2, 3/4, 2/3, 4/6, 6/8.
6 boxes are filled with purple color.
so the fraction 6/8 names the purple part of the model.
B. Does \(\frac{1}{4}\) name the unshaded part of the model? Explain.
Answer:
Yes, the fraction 1/4 names the unshaded part of the model.
Explanation:
In the above-given question,
given that,
the fractions are 1/2, 3/4, 2/3, 4/6, 6/8.
2 boxes are not filled with purple color.
so the fraction 2/8 names the unshaded part of the model.
Question 7.
Carl, Fiona, and Jen each had a sandwich. The sandwiches were the same size and cut into eighths. Carl ate \(\frac{7}{8}\) of a sandwich, Fiona ate \(\frac{3}{8}\) of a sandwich, and Jen ate \(\frac{6}{8}\) of a sandwich. Who ate the most? Explain.
Answer:
Carl ate more sandwiches.
Explanation:
In the above-given question,
given that,
Carl, Fiona, and Jen each had a sandwich.
The sandwiches were the same size and cut into eighths.
Carl ate \(\frac{7}{8}\) of a sandwich.
Fiona ate \(\frac{3}{8}\) of a sandwich.
Jen ate \(\frac{6}{8}\) of a sandwich.
3/8, 6/8, 7/8.
so carl ate more sandwiches.
Question 8.
George wants to know if two pieces of wire are the same length. One wire is \(\frac{6}{8}\) foot. The other is \(\frac{3}{4}\) foot. Are they the same length? Fill in the fractions on the number line to compare the lengths of the pieces of wire. Then explain your answer.
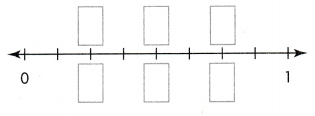
Answer:
The missing fractions are 1/4, 2/4, and 3/4.
2/8, 4/8, and 6/8.
Explanation:
In the above-given question,
given that,
George wants to know if two pieces of wire are the same length.
One wire is \(\frac{6}{8}\) foot.
The other is \(\frac{3}{4}\) foot.
6/8 = 3/4.
2 x 3 = 6.
2 x 4 = 8.
so the missing fractions are 1/4, 2/4, and 3/4.
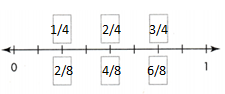
Question 9.
Lezlie hiked \(\frac{3}{8}\) mile on Monday. On Wednesday she hiked \(\frac{3}{6}\) mile. She hiked a mile on Friday. Use benchmark fractions to arrange the lengths of the hikes in order from shortest to longest hike.
Answer:
The lengths of hikes in order from shortest and longest = 3/4, 3/6, and 3/8.
Explanation:
In the above-given question,
given that,
Lezlie hiked \(\frac{3}{8}\) mile on Monday.
On Wednesday she hiked \(\frac{3}{6}\) mile.
She hiked a mile on Friday.
8 – 2 = 6, 6 – 2 = 4.
so the lengths of hikes in order from shortest and longest = 3/4, 3/6, and 3/8.
Question 10.
A mural is divided into 3 equal parts. What fraction represents the entire mural? Explain.
Answer:
The entire mural is 3/3.
Explanation:
In the above-given question,
given that,
A mural is divided into 3 equal parts.
3/3 = 1.
so the entire mural is divided into 3 parts.
Question 11.
Meagan ate \(\frac{3}{4}\) of a cookie. Write an equivalent fraction for the amount of cookie Meagan did NOT eat. Then write a fraction that is equivalent to the amount of the cookie that Meagan did eat, and explain why your answer is correct.
Answer:
Megan did not eat = 1/4.
Explanation:
In the above-given question,
given that,
Meagan ate \(\frac{3}{4}\) of a cookie.
3/4 + 1/4 = 1.
3/4 = 1/4 + 1/4 + 1/4.
so megan did not ate = 1/4.
Question 12.
Circle each fraction that is equivalent to 1. Explain your reasoning. Then give another fraction that is equal to 1.
![]()
Answer:
The fraction that is equivalent to 1 is 3/3 and 6/6.
Explanation:
In the above-given question,
given that,
the fractions are 2/4, 3/3, 3/6, 4/6, and 6/6.
circle each fraction that is equivalent to 1.
3/3 = 1, and 6/6 = 1.

Question 13.
Use the number line to help order the fractions from least to greatest. Then explain how you found your answer.
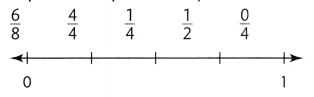
Answer:
The fractions from least to greatest = 0/4, 1/2, 1/4, 6/8, and 4/4.
Explanation:
In the above-given question,
given that,
The fractions are 6/8, 4/4, 1/4, 1/2, and 0/4.
6/8 = 3/4.
2 x 3 = 6.
2 x 4 = 8.
so the fractions from least to greatest = 0/4, 1/2, 1/4, 6/8, and 4/4.
Question 14.
Eva and Landon had the same math homework. Eva finished the homework. Landon finished of the homework. Conjecture: Eva and Landon finished the same amount of their homework.
A. Complete the number lines to help think about the conjecture.
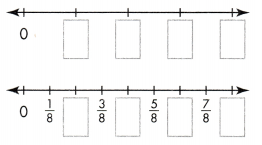
Answer:
The fractions are 1/4, 2/4, 3/4, and 4/4.
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, and 8/8.
Explanation:
In the above-given question,
given that,
Eva and Landon had the same math homework.
Eva finished the homework.
2/4 = 1/2.
2 x 1 = 2.
2 x 2 = 4.
so the missing fractions are 1/4, 2/4, 3/4, and 4/4.
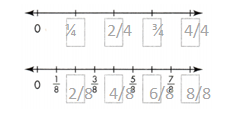
B. Use your diagram to decide if the conjecture is correct. Explain.
Answer:
Question 15.
For each pair of fractions, write the equivalent whole number in the box.
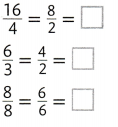
Answer:
16/4 = 8/2 = 4.
6/3 = 4/2 = 2.
8/8 = 6/6 = 1.
Explanation:
In the above-given question,
given that,
the pair of fractions are 16/4, 8/2, 6/3, 4/2, 8/8, and 6/6.
16/4 = 8/2 = 4.
6/3 = 4/2 = 2.
8/8 = 6/6 = 1.
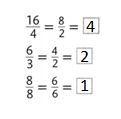
Topic 13 Performance Task
Clothing Store Devin, Jenna, Eli, and Gabby work at a clothing store. On Saturday they each worked the same number of hours.
The Time Spent at Cash Register table shows the fraction of time each person spent checking out customers. The Time Spent on Customer Calls table shows the fraction of an hour Jenna spent answering phone calls for the store.
Use the Time Spent at Cash Register table to answer Questions 1-3.
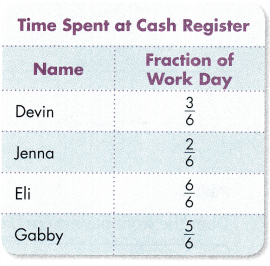
Question 1.
Draw fraction strips to show the fraction of time each person worked at the cash register.

Answer:
The fraction of time each person worked at the cash register = 3/6, 2/6, 6/6, and 5/6.
Explanation:
In the above-given question,
given that,
Devin, Jenna, Eli, and Gabby work at a clothing store.
Devin worked 3/6 hours a day.
Jenna worked 2/6 hours a day.
Eli worked 6/6 hours a day.
Gabby worked 5/6 hours a day.
the fraction of hours is 3/6, 2/6, 6/6, and 5/6.
so the fraction of time each person worked at the cash register = 3/6, 2/6, 6/6, and 5/6.
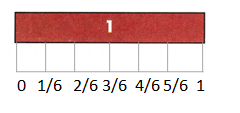
Question 2.
Who spent the most time at the cash register?
Answer:
The most time spent at the cash register = Gabby.
Explanation:
In the above-given question,
given that,
Devin, Jenna, Eli, and Gabby work at a clothing store.
Devin worked 3/6 hours a day.
Jenna worked 2/6 hours a day.
Eli worked 6/6 hours a day.
Gabby worked 5/6 hours a day.
3/6 = 1/2.
3 x 1 = 3.
3 x 2 = 6.
2/6 = 1/3.
2 x 1 = 2.
2 x 3 = 6.
6 / 6 = 1.
so the number of hours Gabby worked = 5/6.
Question 3.
Write a comparison to show the time Gabby spent at the cash register compared to the time Devin spent. Use >, <, or =.
Answer:
Gabby worked more hours than Devin.
Explanation:
In the above-given question,
given that,
Devin, Jenna, Eli, and Gabby work at a clothing store.
Devin worked 3/6 hours a day.
Jenna worked 2/6 hours a day.
Eli worked 6/6 hours a day.
Gabby worked 5/6 hours a day.
5/6 is greater than 3/6.
so Gabby worked more hours than Devin.
Question 4.
Use the Time Spent on Customer Calls table to answer this question: On which day did Jenna spend closest to one hour on the phone? Explain how you know.

Answer:
Jenna spends the closest to one hour on Monday.
Explanation:
In the above-given question,
given that,
on Saturday he spends a 3/6 fraction of an hour.
on Sunday he spends 3/5 fraction of an hour.
on Monday he spends 3/4 fraction of an hour.
3/6 = 1/2.
3/4 is nearest to the 1.
so Jenna spends the closest to one hour on Monday.
The store sells different colors of men’s socks. The Socks table shows the fraction for each sock color in the store.
Use the Socks table to answer Questions 5 and 6.

Question 5.
Part A
Complete the fractions on the number line. Label the fraction that represents each sock color.
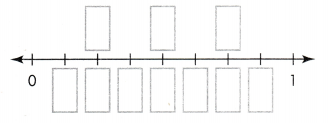
Answer:
The fraction that represents each sock color = 1/4, 2/4, 3/4, and 1.
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, and 1.
Explanation:
In the above-given question,
given that,
The store sells different colors of men’s socks.
the white color socks are 1/8.
the black color sock is 1/4.
the brown color socks are 3/8.
the gray color socks are 2/8.
so the fraction that represents each sock color = 1/4, 2/4, 3/4, and 1.
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, and 1.
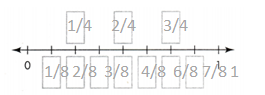
Part B
Does the store have more brown socks or more white socks?
Answer:
The store has more brown socks = 3/8.
Explanation:
In the above-given question,
given that,
The store sells different colors of men’s socks.
the white color socks are 1/8.
the black color sock is 1/4.
the brown color socks are 3/8.
the gray color socks are 2/8.
3/8 is greater than 1/8.
so brown color socks are more than white color socks.
Question 6.
Use the number line in Exercise 5 Part A to construct an argument to justify the following conjecture: The store has an equal number of gray socks and black socks.
Answer:
Yes, the store has an equal number of gray socks and white socks.
Explanation:
In the above-given question,
given that,
The store sells different colors of men’s socks.
the white color socks are 1/8.
the black color sock is 1/4.
the brown color socks are 3/8.
the gray color socks are 2/8.
2/8 = 1/4.
2 x 1 = 2.
4 x 2 = 8.
so the store has the equal number of gray socks and white socks.
Question 7.
Use the Miguel’s Socks table to answer the question.

Miguel bought some socks at the clothing store. After he washed them, he counted the number of individual socks he has. Each sock is \(\frac{1}{2}\) of a pair. How many pairs of black socks does he have? Write this number as a fraction.
Answer:
The number of pairs of black socks does he have = 3 pairs.
Explanation:
In the above-given question,
given that,
Miguel bought some socks at the clothing store.
the number of black color socks = 6.
the number of gray color socks = 8.
3/6 and 4/8.
3/6 = 1/2.
4/8 = 1/2.
so the number of pairs of black socks does he have = 3 pairs.