Go through the enVision Math Common Core Grade 3 Answer Key Topic 4 Use Multiplication to Divide: Division Facts regularly and improve your accuracy in solving questions.
enVision Math Common Core 3rd Grade Answers Key Topic 4 Use Multiplication to Divide: Division Facts
Essential Questions:
How can you use known multiplication facts to find unknown division facts? How are multiplication and division related?

enVision STEM Project: Testing Models
Do Research Tests can be done to see if a model works or if a change makes it better. Use the Internet or other sources to find information about a model or prototype that was tested. Identify how the testing was done.
Journal: Write a Report Include what you found. Also in your report:
- Make a chart that includes the model, what changed in the test, and what stayed the same.
- Explain the results of the test.
- Write an equation to show one of the relationships in the test. Explain what the numbers represent.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- division
- factors
- multiplication
- equation
Question 1.
_________ are multiplied together to give a product.
Answer:
__Factors _______ are multiplied together to give a product.
Question 2.
Use _________ to find how many equal groups or how many are in each group.
Answer:
Use __division_______ to find how many equal groups or how many are in each group.
Question 3.
___________ is an operation that gives the total number when you put together equal groups.
Answer:
__Multiplication_________ is an operation that gives the total number when you put together equal groups.
Division
Solve each problem. You can use bar diagrams, counters, or draw a picture to help.
Question 4.
Stuart has 15 stickers to give to his 3 friends. How many stickers can each friend have?
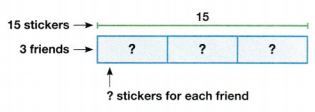
Answer:
Number of stickers each friend gives = 5.
Explanation:
Number of stickers Stuart has = 15.
Number of friends to give = 3.
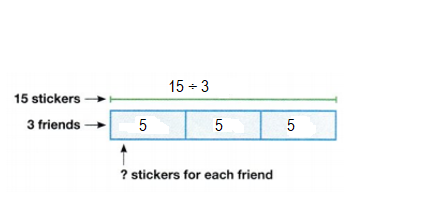
Number of stickers each friend gives = Number of stickers Stuart has ÷ Number of friends to give
= 15 ÷ 3
= 5.
Question 5.
There are 32 muffins. Eight people share them equally. How many muffins does each person get?
Answer:
Number of muffins each person get = 4.
Explanation:
Number of muffins = 32.
Number of people share them equally = 8.
Number of muffins each person get = Number of muffins ÷ Number of people share them equally
= 32 ÷ 8
= 4.
Question 6.
Suzy has 12 granola bars. There are 2 granola bars in each package. How many packages of granola bars are there?
Answer:
Number of packages of granola bars there = 6.
Explanation:
Number of granola bars Suzy has = 12.
Number of granola bars in each package = 2.
Number of packages of granola bars there = Number of granola bars Suzy has ÷ Number of granola bars in each package
= 12 ÷ 2
= 6.
Equations
Question 7.
Brian has 5 boxes. He puts 8 markers in each box. Which equation shows the total number of markers?
A. 5 + 8 = 13
B. 5 × 8 = 40
C. 40 ÷ 5 = 8
D. 40 ÷ 8 = 5
Answer:
Total number of markers = 40.
B. 5 × 8 = 40.
Explanation:
Number of boxes Brian has = 5.
Number of markers in each box = 8.
Total number of markers = Number of boxes Brian has × Number of markers in each box
= 5 × 8
= 40.

Pick a Project
PROJECT 4A
Who are your favorite athletes?
Project: Make a Poster of Your Favorite Athletes

Answer:

PROJECT 4B
Who is on our money?
Project: Write a Report About Money

Answer:

PROJECT 4C
How do you score in horseshoes?
Project: Create a Score Sheet

Answer:

PROJECT 4D
What kind of game would you create?
Project: Develop a Game

Answer:

Lesson 4.1 Relate Multiplication and Division
Solve & Share
Use 24 counters to make arrays with equal rows. Write multiplication and division equations to describe your arrays.
I can … use fact families to see how multiplication and division are related.

Look Back! What relationships do you see between the multiplication and division equations for each of your arrays?
Answer:
The relationships between the multiplication and division equations for each of the arrays may be different in process yet the result value is same.
Explanation:
Process different to multiplication and division equations yet both are done to find the solution to the problem.

Essential Question
How Can Multiplication Question Facts Help You Divide?
Answer:
In multiplication, we find the product of two factors. In division, we find the missing factor if the other factor and the product are known.
Explanation:
In multiplication, we find the product of two factors. In division, we find the missing factor if the other factor and the product are known. This is how Multiplication Question Facts Helps in Divide.
Visual Learning Bridge
This array can show the relationship between multiplication and division.

Multiplication 3 rows of 10 drums
3 × 10 = 30
30 drums
Division 30 drums in 3 equal rows
30 ÷ 3 = 10
10 drums in each row
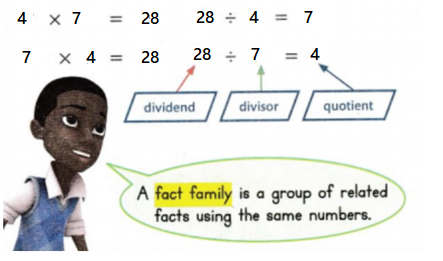
A fact family shows how multiplication and division are related.
Fact family for 3, 10, and 30:

The dividend is the number of objects to be divided.
The divisor is the number by which another number is divided.
The quotient is the answer to a division problem.

Convince Me! Reasoning 4 × 7 = 28 is one fact in a fact family. Draw an array for this fact. Write the other three facts in the fact family.
Answer:
4 × 7 = 28.
28 = dividend.
7 = divisor
4 = quotient.
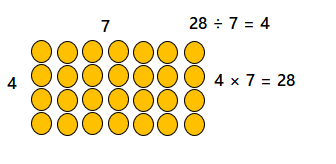
Explanation:
Guided Practice
Do You Understand?
Question 1.
Look at the fact family for 3, 10, and 30 on the previous page. What do you notice about the products and the dividends?
Answer:
It is noticed that the product in mathematics means that the two factors should be multiplied together.
In division, the amount or number to be divided is called the dividend.
Explanation:
Multiplication 3 rows of 10 drums
3 × 10 = 30 drums.
Division 30 drums in 3 equal rows
30 ÷ 3 = 10 drums in each row.
It is noticed that the product in mathematics means that the two factors should be multiplied together.
In division, the amount or number to be divided is called the dividend. Dividend is the whole that is to be divided into parts.
Question 2.
Is 4 × 6 = 24 part of the fact family for 3, 8, and 24? Explain.
Answer:
Yes, 4 × 6 = 24 is a part of the fact family for 3, 8, and 24.
Explanation:
Is 4 × 6 = 24 part of the fact family for 3, 8, and 24.
4 × 6 = 24.
24 ÷ 4 = 6.
Dividend = 24.
Divisor = 4
Quotient = 6
.
3 × 8 = 24.
24 ÷ 3 = 8.
Dividend = 24.
Divisor = 3
Quotient = 8.
Do You Know How?
In 3-5, use the relationship between multiplication and division to complete each equation.
Question 3.
3 × 7 = 21
21 ÷ 3 = ________
Answer:
3 × 7 = 21.
21 ÷ 3 = __7__.
Explanation:
3 × 7 = 21.
21 ÷ 3 = 7.
Dividend ÷ Quotient = Divisor.
Question 4.
18 ÷ 2 = 9
2 × ______ = 18
Answer:
18 ÷ 2 = 9.
2 × __9____ = 18.
Explanation:
18 ÷ 2 = 9.
2 × 9 = 18.
Quotient × divisor = dividend.
Question 5.
2 × 10 = 20
20 ÷ 2 = _________
Answer:
2 × 10 = 20.
20 ÷ 2 = ____10_____.
Explanation:
2 × 10 = 20.
20 ÷ 2 = 10.
Dividend ÷ quotient = Divisor.
Independent Practice
In 6 and 7, use the relationship between multiplication and division to complete each equation.
Question 6.
2 × ______ = 16
16 ÷ 2 = _______
Answer:
2 × __8____ = 16.
16 ÷ 2 = __8_____.
Explanation:
2 × 8 = 16
16 ÷ 2 = 8.
Dividend ÷ quotient = Divisor.
Question 7.
56 ÷ 8 = 7
8 × _____ = 56
Answer:
56 ÷ 8 = 7.
8 × __7___ = 56.
Explanation:
56 ÷ 8 = 7.
8 × 7 = 56.
Dividend = Divisor ÷ quotient.
In 8-13, write the fact family.
Question 8.
Write the fact family for 6, 7, and 42.
Answer:
6 × 7 = 42.
42 ÷ 6 = 7.
Explanation:
6 × 7 = 42.
42 ÷ 6 = 7.
Dividend ÷ quotient = Divisor.

Question 9.
Write the fact family for 9, 10, and 90.
Answer:
9 × 10 = 90.
90 ÷ 9 = 10.
Explanation:
9 × 10 = 90.
90 ÷ 9 = 10.
Dividend ÷ quotient = Divisor.
Question 10.
Write the fact family for 2, 3, and 6.
Answer:
2 × 3 = 6.
6 ÷ 2 = 3.
Explanation:
2 × 3 = 6.
6 ÷ 2 = 3.
Dividend ÷ quotient = Divisor.
Question 11.
Write the fact family for 1, 5, and 5.
Answer:
1 × 5 = 5.
5 ÷ 1 = 5.
Explanation:
1 × 5 = 5.
5 ÷ 1 = 5.
Dividend ÷ quotient = Divisor.
Question 12.
Write the fact family for 3, 8, and 24.
Answer:
3 × 8 = 24.
24 ÷ 3 = 8.
Explanation:
3 × 8 = 24.
24 ÷ 3 = 8.
Dividend ÷ quotient = Divisor.
Question 13.
Write the fact family for 5, 6, and 30.
Answer:
5 × 6 = 30.
30 ÷ 5 = 6.
Explanation:
5 × 6 = 30.
30 ÷ 5 = 6.
Dividend ÷ quotient = Divisor.
Problem Solving
Question 14.
Write a multiplication equation and a division equation for the array.
4 × ______ = 20
20 ÷ ______ = 5

Answer:
4 × _5____ = 20.
20 ÷ __4____ = 5.
Explanation:
4 × 5 = 20.
20 ÷ 4 = 5.
Dividend ÷ quotient = Divisor.
Question 15.
Make Sense and Persevere How many inches shorter is the red fabric than the green and yellow fabrics combined?

Answer:
Length of the red fabric shorter than the green and yellow fabrics combined = 18 inches.
Explanation:
Length of the red fabric = 72 inches.
Length of the green fabric = 36 inches.
Length of the yellow fabric = 54 inches.
Length of the red fabric shorter than the green and yellow fabrics combined = (Length of the green fabric + Length of the yellow fabric) – Length of the red fabric
= (36 + 54) – 72
= 90 – 72
= 18 inches.
Question 16.
Higher Order Thinking
Anya says that with 24 counters she can make only 6 possible arrays. Todd says he can make 8 arrays. Who is correct? Explain.
Answer:
Anya says with 24 counters she can make only 6 possible arrays is incorrect because we can make 8 arrays out of 24 counters as Todd says.
Explanation:
Anya says that with 24 counters she can make only 6 possible arrays.
=> 24 ÷ 6 = 4.
Todd says that with 24 counters he can make 8 arrays.
=> 24 ÷ 8 = 3.
Question 17.
Algebra Carla picked 9 apples a day for three days. Which number tells you how many apples she picked in three days and makes this equation true? ☐ ÷ 3 = 9
Answer:
Number of apples she picked in three days = 27.
Equation: 27 ÷ 3 = 9.
Explanation:
Number of apples Algebra Carla picked a day = 9.
Number of days Algebra Carla picked apples = 3.
Number of apples she picked in three days = Number of apples Algebra Carla picked a day × Number of days Algebra Carla picked apples
= 9 × 3
= 27.
Question 18.
Vocabulary
Can you write a fact family for 3, 5, and 7? Explain.
Answer:
3, 5 , and 7 are nor fact family because there is no product number among this three numbers.
Explanation:
No, you cannot write a fact family for 3, 5 , and 7 because they are odd numbers and there is no product among these three numbers.
Question 19.
Lisa, Bret, and Gary harvested apples. Lisa filled 3 carts with apples. Bret also filled 3 carts with apples. Gary filled another 3 carts with apples. Write a multiplication equation and a division equation for this story.
Answer:
Number of carts each person filled with apples = 9 ÷ 3 = 3.
Total number of carts of apples these three filled = 3 × 3 = 9.
Explanation:
Number of carts Lisa filled with apples = 3.
Number of carts Bret filled with apples = 3.
Number of carts Gary filled with apples = 3.
Total number of carts these three filled = Number of carts Lisa filled with apples + Number of carts Bret filled with apples + Number of carts Gary filled with apples
= 3 + 3 + 3
= 6 + 3
= 9.
Number of people filled carts with apples = 3.
Number of carts each person filled with apples = Total number of carts of apples these three filled ÷ Number of people filled carts with apples
= 9 ÷ 3 = 3.
Total number of carts of apples these three filled = Number of people filled carts with apples × Number of carts each person filled with apples
= 3 × 3 = 9.
Assessment Practice
Question 20.
Select numbers to create a multiplication equation that could be used to solve 20 ÷ 5 = ☐.

Answer:
Numbers to create a multiplication equation that could be used to solve 20 ÷ 5 = ☐.
20 ÷ 5 = 4.
4 × 5 = 20.
Explanation:
Numbers to create a multiplication equation that could be used to solve 20 ÷ 5 = ☐.
20 ÷ 5 = 4.
5 × 4 = 20.
4 × 5 = 20.
Question 21.
Select numbers to create a multiplication equation that could be used to solve 24 ÷ 8 = ☐0

Answer:
Numbers to create a multiplication equation that could be used to solve 24 ÷ 8 = ☐.
24 ÷ 8 = 3.
3 × 8 = 24.
Explanation:
Numbers to create a multiplication equation that could be used to solve 24 ÷ 8 = ☐.
24 ÷ 8 = 3.
8 × 3 = 24.
3 × 8 = 24.
Lesson 4.2 Use Multiplication to Divide with 2, 3, 4, and 5
Solve & Share
Kara puts 30 toys into 5 party bags. She puts the same number of toys into each bag. How many toys are in each bag?
I can … divide by 2, 3, 4, and 5 by thinking about how I multiply with those numbers.

Look Back! Show two pictures you might draw to represent 30 ÷ 5.
Answer:
Number of toys are in each bag = 6.
30 ÷ 5 = 6.
5 × 6 = 30.
6 × 5 = 30.
Explanation:
Number of toys Kara has = 30.
Number of party bags Kara has = 5.
Number of toys are in each bag = Number of toys Kara has ÷ Number of party bags Kara has
= 30 ÷ 5
= 6.
5 × 6 = 30.
6 × 5 = 30.
Essentials Question
What Multiplication Fact Can You Use?
Answer:
Some basic multiplication facts are needed to follow for multiplying numbers. The repeated addition of the same number is expressed by multiplication in short.
Explanation:
Multiplication facts which we commonly use is multiplying two numbers together to get the product.
Visual Learning Bridge
Dee has 14 noisemakers. She puts the same number on each of 2 tables. How many noisemakers are on each table?

Dee has 40 stickers. If she puts 5 stickers on each bag, how many bags can Dee decorate?

Find 40 ÷ 5.
What You Think
What number times 5 is 40?
8 × 5 = 40
What You Write
40 ÷ 5 = 8
Dee can decorate 8 bags.
You can use multiplication to help divide.
Dee wants to put 15 cups in 3 equal stacks on the table. How many cups will Dee put in each stack?

Find 15 ÷ 3.
What You Think
3 times what number is 15?
3 × 5 = 15
What You Write
15 ÷ 3 = 5
Dee will put 5 cups in each stack.
Multiplication and division facts form relationships.
Convince Me! Reasoning How can you use multiplication to help solve 20 ÷ 4? Write the related multiplication fact you use to help solve the problem.
Answer:
20 ÷ 4 = 5.
5 × 4 = 20.
Explanation:
Dee wants to put 20cups in 4 equal stacks on the table. How many cups will Dee put in each stack?
20 ÷ 4 = 5.
5 × 4 = 20.
4 × 5 = 20.
Another Example!
Here are two ways to write a division problem.

Guided Practice
Do You Understand?
Question 1.
How can 5 × 3 = 15 help you divide 15 by 3?
Answer:
5 × 3 = 15.
15 ÷ 3 = 5.
Explanation:
5 × 3 = 15.
15 ÷ 3 = 5.
Question 2.
Mr. Dean has 3 children. He buys 30 pencils to share equally among his children for the school year. How many pencils will each child get? Write the answer and the fact family you used.
Answer:
Number of pencils each child gets = 10.
Explanation:
Number of children Mr. Dean has = 3.
Number of pencils he buys to share equally among his children for the school year = 30.
Number of pencils each child gets = Number of pencils he buys to share equally among his children for the school year ÷ Number of children Mr. Dean has
= 30 ÷ 3
= 10.
Do You Know How?
In 3 and 4, complete each fact family.
Question 3.
3 × 6 = 18 _________
18 ÷ 3 = 6 _________
Answer:
3 × 6 = 18 __Dividend_______.
18 ÷ 3 = 6 ____quotient___.
Explanation:
3 × 6 = 18 (Dividend)
18 ÷ 3 = 6 (quotient).
Question 4.
9 × 4 = 36 _________
36 ÷ 4 = 9 _________
Answer:
9 × 4 = 36 __Dividend_______.
36 ÷ 4 = 9 ___quotient______.
Explanation:
9 × 4 = 36 (Dividend).
36 ÷ 4 = 9 (quotient).
In 5-8, find each quotient.
Question 5.
36 ÷ 4 = ________
Answer:
36 ÷ 4 = ____9____.
Explanation:
36 ÷ 4 = ___9_____.
Question 6.
_______ = 15 ÷ 5
Answer:
___3____ = 15 ÷ 5.
Explanation:
___3____ = 15 ÷ 5.
Question 7.
![]()
Answer:
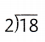
= 9.
Explanation:
![]()
= 9.
Question 8.
![]()
Answer:
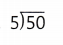 = 10.
= 10.
Explanation:
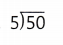 = 10.
= 10.
Independent Practice
In 9-20, find each quotient.
Question 9.
12 ÷ 2 = _______
Answer:
12 ÷ 2 = __6_____.
Explanation:
12 ÷ 2 = 6.
Question 10.
_______ = 12 ÷ 3
Answer:
___4____ = 12 ÷ 3.
Explanation:
4 = 12 ÷ 3.
Question 11.
16 ÷ 4 = _______
Answer:
16 ÷ 4 = ___4____.
Explanation:
16 ÷ 4 = 4.
Question 12.
35 ÷ 5 = _______
Answer:
35 ÷ 5 = ___7____.
Explanation:
35 ÷ 5 = 7.
Question 13.
14 ÷ 2 = _______
Answer:
14 ÷ 2 = ___7___.
Explanation:
14 ÷ 2 = 7.
Question 14.
20 ÷ 4 = ______
Answer:
20 ÷ 4 = __5____.
Explanation:
20 ÷ 4 = 5.
Question 15.
_______ = 24 ÷ 4
Answer:
___6____ = 24 ÷ 4.
Explanation:
6= 24 ÷ 4.
Question 16.
45 ÷ 5 = ______
Answer:
45 ÷ 5 = ___9___.
Explanation:
45 ÷ 5 = 9.
Question 17.
![]()
Answer:
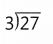
= 9.
Explanation:
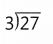
= 9.
Question 18.
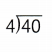
Answer:
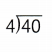
= 10.
Explanation:
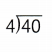
= 10.
Question 19.
![]()
Answer:
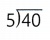
= 8.
Explanation:
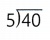
= 8.
Question 20.
![]()
Answer:
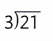
= 7.
Explanation:
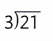
= 7.
Problem Solving
In 21 and 22, use the rectangle at the right.
Question 21.
How many individual squares are inside the rectangle? Write a division equation in which the quotient represents the number of rows.

Answer:
Total number of squares in the rectangle = 20.
Division Equation:
20 ÷ 4 = 5.
Explanation:
Number of squares rows = 5.
Number of squares columns = 4.
Total number of squares in the rectangle = Number of squares rows × Number of squares columns
= 5 × 4
= 20.
Division Equation:
Total number of squares in the rectangle ÷ Number of squares columns = Number of squares rows.
20 ÷ 4 = 5.
Question 22.
Make Sense and Persevere If Anna arranges the squares into an array with 2 columns, how many rows will there be?
Answer:
Number of rows = 10.
Explanation:
Number of squares = 20.
Number of columns = 2
Number of rows = Number of squares ÷ Number of columns
= 20 ÷ 2
= 10.
Question 23.
Number Sense Joey says, “I cannot solve 8 ÷ 2 by using the fact 2 × 8 = 16.” Do you agree or disagree? Explain.
Answer:
Yes, I agree with Joey. We cannot solve 8 ÷ 2 by using the fact 2 × 8 = 16.
Explanation:
2 × 8 = 16.
=> 16 ÷ 8 = 2.
=> 16 ÷ 2 = 8.
8 ÷ 2 = 4.
Question 24.
Miko has 8 counters to arrange in an array. Write multiplication and division equations to represent all the ways Miko might arrange her counters.
Answer:
Way:1: Total number of counters = Number of rows × Number of columns
= 4 × 2
= 8.
Way:2: Total number of counters = Number of rows × Number of columns
= 2 × 4
= 8.
Way:3: Total number of counters = Number of rows × Number of columns
= 8 × 1
= 8.
Way:4: Total number of counters = Number of rows × Number of columns
= 1 × 8
= 8.
Explanation:
Number of counters Miko has = 8.
Way:1:
Number of rows = 4.
Number of columns = 2.
Total number of counters = Number of rows × Number of columns
= 4 × 2
= 8.
Way:2:
Number of rows = 2.
Number of columns = 4.
Total number of counters = Number of rows × Number of columns
= 2 × 4
= 8.
Way:3:
Number of rows = 8.
Number of columns = 1.
Total number of counters = Number of rows × Number of columns
= 8 × 1
= 8.
Way:4:
Number of rows = 1.
Number of columns = 8.
Total number of counters = Number of rows × Number of columns
= 1 × 8
= 8.
Question 25.
Vocabulary Write a division equation. Tell which number is the quotient, the dividend, and the divisor.
Answer:
Division Equation:
Total number of counters ÷ Number of columns = Number of rows
8 ÷ 8 = 1.
Dividend = 8.
Divisor = 8.
Quotient = 1.
Explanation:
Number of rows = 1.
Number of columns = 8.
Total number of counters = Number of rows × Number of columns
= 1 × 8
= 8.
Division Equation:
Total number of counters ÷ Number of columns = Number of rows
8 ÷ 8 = 1.
Dividend = 8.
Divisor = 8.
Quotient = 1.
Question 26.
Higher Order Thinking Chris gives 18 pretzels equally to 3 friends. Martha gives 20 pretzels equally to 4 friends. Whose friends got more pretzels? Use equations to justify your answer.
Answer:
Chris’s friends gets each 6 pretzels more than Martha’s friends.
Explanation:
Number of pretzels Chris gives = 18.
Number of friends Chris gives equally = 3.
Number of pretzels Chris’s friends gets each = Number of pretzels Chris gives ÷ Number of friends Chris gives equally
= 18 ÷ 3
= 6.
Number of pretzels Martha gives = 20.
Number of friends Martha gives equally = 4.
Number of pretzels Martha’s friends gets each = Number of pretzels Martha gives ÷ Number of friends Martha gives equally
= 20 ÷ 4
= 5.
Assessment Practice
Question 27.
Which expression can help you divide 12 ÷ 3?
A. 2 × 3
B. 3 × 3
C. 4 × 3
D. 5 × 3
Answer:
C. 4 × 3 is the expression which helps to divide 12 ÷ 3 = ??.
Explanation:
Expression can help you divide 12 ÷ 3 = ??
12 ÷ 3 = 4.
=> 4 × 3 = 12.
Question 28.
Which expression can help you divide 28 ÷ 4?
A. 7 × 4
B. 6 × 4
C. 5 × 4
D. 4 × 4
Answer:
A. 7 × 4 is the expression which helps to divide 28 ÷ 4 = ??.
Explanation:
Expression can help you divide 28 ÷ 4 = ??
28 ÷ 4 = 7.
=> 7 × 4 = 28.
Lesson 4.3 Use Multiplication to Divide with 6 and 7
Solve & Share
There are 18 children in a ballet class. They are standing in rows of 6 for a dance recital. How many rows of children are there?
I can … divide by 6 and 7 by thinking about how I multiply with those numbers.

Look Back! Draw a bar diagram to represent the problem.
Answer:
Number of children in each row = 3.
Explanation:
Number of children in a ballet class = 18
Number of rows children are standing for a dance recital = 6.
Number of children in each row = Number of children in a ballet class ÷ Number of rows children are standing for a dance recital
= 18 ÷ 6
= 3.
Essential Question
How Do You Divide with 6 and 7?
Answer:
The dividend to be divided with the number 6 or 7 to get the answer which is called quotient.
Explanation:
What is being divided is called the dividend, which is divided by the divisor, and the result is called the quotient. In the example, 24 is the dividend, 6 is the divisor, and 4 is the quotient
Visual Learning Bridge
There are 48 dogs entered in a dog show. The judge wants 6 dogs in each group. How many groups will there be?

Find 48 ÷ 6.
What You Think
What number times 6 is 48?
8 × 6 = 48
What You Write
48 ÷ 6 = 8
There will be 8 groups.
Use a multiplication problem to make sense of a division problem.
Another dog was entered in the show. There will now be 7 dogs in each group. How many groups will there be?
Find 49 ÷ 7.
What You Think
What number times 7 is 49?
7 × 7 = 49
What You Write
49 ÷ 7 = 7
There will be 7 groups.
Convince Me! Model with Math Draw a bar diagram using the numbers 36, 6, and 6. Write the division fact and the related multiplication fact that your bar diagram shows.
Answer:
36 ÷ 6 = 6.
6 × 6 = 36.
Explanation:
Division Equation:
36 ÷ 6 = 6.
Multiplication Equation:
6 × 6 = 36.
Guided Practice
Do You Understand?
Question 1.
How can you tell without dividing that 42 ÷ 6 will be greater than 42 ÷ 7?
Answer:
If the divisor is small, the quotient in division is going to be greater number and vice versa.
Explanation:
42 ÷ 6 will be greater than 42 ÷ 7 you can say without doing division by seeing the divisor. If the divisor is small the quotient in division is going to be greater number and vice versa.
Question 2.
How can 8 × 6 = 48 help you divide 48 by 6?
Answer:
8 × 6 = 48 helps in dividing 48 by 6.
48 ÷ 6 = 8.
Explanation:
8 × 6 = 48 helps in dividing 48 by 6.
48 ÷ 6 = 8.
Do You Know How?
In 3-8, write the related multiplication fact, and then find each quotient.
Question 3.
36 ÷ 6 = ________
Answer:
36 ÷ 6 = ____6____.
Explanation:
36 ÷ 6 = 6 (quotient).
6 × 6 = 36.
Question 4.
______ = 42 ÷ 6
Answer:
___7___ = 42 ÷ 6.
Explanation:
42 ÷ 6 = 7 (quotient).
6 × 7 = 42.
Question 5.
42 ÷ 7 = _______
Answer:
42 ÷ 7 = __6_____.
Explanation:
42 ÷ 7 = 6 (quotient).
7 × 6 = 42.
Question 6.
______ = 18 ÷ 6
Answer:
__3____ = 18 ÷ 6.
Explanation:
18 ÷ 6 = 3 (quotient).
6 × 3 = 18.
Question 7.
![]()
Answer:
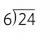 = 4.
= 4.
Explanation:
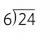 = 4(quotient).
= 4(quotient).
6 × 4 = 24.
Question 8.
![]()
Answer:
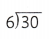
= 5.
Explanation:
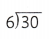
= 5 (quotient).
6 × 5 = 30.
Independent Practice
Leveled Practice In 9-20, use related multiplication and division facts to find the quotient.
Question 9.
12 ÷ 6 = ?
What number times 6 is 12?
6 × ☐ = 12
12 ÷ 6 = ☐
Answer:
12 ÷ 6 = 2.
Explanation:
12 ÷ 6 = ??
6 × 2 = 12.
12 ÷ 6 = 2.
Question 10.
21 ÷ 3 = ?
What number times 3 is 21?
3 × ☐ = 21
21 ÷ 3 = ☐
Answer:
21 ÷ 3 = 7.
Explanation:
21 ÷ 3 = ??
3 × 7 = 21.
21 ÷ 3 = 7.
Question 11.
30 ÷ 6 = ?
What number times 6 is 30?
6 × ☐ = 30
30 ÷ 6 = ☐
Answer:
30 ÷ 6 = 5.
Explanation:
30 ÷ 6 = ??
6 × 5 = 30.
30 ÷ 6 = 5.
Question 12.
![]()
Answer:
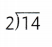 = 7.
= 7.
Explanation:
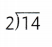 = ??
= ??
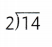 = 7.
= 7.
2 × 7 = 14.
Question 13.
![]()
Answer:
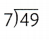 = 7.
= 7.
Explanation:
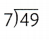 = ??
= ??
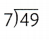 = 7.
= 7.
7 × 7 = 49.
Question 14.
![]()
Answer:
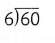 = 10.
= 10.
Explanation:
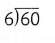 = ??
= ??
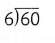 = 10.
= 10.
6 × 10 = 60.
Question 15.
![]()
Answer:
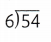 = 9.
= 9.
Explanation:
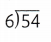 = ??
= ??
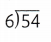 = 9.
= 9.
6 × 9 = 54.
Question 16.
![]()
Answer:
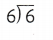 = 1.
= 1.
Explanation:
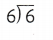 =??
=??
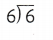 = 1.
= 1.
6 × 1 = 6.
Question 17.
![]()
Answer:
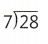 = 4.
= 4.
Explanation:
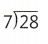 = ??
= ??
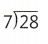 = 4.
= 4.
7 × 4 = 28.
Question 18.
Find 49 divided by 7.
Answer:
49 ÷ 7 = 7.
Explanation:
49 ÷ 7 = 7.
7 × 7 = 49.
Question 19.
Divide 54 by 6.
Answer:
54 ÷ 6 = 9.
Explanation:
54 ÷ 6 = 9.
6 × 9 = 54.
Question 20.
Find 35 divided by 7.
Answer:
35 ÷ 7 = 5.
Explanation:
35 ÷ 7 = 5.
7 × 5 = 35.
Problem Solving
Question 21.
A pizza parlor made 88 deep-dish pizzas. It made 10 more thin-crust pizzas than deep-dish pizzas. How many thin-crust pizzas did the parlor make?
Answer:
10 more thin-crust pizzas the parlor makes than deep-dish pizzas.
Explanation:
Number of deep-dish pizzas pizza parlor made = 88.
It made 10 more thin-crust pizzas than deep-dish pizzas.
=> Number of thin-crust pizzas pizza parlor made = 88 + 10 = 98.
Difference:
Number of thin-crust pizzas pizza parlor made – Number of deep-dish pizzas pizza parlor made
= 98 – 88
= 10.
Question 22.
Higher Order Thinking There are 35 new tires. Each truck will get 6 tires plus 1 tire for a spare. How many trucks will get new tires?
Answer:
Number of trucks gets new tires = 5.
Explanation:
Number of new tires = 35.
Each truck will get 6 tires plus 1 tire for a spare.
=> Number of tires each truck gets = 6 + 1 = 7.
Number of trucks gets new tires = Number of new tires ÷ Number of tires each truck gets
= 35 ÷ 7
= 5.
Question 23.
Make Sense and Persevere Explain the mistake in the fact family below. Give the correct fact.
4 × 7 = 28
7 × 4 = 28
7 ÷ 4= 28
28 ÷ 7 = 4
Answer:
4 × 7 = 28. Correct.
7 × 4 = 28. Correct.
7 ÷ 4= 28. Incorrect.
28 ÷ 7 = 4. Correct.
Explanation:
4 × 7 = 28. Correct.
7 × 4 = 28. Correct.
7 ÷ 4 = 28. Division is not correct. Incorrect.
28 ÷ 7 = 4. Correct.
Question 24.
Gloria mowed 7 lawns and earned $56. She was paid the same amount for each lawn. How much money did Gloria earn for mowing each lawn? Write an equation to represent this problem.
Answer:
Amount Gloria earn for mowing each lawn = $392.
Explanation:
Number of lawns Gloria mowed = 7.
Money Gloria earned = $56.
She was paid the same amount for each lawn.
Amount Gloria earn for mowing each lawn = Number of lawns Gloria mowed × Money Gloria earned
= 7 × $56.
= $392.

Question 25.
Andy bought 35 beads. He bought only one color of beads. Which beads could Andy have bought? How many packages of that color bead did he buy?
Answer:
Andy would have bought red or gold beads.
Number of packets red beads Andy bought = 5.
Number of packets gold beads Andy bought = 7.
Explanation:
Number of beads Andy bought = 35.
Number of beads in green package = 6.
Number of beads in red package = 7.
Number of beads in gold package = 5.
Number of packets red beads Andy bought = Number of beads Andy bought ÷ Number of beads in red package
= 35 ÷ 7
= 5.
Number of packets gold beads Andy bought = Number of beads Andy bought ÷ Number of beads in gold package
= 35 ÷ 5
= 7.
Question 26.
Cassidy bought 48 beads. She bought only one color of beads. Which beads could Cassidy have bought? How many packages of that color bead did she buy?
Answer:
Number of packets green beads Cassidy bought = 8.
Explanation:
Number of beads Cassidy bought = 48.
Number of beads in green package = 6.
Number of beads in red package = 7.
Number of beads in gold package = 5
Number of packets green beads Cassidy bought = Number of beads Cassidy bought ÷ Number of beads in green package
= 48 ÷ 6
= 8.
Assessment Practice
Question 27.
Which multiplication fact can you use to help find the value of the unknown number in the equation 42 ÷ 7 = ☐?
A. 5 × 7
B. 6 × 7
C. 7 × 7
D. 8 × 7
Answer:
Equation 42 ÷ 7 = ☐?
B. 6 × 7 multiplication fact can be used to help, find the value of the unknown number in the equation 42 ÷ 7 = ??.
Explanation:
Equation 42 ÷ 7 = ☐?
42 ÷ 7 = 6.
7 × 6 = 42.
6 × 7 = 42.
Question 28.
Which multiplication fact can you use to help find the value of the unknown number in the equation 36 ÷ 6 = ☐?
A. 5 × 6
B. 6 × 6
C. 7 × 6
D. 8 × 6
Answer:
Equation 36 ÷ 6 = ☐?
B. 6 × 6 multiplication fact can be used to help, find the value of the unknown number in the equation 36 ÷ 6 = ☐?
Explanation:
Equation 36 ÷ 6 = ☐?
36 ÷ 6 = 6.
6 × 6 = 36.
Lesson 4.4 Use Multiplication to Divide with 8 and 9
Solve & Share
An art teacher has 72 crayons. The crayons came in boxes with 8 crayons in each box. How many boxes of crayons were there?
I can … divide by 8 and 9 by thinking about how I multiply with those numbers.

Look Back! Draw a picture you could use to help solve the problem above.
Answer:
Number of boxes crayons are there = 9.
Explanation:
Number of crayons art teacher has = 72.
Number of crayons in each box = 8
Number of boxes crayons are there = Number of crayons art teacher has ÷ Number of crayons in each box
= 72 ÷ 8
= 9.

Essential Question
What Multiplication Fact Can You Use?
Answer:
Some basic multiplication facts are needed to follow for multiplying numbers. The repeated addition of the same number is expressed by multiplication in short.
Explanation:
Basic multiplication facts are needed to follow for multiplying numbers. The repeated addition of the same number is expressed by multiplication in short.
For example: 36 ÷ 6 = 6.
6 × 6 = 36.
Visual Learning Bridge
John has 56 straws. He needs 8 straws to make a spider. How many spiders can John make? Find 56 ÷ 8.
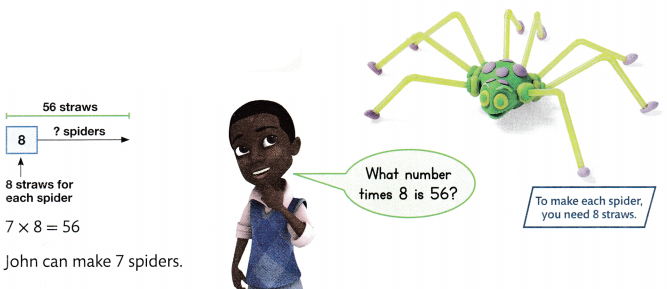
Luz made 9 animals. She used 54 straws. She used the same number of straws for each animal. How many straws did Luz use

Find 54 ÷ 9.
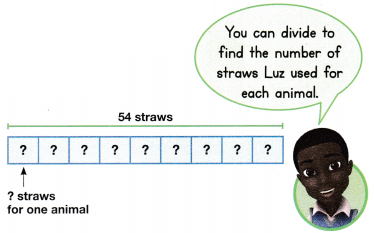
What You Think
9 times what number is 54?
9 × 6 = 54
What You Write
54 ÷ 9 = 6
Luz used 6 straws for each animal.
Convince Me! Look for Relationships Write the related multiplication fact that can be used to complete each division fact.
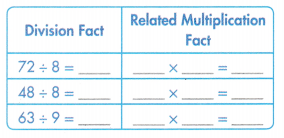
Answer:
Division Fact Related Multiplication Fact.
72 ÷ 8 = 9. 9 × 8 = 72.
48 ÷ 8 = 6. 8 × 6 = 48.
63 ÷ 9 = 7. 9 × 7 = 63.
Explanation:
Related multiplication fact that can be used to complete each division fact is as below:
Division Fact Related Multiplication Fact.
72 ÷ 8 = 9. 9 × 8 = 72.
48 ÷ 8 = 6. 8 × 6 = 48.
63 ÷ 9 = 7. 9 × 7 = 63.
Guided Practice
Do You Understand?
Question 1.
What multiplication fact can you use to find 18 ÷ 9?
Answer:
2 × 9 = 18 multiplication fact can be used to find 18 ÷ 9.
Explanation:
18 ÷ 9 = ??
18 ÷ 9 = 2.
2 × 9 = 18.
Question 2.
Carla and Jeff each use 72 straws. Carla makes animals with 9 legs. Jeff makes animals with 8 legs. Who makes more animals? Explain.
Answer:
Jeff makes 1 more animal with legs than Carla makes.
Explanation:
Number of straws Carla and Jeff each use = 72
Number of animals with legs Carla makes = 9.
Number of animals with legs Jeff makes = 8.
Total number of animals with legs Carla makes = Number of straws Carla and Jeff each use ÷ Number of animals with legs Carla makes
= 72 ÷ 9
= 8.
Total number of animals with legs Jeff makes = Number of straws Carla and Jeff each use ÷ Number of animals with legs Jeff makes
= 72 ÷ 8
= 9.
Do You Know How?
In 3 and 4, use the multiplication equation to help find each quotient.
Question 3.
16 ÷ 8 = ?
What number times 8 is 16?
______ × 8 = 16
So, 16 ÷ 8 = _______
Answer:
16 ÷ 8 = 2.
___2___ × 8 = 16.
So, 16 ÷ 8 = __2_____.
Explanation:
16 ÷ 8 = ?
16 ÷ 8 = 2.
=> 2 × 8 = 16.
So, 16 ÷ 8 =2.
Question 4.
64 ÷ 8 = ?
What number times 8 is 64?
______ × 8 = 64
So, 64 ÷ 8 = _______
Answer:
64 ÷ 8 = 8.
__8____ × 8 = 64.
So, 64 ÷ 8 = __8_____.
Explanation:
64 ÷ 8 = ?
64 ÷ 8 = 8.
8 × 8 = 64
So, 64 ÷ 8 = 8.
Independent Practice
Leveled Practice In 5-7, use the multiplication equation to help find each quotient.
Question 5.
24 ÷ 8= ?
What number times 8 is 24?
______ × 8 = 24
24 ÷ 8 = ______
Answer:
24 ÷ 8= 3.
___3___ × 8 = 24.
24 ÷ 8 = ___3___.
Explanation:
24 ÷ 8= ?
24 ÷ 8= 3.
3 × 8 = 24.
24 ÷ 8 = 3.
Question 6.
45 ÷ 9 = ?
What number times 9 is 45?
______ × 9 = 45
45 ÷ 9 = ______
Answer:
45 ÷ 9 = 5.
___5___ × 9 = 45.
45 ÷ 9 = ___5___.
Explanation:
45 ÷ 9 = ?
45 ÷ 9 = 5.
5 × 9 = 45.
45 ÷ 9 = 5.
Question 7.
27 ÷ 9 = ?
What number times 9 is 27?
______ × 9 = 27
27 ÷ 9 = _______
Answer:
27 ÷ 9 = 3.
___3___ × 9 = 27.
27 ÷ 9 = ___3____.
Explanation:
27 ÷ 9 = ?
27 ÷ 9 = 3.
3 × 9 = 27.
27 ÷ 9 = 3.
In 8-16, find each quotient.
Question 8.
48 ÷ 8 = _______
Answer:
48 ÷ 8 = 8.
Explanation:
48 ÷ 8 = 8. (quotient)
Question 9.
72 ÷ 9 = ______
Answer:
72 ÷ 9 = ___8___.
Explanation:
72 ÷ 9 = 8. (quotient)
Question 10.
______ = 8 ÷ 8
Answer:
__1____ = 8 ÷ 8.
Explanation:
8 ÷ 8 = 1. (quotient)
Question 11.
_____ = 54 ÷ 9
Answer:
__6___ = 54 ÷ 9.
Explanation:
54 ÷ 9 = 6. (quotient)
Question 12.
72 ÷ 8 = ______
Answer:
72 ÷ 8 = ___9___.
Explanation:
72 ÷ 8 = 9. (quotient)
Question 13.
90 ÷ 9 = ________
Answer:
90 ÷ 9 = __10______.
Explanation:
90 ÷ 9 = 10. (quotient)
Question 14.
![]()
Answer:
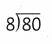 = 10.
= 10.
Explanation:
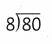 = 10. (quotient)
= 10. (quotient)
Question 15.
![]()
Answer:
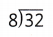 = 4.
= 4.
Explanation:
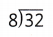 = 4. (quotient)
= 4. (quotient)
Question 16.
![]()
Answer:
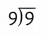 = 1.
= 1.
Explanation:
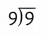 = 1. (quotient)
= 1. (quotient)
Problem Solving
Question 17.
Callie biked 27 miles on Saturday. She biked 9 miles every hour. How many hours did Callie bike? Draw a picture to represent the problem.
Answer:
Total number of hours she biked = 3.
Explanation:
Number of miles Callie biked on Saturday = 27.
Number of miles Callie biked every hour = 9.
Total number of hours she biked = Number of miles Callie biked on Saturday ÷ Number of miles Callie biked every hour
= 27 ÷ 9
= 3.
Question 18.
en Vision® STEM Eight friends decide to test how far 40 paper airplanes with different shapes will fly. If each friend tests the same number of airplanes, how many airplanes does each friend test?
Answer:
Number of airplanes each friend gets to test = 5.
Explanation:
Number of friends of Stem = 8.
Number of paper airplanes with different shapes = 40.
Number of airplanes each friend gets to test = Number of paper airplanes with different shapes ÷ Number of friends of Stem
= 40 ÷ 8
= 5.
Question 19.
Reasoning What other equations are in the same fact family as 18 ÷ 9 = 2?
Answer:
Other equations which are in the same fact family as 18 ÷ 9 = 2:
18 ÷ 2 = 9.
2 × 8 = 18.
9 × 2 = 18.
Explanation:
18 ÷ 9 = 2.
Other equations which are in the same fact family as 18 ÷ 9 = 2:
18 ÷ 2 = 9.
2 × 8 = 18.
9 × 2 = 18.
Question 20.
Higher Order Thinking Jeremy had 30 gummy bears. He ate 6, and then gave the rest to 8 friends. Each friend got the same number of gummy bears. How many did each friend get?
Answer:
Number of gummy bears each friend gets = 3.
Explanation:
Number of gummy bears Jeremy had = 30.
Number of gummy bears Jeremy ate = 6.
Number of friends he gave the rest gummy bears = 8.
Number of gummy bears each friend gets = (Number of gummy bears Jeremy had – Number of gummy bears Jeremy ate) ÷ Number of friends he gave the rest gummy bears
= (30 – 6) ÷ 8
= 24 ÷ 8
= 3.
Question 21.
Mr. Stern spends $36 on tickets. He buys only one type of ticket.

a. Which types of ticket could he buy?
Answer:
Types of tickets he could buy:
Number of child tickets he buys = 9.
Number of adult tickets he buys = 4.
Explanation:
Mr. Stern spends $36 on tickets.
Cost of the child ticket = $4
Amount Mr. Stern spends on child tickets = $36
Number of child tickets he buys = Amount Mr. Stern spends on child tickets ÷ Cost of the child ticket
= $36 ÷ $4
= 9.
Cost of the adult ticket = $9.
Amount Mr. Stern spends on adult tickets = $36
Number of adult tickets he buys = Amount Mr. Stern spends on adult tickets ÷ Cost of the adult ticket
= $36 ÷ $9
= 4.
b. Which type of ticket could Mr. Stern NOT buy? Explain why not.
Answer:
Cost the youth ticket = $8 because the amount cannot be divided exactly by the amount he spent on tickets purchase.
Explanation:
Cost the youth ticket = $8.
This ticket may not be purchased by Mr. Stern because the amount cannot be divided exactly by the amount he spent on tickets purchase.
Assessment Practice
Question 22.
Find 32 ÷ 8 by selecting numbers to complete the following equations. Numbers may be selected more than once.

Answer:
8 × 9 = 32.
32 ÷ 8 = 4.
Explanation:
32 ÷ 8 = 4.
8 × 9 = 32.
Number 4 is selected from the given numbers to complete the following equations.
Question 23.
Find 54 ÷ 9 by selecting numbers to complete the following equations. Numbers may be selected more than once.

Answer:
9 × 6 = 54.
54 ÷ 9 = 6.
Explanation:
54 ÷ 9 = 6.
9 × 6 = 54.
6 number is selected from the given numbers to complete the following equations.
Lesson 4.5 Multiplication Patterns: Even and Odd Numbers
Solve & Share
Prizes for a school fair are packaged with 2 of the same prizes in each package. Which of the prizes listed below can be packaged with none left over? Tell how you decided.
I can … find and explain patterns for even and odd numbers.

You can use reasoning. Think about numbers that can be separated into two equal groups.
Look Back! What do you notice about the numbers for the prizes that can be packaged in 2s with none left over? What do you notice about the numbers for the other prizes?
Answer:
The prizes listed can be packaged with none left over are: car prizes, boats prizes and books prizes.
It is noticed about the numbers for the prizes that can be packaged in 2s with none left over that they are the multiples of 2. It is noticed about the numbers for the other prizes that they are prime numbers and are not multiples of 2.
Explanation:
Number of car prizes = 6.
Number of hats prizes = 15.
Number of balls prizes = 23.
Number of boats prizes = 18.
Number of books prizes = 36.
Number of groups the prizes are packed = 2.
Numbers for the prizes that can be packaged in 2s with none left over:
= Number of car prizes ÷ Number of groups the prizes are packed
= 6 ÷ 2
= 3.
Number of boats prizes ÷ Number of groups the prizes are packed
= 18 ÷ 2
= 9.
Number of books prizes ÷ Number of groups the prizes are packed
= 18 ÷ 2
= 9.
Essential Question
How Can You Explain Multiplication Question Patterns for Even and Odd Numbers?
Answer:
An even number can only be formed by multiplication in three ways:
even × odd, odd × even and even × even.
An odd number can only be formed by multiplication in one way:
odd × odd = odd.
Explanation:
Multiplication Question Patterns for Even and Odd Numbers can be explained as below:
An even number can only be formed by multiplication in three ways:
even × odd, odd × even and even × even.
An odd number can only be formed by multiplication in one way:
odd × odd = odd.
Visual Learning Bridge
Nita says that the product of an even number and an odd number is always even. Is she correct?
Even numbers are whole numbers that can be divided by 2 with none left over.
Odd numbers are whole numbers that cannot be divided by 2 with none left over.

Even numbers greater than 0 can be shown as two equal groups.
Think about 2 × 3 and 2 × 5.
2 is an even number.
2 × 3 means 2 equal groups of 3.
2 × 3 = 6
2 × 5 means 2 equal groups of 5.
2 × 5 = 10
There are always 2 equal groups, so the product of 2 times any number is even.
You can generalize.
All even numbers are multiples of 2.
Think about 4 × 3.
You can think of 4 as 2 groups of 2.
Using properties you can write
4 × 3 = (2 × 2) > 3 as
4 × 3 = 2 × (2 × 3).
So, 4 × 3 = 2 × 6.
There are 2 equal groups of 6. So, the product will be even.
You can write any even number as 2 equal groups. So, Nita is correct: me even X odd = even.
Convince Me! Generalize Does multiplying by 8 also always result in an even product? Explain.
Answer:
Multiplying by 8 also always result in an even product is true because even numbers are whole numbers that can be divided by 2 with none left over. Odd numbers are whole numbers that cannot be divided by 2 with none left over.
Explanation:
Multiplying by 8 also always result in an even product is true because even numbers are whole numbers that can be divided by 2 with none left over. Odd numbers are whole numbers that cannot be divided by 2 with none left over.
2 × 8 = 16.
3 × 8 = 24.
Another Example!
An odd number cannot be divided by 2 with none left over.
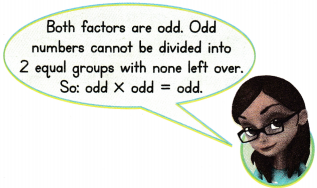
Think about 3 × 5.
3 cannot be divided by 2 with none left over.
5 cannot be divided by 2 with none left over.
3 × 5 = 15
15 is odd.
Guided Practice
Do You Understand?
Question 1.
If you multiply two even numbers, will the product be even or odd? Explain with an example.
Answer:
If you multiply two even numbers, will the product be even not odd.
Explanation:
If you multiply two even numbers, will the product be even not odd.
For example: 2 × 6 = 12.
Do You Know How?
Write or circle to complete the sentences. Then solve.
Question 2.
4 × 6 = ?
Can 4 be divided by 2? _______
Can 6 be divided by 2? _______
So 4 × 6 is even, odd
4 × 6 = _______
Answer:
4 × 6 = 24.
Can 4 be divided by 2? __Yes_____.
Can 6 be divided by 2? ____Yes___.
So 4 × 6 is even.
4 × 6 = _24______.
Explanation:
4 × 6 = 24.
Can 4 be divided by 2? 4 ÷ 2 = 2 yes.
Can 6 be divided by 2? 6 ÷ 2 = 3 yes.
So 4 × 6 is even.
4 × 6 = 24.
Independent Practice
In 3-5, circle the factors that can be divided by 2. Then write even or odd to describe the product and solve the equation.
Question 3.
9 × 5 = ?
9 × 5 is _______
9 × 5 = _______
Answer:
9 × 5 = ?
9 × 5 is __odd_____.
9 × 5 = __45_____.
Explanation:
9 × 5 = ??
9 × 5 is odd.
9 × 5 = 45.
Question 4.
8 × 7 = ?
8 × 7 is ______
8 × 7 = ______
Answer:
8 × 7 = ?
8 × 7 is __even____.
8 × 7 = __56____.
Explanation:
8 × 7 = ?
8 × 7 is even.
8 × 7 = 56.
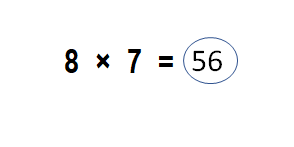
Question 5.
4 × 8 =?
4 × 8 is ______
4 × 8 = ______
Answer:
4 × 8 =?
4 × 8 is _Even_____.
4 × 8 = __32____.
Explanation:
4 × 8 =?
4 × 8 is even.
4 × 8 = 32.
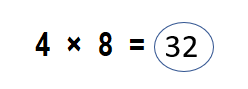
Problem Solving
In 6-8, use the table at the right. Look at the factors. Write even or odd to describe the product. Then solve.
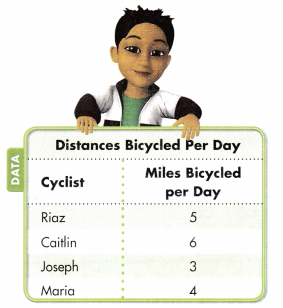
Question 6.
How many miles did Joseph bicycle in 6 days?
The product is ________.
Answer:
Number of miles Joseph bicycled in 6 days = 18.
The product is ___18(Even)_____.
Explanation:
Number of miles Joseph bicycled per day = 3.
Number of miles Joseph bicycled in 6 days = Number of miles Joseph bicycled per day × 6
= 3 × 6
= 18.
Question 7.
How many miles did Caitlin bicycle in 8 days?
The product is ________.
Answer:
Number of miles Caitlin bicycled in 8 days = 48.
The product is ___48 (Even)_____.
Explanation:
Number of miles Caitlin bicycled per day = 6.
Number of miles Caitlin bicycled in 8 days = Number of miles Caitlin bicycled per day × 8
= 6 × 8
= 48.
Question 8.
How many miles did Maria and Riaz bicycle in 3 days?
The total is _________
Answer:
Total number of miles Maria and Riaz bicycled in 3 days = 27.
The total is ___27 (Odd)______.
Explanation:
Number of miles Maria bicycled per day = 4.
Number of miles Maria bicycled in 3 days = Number of miles Maria bicycled per day × 3
= 4 × 3
= 12.
Number of miles Riaz bicycled per day = 5.
Number of miles Riaz bicycled in 3 days = Number of miles Riaz bicycled per day × 3
= 5 × 3
= 15.
Total number of miles Maria and Riaz bicycled in 3 days = Number of miles Maria bicycled in 3 days + Number of miles Riaz bicycled in 3 days
= 12 + 15
= 27.
Question 9.
Critique Reasoning Ryan says that the following patterns are true:
even × odd = even
odd × even = odd
Is he correct? Explain.
Answer:
(even × odd = even) pattern Ryan’s says is correct yet not odd × even = odd pattern.
Explanation:
even × odd = even.
=> 2 × 5 = 10.
odd × even = odd
=> 5 × 4 = 20.
Question 10.
Draw a shape with an odd number of sides. Then write the name of the shape.
Answer:

Explanation:
Number of sides in the shape = 5.
Name of the shape = Pentagon.

Question 11.
Higher Order Thinking The bakery had 84 muffins. Ms. Craig bought 5 packs of 6 muffins. Did she purchase an even or an odd number of muffins? Is the number of muffins left even or odd? Explain.
Answer:
Total number of muffins Ms. Craig bought = 30. (Even)
Number of muffins left = 54. (Even)
Explanation:
Number of muffins bakery had = 84.
Number of muffins Ms. Craig bought = 6.
Number of packs Ms. Craig bought = 5.
Total number of muffins Ms. Craig bought = Number of muffins Ms. Craig bought × Number of packs Ms. Craig bought
= 6 × 5
= 30. (Even)
Number of muffins left = Number of muffins bakery had – Total number of muffins Ms. Craig bought
= 84 – 30
= 54. (Even)
Assessment Practice
Question 12.
Select all of the equations where you can use properties of operations to show that the product will be even.
☐ 7 × 9 = ?
☐ 9 × 2 = ?
☐ 5 × 3 = ?
☐ 1 × 6 = ?
☐ 7 × 5 = ?
Answer:
9 × 2 = 18. => odd × even = even.
1 × 6 = 6. => odd × even = even.
Explanation:
☐ 7 × 9 = 63.
=> odd × odd = odd.
☐ 9 × 2 = 18.
=> odd × even = even.
☐ 5 × 3 = 15.
=> odd × odd = odd.
☐ 1 × 6 = 6.
=> odd × even = even.
☐ 7 × 5 = 35.
=> odd × odd = odd.
Question 13.
Select all of the equations that do NOT have even products.
☐ 5 × 1 = ?
☐ 2 × 7 = ?
☐ 3 × 9 = ?
☐ 8 × 8 = ?
☐ 6 × 4 = ?
Answer:
5 × 1 = 5. => odd × odd = odd.
3 × 9 = 27. => odd × odd = odd.
Explanation:
☐ 5 × 1 = 5.
=> odd × odd = odd.
☐ 2 × 7 = 14.
=> even × odd = even.
☐ 3 × 9 = 27.
=> odd × odd = odd.
☐ 8 × 8 = 64.
=> even × even = even.
☐ 6 × 4 = 24.
=> even × even = even.
Lesson 4.6 Division Involving 0 and 1
Solve & Share
Find 5 ÷ 1,0 ÷ 5, and 5 ÷ 5. Explain how you found each quotient. You can use counters to help.
I can … understand the patterns of division with 0 and 1.

Look Back! Use your understanding of multiplying by 0 to find 0 ÷ 7,0 ÷ 4, and 0 ÷ 10. Describe the patterns you see.
Answer:
0 ÷ 4 = 0.
0 ÷ 7 = 0.
0 ÷ 10 = 0.
It is observed that any number multiplied to zero or zero divided by any number the product of it is same that is zero.
Explanation:
0 × 4 = 0.
0 ÷ 4 = 0.
0 × 7 = 0.
0 ÷ 7 = 0.
0 × 10 = 0.
0 ÷ 10 = 0.
Essential Question
How Do You Divide with 1 or 0?
Answer:
Any number divided by the given number to be divided.
2 ÷ 1 = 2.
2 ÷ 0 = 0.
Explanation:
We divided the number with one or 0 by the following:
2 ÷ 1 = 2.
2 ÷ 0 = 0.
Visual Learning Bridge
Neil has 3 goldfish. He puts 1 goldfish in each bowl. How many bowls did Neil use? Find 3 ÷ 1.

What number times 1 is 3?
3 × 1 = 3
So, 3 ÷ 1 = 3.
Neil used 3 bowls.
1 as a Quotient
Find 3 ÷ 3.
3 times what number equals 3?
3 × 1 = 3
S0, 3 ÷ 3 = 1.
Rule: Any number (except 0) divided by itself is 1.
Dividing O by a Number
Find 0 ÷ 3.
3 times what number equals 0?
3 × 0 = 0
So, 0 ÷ 3 = 0.
Rule: 0 divided by any number (except 0) is 0.
Dividing by 0
Find 3 ÷ 0.
0 times what number equals 3?
There is no such number. So, 3 ÷ 0 can’t be done.
Rule: You cannot divide any number by 0.
Convince Me! Be Precise Sue wrote 9 invitations. She put 1 invitation in each mailbox on her street. How many mailboxes got invitations? Which equation shows the problem and the solution? Explain your thinking.
0 ÷ 9 = 0
9 ÷ 1 = 9
Answer:
Number of mailboxes got invitations = Number of invitations Sue wrote ÷ Number of invitation she puts in each mailbox on her street
= 9 ÷ 1
= 9.
Explanation:
Number of invitations Sue wrote = 9.
Number of invitation she puts in each mailbox on her street = 1.
Number of mailboxes got invitations = Number of invitations Sue wrote ÷ Number of invitation she puts in each mailbox on her street
= 9 ÷ 1
= 9.
Guided Practice
Do You Understand?
Question 1.
How can you tell, without dividing, that 375 ÷ 375 = 1?
Answer:
Any number divided by itself, the product is always 1.
375 ÷ 375 = 1
Explanation:
We can tell without dividing, that 375 ÷ 375 = 1 because any number divided by itself, the product is always 1.
Question 2.
Use a representation to explain why zero divided by any number except zero is zero.
Answer:
In mathematics, division by zero is division where the divisor (denominator) is zero. Such a division can be formally expressed as where a is the dividend. Any number dividend by zero is zero yet not by itself divided.
Explanation:
In mathematics, division by zero is division where the divisor (denominator) is zero. Such a division can be formally expressed as where a is the dividend.
Any number multiplied by zero is zero, the expression is also undefined.
Do You Know How?
In 3 and 4, solve the multiplication equation to find each quotient.

Question 3.
Find 8 ÷ 8.
8 × _____ = 8
So, 8 ÷ 8 = _______
Answer:
8 × __1___ = 8
So, 8 ÷ 8 = ___1____. (quotient)
Explanation:
8 × 1 = 8
So, 8 ÷ 8 = 1.
Question 4.
Find 0 ÷ 9.
9 × ______ = 0
So, 0 ÷ 9 = ______
Answer:
9 × __0____ = 0
So, 0 ÷ 9 = __0____. (quotient)
Explanation:
9 × 0 = 0
So, 0 ÷ 9 = 0.
Independent Practice
Leveled Practice In 5-7, solve the multiplication equation to find each quotient.
Question 5.
Find 0 ÷ 7.
7 × _______ = 0
So, 0 ÷ 7 = _______
Answer:
7 × ___0____ = 0.
So, 0 ÷ 7 = ___0____. (quotient)
Explanation:
7 × 0 = 0
So, 0 ÷ 7 = 0.
Question 6.
Find 4 ÷ 4.
4 × _______ = 4
So, 4 ÷ 4 = ________
Answer:
4 × ___1____ = 4
So, 4 ÷ 4 = ___1_____. (quotient)
Explanation:
4 × 1 = 4
So, 4 ÷ 4 = 1.
Question 7.
Find 6 ÷ 1.
1 × _______ = 6
So, 6 ÷ 1 = _______
Answer:
1 × ___6____ = 6
So, 6 ÷ 1 = ___6____. (quotient)
Explanation:
1 × 6 = 6
So, 6 ÷ 1 = 6.
In 8-18, find each quotient.
Question 8.
3 ÷ 3 = __________
Answer:
3 ÷ 3 = ____1______.(quotient)
Explanation:
3 ÷ 3 = 1.
Question 9.
______ = 0 ÷ 8
Answer:
___0___ = 0 ÷ 8. (quotient)
Explanation:
0 = 0 ÷ 8.
Question 10.
______ = 5 ÷ 5
Answer:
___1___ = 5 ÷ 5. (quotient)
Explanation:
1 = 5 ÷ 5.
Question 11.
7 ÷ 1 = _______
Answer:
7 ÷ 1 = __7_____. (quotient)
Explanation:
7 ÷ 1 = 7.
Question 12.
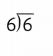
Answer:
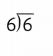 = 1. (quotient)
= 1. (quotient)
Explanation:
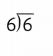 = 1.
= 1.
Question 13.
![]()
Answer:
![]() = 5. (quotient)
= 5. (quotient)
Explanation:
![]() = 5.
= 5.
Question 14.
![]()
Answer:
![]() = 1. (quotient)
= 1. (quotient)
Explanation:
![]() = 1.
= 1.
Question 15.
![]()
Answer:
![]() = 13. (quotient)
= 13. (quotient)
Explanation:
![]() = 13.
= 13.
Question 16.
Find 0 divided by 8.
Answer:
0 ÷ 8 = 0.
Explanation:
0 divided by 8.
=> 0 ÷ 8 = 0.
Question 17.
Find 9 divided by 1.
Answer:
9 ÷ 1 = 9.
Explanation:
9 divided by 1.
9 ÷ 1 = 9.
Question 18.
Find 10 divided by 10.
Answer:
10 ÷ 10 = 1.
Explanation:
10 divided by 10.
=> 10 ÷ 10 = 1.
Problem Solving
In 19-22, use the picture at the right.

Question 19.
Addie hiked 3 different trails for a total distance of 11 miles. Which trails did Addie hike?
Answer:
Trails Addie hiked = Number of miles of White hike + Number of miles of Red hike + Number of miles of Green hike
= 5 + 2 + 4
= 11.
Explanation:
Number of miles of Blue hike = 3.
Number of miles of White hike = 5.
Number of miles of Red hike = 2.
Number of miles of Green hike = 4.
Number of different trails Addie hiked = 3.
Number of total miles distance Addie hiked = 11.
Trails Addie hiked = Number of miles of White hike + Number of miles of Red hike + Number of miles of Green hike
= 5 + 2 + 4
= 7 + 4
= 11.
Question 20.
Marty hikes one of the trails 4 times. In all, he hikes more than 10 miles but less than 16 miles. Which trail does Marty hike? Explain your answer.
Answer:
Blue Trail Marty hiked 4times hiking of 12 miles.
Explanation:
Number of different trails Marty hiked = 1.
Number of times Marty hiked same trail = 4.
Number of miles of Blue hike = 3.
Trail Marty hiked = Number of miles of Blue hike × 4
= 3 × 4
= 12 > 10 < 16.
Question 21.
Four teams are tidying the Green trail. They will each tidy an equal distance. How many miles does each team tidy?
Answer:
Miles each team tidy = 1.
Explanation:
Number of miles of Green hike = 4.
Number of teams hiking the green trial = 4.
Miles each team tidy = Number of miles of Green hike ÷ Number of teams hiking the green trial
= 4 ÷ 4
= 1.
Question 22.
Fiona hiked on Wednesday and Sunday. Each day she hiked all of the trails. How many miles did Fiona hike?
Answer:
Total number of Miles Fiona hiked = 28.
Explanation:
Number of miles of Blue hike = 3.
Number of miles of White hike = 5.
Number of miles of Red hike = 2.
Number of miles of Green hike = 4.
Fiona hiked on Wednesday and Sunday.
=> Number of days Fiona hiked = 2.
Total number of Miles Fiona hiked = Number of miles of Blue hike + Number of miles of White hike + Number of miles of Red hike + Number of miles of Green hike × Number of days Fiona hiked
= (3 + 5 + 2 + 4) × 2
= ( 8 + 2 + 4)
= ( 10 + 4)
= 14 × 2
= 28.
Question 23.
Model with Math Use a representation to explain why any number divided by 1 is itself.
Answer:
Same number divided by itself, always gives the product of 1.
Explanation:
1 ÷ 1 = 1 because same number divided by itself, always gives the product of 1.
2 ÷ 2 = 1.
Question 24.
Higher Order Thinking Yvonne says that 0 ÷ 21 and 21 ÷ 0 both have a quotient of 0. Is Yvonne correct? Explain.
Answer:
Yes, Yvonne is correct 0 ÷ 21 and 21 ÷ 0 both have a quotient of 0 because any number divided by zero or zero divided by any number the quotient is always zero.
Explanation:
0 ÷ 21 = 0.
21 ÷ 0 = 0.
Assessment Practice
Question 25.
Use division properties to match each equation to its quotient.
Answer:
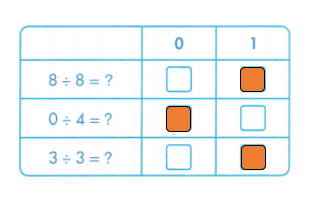
Explanation:
8 ÷ 8 = 1. Any number divided by itself, quotient is always 1.
0 ÷ 4 = 0. Zero divided by any number, quotient is always 0.
3 ÷ 3 = 1. Any number divided by itself, quotient is always 1.
Question 26.
Use division properties to match each equation to its quotient.
Answer:
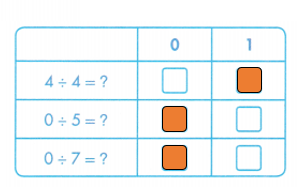
Explanation:
4 ÷ 4 = 1. Any number divided by itself, quotient is always 1.
0 ÷ 5 = 0. Zero divided by any number, quotient is always 0.
0 ÷ 7 = 0. Zero divided by any number, quotient is always 0.
Lesson 4.7 Practice Multiplication and Division Facts
Solve & Share
A tour bus to a national park holds 56 people. There are 7 tour guides at the park to lead equal groups of people from the bus. How many people are in each tour group? Each person in a group pays a $2 entrance fee to a tour guide. How much does 1 tour guide collect?
I can .. use patterns and related facts to solve multiplication and division problems.

Look Back! How can 7 × ? = 56 help you find 56 ÷ 7 = ?
Answer:
Number of people in each tour group = 8.
Amount of each tour guide collects = $16.
Explanation:
Number of people A tour bus to a national park holds = 56.
Number of tour guides at the park to lead equal groups of people from the bus = 7.
Number of people in each tour group = Number of people A tour bus to a national park holds ÷ Number of tour guides at the park to lead equal groups of people from the bus
= 56 ÷ 7
= 8.
Amount of entrance fee each person in a group to pay tour guide = $2.
Amount of each tour guide collects = Number of people in each tour group × Amount of entrance fee each person in a group to pay tour guide
= 8 × $2
= $16.
Essential Question
What Fact Can You Use?
Answer:
To solve the problem we can use multiplication facts or division facts according to the requirment of the question asked.
Explanation:
We can use multiplication facts 1s, 2s, 3s, 4s, 5s…… and division facts to solve the problems to find the asked solution.
Visual Learning Bridge
Sabrina has 28 quarters in her bank. She wants to trade all of them for one-dollar bills. How many one-dollar bills will Sabrina get?
There are 4 quarters in one dollar.
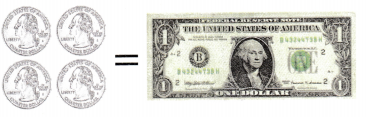
One Way
How many groups of 4 are in 28?
You can draw a bar diagram to help solve the problem

28 ÷ 4 = 7
There are 7 groups of 4 in 28. Sabrina can trade 28 quarters for 7 one-dollar bills.
Another Way
What number times 4 equals 28?
You can use multiplication facts to help solve the problem.
28 quarters
? × 4 = 28
7 × 4= 28
Sabrina can trade 28 quarters for 7 one-dollar bills.
Convince Me! Construct Arguments Why can both 28 ÷ 7 = ? and ? × 7 = 28 be used to solve the problem above?
Answer:
Number of one-dollar bills Sabrina gets = 7.
4 × 7 = 28.
28 ÷ 7 = 4.
We can use both 28 ÷ 7 = ? and ? × 7 = 28 to solve the problem above explained as below:
Number of quarters in one dollar × Number of one-dollar bills Sabrina gets = Number of quarters Sabrina has in her bank.
=> 4 × 7 = 28.
Number of quarters Sabrina has in her bank ÷ Number of one-dollar bills Sabrina gets = Number of quarters in one dollar.
28 ÷ 7 = 4.
Explanation:
There are 4 quarters in one dollar.
Number of quarters Sabrina has in her bank = 28.
Number of quarters in one dollar = 4.
Number of one-dollar bills Sabrina gets = Number of quarters Sabrina has in her bank ÷ Number of quarters in one dollar
= 28 ÷ 4
= 7.
We can use both 28 ÷ 7 = ? and ? × 7 = 28 to solve the problem above explained as below:
Number of quarters in one dollar × Number of one-dollar bills Sabrina gets = Number of quarters Sabrina has in her bank.
=> 4 × 7 = 28.
Number of quarters Sabrina has in her bank ÷ Number of one-dollar bills Sabrina gets = Number of quarters in one dollar.
=> 28 ÷ 7 = 4.
Guided Practice
Do You Understand?
Question 1.
Look back at the problem on the previous page. Suppose Sabrina put 8 more quarters in her bank. How many one-dollar bills can she trade for the quarters in her bank now?
Answer:
Number of one-dollar bills Sabrina gets = 10.
Explanation:
There are 4 quarters in one dollar.
Number of quarters Sabrina has in her bank = 28 + 12 = 40.
Number of quarters in one dollar = 4.
Number of one-dollar bills Sabrina gets = Number of quarters Sabrina has in her bank ÷ Number of quarters in one dollar
= 40 ÷ 4
= 10.
Question 2.
Calvin solves the equation 49 ÷ 7 = ☐. How does this help him complete the equation 7 × ☐ = 49?
Answer:
Yes, this helps Calvin to complete the equation 7 × ☐ = 49.
Explanation:
Equation:
49 ÷ 7 = ☐.
49 ÷ 7 = 7.
=> 7 × 7= 49.
Do You Know How?
In 3-7, use a multiplication or a division fact to complete the equations.
You can use multiplication to help divide.
Question 3.
______ = 45 ÷ 5
45 = 5 × ______
Answer:
___9___ = 45 ÷ 5.
45 = 5 × ___9___.
Explanation:
9 = 45 ÷ 5
45 = 5 × 9.
Question 4.
_____ × 7 = 21
21 ÷ ______ = 7
Answer:
__3___ × 7 = 21.
21 ÷ __3____ = 7.
Explanation:
3 × 7 = 21.
21 ÷ 3 = 7.
Question 5.
6 × _____ = 30
30 ÷ 6 = ______
Answer:
6 × __5___ = 30.
30 ÷ 6 = ___5___.
Explanation:
6 × 5 = 30.
30 ÷ 6 = 5.
Question 6.
4 = 24 ÷ _______
24 = ______ × 4
Answer:
4 = 24 ÷ ___6____.
24 = __6____ × 4.
Explanation:
4 = 24 ÷ 6.
24 = 6 × 4.
Question 7.
6 × _____ = 12
12 ÷ 6 = _______
Answer:
6 × __2___ = 12.
12 ÷ 6 = __2_____.
Explanation:
6 × 2 = 12.
12 ÷ 6 = 2.
Independent Practice
Leveled Practice In 8-10, use fact families to complete the equations.
Question 8.
42 ÷ 7 = ______
7 × _____ = 42
Answer:
42 ÷ 7 = ___6___.
7 × __6___ = 42.
Explanation:
42 ÷ 7 = 6.
7 × 6 = 42.
Question 9.
18 = 6 × ______
_____ = 18 ÷ 6
Answer:
18 = 6 × ___3___.
__3___ = 18 ÷ 6.
Explanation:
18 = 6 × 3.
3 = 18 ÷ 6.
Question 10.
9 = _____ ÷ 8
9 × 8 = ______
Answer:
9 = __2___ ÷ 8.
9 × 8 = ___2___.
Explanation:
9 = 2 ÷ 8.
9 × 8 = 2.
In 11-19, find the product or quotient.
Question 11.
36 ÷ 4 = ______
Answer:
36 ÷ 4 = __9____.
Explanation:
36 ÷ 4 = 9. (quotient)
Question 12.
_____ = 8 × 8
Answer:
__1___ = 8 × 8.
Explanation:
1= 8 × 8. (quotient)
Question 13.
15 ÷ 3 = ________
Answer:
15 ÷ 3 = ___5_____.
Explanation:
15 ÷ 3 = 5. (quotient)
Question 14.
![]()
Answer:
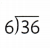 = 6.
= 6.
Explanation:
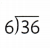 = 6. (quotient)
= 6. (quotient)
Question 15.
![]()
Answer:
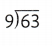 = 7.
= 7.
Explanation:
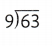 = 7. (quotient)
= 7. (quotient)
Question 16.
![]()
Answer:
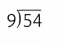 = 6.
= 6.
Explanation:
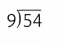 = 6. (quotient)
= 6. (quotient)
Question 17.
Multiply 8 times 5.
Answer:
8 × 5 = 40.
Explanation:
Multiply 8 times 5.
8 × 5 = 40. (product)
Question 18.
Divide 18 by 9.
Answer:
18 ÷ 9 = 2.
Explanation:
18 ÷ 9 = 2. (product)
Question 19.
Divide 27 by 3.
Answer:
27 ÷ 3 = 9.
Explanation:
Divide 27 by 3.
27 ÷ 3 = 9.(product)
Problem Solving
In 20-22, use the recipe at the right.

Question 20.
How many cups of peanuts would Eric need to make 5 batches of trail mix? Write an equation to show your thinking.
Answer:
Number of cups of peanuts would Eric need to make of 5 batches trail mix = 5 × 4 = 20.
Explanation:
Number of cups of peanuts would Eric need to make of trail mix = 4.
Number of batches to make trail mix = 5.
Number of cups of peanuts would Eric need to make of 5 batches trail mix = Number of cups of peanuts would Eric need to make of trail mix × Number of batches to make trail mix
= 5 × 4
= 20.
Question 21.
How many batches of trail mix can Eric make with 16 cups of peanuts, 15 cups of raisins, and 8 cups of walnuts?
Answer:
Number of batches of trail mix can Eric make with 16 cups of peanuts = 16 ÷ 4 = 4.
Number of batches of trail mix can Eric make with 8 cups of walnuts = 8 ÷ 2 = 4.
Number of batches of trail mix can Eric make with 15 cups of raisins = 15 ÷ 3 = 5.
Explanation:
Number of cups of peanuts would Eric need to make of trail mix = 4.
Number of cups of peanuts Eric want the trail mix = 16
Number of batches of trail mix can Eric make with 16 cups of peanuts = Number of cups of peanuts Eric want the trail mix ÷ Number of cups of peanuts would Eric need to make of trail mix
= 16 ÷ 4
= 4.
Number of cups of raisins would Eric need to make of trail mix = 3.
Number of cups of raisins Eric want the trail mix = 15.
Number of batches of trail mix can Eric make with 15 cups of raisins = Number of cups of raisins Eric want the trail mix ÷ Number of cups of raisins would Eric need to make of trail mix
= 15 ÷ 3
= 5.
Number of cups of walnuts would Eric need to make of trail mix = 2.
Number of cups of walnuts Eric want the trail mix = 8.
Number of batches of trail mix can Eric make with 8 cups of walnuts = Number of cups of walnuts Eric want the trail mix ÷ Number of cups of walnuts would Eric need to make of trail mix
= 8 ÷ 2
= 4.
Question 22.
Reasoning Eric spends $30 to buy the ingredients for 5 batches of trail mix. Find the cost of the ingredients Eric needs for one batch. How much would Eric need for 2 batches?
Answer:
Cost of the ingredients Eric needs for one batch = $6.
Amount of money Eric need for buying 2 batches = $12.
Explanation:
Amount of money Eric spends to buy the ingredients for 5 batches of trail mix = $30.
Number of batches of trail mix Eric buys = 5.
Cost of the ingredients Eric needs for one batch = Amount of money Eric spends to buy the ingredients for 5 batches of trail mix ÷ Number of batches of trail mix Eric buys
= $30 ÷ 5
= $6.
Amount of money Eric need for buying 2 batches = Cost of the ingredients Eric needs for one batch × 2
= $6 × 2
= $12.
Question 23.
Emilia drew lines to divide these squares into parts. What is one way to name these parts?
Answer:
One way to name these parts:
Square.
Triangle.
Explanation:
one way to name these parts:
Square.
Triangle.
Question 24.
Higher Order Thinking Wilson is thinking of 2 one-digit numbers. When he multiplies them, the product is 27. What is the sum of the two numbers? Explain your answer.
Answer:
2 one-digit numbers: 3 and 9.
Product: 3 × 9 = 27. or 9 × 3 = 27.
Sum: 3 + 9 = 12. or 9 + 3 = 12.
Explanation:
2 one-digit numbers: 3 and 9.
Product: 3 × 9 = 27.
or 9 × 3 = 27.
Sum: 3 + 9 = 12.
or 9 + 3 = 12.
Assessment Practice
Question 25.
Use the relationship between multiplication and division to find the value of each unknown.
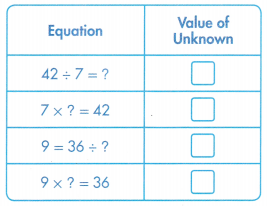
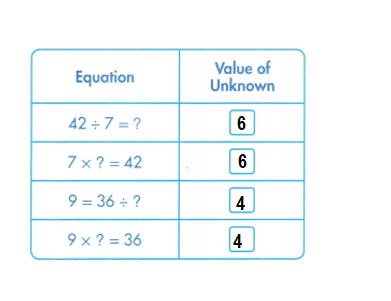
Answer:
Explanation:
42 ÷ 7 = ? => 42 ÷ 7 = 6.
7 × ? = 42. => 7 × 6 = 42.
36 ÷ 4 = ? => 36 ÷ 4 = 9.
9 × 4 = 36. => 9 × 4 = 36.
Question 26.
Use properties of operations to find the value of each unknown.
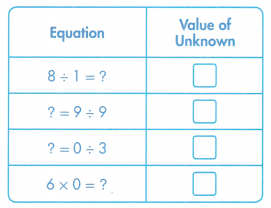
Answer:
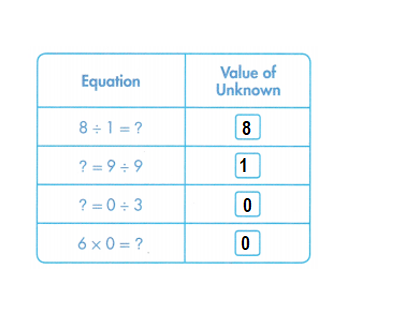
Explanation:
8 ÷ 1 = ? => 8 ÷ 1 = 8.
? = 9 ÷ 9. =>1 = 9 ÷ 9.
? = 0 ÷ 3. => 0 = 0 ÷ 3.
6 × 0 = ? => 6 × 0 = 0.
Lesson 4.8 Solve Multiplication and Division Equations
Solve & Share
The expression 24 ÷ 4 is on the right side of the balance below. What can you write on the left side that will have the same value as the right side? Write 5 different multiplication or division problems that will keep the pans balanced.
I can… use multiplication and division facts to find unknown values in an equation.

Look Back! Would the problem 1 × 3 × 2 × 1 keep the pans above balanced? Explain.
Answer:
Yes, the problem 1 × 3 × 2 × 1 keep the pans above balanced because 24 ÷ 4 = 6.
(1 × 3) × (2 × 1) = 3 × (2 × 1) = 3 × 2 = 6.
Explanation:
Problem 1 × 3 × 2 × 1 keep the pans above balanced.
24 ÷ 4 = 6.
(1 × 3) × (2 × 1) = 3 × (2 × 1) = 3 × 2 = 6.
Essential Question
How Do Multiplication and Division Equations Work?
Answer:
Multiplication works by multiplying the numbers to find the answers and Division works by dividing the numbers to find the answers.
Explanation:
Multiplication is the process of multiplying the numbers and Division means the process of divinding the numbers to find the answers.
Visual Learning Bridge
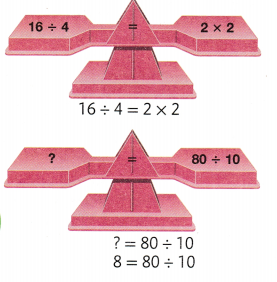
The pan balance shows 35 ÷ 7 = 5.

Remember, in an equation, the symbol = means “is equal to.” It tells you the value on the left is the same as the value on the right.
These are other examples of equations.
Frank has some tubes of tennis balls. Each tube has 4 tennis balls. Frank has 8 tennis balls in all. How many tubes of tennis balls does he have?
You can write an equation to represent the problem.
8 = ? × 4
Some equations have symbols to represent unknowns. The ? represents the number of tubes of tennis balls Frank has.
8 = ? × 4
A multiplication fact that matches this is 8 = 2 × 4.

The value of ? is 2. So, ? = 2.
Convince Me! Reasoning Use the value of ? in the multiplication equation to write and solve two division equations.
7 × ? = 42
42 ÷ ? = ☐
42 ÷ ☐ = ?
Answer:
7 × ? = 42 => 7 × 6 = 42.
42 ÷ ? = ☐ => 42 ÷ 6 = 7.
42 ÷ ☐ = ? => 42 ÷ 7 = 6.
Explanation:
7 × 6 = 42.
42 ÷ 6 = 7.
42 ÷ 7 = 6.
Guided Practice
Do You Understand?
Question 1.
Write an equation that represents the following problem: Walt makes some sandwiches. Each sandwich uses 2 slices of bread. He uses 16 slices of bread. How many sandwiches does Walt make? Use ? to represent the number of sandwiches.
Answer:
Number of sandwiches Walt makes = 8.
Explanation:
Number of slices of bread each sandwich uses = 2.
Number of slices of bread Walt uses = 16.
Number of sandwiches Walt makes = ??
=> Number of slices of bread Walt uses ÷ Number of slices of bread each sandwich uses
=> 16 ÷ 2
=> 8.
Do You Know How?
In 2-5, find the value for ? that makes the equation true.
Question 2.
9 × ? = 27
Answer:
9 × 3 = 27.
Explanation:
9 × ? = 27.
9 × 3 = 27.
Question 3.
8 = 40 ÷ ?
Answer:
8 = 40 ÷ 5.
Explanation:
8 = 40 ÷ ?
8 = 40 ÷ 5.
Question 4.
32 = ? × 8
Answer:
32 = 4 × 8.
Explanation:
32 = ? × 8.
32 = 4 × 8.
Question 5.
? ÷ 3 = 6
Answer:
18 ÷ 3 = 6.
Explanation:
? ÷ 3 = 6.
18 ÷ 3 = 6.
Independent Practice
In 6-9, find the value for ? that makes the equation true.
Question 6.
? ÷ 4 = 7
Answer:
28 ÷ 4 = 7.
Explanation:
? ÷ 4 = 7.
28 ÷ 4 = 7.
Question 7.
25 = 5 × ?
Answer:
25 = 5 × 5.
Explanation:
25 = 5 × ?
25 = 5 × 5.
Question 8.
72 = ? × 9
Answer:
72 = 8 × 9.
Explanation:
72 = ? × 9.
72 = 8 × 9.
Question 9.
4 = 20 ÷ ?
Answer:
4 = 20 ÷ 5.
Explanation:
4 = 20 ÷ ?.
4 = 20 ÷ 5.
In 10-13, write and solve an equation that represents the problem.
Question 10.
Sasha has 21 dimes. She puts them in stacks with the same number of dimes in each stack. In all, she has 3 stacks. How many dimes are in each stack? Use? to represent the number of dimes in each stack.
Answer:
Number of dimes in each stack = 7.
Explanation:
Number of dimes Sasha has = 21.
She puts them in stacks with the same number of dimes in each stack.
Number of stacks Sasha has = 3.
Number of dimes in each stack = Number of dimes Sasha has ÷ Number of stacks Sasha has
= 21 ÷ 3
= 7.
Question 11.
There were some sheep in a barnyard. Each sheep had 4 legs. There were 24 legs in the barnyard. How many sheep were in the barnyard? Use ? to represent the number of sheep in the barnyard.
Answer:
Number of sheep in the barnyard = 6.
Explanation:
Number of legs each sheep has = 4.
Total number of legs in the barnyard = 24.
Number of sheep in the barnyard = ??
=> Total number of legs in the barnyard ÷ Number of legs each sheep has
=> 24 ÷ 4
=> 6.
Question 12.
A football team scored 48 points. The team only scored on touchdowns, worth 6 points each. How many touchdowns did the team score? Use ? to represent the number of touchdowns.
Answer:
Number of touchdowns the team scored = 8.
Explanation:
Number of points football team scored = 48.
Number of points team scored on touchdowns each = 6.
Number of touchdowns the team scored = ??
=> Number of points football team scored ÷ Number of points team scored on touchdowns each
=> 48 ÷ 6
=> 8.
Question 13.
There were 6 ladybugs on a leaf. Each ladybug had the same number of spots. There were 36 spots. How many spots were on each ladybug? Use ? to represent the number of spots on each ladybug.
Answer:
Number of spots on each ladybug = 6.
Explanation:
Number of ladybugs on a leaf = 6.
Each ladybug had the same number of spots.
Total number of spots = 36.
Number of spots on each ladybug =??
=> Total number of spots ÷ Number of ladybugs on a leaf
=> 36 ÷ 6
=> 6.
Problem Solving
Question 14.
A baker is decorating 5 cakes. He uses 9 chocolate flowers to decorate each cake. How many flowers will he need to decorate all the cakes? Write an equation to represent the problem, using ? to represent the missing information. Then solve your equation.
Answer:
Number of flowers he needs to decorate all the cakes = 45.
Explanation:
Number of cakes baker decorating = 5.
Number of chocolate flowers he uses to decorate each cake = 9.
Number of flowers he needs to decorate all the cakes = ??
=> Number of cakes baker decorating × Number of chocolate flowers he uses to decorate each cake
=> 5 × 9
=> 45.
Question 15.
Be Precise Hal asked 20 people to name their favorite sport. The tally chart shows how many people answered baseball and swimming. All the other people he asked said their favorite sport was football. Complete the tally chart to show how many people chose football.

Answer:
Number of people choose Football as their favorite sport = 8.
Explanation:
Total number of people Hal asked to name their favorite sport = 20.
Number of people choose Baseball as their favorite sport = 3.
Number of people choose Swimming as their favorite sport = 5 + 4 = 9.
Number of people choose Football as their favorite sport = ??
=> Total number of people Hal asked to name their favorite sport – ( Number of people choose Baseball as their favorite sport + Number of people choose Swimming as their favorite sport )
=> 20 – ( 3 + 9 )
=> 20 – 12
=> 8.

Question 16.
Higher Order Thinking A building has more than 2 stories but fewer than 10 stories. Each story of the building has the same number of windows. The building has 25 windows. Complete the sentence. Then explain how you found your answer.
The building has each story has ________stories, and each story has ______ windows.
Answer:
The building has each story has ___25_____stories, and each story has ___25___ windows.
Explanation:
A building has more than 2 stories but fewer than 10 stories.
Number of windows building has = 25.
Each story of the building has the same number of windows.
=> Number of stories each building has = 25.
Question 17.
Rosi and Karen are trying to solve 4= ? ÷ 8. Rosi says the value of the unknown is 32. Karen says the value of the unknown is 2. Is Rosi or Karen correct? Explain.
Answer:
Rosi is correct because 32 ÷ 8 = 4 not 2 ÷ 8 = 4.
Explanation:
Equation:
4 = ? ÷ 8.
=> 4 = 32 ÷ 8.
Assessment Practice
Question 18.
What is the value of the unknown in the equation 30 ÷ ? = 6?
A. 4
B. 5
C. 6
D. 7
Answer:
30 ÷ 5 = 6.
C. 6
Explanation:
Equation :
30 ÷ ? = 6
=> 30 ÷ 5 = 6.
Question 19.
What is the value of the unknown in the equation 8 × ? = 64?
A. 5
B. 6
C. 7
D. 8
Answer:
8 × 8 = 64.
D. 8
Explanation:
Equation:
8 × ? = 64
8 × 8 = 64.
Lesson 4.9 Problem Solving
Make Sense and Persevere
Solve & Share
Natalie prepared a crate of oranges for shipment. She packed the oranges in 2 layers. In each layer, she packed 6 rows with 7 oranges in each row. How many oranges did Natalie pack? Use equations to represent your work.
I can… make sense of problems and keep working if I get stuck.
Thinking Habits
Be a good thinker! These questions can help you.
- What do I need to find?
- What do I know?
- What’s my plan for solving the problem?
- What else can I try if get stuck?
- How can I check that my solution makes sense?

Look Back! Make Sense and Persevere How did you find how many oranges Natalie packed in each layer? How did this plan help you solve the problem?
Answer:
Total number of oranges Natalie packed = 84. This plan helped to solve the problem by step by step process and its easy to understand.
Explanation:
Natalie prepared a crate of oranges for shipment. She packed the oranges in 2 layers. In each layer, she packed 6 rows with 7 oranges in each row. How many oranges did Natalie pack?
Number of layers of oranges she packed = 2.
Number of rows of oranges she packed = 6.
Number of oranges in each row she kept = 7.
Total number of oranges Natalie packed = ??
=> Number of layers of oranges she packed ( Number of rows of oranges she packed × Number of oranges in each row she kept )
=> 2 ( 6 × 7)
=> 2 × 42
=> 84.
Essential Question
How Can You Make Sense of a Problem and Persevere in Solving It?
Answer:
According to the Common Core State Standards, mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. You should understand the problem step by step then should try to find out the solve the problem.
Explanation:
According to the Common Core State Standards, mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals.
Visual Learning Bridge
A store has boxes of video games for sale. In each box, the video games are in 2 rows with 3 video games in each row. Each video game costs the same amount. What is the cost of each video game?
To persevere you can check your strategy and your work.

What do I need to do?
I need to make sense of the problem before I can solve it. If I get stuck, I need to persevere until I find the cost of each video game.
How can I make sense of and solve this problem?
I can
- identify what is known from the problem.
- look for and answer hidden questions in the problem.
- make a plan to solve the problem.
- check to make sure my work and answer make sense.
Here’s my thinking…
I know a box costs $54.
There are 2 rows of 3 games in a box.
First, I need to find the total number of games in a box.
I will multiply the number of rows by the number of games in each row.
2 × 3 = 6
6 games are in a box.
Then I will divide the cost of a box by the total number of games to find the cost of each game.
$54 ÷ 6 = $
9 Each game costs $9.
Convince Me! Make Sense and Persevere How can you check to make sure the work and answer given above make sense?
Answer:
CHECK:
Cost of video game box = Total number of video games in a box × Cost of each game
= 6 × $9
= $54.
Explanation:
Number of rows of video games = 2.
Number of video games in each row = 3.
Cost of video game box= $54.
Total number of video games in a box = Number of rows of video games × Number of video games in each row
= 2 × 3
= 6.
Cost of each game = Cost of video game box ÷ Total number of video games in a box
= $54 ÷ 6
= $9.
Guided Practice
Make Sense and Persevere Twelve friends went camping. All except 4 of them went on a hike. The hikers carried 32 water bottles. Each hiker carried the same number of water bottles. How many water bottles did each hiker carry?

Question 1.
Tell what you know. Then explain what you can persevere. Think: need to find first to solve the problem. Does the strategy I am sing make sense?
Answer:
Number of water bottles each hiker carried = 4. Yes, the strategy makes sense which you are singing.
Explanation:
Number of friends went camping = 12.
All except 4 of them went on a hike.
=> Number of friends went on a hike = 12 – 4 = 8.
Number of water bottles the hikers carried = 32.
Number of water bottles each hiker carried = Number of water bottles the hikers carried ÷ Number of friends went on a hike
= 32 ÷ 8
= 4.
Question 2.
Tell which operations you will use. Then solve the problem.
Answer:
Multiplication and Division are the operations used and solved the problem.
Explanation:
The operations used re multiplication and division to solve the problem.
Independent Practice
Make Sense and Persevere Four students went bowling. They bowled 2 games each. The cost was $5 per game. How much money did the students spend on bowling? Explain.
Question 3.
Tell what you know. Then explain what you need to find first to solve the problem.
Answer:
Amount of money the students spend on bowling = $40.
Explanation:
Number of students went for bowling = 4.
Number of games they bowled each = 2.
Cost of each game = $5.
Amount of money the students spend on bowling = ( Number of students went for bowling × Number of games they bowled each ) Cost of each game
= (4 × 2) × $5
= 8 × $5
= $40.
Question 4.
Tell which operations you will use. Then solve the problem.
Answer:
Multiplication and Division are the operations used and solved the problem.
Explanation:
The operations used re multiplication and division to solve the problem.
Question 5.
How can you check that your work is correct?
Answer:
CHECK:
Number of students went for bowling × Number of games they bowled each = Amount of money the students spend on bowling ÷ Cost of each game
=> 4 × 2 = $40 ÷ $5
= 8.
Explanation:
CHECK:
Number of students went for bowling × Number of games they bowled each = Amount of money the students spend on bowling ÷ Cost of each game
=> 4 × 2 = $40 ÷ $5
= 8.
Problem Solving
Performance Task
County Fair
County Fair The table shows costs at the county fair. Mr. Casey spent $24 on admission tickets for himself and the children in his group. How many children are in his group? Answer Exercises 6-9 to solve the problem.

Question 6.
Make Sense and Persevere What do you know? What are you asked to find?
Answer:
Number of children in his group = 4.
Explanation:
Amount spent on admission tickets for himself and the children in his group = $24.
Amount for admission ticket for adult = $8.
Amount for admission ticket for child = $4.
Amount for boat ride ticket for adult = $2.
Amount for boat ride ticket for child = $1.
Number of children in his group = (Amount spent on admission tickets for himself and the children in his group – Amount for admission ticket for adult) ÷ Amount for admission ticket for child
= ($24 – $8) ÷ $4.
= $16 ÷ $4.
= 4.
Question 7.
Be Precise Why is it important to know which kind of tickets Mr. Casey bought?

Answer:
It is important to know which kind of tickets Mr. Casey bought because he needs to go country fair.
Explanation:
Mr. Casey buys the tickets to go country fair he needs to know which kind of tickets he purchased.
Question 8.
Critique Reasoning Dan says there are 6 children in Mr. Casey’s group because $24 ÷ $4 = 6. Does Dan’s reasoning make sense? Explain.
Answer:
Yes, Dan does not make sense because $24 ÷ $4 = 6 because total amount spent divided by amount for admission ticket for child.
Explanation:
Dan equation is correct because total amount spent divided by amount for admission ticket for child.
Question 9.
Reasoning Solve the problem. Write an equation for each step and explain.
Answer:
Number of children took the admission tickets = 6.
Explanation:
Amount spent on admission tickets for himself and the children in his group = $24.
Amount for admission ticket for adult = $8.
Amount for admission ticket for child = $4.
Amount for boat ride ticket for adult = $2.
Amount for boat ride ticket for child = $1.
Number of children in his group = 4.
Number of children took the admission tickets = Amount spent on admission tickets for himself and the children in his group ÷ Amount for admission ticket for child
= $24 ÷ $4.
= 6.
Topic 7 Fluency Review Activity
Find a Match
Work with a partner. Point to a clue. Read the clue.
Look below the clues to find a match. Write the clue letter in the box next to the match.
Find a match for every clue.
I can … add and subtract within 100. man
Clues
A. is equal to 59 + 19
B. is equal to 13 – 6
C. is equal to 48 + 38
D. is equal to 57 – 18
E. Is equal to 72 – 24
F. is equal to 35 + 15
G. is equal to 100 – 19
H. is equal to 65 + 33
I. Is equal to 39 – 17
J. is equal to 29 +44
K. is equal to 56 – 47
L. is equal to 16 + 35
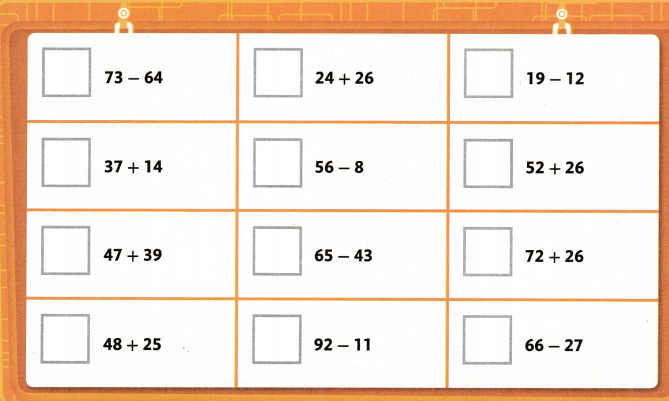
Answer:
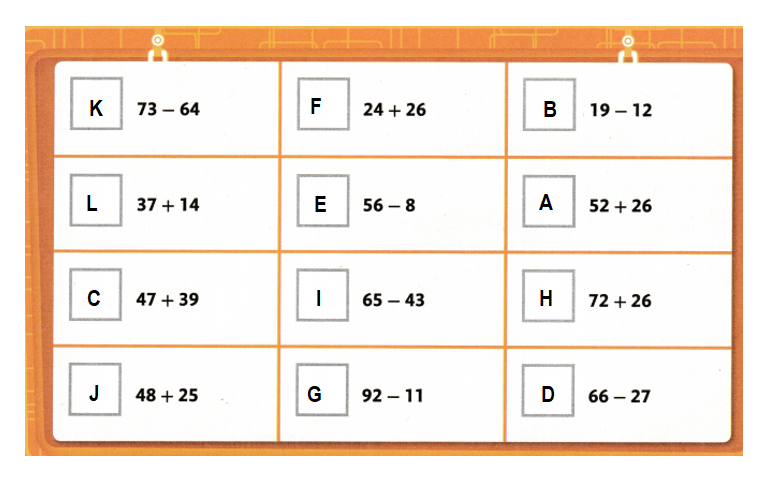
Explanation:
73 – 64 = 9.
37 + 14 = 51.
47 + 39 = 86.
48 + 25 = 73.
24 + 26 = 50.
56 – 8 = 48.
92 – 11 = 81.
65 – 43 = 22.
19 – 12 = 7.
52 + 26 = 78.
72 + 26 = 98.
66 – 27 = 39.
A. is equal to 59 + 19 = 78.
B. is equal to 13 – 6 = 7.
C. is equal to 48 + 38 = 86.
D. is equal to 57 – 18 = 39.
E. Is equal to 72 – 24 = 48.
F. is equal to 35 + 15 = 50.
G. is equal to 100 – 19 = 81.
H. is equal to 65 + 33 = 98.
I. Is equal to 39 – 17 = 22.
J. is equal to 29 +44 = 73.
K. is equal to 56 – 47 = 9.
L. is equal to 16 + 35 = 51.
Topic 4 Vocabulary Review
Understand Vocabulary
Word List
- dividend
- divisor
- even number
- fact family
- odd number product
- quotient
Question 1.
Circle the divisor in each equation.
30 ÷ 6 = 5
24 ÷ 3 = 8
14 ÷ 2=7
45 ÷ 5 = 9
Answer:
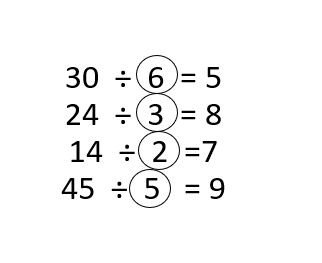
Explanation:
30 ÷ 6 = 5. Divisor – 6.
24 ÷ 3 = 8. Divisor – 3.
14 ÷ 2 =7. Divisor – 2.
45 ÷ 5 = 9. Divisor – 5.
Question 2.
Circle the dividend in each equation.
63 ÷ 7 = 9
4 ÷ 1 = 4
0 ÷ 5 = 0
8 ÷ 4 = 2
Answer:
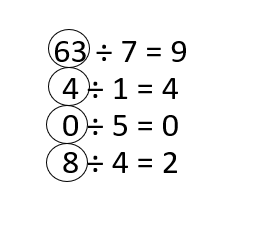
Explanation:
63 ÷ 7 = 9. Dividend – 63.
4 ÷ 1 = 4. Dividend – 4.
0 ÷ 5 = 0. Dividend – 0.
8 ÷ 4 = 2. Dividend – 8.
Question 3.
Circle the quotient in each equation.
21 ÷ 3 = 7
54 ÷ 9 = 6
15 ÷ 5 = 3
16 ÷ 8 = 2
Answer:
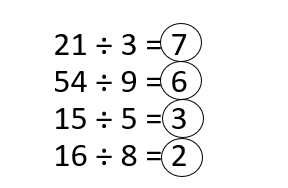
Explanation:
21 ÷ 3 = 7. quotient – 7.
54 ÷ 9 = 6. quotient – 54.
15 ÷ 5 = 3. quotient – 15.
16 ÷ 8 = 2. quotient – 16.
Question 4.
Circle the even numbers.
24
19
45
68
Answer:
Explanation:
24 and 68 are even numbers.
Question 5.
Circle the odd numbers.
21
36
13
47
Answer:
Explanation:
21, 13, 47 are odd numbers.
Question 6.
Look at the equations below. Write Y if the product is 6. Write N if the product is NOT 6.
4 × 6 = 24 _______
2 × 3 = 6 _______
6 = 3 × 2 ________
Answer:
4 × 6 = 24 ___N____.
2 × 3 = 6 ____Y___.
6 = 3 × 2 ____Y____.
Explanation:
4 × 6 = 24. N
2 × 3 = 6. Y
6 = 3 × 2. Y
Question 7.
Look at the equations below. Write Y if the group shows a fact family. Write N if the group does NOT show a fact family.
3 × 9 = 27 _______
27 ÷ 9 = 3
9 × 3 = 27
27 ÷ 3 = 9
12 ÷ 6 = 2 ________
2 × 6 = 12
12 ÷ 3 = 4
6 × 2 = 12
56 ÷ 8 = 7 _________
56 ÷ 7 = 8
8 × 7 = 56
7 × 8 = 56
Answer:
3 × 9 = 27 ___Y____
27 ÷ 9 = 3
9 × 3 = 27
27 ÷ 3 = 9
12 ÷ 6 = 2 ___N_____
2 × 6 = 12
12 ÷ 3 = 4
6 × 2 = 12
56 ÷ 8 = 7 _____Y____
56 ÷ 7 = 8
8 × 7 = 56
7 × 8 = 56
Explanation:
3 × 9 = 27 Y
27 ÷ 9 = 3
9 × 3 = 27
27 ÷ 3 = 9
12 ÷ 6 = 2 N
2 × 6 = 12
12 ÷ 3 = 4
6 × 2 = 12
56 ÷ 8 = 7 Y
56 ÷ 7 = 8
8 × 7 = 56
7 × 8 = 56
Use Vocabulary in Writing
Question 8.
Explain how to find the fact family for 2, 4, and 8. Use at least 2 terms from the Word List in your explanation.
Answer:
2, 4, 8.
2 × 4 = 8.
4 × 2 = 8.
8 ÷ 2 = 4.
8 ÷ 4 = 2.
Explanation:
In math, a fact family can be defined as a group of math facts or equations created using the same set of numbers. The fact family shows the relationships between the three numbers involved.
2, 4, 8.
2 × 4 = 8.
4 × 2 = 8.
8 ÷ 2 = 4.
8 ÷ 4 = 2.
Topic 4 Reteaching
Set A pages 117-120
Monica has 24 chairs to arrange equally in 3 rows. You can use an array to find the number of chairs in each row.

This array shows the relationship between multiplication and division.
3 rows of 8
3 × 8 = 24
24 in 3 equal rows
24 ÷ 3= 8
A fact family shows how multiplication and division are related.
Fact family for 3, 8, and 24:
3 × 8= 24
8 × 3 = 24
24 ÷ 8 = 3
24 ÷ 8 = 3
Remember that a fact family is a group of related facts using the same numbers.
In 1-4, write the other three facts in the fact family
Question 1.
3 × 7 = 21
Answer:
3 × 7 = 21.
7 × 3 = 21.
21 ÷ 7 = 3.
21 ÷ 3 = 7.
Explanation:
Other three facts in the fact family of 3 × 7 = 21:
7 × 3 = 21.
21 ÷ 7 = 3.
21 ÷ 3 = 7.
Question 2.
5 × 3 = 15
Answer:
3 × 5 = 15.
15 ÷ 5 = 3.
15 ÷ 3 = 5.
Explanation:
Other three facts in the fact family of 5 × 3 = 15:
3 × 5 = 15.
15 ÷ 5 = 3.
15 ÷ 3 = 5.
Question 3.
8 × 6 = 48
Answer:
6 × 8 = 48.
48 ÷ 8 = 6.
48 ÷ 6 = 8.
Explanation:
Other three facts in the fact family of 8 × 6 = 48:
6 × 8 = 48.
48 ÷ 8 = 6.
48 ÷ 6 = 8.
Question 4.
4 × 5 = 20
Answer:
5 × 4 = 20.
20 ÷ 5 = 4.
20 ÷ 4 = 5.
Explanation:
Other three facts in the fact family of 4 × 5 = 20:
5 × 4 = 20.
20 ÷ 5 = 4.
20 ÷ 4 = 5.
Set B pages 121-124
You can use multiplication to solve division problems.
Hector has 24 oranges. He puts 4 oranges in each basket. How many baskets does Hector need for all the oranges?

What number times 4 is 24?
6 × 4 = 24
24 ÷ 4 = 6
Hector needs 6 baskets.
Remember that you can use multiplication to help divide.
In 1 and 2, solve each problem. Write the multiplication fact and division fact you use to solve the problem.
Question 1.
Sally has 32 flowers. She puts 8 flowers in each vase. How many vases does Sally need for all the flowers?
Answer:
Number of vases Sally needs for all the flowers = 4.
Division fact:
32 ÷ 8 = 4.
32 ÷ 4 = 8.
Explanation:
Number of flowers Sally has = 32.
Number of flowers she puts in each vase = 8.
Number of vases Sally needs for all the flowers = Number of flowers Sally has ÷ Number of flowers she puts in each vase
= 32 ÷ 8
= 4.
Division fact:
32 ÷ 8 = 4.
32 ÷ 4 = 8.
Question 2.
Jon has 18 peaches. He uses 3 peaches to make a peach tart. How many peach tarts does Jon make if he uses all the peaches?
Answer:
Number of peach tarts Jon makes if he uses all the peaches = 6.
Division fact:
18 ÷ 3 = 6.
18 ÷ 6 = 3.
Explanation:
Number of peaches Jon has = 18.
Number of peaches he uses to make a peach tart = 3.
Number of peach tarts Jon makes if he uses all the peaches = Number of peaches Jon has ÷ Number of peaches he uses to make a peach tart
= 18 ÷ 3
= 6.
Division fact:
18 ÷ 3 = 6.
18 ÷ 6 = 3.
Set C pages 125-128
Brent is putting 42 books on shelves. He puts 6 books on each shelf. How many shelves will Brent need?

What number times 6 is 42?
7 × 6 = 42
42 ÷ 6 = 7
Brent will need 7 shelves.
How many shelves would Brent need if he put 7 books on each shelf?
What number times 7 is 42?
6 × 7 = 42
42 ÷ 7 = 6
Brent would need 6 shelves.
Remember that you can use multiplication facts for 6s and 7s to help you divide by 6s and 7s.
In 1-3, solve each problem. Write the multiplication fact and division fact you use to solve the problem.
Question 1.
There are 36 runners entered in a marathon. They run in groups of 6. How many groups are there?
Answer:
Number of groups = 6.
Division fact:
36 ÷ 6 = 6.
Explanation:
Number of runners entered in a marathon = 36.
Number of runners run in groups = 6.
Number of groups = Number of runners entered in a marathon ÷ Number of runners run in groups
= 36 ÷ 6
= 6.
Question 2.
Lani has 35 bird stickers. There are 5 stickers on each sheet. How many sheets of bird stickers does she have?
Answer:
Number of sheets of bird stickers she has = 7.
Division fact:
35÷ 7 = 5.
Explanation:
Number of bird stickers Lani has = 35.
Number of stickers on each sheet = 5.
Number of sheets of bird stickers she has = Number of bird stickers Lani has ÷ Number of stickers on each sheet
= 35 ÷ 5
= 7.
Division fact:
35÷ 7 = 5.
Question 3.
Jake has 18 remote-controlled boats for 6 friends to share equally. How many boats will each friend get?
Answer:
Number of boats each friend gets = 3.
Division fact:
18÷ 3 = 6.
Explanation:
Number of remote-controlled boats Jake has =18.
Number of friends he shares them equally = 6.
Number of boats each friend gets = Number of remote-controlled boats Jake has ÷ Number of friends he shares them equally
= 18 ÷ 6
= 3.
Division fact:
18÷ 3 = 6.
Set D pages 129-132
Lu made 9 bracelets. He used 72 beads. He used the same number of beads for each bracelet. How many beads did Lu use for each bracelet?
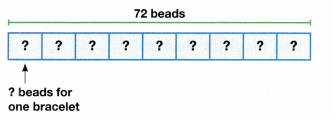
9 times what number is 72?
9 × 8 = 72
72 ÷ 9 = 8
Lu used 8 beads for each bracelet.
Remember that you can use multiplication facts for 8s and 9s to help divide by 8s and 9s.
In 1-5, write the related multiplication fact that can be used to complete each division fact. Then find the quotient.
Question 1.
54 ÷ 9 = ______ _____ × ______ = _______
Answer:
54 ÷ 9 = __6____ __9___ × __6____ = ___54____.
Explanation:
54 ÷ 9 = 6.
9 × 6 = 54.
Question 2.
64 ÷ 8 = ______ _____ × ______ = _______
Answer:
64 ÷ 8 = __8____ __8___ × ___8___ = __64_____.
Explanation:
64 ÷ 8 = 8.
8 × 8 = 64.
Question 3.
36 ÷ 9 = ______ _____ × ______ = _______
Answer:
36 ÷ 9 = __4____ __9___ × ___4___ = __36_____.
Explanation:
36 ÷ 9 = 4.
9 × 4 = 36.
Question 4.
56 ÷ 8 = ______ _____ × ______ = _______
Answer:
56 ÷ 8 = __7____ __8___ × ___7___ = ___56____.
Explanation:
56 ÷ 8 = 7.
8 × 7 = 56.
Question 5.
72 ÷ 8 = ______ _____ × ______ = _______
Answer:
72 ÷ 8 = ___9___ __8__ × ___9___ = __72_____.
Explanation:
72 ÷ 8 = 9.
8 × 9 = 72.
Set E pages 133-136
A whole number is even if it can be divided by 2 with none left over.
A whole number is odd if it cannot be divided by 2 with none left over.
Which product is even? Which is odd?
3 × 7 = odd product
5 × 8 = even product
All even numbers can be thought of as 2 equal groups.
When at least one factor is even, the product is even.
Remember that you can think about dividing by 2 to tell whether a number is even or odd.
In 1-3, circle the factors that can be divided by 2. Then circle even or odd to describe the product.
Question 1.
6 × 4 = ?
even
odd
Answer:
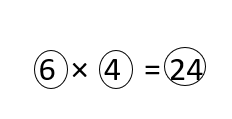
Explanation:
Even factors:
6 and 4 both.
Product 6 × 4 = 24 is also even number.
Question 2.
9 × 1 = ?
even
odd
Answer:
Explanation:
Odd factors:
9 and 1 both.
Product 9 × 1 = 9 is also odd number.
Question 3.
8 × 7 = ?
even
odd
Answer:
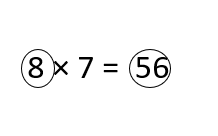
Explanation:
Even factors:
8 is even number.
Product 8 × 7 = 56 is even number.
Set F pages 137-140
Find 5 ÷ 1. Five plants are divided into groups of 1.

What number times 1 is 5?
5 × 1 = 5
So, 5 ÷ 1 = 5.
Find 0 ÷ 8.
8 × 0 = 0
So, 0 ÷ 8 = 0.
Remember that any number divided by 1 is itself. Any number (except 0) divided by itself is 1. Zero divided by any number (except 0) is 0.
In 1-3, use division to solve.
Question 1.
0 ÷ 16 = ______
Answer:
0 ÷ 16 = __0____.
Explanation:
0 ÷ 16 = 0.
Question 2.
10 ÷ 10 = _______
Answer:
10 ÷ 10 = ___1____.
Explanation:
10 ÷ 10 = 1.
Question 3.
Leroy had 4 oranges. He gave one orange to each of his 4 friends. How many oranges did each friend get? Write an equation to show your answer.
Answer:
Number of oranges each friend gets = 1.
Explanation:
Number of oranges Leroy had = 4.
Number of friends he gave one orange each = 4.
Number of oranges each friend gets = Number of oranges Leroy had ÷ Number of friends he gave one orange each
= 4 ÷ 4
= 1.
Set G pages 141-144
How many groups of 4 are in 24?

You can use multiplication facts.
? × 4 = 24
6 × 4 = 24
There are 6 groups of 4 in 24.
Remember that you can use bar diagrams or multiplication facts to help solve a division problem.
In 1 and 2, use related multiplication and division facts to solve.
Question 1.
21 ÷ 7 = _____
7 × ______ = 21
Answer:
21 ÷ 7 = _3___.
7 × __3____ = 21.
Explanation:
21 ÷ 7 = 3.
7 × 3 = 21.
Question 2.
5 × __ = 45
45 ÷ 5 = ______
Answer:
5 × __9__ = 45.
45 ÷ 5 = __9____.
Explanation:
5 × 9 = 45
45 ÷ 5 = 9.
Set H pages 145-148
Look at the equation 3 × ? = 15.

Read the equation like this:
“Multiply 3 by a number. The result is 15.” Then find the value of the unknown. Think of a fact that uses the numbers in the equation.
3 × 5 = 15, so the unknown number is 5.
Remember that you can use multiplication and division facts to find the value of an unknown.
In 1-6, find the value of the unknown.
Question 1.
? ÷ 2 = 6
Answer:
12 ÷ 2 = 6., so the unknown number is 12.
Explanation:
“Divide by 2 number. The result is 6.”
? ÷ 2 = 6
=> 12 ÷ 2 = 6.
Question 2.
7 × ? = 42
Answer:
7 × 6 = 42., so the unknown number is 42.
Explanation:
“Multiply 7 by a number. The result is 42.”
7 × ? = 42
=> 7 × 6 = 42.
Question 3.
20 = 4 × ?
Answer:
20 = 4 × 5., so the unknown number is 5.
Explanation:
“Multiply 4 by a number. The result is 20.”
20 = 4 × ?
=> 20 = 4 × 5.
Question 4.
9 = ? ÷ 3
Answer:
9 = 27 ÷ 3., so the unknown number is 27.
Explanation:
“Divide by 3 number. The result is 9.”
9 = ? ÷ 3
=> 9 = 27 ÷ 3.
Question 5.
16 ÷ ? = 2
Answer:
16 ÷ 8 = 2., so the unknown number is 8.
Explanation:
“16 Divide by. The result is 2.”
16 ÷ ? = 2
=> 16 ÷ 8 = 2.
Question 6.
24 ÷ ? = 6
Answer:
24 ÷ 4 = 6., so the unknown number is 4.
Explanation:
“24 Divide by. The result is 6.”
24 ÷ ? = 6
=> 24 ÷ 4 = 6.
Set I pages 149-152
Think about these questions to help you make sense of problems and persevere in solving them.
Thinking Habits
- What do I need to find?
- What do I know?
- What’s my plan for solving the problem?
- What else can I try if I get stuck?
- How can I check that my solution makes sense?

Remember to use the information in each step to solve the problem.
In 1 and 2, answer to solve a two-step problem.
Fourteen friends went to the county fair. All except 6 of them bought a hot dog. Each hot dog costs $3. How much did the friends spend on hot dogs?
Question 1.
Tell what you know. Then explain what you need to find first to solve the problem.
Answer:
Number of friends went to the county fair = 14.
All except 6 of them bought a hot dog.
=> Number of friends bought a hot dog = 14 – 6 = 8.
Each hot dog costs $3.
=> Cost of each hot dog = $3.
We need to find amount of money the friends spend on hot dogs = ??
Amount of money the friends spend on hot dogs = $24.
Explanation:
Number of friends went to the county fair = 14.
All except 6 of them bought a hot dog.
=> Number of friends bought a hot dog = 14 – 6 = 8.
Each hot dog costs $3.
=> Cost of each hot dog = $3.
We need to find amount of money the friends spend on hot dogs = ??
Amount of money the friends spend on hot dogs = Number of friends bought a hot dog × Cost of each hot dog
= 8 × $3
= $24.
Question 2.
Tell which operations you will use. Then solve the problem.
Answer:
Multiplication and Division operations we use to solve the problem.
Explanation:
The operations used here are multiplication and division to solve the problem to find the answer.
Number of friends went to the county fair = 14.
Number of friends bought a hot dog = 14 – 6 = 8.
Cost of each hot dog = $3.
Amount of money the friends spend on hot dogs = Number of friends bought a hot dog × Cost of each hot dog
= 8 × $3
= $24.
Topic 4 Assessment Practice
Question 1.
A. Heather wrote a multiplication fact and a division fact for the array below. Select all of the equations that show a fact Heather could have written.

☐ 5 × 9 = 45
☐ 5 × 5 = 25
☐ 45 ÷ 5 = 9
☐ 10 × 5 = 50
☐ 50 ÷ 5 = 10
Answer:
Heather wrote a multiplication fact and a division fact for the array below:
☐ 5 × 9 = 45.
☐ 45 ÷ 5 = 9.
Explanation:
Number of rows = 9.
Number of columns = 5.
Heather wrote a multiplication fact and a division fact for the array below:
Multiplication fact:
9 × 5 = 45.
5 × 9 = 45.
Division fact:
45 ÷ 9 = 5.
45 ÷ 5 = 9.
B. Look at the multiplication fact you selected in Part A. Which of these is a way to rewrite the product in it?
☐ (5 × 3) + (5 × 4)
☐ (5 × 5) + (5 × 4)
☐ (5 × 5) + (5 × 2)
☐ 5 × 5 × 4
Answer:
Multiplication fact you selected in Part A:
5 × 9 = (5 × 4) + (5 × 5) = 45.
Explanation:
Multiplication fact you selected in Part A:
5 × 9 = 45.
= (5 × 4) + (5 × 5)
= 20 + 25
= 45.
Question 2.
Colin wrote three equations. What number will make all of Colin’s equations true?
14 = ? × 2
56 ÷ 8 = ?
? × ? = 49
Answer:
7 number will make all of Colin’s equations true.
Explanation:
14 = ? × 2
=> 14 = 7 × 2.
56 ÷ 8 = ?
=> 56 ÷ 8 = 7.
? × ? = 49
7 × 7 = 49.
Question 3.
If a group of objects is divided into 2 equal groups, 1 object is left over. Is the total number of objects even or odd? What could the total number of objects be? Use a drawing to explain.
Answer:
If a group of objects is divided into 2 equal groups, 1 object is left over then the total number of objects going to be odd not even.
Explanation:
If a group of objects is divided into 2 equal groups, 1 object is left over then the total number of objects going to be odd not even.
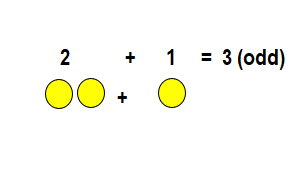
Question 4.
Mrs. Raspa wrote the expression 6 × 3 on the board. Which of the following expressions has the same value?
A. (3 × 3) + (3 × 1)
B. (6 × 2) + (6 × 1)
C. (6 × 0) + (6 × 4)
D. (4 × 3) + (5 × 3)
Answer:
B. (6 × 2) + (6 × 1) has the same value of the expression 6 × 3.
Explanation:
Expression 6 × 3 = 18.
A. (3 × 3) + (3 × 1) = 9 + 3 = 12.
B. (6 × 2) + (6 × 1) = 12 + 6 = 18.
C. (6 × 0) + (6 × 4) = 0 + 24 = 24.
D. (4 × 3) + (5 × 3) = 12 + 15 = 27.
Question 5.
A. Mr. Vargas is buying used computer equipment. He buys 3 keyboards and 4 mice. He spends $42. If the items are all the same price, how much does each item cost?
Answer:
Cost of each item = $6.
Explanation:
Number of keyboards Mr. Vargas buys = 3.
Number of mice Mr. Vargas buys = 4.
Amount he spends = $42.
Total number of items he bought = Number of keyboards Mr. Vargas buys + Number of mice Mr. Vargas buys
= 3 + 4
= 7.
Cost of each item = Amount he spends ÷ Total number of items he bought
= $42 ÷ 7
= $6.
B. Mr. Vargas decides to buy more keyboards that cost another $12 in all. How many more keyboards does Mr. Vargas buy?
Answer:
Number of more keyboards Mr. Vargas buy = 9.
Explanation:
Amount he spends to buy more keyboards in all = $12.
Number of keyboards Mr. Vargas buys = 3.
Amount he spends = $42.
Amount he spends more = $12.
Amount he spends now = Amount he spends + Amount he spends more
= $42 + $12
= $54.
Cost of each keyboard = $6.
Number of more keyboards Mr. Vargas buy = Amount he spends now ÷ Cost of each keyboard
= $54 ÷ $6
= 9.
Question 6.
Look at the counters below.
A. Draw lines around the counters to show 12 ÷ 6.

Answer:
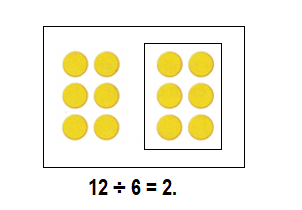
Explanation:
12 ÷ 6 = 2.
B. Write a multiplication fact related to the drawing you completed in Part A.
Answer:
6 × 2 = 12.
2 × 6 = 12.
Explanation:
Multiplication fact related to the drawing you completed in Part A:
6 × 2 = 12.
2 × 6 = 12.
Question 7.
Match each expression on the left with an equivalent expression.
Answer:
Explanation:
9 ÷ 1 = 9.
3 ÷ 3 = 0.
1 × 6 = 6.
7 ÷ 7 = 1.
8 ÷ 8 = 1.
0 × 7 = 0.
24 ÷ 4 = 6.
27 ÷ 3 = 9.
Question 8.
A. Peter wrote five numbers. Which of Peter’s numbers can be divided into 7 equal groups with 0 left over? Select all that apply.
☐ 56
☐ 35
☐ 52
☐ 27
☐ 42
Answer:
Peter’s numbers can be divided into 7 equal groups with 0 left over are as below:
56, 35, 42.
Explanation:
Peter’s numbers can be divided into 7 equal groups with 0 left over:
☐ 56 ÷ 7 = 8.
☐ 35 ÷ 7 = 5.
☐ 52 ÷ 7 = 7.4.
☐ 27 ÷ 7 = 3.8.
☐ 42 ÷ 7 = 6.
B. How can you check to make sure the numbers you chose are divisible by 7?
A. Check that each number is even.
B. Check that each number is odd.
C. Use multiplication to multiply 0 by a number to determine if it is equal to the number you chose.
D. Use multiplication to multiply 7 by a number to determine if it is equal to the number you chose.
Answer:
D. Use multiplication to multiply 7 by a number to determine if it is equal to the number you chose.
Explanation:
To make sure the numbers choosed are divisible by 7, use multiplication facts to determine if it is equal to the number you chose.
Question 9.
Crystal drew this bar diagram to model a division problem. Write a multiplication equation Crystal could use to help solve the problem.
Answer:
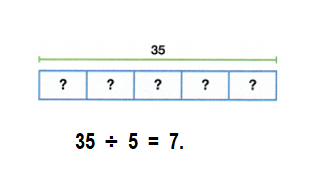
Multiplication Equation:
5 × 7 = 35.
7 × 5 = 35.
Explanation:
Total count given = 35.
Number of boxes divided = 5.
Number value used to divided = Total count given ÷ Number of boxes divided
= 35 ÷ 5
= 7.
Multiplication Equation:
5 × 7 = 35.
7 × 5 = 35.
Question 10.
A. Xavier divided his action figure collection into 2 equal groups. Which describes the number of action figures Xavier has?
A. It is an even number.
B. It is an odd number.
Answer:
The number of action figures Xavier has is an even number because to divide into anything into 2 groups equally it has to be even.
Explanation:
To divide anything into two groups equally means, it has to be even not odd because odd number cannot be divided into two parts.
B. Xavier finds 2 more action figures.
Select all statements that are true.
☐ Including the action figures he found, Xavier has an even number of action figures.
☐ Including the action figures he found, Xavier has an odd number of action figures.
☐ Xavier can divide all of the action figures into 2 equal groups.
☐ Xavier could now have a total of 6 action figures in his collection.
☐ Xavier could now have a total of 8 action figures in his collection.
Answer:
All statements that are true are below:
Including the action figures he found, Xavier has an even number of action figures.
Xavier can divide all of the action figures into 2 equal groups.
Xavier could now have a total of 6 action figures in his collection.
Xavier could now have a total of 8 action figures in his collection.
Explanation:
☐ Including the action figures he found, Xavier has an even number of action figures.
☐ Xavier can divide all of the action figures into 2 equal groups.
☐ Xavier could now have a total of 6 action figures in his collection.
☐ Xavier could now have a total of 8 action figures in his collection.
Question 11.
Mandy is trying to find 6 ÷ 0. She says the answer is 6 because 6 × 0 = 6. Is Mandy correct? Explain.
Answer:
Mandy is incorrect because 6 × 0 = 0 not 6 × 0 = 6.
Explanation:
6 ÷ 0 = 0.
6 × 0 = 0.
Question 12.
Luz has 36 pencil toppers. She sorts her pencil toppers into 6 equal groups.
A. Write an expression that represents how many pencil toppers are in each group.
Answer:
Number of pencil toppers are in each group = 36 ÷ 6 = 6.
Explanation:
Number of pencil toppers Luz has = 36.
Number of equal groups She sorts her pencil toppers = 6.
Number of pencil toppers are in each group = Number of pencil toppers Luz has ÷ Number of equal groups She sorts her pencil toppers
= 36 ÷ 6
= 6.
B. How many are in each group?
Answer:
There are 6 in each group.
Explanation:
Number of pencil toppers are in each group = 6.
Question 13.
Kira has 63 sheets of recycled paper. She gives the same number of sheets to each of 9 friends. How many sheets does Kira give to each friend? Use the bar diagram to help.

A. 6
B. 7
C. 8
D. 9
Answer:
Number of sheets Kira gives to each friend = 7.
B. 7
Explanation:
Number of sheets of recycled paper Kira has = 63.
Number of friends she gives = 9.
Number of sheets Kira gives to each friend = Number of sheets of recycled paper Kira has ÷ Number of friends she gives
= 63 ÷ 9
= 7.
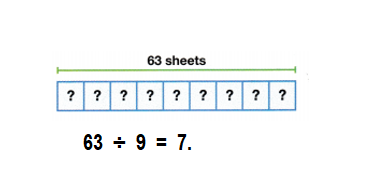
Question 14.
Jules has 4 classes. For each class, he needs 3 folders. Find how many folders he needs in all. Then write the fact family related to this situation.
Answer:
Number of folders he needs in all = 12.
Explanation:
Number of classes Jules has = 4.
Number of folders he needs for each class = 3.
Number of folders he needs in all = Number of classes Jules has × Number of folders he needs for each class
= 4 × 3
= 12.
Fact family:
4 × 3 = 12.
3 × 4 = 12.
12 ÷ 3 = 4.
12 ÷ 4 = 3.
Question 15.
A. Gennaro wrote 4 true statements about even and odd products. Select all of the true statements.
☐ An even number times an even number has an even product.
☐ An even number times an odd number has an even product.
☐ An odd number times an odd number has an odd product.
☐ An odd number times an even number has an odd product.
☐ If one factor is even, then the product is even.
Answer:
All of the true statements are:
An even number times an even number has an even product.
An even number times an odd number has an even product.
An odd number times an odd number has an odd product.
If one factor is even, then the product is even.
Explanation:
All of the true statements are:
☐ An even number times an even number has an even product.
☐ An even number times an odd number has an even product.
☐ An odd number times an odd number has an odd product.
☐ If one factor is even, then the product is even.
B. Look at the statement you did NOT select in Part A. Give an example of why it is not true.
Answer:
An odd number times an even number has an odd product.
For an example:
3 × 4 = 12.
Explanation:
The statement which is NOT selected in Part A is as below:
An odd number times an even number has an odd product.
For an example:
3 × 4 = 12.
Question 16.
Which number makes both equations true?
18 ÷ 9 = ?
? × 9 = 18
Answer:
2 number makes both equations true.
Explanation:
18 ÷ 9 = ?
=> 18 ÷ 9 = 2.
? × 9 = 18
=> 2 × 9 = 18.
Question 17.
Anna drew the bar diagram below. Write two equations that could be used to represent the problem shown in Anna’s bar diagram. Then solve the equations.

Answer:
Way:1:
Value of sector divided = Total number given ÷ Number of sectors divided given
= 18 ÷ 3
= 6.
Way:2:
Total number given = Number of sectors divided given × Value of sector divided
=> 18 = 3 × ??
=> 18 ÷ 3 = ??
=> 6 = ??.
Explanation:
Way:1:
Total number given = 18.
Number of sectors divided given = 3.
Value of sector divided = Total number given ÷ Number of sectors divided given
= 18 ÷ 3
= 6.
Way:2:
Total number given = 18.
Number of sectors divided given = 3.
Value of sector divided = ??
Total number given = Number of sectors divided given × Value of sector divided
=> 18 = 3 × ??
=> 18 ÷ 3 = ??
=> 6 = ??.
Question 18.
A balloon artist wants to make 6 different kinds of balloon animals. She needs 4 balloons to make each animal. How many balloons will she need to buy? Tell which operations you will use. Then solve the problem.
Answer:
We are going to use multiplication operations to solve the problem.
Number of balloons she needs to buy = 24.
Explanation:
We are going to use multiplication operations to solve the problem.
Number of different kinds of balloon animals a balloon artist wants to make = 6.
Number of balloons she needs to make each animal = 4.
Number of balloons she needs to buy = Number of different kinds of balloon animals a balloon artist wants to make × Number of balloons she needs to make each animal
= 6 × 4
= 24.
Topic 4 Performance Task
Relay Race
Mrs. Achilles teaches Physical Education. She is planning a relay race for her school. Each grade forms teams. Each student is on 1 team.
Race Details
- The field is 40 feet wide.
- Each runner gets 1 lane.
- Mrs. Achilles has 7 trophies.
Use the Race Details list to answer the following question.
Question 1.
Each lane must be an equal width. Mrs. Achilles wants to use the entire width of the field for lanes. How wide will each lane be if Mrs. Achilles sets out 10 lanes? 5 lanes? Use multiplication facts to help you.
Answer:
IF,
Number of lanes set out = 10.
Width of the each lane = 4.
IF,
Number of lanes set out = 5.
Width of the each lane = 8.
Explanation:
Number of lanes each runner gets = 1.
Number of trophies Mrs. Achilles has = 7.
Number of students in each team = 1.
IF,
Number of lanes set out = 10.
Width of the field = 40 feet.
Width of the each lane = Width of the field ÷ Number of lanes set out
= 40 ÷ 10
= 4.
IF,
Number of lanes set out = 5.
Width of the field = 40 feet.
Width of the each lane = Width of the field ÷ Number of lanes set out
= 40 ÷ 5
= 8.
Use the Race Details list and Grade Size table to answer the following question.
Question 2.
Each grade gets an equal number of trophies. How many trophies does each grade get? Write a division fact and a related multiplication fact you can use to solve this problem.
Answer:
Number of trophies each grade gets = 1.
Explanation:
Number of trophies Mrs. Achilles has = 7.
Number of grades = 7.
Number of trophies each grade gets = Number of trophies Mrs. Achilles has ÷ Number of grades
= 7 ÷ 7
= 1.
Division fact:
= 7 ÷ 7 = 1.
Multiplication fact:
= 1 × 7 = 7.
Use the Grade Size table to answer the following question.
Question 3.
Mrs. Achilles wonders whether each team can have exactly 2 people. Explain whether or not this is possible.
Answer:
If the students strength is even number, then its possible to have two people in each team and its not possible, if the strength is odd number.
Explanation:
Yes, its possible to have 2 people in each team if the students strength is even. if the strength of students is odd, then its not possible to have 2 people in each team.
Use the Grade Size and Grade 3 Possible Team Sizes tables to answer the following question. Use related multiplication facts to help you.

Question 4.
Mrs. Achilles puts more than 2 students on each team. Each team must have an equal number of students.
Part A
Complete the table to show the 4 different ways Mrs. Achilles can form teams for Grade 3.
Answer:
Way:1: = 24 ÷ 3 = 8.
Way:2: = 3 × 8 = 24.
Way:3: = 8 × 3 = 24.
Way:4: = 24 ÷ 8 = 3.
Explanation:
Total number of students in grade 3 = 24.
Way:1:
Number of people in each team = 3.
Team 1 form = Total number of students in grade 3 ÷ Number of people in each team
= 24 ÷ 3
= 8.
Way:2:
Number of people in each team × Team 1 form = Total number of students in grade 3.
= 3 × 8
= 24.
Way:3:
Team 1 form × Number of people in each team = Total number of students in grade 3.
= 8 × 3
= 24.
Way:4:
Total number of students in grade 3 ÷ Team 1 form = Number of people in each team.
= 24 ÷ 8
= 3.
Part B
Mrs. Achilles tries to make teams of 4 students each. She can do this for some grades but not for all. Which grades can have equal teams of 4?
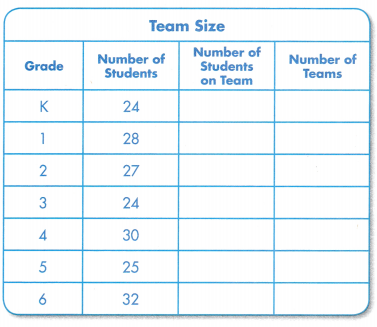
Fill out the table for the grades written above. Use the same-size team for each of these grades.
Answer:
Grade: K, 1, 3 and 6 grades can have equal teams of 4.
Explanation:
Grade: K and 3:
Number of students = 24.
Number of people in team = 4.
Number of teams = Number of students ÷ Number of people in team
= 24 ÷ 4
= 6.
Grade: 1:
Number of students = 28.
Number of people in team = 4.
Number of teams = Number of students ÷ Number of people in team
= 28 ÷ 4
= 7.
Grade: 2 , 4 , 5:
Number of students number is not the multiple of 4 , so they cannot be having 4 people in each team.
Grade: 6:
Number of students = 32.
Number of people in team = 4.
Number of teams = Number of students ÷ Number of people in team
= 32÷ 4
= 8.
Part C
In the Team Size table, write the grades that you did NOT fill out in Part B.
Choose team sizes that let everyone in these grades participate. Use different sizes for each of these grades. Fill out the rest of the table.
Answer:
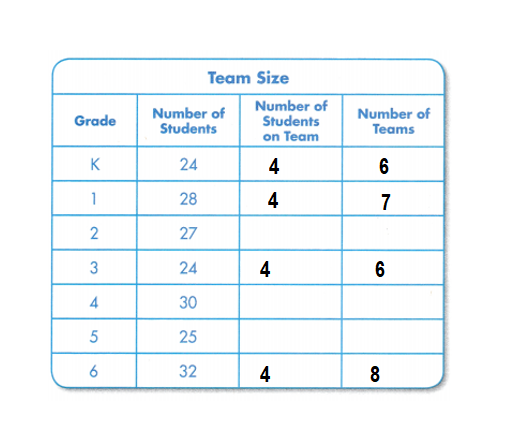
Explanation:
Grade: 2 , 4 , 5:
Number of students are 27, 30, 25 , number is not the multiple of 4 , so they cannot be having 4 people in each team.




