Go through the enVision Math Common Core Grade 4 Answer Key Topic 10 Extend Multiplication Concepts to Fractions regularly and improve your accuracy in solving questions.
enVision Math Common Core 4th Grade Answers Key Topic 10 Extend Multiplication Concepts to Fractions
Essential Questions:
How can you describe a fraction using a unit fraction? How can you multiply a fraction by a whole number?
Answer:
A fraction can be converted into a unit fraction as explained below:
Put the whole number over 1 to turn it into a fraction.
Ex:
The whole number is: 5
The conversion of 5 into a unit fraction is: \(\frac{1}{5}\)
A fraction can be multiplied by a whole number as explained below:
Step 1:
Multiply across the top number by top number (numerator) and bottom number by bottom number (denominator).
Step 2:
Simplify your answer by dividing both numerator and denominator by the same number, when applicable.
enVision STEM Project: Light and Multiplication
Do Research
Use the Internet or other sources to research the words transparent, translucent, and opaque? Write a definition for each word.
Answer:
Transparent:
If any material allows all light to pass through it, then it is called “Transparent”
Translucent:
If any material allows some light to pass through it, then it is called “Translucent”
Opaque:
When any material allows no light to pass through it, then it is called “Opaque”
Journal: Write a Report
Include what you found. Also in your report:
PART A:
List 1 example of each of the items that are transparent, translucent, or opaque.
Answer:
Examples of Transparent items are:
a. Clean glass
b. Water
c. Air
Examples of Translucent items are:
a. Frosted glass
b. Wax paper
c. Smoke
d Butter paper
Examples of Opaque items are:
a. Stone
b. Metal
c. Wood
PART B:
Suppose one-third of each of 5 same-sized posters is covered with opaque paper. What fraction of the posters are not covered by opaque paper? Explain how to use multiplication to find what parts of the posters are not covered by opaque paper?
Answer:
It is given that
One-third of each of 5 same-sized posters is covered with opaque paper
Now,
The representation of the 5 same-sized posters with opaque paper is:
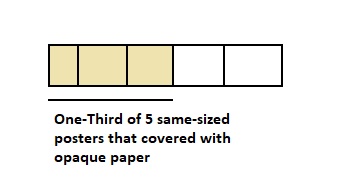
Now,
From the given figure,
We can observe that
The total number of parts are: 5
The number of parts covered with opaque paper is: 3
The number of parts that are not covered with opaque paper is: 2
Now,
The fraction of the posters that are covered by the opaque paper = \(\frac{The number of parts that are covered with opaque paper}{The total number of parts}\)
= \(\frac{3}{5}\)
So,
The fraction of the posters that are not covered by the opaque paper = \(\frac{The number of parts that are not covered with opaque paper}{The total number of parts}\)
= \(\frac{2}{5}\)
Hence, from the above,
We can conclude that
The fraction of the posters that are not covered by the opaque paper is: \(\frac{2}{5}\)

Review What You Know
Vocabulary
- equivalent fractions
- mixed number
- fraction
- whole number
Choose the best term from the box. Write it on the blank.
Question 1.
A _________ has a whole number and a fraction.
Answer:
We know that,
A “Mixed number” has a whole number and a fraction.
Hence, from the above,
We can conclude that
The best term that is suitable for the given sentence is: Mixed number
Question 2.
Fractions that name the same region, part of a set or part of a segment are called __________
Answer:
We know that,
Fractions that name the same region, part of a set, or part of a segment are called “Equivalent fractions”
Hence, from the above,
We can conclude that
The best term that is suitable for the given sentence is: Equivalent fractions
Question 3.
A _________ has a numerator and a denominator.
Answer:
We know that,
A “Fraction” has a numerator and a denominator
Hence, from the above,
We can conclude that
The best term that is suitable for the given sentence is: Fraction
Identifying Fractions
Write the fraction shown by each model.
Question 4.
![]()
Answer:
The given model is:
![]()
Now,
From the given model,
The total number of parts are: 4
The shaded part is: 1
So,
The fraction represented by the given model = \(\frac{The shaded part}{The total number of parts}\)
= \(\frac{1}{4}\)
Hence, from the above,
We can conclude that
The fraction represented by the given model is: \(\frac{1}{4}\)
Question 5.
![]()
Answer:
The given model is:
![]()
Now,
From the given model,
The total number of parts are: 3
The shaded part is: 2
So,
The fraction represented by the given model = \(\frac{The shaded part}{The total number of parts}\)
= \(\frac{2}{3}\)
Hence, from the above,
We can conclude that
The fraction represented by the given model is: \(\frac{2}{3}\)
Question 6.
![]()
Answer:
The given model is:
![]()
Now,
From the given model,
The total number of parts are: 8
The shaded part is: 5
So,
The fraction represented by the given model = \(\frac{The shaded part}{The total number of parts}\)
= \(\frac{5}{8}\)
Hence, from the above,
We can conclude that
The fraction represented by the given model is: \(\frac{5}{8}\)

Question 7.
![]()
Answer:
The given model is:
![]()
Now,
From the given model,
The total number of parts are: 5
The shaded part is: 1
So,
The fraction represented by the given model = \(\frac{The shaded part}{The total number of parts}\)
= \(\frac{1}{5}\)
Hence, from the above,
We can conclude that
The fraction represented by the given model is: \(\frac{1}{5}\)
Question 8.
![]()
Answer:
The given model is:
![]()
Now,
From the given model,
The total number of parts are: 10
The shaded part is: 5
So,
The fraction represented by the given model = \(\frac{The shaded part}{The total number of parts}\)
= \(\frac{5}{10}\)
Hence, from the above,
We can conclude that
The fraction represented by the given model is: \(\frac{5}{10}\)
Question 9.
![]()
Answer:
The given model is:
![]()
Now,
From the given model,
The total number of parts are: 2
The shaded part is: 1
So,
The fraction represented by the given model = \(\frac{The shaded part}{The total number of parts}\)
= \(\frac{1}{2}\)
Hence, from the above,
We can conclude that
The fraction represented by the given model is: \(\frac{1}{2}\)
Unit Fractions
Write a fraction for each statement.
Question 10.
3 copies of \(\frac{1}{6}\) is _______.
Answer:
The given statement is:
3 copies of \(\frac{1}{6}\)
So,
The representation of the given statement is: 3 × \(\frac{1}{6}\)
So,
3 × \(\frac{1}{6}\)
= \(\frac{3}{6}\)
Hence, from the above,
We can conclude that the fraction for the given statement is: \(\frac{3}{6}\)
Question 11.
9 copies of \(\frac{1}{12}\) is _________
Answer:
The given statement is:
9 copies of \(\frac{1}{12}\)
So,
The representation of the given statement is: 9 × \(\frac{1}{12}\)
So,
9 × \(\frac{1}{12}\)
= \(\frac{9}{12}\)
Hence, from the above,
We can conclude that the fraction for the given statement is: \(\frac{9}{12}\)
Question 12.
5 copies of \(\frac{1}{5}\) is ___________
Answer:
The given statement is:
5 copies of \(\frac{1}{5}\)
So,
The representation of the given statement is: 5 × \(\frac{1}{5}\)
So,
5 × \(\frac{1}{5}\)
= \(\frac{5}{5}\)
Hence, from the above,
We can conclude that the fraction for the given statement is: \(\frac{5}{5}\)
Question 13.
3 copies of \(\frac{1}{10}\) is _________.
Answer:
The given statement is:
3 copies of \(\frac{1}{10}\)
So,
The representation of the given statement is: 3 × \(\frac{1}{10}\)
So,
3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)
Hence, from the above,
We can conclude that the fraction for the given statement is: \(\frac{3}{10}\)
Question 14.
6 copies of \(\frac{1}{8}\) is _________.
Answer:
The given statement is:
6 copies of \(\frac{1}{8}\)
So,
The representation of the given statement is: 6 × \(\frac{1}{8}\)
So,
6 × \(\frac{1}{8}\)
= \(\frac{6}{8}\)
Hence, from the above,
We can conclude that the fraction for the given statement is: \(\frac{6}{8}\)
Question 15.
7 copies of \(\frac{1}{10}\) is _________.
Answer:
The given statement is:
7 copies of \(\frac{1}{10}\)
So,
The representation of the given statement is: 7 × \(\frac{1}{10}\)
So,
7 × \(\frac{1}{10}\)
= \(\frac{7}{10}\)
Hence, from the above,
We can conclude that the fraction for the given statement is: \(\frac{7}{10}\)
Equivalent Fractions
Question 16.
Draw a rectangle that shows 8 equal parts. Shade more than \(\frac{3}{8}\) of the rectangle but less than \(\frac{5}{8}\). What fraction did you model? Use multiplication or division to write two equivalent fractions for your model.
Answer:
It is given that
Draw a rectangle that shows 8 equal parts. Shade more than \(\frac{3}{8}\) of the rectangle but less than \(\frac{5}{8}\)
Now,
The representation of the rectangle with the total number of parts and shaded parts is:
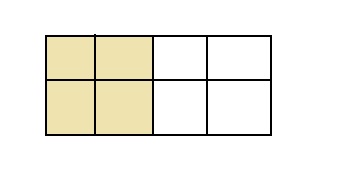
Now,
From the given figure,
We can observe that
The total number of parts are: 8
The number of shaded parts is: 4
The number of non-shaded parts is: 4
Now,
The fraction of the shaded part from the model = \(\frac{The number of shaded parts}{The total number of parts}\)
= \(\frac{4}{8}\)
= \(\frac{1}{2}\)
Hence, from the above,
We can conclude that
The equivalent fractions of the shaded part for your model are:
a. \(\frac{4}{8}\)
b. \(\frac{1}{2}\)
Pick a Project
PROJECT 10A
Would you like to work with tiles?
Project: Design with Tiles

PROJECT 10B
What cause would you donate your time or money to?
Project: Set Up a Charity Event

PROJECT 10C
How fast can a jet aircraft travel?
Project: Write and Perform a Skit

PROJECT 10D
How would you like to run a marathon?
Project: Make a Game about Marathon Winners

Lesson 10.1 Fractions as Multiples of Unit Fractions
Solve & Share
Kalil and Mara were working on their math homework. Mara wrote \(\frac{4}{5}\) as \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\). Kalil looked at Mara’s work and said, “I think you could use multiplication to rewrite your equation.” Is Kalil’s observation correct? Explain.
I can … use fraction strips or number lines to understand a fraction as a multiple of a unit fraction.

Answer:
It is given that
Kalil and Mara were working on their math homework. Mara wrote \(\frac{4}{5}\) as \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\). Kalil looked at Mara’s work and said, “I think you could use multiplication to rewrite your equation.”
Now,
We know that,
“Repeated addition” is also known as “Multiplication”. If the same number is repeated then in short we can write that in the form of multiplication
Ex:
2 is repeated 5 times so in short, we can write this addition as 2 x 5.
So,
According to Kalil, Mara’s work can also be represented in the form of multiplication
So,
\(\frac{4}{5}\) can also be written as:
\(\frac{4}{5}\) = 4 × \(\frac{1}{5}\)
Hence, from the above,
We can conclude that Kalil’s observation is correct
Look Back! Model with Math
Write an equation to show the relationship between Mara’s work and Kalil’s observation.
Answer:
According to Mara,
\(\frac{4}{5}\) = \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)
Now,
We know that,
“Repeated addition” is also known as “Multiplication”. If the same number is repeated then in short we can write that in the form of multiplication
So,
According to Kalil,
Mara’s work can also be represented as:
\(\frac{4}{5}\) = 4 × \(\frac{1}{5}\)
Now,
The relationship between Mara’s work and Kalil’s observation is:
\(\frac{4}{5}\) = 4 × \(\frac{1}{5}\)
So,
\(\frac{1}{5}\) is repeated 4 times
So,
In short, we can write this addition as 4 x \(\frac{1}{5}\)
Hence, from the above,
We can conclude that
The relationship between Mara’s work and Kalil’s observation is:
\(\frac{1}{5}\) is repeated 4 times
So,
In short, we can write this addition as 4 x \(\frac{1}{5}\)
Essential Question
How Can You Describe a Fraction Using a Unit Fraction?
Answer:
A fraction can be converted into a unit fraction as explained below:
Put the whole number over 1 to turn it into a fraction.
Ex:
The whole number is: 5
The conversion of 5 into a unit fraction is: \(\frac{1}{5}\)
Visual Learning Bridge
Courtney ran \(\frac{3}{4}\) of the way to school. Describe \(\frac{3}{4}\) using unit fractions.

A unit fraction is a fraction that describes one part of the whole. Unit fractions always contain the numerator 1.
When a whole is divided into four equal parts, each part is described as the unit fraction \(\frac{1}{4}\).
Decompose \(\frac{3}{4}\) into unit fractions.
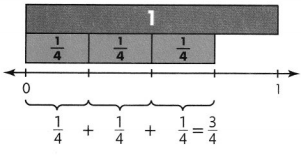
Repeated addition can be represented as multiplication.

Convince Me! Reasoning
The number \(\frac{5}{8}\) is a multiple of what unit fraction? Explain.
Answer:
The given fraction is: \(\frac{5}{8}\)
In the given fraction,
The numerator represents the shaded parts
The denominator represents the total number of parts
Now,
The representation of \(\frac{5}{8}\) is:

Now,
From the given model,
We will add \(\frac{1}{8}\) 5 times
So,
5 × \(\frac{1}{8}\) = \(\frac{5}{8}\)
Hence, from the above,
We can conclude that
\(\frac{5}{8}\) is a multiple of \(\frac{1}{8}\)
Another Example!
Describe \(\frac{5}{4}\) as a multiple of a unit fraction.
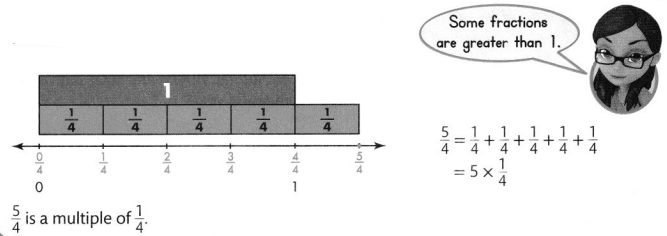
Guided Practice
Do You Understand?
Question 1.
Draw a picture to explain why \(\frac{3}{5}\) = 3 × \(\frac{1}{5}\).
Answer:
The given fraction is: \(\frac{3}{5}\)
In the given fraction,
The numerator represents the shaded parts
The denominator represents the total number of parts
Now,
The representation of the given fraction in the form of unit fractions is:
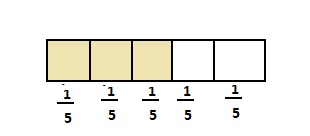
Now,
From the given model,
We will add \(\frac{1}{5}\) 3 times
So,
3 × \(\frac{1}{5}\) = \(\frac{3}{5}\)
Hence, from the above,
We can conclude that
\(\frac{3}{5}\) = 3 × \(\frac{1}{5}\)
Question 2.
Write a multiplication equation to show each part of the following story. Mark’s family ate \(\frac{7}{4}\) chicken pot pies for dinner. There are 7 people in Mark’s family. Each family member ate \(\frac{1}{4}\) of a pie.
Answer:
It is given that
Mark’s family ate \(\frac{7}{4}\) chicken pot pies for dinner. There are 7 people in Mark’s family. Each family member ate \(\frac{1}{4}\) of a pie.
So,
The representation of the given information in the form of a bar diagram is:
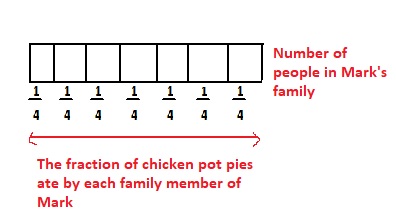
So,
The equation that shows the given information is:
(The total number of people present in Mark’s family) × (The fraction of pie eaten by each family member of Mark) = (The total amount of chicken pot pies eaten by Mark’s family for dinner)
7 × \(\frac{1}{4}\) = \(\frac{7}{4}\)
Hence, from the above,
We can conclude that
The multiplication equation to show the given information is:
(The total number of people present in Mark’s family) × (The fraction of pie eaten by each family member of Mark) = (The total amount of chicken pot pies eaten by Mark’s family for dinner)
Do You Know How?
For 3-6, write each fraction as a multiple of a unit fraction. Use a tool as needed.
Question 3.
\(\frac{2}{3}\) = ______ × \(\frac{1}{3}\)
Answer:
The given fraction is: \(\frac{2}{3}\)
Now,
In the given fraction,
The numerator represents the shaded part
The denominator represents the total number of parts
Now,
The representation of the given fraction as a multiple of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
\(\frac{2}{3}\) = 2 × \(\frac{1}{3}\)
Question 4.
\(\frac{5}{6}\) = 5 × \(\frac{1}{}\)
Answer:
The given fraction is: \(\frac{5}{6}\)
Now,
In the given fraction,
The numerator represents the shaded part
The denominator represents the total number of parts
Now,
The representation of the given fraction as a multiple of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
\(\frac{5}{6}\) = 5 × \(\frac{1}{6}\)
Question 5.
\(\frac{4}{2}\) = 4 × \(\frac{1}{}\)
Answer:
The given fraction is: \(\frac{4}{2}\)
Now,
In the given fraction,
The numerator represents the shaded part
The denominator represents the total number of parts
Now,
The representation of the given fraction as a multiple of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
\(\frac{4}{2}\) = 4 × \(\frac{1}{2}\)
Question 6.
\(\frac{6}{5}\) = 6 × \(\frac{1}{}\)
Answer:
The given fraction is: \(\frac{6}{5}\)
Now,
In the given fraction,
The numerator represents the shaded part
The denominator represents the total number of parts
Now,
The representation of the given fraction as a multiple of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
\(\frac{6}{5}\) = 6 × \(\frac{1}{5}\)
Independent Practice
Leveled Practice For 7-12, write each fraction as a multiple of a unit fraction. Use a tool as needed.
Question 7.

Answer:
The given fraction is: \(\frac{7}{8}\)
So,
The representation of the given fraction as a unit fraction is:
![]()
Hence, from the above model,
We can conclude that
\(\frac{7}{8}\) = 7 × \(\frac{1}{8}\)
Question 8.

Answer:
The given fraction is: \(\frac{3}{6}\)
So,
The representation of the given fraction as a unit fraction is:
![]()
Hence, from the above model,
We can conclude that
\(\frac{3}{6}\) = 3 × \(\frac{1}{6}\)
Question 9.
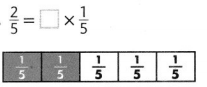
Answer:
The given fraction is: \(\frac{2}{5}\)
So,
The representation of the given fraction as a unit fraction is:
![]()
Hence, from the above model,
We can conclude that
\(\frac{2}{5}\) = 2 × \(\frac{1}{5}\)
Question 10.
\(\frac{6}{4}\)
Answer:
The given fraction is: \(\frac{6}{4}\)
So,
The representation of the given fraction as a unit fraction is:
![]()
Hence, from the above model,
We can conclude that
\(\frac{6}{4}\) = 6 × \(\frac{1}{4}\)
Question 11.
\(\frac{9}{6}\)
Answer:
The given fraction is: \(\frac{9}{6}\)
So,
The representation of the given fraction as a unit fraction is:
![]()
Hence, from the above model,
We can conclude that
\(\frac{9}{6}\) = 9 × \(\frac{1}{6}\)
Question 12.
\(\frac{8}{5}\)
Answer:
The given fraction is: \(\frac{8}{5}\)
So,
The representation of the given fraction as a unit fraction is:
![]()
Hence, from the above model,
We can conclude that
\(\frac{8}{5}\) = 8 × \(\frac{1}{5}\)
Problem Solving
Question 13.
Mark slices \(\frac{4}{6}\) of a tomato. Each slice is of the tomato. How many slices does Mark have? Explain by writing \(\frac{4}{6}\) as a multiple of \(\frac{1}{6}\).
Answer:
It is given that
Mark slices \(\frac{4}{6}\) of a tomato. Each slice is of the tomato
Now,
From the given fraction,
We can observe that
The number of shaded slices of tomato is: 4
The total number of slices of tomato are: 6
So,
The representation of the given fraction as a unit fraction is:
![]()
So,
The representation of the given fraction as a multiple of \(\frac{1}{6}\) is:
\(\frac{4}{6}\) = 4 × \(\frac{1}{6}\)
Hence, from the above,
We can conclude that
The number of slices does Mark have is: 6 slices
The representation of the given fraction as a multiple of \(\frac{1}{6}\) is:
\(\frac{4}{6}\) = 4 × \(\frac{1}{6}\)
Question 14.
Delia flew 2,416 miles the first year on the job. She flew 3,719 miles the second year. Delia flew 2,076 more miles the third year than the first and second years combined. How many miles did Delia fly the third year?
Answer:
It is given that
Delia flew 2,416 miles the first year on the job. She flew 3,719 miles the second year. Delia flew 2,076 more miles the third year than the first and second years combined
So,
The number of miles Deli flew the third year = 2,076 + (The number of miles Delia flew the first and the second years combined)
= 2,076 + (2,416 + 3,719)
= 2,076 + 6,135
= 8,211 miles
Hence, from the above,
We can conclude that
The number of miles did Delia fly the third year is: 8,211 miles
Question 15.
The model with Math
The picture below shows \(\frac{6}{2}\) pears. Write \(\frac{6}{2}\) as repeated addition and as a multiple of a unit fraction.

Answer:
It is given that
The picture below shows \(\frac{6}{2}\) pears
Now,
The given picture is:

So,
The representation of the given fraction as a unit fraction is:
![]()
Now,
The representation of the given fraction as a repeated addition is:
\(\frac{6}{2}\) = \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\)
Now,
The representation of the given fraction as a multiple of the unit fraction is:
\(\frac{6}{2}\) = 6 × \(\frac{1}{2}\)
Hence, from the above,
We can conclude that
The representation of \(\frac{6}{2}\) as a repeated addition and as a multiple of unit fraction respectively is:
a. \(\frac{6}{2}\) = \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\)
b. \(\frac{6}{2}\) = 6 × \(\frac{1}{2}\)
Question 16.
The picture below shows \(\frac{7}{2}\) apples. Write \(\frac{7}{2}\) as repeated addition and as a multiple of a unit fraction.

Answer:
It is given that
The picture below shows \(\frac{7}{2}\) apples
Now,
The given picture is:

So,
The representation of the given fraction as a unit fraction is:
![]()
Now,
The representation of the given fraction as a repeated addition is:
\(\frac{7}{2}\) = \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\)
Now,
The representation of the given fraction as a multiple of the unit fraction is:
\(\frac{7}{2}\) = 7 × \(\frac{1}{2}\)
Hence, from the above,
We can conclude that
The representation of \(\frac{7}{2}\) as repeated addition and as a multiple of unit fraction respectively is:
a. \(\frac{6}{2}\) = \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\)
b. \(\frac{7}{2}\) = 7 × \(\frac{1}{2}\)
Question 17.
enVision® STEM Light travels at a speed of about 186,000 miles per second. How far does light travel in 5 seconds?
Answer:
It is given that
Light travels at a speed of about 186,000 miles per second
So,
The distance traveled by light in 5 seconds = 5 × (The distance traveled by light in 1 second)
= 5 × 186,000
= 930,000 miles
Hence, from the above,
We can conclude that
The distance traveled by light in 5 seconds is: 930,000 miles
Question 18.
Higher-Order Thinking Kobe drinks \(\frac{1}{3}\) cup of juice each day. He has 2\(\frac{1}{3}\) cups of juice left. For how many days will it last? Explain by writing 2\(\frac{1}{3}\) as a fraction and then writing the fraction as a multiple of \(\frac{1}{3}\).
Answer:
It is given that
Kobe drinks \(\frac{1}{3}\) cup of juice each day. He has 2\(\frac{1}{3}\) cups of juice left.
So,
The representation of 2\(\frac{1}{3}\) as a fraction is:
2\(\frac{1}{3}\) = \(\frac{8}{3}\)
But,
It is given that
Kobe drinks \(\frac{1}{3}\) cup of juice each day
So,
The representation of \(\frac{8}{3}\) as a multiple of the unit fraction is:
\(\frac{8}{3}\) = 8 × \(\frac{1}{3}\)
So,
The total number of cups of juice left = (The total number of days) × (The number of cups Kobe drinks each day)
Hence, from the above,
We can conclude that
The number of days that \(\frac{8}{3}\) cups of juice will last is: 8 days
Assessment Practice
Question 19.
Which multiplication equation describes the fraction plotted on the number line?
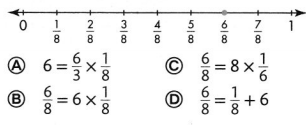
Answer:
The given number line is:
![]()
Now,
We know that,
We will write any fraction in terms of a multiple of the unit fraction as:
\(\frac{x}{y}\) = x × \(\frac{1}{y}\)
Now,
From the given number line,
We can observe that,
The value of y is: 8
So,
From the given options,
We have to check whether the given fraction is in the form of
\(\frac{x}{8}\) = x × \(\frac{1}{8}\)
Hence, from the above,
We can conclude that
The multiplication equation that describes the fraction plotted on the number line is:

Question 20.
Which multiplication equation describes the picture below?
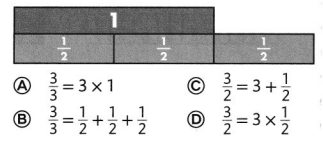
Answer:
The given number line is:

Now,
We know that,
We will write any fraction in terms of a multiple of the unit fraction as:
\(\frac{x}{y}\) = x × \(\frac{1}{y}\)
Now,
From the given number line,
We can observe that,
The value of y is: 2
So,
From the given options,
We have to check whether the given fraction is in the form of
\(\frac{x}{2}\) = x × \(\frac{1}{2}\)
Hence, from the above,
We can conclude that
The multiplication equation that describes the picture is:
Lesson 10.2 Multiply a Fraction by a Whole Number: Use Models
Solve & Share
How much tomato juice is needed for a group of 4 people if each person gets \(\frac{1}{3}\) cup of juice? How much tomato juice is needed if they each get \(\frac{2}{3}\) cup of juice? Solve these problems any way you choose.
I can… use drawings, area models, or number lines to multiply fractions by whole numbers.

Answer:
It is given that
There are 4 people and each person gets \(\frac{1}{3}\) cup of juice and after some time gets \(\frac{2}{3}\) cup of juice
So,
The amount of tomato juice needed for 4 people when each person gets \(\frac{1}{3}\) of juice
= (The number of people) × (The amount of juice each person gets)
= 4 × \(\frac{1}{3}\)
= \(\frac{4}{3}\) cups of tomato juice
So,
The amount of tomato juice needed for 4 people when each person gets \(\frac{2}{3}\) cups of juice
= (The number of people) × (The amount of juice each person gets)
= 4 × \(\frac{2}{3}\)
= \(\frac{4 × 2}{3}\)
= \(\frac{8}{3}\) cups of tomato juice
Hence, from the above,
We can conclude that
a. The amount of tomato juice needed for 4 people when each person gets \(\frac{1}{3}\) cup of juice is: \(\frac{4}{3}\) cups of tomato juice
b. The amount of tomato juice needed for 4 people when each person gets \(\frac{2}{3}\) cups of juice is: \(\frac{8}{3}\) cups of tomato juice
Look Back! Use Structure How does finding the total juice for 4 people with \(\frac{2}{3}\) cup servings compare to finding it for \(\frac{1}{3}\) cup servings? Why?
Answer:
From the above problem,
We can observe that
The amount of tomato juice needed for 4 people when each person gets \(\frac{1}{3}\) cup of juice is: \(\frac{4}{3}\) cups of tomato juice
The amount of tomato juice needed for 4 people when each person gets \(\frac{2}{3}\) cups of juice is: \(\frac{8}{3}\) cups of tomato juice
So,
The amount of tomato juice needed for 4 people when each person gets \(\frac{2}{3}\) cups of juice = \(\frac{8}{3}\) cups of tomato juice
= 4 × \(\frac{2}{3}\)
= 4 × 2 × \(\frac{1}{3}\)
= 2 × (The amount of tomato juice needed for 4 people when each person gets \(\frac{1}{3}\) cups of juice)
Hence, from the above,
We can conclude that
The amount of tomato juice needed for 4 people when each person gets \(\frac{2}{3}\) of juice is “2 Times” of the amount of tomato juice needed for 4 people when each person gets \(\frac{1}{3}\) of juice
Essential Question
How Can You Multiply a Fraction by a Whole Number?
Answer:
A fraction can be multiplied by a whole number as explained below:
Step 1:
Multiply across the top number by top number (numerator) and bottom number by bottom number (denominator).
Step 2:
Simplify your answer by dividing both numerator and denominator by the same number, when applicable.
Visual Learning Bridge
Dori lives \(\frac{1}{4}\) mile from school. If she walks to and from school each day, how far does Dori walk during a school week?
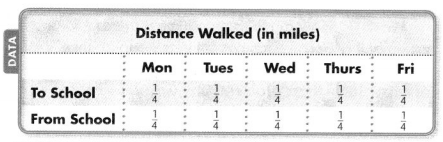
Remember, multiplication is repeated addition. So, you can use addition or multiplication to solve this problem.
One Way
Draw a picture to show Dori walks \(\frac{1}{4}\) mile, 10 times.
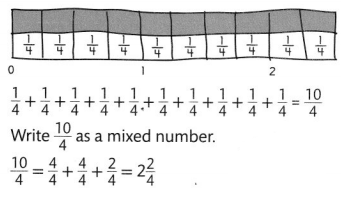
Since \(\frac{2}{4}\) is equivalent to \(\frac{1}{2}\), 2\(\frac{2}{4}\) is equivalent to 2\(\frac{1}{2}\). Dori walks 2\(\frac{1}{2}\)miles to and from school each week.
Another Way
Draw a number line to show Dori walks \(\frac{1}{4}\) mile, 10 times
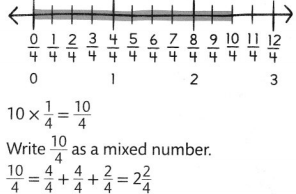
Convince Me! Generalize Why can both addition and multiplication be used to represent the problem above? Write an equation to explain.
Answer:
We know that,
The addition is the process of combining a number of individual items together to form a new total. This means that in multiplication, groups are created to represent the numbers being multiplied, and then the groups are added together to produce a total. Relating addition to multiplication is relatively simple.
Example:
We can write \(\frac{10}{4}\) as the repeated addition of \(\frac{2}{4}\) and as a multiplication as a multiple of \(\frac{2}{4}\)
So,
In the form of addition,
\(\frac{10}{4}\) = \(\frac{2}{4}\) + \(\frac{2}{4}\) + \(\frac{2}{4}\) + \(\frac{2}{4}\) + \(\frac{2}{4}\)
In the form of multiplication,
\(\frac{10}{4}\) = 5 × \(\frac{2}{4}\)
Another Example!
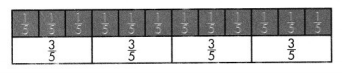
How far did Jess bike to practice if he biked mile each day for 4 days?
Use addition
\(\frac{3}{5}+\frac{3}{5}+\frac{3}{5}+\frac{3}{5}=\frac{12}{5}=\frac{5}{5}+\frac{5}{5}+\frac{2}{5}=2 \frac{2}{5}\)
Jess bikes 2\(\frac{2}{5}\) miles.
Use multiplication.
\(4 \times \frac{3}{5}=\frac{12}{5}=\frac{5}{5}+\frac{5}{5}+\frac{2}{5}=2 \frac{2}{5}\)
Jess bikes 2\(\frac{2}{5}\) miles.
Guided Practice
Do You Understand?
Question 1.
Draw a picture to explain how to find 3 × \(\frac{2}{5}\).
Answer:
The given fraction is:
3 × \(\frac{2}{5}\)
Now,
In the given fraction,
The numerator represents the shaded parts
The denominator represents the total number of parts
So,
The representation of the given fraction in the form of a bar diagram is:

Now,
From the given figure,
We can observe that
3 × \(\frac{2}{5}\) = \(\frac{2}{5}\) + \(\frac{2}{5}\) + \(\frac{2}{5}\)
Hence, from the above,
We can conclude that
The representation of the given fraction is:
3 × \(\frac{2}{5}\) = \(\frac{2}{5}\) + \(\frac{2}{5}\) + \(\frac{2}{5}\)
Do You Know How?
For 2-3, write and solve a multiplication equation.
Question 2.

Answer:
The given figures are:

Now,
From the first figure,
We can observe that
The number of shaded parts is: 2
The total number of parts are: 6
From the second figure,
We can observe that
The number of shaded parts is: 2
The total number of parts are: 6
So,
The representation of the given figures in the form of fractions are:
For the first figure,
The fraction of the shaded part = \(\frac{The number of shaded parts}{The total number of parts}\)
= \(\frac{2}{6}\)
For the second figure,
The fraction of the shaded part = \(\frac{The number of shaded parts}{The total number of parts}\)
= \(\frac{2}{6}\)
So,
The multiplication equation for the given figures is:
\(\frac{2}{6}\) + \(\frac{2}{6}\) = 2 × \(\frac{2}{6}\)
Hence, from the above,
We can conclude that
The multiplication equation for the given figures is:
\(\frac{2}{6}\) + \(\frac{2}{6}\) = 2 × \(\frac{2}{6}\)
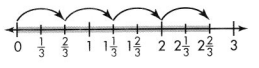
Question 3.
Answer:
The given number line is:

Now,
From the given number line,
We can observe that
The number line is showing the gap of 2 numbers
Now,
The representation of the multiplication equation for the given number line is:
n × \(\frac{1}{3}\)
Where,
n = 2, 4, 6, 8
Hence, from the above,
We can conclude that
The representation of the multiplication equation for the given number line is:
n × \(\frac{1}{3}\)
Where,
n = 2, 4, 6, 8
Independent Practice
For 4-7, write and solve a multiplication equation. Use drawings or number lines as needed.
Question 4.

Answer:
The given model is:

Now,
From the given model,
We can observe that
\(\frac{1}{8}\) is repeated 5 times
So,
The multiplication equation for the given model is:
\(\frac{1}{8}\) + \(\frac{1}{8}\)+ \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) (or) 5 × \(\frac{1}{8}\)
Hence, from the above,
We can conclude that
The multiplication equation for the given model is:
\(\frac{1}{8}\) + \(\frac{1}{8}\)+ \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) (or) 5 × \(\frac{1}{8}\)
Question 5.

Answer:
The given model is:

Now,
From the given model,
We can observe that
\(\frac{2}{10}\) is repeated 3 times
So,
The multiplication equation for the given model is:
\(\frac{2}{10}\) + \(\frac{2}{10}\) + \(\frac{2}{10}\) (or) 3 × \(\frac{2}{10}\)
Hence, from the above,
We can conclude that
The multiplication equation for the given model is:
\(\frac{2}{10}\) + \(\frac{2}{10}\) + \(\frac{2}{10}\) (or) 3 × \(\frac{2}{10}\)
Question 6.
Calculate the distance Margo rides her bike if she rides \(\frac{7}{8}\) mile each day for 4 days.
Answer:
It is given that
Margo rides her bike \(\frac{7}{8}\) mile each day for 4 days
So,
The distance traveled by Margo for 4 days = 4 × (The number of miles Margo rides each day)
= 4 × \(\frac{7}{8}\)
= \(\frac{4 × 7}{8}\)
= \(\frac{28}{8}\) miles
Hence, from the above,
We can conclude that
The distance Margo rides her bike for 4 days is: \(\frac{28}{8}\) miles
Question 7.
Calculate the distance Tom rides his bike if he rides \(\frac{5}{6}\) mile each day for 5 days.
Answer:
It is given that
Tom rides his bike \(\frac{5}{6}\) miles each day
So,
The distance Tom rides his bike for 5 days = 5 × (The number of miles Tom rides his bike each day)
= 5 × \(\frac{5}{6}\)
= \(\frac{5 × 5}{6}\)
= \(\frac{25}{6}\) miles
Hence, from the above,
We can conclude that
The distance Tom rides his bike for 5 days is: \(\frac{25}{6}\) miles
Problem Solving
Question 8.
Kiona fills a measuring cup with \(\frac{3}{4}\) cup of juice 3 times to make punch. Write and solve a multiplication equation with a whole number and a fraction to show the total amount of juice Kiona uses.

Answer:
It is given that
Kiona fills a measuring cup with \(\frac{3}{4}\) cup of juice 3 times to make a punch
So,
The total amount of juice Kiona uses = (The number of times Kiona fills a measuring cup) × (Each cup of juice that Kiona fills)
= 3 × \(\frac{3}{4}\)
= \(\frac{3 × 3}{4}\)
= \(\frac{9}{4}\) cups of juice
Hence, from the above,
We can conclude that
The total amount of juice Kiona uses is: \(\frac{9}{4}\) cups of juice
Question 9.
Each lap around a track is \(\frac{3}{10}\) kilometer. Eliot walked around the track 4 times. How far did Eliot walk?
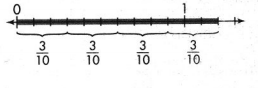
Answer:
It is given that
Each lap around a track is \(\frac{3}{10}\) kilometer. Eliot walked around the track 4 times.
So,
The distance that Eliot walked = (The number of times Eliot walked around the track) × (Each lap Eliot walked around a track)
= 4 × \(\frac{3}{10}\)
= \(\frac{4 × 3}{10}\)
= \(\frac{12}{10}\) Kilometers
Hence, from the above,
We can conclude that
The distance that Eliot walked is: \(\frac{12}{10}\) Kilometers
Question 10.
A chef serves \(\frac{5}{6}\) of a pan of lasagna. Each piece is \(\frac{1}{6}\) of the pan. How many pieces did the chef serve? Solve by writing \(\frac{5}{6}\) as a multiple of \(\frac{1}{6}\).
Answer:
It is given that
A chef serves \(\frac{5}{6}\) of a pan of lasagna. Each piece is \(\frac{1}{6}\) of the pan.
Now,
Let the number of pieces did the chef serve be: x
So,
The amount of a pan of lasagna the chef serves = (The number of pieces did the chef serve) × (Each piece of lasagna)
\(\frac{5}{6}\) = x × \(\frac{1}{6}\)
5 × \(\frac{1}{6}\) = x × \(\frac{1}{6}\)
x = 5 pieces
Hence, from the above,
We can conclude that
The number of pieces did the chef serves is: 5 pieces
Question 11.
Model with Math
Wendy uses \(\frac{2}{12}\) of a loaf of bread to make one sandwich. Write and solve an equation to find b, how much of the loaf of bread she uses to make 4 sandwiches. Use a drawing, as needed.
Answer:
It is given that
Wendy uses \(\frac{2}{12}\) of a loaf of bread to make one sandwich
So,
The amount of the loaf of bread Wendy uses to make 4 sandwiches = 4 × (The loaf of a bread used by Wendy to make one sandwich)
= 4 × \(\frac{2}{12}\)
= \(\frac{4 × 2}{12}\)
= \(\frac{8}{12}\) loaves of bread
Hence, from the above,
We can conclude that
The amount of loaf of bread used by Wendy to make 4 sandwiches is: \(\frac{8}{12}\) loaves of bread
Question 12.
Higher-Order Thinking A baker uses \(\frac{2}{3}\) cup of rye flour in each loaf of bread. How many cups of rye flour will the baker use in 3 loaves? in 7 loaves? in 10 loaves?
Answer:
It is given that
A baker uses \(\frac{2}{3}\) cup of rye flour in each loaf of bread
So,
The number of cups of rye flour will the baker use in 3 loaves = 3 × (The cup of rye flour used by the baker in each loaf of bread)
= 3 × \(\frac{2}{3}\)
= \(\frac{3 × 2}{3}\)
= \(\frac{6}{3}\) cups of rye flour
So,
The number of cups of rye flour will the baker use in 7 loaves = 7 × (The cup of rye flour used by the baker in each loaf of bread)
= 7 × \(\frac{2}{3}\)
= \(\frac{7 × 2}{3}\)
= \(\frac{14}{3}\) cups of rye flour
So,
The number of cups of rye flour will the baker use in 10 loaves = 10 × (The cup of rye flour used by the baker in each loaf of bread)
= 10 × \(\frac{2}{3}\)
= \(\frac{10 × 2}{3}\)
= \(\frac{20}{3}\) cups of rye flour
Hence, from the above,
We can conclude that
The number of cups of rye flour will the baker use in 3 loaves is: \(\frac{6}{3}\) cups
The number of cups of rye flour will the baker use in 7 loaves is: \(\frac{14}{3}\) cups
The number of cups of rye flour will the baker use in 10 loaves is: \(\frac{20}{3}\) cups
Assessment Practice
Question 13.
Elaine jogged \(\frac{4}{5}\) mile each day for 4 days. Select all the expressions that tell how far Elaine jogged in all. Use drawings or number lines as needed.
☐ 4 × \(\frac{4}{5}\)
☐ \(\frac{16}{5}\)
☐ 3 \(\frac{1}{5}\)
☐ 4 × \(\frac{1}{5}\)
☐ 2\(\frac{1}{5}\)
Answer:
It is given that
Elaine jogged \(\frac{4}{5}\) mile each day for 4 days
So,
The number of miles Elaine jogged for 4 days = 4 × (The number of miles Elaine jogged each day)
= 4 × \(\frac{4}{5}\)
= \(\frac{4 × 4}{5}\)
= \(\frac{16}{5}\) miles
= 3\(\frac{1}{5}\) miles
Hence, from the above,
We can conclude that all the expressions that tell how far Elaine jogged are:

Question 14.
Freddie skated \(\frac{1}{2}\) mile each day for 6 days. Select all the equations that can be used to find s, the total distance Freddie skated.
☐ s = \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\)
☐ s = 6 × \(\frac{1}{2}\)
☐ s = 6 + \(\frac{1}{2}\)
☐ s = 6 + 2 × \(\frac{1}{2}\)
☐ s = 6 × 2
Answer:
It is given that
Freddie skated \(\frac{1}{2}\) mile each day for 6 days
So,
The number of miles (s) Freddie skated for 6 days = 6 × (The number of miles Freddie skated each day)
= 6 × \(\frac{1}{2}\)
= \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\)
= \(\frac{6 × 1}{2}\)
= \(\frac{6}{2}\) miles
Hence, from the above,
We can conclude that all the equations that can be used to find s, the total distance Freddie skated are:

Lesson 10.3 Multiply a Fraction by a Whole Number: Use Symbols
Solve & Share
A recipe for 1 gallon of fruit punch calls for \(\frac{3}{4}\) cup of orange juice. How many cups of orange juice are needed to make 8 gallons of fruit punch? Solve this problem any way you choose.
I can… use properties and equations to multiply a fraction by a whole number.

Answer:
It is given that
A recipe for 1 gallon of fruit punch calls for \(\frac{3}{4}\) cup of orange juice
So,
The number of cups of orange juice needed to make 8 gallons of fruit punch = 8 × (The number of cups of orange juice needed to make 1 gallon of fruit punch)
= 8 × \(\frac{3}{4}\)
= \(\frac{8 × 3}{4}\)
= \(\frac{24}{4}\)
= 6 cups of orange juice
Hence, from the above,
We can conclude that
The number of cups of orange juice needed to make 8 gallons of fruit punch is: 6 cups of orange juice
Look Back! Be Precise Look back at your solution. What units should you use to label your answer?
Answer:
From the above problem,
We can observe that
The solution for the above problem is: 6 cups of orange juice (Which is the number of cups)
Hence, from the above,
We can conclude that
There are no units you should use to label your answer
Essential Question
How Can You Use Symbols to Multiply a Fraction by a Whole Number?
Answer:
A fraction can be multiplied by a whole number as explained below:
Step 1:
Multiply across the top number by top number (numerator) and bottom number by bottom number (denominator).
Step 2:
Simplify your answer by dividing both numerator and denominator by the same number, when applicable.
Visual Learning Bridge
Stanley makes ice cream sundaes. Today Stanley made 2 ice cream sundaes. How much ice cream did Stanley use? Find 2 × \(\frac{3}{4}\).
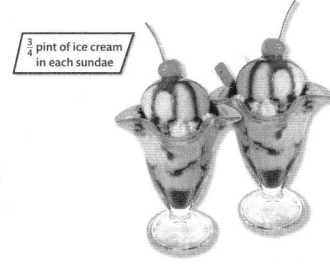
You can use structure when multiplying a fraction and a whole number.

Convince Me! Use Structure Use properties of operations to calculate 3 × \(\frac{3}{6}\). Show your work.
Answer:
The given fraction is: 3 × \(\frac{3}{6}\)
Now,
By using the unit fractions,
3 × \(\frac{3}{6}\)
= 3 × 3 × \(\frac{1}{6}\)
By using he Associative Property of Multiplication,
= (3 × 3) × \(\frac{1}{6}\)
= 9 × \(\frac{1}{6}\)
= \(\frac{9 × 1}{6}\)
= \(\frac{9}{6}\)
= \(\frac{3}{2}\)
Hence, from the above,
We can conclude that
The value of 3 × \(\frac{3}{6}\) is: \(\frac{3}{2}\)
Guided Practice
Do You Understand?
Question 1.
Sarah has \(\frac{1}{2}\) of a granola bar. Her friend has 5 times as many granola bars. How many granola bars does Sarah’s friend have?
Answer:
It is given that
Sarah has \(\frac{1}{2}\) of a granola bar. Her friend has 5 times as many granola bars
So,
The number of granola bars does Sarah’s friend have = (The number of times Sarah’s friend has as many granola bars) × (The number of pieces of each granola bar)
= 5 × \(\frac{1}{2}\)
= \(\frac{5}{2}\) granola bars
Hence, from the above,
We can conclude that
The number of granola bars does Sarah’s friend have is: \(\frac{5}{2}\) granola bars
Question 2.
Sue needs a \(\frac{5}{6}\) cup of cocoa to make one batch of chocolate pudding. She wants to make 4 batches of pudding to take to a party. Write and solve an equation to find how many cups of cocoa, c, Sue will need for all 4 batches of pudding.
Answer:
It is given that
Sue needs a \(\frac{5}{6}\) cup of cocoa to make one batch of chocolate pudding. She wants to make 4 batches of pudding to take to a party
So,
The number of cups of cocoa Sue will need for 4 batches of pudding (c) = 4 × (The amount of cocoa needed to make one batch of chocolate pudding)
= 4 × \(\frac{5}{6}\)
= \(\frac{4 × 5}{6}\)
= \(\frac{20}{6}\)
= \(\frac{10}{3}\) cups of cocoa
Hence, from the above,
We can conclude that
The number of cups of cocoa Sue will need for 4 batches of pudding is: \(\frac{10}{3}\) cups of pudding
Do You Know How?
For 3-4, multiply.
Question 3.
8 × \(\frac{1}{2}\)
Answer:
The given fraction is: 8 × \(\frac{1}{2}\)
So,
8 × \(\frac{1}{2}\)
= \(\frac{8 × 1}{2}\)
= \(\frac{8}{2}\)
= 4
Hence, from the above,
We can conclude that
The value of the given fraction is: 4
Question 4.
3 × \(\frac{3}{4}\)
Answer:
The given fraction is: 3 × \(\frac{3}{4}\)
So,
3 × \(\frac{3}{4}\)
= \(\frac{3 × 3}{4}\)
= \(\frac{9}{4}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{9}{4}\)
For 5-6, write and solve a multiplication equation.
Question 5.
Calculate the amount of medicine taken in 5 days if the dose is \(\frac{3}{4}\) fluid ounce per day.
Answer:
It is given that
The dose is \(\frac{3}{4}\) fluid ounce per day
So,
The amount of medicine taken in 5 days = 5 × (The amount of dose taken per day)
= 5 × \(\frac{3}{4}\)
= \(\frac{5 × 3}{4}\)
= \(\frac{15}{4}\) fluid ounces
Hence, from the above,
We can conclude that
The amount of medicine taken in 5 days is: \(\frac{15}{4}\) fluid ounces
Question 6.
Calculate the total length needed to decorate 9 boxes if each box uses \(\frac{2}{3}\) yard of ribbon.
Answer:
It is given that
Each box uses \(\frac{2}{3}\) yard of ribbon
So,
The total length of ribbon needed to decorate 9 boxes = 9 × (The length of ribbon used for each box)
= 9 × \(\frac{2}{3}\)
= \(\frac{9 × 2}{3}\)
= \(\frac{18}{3}\)
= 6 yards of ribbon
Hence, from the above,
We can conclude that
The total length of the ribbon needed to decorate 9 boxes is: 6 yards of ribbon
Independent Practice
For 7-15, multiply.
Question 7.
4 × \(\frac{1}{3}\)
Answer:
The given fraction is: 4 × \(\frac{1}{3}\)
So,
4 × \(\frac{1}{3}\)
= \(\frac{4 × 1}{3}\)
= \(\frac{4}{3}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{4}{3}\)
Question 8.
6 × \(\frac{3}{8}\)
Answer:
The given fraction is: 6 × \(\frac{3}{8}\)
So,
6 × \(\frac{3}{8}\)
= \(\frac{3 × 6}{8}\)
= \(\frac{18}{8}\)
= \(\frac{9}{4}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{9}{4}\)
Question 9.
8 × \(\frac{2}{5}\)
Answer:
The given fraction is: 8 × \(\frac{2}{5}\)
So,
8 × \(\frac{2}{5}\)
= \(\frac{8 × 2}{5}\)
= \(\frac{16}{5}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{16}{5}\)
Question 10.
2 × \(\frac{5}{6}\)
Answer:
The given fraction is: 2 × \(\frac{5}{6}\)
So,
2 × \(\frac{5}{6}\)
= \(\frac{2 × 5}{6}\)
= \(\frac{10}{6}\)
= \(\frac{5}{3}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{5}{3}\)
Question 11.
4 × \(\frac{2}{3}\)
Answer:
The given fraction is: 4 × \(\frac{2}{3}\)
So,
4 × \(\frac{2}{3}\)
= \(\frac{4 × 2}{3}\)
= \(\frac{8}{3}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{8}{3}\)
Question 12.
5 × \(\frac{7}{8}\)
Answer:
The given fraction is: 5 × \(\frac{7}{8}\)
So,
5 × \(\frac{7}{8}\)
= \(\frac{5 × 7}{8}\)
= \(\frac{35}{8}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{35}{8}\)
Question 13.
7 × \(\frac{3}{4}\)
Answer:
The given fraction is: 7 × \(\frac{3}{4}\)
So,
7 × \(\frac{3}{4}\)
= \(\frac{7 × 3}{4}\)
= \(\frac{21}{4}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{21}{4}\)
Question 14.
9 × \(\frac{3}{4}\)
Answer:
The given fraction is: 9 × \(\frac{3}{4}\)
So,
9 × \(\frac{3}{4}\)
= \(\frac{9 × 3}{4}\)
= \(\frac{27}{4}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{27}{4}\)
Question 15.
4 × \(\frac{5}{8}\)
Answer:
The given fraction is: 4 × \(\frac{5}{8}\)
So,
4 × \(\frac{5}{8}\)
= \(\frac{4 × 5}{8}\)
= \(\frac{20}{8}\)
= \(\frac{5}{2}\)
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{5}{2}\)
For 16-17, write and solve a multiplication equation.
Question 16.
Calculate the total distance Mary runs in one week if she runs a \(\frac{7}{8}\) mile each day.
Answer:
It is given that
Mary runs \(\frac{7}{8}\) miles each day
Now,
We know that,
1 week = 7 days
So,
The total distance Mary runs in 1 week = 7 × (The number of miles Mary runs each day)
= 7 × \(\frac{7}{8}\)
= \(\frac{7 × 7}{8}\)
= \(\frac{49}{8}\) miles
Hence, from the above,
We can conclude that
The total distance Mary runs in 1 week is: \(\frac{49}{8}\) miles
Question 17.
Calculate the length of 5 pieces of ribbon laid end to end if each piece is \(\frac{2}{3}\) yard long.
Answer:
It is given that
Each piece is \(\frac{2}{3}\) yard long
So,
The length of 5 pieces of ribbon laid end to end = 5 × (The length of each piece)
= 5 × \(\frac{2}{3}\)
= \(\frac{5 × 2}{3}\)
= \(\frac{10}{3}\) yards
Hence, from the above,
We can conclude that
The length of 5 pieces of ribbon laid end to end is: \(\frac{10}{3}\) yards
Problem Solving
Question 18.
A baseball team bought 8 boxes of baseballs. If the team spent a total of $1,696, what was the cost of 1 box of baseballs?
Answer:
A baseball team bought 8 boxes of baseballs and the team spent a total of $1,696
Now,
Let the cost of 1 box of baseballs be $x
So,
The total cost team spent = (The number of baseballs) × (The cost of 1 box of baseballs)
$1,696 = 8 × x
x = \(\frac{1,696}{8}\)
x = $212
Hence, from the above,
We can conclude that
The cost of 1 box of baseballs is: $212
Question 19.
Oscar wants to make 4 chicken pot pies. The recipe requires \(\frac{2}{3}\) pound of potatoes for each pot pie. How many pounds of potatoes will Oscar need?
Answer:
It is given that
Oscar wants to make 4 chicken pot pies. The recipe requires \(\frac{2}{3}\) pound of potatoes for each pot pie
So,
The number of pounds of potatoes oscar will need = (The number of chicken pot pies) × (The number of pounds of potatoes for each pot pie)
= 4 × \(\frac{2}{3}\)
= \(\frac{4 × 2}{3}\)
= \(\frac{8}{3}\) pounds of potatoes
Hence, from the above,
We can conclude that
The number of pounds of potatoes Oscar will need is: \(\frac{8}{3}\) pounds of potatoes
Question 20.
It takes Mario \(\frac{1}{4}\) hour to mow Mr. Harris’s lawn. It takes him 3 times as long to mow Mrs. Carter’s lawn. How long does it take Mario to mow Mrs. Carter’s lawn? Write your answer as a fraction of an hour, then as minutes.

Answer:
It is given that
It takes Mario \(\frac{1}{4}\) hour to mow Mr. Harris’s lawn. It takes him 3 times as long to mow Mrs. Carter’s lawn
So,
The time taken for Mario to mow Mrs. harris’s lawn = 3 × (The time taken for Mario to mow Mr.Harris’s lawn)
= 3 × \(\frac{1}{4}\)
= \(\frac{3 × 1}{4}\)
= \(\frac{3}{4}\) hours
Now,
It is given that
\(\frac{1}{4}\) hour = 15 minutes
So,
The time is taken for Mario to mow Mrsharris’s lawn = 3 × 15
= 45 minutes
Hence, from the above,
We can conclude that
The time taken for Mario to mow MrsHarris’s lawn is: \(\frac{3}{4}\) hours (or) 45 minutes
Question 21.
Vocabulary Use numerator, denominator, and whole number.
When you multiply a fraction by a whole number, the __________ in the product is the same as the denominator of the fraction. The ___________ in the product is the product of the and the numerator of the fraction.
Answer:
When you multiply a fraction by a whole number, the “Denominator” in the product is the same as the denominator of the fraction. The “Numerator” in the product is the product of the “Whole number” and the numerator of the fraction.
Question 22.
Model with Math
Malik swims \(\frac{9}{10}\) mile each day. Write and solve an equation to find n, how many miles Malik swims in 4 days.
Answer:
It is given that
Malik swims \(\frac{9}{10}\) mile each day
So,
The number of miles Malik swims in 4 days = 4 × (The number of miles Malik swims each day)
= 4 × \(\frac{9}{10}\)
= \(\frac{4 × 9}{10}\)
= \(\frac{36}{10}\)
= \(\frac{18}{5}\) miles
Hence, from the above,
We can conclude that
The number of miles Malik swims in 4 days is: \(\frac{18}{5}\) miles
Question 23.
Higher-Order Thinking Sam is making 7 fruit tarts. Each tart needs \(\frac{3}{4}\) cup of strawberries and \(\frac{1}{4}\) cup of blueberries. What is the total amount of fruit that Sam needs for his tarts? Use properties of operations to solve.
Answer:
It is given that
Sam is making 7 fruit tarts. Each tart needs \(\frac{3}{4}\) cup of strawberries and \(\frac{1}{4}\) cup of blueberries
So,
The total cups of fruit Sam needs for each tart = (The number of cups of strawberries needed for 1 fruit tart) + (The number of cups of blueberries needed for 1 fruit tart)
= \(\frac{3}{4}\) + \(\frac{1}{4}\)
= \(\frac{3 + 1}{4}\)
= \(\frac{4}{4}\)
= 1 cup
So,
The total amount of fruit Sam needs for his tarts = (The total number of fruit tarts) × (The numebr of cups of fruit Sam needs for each tart)
= 7 × 1
= 7 cups
Hence, from the above,
We can conclude that
The total amount of fruit Sam needs from his tarts is: 7 cups of strawberry and blueberries
Assessment Practice
Question 24.
Sean is making picture frames. Each frame uses \(\frac{4}{5}\) yard of wood. What is the total length of wood Sean will need to make 2 frames? Complete the equation.
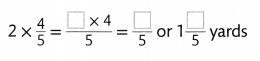
Answer:
It is given that
Sean is making picture frames. Each frame uses \(\frac{4}{5}\) yard of wood.
So,
The total length of the wood Sean will need to make 2 frames = (The total number of frames) × (The length of wood needed to make each frame)
= 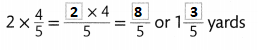
Hence, from the above,
We can conclude that
The total length of the wood Sean will need to make 2 frames is: \(\frac{8}{5}\) yards
Question 25.
Ellen is making plant boxes. Each box uses \(\frac{3}{6}\) yard of wood. What is the total length of wood Ellen will need to make 7 plant boxes? Complete the equation.

Answer:
It is given that
Ellen is making plant boxes. Each box uses \(\frac{3}{6}\) yard of wood
So,
The total length of wood Ellen need to make 7 plant boxes = 7 × (The length of wood used by Ellen for each box)
= 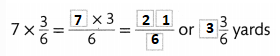
Hence, from the above,
We can conclude that
The total length of wood Ellen need to make 7 plant boxes is: \(\frac{21}{6}\) yards
Lesson 10.4 Solve Time Problems
Solve & Share
The Big Sur International Marathon is run on the California coast each spring. Sean’s mother was the women’s overall winner. How much faster was Sean’s mother than the women’s winner in the Ages 65-69 group? Tell me how you decided. Solve this problem any way you choose.
I can… use addition, subtraction, multiplication, or division to solve problems involving time.

Answer:
It is given that
The Big Sur International Marathon is run on the California coast each spring. Sean’s mother was the women’s overall winner
Now,
The given table is:

Now,
From the given table,
We can observe that
The time is taken by Sean’s mother to complete the marathon = 2 hours 50 minutes
The time is taken by Women’s Age group 65 – 69 to complete the marathon = 3 hours 58 minutes
So,
The time difference between Sean’s mother and women’s Age group 65 – 69 to complete the marathon = 3 hours 58 minutes – 2 hours 50 minutes
= 1 hour 8 minutes
Hence, from the above,
We can conclude that
Sean’s mother was faster by 1 hour 8 minutes than the women’s winner in the Ages 65-69 group
Look Back! The men’s winner in the Ages 70-74 group took 4\(\frac{1}{3}\) hours. Sean’s grandfather, who is only 68, took 3\(\frac{2}{3}\) hours. How can you find the difference in these times?
Answer:
It is given that
The men’s winner in the Ages 70-74 group took 4\(\frac{1}{3}\) hours. Sean’s grandfather, who is only 68, took 3\(\frac{2}{3}\) hours.
Now,
The given table is:

Now,
From the given table,
We can observe that
The time taken by Men’s winner Ages 70 – 74 group = 4 hours 20 minutes
Now,
We know that,
1 hour = 60 minutes
So,
4 hours 20 minutes = 4 + \(\frac{20}{60}\)
= 4\(\frac{1}{3}\) hours
Now,
The time is taken by Sean’s grandfather who is only 68 = 3 hours 34 minutes
≈ 3 hours 40 minutes
= 3 + \(\frac{40}{60}\)
= 3\(\frac{2}{3}\) hours
So,
The difference of time taken between men’s winner Ages 70 – 74 group and Sean’s grandfather
= 4\(\frac{1}{3}\) – 3\(\frac{2}{3}\)
= \(\frac{13}{3}\) – \(\frac{11}{3}\)
= \(\frac{13 – 11}{3}\)
= \(\frac{2}{3}\) hours
Hence, from the above,
We can conclude that
The difference of time taken between men’s winner Ages 70 – 74 group and Sean’s grandfather is about \(\frac{2}{3}\) hours
Essential Question
How Can You Solve Problems Involving Time?
Answer:
We know that,
When we want to find the total time,
We will add the given times
When we want to find the difference between time,
We will subtract the given times
Now,
We know that,
1 hour = 60 minutes
1 minute = \(\frac{1}{60}\) hours
Visual Learning Bridge
Krystal is training for a race. She trains every day for 8 days. How many hours does Krystal train?
Krystal spends an equal amount of time sprinting, walking, and jogging. How many minutes does Krystal spend on each activity during her 8 days of training?

You can use what you know about time to help solve these problems.
Find how many hours Krystal trains.
Find 8 × \(\frac{3}{4}\)
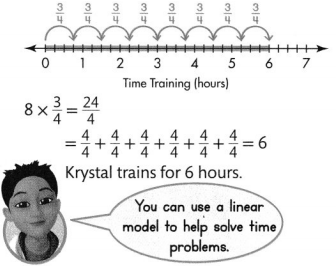
Find how many minutes Krystal spends on each activity during her training.
1 hour = 60 minutes
6 × 60 minutes = 360 minutes of training
In 8 days, Krystal spends 360 minutes sprinting, walking, and jogging.
Divide to find how many minutes Krystal spends on each activity. Find 360 ÷ 3.
![]()
In 8 days, Krystal spends 120 minutes, or 2 hours, training on each activity.
Convince Me! Construct Arguments Why do you multiply to convert 6 hours to minutes?
Answer:
From the previous example,
We can observe that
The amount of time taken by Krystal to train for 8 days is: 6 hours
But,
It is given that we have to find the amount of time in minutes
Now,
We know that,
1 hour = 60 minutes
So,
6 hours = 6 × 60 minutes
= 360 minutes
Hence, from the above,
We can conclude that
We will convert 6 hours into minutes because it has been asked to find the amount of time taken in minutes
Another Example!

Guided Practice
Do You Understand?
Question 1.
How are adding and subtracting measures of time like adding and subtracting whole numbers?
Answer:
The adding and subtracting measures of time is the same as adding and subtracting whole numbers when the measures of time are also whole numbers
But,
When the measures of time are the decimal numbers, we will borrow 60 minutes when the borrowing number is less than the second number
Do You Know How?
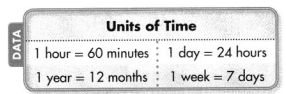
For 2-3, solve. Remember there are 60 minutes in 1 hour and 7 days in 1 week.
Question 2.
How many minutes are in a school day of 7 hours 25 minutes?
Answer:
It is given that
1 hour = 60 minutes
1 week = 7 days
So,
7 hours 25 minutes = (7 × 60) + 25
= 420 + 25
= 445 minutes
Hence, from the above,
We can conclude that
The number of minutes present in a school day of 7 hours 25 minutes is: 445 minutes
Question 3.
How much is 3\(\frac{2}{4}\) weeks + 2\(\frac{3}{4}\) weeks?
Answer:
The given fraction is:
3\(\frac{2}{4}\) weeks + 2\(\frac{3}{4}\) weeks
So,
3\(\frac{2}{4}\) weeks + 2\(\frac{3}{4}\) weeks
= \(\frac{14}{4}\) weeks + \(\frac{11}{4}\) weeks
= \(\frac{14 + 11}{4}\) weeks
= \(\frac{25}{4}\) weeks
Hence, from the above,
We can conclude that the value of 3\(\frac{2}{4}\) weeks + 2\(\frac{3}{4}\) weeks is:
\(\frac{25}{4}\) weeks
Independent Practice
For 4-7, add, subtract, multiply, or divide.
Question 4.
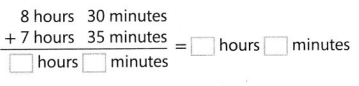
Answer:
We know that,
Now,
We know that,
When the number of minutes is greater than 60,
Convert 60 minutes into 1 hour and add that 1 hour to the number of hours we obtained in the result
Hence,
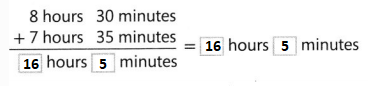
Question 5.

Answer:
We know that,

Now,
We know that,
When the number of months is less than the second number of months,
We have to borrow and we will borrow 12 months and add that 12 months into the first number of months
Hence,

Question 6.

Answer:
We know that,

Hence,
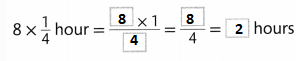
Question 7.
How long must each person work for 4 people to evenly share 48 hours of work?
48 ÷ 4 = ☐ hours
Answer:
We know that,

So,
The amount of time each person work for 4 people to evenly share 48 hours of work is:
![]()
Hence, from the above,
We can conclude that
The amount of time each person work for 4 people to evenly share 48 hours of work is: 12 hours
Problem Solving
For 8-9, use the table at the right.

Question 8.
How long do all of the activities at the reunion last?
Answer:
The given data is:

So,
The time that all of the activities at the reunion last = The total time is taken for all the activities to end
So,
The time that all of the activities at the reunion last = 4 hours 15 minutes + 55 minutes + 1 hour 30 minutes + 1 hour 35 minutes
= 6 hours 135 minutes
= 6 hours + 2 hours + 15 minutes
= 8 hours 15 minutes
Hence, from the above,
We can conclude that
The time that all of the activities at the reunion last is: 8 hours 15 minutes
Question 9.
There are 55 minutes between the time dinner ends and the campfire begins. What is the elapsed time from the beginning of dinner to the beginning of the campfire?
Answer:
It is given that
There are 55 minutes between the time dinner ends and the campfire begins
Now,
The given data is:

So,
The elapsed time from the beginning of dinner to the beginning of the campfire = (The end time of the slide show) – (The end time of Dinner)
= 1 hour 30 minutes – 55 minutes [1 hour = 60 minutes]
= 90 – 55
= 35 minutes
Hence, from the above,
We can conclude that
The elapsed time from the beginning of dinner to the beginning of the campfire is: 35 minutes
Question 10.
Make Sense and Persevere The band boosters spent $4,520 on airline tickets and $1,280 on hotel costs for the 8 members of the color guard. How much was spent for each member of the color guard?
Answer:
It is given that
The band boosters spent $4,520 on airline tickets and $1,280 on hotel costs for the 8 members of the color guard
So,
The total amount spent by the band boosters = (The amount spent by the band boosters on airline tickets) + (The amount spent by the band boosters on hotel costs)
= $4,520 + $1,280
= $5,800
So,
The amount spend for each member of the color guard = \(\frac{The total amount spent by the band boosters}{The total members present in the color guard}\)
= \(\frac{$5,800}{8}\)
= $725
Hence, from the above,
We can conclude that
The amount spend for each member of the color guard is: $725
Question 11.
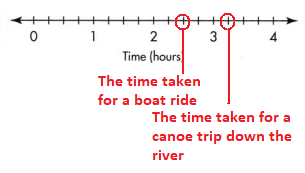
Higher-Order Thinking A boat ride at the lake lasts 2\(\frac{2}{4}\) hours. A canoe trip down the river lasts 3\(\frac{1}{4}\) hours. Show each time on the number line. How much longer is the canoe trip than the boat ride in hours? in minutes?
Answer:
It is given that
A boat ride at the lake lasts 2\(\frac{2}{4}\) hours. A canoe trip down the river lasts 3\(\frac{1}{4}\) hours
So,
The difference of time between the canoe trip and the boat ride in hours = 3\(\frac{1}{4}\) – 2\(\frac{2}{4}\)
= \(\frac{13}{4}\) – \(\frac{10}{4}\)
= \(\frac{13 – 10}{4}\)
= \(\frac{3}{4}\) hours
Now,
The difference of time between the canoe trip and the boat ride in minutes = \(\frac{3}{4}\) × 60 minutes
= \(\frac{3 × 60}{4}\)
= \(\frac{180}{4}\)
= 45 minutes
Now,
The representation of the canoe time and the time taken for a boat ride in the number line is:
Hence, from the above,
We can conclude that
The difference of time between the canoe trip and the boat ride in hours is: \(\frac{3}{4}\) hours
The difference of time between the canoe trip and the boat ride in minutes is: 45 minutes
Assessment Practice
Question 12.
It takes Krys and Glen \(\frac{1}{4}\) hour to walk a mile. This week Krys walked 9 miles and Glen walked 3 miles. How much longer did Krys walk than Glen?
________ hours
Answer:
It is given that
It takes Krys and Glen \(\frac{1}{4}\) hours to walk a mile. This week Krys walked 9 miles and Glen walked 3 miles
So,
The difference between the number of miles walked by Krys ad Glen = 9 – 3
= 6 miles
So,
The difference of time taken for Krys to walk faster than Glen = (The difference between the number of miles walked by Krys and Glen) × (The time taken by Krys and Glan to walk a mile)
= 6 × \(\frac{1}{4}\)
= \(\frac{6 × 1}{4}\)
= \(\frac{6}{4}\)
= \(\frac{3}{2}\)
= 1.5 hours
Hence, from the above,
We can conclude that
The difference of time taken for Krys to walk faster than Glen is: 1.5 hours
Question 13.
Henry’s first flight lasts 1 hour 12 minutes. The second flight lasts 2 hours 41 minutes. How much time did Henry spend on the flights?
_______ hours _______ minutes
Answer:
It is given that
Henry’s first flight lasts 1 hour 12 minutes. The second flight lasts 2 hours 41 minutes
So,
The total time spent by Henry on the flights = 1 hour 12 minutes + 2 hours 41 minutes
= 3 hours 53 minutes
Hence, from the above,
We can conclude that
The total time spent by Henry on the flights is: 3 hours 53 minutes
Lesson 10.5 Problem Solving
Model with Math
Solve & Share
Pierre’s mother owns an ice cream shop. She puts \(\frac{3}{12}\) cup of vanilla extract and \(\frac{1}{12}\) cup of almond extract in each 10-gallon batch of ice cream. How much total extract is used to make 5 batches of ice cream? Use the bar diagrams to represent and solve this problem.
I can …use various representations to solve problems.
Thinking Habits
Be a good thinker! These questions can help you.
- How can I use the math I know to help solve this problem?
- How can I use pictures, objects, or an equation to represent the problem?
- How can I use numbers, words, and symbols to solve the problem?
Answer:
It is given that
Pierre’s mother owns an ice cream shop. She puts \(\frac{3}{12}\) cup of vanilla extract and \(\frac{1}{12}\) cup of almond extract in each 10-gallon batch of ice cream.
So,
The total amount of extract that is used to make 1 batch of icecream = (The amount of vanilla extract) + (The amount of almond extract)
= \(\frac{3}{12}\) + \(\frac{1}{12}\)
= \(\frac{3 + 1}{12}\)
= \(\frac{4}{12}\)
= \(\frac{1}{3}\) cups
So,
The total extract present in 5 batches of icecream = 5 × (The total extract present in 1 batch of icecream)
= 5 × \(\frac{1}{3}\)
= \(\frac{5 × 1}{3}\)
= \(\frac{5}{3}\) cups
Now,
The representation of the given information in the form of a bar diagram is:

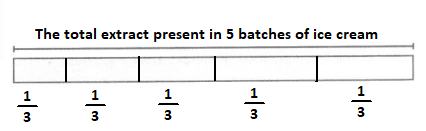
Hence, from the above,
We can conclude that
The total amount of extract present in 5 batches of ice cream is: \(\frac{5}{3}\) cups
Look Back! Model with Math What number sentences can you write to model the problem?
Answer:
The number of sentences that you can write to model the above problem is:
a.
The total amount of extract that is used to make 1 batch of icecream = (The amount of vanilla extract) + (The amount of almond extract)
b.
The total extract present in 5 batches of icecream = 5 × (The total extract present in 1 batch of icecream)
Essential Question
How Can You Represent a Situation with a Math Model?
Answer:
A “Math model” usually describes a system by a set of variables and a set of equations that establish relationships between the variables
Visual Learning Bridge
Mr. Finn gives the number of snacks shown to the baseball team’s coach every time the team wins a game. How many total pounds of snacks does Mr. Finn give the coach after the baseball team wins 3 games?
What hidden question do you need to find and solve first?
How many total pounds of snacks does Mr. Finn give the coach when the baseball team wins one game?
How can I model with math?
I can
- use previously learned concepts and skills.
- find and answer any hidden questions.
- use bar diagrams and equations to represent and solve this problem.
Here’s my thinking.
Let p = the pounds of snacks after one game.
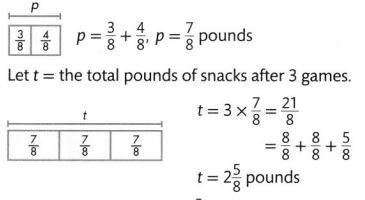
Mr. Finn gives the coach 2\(\frac{5}{8}\) pounds of snacks after the team wins 3 games.
Convince Me! Reasoning Explain how to solve this problem another way.
Answer:
It is given that
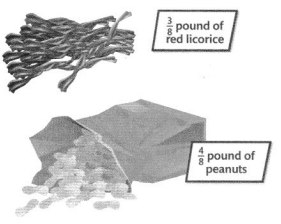
Mr. Finn gives the number of snacks shown to the baseball team’s coach every time the team wins a game.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The total number of pounds of snacks Mr.Finn give the coach after the baseball team wins 1 game =
(The number of pounds of red licorice) + (The number of pounds of peanuts)
= \(\frac{3}{8}\) + \(\frac{4}{8}\)
= \(\frac{3 + 4}{8}\)
= \(\frac{7}{8}\) pounds of snacks
Now,
The total number of pounds of snacks Mr.Finn give the coach after the baseball team wins 3 games =
3 × (The total number of pounds of snacks Mr.Finn give the coach after the baseball team wins 1 game)
= 3 × \(\frac{7}{8}\)
= \(\frac{3 × 7}{8}[/altex]
= [latex]\frac{21}{8}\) pounds of snacks
Hence, from the above,
We can conclude that
The total number of pounds of snacks Mr.Finn give the coach after the baseball team wins 3 games is: \(\frac{21}{8}\) pounds
Guided Practice
Model with Math
Colton and his classmates are making maps of the streets where they live. How much green and black felt does his teacher need to buy so 5 groups of students can each make a map?

Question 1.
Draw the bar diagrams and write equations to find g, the amount of green, and b, the amount of black felt.
Answer:
It is given that
Colton and his classmates are making maps of the streets where they live
Now,
The given information is:

Now,
From the given information,
The amount of green felt needed for each map (g) = \(\frac{4}{6}\) sheet of green
The amount of black felt needed for each map (b) = \(\frac{5}{6}\) sheet of black
Hence,
The representation of the given information in the form of a bar diagram is:

Question 2.
Write and solve an equation to find t, the amount of green and black felt the class will use.
Answer:
From Question 1,
We can observe that
The amount of green felt needed for each map (g) = \(\frac{4}{6}\) sheet of green
The amount of black felt needed for each map (b) = \(\frac{5}{6}\) sheet of black
So,
The total amount of green and black felts needed for each map (t) = (The amount of green felt needed fro each map) + (The amount of black felt needed for each map)
= \(\frac{4}{6}\) + \(\frac{5}{6}\)
= \(\frac{4 + 5}{6}\)
= \(\frac{9}{6}\)
= \(\frac{3}{2}\)
So,
the amount of green and black felt the class will use = 5 × \(\frac{3}{2}\)
= [altex]\frac{5 × 3}{2}[/latex]
= \(\frac{15}{2}\)
Hence, from the above,
We can conclude that
The total amount of green and black felt the class will use is: \(\frac{15}{2}\)
Independent Practice
Model with Math
Moira swims \(\frac{3}{6}\) hour before school 5 days a week and \(\frac{5}{6}\) hour after school 4 days a week. For how long does she swim each week? Use Exercises 3-5 to answer the question.
Question 3.
Draw a bar diagram and write an equation to find b, how many hours Moira swims before school each week.
Answer:
It is given that
Moira swims \(\frac{3}{6}\) hour before school 5 days a week and \(\frac{5}{6}\) hour after school 4 days a week.
So,
The number of hours Moira swims before school a week (b) = (The number of days Moira swims before school in a week) × (The number of hours Moira swims each day before school in a week)
= 5 × \(\frac{3}{6}\)
= \(\frac{5 × 3}{6}\)
= \(\frac{15}{6}\)
= \(\frac{5}{2}\) hours
Hence,
The representation of the information about the number of hours Moira swims before school each week is:

The number of hours Moira swims before school a week is: \(\frac{5}{2}\) hours
Question 4.
Draw a bar diagram and write an equation to find a, how many hours she swims after school each week.
Answer:
It is given that
Moira swims \(\frac{3}{6}\) hour before school 5 days a week and \(\frac{5}{6}\) hour after school 4 days a week.
So,
The number of hours Moira swims after school a week (a) = (The number of days Moira swims after school in a week) × (The number of hours Moira swims each day after school in a week)
= 4 × \(\frac{5}{6}\)
= \(\frac{5 × 4}{6}\)
= \(\frac{20}{6}\)
= \(\frac{10}{3}\) hours
Hence,
The representation of the information about the number of hours Moira swims after school each week is:

The number of hours Moira swims after school a week is: \(\frac{10}{3}\) hours
Question 5.
Draw a bar diagram and write an equation to find h, how many hours Moira swims each week.
Answer:
From Questions 3 and 4,
We can observe that
The number of hours Moira swims before school a week (b) is: \(\frac{5}{2}\) hours
The number of hours Moira swims after school a week (a) is: \(\frac{10}{3}\) hours
So,
The total number of hours Moira swims each week (h) = b + a
= \(\frac{5}{2}\) + \(\frac{10}{3}\)
= \(\frac{15}{6}\) + \(\frac{20}{6}\)
= \(\frac{15 + 20}{6}\)
= \(\frac{35}{6}\) hours
Hence,
The representation of the bar diagram for the number of hours Moira swims each week is:

The number of hours Moira swims each week is: \(\frac{35}{6}\) hours
Problem Solving
Performance Task
Seeing Orange
Perry mixed \(\frac{5}{8}\) gallon of red paint and \(\frac{3}{8}\) gallon of yellow paint to make the right shade of orange paint. He needs 2 gallons of orange paint to paint the basement floor. How many gallons of red and yellow paint should Perry use to make enough orange paint to cover the floor?
Question 6.
Reasoning What do you need to know to find how many gallons of each color Perry should use?
Answer:
It is given that
Perry mixed \(\frac{5}{8}\) gallon of red paint and \(\frac{3}{8}\) gallon of yellow paint to make the right shade of orange paint. He needs 2 gallons of orange paint to paint the basement floor
Hence,
To find how many gallons of each color Perry should use, we have to answer:
How many gallons of red paint and yellow paint are needed to make the right side of orange paint?
Question 7.
Model with Math
Draw the bar diagrams and write equations to find g, how many gallons of paint are in a batch, and b, how many batches Perry needs to make.

Answer:
It is given that
Perry mixed \(\frac{5}{8}\) gallon of red paint and \(\frac{3}{8}\) gallon of yellow paint to make the right shade of orange paint. He needs 2 gallons of orange paint to paint the basement floor
So,
The total amount of paint needed to make the right side of orange paint = (The number of gallons of red paint) + (The number of gallons of yellow paint)
= \(\frac{5}{8}\) + \(\frac{3}{8}\)
= \(\frac{5 + 3}{8}\)
= \(\frac{8}{8}\)
= 1 gallon
Now,
The number of gallons needed for Perry to paint the basement floor = (The number of gallons of orange paint needed to paint the basement floor) × (The total amount of paint needed to make the right side of orange paint)
= 2 × 1
= 2 gallons
Hence,
The representation of the given information in the form of a bar diagram is:

The number of gallons needed for Perry to paint the basement floor is: 2 gallons
Question 8.
Model with Math
Draw the bar diagrams and write and solve equations to show how to find how many gallons of each color Perry should use. Tell what your variables represent.
Answer:
It is given that
Perry mixed \(\frac{5}{8}\) gallon of red paint and \(\frac{3}{8}\) gallon of yellow paint to make the right shade of orange paint. He needs 2 gallons of orange paint to paint the basement floor
So,
The number of gallons of each color Perry should use = 2 × (The number of gallons of red paint) + 2 × (The number of gallons of yellow paint)
= 2 × \(\frac{5}{8}\) + 2 × \(\frac{3}{8}\)
= \(\frac{2 × 5}{8}\) + \(\frac{2 × 3}{8}\)
= \(\frac{10}{8}\) + \(\frac{6}{8}\)
= \(\frac{10 + 6}{8}\)
= \(\frac{16}{8}\)
= 2 gallons
Hence,
The representation of the given information in the form of a bar diagram is:
The number of gallons of red paint Perry should use is: \(\frac{10]{8}\) gallons
The number of gallons of yellow paint Perry should use is: \(\frac{6]{8}\) gallons
Topic 10 Fluency Practice Activity
Pointe Tall
Find a partner. Get paper and a pencil. Each partner chooses a different color: light blue or dark blue.
Partner 1 and Partner 2 each point to a black number at the same time. Each partner adds the two numbers.
If the answer is on your color, you get a tally mark. Work until one partner has twelve tally marks.
I can … add multi-digit whole numbers.
Topic 10 Vocabulary Review
Understand Vocabulary
Word List
- denominator
- equivalent fractions
- fraction
- mixed number
- multiple
- numerator
- unit fraction
Write T for true and F for false.
Question 1.
_______ The fraction \(\frac{3}{4}\) is a multiple of \(\frac{1}{4}\).
Answer:
The given statement is:
The fraction \(\frac{3}{4}\) is a multiple of \(\frac{1}{4}\)
Now,
We know that,
n × \(\frac{1}{y}\) is always a multiple of \(\frac{1}{y}\)
Hence, from the above,
We can conclude that
The fraction \(\frac{3}{4}\) is a multiple of \(\frac{1}{4}\) is: True
Question 2.
__________ Equivalent fractions are fractions where the numerator and the denominator have the same value.
Answer:
The given statement is:
Equivalent fractions are fractions where the numerator and the denominator have the same value
Now,
We know that,
The “Equivalent fractions” are the fractions that have different values of numerator and denominator
Hence, from the above,
We can conclude that
Equivalent fractions are fractions where the numerator and the denominator have the same value is: False
Question 3.
__________ The denominator of a fraction tells the number of equal parts in the whole.
Answer:
The given statement is:
The denominator of a fraction tells the number of equal parts in the whole.
Now,
We know that,
In the fraction \(\frac{x}{y}\),
x represents the number of shaded parts
y represents the total number of equal parts
Hence, from the above,
We can conclude that
The denominator of a fraction tells the number of equal parts in the whole is: True
Question 4.
___________ A fraction names part of a whole, part of a set, or a location on a number line.
Answer:
The given statement is:
A fraction names part of a whole, part of a set, or a location on a number line.
Now,
We know that,
A symbol used to name a part of a whole, a part of a set, or a location on a number line is called a “Fraction”
Hence, from the above,
We can conclude that
A fraction names part of a whole, part of a set, or a location on a number line is: True
Question 5.
________ The numerator is the number below the fraction bar in a fraction.
Answer:
The given statement is:
The numerator is the number below the fraction bar in a fraction.
Now,
We know that,
The “Denominator” is the number below the fraction bar in a fraction
Hence, from the above,
We can conclude that
The numerator is the number below the fraction bar in a fraction is: False
Write always, sometimes, or never.
Question 6.
A unit fraction __________ has a numerator of 1.
Answer:
The given statement is:
A unit fraction __________ has a numerator of 1.
Hence, from the above,
We can conclude that
A unit fraction “always” has a numerator of 1.
Question 7.
A numerator is _________ greater than its denominator.
Answer:
The given statement is:
A numerator is _________ greater than its denominator.
Hence, from the above,
We can conclude that
A numerator is “sometimes” greater than its denominator.
Question 8.
A mixed number _________ has just a fraction part.
Answer:
The given statement is:
A mixed number _________ has just a fraction part.
Hence, from the above,
We can conclude that
A mixed number “never” has just a fraction part.
Use Vocabulary in Writing
Question 9.
Samatha wrote \(\frac{1}{2}\). Use at least 3 terms from the Word List to describe Samantha’s fraction.

Answer:
It is given that
Samatha wrote \(\frac{1}{2}\).
Hence, from the above,
We can conclude that
The 3 terms from the word list to describe Samantha’s fraction are:
a. Fraction
b Unit fraction
c Equivalent fraction
Topic 10 Reteaching
Set A pages 385-388
Talia used \(\frac{5}{8}\) yard of ribbon.
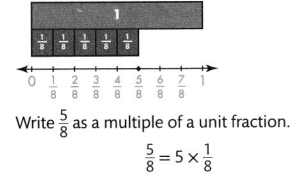
Remember a unit fraction will always have a numerator of 1
Write each fraction as a multiple of a unit fraction.
Question 1.
\(\frac{5}{5}\)
Answer:
The given fraction is: \(\frac{5}{5}\)
So,
The representation of the given fraction in the form of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
The given fraction as a multiple of a unit fraction is:
\(\frac{5}{5}\) = 5 × \(\frac{1}{5}\)
Question 2.
\(\frac{3}{8}\)
Answer:
The given fraction is: \(\frac{3}{8}\)
So,
The representation of the given fraction in the form of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
The given fraction as a multiple of a unit fraction is:
\(\frac{3}{8}\) = 3 × \(\frac{1}{8}\)
Question 3.
\(\frac{4}{3}\)
Answer:
The given fraction is: \(\frac{4}{3}\)
So,
The representation of the given fraction in the form of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
The given fraction as a multiple of a unit fraction is:
\(\frac{4}{3}\) = 4 × \(\frac{1}{3}\)
Question 4.
\(\frac{6}{5}\)
Answer:
The given fraction is: \(\frac{6}{5}\)
So,
The representation of the given fraction in the form of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
The given fraction as a multiple of a unit fraction is:
\(\frac{6}{5}\) = 6 × \(\frac{1}{5}\)
Question 5.
\(\frac{15}{8}\)
Answer:
The given fraction is: \(\frac{15}{8}\)
So,
The representation of the given fraction in the form of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
The given fraction as a multiple of a unit fraction is:
\(\frac{15}{8}\) = 15 × \(\frac{1}{8}\)
Question 6.
\(\frac{7}{4}\)
Answer:
The given fraction is: \(\frac{7}{4}\)
So,
The representation of the given fraction in the form of a unit fraction is:
![]()
Hence, from the above,
We can conclude that
The given fraction as a multiple of a unit fraction is:
\(\frac{7}{4}\) = 7 × \(\frac{1}{4}\)
Set B pages 389-392
James runs \(\frac{3}{5}\) mile each week. How far does James run after 2 weeks?
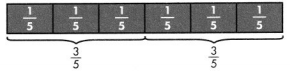
Use multiplication to find the product.
\(2 \times \frac{3}{5}=\frac{3}{5}+\frac{3}{5}=\frac{6}{5}=\frac{5}{5}+\frac{1}{5}=1 \frac{1}{5}\)
James ran \(\frac{6}{5}\) or 1\(\frac{1}{5}\) miles.
Remember you can record answers as fractions or mixed numbers.
Write and solve an equation.
Question 1.
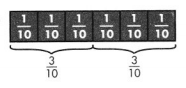
Answer:
The given model is:

Now,
From the given model,
We can observe that
3 × \(\frac{1}{10}\) + 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\) + \(\frac{3}{10}\)
= \(\frac{3 + 3}{10}\)
= \(\frac{6}{10}\)
= \(\frac{3}{5}\)
Hence, from the above,
We can conclude that
The value for the given model is: \(\frac{3}{5}\)
Question 2.
Answer:
The given model is:

Now,
From the given model,
We can observe that
The total number of parts are: 6
The number of shaded parts is: 4
So,
The fraction of the shaded part in the given model = \(\frac{The number of shaded parts}{The total number of parts}\)
= \(\frac{4}{6}\)
= \(\frac{2}{3}\)
Hence, from the above,
We can conclude that
The value for the given model is: \(\frac{2}{3}\)
Set C pages 393-396
Alisa has 7 puppies. Each puppy eats \(\frac{2}{3}\) cup of food each day. How many cups of food does Alisa need to feed the puppies each day?
Multiply 7 × \(\frac{2}{3}\)
Multiply the whole number and the numerator.
\(7 \times \frac{2}{3}=\frac{7 \times 2}{3}\)
= \(\frac{14}{3}\)
= \(\frac{3}{3}+\frac{3}{3}+\frac{3}{3}+\frac{3}{3}+\frac{2}{3}\)
= 4\(\frac{2}{3}\) cups
Alisa needs 4\(\frac{2}{3}\) cups of food to feed the puppies each day.
Remember you multiply the whole number and the numerator and write the product above the denominator of the fraction.
Question 1.
Milo makes 5 batches of muffins. In each batch he uses \(\frac{2}{3}\) bag of walnuts. How many bags of walnuts does Milo use?
Answer:
It is given that
Milo makes 5 batches of muffins. In each batch he uses \(\frac{2}{3}\) bag of walnuts.
So,
The number of bags of walnuts does Milo use = (The number of batches of muffins) × (The amount of bag of walnuts present in each batch)
= 5 × \(\frac{2}{3}\)
= \(\frac{5 × 2}{3}\)
= \(\frac{10}{3}\) bags of walnuts
Hence, from the above,
We can conclude that
The number of bags of walnuts does Milo used is: \(\frac{10}{3}\) bags of walnuts
Question 2.
A bird feeder can hold \(\frac{7}{8}\) pound of seeds. How many pounds of seeds can 4 bird feeders hold?
Answer:
It is given that
A bird feeder can hold \(\frac{7}{8}\) pound of seeds
So,
The number of pounds of seeds can 4 bird feeders hold = 4 × (The number of pounds of seeds a bird feeder can hold)
= 4 × \(\frac{7}{8}\)
= \(\frac{4 × 7}{8}\)
= \(\frac{28}{8}\)
= \(\frac{7}{2}\) pounds of seeds
Hence, from the above,
We can conclude that
The number of pounds of seeds can 4 bird feeders hold is: \(\frac{7}{2}\) pounds of seeds
Set D pages 397-400

Remember you may need to regroup when solving problems with time.
Question 1.

Answer:
We know that,
If the number of minutes is greater than 60 and we know that
1 hour = 60 minutes
Add that hour to the hours present in the result and keep the extra minutes intact
Hence,

Question 2.
7 × \(\frac{3}{4}\) hour
Answer:
The given fraction is: 7 × \(\frac{3}{4}\) hours
So,
7 × \(\frac{3}{4}\)
= \(\frac{7 × 3}{4}\)
= \(\frac{21]{4}\) hours
Hence, from the above,
We can conclude that
The value of the given fraction is: \(\frac{21}{4}\) hours
Question 3.

Answer:
We know that,
1 week = 7 days
So,
When the number of days is less than 7, borrow that 7 days from the number of weeks and add it to the number that is less than 7 and do the subtraction
Hence,

Question 4.
Divide 560 days into groups of 8.
Answer:
It is given that
Divide 560 days into groups of 8.
So,
Using the method of Long division,

Hence, from the above,
We can conclude that
560 days is divided into 70 equal parts when divided by 8
Question 5.
Li Marie practices piano 1\(\frac{2}{3}\) hours during the week and 2\(\frac{1}{3}\) hours on the weekend. Show each time on the number line. How many more hours does she practice on the weekend than on the weekdays?
Answer:
It is given that
Li Marie practices piano 1\(\frac{2}{3}\) hours during the week and 2\(\frac{1}{3}\) hours on the weekend
Now,
We know that,
The number of weekdays is: 5 days
The number of days in a weekend are: 2 days
So,
The number of hours Li Marie practices piano during the week = 5 × 1\(\frac{2}{3}\)
= 5 × \(\frac{5}{3}\)
= \(\frac{5 × 5}{3}\)
= \(\frac{25}{3}\) hours
So,
The number of hours Li Marie practices piano on the weekend = 2 × 2\(\frac{1}{3}\)
= 2 × \(\frac{7}{3}\)
= \(\frac{2 × 7}{3}\)
= \(\frac{14}{3}\) hours
So,
The difference between the number of hours Li Marie practices on the weekend and during the week =
\(\frac{25}{3}\) – \(\frac{14}{3}\)
= \(\frac{25 – 14}{3}\)
= \(\frac{11}{3}\) hours
So,
The representation of the number f hours Li Mario practices piano during the week and on the weekend on a number line is:
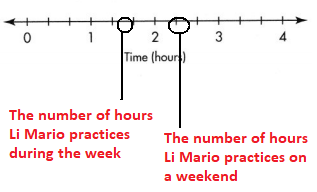
Hence, from the above,
We can conclude that
Li Mario practices \(\frac{11}{3}\) hours more on the weekend than the weekdays
Set E pages 401-404
Think about these questions to help you model math.
Thinking Habits
- How can I use the math I know to help solve this problem?
- How can I use pictures, objects, or an equation to represent the problem?
- How can I use numbers, words, and symbols to solve the problem?

Julie makes chili with 2\(\frac{3}{8}\) cups of red beans, 4\(\frac{1}{8}\) cups of chili beans, and \(\frac{7}{8}\) cup of onions. How many more cups of chili beans did Julie use than red beans and onions combined?
Question 1.
Write and solve an equation to find r, how many cups of red beans and onions Julie uses.
Answer:
It is given that
Julie makes chili with 2\(\frac{3}{8}\) cups of red beans, 4\(\frac{1}{8}\) cups of chili beans, and \(\frac{7}{8}\) cup of onions
So,
The number of cups of red beans and onions Julie uses to make chili (r) = (The number of cups of red beans used to make chili) + (The number of cups of onions used to make chili)
= 2\(\frac{3}{8}\) + \(\frac{7}{8}\)
= \(\frac{19}{8}\) + \(\frac{7}{8}\)
= \(\frac{19 + 7}{8}\)
= \(\frac{26}{8}\)
= \(\frac{13}{4}\) cups
Hence, from the above,
We can conclude that
The number of cups of red beans and onions Julie uses to make chili is: \(\frac{13}{4}\) cups
Question 2.
Write and solve an equation to find c, how many more cups of chili beans Julie used than red beans and onions.
Answer:
It is given that
Julie makes chili with 2\(\frac{3}{8}\) cups of red beans, 4\(\frac{1}{8}\) cups of chili beans, and \(\frac{7}{8}\) cup of onions
Now,
From Question 1,
The number of cups of red beans and onions Julie uses to make chili is: \(\frac{13}{4}\) cups
Now,
The number of more cups of chili beans Julie used than red beans and onions (c) = (The number of cups of chili beans Julie used to amke chili) – (The number of cups of red beans and onions Julie uses to make chili)
= 4\(\frac{1}{8}\) – \(\frac{13}{4}\)
= \(\frac{33}{8}\) – \(\frac{26}{8}\)
= \(\frac{33 – 26}{8}\)
= \(\frac{7}{8}\) cups
Hence, from the above,
We can conclude that
The number of more cups of chili beans Julie used than red beans and onions (c) is: \(\frac{7}{8}\) cups
Topic 10 Assessment Practice
Question 1.
Margo practices her flute \(\frac{1}{4}\) hour each day.

A. Write and solve an equation to find how many hours Margo practices her flute in 1 week.
Answer:
It is given that
Margo practices her flute \(\frac{1}{4}\) hour each day.
Now,
The given information is:

So,
The number of hours Margo practices her flute in 1 week = (The number of days in 1 week) × (The number of hours Margo practices her flute each day)
= 7 × \(\frac{1}{4}\)
= \(\frac{7 × 1}{4}\)
= \(\frac{7}{4}\) hours
Hence, from the above,
We can conclude that
The number of hours Margo practices her flute in 1 week is: \(\frac{7}{4}\) hours
B. Write and solve an equation to find how many minutes Margo practices her flute in 1 day. Then use that to find the number of minutes she practices in 1 week.
Answer:
It is given that
Margo practices her flute \(\frac{1}{4}\) hour each day.
Now,
The given information is:

Now,
We know that,
1 day = 24 hours
So,
The number of minutes Margo practices her flute in 1 day = (The number of hours Margo practices her flute in 1 day) × 60
= \(\frac{1}{4}\) × 60
= \(\frac{60}{4}\)
= 15 minutes
So,
The number of minutes Margo practices her flute in 1 week = (The number of days in 1 week) × (The number of minutes Margo practices her flute in 1 day)
= 7 × 15
= 7 × (10 + 5)
= (7 × 10) + (7 × 5)
= 70 + 35
= 105 minutes
Hence, from the above,
We can conclude that
The number of minutes Margo practices her flute in 1 day is: 15 minutes
The number of minutes Margo practices her flute in 1 week is: 105 minutes
Question 2.
Which of the following represents the fraction \(\frac{8}{9}\) as a multiple of a unit fraction?
A. \(\frac{8}{8}\) = 1 × \(\frac{8}{9}\)
B. \(\frac{8}{9}\) = 8 × 9
C. \(\frac{8}{9}\) = 8 × \(\frac{1}{9}\)
D. \(\frac{8}{9}\) = 4 × \(\frac{2}{9}\)
Answer:
The given fraction is: \(\frac{8}{9}\)
So,
The representation of the given fraction as a multiple of a unit fraction is:
\(\frac{8}{9}\) = 8 × \(\frac{1}{9}\)
Hence, from the above,
We can conclude that
The following equations represent the fraction \(\frac{8}{9}\) as a multiple of a unit fraction are:

Question 3.
Ben played at a friend’s house for 2 hours 35 minutes. Later he played at a park for 1 hour 10 minutes. He played for another 1 hour 20 minutes in his backyard. How long did Ben play in all?
A. 6 hours 27 minutes
B. 5 hours 15 minutes
C. 5 hours 5 minutes
D. 5 hours
Answer:
It is given that
Ben played at a friend’s house for 2 hours 35 minutes. Later he played at a park for 1 hour 10 minutes. He played for another 1 hour 20 minutes in his backyard
So,
The total amount of time taken by Ben to play in all = 2 hours 35 minutes + 1 hour 10 minutes + 1 hour 20 minutes
= 4 hours 65 minutes
= 5 hours 05 minutes
Hence, from the above,
We can conclude that
The time taken by Ben to play in all is:
Question 4.
Choose numbers from the list to fill in the missing values in the multiplication equations. Use each number once.

Answer:
The given number list is:

Hence, from the above,
We can conclude that
The numbers from the list that filled in the missing values in the multiplication equations are:
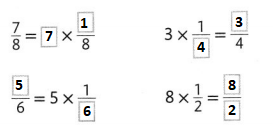
Question 5.
Chris found the products of whole numbers and fractions. Match each expression with its product.
Answer:
The given expressions with their matched products are:
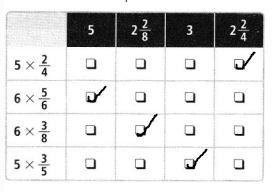
Question 6.
What is the product of 4 and \(\frac{4}{8}\)? Write another expression that is equal to the product of 4 and \(\frac{4}{8}\).
Answer:
The given numbers are: 4 and \(\frac{4}{8}\)
So,
4 × \(\frac{4}{8}\)
= 4 × 4 × \(\frac{1}{8}\)
= \(\frac{4 × 4}{8}\)
= \(\frac{16}{8}\)
= 2
Hence, from the above,
We can conclude that
The product of 4 × \(\frac{4}{8}\) is: 2
The another expression that is equal to 4 × \(\frac{4}{8}\) is: 4 × 4 × \(\frac{1}{8}\)
Question 7.
Complete the multiplication equation that describes that is shown by the model.
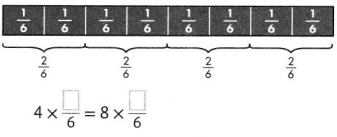
Answer:
The given model is:

Now,
From the given model,
We can observe that
\(\frac{1}{6}\) is repeated 8 times and \(\frac{2}{6}\) is repeated 4 times
So,

Hence, from the above,
We can conclude that
The completed multiplication equation that is shown by the model is:

Question 8.
Use a unit fraction and a whole number to write a multiplication equation equal to a \(\frac{7}{8}\).
Answer:
The given fraction is: \(\frac{7}{8}\)
So,
The representation of the given fraction in the form of a unit fraction and a whole number is:
\(\frac{7}{8}\) = 7 × \(\frac{1}{8}\)
Hence, from the above,
We can conclude that
The multiplication equation for the given fraction in the form of a unit fraction and a whole number is:
\(\frac{7}{8}\) = 7 × \(\frac{1}{8}\)
Question 9.
Juan is making cookies. He makes 2 batches on Monday and 4 batches on Tuesday. He uses \(\frac{3}{4}\) cup of flour in each batch. How much flour does Juan use? Explain.
Answer:
It is given that
Juan is making cookies. He makes 2 batches on Monday and 4 batches on Tuesday. He uses \(\frac{3}{4}\) cup of flour in each batch
So,
The total number of batches = (The number of batches made by Juan on Monday) + (The number of batches made by Juan on Tuesday)
= 2 + 4
= 6 batches
So,
The total amount of flour Juan used = (The total number of batches) × (The amount of flour used in each batch)
= 6 × \(\frac{3}{4}\)
= \(\frac{6 × 3}{4}\)
= \(\frac{18}{4}\)
= \(\frac{9}{2}\) cups of flour
Hence, from the above,
We can conclude that
The total amount of flour Juan used is: \(\frac{9}{2}\) cups of flour
Question 10.
Lee uses \(\frac{1}{5}\) yard of wire for each ornament he makes. He makes 3 ornaments for his grandmother and 2 ornaments for his mother. How many yards of wire did Lee use?
A. \(\frac{3}{5}\)
B. 1\(\frac{2}{5}\)
C. \(\frac{2}{5}\)
D. 1
Answer:
It is given that
Lee uses \(\frac{1}{5}\) yard of wire for each ornament he makes. He makes 3 ornaments for his grandmother and 2 ornaments for his mother
So,
The total number of ornaments Lee made = (The number of ornaments he made for his grandmother) + (The number of ornaments made for his mother)
= 3 + 2
= 5 ornaments
So,
The total number of yards of wire Lee used = (The total number of ornaments Lee made) × (The number of yards of wire he used for each ornament)
= 5 × \(\frac{1}{5}\)
= \(\frac{5 × 1}{5}\)
= \(\frac{5}{5}\)
= 1 yard
Hence, from the above,
We can conclude that
The total number of yards of wire Lee used is:

Question 11.
Lucas is making one dozen snacks for his team. He uses \(\frac{1}{4}\) cup of dried cherries and \(\frac{2}{4}\) cup of dried apricots for each snack. How many cups of dried fruit does Lucas need for his one dozen snacks? Remember, there are 12 snacks in one dozen. Write and solve equations to show how you found the answer.
Answer:
It is given that
Lucas is making one dozen snacks for his team. He uses \(\frac{1}{4}\) cup of dried cherries and \(\frac{2}{4}\) cup of dried apricots for each snack.
So,
The total number of cups of dried cherries and dried apricots for each snack = \(\frac{1}{4}\) + \(\frac{2}{4}\)
= \(\frac{1 + 2}{4}\)
= \(\frac{3}{4}\)
So,
The total number of cups of dried cherries and dried apricot for his 1 dozen snacks = 12 × (The total number of cups of dried cherries and dried apricots for each snack)
= 12 × \(\frac{3}{4}\)
= \(\frac{12 × 3}{4}\)
= \(\frac{36}{4}\)
= 9 cups
Hence, from the above,
We can conclude that
The total number of cups of dried cherries and dried apricot for his 1 dozen snacks are: 9 cups
Topic 10 Performance Task
School Mural
Paul has permission to paint a 20-panel mural for his school. Part of the mural is shown in the Painting a Mural figure. Paul decides he needs help. The Helpers table shows how much several of his friends can paint each day and how many days a week they can paint.

Question 1.
The students want to find how long it will take to paint the mural if each works on a different part of the panels a different number of days a week.
Part A
How many panels can Leeza paint in a week? Use fraction strips to explain.
Answer:
It is given that
Paul has permission to paint a 20-panel mural for his school. Part of the mural is shown in the Painting a Mural figure. Paul decides he needs help. The Helpers table shows how much several of his friends can paint each day and how many days a week they can paint.
Now,
The given table is:
Now,
From the given table,
We can observe that
Leeza can paint \(\frac{3}{4}\) panels a day for 3 days a week
So,
The number of panels Leeza can paint in a week = (The amount Leeza can paint a day) × (The number of days she can paint a week)
= \(\frac{3}{4}\) × 3
= \(\frac{3 × 3}{4}\)
= \(\frac{9}{4}\) panels
Hence,
The representation of the number of panels Leeza can paint in a week in the form of a bar diagram is:
The number of panels Leeza can paint in a week is: \(\frac{9}{4}\) panels
Part B
How many panels can Kelsey paint in a week? Use equations to explain.
Answer:
The given table is:

Now,
From the given table,
We can observe that
Kelsey paints \(\frac{7}{8}\) panels a day for 4 days a week
So,
The number of panels Kelsey can paint in a week = (The number of days can Kelsey paint in a week) × (The number of panels Kelsey can paint in a day)
= 4 × \(\frac{7}{8}\)
= \(\frac{4 × 7}{8}\)
= \(\frac{28}{8}\)
= \(\frac{7}{2}\) panels
Hence, from the above,
We can conclude that
The number of panels Kelsey can paint in a week is: \(\frac{7}{2}\) panels
Part C
Paul can work 5 days a week. How many panels can Paul paint in a week? Explain.
Answer:
It is given that
Paul works \(\frac{9}{10}\) panels a day
So,
The number of panels Paul can paint in a week = (The number of days Paul can paint in a week) × (The number of panels Paul can paint in a day)
= 5 × \(\frac{9}{10}\)
= \(\frac{5 × 9}{10}\)
= \(\frac{45}{10}\)
= \(\frac{9}{2}\) panels
Hence, from the above,
We can conclude that
The number of panels Paul can paint in a week is: \(\frac{9}{2}\) panels
Part D
How many panels can Tony paint in a week? Draw a bar diagram. Write and solve an equation.
Answer:
The given table is:

Now,
From the given table,
We can observe that
Tony paints \(\frac{5}{6}\) panels a day for 3 days a week
So,
The number of panels Tony can paint in a week = (The number of days can Tony paint in a week) × (The number of panels Tony can paint in a day)
= 3 × \(\frac{5}{6}\)
= \(\frac{3 × 5}{6}\)
= \(\frac{15}{6}\)
= \(\frac{5}{2}\) panels
Hence,
The representation of the number of panels Tony can make in a week in the form of a bar diagram is:

The number of panels Tony can paint in a week is: \(\frac{5}{2}\) panels
Question 2.
The Time Spent Painting Each Day table shows how much time each of Paul’s friends helped with the mural each day that they worked on it.

How much more time did Kelsey spend each day than Tony and Leeza combined? Explain.
Answer:
It is given that
The Time Spent Painting Each Day table shows how much time each of Paul’s friends helped with the mural each day that they worked on it.
Now,
The given table is:

Now,
From the given table,
We can observe that
The time spent painting each day by Tony and Leeza combined = 1 hour 45 minutes + 30 minutes
= 1 hour 75 minutes
= 2 hours 15 minutes
So,
The difference between the time spent each day by Kelsey and Tony and Leeza combined = 2 hours 30 minutes – 2 hours 15 minutes
= 15 minutes
Hence, from the above,
We can conclude that
Kelsey spent each day 15 minutes more than Tony and Leeza combined
