enVision Math Common Core Grade 4 Answer Key Topic 14 Algebra Generate and Analyze Patterns

Go through the enVision Math Common Core Grade 4 Answer Key Topic 14 Algebra: Generate and Analyze Patterns regularly and improve your accuracy in solving questions.

enVision Math Common Core 4th Grade Answers Key Topic 14 Algebra Generate and Analyze Patterns

Essential Questions:
How can you use a rule to continue a pattern? How can you use a table to extend a pattern? How can you use a repeating pattern to predict a shape?

enVision STEM Project: Patterns and Waves
Journal: Write a Report Include what you found. Also in your report:
Do Research Use the Internet or other sources to learn about 2 industries where oscilloscopes can be used. Name the industry and what can be observed using the oscilloscope.

Oscilloscopes are used to observe patterns in waves. Suppose a scientist created a pattern with three levels of sounds: quiet, loud, medium. If the scientist repeats the pattern of sounds, what would be the 41st sound in the pattern? Explain.

Review What You Know

Vocabulary
Choose the best term from the box. Write it on the blank.

• even number
• odd number
• inverse operations
• variable

Question 1.
A(n) ________ can be divided into groups of 2 without a remainder.
Answer:
Even number
Explanation:
Even numbers are those numbers that can be divided into two equal groups or pairs and are exactly divisible by 2.

Question 2.
A symbol or letter that stands for a number is called a(n) ___________.
Answer: Variable
Explanation:
A variable is a letter or symbol used as a placeholder for an unknown value

Question 3.
Operations that undo each other are called _________
Answer: Inverse Operation.
Explanation:
Inverse operations are operations that are opposite or “undo” each other.
For example, addition undoes subtraction and division undoes multiplication.
Inverse operations are useful when solving equations

Addition and Subtraction Patterns

Add or subtract to find the missing number in each pattern.
Question 4.
3, 6, 9, 12, ____,18
Answer: 15
Explanation:
Pattern : Add 3

Question 5.
4,8, 12, ____, 20, 24
Answer: 16
Explanation:
Pattern : Add 4

Question 6.
8, 7, 6, ____,4, 3
Answer: 5
Explanation:
Pattern : Add 1 then less 1

Question 7.
30, 25, 20, 15, ____,5
Answer: 10
Explanation:
Pattern : Subtract 5

Question 8.
1, 5, 9, ____, 17, 21
Answer: 13
Explanation:
Pattern : Add 4

Question 9.
12, 10, 8, 6, ___, 2
Answer: 4
Explanation:
Pattern : Subtract 2

Multiplication and Division Patterns

Multiply or divide to find the missing number in each pattern.
Question 10.
1, 3, 9, 27, ___, 243
Answer: 81
Explanation:
Pattern : Multiply 3

Question 11.
64, 32, 16, ____, 4, 2
Answer:  8
Explanation:
Pattern : Divide by 2

Question 12.
1,5, 25, ____, 625
Answer: 125
Explanation:
Pattern : Multiply 5

Question 13.
1, 2, 4, 8, ____, 32
Answer:
Explanation:
Pattern : Multiply by 2

Question 14.
1, 4, 16, ____, 256
Answer: 64
Explanation:
Pattern : Multiply by 4

Question 15.
729, 243, 81,27, 9, ____
Answer: 3
Explanation:
Pattern : Divided by 3

Problem Solving

Question 16.
Look for Relationships James places 1 counter in the first box. He places 2 counters in the second box, 4 counters in the third box, 8 counters in the fourth box, and continues the pattern until he gets to the tenth box. How many counters did James place in the tenth box?

Answer: 512
Explanation:
Pattern is multiply by 2

Pick a Project

PROJECT 14A
How have roller coasters changed through the years?
Project: Make a Model Roller-Coaster Car

PROJECT 14B
How can you use currency from different countries?
Project: Make Your Own Currency

PROJECT 14C
How can patterns be used in sidewalks?
Project: Design Your Own Sidewalk

PROJECT 14D
How many stadiums in the United States have retractable roofs?
Project: Make a Seating Diagram

Lesson 14.1 Number Sequences

Solve & Share
Look at the rules and starting numbers below. What are the next 6 numbers in each pattern? Tell how you decided. Describe features of the patterns. Solve these problems any way you choose.
I can … use a rule to create and extend a number pattern and identify features of the number pattern not described by the rule.

Look Back! Look for Relationships Create two patterns that use the same rule but start with different numbers. Identify a feature of each pattern. For example, identify whether the numbers are all even, all odd, or alternate between even and odd.

Essential Question
How Can You Use a Rule to Continue a Pattern?

Visual Learning Bridge
The house numbers on a street follow the rule “Add 4.” If the pattern continues, what are the next three house numbers? Describe a feature of the pattern.

You can use a number line to help make sense of the problem and find the next three house numbers.

Use a number line to continue the pattern.
A rule is a mathematical phrase that tells how numbers or shapes in a pattern are related. The rule for the house numbers is “Add 4.”

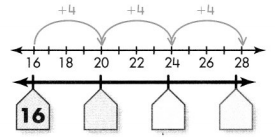
The next three house numbers are 20, 24, and 28.

Describe features of the pattern.
Some patterns have features that are not given in the rule.
16, 20, 24, 28
One of the features of this pattern is all of the house numbers are even numbers.
Another feature is all of the house numbers are multiples of 4.

Convince Me! Generalize Can you use the rule “Add 4” to create a different pattern with all odd numbers? Explain.
Explanation:
No, we cannot apply this rule on odd numbers
when u add 4 to a odd number the answers all will be in odd numbers
but not the multiples.

Another Example!
On another street, the house numbers follow the rule “Subtract 5.” What are the next three house numbers after 825? Describe a feature of the pattern.

The next three house numbers are 820, 815, and 810. All of the house numbers are multiples of 5.

Guided Practice

Do You Understand?
Question 1.
Rudy’s rule is “Add 2.” He started with 4 and wrote the numbers below. Which number does NOT belong to Rudy’s pattern? Explain. 4,6, 8, 9, 10, 12
Answer: 9
Explanation:
9 number does NOT belong to Rudy’s pattern
Because it is not the multiple of 2

Do You Know How?
Continue the pattern. Describe a feature of the pattern.
Question 2.
Subtract 6
48, 42, 36, 30, 24, _____, _____, ______
Answer: 18,12,6.
Explanation:
Pattern = multiples of 6

Independent Practice

For 3-6, continue each pattern. Describe a feature of each pattern.
Question 3.
Subtract 3: 63, 60, 57, _____, _____
Answer: 54,51,48
Explanation:
Pattern is multiples of 3

Question 4.
Add 7: 444, 451, 458, _____, _____
Answer: 465,472.
Explanation:
pattern = Multiples of 7

Question 5.
Add 25: 85, 110, 135, _____, _____
Answer: 160,185
Explanation:
The sequence is completed by adding 25

Question 6.
Subtract 4: 75, 71, 67, _____, _____
Answer: 63,59
Explanation:
The sequence is completed by  subtracting 4

For 7-12, use the rule to generate each pattern.
Question 7.
Rule: Subtract 10
90, _____, _____
Answer: 80,70
Explanation:
The sequence is completed by subtracting 10

Question 8.
Rule: Add 51
16, _____, _____
Answer: 67,83
Explanation:
The sequence is completed by adding 51

Question 9.
Rule: Add 5
96, _____, _____
Answer: 101, 106
Explanation:
The sequence is completed by adding 5

Question 10.
Rule: Add 107
43, _____, _____
Answer:  150, 257
Explanation:
The sequence is completed by adding 107

Question 11.
Rule: Subtract 15
120, _____, _____
Answer: 105, 90
Explanation:
The sequence is completed by Subtracting 15

Question 12.
Rule: Subtract 19
99, _____, _____
Answer: 80, 61
Explanation:
The sequence is completed by Subtracting 19

Problem Solving

Question 13.
Reasoning Orlando delivers mail. He sees one mailbox that does not have a number. If the numbers are in a pattern, what is the missing number?

Answer: 31
Explanation:
Pattern : Add 2
The missing number is 31

Question 14.
A bus tour runs 9 times a day, 6 days a week. The bus can carry 30 passengers. Find the greatest number of passengers who can ride the tour bus each week.
Answer: 1620
Explanation:
6 x 9 = 54 trips
54 x 30 = 1620
The greatest number of passengers who can ride the tour bus each week is 1620 passengers.

Question 15.
The year 2017 was the year of the Rooster on the Chinese calendar. The next year of the Rooster will be 2029. The rule is “Add 12.” What are the next five years of the Rooster?

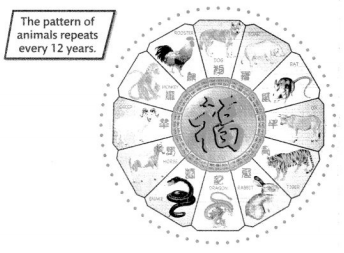
Answer: 2041, 2053, 2065, 2077, 2089
Explanation:
The next five years of the Rooster are 2041, 2053, 2065, 2077, 2089

Question 16.
Describe a feature of the year of the Rooster pattern.
Answer: Multiples of 12
Explanation:
Feature of the year of the Rooster pattern is multiples of 12

Question 17.
Vocabulary Define rule. Create a number pattern using the rule “Subtract 7.”
Answer: Rule = multiples of 7
Explanation:
70, 63, 56, 49
Is the pattern of Subtract 7

Question 18.
Higher Order Thinking Some patterns use both addition and subtraction in their rules. The rule is “Add 3, Subtract 2.” Find the next three numbers in the pattern.
1, 4, 2, 5, 3, 6, 4, 7, _____, _____, _____
Answer: 5, 8 , 6
Explanation:
The next three numbers in the pattern is 5, 8 , 6

Assessment Practice

Question 19.
Rima used “Subtract 3” as the rule to make a pattern. She started with 60, and wrote the next six numbers in her pattern. Which number does NOT belong in Rima’s pattern?

A. 57
B. 54
C. 45
D. 26
Answer: D
Explanation:
26 number does NOT belong in Rima’s pattern

Question 20.
Ivan counted all the beans in a jar. If he counted the beans in groups of 7, which list shows the numbers Ivan could have named?
A. 77, 84, 91, 99
B. 301, 308, 324, 331
C. 574, 581, 588, 595
D. 14, 24, 34, 44
Answer: B
Explanation:
301, 308, 324, 331 list shows the numbers Ivan could have named

Lesson 14.2 Patterns: Number Rules

Solve & Share
There are 6 juice boxes in 1 pack, 12 in 2 packs, and 18 in 3 packs. How many juice boxes are in 4 packs? in 5 packs? in 6 packs? Use the rule to complete the table. Describe features of the pattern. Then find how many juice boxes are in 10 packs and 100 packs.
I can … use a rule to extend a number pattern, identify features of the number pattern, and use the number pattern to solve a problem.

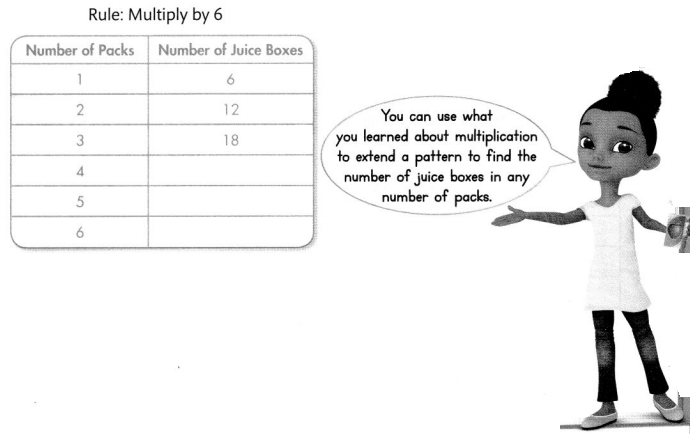
Look Back! Reasoning Create a table showing the relationship between the number of bicycles and the number of bicycle wheels. Start with 1 bicycle. Complete 5 rows of the table using the rule “Multiply by 2.” Describe features of the pattern.
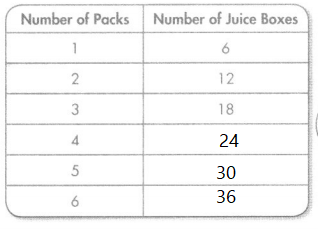gf

Essential Question
What is the Pattern?

Visual Learning Bridge
There are 3 leaflets on 1 cloverleaf. There are 6 leaflets on 2 cloverleaves. There are 9 leaflets on 3 cloverleaves. How many leaflets are on 4 cloverleaves? How many cloverleaves will have 12 leaflets?

You can use a table to create, extend, and identify features of a pattern.

How many leaflets are on 4 cloverleaves?

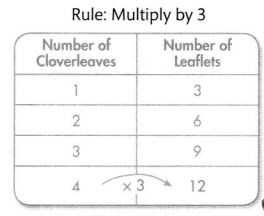
There are 12 leaflets on 4 cloverleaves. The number of leaflets is a multiple of the number of cloverleaves.

How many cloverleaves for 12 leaflets?

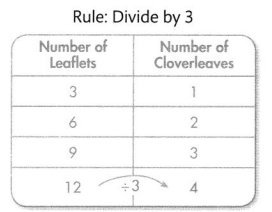
There are 4 cloverleaves for 12 leaflets. The number of cloverleaves is a factor of the number of leaflets.

Convince Me! Model with Math If you know the number of leaflets, l, what expression can you use to find the number of cloverleaves, c? If you know the number of cloverleaves, what expression can you use to find the number of leaflets?

Guided Practice

Do You Understand?
Question 1.
The rule for this table is “Multiply by 4.” What number does not belong?

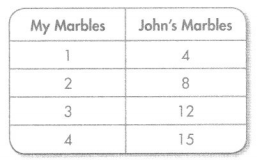
Answer: 15
Explanation:
4 x  4 = 16
15 does not belong to the  group

Do You Know How?
Complete the table. Describe a feature of the pattern.
Question 2.
Rule: Divide by 4

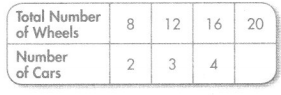
Answer: 5

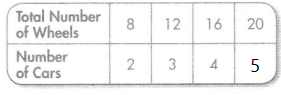
Explanation:
5 x 4 = 20
Multiply by 4 is the pattern

Independent Practice

For 3-6, use the rule to complete each table. Describe a feature of each pattern.
You can multiply or divide to find the patterns in these tables.
Question 3.
Rule: Multiply by 8

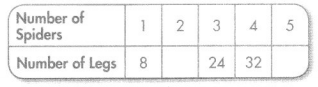
Answer:

Explanation:
2 x 8 = 16
5 x 8 = 40
The sequence is completed by the multiplies of 8

Question 4.
Rule: Divide by 5

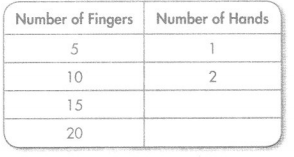
Answer:

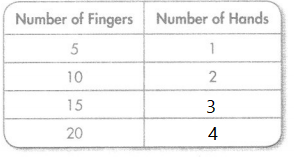
Explanation:
The sequence is completed by Divide by 5

Question 5.
Rule: Multiply by 16

Answer:

Explanation:
The sequence is completed by the multiples of 16

Question 6.
Rule: Divide by 2

Answer:

Explanation:
The sequence is completed by dividing with 2
500 divided by 2 is 250
730 divided by 2 is 365

Problem Solving

Question 7.
The table shows how much money Joe makes painting. How much money will Joe make when he paints for 6 hours?
Rule: Multiply by 45

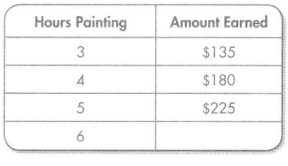
Answer: 270

Explanation:
$270 money will Joe make when he paints for 6 hours

Question 8.
The table shows the total number of pounds of potatoes for different numbers of bags. How many bags does it take to hold 96 pounds of potatoes?
Rule: Divide by 8

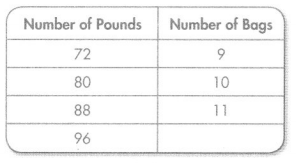
Answer: 12

Explanation:
12 bags it take to hold 96 pounds of potatoes

Question 9.
Number Sense What is the greatest number you can make using each of the digits 1,7,0, and 6 once?
Answer: 7106
Explanation:
7106  is the greatest number you can make using each of the digits 1,7,0, and 6 once

Question 10.
Algebra A penguin can swim 11 miles per hour. At this speed, how far can it swim in 13 hours? Use s as a variable. Write and solve an equation.
Answer: 143 miles
Explanation:
s = 11 x 13
s = 143 miles

For 11-12, the rule is “Multiply by 3.”

Question 11.
Reasoning Using the rule, how many batteries do 8 flashlights need?
Answer: 24
Explanation:
8 x 3 = 24
24 batteries has 8 flashlights needed.

Question 12.
Higher Order Thinking How many more batteries do 20 flashlights need than 15 flashlights? Explain.
Answer:
15 x 3 = 45
20 x 3 = 60
60 – 45 = 15
Explanation:
15 more batteries do 20 flashlights need than 15 flashlights

Assessment Practice

Question 13.
There are 6 rolls in each package. Use the rule “Divide by 6” to show the relationship between the number of rolls and the number of packages. Use each digit from the box once to complete the table.

Answer:

Explanation:
Used each digit from the box once to complete the table.

Lesson 14.3 Patterns: Repeating Shapes

Solve & Share
The rule for the repeating pattern below is “Square, Triangle.” What will be the 37th shape in the pattern? Explain. Solve this problem any way you choose.
I can … use a rule to predict a number or shape in a pattern.

Look Back! When the pattern has 37 shapes, how many are triangles?
Answer:
37 divided by 2 is 18 times triangles
37 is the triangle

Essential Question
How Can You Use a Repeating Pattern to Predict a Shape?

Visual Learning Bridge
Rashad is making a repeating pattern for the rule “Triangle, Square, Trapezoid.” What will be the 49th shape in the pattern?
A repeating pattern is made up of shapes or numbers that form a part that repeats.

Explanation:
49th shape is triangle
48 divided by 3 is 16
so, the next is triangle

Look for Features of the Repeating Pattern

The trapezoid is the 3^rd, 6^th, and 9^th shape in the pattern. The positions of the trapezoids are multiples of 3.

The triangle is the 15^th, 4^th, and 7^th shape in the pattern. The positions of the triangles are 1 more than a multiple of 3.

The square is the 2^nd, 5^th, and 8^th shape in the pattern. The positions of the squares are 1 less than a multiple

Use the Repeating Pattern to Solve
When you divide 49 by 3, the quotient is 16 R1. The pattern repeats 16 times. The 1st shape in the repeating pattern, a triangle, then appears.

49 is one more than a multiple of 3.
The 49th shape is a triangle.

Convince Me! Be Precise Suppose the rule is “Square, Triangle, Square, Trapezoid” in a repeating pattern. What is the 26th shape in the pattern? Describe features of the repeating pattern. Be precise in your description.

Another Example!
Write the next three numbers in the repeating pattern. Then name the 100th number in the pattern.

Rule: 1, 3, 5, 7 1, 3, 5, 7, 1, 3, 5, 7, 1, 3, 5, 7, 1, 3, 5 …
There are 4 items in the repeating pattern. To find the 100^th number, divide by 4. The pattern repeats 25 times. The 100^th number is 7.

Guided Practice

Do You Understand?
Question 1.
In the “Triangle, Square, Trapezoid” example on the previous page, what will be the 48^th shape? the 50^th shape? Explain.
Answer: 48th is trapezoid, 50th is square
Explanation:
When you divide 49 by 3, the quotient is 16 R1. The pattern repeats 16 times. The 1st shape in the repeating pattern, a triangle, then appears.

Do You Know How?
Question 2.
What is the 20^th shape? The rule is “Triangle, Circle, Circle.”

Answer: circle
Explanation:
When you divide 20 by 3, the quotient is 6 R2. The pattern repeats 6 times. The 1st shape in the repeating pattern, a circle, then appears.

Question 3.
Write the next three numbers. The rule is “9, 2, 7, 6.”
9, 2, 7, 6, 9, 2, 7, 6, ____, _____, ______
Answer: 9,2,7
Explanation:
The next three numbers 9, 2, 7

Independent Practice

For 4-7, draw or write the next three items to continue each repeating pattern.
Question 4.
The rule is “Square, Triangle, Square.”

Answer:

Explanation:
The pattern is completed with the help of rule

Question 5.
The rule is “Up, Down, Left, Right.”

Answer:

Explanation:
The pattern is completed with the help of rule

Question 6.
The rule is “1, 1, 2.”
1, 1, 2, 1, 1, 2, ____ , ____, ____ ……
Answer: 1,1,2
Explanation:
The pattern is completed with the help of rule

Question 7.
The rule is “5, 7, 4, 8.”
5, 7, 4, 8, 5, 7, 4, 8, 5, 7, ____, ____, ____ ……
Answer: 4, 8, 5
Explanation:
The pattern is completed with the help of rule

For 8-9, determine the given shape or number in each repeating pattern.
Question 8.
The rule is “Tree, Apple, Apple.” What is the 19^th shape?

Answer:
Explanation:
When you divide 19 by 3, the quotient is 6 R1. The pattern repeats 6 times. The 1st shape in the repeating pattern, a tree, then appears.

Question 9.
The rule is “1, 2.” What is the 42^nd number?
1, 2, 1, 2, 1, 2, …
Answer:
Explanation:
When you divide 42 by 2, the quotient is 21 R0. The pattern repeats 21 times.
The pattern is closed so the pattern end with 2.

Problem Solving

Question 10.
Create a repeating pattern using the rule “Triangle, Square, Square.”
Answer:

Explanation:
Created a repeating pattern using the rule “Triangle, Square, Square.”
Ends with the triangle.

Question 11.
enVision® STEM Margot measured the distance for 6 wavelengths of visible light as 2,400 nanometers. What is the distance for 1 wavelength?
Answer:
2400 divided by 6 = 400
Explanation:
400 is the distance for 1 wavelength

Question 12.
Look for Relationships Hilda is making a repeating pattern with the shapes below. The rule is “Heart, Square, Triangle.” If Hilda continues the pattern, what will be the 11th shape?

Answer:
Explanation:
When you divide 11 by 3, the quotient is 3 R2. The pattern repeats 3 times.
The 2nd shape in the repeating pattern, a square, then appears.

Question 13.
Look for Relationships Josie puts beads on a string in a repeating pattern. The rule is “Blue, Green, Yellow, Orange.” There are 88 beads on her string. How many times did Josie repeat her pattern?
Answer: 22 times
Explanation:
When you divide 88 by 4, the quotient is 22 R0. The pattern repeats 22 times.
The pattern is closed so the pattern end with yellow

Question 14.
How many more years passed between the first steam locomotive and the gasoline-powered automobile than between the gasoline-powered automobile and the first diesel locomotive?

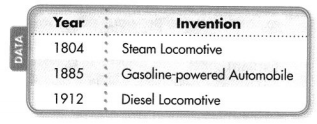
Answer: 81 , 27
Explanation:
steam locomotive and the gasoline-powered automobile
1885 – 1804 = 81
81 years
gasoline-powered automobile and the first diesel locomotive
1912 – 1885= 27

Question 15.
Louisa used the rule “Blue, Green, Green, Green” to make a bracelet with a repeating pattern. She used 18 green beads. How many beads did Louisa use to make the bracelet? How many beads were NOT green?
Answer:
18 divided by 3 is 6
so, pattern repeated 6 times
6 x 4 = 24
24 – 18 = 6
Explanation:
6 beads were NOT green

Question 16.
Higher Order Thinking Marcus is using shapes to make a repeating pattern. He has twice as many circles as squares. Make a repeating pattern that follows this rule.
Answer: The rule is circle , square , square

Explanation:
The pattern is made according to the rule.

Assessment Practice

Question 17.
Which rules give a repeating pattern that has a square as the 15th shape? Select all that apply.
☐ Square, Circle
☐Circle, Square, Triangle
☐ Square, Circle, Triangle
☐ Circle, Triangle, Square
☐ Trapezoid, Circle, Square
Answer:

Explanation:
Selected all that apply
where the 15th shape is a square.

Question 18.
Which rules give a repeating pattern that has a 7 as the 15^th number? Select all that apply.
☐ 1, 7
☐ 1, 7, 9
☐ 1, 9, 7
☐ 1, 7, 7
☐ 7, 1, 9
Answer:

Explanation:
selected pattern rules give a repeating pattern that has a 7 as the 15^th number

Lesson 14.4 Problem Solving

Look For and Use Structure
Solve & Share
Evan’s baby brother is stacking blocks. Using the rule “Add 1 block to the number of blocks in the previous stack,” how many blocks will be in the 6th stack? Explain. Justify your answer.
I can … use patterns to help solve problems.

Thinking Habits
• What patterns can I see and describe?
• How can I use the patterns to solve the problem?
· Can I see expressions and objects in different ways?

Look Back! Look For Relationships How many blocks are in the 10th stack? Explain.

Essential Question
How Can I Look For and Make Use of Structure?

Visual Learning Bridge
Alisa made three walls with cubes. She recorded her pattern. If she continues the pattern, how many cubes will be in a 10-layer wall? a 100-layer wall?

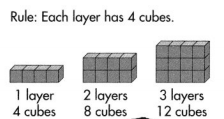
What do you need to do to find the number of cubes in a 10-layer and 100-layer wall?
I need to continue the pattern using the rule and analyze the pattern to find features not stated in the rule itself.

How can I make use of structure to solve this problem?
I can

• look for and describe patterns in three dimensional shapes.
• use the rule that describes how objects or values in a pattern are related.
• use features of the pattern not stated in the rule to generate or extend the pattern.

Here’s my thinking.
Make a table and look for patterns.

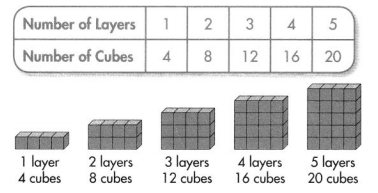
There are 4 cubes in each layer. Multiply the number of layers by 4 to calculate the number of cubes.
A 10-layer wall contains 10 × 4 = 40 cubes.
A 100-layer wall contains 100 × 4 = 400 cubes.

Convince Me! Look for Relationships How could you use multiples to describe Alisa’s pattern?

Guided Practice

Use Structure
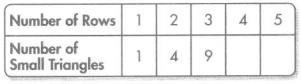
Leah arranged triangular tiles in a pattern like 1 row the one shown. She used the rule “Multiply the number of rows by itself to get the number of small triangles.” How many small triangles would be in the pattern if there were 10 rows?

Question 1.
Complete the table to help describe the pattern.

Answer:

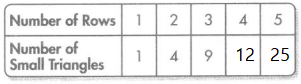
Explanation:
Multiplied the number by itself

Question 2.
Describe the pattern another way.
Answer:
4 x 4 = 12
5 x 5 = 25
Explanation:
used the rule “Multiply the number of rows by itself to get the number of small triangles

Question 3.
How many triangles would be in 10 rows?
Answer: 100
Explanation:
10 x 10= 100
used the rule “Multiply the number of rows by itself to get the number of small triangles

Independent Practice

Look for Relationships
Alan built the towers shown using the rule “Each story has 2 blocks.” How many blocks will a 10-story tower have? Use Exercises 4-6 to answer the question.

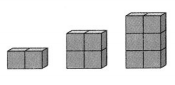
Question 4.
Complete the table to help describe the pattern.

Answer: 10 x 2 = 20

Explanation:
Pattern is add by 2

Question 5.
What is another way to describe the pattern that is not described by the rule?
Answer:
Explanation:
Pattern is add by 2

Question 6.
How many blocks are in a 10-story tower? Explain.
Answer: 10 x 2 = 20
Explanation:
used the rule “Multiply the number with 2″

Problem Solving

Performance Task

Glass Stairs
An art gallery staircase is built using glass cubes. The diagram below shows 4 steps are 4 cubes high and 4 cubes across. Five steps are 5 cubes high and 5 cubes across. How many glass cubes are used to make 7 steps? Use Exercises 7-10 to answer the question.

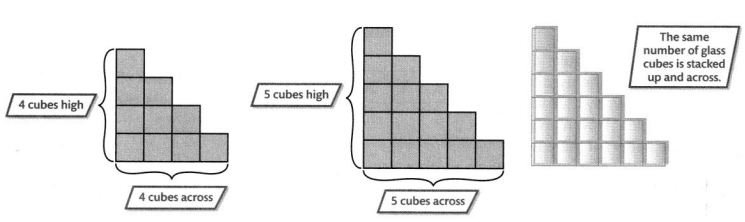
Question 7.
Make Sense and Persevere What do you know, and what do you need to find?
Answer:
4 steps are 4 cubes high and 4 cubes across. Five steps are 5 cubes high and 5 cubes across
is what we know
7 steps is to find
seven steps are 7 cubes high and 7 cubes across

Question 8.
Reasoning Complete the table.

Answer:

Explanation:
Pattern = multiply by 3

Question 9.
Look For Relationships What pattern can you determine from the table?

Answer: Pattern = multiply by 3
Explanation:
multiply by 3 pattern can you determine from the table

Question 10.
Reasoning How many cubes are needed for 7 steps? Write and solve an equation.
Answer: 49 cubes
Explanation:
7 x 7 = 49
seven steps are 7 cubes high and 7 cubes across
49 cubes are needed for 7 steps

Topic 14 Fluency Practice Activity

Point & Tally
Find a partner. Get paper and a pencil. Each partner chooses a different color: light blue or dark blue. Partner 1 and Partner 2 each point to a black number at the same time. Each partner adds the two numbers. If the answer is on your color, you get a tally mark. Work until one partner has twelve tally marks.
I can … add multi-digit whole numbers.

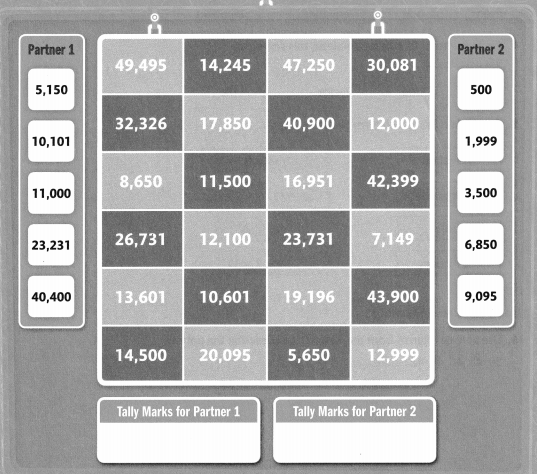
Topic 14 Vocabulary Review

Understand Vocabulary
Word List

• equation
• even number
• factor
• multiple
• odd number
• repeating pattern
• rule
• unknown

Question 1.
Circle the term that best describes 28.
even
odd
equation
unknown
Answer: Even
Explanation:
Even is the word which is divisible by 2

Question 2.
Circle the term that best completes this sentence: 4 is a _________ of 16.
even
odd
factor
multiple
Answer: factor
Explanation:
2, 4 , 8 are the factors of 16

Question 3.
Circle the term that best describes 17.
even
odd
equation
unknown
Answer: Odd
Explanation:
Odd numbers are the numbers that cannot be divided by 2 evenly.

Question 4.
Circle the term that best completes this sentence: 9 is a _________ of 3.
even
odd
factor
multiple
Answer: Multiple of 3
Explanation:
3 x 3 = 9
9 is the multiple of 3

Question 5.
Draw a line from each term to its example.

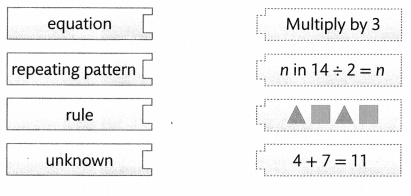
Answer:

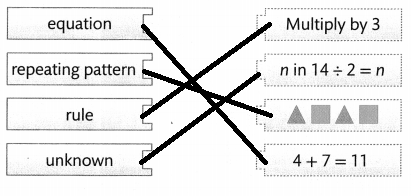
Explanation:
The preview  words are matched with the correct answers.

Use Vocabulary in Writing
Question 6.
Use at least 3 terms from the Word List to describe the pattern.
50, 48, 46, 44, 42 …
Answer:
Even numbers
Multiple
Rule
Explanation:
The above all numbers are even numbers
They are multiples of 2
Rule= less 2

Topic 14 Reteaching

Set A pages 521-524

You can use the rule “Subtract 3” to continue the pattern.

The next three numbers in the pattern are 9,6, and 3
A feature of the pattern is all the numbers are multiples of 3.
Another feature is all the numbers in the pattern alternate even, odd.

Remember to check that the numbers in your pattern follow the rule.

Use the rule to continue each pattern. Describe a feature of the pattern.
Question 1.
Rule: Add 20
771, 791, 811, _____, _____, _____
Answer: 831, 851
Explanation:
A feature of the pattern is all the numbers are odd numbers

Question 2.
Rule: Subtract 12
122, 110, 98, _____, _____, ______
Answer: 86, 74, 62
Explanation:
A feature of the pattern is all the numbers are even numbers

Set B pages 525-528

The regular price is twice the sale price. You can use the rule “Divide by 2” to continue the pattern.

Remember to look for features of the pattern not described by the rule.

Use the rule to continue each pattern. Describe a feature of the pattern.
Question 1.
Rule: Multiply by 18

Answer:

Explanation:
A feature of the pattern is all the numbers are even numbers

Question 2.
Rule: Divide by 9

Answer:  $100

Explanation:
A feature of the pattern is all the numbers are even and odd numbers

Question 3.
Rule: Multiply by 24

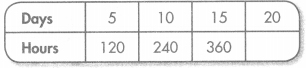
Answer:

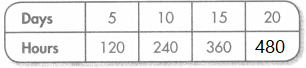
Explanation:
A feature of the pattern is all the numbers are even

Set C pages 529-532

You can use the rule “Circle, Triangle, Square” to continue the repeating pattern.

You can use the rule to find the 25^th shape in the pattern.
25 ÷ 3 = 8 R1.
The pattern will repeat 8 times, then the 1^st shape will appear.
The circle is the 25^th shape in the pattern.

Remember to use the rule to continue the pattern.

Question 1.
a. Draw the next three shapes in the repeating pattern. The rule is “Right, Up, Up.”

Answer:

Explanation:
Up, Up, Right is the next three shapes in the repeating pattern

b. Draw the 50^th shape in the pattern.
Answer:
Explanation:
You can use the rule to find the 50^th shape in the pattern.
50 ÷ 3 = 16 R2.
The pattern will repeat 16 times, then the 1^st shape will appear.
The up is the 50^th shape in the pattern.

Question 2.
a. Write the next three numbers in the repeating pattern. The rule is “3, 5, 7, 9.”
3, 5, 7, 9, 3, 5, 7, ____, _____, ______
Answer: 9, 3, 5, 7
Explanation:
9, 3, 5, 7 the next three numbers in the repeating pattern

b. What will be the 100^th number in the pattern?
Answer:
Explanation:
You can use the rule to find the 100^th number in the pattern.
100 ÷ 4 = 25 R0.
The pattern will repeat 25 times,
There the pattern ends so, the 100th  number is 7

Set D pages 533-536

Think about these questions to help you Look For and Use Structure.
Thinking Habits

• What patterns can I see and describe?
• How can I use the patterns to solve the problem?
• Can I see expressions and objects in different ways?
  

Remember to use the rule that describes how objects or values in a pattern are related.

Sam creates a pattern using the rule “Each story has 3 blocks.”

Question 1.
Draw the next shape in Sam’s pattern.
Answer:

Explanation:
4 x 4 is the Sam’s next shape

Question 2.
Use the rule to continue Sam’s pattern.

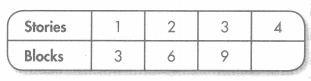
Answer:

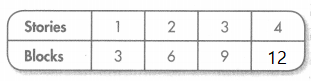
Explanation:
pattern = multiple of 3

Question 3.
How many blocks are in the 10th shape in Sam’s pattern?
Answer:
10 x 10 = 100
Explanation:
100 blocks are in the 10th shape in Sam’s pattern.

Topic 14 Assessment Practice

Question 1.
Football players come out of the tunnel, and their jerseys have the number pattern shown below. They follow the rule “Add 4.”

A. What number belongs on the front of the blank jersey? Explain.
Answer: 24
Explanation:
Number 24 belongs on the front of the blank jersey

B. Describe two features of the pattern.
Answer:
Explanation:
A feature of the pattern is all the numbers are even
A feature of the pattern is all the numbers are multiples of  4

Question 2.
One dozen eggs is 12 eggs. Two dozen eggs is 24 eggs. Match the number of dozens to the number of eggs. The rule is “Multiply by 12.”

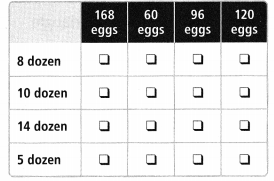
Answer:

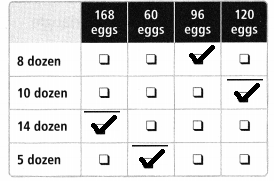
Explanation:
Matched the eggs with the dozen

Question 3.
Use the rule “Multiply by 6” to continue the pattern. Then describe a feature of the pattern.

Answer:

Explanation:
A feature of the pattern is all the numbers are even

Question 4.
Use the rule “Divide by 3” to continue the pattern. Then write 4 terms of a different pattern that follows the same rule.
729, 243, 81, ____, _____
Answer: 27, 9 , 3, 1
Explanation:
4 terms of a different pattern that follows the same rule is 27, 9 , 3, 1

Question 5.
Nicole arranges her shopping purchases by price. Each item costs $6 more than the last. The first item costs $13. The last costs $61. Her brother John says that the price of each item is an odd number. Is John correct? Find the cost of each item to explain.
Answer: 19 , 25 , 31, 37 , 43, 49, 55, 61.
Explanation:
John says that the price of each item is an odd number. yes, John correct

Question 6.
The rule for the repeating pattern is “5, 7, 2, 8.” Write the next three numbers in the pattern. Then tell what will be the 25th number in the pattern. Explain.
5, 7, 2, 8, 5, 7, 2, 8, 5, _____, _____, _____
Answer:
5, 7, 2, 8, 5, 7, 2, 8, 5, 7, 2, 8
Explanation:
You can use the rule to find the 25^th number in the pattern.
25 ÷ 4 = 6 R1.
The pattern will repeat 6 times,
then the 1^st number will appear.
The 5 is the 25^th number in the pattern

Question 7.
Jackson wrote different patterns for the rule “Subtract 5.” Select all of the patterns that he could have written. Then write 4 terms of a different pattern that follows the same rule.
☐ 27, 22, 17, 12,7
☐ 5, 10, 15, 20, 25
☐ 55, 50, 35, 30, 25
☐ 100, 95, 90, 85, 80
☐ 75, 65, 55, 45, 35
Answer:

Explanation:
different patterns for the rule “Subtract 5.”
Selected all of the patterns that he could have written

Question 8.
The rule is “Subtract 7.” What are the next 3 numbers in the pattern? Describe two features of the pattern.
70,63, 56, 49, 42,35
Answer: 28, 21, 14, 7
Explanation:
28, 21, 14, 7 the next 3 numbers in the pattern

Question 9.
The table shows the different number of teams formed by different numbers of players. The rule is “Divide by 8.”

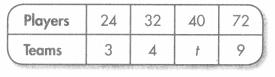
A. How many teams can be formed with 40 players?
_______ teams
Answer: 5
Explanation:
5 teams can be formed with 40 players

B. How many players are there on 13 teams? How do you know?
Answer: 104
Explanation:
104 players are there on 13 teams

Question 10.
A. Select all the true statements for the repeating pattern. The rule is “Circle, Heart, Triangle.”

☐ The next shape is the circle.
☐ The circle only repeats twice.
☐ The 10^th shape is the heart.
☐ The 12^th shape is the triangle.
☐ The circle is the 1^st, 4^th, 7^th, etc. shape.
Answer:

Explanation:
Selected all the true statements for the repeating pattern.

B. How many triangles are there among the first 22 shapes?
Answer: 7
Explanation:
7 triangles are there among the first 22 shapes

Topic 14 Performance Task

Wall Hangings Michael uses knots to make wall hangings to sell.

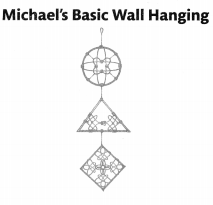
Question 1.
The Michael’s Basic Wall Hanging figure shows a simple wall hanging Michael makes by repeating the shapes shown. What is the 16th shape in the repeating pattern? The rule is “Circle, Triangle, Square.” Explain.
Answer:
Explanation:
You can use the rule to find the 25^th number in the pattern.
16 ÷ 3 =  R1.
The pattern will repeat 5 times,
then the 1^st shape will appear.
The circle is the 16^th shape in the pattern

Question 2.
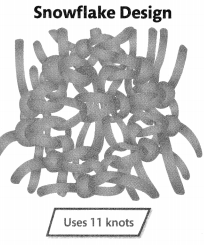
The Snowflake Design figure shows a knot Michael likes to use.

Part A
List the number of knots that Michael uses to form 1 to 6 snowflake designs. The rule is “Add 11.”
Answer: 11 , 22, 33, 44, 55, 66
Explanation:
The number of knots that Michael uses to form 1 to 6 snowflake designs 11 , 22, 33, 44, 55, 66

Part B
Describe a feature of the pattern you listed in Part A that is not part of the rule. Explain why it works.
Answer:
Explanation:
A feature of the pattern is all the numbers are even and odd

Question 3.
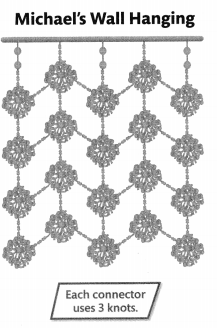
The Michael’s Wall Hanging figure shows the design of a wall hanging Michael makes using the Snowflake Design. Answer the following to find how many knots Michael ties to make a wall hanging with 28 snowflakes.

Part A
Each column of 4 snowflakes has 4 connectors. There are also 4 connectors between columns. Complete the Connectors table using the rule “Add 8 connectors for each column.” Describe a feature of the pattern.

Answer:

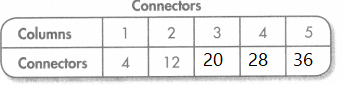
Explanation:
Completed the table by following the rule

Part B
Complete the Total Knots table using the following rules.
Snowflake Knots rule: Multiply the number of snowflakes by 11.
Connector Knots rule: Multiply the number of connectors from the Connectors table by 3.
Total Knots rule: Add the number of snowflake knots and the number of connector knots.

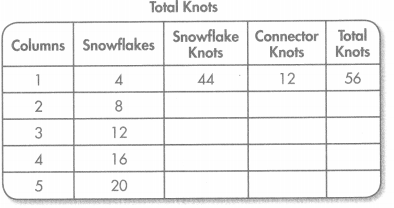
Answer:

Explanation:
Snowflake Knots rule: Multiply the number of snowflakes by 11.
Connector Knots rule: Multiply the number of connectors from the Connectors table by 3.
Total Knots rule: Add the number of snowflake knots and the number of connector knots.