Go through the enVision Math Common Core Grade 4 Answer Key Topic 3 Use Strategies and Properties to Multiply by 1-Digit Numbers regularly and improve your accuracy in solving questions.
enVision Math Common Core 4th Grade Answers Key Topic 3 Use Strategies and Properties to Multiply by 1-Digit Numbers
Essential Questions:
How can you multiply by multiples of 10, 100, and 1,000? How can you multiply whole numbers?

enVision STEM Project: Maps and Math
Do Research Use the Internet or other sources to find information about three of Earth’s features on a topographic map, such as mountains or oceans. Write two facts about each of the features you researched.
Journal: Write a Report Include what you found. Also in your report:
- Write the height or depth of each feature you researched.
- Estimate to find 10 times the heights or depths of the features you researched.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- breaking apart
- compensation
- inverse operations
- partial products
Question 1.
Multiplication and division are _________.
Answer:
Multiplication and division are ____inverse operations____.
Question 2.
A mental math method used to rewrite a number as the sum of numbers to form an easier problem is called __________.
Answer:
A mental math method used to rewrite a number as the sum of numbers to form an easier problem is called __breaking apart________.
Question 3.
Choosing numbers close to the numbers in a problem to make the computation easier, and then adjusting the answer is called ________.
Answer:
Choosing numbers close to the numbers in a problem to make the computation easier, and then adjusting the answer is called ___partial products_____.
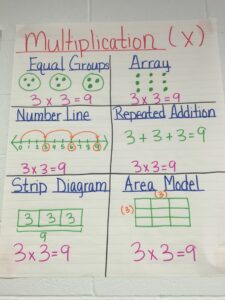
Multiplication
Find each product.
Question 4.
6 × 2
Answer:
6 × 2 = 12.
Explanation:
6 × 2 = (3 × 2) + (3 × 2)
6 × 2 = 6 + 6
6 × 2 =12.
Question 5.
8 × 9
Answer:
8 × 9 = 72.
Explanation:
8 × 9 = (4 × 9) + (4 × 9)
8 × 9 = 36 + 36
8 × 9 = 72.
Question 6.
6 × 5
Answer:
6 × 5 = 30.
Explanation:
6 × 5 = (2 × 5) + (4 × 5)
6 × 5 = 10 + 20
6 × 5 = 30.
Question 7.
7 × 8
Answer:
7 × 8 = 56.
Explanation:
7 × 8 = (3 × 8) + (4 × 8)
7 × 8 = 24 + 32
7 × 8 = 56.
Question 8.
4 × 8
Answer:
4 × 8 = 32.
Explanation:
4 × 8 = (1 × 8) + (3 × 8)
4 × 8 = 8 + 24
4 × 8 = 32.

Question 9.
3 × 7
Answer:
3 × 7 = 21.
Explanation:
3 × 7 = (2 × 7) + (1 × 7)
3 × 7 = 14 + 7
3 × 7 = 21.
Rounding
Round each number to the nearest ten.
Question 10.
16
Answer:
Nearest ten of 16 is 20.
Question 11.
82
Answer:
Nearest ten of 82 is 80.
Question 12.
35
Answer:
Nearest ten of 35 is 40.
Question 13.
53
Answer:
Nearest ten of 53 is 50.
Question 14.
24
Answer:
Nearest ten of 24 is 20.
Question 15.
49
Answer:
Nearest ten of 49 is 50.
Round each number to the nearest hundred.
Question 16.
868
Answer:
Nearest hundred of 868 is 900.
Question 17.
499
Answer:
Nearest hundred of 499 is 500.
Question 18.
625
Answer:
Nearest hundred of 625 is 600.
Question 19.
167
Answer:
Nearest hundred of 167 is 200.
Question 20.
341
Answer:
Nearest hundred of 341 is 300.
Question 21.
772
Answer:
Nearest hundred of 772 is 800.
Question 22.
919
Answer:
Nearest hundred of 919 is 900.
Question 23.
552
Answer:
Nearest hundred of 552 is 600.
Question 24.
321
Answer:
Nearest hundred of 321 is 300.
Problem Solving
Question 25.
Critique Reasoning Tyler says, 9 × 7 is greater than 7 × 9 because the greater number is first.” Explain Tyler’s error.
Answer:
Tyler’s is incorrect because 9 × 7 and 7 × 9 are same value numbers, just numbers are interchanged.
Explanation:
9 × 7 = (5 × 7) + (4 × 7)
9 × 7 = 35 + 28
9 × 7 = 63.
7 × 9 = (3 × 9) + (4 × 9)
7 × 9 = 27 + 36
7 × 9 = 63.
Pick a Project
PROJECT ЗА
How zesty is Key lime pie?
Project: Create Data for Key Lime Pie Ingredients

Answer:

PROJECT ЗВ
What do a dozen Florida panthers weigh?
Project: Draw a Captioned Picture

Answer:

PROJECT 3C
What’s the mass of a giraffe?
Project: Create a Song

Answer:

3-ACT MATH PREVIEW
Math Modeling
Covered Up

I can…model with math to solve a problem that involves estimating and computing with area models.
Lesson 3.1 Multiply by Multiples of 10, 100, and 1,000
Solve & Share
Find the products for 3 × 4, 3 × 40, 3 × 400, and 3 × 4,000. Solve these problems using any strategy you choose.
I can… find the products of multiples of 10, 100, and 1,000 using mental math and place-value strategies.

Look Back! What pattern do you notice in the products?
Answer:
The patern noticed in the products is that for every product extra zero is added after the number.
Explanation:
3 × 4 = (3 × 1) + ( 3 × 3) = 3 + 9 = 12.
3 × 40 = (3 × 10) + (3 × 30) = 30 + 90 = 120.
3 × 400 = (3 × 100) + ( 3 × 300) = 300 + 900 = 1200.
3 × 4,000 = (3 × 1000) + ( 3 × 3000) = 3000 + 9000 = 12000.
Essential Question
How Can You Multiply by Multiples of 10, 100, and 1,000?
Answer:
We multiply the multiplicand by the non-zero digit of the multiplier. Then we add the same number of zero to the extreme right of the product as the multiplier has.
Explanation:
We use Multiply by Multiples of 10, 100, and 1,000 as follow:
We can understand this method as follows.
1. First we count the zeros.
2. We multiply the non – zero numbers.
3. We place the same number of zero to the extreme right of the product
Visual Learning Bridge
Calculate 3 × 50, 3 × 500, and 3 × 5,000 using basic multiplication facts and properties of operations.
The Associative Property of Multiplication states that you can change the grouping of the factors and the product stays the same.

One Way
Find 3 × 50, 3 × 500, and 3 × 5,000.
Use basic facts and place value.
3 × 50 = 3 × 5 tens
= 15 tens
= 150
3 × 500 = 3 × 5 hundreds
= 15 hundreds
= 1,500
3 × 5,000 = 3 × 5 thousands
= 15 thousands
= 15,000
Another Way
Find 3 × 50, 3 × 500, and 3 × 5,000.
Break apart numbers. Use the Associative Property of Multiplication.
3 × 50 = 3 × (5 × 10)
= (3 × 5) × 10
= 15 × 10
= 150
3 × 500 = 3 × (5 × 100)
= (3 × 5) × 100
= 15 × 100
= 1,500
3 × 5,000 = 3 × (5 × 1,000)
= (3 × 5) × 1,000
= 15 × 1,000
= 15,000
Convince Me! Reasoning What patterns do you see in the number of zeros in the products above?
Answer:
The pattern noticed in the zero’s in the products above is that for every number zero is added more from one to last number products.
Explanation:
Extra zero is added for every product from one to last number.
Another Example!
Use place value to calculate 5 × 400 and 6 × 5,000.
5 × 400 = 5 × 4 hundreds
= 20 hundreds
= 2,000
6 × 5,000 = 6 × 5 thousands
= 30 thousands
= 30,000
If the product of the basic fact ends in zero, the product has one more zero than you see in the factors.
Guided Practice
Do You Understand?
Question 1.
Show how you can use the basic fact 5 × 8 = 40 to determine the product of 5 × 800.
Answer:
5 × 800 = (5 × 8 × 100) = 4000.
Explanation:
5 × 8 = 40.
5 × 800 = (5 × 8 × 100)
5 × 800 = 40 × 100
5 × 800 = 4000.
Question 2.
Bob said 4 × 500 = 200. Explain his error using place value.
Answer:
His error is he missed zero to write in place value of the number.
4 × 500 = 2000 not 4 × 500 = 200.
Explanation:
4 × 500 = 200.
4 × 500 = 4 × 5 × 100
4 × 500 = 20 × 100
4 × 500 = 2000.
Do You Know How?
For 3-5, use strategies you learned to help multiply.
Question 3.
8 × 7 = ________
8 × 70 = ________
8 × 700 = ________
8 × 7,000 = ________
Answer:
8 × 7 = __56______.
8 × 70 = __560______.
8 × 700 = __5600______.
8 × 7,000 = ___56000_____.
Explanation:
8 × 7 = 56.
8 × 70 = 8 × 7 tens
= 56 tens
= 560.
8 × 700 = 8 × 7 hundreds
= 56 hundreds
= 5600.
8 × 7,000 = 8 × 7 thousands
= 56 thousands
= 56000.
Question 4.
7 × 70
Answer:
7 × 70 = 490.
Explanation:
7 × 70 = 7 × 7 tens
= 49 tens
= 490.
Question 5.
2 × 700
Answer:
2 × 700 = 1400.
Explanation:
2 × 700 = 2 × 7 hundreds
= 14 hundreds
= 1400.
Independent Practice
Leveled Practice For 6-11, use basic facts, place value, and properties to help multiply.
You can use place-value strategies to calculate each product.
Question 6.
3 × 70 = ________
3 × 700 = ________
3 × 7,000 = ________
Answer:
3 × 70 = __210______.
3 × 700 = ___2100_____.
3 × 7,000 = ___21000_____.
Explanation:
3 × 70 = 3 × 7 tens
= 21 tens
= 210.
3 × 700 = 3 × 7 hundreds
= 21 hundreds
= 2100.
3 × 7,000 = 3 × 7 thousands
= 21 thousands
= 21000.
Question 7.
________ = 6 × 40
________ = 6 × 400
________ = 6 × 4,000
Answer:
___240_____ = 6 × 40.
____2400____ = 6 × 400.
__24000______ = 6 × 4,000.
Explanation:
6 × 40 = 6 × 4 tens
= 24 tens
= 240.
6 × 400 = 6 × 4 hundreds
= 24 hundreds
= 2400.
6 × 4,000 = 6 × 4 thousands
= 24 thousands
= 24000.
Question 8.
8 × 50 = ________
8 × 500 = ________
8 × 5,000 = ________
Answer:
8 × 50 = ___400_____.
8 × 500 = ___4000_____.
8 × 5,000 = __40000______.
Explanation:
8 × 50 = 8 × 5 tens
= 4 hundreds
= 400.
8 × 500 = 8 × 5 hundreds
= 4 thousands
= 4000.
8 × 5,000 = 8 × 5 thousands
= .4 ten thousands
= 40000.
Question 9.
4 × 2,000
Answer:
4 × 2,000 = 8000.
Explanation:
4 × 2,000 = 4 × 2 thousands
= 8 thousands
= 8000.
Question 10.
700 × 4
Answer:
700 × 4 = 2800.
Explanation:
700 × 4 = 7 hundreds × 4
= 28 hundreds
= 2800.
Question 11.
6 × 60
Answer:
6 × 60 = 360.
Explanation:
6 × 60 = 6 × 6 tens
= 36 tens
= 360.
Problem Solving
Question 12.
enVision® STEM The Mississippi River is about 8 times the length of the Hudson River. If the Hudson River is about 300 miles long, about how many miles long is the Mississippi River? Write and solve an equation.
Answer:
Length of Mississippi River = 2400 miles.
Explanation:
Length of the Hudson River = 300 miles long.
The Mississippi River is about 8 times the length of the Hudson River.
=> Length of Mississippi River = 8 × Length of the Hudson River
= 8 × 300
= 8 × 3 hundreds
= 24 hundreds
= 2400 miles.
Question 13.
Ted, Jason, and Angelina are trying to raise $200 for a local shelter. Ted raised $30. Jason raised $90. How much money m does Angelina need to raise to reach their goal?

Answer:
Amount to be raised by m, Angelina = $80.
Explanation:
Amount raised by Ted = $30.
Amount raised by Jason = $90.
Total amount Ted, Jason, and Angelina are trying to raise = $200.
Amount to be raised by m, Angelina = Total amount Ted, Jason, and Angelina are trying to raise – (Amount raised by Ted + Amount raised by Jason )
= $200 – ($30 + $90)
= $200 – $120
= $80.

For 14-15, use the table at the right.

Question 14.
Make Sense and Persevere There are 9 girls and 4 adults in Aimee’s scout troop. How much did the troop pay for tickets to the amusement park?
Answer:
Total amount of fee to 9 girls and 4 adults troop paying for tickets to the amusement park = $430.
Explanation:
Number of girls to the amusement park = 9.
Amount of fee to each girl to the amusement park = $30.
Number of adults to the amusement park = 4.
Amount of fee to each adult to the amusement park = $40.
Total amount of fee to 9 girls and 4 adults troop paying for tickets to the amusement park = ( Number of girls to the amusement park × Amount of fee to each girl to the amusement park =) + ( Number of adults to the amusement park × Amount of fee to each adult to the amusement park )
= (9 × $30) + ( 4 × $40)
= $270 + $160
= $430.
Question 15.
Higher Order Thinking Tina visited Funland with her mom and a friend They bought tickets for Plan C. How much money did they save on the two children’s tickets for Plan C instead of buying separate tickets for Plan A and Plan B?
Answer:
Amount of money they saved on the two children’s tickets for Plan C instead of buying separate tickets for Plan A and Plan B = $20.
Explanation:
Amount of fee to each girl to the amusement park in Plan A = $20.
Amount of fee to each girl to the amusement park in Plan B = $30.
Amount of fee to each adult to the amusement park = $40.
Amount of tickets for Plan C (combined A and B) for adult = $60.
Amount of tickets for Plan C (combined A and B) for kids = $40.
Amount for two children in Plan A = 2 × $20 = $40.
Amount for two children in Plan B = 2 × $30 = $60.
Amount for two children in Plan C (combined A and B) = 2 × $40 = $80.
Difference:
Amount of money they saved on the two children’s tickets for Plan C instead of buying separate tickets for Plan A and Plan B = (Amount for two children in Plan A + Amount for two children in Plan B ) – Amount for two children in Plan C (combined A and B)
= ($40 + $60) – $80.
= $100 – $80
= $20.
Assessment Practice
Question 16.
Brandon says 4 × 800 is greater than 8 × 4,000.
Renee says 4 × 800 is less than 8 × 4,000.
A. Without calculating the answer, explain ” how to use place-value strategies or the Associative Property to find which is greater.
Answer:
Brandon says 4 × 800 is greater than 8 × 4,000 and Renee says 4 × 800 is less than 8 × 4,000 both are correct.
Explanation:
4 × 800 is greater than 8 × 4,000.
=> place value of 4000 is thousand greater than 800.
4 × 800 is less than 8 × 4,000.
=> place value of 800 is hundred less than thousands.
B. Without calculating the answer, explain how to use relationships or basic facts to find which is less.
Answer:
Without calculating the answer, we can use relationships or basic facts to find which is less by the place value of the numbers given.
Explanation:
We can use relationships or basic facts to find which is less by the place value of the numbers given without calculating the answer. Which is having less place value that is considered as less and vice versa.
Lesson 3.2 Estimate Products
Solve & Share
Sarah earns $48 a week babysitting. She saves all of her earnings for 6 weeks. Estimate to determine about how much money Sarah saves. Solve this problem using any strategy you choose.
I can …use rounding to estimate products and check if my answer is reasonable

Look Back! Is your estimate more or less than the amount Sarah actually earned? Explain.
Answer:
My estimation for Sarah earnings is around $290. My estimation saving is more than the actual savings of her.
Explanation:
Amount of money Sarah earns for babysitting for a week = $48.
Number of weeks She saves all of her earnings = 6.
Amount of money Sarah saves = Amount of money Sarah earns for babysitting for a week × Number of weeks She saves all of her earnings
= $48 × 6
= $288.
Essential Question
How Can You Estimate When You Multiply?
Answer:
We can estimate when we multiply by using multiplication facts to get the solution and solve the problem.
Explanation:
We can estimate when we multiply by checking the numbers given and doing their multiplication or by using multiplication facts to get the solution and solve the problem.
Visual Learning Bridge
Mr. Hector’s class sold calendars and note pads for 3 weeks as a class fundraiser. About how much did Mr. Hector’s class make selling calendars? selling note pads?

Use compatible numbers to estimate how many calendars C, were sold.
28 + 73 + 63 = C
164 = C
Estimate $4 × 164.
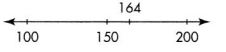
Estimate by using compatible numbers. 164 is close to 150.
4 × 150 = 600
Mr. Hector’s class made about $600 selling calendars.
Use rounding to estimate how many note pads n, were sold.
272 + 475 + 232 = n
979 = n
Estimate $3 × 979.
![]()
To the nearest thousand, 979 rounds to 1,000.
3 × 1,000 = 3,000
Mr. Hector’s class made about $3,000 selling note pads.
Convince Me! Construct Arguments Could you solve the problem above by rounding to estimate the total number of calendars and the total number of note pads? Explain.
Answer:
We can estimate by rounding to estimate the total number of calendars and the total number of note pads and solve the problem.
Explanation:
We can estimate by rounding to estimate the total number of calendars and the total number of note pads and solve the problem. By rounding the total there cannot be any difference much its just rounding the number to the nearest tens, hundreds or thousands.
Another Example!
Mrs. Li’s class made $2,089 selling neon pencil packs. A student calculated that Mr. Hector’s class and Mrs. Li’s class together made $8,865 selling the school supplies. Is the student’s calculation reasonable?
You can estimate to check if an answer is reasonable.
Round Mrs. Li’s total to the nearest thousand: $2,000. Then, add the rounded amounts. $2,000 + $600 + $3,000 = $5,600
The student’s calculation is not reasonable because $8,865 is not close to $5,600.
Guided Practice
Do You Understand?
Question 1.
Mr. Harm’s class sold 1,275 items at $5 per item. One of his students calculates the class raised $2,375. Is the student’s calculation reasonable? Explain.
Answer:
No, student’s calculation is not reasonable because class raised $6375 not $2375.
Explanation:
Number of items Mr. Harm’s class sold = 1275.
Cost of each item Mr. Harm’s class sold = $5
Total cost of amount of items Mr. Harm’s class sold = Number of items Mr. Harm’s class sold × Cost of each item Mr. Harm’s class sold
= 1275 × $5
= $6375.
One of his students calculates the class raised $2,375.
Do You Know How?
For 2-5, estimate the product.
Question 2.
6 × 125
Answer:
6 × 125 = 15000.
Explanation:
6 × 125 = 6 × (100 + 25)
6 × 125 = 600 + 150
6 × 125 = 750.
Question 3.
4 × 2,610
Answer:
4 × 2,610 = 10440.
Explanation:
4 × 2,610 = 4 × (2000 + 600 + 10)
4 × 2,610 = 8000 + 2400 + 40
4 × 2,610 = 10400 + 40
4 × 2,610 = 10440.
Question 4.
538 × 3
Answer:
538 × 3 = 1614.
Explanation:
538 × 3 = (500 + 30 + 8) × 3
538 × 3 = 1500 + 90 + 24
538 × 3 = 1590 + 24
538 × 3 = 1614.
Question 5.
314 × 7
Answer:
314 × 7 = 2198.
Explanation:
314 × 7 = (300 + 10 + 4) × 7
314 × 7 = 2100 + 70 + 28
314 × 7 = 2170 + 28
314 × 7 = 2198.
Independent Practice
Leveled Practice For 6-8, estimate the product.
Question 6.

Answer:

Explanation:
287 Rounded to 290.
=> 3 × 290=270.
Question 7.

Answer:
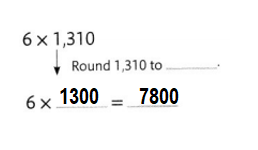
Explanation:
1310 Rounded to 1300.
=> 6 × 1300 = 7800.
Question 8.

Answer:

Explanation:
62 Rounded to 60.
=> 9 × 60 = 540.
For 9-11, estimate to check if the answer is reasonable.
Question 9.

Answer:
Its reasonable because 3430 is the rounded number of 3402 and there is not much difference.
Explanation:
7 × 486 = 3402.
486 is rounded to 490.
=> 7 × 490 = 3430.
Question 10.

Answer:
Its not reasonable because 5 × 1240 = 6200 not 9200.
Explanation:
5 × 1240 = 6200.
1240 Rounded to 1240.
=> 5 × 1240 = 6200
Question 11.
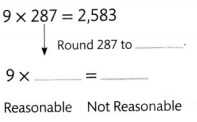
Answer:
Its reasonable because 2610 is the rounded figure is 2583 and there is not much difference.
Explanation:
9 × 287 = 2583.
287 Rounded to 290.
9 × 290 = 2610.
Problem Solving
For 12-13, use the graph at the right.
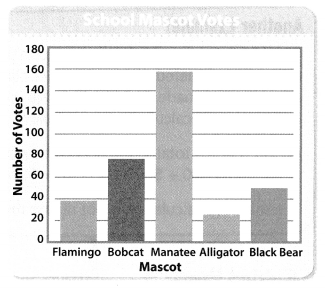
Question 12.
The students voted on a school mascot. Which mascot had 4 times as many of votes as the flamingo?
Answer:
Mascot had 4 times as many of votes as the flamingo = Manatee = 158 votes.
Explanation:
Number of votes on Flamingo = 38.
Number of votes on Bobcat = 78.
Number of votes on Manatee = 158.
Number of votes on Alligator = 22.
Number of votes on Black Bear = 50.
Comparison:
Mascot had 4 times as many of votes as the flamingo = 4 × Number of votes on Flamingo
= 4 × 38
= 152.
=> Number of votes on Manatee = 158.
Question 13.
Construct Arguments Explain how you could estimate the number of students who voted on a school mascot. Then give your estimate.
Answer:
We can estimate by by adding the number of votes, they voted in school.
Total number of students = 346.
Explanation:
Number of votes on Flamingo = 38.
Number of votes on Bobcat = 78.
Number of votes on Manatee = 158.
Number of votes on Alligator = 22.
Number of votes on Black Bear = 50.
Total number of students = Number of votes on Flamingo + Number of votes on Bobcat + Number of votes on Manatee + Number of votes on Alligator + Number of votes on Black Bear
= 38 + 78 + 158 + 22 + 50
= 116 + 158 + 22 + 50
= 274 + 22 + 50
= 296 + 50
= 346.
Question 14.
Number Sense Ellie says the product of 211 and 6 is 1,866. Is this calculation reasonable? Explain.
Answer:
This calculation is not reasonable because 211 × 6 = 1266 not 1866.
Explanation:
211 × 6 = (200 + 11) × 6
= 1200 + 66
= 1266.
Question 15.
Higher Order Thinking An adult sleeps about 480 minutes per day. An infant sleeps about 820 minutes per day. About how many more minutes does an infant sleep than an adult in one week? Solve the problem two different ways.
Answer:
1Way:
Time taken more by infant than an adult to sleep per one week = Time an infant sleeps per day – Time an adult sleeps per day
= 820 – 480
= 340 minutes.
2Way:
Time an adult sleeps per day = Time taken more by infant than an adult to sleep per one week + Time an infant sleeps per day
=> 820 = ??? + 480
=> 820 – 480 = ???
= 340 minutes = ???
Explanation:
1Way:
Time an adult sleeps per day = 480 minutes.
Time an infant sleeps per day = 820 minutes.
Time taken more by infant than an adult to sleep per one week = Time an infant sleeps per day – Time an adult sleeps per day
= 820 – 480
= 340 minutes.
2Way:
Time an adult sleeps per day = 480 minutes.
Time an infant sleeps per day = 820 minutes.
Time an adult sleeps per day = Time taken more by infant than an adult to sleep per one week + Time an infant sleeps per day
=> 820 = ??? + 480
=> 820 – 480 = ???
= 340 minutes = ???
Assessment Practice
Question 16.
Gul can run 800 meters in 139 seconds. About how long would it take her to run 6 times as far if she runs at the same speed? Choose the best estimate.
A. About 140 seconds
B. About 600 seconds
C. About 1,200 seconds
D. About 6,000 seconds
Answer:
Time taken by Gul to run 6 times as far if she runs at the same speed = 834 seconds.
C. About 1,200 seconds
Explanation:
Time taken by Gul to run 800 meters = 139 seconds.
Time taken by Gul to run 6 times as far if she runs at the same speed = 6 × Time taken by Gul to run 800 meters
= 6 × 139
= 834 seconds.
Question 17.
A new two-seater car weighs 1,785 pounds. About how much would 8 of the two-seater cars weigh? Choose the best estimate.
A. About 160 pounds
B. About 1,600 pounds
C. About 16,000 pounds
D. About 60,000 pounds
Answer:
Weight of 8 of the two-seater cars weigh = 14280 pounds.
C. About 16,000 pounds
Explanation:
Weight of new two-seater car = 1,785 pounds.
Weight of 8 of the two-seater cars weigh = 8 × Weight of new two-seater car
= 8 × 1785
= 14280 pounds.
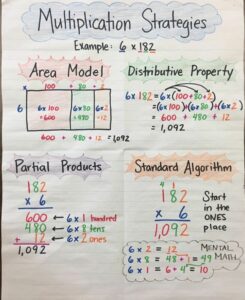
Lesson 3.3 Use Arrays and Partial Products to Multiply
Solve & Share
A music room has chairs arranged in rows. There are 6 rows. Each row has 18 chairs. How many chairs are in the music room? Solve this problem any way you choose. Explain your answer.
I can … use arrays and partial products to multiply.

Look Back! Would the answer be different if there were 18 rows with 6 chairs in each row? Explain.
Answer:
No, there won’t be any change in the answer because 18 × 6 or 6 × 18 are both the same just numbers are interchanged, product = 108.
Explanation:
Number of rows chairs arranged = 18.
Number of chairs in each row = 6.
Total number of chairs used = Number of rows chairs arranged × Number of chairs in each row
= 18 × 6
= 108.
Total number of chairs used = Number of chairs in each row × Number of rows chairs arranged
= 6 × 18
= 108.
Essential Question
How Can You Use an Array and Partial Products to Multiply?
Answer:
We can use an array and Partial Products to Multiply by multiplying each digit of a number in turn with each digit of another where each digit maintains its place.
Explanation:
The partial product method involves multiplying each digit of a number in turn with each digit of another where each digit maintains its place.
Visual Learning Bridge
The windows of a building on International Drive are in an array. There are 5 rows with 13 windows in each row. How many windows are in this array?

What You Show

What You Think
Find 5 × 13.
Estimate: 5 × 13 is about 5 × 10 = 50.
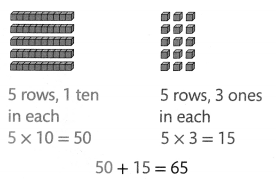
The numbers 15 and 50 are called partial products. 65 is the product.
What You Record
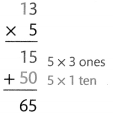
There are 65 windows in the array.
The product, 65, is close to the estimate of 50. The answer is reasonable.
You can use place value to break factors apart and the Distributive Property to find partial products.
Convince Me! Use Structure How are the partial products represented with the place-value blocks?
Answer:
The partial product method involves multiplying each digit of a number in turn with each digit of another where each digit maintains its place.
Explanation:
The partial product method involves multiplying each digit of a number in turn with each digit of another where each digit maintains its place.
For Example:
2 in 23 would actually be 20.
For instance, 23 x 42 would become (20 x 40) + (20 x 2) + (3 x 40) + (3 x 2).
Another Example!
Find 2 × 126.
Estimate: 2 × 126 is about 2 × 100 = 200.

Guided Practice
Do You Understand?
Question 1.
Explain how an array shows multiplication.
Answer:
An array is a way to represent multiplication and division using rows and columns. The word problem will determine which way to draw the array.
Explanation:
Rows represent the number of groups. Columns represent the number in each group or the size of each group. The word problem will determine which way to draw the array.
Do You Know How?
For 2-3, complete each calculation.
Question 2.
2 × 24
Answer:
2 × 24 = 48.
Explanation:
2 × 24 = ??
=> 2 × 2 tens = 2 × 20 = 40.
=> 2 × 4 ones = 2 × 4 = 8.
2 × 24 = 40 + 8 = 48.
Question 3.
3 × 218
Answer:
3 × 218 = 654.
Explanation:
3 × 218 = ??
=> 3 × 2 hundreds = 3 × 200 = 600.
=> 3 × 1 tens = 3 × 10 = 30.
=> 3 × 8 ones = 3 × 8 = 24.
3 × 218 = 600 + 30 + 24 = 654.
Independent Practice
Leveled Practice For 4-5, multiply. Complete each equation.
Question 4.
Find 3 × 13.
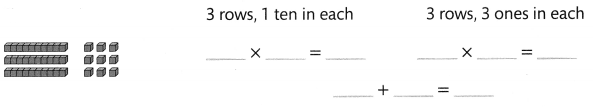
Answer:
3 × 13 = 39.
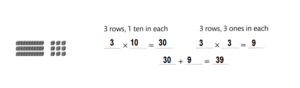
Explanation:
3 × 13 = ??
3 rows, 1 ten in each.
=> 3 × 10 = 30.
3 rows, 3 ones in each.
=> 3 × 3= 9.
=> 30 + 9 = 39..
Question 5.
Find 2 × 105
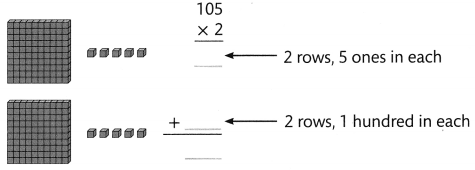
Answer:
2 × 105 = 210.

Explanation:
2 × 105 = ??
2 rows, 1 hundred in each.
=> 2 × 100 = 200.
2 rows, 5 ones in each.
=> 2 × 5 = 10.
=> 200 + 10 = 210.
Problem Solving
Question 6.
Model with Math What multiplication equation do the place-value blocks show? Find the product. Then write a problem that could be solved using this model.

Answer:
300 + 20 + 4 = 324 blocks 3 rows.
Multiplication equation:
3 × 324 = 972.
Explanation:
3 rows, 3 hundred in each.
=> 3 × 300 = 900.
3 rows, 2 tens in each.
=> 3 × 20 = 60.
3 rows, 4 ones in each.
=> 3 × 4 = 12.
3 × 324 = 900 + 60+ 12 = 972.
Question 7.
How many marbles are in 3 large bags and 4 small bags?
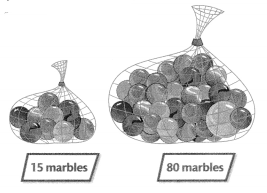
Answer:
Total number of marbles in 4 small bags = 60.
Total number of marbles in 3 large bags = 240.
Explanation:
Number of marbles in small bag = 15.
Total number of marbles in 4 small bags = 4 × Number of marbles in small bag
= 4 × 15
= 60.
Number of marbles in large bag = 80.
Total number of marbles in 3 large bags = 3 × Number of marbles in large bag
= 3 × 80
= 240.
Question 8.
Higher Order Thinking How can the Distributive Property be used to find 4 × 875? Draw an array.
Answer:
4 × 875 = 3500.

Explanation:
4 × 875 =???
= 4 × 8hundreds = 4 × 800 = 3200.
= 4 × 7tens = 4 × 70 = 280.
= 4 × 5ones = 4 × 5 = 20.
4 × 875 = 3200 + 280 + 5 = 3500.
Question 9.
Select all the expressions that have a value of 312.
☐ (3 × 100) + (3 × 4)
☐ 3 × 12
☐ 3 × 112
☐ (30 × 10) + (3 × 12)
☐ 3 × 104
Answer:
(3 × 100) + (3 × 4) and 3 × 104 expressions have 312.
Explanation:
312 = ???
(3 × 100) + (3 × 4) = 300 + 12 = 312.
3 × 12 = 36.
3 × 112 = 336.
(30 × 10) + (3 × 12) = 300 + 36 = 336.
3 × 104 = 312.
Question 10.
Which are correct partial products for 54 × 9?
A. 36, 45
B. 36, 450
C. 540, 36
D. 32, 450
Answer:
54 × 9 = 450 + 36 = 486.
B. 36, 450 is the correct partial products for 54 × 9.
Explanation:
54 × 9 = ??
= 5tens × 9 = 9 × 50 = 450.
= 4ones × 9 = 4 × 9 = 36.
54 × 9 = 450 + 36 = 486.
Lesson 3.4 Use Area Models and Partial Products to Multiply
Solve & Share
Use only the numbers shown on the diagram and the operation symbols (+, -, ×, +) to determine the area of the unshaded rectangle below. Solve this problem using any strategy you choose.
I can use area models and partial products to multiply.

Look Back! Use Structure Are these equations equal? Explain. 8 × (10 – 4) = (8 × 10) – (8 × 4)
Answer:
Yes, these equations are equal 8 × (10 – 4) = (8 × 10) – (8 × 4) = 48.
Explanation:
8 × (10 – 4) = (8 × 10) – (8 × 4) = ??
8 × (10 – 4) = 80 – 32 = 48.
(8 × 10) – (8 × 4) = 80 – 32 = 48.
Essential Question
How Can You Use an Area Model and Partial Products to Multiply?
Answer:
The partial product method involves multiplying each digit of a number in turn with each digit of another where each digit maintains its place. Write each factor in expanded form. Then, draw your model. Next, multiply to find the area of each smaller rectangle. Finally, add those products to find the total area.
Explanation:
First, write each factor in expanded form. Then, draw your model. Next, multiply to find the area of each smaller rectangle. Finally, add those products to find the total area.
The partial product method involves multiplying each digit of a number in turn with each digit of another where each digit maintains its place.
Visual Learning Bridge
A garden is in the shape of a rectangle. It is 8 feet wide and 25 feet long. What is the area of the garden?
A numerical expression contains numbers and at least one operation. 8 × 25 is a numerical expression.
What You Show

What You Think
Estimate: 8 × 25 is about 8 × 30 = 240. 20

What You Record
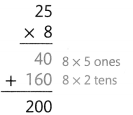
The area of the garden is 200 square feet.
The product, 200, is close to the estimate of 240. The answer is reasonable.
Convince Me! Use Structure Does 12 – (4 × 2) = (12 – 4) (12 – 2)? Explain.
Answer:
No, this equation is not correct because 12 – (4 × 2) = 24 where as (12 – 4) (12 – 2) =80.
Explanation:
12 – (4 × 2) = (12 × 4) – (12 × 2) = 48 – 24 = 24.
(12 – 4) (12 – 2) = 8 × 10 = 80.
Another Example!
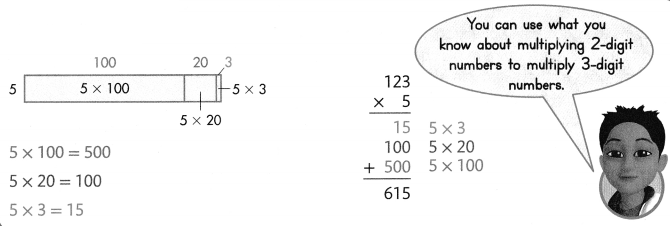
Guided Practice
Do You Understand?
Question 1.
What numerical expression is shown by the area model below?

Answer:
265 × 7 = 1855.
Explanation:
(200 + 60 + 5) 7 = 265 × 7
=> 7 × 200 = 1400.
=> 7 × 60 = 420.
=> 7 × 5 = 35.
1400 + 420 + 35 = 1855.
Do You Know How?
Question 2.
Multiply. Use the area model and partial products.

Answer:
560 × 7 = 3920.
Explanation:
(500 + 60 ) 7 = 560 × 7
=> 7 × 500 = 3500
=> 7 × 60 = 420.
3500 + 420 = 3920.
Independent Practice
Leveled Practice For 3-6, multiply. Use the area model and partial products.
Question 3.
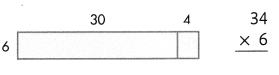
Answer:
34 × 6 = 204.
Explanation:
(30+ 4) 6 = 34 × 6
=> 6 × 30 = 180.
=> 6 × 4 = 24.
180 + 24 = 204.
Question 4.

Answer:
99 × 2 = 198.
Explanation:
(90 + 9) 2 = 99 × 2
=> 2 × 90 = 180.
=> 2 × 9 = 18.
180 + 18 = 198.
Question 5.

Answer:
3 × 185 = 555.
Explanation:
3 (100 + 80 + 5) = 3 × 185
=> 3 × 100 = 300.
=> 3 × 80 = 240.
=> 3 × 5 = 15.
300 + 240 + 15 = 555.
Question 6.

Answer:
8 × 440 = 3520.
Explanation:
8 ( 400 + 40) = 8 × 440
=> 8 × 400 = 3200.
=> 8 × 40 = 320.
3200 + 320 = 3520.
Problem Solving
Question 7.
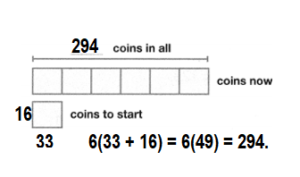
Model with Math Last year, Anthony’s grandmother gave him 33 silver coins and 16 gold coins to start a coin collection. Now Anthony has six times as many coins in his collection. How many coins does Anthony have in his collection? Complete the bar diagram to show your work.
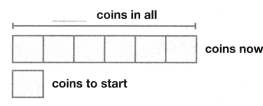
Answer:
Number of coins Anthony have in his collection now = 294.
Explanation:
Number of silver coins Anthony’s grandmother gave him = 33.
Number of gold coins Anthony’s grandmother gave him = 16.
Now Anthony has six times as many coins in his collection.
Number of coins Anthony have in his collection now = 6 × (Number of silver coins Anthony’s grandmother gave him + Number of gold coins Anthony’s grandmother gave him)
= 6 × (33 + 16)
= (6 × 33) + (6 × 16)
= 198 + 96
= 294.
Question 8.
Wyatt said he used partial products to write 7 × 870 = 5,600 + 49. Explain Wyatt’s error and use math to justify your explanation.
Answer:
7 × 870 = 5600 + 490 not 5,600 + 49 because Wyatt’s error is that he took partial products value wrong and got the result wrong answer.
Explanation:
7 × 870 = (7 × 800) + (7 × 70)
7 × 870 = 5600 + 490
7 × 870 = 6090.
5,600 + 49 = 5649.
Question 9.
Higher Order Thinking Tod Mountain is a mountain peak near Tyler, Texas. A ranger hiked 607 feet to and from the peak, each way. The ranger hiked 3 times in the past four weeks. How far did the ranger hike on Tod Mountain over the past four weeks?
Answer:
Length of the ranger hiked on Tod Mountain over the past four weeks = 1821 feet.
Explanation:
Length of the ranger hiked to and from the peak, each way of Tod Mountain = 607 feet.
The ranger hiked 3 times in the past four weeks.
Length of the ranger hiked on Tod Mountain over the past four weeks = 3 × Length of the ranger hiked to and from the peak, each way of Tod Mountain
= 3 × 607
= (3 × 600) + (3 × 7)
= 1800 + 21
= 1821 feet.
Question 10.
Wendy plans to bring beverages for the school picnic. She has 5 gallons of iced tea. Also, she will bring 2 gallons of lemonade for every 10 people. How many total gallons of lemonade and iced tea does Wendy need to bring for 40 people? Complete the table.
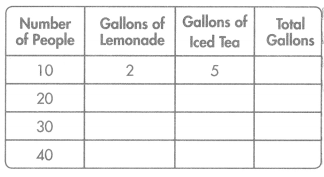
Answer:
Total gallons of lemonade and iced tea Wendy needs to bring for 40 people = 28.
Explanation:
Number of gallons of iced tea Wendy has for every 10 people = 5.
Number of gallons of lemonade Wendy has for every 10 people = 2.
Total gallons of lemonade and iced tea Wendy needs to bring for 40 people = 4 × (Number of gallons of iced tea Wendy has for every 10 people + Number of gallons of lemonade Wendy has for every 10 people)
= 4 × (5 + 2)
= (4 × 5) + (4 × 2)
= 20 + 8
= 28.
Assessment Practice
Question 11.
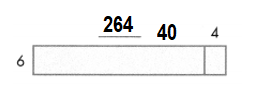
What is the missing factor?
6 × ? = 264

A. 50
B. 44
C. 40
D. 30
Answer:
6 × 44 = 264.
B. 44
Explanation:
6 × ? = 264
=> ? = 264 ÷ 6
=> ? = 44.
Question 12.
Which are the partial products for this area model?
7 × 228
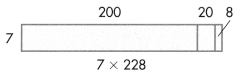
A. 1,400, 144, 56
B. 14,000, 140, 56
C. 56, 14, 1,400
D. 56, 140, 1,400
Answer:
7 × 228 = 1400 + 140 + 56 = 1596.
D. 56, 140, 1,400
Explanation:
7 × 228 = (7 × 200) + (7 × 20) + (7 × 8)
7 × 228 = 1400 + 140 + 56
7 × 228 =1540 + 56
7 × 228 = 1596.
Lesson 3.5 More Use Area Models and Partial Products to Multiply
Solve & Share
The horseshoe-pit model below has an area of 228 square feet. The length of one part of the pit was erased by mistake. What is the length of the missing section, x? Solve any way you choose. Explain how you found the answer.
I can … use area models and partial products to multiply.

Look Back! What multiplication equation can be used to represent the horseshoe-pit model above?
Answer:
Length of the second section missing horseshoe-pit model = x = 8 feet.
Explanation:
The horseshoe-pit model below has an area of 228 square feet. The length of one part of the pit was erased by mistake. What is the length of the missing section, x? Solve any way you choose.
Area of the horseshoe-pit model = 228 square feet.
Length of the first section horseshoe-pit model = 30 feet.
Length of the second section missing horseshoe-pit model = x feet.
Breadth of the horseshoe-pit model = 6 feet.
Area of the horseshoe-pit model = length × Breadth
=> 228 = (Length of the first section horseshoe-pit model + Length of the second section missing horseshoe-pit model) × 6
=> 228 = (30 + x) × 6
=> 228 ÷ 6 = 30 + x
=> 38 = 30 + x
=> 38 – 30 = x
=> 8 feet = x.
Essential Question
How Do You Multiply with Greater Numbers?
Answer:
We multiply greater number Multiplication by using the place values of each number given and multiply and get the result to that problem.
Explanation:
When multiplying by larger numbers with two digits or more, use one placeholding zero when multiplying by the tens digit, two placeholding zeros when multiplying by the hundreds digit, three zeros when multiplying by the thousands digit, and so forth.
Visual Learning Bridge
The Rails-to-Trails Preservation opened a new section of a biking trail. The section is 6 yards wide. What is its area? Calculate 6 × 1,842.
The process for multiplying is the same regardless of the number of digits.

Find 6 × 1,842 using an area model and partial products.
Estimate: 6 × 1,842 is about 6 × 2,000 = 12,000.
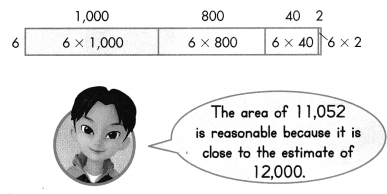
Remember you can find partial products in any order.
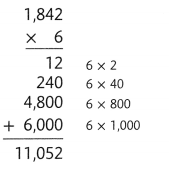
The new section is 11,052 square yards.
Convince Me! Use Structure How is the process of using partial products to find the final product the same for each of these calculations? How is it different? Explain.
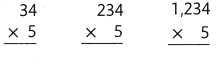
Answer:
The process of using partial products to find the final product for each of these calculations is not same, its completely different because the numbers given for multiplication having different place values and result of their products also different.
Explanation:
5 × 34 = (5 × 30) + (5 × 4)
5 × 34 = 150 + 20
5 × 34 = 170.
5 × 234 = (5 × 200) + (5 × 30) + (5 × 4)
5 × 234 = 1000 + 150 + 20
5 × 234 = 1150 + 20
5 × 234 = 1170.
5 × 1234 = (5 × 1000) + (5 × 200) + (5 × 30) + (5 × 4)
5 × 1234 = 5000 + 1000 + 150 + 20
5 × 1234 = 6000 + 150 + 20
5 × 1234 = 6150 + 20
5 × 1234 = 6170.
Guided Practice
Do You Understand?
Question 1.
What multiplication expression is shown by the area model below?
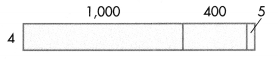
Answer:
4 × (1000 + 400 + 5) = 4 × 1405 = 5620.
Explanation:
4 × (1000 + 400 + 5) = ????
4 × (1000 + 400 + 5) = (4 × 1000) + (4 × 400) + ( 4 × 5)
4 × (1000 + 400 + 5) = 4000 + 1600 + 20
4 × (1000 + 400 + 5) = 5600 + 20
4 × (1000 + 400 + 5) = 5620.
=> 4 × 1405 = 5620. (1000 + 400 + 5 = 1405)
Do You Know How?
For 2, multiply. Use the area model and partial products.
Question 2.
5 × 1,117

Answer:
5 × 1,117 = 5585.
Explanation:
Length of the given rectangle figure = 1000 + 100 + 10 + 7 = 1117.
Breadth of the given rectangle figure = 5.
Area of the given rectangle figure = Length of the given rectangle figure × Breadth of the given rectangle figure
= 1117 × 5
= (1000 × 5) + (100 × 5) + (10 × 5) + (7 × 5)
= 5000 + 500 + 50 + 35
= 5500 + 50 + 35
= 5550 + 35
= 5585.
Independent Practice
For 3-8, multiply. Use the area model and partial products.

Question 3.
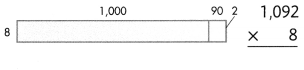
Answer:
1092 × 8 = (1000 × 8) + (90 × 8) + (2 × 8) = 8736.
Explanation:
Length of the given rectangle figure = 1000 + 90+ 2 = 1092.
Breadth of the given rectangle figure = 8.
Area of the given rectangle figure = Length of the given rectangle figure × Breadth of the given rectangle figure
= 1092× 8
= (1000 × 8) + (90 × 8) + (2 × 8)
= 8000 + 720 + 16
= 8720 + 16
= 8736.
Question 4.

Answer:
4261 × 3 = (4000 × 3) + (200× 3) + (60 × 3) + (1 × 3) = 12783.
Explanation:
Length of the given rectangle figure = 4000 + 200 + 60 + 1= 4261.
Breadth of the given rectangle figure = 3.
Area of the given rectangle figure = Length of the given rectangle figure × Breadth of the given rectangle figure
= 4261 × 3
= (4000 × 3) + (200× 3) + (60 × 3) + (1 × 3)
= 12000 + 600 + 180 + 3
= 12600 + 180 + 3
= 12780 + 3
= 12783.
Question 5.
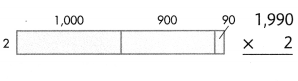
Answer:
1990× 2 = (1000 × 2) + (900× 2) + (90 × 2) = 3980.
Explanation:
Length of the given rectangle figure = 1000 + 900 + 90 = 1990
Breadth of the given rectangle figure = 2.
Area of the given rectangle figure = Length of the given rectangle figure × Breadth of the given rectangle figure
= 1990× 2
= (1000 × 2) + (900× 2) + (90 × 2)
= 2000 + 1800 + 180
= 3800 + 180
= 3980.
Question 6.
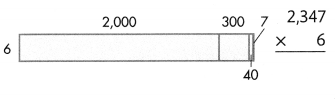
Answer:
2347 × 6 = (2000 × 6) + (300× 6) + (40 × 6) + (7 × 6) = 14082.
Explanation:
Length of the given rectangle figure = 2000 + 300 + 40 + 7 = 2347
Breadth of the given rectangle figure = 6.
Area of the given rectangle figure = Length of the given rectangle figure × Breadth of the given rectangle figure
= 2347 × 6
= (2000 × 6) + (300× 6) + (40 × 6) + (7 × 6)
= 12000 + 1800 + 240 + 42
= 13800 + 240 + 42
= 14040 + 42
= 14082.
Question 7.

Answer:
3022 × 5 = (3000 × 5) + (20 × 5) + (2 × 5) = 15110.
Explanation:
Length of the given rectangle figure = 3000 + 20 + 2 = 3022.
Breadth of the given rectangle figure = 5.
Area of the given rectangle figure = Length of the given rectangle figure × Breadth of the given rectangle figure
= 3022 × 5
= (3000 × 5) + (20 × 5) + (2 × 5)
= 15000 + 100 + 10
= 15100 + 10
= 15110.
Question 8.
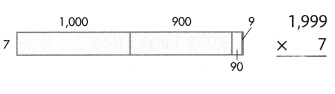
Answer:
1999 × 7 = (1000 × 7) + (900 × 7) + (90 × 7) + (9 × 7) = 13993.
Explanation:
Length of the given rectangle figure = 1000 + 900 + 90 + 9 = 1999.
Breadth of the given rectangle figure = 7.
Area of the given rectangle figure = Length of the given rectangle figure × Breadth of the given rectangle figure
= 1999 × 7
= (1000 × 7) + (900 × 7) + (90 × 7) + (9 × 7)
= 7000 + 6300 + 630 + 63
= 13300 + 630 + 63
= 13930 + 63
= 13993.
Problem Solving
Question 9.
Be Precise There are usually 365 days in each year. Every fourth year is called a leap year and has one extra day in February. How many days are there in 8 years if 2 of the years are leap years?
Answer:
Number of days in 8 years = 2922.
Explanation:
Number of days in each year = 365.
Every fourth year is called a leap year and has one extra day in February.
=> Number of days in leap year = 366.
Number of days in 8 years = 6 ( Number of days in each year) + 2 (Number of days in leap year)
= (6 × 365) + (2 × 366)
= 2190 + 732
= 2922.
Question 10.
There are 1,250 seeds in each package. There are 5 packages. How many seeds are there in all?
Answer:
1250 × 5 = (1000 × 5) + (200 × 5) + ( 50 × 5) = 6250.
Explanation:
Number of seeds in each package = 1250.
Number of packages = 5.
Total number of seeds in all = Number of seeds in each package × Number of packages
= 1250 × 5
= (1000 × 5) + (200 × 5) + ( 50 × 5)
= 5000 + 1000 + 250
= 6000 + 250
= 6250.
Question 11.
A cat breeder has 6 Sphynx kittens and 7 Persian kittens for sale. If all 13 kittens sell, how much money will the breeder earn? Write and solve equations. Tell what your variables represent.

Answer:
Total money the breeder earns = $9613.
Explanation:
Number of Sphynx kittens a cat breeder has for sale = 6.
Number of Persian kittens a cat breeder has for sale = 7.
Cost of each Sphynx kitten = $698.
Cost of each Persian kitten = $775.
Total money the breeder earns = ( Number of Sphynx kittens a cat breeder has for sale × Cost of each Sphynx kitten) + (Number of Persian kittens a cat breeder has for sale × Cost of each Persian kitten )
= (6 × $698) + (7 × $775)
= $4188 + $5425
= $9613.
Question 12.
Higher Order Thinking Patricia creates a design using 1,025 tiles. She doubles the number of tiles to make a second design. Her third design uses 3 times as many tiles as the second design. How many tiles does Patricia use in her third design? Explain.
Answer:
Number of tiles Patricia uses for creating third design = 6150.
Explanation:
Number of tiles Patricia uses for creating first design = 1025.
She doubles the number of tiles to make a second design.
=> Number of tiles Patricia uses for creating second design = 2×1025 = 2050.
Her third design uses 3 times as many tiles as the second design.
=> Number of tiles Patricia uses for creating third design = 3 × Number of tiles Patricia uses for creating second design
=> 3 × 2050
=> 6150.
Assessment Practice
Question 13.
Which are the correct partial products of 3 × 3,672?
A. 6; 21; 1,800; 9,000
B. 9,000; 1,800; 210; 6
C. 210; 1,800; 9,000
D. 6; 210; 180; 9,000
Answer:
The correct partial products of 3 × 3,672:
B. 9,000; 1,800; 210; 6
Explanation:
3 × 3,672 = (3 × 3000) + (3 × 600) + (3 × 70) + (3 × 2)
3 × 3,672 = 9000 + 1800 + 210 + 6
3 × 3,672 = 10800 + 210 + 6
3 × 3,672 = 11010 + 6
3 × 3,672 = 11016.
Question 14.
Select all the expressions that have 1,600 as a partial product.
☐ 4 × 4,381
☐ 8 × 3,240
☐ 4 × 1,408
☐ 2 × 7,881
☐ 8 × 2,021
Answer:
Expressions that have 1,600 as a partial product:
8 × 3,240
4 × 1,408
2 × 7,881.
Explanation:
4 × 4,381 = (4 × 4000) + (4 ×300) + (4 × 80) + (4 × 1)
4 × 4,381 = 16000 + 1200 + 320 + 4
4 × 4,381 = 17200 + 320 + 4
4 × 4,381 = 17520 + 4
4 × 4,381 = 17524.
8 × 3,240 = (8 × 3000) + (8 ×200) + (8 × 40) + (8 × 1)
8 × 3,240 = 24000 + 1600 + 320 + 8
8 × 3,240 = 25600 + 320 + 8
8 × 3,240 = 25920 + 8
8 × 3,240 = 25928.
4 × 1,408 = (4 × 1000) + (4 ×400) + (4 × 8)
4 × 1,408 = 4000 + 1600 + 32
4 × 1,408 = 5600 + 32
4 × 1,408 = 5632.
2 × 7,881 = (2 × 7000) + (2 ×800) + (2 × 80) + (2 × 1)
2 × 7,881 = 14000 + 1600 + 160 + 2
2 × 7,881 = 15600 + 160 + 2
2 × 7,881 = 15760 + 2
2 × 7,881 = 15762.
8 × 2,021 = (8 × 2000) + (8 × 20) + (8 × 1)
8 × 2,021 = 16000 + 160 + 8
8 × 2,021 = 16160 + 8
8 × 2,021 = 16168.
Lesson 3.6 Mental Math Strategies for Multiplication
Solve & Share
Determine the products for the expressions given below. Use mental math to solve. Explain your thinking. Solve these problems using any strategy you choose.
I can … use mental math strategies based on place value and properties of operations to multiply.

Look Back! Describe two different ways to find 4 × 97.
Answer:
Way:1:
4 × 97 = (4 × 100) – (4 × 3) = 400 – 12 = 388.
Way:2:
4 × 97 = 4 × (90 + 7) = (4 × 90) + (4 × 7) = 360 + 28 = 388.
Explanation:
Way:1:
4 × 97 = 4 × (100 – 3)
4 × 97 = (4 × 100) – (4 × 3)
4 × 97 = 400 – 12
4 × 97 = 388.
Way:2:
4 × 97 = 4 × (90 + 7)
4 × 97 = (4 × 90) + (4 × 7)
4 × 97 = 360 + 28
4 × 97 = 388.
Essential Question
How Can You Multiply Mentally?
Answer:
We can Multiply Mentally by rounding the numbers to nearest place and doing the required operation necessary to solve the problem.
Explanation:
For example: Any time you square a two-digit number that ends in 5, the last digits of the answer will be 25 and the digits before that are given by multiplying the first digit of the number by the number that’s one greater.
Visual Learning Bridge
Three cyclists rode their bikes the distances shown in the table. Use mental math to calculate the total distance Pam and Anna each rode.

Multiply 4 × 325 to find the distance Pam rode.
To multiply mentally, you can break apart numbers using place value and the Distributive Property.
Think:
4 × 325 = 4 × 300 + 4 × 25
= 1,200 + 100
= 1,300
Pam rode 1,300 miles.
Multiply 8 × 25 to find the distance Anna rode.
To multiply mentally, you can break apart and rearrange numbers using the Commutative and Associative Properties.
Think: 8 × 25 = (4 × 2) × 25
= 2 × (4 × 25)
= 2 × 100
= 200
Anna rode 200 miles.
Convince Me! Use Structure in the work for 4 × 325 above, why was 25 not broken into 20 and 5? Explain.
Answer:
25 was not broken into 20 and 5 because 325 already was broken into two parts 300 and 25 , so its not broken again.
Explanation:
To multiply mentally, you can break apart numbers using place value and the Distributive Property.
4 × 325 = 4 × 300 + 4 × 25
4 × 325 = 1,200 + 100
4 × 325 = 1,300.
Pam rode 1,300 miles.
Another Example!
Determine the distance George rode.
Find 3 × 398. 400 is close to 398.
Find 3 × 400 and adjust the answer.
3 × 400 = 1,200
398 + 2 = 400 3 × 2 = 6
Adjust the answer by subtracting 6. 1,200 – 6 = 1,194
George rode 1,194 miles in 3 months.

Guided Practice
Do You Understand?
Question 1.
Why was 6 subtracted from 1,200 in the problem above?
Answer:
6 was subtracted from 1,200 in the problem above, because 398 was rounded nearest to hundreds number 400 and it was rearranged to get its actual figure.
Explanation:
George rode ???? miles in 3 months.
3 × 398. 400 is close to 398.
3 × 400 = 1,200
398 + 2 = 400.
3 × 2 = 6.
Adjust the answer by subtracting 6.
1,200 – 6 = 1,194.
George rode 1,194 miles in 3 months.
Do You Know How?
For 2, multiply mentally to find the product. Explain which strategy you used.
Question 2.
8 × 903?
Answer:
8 × 903 = 7224.
Explanation:
8 × 903 = (8 × 900) + (8 × 3)
8 × 903 = 7200 + 24
8 × 903 = 7224.
Independent Practice
Leveled Practice For 3-10, multiply mentally to find each product. Explain which strategy you used.
Question 3.
6 × 250 = (3 + _____) × 250
Answer:
6 × 250 = (3 + __3___) × 250 = 1500.
Explanation:
6 × 250 = (3 + 3) × 250
6 × 250 = (3 × 250) + (3 × 250)
6 × 250 = 750 + 750
6 × 250 = 1500.
Question 4.
4 × 506 = 4 × (_____+ _____)
Answer:
4 × 506 = 4 × (__500___+ ___6__) = 2024.
Explanation:
4 × 506 = 4 × (__500___+ ___6__)
4 × 506 = (4 × 500) + (4 × 6)
4 × 506 = 2000 + 24
4 × 506 = 2024.
Question 5.
4 × 1,995
Answer:
4 × 1,995 = 4 (2000 – 5) = 7980.
Explanation:
4 × 1,995 = 4 (2000 – 5)
4 × 1,995 = (4 × 2000) – (4 × 5)
4 × 1,995 = 8000 – 20
4 × 1,995 = 7980.
Question 6.
22 × 5
Answer:
22 × 5 = (20 + 2) 5 = 100 + 10 = 110.
Explanation:
22 × 5 = (20 + 2) 5
22 × 5 = (20 × 5) + (2 × 5)
22 × 5 = 100 + 10
22 × 5 = 110.
Question 7.
404 × 6
Answer:
404 × 6 = (400 + 4) 6 = (400 × 6) + ( 4 × 6) = 2424.
Explanation:
404 × 6 = (400 + 4) 6
404 × 6 = (400 × 6) + ( 4 × 6)
404 × 6 = 2400 + 24
404 × 6 = 2424.
Question 8.
7 × 250
Answer:
7 × 250 = 7 ( 200 + 50) = 1400 + 350 = 1750.
Explanation:
7 × 250 = 7 ( 200 + 50)
7 × 250 = (7 × 200) + (7 × 50)
7 × 250 = 1400 + 350
7 × 250 = 1750.
Question 9.
2 × 395
Answer:
2 × 395 = 2 (400 – 5) = 800 – 10 = 790.
Explanation:
2 × 395 = 2 (400 – 5)
2 × 395 = (2 × 400) – (2 × 5)
2 × 395 = 800 – 10
2 × 395 = 790.
Question 10.
9 × 56
Answer:
9 × 56 = 9 (50 + 6) = (9 × 50) + ( 9 × 6) = 450 + 54 = 504.
Explanation:
9 × 56 = 9 (50 + 6)
9 × 56 = (9 × 50) + ( 9 × 6)
9 × 56 = 450 + 54
9 × 56 = 504.
Problem Solving
Question 11.
Each elephant at a zoo eats 100 pounds of hay and 5 pounds of fruits and vegetables every day. How many pounds of food does the zoo need to feed one elephant for one week? Use mental math to solve.
Answer:
Number of pounds of food the zoo needs to feed one elephant for one week = 735.
Explanation:
Number of pounds of hay every day each elephant at a zoo eats = 100.
Number of pounds of fruits and vegetables every day each elephant at a zoo eats = 5.
1 Week = 7 days.
Number of pounds of food the zoo needs to feed one elephant for one week = 7 (Number of pounds of hay every day each elephant at a zoo eats + Number of pounds of fruits and vegetables every day each elephant at a zoo eats)
= 7 (100 + 5)
= (7 × 100) + (7 × 5)
= 700 + 35
= 735.
Question 12.
Ashley and 3 friends are planning a trip. The cost of the trip is $599 per person. How much will the trip cost Ashley and her friends? Explain the mental math strategy you used to find the answer.
Answer:
Total trip cost of Ashley and her friends = $2396.
The mental math strategy you used to find the answer is break apart numbers using place value and the Distributive Property.
Explanation:
Number of people planning for a trip =(Ashley and 3 friends) = 1 + 3 = 4.
Cost of the trip per person = $599.
Total trip cost of Ashley and her friends = Number of people planning for a trip × Cost of the trip per person
= 4 × $599
= (4 × 500) + (4 × 99)
= 2000 + 396
= $2396.
Question 13.
Kyle has a rock collection. On Monday, he found 16 new rocks. On Tuesday, he gave 9 rocks to his friends. After giving away the rocks, Kyle had 122 rocks left in his collection. How many rocks did Kyle have to start with?
Answer:
Number of rocks Kyle have to start with = 129.
Explanation:
Number of new rocks on Monday, Kyle found = 16.
Number of rocks on Tuesday, Kyle gave to his friends = 9.
Number of rocks left in his collection after giving = 122.
Number of rocks Kyle have to start with = Number of new rocks on Monday, Kyle found – Number of rocks on Tuesday, Kyle gave to his friends + Number of rocks left in his collection after giving
= 16 – 9 + 122
= 7 + 122
= 129.
Question 14.
Critique Reasoning Quinn used compensation to find the product of 4 × 307. First, she found 4 × 300 = 1,200. Then she adjusted the product by subtracting 4 groups of 7 to get her final answer of 1,172. Explain Quinn’s mistake and find the correct answer.
Answer:
4 × 307 = 1228 not 1172. Quinn’s mistake is that 4 × 300 = 1200 is correct yet subtracting did 4 groups of 7 is wrong, they needed to be added to get the correct answer.
Explanation:
4 × 307 = 4 (300 + 7)
4 × 307 = (4 × 300) + (4 × 7)
4 × 307 = 1200 + 28
4 × 307 = 1228.
Question 15.
Higher Order Thinking Do you think it would be better to use breaking apart and the Distributive Property or compensation to find the product of 5 × 328? Explain why and show how to find the product.
Answer:
It would be better to use breaking apart and the Distributive Property or compensation to find the product of 5 × 328 because its a big number to do multiplication at once, so breaking them into parts and doing the process helps to get correct answer without any mistakes.
Explanation:
5 × 328 = 5 (300 + 28)
5 × 328 = (5 × 300) + (5 × 28)
5 × 328 = 1500 + 140
5 × 328 =1640.
Assessment Practice
Question 16.
Select all of the expressions that show how to use mental math to find the product of 4 × 27.

☐ (4 × 20) + (4 × 7)
☐ 4 × (20 × 7)
☐ (4 × 30) – (4 × 3)
☐ (4 × 25) + (4 × 2)
☐ 4 × 2 × 7
Answer:
The expressions that show how to use mental math to find the product of 4 × 27:
(4 × 20) + (4 × 7)
4 × (20 × 7)
(4 × 30) – (4 × 3)
(4 × 25) + (4 × 2)
Explanation:
4 × 27 = 4 (20 + 7)
4 × 27 = (4 × 20) + (4 × 7)
4 × 27 = 80 + 28
4 × 27 = 108.
4 × 27 = 4 (30 – 3)
4 × 27 = (4 × 30) – (4 × 3)
4 × 27 = 120 – 12
4 × 27 = 108.
4 × 27 = 4 (25 + 2)
4 × 27 = (4 × 25) + (4 × 2)
4 × 27 = 100 + 8
4 × 27 = 108.
Lesson 3.7 Choose a Strategy to Multiply
Solve & Share
A cineplex has 4 movie theaters. Each theater has 342 floor seats and 85 mezzanine seats. How many people can the cineplex seat? Solve this problem using any strategy you choose. Explain your solution.
I can… choose an appropriate strategy to multiply.

Look Back! What strategy or strategies did you use to solve this problem? Explain why.
Answer:
Manipulation tools strategy the use of blocks, fruits, balls, or other manipulation tools help students learn the basics of place value, addition, subtraction, and other areas of basic math. It is used to solve this problem.
Number of people in the cineplex seat = 1708.
Explanation:
A cineplex has 4 movie theaters. Each theater has 342 floor seats and 85 mezzanine seats. How many people can the cineplex seat.
Number of floor seats each theater has = 342.
Number of mezzanine seats each theater has = 85.
Number of movie theaters a cineplex has = 4.
Number of people in the cineplex seat = 4 (342 + 85)
= (4 × 342) + (4 × 85)
= 1368 + 340
= 1708.
Essential Question
What Strategy Will You Use to Multiply?
Answer:
The Strategy Used to do Multiply is using the place value of the numbers given and do the required operation to solve the problem.
Explanation:
The place value of the numbers given and do the required operation to solve the problem can be followed to multiply.
Visual Learning Bridge
Paying for pothole damage to cars can be costly. The table shows the cost of some car repairs. What is the total cost of the repairs?

Find the cost for the tires, c.
4 × $125 = 0
Estimate: 4 × 125 is about 4 × 120 = 480.
Break apart 125 using place value and the Distributive Property.
4 × 125 = 4 × (100 + 25)
= 4 × 100 + 4 × 25
= 400 + 100
= 500
c = 500
The tire repairs cost $500.
Find the cost of the paint, y.
2 × $1,450 = y
Estimate: 2 × 1,450 is about 2 x× 1,500 = 3,000.
Use an area model and partial products.
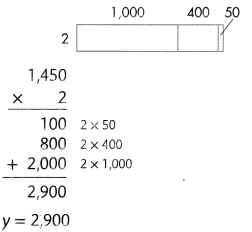
To paint the car costs $2,900.
Find the total cost of the repairs, z.
$500 + $2,900 = 2
Estimate: 500 + 2,900 is about 500 + 3,000 = 3,500.
Use compensation to add.
500 + 3,000 = 3,500
3,000 is 100 more than 2,900.
Subtract 100.
3,500 – 100 = 3,400
z = 3,400
The total cost of the repairs was $3,400.
Convince Me! Reasoning Explain why the answers to each part of the problem above are reasonable.
Answer:
The total cost of the repairs was $3,400. The answers to each part of the problem above are reasonable because they are correctly solved using all required strategies.
Explanation:
The cost for the tires, c.
4 × $125 = c.
4 × 125 = 4 × (100 + 25)
4 × 125 = 4 × 100 + 4 × 25
4 × 125 = 400 + 100
4 × 125 = 500.
c = 500
The tire repairs cost $500.
The cost of the paint, y.
2 × $1,450 = y
2 × 1,450 = 2 (1000 + 450)
2 × 1,450 = (2 × 1000) + (2 × 450)
2 × 1,450 = 2000 + 900
2 × 1,450 = $2900.
The total cost of the repairs, z.
x + y = z.
=> $500 + $2,900
=> $3400.
Guided Practice
Do You Understand?
Question 1.
A tire shop sells 3 tires that cost $175 each, which includes a fourth tire for free. Is this more or less expensive than buying 4 tires that cost $135 each?
Answer:
Cost of all tires a tire shop sells = $700 is more than Cost of all tires = $540.
Explanation:
Number of tires a tire shop sells = 3.
Cost of each tire a tire shop sells = $175.
Number of tires includes a fourth tire for free a tire shop sells = 1.
Cost of all tires a tire shop sells = (Number of tires a tire shop sells + Number of tires includes a fourth tire for free a tire shop sells) × Cost of each tire a tire shop sells
= (3 + 1) 175
= (3 × 175) + (1 × 175)
= 525 + 175
= $700.
Number of tires = 4.
Cost of each tire = $135.
Cost of all tires = Number of tires × Cost of each tire
= 4 × 135
= 4 (100 + 35)
= (4 × 100) + (4 × 35)
= 400 + 140
= $540.
Do You Know How?
For 2-5, find each product by choosing an appropriate strategy.
Question 2.
![]()
Answer:
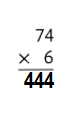
Explanation:
74 × 6 = (70 × 6) + (4 × 6)
74 × 6 = 420 + 24
74 × 6 = 444.
Question 3.
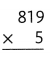
Answer:
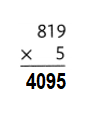
Explanation:
819 × 5 = (800 × 5) + (19 × 5)
819 × 5 = 4000 + 95
819 × 5 = 4095.
Question 4.
4 × 309
Answer:
4 × 309 = 1236.
Explanation:
4 × 309 = (4 × 300) + (4 × 9)
4 × 309 = 1200 + 36
4 × 309 = 1236.
Question 5.
3 × 354
Answer:
3 × 354 = 1062.
Explanation:
3 × 354 = (3 × 300) + (3 × 50) + (3 × 4)
3 × 354 = 900 + 150 + 12
3 × 354 = 1050 + 12
3 × 354 = 1062.
Independent Practice
For 6-21, find each product by choosing an appropriate strategy.
Question 6.
![]()
Answer:
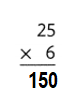
Explanation:
25 × 6 = (20 × 6 ) + ( 5 × 6)
25 × 6 = 120 + 30
25 × 6 = 150.
Question 7.
![]()
Answer:
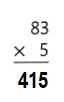
Explanation:
83 × 5 = (80 × 5) + ( 3 × 5)
83 × 5 = 400 + 15
83 × 5 = 415.
Question 8.
![]()
Answer:
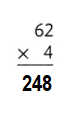
Explanation:
62 × 4 = (60 × 4) + (2 × 4)
62 × 4 = 240 + 8
62 × 4 = 248.
Question 9.
![]()
Answer:

Explanation:
89 × 7 = (100 × 7) – (11 × 7)
89 × 7 = 700 – 77
89 × 7 = 623.
Question 10.
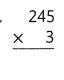
Answer:
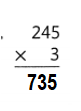
Explanation:
245 × 3 = (250 × 3) – (5 × 3)
245 × 3 = 750 – 15
245 × 3 = 735.
Question 11.
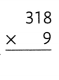
Answer:
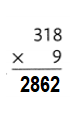
Explanation:
318 × 9 = (300 × 9) + (18 × 9)
318 × 9 = 2700 + 162
318 × 9 = 2862.
Question 12.
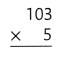
Answer:
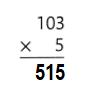
Explanation:
103 × 5 = (100 × 5) + (3 × 5)
103 × 5 = 500 + 15
103 × 5 = 515.
Question 13.
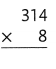
Answer:
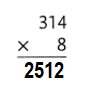
Explanation:
314 × 8 = (300 × 8) + (14 × 8)
314 × 8 = 2400 + 112
314 × 8 = 2512.
Question 14.
4 × 4,347
Answer:
4 × 4,347 = 17388.
Explanation:
4 × 4,347 = (4 × 4000) + (4 × 300) + (4 × 40) + (4 × 7)
4 × 4,347 = 16000 + 1200 + 160 + 28
4 × 4,347 = 17200 + 160 + 28
4 × 4,347 = 17360 + 28
4 × 4,347 =17388.
Question 15.
6 × 2,716
Answer:
6 × 2,716 = 16296.
Explanation:
6 × 2,716 = (6 × 2000) + ( 6 × 700) + ( 6 × 10) + (6 × 6)
6 × 2,716 = 12000 + 4200 + 60 + 36
6 × 2,716 = 16200 + 60 + 36
6 × 2,716 = 16260 + 36
6 × 2,716 = 16296.
Question 16.
7 × 1,287
Answer:
7 × 1,287 = 9009.
Explanation:
7 × 1,287 = (7 × 1000) + (7 × 200) + (7 × 80) + (7 × 7)
7 × 1,287 = 7000 + 1400 + 560 + 49
7 × 1,287 = 8400 + 560 + 49
7 × 1,287 = 8960 + 49
7 × 1,287 = 9009.
Question 17.
3 × 1,942
Answer:
3 × 1,942 = 5826.
Explanation:
3 × 1,942 = (3 × 1000) + ( 3 × 900) + (3 × 40) + (3 × 2)
3 × 1,942 = 3000 + 2700 + 120 + 6
3 × 1,942 = 5700 + 120 + 6
3 × 1,942 = 5820 + 6
3 × 1,942 = 5826.
Question 18.
2,319 × 5
Answer:
2,319 × 5 = 11595.
Explanation:
2,319 × 5 = (2000 × 5) + (300 × 5) + (10 × 5) + (9 × 5)
2,319 × 5 = 10000 + 1500 + 50 + 45
2,319 × 5 = 11500 + 50 + 45
2,319 × 5 = 11550 + 45
2,319 × 5 = 11595.
Question 19.
1,467 × 5
Answer:
1,467 × 5 = 7335.
Explanation:
1,467 × 5 = (1000 × 5) + (400 × 5) + (60 × 5) + (7 × 5)
1,467 × 5 = 5000 + 2000 + 300 + 35
1,467 × 5 = 7000 + 300 + 35
1,467 × 5 = 7300 + 35
1,467 × 5 = 7335.
Question 20.
6,006 × 9
Answer:
6,006 × 9 = 54054.
Explanation:
6,006 × 9 = (6000 × 9) + (6 × 9)
6,006 × 9 = 54000 + 54
6,006 × 9 = 54054.
Question 21.
9,749 × 5
Answer:
9,749 × 5 = 48745.
Explanation:
9,749 × 5 = (9000 × 5) + (700 × 5) + (40 × 5) + (9 × 5)
9,749 × 5 = 45000 + 3500 + 200 + 45
9,749 × 5 = 48500 + 200 + 45
9,749 × 5 = 48700 + 45
9,749 × 5 = 48745.
Problem Solving
Question 22.
Make Sense and Persevere Maura’s dance team wants to buy costumes that cost $56 each. They have $523 saved in a fund. How much money will they have left in the fund after they buy 9 costumes?

Answer:
Amount of money left in the fund after they buy 9 costumes = $19.
Explanation:
Cost of each costumes Maura’s dance team wants to buy = $56.
Total amount saved in fund by Maura’s dance team = $523.
Cost of 9 costumes Maura’s dance team wants to buy = 9 × Cost of each costumes Maura’s dance team wants to buy
= 9 × $56
= (9 × 50) + (9 × 6)
= 450 + 54
= $504.
Amount of money left in the fund after they buy 9 costumes = Total amount saved in fund by Maura’s dance team – Cost of 9 costumes Maura’s dance team wants to buy
= $523 – $504
= $19.
Question 23.
Elaine rents a car for 5 days. It costs $44 each day to rent the car and $7 each day for insurance. At the end of the trip she spends $35 to fill the car with gas. What is the total cost for Elaine to use the car?
Answer:
Total cost for Elaine to use the car = $86.
Explanation:
Number of days Elaine rents a car = 5.
Cost of renting car each day = $44.
Cost of each day for insurance = $7.
Cost for filling car with gas = $35.
Total cost for Elaine to use the car = Cost of renting car each day + Cost of each day for insurance + Cost for filling car with gas
= $44 + $7 + $35
= $51 + $35
= $86.
Question 24.
At the Math Club ceremony, there were 17 tables with 8 people seated at each table. Each guest received 2 certificates. How many certificates were distributed at the ceremony?
Answer:
Total number of certificates were distributed at the ceremony = 272.
Explanation:
Number of tables at the Math Club ceremony = 17.
Number of people seated at each table = 8.
Number of certificates each guest received = 2.
Total number of people at the Math Club ceremony = Number of tables at the Math Club ceremony × Number of people seated at each table
= 17 × 8
= 136.
Total number of certificates were distributed at the ceremony = Total number of people at the Math Club ceremony × Number of certificates each guest received
= 136 × 2
= (100 × 2) + (36 × 2)
= 200 + 72
= 272.
Question 25.
Water erupting from geysers can reach a temperature of 244°F. The average temperature in Yellowstone National Park is 35°F. Calculate the difference between these two temperatures.
Answer:
Difference between these two temperatures = 87°F.
Explanation:
Temperature of Water erupting from geysers = 244°F
Average temperature in Yellowstone National Park = 35°F
Average temperature of Water erupting from geysers = 244°F ÷ 2
= 122°F
Difference between these two temperatures = Average temperature of Water erupting from geysers – Average temperature in Yellowstone National Park
= 122°F – 35°F
= 87°F.
Question 26.
Higher Order Thinking On Monday, Paolo sold 21 tickets to the dance. On Tuesday, he sold three times as many tickets as he sold on Monday. On Wednesday, he sold twice as many tickets as he sold on Tuesday. How many total tickets did Paolo sell in the three days?
Answer:
Total number of tickets Paolo sells in the three days = 210.
Explanation:
Number of tickets to the dance Paolo sold on Monday = 21.
On Tuesday, he sold three times as many tickets as he sold on Monday.
=> Number of tickets to the dance Paolo sold on Tuesday = 3 × Number of tickets to the dance Paolo sold on Monday
= 3 × 21
= 63.
On Wednesday, he sold twice as many tickets as he sold on Tuesday.
=> Number of tickets to the dance Paolo sold on Wednesday = 3 × Number of tickets to the dance Paolo sold on Tuesday
=> 2 × 63
=> 126.
Total number of tickets Paolo sells in the three days = Number of tickets to the dance Paolo sold on Monday + Number of tickets to the dance Paolo sold on Tuesday + Number of tickets to the dance Paolo sold on Wednesday
= 21 + 63 + 126
= 84 + 126
= 210.
Assessment Practice
Question 27.
Mr. Tran would like to buy a new sofa that costs $934. He can pay the total all at once, or he can make a $125 payment each month for 8 months. How much less does it cost to pay all at once? Write equations to show how you solve. Tell what your variables represent.

Answer:
$66 less it costs to pay all at once for Mr. Tran.
Explanation:
Cost of new sofa Mr. Tran wants to buy = $934.
Cost of each month payment = $125.
Number of months for each month payment = 8.
Total amount for each month payment = Cost of each month payment × Number of months for each month payment
= $125 × 8
= $1000.
Difference:
Total amount for each month payment – Cost of new sofa Mr. Tran wants to buy
= $1000 – $934
= $66.
Lesson 3.8 Problem Solving
Model with Math
Solve & Share
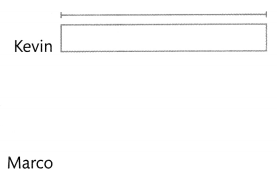
Kevin took 120 color photos and 128 black and white photos on a field trip. Marco took 2 times as many photos as Kevin. How many photos did Marco take? Solve this problem using any strategy you choose. Use the bar diagram to help.
I can … apply the math I know to solve problems.
Answer:
Number of photos Marco took = 496.
Explanation:
Number of color photos Kevin took on a field trip = 120.
Number of white photos Kevin took on a field trip = 128.
Marco took 2 times as many photos as Kevin.
=> Number of photos Marco took = 2 (Number of color photos Kevin took on a field trip + Number of white photos Kevin took on a field trip)
=> 2 (120 + 128)
=> 2 × 248
=> 496.
Thinking Habits
Be a good thinker! These questions can help you.
- How can I use math I know to solve this problem?
- How can I use pictures, objects, or an equation to represent the problem?
- How can I use numbers, words, and symbols to solve the problem?
Look Back! Model with Math What representation did you use to solve the problem and show relationships?
Answer:
Number of photos Marco took = 2 (Number of color photos Kevin took on a field trip + Number of white photos Kevin took on a field trip)
=> 2 (120 + 128)
=> 2 × 248
=> 496.
Explanation:
Number of color photos Kevin took on a field trip = 120.
Number of white photos Kevin took on a field trip = 128.
Marco took 2 times as many photos as Kevin.
=> Number of photos Marco took = 2 (Number of color photos Kevin took on a field trip + Number of white photos Kevin took on a field trip)
=> 2 (120 + 128)
=> 2 × 248
=> 496.
Essential Question
How Can You Represent a Situation with a Math Model?
Answer:
We can represent a Situation with a Math Model using the given data, knowing what is asked and then solving the problem to find the solution asked for.
Explanation:
A mathematical model is a description of a system using mathematical concepts and language . The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences and engineering disciplines, as well as in non-physical systems such as the social sciences.
Visual Learning Bridge
An art show uses 9 teams of art judges. If each team judges the work of 13 painters and 14 sculptors, how many artists attend the show?
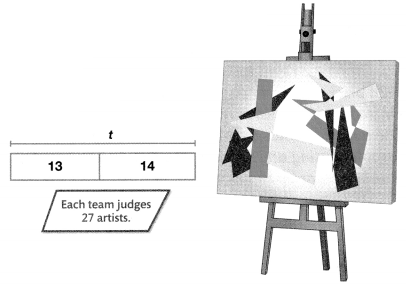
What do you need to find?
I need to find how many artists each team judges.
I need to find the total number of artists.
How can I model with math?
I can
use bar diagrams and equations to represent and solve this problem.
decide if my results make sense.
Here’s my thinking.
Find 9 × 27.
Use a bar diagram. Write and solve an equation.

a = 9 × 27
a = 243
There are 243 artists at the show.
Convince Me! Model with Math How could you decide if your answer makes sense?
Answer:
Number of artists attended the show = 243.
Explanation:
An art show uses 9 teams of art judges. If each team judges the work of 13 painters and 14 sculptors, how many artists attend the show?
Number of teams of art judges an art show uses = 9.
Number of painters each team judges the work = 13.
Number of sculptors each team judges the work = 14.
Number of artists attended the show = Number of teams of art judges an art show uses (Number of painters each team judges the work + Number of sculptors each team judges the work)
= 9 (13 + 14)
= 9 × 27
= (9 × 20) + (9 × 7)
= 180 + 63
= 243.
Guided Practice
Model with Math
When you model with Sharon’s Stationery Store contains 1,219 boxes of cards. May’s Market contains 3 times as many boxes of cards. How many boxes, b, does May’s Market contain?

Question 1.
Explain how to use a picture to represent the problem and show relationships.
Answer:
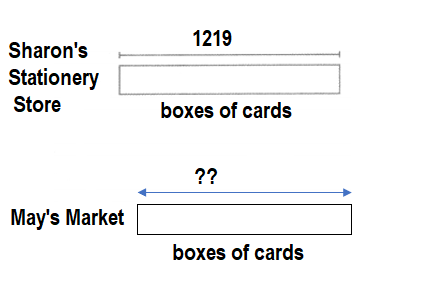
Explanation:
Number of boxes of cards Sharon’s Stationery Store contains = 1,219.
May’s Market contains 3 times as many boxes of cards.
Number of boxes May’s Market contains = ???
Question 2.
What equation can you write to represent the problem?
Answer:
Number of boxes May’s Market contains = 3 × Number of boxes of cards Sharon’s Stationery Store contains
=> 3 × 1219 = ???
Explanation:
Number of boxes of cards Sharon’s Stationery Store contains = 1,219.
May’s Market contains 3 times as many boxes of cards.
=> Number of boxes May’s Market contains = 3 × Number of boxes of cards Sharon’s Stationery Store contains
=> 3 × 1219
Question 3.
What is the solution to the problem?
Answer:
Number of boxes May’s Market contains = 3 × 1219 = 3657.
Explanation:
Number of boxes of cards Sharon’s Stationery Store contains = 1,219.
May’s Market contains 3 times as many boxes of cards.
=> Number of boxes May’s Market contains = 3 × Number of boxes of cards Sharon’s Stationery Store contains
=> 3 × 1219
=> (3 × 1000) + (3 × 200) + (3 × 10) + (3 × 9)
=> 3000 + 600 + 30 + 27
=> 3600 + 30 + 27
=> 3630 + 27
=> 3657.
Independent Practice
Model with Math Annie has 6 albums of stamps in her stamp collection. Each album contains 440 stamps. How many stamps, does Annie have in her collection? Use Exercises 4-6 to answer the question.
Question 4.
Draw a picture and write an equation to represent the problem.
Answer:

Explanation:
Number of albums of stamps in her stamp collection Annie has = 6.
Number of stamps each album contains = 440.
Total number of stamps Annie have in her collection = ???
Question 5.
What previously learned math can you use to solve the problem?
Answer:
Number of albums of stamps in her stamp collection Annie has = 6.
Number of stamps each album contains = 440.
Total number of stamps Annie have in her collection = Number of albums of stamps in her stamp collection Annie has × Number of stamps each album contains
= 6 × 440
Explanation:
Number of albums of stamps in her stamp collection Annie has = 6.
Number of stamps each album contains = 440.
Total number of stamps Annie have in her collection = Number of albums of stamps in her stamp collection Annie has × Number of stamps each album contains
= 6 × 440
Question 6.
What is the solution to the problem? Explain why your solution makes sense.
Answer:
Total number of stamps Annie have in her collection = 2640.
Explanation:
Number of albums of stamps in her stamp collection Annie has = 6.
Number of stamps each album contains = 440.
Total number of stamps Annie have in her collection = Number of albums of stamps in her stamp collection Annie has × Number of stamps each album contains
= 6 × 440
= (6 × 400) + (6 × 40)
= 2400 + 240
= 2640.
Problem Solving
Performance Task
Hauling Fuel A truck like the one shown delivers a load of gasoline to a gas station 3 times a week. The storage tank at the gas station holds 9 loads of fuel. How much more gas does the storage tank hold than the truck?

Question 7.
Make Sense and Persevere What do you know and what do you need to determine?
Answer:
Number of times a truck delivers a load of gasoline to a gas station a week = 3.
Quantity of loads of fuel a storage tank at the gas station holds = 9.
Quantity of loads of fuel a storage tank holds = 2700 gallons.
Quantity of gas the storage tank holds = ???
Quantity of gas the truck holds = ???
Explanation:
Known information:
Number of times a truck delivers a load of gasoline to a gas station a week = 3.
Quantity of loads of fuel a storage tank at the gas station holds = 9.
Quantity of loads of fuel a storage tank holds = 2700 gallons.
To determine:
Quantity of gas the storage tank holds = ???
Quantity of gas the truck holds = ???
Question 8.
Make Sense and Persevere What do you need to know to determine how much more the tank holds than the truck?

Answer:
16200 gallons more gas the storage tank hold than the truck.
Explanation:
Number of times a truck delivers a load of gasoline to a gas station a week = 3.
Quantity of loads of fuel a storage tank at the gas station holds = 9.
Quantity of loads of fuel a storage tank holds = 2700 gallons.
Quantity of gas the storage tank holds = ???
Quantity of gas the truck holds = ???
Quantity of gas the storage tank holds = Quantity of loads of fuel a storage tank at the gas station holds × Quantity of loads of fuel a storage tank holds
= 9 × 2700
= 9 ( 2000 + 700)
= (9 × 2000) + (9 × 700)
= 18000 + 6300
= 24300 gallons.
Quantity of gas the truck holds = Number of times a truck delivers a load of gasoline to a gas station a week × Quantity of loads of fuel a storage tank holds
= 3 × 2700
= 3 ( 2000 + 700)
= (3 × 2000) + (3 × 700)
= 6000 + 2100
= 8100 gallons.
Difference:
= Quantity of gas the storage tank holds – Quantity of gas the truck holds
= 24300 – 8100
= 16200 gallons.
Question 9.
Model with Math Explain how to use bar diagrams and equations to represent the problem and solve.
Answer:
Explanation:
Quantity of gas the storage tank holds = Quantity of loads of fuel a storage tank at the gas station holds × Quantity of loads of fuel a storage tank holds
= 9 × 2700
= 9 ( 2000 + 700)
= (9 × 2000) + (9 × 700)
= 18000 + 6300
= 24300 gallons.
Quantity of gas the truck holds = Number of times a truck delivers a load of gasoline to a gas station a week × Quantity of loads of fuel a storage tank holds
= 3 × 2700
= 3 ( 2000 + 700)
= (3 × 2000) + (3 × 700)
= 6000 + 2100
= 8100 gallons.
Difference:
= Quantity of gas the storage tank holds – Quantity of gas the truck holds
= 24300 – 8100
= 16200 gallons.

Topic 3 Fluency Practice Activity
Follow the Path
Shade a path from START to FINISH. Follow the differences that are correct. You can only move up, down, right, or left.
I can … subtract multi-digit whole numbers.
Answer:

Explanation:
812 – 44 = 768. (Correct)
621 – 85 = 536. (Correct)
543 – 97 = 446. (Correct)
111 – 87 = 76. (Incorrect)
684 – 485 = 299. (Incorrect)
929 – 879 = 150. (Incorrect)
341 – 299 = 142. (Incorrect)
836 – 788 = 48. (Correct)
876 – 55 = 72. (Incorrect)
922 – 87 = 865. (Incorrect)
511 – 423 = 112. (Incorrect)
486 – 230 =256. (Correct)
178 – 98 =80. (Correct)
912 – 842 = 170. (Incorrect)
312 – 219 = 193. (Incorrect)
767 – 31 = 636. (Incorrect)
825 – 789 = 36. (Correct)
123 – 53 = 30. (Incorrect)
282 – 32 = 150. (Incorrect)
986 – 887 = 199. (Incorrect)
698 – 12 = 586. (Incorrect)
333 – 111 = 222. (Correct)
342 – 88 = 254. (Correct)
293 – 95 = 198. (Correct)
876 – 543 = 333. (Correct)
Topic 3 Vocabulary Review
Understand Vocabulary
Word List
- array
- Associative Property of Multiplication
- Commutative Property of Multiplication
- compensation
- Distributive Property
- estimate
- numerical expression
- partial product
Question 1.
Circle the property shown by 4 × (6 + 2) = (4 × 6) + (4 × 2).
Associative
Commutative
Distributive
Answer:

Explanation:
The property shown by 4 × (6 + 2) = (4 × 6) + (4 × 2):
Associative
Question 2.
Circle the property shown by 2 × 134 = 134 × 2.
Associative
Commutative
Distributive
Answer:

Explanation:
The property shown by 2 × 134 = 134 × 2:
Commutative
Question 3.
Circle the property shown by (1 × 3) × 7 = 1 × (3 × 7).
Associative
Commutative
Distributive
Answer:

Explanation:
The property shown by (1 × 3) × 7 = 1 × (3 × 7):
Distributive
Question 4.
Draw a line from each vocabulary word to its example.
Answer:
Explanation:
Each vocabulary word is matched to the examples:

Use Vocabulary in Writing
Question 5.
Find 4 × 114. Use at least three terms from the Word List to describe how to find the product.
Answer:
4 × 114 = 456.
Explanation:
4 × 114 = ??? { Estimate}
4 × 114 = (4 × 100) + (4 × 10) + (4 × 4) { numerical expression}
4 × 114 = 400 + 40+ 16
4 × 114 = 440 + 16 {partial products}
4 × 114 = 456.
Topic 3 Reteaching
Set A pages 81-84
Use basic facts, place value, and multiplication properties to multiply by multiples of 10 and 100.
Find 4 × 60.
4 × 60 = 4 × 6 tens
4 × 60 = (4 × 6) tens
4 × 60 = 24 × 10
4 × 60 = 240
Find 4 × 600.
4 × 600 = 4 × 6 hundreds
4 × 600 = (4 × 6) hundreds
4 × 600 = 24 × 100
4 × 600 = 2,400
Find 4 × 6,000.
4 × 6,000 = 4 × 6 thousands
4 × 6,000 = (4 × 6) thousands
4 × 6,000 = 24 × 1,000
4 × 6,000 = 24,000
Remember when the product of a basic fact ends in zero, the answer will have an extra zero.
Question 1.
8 × 60
Answer:
8 × 60 = 480.
Explanation:
8 × 60 = (8 × 6) tens
8 × 60 = 48 tens
8 × 60 = 48 × 10
8 × 60 = 480.
Question 2.
3 × 10
Answer:
3 × 10 = 30.
Explanation:
3 × 10 = (3 × 1) tens
3 × 10 = 3 tens
3 × 10 = 3 × 10
3 × 10 = 30.
Question 3.
6 × 50
Answer:
6 × 50 = 300.
Explanation:
6 × 50 = (6 × 5) tens
6 × 50 = 30 tens
6 × 50 = 30 × 10
6 × 50 = 300.
Question 4.
5 × 300
Answer:
5 × 300 = 1500.
Explanation:
5 × 300 = (5 × 3) hundreds
5 × 300 = 15 × hundreds
5 × 300 = 15 × 100
5 × 300 = 1500.
Question 5.
7,000 × 4
Answer:
7,000 × 4 = 28000.
Explanation:
7,000 × 4 = thousands (7 × 4)
7,000 × 4 = thousands × 28
7,000 × 4 = 1000 × 28
7,000 × 4 = 28000.
Question 6.
2 × 900
Answer:
2 × 900 = 1800.
Explanation:
2 × 900 = (2 × 9) hundreds
2 × 900 = 18 × hundreds
2 × 900 = 18 × 100
2 × 900 = 1800.
Question 7.
80 × 8
Answer:
80 × 8 = 640.
Explanation:
80 × 8 = tens (8 × 8)
80 × 8 = tens × 64
80 × 8 = 10 × 64
80 × 8 = 640.
Question 8.
400 × 5
Answer:
400 × 5 = 2000.
Explanation:
400 × 5 = hundreds (4 × 5)
400 × 5 = hundreds × 20
400 × 5 = 100 × 20
400 × 5 = 2000.
Question 9.
30 × 9
Answer:
30 × 9 = 270.
Explanation:
30 × 9 = tens ( 3 × 9)
30 × 9 = tens × 27
30 × 9 = 10 × 27
30 × 9 = 270.
Question 10.
5 × 8,000
Answer:
5 × 8,000 = 40000.
Explanation:
5 × 8,000 = (5 × 8) thousands
5 × 8,000 = 40 × thousands
5 × 8,000 = 40 × 1000
5 × 8,000 = 40000.
Question 11.
700 × 8
Answer:
700 × 8 = 5600.
Explanation:
700 × 8 = hundreds (7 × 8)
700 × 8 = hundreds × 56
700 × 8 = 100 × 56
700 × 8 = 5600.
Question 12.
9,000 × 6
Answer:
9,000 × 6 = 54000.
Explanation:
9,000 × 6 = thousands (9 × 6)
9,000 × 6 = thousands × 54
9,000 × 6 = 1000 × 54
9,000 × 6 = 54000.
Question 13.
7 × 9,000
Answer:
7 × 9,000 = 63000.
Explanation:
7 × 9,000 = (7 × 9) thousands
7 × 9,000 = 63 × thousands
7 × 9,000 = 63 × 1000
7 × 9,000 = 63000.
Question 14.
5 × 100
Answer:
5 × 100 = 500.
Explanation:
5 × 100 = (5 × 1) hundreds
5 × 100 = 5 × hundreds
5 × 100 = 5 × 100
5 × 100 = 500.
Question 15.
20 × 5
Answer:
20 × 5 = 100.
Explanation:
20 × 5 = tens (2 × 5)
20 × 5 = tens × 10
20 × 5 = 10 × 10
20 × 5 = 100.
Question 16.
5 × 4,000
Answer:
5 × 4,000 = 20000.
Explanation:
5 × 4,000 = (5 × 4) thousands
5 × 4,000 = 20 × thousands
5 × 4,000 = 20 × 1000
5 × 4,000 = 20000.
Question 17.
5 × 500
Answer:
5 × 500 = 2500.
Explanation:
5 × 500 = (5 × 5) hundreds
5 × 500 = 25 × hundreds
5 × 500 = 25 × 100
5 × 500 = 2500.
Question 18.
3 × 2,000
Answer:
3 × 2,000 = 6000.
Explanation:
3 × 2,000 = (3 × 2) thousands
3 × 2,000 = 6 × thousands
3 × 2,000 = 6 × 1000
3 × 2,000 = 6000.
Set B pages 85-88
Use rounding to estimate 9 × 1,993.
Round 1,993 to 2,000.

So, 9 × 1,993 is about 18,000.
Remember to round a three-digit number to the nearest hundred and a four-digit number to the nearest thousand.
Estimate each product.
Question 1.
8 × 7,632
Answer:
8 × 7,632 is about 64000.
Explanation:
8 × 7,632 = ?????
Rounding 7632 to nearest thousand.
=> 8 × 7,632 = 8 × 8000
=> 8 × 7,632 = 64000.
Question 2.
493 × 3
Answer:
493 × 3 is about 1500.
Explanation:
493 × 3 = ????
Rounding 493 to nearest hundred.
=> 493 × 3 = 500 × 3
=> 493 × 3 = 1500.
Question 3.
9,379 × 5
Answer:
9,379 × 5 is about 45000.
Explanation:
9,379 × 5 = ?????
Rounding 9379 to nearest thousand.
=> 9,379 × 5 = 9000 × 5
=> 9,379 × 5 = 45000.
Question 4.
678 × 6
Answer:
678 × 6 is about 4200.
Explanation:
678 × 6 = ????
Rounding 678 to nearest hundred.
=> 678 × 6 = 700 × 6
=> 678 × 6 = 4200.
Question 5.
707 × 4
Answer:
707 × 4 is about 2800.
Explanation:
707 × 4 = ????
Rounding 707 to nearest hundred.
=> 707 × 4 = 700 × 4
=> 707 × 4 = 2800.
Question 6.
5,703 × 3
Answer:
5,703 × 3 is about 18000.
Explanation:
5,703 × 3 = ?????
Rounding 5703 to nearest thousand.
=> 5,703 × 3 = 6000 × 3
=> 5,703 × 3 = 18000.
Question 7.
483 × 6
Answer:
483 × 6 is about 3000.
Explanation:
483 × 6 = ????
Rounding 483 to nearest hundred.
=> 483 × 6 = 500 × 6
=> 483 × 6 = 3000.
Question 8.
6 × 8,166
Answer:
6 × 8,166 is about 48000.
Explanation:
6 × 8,166 = ?????
Rounding 9379 to nearest thousand.
=> 6 × 8,166 = 6 × 8000
=> 6 × 8,166 = 48000.
Set C pages 89-92
Use an array and partial products to find 3 × 121.
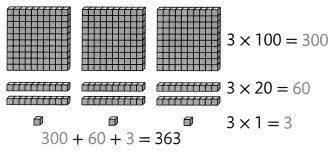
Remember to line up the partial products carefully.
Question 1.
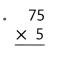
Answer:
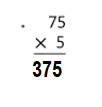
Explanation:
75 × 5 = (70 × 5) + ( 5 × 5)
75 × 5 = 350 + 25
75 × 5 = 375.
Question 2.
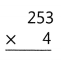
Answer:
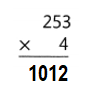
Explanation:
253 × 4 = (200 × 4) + ( 50 × 4) + (3 × 4)
253 × 4 = 800 + 200 + 12
253 × 4 = 1000 + 12
253 × 4 = 1012.
Question 3.
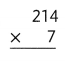
Answer:
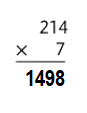
Explanation:
214 × 7 = (200 × 7) + (10 × 7) + (4 × 7)
214 × 7 = 1400 + 70 + 28
214 × 7 = 1470 + 28
214 × 7 = 1498.
Question 4.

Answer:
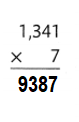
Explanation:
1341 × 7 = (1000 × 7) + (300 × 7) + (40 × 7) + (1 × 7)
1341 × 7 = 7000 + 2100 + 280 + 7
1341 × 7 = 9100 + 280 + 7
1341 × 7 = 9380 + 7
1341 × 7 = 9387.
Set D pages 93-96
Use the Distributive Property to find 5 × 45.
Use place value to break apart 45 as 40 + 5.
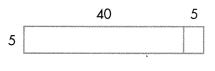
Use the Distributive Property:
5 × 45 = 5 × (40 + 5)
= (5 × 40) + (5 × 5)
= 200 + 25
= 225
So, 5 × 45 = 225.
Remember that you can use the Distributive Property to help multiply larger numbers.
Question 1.
7 × 45
Answer:
7 × 45 = 315.
Explanation:
7 × 45 = 7 × (40 + 5)
= (7 × 40) + (7 × 5)
= 280+ 35
= 315.
Question 2.
326 × 9
Answer:
326 × 9 = 2934.
Explanation:
326 × 9 = (300 + 26) 9
= (300 × 9) + (26 × 9)
= 2700 + 234
= 2934.
Question 3.
720 × 6
Answer:
720 × 6 = 4320.
Explanation:
720 × 6 = (700 + 20) 6
= (700 × 6) + (20 × 6)
= 4200 + 120
= 4320.
Question 4.
3 × 46
Answer:
3 × 46 = 138.
Explanation:
3 × 46 = 3 ( 40 + 6)
= (3 × 40) + (3 × 6)
= 120 + 18
= 138.
Question 5.
371 × 8
Answer:
371 × 8 = 2968.
Explanation:
371 × 8 = (300 + 71) 8
= (300 × 8) + (71 × 8)
= 2400 + 568
= 2968.
Question 6.
5 × 95
Answer:
5 × 95 = 475.
Explanation:
5 × 95 = 5 ( 90 + 5)
= (5 × 90) + (5 × 5)
= 450 + 25
= 475.
Question 7.
88 × 3
Answer:
88 × 3 = 264.
Explanation:
88 × 3 = (80 + 8) 3
= (80 × 3) + ( 8 × 3)
= 240 + 24
= 264.
Question 8.
4 × 1,865
Answer:
4 × 1,865 = 7460.
Explanation:
4 × 1,865 = 4 ( 1000 + 800 + 60 + 5)
= (4 × 1000) + ( 4 × 800) + (4 × 60) + (4 × 5)
= 4000 + 3200 + 240 + 20
= 7200 + 240 + 20
= 7440 + 20
= 7460.
Question 9.
57 × 3
Answer:
57 × 3 = 171.
Explanation:
57 × 3 = (50 + 7) 3
= (50 × 3) + ( 7 × 3)
= 150 + 21
= 171.
Question 10.
209 × 7
Answer:
209 × 7 = 1463.
Explanation:
209 × 7 = (200 + 9) 7
= (200 × 7) + (9 × 7)
= 1400 + 63
= 1463.
Set E pages 97-100
All your strategies may be used to find larger products.
Use the Distributive Property to find 3 × 1,275.
Use expanded notation and place value to construct an area model. 1,000
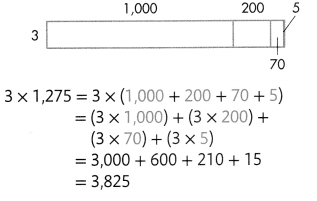
Remember to estimate to check that your answer is reasonable.
Question 1.
1,468 × 4
Answer:
1,468 × 4 = 5872.
Explanation:
1,468 × 4 = (1000 + 400 + 60 + 8) 4
1,468 × 4 = (1000 × 4) + (400 × 4) + ( 60 × 4) + (8 × 4)
1,468 × 4 = 4000 + 1600 + 240 + 32
1,468 × 4 = 5600 + 240 + 32
1,468 × 4 = 5840 + 32
1,468 × 4 = 5872.
Check:
??? × 4 = 5872
= ??? = 5872 ÷ 4
= ??? = 1468. (Answer is reasonable)
Question 2.
361 × 3
Answer:
361 × 3 = 1083.
Explanation:
361 × 3 = (300 + 60 + 1) 3
361 × 3 = (300 × 3) + (60 × 3) + (1 × 3)
361 × 3 = 900 + 180 + 3
361 × 3 = 1080 + 3
361 × 3 = 1083.
Check:
??? × 3 = 1083.
??? = 1083 ÷ 3
??? = 361. (Answer is reasonable)
Question 3.
25 × 7
Answer:
25 × 7 = 175.
Explanation:
25 × 7 = (20 + 5) 7
25 × 7 = (20 × 7) + (5 × 7)
25 × 7 = 140 + 35
25 × 7 = 175.
Check:
?? × 7 = 175.
=> ??= 175 ÷ 7
=> ?? = 25. (Answer is reasonable)
Question 4.
2,189 × 7
Answer:
2,189 × 7 = 15323.
Explanation:
2,189 × 7 = (2000 + 100 + 80 + 9) 7
2,189 × 7 = (2000 × 7) + ( 100× 7) + (80 × 7) + ( 9 × 7)
2,189 × 7 = 14000 + 700 + 560 + 63
2,189 × 7 = 14700 + 560 + 63
2,189 × 7 = 15260 + 63
2,189 × 7 = 15323.
Check:
???? × 7 = 15323.
???? = 15323 ÷ 7
???? = 2189. (Answer is reasonable)
Question 5.
6 × 987
Answer:
6 × 987 = 5922.
Explanation:
6 × 987 = 6 ( 900 + 80 + 7)
6 × 987 = (6 × 900) + (6 × 80) + (6 × 7)
6 × 987 = 5400 + 480 + 42
6 × 987 = 5880 + 42
6 × 987 = 5922.
Check:
6 × ??? = 5922.
??? = 5922 ÷ 6
??? = 987.(Answer is reasonable)
Question 6.
8 × 22
Answer:
8 × 22 = 176.
Explanation:
8 × 22 = 8 (20 + 2)
8 × 22 = (8 × 20) + (8 × 2)
8 × 22 = 160 + 16
8 × 22 = 176. (Answer is reasonable)
Question 7.
763 × 5
Answer:
763 × 5 = 3815.
Explanation:
763 × 5 = (700 + 60 + 3) 5
763 × 5 = (700 × 5) + (60 × 5) + (3 × 5)
763 × 5 = 3500 + 300 + 15
763 × 5 = 3800 + 15
763 × 5 = 3815. (Answer is reasonable)
Question 8.
14 × 9
Answer:
14 × 9 = 126.
Explanation:
14 × 9 = (10 + 4) 9
14 × 9 = (10 × 9) + (4 × 9)
14 × 9 = 90 + 36
14 × 9 = 126. (Answer is reasonable)
Question 9.
171 × 8
Answer:
171 × 8 = 1368.
Explanation:
171 × 8 = (100 + 70 + 1) 8
171 × 8 = (100 × 8) + (70 × 8) + (1 × 8)
171 × 8 = 800 + 560 + 8
171 × 8 = 1360 + 8
171 × 8 = 1368. (Answer is reasonable)
Question 10.
22 × 9
Answer:
22 × 9 = 198.
Explanation:
22 × 9 = (20 + 2) 9
22 × 9 = (20 × 9) + (2 × 9)
22 × 9 = 180 + 18
22 × 9 = 198. (Answer is reasonable)
Question 11.
1,409 × 5
Answer:
1,409 × 5 = 7045.
Explanation:
1,409 × 5 = (1000 + 400 + 9) 5
1,409 × 5 = (1000 × 5) + (400 × 5) + (9 × 5)
1,409 × 5 = 5000 + 2000 + 45
1,409 × 5 = 7000 + 45
1,409 × 5 = 7045. (Answer is reasonable)
Question 12.
17 × 6
Answer:
17 × 6 = 102.
Explanation:
17 × 6 = (10 + 7) 6
17 × 6 = (10 × 6) + (7 × 6)
17 × 6 = 60 + 42
17 × 6 = 102. (Answer is reasonable)
Set F pages 101-104
You can use properties of operations or compensation to multiply mentally.
Use the Commutative and Associative Properties to find 8 × 50.
8 × 50 = (2 × 4) 50
= (4 × 2) × 50
= 4 × (2 × 50)
= 4 × 100
= 400
Use compensation to find 9 × 67.
Think: 67 = 70 – 3
Multiply mentally 9 × 70.
9 × 70 = 630
Adjust by subtracting
9 × 3, or 27.
Subtract: 630 – 27 = 603
So, 9 × 67 = 603.
Remember that you can use diagrams or properties of operations to help multiply mentally
Question 1.
18 × 2
Answer:
18 × 2 = 36.
Explanation:
18 × 2 = (10 + 8) 2
18 × 2 = (10 × 2) + (8 × 2)
18 × 2 = 20 + 16
18 × 2 = 36.
Question 2.
48 × 5
Answer:
48 × 5 = 240.
Explanation:
48 × 5 = (50 – 2) 5
48 × 5 = (50 × 5) – (2 × 5)
48 × 5 = 250 – 10
48 × 5 = 240.
Question 3.
52 × 7
Answer:
52 × 7 = 364.
Explanation:
52 × 7 = (50 + 2) 7
52 × 7 = (50 × 7) + (2 × 7)
52 × 7 = 350 + 14
52 × 7 = 364.
Question 4.
33 × 6
Answer:
33 × 6 = 198.
Explanation:
33 × 6 = (30 + 3) 6
33 × 6 = (30 × 6) + (3 × 6)
33 × 6 = 180 + 18
33 × 6 = 198.
Question 5.
97 × 7
Answer:
97 × 7 = 679.
Explanation:
97 × 7 = (100 – 3) 7
97 × 7 = (100 × 7) – (3 × 7)
97 × 7 = 700 – 21
97 × 7 = 679.
Question 6.
88 × 4
Answer:
88 × 4 = 352.
Explanation:
88 × 4 = (90 – 2) 4
88 × 4 = (90 × 4) – (2 × 4)
88 × 4 = 360 -8
88 × 4 = 352.
Question 7.
239 × 4
Answer:
239 × 4 = 956.
Explanation:
239 × 4 = (200 + 30 + 9) 4
239 × 4 = (200 × 4) + (30 × 4) + (9 × 4)
239 × 4 = 800 + 120 + 36
239 × 4 = 920 + 36
239 × 4 = 956.
Question 8.
148 × 5
Answer:
148 × 5 = 740.
Explanation:
148 × 5 = (100 + 40 + 8) 5
148 × 5 = (100 × 5) + (40 × 5) + (8 × 5)
148 × 5 = 500 + 200 + 40
148 × 5 = 700 + 40
148 × 5 = 740.
Question 9.
233 × 6
Answer:
233 × 6 = 1398.
Explanation:
233 × 6 = (200 + 30 + 3) 6
233 × 6 = (200 × 6) + (30 × 6) + (3 × 6)
233 × 6 = 1200 + 180 + 18
233 × 6 = 1380 + 18
233 × 6 = 1398.
Question 10.
937 × 7
Answer:
937 × 7 = 6559.
Explanation:
937 × 7 = (900 + 30 + 7) 7
937 × 7 = (900 × 7) + (30 × 7) + (7 × 7)
937 × 7 = 6300 + 210 + 49
937 × 7 = 6510 + 49
937 × 7 = 6559.
Set G pages 105-108
You can use the strategy that fits the problem best. You know place-value strategies, the Distributive Property, area models, and compensation.
Place value: 8 × 359 = 8 × 3 hundreds + 8 × 5 tens + 8 × 9 ones
The Distributive Property: 7 × 4,056 = 7 × (4,000 + 50 + 6)
= (7 × 4,000) + (7 × 50) + (7 × 6)
Compensation: 6 × 495
(6 × 500) – (6 × 5)
Remember to use an estimate to check if your answer is reasonable.
Question 1.
![]()
Answer:
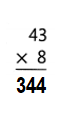
Explanation:
43 × 8 = (40 + 3) 8
43 × 8 = (40 × 8) + (3 × 8)
43 × 8 = 320 + 24
43 × 8 = 344.
Check:
?? × 8 = 344.
=> ?? = 344 ÷ 8
=> ?? = 43.
Question 2.
![]()
Answer:
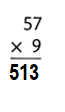
Explanation:
57 × 9 = (60 – 3) 9
57 × 9 = (60 × 9) – (3 × 9)
57 × 9 = 540 – 27
57 × 9 = 513.
Check:
?? × 9 = 513.
=> ?? = 513 ÷ 9
=> ?? = 57.
Question 3.
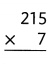
Answer:
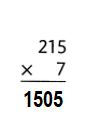
Explanation:
215 × 7 = (200 + 10 + 5) 7
215 × 7 = (200 × 7) + (10 × 7) + (5 × 7)
215 × 7 = 1400 + 70 + 35
215 × 7 = 1470 + 35
215 × 7 = 1505.
Check:
?? × 7 = 1505.
=> ?? = 1505 ÷ 7
=> ?? = 215.
Question 4.
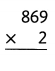
Answer:
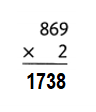
Explanation:
869 × 2 = (800 + 60 + 9) 2
869 × 2 = (800 × 2) + (60 × 2) + (9 × 2)
869 × 2 = 1600 + 120 + 18
869 × 2 = 1720 + 18
869 × 2 = 1738.
Check:
??? × 2 = 1738.
=> ??? = 1738 ÷ 2
=> ??? = 869.
Question 5.
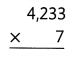
Answer:
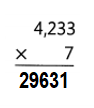
Explanation:
4233 × 7 = (4000 + 200 + 30 + 3) 7
4233 × 7 = (4000 × 7) + (200 × 7) + (30 × 7) + (3 × 7)
4233 × 7 = 28000 + 1400 + 210 + 21
4233 × 7 = 29400 + 210 + 21
4233 × 7 = 29610 + 21
4233 × 7 = 29631.
Check:
??? × 7 = 29631.
=> ??? = 29631 ÷ 7
=>??? = 4233.
Question 6.
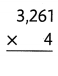
Answer:
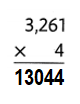
Explanation:
3261 × 4 = (3000 + 200 + 60 + 1) 4
3261 × 4 = (3000 × 4) + ( 200 × 4) + (60 × 4) + (1 × 4)
3261 × 4 = 12000 + 800 + 240 + 4
3261 × 4 = 12800 + 240 + 4
3261 × 4 = 13040 + 4
3261 × 4 = 13044.
Check:
??? × 4 = 13044.
=> ??? = 13044 ÷ 4
=> ??? = 3261.
Question 7.
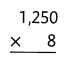
Answer:
Explanation:
1250 × 8 = (1000 + 200 + 50) 8
1250 × 8 = (1000 × 8) + (200 × 8) + (50 × 8)
1250 × 8 = 8000 + 1600 + 400
1250 × 8 = 9600 + 400
1250 × 8 = 10000.
Check:
??? × 8 = 10000.
=> ??? = 10000 ÷ 8
=> ??? = 1250.
Question 8.
Answer:

Explanation:
2239 × 5 = (2000 + 200 + 30 + 9) 5
2239 × 5 = (2000 × 5) + (200 × 5) + (30 × 5) + (9 × 5)
2239 × 5 = 10000 + 1000 + 150 + 45
2239 × 5 = 11000 + 150 + 45
2239 × 5 = 11150 + 45
2239 × 5 = 11195.
Check:
??? × 5 = 11195.
=> ??? = 11195 ÷ 5
=> ??? = 2239.
Set H pages 109-112
Think about these questions to help you model with math.
Thinking Habits
- How can I use math I know to help solve this problem?
- How can I use pictures, objects, or an equation to represent the problem?
- How can I use numbers, words, and symbols to solve the problem?

Remember that a bar diagram can help you write an equation.
Mia has a collection of 34 dolls. A toy store’s warehouse has 5 times as many dolls.
Question 1.
Use pictures, a bar diagram, or an equation to find the number of dolls in the warehouse.
Answer:
Number of dolls in the warehouse = 5 × Number of dolls collection Mia has
= 5 × 34
= 170.
Explanation:
Number of dolls collection Mia has = 34.
A toy store’s warehouse has 5 times as many dolls.
=> Number of dolls in the warehouse = 5 × Number of dolls collection Mia has
= 5 × 34
= 170.
Question 2.
How can you decide if your answer is reasonable?
Answer:
To be reasonable means to be as much as is appropriate or fair.
Explanation:
In math, reasonableness can be defined as checking to verify that the result of the solution or the calculation of the problem is correct or not, be either estimating or by plugging in your result to check it.
Topic 3 Assessment Practice
Question 1.
Use numbers from the box to show how to multiply 126 by 3.

Answer:
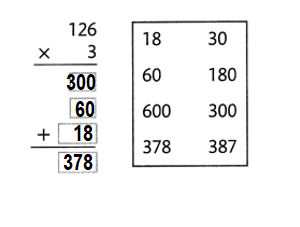
Explanation:
126 × 3 = (100 + 20 + 6) 3
126 × 3 = (100 × 3) + ( 20 × 3) + (6 × 3)
126 × 3 = 300 + 60 + 18
126 × 3 = 360 + 18
126 × 3 = 378.
Question 2.
Alberto rode the train 198 miles round trip 4 times last month. Explain how to use mental math to find the total distance Alberto traveled.
Answer:
Total distance Alberto traveled = 792.
Explanation:
Number of miles Alberto rode the train = 198.
Number of trips he did last month = 4.
Total distance Alberto traveled = Number of miles Alberto rode the train × Number of trips he did last month
= 198 × 4
= (100 + 90 + 8) 4
= (100 × 4) + (90 × 4) + (8 × 4)
= 400 + 360 + 32
= 760 + 32
= 792.
Question 3.
Mr. Ortiz sells tortillas in bags of 25 and in bags of 50. If he sells 4 bags of 50 and 6 bags of 25, how many tortillas did Mr. Ortiz sell?
A. 10 tortillas
B. 350 tortillas
C. 170 tortillas
D. 3,500 tortillas
Answer:
Total number of tortillas Mr. Ortiz sells = 350.
B. 350 tortillas
Explanation:
Number of tortillas in bags of 25 Mr. Ortiz sells = 6.
Number of tortillas in bags of 50 Mr. Ortiz sells = 4.
Total number of tortillas Mr. Ortiz sells = (25 × Number of tortillas in bags of 25 Mr. Ortiz sells) + 50 ×Number of tortillas in bags of 50 Mr. Ortiz sells)
= (25 × 6) + (50 × 4)
= 150 + 100
= 350.
Question 4.
A. What are the partial products when finding 1,874 × 3? Select all that apply.
☐ 5,400
☐ 2,000
☐ 3,000
☐ 210
☐ 2,400
☐ 12
Answer:
The partial products when finding 1,874 × 3 are:
☐ 5,400
☐ 3,000
☐ 210
☐ 2,400
☐ 12
Explanation:
1,874 × 3 = (1000 + 800 + 70 + 4) 3
1,874 × 3 = (1000 × 3) + (800 × 3) + (70 × 3) + (4 × 3)
1,874 × 3 = 3000 + 2400 + 210 + 12
1,874 × 3 = 5400 + 210 + 12
1,874 × 3 = 5610 + 12
1,874 × 3 = 5622.
B. Find the product of 1,874 and 3.
Answer:
1,874 × 3 = 5622.
Explanation:
1,874 × 3 = (1000 + 800 + 70 + 4) 3
1,874 × 3 = (1000 × 3) + (800 × 3) + (70 × 3) + (4 × 3)
1,874 × 3 = 3000 + 2400 + 210 + 12
1,874 × 3 = 5400 + 210 + 12
1,874 × 3 = 5610 + 12
1,874 × 3 = 5622.
Question 5.
A science class is growing some fruit and vegetable plants on a plot of land behind their school. Each section is laid out in rows.

A. There are 9 strawberry plants planted in each row. Write and solve an equation to find how many strawberry plants were planted.
Answer:
Total number of strawberry plants were planted = 585.
Explanation:
Number of strawberry plants planted in each row = 9.
Number of rows strawberry plants planted = 65.
Total number of strawberry plants were planted = Number of rows strawberry plants planted × Number of strawberry plants planted in each row
= 65 × 9
= (60 + 5) 9
= (60 × 9) + (5 × 9)
= 540 + 45
= 585.
B. There are 9 pepper plants planted in each row. Draw an area model and show the partial products to find how many pepper plants are planted behind the school.
Answer:
Number of pepper plants are planted behind the school = 162.
Explanation:
Number of pepper plants planted in each row = 9.
Number of rows pepper plants planted = 18.
Number of pepper plants are planted behind the school = Number of pepper plants planted in each row × Number of rows pepper plants planted
= 9 × 18
= 9 (10 + 8)
= (9 × 10) + (9 × 8)
= 90 + 72
= 162.
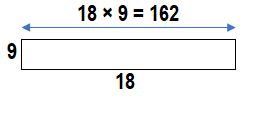
Question 6.
Select all the expressions that could be used to find 1,235 × 9.
☐ 9 × (1,000 + 200 + 20 + 5)
☐ 9 × (1,000 + 200 + 30 + 5)
☐ (9 × 1,000) + (9 × 200) + (9 × 30) + (9 × 5)
☐ 9 × 1,235
☐ 1,235 + 9
Answer:
1,235 × 9 = 11115.
The expressions that are used to find 1,235 × 9:
9 × (1,000 + 200 + 30 + 5)
(9 × 1,000) + (9 × 200) + (9 × 30) + (9 × 5)
9 × 1,235
Explanation:
1,235 × 9 = (1000 + 200 + 30 + 5) 9
1,235 × 9 = (1000 × 9) + (200 × 9) + (30 × 9) + (5 × 9)
1,235 × 9 = 9000 + 1800 + 270 + 45
1,235 × 9 = 10800 + 270 + 45
1,235 × 9 = 11070 + 45
1,235 × 9 = 11115.
Question 7.
Draw a model to find 365 × 3.
365 × 3 = _________
Answer:
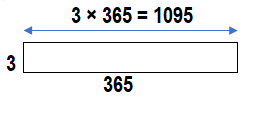
365 × 3 = __1095____.
Explanation:
365 × 3 = (300 + 60 + 5) 3
365 × 3 = (300 × 3) + (60 × 3) + (5 × 3)
365 × 3 = 900 + 180 + 15
365 × 3 = 1080 + 15
365 × 3 = 1095.
Question 8.
Select all of the expressions that have a product of 640.
☐ (6 × 100) + (4 × 10)
☐ 9 × 54
☐ 60 × 4 × 1
☐ 160 × 4
☐ (6 × 100) × (4 × 10)
Answer:
The expressions that have a product of 640:
☐ 160 × 4
Explanation:
640 = (600 + 40)
640 = 160 × 4
Question 9.
The table shows the number of hot drinks sold in a busy coffee shop in 1 week.

A. If the same number of cups of coffee were sold for 6 weeks in a row, how many cups would be sold in all?
Answer:
Number of cups of coffee were sold in all = 5010.
Explanation:
Number of cups of coffee were sold in a week = 835.
Number of cups of coffee were sold in all = 6 × Number of cups of coffee were sold in a week
= 6 × 835
= 6 (800 + 30 + 5)
= (6 × 800) + ( 6 × 30) + ( 5 × 6)
= 4800 + 180 + 30
= 4980 + 30
= 5010.
B. The special drink of the month was an iced mocha. The shop sold 5 times as many iced mochas in one week as hot mochas. How many more iced mochas were sold than hot mochas in 4 weeks? Explain.
Answer:
1468 more iced mochas were sold than hot mochas in 4 weeks.
Explanation:
The shop sold 5 times as many iced mochas in one week as hot mochas.
Number of iced mochas were sold in a week = 567.
Number of hot mochas were sold in a week = 200.
Number of more iced mochas were sold than hot mochas in 4 weeks = (4 × Number of iced mochas were sold in a week) – (4 × Number of hot mochas were sold in a week )
= (4 × 567) – (4 × 200)
= 2268 – 800
= 1468.
Question 10.
Tickets for a resort cost $1,182 each for adults and $459 each for children. Find the cost for 3 adult tickets and 3 child tickets. Explain how you know your answer is reasonable.
Answer:
Cost for 3 adult tickets and 3 child tickets = $4923.
Answer is reasonable because the solution is correct for given problem.
Explanation:
Cost of Tickets for each adult = $1182.
Cost of Tickets for each children = $459.
Cost for 3 adult tickets and 3 child tickets = (3 × Cost of Tickets for each adult ) + (3 × Cost of Tickets for each children)
= (3 × $1182) + (3 × $459)
= $3546 + $1377
= $4923.
Question 11.
Which expression has the same value as 5 × 617?
A. (5 × 6) + (5 ×1) + (5 × 7)
B. (5 × 60) + (5 × 10) + (5 × 70)
C. (5 × 600) + (5 × 1) + (5 × 7)
D. (5 × 600) + (5 × 10) + (5 × 7)
Answer:
Expression has the same value as 5 × 617 is:
D. (5 × 600) + (5 × 10) + (5 × 7)
Explanation:
5 × 617 = 5 (600 10 + 7)
5 × 617 = (5 × 600) + (5 × 10) + (5 × 7)
5 × 617 = 3000 + 50 + 35
5 × 617 = 3050 + 35
5 × 617 = 3085.
A. (5 × 6) + (5 ×1) + (5 × 7) = 30 + 5 + 35 = 35 + 335 = 70.
B. (5 × 60) + (5 × 10) + (5 × 70) = 300 + 50 + 350 = 350 + 350 = 700.
C. (5 × 600) + (5 × 1) + (5 × 7) = 3000 + 5 + 35 = 3005 + 35 = 3040.
D. (5 × 600) + (5 × 10) + (5 × 7) = 3000 + 50 + 35 = 3050 + 35 = 3085.
Question 12.
Which of the following is equivalent to (400 × 3) + (36 × 3)?
A. 436 ÷ 3
B. 400 × 10
C. 436 × 3
D. 400 × 3 + 36
Answer:
Equivalent to (400 × 3) + (36 × 3) is:
C. 436 × 3 = 1308.
Explanation:
(400 × 3) + (36 × 3) = 1200 + 108
(400 × 3) + (36 × 3) = 1308.
A. 436 ÷ 3 = 145.33
B. 400 × 10 = 4000.
C. 436 × 3 = 1308.
D. 400 × 3 + 36 = 1200 + 36 = 1236.
Question 13.
Find 3 × 312. Draw a bar diagram to solve.
Answer:

Explanation:
3 × 312 = 3 (300 + 10 + 2)
3 × 312 = (3 × 300) + (3 × 10) + (3 × 2)
3 × 312 = 900 + 30 + 6
3 × 312 = 930 + 6
3 × 312 = 936.
Question 14.
Bea’s Bakery bakes 215 cookies and 45 muffins every hour. How many baked goods are baked in 4 hours?
Answer:
Number of baked goods are baked in 4 hours = 1040.
Explanation:
Number of cookies Bea’s Bakery bakes every hour = 215.
Number of muffins Bea’s Bakery bakes every hour = 45.
Number of baked goods are baked in 4 hours = (4 × Number of cookies Bea’s Bakery bakes every hour) + (4 × Number of muffins Bea’s Bakery bakes every hour)
= (4 × 215)+ (4 × 45)
= 860 + 180
= 1040.
Question 15.
Write and solve an equation that represents the given bar diagram.
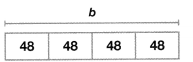
Answer:
Total number of biscuits made in 4 hours = b = 192.
Explanation:
Number of hours used to make them = 1.
Number of biscuits made every hour = 48.
Total number of biscuits made in 4 hours = b = 4 × Number of biscuits made every hour
= 4 × 48
= 4 (40 + 8)
= (4 × 40) + (4 × 8)
= 160 + 32
= 192.
Question 16.
Which of the following is equivalent to 8 × 493? Select all that apply.
☐ (8 × 400) + (8 × 90) + (8 × 3)
☐ (8 × 400) + 93
☐ 493 × 8
☐ (8 × 500) – (8 × 93)
☐ (8 × 500) – (8 × 7)
Answer:
8 × 493 = 3944.
Equivalent to 8 × 493 is:
(8 × 400) + (8 × 90) + (8 × 3)
493 × 8
(8 × 500) – (8 × 7)
Explanation:
8 × 493 = 8 (400 + 90 + 3)
8 × 493 = (8 × 400) + (8 × 90) + (8 × 3)
8 × 493 = 3200 + 720 + 24
8 × 493 = 3920 + 24
8 × 493 = 3944.
Expression given:
(8 × 400) + (8 × 90) + (8 × 3) = 3200 + 720 + 24 = 3920 + 24 = 3944.
(8 × 400) + 93 = 3200 + 93 = 3293.
493 × 8 = (400 × 8) + (90 × 8) + (3 × 8) = 3200 + 720 + 24 = 3920 + 24 = 3944.
(8 × 500) – (8 × 93) = 4000 – 744 = 3256.
(8 × 500) – (8 × 7) = 4000 – 56 = 3944.
Question 17.
Mr. Luca would like to purchase a digital keyboard for each of his 3 nieces and 1 nephew. The keyboard costs $105.
A. Mr. Luca thinks the total cost should be about $200. Is this amount reasonable? Explain.
Answer:
No, the amount is not reasonable because total cost of the keyboard Mr. Luca wants to buy for each of his 3 nieces and 1 nephew is $420 not $200. His estimation is wrong.
Explanation:
Cost of the keyboard = $105.
Number of nieces Mr. Luca has = 3.
Number of nephew Mr. Luca has = 1.
Total cost of the keyboard Mr. Luca wants to buy for each of his 3 nieces and 1 nephew = (3 × $105) + (1 × $105)
= $315 + $105
= $420.
B. Write and solve an equation to find the total cost of the keyboards. Explain why your answer is reasonable.
Answer:
Total cost of the keyboard Mr. Luca wants to buy for each of his 3 nieces and 1 nephew = (3 × $105) + (1 × $105)
= $315 + $105
= $420.
My answer is reasonable because its calculation is correct with correct solution for the problem.
Explanation:
Cost of the keyboard = $105.
Total cost of the keyboard Mr. Luca wants to buy for each of his 3 nieces and 1 nephew = (3 × $105) + (1 × $105)
= $315 + $105
= $420.
Question 18.
What is the product of 5 × 1,903?
A. 9,515
B. 9,505
C. 9,155
D. 965
Answer:
5 × 1,903 = 9515.
A. 9,515
C. 9,155
Explanation:
5 × 1,903 = 5 (1000 + 900 + 3)
5 × 1,903 = (5 × 1000) + (5 × 900) + (5 × 3)
5 × 1,903 = 5000 + 4500 + 15
5 × 1,903 = 9500 + 15
5 × 1,903 = 9515.
Question 19.
How can you use mental math to find the product of 6 × 295?
Answer:
We can use mental math to find the product of 6 × 295 by using partial products or by distributive property.
Explanation:
6 × 295 = 6 (200 + 95)
6 × 295 = (6 × 200 ) + (6 × 95)
6 × 295 = 1200 + 570
6 × 295 = 1770.
Question 20.
A. Select all the partial products for 8 × 321.
☐ 8
☐ 80
☐ 160
☐ 1,600
☐ 2,400
Answer:
Partial products for 8 × 321 :
☐ 8
☐ 160
☐ 2,400
Explanation:
8 × 321 = 8 ( 300 + 20 + 1)
8 × 321 = (8 × 300) + (8 × 20) + (8 × 1)
8 × 321 = 2400 + 160 + 8
8 × 321 = 2560 + 8
8 × 321 = 2568.
B. Find the product for Part A using the partial products.
Answer:
8 × 321 = 2568.
Explanation:
8 × 321 = 8 ( 300 + 20 + 1)
8 × 321 = (8 × 300) + (8 × 20) + (8 × 1)
8 × 321 = 2400 + 160 + 8
8 × 321 = 2560 + 8
8 × 321 = 2568.
Topic 3 Performance Task
Buying Classroom Computers Jorge’s school can purchase computers and printers for the prices shown. Information about the fourth-grade classes are given in the table.

Question 1.
Jorge’s teacher is Ms. Sanchez. His class wants to buy 8 desktop computers and 3 printers.
Part A
What is the total cost of 8 desktop computers? Use place-value strategies and properties of operations.
Answer:
Cost of 8 desktop computers = $8400.
Explanation:
Cost of desktop computers = $1050.
Cost of 8 desktop computers = 8 × $1050
= 8 (1000 + 50)
= (8 × 1000) + (8 × 50)
= 8000 + 400
= $8400.
Part B
What is the total cost of 3 printers? Draw an array and show the partial products to find the cost.
Answer:
Total cost of 3 printers = $1024.
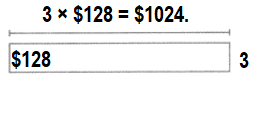
Explanation:
Cost of printers= $128.
Total cost of 3 printers = 8 × $128
= 8(100 + 20 + 8)
= (8 × 100) + (8 × 20) + (8 × 8)
= 800 + 160 + 64
= 960 + 64
= $1024.
Part C
Did Jorge’s class raise enough money to buy 8 computers and 3 printers? Explain.
Answer:
No, Jorge’s class did not raise enough money to buy 8 computers and 3 printers because cost of them is $9424 and their raise amount $9000 is less to buy them.
Explanation:
Total cost of 3 printers = $1024.
Cost of 8 desktop computers = $8400.
Money raised by Jorge’s class = $9000.
Total amount of money to buy 8 computers and 3 printers = Total cost of 3 printers + Cost of 8 desktop computers
= $1024 + $8400
= $9424.
Difference:
= Total amount of money to buy 8 computers and 3 printers – Money raised by Jorge’s class
= $9424 – $9000
= $424.
Question 2.
Rachel’s teacher is Mr. Jones. Her class wants to buy 7 computers and 2 printers.
Part A
How much more do 7 desktop computers cost than 7 laptop computers? Use bar diagrams and equations to represent and solve the problem.
Answer:
$1904 Cost of 7 desktop computers is more cost than 7 laptop computers.
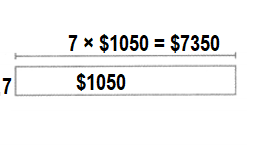
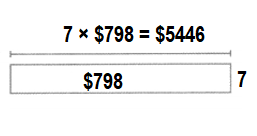
Explanation:
Cost of desktop computers = $1050.
Total cost of 7 desktop computers = 7 × Cost of desktop computers
= 7 × $1050
= 7 ( 1000 + 50)
= (7 × 1000) + (7 × 50)
= 7000 + 350
= $7350.
Cost of laptop computers = $798.
Total cost of 7 laptop computers = 7 × Cost of laptop computers
= 7 × $798
= 7 ×( 700+ 90 + 8)
= (7 × 700) + (7 × 90) + (7 × 8)
= 4900 + 490 + 56
= 5390 + 56
= $5446.
Cost of 7 desktop computers more cost than 7 laptop computers = Total cost of 7 desktop computers – Total cost of 7 laptop computers
= $7350 – $5446
= $1904.
Part B
What is another way to find the difference in the cost of 7 desktop computers and 7 laptop computers? Explain.
Answer:
Difference between 7 desktop computers and 7 laptop computers is $1904.
Explanation:
Another way:
Cost of 7 desktop computers = $7350.
Cost of 7 laptop computers = $5446.
Difference:
= Total cost of 7 desktop computers – Total cost of 7 laptop computers
= $7350 – $5446
= $1904.
Question 3.
Miranda’s teacher is Ms. Katz. Her class wants to buy 9 laptop computers and 4 printers. Miranda said the total cost should be $7,494. Is this amount reasonable? Explain. Does the class have enough money?
Answer:
No, the amount is not reasonable because there is a difference $200 less than the actual amount to that of expected amount.
Explanation:
Cost of laptop computer = $798.
Cost of printer = $128.
Total cost expected to be by Miranda = $7,494
Cost of 9 laptop computers and 4 printers = (9 × Cost of laptop computer) + ( 4 × Cost of printer)
= (9 × $798) + (4 × $128)
= $7182 + $512
= $7694.
Difference:
= Cost of 9 laptop computers and 4 printers – Total cost expected to be by Miranda
= $7694 – $7494
= $200.
