Go through the enVision Math Common Core Grade 4 Answer Key Topic 4 Use Strategies and Properties to Multiply by 2-Digit Numbers regularly and improve your accuracy in solving questions.
enVision Math Common Core 4th Grade Answers Key Topic 4 Use Strategies and Properties to Multiply by 2-Digit Numbers
Essential Questions:
How can you use a model to multiply? How can you use the Distributive Property to multiply? How can you use multiplication to solve problems?
Answer:
Multiplication using the “Area model”:
We know that,
An “Area” is the amount of flat space occupied by a figure, You can find the area of a figure by filling it with unit squares and then counting how many squares entirely fill the shape
The total area of the figure is the multiplication of the number of rows and columns
Multiplication using the Distributive Property:
Let the three numbers be a, b, c
Now,
According to the Distributive Property of Multiplication,
a × (b + c) = (a × b) + (a × c)
(a + b) × c = (a × c ) + (b × c)
Ex:
We have to find the product of 12 × 4
Now,
The steps to find the product of the given expression using the Distributive Property of Multiplication are:
Step 1:
Simplify the terms
So,
12 × 4 = (10 + 2) × 4
Step 2:
Use the Distributive Property of Multiplication on the simplified expression that we obtained in Step 1
So,
(10 + 2) × 4 = (10 × 4) + (2 × 4)
= 40 + 8
Step 3:
Add the values that we obtained in the last step of Step 2
So,
40 + 8 = 48
Hence,
The value of the given expression is: 48

enVision STEM Project: Renewable Energy and Multiplication
Do Research
Use the Internet or other sources to find information about different sources of renewable energy?
Answer:
The major types of renewable energy sources are:
A. Biomass:
Obtained from wood and wood waste, municipal solid waste etc
B. Hydropower energy:
Obtained from water
C. Geothermal energy:
Obtained from land
D. Wind energy:
Obtained from wind turbines
E. Solar energy:
Obtained from the sun

Journal: Write a Report that Includes what you found. Also in your report:
A)
A wind farm is an area of land with a large number of turbines. Draw an array with 15 rows to show the turbines in a wind farm. How many turbines are in your wind farm?
Answer:
It is given that
A wind farm is an area of land with a large number of turbines
Now,
The representation of an array with 15 rows to show the turbines in a wind farm is:

Hence, from the above figure,
We can conclude that there are 15 turbines in your wind farm
B)
Some turbines produce 63 megawatt-hours of energy every week. Find how much energy one of these turbines would produce in one year. Remember, one year is 52 weeks?
Answer:
It is given that
Some turbines produce 63 megawatt-hours of energy every week.
So,
The amount of energy these turbines produce in 1 year = (The amount of energy produced by one of these turbines in a week) × (The number of weeks in a year)
= 63 × 52
= 63 × (50 + 2) [By using the Distributive Property of Multiplication]
= (63 × 50) + (63 × 2)
= 3,150 + 126
= 3,276 megawatt-hours
Hence, from the above,
We can conclude that the amount of energy produced by one of these turbines in one year is: 3,276 megawatt-hours
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- algorithm
- product
- variable
- array
Question 1.
You multiply numbers to find a(n) __________.
Answer:
We know that,
You multiply numbers to find a “Product”
Hence, from the above,
We can conclude that the best term that fits the given definition is a “Product”
Question 2.
A(n) _________ shows the number of objects in rows and columns.
Answer:
We know that,
An “Array” shows the number of objects in rows and columns.
Hence, from the above,
We can conclude that the best term that fits the given definition is an “Array”
Question 3.
A symbol or letter that stands for a number is called a(n) ______________.
Answer:
We know that,
A symbol or letter that stands for a number is called a “Variable”
Hence, from the above,
We can conclude that the best term that fits the given definition is a “Variable”
Multiplication
Find each product.
Question 4.
4 × 8
Answer:
The given expression is: 4 × 8
Now,
By using the Distributive Property of Multiplication,
4 × 8
= 4 × (4 + 4)
= (4 × 4) + (4 × 4)
= 16 + 16
= 32
Hence, from the above,
We can conclude that the value of the given expression is: 32
Question 5.
2 × 9
Answer:
The given expression is: 2 × 9
Now,
By using the Distributive Property of Multiplication,
2 × 9
= 2 × (6 + 3)
= (2 × 6) + (2 × 3)
= 12 + 6
= 18
Hence, from the above,
We can conclude that the value of the given expression is: 18
Question 6.
9 × 5
Answer:
The given expression is: 9 × 5
Now,
By using the Distributive Property of Multiplication,
9 × 5
= 9 × (4 + 1)
= (9 × 4) + (9 × 1)
= 36 + 9
= 45
Hence, from the above,
We can conclude that the value of the given expression is: 45
Question 7.
6 × 8
Answer:
The given expression is: 6 × 8
Now,
By using the Distributive Property of Multiplication,
6 × 8
= 6 × (4 + 4)
= (6 × 4) + (6 × 4)
= 24 + 24
= 48
Hence, from the above,
We can conclude that the value of the given expression is: 48
Question 8.
16 × 4
Answer:
The given expression is: 16 × 4
Now,
By using the Distributive Property of Multiplication,
16 × 4
= (8 + 8) × 4
= (4 × 8) + (4 × 8)
= 32 + 32
= 64
Hence, from the above,
We can conclude that the value of the given expression is: 64
Question 9.
6 × 68
Answer:
The given expression is: 6 × 68
Now,
By using the Distributive Property of Multiplication,
6 × 68
= (3 + 3) × 68
= (3 × 68) + (3 × 68)
= 204 + 204
= 408
Hence, from the above,
We can conclude that the value of the given expression is: 408
Question 10.
87 × 5
Answer:
The given expression is: 87 × 5
Now,
By using the Distributive Property of Multiplication,
87 × 5
= 87 × (3 + 2)
= (87 × 3) + (87 × 2)
= 261 + 174
= 435
Hence, from the above,
We can conclude that the value of the given expression is: 435
Question 11.
19 × 9
Answer:
The given expression is: 19 × 9
Now,
By using the Distributive Property of Multiplication,
19 × 9
= 19 × (3 + 6)
= (19 × 3) + (19 × 6)
= 57 + 114
= 171
Hence, from the above,
We can conclude that the value of the given expression is: 171
Question 12.
128 × 6
Answer:
The given expression is: 128 × 6
Now,
By using the Distributive Property of Multiplication,
128 × 6
= (100 + 28) × 6
= (100 × 6) + (28 × 6)
= 600 + 168
= 768
Hence, from the above,
We can conclude that the value of the given expression is: 768
Rounding
Round each number to the nearest hundred.

Question 13.
164
Answer:
The given number is: 164
Hence, from the above,
We can conclude that the number that is to the nearest hundred for the given number is: 200
Question 14.
8,263
Answer:
The given number is: 8,263
Hence, from the above,
We can conclude that the number that is to the nearest hundred for the given number is: 8,300
Question 15.
527
Answer:
The given number is: 527
Hence, from the above,
We can conclude that the number that is to the nearest hundred for the given number is: 500
Question 16.
2,498
Answer:
The given number is: 2,498
Hence, from the above,
We can conclude that the number that is to the nearest hundred for the given number is: 2,500
Question 17.
7,892
Answer:
The given number is: 7,892
Hence, from the above,
We can conclude that the number that is to the nearest hundred for the given number is: 7,900
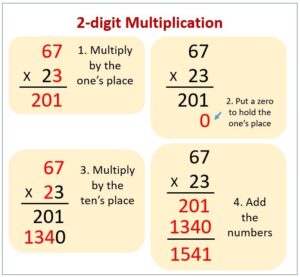
Question 18.
472
Answer:
The given number is: 472
Hence, from the above,
We can conclude that the number that is to the nearest hundred for the given number is: 500
Round each number to the nearest thousand.
Question 19.
8,685
Answer:
The given number is: 8,685
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 9,000
Question 20.
4,991
Answer:
The given number is: 4,991
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 5,000
Question 21.
62,549
Answer:
The given number is: 62,549
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 62,000
Question 22.
167,241
Answer:
The given number is: 167,241
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 167,200
Question 23.
77,268
Answer:
The given number is: 77,268
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 77,000
Question 24.
34,162
Answer:
The given number is: 34,162
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 34,000
Question 25.
1,372
Answer:
The given number is: 1,372
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 1,000
Question 26.
9,009
Answer:
The given number is: 9,009
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 9,000
Question 27.
121,619
Answer:
The given number is: 121,619
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 122,000
Question 28.
Construct Arguments Explain how to round 608,149 to the nearest thousands place.
Answer:
The given number is: 608,149
Now,
From the given number,
We can observe that the total number is less than 608,500
Hence, from the above,
We can conclude that the number that is to the nearest thousand for the given number is: 608,000
Pick a Project
PROJECT 4A
How high would a stack of sabal palms be?
Project: Explain the Processes

PROJECT 4B
Can you estimate the weight of dozens of birds?
“Project: Write a Report About the Northern Mockingbird

PROJECT 4C
How many soccer players start in the Women’s World Cup ?
Project: Create an Array Poster

PROJECT 4D
How much weight can shotputters throw?
Project: Compare Shot Masses

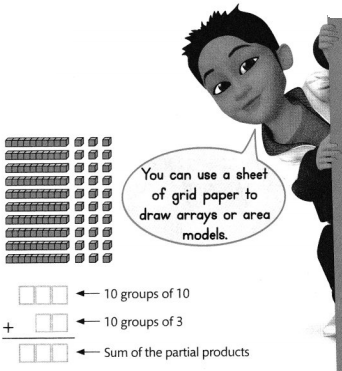
Lesson 4.1 Multiply Multiples of 10
Solve & Share
The principal of a school needs to order supplies for 20 new classrooms. Each classroom needs the following items: 20 desks, 30 chairs, and 40 pencils. How many of each item does the principal need to order? Solve these problems using any strategy you choose.
I can … use place-value strategies or properties of operations to multiply by multiples of 10.

Answer:
It is given that
The principal of a school needs to order supplies for 20 new classrooms. Each classroom needs the following items: 20 desks, 30 chairs, and 40 pencils
So,
The total number of desks the principal needs to order = (The total number of classrooms) × (The number of desks needed for each classroom)
= 20 × 20
= 2 tens × 2 tens [By using the Place-Value strategy]
= 4 hundred
= 400
So,
The total number of chairs the principal needs to order = (The total number of classrooms) × (The number of chairs needed for each classroom)
= 20 × 30
= 2 tens × 3 tens [By using the Place-Value strategy]
= 6 hundred
= 600
So,
The total number of pencils the principal needs to order = (The total number of classrooms) × (The number of pencils needed for each classroom)
= 20 × 40
= 2 tens × 4 tens [By using the Place-Value strategy]
= 8 hundred
= 800
Hence, from the above,
We can conclude that
The total number of desks the principal needs to order is: 400
The total number of chairs the principal needs to order is: 600
The total number of pencils the principal needs to order is: 800
Look Back! Look at the factors and products. What patterns do you notice?
Answer:
The patterns we noticed from the above factors and products are:
a. All multiples of 2 have a pattern of 2, 4, 6, 8, or 0 in the 1’s place.
b. When multiplying Any number by 2, the result is even
c. There are 5 even numbers and 5 odd numbers in each range of 10 numbers
Essential Question
How Can You Multiply on by Multiples of 10?
Answer:
When we multiply any number by 10, the last digit will always be 0
Ex:
2 × 20 = 2 × 2 × 10
= 4 × 10
= 40
Visual Learning Bridge
The number of visitors of each age group for the Sunny Day Amusement Park is shown below. How many children visit the park in 30 days?

One Way
Find 30 × 80.
Use basic facts and place value.
30 × 80 = 3 tens × 8 tens
= 24 hundreds
= 2,400
2,400 children visit the park in 30 days.
10 × 10 = 100
Another Way
Find 30 × 80
Break apart numbers. Use the Commutative Property and the Associative Property of Multiplication.
30 × 80 = (3 × 10) (8 × 10)
= 3 × 8 × 10 × 10
= (3 × 8) (10 × 10)
= 24 × 100
= 2,400
2,400 children visit the park in 30 days.
Convince Me!
Look for Relationships Use place value or properties of operations to determine how many adults age 65 and older visit the park in 30 days.

Answer:
From the given figure,
We can observe that
The number of visitors each day that are Adults 65 and over are: 40
So,
The number of visitors in 30 days that are Adults 65 and over = 30 × (The number of visitors each day that are Adults 65 and over)
= 30 × 40
= 3 tens × 4 tens [By using the Place-Value strategy]
= 12 hundred
= 1,200
Hence, from the above,
We can conclude that the number of visitors in 30 days that are Adults 65 and over is: 1,200
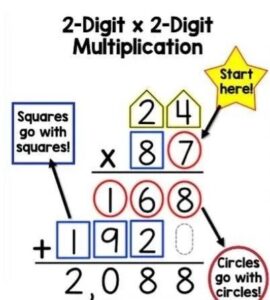
Another Example!
Use the properties of operations to find 50 × 60.
50 × 60 = 5 × 10 × 6 × 10
= (5 × 6) × (10 × 10)
= 30 × 100
= 3,000
If the product of the basic fact ends in zero, the product has one more zero than you see in the factors.
Guided Practice
Do You Understand?
Question 1.
Find 50 × 20. How many zeros are in the product? Explain.
Answer:
The given expression is: 50 × 20
Now,
By using the Place-Value Property,
50 × 20
= 5 tens × 2 tens
= 10 hundred
= 10 × 100
= 1,000
Hence, from the above,
We can conclude that
The value of the product of the given expression is: 1,000
The number of zeroes in the obtained product is: 3
Question 2.
How many adults under 65 visit the park in 30 days?

Answer:
From the given figure,
We can observe that
The number of visitors each day that are adults under 65 are: 60
So,
The number of visitors in 30 days that are Adults under 65 = 30 × (The number of visitors each day that are adults under 65)
= 30 × 60
= 3 × 10 × 6 × 10
= (3 × 6) × (10 × 10)
= 18 × 100
= 1,800
Hence, from the above,
We can conclude that
The number of visitors in 30 days that are Adults under 65 is: 1,800
Do You Know How?
For 3-8, use basic facts and place-value or properties of operations to find each product.
Question 3.
30 × 10
Answer:
The given expression is: 30 × 10
Now,
By using the Properties of Operations,
30 × 10
= 3 × 10 × 1 × 10
= (3 × 1) × (10 × 10)
= 3 × 100
= 300
Hence, from the above,
We can conclude that the value of the given expression is: 300
Question 4.
50 × 10
Answer:
The given expression is: 50 × 10
Now,
By using the Properties of Operations,
50 × 10
= 5 × 10 × 1 × 10
= (5 × 1) × (10 × 10)
= 5 × 100
= 500
Hence, from the above,
We can conclude that the value of the given expression is: 500
Question 5.
20 × 10
Answer:
The given expression is: 20 × 10
Now,
By using the Properties of Operations,
20 × 10
= 2 × 10 × 1 × 10
= (2 × 1) × (10 × 10)
= 2 × 100
= 200
Hence, from the above,
We can conclude that the value of the given expression is: 200
Question 6.
60 × 20
Answer:
The given expression is: 60 × 20
Now,
By using the Properties of Operations,
60 × 20
= 6 × 10 × 2 × 10
= (6 × 2) × (10 × 10)
= 12 × 100
= 1,200
Hence, from the above,
We can conclude that the value of the given expression is: 1,200
Question 7.
90 × 40
Answer:
The given expression is: 90 × 40
Now,
By using the Properties of Operations,
90 × 40
= 9 × 10 × 4 × 10
= (9 × 4) × (10 × 10)
= 36 × 100
= 3,600
Hence, from the above,
We can conclude that the value of the given expression is: 3,600

Question 8.
80 × 50
Answer:
The given expression is: 80 × 50
Now,
By using the Properties of Operations,
80 × 50
= 8 × 10 × 5 × 10
= (8 × 5) × (10 × 10)
= 40 × 100
= 4,000
Hence, from the above,
We can conclude that the value of the given expression is: 4,000
Independent Practice
For 9-16, use basic facts and place-value or properties of operations to find each product.
Question 9.
20 × 70
Answer:
The given expression is: 20 × 70
Now,
By using the Properties of Operations,
20 × 70
= 2 × 10 × 7 × 10
= (2 × 7) × (10 × 10)
= 14 × 100
= 1,400
Hence, from the above,
We can conclude that the value of the given expression is: 1,400
Question 10.
70 × 90
Answer:
The given expression is: 70 × 90
Now,
By using the Properties of Operations,
70 × 90
= 7 × 10 × 9 × 10
= (7 × 9) × (10 × 10)
= 63 × 100
= 6,300
Hence, from the above,
We can conclude that the value of the given expression is: 6,300
Question 11.
40 × 20
Answer:
The given expression is: 40 × 20
Now,
By using the Properties of Operations,
40 × 20
= 4 × 10 × 2 × 10
= (4 × 2) × (10 × 10)
= 8 × 100
= 800
Hence, from the above,
We can conclude that the value of the given expression is: 800
Question 12.
40 × 30
Answer:
The given expression is: 40 × 30
Now,
By using the Properties of Operations,
40 × 30
= 4 × 10 × 3 × 10
= (4 × 3) × (10 × 10)
= 12 × 100
= 1,200
Hence, from the above,
We can conclude that the value of the given expression is: 1,200
Question 13.
70 × 40
Answer:
The given expression is: 70 × 40
Now,
By using the Properties of Operations,
70 × 40
= 7 × 10 × 4 × 10
= (7 × 4) × (10 × 10)
= 28 × 100
= 2,800
Hence, from the above,
We can conclude that the value of the given expression is: 2,800
Question 14.
20 × 30
Answer:
The given expression is: 20 × 30
Now,
By using the Properties of Operations,
20 × 30
= 2 × 10 × 3 × 10
= (2 × 3) × (10 × 10)
= 6 × 100
= 600
Hence, from the above,
We can conclude that the value of the given expression is: 600
Question 15.
60 × 40
Answer:
The given expression is: 60 × 40
Now,
By using the Properties of Operations,
60 × 40
= 6 × 10 × 4 × 10
= (6 × 4) × (10 × 10)
= 24 × 100
= 2,400
Hence, from the above,
We can conclude that the value of the given expression is: 2,400
Question 16.
60 × 90
Answer:
The given expression is: 60 × 90
Now,
By using the Properties of Operations,
60 × 90
= 6 × 10 × 9 × 10
= (6 × 9) × (10 × 10)
= 54 × 100
= 5,400
Hence, from the above,
We can conclude that the value of the given expression is: 5,400
For 17-22, find the missing factor.
Question 17.
10 × ______ = 100
Answer:
The given expression is: 10 × _______ = 100
Now,
Let the missing factor be x
So,
10 × x = 100
x = \(\frac{100}{10}\)
x = 10
Hence, from the above,
We can conclude that the missing factor is: 10
Question 18.
_______ × 20 = 1,600
Answer:
The given expression is: ______ × 20 = 1,600
Now,
Let the missing factor be x
So,
x × 20 = 1,600
x = \(\frac{1,600}{20}\)
x = 80
Hence, from the above,
We can conclude that the missing factor is: 80
Question 19.
_______ × 30 = 1,500
Answer:
The given expression is: ______ × 30 = 1,500
Now,
Let the missing factor be x
So,
x × 30 = 1,500
x = \(\frac{1,500}{30}\)
x = 50
Hence, from the above,
We can conclude that the missing factor is: 50
Question 20.
20 × ______ = 1,000
Answer:
The given expression is: 20 × _______ = 1,000
Now,
Let the missing factor be x
So,
20 × x = 1,000
x = \(\frac{1,000}{20}\)
x = 50
Hence, from the above,
We can conclude that the missing factor is: 50
Question 21.
_______ × 90 = 8,100
Answer:
The given expression is: _______ × 90 = 8,100
Now,
Let the missing factor be x
So,
x × 90 = 8,100
x = \(\frac{8,100}{90}\)
x = 90
Hence, from the above,
We can conclude that the missing factor is: 90
Question 22.
60 × _______ = 4,200
Answer:
The given expression is: 60 × _______ = 4,200
Now,
Let the missing factor be x
So,
60 × x = 4,200
x = \(\frac{4,200}{60}\)
x = 70
Hence, from the above,
We can conclude that the missing factor is: 70
Problem Solving
Question 23.
Reasoning
The product of two factors is 4,200. If one of the factors is 60, what is the other factor? Explain.
Answer:
It is given that
The product of two factors is 4,200 and one of the factors is 60
Now,
Let the other factor be z
So,
60 × z = 4,200
z = \(\frac{4,200}{60}\)
z = 70
Hence, from the above,
We can conclude that the other factor for the given product is: 70
Question 24.
Algebra There is 30 players on each high school football team. Explain how you can find the total number of players if there are 40 teams. Write and solve an equation.
Answer:
It is given that
There is 30 players on each high school football team and there are 40 teams
So,
The total number of players = (The number of players present in each team) × (The total number f teams)
= 30 × 40
= 3 × 10 × 4 × 10
= (3 × 4) × (10 × 10)
= 12 × 100
= 1,200
Hence, from the above,
We can conclude that the total number of players are: 1,200
Question 25.
Bob uses 2 gallons of water while brushing his teeth. He uses 10 gallons of water to wash clothes. How many more cups of water did Bob use while washing his clothes than brushing his teeth?
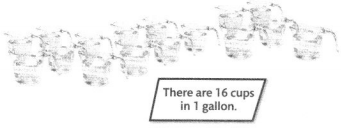
Answer:
It is given that
Bob uses 2 gallons of water while brushing his teeth. He uses 10 gallons of water to wash clothes.
Now,
The given figure is:

So,
The number of cups Bob uses to wash his clothes = (The number of gallons Bob uses to wash his clothes) × (The number of cups in each gallon)
= 10 × 16
= 10 × (8 + 8) [By using the Distributive Property of Multiplication]
= (10 × 8) + (10 × 8)
= 80 + 80
= 160 cups
So,
The number of cups Bob uses while brushing his teeth = (The number of gallons Bob uses to brush his teeth) × (The number of cups in each gallon)
= 2 × 16
= 2 (8 + 8) [By using the Distributive Property of Multiplication]
= (2 × 8) + (2 × 8)
= 16 + 16
= 32 cups
So,
The number of more cups that Bob uses to wash his clothes than while brushing his teeth
= (The number of cups Bob uses to wash his clothes) – (the number of cups Bob uses while brushing his teeth)
= 160 – 32
= 128 cups
Hence, from the above,
We can conclude that
The number of more cups that Bob uses to wash his clothes than while brushing his teeth is: 128 cups
Question 26.
James walked 30 minutes each day for 90 days. Show how you can use place value or properties to find how many minutes James walked.
Answer:
It is given that James walked 30 minutes each day for 90 days
So,
The total number of minutes James walked = (The number of minutes James walks each day) × (The total number of days James walked)
= 30 × 90
= 3 × 10 × 9 × 10
= (3 × 9) × (10 × 10)
= 27 × 100
= 2,700
Hence, from the above,
We can conclude that
The total number of minutes James walked is: 2,700 minutes
Question 27.
Higher-Order Thinking What is one example of a product that will have the same number of zeros in the factors and the product? What is one example of a product that will NOT have the same number of zeros in the factors as the product?
Answer:
The example of a product that will have the same number of zeros in the factors and the product is:
10 × 15
= 10 × (10 + 5) [By usingthe Distributive Property of Multiplication]
= (10 × 10) + (10 × 5)
= 100 + 50
= 150
The example of a product that will not have the same number of zeros in the factors as the product is:
40 × 5
= 4 × 10 × 5
= (4 × 5) × 10
= 20 × 10
= 2 × 10 × 10
= 200
Assessment Practice
Question 28.
Select all of the expressions that have a product of 1,600.
☐ 20 × 80
☐ 20 × 60
☐ 40 × 40
☐ 60 × 30
☐ 90 × 20
Answer:
It is given that
To have a product of 1,600,
The expressions must be even numbers as factors and if we neglect zeroes, the product must be equal to 16
Hence, from the above,
We can conclude that
All the expressions that have a product of 1,600 are:

Question 29.
Which expression has 50 as the missing factor?
A. 20 × ? = 1,000
B. 50 × ? = 3,000
C. 30 × ? = 1,800
D. 10 × ? = 1,000
Answer:
Let the missing factor be x
Now,
A.
20 × x = 1,000
x = \(\frac{1,000}{20}\)
= 50
B.
50 × x =3,000
x = \(\frac{3,000}{50}\)
= 60
C.
30 × x =1,800
x = \(\frac{1,800}{30}\)
= 60
D.
10 × x =1,000
x = \(\frac{1,000}{10}\)
= 100
Hence, from the above,
We can conclude that the expression that has 50 as a missing factor is:
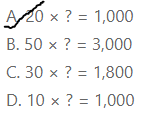
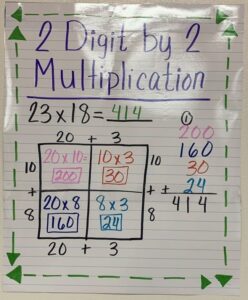
Lesson 4.2 Use Models to Multiply 2-Digit Numbers by Multiples of 10
Solve & Share
There are 10 teams in a baseball league. Each team has 25 players. How many players are in the league? Solve this problem using any strategy you choose.
I can .. use models and properties of operations to help multiply.

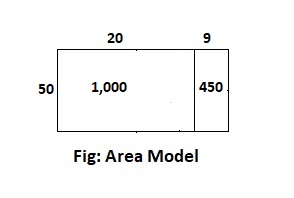
Answer:
It is given that
There are 10 teams in a baseball league. Each team has 25 players
Now,
The area-model that represents the number of teams and the number of players is:
So,
From the above Area-Model,
The total number of players in the league = (The number of players in each team) × (The total number of teams)
= 25 × 10
= 250 players
Hence, from the above,
We can conclude that the total number of players present in the league is: 250
Look Back!
How many players are in the league if there are 30 teams?
Answer:
We know that,
The total number of players in the league = (The number of players in each team) × (The total number of teams)
Now,
If there are 30 teams and each team consists of the same number of players as mentioned above, then
The total number of players present in the league
= 25 × 30
= 25 × 3 × 10
= (25 × 3) × 10
= 750 players
Hence, from the above,
We can conclude that the total number of players present in the league is: 750
Explain how you can use your answer above to help solve this problem.
Answer:
Multiplication using the “Area model”:
We know that,
An “Area” is the amount of flat space occupied by a figure, You can find the area of a figure by filling it with unit squares and then counting how many squares entirely fill the shape
The total area of the figure is the multiplication of the number of rows and columns i.e., the value of the product
Hence, from the above process,
We can conclude that we used the above process to solve the above-given problems
Essentials Question
How Can You Use an Array or an Area Model to Multiply?
Answer:
The steps to find the product that uses an Array or an Area Model to multiply is:
a. First, write each factor in expanded form.
b. Then, draw your model.
c. Next, multiply to find the area of each smaller rectangle.
d. Finally, add those products to find the total area.
Visual Learning Bridge
Max’s Moving Company has boxes for packing books. If each box holds 24 books, how many books would fit into 20 boxes?

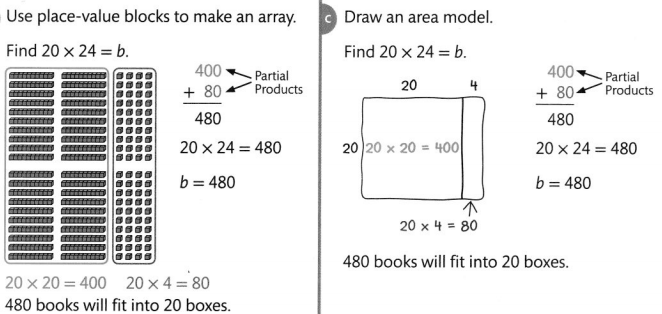
Convince Me!
Reasoning in the problem above, is the product, 480, reasonable? Explain.
Answer:
From the above,
It is given that there are 24 books in each box
So,
The total number of books that would fit in 20 boxes = (The total number of boxes) × (The number of books in each box)
= 20 × 24
= 2 × 10 × 24
= 48 × 10
= 480 books
Hence, from the above,
We can conclude that the product 480 is reasonable that we got in the above problem
Guided Practice
Do You Understand?
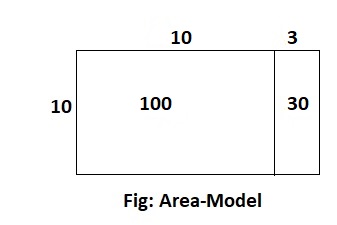
Question 1.
Draw an area model to show 20 × 26. Then find the product.
Answer:
The given expression is: 20 × 26
Now,
By using the Area-Model,
20 × 26
= (10 + 10) × (20 + 6)
= (10 × 20) + (10 × 6) + (10 × 20) + (10 × 6)
= 200 + 60 + 200 + 60
= 400 + 120
= 520
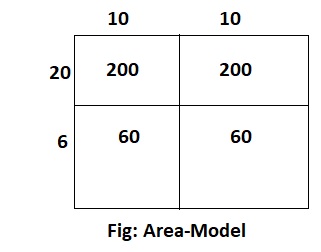
Hence, from the above,
We can conclude that the value of the given expression using the Area-Model is: 520
Do You Know How?
Question 2.
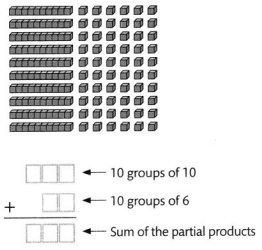
The place-value block array shows 10 × 16. Find the product.
Answer:
The given expression is: 10 × 16
Now,
By using the Area-Model,
10 × 16
= 10 × (10 + 6)
= (10 × 10) + (10 × 6)
= 100 + 60
= 160
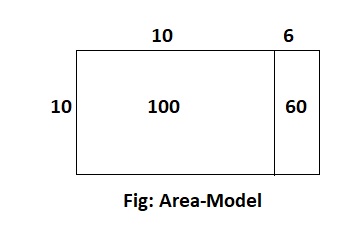
Hence, from the above,
We can conclude that the value of the given expression by using the Area-Model is: 160
Independent Practice
Leveled Practice For 3-8, use place-value blocks, area models, or arrays to find each product.
Question 3.
10 × 22
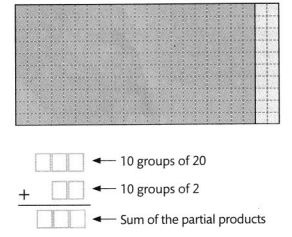
Answer:
The given expression is: 10 × 22
Now,
By using the Area-Model,
10 × 22
= 10 × (20 + 2)
= (10 × 20) + (10 × 2)
= 200 + 20
= 220
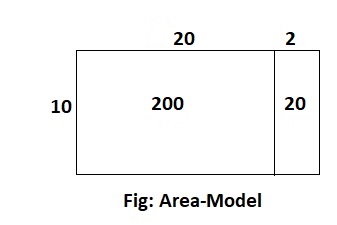
Hence, from the above,
We can conclude that the value of the given expression by using the Area-Model is: 220
Question 4.
10 × 13
Answer:
The given expression is: 10 × 13
Now,
By using the Area-Model,
10 × 13
= 10 × (10 + 3)
= (10 × 10) + (10 × 3)
= 100 + 30
= 130
Hence, from the above,
We can conclude that the value of the given expression by using the Area-Model is: 130
Question 5.
20 × 35
Answer:
The given expression is: 20 × 35
Now,
By using the Area-Model,
20 × 35
= (10 + 10) × (30 + 5)
= (10 × 30) + (10 × 5) + (10 × 30) + (10 × 5)
= 300 + 50 + 300 + 50
= 600 + 100
= 700
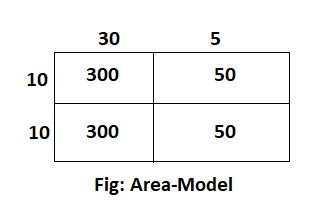
Hence, from the above,
We can conclude that the value of the given expression by using the Area-Model is: 700
Question 6.
20 × 41
Answer:
The given expression is: 20 × 41
Now,
By using the Area-Model,
20 × 41
= (10 + 10) × (40 + 1)
= (10 × 40) + (10 × 1) + (10 × 40) + (10 × 1)
= 400 + 10 + 400 + 10
= 800 + 20
= 820
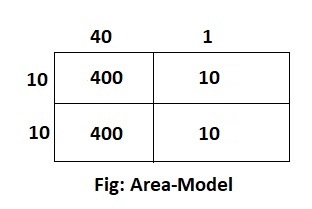
Hence, from the above,
We can conclude that the value of the given expression by using the Area-Model is: 820
Question 7.
30 × 29
Answer:
The given expression is: 30 × 29
Now,
By using the Area-Model,
30 × 29
= (20 + 10) × (20 + 9)
= (20 × 20) + (20 × 9) + (10 × 20) + (10 × 9)
= 400 + 180 + 200 + 90
= 600 + 270
= 870
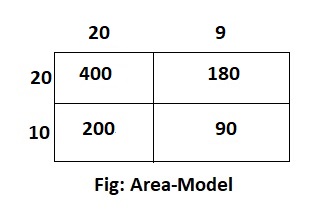
Hence, from the above,
We can conclude that the value of the given expression by using the Area-Model is: 870
Question 8.
40 × 37
Answer:
The given expression is: 40 × 37
Now,
By using the Area-Model,
40 × 37
= (20 + 20) × (30 + 7)
= (20 × 30) + (20 × 7) + (20 × 30) + (20 × 7)
= 600 + 140 + 600 + 140
= 1,200 + 280
= 1,480

Hence, from the above,
We can conclude that the value of the given expression by using the Area-Model is: 1,480
Problem Solving
Camera Sales

Question 9.
Algebra In the first 3 months of the year, an electronics store sold 1,446 cameras. How many cameras did the store sell in March? Write and solve an equation.
Answer:
It is given that
In the first 3 months of the year, an electronics store sold 1,446 cameras
Now,
The given data is:

So,
The number of cameras sold in the three months = (The number of cameras sold in January) + (The number of cameras sold in February) + (The number of cameras sold in March)
Now,
Let the number of cameras sold in March be x
So,
1,446 = 486 + 385 + x
x = 1,446 – (486 + 385)
x = 1,446 – 871
x = 575 cameras
Hence, from the above,
We can conclude that the number of cameras that the store sold in March is: 575
Question 10.
For every camera sold in February, the store donated $2 to a charity. How much did the store donate?
Answer:
It is given that
For every camera sold in February, the store donated $2 to a charity
Now,
The given data is:

So,
The total amount of money the store donated in February to a charity = (The number of cameras sold in February) × (The amount of money the store donated to a charity for every camera)
= 385 × $2
= (300 + 80 + 5) × $2
= (300 × $2) + (80 × $2) + (5 × $2)
= $600 + $160 + $10
= $770
Hence, from the above,
We can conclude that
The total amount of money the store donated in Februaryto a charity is: $770
Question 11.
Model with Math
During a basketball game, 75 cups of fruit punch was sold. Each cup holds 20 fluid ounces. How many total fluid ounces of fruit punch were sold?
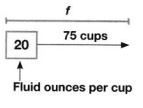
Answer:
It is given that
During a basketball game, 75 cups of fruit punch was sold. Each cup holds 20 fluid ounces.
So,
The amount of total fluid ounces of fruit punch that were sold = (The total number of cups) × (The amount of fluid ounces that each cup holds)
= 75 × 20
= (70 + 5) × (10 + 10)
= (70 × 10) + (70 × 10) + (5 × 10) + (5 × 10)
= 700 + 700 + 50 + 50
= 1,400 + 100
= 1,500 fluid ounces
Hence, from the above,
We can conclude that the amount of fluid ounces of fruit punch that were sold is: 1,500 fluid ounces
Question 12.
Higher-Order Thinking Describe how to correct the partial product that is not correct in the worked problem below. What is the correct product?

Answer:
The given expression is: 27 × 73
Now,
By using the Area-Model,
27 × 73
= (20 + 7) × (70 + 3)
= (20 × 70) + (20 × 3) + (7 × 70) + (7 × 3)
= 1,400 + 60 + 490 + 21
= 1,971
Hence, from the above,
We can conclude that
The partial product that is not correct is: 490
The correct product for the given expression is: 1,971
Assessment Practice
Question 13.
Which is greater?
15 × 30 or 22 × 20 Show your thinking.

Answer:
The given expressions are:
a. 15 × 30 b. 22 × 20
Now,
By using the Area-Model,
a.
15 × 30
= (10 + 5) × (20 + 10)
= (10 × 20) + (10 × 10) + (5 × 20) + (5 × 10)
= 200 + 100 + 100 + 50
= 400 + 50
= 450
b.
22 × 20
= (20 + 2) × (10 + 10)
= (20 × 10) + (20 × 10) + (2 × 10) + (2 × 10)
= 200 + 200 + 20 + 20
= 400 + 40
= 440
Hence, from the above,
We can conclude that the value of the expression 15 × 30 is greater
Lesson 4.3 Estimate: Use Rounding or Compatible Numbers
Solve & Share
Choose two factors from the numbers below to find a product that is as close to 1,600 as possible. Solve this problem using any strategy you choose.
I can .. use rounding or compatible numbers to estimate.

Answer:
The given numbers are: 24, 32, 61, and 78
So,
The numbers that are closest to the given numbers are: 20, 30, 60, and 80
Now,
To find the two factors from the given numbers to find a product that is as close to 1,600 as possible,
We have to find the product of the factors that are close to the given factors
So,
a.
20 × 30
= 2 × 10 × 3 × 10
= (2 × 3) × 100
= 6 × 100
= 600
b.
20 × 60
= 2 × 10 × 6 × 10
= (2 × 6) × 100
= 12 × 100
= 1,200
c.
20 × 80
= 2 × 10 × 8 × 10
= (2 × 8) × 100
= 16 × 100
= 1,600
d.
30 × 60
= 3 × 10 × 6 × 10
= (3 × 6) × 100
= 18 × 100
= 1,800
e.
30 × 80
= 3 × 10 × 8 × 10
= (3 × 8) × 100
= 24 × 100
= 2,400
f.
60 × 80
= 6 × 10 × 8 × 10
= (6 × 8) × 100
= 48 × 100
= 4,800
Hence, from the above,
We can conclude that
The two factors that are closest to the product 1,600 are: 24, 78
Look Back!
Construct Arguments Why did you choose the two factors that you did? How do you know your factors will give the closest estimate of the product?
Answer:
We know that,
The difference between the product of the two exact numbers and the product of the numbers that are closest to the exact numbers must be small
So,
When we observe the above products which we obtained in the above problem,
We can observe that there are two products that are closest to the given product
But,
When we find the difference between the exact product and the estimated product,
The product of the factors 25 and 60 is close to the product of the exact factors 24, 78
Essential Question
What Strategies Can I Use When Estimating?
Answer:
The front-end strategy is a method of estimating computations by keeping the first digit in each of the numbers and changing all the other digits to zeros. This strategy can be used to estimate sums, differences, products and quotients.
Visual Learning Bridge
The workers picked 14 dozen apples at Ms. Piper’s apple grove and 12 dozen apples at Mr. Stuart’s apple grove. There are 12 apples in one dozen. About how many apples did the workers pick?
14 + 12 = 26 dozen apples picked in total

One Way
Use rounding to estimate 26 × 12.
Round 26 to the nearest ten.
Round 12 to the nearest ten.
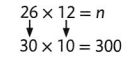
The workers picked about 300 apples.
Some problems do not need an exact answer.
Another Way
Use compatible numbers to estimate 26 × 12.
Replace the factors with numbers that are close and easy to multiply.
26 is close to 25.
12 is close to 10.
25 × 10 = n
250 = n
The workers picked about 250 apples.
Convince Me!
Reasoning Sue said she could find an estimate for 26 × 12 by rounding only 1 factor and multiplying 26 × 10. Do you agree? Explain.
Answer:
Sue said she could find an estimate for 26 × 12 by rounding only 1 factor and multiplying 26 × 10
Now,
We know that,
When we want to find an estimate of the factors, we have to estimate all the factors and it is possible when you do partial estimation i.e., rounding off 1 number and not rounding off another number
Hence, from the above,
We can conclude that we can agree with Sue
Guided Practice
Do You Understand?
Question 1.
In the example on the previous page, how do you know you only need an estimate and not an exact answer?
Answer:
We know that,
There are two types of estimations. They are:
a. Round-off method b. Closest estimated method
Now,
When we use the above two types of eatimations,
The answers we will get may differ
So,
In the example of previous page,
We got different answers when we use different types of estimation methods
Now,
From the example of previous page,
We can observe that the number of fruits had been asked in terms of estimations but not an exact number
Hence, from the above,
We can conclude that we only need an estimate and not an exact answer because of the mentioned quaestion
Question 2.
In the example on the previous page, what is another way you can multiply using compatible numbers by changing only one of the factors? Explain how you would find the estimated product.
Answer:
The given expression on the previous page is: 26 × 12
Now,
By using the closest number estimation,
The factors will be changed into: 25 and 12; or 26 and 10
So,
The estimation of the product using compatible numbers will be:
26 × 12
= 25 × 12 (or) 26 × 10
= 300 (or) = 260
Hence, from the above,
We can coclude that the estimated product is approximatelu 300 (or) 260
Do You Know How?
For 3-6, estimate each product. Explain why you chose the strategy you used to estimate the product.
Question 3.
24 × 18
Answer:
The given expression is: 24 × 18
Now,
By using the Compatible method estimation,
The given expression will become: 25 × 20
So,
25 × 20
= 25 × 2 × 10
= (25 ×2) × 10
= 50 ×10
= 500
Hence, from the above,
We can conclude that the estimated product for the given expression is: 500
Question 4.
33 × 31
Answer:
The given expression is: 33 × 31
Now,
By using the Compatible method estimation,
The given expression will become: 35 × 30
So,
35 × 30
= 35 × 3 × 10
= (35 × 3) × 10
= 105 × 10
= 1,050
Hence, from the above,
We can conclude that the estimated product for the given expression is: 1,050
Question 5.
38 × 22
Answer:
The given expression is: 38 × 32
Now,
By using the Compatible method estimation,
The given expression will become: 40 × 30
So,
40 × 30
= 4 × 10 × 3 × 10
= (4 × 3) × 100
= 12 × 100
= 1,200
Hence, from the above,
We can conclude that the estimated product for the given expression is: 1,200
Question 6.
45 × 48
Answer:
The given expression is: 45 × 48
Now,
By using the Rounding-off method estimation,
The given expression will become: 50 × 50
So,
50 × 50
= 5 ×10 × 5 × 10
= (5 × 5) × 100
= 25 × 100
= 2,500
Hence, from the above,
We can conclude that the estimated product for the given expression is: 2,500
Independent Practice
For 7-12, estimate each product. Explain why you chose the strategy you used to estimate the product.
Question 7.
39 × 19
Answer:
The given expression is: 39 × 19
Now,
By using the Rounding-off estimation method,
The given expression will become: 40 × 20
So,
40 × 20
= 4 × 10 × 2 × 10
= (4 × 2) ×100
= 8 × 100
= 800
Hence, from the above,
We can conclude that the estimated product for the given expression is: 800
Question 8.
28 × 27
Answer:
The given expression is: 28 × 27
Now,
By using the Rounding-off estimation method,
The given expression will become: 30 × 30
So,
30 × 30
= 3 × 10 × 3 × 10
= (3 × 3) ×100
= 9 × 100
= 900
Hence, from the above,
We can conclude that the estimated product for the given expression is: 900
Question 9.
64 × 13
Answer:
The given expression is: 64 × 13
Now,
By using the Compatible estimation method,
The given expression will become: 65 × 15
So,
65 × 15
= (60 + 5) × (10 + 5)
= (60 × 10) + (60 × 5) + (5 × 10) + (5 × 5)
= 600 + 300 + 50 + 25
= 975
Hence, from the above,
We can conclude that the estimated product for the given expression is: 975
Question 10.
42 × 17
Answer:
The given expression is: 42 × 17
Now,
By using the Rounding-off estimation method,
The given expression will become: 40 × 20
So,
40 × 20
= 4 × 10 × 2 × 10
= (4 × 2) ×100
= 8 × 100
= 800
Hence, from the above,
We can conclude that the estimated product for the given expression is: 800
Question 11.
82 × 36
Answer:
The given expression is: 82 × 36
Now,
By using the Compatible way estimation method,
The given expression will become: 80 × 35
So,
80 × 35
= (40 + 40) × (30 + 5)
= (40 × 30) + (40 × 5) + (40 × 30) + (40 × 5)
= 1,200 + 200 + 1,200 + 200
= 2,400 + 400
= 2,800
Hence, from the above,
We can conclude that the estimated product for the given expression is: 2,800
Question 12.
54 × 18
Answer:
The given expression is: 54 × 18
Now,
By using the Compaible way estimation method,
The given expression will become: 55 × 20
So,
55 ×20
= 55 × 2 × 10
= (55 × 2) × 10
= 110 × 10
= 1,100
Hence, from the above,
We can conclude that the estimated product for the given expression is: 1,100
For 13-14, estimate to check if the given answer is reasonable.
Compare your estimate to the given answer to check if the answer is reasonable.
Question 13.
66 × 41 = 2,706
Rounds to ________ × ________ = ________
Reasonable
Not Reasonable
Answer:
The given expression is: 66 × 41
Now,
By using the Rounding-off method,
66 × 41
= 70 × 40
= 7 × 10 × 4 × 10
= (7 × 4) × 100
= 28 × 100
= 2,800
Hence, from the above,
We can conclude that the Rounding is “Reasonable” since the difference between the estimated answer and the exact answer is small
Question 14.
34 × 52 = 2,288
Rounds to ________ × ________ = ________
Reasonable
Not Reasonable
Answer:
The given expression is: 34 × 52
Now,
By using the Rounding-off method,
34 × 52
= 30 × 50
= 3 × 10 × 5 ×10
= (3 × 5) × 100
= 15 × 100
= 1,500
Hence, from the above,
We can conclude that the Rounding is not “Reasonable” since the difference between the estimated answer and the exact answer is large
Problem Solving
For 15-16, use the table at the right.

Question 15.
About how many more Valencia orange trees than Temple orange trees does Mr. Gonzalez have? Explain.
Answer:
The given data is:

Now,
From the given data,
We can find:
a.
The number of Orange trees in Valencia = (The number of trees in each row) × (The number of rows)
= 46 × 31
Now,
By using the rounding-off method,
46 × 31
= 50 × 30
= 5 × 10 × 3 × 10
= (5 × 3) × 100
= 1,500
b.
The number of Orange trees in Temple = (The number of trees in each row) × (The number of rows)
= 38 × 28
Now,
By using the rounding-off method,
38 × 28
= 40 × 30
= 4 × 10 × 3 × 10
= (4 × 3) × 100
= 12 × 100
= 1,200
So,
The number of Valencia orange trees more than Temple orange trees does Mr. Gonzalez have
= (The number of Valencia Orange trees) – (The number of Temple Orange trees)
= 1,500 – 1,200
= 300
Hence, from the above,
We can conclude that Mr Gonzalez have about 300 Valencia Orange trees more than temple Orange trees
Question 16.
About how many orange trees does Mr. Gonzalez have? Explain.
Answer:
The given data is:

Now,
From the given data,
We can find that the total number of Mr. Gonzalez’s trees can be obtained by adding the given three types of Orange trees
So,
The number of Orange trees does Mr Gonzalez have = (The total number of trees in each row) × (The total number of rows)
= (38 + 28 + 46) × (28 + 38 + 31)
= 112 × 97
Now,
By using the Rounding-off method,
112 × 97
= 110 × 100
= 11 × 10 × 100
= 11,000
Hence, from the above,
We can conclude that there are about 11,000 Orange trees does Mr. Gonzalez have
Question 17.
Higher-Order Thinking How is using compatible numbers to estimate similar to using rounding? How is it different?
Answer:
A)
Compatible numbers:
Round the whole number to the closest compatible number. “Compatible numbers” are numbers that are close in value to the real number that would make it easier to find an estimate calculation.
B)
Rounding-off numbers:
Rounding off means a number is made simpler by keeping its value intact but closer to the next number. It is done for whole numbers, and for decimals at various places of hundreds, tens, tenths, etc. Rounding off numbers is done to preserve the significant figures
Question 18.
Construct Arguments Explain how you would use estimation to decide which has the greater product, 39 × 21 or 32 × 32.
Answer:
The given expressions are: 39 × 21 and 32 × 32
Now,
A)
By using the rounding-off method:
a.
39 × 21
= 40 × 20
= 4 × 10 × 2 × 10
= (4 × 2) × 100
= 8 × 100
= 800
b.
32 × 32
= 30 × 30
= 3 × 10 × 3 × 10
= (3 × 3) × 100
= 9 × 100
= 900
B)
By using the compatible nembers method:
a.
39 × 21
= 40 × 20
= 4 × 10 × 2 × 10
= 8 × 100
= 800
b.
32 × 32
= 30 × 30
= 3 × 10 × 3 × 10
= (3 × 3) × 100
= 9 × 100
= 900
Hence, from the above,
We can conclude that the estimated product of 32 × 32 is greater
Assessment Practice
Question 19.
Select all of the expressions that could be used to estimate 32 × 14.
☐ 30 × 20
☐ 30 × 10
☐ 14 × 32
☐ 40 × 10
☐ 32 × 10
Answer:
The given expression is: 32 × 14
Now,
By using the Rounding-off method,
The given expression will become: 30 × 10 and 32 × 10 and 30 × 14
Now,
By using the Compatible numbers method,
The given expression will become: 30 × 15 and 30 × 14 and 32 × 15
Hence, from the above,
We can conclude that the expressions that can be used to estimate 32 × 14 are:

Question 20.
Select all of the equations that use compatible numbers to find an estimate for 28 × 24.
☐ 30 × 25 = 750
☐ 28 × 10 = 280
☐ 28 × 25 = 700
☐ 25 × 20 = 500
☐ 30 × 300 = 9,000
Answer:
The given expression is: 28 × 24
Now,
By usin the compatible numbers method,
The given expression will become: 30 × 25 and 28 × 25 and 30 × 24
Hence, from the above,
We can conclude that
The equations that use compatible numbers to find an estimate for 28 × 24 are:
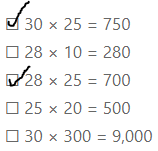
Lesson 4.4 Arrays and Partial Products
Solve & Share
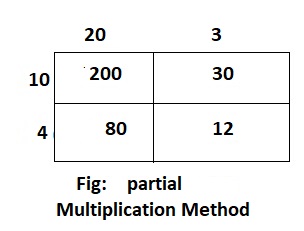
A theater contains 14 rows of seats with 23 seats in each row. How many seats are in the theater? Solve this problem using any strategy you choose.
I can … use place-value concepts and properties to multiply.

Answer:
It is given that
A theater contains 14 rows of seats with 23 seats in each row.
So,
The total number of seats that are present in a theater = (The number of rows of seats a theater contains) × (The number of seats in each row)
= 14 × 23
Now,
By using the Partial multiplication method,
14 × 23
= (10 + 4) × (20 + 3)
= (10 × 20) + (10 × 3) + (4 × 20) + (4 × 3)
= 200 + 30 + 80 + 12
= 322
Hence, from the above,
We can conclude that
The total number of seats that are present in a theater is: 322 seats
Look Back!
Use Structure Theater seating is an example of objects that are arranged in rows and columns, or arrays. How do the number of rows and the number of seats in each row relate to the total number of seats?
Answer:
It is given that
Theater seating is an example of objects that are arranged in rows and columns or arrays
Now,
We know that,
The total number of seats in a theater can be given by the multiplication of the number of rows present in a theater with the number of seats that are present in a row
Hence, from the above,
We can conclude that
The total number of seats in a theater = (The number of rows) × (The number of seats in each row)
Essential Question
How Can You Multiply Using an Array?
Answer:
The steps that are to be followed when you multiply using an Array are:
STEP 1:
Label the height and width of a rectangle with the key numbers in the question.
STEP 2:
a. Break down the numbers into tens and ones.
b Draw a separate column and row for each of these numbers.
STEP 3:
Multiply each column and row with each other, until you get four numbers.
Visual Learning Bridge
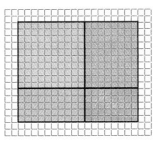
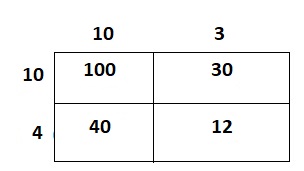
There are 13 toy dogs in each row of a carnival booth. Twenty rows contain toy bulldogs and 4 rows contain toy huskies. How many toy dogs are there?


Convince Me!
Model with Math What 2-digit by 2-digit multiplication is shown by the model at the right? What is the product? Explain how you used the model to find the product.
Answer:
The given model is:

Now,
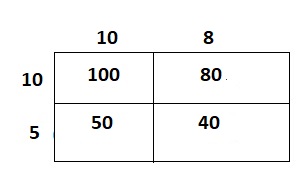
The representation of the given model in the simplest form is:
Now,
From the above,
We can observe that
The two-digit numbers that are used for multiplication is:
(10 + 8) × (10 + 5)
= 18 × 15
Now,
By using the Partial Multiplication method,
18 × 15
= (10 + 8) × (10 + 5)
= (10 × 10) + (10 × 5) + (8 × 10) + (8 × 5)
= 100 + 50 + 80 + 40
= 270
Hence, from the above,
We can conclude that
The 2-digit by 2-digit multiplication that is shown in the given model is: 18 × 15
The product of the obtained 2-digit by 2-digit multiplication using the partial multiplication method is: 270
Guided Practice
Do You Understand?
Question 1.
In the example on the previous page, what four simpler multiplication problems were used to find 24 × 13?
Answer:
The given expression is: 24 × 13
Now,
By using the Partial Multiplication method,
24 × 13
= (20 + 4) × (10 + 3)
= (20 × 10) + ( 20 × 3) + (4 × 10) + (4 × 3)
= 200 + 60 + 40 + 12
= 312
Hence, from the above,
We can conclude that
The four simpler multiplication problems that were used to find 24 × 13 that is the example on the previous page is:
a. 20 × 10 = 200
b. 20 × 3 = 60
c. 4 × 10 = 40
d. 4 × 3 = 12
Question 2.
How can you use properties to help find the product of 24 × 13?
Answer:
The given expression is: 24 × 13
Now,
We know that,
Distributive Property of Multiplication:
a (b + c) = a.b + a.c
Now,
Divide 24 × 13 into parts
So,
24 × 13
= (20 + 4) × (10 + 3)
Now,
By using the Distributive Property of Multiplication,
20 × (10 + 3) = (20 × 10) + (20 × 3)
= 200 + 60
= 260
4 × (10 + 3) = (4 × 10) + (4 × 3)
= 40 + 12
= 52
So,
24 × 13 = 260 + 52
= 312
Hence, from the above,
We can conclude that the product of the given expression by using the properties is: 312
Do You Know How?
For 3, use the array drawn on a grid to find the product. Check if your answer is reasonable.
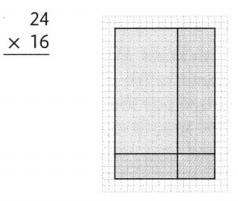
Question 3.
Answer:
The given expression is: 24 × 16
Now,
By using the estimation of the Compatible numbers,
The given expression will become: 24 × 15
Now,
By using the Partial Multiplication method,
24 × 16 24 ×15
= (20 + 4) × (10 + 6) = (20 + 4) × (10 + 5)
= (20 × 10) + (20 × 6) + (4 × 10) + (4 × 6) = (20 × 10) + (20 × 5) + (4 × 10) + (4 × 5)
= 200 + 120 + 40 + 24 = 200 + 100 + 40 + 20
= 384 = 360
Hence, from the above,
We can conclude that
The product of the given expression is: 384
The product for the given expression is “Reasonable” since there is a small difference between the exact product and the estimated product
Independent Practice
For 4-7, use the array drawn on a grid to find each product.
Using the Commutative Property of Addition, you can add the partial products in any order.
Question 4.
14 × 21
Answer:
The given expression is: 14 × 21
Now,
By using the Partial Multiplication method,
14 × 21
= (10 + 4) × (20 + 1)
= (10 × 20) + (10 × 1) + (4 × 20) + (4 × 1)
= 200 + 10 + 80 + 4
= 294
Hence, from the above,
We can conclude that the product for the given expression is: 294
Question 5.
14 × 12

Answer:
The given expression is: 14 × 12
Now,
By using the Partial Multiplication Method,
14 × 12
= (10 + 4) × (10 + 2)
= (10 × 10) + (10 × 2) + (4 × 10) + (4 × 2)
= 100 + 20 + 40 + 8
= 168
Hence, from the above,
We can conclude that the product for the given expression is: 168
Question 6.
18 × 18

Answer:
The given expression is: 18 × 18
Now,
By using the Partial Multiplication method,
18 × 18
= (10 + 8) × (10 + 8)
= (10 × 10) + (10 × 8) + (8 × 10) + (8 × 8)
= 100 + 80 + 80 + 64
= 324
Hence, from the above,
We can conclude that the product for the given expression is: 324
Question 7.
15 × 13

Answer:
The given expression is: 15 × 13
Now,
By using the Partial Multiplication ethod,
15 × 13
= (10 + 5) × (10 + 3)
= (10 × 10) + (5 × 10) + (10 × 3) + (5 × 3)
= 100 + 50 + 30 + 15
= 195
Hence, from the above,
We can conclude that the product for the given expression is: 195
Problem Solving
Question 8.
Find the missing factor. 20 × ? = 420 Explain how you solved.
Answer:
The given expression is: 20 ×? = 420
Now,
Let the missing factor be x
So,
20 × x = 420
x = \(\frac{420}{20}\)
x = 21
Hence, from the above,
We can conclude that the missing factor for the given expression is: 21
Question 9.
The flagpole in front of City Hall in Lou’s town is 35 feet tall. How many inches tall is the flagpole? Remember, there are 12 inches in 1 foot.
Answer:
It is given that
The flagpole in front of City Hall in Lou’s town is 35 feet tall
Now,
We know that,
1 foot = 12 inches
So,
The height of the flagpole in inches = (The height of the flagpole in feet) × (The number of inches for 1 foot)
= 35 × 12
Now,
By using the Partial Multiplication method,
35 × 12
= (30 + 5) × (10 + 2)
= (30 × 10) + (30 × 2) + (5 × 10) + (5 × 2)
= 300 + 60 + 50 + 10
= 420
Hence, from the above,
We can conclude that the height of the flagpole in inches is: 420 inches
For 10-11, use the array at the right.
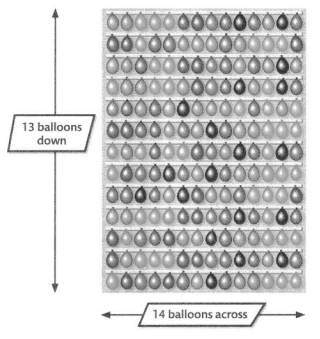
Question 10.
Model with Math Maggie is making a balloon game for the school fair. Students throw darts to pop the balloons. Draw lines on the array to separate each factor into tens and ones. How many balloons are used to set up the game?
Answer:
It is given that
Maggie is making a balloon game for the school fair. Students throw darts to pop the balloons
Now,
The given array is:

So,
The total number of balloons used to set up the game = (The total number of rows of balloons) × (The total number of columns of balloons)
= 13 × 14
Now,
By using the Partial Multiplication method,
13 × 14
= (10 + 3) × (10 + 4)
= (10 × 10) + (10 × 4) + (3 × 10) + (3 × 4)
= 100 + 40 + 30 + 12
= 182
Hence, from the above,
We can conclude that the total number of balloons that are used to set up the game is: 182 balloons
Question 11.
Higher-Order Thinking Maggie knows she will have to completely refill the balloon board about 15 times. Write an equation to show the number of balloons Maggie will need.
Answer:
From Problem 10,
We know that,
The total number of balloons that are used to set up the game is: 182
Now,
It is given that
Maggie knows she will have to completely refill the balloon board about 15 times.
So,
The total number of balloons maggie will need to refill = (The total number of balloons that are used to set up the game) × (The number of times the balloon board will have to refill)
= 182 × 15
Now,
By using the Partial Multiplication method,
182 × 15
= (100 + 80 + 2) × 15
= (100 × 15) + (80 × 15) + (2 × 15)
= 1,500 + 1,200 + 30
= 2,730
Hence, from the above,
We can conclude that
The total number of balloons that Maggie will need to refill the balloon board 15 times is: 2,730 balloons
Assessment Practice
Question 12.
Insert the missing partial products. Then add to find the product.
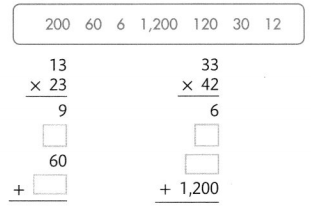
Answer:
The given expressions are:
a. 13 × 23 b 33 × 42
Now,
By using the Partial Multiplication Method,
a
13 × 23
= (10 + 3) × (20 + 3)
= (10 × 20) + (10 × 3) + (3 × 20) + (3 × 3)
= 200 + 30 + 60 + 9
= 299
b
33 × 42
= (30 + 3) × (40 + 2)
= (30 × 40) + (30 × 2) + (3 × 40) + (3 × 2)
= 1,200 + 60 + 120 + 6
= 1,386
Hence, from the above,
We can conclude that
The missing partial products and the addition of partial products for the given expressions are:

Question 13.
Insert the missing factor in each equation.

Answer:
Let the missing factor be x
Now,
The given expressions are with the representation of missing factor are:
a. 19 × x = 1,007
b. 62 × x = 1,736
c. x × 37 = 1,813
d. 15 × x = 1,260
So,
The missing factors for the given expressions will be:
a.
x = \(\frac{1,007}{19}\)
x = 53
b.
x = \(\frac{1,736}{62}\)
x = 28
c.
x = \(\frac{1,813}{37}\)
x = 49
d.
x = \(\frac{1,260}{15}\)
x = 84
Hence, from the above,
We can conclude that
The missing factor in each equation is:
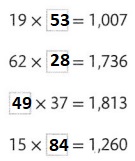
Lesson 4.5 Area Models and Partial Products
Solve & Share
A playground is divided into four sections as shown in the diagram below. Find the area of the playground. Explain how you found the answer. Solve this problem using any strategy you choose.
I can … use area models and properties of operations to multiply two 2-digit numbers.
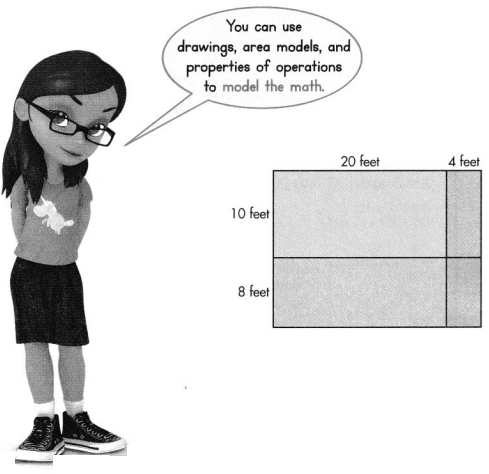
Answer:
It is given that
A playground is divided into four sections as shown in the diagram below.

Now,
From the given shape of the playground,
We can observe that the shape is like an “Area-Model” used for multiplication
So,
By using the Area-Model for multiplication,
The area of the playground = The sum of all the areas of the parts of the playground
Now,
By using the partial Multiplication method,
The area of the playground = (10 × 20) + (10 × 4) + (8 × 20) + (8 × 4)
= 200 + 40 + 160 + 32
= 432 feet²
Hence, from the above,
We can conclude that the area of the given playground is: 432 feet²
Look Back! Explain how you found the area of the blue part of the playground?
Answer:
The given figure is:

Now,
From the above problem,
We can observe that
We had found out the area of the playground by using the Partial Multiplication method
Now,
By using the Partial Multiplication Method,
The area of the blue part of the playground = (20 × 10) + (8 × 20)
= 200 + 160
= 360 feet²
Hence, from the above,
We can conclude that the area of the blue part of the playground is: 360 feet²
Essential Question
How Can You Use the Distributive Property to Multiply?
Answer:
The steps to use the Distributive Property of Multiplication are:
a. Simplify the numbers.
b. Split the problem into two easier problems.
c Take the number outside the parentheses and multiply it by each number inside the parentheses, one at a time.
d. Add the products.
Visual Learning Bridge
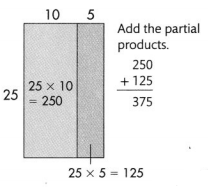
There are 15 players on each baseball team of the Strike Out Club. How many players are on all of the teams in the Strike Out Club?

One Way
Use an area model and the Distributive Property to find 25 × 15.
Break apart 15 into 10+ 5.
25 × (10+5)
(25 × 10) + (25 × 5)
Another Way
Use an area model and the Distributive Property to find 25 × 15.
Break apart 25 into 20 + 5.
(20 + 5) 15)
(20 × 15) + (5 × 15)
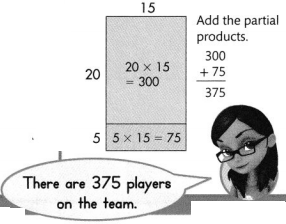
Another Way
Use an area model and the Distributive Property to find 25 × 15.
Break apart both factors.
Break apart 25 into 20 + 5.
Break apart 15 into 10+ 5.
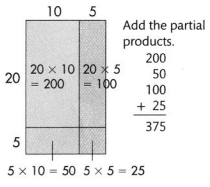
Convince Me!
Use Structure How does an area model illustrate the Distributive Property?
Answer:
The distributive property says that multiplication distributes over addition.
The representation of the area model will be in two ways:
A) a(b + c)
B) ab + ac
The equality of the expressions,
a(b + c) = ab + ac
is the distributive property.
Guided Practice
Do You Understand?
Question 1.
What four simpler multiplication problems are used to find 24 × 23?
Answer:
The given expression is: 24 × 23
Now,
By using the Partial multiplication method,
24 × 23
= (20 + 4) × (20 + 3)
= (20 × 20) + (20 × 3) + (4 × 20) + (4 × 3)
= 400 + 60 + 80 + 12
= 552
Hence, from the above,
We can conclude that
The four simpler multiplication problems used to find 24 × 23 are:
a. 20 × 20 = 400
b. 20 × 3 = 60
c. 4 × 20 = 80
d. 4 × 3 = 12
Question 2.
How can an area model and the Distributive Property help you multiply? Use 12 × 16 to explain.
Answer:
We know that,
The distributive property says that multiplication distributes over addition.
The representation of the area model will be in two ways:
A) a(b + c)
B) ab + ac
The equality of the expressions,
a(b + c) = ab + ac
is the distributive property.
Now,
By using the Distributive Property of Multiplication,
12 × 16
= 12 × (10 + 6)
= (12 × 10) + (12 × 6)
= 120 + 72
= 192
Hence, from the above,
We can conclude that the product for the expression 12 × 16 is: 192
Do You Know How?
Question 3.
Use the area model and the Distributive Property to find 35 × 12.
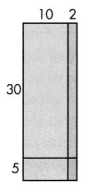
35 × 12 =
30 × 10 =
5 × 10 =
30 × 2 =
5 × 2 =
______ + _____ + ______ + _______ = _________
Answer:
The given expression is: 35 × 12
Now,
By using the area model and the Distributive Property of Multiplication,
35 × 12
= (30 + 5) × (10 + 2)
= (30 × 10) + (30 × 2) + (5 × 10) + (5 × 2)
= 300 + 60 + 50 + 10
= 420
Hence, from the above,
We can conclude that the value of the product for the given expression is: 420
Independent Practice
For 4-10, draw an area model to find each product.
Question 4.
18 × 25
Answer:
The given expression is: 18 × 25
Now,
By using the area model,
18 × 25
= (10 + 8) × (20 + 5)
= (10 × 20) + (10 × 5) + (8 × 20) + (8 × 5)
= 200 + 50 + 160 + 40
= 450
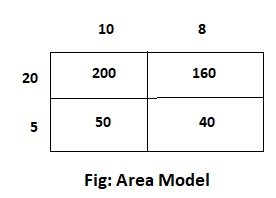
Hence, from the above,
We can conclude that the product value for the given expression is: 450
Question 5.
14 × 25
Answer:
The given expression is: 14 × 25
Now,
By using the area model,
14 × 25
= (10 + 4) × (20 + 5)
= (10 × 20) + (10 × 5) + (4 × 20) + (4 × 5)
= 200 + 50 + 80 + 20
= 350
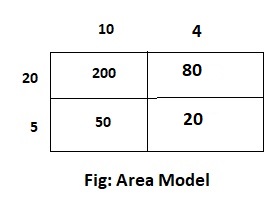
Hence, from the above,
We can conclude that the product value for the given expression is: 450
Question 6.
22 × 88
Answer:
The given expression is: 22 × 88
Now,
By using the area model,
22 × 88
= (20 + 2) × (80 + 8)
= (20 × 80) + (20 × 8) + (2 × 80) + (2 × 8)
= 1,600 + 160 + 160 + 16
= 1,936

Hence, from the above,
We can conclude that the product value for the given expression is: 1,936
Question 7.
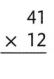
Answer:
The given expression is: 41 ×12
Now,
By using the area model,
41 × 12
= (40 + 1) × (10 + 2)
= (40 × 10) + (40 × 2) + (1 × 10) + (1 × 2)
= 400 + 80 + 10 + 2
= 492
Hence, from the above,
We can conclude that the product value for the given expression is: 492
Question 8.
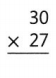
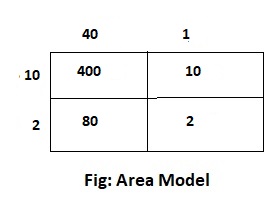
Answer:
The given expression is: 30 × 27
Now,
By using the area model,
30 × 27
= 30 × (20 + 7)
= (30 × 20) + (30 × 7)
= 600 + 210
= 810
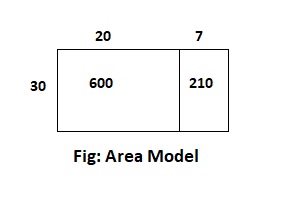
Hence, from the above,
We can conclude that the product value for the given expression is: 810
Question 9.
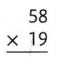
Answer:
The given expression is: 58 × 19
Now,
By using the area model,
58 × 19
= (50 + 8) × (10 + 9)
= (50 × 10) + (50 × 9) + (8 × 10) + (8 × 9)
= 500 + 450 + 80 + 72
= 1,102
Hence, from the above,
We can conclude that the product value for the given expression is: 1,102
Question 10.
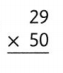
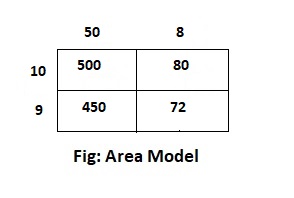
Answer:
The given expression is: 29 × 50
Now,
By using the area model,
29 × 50
= (20 + 9) × 50
= (20 × 50) + (9 × 50)
= 1,000 + 450
= 1,450
Hence, from the above,
We can conclude that the product value for the given expression is: 1,450
Problem Solving
Question 11.
Write 652,079 using number names and in expanded form.
Answer:
The given number is: 652,079
Now,
We know that,
“Expanded form” or the “Expanded notation” is a way of writing numbers to see the math value of individual digits. When numbers are separated into individual place values and decimal places they can also form a mathematical expression
Hence,
The representation of the given number in the word form is:
Six hundred fifty-two thousand, and Seventy-nine
The representation of the given number in the expanded form is:
600,000 + 50,000 + 2,000 + 0 + 70 + 9
Question 12.
Number Sense Sara estimated 23 × 43 using 20 × 40. Sam estimated 23 × 43 using 25 × 40. Will Sara’s or Sam’s method give an estimate closer to the exact answer? Explain.
Answer:
It is given that
Sara estimated 23 × 43 using 20 × 40. Sam estimated 23 × 43 using 25 × 40
Now,
The given expression is: 23 × 43
Now,
By using the Rounding method,
The given expression will become: 20 × 40
By using the Compatible numbers method,
The given expression will become: 25 × 40 (or) 25 × 45
Now,
The exact answer is:
23 × 43
= (20 + 3) × (40 + 3)
= (20 × 40) + (20 × 3) + (3 × 40) + (3 × 3)
= 800 + 60 + 120 + 9
= 989
Now,
The estimation of Sara is:
20 × 40
= 2 × 10 × 4 × 10
= (2 × 4) × 100
= 8 × 100
= 800
Now,
The estimation of Sam is:
25 × 40
= (20 + 5) × 40
= (20 × 40) + (5 × 40)
= 800 + 200
= 1,000
Hence, from the above,
We can conclude that
Sam’s method gives an estimate closer to the exact answer
Question 13.
Use Structure Each family of Florida Scrub-Jays inhabits 25 acres of land. No other Scrub-Jay families live within this area. How many acres of land are needed for 24 families of Florida Scrub-Jays? Show how you can use the Distributive Property to solve this problem.

Answer:
It is given that
Each family of Florida Scrub-Jays inhabits 25 acres of land. No other Scrub-Jay families live within this area.
So,
The acres of land that is needed for 24 families of Florida Scrub-jays = (The amount of land needed by each family of Florida Scrub-Jays) × (The total number of families)
= 25 × 24
Now,
By using the Distributive Property of Multiplication,
25 × 24
= (20 + 5) × (20 + 4)
= (20 × 20) + (20 × 4) + (5 × 20) + (5 × 4)
= 400 + 80 +100 + 20
= 600 acres of land
Hence, from the above,
We can conclude that
The total amount of acres of land needed for 24 families of Florida Scrub-Jays is: 600 acres of land
Question 14.
Marla wants to buy a new tablet that costs $565, including tax. She saved $15 per week for 30 weeks. Does Marla have enough money saved to buy the tablet? Explain.
Answer:
It is given that
Marla wants to buy a new tablet that costs $565, including tax. She saved $15 per week for 30 weeks.
Now,
The amount of money that Marla saved = (The amount of money she saved per week) × (Total number of weeks)
= $15 × 30
= (10 + 5) × 30
= (10 ×30) + (5 × 30)
= 300 + 150
= $450
So,
The amount of money saved by Marla < The cost of a new tablet
$450 < $565
Hence, from the above,
We can conclude that Marla does not have enough money saved to buy the tablet
Question 15.
Higher-Order Thinking Which costs less: 13 oranges that cost 29 cents each or 17 apples that cost 25 cents each? How much less?
Answer:
It is given that
13 oranges cost 29 cents each and 17 apples cost 25 cents each
Now,
The total cost of Oranges = (The number of Oranges) × (The cost of each Orange)
= 13 × 29
= (10 + 3) × (20 + 9)
= (10 × 20) + (10 × 9) + (3 × 20) + (3 × 9)
= 200 + 90 + 60 + 27
= $377
Now,
The total cost of apples = (The number of apples) × (The cost of each apple)
= 17 × 25
= (10 + 7) × (20 + 5)
= (10 × 20) + (10 × 5) + (7 × 20) + (7 × 5)
= 200 + 50 + 140 + 35
= $425
So,
The difference between the cost of Oranges and the cost of apples = $425 – $377
= $48
Hence, from the above,
We can conclude that
The cost of Oranges is less
The cost of Oranges is less by $48 than the cost of apples
Assessment Practice
Question 16.
Select all of the partial products which would be used to find 19 × 26.
☐ 45; 60; 180; 200
☐ 200; 180; 60; 54
☐ 6; 45; 180; 200
☐ 200; 60; 180; 54
☐ 0; 54; 180; 200
Answer:
The given expression is: 19 × 26
Now,
By using the area model,
19 × 26
= (10 + 9) × (20 + 6)
= (10 × 20) + (10 × 6) + (9 × 20) + (9 × 6)
= 200 + 60 + 180 + 54
Hence, from the above,
We can conclude that all the partial products that are used to find 19 × 26 are:

Question 17.
Select all of the ways you can use breaking apart and the Distributive Property to find the product of 35 × 12.
☐ 35 × (10 + 2)
☐ (12 × 30) + (12 × 5)
☐ (12 × 5) + (35 × 5)
☐ (30 × 5) + (10 × 2)
☐ (30 × 10) + (5 × 10) + (30 × 2) + (5 × 2)
Answer:
The given expression is: 35 × 12
Now,
By using the Distributive Property of Multiplication,
35 × 12
= 35 × (10 + 2) —- (1)
= (30 + 5) × 12
= (30 × 12) + (5 × 12) —- (2)
= (30 + 5) × (10 + 2)
= (30 × 10) + (30 × 2) + (5 × 10) + (5 × 2) —– (3)
Hence, from the above,
We can conclude that
All of the ways you can use breaking apart and the Distributive Property to find the product of 35 × 12 are:
Lesson 4.6 Use Partial Products to Multiply by 2-Digit Numbers
Solve & Share
There are 11 regular players and 5 substitute players on a soccer team. How many players are on 15 soccer teams? Solve this problem using any strategy you choose.
I can … use place value and partial products to multiply.

Answer:
It is given that
There are 11 regular players and 5 substitute players on a soccer team.
So,
The total number of players in 15 teams = (The number of players) × (The number of teams)
= (Regular players + Substitute players) × (The number of teams)
= (11 + 5) × 15
= (11 × 15) + (5 × 15)
= 165 + 75
= 240 players
Hence, from the above,
We can conclude that there are a total of 240 players in 15 teams
Look Back! How could you use an array and rounding or an array and compatible numbers to estimate the product for the problem above?
Answer:
From the above problem,
We can observe that
We have to use the area model or the Distributive property to find the total number of players because there are different types of players i.e., Regular players, Substitute players, etc.
Essential Question
How Can You Record Multiplication?
Answer:
The ways to record Multiplication are:
a. Grid method.
b. Long multiplication.
c. Lattice multiplication.
d. Binary or Peasant multiplication.
e. Binary multiplication in computers.
f. Shift and add.
g Quarter square multiplication.
h. Fast multiplication algorithms for large inputs
Visual Learning Bridge
Marcia put 7 oranges and 8 apples into each of 12 bags. How many pieces of fruit did Marcia put into all of the bags?
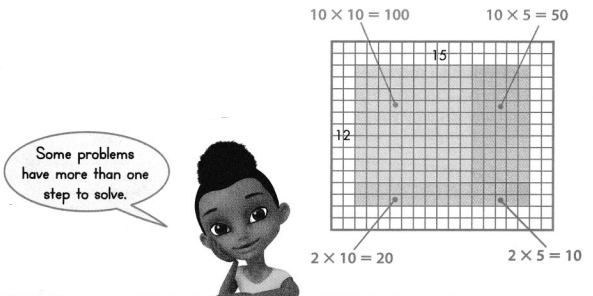
Find 12 × 15.
Estimate: 12 × 15 is about 10 × 15 = 150.
First, multiply the ones.

Then, multiply the tens.

Convince Me!
Reasoning Which partial products are incorrect? What is the correct final product?

Answer:
The given expression is: 26 × 12
Now,
By using the Partial multiplication method,
26 × 12
= (20 + 6) × (10 + 2)
= (20 × 10) + (20 × 2) + (6 × 10) + (6 × 2)
= 200 + 40 + 60 + 12
= 312
Hence, from the above,
We can conclude that
The given incorrect partial products are: 200, 60
The correct final product is: 312
Guided Practice
Do You Understand?
Question 1.
In the example on the previous page, why do you find 2 × 1 ten, rather than 2 × 1?
Answer:
We know that,
1 ten = 10 —–> 10’s place-value
1 = 1 ——> Unit’s place-value
Now,
From the above,
We can observe that there is a lot of difference 10’s position and unit’s position
Hence, from the above,
We can conclude that
We would write 2 × 1 ten rather than 2 × 1 as we observed in the example on the previous page
Question 2.
In the example on the previous page, could you record the 4 partial products in a different order? Explain.
Answer:
The given expression in the example on the previous page is: 15 × 12
Now,
By using the partial Products method,
15 × 13
= (10 + 5) × (10 + 2)
= (10 × 10) + (10 × 2) + (5 × 10) + (5 × 2)
= 100 + 20 + 50 + 10
= 180
Hence, from the above,
We can conclude that
We can record the 4 partial products in a different order for the example that is present in the previous page
Do You Know How?
For 3-4, find all the partial products. Then add to find the final product. Draw area models as needed.
Question 3.
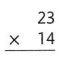
Answer:
The given expression is: 23 × 14
Now,
By using the Partial Products method,
23 × 14
= (20 + 3) × (10 + 4)
= (20 × 10) + (20 × 4) + (3 × 10) + (3 × 4)
= 200 + 80 + 30 + 12
= 322
Hence, from the above,
We can conclude that the final product for the given expression is: 322
Question 4.
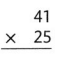
Answer:
The given expression is: 41 × 25
Now,
By using the Partial Products method,
41 × 25
= (40 + 1) × (20 + 5)
= (40 × 20) + (40 × 5) + (1 × 20) + (1 × 5)
= 800 + 200 + 20 + 5
= 1,025
Hence, from the above,
We can conclude that the final product for the given expression is: 1,025
Independent Practice
For 5-12, estimate. Find all the partial products. Then add to find the final product. Draw area models as needed.
Remember to check if your final product is reasonable.
Question 5.
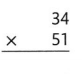
Answer:
The given expression is: 34 × 51
Now,
By using the Partial Products method,
34 × 51
= (30 + 4) × (50 + 1)
= (30 × 50) + (30 × 1) + (4 × 50) + (4 × 1)
= 1,500 + 30 + 200 + 4
= 1,734
Estimate:
35 × 50
= (30 + 5) × 50
= (30 × 50) + (5 × 50)
= 1,500 + 250
= 1,750
Hence, from the above,
We can conclude that
The final product for the given expression is: 1,750
The final product is reasonalble when we compare to its estimate
Question 6.
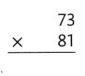
Answer:
The given expression is: 73 × 81
Now,
By using the Partial Products method,
73 × 81
= (70 + 3) × (80 + 1)
= (70 × 80) + (70 × 1) + (3 × 80) + (3 × 1)
= 5,600 + 70 + 240 + 3
= 5,913
Estimate:
75 × 80
= (70 + 5) × 80
= (70 × 80) + (5 × 80)
= 5,600 + 400
= 6,000
Hence, from the above,
We can conclude that
The final product for the given expression is: 5,913
The final product is reasonalble when we compare to its estimate
Question 7.
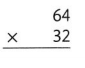
Answer:
The given expression is: 64 × 32
Now,
By using the Partial products method,
64 × 32
= (60 + 4) × (30 + 2)
= (60 × 30) + (60 × 2) + (4 × 30) + (4 × 2)
= 1,800 + 120 + 120 + 8
= 2,048
Estimate:
65 × 30
= (60 + 5) × 30
= (60 × 30) + (5 × 30)
= 1,800 + 150
= 1,950
Hence, from the above,
We can conclude that
The final product for the given expression is: 2,048
The final product is reasonalble when we compare to its estimate
Question 8.
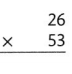
Answer:
The given expression is: 26 × 53
Now,
By using the Partial Products method,
26 × 53
= (20 + 6) × (50 + 3)
= (20 × 50) + (20 × 3) + (6 × 50) + (6 × 3)
= 1,000 + 60 + 300 + 18
= 1,378
Estimate:
25 × 50
= (20 + 5) × 50
= (20 × 50) + (5 × 50)
= 1,000 + 250
= 1,250
Hence, from the above,
We can conclude that
The final product for the given expression is: 1,378
The final product is not reasonalble when we compare to its estimate
Question 9.
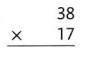
Answer:
The given expression is: 38 × 17
Now,
By using the partial products method,
38 × 17
= (30 +8) × (10 + 7)
= (30 × 10) + (30 × 7) + (8 × 10) + (8 × 7)
= 300 + 210 + 80 + 56
= 646
Estimate:
40 × 15
= 40 × (10 + 5)
= (40 × 10) + (40 × 5)
= 400 + 200
= 600
Hence, from the above,
We can conclude that
The final product for the given expression is: 646
The final product is reasonalble when we compare to its estimate
Question 10.
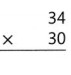
Answer:
The given expression is: 34 × 30
Now,
By using the Partial Products method,
34 × 30
= (30 + 4) × 30
= (30 × 30) + (4 × 30)
= 900 + 120
= 1,020
Estimate:
35 × 30
= (30 + 5) × 30
= (30 × 30) + (5 × 30)
= 900 + 150
= 1,050
Hence, from the above,
We can conclude that
The final product for the given expression is: 1,020
The final product is reasonalble when we compare to its estimate
Question 11.
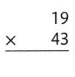
Answer:
The given expression is: 19 × 43
Now,
By using the Partial products method,
19 × 43
= (10 + 9) × (40 + 3)
= (10 × 40) + (10 × 3) + (9 × 40) + (9 × 3)
= 400 + 30 + 360 + 27
= 817
Estimate:
20 × 45
= 20 × (40 + 5)
= (20 × 40) + (20 × 5)
= 800 + 100
= 900
Hence, from the above,
We can conclude that
The final product for the given expression is: 817
The final product is reasonalble when we compare to its estimate
Question 12.
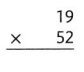
Answer:
The given expression is: 19 × 52
Now,
By using the Partial Products method,
19 × 52
= (10 + 9) × (50 + 2)
= (10 × 50) + (10 × 2) + (9 × 50) + (9 × 2)
= 500 + 20 + 450 + 18
= 988
Estimate:
20 ×50
= 2 × 10 × 5 × 10
= (2 × 5) × 100
= 10 × 100
= 1,000
Hence, from the above,
We can conclude that
The final product for the given expression is: 988
The final product is reasonalble when we compare to its estimate
Problem Solving
Question 13.
The Castillo de San Marcos is a Spanish fortress that was built between 1672 and 1695.

a. Rounded to the nearest ten thousand, how many pesos did it cost to build the fortress?
Answer:
It is given that
The Castillo de San Marcos is a Spanish fortress that was built between 1672 and 1695.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
It is given that it costs 138,375 pesos to build the given fortress
Now,
From the given number,
We can observe that
From the left of the digits’ positions, the 5th position value is “Ten-Thousand”
So,
The given number when it is rounded to the nearest ten thousand is: 140,000
Hence, from the above,
We can conclude that
The number we can obtain when we rounded the given number to the nearest ten thousand is: 140,000
It costs about 140,000 pesos to build the fortress
b. How many years did it take to build the fortress?
Answer:
It is given that
The Castillo de San Marcos is a Spanish fortress that was built between 1672 and 1695.
So,
The number of years did it take to build the fortress = 1695 – 1672
= 23 years
Hence, from the above,
We can conclude that it took 23 years to build a fortress
Question 14.
Construct Arguments A school has 2 large patios. One is rectangular and is 24 feet long by 18 feet wide. The other is square and each side is 21 feet long. Which patio has a greater area? Explain.
Answer:
It is given that
A school has 2 large patios. One is rectangular and is 24 feet long by 18 feet wide. The other is square and each side is 21 feet long
Now,
We know that,
The area of a rectangle = Length × Width
The area of a square = Side × Side
Now,
The area of a rectangular patio = 24 × 18
= (20 + 4) × (10 + 8)
= (20 × 10) + (20 × 8) + (4 × 10) + (4 × 8)
= 200 + 160 + 40 + 32
= 432 feet²
Now,
The area of a square patio = 21 × 21
= (20 + 1) × (20 + 1)
= (20 ×20) + (20 × 1) + (1 × 20) + (1 × 1)
= 400 + 20 + 20 + 1
= 441 feet²
So,
The area of a square patio > The area of a rectangular patio
Hence, from the above,
We can conclude that square patio has a greater area
Question 15.
Higher Order Thinking Show two ways! to break apart the factors, and then find the product of 14 × 22.
Answer:
The given expression is: 14 × 22
Now,
By using the Distributive Property of Multiplication,
Way 1:
14 × 22
= (10 + 4) × (20 + 2)
= (10 × 20) × (10 × 2) + (4 × 20) + (4 × 2)
= 200 + 20 + 80 + 8
= 308
Way 2:
14 × 22
= 14 × (20 + 2)
= (14 × 20) + (14 × 2)
= 280 + 28
= 308
Hence, from the above,
We can conclude that the product value for the given expression is: 308
Assessment Practice
Question 16.
Which set of numbers has the missing partial product and the final product?
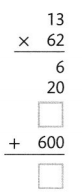
A. 210; 836
B. 18; 806
C. 180; 806
D. 18; 644
Answer:
The given expression is: 13 × 62
Now,
By using the Partial Products method,
13 × 62
= (10 + 3) × (60 + 2)
= (10 × 60) + (10 × 2) + (3 × 60) + (3 × 2)
= 600 + 20 + 180 + 6
= 806
Hence, from the above,
We can conclude that
The missing partial product and the final product are:

Question 17.
Select all the equations in which 12 is the missing factor
☐ b × 14 = 336
☐ b × 36 = 432
☐ 18 × b = 216
☐ 39 × b = 468
☐ 21 × b = 231
Answer:
The given equations are:
a. b × 14 = 336 b. b ×36 = 432 c. 18 × b = 216
d. 39 × b = 468 e. 21 × b = 231
Now,
a.
b × 14 = 336
b = \(\frac{336}{14}\)
b = 24
b.
b × 36 = 432
b = \(\frac{432}{36}\)
b = 12
c.
18 × b = 216
b = \(\frac{216}{18}\)
b = 12
d.
39 × b = 468
b = \(\frac{468}{39}\)
b = 12
e.
21 × b = 231
b = \(\frac{231}{21}\)
b = 11
Hence, from the above,
We can conclude that the expressions that have the missing factor 12 are:
Lesson 4.7 Problem Solving
Make Sense and Persevere
Solve & Share
Five students set a goal to raise $500 from their charity walk. Sponsors donated $25 for each mile walked. By how much did these students exceed or miss their goals? Solve this problem using any strategy you choose.
I can … make sense of problems and keep working if I get stuck.

Thinking Habits
Be a good thinker! These questions can help you.
1. What do I need to find?
2. What do I know?
3. What’s my plan for solving the problem?
4. What else can I try if I get stuck?
5. How can I check that my solution makes sense?
Answer:
It is given that
Five students set a goal to raise $500 from their charity walk. Sponsors donated $25 for each mile walked
Now,
The given table is:

Now,
From the given table,
The total number of miles walked by all the students = 5 + 5 + 3 + 4 + 4
= 21 miles
So,
The amount of money raised by the given students = (The total number of miles walked by all the students) × (The amount of money donated by the sponsor for each mile)
= 21 × 25
= (20 + 1) × (20 + 5)
= (20 × 20) + (20 × 5) + (1 × 20) + (1 × 5)
= 400 + 100 + 20 + 5
= $525
So,
$500 < $525
Now,
The amount of money exceeded = (The amount of money raised by all the students) – (The amount of money that have to be raised by the students)
= $525 – $500
= $25
Hence, from the above,
We can conclude that the amount of money exceeded is: $25
Look Back!
Make Sense and Persevere Is there more than one way to solve the problem? Explain.
Answer:
No, there is no other way to solve the above problem because we must find the total number of miles traveled by all the students and the amount of money raised by them by walking the number of miles
Essential Question
How Can You Make Sense of and Persevere in Solving Problems with More Than One Step?
Answer:
Mathematically, proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals
Visual Learning Bridge
The park has a large garden with a walkway around it. The park’s ground crew are going to paint the walkway. What is the area of the walkway?
What is a good plan for solving this problem?
I need to find the area of the garden and walkway together. Then I need to subtract to find only the area of the walkway.
How can I make sense of and solve this problem?
I can
- identify the quantities given.
- understand how the quantities are related.
- choose and implement an appropriate strategy.
- check to be sure my work and answer make sense.
First find the area of the whole park.
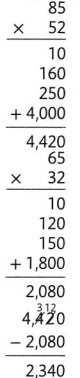
52 × 85 = p
4,420 = p
Next, find the area of the of the garden.
32 × 65 = g
2,080 = g
Subtract to find the area of the walkway. 4,420 – 2,080 = w
The area of the walkway is 2,340 square feet.
Convince Me!
Make Sense and Persevere Can you solve the problem a different way and still calculate the same answer? Explain.
Answer:
There is no other way to solve the above problem because we must calculate the area of the park and the area of the garden to find the area of the walkway since the walkway is enclosed between the park and the garden
Guided Practice
Make Sense and Persevere On her vacation, Julia filled 3 memory cards like the one shown. She printed 2 copies of each picture. How many pictures did Julia print?

Question 1.
What do you know and what do you need to find?
Answer:
It is given that
On her vacation, Julia filled 3 memory cards like the one shown. She printed 2 copies of each picture.
Now,
We know that,
a. The number of filled memory cards
b. The number of copies of each picture
c. The number of pictures in each memory card
We need to find:
a. The number of pictures in all the filled memory cards
b. The total number of copies of pictures
Question 2.
What steps might you take to solve the problem?
Answer:
The steps you have to take to solve the given problem are:
Step 1:
Find the number of pictures in all the filled cards by multiplying the number of filled memory cards and the number of pictures in each memory card
Step 2:
After finding the number of pictures in all the filled memory cards, find the number of copies of pictures by multiplying the number of pictures in all the filled memory cards with 2
Question 3.
How many pictures did Julia print? Explain.
Answer:
It is given that
On her vacation, Julia filled 3 memory cards like the one shown. She printed 2 copies of each picture.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
A memory card holds 28 pictures
So,
The number of pictures present in 3 memory cards = (The number of filled memory cards) × (The number of pictures in each memory card)
= 28 × 3
= (20 + 8) × 3
= (20 × 3) + (8 × 3)
= 60 + 24
= 84 pictures
Now,
The total number of copies of pictures = (The number of pictures present in 3 memory cards) × 2
= 84 × 2
= (80 + 4) × 2
= (80 × 2) + (4 × 2)
= 160 + 8
= 168 pictures
Hence, from the above,
We can conclude that
The total number of pictures did Julia print are: 168
Independent Practice
Make Sense and Persevere Jarrod delivers 63 newspapers each Monday through Saturday and 78 newspapers each Sunday. Last month consisted of 4 Sundays and 26 other days. How many newspapers did Jarrod deliver last month? Use Exercises 4-6 to solve this problem.
Question 4.
What strategies can you use to find how many newspapers Jarrod delivered last month?
Answer:
It is given that
Jarrod delivers 63 newspapers each Monday through Saturday and 78 newspapers each Sunday. Last month consisted of 4 Sundays and 26 other days
Now,
The strategy can you use to find the number of newspapers Jarrod delivered last month is:
Step 1:
Find the total number of newspapers Jarrod delivered on other days
Step 2:
Find the total number of newspapers Jarrod delivered only on Sunday
Step 3:
Add the results we obtained in Step 1 and Step 2
Question 5.
How are the quantities related?
Answer:
The given quantities are related in a way such as:
The total number of newspapers Jarrod delivered last month = (The total amount of newspapers Jarrod delivered on other days) + (The total number of newspapers Jarrod delivered on Sunday)
Question 6.
Explain how to solve the problem.
Answer:
The steps to solve the given problem are:
Step 1:
Find the total number of newspapers Jarrod delivered on other days
Step 2:
Find the total number of newspapers Jarrod delivered only on Sunday
Step 3:
Add the results we obtained in Step 1 and Step 2
Problem Solving
Performance Task
Uniforms
The Stillwater Storm soccer team consists of 16 players. Each player needs a uniform set. The uniform set includes two jerseys, a pair of shorts, and a pair of socks. The price for each separate item is shown. Nine of the players need a medium size and the others need a small size. If the team buys more than 10 sets, the team price for each set is $56. How much money is saved if the team buys all the uniform sets together rather than separately?

Question 7.
Reasoning What are the quantities in the problem and how are they related?
Answer:
It is given that
The Stillwater Storm soccer team consists of 16 players. Each player needs a uniform set. The uniform set includes two jerseys, a pair of shorts, and a pair of socks. The price for each separate item is shown. Nine of the players need a medium size and the others need a small size. If the team buys more than 10 sets, the team price for each set is $56
So,
The quantities related to the given problem are;
a. The price for 2 pairs of jerseys
b. The price for a pair of shorts
c. The price for a pair of socks
Hence,
The relation between the quantities are:
The total cost of a set = (The cost of 2 pairs of jerseys) + (The cost of a pair of shorts) + (The cost of a pair of socks)
Question 8.
Model with Math
Use the bar diagram to write an addition equation and find the total cost of the uniform sets when purchased separately. Then find the total cost if 10 sets or more are purchased.
When you make sense and persevere, you think about the amounts given.

Answer:
Question 9.
Be Precise What is the difference in cost if the team bought all the uniform sets together or if they bought them separately?
Answer:
Topic 4 Fluency Practice Activity
Find a Match
Work with a partner. Point to a clue. Read the clue. Look below the clues to find a match. Write the clue letter in the box next to the match. Find a match for every clue.
I can … add and subtract multi-digit whole numbers.
Clues
A. The difference is between 950 and 1,000.
B. The difference is exactly 913.
C. The sum is between 600 and 700.
D. The sum is exactly 500.
E. The difference is between 700 and 800.
F. The sum is greater than 300 but less than 400.
G. The sum is exactly 753.
H. The difference is exactly 413.

Topic 4 Vocabulary Review
Understand Vocabulary
Word List
- array
- compatible numbers
- estimate
- factors
- partial product
- product
- rounding
- variable
Question 1.
Cross out the numbers that are NOT factors of 12.
1
3
5
6
8
Answer:
We know that,
A “factor” is defined as a number or algebraic expression that divides another number or expression evenly i.e., with no remainder
Hence, from the above,
We can conclude that
The numbers that are not factors of 12 are:
![]()
Question 2.
Cross out the numbers that are NOT good estimates for the product of 17 × 23.
600
400
300
200
100
Answer:
The given expression is: 17 × 23
Now,
The estimate of the given expression is: 20 × 25 (or) 15 × 25 (or) 20 × 20
Hence, from the above,
We can conclude that
The numbers that are not good estimates for the product 17 × 23 are:
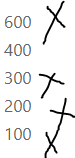
Question 3.
Cross out the numbers that are NOT partial products for 12 × 41.
2
10
18
80
400
Answer:
The given expression is: 12 × 41
Now,
By using the Partial products method,
12 × 41
= (10 + 2) × (40 +1)
= (10 × 40) + (10 × 1) + (2 × 40) + (2 × 1)
= 400 + 10 + 80 + 2
= 492
Hence, from the above,
We can conclude that
The numbers that are not the partial products for the given expression are:
Label each example with a term from the Word List.

Question 4.
 _________
_________
Answer:
The given figure is:

Now,
We know that,
An “Array” is a collection of rows and columns
Hence, from the above,
We can conclude that the term that is sutable for the given figure is: Array
Question 5.
n. __________
Answer:
We know that,
A “Variable”, in algebra, is a symbol (usually a letter) standing in for an unknown numerical value in an equation
Hence, from the above,
We can conclude that the term that is best suitable for the given problem is: Variable
Question 6.
2,318 to the nearest thousand is 2,000 _________
Answer:
We know that,
The “Rounding-off” is a mathematical technique of adjusting the number’s digits to make the number easier to use during calculations
Hence, from the above,
We can conclude that the term that is suitable for the given sentence is: Rounding
Question 7.
3 × 4 = 12 _________
Answer:
We know that,
A “Product” is a final value when we multiply the number of factors
Hence, from the above,
We can conclude that the term that is suitable for the given problem is: product
Use Vocabulary in Writing
Question 8.
Alicia needs to find 23 × 47. Use at least 3 terms from the Word List to explain how Alicia might find 23 × 47.
Answer:
It is given that
Alicia needs to find 23 × 47
Hence, from the above,
We can conclude that
The three words from the given word list to explain how Alicia might find the product for the given expression is:
a. Compatible numbers
b. Estimate
c. partial Product
Topic 4 Reteaching
Set A pages 129-132
Use place-value strategies to find 20 × 80.
Think about the pattern.
20 × 80 = 2 tens × 8 tens
= 16 hundreds
= 1,600
50 × 40 = (5 × 10) × (4 × 10)
= (5 × 4) × (10 × 10)
= 20 × 100
= 2,000
Remember when the product of a basic fact has a zero, there is one more zero in the answer.
Use a pattern to find each product.
Question 1.
40 × 10
Answer:
The given expression is: 40 × 10
Now,
By using the Place-value method,
40 × 10
= 4 × 10 × 1 × 10
= (4 × 1) × 100
= 400
Hence, from the above,
We can conclude that the product value for the given expression is: 400
Question 2.
60 × 20
Answer:
The given expression is: 60 × 20
Now,
By using the Place-value method,
60 × 20
= 6 × 10 × 2 × 10
= (6 × 2) × 100
= 1,200
Hence, from the above,
We can conclude that the product value for the given expression is: 1,200
Question 3.
80 × 50
Answer:
The given expression is: 80 × 50
Now,
By using the Place-value method,
80 × 50
= 8 × 10 × 5 × 10
= (8 × 5) × 100
= 4,000
Hence, from the above,
We can conclude that the product value for the given expression is: 4,000
Question 4.
30 × 90
Answer:
The given expression is: 30 × 90
Now,
By using the Place-value method,
30 × 90
= 3 × 10 × 9 × 10
= (3 × 9) × 100
= 2,700
Hence, from the above,
We can conclude that the product value for the given expression is: 2,700
Question 5.
80 × 70
Answer:
The given expression is: 80 × 70
Now,
By using the Place-value method,
80 × 70
= 8 × 10 × 7 × 10
= (8 × 7) × 100
= 5,600
Hence, from the above,
We can conclude that the product value for the given expression is: 5,600
Question 6.
60 × 60
Answer:
The given expression is: 60 × 60
Now,
By using the Place-value method,
60 × 60
= 6 × 10 × 6 × 10
= (6 × 6) × 100
= 3,600
Hence, from the above,
We can conclude that the product value for the given expression is: 3,600
Question 7.
80 × 30
Answer:
The given expression is: 80 × 30
Now,
By using the Place-value method,
80 × 30
= 8 × 10 × 3 × 10
= (8 × 3) × 100
= 2,400
Hence, from the above,
We can conclude that the product value for the given expression is: 2,400
Question 8.
20 × 50
Answer:
The given expression is: 20 × 50
Now,
By using the Place-value method,
20 × 50
= 2 × 10 × 5 × 10
= (2 × 5) × 100
= 1,000
Hence, from the above,
We can conclude that the product value for the given expression is: 1,000
Set B pages 133-136
Use an array or an area model to multiply 20 × 14.
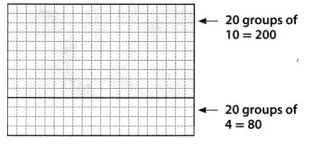
200 + 80 = 280
So, 20 × 14 = 280.
Remember you can draw arrays or area models to represent multiplication problems.
Draw a model to find each product.
Question 1.
10 × 23
Answer:
The given expression is: 10 × 23
Now,
By using the Area-model,
10 × 23
= 10 × (20 + 3)
= (10 × 20) + (10 × 3)
= 200 + 30
= 230

Hence, from the above,
We can conclude that the product value for the given expression is: 230
Question 2.
16 × 20
Answer:
The given expression is: 16 × 20
Now,
By using the Area-model,
16 × 20
= (10 + 6) × 20
= (10 × 20) + (6 × 20)
= 200 + 120
= 320

Hence, from the above,
We can conclude that the product value for the given expression is: 320
Set C pages 137-140
Use compatible numbers to estimate 28 × 19.
28 is close to 25.
19 is close to 20.
If 25 × 2 = 50, then
25 × 20 = 500.
So, 28 × 19 is about 500.
Remember that compatible numbers are numbers that are easy to compute mentally.
Estimate each product.
Question 1.
29 × 31
Answer:
The given expression is: 29 × 31
Now,
By using the estimation of the Compatible number,
The given expression will become: 30 × 30
So,
30 × 30
= 3 × 10 × 3 × 10
= (3 × 3) × 100
= 9 × 100
= 900
Hence, from the above,
We can conclude that the product value for the given expression is about 900
Question 2.
42 × 49
Answer:
The given expression is: 42 × 49
Now,
By using the estimation of the Compatible number,
The given expression will become: 40 × 50
So,
40 × 50
= 4 × 10 × 5 × 10
= (4 × 5) × 100
= 20 × 100
= 2,000
Hence, from the above,
We can conclude that the product value for the given expression is about 2,000
Question 3.
73 × 18
Answer:
The given expression is: 73 × 18
Now,
By using the estimation of the Compatible number,
The given expression will become: 70 × 20
So,
70 × 20
= 7 × 10 × 2 × 10
= (7 × 2) × 100
= 14 × 100
= 1,400
Hence, from the above,
We can conclude that the product value for the given expression is about 1,400
Question 4.
24 × 38
Answer:
The given expression is: 24 × 38
Now,
By using the estimation of the Compatible number,
The given expression will become: 25 × 40
So,
25 × 40
= (20 +5) × 40
= (20 × 40) + (5 × 40)
= 800 + 200
= 1,000
Hence, from the above,
We can conclude that the product value for the given expression is about 1,000
Question 5.
19 × 31
Answer:
The given expression is: 19 × 31
Now,
By using the estimation of the Compatible number,
The given expression will become: 20 × 30
So,
20 × 30
= 2 × 10 × 3 × 10
= (2 × 3) × 100
= 6 × 100
= 600
Hence, from the above,
We can conclude that the product value for the given expression is about 600
Question 6.
63 × 87
Answer:
The given expression is: 63 × 87
Now,
By using the estimation of the Compatible number,
The given expression will become: 60 × 90
So,
60 × 90
= 6 ×10 ×9 × 10
= (6 × 9) × 100
= 54 × 100
= 5,400
Hence, from the above,
We can conclude that the product value for the given expression is about 5,400
Set D pages 141-144
Find 14 × 12. Draw a 14 × 12 array.
Separate each factor into tens and ones. Color each section a different color. Add each part to find the product.
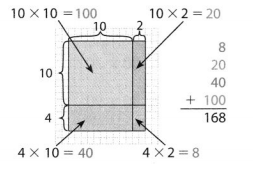
Remember when you break apart a multiplication problem, you can solve the simpler problems in any order and the answer will remain the same.
Question 1.
14 × 32
Answer:
The given expression is: 14 × 32
Now,
By using the Partial Products method,
14 × 32
= (10 + 4) × (30 + 2)
= (10 × 30) + (10 × 2) + (4 × 30) + (4 × 2)
= 300 + 20 + 120 + 8
= 448
Hence, from the above,
We can conclude that the product value for the given expression is: 448
Question 2.
64 × 12
Answer:
The given expression is: 64 × 12
Now,
By using the Partial Products method,
64 × 12
= (60 + 4) × (10 + 2)
= (60 × 10) + (60 × 2) + (4 × 10) + (4 × 2)
= 600 + 120 + 40 + 8
= 768
Hence, from the above,
We can conclude that the product value for the given expression is: 768
Question 3.
56 × 17
Answer:
The given expression is: 56 × 17
Now,
By using the Partial Products method,
56 × 17
= (50 + 6) × (10 + 7)
= (50 × 10) + (50 × 7) + (6 × 10) + (6 × 7)
= 500 + 350 + 60 + 42
= 952
Hence, from the above,
We can conclude that the product value for the given expression is: 952
Question 4.
72 × 15
Answer:
The given expression is: 72 × 15
Now,
By using the Partial Products method,
72 × 15
= (70 + 2) × (10 + 5)
= (70 × 10) + (70 × 5) + (2 × 10) + (2 × 5)
= 700 + 350 + 20 + 10
= 1,080
Hence, from the above,
We can conclude that the product value for the given expression is: 1,080
Question 5.
26 × 63
Answer:
The given expression is: 26 × 63
Now,
By using the Partial Products method,
26 × 63
= (20 + 6) × (60 + 3)
= (20 × 60) + (20 × 3) + (6 × 60) + (6 × 3)
= 1,200 + 60 + 360 + 18
= 1,638
Hence, from the above,
We can conclude that the product value for the given expression is: 1,638
Question 6.
47 × 27
Answer:
The given expression is: 47 × 37
Now,
By using the Partial Products method,
47 × 37
= (40 + 7) × (30 + 7)
= (40 × 30) + (40 × 7) + (7 × 30) + (7 × 7)
= 1,200 + 280 + 210 + 49
= 1,739
Hence, from the above,
We can conclude that the product value for the given expression is: 1,739
Question 7.
19 × 51
Answer:
The given expression is: 19 × 51
Now,
By using the Partial Products method,
19 × 51
= (10 + 9) × (50 + 1)
= (10 × 50) + (10 × 1) + (9 × 50) + (9 × 1)
= 500 + 10 + 450 + 9
= 969
Hence, from the above,
We can conclude that the product value for the given expression is: 969
Question 8.
12 × 56
Answer:
The given expression is: 12 × 56
Now,
By using the Partial Products method,
12 × 56
= (10 + 2) × (50 + 6)
= (10 × 50) + (10 × 6) + (2 × 50) + (2 × 6)
= 500 + 60 + 100 + 12
= 662
Hence, from the above,
We can conclude that the product value for the given expression is: 662
Question 9.
76 × 23
Answer:
The given expression is: 76 × 23
Now,
By using the Partial Products method,
76 × 23
= (70 + 6) × (20 + 3)
= (70 × 20) + (70 × 3) + (6 × 20) + (6 × 3)
= 1,400 + 210 + 120 + 18
= 1,748
Hence, from the above,
We can conclude that the product value for the given expression is: 1,748
Question 10.
84 × 37
Answer:
The given expression is: 84 × 37
Now,
By using the Partial Products method,
84 × 37
= (80 + 4) × (30 + 7)
= (80 × 30) + (80 × 7) + (4 × 30) + (4 × 7)
= 2,400 + 560 + 120 + 28
= 3,108
Hence, from the above,
We can conclude that the product value for the given expression is: 3,108
Question 11.
14 × 72
Answer:
The given expression is: 14 × 72
Now,
By using the Partial Products method,
14 × 72
= (10 + 4) × (70 + 2)
= (10 × 70) + (10 × 2) + (4 × 70) + (4 × 2)
= 700 + 20 + 280 + 8
= 1,008
Hence, from the above,
We can conclude that the product value for the given expression is: 1,008
Question 12.
21 × 51
Answer:
The given expression is: 21 × 51
Now,
By using the Partial Products method,
21 × 51
= (20 + 1) × (50 + 1)
= (20 × 50) + (20 × 1) + (1 × 50) + (1 × 1)
= 1,000 + 20 + 50 + 1
= 1,071
Hence, from the above,
We can conclude that the product value for the given expression is: 1,071
Set E pages 145-152
Use the Distributive Property to find 13 × 55.
13 × 55
= (10 + 3) (50 + 5)
= (10 + 3) 50 + (10 + 3) × 5
= (10 × 50) + (3 × 50) + (10 × 5) + (3 × 5)
= 500 + 150 + 50 + 15
= 715
Remember you can break numbers apart in more than one way when using the Distributive Property to solve multiplication problems.
Question 1.
12 × 19
Answer:
The given expression is: 12 × 19
Now,
By using the Distributive Property of Multiplication,
12 × 19
= (10 + 2) × (10 + 9)
= (10 × 10) + (10 × 9) + (2 × 10) + (2 × 9)
= 100 + 90 + 20 + 18
= 228
Hence, from the above,
We can conclude that the product value for the given expression is: 228
Question 2.
38 × 12
Answer:
The given expression is: 38 × 12
Now,
By using the Distributive Property of Multiplication,
38 × 12
= (30 + 8) × (10 + 2)
= (30 × 10) + (30 × 2) + (8 × 10) + (8 × 2)
= 300 + 60 + 80 + 16
= 456
Hence, from the above,
We can conclude that the product value for the given expression is: 456
Question 3.
19 × 25
Answer:
The given expression is: 19 × 25
Now,
By using the Distributive Property of Multiplication,
19 × 25
= (10 + 9) × (20 + 5)
= (10 × 20) + (10 × 5) + (9 × 20) + (9 × 5)
= 200 + 50 + 180 + 45
= 475
Hence, from the above,
We can conclude that the product value for the given expression is: 475
Question 4.
45 × 23
Answer:
The given expression is: 45 × 23
Now,
By using the Distributive Property of Multiplication,
45 × 23
= (40 + 5) × (20 + 3)
= (40 × 20) + (40 × 3) + (5 × 20) + (5 × 3)
= 800 + 120 + 100 + 15
= 1,035
Hence, from the above,
We can conclude that the product value for the given expression is: 1,035
Question 5.
62 × 11
Answer:
The given expression is: 62 × 11
Now,
By using the Distributive Property of Multiplication,
62 × 11
= (60 + 2) × (10 + 1)
= (60 × 10) + (60 × 1) + (2 × 10) + (2 × 1)
= 600 + 60 + 20 + 2
= 682
Hence, from the above,
We can conclude that the product value for the given expression is: 682
Question 6.
46 × 26
Answer:
The given expression is: 46 × 26
Now,
By using the Distributive Property of Multiplication,
46 × 26
= (40 + 6) × (20 + 6)
= (40 × 20) + (40 × 6) + (6 × 20) + (6 × 6)
= 800 + 240 + 120 + 36
= 1,196
Hence, from the above,
We can conclude that the product value for the given expression is: 1,196
Set F pages 153-156
Think about these questions to help you make sense and persevere in solving problems.
Thinking Habits
- What do I need to find?
- What do I know?
- What’s my plan for solving the problem?
- What else can I try if I get stuck?
- How can I check that my solution makes sense?

Remember to use the information given to solve the problem.
Rose visited 14 cities on her vacation. She bought 8 souvenirs in each city to send to her friends. Rose paid $2 in postage for each souvenir to be sent.
Question 1.
What hidden question do you need to answer to find how much it cost Rose to send all of the souvenirs?
Answer:
It is given that
Rose visited 14 cities on her vacation. She bought 8 souvenirs in each city to send to her friends. Rose paid $2 in postage for each souvenir to be sent.
So,
The hidden question you need to answer to find how much it cost Rose to send all of the souvenirs is:
a. What is the total number of souvenirs Rose bought from all the cities?
Question 2.
How much did Rose spend on the souvenirs and postage?
Answer:
It is given that
Rose visited 14 cities on her vacation. She bought 8 souvenirs in each city to send to her friends. Rose paid $2 in postage for each souvenir to be sent.
So,
The total number of souvenirs Rose bought from all the cities = (The total number of cities) × (The number of souvenirs bought by Rose in each city)
= 14 × 8
= (10 +4) × 8
= (10 × 8) + (4 × 8)
= 80 + 32
= 112 souvenirs
So,
The total cost to send all the souvenirs in postage by Rose = (The total number of souvenirs Rose bought) × (The cost of each souvenir to be sent by Rose in postage)
= 112 × $2
= (100 + 2) × 2
= (100 × 2) + (2 × 2)
= 200 + 4
= $204
Hence, from the above,
We can conclude that the total money spent by Rose on souvenirs and postage is: $204
Topic 4 Assessment Practice
Question 1.
Don works 18 hours a week. Which expression shows a good way to use rounding to estimate how many hours Don will work in 52 weeks?
A. 10 × 50
B. 10 × 600
C. 20 × 50
D. 18 × 60
Answer:
It is given that Don works 18 hours a week
So,
The number of hours Don will work in 52 weeks = (The number of hours Don works in a week) × (The number of weeks)
= 18 × 52
Now,
By using the rounding-off estimation,
The number of hours Don will work in 52 weeks is about 20 × 50
Hence,
The number of hours Don will work in 52 weeks is about:

Question 2.
Find the product 21 × 40. Show your work.
Answer:
The given expression is: 21 × 40
Now,
By using the Distributive Property of Multiplication,
21 × 40
= (20 + 1) × 40
= (20 × 40) + (1 × 40)
= 800 + 40
= 840
Hence, from the above,
We can conclude that the product value for the given expression is: 840
Question 3.
The product of two factors is 2,000. One of the factors is 50. What is the other factor?
A. 20
B. 40
C. 200
D. 400
Answer:
It is given that
The product of two factors is 2,000. One of the factors is 50
Now,
Let the other factor be x
So,
50 × x = 2,000
x = \(\frac{2,000}{50}\)
x = 40
Hence, from the above,
We can conclude that the other factor is:

Question 4.
Select all the expressions that are equal to 260.
☐ 23 × 10
☐ 20 × 10 + 3 × 10
☐ 13 × 20
☐ 1 × 20 + 3 × 20
☐ 10 × 20 + 3 × 20
Answer:
The given expressions are:
a. 23 × 10
b. (20 × 10) + (3 × 10)
c. 13 × 20
d. (1 × 20) + (3 × 20)
e. (10 × 20) + (3 × 20)
So,
The product values for the given expressions are:
a.
23 × 10
= (20 + 3) × 10
= (20 × 10) + (3 × 10)
= 200 + 30
= 230
b.
(20 × 10) + (3 × 10)
= 230
c.
13 × 20
= (10 + 3) × 20)
= (10 × 20) + (3 × 20)
= 200 + 60
= 260
d.
(1 × 20) + (3 × 20)
= 70
e.
(10 × 20) + (3 × 20)
= 200 + 60
= 260
Hence, from the above,
We can conclude that all of the expressions that are equal to 260 are:
Question 5.
A florist makes centerpieces. He puts 18 roses in each centerpiece. Which is the best way to use compatible numbers to estimate the number of roses the florist needs for 24 centerpieces? What is the exact number of roses?
A. 10 × 25 = 250; 360
B. 20 × 25 = 500; 432
C. 25 × 30 = 750; 672
D. 30 × 30 = 900; 784
Answer:
It is given that
A florist makes centerpieces. He puts 18 roses in each centerpiece
So,
The number of roses the florist needs for 24 centerpieces = (The number of centerpieces) × (The number of roses in each centerpiece)
= 18 × 24
Now,
By using the partial Products method,
18 × 24
= (10 + 8) × (20 + 4)
= (10 × 20) + (10 × 4) + (8 × 20) + (8 × 4)
= 200 + 40 + 160 + 32
= 432
Now,
Estimate:
18 × 24
= 20 × 25 [Estimate of the total number of roses]
Now,
By using the Partial Products method,
20 × 25
= 20 × (20 + 5)
= (20 × 20) + (20 × 5)
= 400 + 100
= 500
Hence, from the above,
We can conclude that
The estimated and the exact number of the total number of roses in 24 centerpieces are:
Question 6.
Margo hiked 12 miles 13 times last month. She hiked 14 miles 12 times this month.
A. Draw arrays or area models to find the number of miles Margo hiked during the past two months.
Answer:
It is given that
Margo hiked 12 miles 13 times last month. She hiked 14 miles 12 times this month.
So,
The number of miles Margo hiked during the past month = (The number of miles margo hiked past month) × (The number of times Margo hiked during the past month)
= 12 × 13
= (10 + 2) × (10 + 3)
The number of miles Margo hiked during this month = (The number of miles margo hiked this month) × (The number of times Margo hiked during this month)
= 14 × 12
= (10 + 4) × (10 + 2)
Hence, from the above,
The representations of the area models for the number of miles Margo hiked this month and the past month is:
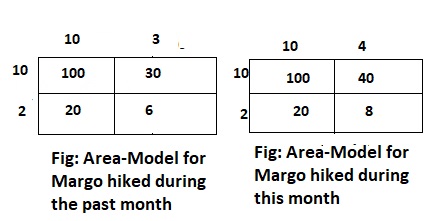
B. Write and solve equations to represent your arrays or area models.
Answer:
From part (A),
We know that,
The number of miles Margo hiked during the past month = (The number of miles margo hiked past month) × (The number of times Margo hiked during the past month)
= 12 × 13
The number of miles Margo hiked during this month = (The number of miles margo hiked this month) × (The number of times Margo hiked during this month)
= 14 × 12
So,
By using the Partial Products method,
12 × 13
= (10 + 2) × (10 + 3)
= (10 × 10) + (10 × 3) + (2 × 10) + (2 × 3)
= 100 + 30 + 20 + 6
= 156 miles
So,
By using the Partial products method,
14 × 12
= (10 + 4) × (10 + 2)
= (10 × 10) + (10 × 2) + (4 × 10) + (4 × 2)
= 100 + 20 + 40 + 8
= 168 miles
Hence, from the above,
We can conclude that
The number of miles Margo hiked the past month is: 156 miles
The number of miles Margo hiked this month is: 168 miles
Question 7.
Liz makes necklaces. Each has 16 beads. Use the numbers in the box to complete the table.
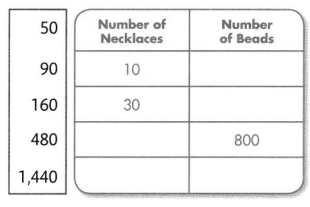
Answer:
It is given that
Liz makes necklaces. Each has 16 beads
So,
The total number of beads = (The number of necklaces) × (The number of beads in each necklace)
The number of beads in each necklace = \(\frac{The total number of beads}{The number of encklaces}\)
Hence from the above,
We can conclude that
The completed table is:
Question 8.
Justine’s plant shop has 7 shelves. Each shelf holds 18 plants. Suppose she adds 2 more shelves to the shop. Write and solve equations to find the number of plants all of the shelves can hold. Check if your answer is reasonable.
Answer:
It is given that
Justine’s plant shop has 7 shelves. Each shelf holds 18 plants. Suppose she adds 2 more shelves to the shop.
So,
The total number of shelves in the shop = 7 + 2
= 9 shelves
Now,
The total number of plants all of the shelves can hold = (The total number of shelves) × (The number of plants each shelf can hold)
= 9 × 18
= 9 × (10 + 8)
= (9 × 10) + (9 × 8)
= 90 + 72
= 162 plants
Estimate:
10 × 20
= 1× 10 × 2 × 10
= (1 × 2) × 100
= 2 × 100
= 200 plants
Hence, from the above,
We can conclude that the total number of plants all of the shelves can hold is exactly: 162 plants
As the estimated and the exact answer does not have much difference, the answer is reasonable
Question 9.
Jack’s landscape service charges $78 to plant a tree. What is the total cost to plant 18 trees on Tuesday and 23 trees on Wednesday? Write and solve equations.
Answer:
It is given that
Jack’s landscape service charges $78 to plant a tree
So,
The total cost to plant the trees on Tuesday = (The total number of trees planted on Tuesday) × (The cost to plant each tree)
= 18 × 78
= (10 + 8) × (70 + 8)
= (10 × 70) + (10 × 8) + (8 × 70) + (8 × 8)
= 700 + 80 +560 + 64
= $1,404
So,
The total cost to plant the trees on Wednesday = (The total number of trees planted on Wednesday) × (The cost to plant each tree)
= 23 × 78
= (20 + 3) × (70 + 8)
= (20 × 70) + (20 × 8) + (3 × 70) + (3 × 8)
= 1,400 + 160 +210 + 24
= $1,794
Hence, from the above,
We can conclude that
The total cost to plant trees on Tuesday is: $1,404
The total cost to plant trees on Wednesday is: $1,794
Question 10.
Which of the following uses properties of operations to help find 27 × 14?
A. 20 + 7 + 10 + 4
B. 20 × 7 × 10 × 4
C. 27 + 14
D. (20 + 7) (10 + 4)
Answer:
The given expression is: 27 × 14
Now,
By using the Distributive Property of Multiplication,
27 × 14
= (20 + 7) × (10 + 4)
Hence, from the above,
We can conclude that the properties of operations used to find 27 × 14 are:
Question 11.
Lorin drew an area model to find 19 × 15. Write the partial product for each rectangle in the area model.
Answer:
The given expression is: 19 × 15
Now,
By using the Partial products method,
19 × 15
= (10 + 9) × (10 + 5)
= (10 × 10) + (10 × 5) + (9 × 10) + (9 × 5)
= 100 + 50 + 90 + 45
= 285
Hence, from the above,
We can conclude that the partial products for the given expression are:
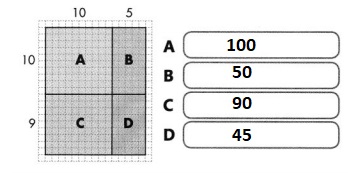
Question 12.
The biggest painting in an art show is 31 inches long and 28 inches wide. The smallest painting is 14 inches long and 11 inches wide. What is the difference between the areas of the two paintings? Use equations to show your work.
________ square inches
Answer:
It is given that
The biggest painting in an art show is 31 inches long and 28 inches wide. The smallest painting is 14 inches long and 11 inches wide.
Now,
The area of the biggest painting = Length × Width
= 31 × 28
= (30 + 1) × (20 + 8)
= (30 × 20) + (30 × 8) + (1 × 20) + (1 × 8)
= 600 +240 + 20 + 8
= 868 inches²
Now,
The area of the samllest painting = Length × Width
= 14 × 11
= (10 + 4) × (10 + 1)
= (10 × 10) + (10 × 1) + (4 × 10) + (4 × 1)
= 100 + 10 + 40 + 4
= 154 inches²
So,
The difference between the areas of the biggest painting and the smallest painting = 868 – 154
= 714 square inches
Hence, from the above,
We can conclude that the difference between the areas between the two paintings is: 714 square inches
Topic 4 Performance Task
Raising Money
The fourth-grade students at Skyline School sold candles to raise money. The money raised will be used to buy toys for children who live in a group home. The Candle Fundraiser table shows how many candles each class sold.
 Beehive candles sell for $20 each. The class raised $12 for each candle sold.
Beehive candles sell for $20 each. The class raised $12 for each candle sold.
 Soybean candles sell for $22 each. The class raised $14 for each candle sold.
Soybean candles sell for $22 each. The class raised $14 for each candle sold.

Question 1.
About how much money did the fourth-grade students raise? Explain.
Answer:
It is given that
Beehive candles sell for $20 each. The class raised $12 for each candle sold.
Soybean candles sell for $22 each. The class raised $14 for each candle sold.
So,
The total cost of each Beehive candle = $20 + $12
= $32
The total cost of each Soybean candle = $22 + $14
= $36
Now,
The given table is:

So,
The money raised by the fourth-grade students = (The total number of candles sold) + (The amount raised for each candle)
= (32 × 32) + (25 × 36) + (18 × 36) + (47 × 32)
= 1,024 + 900 + 648 + 1,504
= $4,076
Hence, from the above,
We can conclude that
The total money raised by the fourth-grade students is: $4,076
Question 2.
The school secretary needs to know exactly how much money was raised.
Part A
How much money did Ms. Schmidt’s class raise? Use an area model and partial products to find the product.
Answer:
The given data is:

Now,
From the given table,
We can observe that
The amount of money raised by Mr. Schmidt’s class = (The number of candles sold by Mr.Schmidt’s class) × (The total amount raised for each candle sold)
= 25 × 36
Now,
By using the area-Model,
25 × 36
= (20 + 5) × (30 + 6)
= (20 × 30) + (20 × 6) + (5 × 30) + (5 × 6)
= 600 + 120 + 150 + 30
= 900
Hence, from the above,
We can conclude that the money raised by Mr. Schmidt’s class is: $900
Part B
How much money did Ms. Picard’s class raise? Use the Distributive Property to find the product.
Answer:
The given data is:

Now,
From the given table,
We can observe that
The amount of money raised by Ms. Picard’s class = (The number of candles sold by Ms.Picord’s class) × (The total amount raised for each candle sold)
= 18 × 36
Now,
By using the Distributive Property of Multiplication,
18 × 36
= (10 + 8) × (30 + 6)
= (10 × 30) + (10 × 6) + (8 × 30) + (8 × 6)
= 300 + 60 + 240 + 48
= 648
Hence, from the above,
We can conclude that the amount of money raised by Ms. Picard’s class is: $648
Part C
How much money did the fourth-grade students raise? Explain.
Answer:
It is given that
Beehive candles sell for $20 each. The class raised $12 for each candle sold.
Soybean candles sell for $22 each. The class raised $14 for each candle sold.
So,
The total cost of each Beehive candle = $20 + $12
= $32
The total cost of each Soybean candle = $22 + $14
= $36
Now,
The given table is:

So,
The money raised by the fourth-grade students = (The total number of candles sold) + (The amount raised for each candle)
= (32 × 32) + (25 × 36) + (18 × 36) + (47 × 32)
= 1,024 + 900 + 648 + 1,504
= $4,076
Hence, from the above,
We can conclude that
The total money raised by the fourth-grade students is: $4,076
Part D
Is the total amount of money raised from Part C reasonable based on the estimate you found in Exercise 1? Explain.
Answer:
From part (C) and Exercise 1,
We can observe that
In Exercise 1,
We found out the total amount of money raised by the fourth-grade students
In part (C),
We found out the total amount of money raised by the fourth-grade students
So,
From the above,
We can observe that
We found the same value in both
Hence, from the above,
We can conclude that
The total amount of money raised from Part C is reasonable based on the estimate you found in Exercise 1
The fourth-grade students at Skyline School decide to buy the toys shown.

Buying Toys
- They buy 68 toys in all.
- They buy at least 25 of each type.
- They cannot spend more money than was raised.
Question 3.
How many of each toy can be bought following the directions from the Buying Toys list? Find the total cost for the numbers you choose.
Answer:
It is given that
The cost of each teddy bear is: $17
The cost of each scooter is: $28
The total number of toys are: 68
Now,
Let there be an equal number of teddy bears and scooters
So,
The number of each toy = \(\frac{68}{2}\)
= 34
So,
The total cost of the toys = (34 × 17) + (34 × 28)
= $1,530
Hence, from the above,
We can conclude that
The total cost for the number of toys you choose is: $1,530
