Go through the enVision Math Common Core Grade 4 Answer Key Topic 8 Extend Understanding of Fraction Equivalence and Ordering regularly and improve your accuracy in solving questions.
enVision Math Common Core 4th Grade Answers Key Topic 8 Extend Understanding of Fraction Equivalence and Ordering
Essential Questions:
What are some ways to name the same part of a whole?
How can you compare fractions with unlike numerators and denominators?

Answer:
Fraction,
To compare fractions with unlike numerators and denominators we
multiply the numerator and denominator of one fraction by the same number,
so both fractions will have the same denominator then if denominators
of both are same we compare numerators,
Explanation:
A part or parts of a whole is called fraction,
A number that names part of a whole or part of a group is called fraction.
Fractions represent equal parts of a whole or a collection.
If two fractions have different numerators and denominators
it is difficult to determine which fraction is larger. So we multiply
the numerator and denominator of one fraction by the same number,
so both fractions will have the same denominator.
For example, if 5/12 and 1/3 are being compared,
1/3 should be multiplied by 4/4. It does not change the value of
1/3 to be multiplied by 4/4 (which is equal to 1) because any number
multiplied by 1 is still the same number.
After the multiplication (1/3 * 4/4 = 4/12),
the comparison can be made between 5/12 and 4/12.
We may have to multiply both fractions by different numbers
to produce the same denominator for both fractions.
For example if 2/3 and 3/4 are compared, we need to
multiply 2/3 by 4/4 to give 8/12 and multiply 3/4 by 3/3 to give 9/12.
The fraction 3/4 which is equal to 9/12 is larger than 2/3 which is equal to 8/12.
The fraction with the larger numerator is the larger fraction if the
denominators are the same.
Envision STEM Project: Senses
Do Research Use the Internet or other resources to find information
about how animals use special senses, such as echolocation,
electricity, or magnetism. Include information about where the
animal lives and how the special sense is used.
Journal: Write a Report Include what you found. Also in your report:
- Some spiders rely on sight to receive information about food.
Most spiders have 8 eyes. Draw a picture of a spider with many eyes,
using some shaded circles as eyes and some empty circles as eyes. - Write a fraction that names shaded spider eyes to total spider eyes.
Write three equivalent fractions.
Answer:
Senses also allow animals to see, feel, hear, taste, and smell,
Echolocation : Using reflected sound animals hunt, Ex: Bats,
Explanation:
Senses also allow animals to see, feel, hear, taste, and smell,
Information from these senses is transferred to the brain,
allowing reaction and interpretation of external stimuli.
Echolocation is a technique used by bats, dolphins and
other animals to determine the location of objects using
reflected sound. This allows the animals to move around
in pitch darkness, so they can navigate, hunt, identify friends and
enemies, and avoid obstacles.
Saltwater creatures, such as sharks, rays, and even one
species of dolphin also rely on special sensory organs to
hunt underwater. Though less common, land animals such as
the bumblebee, platypus and echidna harness electricity to
forage and communicate.

Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- denominator
- fraction
- numerator
- unit fraction
Question 1.
A symbol, such as \(\frac{2}{3}\) or \(\frac{1}{2}\),
used to name part of a whole, part of a set, or a
location on a number line is called a __fraction_______.
Answer:
Fraction
Explanation:
A numerical quantity that is not a whole number.
Question 2.
The number above the fraction bar in a fraction is called the ___numerator______.
Answer:
Numerator
Explanation:
The number above the line in a fraction showing how many of the parts
indicated by the denominator are taken or the term of a fraction,
usually above the line, that indicates the number of equal parts that are to
be added together; the dividend placed over a divisor is called numerator.
Question 3.
A fraction with a numerator of 1 is called a ____Unit Fraction______
Answer:
Unit Fraction
Explanation:
A unit fraction is any fraction with 1 as its numerator and whole number as its denominator.
Unit Fractions
Write a fraction for each statement.
Question 4.
2 copies of \(\frac{1}{6}\) is ___1/3_____.
Answer:
1/3 or \(\frac{1}{3}\)
Explanation:
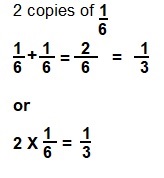
Question 5.
3 copies of \(\frac{1}{3}\) is _______
Answer:
1
Explanation:
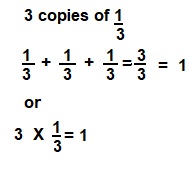
Question 6.
4 copies of \(\frac{1}{5}\) is __4/5______.
Answer:
4/5 or \(\frac{4}{5}\)
Explanation:
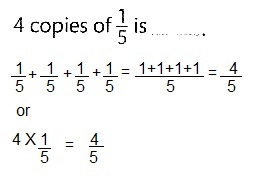
Question 7.
2 copies of \(\frac{1}{10}\) to is ___1/5______.
Answer:
1/5 or \(\frac{1}{5}\)
Explanation:
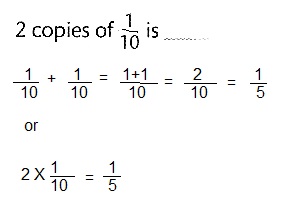
Question 8.
7 copies of \(\frac{1}{12}\) is ____7/12______
Answer:
7/12 or \(\frac{7}{12}\)
Explanation:
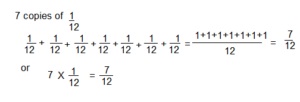
Question 9.
3 copies of \(\frac{1}{8}\) is ____3/8_______
Answer:
3/8 or \(\frac{3}{8}\)
Explanation:
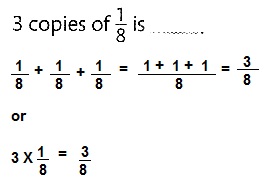
Fraction Concepts
Write the fraction shown by each figure.
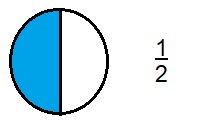
Question 10.

Answer:
\(\frac{1}{2}\)
Explanation:
In the given circle the whole is equally divided into 2 halves and one part is shaded.
So fraction is 1/2 or \(\frac{1}{2}\)
Question 11.

Answer:
\(\frac{3}{8}\)
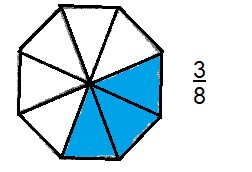
Explanation:
In given picture the whole is equally divided into 8 parts and 3 parts are shaded.
So the fraction is 3/8 or \(\frac{3}{8}\)
Question 12.

Answer:
1 (Whole)
Explanation:
The whole is divided into 6 equal parts and no shaded parts.
So 6/6 or \(\frac{6}{6}\) = 1.

Question 13.

Answer:
\(\frac{1}{3}\)
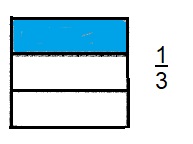
Explanation:
The given whole is divided equally into 3 parts, among that one is shaded.
So, the fraction is 1/3 or \(\frac{1}{3}\)
Question 14.
Answer:
\(\frac{5}{10}\) or \(\frac{1}{2}\)
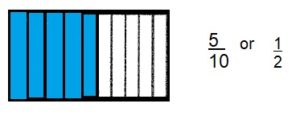
Explanation:
The given whole is equally divided into 10 parts,
among that 5 parts are shaded.
So the fraction is \(\frac{5}{10}\) or \(\frac{1}{2}\) (as both goes in 5).
Question 15.

Answer:
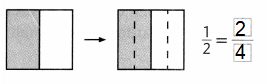
\(\frac{2}{4}\) or \(\frac{1}{2}\)
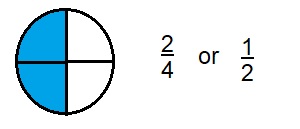
Explanation:
The given whole is equally divided into 4 parts, out of that 2 parts are shaded.
So the fraction is \(\frac{2}{4}\) or \(\frac{1}{2}\)
Parts of Wholes
Question 16.
Construct Arguments is \(\frac{1}{4}\) of the figure below green? Explain.

Answer:
Argument:
\(\frac{1}{4}\) is not the figure shown it is \(\frac{1}{5}\)
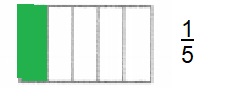
Explanation:
It is not \(\frac{1}{4}\), there are five parts and one part shaded green,
it will be written as 1/5 or \(\frac{1}{5}\).
Question 17.
This picture shows a square. Shade in \(\frac{3}{4}\) of the square.
Answer:
\(\frac{3}{4}\)
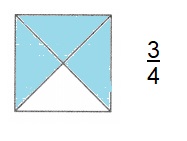
Explanation:
The given square is equally divided into 4 parts, out of that 3 parts are shaded.
So the fraction is \(\frac{3}{4}\) is as shown above.
Pick a Project
PROJECT 8A
How much do you know about the Indianapolis Motor Speedway?
Project: Create a Fraction Game

Answer:
The Indianapolis Motor Speedway is the largest sports venue in the world.
It is located on the corner of 16th Street and Georgetown Road,
approximately six miles (10 km) west of Downtown Indianapolis.
Constructed in 1909, it is the second purpose-built,
banked oval racing circuit after Brook lands and the first to be called a ‘speedway’.
A Fraction Game
The objective of the game is to get all of the markers to the right side of the game board, using as few cards as possible.
How to Play
Click on the pile to turn over one card. This is your target fraction. Move the markers so that the sum of your moves is a fraction that is less than or equal to the target fraction.
For example, if the first card turned over is 4/5,
You could move the fifths marker to 3/5 and the tenths marker to 2/1,
because .
These moves are shown below.
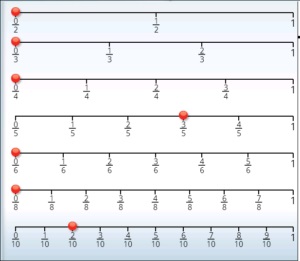
In addition, any of the following moves would also be acceptable:
The fifths marker to .
The tenths marker to , because
.
The thirds marker to , because
.
The fifths marker to and the tenths marker to
, because
.
The halves marker to , the sixths marker to
, and the eighths marker to
, because
.
There are many other moves that would also be acceptable, as long as the sum of the moves is less than or equal to 4/5.
PROJECT 8B
Who does all the stage work for a play or musical?
Project: Build a Model

The stage is usually indicated by the playwright,
but the degree of detail and specificity of this rendering vary
from one playwright to another and from one literary period to another.
- Record Producer. We’ve all heard of the title record producer.
- Audio Technician.
Recording Studio Manager. - Sound Designer.
- Instrument Tech.
- Sound Mixer.
- Radio Broadcast Engineer.
- Digital Audio Editor.
PROJECT:

PROJECT 8C
What is your favorite pie?
Project: Write and Perform a Skit

Answer:
PUMPKIN PIE,

PROJECT
PUMPKIN PRINCESS
Halloween was over and Jessica was wondering what to do with leftover
pumpkin she was not ready to throw them away because they were all in
good condition. She got an idea to prepare a Pie with that and
she gathered all the ingredients needed to make her pie,
she rolled out the dough mashed up the pumpkin and
made sure all the seeds were taken out, than she added
some Cinnamon and nutmeg and then she put the Pie in oven.
Wow! said mom when she came into the kitchen.
That’s your sure smells Yummy. I can’t wait for the Pie to finish and
she said to invite all her friends for the party. Jessica was proud of her
Pie and her mother crowned her with PUMPKIN PRINCESS

PROJECT 8D
How do you make clothes that could fit anyone?
Project: Create a Game

Lesson 8.1 Equivalent Fractions: Area Models
Solve & Share
Lena has yellow tile on \(\frac{1}{4}\) of her kitchen floor.
Write another fraction equivalent to \(\frac{1}{4}\).
Solve this problem any way you choose.
I can … recognize and generate equivalent fractions.

Look Back! How do you know your fraction is equivalent to \(\frac{1}{4}\)?
Answer:
Equivalent fraction for \(\frac{1}{4}\) can be \(\frac{2}{8}\),
Explanation:
Equivalent fractions can be defined as fractions that may have
different numerators and denominators but they represent the same value.
So given \(\frac{1}{4}\) if multiply numerator and denominator by 2
the value will not differ so \(\frac{1}{4}\) = \(\frac{2}{8}\).
Essential Question
What Are Some Ways to Name the Same Part of a Whole?
Answer:
The following are some ways to name the same part of a whole.
A part or parts of a whole is called fraction,
A number that names part of a whole or part of a group is called fraction.
Fractions represent equal parts of a whole or a collection.
Visual Learning Bridge
James ate part of the pizza shown in the picture at the right.
He said \(\frac{5}{6}\) of the pizza is left.
Cardell said \(\frac{10}{12}\) of the pizza is left. Who is correct?
Equivalent fractions name the same part of the same whole.
Answer:
Both James and Cardell are correct,
Explanation:
Given James ate part of the pizza shown in the picture at the right.
He said \(\frac{5}{6}\) of the pizza is left.
Cardell said \(\frac{10}{12}\) of the pizza is left as
\(\frac{10}{12}\) can be further simplified as both goes
by 2 it becomes \(\frac{5}{6}\) which is equivalent to
again \(\frac{5}{6}\) ,Both James and Cardell are correct because
\(\frac{5}{6}\) = \(\frac{10}{12}\).
One Way
Use an area model. Draw a rectangle and divide it into sixths.
Shade \(\frac{5}{6}\). Then divide the rectangle into twelfths.
Answer:

Explanation:
Drawn a rectangle and divided it into sixths.
Shaded \(\frac{5}{6}\). Then divided the rectangle into twelfths
as shown above.
The number and size of parts differ, but the shaded part
of each rectangle is the same \(\frac{5}{6}\) and \(\frac{10}{12}\)
are equivalent fractions.
Another Way
Use a different area model. Draw a circle and divide it into sixths.
Shade \(\frac{5}{6}\). Then divide the circle into twelfths.
Answer:
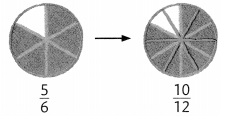
Explanation:
Drawn a circle and divided it into sixths.
Shaded \(\frac{5}{6}\). Then divide the
circle into twelfths as shown above, The number and size
of parts differ, but the shaded part of each circle is the same.
\(\frac{5}{6}\) and \(\frac{10}{12}\) are equivalent fractions.
Convince Me! Reasoning Mia ate \(\frac{1}{4}\) of a pizza.
Matt ate \(\frac{2}{8}\) of another pizza.
Did Mia and Matt eat the same amount of pizza? Explain.
Answer:
Yes, both ate same fraction of pizza,
Explanation:
Given Mia ate \(\frac{1}{4}\) of a pizza and
Matt ate \(\frac{2}{8}\) of another pizza, as 2 and 8 goes
by 2 we get \(\frac{1}{4}\) and 1/4 of a pizza is
equivalent to 2/8 of another pizza so both Mia and Matt ate
same amount of pizza.
Guided Practice
Do You Understand?
Question 1.
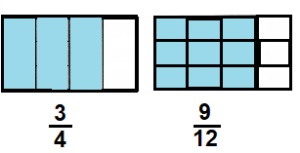
Use the area model to explain why \(\frac{3}{4}\) and
\(\frac{9}{12}\) are equivalent.
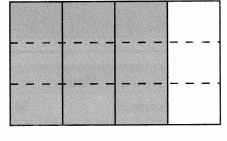
Answer:
\(\frac{3}{4}\) and \(\frac{9}{12}\) are equivalent fractions.
Explanation:
By using the given area model. Given rectangle is
divide into four parts. Shaded \(\frac{3}{4}\) parts.
Then divide the rectangle into twelve parts.
The number and size of parts differ, but the shaded part of
each rectangle is the same \(\frac{3}{4}\) and \(\frac{9}{12}\) are equivalent fractions,
as shown in below picture.
Do You Know How?
For 2-3, use the area model to solve each problem.
Question 2.
Find the missing numerator.
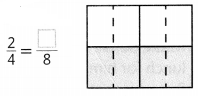
Answer:
Missing number is 4,
Explanation:
The shaded part of each rectangle is the same \(\frac{2}{4}\) and \(\frac{4}{8}\)
are equivalent fractions as shown in the above picture.

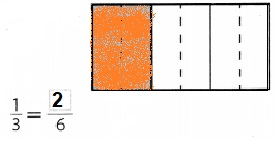
Question 3.
Find the missing numerator.

Answer:
Missing number is 2,
Explanation:
The shaded part of each rectangle is the same \(\frac{1}{3}\) and \(\frac{2}{6}\)
are equivalent fractions as shown in the above picture.
Independent Practice
Question 4.
Write a fraction equivalent to \(\frac{1}{5}\).
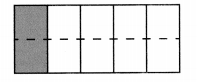
Answer:
Equivalent fraction is \(\frac{2}{10}\).
Explanation:
The Equivalent fraction for \(\frac{1}{5}\) is \(\frac{2}{10}\)
If we multiply both numerator and denominator by 2 to \(\frac{1}{5}\)
we get \(\frac{2}{10}\) which is equivalent fraction to \(\frac{2}{10}\).
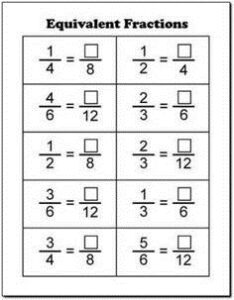
Question 5.
Write two fractions equivalent to \(\frac{4}{12}\).
Answer:
The two equivalent fractions for \(\frac{4}{12}\) are
\(\frac{1}{3}\) and \(\frac{2}{6}\),
Explanation:
Given \(\frac{4}{12}\) if we divide numerator and
denominator by 4 we get \(\frac{1}{3}\) and
if we divide numerator and denominator by 2 we get \(\frac{2}{6}\),
So two equivalent fractions for \(\frac{4}{12}\) are
\(\frac{1}{3}\) and \(\frac{8}{24}\).
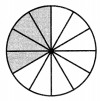
Question 6.
Write a fraction equivalent to \(\frac{2}{6}\).
Answer:
Equivalent fraction is \(\frac{1}{3}\).
Explanation:
The Equivalent fraction for \(\frac{2}{6}\) is \(\frac{1}{3}\)
If we divide both numerator and denominator by 2
we get \(\frac{1}{3}\) which is equivalent fraction to \(\frac{2}{6}\).
Question 7.
Write two fractions equivalent to \(\frac{1}{2}\).

Answer:
The two equivalent fractions for \(\frac{1}{2}\) are
\(\frac{2}{4}\) and \(\frac{3}{6}\),
Explanation:
Given \(\frac{1}{2}\) if we multiply numerator and
denominator by 2 we get \(\frac{2}{4}\) and
if we multiply numerator and denominator by 3 we get \(\frac{3}{6}\),
So two equivalent fractions for \(\frac{1}{2}\) are
\(\frac{2}{4}\) and \(\frac{3}{6}\).
For 8-15, draw an area model or use fraction strips to solve each problem.
Question 8.
\(\frac{2}{8}=\frac{}{4}\)
Answer:
\(\frac{2}{8}=\frac{}{4}\)
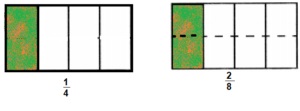
Explanation:
Given \(\frac{2}{8} = \frac{}{4}\) other side denominator is 4
means if we divided \(\frac{2}{8} both by 2 we get denominator as 4
so we get numerator as 1, therefore
[latex]\frac{2}{8}\) = \(\frac{1}{4}\) as shown above.
Question 9.
\(\frac{2}{4}=\frac{ }{8}\)
Answer:
\(\frac{2}{4}=\frac{ 4}{8}\)
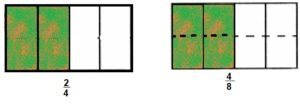
Explanation:
Given \(\frac{2}{4}=\frac{}{8}\) other side denominator is 8
means if we multiply \(\frac{2}{4} both by 2 we get denominator as 8
and we get numerator as 4,
therefore [latex]\frac{2}{4}\) = \(\frac{4}{8}\) as shown above.
Question 10.
\(\frac{1}{2}=\frac{ }{6}\)
Answer:
\(\frac{1}{2}=\frac{ 3}{6}\)
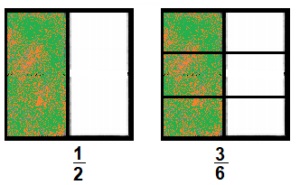
Explanation:
Given \(\frac{1}{2}=\frac{}{6}\) other side denominator is 6
means if we multiply \(\frac{1}{2} both by 3 we get denominator as 6
and we get numerator as 3,
therefore [latex]\frac{1}{2}\) = \(\frac{3}{6}\) as shown above.
Question 11.
\(\frac{3}{3}=\frac{6}{}\)
Answer:
\(\frac{3}{3}=\frac{6}{6}\)

Explanation:
Given \(\frac{3}{3}=\frac{6}{}\) other side numerator is 6
means if we multiply \(\frac{3}{3} both by 2 we get numerator as 6
and we get denominator also as 6,
therefore [latex]\frac{3}{3}\) = \(\frac{6}{6}\) as shown above.
Question 12.
\(\frac{1}{5}=\frac{ }{10}\)
Answer:
\(\frac{1}{5}=\frac{2 }{10}\)
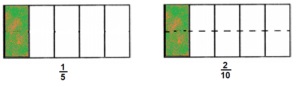
Explanation:
Given \(\frac{1}{5}=\frac{}{10}\) other side denominator is 10
means if we multiply \(\frac{1}{5} both by 2 we get denominator as 10
and we get numerator as 1 X 2 = 2,
therefore [latex]\frac{1}{5}\) = \(\frac{2}{5}\) as shown above.
Question 13.
\(\frac{5}{6}=\frac{10}{}\)
Answer:
\(\frac{5}{6}=\frac{10}{12}\)
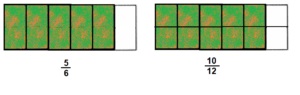
Explanation:
Given \(\frac{5}{6}=\frac{10}{}\) other side numerator is 10
means if we multiply \(\frac{5}{6} both by 2 we get numerator as 10
and we get denominator as 12,
therefore [latex]\frac{5}{6}\) = \(\frac{10}{12}\) as shown above.
Question 14.
\(\frac{8}{12}=\frac{2}{}\)
Answer:
\(\frac{8}{12}=\frac{2}{3}\)
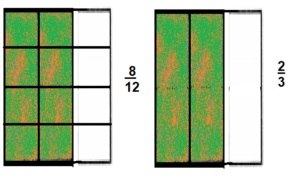
Explanation:
Given \(\frac{8}{12}=\frac{2}{}\) other side numerator is 2
means if we divide \(\frac{8}{12} both by 4 we get numerator as 2
and we get denominator as 3,
therefore [latex]\frac{8}{12}\) = \(\frac{2}{3}\) as shown above.
Question 15.
\(\frac{4}{5}=\frac{8}{}\)
Answer:
\(\frac{4}{5}=\frac{8}{10}\)
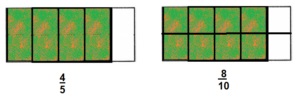
Explanation:
Given \(\frac{4}{5}=\frac{8}{}\) other side numerator is 8
means if we multiply \(\frac{4}{5} both by 2 we get numerator as 8
and we get denominator as 10,
therefore [latex]\frac{4}{5}\) = \(\frac{8}{10}\) as shown above.
Problem Solving
Question 16.
Envision®STEM Monarch butterflies migrate when they sense
daylight hours are shorter and temperatures get colder.
Write two equivalent fractions for the part of the migration a monarch butterfly can complete in 1 week.

Answer:
\(\frac{7}{35} and \frac{14}{70}\),
Two equivalent fractions for the part of the migration a
monarch butterfly can complete in 1 week are
\(\frac{7}{35} and \frac{14}{70}\),
Explanation:
Given Monarch butterflies travel \(\frac{1}{5}\)
the total migration in 1 week,
its equivalent fraction can be written by multiplying both numerator and
denominator by 7 we get
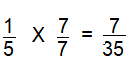
\(\frac{1}{5}\). = \(\frac{7}{35}\) and if we multiply numerator and denominator by 2
we get another equivalent fraction as \(\frac{14}{35}\).
Question 17.
Make Sense and Persevere Garrett buys lunch for himself and his friend.
He buys 2 sandwiches, 2 fries, and 2 malts. How much did Garrett spend on lunch?

Answer:
Garrett spend $30 on lunch,
Explanation:
2 X $8 + 2 X $3 + 2 X $4 = $16 + $6 + $8 = $30,
Therefore Garrett spent total $30.
Question 18.
Connor said, “To the nearest hundred, I’ve attended
school for 800 days of my life!” Write three numbers that
could be the actual number of days Connor has attended school.
Answer:
The numbers can be anything between 750 to 849,
can be 790, 812 and 801,
Explanation:
Given Connor said, “To the nearest hundred, I’ve attended
school for 800 days of my life!” Write three numbers that
could be the actual number of days Connor has attended school.
So nearest hundred to 800 can be any numbers between 750 to 849,
so it can be 790, 812 and 801.
Question 19.
Higher Order Thinking Josh, Lisa, and Vicki each ate \(\frac{1}{4}\)
of their own pizza. Each pizza was the same size,
but Josh ate 1 slice, Lisa ate 2 slices, and Vicki ate 3 slices. How is this possible?
Answer:
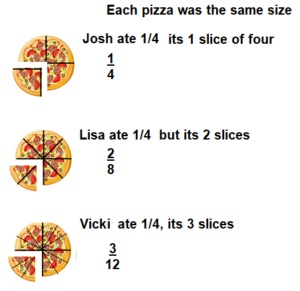
Explanation:
Each pizza was of the same size but the portion of slices are different
Josh ate \(\frac{1}{4}\), Lisa ate 2 slices means
2 X \(\frac{1}{4}\) = \(\frac{2}{8}\) and
Vicki ate 3 slices means 3 X \(\frac{1}{4}\) = \(\frac{3}{12}\).
Assessment Practice
Question 20.
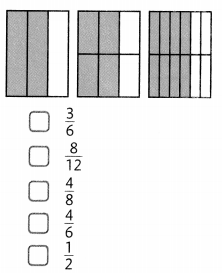
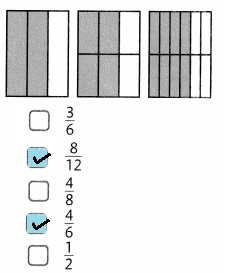
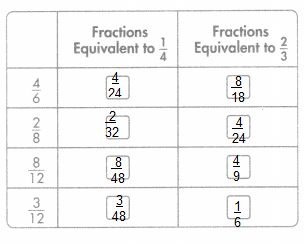
Select all the fractions that are equivalent to \(\frac{2}{3}\).
Use the area models to help.
Answer:
Explanation:
As \(\frac{8}{12}\), \(\frac{4}{6}\) are
the equivalent fractions of \(\frac{2}{3}\) when
\(\frac{8}{12}\) if numerator and denominator is
divided by 4 we get \(\frac{2}{3}\) and
\(\frac{4}{6}\) if numerator and denominator is
divided by 2 we get \(\frac{2}{3}\), therefore \(\frac{8}{12}\), \(\frac{4}{6}\) are the equivalent fractions of \(\frac{2}{3}\).
Question 21.
Select all the pairs that are equivalent fractions. Use the area models to help.

Answer:
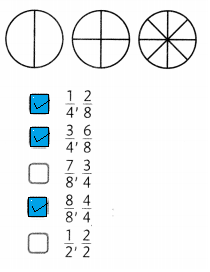
Explanation:
As \(\frac{1}{4}\) if numerator and denominator is
multiplied by 2 we get the equivalent fractions of \(\frac{2}{8}\) if
\(\frac{3}{4}\) if numerator and denominator is
multiplied by 2 we get the equivalent fractions of \(\frac{6}{8}\) and
\(\frac{8}{8}\) we get 1 and the equivalent fractions of
\(\frac{4}{4}\) we get 1 so selected all the pairs that are
equivalent fractions as shown above.
Lesson 8.2 Equivalent Fractions: Number Lines
Solve & Share
Suppose you have a ruler showing fourths. Use your ruler to name a fraction that is equivalent to . Tell how you know the fraction is equivalent.
I can … name the same point on a number line using equivalent fractions.
Look Back! Model with Math Do you think there is more than one fraction equivalent to \(\frac{2}{4}\)? Draw a picture to explain.
Answer:
2/4 Equivalent fraction is 1/2
Explanation:
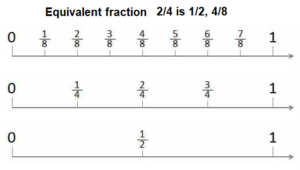
Essential Question
How Can You Use a Number Line to Explain Why Fractions Are Equivalent?

Answer:
A part or parts of a whole is called fraction, A number that names part of a whole or part of a group is called fraction. the sum of all fractions is a whole.
Explanation:
So Number Line can be used to explain the equivalent fractions.
Visual Learning Bridge
Sal rode his bike \(\frac{3}{4}\) mile to school. Name two fractions that are equivalent to \(\frac{3}{4}\).
A number line is another appropriate tool for finding equivalent fractions.
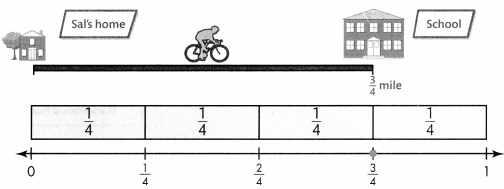
Show \(\frac{3}{4}\) on the number line.
Divide each fourth into two equal parts to show eighths.
Divide each fourth into three equal parts to show twelfths.
\(\frac{3}{4}, \frac{6}{8}\) and \(\frac{9}{12}\) are at the same point on the number lines that are all the same length. \(\frac{6}{8}\) and \(\frac{9}{12}\) are equivalent to \(\frac{3}{4}\).
Convince Me! The number and size of each part on two number lines are different. Can the number lines show equivalent fractions? Use the number lines above to explain.
Answer:
Yes, the number and size of each part on two number lines are different can also show equivalent fractions.
Explanation:
\(\frac{3}{6}\) = \(\frac{6}{8}\) = \(\frac{9}{12}\)
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
2 x 3 = 6
2 x 4 = 8
2 x 6 = 12
Another Example!
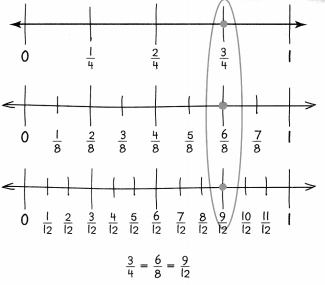
You can use a number line to find equivalent fractions that are greater than or equal to 1.
Guided Practice
Do You Understand?
Question 1.
Use the number line above to write a fraction equivalent to \(\frac{9}{6}\). Why are the fractions equivalent? Explain.
Answer:
\(\frac{3}{2}\) is equivalent fraction to \(\frac{9}{6}\)
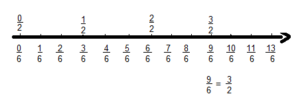
\(\frac{9}{6}\) = \(\frac{3}{2}\)
3 x 3 = 9
3 x 2 = 6
Explanation:
If the numerator and denominator of a fraction are equal, then the fraction is less then 1, greater then 1, equal to 1.
These fractions are actually the same because when we multiply or divide both the numerator and the denominator by the same number, the value of the fraction actually doesn’t change. Therefore, equivalent fractions, when reduced to their simplified value, will all be the same.
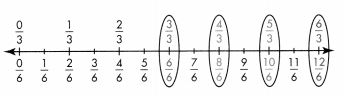
Do You Know How?
For 2-3, use the number line below.
Question 2.
Write an equivalent fraction for \(\frac{1}{3}\).
Answer:
\(\frac{2}{6}\) is an equivalent fraction for \(\frac{1}{3}\).
Explanation:
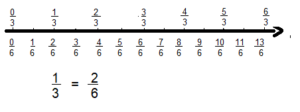
Question 3.
Write an equivalent fraction for \(\frac{1}{2}\).
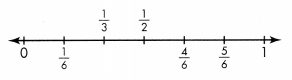
Answer:
\(\frac{3}{6}\) is an equivalent fraction for \(\frac{1}{2}\).
Explanation:
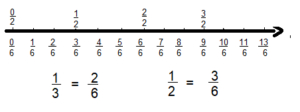
Independent Practice
For 4-7, use the number line to find equivalent fractions. Circle the correct answers.

Question 4.
Which of the following fractions is an equivalent fraction for point A?
\(\begin{array}{lllll}
\frac{1}{4} & \frac{1}{3} & \frac{2}{3} & \frac{1}{6} & \frac{2}{6}
\end{array}\)
Answer:
\(\frac{1}{3}\), \(\frac{2}{6}\) are the equivalent fractions for point A.
Explanation:
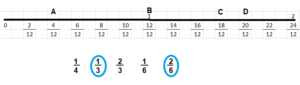
Question 5.
Which of the following fractions is an equivalent fraction for point B?
\(\begin{array}{lllll}
\frac{11}{12} & \frac{12}{12} & \frac{13}{12} & \frac{7}{6} & \frac{6}{6}
\end{array}\)
Answer:
\(\frac{12}{12}\) and \(\frac{6}{6}\) are the equivalent fractions for point B.
Explanation:
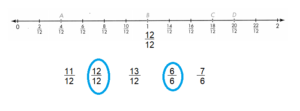
Question 6.
Which of the following fractions is an equivalent fraction for point C?
\(\begin{array}{lllll}
\frac{8}{6} & \frac{2}{3} & \frac{1}{2} & \frac{3}{2} & \frac{6}{4}
\end{array}\)
Answer:
\(\frac{3}{2}\)and \(\frac{6}{4}\) are the equivalent fractions for point C.
Explanation:

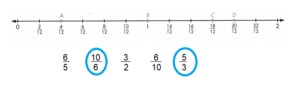
Question 7.
Which of the following fractions is an equivalent fraction for point D?
\(\begin{array}{lllll}
\frac{6}{5} & \frac{10}{6} & \frac{3}{2} & \frac{6}{10} & \frac{5}{3}
\end{array}\)
Answer:
\(\frac{10}{6}\) and \(\frac{5}{3}\) are the equivalent fractions for point D.
Explanation:
Problem Solving
Question 8.
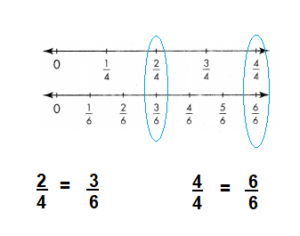
What equivalent fractions are shown by the two number lines?
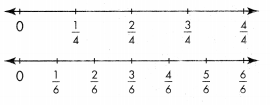
Answer:
\(\frac{2}{4}\) and \(\frac{3}{6}\)
\(\frac{4}{4}\) and \(\frac{6}{6}\) are equivalent fractions
Explanation:
Question 9.
Make Sense and Persevere Randy and Carla like to walk the path around their town park. The path is 2 miles long. Last month Randy walked the path 13 times, and Carla walked it 22 times. How many more miles did Carla walk than Randy last month?
Answer:
18 miles more.
Explanation:
Randy walk 13 X 2 = 26 miles
Carla walk 22 X 2 = 44 miles
44 – 26 = 18 miles
Question 10.
Higher Order Thinking Jarred says these number lines show \(\frac{3}{4}\) is equivalent to \(\frac{2}{3}\). Is Jarred correct? Explain.
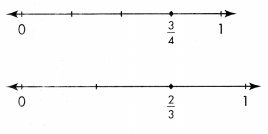
Answer:
NO, Jarred is not correct.
Explanation:

As blue line is smaller then the red line in the bench mark number line picture3/4 and 2/3 are not correct, Jarred said wrong.
Assessment Practice
Question 11.
Kevin and Gabbie use a number line to find fractions that are equivalent to \(\frac{4}{10}\).
Kevin says he can find an equivalent fraction with a denominator greater than 10. Gabbie says she can find an equivalent fraction with a denominator less than 10.
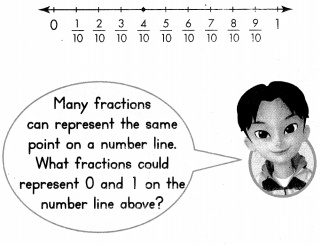
Part A
Write to explain how Kevin can use the number line to find his equivalent fraction.
Answer:
\(\frac{4}{10}\) = \(\frac{4}{100}\)

Explanation:
10 x 4 = 40
10 x 10 = 100
So, \(\frac{4}{10}\) = \(\frac{4}{100}\)
Part B
Write to explain how Gabbie can use the number line to find her equivalent fraction.
Answer:
\(\frac{4}{10}\) = \(\frac{2}{5}\)

Explanation:
2 x 2 = 4
2 x 5 = 10
So, \(\frac{4}{10}\) = \(\frac{2}{5}\)
8.3 Generate Equivalent Fractions: Multiplication
Solve & Share
Wayne bought a box of muffins. Four sixths of the muffins are blueberry. Write a fraction equivalent to solve this problem any way you choose.
I can … use multiplication to find equivalent fractions.

Look Back! How are the numerator and denominator of your fraction related to the numerator and denominator of \(\frac{4}{6}\)?
Answer:
\(\frac{2}{3}\) related to \(\frac{4}{6}\).
Explanation:
By multiplying the numerator and denominator of a fraction with 2 factor
2 x2 = 4
2 x 3 = 6
So, \(\frac{4}{6}\) = \(\frac{2}{3}\)
Essential Question
How Can You Use Multiplication to Find Equivalent Fractions?
Answer:
Multiplications can be used to find an equivalent fraction by multiplying the numerator and denominator by the same number.
Explanation:
If you are given the fraction \(\frac{1}{2}\).
You can multiply the numerator by 3 and the denominator by 3.
1 x 3 = 3
2 x 3 = 6
So, \(\frac{1}{2}\) = \(\frac{3}{6}\)
Visual Learning Bridge
A librarian said \(\frac{1}{2}\) of the books checked out yesterday were nonfiction. What are some fractions equivalent to \(\frac{1}{2}\)?

To find equivalent fractions, multiply by a fraction equal to one.
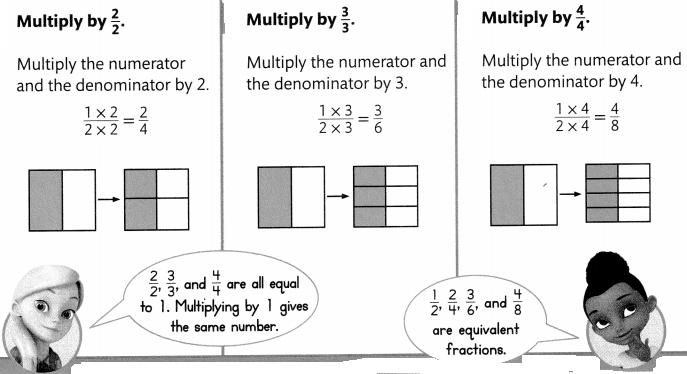
Convince Me! Critique Reasoning Kevin said, “In each of the examples above, all you are doing is multiplying by one. When you multiply by 1, the value doesn’t change.” Is Kevin correct? Explain.
Answer:
Yes, Kelvin is correct,
Explanation:
Multiplying by one doesn’t change the value. So we call 1 the multiplicative identity.
Guided Practice
Do You Understand?
Question 1.
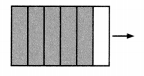
Use an area model and multiplication to show why \(\frac{5}{6}\) and \(\frac{10}{12}\) are equivalent fractions.
Answer:
Yes, \(\frac{5}{6}\) and \(\frac{10}{12}\) are Equivalent fractions.
Explanation:
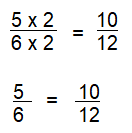
Question 2.
Use multiplication to explain why \(\frac{3}{4}\) and \(\frac{8}{12}\) are NOT equivalent fractions.
Answer:
No, \(\frac{3}{4}\) and \(\frac{8}{12}\) are not equivalent fractions,
Explanation:
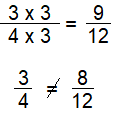
\(\frac{8}{12}\) = \(\frac{2}{3}\),
So \(\frac{3}{4}\) = \(\frac{2}{3}\) are NOT Equivalent fractions
Do You Know How?
For 3-7, multiply to find equivalent fractions.
Question 3.
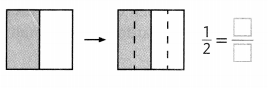
Answer:
\(\frac{2}{4}\)
Explanation:
Question 4.
\(\frac{3}{4}=\frac{}{12}\)
Answer:
\(\frac{9}{12}\)]
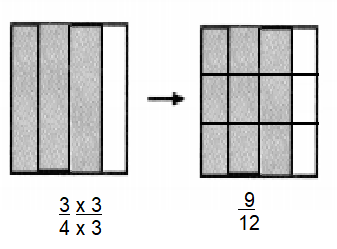
Explanation:
To find equivalent fractions, multiply by a fraction equal to one in both numerator and denominator.
So in the given fraction multiply with 3 in both numerator and denominator.
Question 5.
\(\frac{5}{5}=\frac{10}{}\)
Answer:
\(\frac{10}{10}\)
Explanation:
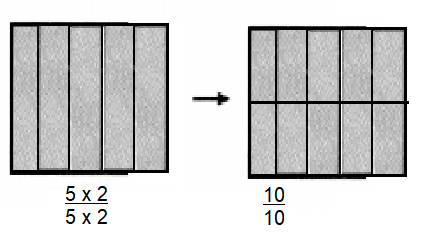
To find equivalent fractions, multiply by a fraction equal to one in both numerator and denominator.
So in the given fraction multiply with 2 in both numerator and denominator.
Question 6.
\(\frac{3}{2}=\frac{6}{}\)
Answer:
\(\frac{6}{4}\)
Explanation:
Total 3 box, 2 are shaded
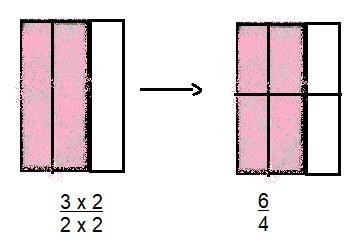
To find equivalent fractions, multiply by a fraction equal to one in both numerator and denominator.
So in the given fraction multiply with 2 in both numerator and denominator.
Question 7.
\(\frac{1}{6}=\frac{}{12}\)
Answer:
\(\frac{2}{12}\)
Explanation:
Total six box, one box is shaded
To find equivalent fractions, multiply by a fraction equal to one in both numerator and denominator.
So in the given fraction multiply with 2 in both numerator and denominator.
Independent Practice
Leveled Practice For 8-13, fill in the missing numbers to find equivalent fractions.
Question 8.
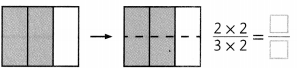
Answer:
\(\frac{4}{6}\)
Explanation:
Write the product of numerator and denominator in the missing boxes.
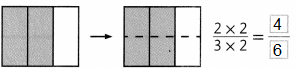
Question 9.
Answer:
\(\frac{6}{12}\) is missing.
Explanation:
Write the product of numerator and denominator in the missing boxes.
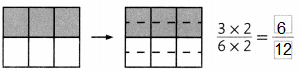
Question 10.

Answer:
Missing number is 2.
Explanation:
Write the product of numerator and denominator in the missing boxes.
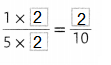
Question 11.
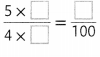
Answer:
Missing number is 25.
Explanation:
Write the product of numerator and denominator in the missing boxes.
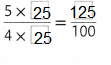
Question 12.
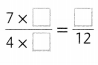
Answer:
Missing number is 3.
Explanation:
Write the product of numerator and denominator in the missing boxes.
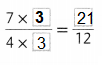
Question 13.
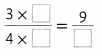
Answer:
Missing number is 3
Explanation:
Write the product of numerator and denominator in the missing boxes.
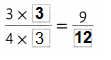
For 14-21, write two equivalent fractions for each given fraction.
Question 14.
\(\frac{1}{10}\)
Answer:
\(\frac{2}{20}\)
Explanation:
Multiply with 2 in numerator and denominator to get \(\frac{2}{20}\)

Question 15.
\(\frac{4}{2}\)
Answer:
\(\frac{8}{4}\)
Explanation:
Multiply with 2 in numerator and denominator to get \(\frac{8}{4}\)
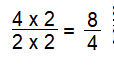
Question 16.
\(\frac{5}{6}\)
Answer:
\(\frac{10}{2}\)
Explanation:
Multiply with 2 in numerator and denominator to get \(\frac{10}{2}\)

Question 17.
\(\frac{1}{3}\)
Answer:
\(\frac{3}{9}\)
Explanation:
Multiply with 3 in numerator and denominator to get \(\frac{3}{9}\)
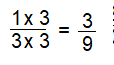
Question 18.
\(\frac{2}{5}\)
Answer:
\(\frac{4}{10}\)
Explanation:
Multiply with 2 in numerator and denominator to get \(\frac{4}{10}\)

Question 19.
\(\frac{3}{4}\)
Answer:
\(\frac{6}{8}\)
Explanation:
Multiply with 2 in numerator and denominator to get \(\frac{6}{8}\)

Question 20.
\(\frac{9}{2}\)
Answer:
\(\frac{18}{4}\)
Explanation:
Multiply with 2 in numerator and denominator to get \(\frac{18}{4}\)
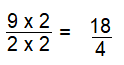
Question 21.
\(\frac{7}{12}\)
Answer:
\(\frac{14}{21}\)
Explanation:
Multiply with 2 in numerator and denominator to get \(\frac{14}{21}\)
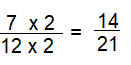
Problem Solving
For 22-23, use the chart at the right.

Question 22.
Write three equivalent fractions to describe the portion of .
Answer:
\(\frac{1}{6}\), \(\frac{2}{12}\), \(\frac{3}{18}\) are three equivalent fractions.
Explanation:
Three equivalent fractions of \(\frac{1}{6}\) are…
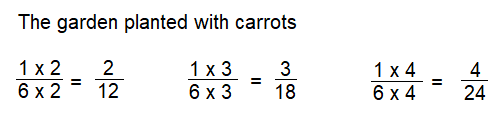
Question 23.
Reasoning Which vegetable takes up the same amount of the garden as the tomatoes? Explain.
Answer:
Beans = \(\frac{3}{12}\) and Tomatoes = \(\frac{1}{4}\)
Beans take up the same amount of the garden as the tomatoes
Explanation:
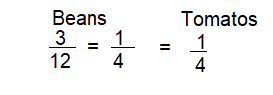
Question 24.
Jeena has 5 packets of seeds. Each packet has 12 seeds. Jeena wants to divide the seeds evenly among 10 flower pots. How many seeds can she plant in each flower pot?
Answer:
6 seeds in one flower pot
Explanation:
5 packets X 12 Seeds = 60 Seeds total
60 seeds,10 flower pots
\(\frac{60}{10}\) = 6
Question 25.
Higher Order Thinking Jen says, “I can use this equation to find equivalent fractions but n cannot be zero.”
\(\frac{a}{b}=\frac{(n \times a)}{(n \times b)}\)
Do you agree with Jen? Explain. Give examples to support your reasoning.
Answer:
YES, I agree with Jen.
Explanation:
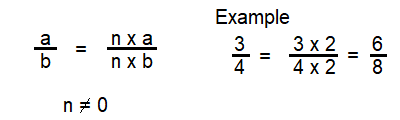
By multiplying the numerator and denominator with the same number, we get equivalent fractions, n should not be zero.
Assessment Practice
Question 26.
Select the equivalent fraction.
Answer:
Explanation:
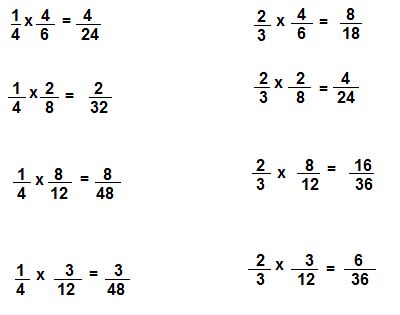
Question 27.
Nia found a fraction that is equivalent to \(\frac{1}{2}\). Is Nia’s fraction work, shown below, correct? Explain.
\(\frac{3 \times 4}{8 \times 3}=\frac{12}{24}\)
Answer:
YES, Nia’s fraction work is Correct.
Explanation:
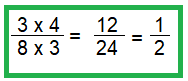
The equivalent fraction is \(\frac{1}{2}\) for both the fraction Nai found
Lesson 8.4 Generate Equivalent Fractions: Division
Solve & Share
Sara bought a piece of ribbon. The length of the ribbon is given in tenths. Write the length as two other equivalent fractions. Solve this problem any way you choose.
I can … use division to find equivalent fractions.
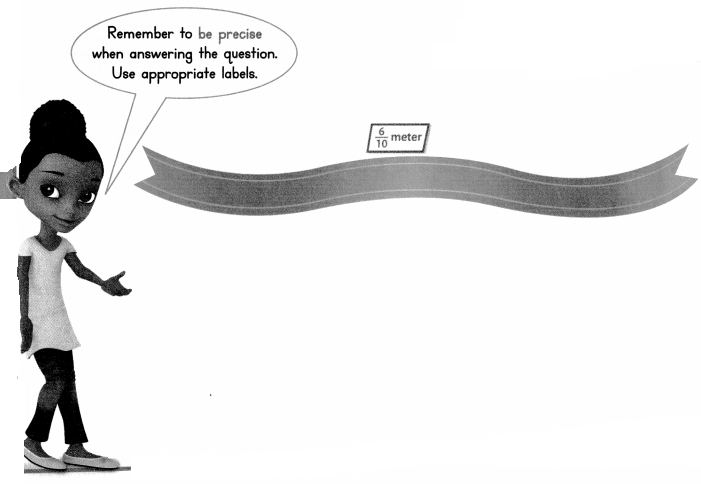
Look Back! Sara wrote the following equivalent fractions: \(\frac{6}{10}=\frac{3}{5}\). What two operations could Sara have used to find her equivalent fractions? Explain.
Answer:
Sara could use common factorization, cross multiplication operations.
Explanation:
To find equivalent fractions, divide the numerator and the denominator by a common factor.
A common factor is a factor two or more numbers have in common.
Essential Question
How Can You Use Division to Find Equivalent Fractions?
Answer:
You can multiply or divide to find an equivalent fraction.
Adding or subtracting does not work for finding an equivalent fraction.
If you multiply or divide by the top of the fraction, you must do the same to the bottom.
Use cross multiplication to determine if two fractions are equivalent.
Visual Learning Bridge
In early May, Fairbanks, Alaska, has daylight for \(\frac{18}{24}\) of the day. What are some fractions equivalent to \(\frac{18}{24}\)?
Answer:
\(\frac{3}{4}\)
Explanation:
Here 18 and 24 can be divided by 6
18 can be divided by 6 in 3 times so 18 ÷ 6 = 3
24 can be divided by 6 in 4 times so 24÷ 6 = 4
so we get
\(\frac{18}{24}\) = \(\frac{3}{4}\)

Two common factors of 18 and 24 are 2 and 3.
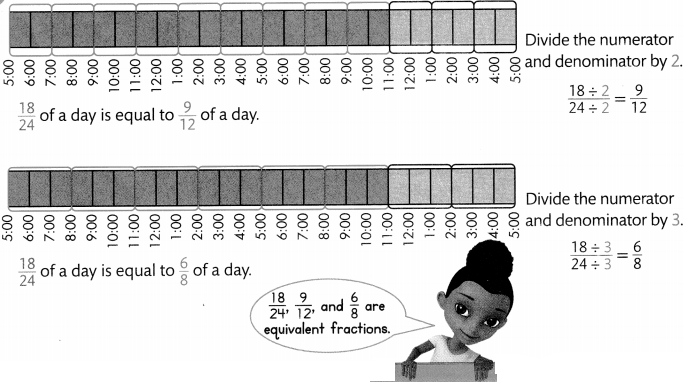
Convince Me! Model with Math Draw a number line and label it with equivalent fractions to show \(\frac{18}{24}=\frac{9}{12}=\frac{6}{8}=\frac{3}{4}\).
Guided Practice
Do You Understand?
Question 1.
Use division to show \(\frac{9}{12}\) and \(\frac{3}{4}\) are equivalent fractions.
Answer:
yes, these are equivalent fractions.
\(\frac{9}{12}\) and \(\frac{3}{4}\) are equivalent fractions.
Explanation:
Here 9 and 12 can be divided by 3
9 can be divided by 3 in 3 times so 9 ÷ 3 = 3
12 can be divided by 3 in 4 times so 12 ÷ 3 = 4
so we get
\(\frac{9}{12}\) = \(\frac{3}{4}\)
Question 2.
Is there a fraction with a smaller numerator and denominator that is equivalent to \(\frac{4}{12}\)? Explain.
Answer:
Yes, a fraction with a smaller numerator and denominator that is equivalent to 4/12 is 1/3
Explanation:
Here 4 and 12 can be divided by 4
4 can be divided by 4 in 1 time so 4 ÷ 4 = 1
12 can be divided by 4 in 3 times so 12 ÷ 4 = 3
so we get
\(\frac{4}{12}\) = \(\frac{1}{3}\)
Do You Know How?
For 3-8, divide to find equivalent fractions.
Question 3.
\(\frac{6}{10}=\frac{}{}\)
Answer:
\(\frac{3}{5}\)
Explanation:
Here 6 and 10 can be divided by 2
6 can be divided by 2 in 3 times so 6 ÷ 2 = 3
10 can be divided by 2 in 5 times so 10 ÷ 2 = 5
so we get
\(\frac{6}{10}\) = \(\frac{3}{5}\)
Question 4.
\(\frac{8}{12}=\frac{ }{ }\)
Answer:
\(\frac{2}{3}\)
Explanation:
Here 8 and 12 can be divided by 4
8 can be divided by 4 in 2 times so 8 ÷ 4 = 2
12 can be divided by 4 in 3 times so 12 ÷ 4 = 3
so we get
\(\frac{8}{12}\) = \(\frac{2}{3}\)
Question 5.
\(\frac{8}{12}=\frac{ }{3}\)
Answer:
\(\frac{2}{3}\)
Explanation:
Here 8 and 12 can be divided by 4
8 can be divided by 4 in 2 times so 8 ÷ 4 = 2
12 can be divided by 4 in 3 times so 12 ÷ 4 = 3
so we get
\(\frac{8}{12}\) = \(\frac{2}{3}\)
Question 6.
\(\frac{10}{12}=\frac{5}{}\)
Answer:
\(\frac{5}{6}\)
Explanation:
Here 10 and 12 can be divided by 2
10 can be divided by 2 in 5 times so 10 ÷ 2 = 5
12 can be divided by 2 in 6 times so 12 ÷ 2 = 6
so we get
\(\frac{10}{12}\) = \(\frac{5}{6}\)
Question 7.
\(\frac{2}{10}=\frac{ }{5}\)
Answer:
\(\frac{1}{5}\)
Explanation:
Here 2 and 10 can be divided by 2
2 can be divided by 2 in 1 time so 2 ÷ 2 = 1
10 can be divided by 2 in 5 times so 10 ÷ 2 = 5
so we get
\(\frac{2}{10}\) = \(\frac{1}{5}\)
Question 8.
\(\frac{10}{100}=\frac{ }{10}\)
Answer:
\(\frac{1}{10}\)
Explanation:
Here 10 and 100 can be divided by 10
10 can be divided by 10 in 1 time so 10 ÷ 10 = 1
100 can be divided by 10 in 10 times so 100 ÷ 10 = 10
so we get
\(\frac{10}{100}\) = \(\frac{1}{10}\)
Independent Practice
Leveled Practice For 9-16, fill in the missing numbers to find equivalent fractions.
Question 9.
\(\frac{6 \div 6}{12 \div 6}=\)
Answer:
Missing number is \(\frac{1}{2}\)
Explanation:
![]()
Question 10.
\(\frac{70 \div 5}{10 \div 5}=\)
Answer:
Missing number is \(\frac{35}{2}\)
Explanation:
![]()
Question 11.
\(\frac{2 \div 2}{6 \div 2}=\)
Answer:
Missing number is \(\frac{1}{3}\)
Explanation:
![]()
Question 12.
\(\frac{50 \div 10}{100 \div 10}=\)
Answer:
Missing number is \(\frac{1}{2}\)
Explanation:
![]()
Question 13.

Answer:
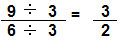
Explanation:
Dividing \(\frac{9}{6}\) with 3 on both the sides we get \(\frac{3}{2}\)
Question 14.
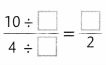
Answer:
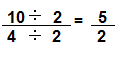
Explanation:
Dividing 10/4 with 2 on both the sides we get \(\frac{5}{2}\)
Question 15.

Answer:
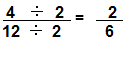
Explanation:
Dividing \(\frac{4}{12}\) with 2 on both the sides we get \(\frac{2}{6}\)
Question 16.
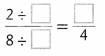
Answer:

Explanation:
Dividing \(\frac{2}{8}\) with 2 on both the sides we get \(\frac{1}{4}\)
For 17-24, divide to find two equivalent fractions.
Question 17.
\(\frac{20}{100}\)
Answer:
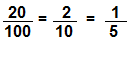
Explanation:
\(\frac{20}{10}\) = 2
\(\frac{100}{10}\) = 10
So,
\(\frac{2}{10}\) =\(\frac{1}{5}\)
Question 18.
\(\frac{40}{10}\)
Answer:
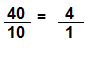
Explanation:
10 x 1 = 10
10 x 4 = 40
So \(\frac{40}{10}\) = \(\frac{4}{1}\) are equivalent fractions.
Question 19.
\(\frac{16}{12}\)
Answer:
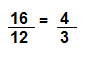
Explanation:
4 x 4 = 16
4 x 3 = 12
So \(\frac{16}{12}\) = \(\frac{4}{3}\) are equivalent fractions.
Question 20.
\(\frac{12}{8}\)
Answer:
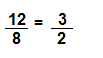
Explanation:
4 x 3 = 12
4 x 2 = 8
So, \(\frac{12}{8}\) = \(\frac{3}{2}\) are equivalent fractions.
Question 21.
\(\frac{24}{12}\)
Answer:
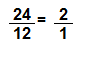
Explanation:
12 x 2 = 24
12 x 1 = 12
So, \(\frac{24}{12}\) = \(\frac{2}{1}\) are equivalent fractions.
Question 22.
\(\frac{10}{100}\)
Answer:
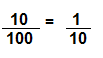
Explanation:
10 x 1 = 10
10 x 10 =100
So, \(\frac{10}{100}\) = \(\frac{1}{10}\) are equivalent fractions.
Question 23.
\(\frac{90}{10}\)
Answer:
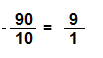
Explanation:
10 x 1 = 10
10 x 9 = 90
So, \(\frac{90}{10}\) = \(\frac{9}{1}\) are equivalent fractions.
Question 24.
\(\frac{80}{100}\)
Answer:
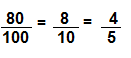
Explanation:
10 x 8 = 80
10 x 10 = 100
2 x 4 = 8
2 x 5 = 10
So, \(\frac{80}{100}\) = \(\frac{4}{5}\)
Problem Solving
For 25-27, use the table at the right.
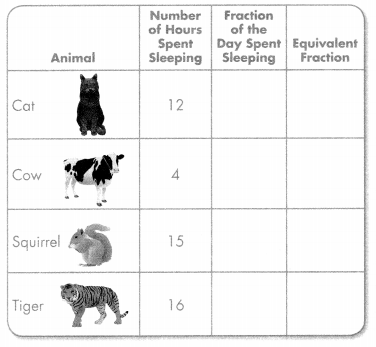
Question 25.
Complete the table at the right by writing the fraction of the day each animal sleeps and an equivalent fraction. Remember, there are 24 hours in a day.
Answer:

Explanation:
\(\frac{12}{24}\) divide both numerator and denominator with 2 to get equivalent fraction \(\frac{1}{2}\)
\(\frac{4}{24}\) divide both numerator and denominator with 4 to get equivalent fraction \(\frac{1}{6}\)\(\frac{15}{24}\) divide both numerator and denominator with 3 to get equivalent fraction \(\frac{5}{8}\)
\(\frac{16}{24}\)divide both numerator and denominator with 8 to get equivalent fraction \(\frac{2}{3}\)
Question 26.
Suppose the cow slept 4 more hours. What fraction of the day would the cow spend sleeping?
Answer:
The Cow spend \(\frac{1}{3}\) of sleeping hours.
Explanation:
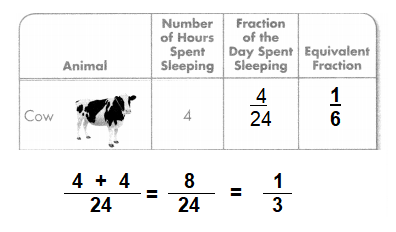
Question 27.
How many hours does a tiger sleep in 7 days?
Answer:
Tiger sleeps 112 hours in 7 days.
Explanation:

Question 28.
Use Structure Ethan ate \(\frac{4}{8}\) of his sandwich. Andy ate \(\frac{1}{2}\) of his sandwich. The sandwiches were the same size.
a. Whose sandwich had more equal parts?
Answer:
Ethan sandwich had more equal parts.
Explanation:

b. Whose sandwich had larger equal parts?
Answer:
Andy had larger equal parts.
Explanation:

c. Who ate more? Explain.
Answer:
Both of them ate same,
As, the sandwiches were of the same size.
Explanation:

Question 29.
Higher Order Thinking If the numerator and denominator of a fraction are both odd numbers, can you write an equivalent fraction with a smaller numerator and denominator? Give an example to explain.
Answer:
The numerator and denominator of a fraction are both odd numbers,
As shown in the bench mark number line 1/3 and 3/9 are the odd numbers fraction and they are equivalent fractions.
Explanation:
Example,
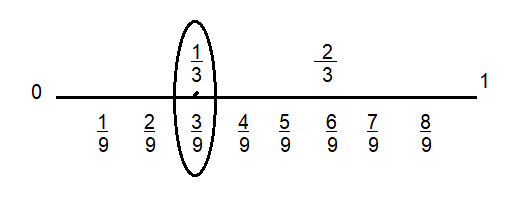
Assessment Practice
Question 30.
Select all the equations that are correct.
☐ \(\frac{12 \div 3}{3 \div 3}=\frac{3}{1}\)
☐ \(\frac{4 \div 2}{8 \div 2}=\frac{2}{4}\)
☐ \(\frac{5 \div 5}{10 \div 5}=\frac{1}{5}\)
☐ \(\frac{10 \div 2}{4 \div 2}=\frac{5}{2}\)
☐ \(\frac{12 \div 4}{8 \div 4}=\frac{3}{2}\)
Answer:
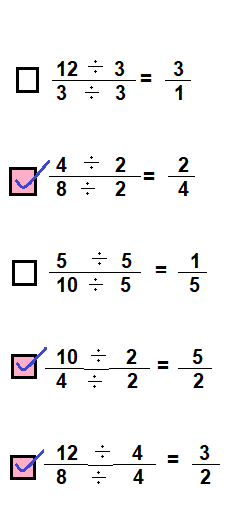
Explanation:
In the above equation 4/8 divide both numerator and denominator with 2 to get equivalent fraction 2/4.
In the above equation10/4 divide both numerator and denominator with 2 to get equivalent fraction 5/2.
In the above equation 12/8 divide both numerator and denominator with 4 to get equivalent fraction 1/2.
Question 31.
There are 12 students in DeLynn’s class. Eight students own pets. Which pair of fractions show the fraction of the class that owns pets?
A. \(\frac{8}{12}, \frac{2}{3}\)
B. \(\frac{1}{2}, \frac{2}{3}\)
C. \(\frac{6}{4}, \frac{3}{2}\)
D. \(\frac{12}{8}, \frac{3}{2}\)
Answer:
Option A
Explanation:
In 8/12 fraction divide both numerator and denominator with 4 to get equivalent fraction 2/3.

Lesson 8.5 Use Benchmarks to Compare Fractions
Solve & Share
Color a part of each strip of paper below. Estimate what fraction of each strip is colored. Explain how you made your estimate. Solve this problem any way you choose.
I can … use benchmarks, area models, and number lines to compare fractions.

Look Back! Generalize How could you tell if a fraction is greater than, less than, or equal \(\frac{1}{2}\) to just by looking at the numerator and the denominator?
Answer:
Fractions greater than 1 have numerators larger than their denominators; those that are less than 1 have numerators smaller than their denominators; the rest are equal to 1..
Essential Question
How Can You Use Benchmarks to Compare Fractions?
Answer:
Compare fractions with different denominators by finding the least common denominators and converting the fractions to it so the numerators can be compared.
Explanation:
For example,
Determine whether \(\frac{8}{15}\) is less than or equal to \(\frac{4}{5}\)
Note that because 5 is a multiple of 15, the least common denominator is 15.
Convert the fractions: \(\frac{8}{15}\) remains the same and \(\frac{4}{5}\) becomes \(\frac{12}{15}\)
Write that \(\frac{8}{15}\) is less than \(\frac{4}{5}\) since the 8 is smaller than the 12.
Visual Learning Bridge
Robert needs \(\frac{3}{8}\) stick of butter to make muffins and stick of butter to make cookies. Which recipe uses more butter?

Compare \(\frac{3}{8}\) to the benchmark fraction \(\frac{1}{2}\).
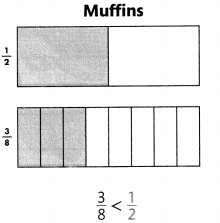
You can compare these fractions because they refer to the same whole, a stick of butter.
Compare \(\frac{2}{3}\) to the benchmark fraction \(\frac{1}{2}\)?
Answer:
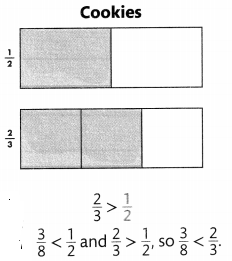
The cookie recipe uses more butter.
Explanation:

Convince Me! Critique Reasoning Ernesto said, “I know \(\frac{3}{8}\) is less than \(\frac{2}{3}\) because \(\frac{3}{8}\) is closer to 0 than it is to 1 and \(\frac{2}{3}\) is closer to 1 than it is to 0.” Does Ernesto’s reasoning make sense? Draw two number lines to support your answer.
Answer:
i) we can use benchmarks to compare fractions
ii) A benchmark is a known size or amount that helps us understand a different size or amount.
iii) we can use models or benchmarks on a number line to compare fractions.
Explanation:
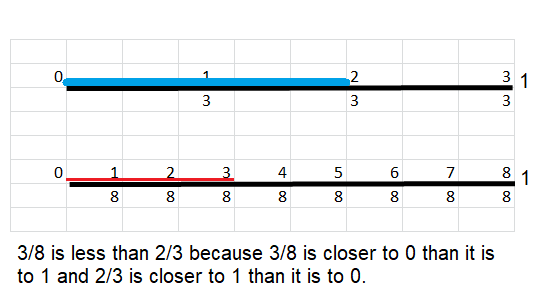
Another Example!
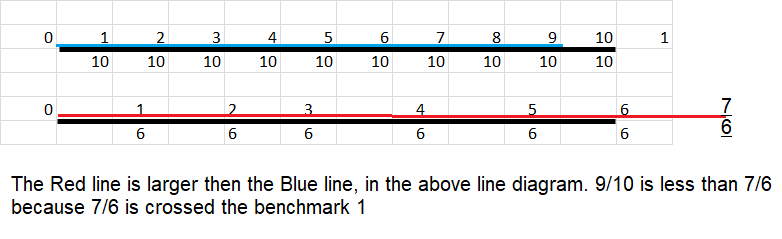
Compare \(\frac{9}{10}\) and \(\frac{7}{6}\). Use 1 whole as a benchmark.
\(\frac{9}{10}\) < 1 and \(\frac{7}{6}\) > 1, so \(\frac{9}{10}\) < \(\frac{7}{6}\).
Answer:
Guided Practice
Do You Understand?
Question 1.
Carl found \(\frac{4}{8}\) is equal to \(\frac{1}{2}\), and \(\frac{1}{3}\) is less than \(\frac{1}{2}\). How can Carl compare \(\frac{4}{8}\) to \(\frac{1}{3}\).
Answer:
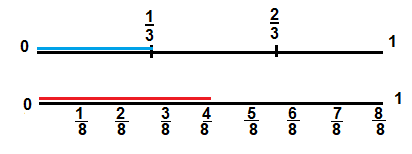
Explanation:
carl – by comparing the blue line with the red line in the above number line picture, it shown that \(\frac{1}{3}\) is less then \(\frac{4}{8}\)
\(\frac{4}{8}\) and \(\frac{1}{2}\) are equal.
Question 2.
Write a fraction that is closer to 0 than to 1. Write another fraction that is closer to 1 than to 0. Use your fractions to complete the comparison.
\(\frac{}{}\) < \(\frac{}{}\)
Answer:
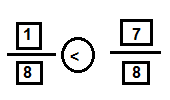
Explanation:
Lets take example \(\frac{1}{8}\) and \(\frac{7}{8}\) are the two fractions
By applying division rule
\(\frac{1}{8}\) = 0.1
So, \(\frac{1}{8}\) is closer to the 0
\(\frac{7}{8}\) = 0.8
So, \(\frac{7}{8}\)is closer to the 1
Do You Know How?
For 3-4, compare. Write <, >, or =.
Question 3.
\(\frac{2}{6}\) ![]() \(\frac{4}{5}\)
\(\frac{4}{5}\)
Answer:
![]()
Explanation:
By applying division rule
\(\frac{2}{6}\) = 0.3 and \(\frac{4}{5}\) = 0.8
So, \(\frac{2}{6}\) is less than \(\frac{4}{5}\)
Question 4.
\(\frac{11}{12}\) ![]() \(\frac{9}{8}\)
\(\frac{9}{8}\)
Answer:

Explanation:
By applying division rule
\(\frac{11}{12}\) = 0.9 and \(\frac{9}{8}\) = 1.1
So, \(\frac{11}{12}\) smaller then \(\frac{9}{8}\)
Question 5.
Circle the fractions that are less than \(\frac{1}{2}\).
\(\begin{array}{llllll}
\frac{5}{4} & \frac{1}{4} & \frac{1}{5} & \frac{2}{3} & \frac{2}{12} & \frac{51}{100}
\end{array}\)
Answer:
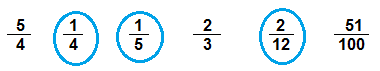
Explanation:
By applying division rule
\(\frac{5}{4}\) = 1.2
\(\frac{1}{4}\) = 0.2
\(\frac{1}{5}\) = 0.2
\(\frac{2}{3}\) = 0.3
\(\frac{2}{12}\) =0.2
\(\frac{51}{100}\) = 0.4
So, Fractions \(\frac{1}{4}\), \(\frac{1}{5}\) and \(\frac{2}{12}\) are less then \(\frac{1}{2}\)
Question 6.
Circle the fractions that are greater than 1.
\(\begin{array}{llllll}
\frac{99}{100} & \frac{6}{5} & \frac{7}{8} & \frac{14}{8} & \frac{11}{10} & \frac{11}{12}
\end{array}\)
Answer:
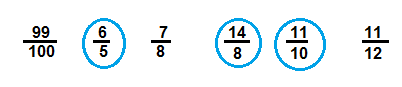
Explanation:
By applying division rule
\(\frac{99}{100}\) = 0.9
\(\frac{6}{5}\) = 1.2
\(\frac{7}{8}\) = 0.8
\(\frac{14}{8}\) = 1.7
\(\frac{11}{10}\) = 1.1
\(\frac{11}{12}\) = 0.9
So, Fractions \(\frac{6}{5}\), \(\frac{14}{8}\) and \(\frac{11}{10}\) are greater then 1
Independent Practice
For 7-10, circle all the fractions that match each statement.
Question 7.
Fractions less than \(\frac{1}{2}\)
\(\begin{array}{llllll}
\frac{3}{4} & \frac{1}{6} & \frac{6}{12} & \frac{4}{10} & \frac{5}{8} & \frac{5}{2}
\end{array}\)
Answer:

Explanation:
Perform the divisions:
\(\frac{1}{6}\) = 0.15 (rounded) and \(\frac{4}{10}\) = 0.8 (rounded).
\(\frac{1}{6}\) and \(\frac{4}{10}\) are the fractions less than \(\frac{1}{2}\)
\(\frac{3}{4}\); \(\frac{6}{12}\); \(\frac{5}{8}\); \(\frac{5}{2}\) are the fractions less than \(\frac{1}{2}\)
Question 8.
Fractions greater than \(\frac{1}{2}\)
\(\begin{array}{llllll}
\frac{5}{8} & \frac{1}{4} & \frac{6}{3} & \frac{7}{10} & \frac{5}{12} & \frac{6}{12}
\end{array}\)
Answer:
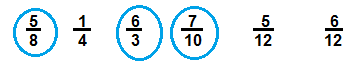
Explanation;
Perform the divisions
\(\frac{5}{8}\) = 0.62 ; \(\frac{6}{3}\) = 2.0; \(\frac{7}{10}\) = 0.7
So, \(\frac{5}{8}\); \(\frac{6}{3}\); \(\frac{7}{10}\) are the fractions greater than \(\frac{1}{2}\)
where as \(\frac{1}{4}\); \(\frac{5}{12}\); \(\frac{6}{12}\) are the fractions less than \(\frac{1}{2}\)
Question 9.
Fractions greater than \(\frac{1}{2}\)
\(\begin{array}{llllll}
\frac{5}{4} & \frac{2}{3} & \frac{6}{6} & \frac{1}{10} & \frac{15}{12} & \frac{7}{8}
\end{array}\)
Answer:

Explanation:
when we perform the divisions
\(\frac{5}{4}\) = 1.24
\(\frac{15}{12}\) = 1.3
So, \(\frac{5}{4}\)and \(\frac{15}{12}\) fractions are greater than \(\frac{1}{2}\)
Question 10.
Fractions closer to 0 than to 1
\(\begin{array}{llllll}
\frac{3}{4} & \frac{1}{8} & \frac{1}{4} & \frac{7}{5} & \frac{2}{4} & \frac{3}{10}
\end{array}\)
Answer:
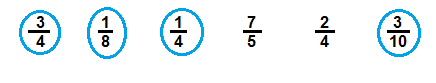
Explanation:
when we perform the divisions
\(\frac{3}{4}\) = 0.7
\(\frac{1}{8}\) = 0.1
\(\frac{1}{4}\) = 0.2
\(\frac{3}{10}\) = 0.3
So, \(\frac{3}{4}\); \(\frac{1}{8}\); \(\frac{1}{4}\)and \(\frac{3}{10}\) fractions are closer to 0 than 1.
For 11-18, compare using benchmark fractions or 1. Then write >,<, or =.
Question 11.
\(\frac{1}{3}\) ![]() \(\frac{4}{6}\)
\(\frac{4}{6}\)
Answer:

Explanation:
Perform the divisions:
\(\frac{1}{3}\) = 0.33 (rounded) and \(\frac{4}{6}\) = 0.58
The decimal form of \(\frac{1}{3}\) is less than \(\frac{4}{6}\)
Question 12.
\(\frac{4}{8}[/latex] ![]() [latex]\frac{2}{4}\)
[latex]\frac{2}{4}\)
Answer:

Explanation:
By applying division rule
\(\frac{4}{8}\) = 0.5
\(\frac{2}{4}\) = 0.5
so, \(\frac{4}{8}\) and \(\frac{2}{4}\) are equivalent fractions.
Question 13.
\(\frac{7}{5}\) ![]() \(\frac{7}{8}\)
\(\frac{7}{8}\)
Answer:

Explanation:
Perform the divisions:
\(\frac{7}{5}\)= 1.4 (rounded) and \(\frac{7}{8}\)= 0.87
The decimal form of \(\frac{7}{5}\) is greater than \(\frac{7}{8}\)
Question 14.
\(\frac{6}{12}\) ![]() \(\frac{4}{5}\)
\(\frac{4}{5}\)
Answer:

Explanation:
Perform the divisions:
\(\frac{6}{12}\) = 0.5 (rounded) and \(\frac{4}{5}\) = 0.8
The decimal form of \(\frac{6}{12}\) is less than \(\frac{4}{5}\)
Question 15.
\(\frac{4}{5}\) ![]() \(\frac{2}{5}\)
\(\frac{2}{5}\)
Answer:

Explanation:
Perform the divisions:
\(\frac{4}{5}\) = 0.8 (rounded) and \(\frac{2}{5}\) = 0.4
The decimal form of \(\frac{4}{5}\) is greater than \(\frac{2}{5}\)
Question 16.
\(\frac{6}{6}\) ![]() \(\frac{13}{12}\)
\(\frac{13}{12}\)
Answer:

Explanation:
Perform the divisions:
\(\frac{6}{6}\) = 1 and \(\frac{13}{12}\) = 1.08
The decimal form of \(\frac{6}{6}\) is less than \(\frac{13}{12}\)
Question 17.
\(\frac{8}{10}\) ![]() \(\frac{1}{8}\)
\(\frac{1}{8}\)
Answer:

Explanation:
Perform the divisions:
\(\frac{8}{10}\) = 0.8 (rounded) and \(\frac{1}{8}\) = 0.12
The decimal form of \(\frac{8}{10}\) is greater than \(\frac{1}{8}\)
Question 18.
\(\frac{4}{4}\) ![]() \(\frac{10}{10}\)
\(\frac{10}{10}\)
Answer:
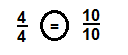
Explanation:
Perform the divisions:
\(\frac{4}{4}\) = 1 and \(\frac{10}{10}\) = 1
So, The decimal form of \(\frac{4}{4}\) is equal to \(\frac{10}{10}\)
Problem Solving
Question 19.
Reasoning Jordan has \(\frac{5}{8}\) can of green paint and \(\frac{3}{6}\) can of blue paint. If the cans are the same size, does Jordan have more green paint or blue paint? Explain.
Answer:
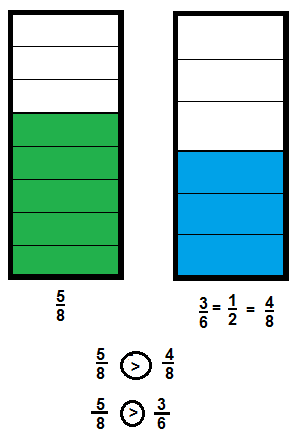
Explanation:
By applying division rule
\(\frac{5}{8}\) = 0.6
\(\frac{4}{8}\) = 0.5
\(\frac{3}{6}\) = 0.5
So, \(\frac{5}{8}\) is greater than \(\frac{4}{8}\) and \(\frac{3}{6}\)
So, Jordan has more green paints rather than blue paints.
Question 20.
Vocabulary Write two examples of a benchmark fraction.
Answer:
Benchmark fractions are fractions that are easy to picture mentally, like \(\frac{1}{4}\), \(\frac{1}{2}\), or \(\frac{3}{4}\)
For example, the fraction \(\frac{1}{2}\) is a very well-known fraction that means 1 of 2 equal parts, or exactly a half of a whole.
Benchmark fractions can be used on number line to compare fractions.
Explanation:

Question 21.
Four neighbors each have gardens that are the same size.


a. Which neighbors planted vegetables in less than half of their gardens?
Answer:
James and Claudia planted vegetables in less than half of their gardens
Explanation:
By Multiple fraction method
James \(\frac{5}{12}\) fraction is written as
5 x 5 = 25
12 x 5 = 60
So, \(\frac{5}{12}\) = \(\frac{25}{60}\) < \(\frac{1}{2}\)
Claudia fraction \(\frac{1}{6}\) is written as
10 x 1 = 10
10 x 6 = 60
So, \(\frac{1}{6}\) = \(\frac{10}{60}\) < \(\frac{1}{2}\)
b. Who has a larger section of vegetables in their garden, Margaret or Wayne?
Answer:
Wayne has a larger section of vegetables.
Explanation:
Margaret planted \(\frac{1}{2}\) vegetables of their gardens,
\(\frac{5}{10}\) = \(\frac{30}{60}\)
6 x 5 = 30
6 x 10 = 60
Wayne more then half planted vegetables of their gardens
\(\frac{2}{3}\) = \(\frac{40}{60}\)
20 x 2 = 40
20 x 3 = 60
Question 22.
Gavin bought 3 pizzas for a party. Each pizza had 8 slices. There were 8 other people at the party. Everyone ate the same number of slices. How many slices did each person eat? How many slices were left over?
Answer:
Each person ate 2 slices
6 slices were left
Explanation:

Question 23.
Higher Order Thinking How can you tell just by looking at the numerator and denominator of a fraction if it is closer to O or to 1? Give some examples in your explanation.
Answer:

If the numerators are with smaller number and denominators are with greater number, we can conclude that the fraction is closer to 0 or to 1.
Examples:
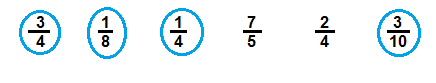
Explanation:
Perform division rule
\(\frac{3}{4}\) = 0.7;
\(\frac{1}{8}\) = 0.1
\(\frac{1}{4}\) = 0.2
\(\frac{3}{10}\) = 0.3
So, \(\frac{3}{4}\); \(\frac{1}{8}\); \(\frac{1}{4}\)and \(\frac{3}{10}\) fractions are closer to 0 than 1.
Assessment Practice
Question 24.
Donna ate \(\frac{7}{12}\) box of popcorn. Jack ate \(\frac{4}{10}\) box of popcorn. The boxes of popcorn are the same size. Write to explain how to use a benchmark fraction to determine who ate more popcorn.
Answer:
Donna ate more
\(\frac{7}{12}\) > \(\frac{4}{10}\)
Explanation
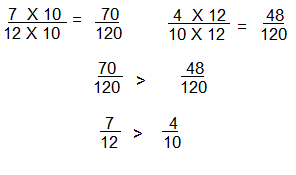
Lesson 8.6 Compare Fractions
Solve & Share
Juan read for \(\frac{5}{6}\) of an hour. Larissa read for \(\frac{10}{12}\) of an hour. Who read for a longer period of time? Explain. Solve this problem any way you choose.
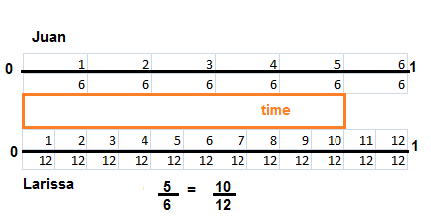
I can … use equivalent fractions to compare fractions.

Look Back! Carlos read for \(\frac{8}{12}\) of an hour. Did Carlos read for more or less time than Juan? Write your answer as a number sentence using >, <, or =.
Answer:
\(\frac{5}{6}\)> \(\frac{8}{12}\)
Explanation:
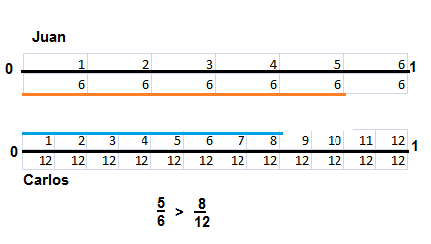
Essential Question
How Can You Compare Fractions with Unlike Denominators?
Answer:
We can compare fractions with unlike denominators by finding the least common denominator, or the smallest multiple the denominators share. Then we make equivalent fractions, or fractions that represent the same part of the whole.
Explanation:
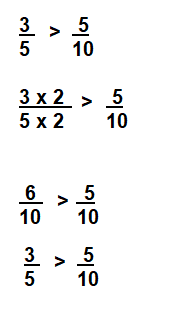
\(\frac{3}{5}\) > \(\frac{5}{10}\)
Visual Learning Bridge
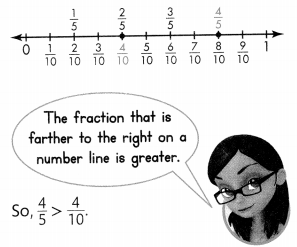
Isabella’s father is building a model dinosaur with small pieces of wood. Compare the lengths of the pieces of wood. Compare \(\frac{1}{4}\) inch and \(\frac{5}{6}\) inch. Then, compare \(\frac{4}{5}\) inch and \(\frac{4}{10}\) inch.
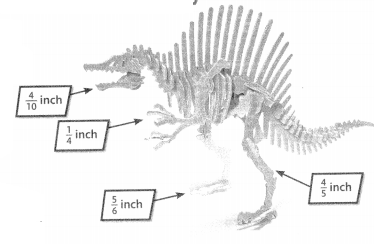
You can compare these fractions because they refer to the same whole, an inch.
Compare \(\frac{1}{4}\) and \(\frac{5}{6}\) by renaming each fraction so they both have the same denominator.
\(\frac{1}{4}=\frac{1 \times 3}{4 \times 3}=\frac{3}{12} \quad \frac{5}{6}=\frac{5 \times 2}{6 \times 2}=\frac{10}{12}\)
Compare the numerators of the renamed fractions.
\(\frac{1}{2}\) < \(\frac{1}{2}\)
So, \(\frac{1}{2}\) < \(\frac{1}{2}\).
Compare \(\frac{4}{5}\) and \(\frac{4}{10}\) on a number line.
Convince Me! Critique Reasoning The fractions on the right refer to the same whole. Kelly said, “These are easy to compare. I just think about \(\frac{1}{8}\) and \(\frac{1}{6}\).” Circle the greater fraction. Explain what Kelly was thinking.
\(\frac{5}{8}\)
\(\frac{5}{6}\)
Another Example!
Compare \(\frac{3}{4}\) and \(\frac{6}{10}\).
Create an equivalent fraction for either \(\frac{3}{4}\) or \(\frac{6}{10}\)
so that the numerators are the same.
\(\frac{6 \div 2}{10 \div 2}=\frac{3}{5}\)
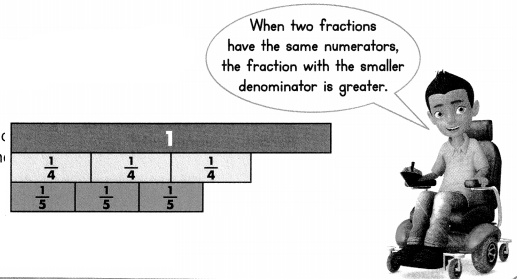
\(\frac{3}{4}>\frac{3}{5}\) When you divide a whole into 4 equal parts, each part is larger than when you divide it into 5 equal parts.
Guided Practice
Do You Understand?
Question 1.
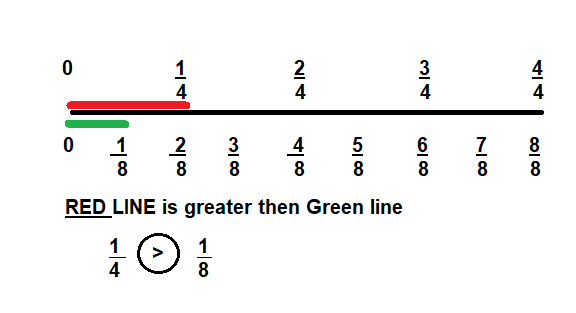
Mary says \(\frac{1}{8}\) is greater than \(\frac{1}{4}\), because 8 is greater than 4. Is Mary’s reasoning correct? Explain.
Answer:
NO, Mary’s reasoning is wrong
Explanation:
Do You Know How?
For 2-5, write >, <, or =. Use number lines, fraction strips, benchmark or equivalent fractions.
Question 2.
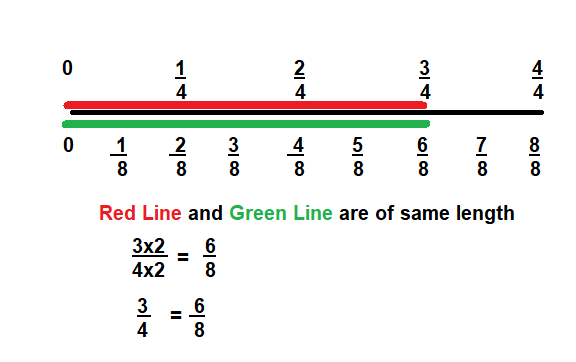
\(\frac{3}{4}\) ![]() \(\frac{6}{8}\)
\(\frac{6}{8}\)
Answer:
\(\frac{3}{4}\) = \(\frac{6}{8}\)
Explanation:
Question 3.
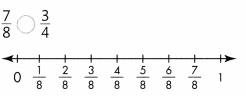
\(\frac{1}{4}\) ![]() \(\frac{1}{10}\)
\(\frac{1}{10}\)
Answer:
\(\frac{1}{4}\) > \(\frac{1}{10}\)
Explanation:
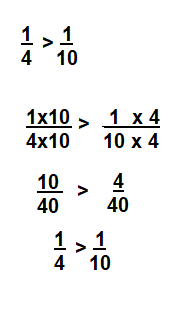
Question 4.
\(\frac{3}{5}\) ![]() \(\frac{5}{10}\)
\(\frac{5}{10}\)
Answer:
\(\frac{3}{5}\) > \(\frac{5}{10}\)
Explanation:
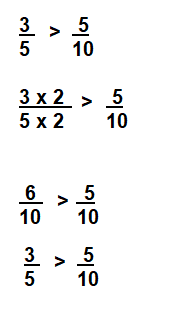
Question 5.
\(\frac{1}{2}\) ![]() \(\frac{4}{5}\)
\(\frac{4}{5}\)
Answer:
\(\frac{1}{2}\) < \(\frac{4}{5}\)
Explanation:
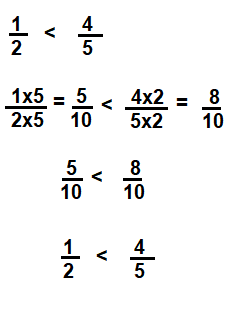
Independent Practice
Leveled Practice For 6-15, find equivalent fractions to compare. Then, write >, <, or =.
Question 6.
Answer:
7/8 > 6/8
Explanation:
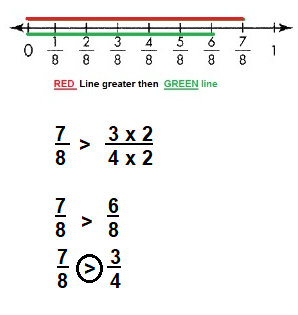
Question 7.
\(\frac{5}{6}\) ![]() \(\frac{10}{12}\)
\(\frac{10}{12}\)
Answer:
\(\frac{5}{6}\) = \(\frac{10}{12}\)
Explanation:
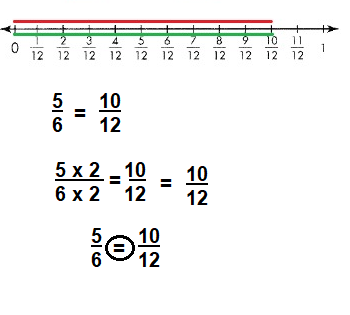
Question 8.
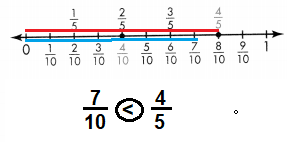
\(\frac{7}{10}\) ![]() \(\frac{4}{5}\)
\(\frac{4}{5}\)
Answer:
\(\frac{7}{10}\) < \(\frac{4}{5}\)
Explanation:
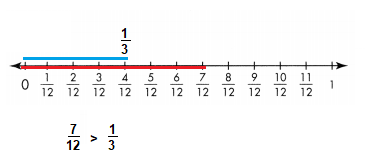
Question 9.
\(\frac{7}{12}\) ![]() \(\frac{1}{3}\)
\(\frac{1}{3}\)
Answer:
\(\frac{7}{12}\) > \(\frac{1}{3}\)
Explanation:
Question 10.
\(\frac{5}{12}\) ![]() \(\frac{4}{5}\)
\(\frac{4}{5}\)
Answer:
\(\frac{5}{12}\) < \(\frac{4}{5}\)5/12 < 4/5
Explanation:
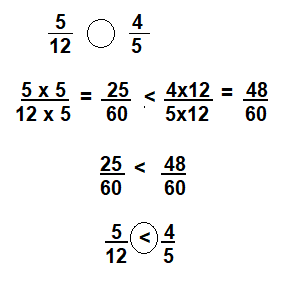
Question 11.
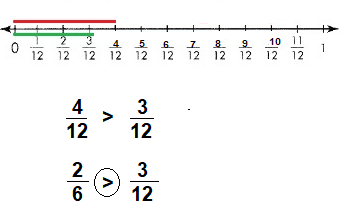
\(\frac{2}{6}\) ![]() \(\frac{3}{12}\)
\(\frac{3}{12}\)
Answer:
\(\frac{2}{6}\) > \(\frac{3}{12}\)
Question 12.
\(\frac{6}{8}\) ![]() \(\frac{3}{4}\)
\(\frac{3}{4}\)
Answer:
\(\frac{6}{8}\) = \(\frac{3}{4}\)
Explanation:

Question 13.
\(\frac{6}{10}\) ![]() \(\frac{3}{6}\)
\(\frac{3}{6}\)
Answer:
\(\frac{6}{10}\) > \(\frac{3}{6}\)
Explanation:
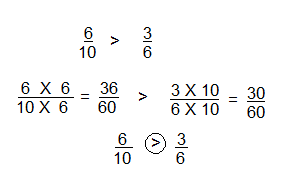
Question 14.
\(\frac{2}{10}\) ![]() \(\frac{1}{6}\)
\(\frac{1}{6}\)
Answer:
\(\frac{2}{10}\) > \(\frac{1}{6}\)
Explanation:

Question 15.
\(\frac{5}{6}\) ![]() \(\frac{2}{3}\)
\(\frac{2}{3}\)
Answer:
\(\frac{5}{6}\) > \(\frac{2}{3}\)
Explanation:
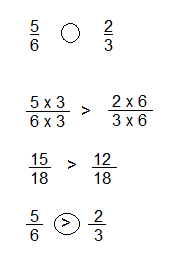
Problem Solving
Question 16.
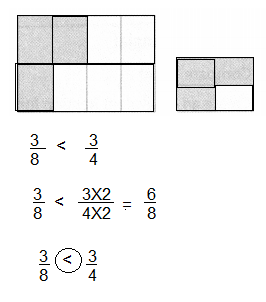
Felicia drew the pictures at the right to show \(\frac{3}{8}\) is greater than \(\frac{3}{4}\). What was Felicia’s mistake?
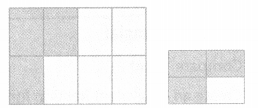
Answer:
YES, Felicia mistake
\(\frac{3}{8}\) < \(\frac{3}{4}\)
Explanation:
Question 17.
Critique Reasoning Jake said you can compare two fractions with the same denominator by only comparing the numerators. Is Jake correct? Explain.
Answer:
Yes, Jake is correct.
Explanation:
Jack said correct
Only compare numerators of two fractions, with same denominator, if different denominators are there, either by multiplying or dividing the fraction to make the denominator same for comparing the fractions.
Example : \(\frac{A}{D}\) < \(\frac{B}{D}\)
A and B are numerators are compared (A<B), D denominator is same for both the fractions.
Question 18.
Tina completed \(\frac{2}{3}\) of her homework. George completed \(\frac{8}{9}\) of his homework. Tina and George have the same amount of homework. Who completed a greater fraction of homework?
Answer:
\(\frac{2}{3}\) < \(\frac{8}{9}\)
Explanation:
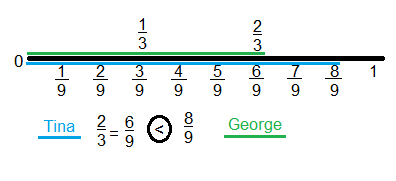
Question 19.
If 34 × 2 = 68 then what does 34 × 20 equal?
Answer:
680
Explanation:
34 X 2 = 68
34 X 20 =680
Question 20.
What can you conclude about \(\frac{3}{5}\) and \(\frac{60}{100}\) if you know \(\frac{3}{5}\) is equivalent to \(\frac{6}{10}\) and \(\frac{6}{100}\) is equivalent to \(\frac{60}{100}\)?
Answer:
Equivalent fractions.
\(\frac{6}{100}\) Not Equal to \(\frac{60}{100}\)
\(\frac{3}{5}\) = \(\frac{6}{10}\) and \(\frac{6}{10}\) = \(\frac{60}{100}\)
Explanation:
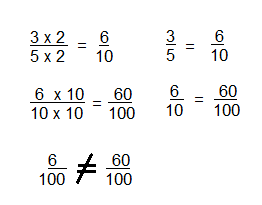
Question 21.
Jackson played a video game for \(\frac{1}{6}\) hour. Hailey played a video game for \(\frac{1}{3}\) hour. Who played the video game for a greater amount of time? Explain.
Answer:
Hailey played greater amount of time.
\(\frac{1}{6}\) < \(\frac{1}{3}\)
Explanation:
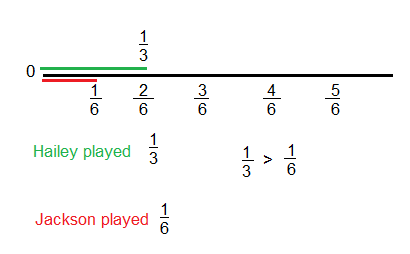
Question 22.
Higher Order Thinking Write a fraction that is greater than \(\frac{3}{12}\), is less than \(\frac{75}{100}\) and has 6 as a denominator.
Answer:
\(\frac{5}{6}\)
Explanation:
(\(\frac{75}100}]\) = \(\frac{3}{4}\) or \(\frac{9}{12}\) are equivalent fractions)
\(\frac{3}{12}\) < \(\frac{75}{100}\) < \(\frac{X}{6}\) X \(\frac{2}{2}\)
\(\frac{3}{12}\) < \(\frac{3}{4}\) X \(\frac{3}{3}\)< \(\frac{10}{12}\)
\(\frac{3}{12}\) < \(\frac{9}{12}\)< \(\frac{10}{12}\)
\(\frac{3}{12}\) < \(\frac{75}{100}\) < \(\frac{5}{6}\)
Assessment Practice
Question 23.
Select all fractions that would make the comparison true.
\(\frac{3}{4}\) = ________
☐ \(\frac{5}{12}\)
☐ \(\frac{75}{100}\)
☐ \(\frac{9}{12}\)
☐ \(\frac{7}{10}\)
☐ \(\frac{6}{8}\)
Answer:

Question 24.
Select all answer choices that show a correct comparison
☐ \(\frac{5}{6}\) > \(\frac{7}{12}\)
☐ \(\frac{1}{2}\) > \(\frac{10}{10}\)
☐ \(\frac{4}{10}\) > \(\frac{2}{6}\)
☐ \(\frac{1}{5}\) < \(\frac{2}{3}\)
☐ \(\frac{2}{3}\) > \(\frac{9}{12}\)
Answer:

Lesson 8.7 Problem Solving
Construct Arguments
Solve & Share
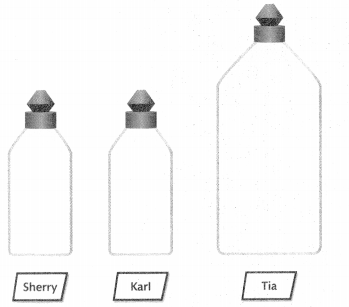
Sherry and Karl both started their hike with a small bottle filled with water. Tia started her hike with a larger bottle that was \(\frac{1}{2}\) full. At the end of the hike, Sherry and Tia’s bottles were each half filled with water. Karl’s bottle was \(\frac{1}{3}\) filled with water. Who has the most water left? Construct a math argument to support your answer.
I can … construct math arguments using what I know about fractions.
Thinking Habits
Be a good thinker! These questions can help you.
- How can I use numbers, objects, drawings, or actions to justify my argument?
- Am I using numbers and symbols correctly?
- Is my explanation clear and complete?
Look Back! Construct Arguments if Tia’s bottle was filled with water at the end of the hike, would you be able to decide who had the most water left? Construct an argument to support your answer.
Answer:
Tia left with most water
Explanation:
Sherry and Karl starter with say \(\frac{6}{12}\) and left with \(\frac{3}{12}\)
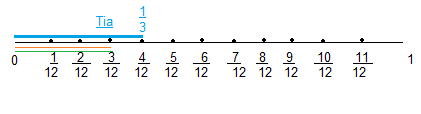
Sherry and Karl both started small bottle filled with water.
Tia started larger bottle \(\frac{1}{2}\) filled.
As the sizes of the bottles are different, a common denominator to be find to compare these three fractions.
Let 12 be the common denominator for these three fractions.
Sherry and Karl both started small bottle filled with water \(\frac{6}{12}\) = \(\frac{1}{2}\) of water compared to larger bottle.
After hike Tia is with \(\frac{1}{3}\) of water in her larger water bottle = \(\frac{4}{12}\) of water left.
Essential Question
How Can You Construct Arguments?
Answer:
I can
- use numbers, objects, drawings, or models to justify my arguments.
- use a counterexample in my argument.
- give an explanation of my argument that is clear and complete.
Visual Learning Bridge
Erin said \(\frac{1}{2}\) is the same amount as \(\frac{2}{4}\).
Matt said \(\frac{1}{2}\) and \(\frac{2}{4}\) can be different amounts.
Which student is correct?
A good math argument is correct, simple, complete, and easy to understand.
What do you need to do to solve this problem?
I need to construct an argument with what I know about fraction models and ways to show \(\frac{1}{2}\) and \(\frac{2}{4}\).
How can I construct an argument?
I can
- use numbers, objects, drawings, or models to justify my arguments.
- use a counterexample in my argument.
- give an explanation of my argument that is clear and complete.
Here’s my thinking.
I will use drawings to show which student is correct.
Both wholes are the same size. The \(\frac{1}{2}\) and \(\frac{2}{4}\) represent the same part of the whole.
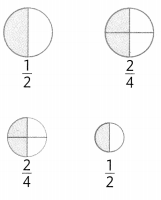
These wholes are not the same size. So, \(\frac{2}{4}\) of the larger circle represents more than \(\frac{1}{2}\) of the smaller circle.
Both students are correct. \(\frac{1}{2}\) and \(\frac{2}{4}\) of the same-size whole are the same amount. \(\frac{1}{2}\) and \(\frac{2}{4}\) of different-size wholes are different amounts.
Convince Me! Critique Reasoning Erin also said \(\frac{3}{6}\) and \(\frac{5}{10}\) are NOT the same size because the denominators are not factors of each other. Is Erin’s argument correct? Explain.
Answer:
No, Erin’s argument is not correct.
As both fractions are same even though there denominators are different.
\(\frac{3}{6}\) and \(\frac{5}{10}\)
Explanation:
With reference to benchmark reference,
\(\frac{3}{6}\) ÷ \(\frac{3}{3}\) = \(\frac{1}{2}\)
\(\frac{5}{10}\) ÷ \(\frac{5}{5}\) = \(\frac{1}{2}\)
Guided Practice
Construct Arguments Margie and Parker ordered the same-size burritos. Margie ate of her burrito. Parker ate of his burrito. Margie concluded she ate more than Parker because the fraction of the burrito she ate has a greater denominator.
Question 1.
What is Margie’s argument? How does she support her argument?
Answer:
Same – size of burrito
Burrito made 2 slices or 4 slices
Parker ate 2 slices and Margei ate 4 slice
\(\frac{2}{2}\) = \(\frac{4}{4}\)
Question 2.
Does Margie’s conclusion make sense?
Answer:
No, Margies conclusion does not make sense,
Because both ate same quantity of burrito.
Independent Practice
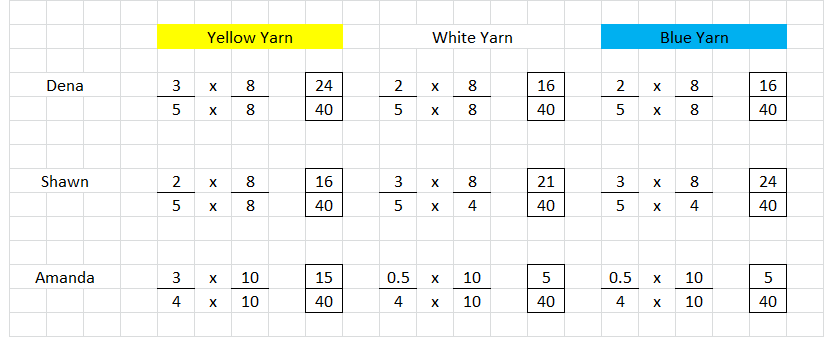
Construct Arguments In the after-school club, Dena, Shawn, and Amanda knit scarves that are all the same size with yellow, white, and blue yarn. Dena’s scarf is \(\frac{3}{5}\) yellow, Shawn’s scarf is \(\frac{2}{5}\) yellow, and Amanda’s scarf is \(\frac{3}{4}\) yellow. The rest of each scarf has an equal amount of white and blue.

Question 3.
Describe how Amanda could make the argument that her scarf has the most yellow.
Answer:
As per the above mathematical calculations
\(\frac{15}{40}\) > \(\frac{5}{40}\) white and \( \frac{5}{40} blue \)
Amanda argument is correct, her scarf has the most yellow
Question 4.
How much of Dena’s scarf is blue?
Answer:
Dena’s scarf is \(\frac{2}{5}\) or \(\frac{16}{40}\) blue.
Question 5.
Dena has a scarf at home that is the same size as the scarf she made in the club. The scarf at home is \(\frac{6}{8}\) yellow. Dena said the scarf at home has more yellow. Is she correct? Explain. Include an explanation of how you make the comparison.
Answer:
YES, Dena is correct.
Explanation:
The denominators are made common by multiplying with same number, as shown below
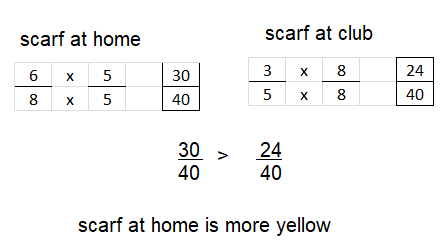
Problem Solving
Performance Task
Snail Race Mr. Aydin’s science class had a snail race to see which snail would crawl the farthest from a starting line in two minutes. The table shows the distances the snails crawled.

Question 6.
Use Appropriate Tools Curly and Stylo traveled the same distance. Justify this conjecture using a number line or fraction strips.
Answer:
Yes, Curly and Stylo traveled the same distance.
\(\frac{12}{60}\) = \(\frac{12}{60}\)
\(\frac{1}{5}\) = \(\frac{2}{10}\)

Question 7.
Construct Arguments who traveled farther, Slimy or Slinky? Change the fractions to have the same denominator.

Answer:
Slimy traveled farther
\(\frac{15}{60}\) > \(\frac{10}{60}\)
Question 8.
Reasoning Who traveled farther, Creeper or Slimy? Change the fractions to have the same numerator.
Answer:
Creeper travelled farther.
\(\frac{20}{60}\) > \(\frac{15}{60}\)
Question 9.
Make Sense and Persevere Who won the race?
Answer:
Creeper won the race.
Topic 8 Fluency Practice Activity
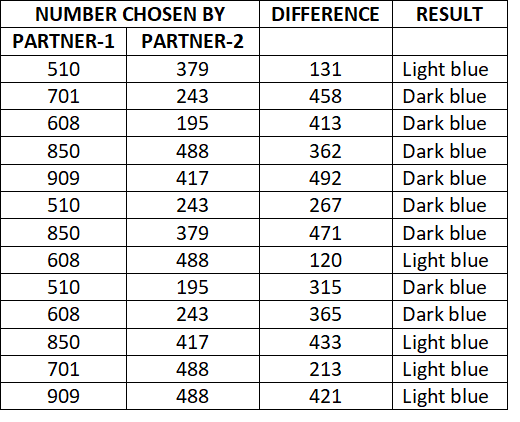
Point & Tally
Find a partner. Get paper and a pencil. Each partner chooses a different color: light blue or dark blue.
Partner 1 and Partner 2 each point to a black number at the same time. Each partner subtracts the two numbers.
If the answer is on your color, you get a tally mark. Work until one partner has twelve tally marks.
I can … subtract multi-digit whole numbers.
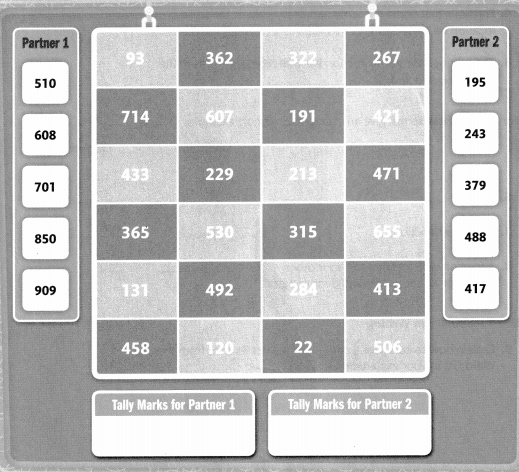
Answer:
Let partner one choose light blue,
Let partner two choose dark blue.
Now partner one and partner two choose a black number from the columns at the same time.
Now subtract the chosen numbers.
Topic 8 Vocabulary Review
Understand Vocabulary
Word List
- benchmark fraction
- common factor
- denominator
- equivalent fractions
- fraction
- numerator
Choose the best term from the box. Write it on the blank.
Question 1.
A number that names part of a whole, part of a set, or a location on a number line is a(n) ___________
Answer:
Fraction.
Question 2.
A commonly used fraction that helps you understand a different size or amount is called a(n) ___________
Answer:
Benchmark Fraction.
Question 3.
The number below the fraction bar in a fraction that shows the total number of equal parts is the ___________
Answer:
Denominator.
Question 4.
Fractions that name the same part of a whole or the same location on a number line are called ____________
Answer:
Equivalent Fractions.
Question 5.
The number above the fraction bar that represents part of the whole is called a(n) ____________
Answer:
Numerator.
For each of these terms, give an example and a non-example.

Answer:

Use Vocabulary in Writing
Question 9.
Explain how to compare \(\frac{5}{8}\) and \(\frac{3}{8}\). Use at least 3 terms from the Word List in your explanation.
Answer:
\(\frac{5}{8}\) and \(\frac{3}{8}\)
Explanation:
First the denominators are compared, both the fraction must be of same denominator then numerators are compared.
here in the given fractions, numerator 5 is greater then the 3.
\(\frac{5}{8}\) > \(\frac{3}{8}\)
Topic 8 Reteaching
Set A pages 293-300
Use an area model to write an equivalent fraction for \(\frac{1}{2}\).
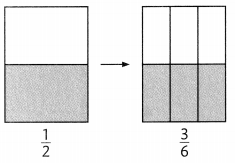
\(\frac{1}{2}\) and \(\frac{3}{6}\)name the same part of the whole.
\(\frac{1}{2}\) and \(\frac{3}{6}\) are equivalent fractions.
Use a number line to write an equivalent fraction for \(\frac{1}{3}\).
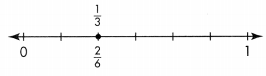
\(\frac{1}{3}\) and \(\frac{2}{6}\) name the same part of the whole.
\(\frac{1}{3}\) and \(\frac{2}{6}\) are equivalent fractions.
Remember that equivalent fractions name the same part of a whole.
Write an equivalent fraction for each fraction given.
Question 1.
\(\frac{2}{8}\)
Answer:
\(\frac{1}{4}\)
Explanation:
By dividing the fraction with the common factor [2] we get:
2 ÷ 2 = 1
8 ÷ 2 = 4
so we get an equivalent fraction \(\frac{1}{4}\)
Question 2.
\(\frac{2}{3}\)
Answer:
\(\frac{4}{6}\)
Explanation:
By multiplying the fraction with the common factor [2] we get:
2 X 2 = 4
2 X 3 = 6
so we get an equivalent fraction \(\frac{4}{6}\)
Question 3.
\(\frac{1}{4}\)
Answer:
\(\frac{2}{8}\)
Explanation:
By dividing the fraction with the common factor [2] we get:
2÷ 2 = 1
8÷ 2 = 4
so we get an equivalent fraction \(\frac{2}{8}\)
Question 4.
\(\frac{3}{4}\)
Answer:
\(\frac{9}{12}\)
Draw a number line to shown each fraction and an equivalent fraction.
Question 5.
\(\frac{4}{6}\)
Answer:
\(\frac{2}{3}\)
Explanation:
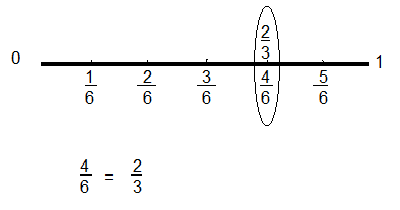
Question 6.
\(\frac{4}{10}\)
Answer:
\(\frac{2}{5}\)
Explanation:

Set B pages 301-308
Find two equivalent fractions for \(\frac{1}{2}\).
\(\frac{1}{2} \times \frac{2}{2}=\frac{2}{4} \quad \frac{1}{2} \times \frac{3}{3}=\frac{3}{6}\)
\(\frac{1}{2}, \frac{2}{4}\), and \(\frac{3}{6}\) are equivalent fractions.
Find two equivalent fractions for \(\frac{8}{12}\).
\(\frac{8}{12} \div \frac{2}{2}=\frac{4}{6} \quad \frac{8}{12} \div \frac{4}{4}=\frac{2}{3}\)
\(\frac{8}{12}, \frac{4}{6}\), and \(\frac{2}{3}\) are equivalent fractions.
Remember that you can multiply or divide to find equivalent fractions.
Multiply or divide to find equivalent fractions.
Question 1.
\(\frac{2}{3}=\frac{8}{}\)
Answer:
\(\frac{8}{12}\)
Explanation:
Multiply the given fraction with common factor 4, then
\(\frac{2}{3}×\frac{4}{4}=\frac{8}{12}\)
Question 2.
\(\frac{1}{4}=\frac{}{8}\)
Answer:
\(\frac{2}{8}\)
Explanation:
Multiply numerattor and denominator with common factor 2, then
\(\frac{1}{4}×\frac{2}{2}=\frac{2}{8}\)
Question 3.
\(\frac{1}{6}=\frac{2}{}\)
Answer:
\(\frac{2}{12}\)
Explanation:
Multiply numerator and denominator with common factor in numerator and denominator then,
\(\frac{1}{6}×\frac{2}{2}=\frac{2}{12}\)
Question 4.
\(\frac{3}{5}=\frac{}{10}\)
Answer:
\(\frac{6}{10}\)
Explanation:
Multiply numerator and denominator with common factor 2 then,
\(\frac{3}{5}×\frac{2}{2}=\frac{6}{10}\)
Question 5.
\(\frac{10}{12}=\frac{5}{}\)
Answer:
\(\frac{5}{6}\)
Explanation:
Divide numerator and denominator with common factor 2, then
\(\frac{10}{12}÷\frac{2}{2}=\frac{5}{6}\)
Question 6.
\(\frac{4}{10}=\frac{}{5}\)
Answer:
\(\frac{2}{5}\)
Explanation:
Divide numerator and denominator with common factor 2, then
\(\frac{4}{10}÷\frac{2}{2}=\frac{2}{5}\)
Question 7.
\(\frac{2}{6}=\frac{1}{}\)
Answer:
\(\frac{1}{3}\)
Explanation:
Divide numerator and denominator with common factor 2, then
\(\frac{2}{6}÷\frac{2}{2}=\frac{1}{3}\)
Question 8.
\(\frac{6}{10}=\frac{}{5}\)
Answer:
\(\frac{3}{5}\)
Explanation:
Divide numerator and denominator with common factor 2, then
\(\frac{6}{10}÷\frac{2}{2}=\frac{3}{5}\)
Set C pages 309-316
Compare \(\frac{5}{8}\) and \(\frac{4}{10}\). Use benchmark fractions.
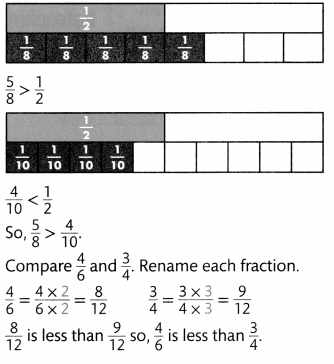
Remember when the numerators of two fractions are the same, the fraction with the lesser denominator is greater.
Use benchmark fractions to compare. Write >, <, or = for each ![]() .
.
Question 1.
\(\frac{5}{5}\) ![]() \(\frac{4}{6}\)
\(\frac{4}{6}\)
Answer:
\(\frac{5}{5}\) > \(\frac{4}{6}\)
Explanation:
Multiply the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{5}{5}\) × \(\frac{6}{6}\) = \(\frac{30}{30}\)
\(\frac{4}{6}\) × \(\frac{5}{5}\) = \(\frac{20}{30}\)
\(\frac{30}{30}\) > \(\frac{20}{30}\)
So, \(\frac{5}{5}\) > \(\frac{4}{6}\)
Question 2.
\(\frac{4}{8}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
Answer:
\(\frac{4}{8}\) = \(\frac{1}{2}\)
Explanation:
Divide the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{4}{8}\) ÷ \(\frac{4}{4}\) = \(\frac{1}{2}\)
\(\frac{1}{2}\) ÷ \(\frac{1}{1}\) = \(\frac{1}{2}\)
So \(\frac{4}{8}\) = \(\frac{1}{2}\)
Question 3.
\(\frac{5}{12}\) ![]() \(\frac{7}{8}\)
\(\frac{7}{8}\)
Answer:
\(\frac{5}{12}\) < \(\frac{7}{8}\)
Explanation:
Multiply the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{5}{12}\) × \(\frac{2}{2}\) = \(\frac{10}{24}\)
\(\frac{7}{8}\) × \(\frac{3}{3}\) = \(\frac{21}{24}\)
\(\frac{10}{24}\) < \(\frac{21}{24}\)
So, \(\frac{5}{12}\) < \(\frac{7}{8}\)
Question 4.
\(\frac{2}{3}\) ![]() \(\frac{4}{6}\)
\(\frac{4}{6}\)
Answer:
\(\frac{2}{3}\) = \(\frac{4}{6}\)
Explanation:
Divide the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{2}{3}\) ÷ \(\frac{1}{1}\) = \(\frac{2}{3}\)
\(\frac{4}{6}\) ÷ \(\frac{2}{2}\) = \(\frac{2}{3}\)
\(\frac{2}{3}\) = \(\frac{4}{6}\)
Compare. Write >, <, or = for each ![]() .
.
Question 5.
\(\frac{3}{4}\) ![]() \(\frac{5}{8}\)
\(\frac{5}{8}\)
Answer:
\(\frac{3}{4}\) > \(\frac{5}{8}\)
Explanation:
Multiply the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{3}{4}\) × \(\frac{2}{2}\) = \(\frac{6}{8}\)
\(\frac{5}{8}\) × \(\frac{1}{2}\) = \(\frac{5}{8}\)
\(\frac{3}{4}\) > \(\frac{8}{6}\)
Question 6.
\(\frac{1}{5}\) ![]() \(\frac{2}{10}\)
\(\frac{2}{10}\)
Answer:
\(\frac{1}{5}\) = \(\frac{2}{10}\)
Explanation:
Multiply the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{1}{5}\) × \(\frac{2}{2}\) = \(\frac{2}{10}\)
\(\frac{2}{10}\) × \(\frac{1}{1}\) = \(\frac{2}{10}\)
\(\frac{1}{5}\) = \(\frac{2}{10}\)
Question 7.
\(\frac{2}{5}\) ![]() \(\frac{1}{4}\)
\(\frac{1}{4}\)
Answer:
\(\frac{2}{5}\) > \(\frac{1}{4}\)
Explanation:
Multiply the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{2}{5}\) × \(\frac{4}{4}\) = \(\frac{8}{20}\)
\(\frac{1}{4}\) × \(\frac{5}{5}\) = \(\frac{5}{120}\)
\(\frac{2}{5}\) = \(\frac{1}{4}\)
Question 8.
\(\frac{3}{6}\) ![]() \(\frac{3}{4}\)
\(\frac{3}{4}\)
Answer:
\(\frac{3}{6}\) < \(\frac{3}{4}\)
Explanation:
Multiply the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{3}{6}\) × \(\frac{2}{2}\) = \(\frac{6}{12}\)
\(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
\(\frac{3}{6}\) < \(\frac{3}{4}\)
Question 9.
\(\frac{2}{4}\) ![]() \(\frac{2}{3}\)
\(\frac{2}{3}\)
Answer:
\(\frac{2}{4}\) < \(\frac{2}{3}\)
Explanation:
Multiply the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{2}{4}\) × \(\frac{3}{3}\) = \(\frac{6}{12}\)
\(\frac{2}{3}\) × \(\frac{4}{4}\) = \(\frac{8}{12}\)
\(\frac{2}{4}\) < \(\frac{2}{3}\)
Question 10.
\(\frac{8}{10}\) ![]() \(\frac{4}{6}\)
\(\frac{4}{6}\)
Answer:
\(\frac{8}{10}\) >\(\frac{4}{6}\)
Explanation:
Multiply the fractions on both sides with common number to get same denominator, then compare the numerator
\(\frac{8}{10}\) × \(\frac{6}{6}\) = \(\frac{48}{60}\)
\(\frac{4}{6}\) × \(\frac{10}{10}\) = \(\frac{40}{60}\)
\(\frac{8}{10}\) > \(\frac{4}{6}\)
Set D pages 317-320
Think about these questions to help you construct arguments.
Thinking Habits
- How can I use numbers, objects, drawings, or actions to justify my argument?
- Am I using numbers and symbols correctly?
- Is my explanation clear and complete?

Remember you can use drawings and numbers to construct arguments.
Peter says \(\frac{3}{4}\) of a pizza is always the same as of a pizza. Nadia says while \(\frac{3}{4}\) and \(\frac{6}{8}\) are equivalent fractions, \(\frac{3}{4}\) and \(\frac{6}{8}\) of a pizza could represent different amounts.
Question 1.
Who is correct? Explain. Use a drawing to justify your argument.
Answer:
Nadia is correct
\(\frac{3}{4}\) = \(\frac{6}{8}\)
Explanation:

Question 2.
Use a counter example to explain who is correct.
Answer:
\(\frac{1}{2}\) = \(\frac{2}{4}\)
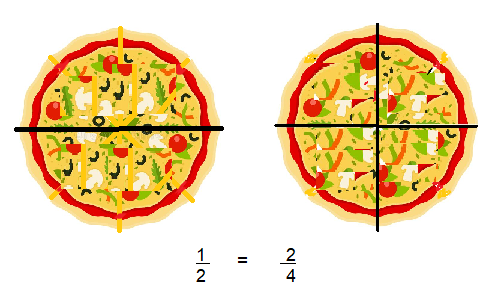
Topic 8 Assessment Practice
Question 1.
Draw a model to show that \(\frac{3}{4}=\frac{6}{8}\).
Answer:

Question 2.
Leslie will use more than \(\frac{1}{2}\) cup but less than 1 whole cup of flour for a recipe. What fraction of a cup might Leslie use? Explain.
Answer:
\(\frac{3}{4}\)
\(\frac{1}{2}\) < \(\frac{3}{4}\) < 1
Explanation:
Leslie use \(\frac{3}{4}\) cup of flour
Question 3.
Jared has mowed \(\frac{2}{5}\) of the yard. Abby says that Jared has mowed \(\frac{4}{6}\) of the yard. Is Abby correct? Explain.
Answer:
No, Abby is wrong.
Explanation:
\(\frac{2}{5}\) and \(\frac{4}{6}\) are not equivalent fractions
Question 4.
Explain how to use division to find an equivalent fraction for \(\frac{9}{12}\).
Answer:
\(\frac{3}{4}\) is an equivalent fraction for \(\frac{9}{12}\).
Explanation:
Divide both numerator and denominator with common factor 3, then
\(\frac{9}{12}÷\frac{3}{3}=\frac{3}{4}\)
Question 5.
Write two fractions that are equivalent to \(\frac{3}{6}\). Describe how you can show they are equivalent.
Answer:
\(\frac{1}{2}\) and \(\frac{6}{12}\) are two equivalent fractions of \(\frac{3}{6}\)
Explanation
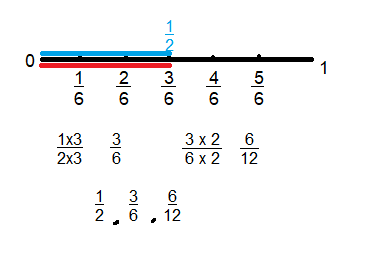
Question 6.
Compare the fractions to \(\frac{1}{2}\). Write each fraction in the correct answer space.

Answer:

Question 7.
Sarah and Cole both ordered large subs for lunch. Sarah had \(\frac{1}{2}\) of a sub and Cole had \(\frac{2}{5}\) of a sub. Who ate more? Explain.
A. The subs are different sizes, so it is impossible to compare the fractions and tell who ate more.
B. Sarah ate more than Cole, as \(\frac{2}{5}\) < \(\frac{1}{2}\).
C. Sarah’s sub was bigger than Cole’s, so Sarah ate more.
D. They ate the same amount because \(\frac{1}{2}\) is the same as \(\frac{2}{4}\).
Answer:
Option B
Explanation:
\(\frac{2}{5}×\frac{2}{2}\) < \(\frac{1}{2}×\frac{5}{5}\)
\(\frac{4}{10}\) < \(\frac{5}{10}\).
\(\frac{2}{5}\) < \(\frac{1}{2}\) is correct
Question 8.
The Sahas were reading a best-selling novel as a family. After the first week, they checked in with each other to see how much of the book each had read.
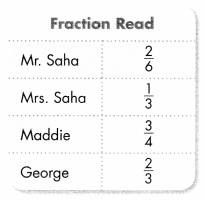
A. Who read the greatest fraction of the book?
Answer:
Maddie read the greatest fraction of the book
Explanation:
Apply division rule
\(\frac{3}{4}\) = 0.7
When compared with others Maddie read more.
B. Name the two family members who read the same fraction of the book. Explain.
Answer:
Mr Saha and Mrs Saha read the same fraction of the book
\(\frac{2}{6}\) = \(\frac{1}{3}\)
Explanation:
Apply division rule
\(\frac{3}{4}\) = 0.7
\(\frac{1}{3}\) = 0.3
Question 9.
Johnny found a fraction equivalent to the one shown by the point on the number line. Which fraction could Johnny have found? Explain.

Answer:
Option C
Explanation:
\(\frac{1}{2}\) = \(\frac{4}{8}\).
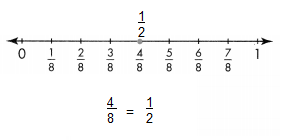
Question 10.
Bill and Gina each ate \(\frac{1}{2}\) of their own pizza. Bill ate more pizza than Gina. Draw a picture and explain how that is possible.
Answer:
Bill pizza is bigger in size
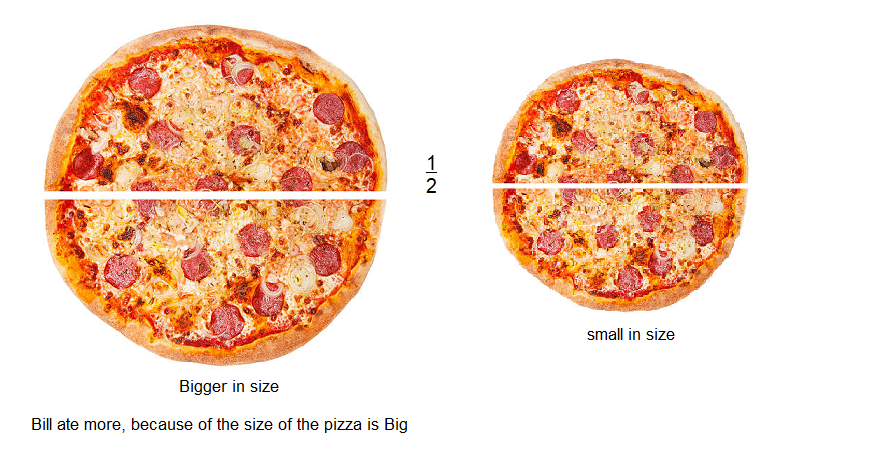
Explanation:
As the sizes of pizza are different.
So, Bill ate more.
Question 11.
Order \(\frac{1}{2}\), from least to greatest.
Answer:
Question 12.
Only one of the comparisons below is correct. Which is correct? What benchmark was used to check your answer?
A. \(\frac{2}{3}\) < \(\frac{1}{2}\); I used \(\frac{1}{2}\) as a benchmark.
B. \(\frac{1}{2}\) = \(\frac{3}{5}\); I used \(\frac{1}{4}\) as a benchmark.
C. \(\frac{2}{3}\) < \(\frac{9}{10}\); I used \(\frac{3}{4}\) as a benchmark.
D. \(\frac{3}{4}\) < \(\frac{2}{3}\); I used \(\frac{1}{2}\) as a benchmark.
Answer:
Option C
\(\frac{2}{3}\) < \(\frac{9}{10}\); I used \(\frac{3}{4}\) as a benchmark.
Question 13.
Draw a model to compare \(\frac{1}{3}\) and \(\frac{3}{5}\).
Answer:
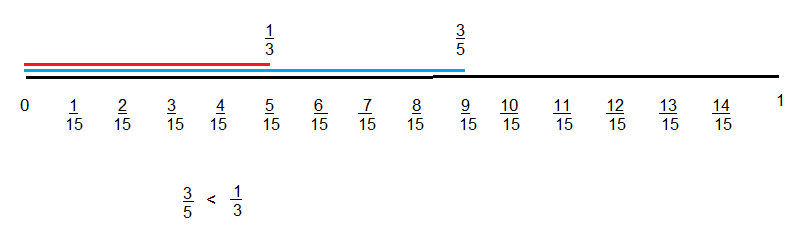
\(\frac{1}{3}×\frac{5}{5}\) and \(\frac{3}{5}×\frac{3}{3}\)
Explanation:
Frist the denominators are multiplied with common number to get same denominator for the both the fractions such that they can compare each other, as shown below
\(\frac{5}{15}\) and \(\frac{9}{15}\)
Topic 8 Performance Task
Comparing Grasshoppers
Mrs. Rakin’s class measured the lengths of some grasshoppers. The Grasshopper Lengths table shows the lengths they found.

Question 1.
Mrs. Rakin asked the students to choose two grasshoppers and compare their lengths.
Part A
Henry used benchmark fractions to compare the lengths of grasshoppers A and C. Which grasshopper is longer? Explain.
Answer:

Explanation:
By using above benchmark number line. Grasshopper F is nearer to 0 and C too far to 0, that means F is smaller and C is bigger in size.
\(\frac{3}{8}\) < \(\frac{14}{8}\)
Part B
Riley used a number line to compare the lengths of grasshoppers A and E. Which grasshopper is longer? Use the number line to show the comparison.

Answer:

Part C
Jack compared the lengths of grasshoppers D and E. He said grasshopper D is longer. Is Jack correct? Justify the comparison using fraction strips.
Answer:
YES, Jack is correct.
Grasshopper D is longer
\(\frac{7}{8}\) > \(\frac{6}{8}\)
Explanation:
As denominators are same numerators are compared to find the longer one.
So, \(\frac{7}{8}\) > \(\frac{6}{8}\)
Question 2.
One group of students measured the lengths of grasshoppers in centimeters, instead of inches. The More Grasshopper Lengths table shows the lengths they found.

Part A
Tommy compared the lengths of grasshoppers G and H. Which grasshopper is longer? Explain how to rename the fractions using multiplication so they have the same denominator to compare.
Answer:
H is longer
I < G < H
\(\frac{6}{10} < \frac{7}{10} < \frac{8}{10}\)
Explanation:
As denominators are same numerators are compared to find the longer one.
So, \(\frac{6}{10} < \frac{7}{10} < \frac{8}{10}\)
Part B
Venon compared the lengths of grasshoppers Hand I. Which grasshopper is longer? Explain how to rename the fractions using division so they have the same denominator to compare.
Answer:
Grasshopper G is longer.
\(\frac{6}{10} < \frac{7}{10} < \frac{4}{5}\)
Explanation:
\(\frac{30}{50} < \frac{35}{50} < \frac{40}{50}\)
Part C
Rina wants to determine if grasshopper D is longer or shorter than grasshopper G. Explain how Rina can compare the fractions.
Answer:
D = \(\frac{7}{8}\)
G = \(\frac{7}{10}\)
Explanation:
\(\frac{7}{8}\) > \(\frac{7}{10}\)
\(\frac{7}{8}×\frac{10}{10}\) > \(\frac{7}{10}×\frac{8}{8}\)
\(\frac{70}{80}\) > \(\frac{56}{80}\)