enVision Math Common Core Grade 4 Answer Key Topic 9 Understand Addition and Subtraction of Fractions

Go through the enVision Math Common Core Grade 4 Answer Key Topic 9 Understand Addition and Subtraction of Fractions regularly and improve your accuracy in solving questions.

enVision Math Common Core 4th Grade Answers Key Topic 9 Understand Addition and Subtraction of Fractions

Essential Questions:
How do you add and subtract fractions and mixed numbers with like denominators?
How can fractions be added and subtracted on a number line?

Answer:
Adding and subtracting like denominators is simple as denominators
are same we add numerators or subtract numerators.
In mixed numbers with like denominators we convert
first mixed numbers into fractions then as denominators
are same we add or subtract numerators,

Explanation:
Adding and subtracting like denominators is simple as denominators
are same we add numerators or subtract numerators example
let’s take fractions as 5/6 and 4/6  with like denominator 6 so
first in addition we add numerators as 5 and 4 and denominator is
same 6 so result is (5 + 4)/6 = 9/6,
In subtraction we subtract numerators and denominator being same as
(5 – 4)/6 = 1/6, Now in mixed fractions 5(3/4) and 2(1/4) first we convert
mixed fractions into fractions as (5 X 4 + 3)/ 4 = 23/4 and (2 X 4 + 1)/4 = 9/4,
now we add numerators and denominator being same as (23 + 9 )/4 = 32/4,
In subtraction we subtract numerators and denominator being same as
(23 – 9)/4 = 14/4.

Any fractional number can be represented on a number line which is
known as fractions on the number line. Here we will see how to represent
fraction on a number line. We will also see how to add or subtract with the
help of a fraction number line.
Follow the examples step-by-step how to add or subtract
using a fraction number line.
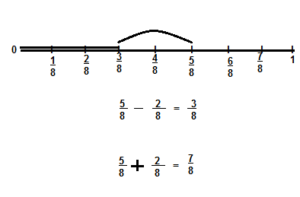
Calculating the sum of 3/10 + 4/10 on the fraction number line as shown below

= 3/10 + 4/10 (as denominators are same we add numerators),
= (3 + 4)/10,
= 7/10,
The difference of 9/10 and 7/10,

9/10 – 7/10 (as denominators are same we subtract numerators),
= 2/10 or 2/10 ÷ 2/2,
= 1/5 as shown above.

Envision STEM Project: Fractions and Information Transfer
Do Research Morse code uses patterns to transfer information.
Any word can be written using Morse code. Use the Internet or
other sources to find how to write fourth, grade, and school using Morse code.
Journal: Write a Report Include what you found. Also in your report:

• Write three in Morse code. Write a fraction that tells what part of
  the code for three is dots.
• Write and solve an equation to find how much greater the fraction for
  dots is than the fraction for dashes in the word three.

Review What You Know

Vocabulary

• benchmark fractions
• equivalent fractions
• denominator
• numerator

Choose the best term from the box. Write it on the blank.
Question 1.
In \(\frac{2}{3}\), 2 is the _numerator_ of the fraction and
3 is the __denominator_______ of the fraction.
Answer:
2 is the numerator and 3 is the denominator,

Explanation:
Given In \(\frac{2}{3}\) as first, a fraction is made up
of two integers one on the top, and one on the bottom.
The top one is called the numerator, the bottom one is called
the denominator, and these two numbers are separated by a line.
So here 2 is the numerator of the fraction and 3 is the denominator of the fraction.

Question 2.
Fractions that name the same region or part of a segment are
called _equivalent fractions_.
Answer:
Equivalent fractions,

Explanation:
Equivalent fractions can be defined as fractions that may have different
numerators and denominators but they represent the same value.
For example, 9/12 and 6/8 are equivalent fractions because both are equal to 3/4.

Equivalent Fraction

Write the missing values to show pairs of equivalent fractions.
Question 3.
\(\frac{2}{3}=\frac{ }{6}\)
Answer:
4,
\(\frac{2}{3}=\frac{4}{6}\),

Explanation:
As denominator is 3 and other side is 6 means if we divide 6 by 3 we get 2,
means both numerator and denominator are multiplied by 2,
So, 2 should be multiplied to 2 then we get missing numerator as 4,
therefore \(\frac{2}{3}=\frac{4}{6}\).

Question 4.
\(\frac{ }{4}=\frac{3}{12}\),
Answer:
1,
\(\frac{1}{4}=\frac{3}{12}\),

Explanation:
As denominator is 12 and other side is 4 means if we divide 12 by 4 we get 3,
means to get missing numerator we divide 3 by 3 we get 1,
therefore \(\frac{1}{4}=\frac{3}{12}\).

Question 5.
\(\frac{6}{5}=\frac{ }{10}\)
Answer:
12,
\(\frac{6}{5}=\frac{12}{10}\),

Explanation:
As denominator is 5 and other side is 10 means if we divide 10 by 5 we get 2,
means both numerator and denominator are multiplied by 2,
So, 6 should be multiplied to 2 then we get missing numerator as 12,
therefore \(\frac{6}{5}=\frac{12}{10}\).

Question 6.
\(\frac{1}{2}=\frac{50}{}\)
Answer:
100,
\(\frac{1}{2}=\frac{50}{100}\),

Explanation:
As numerator is 50 and other side is 1 means if we divide 50 by 1 we get 50,
means both numerator and denominator are multiplied by 50,
So, 2 should be multiplied to 50 then we get missing denominator as 100,
therefore \(\frac{1}{2}=\frac{50}{100}\).

Question 7.
\(\frac{1}{5}=\frac{ }{10}\)
Answer:
2,
\(\frac{1}{5}=\frac{2}{10}\),

Explanation:
As denominator is 5 and other side is 10 means if we divide 10 by 5 we get 2,
means both numerator and denominator are multiplied by 2,
So, 1 should be multiplied to 2 then we get missing numerator as 2,
therefore \(\frac{1}{5}=\frac{2}{10}\).

Question 8.
\(\frac{3}{}=\frac{30}{100}\)
Answer:
10,
\(\frac{3}{10}=\frac{30}{100}\),

Explanation:
As numerator is 3 and other side is 30 means if we divide 30 by 3 we get 10,
So, 100 should be divided by 10 then we get missing denominator as 10,
therefore \(\frac{3}{10}=\frac{30}{100}\).

Benchmark Fractions

Use the number line to find a benchmark fraction or whole number for each given fraction.

Question 9.
\(\frac{11}{2}\) is close to __5\(\frac{1}{2}\)_____.
Answer:

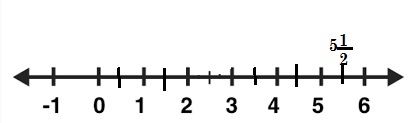
Explanation:
Given \(\frac{11}{2}\) as numerator is greater than denominator,
11 can be written as 5 X 2 + 1, so we write in mixed fraction
as 5\(\frac{1}{2}\) as shown above on the number line.

Question 10.
\(\frac{8}{12}\) is close to _\(\frac{2}{3}\)_________
Answer:

Explanation:
Given \(\frac{8}{12}\) as both numerator and denominators goes in 4,
we divide both by 4 as 8/4 = 2 and 12/4 = 3 so we get \(\frac{2}{3}\)
as shown above on the number line.

Question 11.
\(\frac{2}{6}\) is close to ___\(\frac{1}{3}\) ______
Answer:

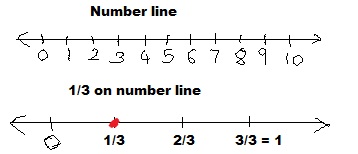
Explanation:
Given \(\frac{2}{6}\) as both numerator and denominators goes in 2,
we divide both by 2 as 2/2 = 1 and 6/2 = 3, so we get \(\frac{1}{3}\)
as shown above on the number line.

Problem Solving

Question 12.
Adult admission to the dog show is $16. Children’s admission is $9.
How much would it cost 3 adults and 2 children to enter the dog show?
Answer:
It cost $66 for 3 adults and 2 children to enter the dog show,

Explanation:
Given Adult admission to the dog show is $16 and
Children’s admission is $9 so for $16
for 3 Adults and 2 Children it will be 3 X $16 + 2 X $9 =
$48 + $18 = $66, So the total cost will be $66 to enter
the dog show.

Question 13.
Meg saved coins she found for a year. She found a total of
95 pennies, 13 nickels, 41 dimes, and 11 quarters.
She would like to evenly divide the coins into 4 piggy banks.
How many coins will go in each piggy bank?
Answer:
40 coins will go in each piggy bank,

Explanation:
Given Meg saved coins she found for a year. She found a total of
95 pennies, 13 nickels, 41 dimes, and 11 quarters.
She would like to evenly divide the coins into 4 piggy banks.
So first total number of coins Meg have are 95 + 13 + 41 + 11 = 160 coins,
As coins are evenly divide the coins into 4 piggy banks, each piggy bank will
have 160/4 = 40 coins respectively.

Pick a Project

PROJECT 9A
How do you follow a recipe?
Project: Exploring Recipes

Answer:
Follow a recipe

Exploring Cookie Recipe:

PROJECT 9B
Would you like to be a code breaker?
Project: Create a Fraction Code

PROJECT 9C
What is a farmers’ market?
Project: Write and Perform a Skit

A farmers’ market is a physical retail market place intended to sell foods directly by
farmers to consumers. Farmers’ markets may be indoors or outdoors and typically
consist of booths, tables or stands where farmers sell their produce, live animals and
plants, and sometimes prepared foods and beverages. Farmers’ markets exist in many
countries worldwide and reflect the local culture and economy. The size of the market
may be just a few stalls or it may be as large as several city blocks. Due to their nature,
they tend to be less rigidly regulated than retail produce shops.
They are distinguished from public markets which are generally housed in
permanent structures, open year-round, and offer a variety of non-farmer/non-producer vendors, packaged foods and non-food products.

3-ACT MATH PREVIEW

Math Modeling
Just Add Water

I can … model with math to solve a problem that involves estimating,
adding fractions and mixed numbers, and comparing quantities.

Lesson 9.1 Model Addition of Fractions

Solve & Share
Kyle and Jillian are working on a sports banner. They painted \(\frac{3}{8}\)
of the banner green and \(\frac{4}{8}\) purple. How much of the banner
have they painted? Solve this problem any way you choose.
I can … use tools such as fraction strips or area models to add fractions.

Look Back! Use Appropriate Tools Kyle says \(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}\).
Jillian says \(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{24}\).
Use a tool to decide who is correct and explain.
Answer:
Kyle and Jillian painted \(\frac{7}{8}\)  banner,

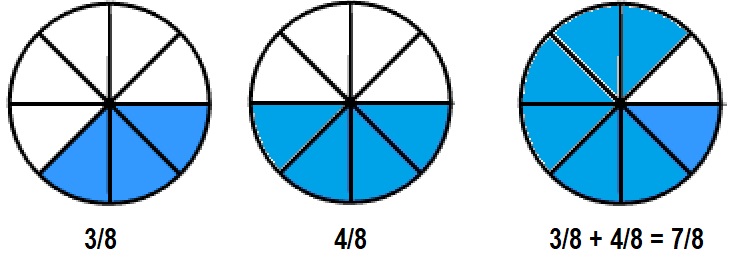
Kyle is correct,

Explanation:
Given Kyle and Jillian are working on a sports banner. They painted \(\frac{3}{8}\)
of the banner green and \(\frac{4}{8}\) purple. Therefore the banner
have they painted is \(\frac{3}{8}\) + \(\frac{4}{8}\) used
area model to add fractions as shown above.
Given Kyle says \(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}\).
Jillian says \(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{24}\) but Kyle
is correct as \(\frac{1}{8}+\frac{1}{8}+\frac{1}{8} is \frac{3}{8}\) not
Jillian says \(\frac{1}{8}+\frac{1}{8}+\frac{1}{8} ≠ \frac{3}{24}\) as
\(\frac{1}{8}+\frac{1}{8}+\frac{1}{8} is \frac{3}{8}\)  because as denominators
are same we add numerators only so Jillian is incorrect.

Essential Question
How Can You Use Tools to Add Fractions?
We can use tools such as fraction strips to add two or more fractions,

Explanation:

Visual Learning Bridge
Ten canoeing teams are racing downriver. Five teams have silver canoes and
two teams have brown canoes. What fraction of the canoes are either silver or brown?

You can use tools such as fraction strips to add two or more fractions.

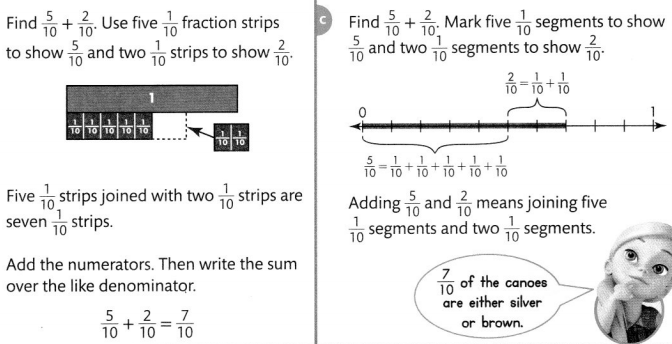
Convince Me! Make Sense and Persevere What two fractions would you add to
find the fraction of the canoes that are either green or brown?
What is the sum? How do you know your sum is correct?

Guided Practice

Do You Understand?
Question 1.
In the problem on the previous page, would you get the same answer if you
used an area model instead of fraction strips or a number line? Explain.
Answer:

Question 2.
What two fractions are being added below? What is the sum?

Answer:
The two fractions are \(\frac{2}{8}\) and \(\frac{3}{8}\),
The sum is \(\frac{5}{8}\),

Explanation:
Given two fractions are \(\frac{2}{8}\) and \(\frac{3}{8}\),
as denominators are same 8 we add numerators 2 and 3 we get 5,
therefore sum is \(\frac{5}{8}\).

Do You Know How?
For 3-4, find each sum.
Question 3.

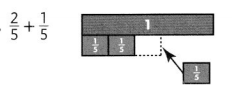
Answer:
\(\frac{3}{5}\),

Explanation :
As \(\frac{2}{5}\) and \(\frac{1}{5}\)
are like fraction as denominators are same ,
we can add numerators 2 and 1 = 3,
therefore \(\frac{2}{5}\)+ \(\frac{1}{5}\) =\(\frac{3}{5}\).

Question 4.

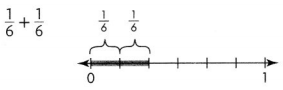
Answer:
\(\frac{2}{6}\),
Simplest form : \(\frac{1}{3}\),

Explanation :
As \(\frac{1}{6}\) and \(\frac{1}{6}\)
are like fraction, we can add numerators 1 and 1 so
\(\frac{2}{6}\) as it can be further simplified
2 and 6 goes in 3 table so answer in simplest form \(\frac{1}{3}\).

Independent Practice

Leveled Practice For 5-16, find each sum. Use a tool as needed.
Question 5.

Answer:
\(\frac{7}{12}\),

Explanation:
As \(\frac{3}{12}\) and \(\frac{4}{12}\)
are like fraction as denominators are same ,
we can add numerators 3 and 4 as 7,
therefore \(\frac{3}{12}\) + \(\frac{4}{12}\) =\(\frac{7}{12}\).

Question 6.

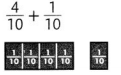
Answer:
\(\frac{5}{10}\),
Simplest form = \(\frac{1}{2}\),

Explanation:
As \(\frac{4}{10}\) and \(\frac{1}{10}\)
are like fraction as denominators are same,
we can add numerators 4 and 1 as 5,
therefore \(\frac{4}{10}\)+ \(\frac{1}{10}\) =\(\frac{5}{10}\).
As \(\frac{5}{10}\) can be further simplified because
5 and 10 goes in 5 table so answer in the simplest form is \(\frac{1}{2}\).

Question 7.

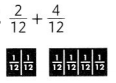
Answer:
\(\frac{6}{12}\),
Simplest form = \(\frac{1}{2}\),

Explanation:
As \(\frac{2}{12}\) and \(\frac{4}{12}\)
are like fraction as denominators are same,
we can add numerators 2 and 4 = 6,
therefore \(\frac{2}{12}\)+ \(\frac{4}{12}\) =\(\frac{6}{12}\).
As \(\frac{6}{12}\) can be further simplified because
6 and 12 goes in 6 table so answer in the simplest form is \(\frac{1}{2}\).

Question 8.

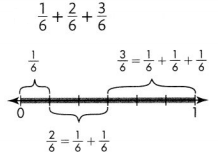
Answer:
\(\frac{6}{6}\),
Simplest form = \(\frac{1}{1}\) = 1,

Explanation:
As \(\frac{1}{2}\), \(\frac{2}{6}\) and \(\frac{3}{6}\)
are like fraction as denominators are same ,
we can add numerators 1, 2 and 3 = 6,
therefore \(\frac{1}{2}\)+ \(\frac{2}{6}\) + \(\frac{3}{6}\) =\(\frac{6}{6}\).
As \(\frac{6}{6}\) can be further simplified because
6 and 6 can be cancelled so answer in the simplest form is \(\frac{1}{1}\) = 1.

Question 9.

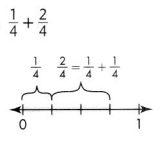
Answer:
\(\frac{3}{4}\),

Explanation:
As \(\frac{1}{4}\) and \(\frac{2}{4}\)
are like fraction as denominators are same ,
we can add numerators 1 and 2 =3,
therefore \(\frac{1}{4}\) + \(\frac{2}{4}\) = \(\frac{3}{4}\).

Question 10.

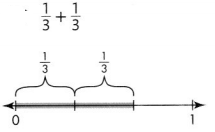
Answer:
\(\frac{2}{3}\),

Explanation:
Given \(\frac{1}{3}\) and \(\frac{1}{3}\)
are like fraction as denominators are same ,
we can add numerators 1 and 1 = 2,
therefore \(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\).

Question 11.
\(\frac{5}{8}+\frac{1}{8}\)
Answer:
\(\frac{6}{8}\) or \(\frac{3}{4}\),

Explanation:
As \(\frac{5}{8}\) and \(\frac{1}{8}\)
are like fraction as denominators are same,
we can add numerators 5 and 1 = 6,
therefore \(\frac{5}{8}\) + \(\frac{1}{8}\) = \(\frac{6}{8}\),
As \(\frac{6}{8}\) can be further simplified because
6 and 8 can be cancelled by 2, we get 3 X 2 =6 and 4 X 2 = 8,
so answer in the simplest form is \(\frac{3}{4}\).

Question 12.
\(\frac{1}{4}+\frac{3}{4}\)
Answer:
\(\frac{4}{4}\) or 1,

Explanation:
As \(\frac{1}{4}\) and \(\frac{3}{4}\)
are like fraction as denominators are same,
we can add numerators 1 and 3 = 4,
therefore \(\frac{1}{4}\) + \(\frac{3}{4}\) = \(\frac{4}{4}\),
As \(\frac{4}{4}\) can be further simplified because
4 and 4 can be cancelled by 4, so answer in the simplest form is 1.

Question 13.
\(\frac{7}{12}+\frac{2}{12}\)
Answer:
\(\frac{9}{12}\) or \(\frac{3}{4}\),

Explanation:
As \(\frac{7}{12}\) and \(\frac{2}{12}\)
are like fraction as denominators are same,
we can add numerators 7 and 2 = 9,
therefore \(\frac{7}{12}\) + \(\frac{2}{12}\) = \(\frac{9}{12}\),
As \(\frac{9}{12}\) can be further simplified because
9 and 12 can be cancelled by 3, 3 X 3 = 9 and 4 X 3 = 12,
we get (3,4) so answer in the simplest form is \(\frac{3}{4}\).

Question 14.
\(\frac{1}{4}+\frac{1}{4}\)
Answer:
\(\frac{2}{4}\) or \(\frac{1}{2}\),

Explanation:
As \(\frac{1}{4}\) and \(\frac{1}{4}\)
are like fraction as denominators are same,
we can add numerators 1 and 1 = 2,
therefore \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\),
As \(\frac{2}{4}\) can be further simplified because
2 and 4 can be cancelled by 2, 1 X 2 = 2 and 2 X 2 = 4,
we get (1,2) so answer in the simplest form is \(\frac{1}{2}\).

Question 15.
\(\frac{2}{5}+\frac{2}{5}\)
Answer:
\(\frac{4}{5}\),

Explanation:
As \(\frac{2}{5}\) and \(\frac{2}{5}\)
are like fraction as denominators are same,
we can add numerators 2 and 2 = 4,
therefore \(\frac{2}{5}\) + \(\frac{2}{5}\) = \(\frac{4}{5}\).

Question 16.
\(\frac{1}{10}+\frac{2}{10}+\frac{1}{10}\)
Answer:
\(\frac{4}{10}\) or \(\frac{2}{5}\),

Explanation:
As \(\frac{1}{10}\), \(\frac{2}{10}\) and \(\frac{1}{10}\)
are like fraction as denominators are same,
we can add numerators 1,2 and 1 = 4,
therefore \(\frac{1}{10}\) + \(\frac{2}{10}\) + \(\frac{1}{10}\) = \(\frac{4}{10}\),
As \(\frac{4}{10}\) can be further simplified because
4 and 10 can be cancelled by 2, 2 X 2 = 4 and 2 X 5 = 10,
we get (2,5) so answer in the simplest form is \(\frac{2}{5}\).

Problem Solving

Question 17.
Number Sense Using three different numerators, write an equation in
which three fractions, when added, have a sum of 1.
Answer:
\(\frac{1}{6}\), \(\frac{2}{6}\) and \(\frac{3}{6}\),
As \(\frac{1}{6}\) + \(\frac{2}{6}\) + \(\frac{3}{6}\) =
\(\frac{6}{6}\),
Simplest form = \(\frac{1}{1}\) = 1,

Explanation:
As \(\frac{1}{6}\), \(\frac{2}{6}\) and \(\frac{1}{6}\)
are like fraction as denominators are same ,
we can add numerators 1, 2 and 3 = 6,
therefore \(\frac{1}{6}\)+ \(\frac{2}{6}\) + \(\frac{3}{6}\) =
\(\frac{6}{6}\).
As \(\frac{6}{6}\) can be further simplified because
6 and 6 can be cancelled so answer in the simplest form is \(\frac{1}{1}\) = 1.

Question 18.
Use Appropriate Tools Diane added \(\frac{3}{8}\) to \(\frac{1}{8}\).
Draw a picture to show \(\frac{1}{8}\) + \(\frac{3}{8}\) = \(\frac{4}{8}\).
Answer:
\(\frac{4}{8}\)= \(\frac{1}{2}\),

Explanation :
\(\frac{3}{8}\) + \(\frac{1}{8}\) = \(\frac{4}{8}\)
further it can be simplified as \(\frac{1}{2}\) as 4 and 8 goes in 4 table.

Question 19.
A bakery sells about 9 dozen bagels per day. About how many bagels
does the bakery sell in a typical week? Explain.

Answer:
756 bagels,

Explanation:
1 dozen = 12,
so 9 dozen = 9 times 12 = 108,
so the bakery sells 108 bagels per day.
now to calculate for a typical week one week = 7 days,
so bagels sold in a week = 108 times 7 = 756 bagels.
Therefore the bakery sells in a typical week about 756 bagels.

Question 20.
During a field trip to a baseball game, \(\frac{3}{8}\) of the students
are wearing red caps and \(\frac{3}{8}\) are wearing blue caps.
Write and solve an equation to find the number of students, s,
who are wearing red or blue caps.

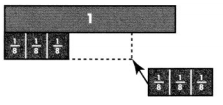
Answer:
Equation:
\(\frac{3}{8}\) + \(\frac{3}{8}\)  + (Number of red + Number of blues) = s,
Number of red and Number of blues wearing caps are
\(\frac{2}{8}\) or \(\frac{1}{4}\),

Explanation:
Given during a field trip to a baseball game, \(\frac{3}{8}\) of the students
are wearing red caps and \(\frac{3}{8}\) are wearing blue caps.
Equation to find the number of students, s, who are wearing red or blue caps is
\(\frac{3}{8}\) + \(\frac{3}{8}\)  + (Number of red + Number of blues) = s,
as s = 1, Substituting above we get
\(\frac{3}{8}\) + \(\frac{3}{8}\)  + (Number of red + Number of blues) = 1,
solving above (Number of red + Number of blues) =
1 – (\(\frac{3}{8}\) + \(\frac{3}{8}\)),
(Number of red + Number of blues) = 1 – \(\frac{6}{8}\),
(Number of red + Number of blues) = \(\frac{8-6}{8}\),
(Number of red + Number of blues) = \(\frac{2}{8}\) or \(\frac{1}{4}\).

Question 21.
Higher Order Thinking Terry ran \(\frac{1}{10}\) of the distance from
school to home. He walked more \(\frac{3}{10}\) of the distance and
then skipped \(\frac{2}{10}\) more of the distance.
What fraction of the distance home does Terry still have to go?

Answer:
The fraction of the distance home does Terry still have to go is
\(\frac{8}{10}\) or \(\frac{4}{5}\),

Explanation:
Given Terry ran \(\frac{1}{10}\) of the distance from
school to home. He walked more \(\frac{3}{10}\) of the distance and
then skipped \(\frac{2}{10}\) more of the distance.
So let x be fraction of the distance home does Terry still have to go therefore
\(\frac{1}{10}\) + \(\frac{3}{10}\) – \(\frac{2}{10}\) + x = 1,
\(\frac{4}{10}\) – \(\frac{2}{10}\) + x = 1,
\(\frac{4-2}{10}\) + x = 1,
\(\frac{2}{10}\) + x = 1,
x = 1- \(\frac{2}{10}\),
x = \(\frac{10 – 2}{10}\),
x = \(\frac{8}{10}\) or \(\frac{4}{5}\).

Assessment Practice

Question 22.
Which is the sum of \(\frac{3}{12}\) + \(\frac{7}{12}\)?

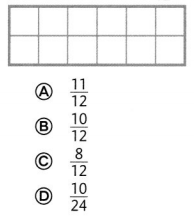
Answer:
B,
\(\frac{10}{12}\),

Explanation:
As \(\frac{3}{12}\) and \(\frac{7}{12}\)
are like fraction as denominators are same,
we can add numerators 3 and 7
so answer is 3 + 7 = 10,
therefore \(\frac{3}{12}\)+ \(\frac{7}{12}\) =\(\frac{10}{12}\).

Question 23.
Lindsay had \(\frac{5}{10}\) cup of flour in the mixing bowl.
She added \(\frac{2}{10}\) cup of cocoa powder and
\(\frac{3}{10}\) cup of sugar. What is the total amount of dry ingredients in the mixing bowl?
A. 1 cup
B. \(\frac{7}{10}\)
C. \(\frac{5}{10}\)
D. \(\frac{1}{10}\)
Answer:
A,
1 cup,

Explanation:
As \(\frac{5}{10}\), \(\frac{2}{10}\) and \(\frac{3}{10}\)
are like fraction as denominators are same ,
we can add numerators 5, 2 and 3
so answer is 5 + 2 + 3 = 10,
therefore \(\frac{5}{10}\)+ \(\frac{2}{10}\) + \(\frac{3}{10}\) =\(\frac{10}{10}\).
\(\frac{10}{10}\) as it can be further simplified
10 and 10 can be cancelled so answer in the simplest form is \(\frac{1}{1}\) = 1.

Lesson 9.2 Decompose Fractions

Solve & Share
Karyn has 1 pounds of chili to put into three bowls. The amount of chili in each bowl does not have to be the same. How much chili could Karyn put into each bowl? Solve this problem any way you choose.
| can…use number lines, area models, or drawings to decompose fractions.

Look Back! Use a drawing or fraction strips to help write equivalent fractions
for the amount of chili in one of the bowls.

Essential Question
How Can You Represent a Fraction in a Variety of Ways?
Answer:
In 5 ways we can represent fractions,

Explanation:
1. Sales: If you get reduction of 20%, 20% is a fraction: 20/100,
2. Comparisons: Ship A is half as big as Ship B. Half is a fraction: 1/2,
3. Taking a part of something: You eat two slices of pizza.
Two out of eight is a fraction: 2/8,
4. Division of integers: If the quotient is not an integer,
it will necessarily be a fraction,
5. Ratios: One of the definitions of π is that it is the ratio of the
Circumference to the Diameter. It is a fraction, although it can’t be
expressed with both terms of it being integers.

Visual Learning Bridge
Charlene wants to leave \(\frac{1}{6}\) of her garden empty.
What are some different ways Charlene can plant the rest of her garden?

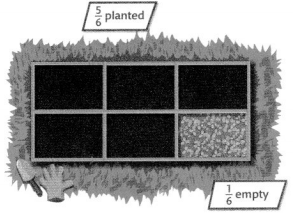
Decompose means to break into parts. Compose means to combine parts. The fraction of the garden that Charlene will plant can be decomposed in more than one way.

One Way
Charlene could plant four \(\frac{1}{6}\) sections with blue flowers and one \(\frac{1}{6}\) section with red peppers.

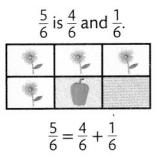
Another Way
Charlene could plant one \(\frac{1}{6}\) section with green beans, one \(\frac{1}{6}\) section with yellow squash, one \(\frac{1}{6}\) section with red peppers, and two \(\frac{1}{6}\) sections with blue flowers.

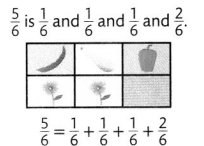
Convince Me! Use Appropriate Tools Draw pictures or use fraction strips to show why these equations are true.
\(\frac{5}{6}=\frac{3}{6}+\frac{2}{6} \quad \frac{5}{6}=\frac{1}{6}+\frac{2}{6}+\frac{2}{6}\)

Another Example!
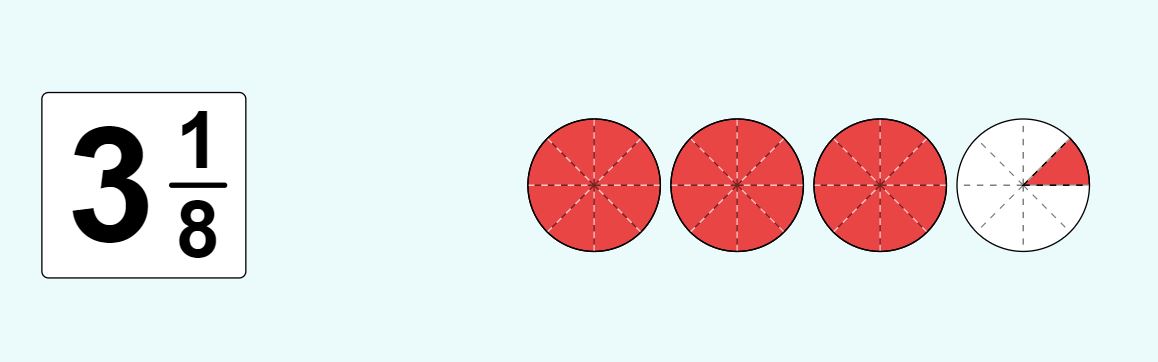
What is one way you can decompose 3\(\frac{1}{8}\)?
A mixed number has a whole number part and a fraction part.
3 \(\frac{1}{8}\) is 1 whole + 1 whole + 1 whole + \(\frac{1}{8}\).
Each whole can also be shown as eight equal parts.

Guided Practice

Do You Understand?
Question 1.
What is another way to decompose 3\(\frac{1}{8}\)?
Answer:

Question 2.
Look at the area model above. What fraction with a greater numerator than
denominator is equivalent to 3\(\frac{1}{8}\)? Explain.
Answer:
\(\frac{25}{8}\),

Explanation:
Given the area model of 3\(\frac{1}{8}\) which is
equivalent to \(\frac{25}{8}\) because we convert mixed
fraction into fraction as (3 X 8 + 1) by 8 = \(\frac{25}{8}\),
where numerator is greater than denominator.

Do You Know How?
For 3-4, decompose each fraction or mixed number in two different ways.
Use a tool if needed.
Question 3.

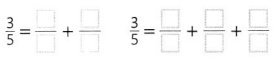
Answer:
,

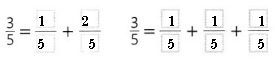Explanation:
Given to find \(\frac{3}{5}\) equivalent to
\(\frac{1}{5}\) + \(\frac{2}{5}\) and
\(\frac{3}{5}\) equivalent to
\(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\).

Question 4.

Answer:
,

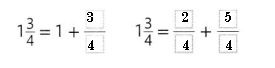Explanation:
Given to find 1\(\frac{3}{4}\) equivalent to as
1\(\frac{3}{4}\)= (1 X 4 + 3) by 4 = \(\frac{7}{4}\)
which is equivalent to 1 + \(\frac{3}{4}\) and
\(\frac{2}{4}\) + \(\frac{5}{4}\).

Independent Practice

Leveled Practice For 5-10, decompose each fraction or
mixed number in two different ways. Use a tool if needed.
Question 5.
\(\frac{4}{6}\) =
Answer:
\(\frac{4}{6}\) = \(\frac{2}{3}\),

Explanation:
Given \(\frac{4}{6}\) to decompose each fraction or mixed number
so as 4 and 6 can be divided by 2,
we get 2 and 3, so \(\frac{4}{6}\) = \(\frac{2}{3}\).

Question 6.
\(\frac{7}{8}\) =
Answer:
\(\frac{7}{8}\) =\(\frac{3}{8}\) + \(\frac{4}{8}\),

Explanation:
Given \(\frac{7}{8}\) to decompose each fraction or mixed number,
so \(\frac{7}{8}\) = \(\frac{3}{8}\) + \(\frac{4}{8}\).

Question 7.
1\(\frac{3}{5}\) =
Answer:
1\(\frac{3}{5}\) = \(\frac{8}{5}\) or \(\frac{5}{5}\) + \(\frac{3}{5}\),

Explanation:
Given 1\(\frac{3}{5}\) to decompose each fraction or mixed number,
so 1\(\frac{3}{5}\) = \(\frac{1 X 5 + 3}{5}\) = \(\frac{8}{5}\) or
1\(\frac{3}{5}\) = \(\frac{5}{5}\) + \(\frac{3}{5}\).

Question 8.
2\(\frac{1}{2}\) =
Answer:
2\(\frac{1}{2}\) = \(\frac{5}{2}\) or \(\frac{4}{2}\) + \(\frac{1}{2}\),

Explanation:
Given 2\(\frac{1}{2}\) to decompose each fraction or mixed number,
so 2\(\frac{1}{2}\) = \(\frac{2 X 2 + 1}{5}\) = \(\frac{5}{2}\) or
2\(\frac{1}{2}\) = \(\frac{4}{2}\) + \(\frac{1}{2}\).

Question 9.
\(\frac{9}{12}\) =
Answer:
\(\frac{9}{12}\) = \(\frac{3}{4}\),

Explanation:
Given \(\frac{9}{12}\) to decompose each fraction or mixed number,
as \(\frac{9}{12}\) can be divided by 3,
we get 3 and 4, so \(\frac{3}{4}\) therefore \(\frac{9}{12}\) = \(\frac{3}{4}\).

Question 10.
1\(\frac{1}{3}\) =
Answer:
1\(\frac{1}{3}\) = \(\frac{4}{3}\) or \(\frac{3}{3}\) + \(\frac{1}{3}\)

Explanation:
Given 1\(\frac{1}{3}\) to decompose each fraction or mixed number,
so 1\(\frac{1}{3}\) = \(\frac{1 X  3 + 1}{3}\) = \(\frac{4}{3}\) or
1\(\frac{1}{3}\) = \(\frac{3}{3}\) + \(\frac{1}{3}\).

 Problem Solving

Question 11.
Jackie ate \(\frac{1}{5}\) of a bag of popcorn. She shared the rest with Enrique.
List three ways they could have shared the remaining popcorn.
Answer:
The list of three ways they shared the remaining popcorn is
1.

\(\frac{1}{5}\) and \(\frac{3}{5}\) = \(\frac{1+3}{5}\)= \(\frac{4}{5}\),
2. \(\frac{2}{5}\) and \(\frac{2}{5}\) = \(\frac{2+2}{5}\)= \(\frac{4}{5}\),
3. \(\frac{3}{5}\) and \(\frac{1}{5}\) = \(\frac{3+1}{5}\)= \(\frac{4}{5}\),

Explanation:
Given Jackie ate \(\frac{1}{5}\) of a bag of popcorn.
She shared the rest with Enrique, So the rest bag of popcorn is
1 – \(\frac{1}{5}\) = \(\frac{1 X 5 – 1}{5}\) = \(\frac{4}{5}\),
The list of three ways they shared the remaining popcorn is
1.  \(\frac{1}{5}\) and \(\frac{3}{5}\) = \(\frac{1+3}{5}\)= \(\frac{4}{5}\),
2. \(\frac{2}{5}\) and \(\frac{2}{5}\) = \(\frac{2+2}{5}\)= \(\frac{4}{5}\),
3. \(\frac{3}{5}\) and \(\frac{1}{5}\) = \(\frac{3+1}{5}\)= \(\frac{4}{5}\).

Question 12.
Use Appropriate Tools Draw an area model to show
\(\frac{4}{10}+\frac{3}{10}+\frac{2}{10}=\frac{9}{10}\)
Answer:

 

Question 13.
In a class of 12 students, 8 students are boys. Write two equivalent fractions
that tell which part of the class is boys.

Answer:

Question 14.
Use Appropriate Tools Find three different ways to decompose 1\(\frac{5}{6}\).
Use number lines to justify your answer.
Answer:

Question 15.
Higher Order Thinking Jason wrote 1\(\frac{1}{3}\) as the sum of three fractions.
None of the fractions had a denominator of 3. What fractions might Jason have used?
Answer:

Assessment Practice

Question 16.
A teacher distributes a stack of paper to 3 groups. Each group receives a different amount of paper.
Select all the ways the teacher can distribute the paper by decomposing 1\(\frac{2}{3}\) inches.
Use a fraction model if needed.

Answer:

Lesson 9.3 Add Fractions with Like Denominators

Solve & Share
Jonas is making nachos and tacos for a family party.
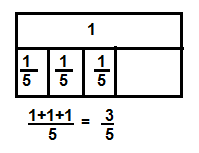
He uses \(\frac{2}{5}\) bag of shredded cheese for the nachos and \(\frac{1}{5}\) bag for the tacos. How much of the bag of shredded cheese does Jonas use?
Solve this problem any way you choose.
I can … use my understanding of addition as joining parts of the same whole to add fractions with like denominators.

Look Back! Look for Relationships What do you notice about the denominators in your equation?
Answer:
Denominators in the equation are same.
\(\frac{2}{5}\) + \(\frac{1}{5}\)
Total \(\frac{3}{5}\) bag of shredded cheese used for the nachos and tacos.
Explanation:

Essential Question
How Can You Add Fractions with Like Denominators?
Answer:
Build each fraction (if needed) so that both denominators are equal.
Add the numerators of the fractions.
The new denominator will be the denominator of the built-up fractions.
Reduce or simplify the answer, if needed.
Explanation:

Visual Learning Bridge
The table shows the results of a fourth-grade Pets Club survey. What fraction of the
club members chose a hamster or a dog as their favorite pet?

Find \(\frac{2}{12}+\frac{4}{12}\) using a model.

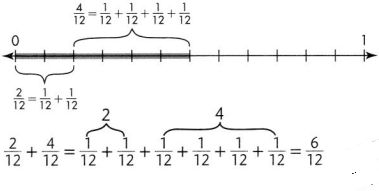
Find \(\frac{2}{12}+\frac{4}{12}\) by joining parts.
Add the numerators. Write the sum over the like denominator.
\(\frac{2}{12}+\frac{4}{12}=\frac{2+4}{12}=\frac{6}{12}\)
\(\frac{6}{12}\) is equivalent to \(\frac{1}{2}\) One half of the club members chose a hamster or a dog as
their favorite pet.

Convince Me! Critique Reasoning Frank solved the problem above and found \(\frac{2}{12}+\frac{4}{12}=\frac{6}{24}\). What error did Frank make? Explain.
Answer:
After solving the problem Frank wrote 24 in denominator, which is not correct.
Explanation:
A it was discussed above in addition when the given fraction with same denominators then only numerators to be added.
But Frank added denominators also, which is wrong.
\(\frac{2}{12}+\frac{4}{12}=\frac{2+4}{12}=\frac{6}{24}\)

Another Example!

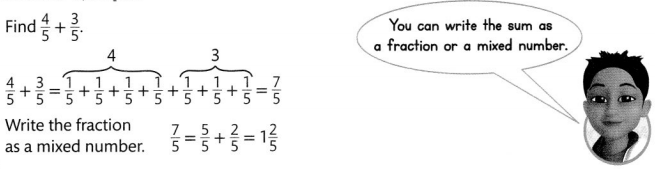
Guided Practice

Do You Understand?
Question 1.
Using the survey on the previous page, what fraction of the club members chose either a bird or a cat?
Answer:
\(\frac{5}{12}+\frac{1}{12}=\frac{6}{12}\)
Explanation:

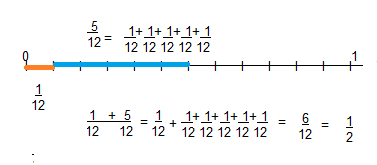
Question 2.
Greg found \(\frac{1}{3}+\frac{2}{3}=\frac{3}{6}\). What error did Greg make?
Answer:
Adding of denominators is the error did by Greg.
Explanation:
Greg added both the numerator and denominators
For adding fractions Numerators should be added and the denominators should be same.
\(\frac{1}{3}+\frac{2}{3}=\frac{3}{3}\) = 1

Do You Know How?
For 3-6, find each sum. Use drawings or fraction strips as needed.
Question 3.
\(\frac{2}{4}+\frac{1}{4}\)
Answer:
\(\frac{3}{4}\)
Explanation:
\(\frac{2}{4}+\frac{1}{4}\) = \(\frac{3}{4}\)

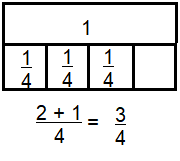
Question 4.
\(\frac{1}{3}+\frac{2}{3}\)
Answer:
\(\frac{3}{3}\)
Explanation:
\(\frac{1}{3}+\frac{2}{3}\) = \(\frac{3}{3}\)

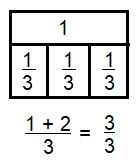
Question 5.
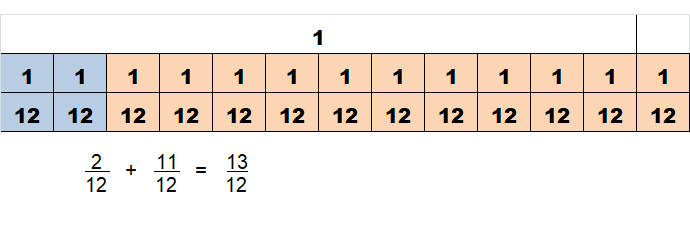
\(\frac{2}{12}+\frac{11}{12}\)
Answer:
1\(\frac{1}{12}\)
Explanation:
\(\frac{2}{12}+\frac{11}{12}\) = \(\frac{13}{12}\) = 1\(\frac{1}{12}\)

Question 6.
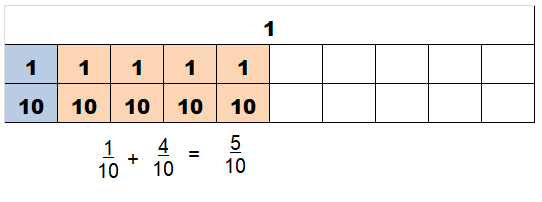
\(\frac{1}{10}+\frac{4}{10}\)
Answer:
\(\frac{5}{10}\)

Explanation:
\(\frac{1}{10}+\frac{4}{10}\) = \(\frac{5}{10}\)

Independent Practice

For 7-18, find each sum. Use drawings or fraction strips as needed.
Question 7.
\(\frac{2}{8}+\frac{1}{8}\)
Answer:
\(\frac{3}{8}\)
Explanation:
\(\frac{2}{8}+\frac{1}{8}\) = \(\frac{3}{8}\)

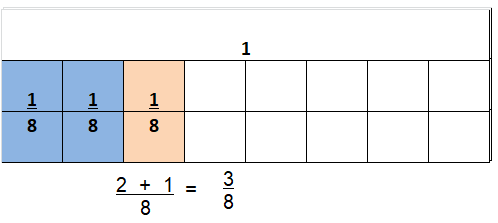
Question 8.
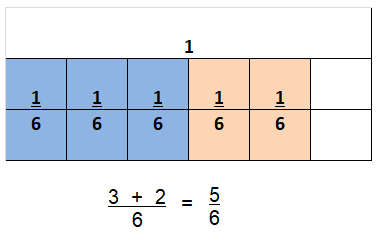
\(\frac{3}{6}+\frac{2}{6}\)
Answer:
\(\frac{5}{6}\)
Explanation:
\(\frac{3}{6}+\frac{2}{6}\) = \(\frac{5}{6}\)

Question 9.
\(\frac{1}{8}+\frac{4}{8}\)
Answer:
\(\frac{5}{8}\)
Explanation:
\(\frac{1}{8}+\frac{4}{8}\) = \(\frac{5}{8}\)

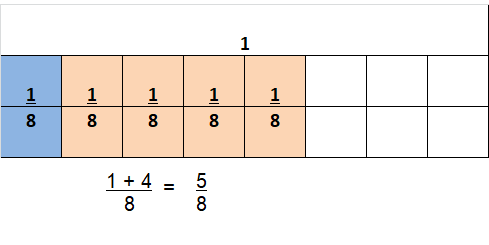
Question 10.
\(\frac{3}{10}+\frac{2}{10}\)
Answer:
\(\frac{5}{10}\)
Explanation:
\(\frac{3}{10}+\frac{2}{10}\) = \(\frac{5}{10}\)

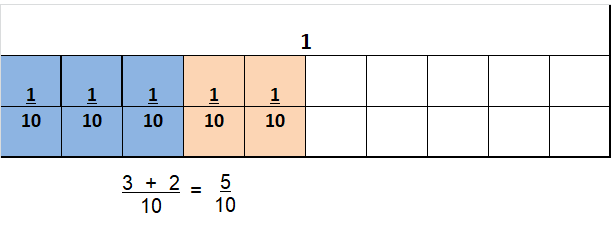
Question 11.
\(\frac{3}{10}+\frac{5}{10}\)
Answer:
\(\frac{8}{10}\)
Explanation:
\(\frac{3}{10}+\frac{5}{10}\) = \(\frac{8}{10}\)

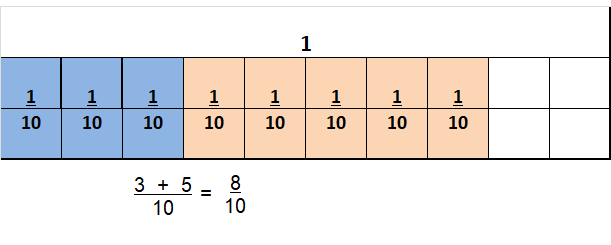
Question 12.
\(\frac{5}{12}+\frac{4}{12}\)
Answer:
\(\frac{9}{12}\)
Explanation:
\(\frac{5}{12}+\frac{4}{12}\) = \(\frac{9}{12}\)

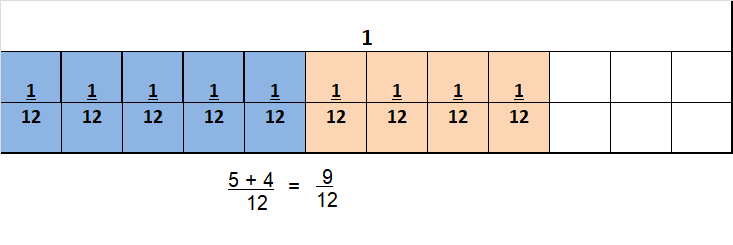
Question 13.
\(\frac{4}{5}+\frac{3}{5}+\frac{2}{5}\)
Answer:
1\(\frac{4}{5}\)
Explanation:
\(\frac{4}{5}+\frac{3}{5}+\frac{2}{5}\) =1\(\frac{4}{5}\)

Question 14.
\(\frac{3}{10}+\frac{2}{10}+\frac{6}{10}\)
Answer:
1\(\frac{1}{10}\)
Explanation:
\(\frac{3}{10}+\frac{2}{10}+\frac{6}{10}\) = \(\frac{10}{10}\)+\(\frac{1}{10}\)=1\(\frac{1}{10}\)

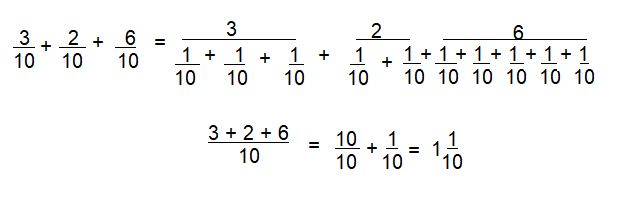
Question 15.
\(\frac{2}{6}+\frac{5}{6}\)
Answer:
\(\frac{7}{6}\)

Explanation:
\(\frac{2}{6}+\frac{5}{6}\) = \(\frac{6}{6}+\frac{1}{6}\) = 1\(\frac{1}{6}\)

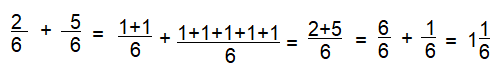
Question 16.
\(\frac{3}{6}+\frac{9}{6}\)
Answer: 2
\(\frac{12}{6}\) = \(\frac{6}{6}\) + \(\frac{6}{6}\) =  2
Explanation:

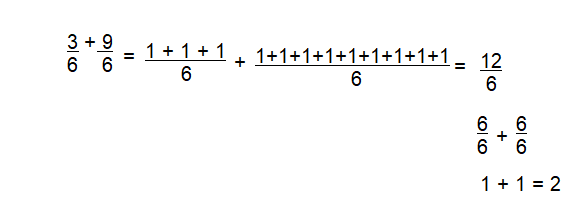
\(\frac{3}{6}+\frac{9}{6}\) = \(\frac{6}{6}+\frac{6}{6}\) = 1+1 = 2

Question 17.
\(\frac{11}{10}+\frac{11}{10}\)
Answer:
2\(\frac{2}{10}\)
Explanation:
\(\frac{11}{10}+\frac{11}{10}\)

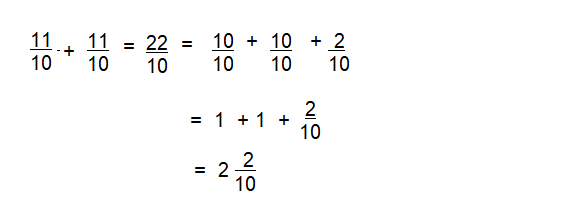
\(\frac{10}{10}\)+ \(\frac{10}{10}\)+\(\frac{2}{10}\)

2\(\frac{2}{10}\)

Question 18.
\(\frac{7}{8}+\frac{1}{8}\)
Answer: 1
\(\frac{8}{8}\)
Explanation:

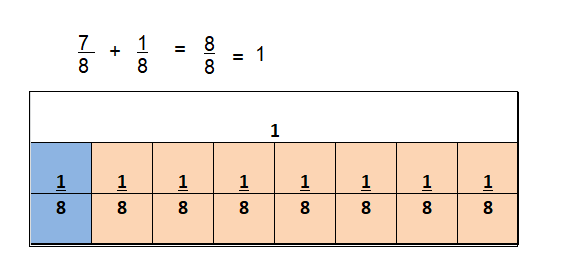
\(\frac{7}{8}+\frac{1}{8}\) = \(\frac{8}{8}\) = 1

Problem Solving

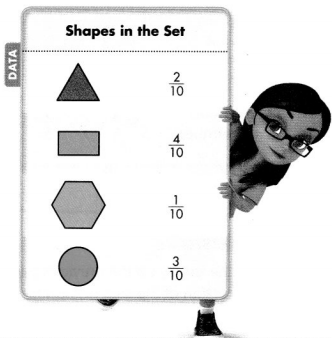
For 19-21, use the table at the right.

Question 19.
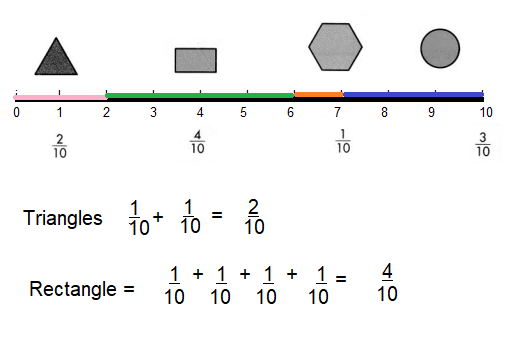
What fraction of the set is either triangles or rectangles?
Answer:
Triangles are \(\frac{2}{10}\)
Rectangles are \(\frac{4}{10}\)
Explanation:

Question 20.
Model with Math Write and solve an equation to find what fraction, f, of the set is either circles or rectangles.
Answer: f = 1 – \(\frac{x}{10}\)

Rectangles = \(\frac{4}{10}\)
Circles = \(\frac{3}{10}\)

Question 21.
Which two shapes make up half of the set? Find two possible answers.
Answer:
Circles and Triangles
\(\frac{3}{10}+\frac{2}{10}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\)

Rectangle and Hexogon
\(\frac{4}{10}+\frac{1}{10}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\)

Question 22.
There are 64 crayons in each box. A school bought 25 boxes of crayons for the art classes. If the crayons are shared equally among 5 classes, how many crayons will each class receive? Explain.
Answer:
Each class receives 320 crayons

Explanation:
64 crayons X 25 boxes = 1600 crayons

1600 crayons / 5 classes = 320 crayons for each class

Question 23.
Higher Order Thinking Three-tenths of Ken’s buttons are blue, \(\frac{4}{10}\) are green, and the rest are black. What fraction of Ken’s buttons are black?
Answer:
\(\frac{3}{10}\)
Explanation

f=1 – (\(\frac{3}{10}\) + \(\frac{4}{10}\)),
= 1 – (\(\frac{3 + 4 }{10}\)),
= 1 – (\(\frac{7}{10}\)),
=(\(\frac{1}{1}\) – \(\frac{7}{10}\)),
=\(\frac{3}{10}\).

Assessment Practice

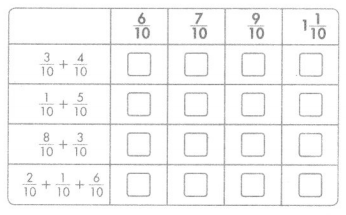
Question 24.
Match each expression with its sum.

Answer:

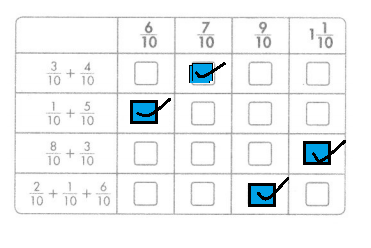
Question 25.
Jayla did some chores in the morning. She did \(\frac{3}{12}\) of her chores in the evening. By the end of the day, she had completed \(\frac{7}{12}\) of her chores. What fraction of the chores c, did Jayla do in the morning?
A. c = \(\frac{1}{12}\)
B. c = \(\frac{2}{12}\)
C. c = \(\frac{3}{12}\)
D. c = \(\frac{4}{12}\)
Answer: D.
\(\frac{4}{12}\)

Explanation:

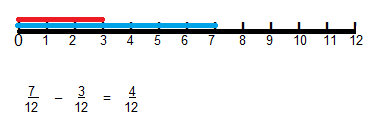
Lesson 9.4 Model Subtraction of Fractions

Solve & Share
Mr. Yetkin uses \(\frac{4}{6}\) of a sheet of plywood to board up a window. How much of the plywood is left? Solve this problem any way you choose.
I can … use tools such as fraction strips or area models to subtract fractions with like denominators.

Look Back! Be Precise Explain why \(\frac{4}{6}\) is subtracted from \(\frac{6}{6}\) to find how much of the plywood is left.
Answer
\(\frac{2}{6}\)

Explanation

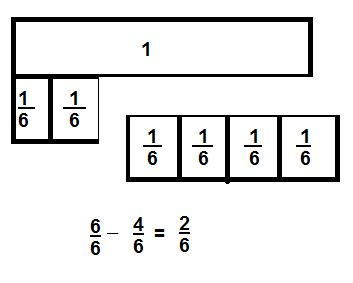
\(\frac{6}{6}\) – \(\frac{4}{6}\) = \(\frac{2}{6}\)

Essential Question
How Can You Use Tools to Subtract Fractions?
Answer:
To subtract fractions with like denominators, subtract the numerator and write the difference over the denominator.
We can use tools such as Fraction Strips or Number line.
For example,

Number line.

Fraction Strip

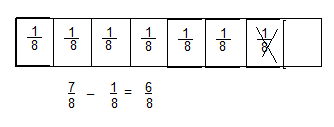
Visual Learning Bridge
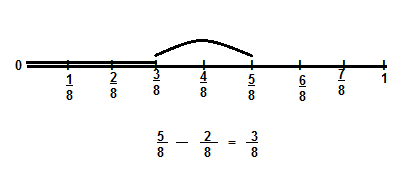
A flower garden is divided into eighths. If \(\frac{2}{8}\) of the garden is used to grow yellow roses, what fraction is left to grow other flowers?

You can use tools such as fraction strips to represent subtraction.

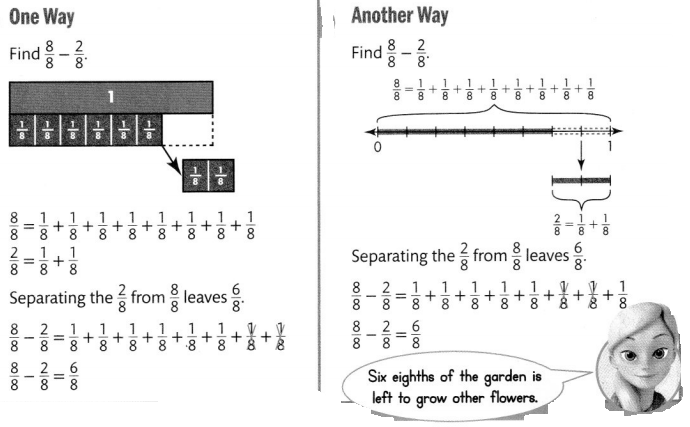
Convince Me! Use Appropriate Tools In the problem above, suppose six sections of the garden are used for yellow roses and two other sections are used for petunias. How much more of the garden is used for yellow roses than is used for petunias? Use fraction strips or another tool to help. Write your answer as a fraction.

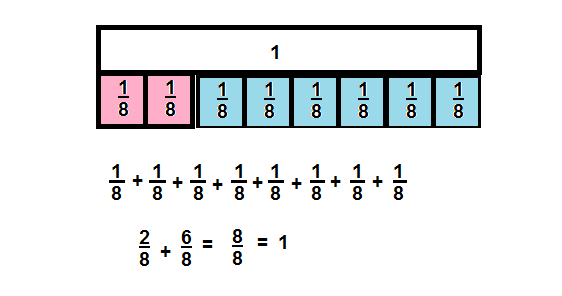
f = \(\frac{6}{8}\) + \(\frac{2}{8}\) =\(\frac{6 + 2}{8}\) = \(\frac{8}{8}\) = 1

Another Example!

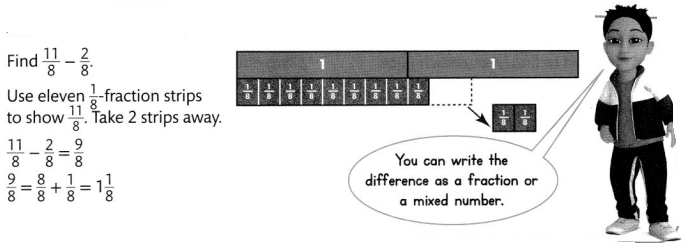
Guided Practice

Do You Understand?
Question 1.
In the problem at the top of the previous page, suppose one other section was used to grow peonies. What fraction of the garden is now available for flowers?
Answer:
f = \(\frac{8}{8}\) – ( \(\frac{2}{8}\) + \(\frac{1}{8}\)) 

  = \(\frac{8}{8}\) – \(\frac{2 + 1}{8}\)

  = \(\frac{8}{8}\) – \(\frac{3}{8}\)

=\(\frac{5}{8}\)

Do You Know How?
For 2-5, use fraction strips or other tools to subtract.
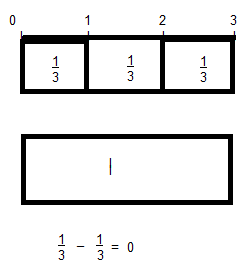
Question 2.
\(\frac{1}{3}-\frac{1}{3}\)
Answer: 0
Explanation:
By using fraction strip \(\frac{1}{3}-\frac{1}{3}\) = 0

Question 3.
\(\frac{5}{5}-\frac{2}{5}\)
Answer:
\(\frac{3}{5}\)
Explanation:

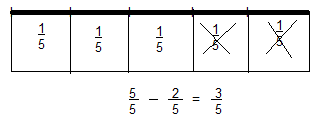
Question 4.
\(\frac{7}{12}-\frac{3}{12}\)
Answer:
\(\frac{4}{12}\)

Explanation:

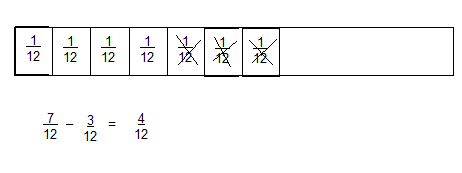
Question 5.
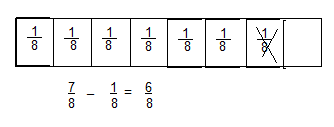
\(\frac{7}{8}-\frac{1}{8}\)
Answer:
\(\frac{6}{8}\)
Explanation:

Independent Practice

Leveled Practice For 6-14, find each difference. Use fraction strips or other tools as needed.
Question 6.

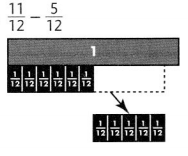
Answer:
\(\frac{6}{12}\)

\(\frac{1}{2}\)

Question 7.

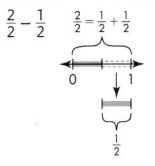
Answer:
\(\frac{1}{2}\)

Question 8.

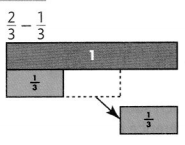
Answer:
\(\frac{1}{3}\)

Question 9.
\(\frac{4}{5}-\frac{2}{5}\)
Answer:
\(\frac{2}{5}\)
Explanation:

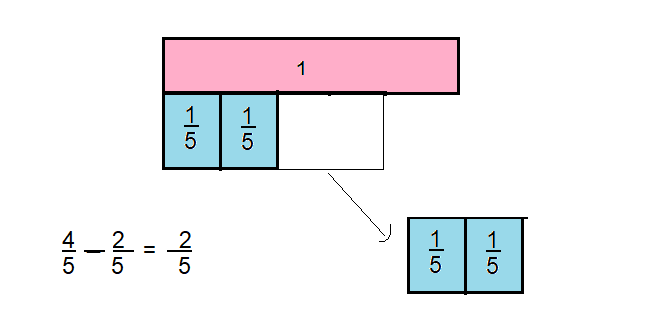
Question 10.
\(\frac{17}{10}-\frac{3}{10}\)
Answer:
1\(\frac{4}{10}\)
Explanation:

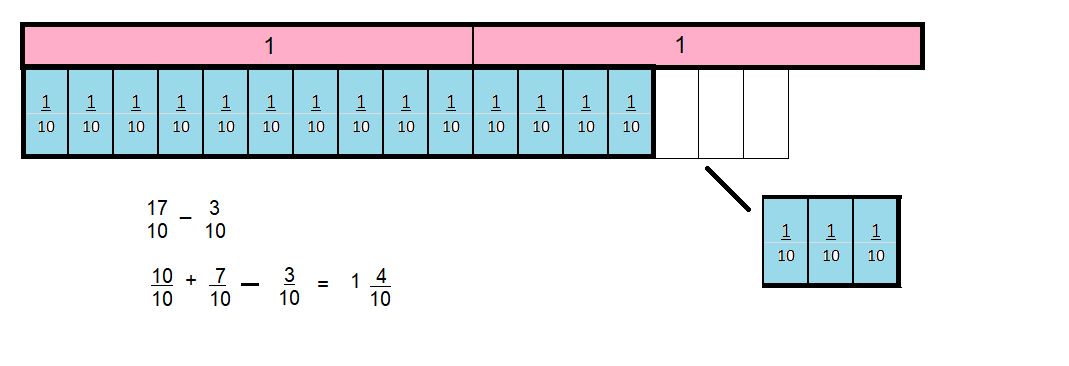
Question 11.
\(\frac{8}{6}-\frac{2}{6}\)
Answer:
\(\frac{8}{6}-\frac{2}{6}\) =1
Explanation:

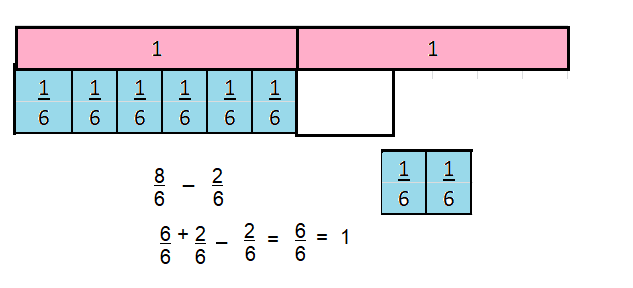
Question 12.
\(\frac{9}{6}-\frac{1}{6}\)
Answer:
1\(\frac{2}{6}\) = 1\(\frac{1}{3}\)
Explanation:

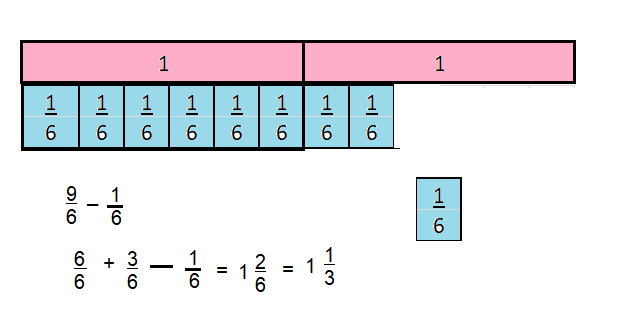
Question 13.
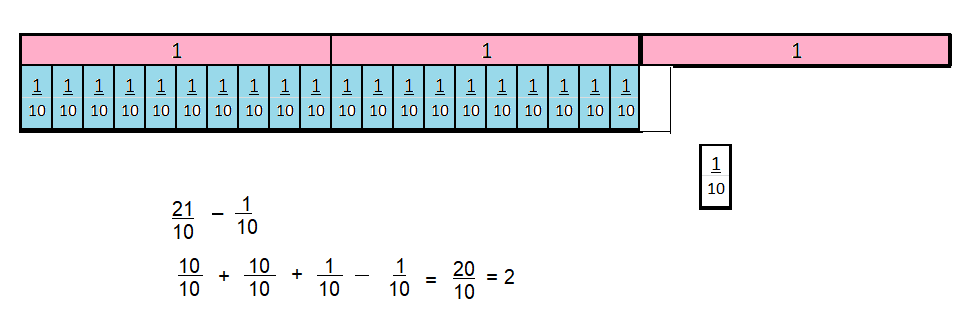
\(\frac{21}{10}-\frac{1}{10}\)
Answer:
\(\frac{20}{10}\) = 2
Explanation:

Question 14.
\(\frac{1}{5}-\frac{1}{5}\)
Answer:
\(\frac{1}{5}-\frac{1}{5}\) = 0
Explanation:

Problem Solving

Question 15.
Model with Math Leesa has \(\frac{7}{8}\) gallon of juice. She shares \(\frac{3}{8}\) gallon. Write and solve an equation to find j, how much juice Leesa has left.

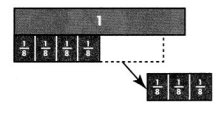
Answer:
\(\frac{4}{8}\)
Explanation:
\(\frac{7}{8}\) – \(\frac{3}{8}\) = \(\frac{4}{8}\) = \(\frac{1}{2}\)

Question 16.
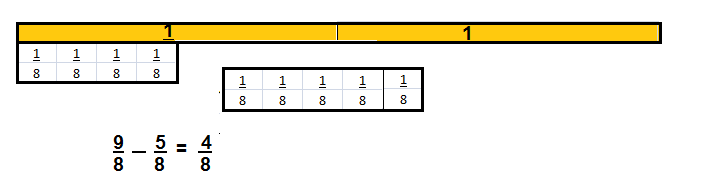
Higher Order Thinking Using only odd numbers for numerators, write two different subtraction problems that have a difference of \(\frac{1}{2}\). Remember, you can find equivalent fractions for \(\frac{1}{2}\).
Answer:
\(\frac{1}{2}\)

Explanation:
\(\frac{9}{8}\) – \(\frac{5}{8}\) = \(\frac{4}{8}\) = \(\frac{1}{2}\)

Question 17.
In Kayla’s class, some of the students are wearing blue shirts. \(\frac{6}{8}\) of the students are NOT wearing blue shirts. What fraction of the students are wearing blue shirts? Show your work.
Answer:
\(\frac{2}{8}\) = \(\frac{1}{4}\)

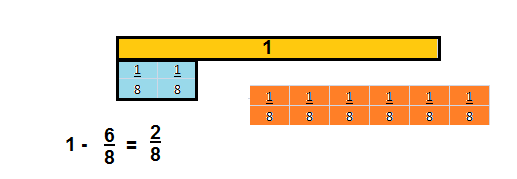
Explanation:
f= 1- \(\frac{6}{8}\) = \(\frac{1}{1}\) – \(\frac{6}{8}\) = \(\frac{2}{8}\) =
\(\frac{1}{4}\)

Question 18.
In Exercise 17, what number represents the whole class? How do you
know what fraction to use to represent this number?
Answer:
1 number represents the whole class
\(\frac{1}{1}\)
Explanation:

Question 19.
Rick shared his bag of grapes with friends. He gave \(\frac{2}{10}\) of the bag to Melissa and \(\frac{4}{10}\) of the bag to Ryan. What fraction of the bag of grapes does Rick have left? Show your work.
Answer:
\(\frac{4}{10}\)
Explanation:

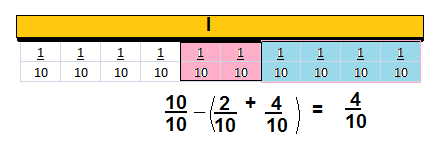
f=1-{\(\frac{4}{10}\) + \(\frac{2}{10}\)}=\(\frac{1}{1}\) – \(\frac{6}{10}\) = \(\frac{4}{10}\)

Question 20.
Teresa gave away 8 baseball cards and has 4 baseball cards left. Write a subtraction problem to show the fraction of the baseball cards Teresa has left.
Answer:
\(\frac{12}{12}\) – \(\frac{8}{12}\) = \(\frac{4}{12}\)
Explanation:

Assessment Practice

Question 21.
Which subtraction problem has a difference of \(\frac{1}{3}\)?
A. \(\frac{2}{2}-\frac{1}{2}\)
B. \(\frac{5}{3}-\frac{3}{3}\)
C. \(\frac{4}{3}-\frac{3}{3}\)
D. \(\frac{5}{3}-\frac{1}{3}\)
Answer:
Option C
\(\frac{4}{3}-\frac{3}{3}\) = \(\frac{1}{3}\)

Question 22.
Which subtraction problem has a difference of \(\frac{10}{8}\)?
A. \(\frac{20}{8}-\frac{10}{8}\)
B. \(\frac{8}{10}+\frac{2}{10}\)
C. \(\frac{10}{8}-\frac{4}{8}\)
D. \(\frac{6}{8}-\frac{1}{4}\)
Answer:
Option A,
\(\frac{20}{8}-\frac{10}{8}\) = \(\frac{10}{8}\)

Lesson 9.5 Subtract Fractions with Like Denominators

Solve & Share
Leah and Josh live the same direction from school and on the same side of Forest Road. Leah’s house is \(\frac{8}{10}\) mile from school. Josh’s house is \(\frac{5}{10}\) mile from school. How much farther does Leah have to walk home when she reaches Josh’s house? Solve this problem any way you choose.
I can … use my understanding of subtraction as separating parts of the same whole to subtract fractions with like denominators.

Look Back! Model with Math How could you represent the problem above with a bar diagram and an equation? Tell what your variable means.

Answer
\(\frac{3}{10}\)

Explanation

Leah’s house is \(\frac{8}{10}\) mile and
Josh’s house is \(\frac{5}{10}\) mile from school.

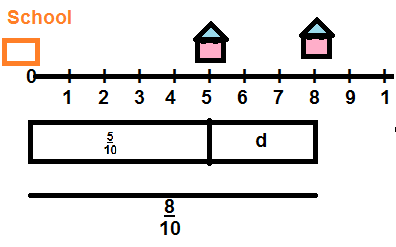
\(\frac{8}{10}\) – \(\frac{5}{10}\) = \(\frac{3}{10}\)

Essential Question
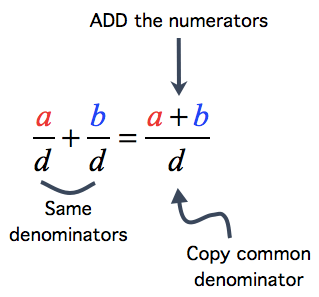
How Can You Subtract Fractions with Like Denominators?
Answer:
To subtract fractions with like denominators, just subtract the numerators and write the difference over the denominator.
Always reduce your final answer to its lowest term.

Explanation:
For Example,
\(\frac{4}{10}\) + \(\frac{5}{10}\) = \(\frac{9}{10}\)

Visual Learning Bridge
Tania is squeezing lemons to make lemonade. The recipe calls for \(\frac{5}{8}\) cup of lemon juice. The amount Tania has squeezed is shown at the right. What fraction of a cup of lemon juice does Tania still need to squeeze?

Subtract the fractions to find the difference.

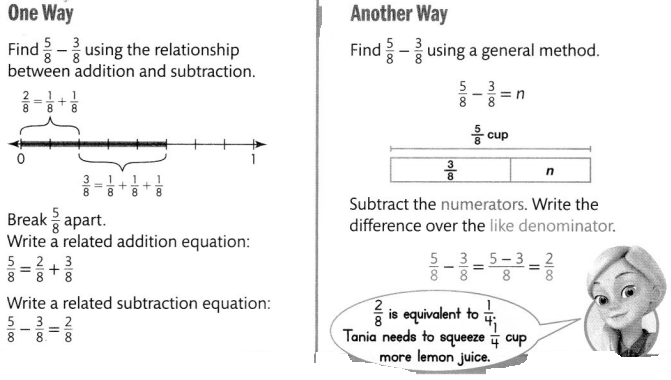
Convince Me! Reasoning in the problem above, suppose Tania decided to double the amount of lemonade she wants to make. Then how much more lemon juice would Tania need to squeeze?

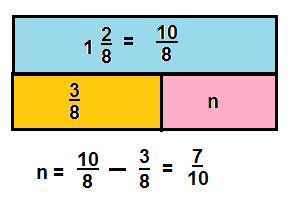
Guided Practice

Do You Understand?
Question 1.
Jesse has a bottle that contains \(\frac{7}{10}\) liter of water. He drinks \(\frac{2}{10}\) liter. Jesse says he has \(\frac{1}{2}\) liter left. Is he correct? Explain.
Answer:
YES, JESSE IS CORRECT
Explanation:

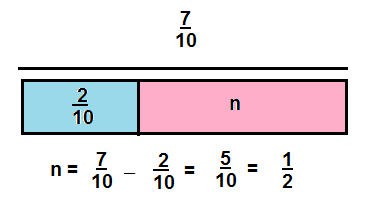
Question 2.
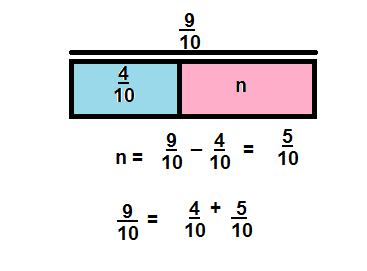
What addition sentence can you use to subtract \(\frac{4}{10}\) from \(\frac{9}{10}\)?
Answer:
\(\frac{4}{10}\) + \(\frac{5}{10}\)= \(\frac{9}{10}\)
\(\frac{9}{10}\) – \(\frac{4}{10}\) = \(\frac{5}{10}\)
Explanation:

Do You Know How?
For 3-10, subtract the fractions.
Question 3.
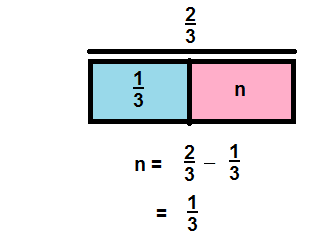
\(\frac{2}{3}-\frac{1}{3}\)
Answer:
\(\frac{1}{3}\)
Explanation:

Question 4.
\(\frac{3}{4}-\frac{2}{4}\)
Answer:
\(\frac{1}{4}\)
Explanation:

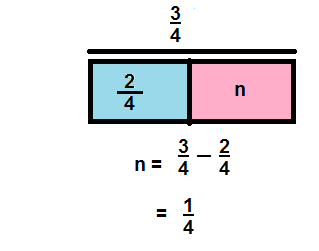
Question 5.
\(\frac{5}{6}-\frac{2}{6}\)
Answer:
\(\frac{3}{6}\)
Explanation:

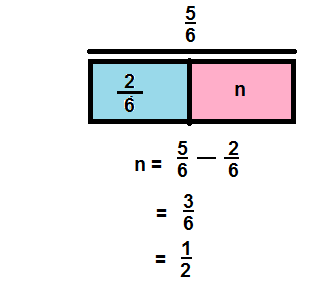
Question 6.
\(\frac{9}{12}-\frac{3}{12}\)
Answer:
\(\frac{6}{12}\)
Explanation:

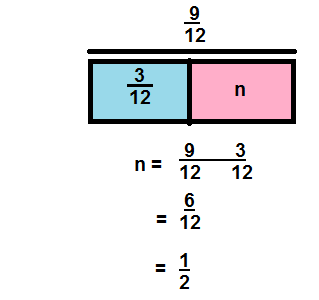
Question 7.
\(\frac{9}{8}-\frac{3}{8}\)
Answer:
\(\frac{6}{8}\)
Explanation:

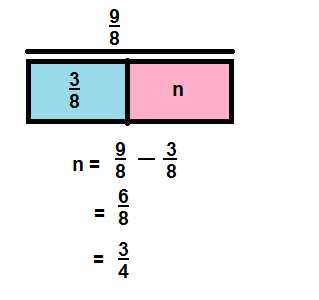
Question 8.
\(\frac{17}{10}-\frac{9}{10}\)
Answer:
\(\frac{8}{10}\)
Explanation:

Question 9.
\(\frac{4}{8}-\frac{1}{8}\)
Answer:
\(\frac{3}{8}\)
Explanation:

Question 10.
\(\frac{1}{2}-\frac{1}{2}\)
Answer:
0

Independent Practice

Leveled Practice For 11-18, subtract the fractions.
Question 11.

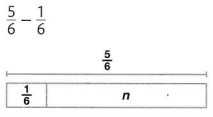
Answer:
n = \(\frac{4}{6}\)
Explanation:

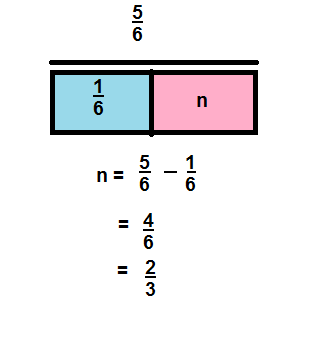
Question 12.

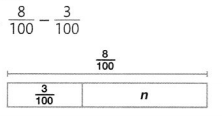
Answer:
n = \(\frac{5}{100}\)
= \(\frac{1}{20}\)
Explanation:

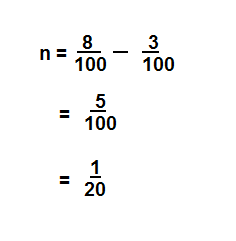
Question 13.

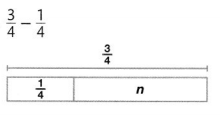
Answer:
n = \(\frac{2}{4}\)
Explanation:

Question 14.

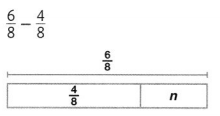
Answer:
n = \(\frac{2}{8}\)
Explanation:

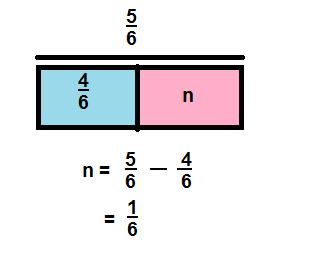
Question 15.
\(\frac{5}{6}-\frac{4}{6}\)
Answer:
\(\frac{1}{6}\)
Explanation:

Question 16.
\(\frac{40}{10}-\frac{20}{10}\)
Answer:
\(\frac{20}{10}\) = 2
Explanation:

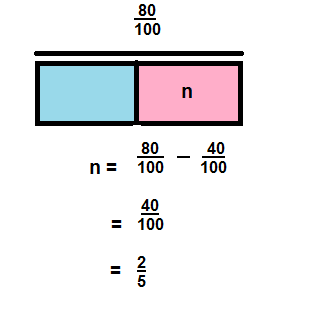
Question 17.
\(\frac{80}{100}-\frac{40}{100}\)
Answer:
\(\frac{40}{100}\)
Explanation:

Question 18.
\(\frac{19}{10}-\frac{8}{10}\)
Answer:
1\(\frac{1}{10}\)
Explanation:

Problem Solving

Question 19.
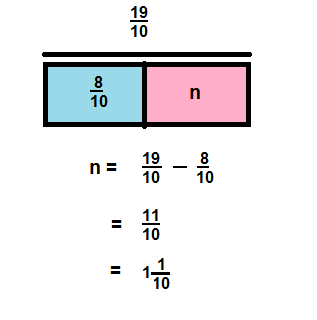
Joey ran \(\frac{1}{4}\) mile in the morning and \(\frac{1}{4}\) mile farther than in the morning in the afternoon. If he wants to run a full mile, how much more does Joey have to run? Write equations to explain.
Answer:
\(\frac{1}{4}\)

Explanation:

Question 20.
Reasoning Explain how subtracting \(\frac{4}{5}-\frac{3}{5}\) involves subtracting 4 – 3.
Answer:
n = \(\frac{1}{5}\)

n = \(\frac{4}{5}\) –  \(\frac{3}{5}\)

n = \(\frac{4 – 3}{5}\)

n = \(\frac{1}{5}\)

Question 21.
Higher Order Thinking The flags of all 5 Nordic countries are displayed. What fraction describes how many more of the flags displayed are 2-color flags than are 3-color flags?

Answer:
\(\frac{1}{5}\)
Explanation:

Assessment Practice

Question 22.
Brian had a piece of chalk \(\frac{9}{10}\) centimeter long. A piece cracked off as he was drawing on the sidewalk. Then Brian’s chalk was only \(\frac{6}{10}\) centimeter long. How long was the piece of chalk that cracked off?

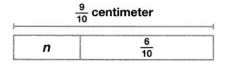
Answer:
\(\frac{3}{10}\)

Explanation:
n = \(\frac{9}{10}\) – \(\frac{6}{10}\)

n = \(\frac{3}{10}\)

Question 23.
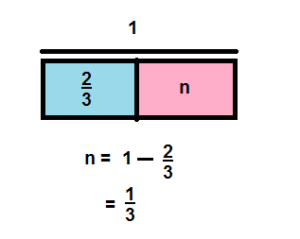
Marietta baked a chicken pot pie. She serves \(\frac{2}{3}\) of the pie at dinner. How much of the pie remains?
Answer:
\(\frac{1}{3}\)
Explanation:

Lesson 9.6 Add and Subtract Fractions with Like Denominators

Solve & Share
The dirt bike track shown is \(\frac{7}{8}\) of a mile long from start to finish. The track is divided into four sections. What is the length of the longest section? Solve this problem any way you choose.
I can … use a number line to add and subtract fractions when the fractions refer to the same whole.

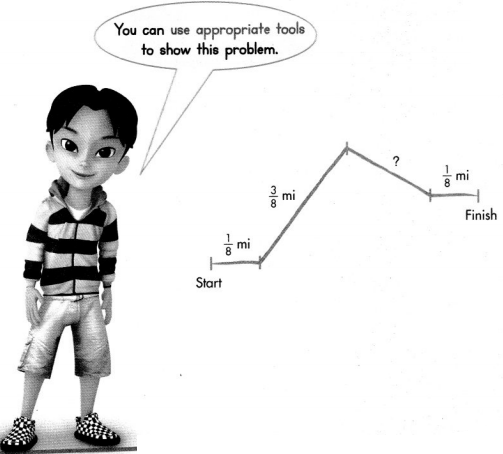
Answer:

\(\frac{2}{8}\)
Explanation:

Number line

Look Back! How did you decide which section of the track was the longest?
Answer:
The length of the longest section = \(\frac{3}{8}\)

Essential Question
How Do You Add and Subtract Fractions on a Number Line?
Answer:
In math, a number line is a straight line with numbers placed at equal intervals or segments along its length.
A number line can be extended infinitely in any direction, and we usually represent it horizontally.
The numbers on the number line in addition increase as we move from left to right and in subtraction decrease moving from right to left.
Explanation:
For Example,

Visual Learning Bridge
Mary rides her bike \(\frac{2}{10}\) mile to pick up her friend Marcy for soccer practice. Together, they ride \(\frac{5}{10}\) mile to the soccer field. What is the distance from Mary’s house to the soccer field?
You can use jumps on the number line to add or subtract fractions.

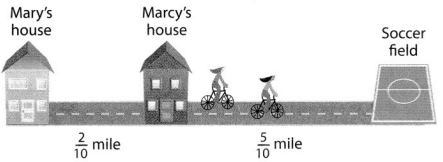
Use a number line to show \(\frac{2}{10}+\frac{5}{10}\).
Draw a number line for tenths. Locate \(\frac{2}{10}\) on the number line.
To add, move \(\frac{5}{10}\) to the right.

When you add, you move to the right on the number line.

Write the addition equation.
Add the numerators. Write the sum over the like denominator.
\(\frac{2}{10}+\frac{5}{10}=\frac{2+5}{10}=\frac{7}{10}\)
The distance from Mary’s house to the soccer field is \(\frac{7}{10}\) mile.

Convince Me! Use Appropriate Tools Use the number line below to find \(\frac{5}{8}+\frac{2}{8}\). Can you also use the number line to find \(\frac{5}{8}-\frac{2}{8}\)? Explain.

Answer:
\(\frac{5}{8}+\frac{2}{8}\) = \(\frac{7}{8}\)

\(\frac{5}{8}-\frac{2}{8}\) = \(\frac{3}{8}\)

Explanation:

Another Example!
Find \(\frac{6}{8}-\frac{4}{8}\)
Start at \(\frac{6}{8}\). To subtract, move \(\frac{4}{8}\) to the left.
The ending point is \(\frac{2}{8}\)
So, \(\frac{6}{8}-\frac{4}{8}=\frac{2}{8}\)

Guided Practice

Do You Understand?
Question 1.
In the example above, how is the denominator illustrated on the number line?
Answer:
The denominator illustrates the number of parts of the whole,
In the above example 8 is the denominator, that is 8 parts.
\(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)

Question 2.
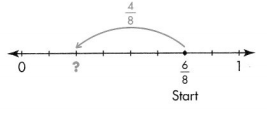
Draw a number line to represent \(\frac{3}{12}+\frac{5}{12}\).
Answer:
\(\frac{3}{12}+\frac{5}{12}\) = \(\frac{8}{12}\)
Explanation:

Do You Know How?
For 3-4, write the equation shown by each number line.
Question 3.

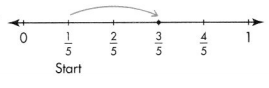
Answer:
\(\frac{3}{5}\)

\(\frac{1}{5}+\frac{2}{5}\) = \(\frac{3}{5}\)

Question 4.

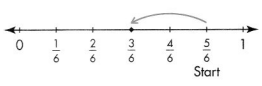
Answer:
\(\frac{2}{6}\)

\(\frac{5}{6} – \frac{3}{6}\) = \(\frac{2}{6}\)

Independent Practice

For 5-8, write the equation shown by each number line.
Question 5.

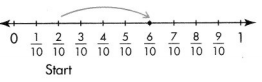
Answer:

\(\frac{6}{10}\)

\(\frac{2}{10} + \frac{4}{10}\) = \(\frac{6}{10}\)

Question 6.

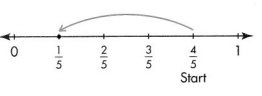
Answer:

\(\frac{1}{5}\)

\(\frac{4}{5} – \frac{3}{5}\) = \(\frac{1}{5}\)

Question 7.

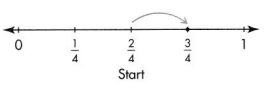
Answer:
\(\frac{3}{4}\)

\(\frac{2}{4} + \frac{1}{4}\) = \(\frac{3}{4}\)

Question 8.

Answer:
\(\frac{2}{6}\)

\(\frac{4}{6} – \frac{2}{6}\) = \(\frac{2}{6}\)

Problem Solving

Question 9.
Number Sense How do you know the quotient 639 ÷ 6 is greater than 100 before you actually divide?
Answer:
106 \(\frac{3}{6}\)
Explanation:
= \(\frac{600}{6}\)  + \(\frac{36}{6}\) + \(\frac{3}{6}\)
= 100 + 6 + \(\frac{3}{6}\)
=106 \(\frac{3}{6}\)

Question 10.
On average, a largemouth bass weighs about 12 pounds. Two fishermen weighed the largemouth bass they both caught and found their catch weighed 82 pounds. What is the greatest number of largemouth bass caught that are average weight?
Answer:
22 pounds
1 \(\frac{10}{12}\)

Explanation:

= \(\frac{82}{12}\)

= \(\frac{60}{12}\) + \(\frac{22}{12}\)

= 5 + 1\(\frac{10}{12}\)

Question 11.
Isaac started his bike ride at the trailhead. He reached the picnic area and continued to the lookout tower. If Isaac rode his bike for a total of \(\frac{10}{4}\) miles, how much farther did he ride beyond the lookout tower?

Answer:
\(\frac{5}{4}\)

Explanation:

n = \(\frac{10}{4}\) – [\(\frac{2}{4}\)+ \(\frac{3}{4}\)]

n = \(\frac{10}{4}\) – \(\frac{5}{4}\)

n = \(\frac{5}{4}\)

n = 1 \(\frac{1}{4}\)

Question 12.
Model with Math Ricky completely filled a bucket to wash his car. After he finished washing the car, \(\frac{5}{8}\) of the water remained in the bucket. Write and solve an equation to find n, the fraction of the water Ricky used.
Answer:
n = \(\frac{3}{8}\) water used by Ricky.
Explanation:
n = \(\frac{1}{1}\) – \(\frac{5}{8}\)
n = \(\frac{3}{8}\)

Question 13.
Higher Order Thinking Sarah and Jenny are running an hour-long endurance race. Sarah ran \(\frac{2}{6}\) hour before passing the baton to Jenny. Jenny ran \(\frac{3}{6}\) hour, then passed the baton back to Sarah. What fraction of the hour does Sarah still need to run to complete the race?
Answer:
\(\frac{1}{6}\) to complete the race.
Explanation:

n = 1 – \(\frac{2}{6}\) + \(\frac{3}{6}\)

n = 1 – \(\frac{2 + 3}{6}\)

n = 1 – \(\frac{5}{6}\)

n = \(\frac{1}{6}\)

Assessment Practice

Question 14.
Choose numbers from the box to fill in the missing numbers in each equation. Use each number once.

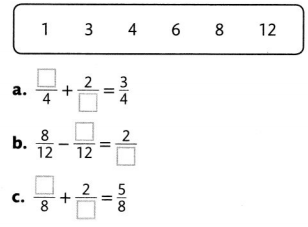
Answer:

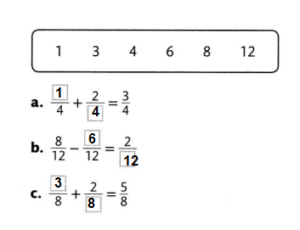
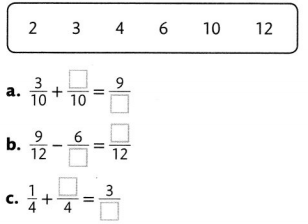
Question 15.
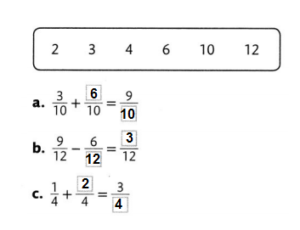
Choose numbers from the box to fill in the missing numbers in each equation. Use each number once.

Answer:

Lesson 9.7 Model Addition and Subtraction of Mixed Numbers

Solve & Share
Tory is cutting loaves of bread into fourths. She needs to wrap 3\(\frac{3}{4}\) loaves to take to a luncheon and 1\(\frac{2}{4}\) loaves for a bake sale. How many loaves does Tory need to wrap for the luncheon and the bake sale? Solve this problem any way you choose.
I can ….. use models and equivalent fractions to help add and subtract mixed numbers.

Look Back! Reasoning How can you estimate the sum above?

3\(\frac{3}{4}\) + 1\(\frac{2}{4}\)

= (3 + 1)(\(\frac{3}{4}\) + \(\frac{2}{4}\))

= (3 + 1)(\(\frac{3 + 2}{4}\))

= (4)(\(\frac{3 + 2}{4}\))

= 4(\(\frac{5}{4}\))

= (4 + 1)(\(\frac{1}{4}\))

= \(5\frac{1}{4}\)

Essential Question
How Can You Add or Subtract Mixed Numbers?
Answer:
To add or subtract mixed numbers, firstly convert the mixed numbers to improper fractions and find the least common denominator, then add or subtract the whole numbers. Finally write the lowest terms.
For example,

3\(\frac{3}{4}\) + 1\(\frac{2}{4}\)

= \(\frac{15}{4}\) + \(\frac{6}{4}\)

= \(\frac{15 + 6}{4}\)

= \(\frac{21}{4}\)

Visual Learning Bridge
Bill has 2 boards to use to make picture frames. What is the total length of the two boards? How much longer is one board than the other?

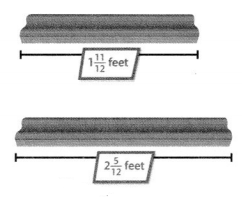
You can use addition to find the total length of the two boards.
You can use subtraction to find how much longer one board is than the other.

Convince Me! Use Appropriate Tools Suppose Bill’s boards were 2\(\frac{11}{12}\) feet and 1\(\frac{5}{12}\) feet. What would be the total length of the two boards? How much longer is one board than the other? Use fraction strips or draw number lines to show your work.

Answer

4\(\frac{4}{12}\)

Explanation

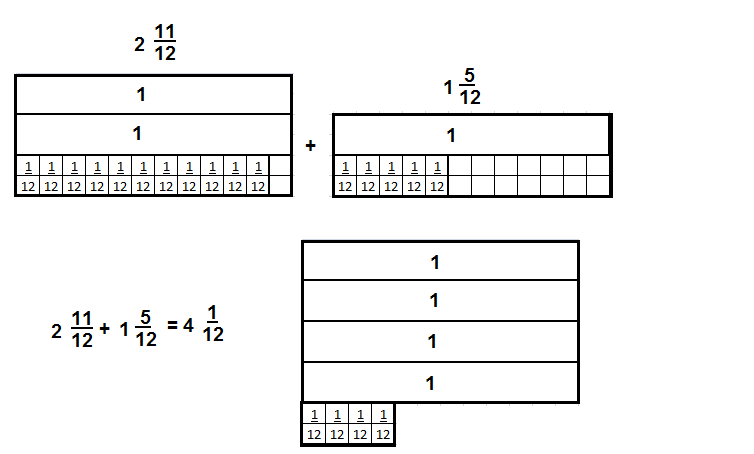
Another Example!

Guided Practice

Do You Understand?
Question 1.
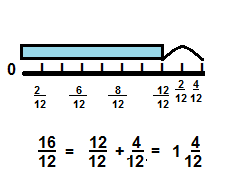
In the problem on the previous page, why does \(\frac{16}{12}\) = 1\(\frac{4}{12}\)? Use decomposing to explain.
Answer:
\(\frac{16}{12}\) = 1\(\frac{4}{12}\)
Explanation:

Do You Know How?
For 2-3, use a tool to find each sum or difference.
Question 2.
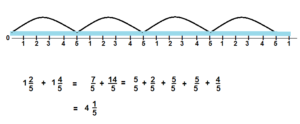
1\(\frac{2}{5}\) + 2\(\frac{4}{5}\)
Answer:
4\(\frac{1}{5}\)
Explanation:

Question 3.
1\(\frac{1}{4}\) + 2\(\frac{3}{4}\)
Answer:  4
Explanation:

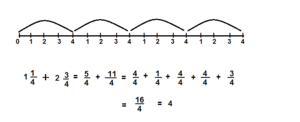
Independent Practice

For 4-11, use a tool to find the sum or difference.
Question 4.

Answer:
\(\frac{2}{4}\)

\(\frac{1}{2}\)

Question 5.

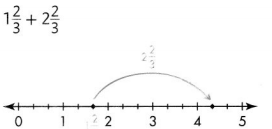
Answer:
4 \(\frac{13}{3}\)
Explanation:

1\(\frac{2}{3}\) + 2\(\frac{2}{3}\)

\(\frac{5}{3}\) + \(\frac{8}{3}\)

\(\frac{13}{3}\)

4 \(\frac{13}{3}\)

Question 6.

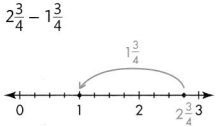
Answer:
1
Explanation:

2\(\frac{3}{4}\) – 1\(\frac{3}{4}\)

\(\frac{11}{4}\) – \(\frac{7}{4}\)

\(\frac{4}{4}\)  =  1

Question 7.

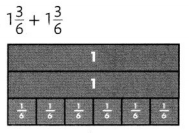
Answer:
3,

Explanation:
1\(\frac{3}{6}\) + 1\(\frac{3}{6}\),
\(\frac{9}{6}\) + \(\frac{9}{6}\),
\(\frac{18}{6}\), 3

Question 8.
\(2 \frac{3}{5}+1 \frac{3}{5}\)
Answer:
4 \(\frac{1}{5}\),

Explanation:

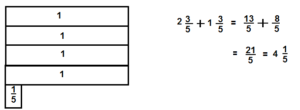
Question 9.
\(4 \frac{5}{12}+1 \frac{7}{12}\)
Answer:
6

Explanation:

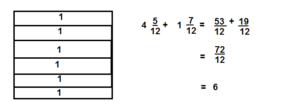
Question 10.
\(4 \frac{9}{10}+3 \frac{7}{10}\)
Answer:
8 \( \frac{2}{10}\)
Explanation:

Question 11.
\(5 \frac{3}{4}+2 \frac{3}{4}\)
Answer:
8 \( \frac{2}{4}\),

Explanation:

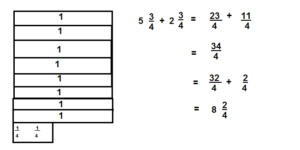
Problem Solving

Question 12.
Use Appropriate Tools Kit said, “On summer vacation, I spent 1\(\frac{1}{2}\) weeks with my grandma and one week more with my aunt than with my grandma.” How many weeks did she spend visiting family? Use a tool to find the sum.
Answer:
2\(\frac{1}{2}\)
Explanation:

1\(\frac{1}{2}\) + 1  week

\(\frac{3}{2}\) + 1 = \(\frac{3 + 2}{2}\)

=   \(\frac{5}{2}\)

=   \(\frac{4}{2}\) + \(\frac{1}{2}\)

=   2\(\frac{1}{2}\)

Question 13.
Use Appropriate Tools If Kit spent 3\(\frac{1}{2}\) weeks in swimming lessons, how much more time did Kit spend visiting family than in swimming lessons? Use a tool to find the difference.
Answer:
6 weeks
Explanation:
1\(\frac{1}{2}\) + 1  week + 3\(\frac{1}{2}\)
\(\frac{3}{2}\) + 1 + \(\frac{7}{2}\) = \(\frac{3 + 2 + 7}{2}\)
=   \(\frac{12}{2}\)
=  6

Question 14.
Hannah used 1\(\frac{5}{8}\) gallons of paint for theceiling. Hannah used 6 gallons of paint for the walls and ceiling combined. How much paint did Hannah use for the walls?
Answer:
4\(\frac{3}{8}\) gallons of Paint Hannah use for the walls
Explanation:
Total paint (Wall + Ceiling) = Paint for Ceiling + Paint for Wall
6 gallons = 1\(\frac{5}{8}\) + Paint for Wall
Paint for Wall = 6 – 1\(\frac{5}{8}\) = 6 – \(\frac{13}{8}\)= \(\frac{35}{8}\)
Paint for Wall = 4\(\frac{3}{8}\)
Paint for Wall = Total paint (Wall + Ceiling) – Total paint Ceiling

Question 15.
A furlong is a unit of length still used today in racing and agriculture. A race that is 8 furlongs is 1 mile. A mile is 5,280 feet. How many feet are in a furlong?
Answer:
660 feet is one furlong
Explanation:
8 furlongs is 1 mile.
A mile is 5,280 feet
one furlong \(\frac{5280}{8}\) = 660 feet

Question 16.
Higher Order Thinking A recipe calls for 1\(\frac{2}{3}\) cups of brown sugar for the granola bars and 1\(\frac{1}{3}\) cups of brown sugar for the topping. Dara has 3\(\frac{1}{4}\) cups of brown sugar. Does she have enough brown sugar to make the granola bars and the topping? Explain.

You can use fraction strips or a number line to compare amounts.
Answer: YES
Dara has enough sugar
She need 3 cups of brown sugar, she has 3\(\frac{1}{4}\) cups

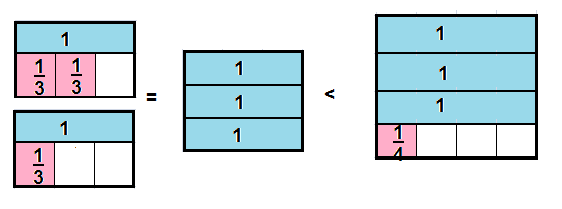
1\(\frac{2}{3}\) + 1\(\frac{1}{3}\) = \(\frac{5 + 4}{3}\)=\(\frac{9}{3}\) = 3

3\(\frac{1}{4}\) >3

Assessment Practice

Question 18.
Megan finishes the scarf. It is 5\(\frac{6}{12}\) feet in length. She finds a mistake in her knitting and unravels 2\(\frac{4}{12}\) feet to correct the mistake. How long is the scarf now?
A. s = \(2 \frac{7}{12}+2 \frac{11}{12}\)
B. s = \(2 \frac{5}{12}+2 \frac{7}{12}\)
C. s = \(2 \frac{11}{12}-2 \frac{7}{12}\)
D. s = \(4 \frac{11}{12}-2 \frac{7}{12}\)
Answer:
\(3 \frac{4}{12}\)

Explanation:
\(5 \frac{6}{12} – 2 \frac{4}{12}\)

\( \frac{66}{12} –  \frac{28}{12}\)

= 3\( \frac{4}{12}\)

D. s = \(4 \frac{11}{12}-1\frac{9}{12}\) {some correction may required in option D}

Question 17.
Megan is knitting a scarf. She has knitted 2\(\frac{7}{12}\) feet so far. She needs to knit another 2\(\frac{11}{12}\) feet. Which of the following equations can Megan use to find s, the length of the completed scarf?
A. 8 \(\frac{10}{12}\) feet
B. 5 \(\frac{4}{12}\) feet
C. 3 \(\frac{2}{12}\) feet
D. 1 \(\frac{4}{12}\) feet
Answer:
Option B.
5 \(\frac{6}{12}\) feet {some correction may required in option B}
Explanation:
s = \(2 \frac{7}{12} + 2 \frac{11}{12}\)

s = \( \frac{31}{12} +  \frac{35}{12}\) =  \( \frac{66}{12}\)

s = 5\( \frac{6}{12}\)

Lesson 9.8 Add Mixed Numbers

Solve & Share
Joaquin used 1\(\frac{3}{6}\) cups of apple juice and 1\(\frac{4}{6}\) cups of orange juice in a recipe for punch. How much juice did Joaquin use? Solve this problem any way you choose.
I can… use equivalent fractions and properties of operations to add mixed numbers with like denominators.

Generalize. You can use what you know about adding fractions to solve this problem.

Look Back! Could you find the sum of \(1 \frac{3}{6}+1 \frac{4}{6}\) by adding (1 + 1) + \(\left(\frac{3}{6}+\frac{4}{6}\right)\)? Explain..

Answer

3\( \frac{1}{6}\)

Explanation

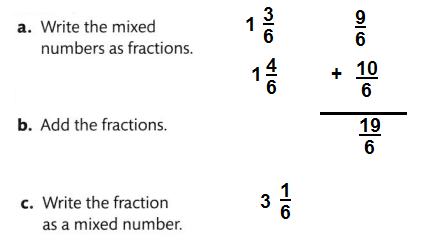
Essential Question
How Can You Add Mixed Numbers?
Answer:
As you may recall, a mixed number consists of an integer and a proper fraction. Any mixed number can also be written as an improper fraction, in which the numerator is larger than the denominator.
For example,
3\(\frac{1}{8}\) = \(\frac{25}{8}\)
The whole numbers, 3 and 1 sum to 4.
The fractions\(\frac{2}{5}\) and \(\frac{3}{5}\) add upto

\(\frac{5}{5}\) or 1.
Add the 1 to 4 to get the answer which is 5.

Visual Learning Bridge
Brenda mixes sand with 2\(\frac{7}{8}\) cups of potting mixture to prepare soil for her plant. After mixing them together, how many cups of soil does Brenda have?

You can use properties of operations to add mixed numbers. When you break apart a mixed number to add, you are using the Commutative and the Associative Properties.

Convince Me! Reasoning How is adding mixed numbers like adding fractions and whole numbers?

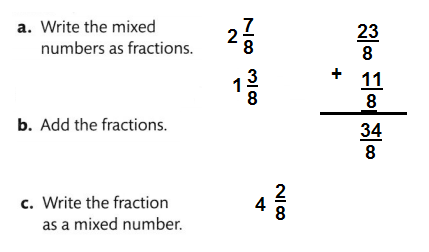
Guided Practice

Do You Understand?
Question 1.
How do the Commutative and Associative Properties allow you to add the fraction parts, add the whole number parts, and then add them together? Use \(2 \frac{5}{10}+1 \frac{9}{10}=\left(2+\frac{5}{10}\right)+\left(1+\frac{9}{10}\right)\) as an example.
Answer:
\(4 \frac{4}{10}\)
Explanation:

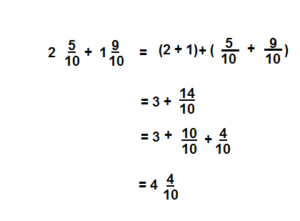
Question 2.
How can you use equivalent fractions to find \(4 \frac{2}{8}+1 \frac{1}{8}\)?
Answer:
\(5 \frac{3}{8}\)
Explanation:

 

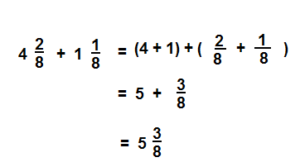
Do You Know How?
For 3-8, find each sum.
Question 3.

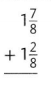
Answer:
\(3 \frac{1}{8}\)
Explanation:

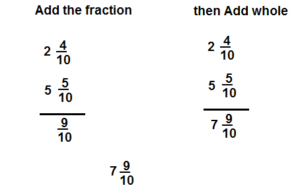
Question 4.

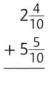
Answer:
\(7 \frac{9}{10}\)
Explanation:

Question 5.
\(4 \frac{2}{3}+1 \frac{2}{3}\)
Answer:
\(6 \frac{1}{3}\)
Explanation:

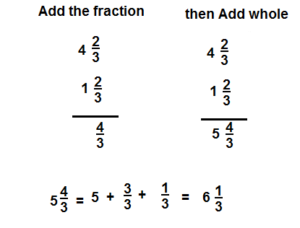
Question 6.
\(6 \frac{5}{12}+4 \frac{11}{12}\)
Answer:
\(11 \frac{4}{12}\)
Explanation:

Question 7.
\(2 \frac{1}{3}+2 \frac{1}{3}\)
Answer:

\(4 \frac{2}{3}\)

Explanation:

Question 8.
\(1 \frac{9}{12}+2 \frac{5}{12}\)
Answer:
\(4 \frac{2}{12}\)
Explanation:

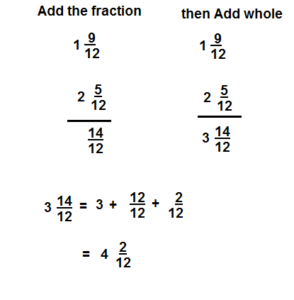
Independent Practice

Leveled Practice For 9-22, find each sum by adding mixed numbers or by adding equivalent fractions.
Question 9.

Answer:
\(4 \frac{1}{6}\)
Explanation:

Question 10.

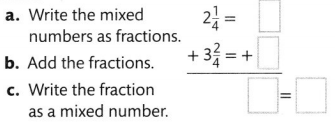
Answer:
\(5 \frac{3}{4}\)
Explanation:

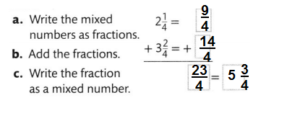
Question 11.

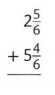
Answer:
\(8 \frac{3}{6}\)
Explanation:

Question 12.

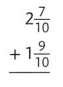
Answer:
\(4 \frac{6}{10}\)
Explanation:

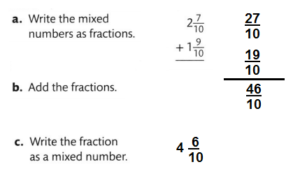
Question 13.

Answer:
\(5 \frac{4}{8}\)
Explanation:

Question 14.

Answer:
\(15 \frac{2}{8}\)
Explanation:

Question 15.
\(4 \frac{1}{10}+6 \frac{5}{10}\)
Answer:
\(10 \frac{6}{10}\)
Explanation:

Question 16.
\(1 \frac{7}{12}+4 \frac{9}{12}\)
Answer:
\(6 \frac{4}{12}\)
Explanation:

Question 17.
\(5+3 \frac{1}{8}\)
Answer:
\(8 \frac{1}{8}\)
Explanation:

Question 18.
\(3 \frac{3}{4}+2 \frac{3}{4}\)
Answer:
\(6 \frac{2}{4}\)
Explanation:

Question 19.
\(2 \frac{4}{5}+2 \frac{3}{5}\)
Answer:
\(5 \frac{2}{5}\)
Explanation:

Question 20.
\(3 \frac{2}{6}+2 \frac{5}{6}\)
Answer:
\(6 \frac{1}{6}\)
Explanation:

Question 21.
\(1 \frac{7}{12}+2 \frac{10}{12}\)
Answer:
\(4 \frac{5}{12}\)
Explanation:

Question 22.
\(3 \frac{6}{8}+1 \frac{3}{8}\)
Answer:
\(5 \frac{1}{8}\)
Explanation:

Problem Solving

For 23, use the map at the right.

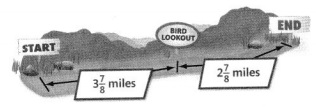
Question 23.
a. Find the distance from the start of the trail to the end of the trail.
Answer:
6 \(\frac{6}{8}\)
Explanation:

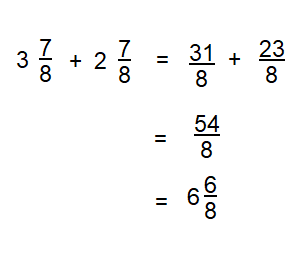
b. Linda walked from the start of the trail to the bird lookout and back. Did Linda walk more or less than if she had walked from the start of the trail to the end?
Answer:
Linda neither walked more nor less, when it comes to start of the trail to the end.
Explanation:
Linda walked from the start of the trail to the bird lookout and back
is  1+1 = 2
she had walked from the start of the trail to the end is one way.
its only 1.

Question 24.
Joe biked 1\(\frac{9}{12}\) miles from home to the lake, then went some miles around the lake, and then back home. Joe biked a total of 4\(\frac{9}{12}\) miles. How many miles did Joe bike around the lake?
Answer:
3 miles – Joe bike around the lake
Explanation:
Let f is miles around the lake
4\(\frac{9}{12}\) miles = 1\(\frac{9}{12}\) miles + f
f = 4\(\frac{9}{12}\) – 1\(\frac{9}{12}\)
f = \(\frac{57}{12}\) – \(\frac{21}{12}\)
f = \(\frac{57 – 21}{12}\)
f = \(\frac{36}{12}\)
f = 3 miles

Question 25.
Reasoning The bus took 4\(\frac{3}{5}\) hours to get from Jim’s home station to Portland and 3\(\frac{4}{5}\) hours to get from Portland to Seattle. How long did the bus take to get from Jim’s home station to Seattle?
Answer:
8\(\frac{2}{5}\) hours
Explanation:
f = 4\(\frac{3}{5}\) + 3\(\frac{4}{5}\)
f = \(\frac{23}{5}\) + \(\frac{19}{5}\)
f = \(\frac{23 + 19}{5}\)
f = \(\frac{42}{5}\)
f = 8\(\frac{2}{5}\)

Question 26.
Higher Order Thinking A male Parson’s chameleon is 23\(\frac{3}{4}\) inches long. It can extend its tongue up to 35\(\frac{1}{4}\) inches. What are 3 possible lengths for the chameleon when its tongue is extended?

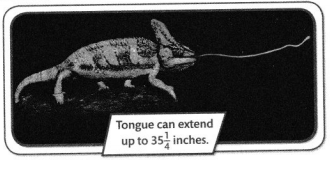
Answer:
3 possible lengths for the chameleon when its tongue is extended are ass follows,
i) 23\(\frac{3}{4}\) + 35\(\frac{1}{4}\) inches

ii) \(\frac{95}{4}\) + \(\frac{141}{4}\)

iii)  23 + \(\frac{3}{4}\) + 35 + \(\frac{1}{4}\)

Assessment Practice

Question 27.
Julie attaches an extension cord that is 2\(\frac{6}{8}\) yards long to a cord that is 2\(\frac{3}{8}\) yards long. How long are the two cords together? Select all the correct ways to find the sum.

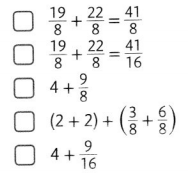
Answer:

Question 28.
Select all the correct sums.

Answer:

Lesson 9.9 Subtract Mixed Numbers

Solve & Share
Evan is walking 2 miles to his aunt’s house. He has already walked mile. How much farther does Evan have to go? Solve this problem any way you choose.
Generalize. You can use what you know about subtracting fractions to solve this problem.
I can … use equivalent fractions, properties of operations, and the relationship between addition and subtraction to subtract mixed numbers with like denominators.

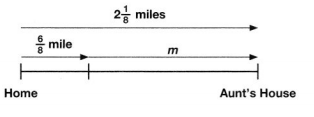
Look Back! You found 2\(\frac{1}{8}\) – \(\frac{6}{8}\) = m. Write a related addition equation.

Essential Question
How Can You Subtract Mixed Numbers?
Change the mixed number (with 1 as the whole number) into an improper fraction. Subtract the whole number of the smaller mixed number from the whole number of the new larger mixed number. If the proper fractions have similar denominators, subtract the numerators directly and remain the denominator as it is.
For example,

Visual Learning Bridge
A golf ball measures about 1\(\frac{4}{6}\) inches across the center. What is the difference between the distances across the centers of a tennis ball and a golf ball?

You can use properties of operations and the relationship between addition and subtraction to help subtract mixed numbers.

Convince Me! Reasoning Explain why you rename 4\(\frac{1}{4}\) to find 4\(\frac{1}{4}\) – \(\frac{3}{4}\).

Guided Practice

Do You Understand?
Question 1.
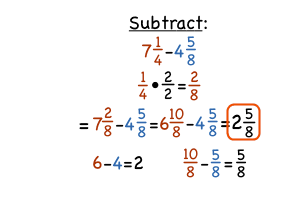
A hole at the golf course is 3\(\frac{3}{6}\) inches wide. How much wider is the hole than the golf ball?
Answer:
1\(\frac{5}{6}\)
Explanation:

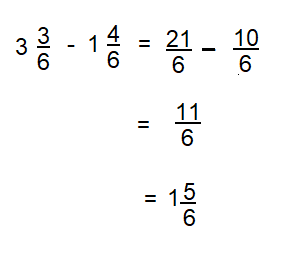
Question 2.
How could you use the relationship between addition and subtraction with counting up to find 3\(\frac{1}{4}\) – 1\(\frac{3}{4}\)?
Answer:
3\(\frac{1}{4}\) – 1\(\frac{3}{4}\) = 1 \(\frac{2}{4}\)

3\(\frac{1}{4}\) = 1\(\frac{3}{4}\) + 1 \(\frac{2}{4}\)

Explanation:
3\(\frac{1}{4}\) – 1\(\frac{3}{4}\)

= \(\frac{13}{4}\) – \(\frac{7}{4}\)

= \(\frac{13 – 7}{4}\)

= \(\frac{6}{4}\)

= 1 \(\frac{2}{4}\)

Do You Know How?
For 3-8, find each difference.
Question 3.

Answer:
5 \(\frac{1}{8}\)
Explanation:

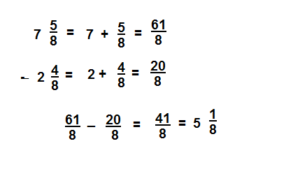
Question 4.

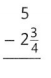
Answer:
\( 2 \frac{1}{4}\)
Explanation:

Question 5.
\(6 \frac{3}{10}-1 \frac{8}{10}\)
Answer:
\(4 \frac{5}{10}\)
Explanation:

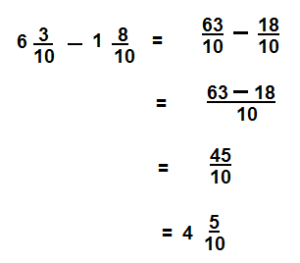
Question 6.
\(9 \frac{4}{12}-4 \frac{9}{12}\)
Answer:
\(4 \frac{7}{12}\)
Explanation:

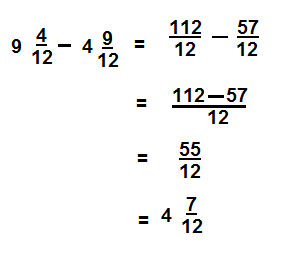
Question 7.
\(4 \frac{5}{6}-2 \frac{1}{6}\)
Answer:
\( 2\frac{4}{6}\)
Explanation:

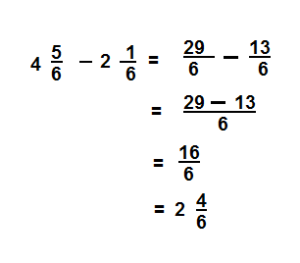
Question 8.
\(1 \frac{9}{12}-\frac{10}{12}\)
Answer:
\( \frac{11}{12}\)
Explanation:

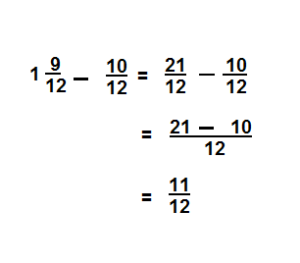
Independent Practice

For 9-24, find each difference.
Question 9.

Answer:
\(6 \frac{3}{8}\)
Explanation:
\(8 \frac{7}{8}-2\frac{4}{8}\)
= \( \frac{71}{8}-\frac{20}{8}\)
= \( \frac{71 – 20}{8}\)
= \( \frac{51}{8}\)
= \(6 \frac{3}{8}\)

Question 10.

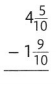
Answer:
\(2 \frac{6}{10}\)

Explanation:

\(4 \frac{5}{10}-1\frac{9}{10}\)

= \( \frac{45}{10}-\frac{19}{10}\)

= \( \frac{45 – 19}{10}\)

= \( \frac{26}{10}\)

= \(2 \frac{6}{10}\)

Question 11.

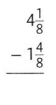
Answer:

\(2 \frac{5}{8}\)

Explanation:

\(4 \frac{1}{8}-1\frac{4}{8}\)

= \( \frac{33}{8}-\frac{12}{8}\)

= \( \frac{33 – 12}{8}\)

= \( \frac{21}{8}\)

= \(2 \frac{5}{8}\)

Question 12.

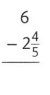
Answer:

\(3 \frac{1}{5}\)

Explanation:

6 – \(2\frac{4}{5}\)

= \( \frac{6}{1}-2\frac{4}{5}\)

= \( \frac{6}{1}-\frac{14}{5}\)

= \( \frac{30 – 14}{5}\)

= \( \frac{16}{5}\)

= \(3 \frac{1}{5}\)

Question 13.
\(6 \frac{1}{3}-5 \frac{2}{3}\)
Answer:

\( \frac{2}{3}\)

Explanation:

\(6 \frac{1}{3}-5 \frac{2}{3}\)

= \( \frac{19}{3}-\frac{17}{3}\)

= \( \frac{19 – 17}{3}\)

= \( \frac{2}{3}\)

Question 14.
\(9 \frac{2}{4}-6 \frac{3}{4}\)
Answer:

\( 2\frac{3}{4}\)

Explanation:

\(9 \frac{2}{4}-6 \frac{3}{4}\)

= \( \frac{38}{4}-\frac{27}{4}\)

= \( \frac{38 – 27}{4}\)

= \( \frac{11}{4}\)

= \(2 \frac{3}{4}\)

Question 15.
\(8 \frac{3}{8}-3 \frac{5}{8}\)
Answer:

\( 4\frac{6}{8}\)

Explanation:

\(8 \frac{3}{8}-3 \frac{5}{8}\)

= \( \frac{67}{8}-\frac{29}{8}\)

= \( \frac{67 – 29}{8}\)

= \( \frac{38}{8}\)

= \(4 \frac{6}{8}\)

Question 16.
\(7-3 \frac{1}{2}\)
Answer:

\(3 \frac{1}{2}\)

Explanation:

7 – \(3\frac{1}{2}\)

= \( \frac{7}{1}-3\frac{1}{2}\)

= \( \frac{7}{1}-\frac{7}{2}\)

= \( \frac{14 – 7}{2}\)

= \( \frac{7}{2}\)

= \(3 \frac{1}{2}\)

Question 17.
\(6 \frac{1}{6}-4 \frac{5}{6}\)
Answer:

\( 1\frac{2}{6}\)

Explanation:

\(6 \frac{1}{6}-4 \frac{5}{6}\)

= \( \frac{37}{6}-\frac{29}{6}\)

= \( \frac{37 – 29}{6}\)

= \( \frac{8}{6}\)

= \(1 \frac{2}{6}\)

Question 18.
\(3 \frac{1}{12}-1 \frac{3}{12}\)
Answer:

\( 1\frac{10}{12}\)

Explanation:

\(3 \frac{1}{12}-1 \frac{3}{12}\)

= \( \frac{37}{12}-\frac{15}{12}\)

= \( \frac{37 – 15}{12}\)

= \( \frac{22}{12}\)

= \(1 \frac{10}{12}\)

Question 19.
\(6 \frac{2}{5}-2 \frac{3}{5}\)
Answer:

\( 3\frac{4}{5}\)

Explanation:

\(6 \frac{2}{5}-2 \frac{3}{5}\)

= \( \frac{32}{5}-\frac{13}{5}\)

= \( \frac{32 – 13}{5}\)

= \( \frac{19}{5}\)

= \(3 \frac{4}{5}\)

Question 20.
\(4 \frac{5}{10}-1 \frac{7}{10}\)
Answer:

\( 2\frac{8}{10}\)

Explanation:

\(4 \frac{5}{10}-1 \frac{7}{10}\)

= \( \frac{45}{10}-\frac{17}{10}\)

= \( \frac{45 – 17}{10}\)

= \( \frac{28}{10}\)

= \(2 \frac{8}{10}\)

Question 21.
\(12 \frac{9}{12}-10 \frac{7}{12}\)
Answer:

\( 2\frac{2}{12}\)

Explanation:

\(12 \frac{9}{12}-10 \frac{7}{12}\)

= \( \frac{153}{12}-\frac{127}{12}\)

= \( \frac{153 – 127}{12}\)

= \( \frac{26}{12}\)

= \(2 \frac{2}{12}\)

Question 22.
\(25 \frac{1}{4}-20\)
Answer:
= \(5 \frac{1}{4}\)

Explanation:

\(25\frac{1}{4} – 20\)

= \(25 \frac{1}{4}-\frac{20}{1}\)

= \( \frac{101}{4}-\frac{20}{1}\)

= \( \frac{101 – 80}{4}\)

= \( \frac{21}{4}\)

= \(5 \frac{1}{4}\)

Question 23.
\(7-2 \frac{1}{8}\)
Answer:
= \(4 \frac{7}{8}\)

Explanation:

7 – \(2\frac{1}{8}\)

= \( \frac{7}{1}-2\frac{1}{8}\)

= \( \frac{7}{1}-\frac{17}{8}\)

= \( \frac{56 – 17}{8}\)

= \( \frac{39}{8}\)

= \(4 \frac{7}{8}\)

Question 24.
\(6 \frac{3}{5}-3 \frac{4}{5}\)
Answer:

\( 2\frac{4}{5}\)

Explanation:

\(6 \frac{3}{5}-3 \frac{4}{5}\)

= \( \frac{33}{5}-\frac{19}{5}\)

= \( \frac{33 – 19}{5}\)

= \( \frac{14}{5}\)

= \(2 \frac{4}{5}\)

Problem Solving

Question 25.
The average weight of a basketball is 21\(\frac{1}{8}\) ounces. The average weight of a baseball is 5\(\frac{2}{8}\) ounces. How many more ounces does the basketball weigh?
Answer:

15\(\frac{7}{8}\) ounces

Explanation

21\(\frac{1}{8}\) – 5\(\frac{2}{8}\)

= \(\frac{169}{8}\) – \(\frac{42}{8}\)

= \(\frac{169 – 42}{8}\)

= \(\frac{127}{8}\)

= 15\(\frac{7}{8}\)

Question 26.
What is the value of the 4 in 284,612?
Answer:
place value : 4000
face value   : 4
Explanation :
the value of 4 in 284612 is 4000, as its in thousands place
and value of four is 4

Question 27.
Two of the smallest mammals on Earth are the bumblebee bat and the Etruscan pygmy shrew. How much shorter is the bat than the shrew?

Answer:
\(\frac{1}{5}\) inches

Explanation:

1\(\frac{2}{5}\) – 1\(\frac{1}{5}\)

= \(\frac{7}{5}\) – \(\frac{6}{5}\)

= \(\frac{7 – 6}{5}\)

= \(\frac{1}{5}\)

Question 28.
Make Sense and Persevere The average length of an adult female hand is about 6 \(\frac{3}{5}\) inches. About how much longer is the hand than the lengths of the bat and shrew combined?

Answer:
4 inches
Explanation:
6 \(\frac{3}{5}\) – (1\(\frac{2}{5}\) + 1\(\frac{1}{5}\))

= 6 \(\frac{3}{5}\)-(\(\frac{7}{5}\) + \(\frac{6}{5}\))

= \(\frac{33}{5}\)-(\(\frac{7 + 6}{5}\))

= \(\frac{33}{5}\)–\(\frac{13}{5}\)

= \(\frac{33 – 13}{5}\)

= \(\frac{20}{5}\)

= 4

Question 29.
Jack made 5\(\frac{1}{4}\) dozen cookies for the bake sale, and his sister made 3\(\frac{3}{4}\) dozen cookies. How many more dozen cookies did Jack make than his sister?
Answer:
1\(\frac{2}{4}\)
Explanation:

5\(\frac{1}{4}\) – 3\(\frac{3}{4}\)

= \(\frac{21}{4}\) – \(\frac{15}{4}\)

= \(\frac{21 – 15}{4}\)

= \(\frac{6}{4}\)

= 1\(\frac{2}{4}\)

Question 30.
Higher Order Thinking Jenna has a spool that contains 5\(\frac{3}{4}\) meters of ribbon. She uses 3\(\frac{2}{4}\) meters for a school project and 1\(\frac{1}{4}\) meters for a bow. How much ribbon remains on the spool?
Answer:
1 meter
Explanation:

5\(\frac{3}{4}\) – (3\(\frac{2}{4}\) + 1\(\frac{1}{4}\))

= \(\frac{23}{4}\) – (\(\frac{14}{4}\) + \(\frac{5}{4}\))

= \(\frac{23}{4}\) – (\(\frac{14 + 5}{4}\))

= \(\frac{23}{4}\) – \(\frac{19}{4}\)

= \(\frac{23 – 19}{4}\)

= \(\frac{4}{4}\)

=1

Assessment Practice

Question 31.
Last week, the office used 5\(\frac{1}{12}\) boxes of paper. This week, they used 1\(\frac{5}{12}\) boxes of paper. How many more boxes did they use last week than this week?
A. 10 \(\frac{6}{12}\) boxes
B. 4 \(\frac{8}{12}\) boxes
C. 4 \(\frac{4}{12}\) boxes
D. 3 \(\frac{8}{12}\) boxes
Answer:
Option D.
3 \(\frac{8}{12}\) boxes

Explanation:

5\(\frac{1}{12}\) – 1\(\frac{5}{12}\)

= 5\(\frac{1}{12}\) – 1\(\frac{5}{12}\)

= \(\frac{61}{12}\) – \(\frac{17}{12}\)

= \(\frac{61 – 17}{12}\)

= \(\frac{44}{12}\)

= 3\(\frac{8}{12}\)

Question 32.
A store sold 6\(\frac{1}{5}\) cases of juice on Friday and 4\(\frac{4}{5}\) cases of juice on Saturday. How many more cases of juice did the store sell on Friday than on Saturday?
A. 11 cases
B. 3 \(\frac{1}{5}\) cases
C. 2 \(\frac{2}{5}\) cases
D. 1 \(\frac{2}{5}\) cases
Answer:

D. 1 \(\frac{2}{5}\) cases

Explanation:

6\(\frac{1}{5}\) – 4\(\frac{4}{5}\)

=6\(\frac{1}{5}\) – 4\(\frac{4}{5}\)

=\(\frac{31}{5}\) – \(\frac{24}{5}\)

=\(\frac{31 – 24}{5}\)

=\(\frac{7}{5}\)

=1\(\frac{2}{5}\)

Lesson 9.10 Problem Solving

Model with Math
Solve & Share
The table shows how long Jamie studied for a math test over 3 days. How much more time did Jamie spend studying on Tuesday and Wednesday than on Thursday?
I can … use math I know to represent and solve problems.

Answer:

=\(\frac{2}{4}\)

Explanation:

(1\(\frac{3}{4}\) + \(\frac{3}{4}\)) – (\(\frac{2}{4}\))

=(1\(\frac{3}{4}\) + \(\frac{3}{4}\)) – (\(\frac{2}{4}\))

=(\(\frac{7}{4}\) + \(\frac{3}{4}\)) – (\(\frac{2}{4}\))

=(\(\frac{7 – 3}{4}\) – \(\frac{2}{4}\))

=(\(\frac{4}{4}\) – \(\frac{2}{4}\))

=\(\frac{4-2}{4}\)

=\(\frac{2}{4}\)

Thinking Habits
Be a good thinker! These questions can help you.

• How can I use math I know to help solve this problem?
• How can I use pictures, objects, or an equation to represent the problem?
• How can I use numbers, words, and symbols to solve the problem?

Look Back! Model with Math What representations can you use to help solve this problem?

Essential Question
How Can You Use Math to Model Problems?

Visual Learning Bridge
Brad and his father hiked the Gadsen Trail and the Rosebriar Trail on Saturday. They hiked the Eureka Trail on Sunday. How much farther did they hike on Saturday than on Sunday?

What do you need to find?
I need to find how far Brad and his father hiked on Saturday and how much farther they hiked on Saturday than on Sunday.

How can I model with math?
I can

• use previously learned concepts and skills.
• use bar diagrams and equations to represent and solve this problem.
• decide if my results make sense.

Here’s my thinking.

Find 2\(\frac{4}{10}\) – \(\frac{6}{10}\).
Use a bar diagram and write an equation to solve.

Brad and his father hiked 1\(\frac{8}{10}\) miles farther on Saturday than on Sunday.

Convince Me! Model with Math How do the bar diagrams help you decide if your answer makes sense?

Answer :

Bar diagram is the pictorial representation of  math model
as per the above picture on Saturday, Brad and his father hiked
1\(\frac{9}{10}\) + \(\frac{5}{10}\) = 2\(\frac{4}{10}\)

and on Sunday \(\frac{6}{10}\)
the difference is denoted by d and is calculated as below
d = 2\(\frac{4}{10}\) – \(\frac{6}{10}\) = 1\(\frac{8}{10}\)

Guided Practice

Model with Math
Alisa hiked a trail that was \(\frac{9}{10}\) mile and Joseph hiked a trail that was \(\frac{5}{10}\) mile. How much farther, d, did Alisa hike than Joseph?

Question 1.
Draw a bar diagram to represent the problem and show the relationships among the quantities.
Answer:

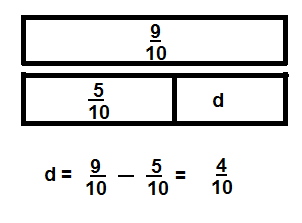
Question 2.
What equation can you write to represent the problem?
Answer:
d = \(\frac{9}{10}\) – \(\frac{5}{10}\)

Explanation:

d = \(\frac{9}{10}\) – \(\frac{5}{10}\)
d = \(\frac{9 – 5}{10}\)

d = \(\frac{4}{10}\)

Question 3.
How much farther did Alisa hike than Joseph?
Answer:
\(\frac{4}{10}\)
Explanation:

d = \(\frac{9}{10}\) – \(\frac{5}{10}\)
d = \(\frac{9 – 5}{10}\)

d = \(\frac{4}{10}\)

Independent Practice

Model with Math

The smallest female spider measures about \(\frac{3}{5}\) millimeter in length. The smallest male spider measures about \(\frac{1}{5}\) millimeter in length. How much longer, n, is the smallest female spider than the smallest male spider? Use Exercises 4-6 to answer the question.
Question 4.
Draw a picture and write an equation to represent the problem.
Answer:

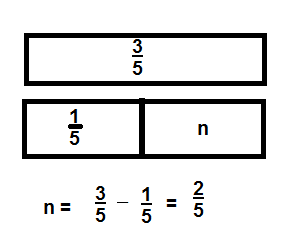
Question 5.
What previously learned math can you use to solve the problem?
Answer: YES
Explanation:
n = \(\frac{3}{5}\) – \(\frac{1}{5}\)

n = \(\frac{3 – 1}{5}\)

n = \(\frac{2}{5}\)

Question 6.
How much longer is the smallest female spider than the smallest male spider?
Answer:

\(\frac{2}{5}\)

Explanation:

n = \(\frac{3}{5}\) – \(\frac{1}{5}\)

n = \(\frac{3 – 1}{5}\)

n = \(\frac{2}{5}\)

Problem Solving

Performance Task
On Safari
Sandra and Ron traveled in a safari car while they were in Tanzania. The diagram shows the distances in miles they traveled from start to finish. How far did Sandra and Ron travel from the leopards to the elephants?

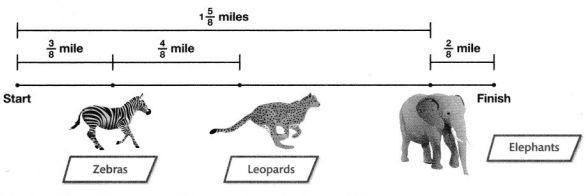
Question 7.
Reasoning What quantities are given in the problem and what do they mean?
Answer:
Sandra and Ron traveled in a safari car in Tanzania
Quantities are given in the problem
from starting point
\(\frac{3}{8}\) mile to see zebras
2\(\frac{4}{8}\) miles to see Leopards
1\(\frac{5}{8}\) miles to see Elephants
1\(\frac{7}{8}\) miles to Finish

Question 8.
Make Sense and Persevere What is a good plan for solving the problem?.
Answer:
First add the distances from start point to zebra and Leopards fractions

\(\frac{3}{8}\)+\(\frac{4}{8}\)  = \(\frac{7}{8}\)

then subtract the above fraction from distance from start to Elephant

1\(\frac{5}{8}\) – \(\frac{7}{8}\) = \(\frac{13 – 7}{8}\) = \(\frac{6}{8}\)

Question 9.
Model with Math Draw pictures and write and solve equations to find how far Sandra and Ron travel from the leopards to the elephants.

Answer:

Sandra and Ron travel from the leopards to the elephants
n = 1\(\frac{5}{8}\) – \(\frac{7}{8}\)
n = \(\frac{13}{8}\) – \(\frac{7}{8}\)
n = \(\frac{13 – 7}{8}\)
n = \(\frac{6}{8}\)

Topic 9 Fluency Practice Activity

Find a Match
Work with a partner. Point to a clue. Read the clue.
Look below the clues to find a match. Write the clue letter in the box next to the match.
Find a match for every clue.
I can … add and subtract multi-digit whole numbers.

Clues
A. The sum is exactly 1,000.
B. The sum is exactly 1,001.
C. The difference is exactly 371.
D. The difference is between 40 and 45.
E. The difference is exactly 437.
F. The difference is between 150 and 160.
G. The sum is between 995 and 1,000.
H. The sum is exactly 1,899.

Answer:

Topic 9 Vocabulary Review

Understand Vocabulary
Word List

• decompose
• denominator
• equivalent fractions
• fraction
• like denominators
• mixed number
• numerator
• whole number

Question 1.
Circle the label that best describes \(\frac{1}{2}\).
fraction
mixed number
whole number
Answer:

Question 2.
Circle the label that best describes 1\(\frac{1}{3}\).
fraction
mixed number
whole number
Answer:

Question 3.
Circle the label that best describes 4.
fraction
mixed number
whole number
Answer:

Question 4.
Draw a line from each term to its example.

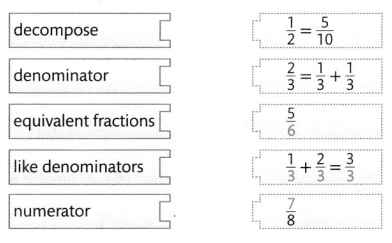
Answer:

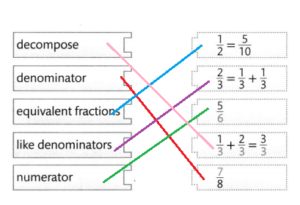
Use Vocabulary in Writing
Question 5.
Find 1\(\frac{1}{3}\) + 2\(\frac{2}{3}\). Use at least 3 terms from the Word List to describe how to find the sum.
Answer:
To add mixed numbers, firstly convert the mixed numbers to improper fractions and find the least common denominator, then add or subtract the whole numbers. Finally write the lowest terms.

Sum = 1\(\frac{1}{3}\) + 2\(\frac{2}{3}\) = 4

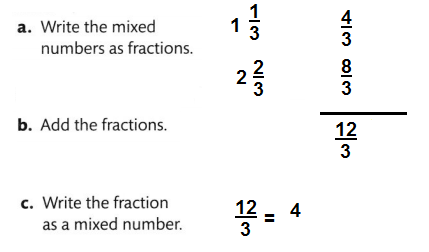
Topic 9 Reteaching

Set A pages 333-336, 341-344

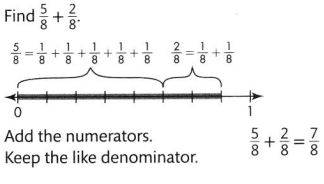
Remember you can use tools or add the numerators and write the sum over the like denoninator.
Question 1.
\(\frac{2}{5}+\frac{2}{5}\)
Answer:
\(\frac{4}{5}\)

Explanation:

\(\frac{2}{5}+\frac{2}{5}\)

=\(\frac{2 + 2}{5}\)

=\(\frac{4}{5}\)

Question 2.
\(\frac{2}{4}+\frac{1}{4}+\frac{1}{4}\)
Answer:

\(\frac{4}{4}\) = 1

Explanation:

\(\frac{2}{4}+\frac{1}{4}+\frac{1}{4}\)

= \(\frac{2 + 1 + 1}{4}\)

= \(\frac{4}{4}\) = 1

Question 3.
\(\frac{3}{8}+\frac{4}{8}\)
Answer:

\(\frac{7}{8}\)

Explanation:

\(\frac{3}{8}+\frac{4}{8}\)

= \(\frac{3 + 4}{8}\)

= \(\frac{7}{8}\)

Question 4.
\(\frac{4}{10}+\frac{2}{10}+\frac{3}{10}\)
Answer:

\(\frac{9}{10}\)

Explanation:

\(\frac{4}{10}+\frac{2}{10}+\frac{3}{10}\)

= \(\frac{4 + 2 + 3}{10}\)

= \(\frac{9}{10}\)

Question 5.
\(\frac{4}{10}+\frac{3}{10}\)
Answer:
\(\frac{7}{10}\)

Explanation:

\(\frac{4}{10}+\frac{3}{10}\)

= \(\frac{4 + 3}{10}\)

= \(\frac{7}{10}\)

Question 6.
\(\frac{7}{12}+\frac{2}{12}\)
Answer:

\(\frac{9}{12}\)

Explanation:

\(\frac{7}{12}+\frac{2}{12}\)

= \(\frac{7 + 2}{12}\)

= \(\frac{9}{12}\)

Set B pages 337-340

Decompose 1\(\frac{5}{6}\) two different ways.

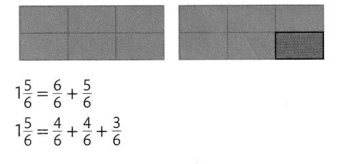
Remember you can decompose fractions in more than one way.

Decompose each fraction or mixed number in two different ways.
Question 1.
\(\frac{3}{5}\)
Answer:

\(\frac{1}{5}\) + \(\frac{1}{5}\) + \(\frac{1}{5}\)

\(\frac{2}{5}\) + \(\frac{1}{5}\)

Explanation:

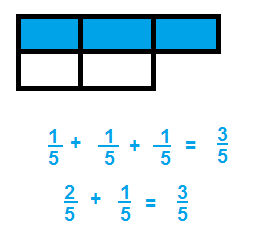
Question 2.
\(\frac{9}{12}\)
Answer:

\(\frac{6}{12}\) + \(\frac{3}{12}\)

\(\frac{3}{12}\) +\(\frac{3}{12}\) + \(\frac{3}{12}\)

Explanation:

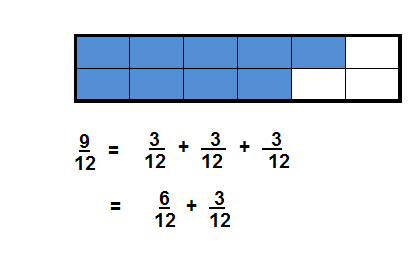
Question 3.
1\(\frac{1}{2}\)
Answer:

\(\frac{1}{2}\) + 1\(\frac{2}{2}\)

\(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\)

Explanation:

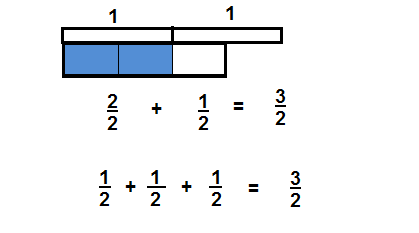
Question 4.
2\(\frac{2}{3}\)
Answer:

\(\frac{3}{3}\) + \(\frac{3}{3}\) +\(\frac{2}{3}\)

\(\frac{2}{3}\) + \(\frac{2}{3}\) +\(\frac{2}{3}\) + \(\frac{2}{3}\)

Explanation:

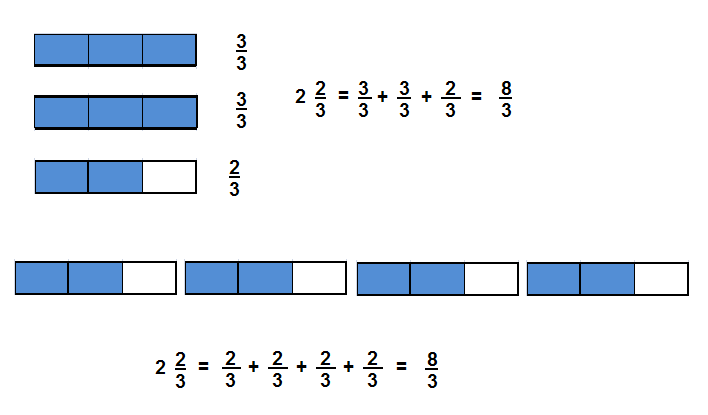
Set C pages 345-352

Find \(\frac{5}{8}-\frac{2}{8}\)

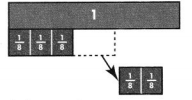
\(\frac{5}{8}-\frac{2}{8}=\frac{3}{8}\)
Subtract the numerators. Keep the like denominator.

Remember you can use different tools to show how to subtract fractions.

Question 1.
\(\frac{3}{3}-\frac{1}{3}\)
Answer:

\(\frac{2}{3}\)

Explanation:

\(\frac{3}{3}-\frac{1}{3}\)

=\(\frac{3 – 1}{3}\)

=\(\frac{2}{3}\)

Question 2.
\(\frac{5}{6}-\frac{2}{6}\)
Answer:

\(\frac{3}{6}\) =\(\frac{1}{2}\)

Explanation:

\(\frac{5}{6}-\frac{2}{6}\)

=\(\frac{5 – 2}{6}\)

=\(\frac{3}{6}\) =\(\frac{1}{2}\)

Question 3.
\(\frac{6}{8}-\frac{3}{8}\)
Answer:
\(\frac{3}{8}\)

Explanation:

\(\frac{6}{8}-\frac{3}{8}\)

=\(\frac{6 – 3}{8}\)

=\(\frac{3}{8}\)

Question 4.
\(\frac{4}{10}-\frac{3}{10}\)
Answer:

\(\frac{1}{10}\)

Explanation:

\(\frac{4}{10}-\frac{3}{10}\)

=\(\frac{4 – 3}{10}\)

=\(\frac{1}{10}\)

Question 5.
\(\frac{5}{5}-\frac{3}{5}\)
Answer:

\(\frac{2}{5}\)

Explanation:

\(\frac{5}{5}-\frac{3}{5}\)

=\(\frac{5 – 3}{5}\)

=\(\frac{2}{5}\)

Question 6.
\(\frac{4}{6}-\frac{2}{6}\)
Answer:

\(\frac{2}{6}\) = \(\frac{1}{3}\)

Explanation:
\(\frac{4}{6}-\frac{2}{6}\)

=\(\frac{4-2}{6}\)

=\(\frac{2}{6}\) = \(\frac{1}{3}\)

Set D pages 353-356

Find the sum or difference shown on each number line.

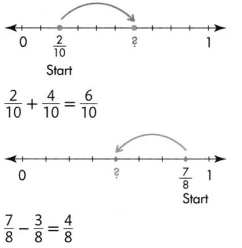
Remember you can show adding or subtracting fractions on a number line.

Write each equation shown.
Question 1.

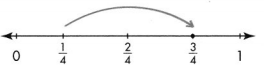
Answer:

\(\frac{3}{4}\)

Explanation:

\(\frac{1}{4}+\frac{2}{4}\) = \(\frac{3}{4}\)

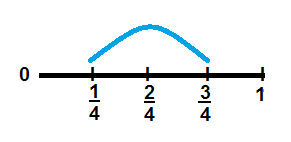
Question 2.

Answer:

\(\frac{4}{6}\)

Explanation:

\(\frac{5}{6}+\frac{1}{6}\) = \(\frac{4}{6}\)

 

Set E pages 357-368

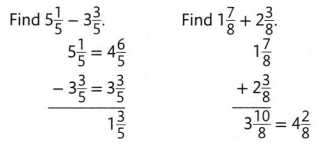
Remember you can use different tools to add and subtract mixed numbers.

Question 1.
\(5 \frac{4}{8}+2 \frac{1}{8}\)
Answer:

7\(\frac{5}{8}\)

Explanation:

Question 2.
\(3 \frac{3}{6}+1 \frac{5}{6}\)
Answer:

5\( \frac{3}{8}\)

Explanation:

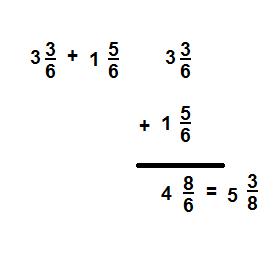
Question 3.
\(5 \frac{7}{10}+4 \frac{4}{10}\)
Answer:

10\(\frac{1}{10}\)

Explanation:

Question 4.
\(9-3 \frac{3}{8}\)
Answer:

5\( \frac{3}{8}\)

Explanation:

Set F pages 369-372

Think about these questions to help you model with math.
Thinking Habits

• How can I use math I know to help solve this problem?
• How can I use pictures, objects, or an equation to represent the problem?
• How can I use numbers, words, and symbols to solve the problem?

Remember to draw a bar diagram and write an equation to help solve a problem.

Bonnie ran \(\frac{1}{4}\) mile, Olga ran \(\frac{3}{4}\) mile, Gracie ran \(\frac{5}{4}\) miles, and Maria ran \(\frac{2}{4}\) mile. How much farther, f, did Gracie run than Bonnie and Maria combined, c?
Answer:

\(\frac{2}{4}\)

Explanation:
\(\frac{5}{4}\) – ( \(\frac{2}{4}\) + \(\frac{1}{4}\))

= \(\frac{5}{4}\) – \(\frac{2+1}{4}\)

= \(\frac{5 }{4}\) – \(\frac{3}{4}\)

= \(\frac{5 – 3 }{4}\)

= \(\frac{2}{4}\)

Topic 9 Assessment Practice

Question 1.
Match each expression on the left to an equivalent expression.

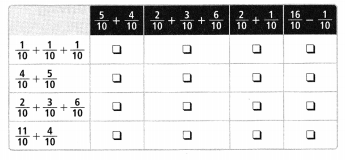
Answer:

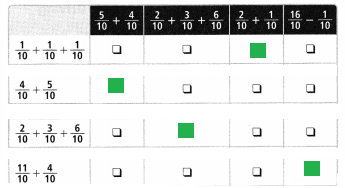
Question 2.
On Monday, \(\frac{3}{12}\) of the students went on a field trip. What fraction of the students did NOT go on the field trip? Explain.

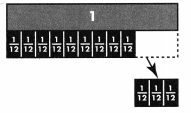
Answer:

\(\frac{9}{12}\)

Explanation:

1 – \(\frac{3}{12}\)

= \(\frac{12}{12}\) – \(\frac{3}{12}\) =\(\frac{9}{12}\)

Question 3.
Riley planted flowers in some of her garden. Then, she planted vegetables in \(\frac{2}{8}\) of her garden. Now, \(\frac{7}{8}\) of Riley’s garden is planted. What fraction of Riley’s garden is planted with flowers? How much of her garden is not planted?
A. \(\frac{2}{8}\) of her garden; \(\frac{1}{8}\) of her garden is not planted
B. \(\frac{3}{8}\) of her garden; \(\frac{2}{8}\) of her garden is not planted
C. \(\frac{4}{8}\) of her garden; \(\frac{5}{8}\) of her garden is not planted
D. \(\frac{5}{8}\) of her garden; \(\frac{1}{8}\) of her garden is not planted
Answer:
Option (D)
 \(\frac{5}{8}\) of her garden; \(\frac{1}{8}\) of her garden is not planted
Explanation:

f + \(\frac{2}{8}\) = \(\frac{7}{8}\)

f = \(\frac{7}{8}\) – \(\frac{2}{8}\)

f = \(\frac{7 – 2}{8}\)

f = \(\frac{5}{8}\) (flowers)

1- \(\frac{7}{8}\) = \(\frac{1}{8}\) (garden is not planted)

Question 4.
Select all the expressions that show a way to decompose \(\frac{7}{8}\).

Answer:

Question 5.
Which equation is NOT true when \(\frac{4}{12}\)is the missing number?

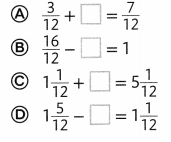
Answer:

Option(C) equation is NOT true

Explanation:

Question 6.
Zoe had 3\(\frac{1}{8}\) feet of orange ribbon. She used some ribbon to make a bow for a gift. Now she has 1\(\frac{1}{8}\) feet of ribbon left. How much orange ribbon did Zoe use? Use the model to write an equation, and solve.

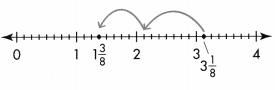
Answer:

1\(\frac{3}{8}\)

Explanation:

3\(\frac{1}{8}\) – 2\(\frac{1}{8}\)

= 3\(\frac{1}{8}\) – 1

= \(\frac{25}{8}\) – 1

= \(\frac{25 – 8}{8}\)

= \(\frac{17}{8}\)

= 2\(\frac{1}{8}\)

2\(\frac{1}{8}\) – \(\frac{6}{8}\)

=\(\frac{17}{8}\) – \(\frac{6}{8}\)

=\(\frac{17 – 6}{8}\)

=\(\frac{11}{8}\)

=1\(\frac{3}{8}\)

Question 7.
Roger and Sulee each decomposed 1\(\frac{1}{6}\). Roger wrote \(\frac{1}{6}+\frac{1}{6}+\frac{2}{6}+\frac{3}{6}\). Sulee wrote \(\frac{3}{6}+\frac{4}{6}\) Who was correct? Explain.
Answer:
Both are correct, as no change is answer
Explanation:
1\(\frac{1}{6}\) =\(\frac{7}{6}\)

Roger    \(\frac{1}{6}+\frac{1}{6}+\frac{2}{6}+\frac{3}{6}\) = \(\frac{1+1+2+3}{6}\) = \(\frac{7}{6}\)

Sulee    \(\frac{3}{6}+\frac{4}{6}\) = \(\frac{3+4}{6}\) = \(\frac{7}{6}\)

Question 8.
The number line shows which of the following equations?

Answer:
Option (B)

Explanation:

\(\frac{6}{10}\)+\(\frac{2}{10}\) = \(\frac{6+2}{10}\)= \(\frac{8}{10}\)

Question 9.
Ryan kayaks 1\(\frac{7}{8}\) miles before lunch and 2\(\frac{3}{8}\) miles after lunch. Select all of the equations you would use to find how far Ryan kayacked.

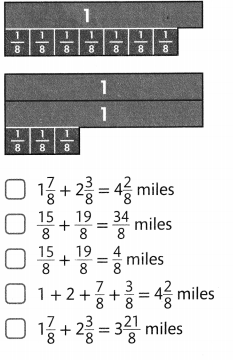
Answer:

 

Question 10.
The Jacobys kept track of the time they spent driving on their trip.

A. Find how many hours the Jacobys drove on Monday and Tuesday. Draw a bar diagram to represent the problem.
Answer:
10\(\frac{2}{4}\)

Explanation:

5\(\frac{3}{4}\)+4\(\frac{3}{4}\)

= \(\frac{23}{4}\)+\(\frac{19}{4}\)

= \(\frac{23 + 19}{4}\)

= \(\frac{42}{4}\)

= 10\(\frac{2}{4}\)

B. Find how many hours the Jacobys drove in all. Explain your work.
Answer:

19\(\frac{2}{4}\)

Explanation:

5\(\frac{3}{4}\)+4\(\frac{3}{4}\) +2\(\frac{1}{4}\)+6\(\frac{3}{4}\)

= \(\frac{23}{4}\)+\(\frac{19}{4}\) +\(\frac{9}{4}\)+\(\frac{27}{4}\)

= \(\frac{23 + 19 + 9 + 27}{4}\)

= \(\frac{23 + 19 + 9 + 27}{4}\)

= \(\frac{78}{4}\)

= 19\(\frac{2}{4}\)

Topic 9 Performance Task

Water Race
In one of the games at the class picnic, students balanced containers filled with water on their heads. The goal was to carry the most water to the finish line. The teams are listed in the Water Race Teams table. The amount of water each student carried is listed in the Water Race Results table.

Question 1.
Mia will hand out the prize to the winning team.
Part A
Draw a bar diagram and write an equation to find c, the cups of water Team 1 carried.
Answer:

c = 1\(\frac{5}{8}\)

Explanation:

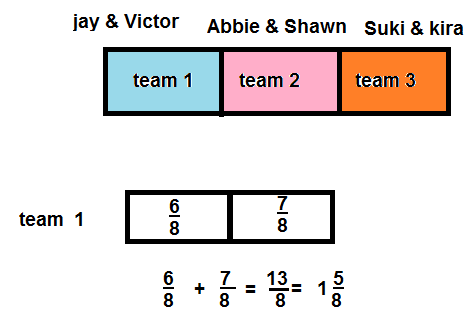
c = \(\frac{6}{8}\) + \(\frac{7}{8}\)

c =\(\frac{6 + 7}{8}\)

c =1\(\frac{5}{8}\)

Part B
How many cups of water did Team 2 carry? Use fraction strips to show the sum.
Answer:

2\(\frac{4}{8}\)

Explanation:

n = \(\frac{5}{8}\) + 1\(\frac{7}{8}\)

n = \(\frac{5}{8}\) + \(\frac{15}{8}\)

n =\(\frac{5 + 15}{8}\)

n =\(\frac{20}{8}\)

n =2\(\frac{4}{8}\)

Part C
How many cups of water did Team 3 carry? Use the number line to show the sum.

Answer:

2\(\frac{3}{8}\)

Explanation:

f = 1\(\frac{6}{8}\) + \(\frac{5}{8}\)

f = \(\frac{14}{8}\) + \(\frac{5}{8}\)

f =\(\frac{14 + 5}{8}\)

f =\(\frac{19}{8}\)

f =2\(\frac{3}{8}\)

Part D
Which team carried the most water?
Answer:
Team 2
2\(\frac{4}{8}\)

Explanation:

n = \(\frac{5}{8}\) + 1\(\frac{7}{8}\)

n = \(\frac{5}{8}\) + \(\frac{15}{8}\)

n =\(\frac{5 + 15}{8}\)

n =\(\frac{20}{8}\)

n =2\(\frac{4}{8}\)

Question 2.
Team 1 wanted to know how they did compared to Team 2.
Part A
Draw a bar diagram and write an equation that could be used to find m, how much more water Team 2 carried than Team 1.
Answer:
m = Team 2 – Team 1 = \(\frac{7}{8}\)

Explanation:

 

Part B
How much more water did Team 2 carry than Team 1? Explain how to solve the problem using your equation from Part A. Show your work.
Answer:
\(\frac{7}{8}\)

Explanation:

Team 2 = \(\frac{5}{8}\) + 1\(\frac{7}{8}\) = \(\frac{5}{8}\) + \(\frac{15}{8}\) = \(\frac{5 + 15}{8}\) =\(\frac{20}{8}\) =2\(\frac{4}{8}\)

Team 1 = \(\frac{6}{8}\) + \(\frac{7}{8}\) =\(\frac{6 + 7}{8}\) =1\(\frac{5}{8}\)

m = 2\(\frac{4}{8}\) – 1\(\frac{5}{8}\)

= \(\frac{20}{8}\) – \(\frac{13}{8}\)

= \(\frac{20 – 13}{8}\)

= \(\frac{7}{8}\)