enVision Math Common Core Grade 5 Answer Key Topic 1 Understand Place Value

Go through the enVision Math Common Core Grade 5 Answer Key Topic 1 Understand Place Value regularly and improve your accuracy in solving questions.

enVision Math Common Core 5th Grade Answers Key Topic 1 Understand Place Value

Envision Math Common Core 5th Grade Answers Key Topic 1 Understand Place Value has all the topics covered , which are related to the basics of Math by giving live examples of our daily life. This chapter is loaded with Decimals, Fractions, and how to do rounding to the nearest numbers, which are quite helpful for students to deal with Math basics. Experience the most satisfying and understandable answers and easy methods with Envision Math Common Core 5th Grade Answers Key Topic 1 Understand Place Value.

Envision Math Common Core 5th Grade Answers Key Topic 1 Understand Place Value

Are you facing difficulties to understand the simple Math problems or numbers , that we have to use in day to day life. Then you have come to the right place to grasp the simple tricks of small calculations. Envision Math Common Core 5th Grade Answers Key Topic 1 Understand Place Value. will help you with rounding the numbers , understand the place values , converting decimal into fractions .These are the major topics covered, get on the track with your kids to know them a better way of learning.

Envision STEM Project: Pollinating Insects

• Envision STEM Project Pollinating Insects

Lesson 1 Patterns with exponents and Powers of 10

• Lesson 1.1 Patterns with exponents and Powers of 10

Lesson 2 Understand Whole Number Place Value

• Lesson 1.2 Understand Whole Number Place Value

Lesson 3 Decimals to Thousandths

• Lesson 1.3 Decimals to Thousandths

Lesson 4 Understand Decimal Place Value

• Lesson 1.4 Understand Decimal Place Value

Lesson 5 Compare Decimals

• Lesson 1.5 Compare Decimals

Lesson 6 Round Decimals

• Lesson 1.6 Round Decimals

Lesson 7 Look For and Use Structure

• Lesson 1.7 Look For and Use Structure

 Performance Task

• Topic 1 Fluency Review
• Topic 1 Assessment Practice
• Topic 1 Performance Task

Essential Question: How are whole numbers and decimals written, compared, and ordered?

Envision STEM Project Pollinating Insects
Do Research Use the Internet or other sources to find out more about pollinating insects in the United States. What types of insects are they? How many are there of each type? How many crops and flowering plants depend on pollinating insects in order to produce the foods we eat?
Journal: Write a Report Include what you found. Also in your report:

• Choose two of the pollinating insects. Estimate how many crop plants each type of insect pollinates.
• Estimate how many of your favorite foods and beverages come from pollinated plants.
• Make up and solve ways to compare and order your data.

Answer: Pollinated insects are nothing but, the insects which are helpful to carry the pollinated grains along with them with the help of their legs or wings from the flower to promote the vast growth of new plants and are commonly known as insect pollinators.

Report for the project :

•  Insect pollinators include bees, flies, butterflies, beetles, wasps, moths, midges and ants, among others. Of these, bees are the most important group, with both wild and managed species acting as pollinators.
• Pollinators are essential for continued plant growth in the wild. There are seven insect pollinators other than bees and butterflies that also help spread plant seeds and enable plant growth.
• Three-fourths of the world’s flowering plants and about 35 percent of the world’s food crops depend on animal pollinators to reproduce. More than 3,500 species of native bees help increase crop yields.
• More than 75 percent of the world’s food crops depend on pollination . When a seed forms in flowering plants, a fruit is able to grow to protect the seed.

Among these two major pollinators are honey bees and butterflies,
Honey bees are the commonly known pollinators which are helpful for the crops like Okra, kiwifruit, Onion, cashew, strawberry, Broccoli, Cauliflower , Cabbage etc.
Butterflies are mostly the pollinators of vegetables and herbs and are helpful for the crops like especially those in the carrot family (dill, fennel, celery, cilantro, parsnip), sunflower family (artichokes, lettuce, chicory, chamomile), legume family (peas, beans), mint family (lavender, basil).

Review What You Know

Vocabulary

Choose the best term from the box. Write it on the blank.

• digits
• place value
• period
• whole numbers

Question 1.
____ are the symbols used to show numbers.
Answer: Digits are the symbols used to show numbers.

Explanation:
Because, A digit is a single symbol used to make numerals or numbers ,
That is 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are the ten digits we use in everyday numerals.
For example, the number 78 is a two digit number which is made up of two digits that is ‘7’ and ‘8’.

Question 2.
A group of 3 digits in a number is a ____
Answer: A group of 3 digits in a number is a Period.

Explanation:
Every number consists of digits. The place value is the position of each digit in a number.
Digits are separated into groups of three by commas. So, a period is a group of three digits,
For example, The number 13,456 is a 5 digit number and the ending 3 digits are called a period, because it is separated by the commas in the number which is referred to a period.

Question 3.
____ is the position of a digit in a number that is used to determine the value of the digit.
Answer: Place value is the position of a digit in a number that is used to determine the value of the digit.

Explanation:
The value of a digit depends on its place, or position, in the number.
Place value is the value of a digit according to its position in the number such as ones, tens, hundreds, and so on.
For example, In the number 3,548
3 is in thousands place and its place value is 3,000,
5 is in hundreds place and its place value is 500,
4 is in tens place and its place value is 40,
8 is in ones place and its place value is 8.

Comparing

Compare. Use <,>, or = for each .

Question 4.
869 912
Answer: 869 < 912.

Explanation:
Because 869 is less than 912.
For the number 869
8 is in hundreds place and its place value is 800,
6 is in tens place and its place value is 60,
9 is in ones place and its place value is 9.

And For the number 912
9 is in hundreds place and its place value is 900,
1 is in tens place and its place value is 10,
2 is in ones place and its place value is 2.

So, 869 is less than 912.

Question 5.
9,033 9,133
Answer: 9,033 < 9,133

Explanation:
Because 9,033 is less than 9,133
For the number 9,033
9 is in thousands place and its place value is 9,000,
0 is in hundreds place and its place value is 000,
3 is in tens place and its place value is 30,
3 is in ones place and its place value is 3.

And For the number 9,133
9 is in thousands place and its place value is 9,000,
1 is in hundreds place and its place value is 100,
3 is in tens place and its place value is 30,
3 is in ones place and its place value is 3.

So, 9,033 is less than 9,133

Question 6.
1,338 1,388
Answer:  1,338 < 1,388

Explanation:
Because 1,338 is less than 1,388
For the number 1,338
1 is in thousands place and its place value is 1,000,
3 is in hundreds place and its place value is 300,
3 is in tens place and its place value is 30,
8 is in ones place and its place value is 8.

And For the number 1,388
1 is in thousands place and its place value is 1,000,
3 is in hundreds place and its place value is 300,
8 is in tens place and its place value is 80,
8 is in ones place and its place value is 8.

So, 1,338 is less than 1,388

Question 7.
417,986 417,986
Answer: 417,986 = 417,986

Explanation:
Because, Numbers given are the same digits having the same place value .

So, 417,986 Equal to 417,986

Question 8.
0.25 0.3
Answer:  0.25 < 0.3

Explanation:
Because, regarding with its place value the number  0.25 is less than 0.3

Question 9.
0.5 0.50
Answer:  0.5 = 0.50

Explanation:
Because the 0 after the number next to decimal is exactly the same number with or without 0
Both the given numbers are in their same places with respect to each other
So, 0.5 is equal to 0.50.

Question 10.
Kamal has 7,325 songs on his computer. Benito has 7,321 songs on his computer. Who has more songs?
Answer:  Kamal has more songs than Benito.

Explanation:
Given , Kamal has 7,325 songs on his computer.
Benito has 7,321 songs on his computer.
Then 7,325 > 7,321 or 7,325 is greater than 7,321

So, Kamal has more songs than Benito.

Adding Whole Numbers

Find each sum.

Question 11.
10,000 + 2,000 + 60 + 1
Answer: 12,061

Explanation:

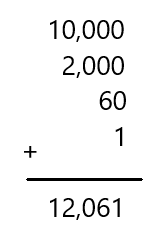
Adding all the given numbers by placing them in order of their place value of the digit
So, the total sum is 12,061.

Question 12.
20,000 + 5,000 + 400 + 3
Answer: 25,403

Explanation:

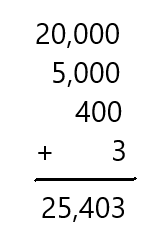
Adding all the given numbers by placing them in order of their place value of the digit
So, the total sum is 25,403.

Question 13.
900,000 + 8,000 + 200 + 70 + 6
Answer: 9,08,276

Explanation:

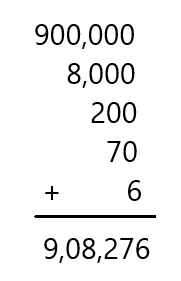
Adding all the given numbers by placing them in order of their place value of the digit
So, the total sum is 9,08,276.

Question 14.
7,000,000 + 50,000 + 900 + 4
Answer: 70,50,904

Explanation:

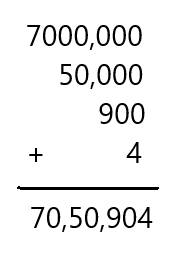
Adding all the given numbers by placing them in order of their place value of the digit
So, the total sum is 70,50,904.

Place Value

Question 15.
The largest playing card structure was made of 218,792 cards. What is the value of the digit 8 in 218,792?
A. 80
B. 800
C. 8,000
D. 80,000
Answer: C

Explanation:
Given, The largest playing card structure was made of 218,792 cards.
According to the place value method, the value of the digit 8 in 218,792 is 8,000

Question 16.
Construct Arguments In the number 767, does the first 7 have the same value as the final 7? Why or why not?
Answer: In the number  767, The first 7 does not have the same value as the final 7.

Explanation:
Given , number is 767 , The first 7 does not have the same value as the final 7.
Because, the place value is counted from right to left by ones, tens, hundreds, thousand and so on.
So, in this number 767, the first  number 7 holds the hundreds place and the final number 7 holds the ones place, giving it a different value for both the numbers in their place respectively.

Pick a Project

PROJECT 1A
Manatees or sea cows?
Project: Create a Manatee Poster

Answer:

PROJECT 1B
What makes a game fun?
Project: Design a Game with Place-Value Blocks

Answer: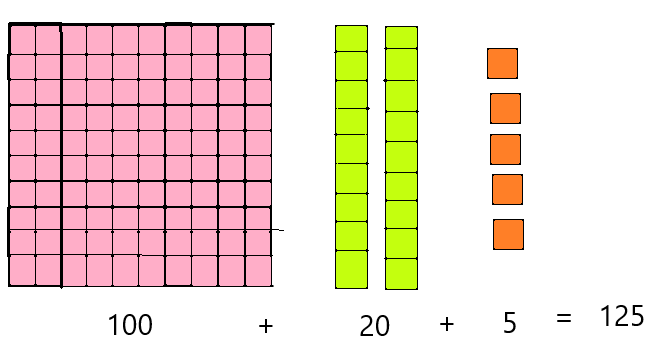

PROJECT 1С
How far are we from the sun?
Project: Research Measurements in Our Solar System

Answer: The Sun is at an average distance of about 93,000,000 miles (150 million kilometers) away from Earth. It is so far away that light from the Sun, traveling at a speed of 186,000 miles (300,000 kilometers) per second, takes about 8 minutes to reach us.

Lesson 1.1 Patterns with exponents and Powers of 10

Solve & share
A store sells AA batteries in packages of 10 batteries. They also sell boxes of 10 packages, cases of 10 boxes, and cartons of 10 cases. How many AA batteries are in one case? One carton? 10 cartons? Solve these problems any way you choose.

You can use appropriate tools, such as place-value blocks, to help solve the problems. However you choose to solve it, show your work!

Look Back! How many 10s are in 100? How many 10s are in 1,000? Write equations to show your work.

Answer: There are 1000 AA batteries in one case , 10,000 batteries in one carton and 1,00,000 batteries in 10 cartons.

Explanation:
Given, A store sells AA batteries in packages of 10 batteries, boxes of 10 packages, cases of 10 boxes, and cartons of 10 cases.
Then we have 10 batteries for one package and given that 1 box contains 10 packages ,
10 × 10 = 100 , that is 100 batteries for each box.
Next for 10 boxes we have a case which means 100 × 10 = 1000 batteries ,
That is each case contains 1000 batteries.
Now for 10 cases we have a carton which means 1000 × 10 = 10,000 batteries ,
That is each carton contains 10,000 batteries.
And now they asked for 10 cartons ,
So, for 10 cartons we have 10,000 × 10 = 1,00,000 batteries .

Visual Learning Bridge

Essential Question
How Can You Explain Patterns in the Number of Zeros in a Product?
Answer: An exponent identifies a quantity representing the power to which a given number or expression is to be raised.

Explanation:
For example , 4 × 60
= 4 x (6 x 10)
= (4 x 6) x 10
= 24 x 10
=240
or
50 x 700
= (5 x 10) + (7 x 100)
= (5 x 7) x (10 x 100)
= 35 x 1,000
= 35,000.

A.
Tamara’s new horse weighs about 1,000 pounds. How can you show 1,000 as a power of 10 using an exponent?

The exponent is the number that tells how many times a base number is used as a factor.

Answer: 10³

Explanation:
Given, horse weighs about 1,000 pounds. then show 1,000 as a power of 10 using an exponent
So we can write 1000 as 10 × 10 × 10 = 10³.

B.
Write 1,000 as a product using 10 as a factor.

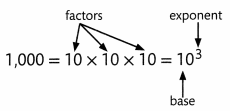
The exponent, 3, shows that the base number, 10, is multiplied 3 times.
So, 1,000 is written as 10³ using exponents.

C.
Tamara estimates that her horse will eat about 5,000 pounds of hay each year. How can you write 5,000 using exponents? 5 × 10¹ = 5 × 10 = 50
5 × 10² = 5 × 10 × 10 = 500
5 × 10³ = 5 × 10 × 10 × 10 = 5,000
The number of zeros in the product is the same as the exponent.
So, 5,000 is written as 5 × 10³ using exponents.

Convince Me! Look for Relationships What pattern do you notice in the number of zeros in the products in box C above?

Guided Practice

Do You Understand?

Question 1.
Why are there three zeros in the product of 6 × 10³?
Answer: The product of 6 × 10³ is 6,000 so it contains three zeros.

Explanation:
The product of 6 × 10³ is 6,000,
Because, 6 × 10 × 10 × 10 = 6,000.
So it contains three zeros.

Question 2.
Susan said that 10⁵ is 50. What mistake did Susan make? What is the correct answer?
Answer: The correct answer is 1,00,000.

Explanation:
10 × 10 × 10 × 10 × 10 = 1,00,000.
The mistake Susan made is he multiplied the exponent with the base.

Do You Know How?

In 3 and 4, complete the pattern.

Question 3.
10¹ =
10² =
10³ =
10⁴ =
Answer:
10¹ = 10
10² = 100
10³ = 1000
10⁴ =  10,000

Explanation:
10  = 10
10 × 10  =  100
10 × 10 × 10  =  1000
10 × 10 × 10 × 10  = 10,000.

Question 4.
= 7 × 10¹
= 7 × 10²
= 7 × 10³
= 7 × 10⁴
Answer:
70 = 7 × 10¹
700 = 7 × 10²
7,000 = 7 × 10³
70,000  = 7 × 10⁴

Explanation:
Given, 7 ×10  = 70
7 × 10 × 10  =  700
7 ×10 × 10 × 10  =  7,000
7 × 10 × 10 × 10 × 10  = 70,000.

Independent Practice

In 5-15, find each product. Use patterns to help.

Question 5.
3 × 10¹ =
3 × 10² =
3 × 10³ =
3 × 10⁴ =
Answer:
3 × 10¹ = 30
3 × 10² = 300
3 × 10³ = 3,000
3 × 10⁴ = 30,000

Explanation:
3 ×10  = 30
3 × 10 × 10  =  300
3 ×10 × 10 × 10  =  3,000
3 × 10 × 10 × 10 × 10  = 30,000.

Question 6.
2 × 10 =
2 × 100 =
2 × 1,000 =
2 × 10,000 =
Answer:
2 × 10 =  20
2 × 100 = 200
2 × 1,000 = 2,000
2 × 10,000 = 20,000

Explanation:
2 × 10 =  2 × 10¹ = 20
2 × 100 = 2 ×  10² =  2 × 10 × 10 = 200
2 × 1,000 = 2 × 10³  =  2 × 10 × 10 × 10 = 2,000
2 × 10,000 = 2 × 10⁴  = 2 × 10 × 10 × 10  × 10 = 20,000

Question 7.
= 9 × 10¹
= 9 × 10²
= 9 × 10³
= 9 × 10⁴
Answer:

90 = 9 × 10¹
900 = 9 × 10²
9,000 = 9 × 10³
90,000  = 9 × 10⁴

Explanation:
Given, 7 ×10  = 70
7 × 10 × 10  =  700
7 ×10 × 10 × 10  =  7,000
7 × 10 × 10 × 10 × 10  = 70,000.

Question 8.
8 × 10⁴
Answer:  8 × 10⁴ = 80,000

Explanation:
8 × 10⁴ = 8 × 10 × 10 × 10 × 10  = 80,000

Question 9.
4 × 1,000
Answer:  4 × 1,000 = 4,000

Explanation:
4 × 10³  = 4 ×10 × 10 × 10  =  4,000

Question 10.
5 × 10²
Answer:  5 × 10² = 500

Explanation:
5 × 10² =  5 × 10 × 10  = 500

Question 11.
6 × 10,000
Answer:  6 × 10,000 = 60,000

Explanation:
6 × 10,000 =  6 × 10 × 10 × 10 × 10  = 6 × 10⁴ = 60,000

Question 12.
4 × 10¹
Answer:  4 × 10¹  =  40

Explanation:
4 × 10¹  =  40

Question 13.
100 × 9
Answer: 100 × 9 = 900

Explanation:
100 × 9  = 10 × 10  × 9 = 900

Question 14.
10³ × 6
Answer:  10³ × 6 = 6,000

Explanation:
10³ × 6 = 10 × 10 × 10 × 6  = 6,000

Question 15.
8 × 10⁵
Answer: 8 × 10⁵  = 8,00,000

Explanation:
8 × 10⁵  = 8 × 10 × 10 × 10 × 10 × 10 = 8,00,000

Question 16.
Write 10 × 10 × 10 × 10 × 10 × 10 with an exponent. Explain how you decided what exponent to write.
Answer: 10⁶

Explanation:
As Given there are 6 tens together
So, 10 × 10 × 10 × 10 × 10 × 10  = 10⁶

Problem Solving

Question 17.
One box of printer paper has 3 × 10² sheets of paper. Another box has 103 sheets of paper. What is the total number of sheets in both boxes?
Answer: The total number of sheets in both boxes is 403

Explanation:
Given, One box of printer paper has 3 × 10² sheets of paper. then , 3 × 10² = 300
Another box has 103 sheets of paper.
So, 300 + 103  = 403
The total number of sheets in both boxes is 403

Question 18.
A post is put every 6 feet along a fence around a rectangular field that is 42 ft long and 36 ft wide. How many posts are needed?
Answer: 26 posts are needed.

Explanation:
42 feet for one side, 42 feet for the parallel side
36 feet for one side, 36 feet for the parallel side
42 ÷ 6 = 7 ,One of these posts is a corner, so make it 6 because we do not want to count a corner post more than once.
36 ÷ 6 = 6 ,One of these posts is a corner, so make it 5 because we do not want to count a corner post more than once
We now add these: 2 x 6 + 2 x 5 = 12 + 10 = 22
Add in the four corner posts: 22 + 4 = 26 posts.
So , 26 posts are needed.

Question 19.
Number Sense A company had 9 × 10⁶ dollars in sales last year. Explain how to find the product 9 × 10⁶.
Answer:  9 × 10⁶   = 9,000,000.

Explanation:
9 × 10⁶  =  9 ×10 × 10 × 10 × 10 × 10 × 10  = 9,000,000.

Question 20.
An aquarium has the same shape as the solid figure shown below. What is the name of this solid figure?

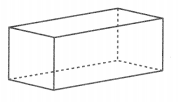
Answer: A Rectangular prism.

Explanation:
a solid figure that has six sides, called faces, that are rectangles.
So, they are known as Rectangular prism.

Question 21.
Model with Math Isaac takes 5 minutes to ride his bike down the hill to school and 10 minutes to ride up the hill from school. He attends school Monday through Friday. How many minutes does he spend biking to and from school in two weeks? Write an equation to model your work.
Answer:  It takes 150 minutes

Explanation:
Given, Issac take 5 minutes to ride his bike down the hill to school
And 10 minutes to ride up the hill from school .
So, it takes 15 min each day to and from school He attends school Monday through Friday,
So, 5 days in a week for 5 days it takes  15 × 5 = 75 minutes
For 2 weeks , 75 × 2 = 150 minutes.

Question 22.
Higher Order Thinking Santiago hopes to buy a 4-horse trailer for about $12,000. Describe all the numbers that when rounded to the nearest hundred are 12,000.
Answer: Any number from 11,950 to 12,049, will result to 12,000 when rounded to the nearest hundred. 

Explanation:
Since we have given that,
Number of horse trailer = 4 Cost of 4 horse trailer = $12000 ,
As we know about the “Estimation”, if there is a number greater or equal to 5 in tens place then it will be rounded off to the nearest next greatest integer.
So, if this number is $11950 to 12049.
So, the possible numbers that when rounded to the nearest hundred are 12000 are from 11500 to 12049.

Assessment Practice

Question 23.
Choose all the equations that are true.
10 × 10 × 10 × 10 = 40
10 × 10 × 10 × 10 = 10⁴
10 × 10 × 10 × 10 = 1,000,
10 × 10 × 10 × 10 = 10,000
10 × 10 × 10 × 10 = 4 × 10⁴
Answer:  10 × 10 × 10 × 10 = 10⁴  and  10 × 10 × 10 × 10 = 10,000

Explanation:
There are 4 tens in 10 × 10 × 10 × 10 = 10⁴
So, 10 × 10 × 10 × 10 = 10,000.

Question 24.
Choose all the equations that are true.
6 × 10⁵ = 6 × 100,000
6 × 10⁵ = 6 × 10,000
6 × 10⁵ = 600,000
6 × 10⁵ = 60,000
6 × 10⁵ = 650,000
Answer: 6 × 10⁵ = 6 × 100,000 and  6 × 10⁵ = 600,000

Explanation:
6 × 10⁵ = 6 × 10 × 10 × 10 × 10  × 10 = 6,00,000. or
6 × 10⁵ = 6 × 10 × 10 × 10 × 10  × 10 = 6 × 100,000.

Lesson 1.2 Understand Whole Number Place Value

Activity

Solve & Share

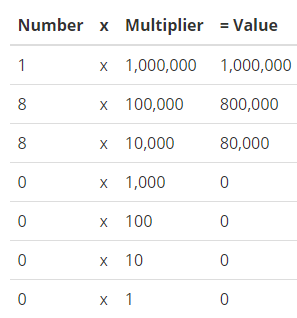
The population of a city is 1,880,000. What is the value of each of the two 8s in this number? How are the two values related? Use tools like this place-value chart to help solve the problem.

Answer: These are the values of each number

Explanation:
Add up all these values and we will have 1,880,000.

Use Structure You can use place value to analyze the relationship between the digits of a number. Show your work!

Look Back! Is the relationship between the value of the two 85 in 1,088,000 the same as the relationship between the value of the two 8s in the problem above? Explain.

Visual Learning Bridge

Essential Question
How Are Place-Value Positions Related?

A.
According to the 2010 U.S. Census, the population of Phoeni×, Arizona is about 1,440,000. What is the relationship between the value of the two 4s in this number?

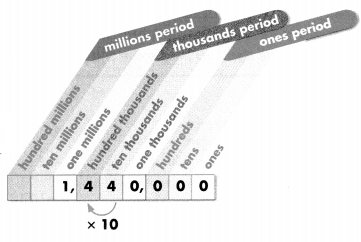
Writing the number in expanded form can help.

C.
Look at the expanded form of 1,440,000. The value of the 4 in the hundred thousands place is 400,000. The value of the 4 in the ten thousands place is 40,000.
400,000 is 10 times as great as 40,000.
40,000 is \(\frac{1}{10}\) of 400,000.

Sometimes word form is used instead of number name.

Standard form
1,440,000
Expanded form:
1 × 1,000,000 + 4 × 100,000 + 4 × 10,000
Using exponents, this can be written as:
(1 × 10⁶) + (4 × 10⁵) + (4 × 10⁴)
Number name:
one million, four hundred forty thousand

Convince Me! Construct Arguments is the value of the 1 in 1,440,000 10 times as great as the value of the 4 in the hundred thousands place? Explain.

Another example
When two digits next to each other in a number are the same, the digit on the left has 10 times the value of the digit to its right.
When two digits next to each other are the same, the digit on the right has to the value of the digit to its left.

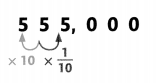
Guided Practice

Do You Understand?

Question 1.
In 9,290, is the value of the first 9 ten times as great as the value of the second 9? Explain.
Answer:  No

Explanation:
The first 9 is on the place of the thousands, while the second 9 is on the place of the tens. so the first 9 is a hundred times as great as the second 9

Do You Know How?

Question 2.
Write 4,050 in expanded form.
Answer:  4,000 + 50

Explanation:
4,000 + 50  = 4,050.

In 3 and 4, write the values of the given digits.

Question 3.
the 7s in 7,700
Answer:  7,000 + 700

Explanation:
The first 7 is on the place of the thousands, while the second 7 is on the place of the hundreds.

Question 4.
the 2s in 522
Answer:  500 + 22

Explanation:
The first 2 is on the place of the tens, while the second 2 is on the place of the ones.

Independent Practice

In 5-7, write each number in standard form.

Question 5.
8,000,000 + 300 + 9
Answer: 8,000,309.

Explanation:
8,000,000 + 300 + 9 = 8,000,309.

Question 6.
(4 × 10⁴) + (6 × 10²)
Answer: 40,600

Explanation:
4 × 10⁴ =4 × 10 × 10 × 10 × 10  =  40,000
6 × 10²  = 6 × 10 × 10 =  600
So, 40,000 + 600 = 40,600

Question 7.
10,000 + 20 + 3
Answer:   10023

Explanation:
10,000 + 20 + 3 = 10023.

In 8-10, write each number in expanded form.

Question 8.
5,360
Answer: (5 × 10³) + (3 × 10²) + (6 × 10)

Explanation:
5,360 =  5000 + 300 + 60  = (5 × 10³) + (3 × 10²) + (6 × 10)

Question 9.
102,200
Answer:  10⁵ + (2 × 10³) + ( 2 × 10²)

Explanation:
102,200 = 1,00,000 + 2000 + 200 =  10⁵ + (2 × 10³) + ( 2 × 10²)

Question 10.
85,000,011
Answer:  (85 ×  10⁶) + 10 + 1

Explanation:
85,000,011 = 85,000,000 + 10 + 1 = (85 ×  10⁶) + 10 + 1

In 11-13, write the values of the given digits.

Question 11.
the 7s in 6,778
Answer: 6,000 + 700 + 70 + 8

Explanation:
The first 7 is on the place of the hundreds, while the second 7 is on the place of the tens.

Question 12.
the 9s in 990,250
Answer: 9,00,000 + 90,000 + 200 + 50

Explanation:
The first 9 is on the place of the hundred thousands, while the second 9 is on the place of the thousands.

Question 13.
the 1s in 2,011,168
Answer: 2,000,000 + 11,000 + 100 + 60 + 8

Explanation:
The first 1 is on the place of the ten thousands, while the second 1 is on the place of the thousands and the third 1 is on the place of hundreds.

Problem Solving

Question 14.
Write the number name and expanded form for the number of driver ants that could be in two colonies.

Up to 22,000,000 driver ants can live in a single colony.

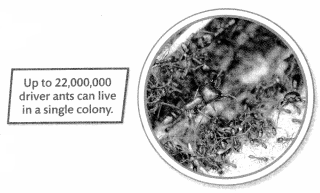
Answer:  For 2 colonies  44,000,000
The number name is Forty four million
The expanded form is (4 ×10⁶) + (4 ×10⁶)

Explanation:
Given , Up to 22,000,000 driver ants can live in a single colony.
For 2 colonies 22,000,000 + 22,000,000 = 44,000,000
The expanded form is 40,000,000 + 4,000,000 = (4 ×10⁶) + (4 ×10⁶)

Question 15.
enVision® STEM A queen ant can produce about nine million ants in her lifetime. Write this number in standard form.
Answer: The number in standard form is 9,000,000

Explanation:
Given, A queen ant can produce about nine million ants in her lifetime.
The number in standard form is 9,000,000.

Question 16.
Critique Reasoning Paul says that in the number 6,367, one 6 is 10 times as great as the other 6. Is he correct? Explain why or why not.
Answer: No

Explanation:
Given in the number 6,367, one 6 is 10 times as great as the other 6.
The first 6 is on the place of the thousands, while the second 6 is on the place of the tens. so the first 6 is a hundred times as great as the second 6.

Question 17.
Jorge drew a square that had a side length of 8 inches. What is the perimeter of Jorge’s square?
Remember, the perimeter of a shape is the distance around it.

Answer: The perimeter of Jorge’s square is 32 inches.

Explanation:
Given, Jorge drew a square that had a side length of 8 inches.
Square has all equal sides, so perimeter of the square P = 4a = 4 × 8 = 32 inches

Question 18.
Higher Order Thinking
Dan wrote (2 × 10⁶) + (3 × 10⁴) + (5 × 10³) + 4 for the expanded form of two million, three hundred fifty thousand, four. What error did he make in the expanded form? What is the standard form of the number?

Answer: The standard form of the number is 20,35,004.
The number name is two million, thirty five thousand and four.

Explanation:
(2 × 10⁶) + (3 × 10⁴) + (5 × 10³) + 4
= 2,000,000 + 30,000 + 5,000 + 4
= 20,35,004.
The standard form of the number is 20,35,004.
The number name is two million, thirty five thousand and four.
He made mistake with the three hundred fifty thousand, instead of  thirty five thousand

Assessment Practice

Question 19.
Colleen says she is thinking of a 4-digit number in which all the digits are the same. The value of the digit in the hundreds place is 200.
Part A
What is the number? Explain.

Part B
Describe the relationship between the values of the digits in the number.
Answer:  The number is 2,222.
The first 2 is on the place of the thousands, while the second 2 is on the place of the hundreds, The third 2 is on the place of the tens, and the last 2 is on the place of the ones.

Explanation:
Given,  Colleen says she is thinking of a 4-digit number in which all the digits are the same. The value of the digit in the hundreds place is 200.
The number is 2,222.
The first 2 is on the place of the thousands, while the second 2 is on the place of the hundreds, The third 2 is on the place of the tens, and the last 2 is on the place of the ones.

Lesson 1.3 Decimals to Thousandths

Solve & Share
At Suzie’s Sticker City, customers can buy a book of stickers, a page, a strip, or a single sticker. Provide the missing fractions in the boxes below.

How can you use what you know about powers of 10 to help you fill in the boxes?

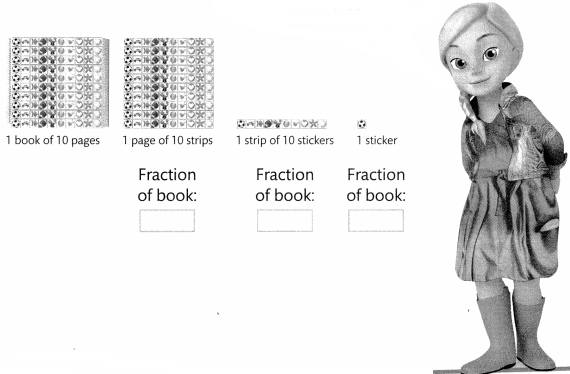
Look Back! Use Structure Describe any patterns you notice in the fractions.

Visual Learning Bridge

Essential Question
How Can You Read and Write Question Decimals to the Thousandths?

A.
A box is filled with 1,000 cubes. Amy picks out 4 cubes. How can you represent 4 out of 1,000 cubes as a decimal?

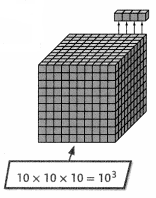
You can write 4 out of 1,00 as the fraction \(\frac{4}{1,000}\).

B.
The number name for \(\frac{4}{1,000}\) is four thousandths. A decimal place-value chart can help you determine the decimal. Notice that the thousandths place is three places to the right of the decimal point.

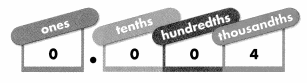
So, \(\frac{4}{1,000}\) can be represented by the decimal 0.004.

C.
How can \(\frac{444}{1,000}\) be represented by a decimal? \(\frac{444}{1,000}\) is read as four hundred forty-four thousandths and represented by the decimal 0.444.

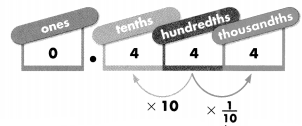
The value of the digit 4 in the hundredths place has 10 times the value of the digit 4 in the thousandths place and \(\frac{1}{10}\) the value of the digit 4 in the tenths place.

Convince Me! Reasoning How is 0.004 the same as and different from 0.444?

Answer: 0.004 and 0.444 both have 4 in the thousandth place

Explanation:
0.004 and 0.444 both have 4 in the thousandth place,
both are in thousandth place
different: 0.444 is greater than 0.004 when divide by 1000
444/1000 is greater than 4/1000
if convert to percentage : 0.444 is 44.4% and 0.004 is 0.4%

Guided Practice

Do You Understand?

Question 1.
If four cubes are pulled from the box on the previous page, how would you write the fraction representing the cubes that are left? the decimal representing the cubes that are left?
Answer:  In decimal form we can write it as 0.996.

Explanation:
Given, A box is filled with 1,000 cubes, picking out 4 cubes,
1000 – 4 = 996,
Then \(\frac{996}{1000}\) are the remaining of the cubes which are left in the box
In decimal form we can write it as 0.996.

Do You Know How?

Question 2.
0.3 is 10 times as great as what decimal? 0.003 is \(\frac{1}{10}\) of what decimal?
Answer: 0.3 is 10 times as great as 0.03 and 0.003 is \(\frac{1}{10}\) of 0.03

Explanation:
0.3 × \(\frac{1}{10}\) = 0.03
0.03 = 0.003 × \(\frac{1}{10}\)
So, 0.3 is 10 times as great as 0.03 and 0.003 is \(\frac{1}{10}\) of 0.03

In 3-6, write each decimal as a fraction.

Question 3.
0.001 =
Answer: \(\frac{1}{1000}\)

Explanation:
Given 0.001 ,
In fraction form we can write it in to \(\frac{1}{1000}\)

Question 4.
0.05 =
Answer: \(\frac{5}{100}\)

Explanation:
Given 0.05 ,
In fraction form we can write it in to \(\frac{5}{100}\)

Question 5.
0.512 =
Answer: \(\frac{512}{1000}\)

Explanation:
Given 0.512 ,
In fraction form we can write it in to \(\frac{512}{1000}\)

Question 6.
0.309 =
Answer: \(\frac{309}{1000}\)

Explanation:
Given 0.309 ,
In fraction form we can write it in to \(\frac{309}{1000}\)

In 7-10, write each fraction as a decimal.

Question 7.
\(\frac{2}{1,000}\) =
Answer: 0.002

Explanation:
Given , \(\frac{2}{1,000}\)
In decimal form we can  write it into 0.002

Question 8.
\(\frac{34}{100}\) =
Answer: 0.34

Explanation:
Given , \(\frac{34}{100}\)
In decimal form we can  write it into 0.34

Question 9.
\(\frac{508}{1,000}\) =
Answer: 0.508

Explanation:
Given , \(\frac{508}{1,000}\)
In decimal form we can  write it into 0.508

Question 10.
\(\frac{99}{1,000}\) = =
Answer:

Explanation:
Given , \(\frac{99}{1,000}\)
In decimal form we can  write it into 0.099

Independent Practice

In 11-18, write each decimal as a fraction.

Question 11.
0.007
Answer: \(\frac{7}{1000}\)

Explanation:
Given 0.007 ,
In fraction form we can write it in to \(\frac{7}{1000}\)

Question 12.
0.08
Answer: \(\frac{8}{100}\)

Explanation:
Given 0.08 ,
In fraction form we can write it in to \(\frac{8}{100}\)

Question 13.
0.065
Answer: \(\frac{65}{1000}\)

Explanation:
Given 0.08 ,
In fraction form we can write it in to \(\frac{65}{1000}\)

Question 14.
0.9
Answer: \(\frac{9}{10}\)

Explanation:
Given 0.9 ,
In fraction form we can write it in to \(\frac{9}{10}\)

Question 15.
0.832
Answer: \(\frac{832}{1000}\)

Explanation:
Given 0.832 ,
In fraction form we can write it in to \(\frac{832}{1000}\)

Question 16.
0.203
Answer: \(\frac{203}{1000}\)

Explanation:
Given 0.203 ,
In fraction form we can write it in to \(\frac{203}{1000}\)

Question 17.
0.78
Answer:  \(\frac{78}{100}\)

Explanation:
Given 0.78 ,
In fraction form we can write it in to \(\frac{78}{100}\)

Question 18.
0.999
Answer: \(\frac{999}{1000}\)

Explanation:
Given 0.999 ,
In fraction form we can write it in to \(\frac{999}{1000}\)

In 19-26, write each fraction as a decimal.

Question 19.
\(\frac{434}{1,000}\) =
Answer:  0.434

Explanation:
Given, \(\frac{434}{1,000}\)
In decimal form we can  write it into 0.0.434

Question 20.
\(\frac{3}{10}\) =
Answer: 0.3

Explanation:
Given, \(\frac{3}{10}\)
In decimal form we can  write it into 0.3

Question 21.
\(\frac{873}{1,000}\) =
Answer: 0.873

Explanation:
Given, \(\frac{873}{1,000}\)
In decimal form we can  write it into 0.873

Question 22.
\(\frac{17}{1,000}\) =
Answer:0.017

Explanation:
Given, \(\frac{17}{1,000}\)
In decimal form we can  write it into 0.017

Question 23.
\(\frac{309}{1,000}\) =
Answer: 0.309

Explanation:
Given, \(\frac{309}{1,000}\)
In decimal form we can  write it into 0.309

Question 24.
\(\frac{5}{1,000}\) =
Answer: 0.005

Explanation:
Given, \(\frac{5}{1,000}\)
In decimal form we can  write it into 0.005

Question 25.
\(\frac{6}{100}\) =
Answer: 0.06

Explanation:
Given, \(\frac{6}{100}\)
In decimal form we can  write it into 0.06

Question 26.
\(\frac{999}{1,000}\) =
Answer: 0.999

Explanation:
Given, \(\frac{999}{1,000}\)
In decimal form we can  write it into 0.999

Question 27.
Look at the middle 9 in exercise 18. How is its value related to the value of the 9 to its left? to the value of the 9 to its right?
Answer: The value of the digit 9 in the hundredths place has 10 times the value of the digit 9 in the thousandths place and \(\frac{1}{10}\) the value of the digit 9 in the tenths place.

Explanation:
The value of the number given in exercise 18 is 0.999,
The first 9 is on the place of the tenths, while the second 9 is on the place of the hundredths and the second 9 is  on the place of thousandths.
So, The value of the digit 9 in the hundredths place has 10 times the value of the digit 9 in the thousandths place and \(\frac{1}{10}\) the value of the digit 9 in the tenths place.

Problem Solving

Question 28.
The Palmers’ property tax bill for the year is $3,513. In their first installment, they paid $1,757. How much do they still owe on their bill? Write an equation to model your work.
Answer:  They still owe $1,756 on their bill .

Explanation:
Given, The Palmers’ property tax bill for the year is $3,513.
In their first installment, they paid $1,757.
$3,513 – $1,757 = $1,756.
So, they still have to pay the half amount that is $1,756
Then $1,757 × 2 = $3,513.
They still owe $1,756 on their bill .

Question 29.
Write the fractions \(\frac{22}{100}\) and \(\frac{22}{1,000}\) as decimals. How are the values of the digit 2 related in each of the decimals?
Answer: 0.22 and 0.022

Explanation:
Given, \(\frac{22}{100}\)
In decimal form we can write it as 0.22,
The value of the digit 2 in the tenths place has 10 times the value of the digit 4 in the hundredths place .

And \(\frac{22}{1,000}\)
In decimal form we can write it as 0.022,
The value of the digit 2 in the hundredths place has 10 times the value of the digit 4 in the thousandths place.

Question 30.
Simon scored 4 × 10² points in a game. Joe scored 2 × 10³ points in the same game. Whose score is higher? How much higher?
Answer: Joe scored 5 times as many as Simon.

Explanation:
Given, Simon scored 4 × 10² points in a game.
Joe scored 2 × 10³ points in the same game.
Now we have  4 × 10² =  4 × 10 × 10 = 400
2 × 10³ =  2 × 10 × 10 × 10 = 2000
Finally, Simon scored 400 point and Joe scored 2000 points
So, Joe scored 5 times as many as Simon.

Question 31.
Higher Order Thinking Kelly said that \(\frac{97}{1,000}\) can be written as 0.97. Is she correct? Explain.
Answer: No , \(\frac{97}{1,000}\)  should be 0.097 not 0.97

Explanation:
Given, Kelly said that \(\frac{97}{1,000}\) can be written as 0.97
The decimal form can written according to the number of zeros in the denominator
So , \(\frac{97}{1,000}\)  should be 0.097 not 0.97

Question 32.
Critique Reasoning Frank reasoned that in the number 0.555, the value of the 5 in the thousandths place is ten times as great as the 5 in the hundredths place. Is he correct? Explain.
Answer: NO

Explanation:
Given, the number 0.555
The value of the digit 5 in the hundredths place has 10 times the value of the digit 5 in the thousandths place

Question 33.
How many cubes are in the box? What fraction of the entire box do the 7 cubes represent? Explain your answer.

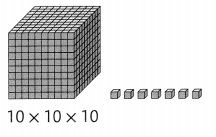
Answer: \(\frac{7}{1000}\)

Explanation:
Given, 10 × 10 × 10  = 1000
And we have the 7 cubes
So, the fraction will be  \(\frac{7}{1000}\)

Assessment Practice

Question 34.
0.04 is 10 times as great as which decimal?
A. 0.4
B. 0.1
C. 0.004
D. 0.001
Answer: C , 0.04 is 10 times as great as 0.004

Explanation:
0.04 × \(\frac{1}{10}\) = 0.004
So, 0.04 is 10 times as great as 0.004

Question 35.
0.009 is o of which decimal?
A. 0.01
B. 0.09
C. 0.1
D. 0.9
Answer:  B, 0.009 is \(\frac{1}{10}\) of 0.09

Explanation:
0.09 × \(\frac{1}{10}\) = 0.009
So, 0.009 is \(\frac{1}{10}\) of 0.09

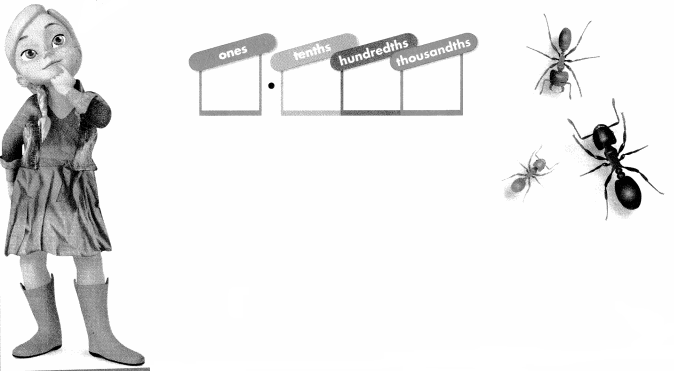
Lesson 1.4 Understand Decimal Place Value

Solve & Share

A runner won a 100-meter race with a time of 9.85 seconds. How can you use place value to Explain this time? Complete a place-value chart to show this time.

Generalize You can use what you know about whole-number place value to help you think about place value of decimal numbers.

Look Back! In the decimal 9.85, what is the value of the 8? What is the value of the 5?

Visual Learning Bridge

Essential Question How Can You Represent Decimals?

A.
Jo picked a seed from her flower. The seed has a mass of 0.245 gram. What are some different ways you can represent 0.245?

You can write the standard form, expanded form, and number name for a decimal just like you can for a whole number.

B.

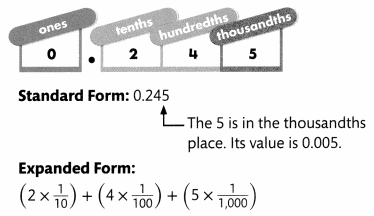
Number Name: two hundred forty-five

A place-value chart can help you identify the tenths, hundredths, and thousandths places in a decimal.

Convince Me! Use Structure How many hundredths are in one tenth? How many thousandths are in one hundredth? Tell how you know.

Another example
Equivalent decimals name the same amount.
What are two other decimals equivalent to 1.4?
One and four tenths is the same as one and forty hundredths.
1.4 = 1.40
One and four tenths is the same as one and four hundred thousandths.
1.4 = 1.400.

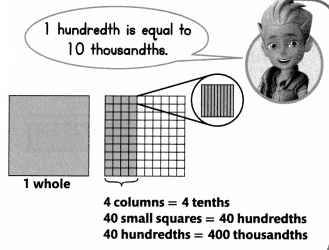
So, 1.4 = 1.40 = 1.400.

Guided Practice

Do You Understand?

Question 1.
The number 3.453 has two 3s. Why does each 3 have a different value?
Answer: These are different due to the place values. 3 and 0.003

Explanation:
The given number is 3.453.
The first 3 that is before the decimal is at ones place, that is 3 × 1 = 3
But the second 3 which is after the decimal is at thousandth place, \(\frac{3}{1000}\) = 0.003
Hence, you can clearly see the different values of both three’s. These are different due to the place values.

Do You Know How?

In 2 and 3, write each number in standard form.

Question 2.
4 × 100 + 7 × 10 + 6 × 1 + 6 × \(\left(\frac{1}{10}\right)\) + 3 × \(\left(\frac{1}{100}\right)\) + 7 × \(\left(\frac{1}{1,000}\right)\)
Answer:  The standard form is 476.637.

Explanation:
Given,
(4 × 100)+ (7 × 10) + (6 × 1) + {6 × \(\left(\frac{1}{10}\right)\) + 3 × \(\left(\frac{1}{100}\right)\) + 7 × \(\left(\frac{1}{1,000}\right)\)}
Solve for the brackets,
we have 400 + 70 + 6 + [ 0.6 + 0.03 + 0.007]
= 476 + 0.637
= 476.637
The standard form is 476.637.

Question 3.
four and sixty-eight thousandths
Answer: The standard form is 0.468.

Explanation:
Given, four and sixty-eight thousandths
The expanded form is 4 × \(\left(\frac{1}{10}\right)\) + 6 × \(\left(\frac{1}{100}\right)\) + 8 × \(\left(\frac{1}{1,000}\right)\)
Then, 0.4 + 0.06 + 0.008 = 0.468
So, the standard form is 0.468

Independent Practice

In 4-6, write each number in standard form.

Question 4.
(2 × 1) + (6 × \(\frac{1}{1,000}\))
Answer: The standard form is 2.006

Explanation:
Given, (2 × 1) + (6 × \(\frac{1}{1,000}\))
= 2 + 0.006
= 2.006
The standard form is 2.006

Question 5.
(3 × 1) + (3 × \(\frac{1}{10}\)) + (9 × \(\frac{1}{1,000}\))
Answer: The standard form is 3.309

Explanation:
Given, (3 × 1) + (3 × \(\frac{1}{10}\)) + (9 × \(\frac{1}{1,000}\))
= 3 + 0.3 + 0.009
= 3.309
So, The standard form is 3.309

Question 6.
nine and twenty hundredths
Answer: The standard form is 0.920.

Explanation:
Given, nine and twenty hundredths
The expanded form is (9 × \(\frac{1}{10}\)) + (20 × \(\frac{1}{100}\))
= 0.9 + 0.020
= 0.920
The standard form is 0.920

In 7-10, write two decimals that are equivalent to the given decimal.

Question 7.
2.200
Answer: The two decimals that are equivalent to the given decimal are 2.2 and 2.20

Explanation:
Given, 2.200
Two and two tenths is the same as two and twenty hundredths.
2.2 = 2.20
Two and Two tenths is the same as two and twenty tenths.
2.2 = 2.2.
So, The two decimals that are equivalent to the given decimal are 2.2 and 2.20

Question 8.
8.1
Answer: The two decimals that are equivalent to the given decimal are 8.10 and 8.100

Explanation:
Given, 8.1
Eight and one tenths is the same as eight and one hundredths.
8.1 = 8.10
Eight and one tenths is the same as eight and one hundred thousandths.
8.1 = 8.100.
So, The two decimals that are equivalent to the given decimal are 8.10 and 8.100

Question 9.
9.50
Answer: The two decimals that are equivalent to the given decimal are 9.5 and 9.500

Explanation:
Given, 9.50
Nine and five tenths is the same as nine and  fifty tenths.
9.50 = 9.5.
Nine and five tenths is the same as nine and fifty hundred thousandths.
9.50 = 9.500.
So, The two decimals that are equivalent to the given decimal are 9.5 and 9.500

Question 10.
4.200
Answer: The two decimals that are equivalent to the given decimal are 4.2 and 4.20

Explanation:
Given, 4.200
Four and two tenths is the same as four and twenty hundredths.
4.200 = 4.20
Four and two tenths is the same as two and twenty tenths.
4.200 = 4.2.
So, The two decimals that are equivalent to the given decimal are 4.2 and 4.20

Problem Solving

Question 11.
The annual fundraising goal of a charity is $100,000. So far $63,482 has been raised. How much more money is needed to reach the goal?

Answer: To reach the goal they need $36,518.

Explanation:
Given, The annual fundraising goal of a charity is $100,000.
So far $63,482 has been raised.
Then, $100,000 – $63,482 = $36,518.
So, To reach the goal they need $36,518.

Question 12.
Santiago has a rope that measures 205.95 centimeters. Write this number in expanded form.
Answer:

Explanation:
Given, Santiago has a rope that measures 205.95 centimeters
The standard form is 205.95
Then, The expanded form is (2 × 100) + (5 × 1) + (9 × \(\frac{1}{10}\)) + (5 × \(\frac{1}{100}\))
= 200 + 5 +[ 0.9 + 0.05 ]
= 205 + 0.95
= 205.95
So, The expanded form is (2 × 100) + (5 × 1) + (9 × \(\frac{1}{10}\)) + (5 × \(\frac{1}{100}\))

Question 13.
How can you tell that 7.630 and 7.63 are equivalent decimals?
Answer: The two decimals that are equivalent to both the numbers

Explanation:
Given, 7.630 and 7.63
Seven and sixty three tenths is the same as Seven and sixty three hundredths.
7.63 = 7.630
So, The two decimals that are equivalent to both the numbers

Question 14.
In Justin’s school, 0.825 of the students participate in a sport. If there are one thousand students in Justin’s school, how many participate in a sport?
Answer: Totally 825 students are participating in the school.

Explanation:
Given, In Justin’s school, 0.825 of the students participate in a sport.
Since, there are 1 thousand students, and the decimal is 0.825,
So, there are 825 students participating.

Question 15.
Be Precise Maria incorrectly placed the decimal point when she wrote 0.65 inch for the width of her tablet computer. What is the correct decimal number for the width?

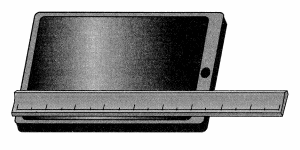
Answer: The correct decimal number for the width is 6.5.

Explanation:
Given, Maria incorrectly placed the decimal point when she wrote 0.65 inch for the width of her tablet computer.
As shown in the figure, the scale placed there to measure the width , as per the scale the width is 6.5.
So, The correct decimal number for the width is 6.5.

Question 16.
Higher Order Thinking Three boys cut out hundredths decimal models. Derrick does not shade any of his models. Ari shades half of one model. Wesley shades two models and one tenth of another model. What decimal represents the amount each boy shades?

Answer: Derrick’s value = 0,
Ari’s value = 0.5,
Wesley’s value = 2.1 ,

Explanation:
Given, Derrick does not shade any of his models. Ari shades half of one model. Wesley shades two models and one tenth of another model.
Derrick doesn’t shade anything, so his value is 0.
Ari shades half of one model, so 1/2 = 0.5 is his value Wesley shades 2 full models, plus 1/10 = 0.1 of another one, leading to 2+0.1 = 2.1 as his value. 
Derrick’s value = 0,
Ari’s value = 0.5,
Wesley’s value = 2.1 ,

Assessment Practice

Question 17.
Find two decimals that are equivalent to (4 × 10) + (7 × \(\frac{1}{100}\)). Write the decimals in the box.

Answer:  The two decimals that are equivalent to the 40.07 are 40.070 and 40.07

Explanation:
Given, (4 × 10) + (7 × \(\frac{1}{100}\)).
= 40 + 0.07
= 40.07
The standard form is 40.07
The two decimals that are equivalent to the 40.07 are 40.070 and 40.07 , from the given box of decimals.

Lesson 1.5 Compare Decimals

Activity

Solve & Share

The lengths of three ants were measured in a laboratory. The lengths were 0.521 centimeter, 0.498 centimeter, and 0.550 centimeter. Which ant was the longest? Which ant was the shortest?

How can you use the math you know to compare and order the decimals? Tell how you decided.

Look Back! Be Precise What are the lengths of the ants in order from least to greatest?

Visual Learning Bridge

Essential Question How Can You Compare Decimals?

A.
Scientists collected and measured the lengths of different cockroach species. Which cockroach had the greater length, the American or the Oriental cockroach?

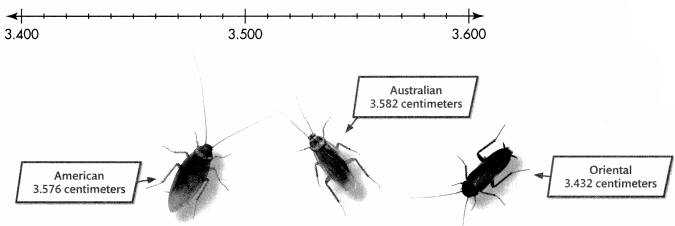
Comparing decimals is like comparing whole numbers!

B.
Step 1
Line up the decimal points.
Start at the left.
Compare digits of the same place value.
3.576
3.432

C.
Step 2
Find the first place where the digits are different.
3.576
3.432

D.
Step 3
Compare.
5 > 4
0.5 > 0.4
So, 3.576 > 3.432.
The American cockroach is longer than the Oriental cockroach.

Convince Me! Critique Reasoning Valerie said, “12.68 is greater than 12.8 because 68 is greater than 8.” Is she correct? Explain.

Answer: No, 12.8 is greater than 12.68

Explanation:
Given  : 12.68 is greater than 12.8
We have given 12.68 and 12.8
In 12.68,
Tens place is 1,
Ones place is 2,
Tenth place is 6,
Hundredth place is 8.
In 12.8,
Tens place is 1 .
Ones place is 2,
Tenth place is 8,
So, We can see Tens place and ones place of both number are same but tenth place of 12.8 is greater than 12.68.
Therefore, 12.8 is greater than 12.68 . 

Another example
Order the cockroaches from least to greatest length.
Step 1
Write the numbers, lining up the decimal points. Start at the left. Compare digits of the same place value.
3.576
3.582
3.432 is the least.

Step 2
Write the remaining numbers, lining up the decimal points. Start at the left. Compare.
3.576
3.582
3.582 is greater than 3.576.

Step 3
Write the numbers from least to greatest.
3.432 3.576 3.582
From least to greatest lengths are the Oriental, the American, and the Australian.

Guided Practice

Do You Understand?

Question 1.
Scientists measured a Madeira cockroach and found it to be 3.44 centimeters long. Toby says that the Madeira is shorter than the Oriental because 3.44 has fewer digits than 3.432. Is he correct? Explain.
Answer: 3.44cm cockroach is the longest.

Explanation:
Given,  3.44  and  3.432
3.44
3.432
Comparing the numbers after decimals,
4 > 3
So, 3.44cm cockroach is the longest.

Do You Know How?

In 2 and 3, write >, <, or = for each .

Question 2.
3.692 3.697
Answer: 3.692 < 3.697

Explanation:
Given,  3.692  and  3.697
3.692
3.697
Comparing the numbers after decimals, we have
2 < 7
So, 3.692 < 3.697.

Question 3.
7.216 7.203
Answer:  7.216 > 7.203.

Explanation:
Given,  7.216  and  7.203
7.216
7.203
Comparing the numbers after decimals, we have
1 > 0
So, 7.216 > 7.203.

In 4 and 5, order the decimals from least to greatest.

Question 4.
5.540, 5.631, 5.625
Answer: The order from least to greatest is  5.540, 5.625, 5.631.

Explanation:
Given, 5.540, 5.631, 5.625
lining up the decimal points.
5.540, is the least
5.631,
5.625,
Comparing the numbers after decimals, we have
5.631,
5.625,
Compare digits of the same place value.
3 > 2
5.631 is the greatest
So, The order from least to greatest is  5.540, 5.625, 5.631.

Question 5.
0.675, 1.529, 1.35, 0.693
Answer: The order from least to greatest is 0.675, 0.693, 1.35, 1.529.

Explanation:
Given, 0.675, 1.529, 1.35, 0.693
lining up the decimal points.
0.675,
1.529,
1.35,
0.693
Comparing the numbers after decimals, we have
0.675,
0.693,
Compare digits of the same place value.
7 < 9
0.675 is the less than 0.693
Then 1.529,
1.35,
Compare digits of the same place value.
5 > 3
1.529 is greater than 1.35
So, The order from least to greatest is 0.675, 0.693, 1.35, 1.529.

Independent Practice

In 6-8, compare the two numbers. Write >, <, or = for each .

Question 6.
0.890 0.890
Answer: 0.890 = 0.890

Explanation:
Given,  0.890  and 0.890
0.890
0.890
Comparing the numbers after decimals, we have
All the numbers are equal
So, 0.890 = 0.890.

Question 7.
5.733 5.693
Answer: 5.733 > 5.693.

Explanation:
Given,  5.733  and  5.693
5.733
5.693
Comparing the numbers after decimals, we have
7 > 6
So, 5.733 > 5.693.

Question 8.
9.707 9.717
Answer: 9.707 < 9.717

Explanation:
Given,  9.707  and  9.717
lining up the decimal points
9.707
9.717
Comparing the numbers after decimals, we have, Compare digits of the same place value.
0 < 1
So, 9.707 < 9.717.

In 9 and 10, order the decimals from greatest to least.

Question 9.
878.403, 887.304,887.043
Answer: The order from least to greatest is 878.403 ,887.043 , 887.304.

Explanation:
Given, 878.403, 887.304,887.043
lining up the decimal points.
878.403, is the least
887.304,
887.043
Comparing the numbers after decimals, we have
887.304,
887.043
Compare digits of the same place value.
3 > 0
887.304 is greater than 887.043
So, The order from least to greatest is 878.403 ,887.043 , 887.304.

Question 10.
435.566, 436.565, 435.665
Answer: The order from least to greatest is 435.566, 435.665 , 436.565.

Explanation:
Given, 435.566, 436.565, 435.665
lining up the decimal points.
435.566,
436.565, is the greatest
435.665
Comparing the numbers after decimals, we have
435.566,
435.665
Compare digits of the same place value.
5 < 6
435.566 is less than 435.665
So, The order from least to greatest is 435.566, 435.665 , 436.565.

Problem Solving

Question 11.
Critique Reasoning Explain why it is not reasonable to say that 4.23 is less than 4.135 because 4.23 has fewer digits after the decimal point than 4.135.
Answer: 4.23 is greater than 4.135.

Explanation:
Given, 4.23 and 4.135
lining up the decimal points.
4.23,
4.135
Comparing the numbers after decimals, we have ,Compare digits of the same place value.
2 < 1
So, 4.23 is greater than 4.135.

Question 12.
Number Sense Carlos wrote three numbers between 0.33 and 0.34. What numbers could Carlos have written?
Answer: there can be any three numbers mentioned Below between 0.33 and 0.34.

Explanation:
Given, three numbers between 0.33 and 0.34
The numbers between the 0.33 and 0.34 are 0.331, 0.332, 0.333, 0.334, 0.335, 0.336, 0.337, 0.338 and 0.339,
Then the next number will be 0.340 that is same as 0.34
So, there can be any three numbers mentioned above between 0.33 and 0.34.

Question 13.
Vocabulary Draw lines to match each decimal on the left to its equivalent decimal on the right.

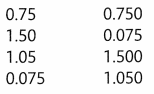
Answer: The given decimals are compared to its nearest decimals by place value method.

Explanation:

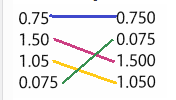
Question 14.
Is 0.5 greater than or less than \(\frac{6}{10}\)? Draw a number line to show your answer.
Answer: 0.5 is < 0.6

Explanation:

Given,  0.5 and \(\frac{6}{10}\)
We can write \(\frac{6}{10}\) as 0.6 in decimal form,
Compare digits of the same place value.
5 < 6
So, 0.5 is < 0.6

Question 15.
Higher Order Thinking Ana’s gymnastics scores were posted on the scoreboard in order from highest to lowest score. One digit in her floor score is not visible. List all the possible digits for the missing number.

Answer: The possible digits are 1 , 2 , 3 , 4

Explanation:
Given,
The floor score must be higher than 15.133 and lower than 15.500
Then all the possible scores are: 15.166 , 15.266 , 15.366 and 15.466
Because 15.166 > 15.133 and 15.466 < 15.500
Then all the possible digits are 1 , 2 , 3 , 4 

Question 16.
Marcia’s vault score is 15.050. How does it compare to Ana’s vault score?
Answer: Marcia’s vault score is less than Ana’s vault score

Explanation:
Given, Marcia’s vault score is 15.050
Ana’s vault score is 15.500
Lining up the decimal points.
15.050
15.500
Comparing the numbers after decimals, we have ,Compare digits of the same place value.
0 < 5
So, 15.050 is less than 15.500.
Finally, Marcia’s vault score is less than Ana’s vault score

Assessment Practice

Question 17.
Which statements correctly compare two numbers?
0.1 <0.125
0.2 < 0.125
125 > 0.13
0.125 > 0.12
0.126 < 0.125
Answer: 0.1 < 0.125 , 125 > 0.13 , 0.125 > 0.12 .

Explanation:
Compare digits of the same place value.
0.1 < 0.125 , because 0 < 2
125 > 0.13 , because .0 > 0.
0.125 > 0.12 . because 5 > 0

Question 18.
Cara weighed 4.16 pounds of apples at the grocery store. Which numbers make the statement true? > 4.16
04.15
04.19
4.2
4.09
4.1
Answer: 04.15

Explanation:
Given, Cara weighed 4.16 pounds of apples at the grocery store
4.16 and 04.15 are the closest decimals
Compare digits of the same place value.
5 < 6
So, the immediate number of 4.16 is 04.15.

Lesson 1.6 Round Decimals

Activity

Solve & Share

In science class, Marci recorded numbers from an experiment as 12.87, 12.13, 12.5, and 12.08. Which numbers are closer to 12? Which are closer to 13? How can you tell?

You can use structure to help determine what number is halfway between two whole numbers. Show your work!

Look Back! What is the halfway point between 12 and 13? Is that point closer to 12 or 13?

Visual Learning Bridge

Essential Question How Can You Round Decimals?

A.
Rounding replaces one number with another number that tells about how many or about how much. Round 2.36 to the nearest tenth. Is 2.36 closer to 2.3 or 2.4?

A number line can help you round a decimal.

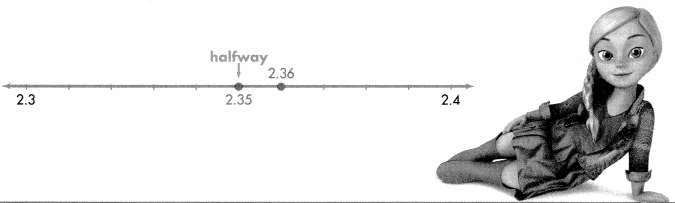
B.
Step 1
Find the rounding place. Look at the digit to the right of the rounding place.
2.36

C.
Step 2
If the digit is 5 or greater, add 1 to the rounding digit. If the digit is less than 5, leave the rounding digit alone.
Since 6 >5, add 1 to the 3.

D.
Step 3
Drop the digits to the right of the rounding digit.
2.36 rounds to 2.4

Rounding can help (you find which tenth or hundredth a decimal is closest to.

Convince Me! Critique Reasoning Carrie said, “448 rounds to 500 because 448 rounds to 450 and 450 rounds to 500.” Is she correct? Explain. Use the number line in your explanation.

Answer: No

Explanation:
Given, 448 rounds to 500 because 448 rounds to 450 and 450 rounds to 500.”
The nearest number to 448 is 450 and that is correct but,
450 is not near the number 500 ,
The difference between these numbers is 50 ,
So, Carrie is wrong.

Another example
Round 3.2 to the nearest whole number. Is 3.2 closer to 3 or 4?

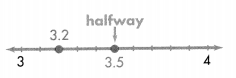
Step 1
Find the rounding place. Look at the digit to the right of the rounding place.
3.2
Step 2
If the digit is 5 or greater, add 1 to the rounding digit. If the digit is less than 5, leave the rounding digit alone. Since 2 < 5, leave 3 the same.
Step 3
Drop the digits to the right of the decimal point. Drop the decimal point.
3.2 rounds to 3.

Guided Practice

Do You Understand?

Question 1.
To round 74.58 to the nearest tenth, which digit do you look at? What is 74.58 rounded to the nearest tenth?
Answer: the nearest tenth to 74.58 is 74.6

Explanation:
Given, To round 74.58 to the nearest tenth,
Find the rounding place. Look at the digit to the right of the rounding place.
8 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point.
74.6
So, the nearest tenth to 74.58 is 74.6

Question 2.
A car-rental service charges customers for the number of miles they travel, rounded to the nearest whole mile. George travels 40.8 miles. For how many miles will he be charged? Explain.
Answer: He will be charged for 41 miles

Explanation:
Given, George travels 40.8 miles.
Find the rounding place. Look at the digit to the right of the rounding place.
8 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point.
The nearest to 40.8 is 41
So, He will be charged for 41 miles

Do You Know How?

In 3-10, round each number to the place of the underlined digit.

Question 3.
16.5
Answer: 17

Explanation:
Given, 16.5
6 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 17
The rounding number is 17.

Question 4.
56.1
Answer: 56

Explanation:
Given, 56.1
6 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 56
The rounding number is 56.

Question 5.
1.32
Answer: 1.3

Explanation:
Given, 1.32
3 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 1.3
The rounding number is 1.3.

Question 6.
42.78
Answer: 42.8

Explanation:
Given, 42.78
7 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 42.8
The rounding number is 42.8.

Question 7.
1.652
Answer: 1.65

Explanation:
Given, 1.652
5 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 1.65
The rounding number is 1.65.

Question 8.
582.04
Answer: 582.0

Explanation:
Given, 582.04
4 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 582.0
The rounding number is 582.0.

Question 9.
80,547.645
Answer: 80,547.65

Explanation:
Given, 80,547.645
4 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 80,547.65
The rounding number is 80,547.65.

Question 10.
135,701.949
Answer: 135,701.9

Explanation:
Given, 135,701.949
9 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 135,701.9
The rounding number is 135,701.9.

Independent Practice

In 11-14, round each decimal to the nearest whole number.

Question 11.
4.5
Answer: 5

Explanation:
Given, 4.5
4 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 5
The rounding number is 5.

Question 12.
57.3
Answer: 57

Explanation:
Given, 57.3
7 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 57
The rounding number is 57.

Question 13.
34.731
Answer: 34.73

Explanation:
Given, 34.731
3 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 34.73
The rounding number is 34.73.

Question 14.
215.39
Answer: 215.4

Explanation:
Given,215.39
3 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 215.4
The rounding number is 215.4.

In 15-18, round each number to the place of the underlined digit.

Question 15.
7.158
Answer: 7.2

Explanation:
Given, 7.158
1 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 7.2
The rounding number is 7.2.

Question 16.
0.758
Answer: 0.76

Explanation:
Given, 0.758
5 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 0.76
The rounding number is 0.76.

Question 17.
6.4382
Answer: 6.44

Explanation:
Given, 6.4382
3 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 6.44
The rounding number is 6.44.

Question 18.
84.732
Answer: 84.7

Explanation:
Given, 84.732
7 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 84.7
The rounding number is 84.7.

Problem Solving

Question 19.
The picture at the right shows the length of an average American alligator. What is the length of the alligator rounded to the nearest tenth?

Answer: 4.4 is the length of the alligator rounded to the nearest tenth.

Explanation:
Given, 4.39
3 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 4.4
The rounding number is 4.4.
So,4.4  is the length of the alligator rounded to the nearest tenth

Question 20.
Name two different numbers that round to 8.21 when rounded to the nearest hundredth.
Answer: 8.211 and 8.212

Explanation:
Given, 8.21 rounded to the nearest hundredth,
2 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 8.211 and 8.212
The rounding number is 8.211 and 8.212.

Question 21.
Number Sense To the nearest hundred, what is the greatest whole number that rounds to 2,500? the least whole number?
Answer: 2,499 and 2,491.

Explanation:
Given, 2,500
The greatest whole number to nearest hundred of 2,500 is 2,499
And, The less whole number to nearest hundred of 2,500 is 2,491

Question 22.
Draw all of the lines of symmetry in the figure shown below.

Answer: There are 2 line lines of symmetry.

Explanation:

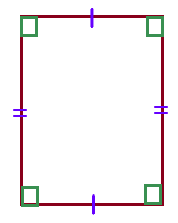
The given figure is in the form of a Rectangle
So, it has 2 lines of symmetry.

Question 23.
Higher Order Thinking Emma needs 2 pounds of ground meat to make a meatloaf. She has one package with 2.36 pounds of ground meat and another package with 2.09 pounds of ground meat. She uses rounding and finds that both packages are close to 2 pounds. Explain how Emma can choose the package closer to 2 pounds.
Answer: She can use the package of 2.09 because it is close to 2 pounds.

Explanation:
Given, 2.09 and 2.36
For 2.09 , 0 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point. 2.1
For 2.36, 3 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point. 2.4
So, She can use the package of 2.09 because it is close to 2 pounds.

Question 24.
Make Sense and Persevere Robert slices a large loaf of bread to make 12 sandwiches. He makes 3 turkey sandwiches and 5 veggie sandwiches. The rest are ham sandwiches. What fraction of the sandwiches Robert makes are ham?
Answer: \(\frac{3}{12}\), \(\frac{5}{12}\), \(\frac{4}{12}\).

Explanation:
Given, Robert slices a large loaf of bread to make 12 sandwiches,
He makes 3 turkey sandwiches and 5 veggie sandwiches
The rest are ham sandwiches.
The number of turkey sandwiches are \(\frac{3}{12}\),
The number of veggie sandwiches are \(\frac{5}{12}\),
The number of ham sandwiches are \(\frac{4}{12}\),
Total 12 sandwiches are there made by Robert.

Question 25.
Algebra After buying school supplies, Ruby had $32 left over. She spent $4 on notebooks, $18 on a backpack, and $30 on a new calculator. How much money, m, did Ruby start with? Write an equation to show your work.
Answer: Ruby started with $84.

Explanation:
Given, Ruby had $32 left over.
She spent $4 on notebooks, $18 on a backpack, and $30 on a new calculator.
The total money spent =  $4 + $18  +  $30  = $52
Add the money she had left over and money she had spent
we have, $52 + $32 = $84
So, Ruby started with $84.

Assessment Practice

Question 26.
Find two numbers that round to 35.4 when rounded to the nearest tenth. Write the numbers in the box.

Answer: 35.45 and 35.391

Explanation:
Given, 35.40
4 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 35.45
if the digit is 5 or greater, add 1 to the rounding digit. 35.391
The rounding number is 35.45 and 35.391.

Lesson 1.7 Look For and Use Structure

Problem Solving

Activity

Solve & Share
Angie volunteers in the school library after school. The librarian gave her a stack of books and told her to use the number on each book to shelve it where it belongs.
How can Angie arrange the books in order from least to greatest to make shelving them easier?

Thinking Habits
Be a good thinker! These questions can help you.
• What patterns can I see and describe?
• How can I use the patterns to solve the problem?
• Can I see expressions and objects in different ways?
• What equivalent expressions can I use?

Look Back! Use Structure Explain why 323.202 is less than 323.21 even though 202 is greater than 21.

Answer: Because , when rounding the decimals we have to look for the place values to decide which is greater or least.

Explanation:
Given, 323.202
0 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 323.21
The rounding number is 323.21.

Visual Learning Bridge

Essential Question
How Can You Use Structure to Solve Problems?

A.
Analyze the chart. What do you notice that can help you complete the chart?

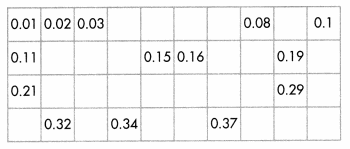
What do I need to do to solve this problem?

I can use the structure of the decimal place-value system to complete the chart.

You can look for patterns to find the missing numbers.

B.
How can I make use of structure to solve this problem?
I can
• find and describe patterns.
• use the patterns to see how the numbers are organized.
• analyze patterns to see the structure in the table.
• break the problem into simpler parts.

C.
Solve
Here’s my thinking…

As you move down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same, except for the last number, while the hundredths increase by 1.

Convince Me! Use Structure Write the missing numbers. Explain how you can use structure to find the last number in the bottom row.

Answer: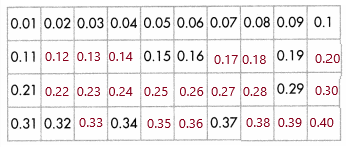   

Explanation:
Because, down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same,
except for the last number, while the hundredths increase by 1.

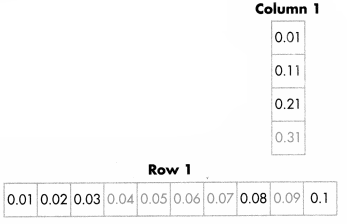
Guided Practice
Use Structure Each of these grids is a part of a decimal number chart similar to the one on page 30.

You can use what you know about place value when you look for patterns with decimals.

Question 1.
Describe the pattern for moving from a pink square to a green square. Then write the missing numbers.

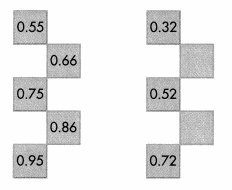
Answer:

Explanation:
Because, down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same,
except for the last number, while the hundredths increase by 1.

Question 2.
How can you use patterns to find the number that would be in the box below 0.52?
Answer: the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same,
except for the last number, while the hundredths increase by 1. and completing the pattern.

Independent Practice

Use Structure Pamela is hiking. When she returns to camp, she passes the mile markers shown at the right.

Question 3.
Explain how you can use structure to find the decimal numbers that will be shown on the next four mile markers.

Answer:  the next four mile markers will be 2.2 , 2.1 , 2.0 , 1.9

Explanation:

Moving from left to right in the rows, tenths stay the same,
except for the last number, while the hundredths increase by 1
So, the next four mile markers will be 2.2 , 2.1 , 2.0 , 1.9

Question 4.
Pamela stops at the 1.8 mile marker. Where will she be if she walks one tenth of a mile towards camp? one mile towards camp? Explain.
Answer: she will be on 0.18 if she walks one tenth of a mile towards camp and 1.7 if she walks one mile towards the camp.

Explanation:
Given, 1.8
8 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 1.7
The reducing mile as reaching out for camp is 1.7
If she will be on 0.18 if she walks one tenth of a mile towards camp, That is 1.8 × \(\frac{1}{10}\)
Finally, she will be on 0.18 if she walks one tenth of a mile towards camp and 1.7 if she walks one mile towards the camp.

Problem Solving

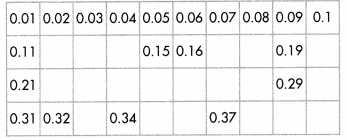
Performance Task

Thousandths Chart
The students in Ms. Lowell’s class wrote a thousandths decimal chart on the board. Some of the numbers got erased.

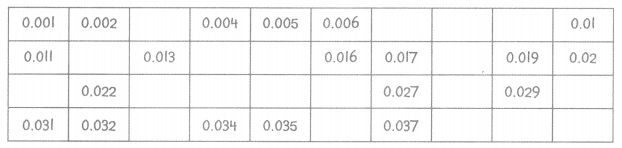
Answer: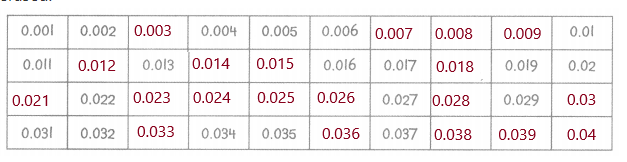

Explanation:
Because, down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same,
except for the last number, while the hundredths increase by 1.

Question 5.
Use Structure Describe the pattern for moving across a row from left to right.
Answer:

Explanation:
Moving from left to right in the rows, tenths stay the same, except for the last number, while the hundredths increase by 1.

You can use structure to decide if decimal numbers are following a pattern.

Answer:

Explanation:
Above question has the figure, we have the decimal numbers following a pattern of  tenths stay the same, except for the last number, while the hundredths increase by 1.

Question 6.
Be Precise How does the pattern change in the last square of each row?
Answer: As you move down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.

Explanation:

As you move down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.

Question 7.
Use Structure Describe the pattern for moving down a column.
Answer: As you move down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.

Explanation:

As you move down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.

Question 8.
Use Repeated Reasoning Write the missing numbers in the decimal chart above.
Answer:

Explanation:
Because, down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same,
except for the last number, while the hundredths increase by 1.

Question 9.
Use Structure Suppose the students add to the chart. Write the missing numbers in the row and the column below.

Answer:  The complete chart is as follows,

Explanation:
Because, down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same,
except for the last number, while the hundredths increase by 1.

Topic 1 Fluency Review

Activity

Find a Match

Work with a partner. Point to a clue. Read the clue. Look below the clues to find a match. Write the clue letter in the box above the match. Find a match for every clue.

Clues
A The sum is between 15,000 and 20,000.
B The difference is less than 10,000.
C The difference is between 41,000 and 42,000.
D The sum is exactly 52,397.
E The difference is between 82,000 and 84,000.
F The sum is greater than 79,000.
G The sum is exactly 52,407,
H The difference is exactly 42,024.

Answer:

Topic 1 Vocabulary Review

Understand Vocabulary

Glossary

Word List
• base
• equivalent decimals
• expanded form
• exponent
• power
• thousandths
• value

Choose the best term from the Word List. Write it on the blank.

Question 1.
Decimal numbers that name the same part of a whole or the same point on a number line are called ____
Answer: Decimal numbers that name the same part of a whole or the same point on a number line are called Equivalent decimals

Question 2.
The ____ of a digit in a number depends on its place in the number.
Answer: The value of a digit in a number depends on its place in the number.

Question 3.
The product that results from multiplying the same number over and over is a(n) ____ of that number.
Answer:  The product that results from multiplying the same number over and over is a(n) POWER of that number.

Question 4.
A digit in the hundredths place has ten times the value of the same digit in the ___ place.
Answer: A digit in the hundredths place has ten times the value of the same digit in the thousandths place.

Question 5.
In 10⁵, the number 10 is the _____.
Answer: In 10⁵, the number 10 is the BASE.

Draw a line from each number in Column A to the same number in Column B.

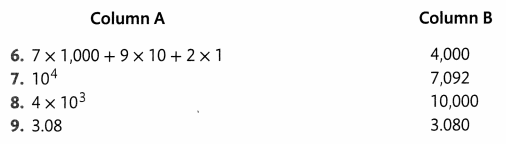
Answer:

Use Vocabulary in Writing

Question 10.
Explain why each 8 in the number 8.888 has a different value. Use one or more terms from the Word List in your explanation.
Answer:  Because of its place value.

Explanation:
Given, 8.888
The first 8 has the place value of tenths, The second 8 has the place value of hundredths and the final 8 has the place value of thousandths.

Set A
pages 5-8
How can you write 7,000 using exponents?
7,000 = 7 × 10 × 10 × 10 = 7 × 10³
So, using exponents, you can write 7,000 as 7 × 10³

Remember the number of zeros in the product is the same as the exponent.

Find each product.

Question 1.
9 × 10¹
Answer: 90

Explanation:
9 × 10¹ = 9 × 10 = 90

Question 2.
8 × 1,000
Answer: 8,000

Explanation:
8 × 10 × 10 × 10 = 8,000

Question 3.
5 × 10²
Answer: 5 × 10² = 500

Explanation:
5 × 10² =  5 × 10 × 10  = 500

Question 4.
2 × 10⁵
Answer: 2 × 10⁵  = 2,00,000

Explanation:
2 × 10⁵  = 2 × 10 × 10 × 10 × 10 × 10 = 2,00,000

Set B
pages 9-12
Write the number name and tell the value of the underlined digit for 930,365.
Nine hundred thirty thousand, three hundred sixty-five
Since the 0 is in the thousands place, its value is 0 thousands, or 0.
Use digital tools to solve these and other problems.

Remember you can find the value of a digit by its place in a number.

Write the number name and tell the value of the underlined digit.

Question 1.
9,000,000
Answer: Nine million

Explanation:
the value of the underlined digit is in millions place.

Question 2.
485,002,000
Answer: four hundred and eighty five million and two thousands

Explanation:
the value of the underlined digit is in millions place.

Question 3.
25,678
Answer: Twenty five thousand and six hundred and seventy eight

Explanation:
the value of the underlined digit is in thousands place.

Question 4.
17,874,000
Answer: seventeen million and eight hundred and seventy four thousand

Explanation:
the value of the underlined digit is in ten millions place.

Set C
pages 13-16, 17-20
A place-value chart can help you write the standard form, expanded form, and number name for a decimal.

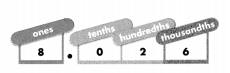
Standard form: 8.026
expanded form: 8 + 2 × \(\frac{1}{100}\) + 6 × \(\frac{1}{1,000}\)
Number name: Eight and twenty-six thousandths

Remember the word and is written for the decimal point.

Question 1.
How can you write 0.044 as a fraction?
How are the values of the two 4s related in 0.044?
Answer: \(\frac{44}{1,000}\) and The first 4 is in hundredths place and last 4 is in thousandths place

Explanation:
\(\frac{44}{1,000}\) = 0.044,
The first 4 is in hundredths place and last 4 is in thousandths place

Write each number in standard form.

Question 2.
eight and fifty-nine hundredths
Answer: 8.59

Question 3.
seven and three thousandths + 4. 3 + 2 × \(\frac{1}{10}\) + 4 × \(\frac{1}{1000}\)
Answer: 11.507

Explanation:
Given, seven and three thousandths + 4. 3 + 2 × \(\frac{1}{10}\) + 4 × \(\frac{1}{1000}\)
7.003 + 4.3 + [ 0.2 + 0.004]
= 11.303 + 0.204
= 11.507

Set D
pages 21-24 Compare. Write >, <, or =.

8. 45 8.47
Line up the decimal points. Start at the left to compare. Find the first place where the digits are different.
8.45
8.47 0.05 < 0.07
So, 8.45 < 8.47.

Remember that equivalent decimals, such as 0.45 and 0.450, can help you compare numbers.
Compare. Write >, <, or =.

Question 1.
0.584 0.58
Answer: 0.584 > 0.58

Explanation:
Given,  0.584 and 0.58
0.584
0.58
Comparing the numbers after decimals,
4 > 0
So, 0.584 > 0.58

Question 2.
9.327 9.236
Answer: 9.327 > 9.236

Explanation:
Given, 9.327 and 9.236
9.327
9.236
Comparing the numbers after decimals,
3 > 2
So, 9.327 > 9.236

Question 3.
5.2 5.20
Answer: 5.2 = 5.20

Explanation:
Given, 5.2 and 5.20
5.2
5.20
Comparing the numbers after decimals, we have
All the numbers are equal
So, 5.2 = 5.20

Question 4.
5.643 5.675
Answer: 5.643 < 5.675

Explanation:
Given, 5.643 and 5.675
5.643
5.675
Comparing the numbers after decimals, we have
4 < 7
So, 5.643 < 5.675

Question 5.
0.07 0.08
Answer: 0.07 < 0.08.

Explanation:
Given,  0.07 and 0.08
0.07
0.08
Comparing the numbers after decimals, we have
7 < 8
So, 0.07 < 0.08.

Set E
pages 25-28
Round 12.087 to the place of the underlined digit.
12.087 Look at the digit following the underlined digit. Look at 7.
Round to the next greater number of hundredths because 7 > 5.
12.087 rounded to the nearest hundredth is 12.09.

Remember that rounding a number means replacing it with a number that tells about how many or how much.
Round each number to the place of the underlined digit.

Question 1.
10.245
Answer: 10.2

Explanation:
Given, 10.245
2 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 10.2
The rounding number is 10.2.

Question 2.
73.4
Answer: 73

Explanation:
Given, 73.4
7 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 73
The rounding number is 73.

Question 3.
0.145
Answer: 0.1

Explanation:
Given, 0.145
1 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 0.1
The rounding number is 0.1.

Question 4.
3.999
Answer: 4

Explanation:
Given, 3.999
9 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 4
The rounding number is 4.

Question 5.
13.023
Answer: 13

Explanation:
2 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 13
The rounding number is 13.

Question 6.
45.398
Answer: 45

Explanation:
3 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 45
The rounding number is 45.

Set F
pages 29-32
Think about these questions to help you look for and use structure to understand and Explain patterns with decimal numbers.

Thinking Habits
• What patterns can I see and describe?
• How can I use the patterns to solve the problem?
• Can I see expressions and objects in different ways?
• What equivalent expressions can I use?

Remember to check that all of your answers follow a pattern.
Each grid is part of a decimal number chart. Write the missing numbers to complete the grids.

Question 1.

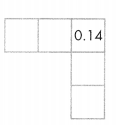
Answer:

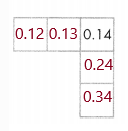
Explanation:
As you move down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same, except for the last number, while the hundredths increase by 1.

Question 2.

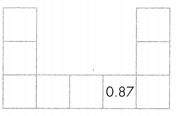
Answer:

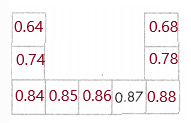
Explanation:
As you move down the columns, tenths increase by 1 while the Column 1 hundredths stay the same.
Moving from left to right in the rows, tenths stay the same, except for the last number, while the hundredths increase by 1.

Topic 1 Assessment Practice

Question 1.
Complete the sentences to make true statements.
6 is 100 times ____.
0.06 is 10 times ______.
60 is \(\frac{1}{100}\) of ____.
Answer: 600, 0.6, 0.6

Explanation:
6 × 100 = 600
0.06 × 10 = 0.6
60 × \(\frac{1}{100}\) = 0.6

Question 2.
A national park has eighty thousand, nine-hundred twenty-three and eighty-six hundredths acres of land. Which shows this in standard form?
A. 80,923.086
B. 80,923.68
C. 80,923.806
D. 80,923.86
Answer: A , that is 80,923.086

Explanation:
Because, the number name of 80,923.086 is eighty thousand, nine-hundred twenty-three and eighty-six hundredths

Question 3.
Which numbers have a digit in the ones place that is \(\frac{1}{10}\) the value of the digit in the tens place? Select all that apply.
9,077
9,884
1,303
1,055
3,222
Answer: 9,884 and  3,222

Explanation:
These numbers 9,884 and  3,222 have a digit in the ones place that is \(\frac{1}{10}\) the value of the digit in the tens place

Question 4.
Mrs. Martin has $7,000 in her savings account. Alonzo has \(\frac{1}{10}\) to as much money in his account as Mrs. Martin. How much money does Alonzo have in his account?
Answer: Amount Alonzo has is $ 700

Explanation:
he amount Martin has in her account is $ 7000
Alonzo has 1/10th the amount Martin has
Therefore Alonzo has \(\frac{1}{10}\) of 7000 ;
= 7000/10 = $ 700
Amount Alonzo has is $ 700 .

Question 5.
Select all the comparisons that are true.
04.15 > 4.051
1.054 > 1.45
5.14 < 5.041
5.104 < 5.41
5.014 < 5.41
Answer:  04.15 > 4.051, 5.104 < 5.41 and 5.014 < 5.41

Explanation:
Because of their place value ,
04.15 > 4.051
1 > 0
So, 04.15 > 4.051

5.104 < 5.41
1 < 4
So, 5.104 < 5.41

5.014 < 5.41
0 < 4
So, 5.014 < 5.41

Question 6.
Luke shaded 20 squares on his hundredths grid. Bekka shaded 30 squares on her hundredths grid.

A. Whose grid represents the larger decimal?
B. Write two decimals equivalent to Luke’s decimal.
Answer: 0.2 < 0.3, The two decimals equivalent to Luke’s decimal are 0.20 and 0.21

Explanation:
Given, Luke shaded 20 squares on his hundredths grid, \(\frac{20}{100}\) that is 0.2
Bekka shaded 30 squares on her hundredths grid. \(\frac{30}{100}\)that is 0.3
Bekka has largest decimal.

The two decimals equivalent to Luke’s decimal are 0.20 and 0.21

Question 7.
Which statements about the values of 2.044 and 20.44 are true? Select all that apply.
2.044 is \(\frac{1}{10}\) of 20.44.
2.044 is \(\frac{1}{100}\) of 20.44.
20.44 is 10 times 2.044.
20.44 is 100 times 2.044.
2.044 is 10 times 20.44.
Answer:  20.44 is 10 times 2.044.

Explanation:
Given, 20.44 is 10 times 2.044.
20.44 × 10 = 2.044.

Question 8.
The weight of Darrin’s phone is 3.405 ounces. What is 3.405 written in expanded form?
A. 3 × 1 + 4 × \(\frac{1}{10}\) + 5 × \(\frac{1}{1,000}\)
B. 3 × 10 + 4 × \(\frac{1}{10}\) + 5 × \(\frac{1}{1,000}\)
C. 3 × 10 + 4 × \(\frac{1}{10}\) + 5 × \(\frac{1}{100}\)
D. 3 × 1 + 4 × \(\frac{1}{100}\) + 5 × \(\frac{1}{1,000}\)
Answer:  D

Explanation:
Given, 3.405
The expanded form, 3 × 1 + 4 × \(\frac{1}{100}\) + 5 × \(\frac{1}{1,000}\)
= 3 +0.04 + 0.005
= 3.405

Question 9.
Elaine has a piece of wire that is 2.16 meters long. Dikembe has a piece of wire that is 2.061 meters long. Whose piece of wire is longer? How can you tell?
Answer: Dikembe has the longest wire.

Explanation:
Given, 2.16 and 2.061
2.16
2.061
Comparing the place values of the digits after decimal
1 > 0
So, 2.16 > 2.061
Dikembe has the longest wire.

Question 10.
In a basketball tournament, Dimitri averaged 12.375 rebounds per game. What is 12.375 written in expanded form? How is it written with number names?
Answer: The expanded form is (12 × 1) + {3 × \(\frac{1}{10}\) + 7 × \(\frac{1}{100}\) + 5 × \(\frac{1}{1,000}\)}

Explanation:
Given, 12.375
The expanded form is (12 × 1) + {3 × \(\frac{1}{10}\) + 7 × \(\frac{1}{100}\) + 5 × \(\frac{1}{1,000}\)}
12 + 0.3 + 0.07 + 0.005
= 12.375.
The number name is twelve thousand and three hundred and seventy five.

Question 11.
The numbers below follow a pattern.
0.006 0.06 0.6 6 ____ _____
A. What are the next two numbers in the pattern?
B. What is the relationship between the terms in the pattern?
Answer:  60 and 600 , The terms relate to each other in that the next term is 10 times the previous term.

Explanation:
Relationship between term: The next term is ten times the previous term.
0.006 = 6/1000
0.06 = 6/100
0.6 = 6/10
6 = 6/1
This is a geometric sequence, where the common ratio is 10. 0.6/0.06 = 6/0.6 = 0.06/0.006 = 10
To get next number we simply multiply the previous number by 10.
The terms relate to each other in that the next term is 10 times the previous term. 

Question 12.
Kendra and her horse completed the barrel racing course in 15.839 seconds. What is this number rounded to the nearest tenth? Explain how you decided.
Answer: The rounding number is 16.

Explanation:
Given, 15.839
5 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 16
The rounding number is 16.

Topic 1 Performance Task

Fruits and Vegetables
Henry recorded how many pounds of fruits and vegetables his family bought during the past two months.

Question 1.
Pick four fruits and list them in the table below.
Part A
Round each fruit’s weight to the nearest 0.1 pound. Write the rounded weight in the next column.

Answer:

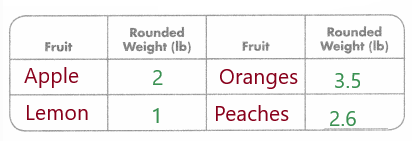
Part B
Explain how you rounded the weights of the fruits.
Answer:  detailed explanation is given below.

Explanation:
For Apples, given 2.068
5 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 2
The rounding number is 2.

For Blueberries 1.07
0 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 1.1
The rounding number is 1.1.

For lemons 1.031
0 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 1
The rounding number is 1.

For oranges 3.502
0 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 3.5
The rounding number is 3.5.

For peaches 2.608
0 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 2.6
The rounding number is 2.6.

For pears 3.592
5 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 3.6
The rounding number is 3.6.

Question 2.
Pick four vegetables and list them in the table below.

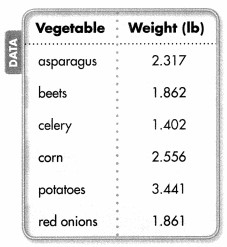
Part A
Round each vegetable’s weight to the nearest 0.01 pound. Write the rounded weight in the next column.

Answer:

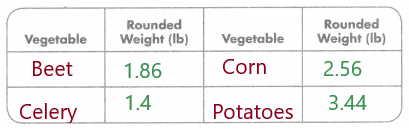
Part B
Explain how you rounded the weights of the vegetables.
Answer: Detailed explanation is given below

Explanation:

For Beets 1.862
6 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 1.86
The rounding number is 1.86.

For Celery 1.402
0 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 1.4
The rounding number is 1.4.

For Corn 2.556
5 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 2.56
The rounding number is 2.56.

For potatoes 3.441
4 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 3.44
The rounding number is 3.44.

Question 3.
Use <, >, or= to compare the weights of blueberries and lemons.
Answer:

Question 4.
When rounded to the nearest hundredth, two items will round to the same decimal. What two items are they?
Answer:

Question 5.
How does writing the weight for potatoes in expanded form show why the same digit can have different values?
Answer: Because of the place value of the numbers in the decimals

Explanation:
For potatoes 3.441
4 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 3.44
The rounding number is 3.44.

The first 4 has the place value of tenths and the last 4 has the place value of hundredths.

Question 6.
What is the relationship between the values of the two 4s in the weight of the potatoes?
Answer: The first 4 has the place value of tenths and the last 4 has the place value of hundredths. and the first 4 is ten times the value of second 4.

Explanation:

For potatoes 3.441
4 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 3.44
The rounding number is 3.44.

The first 4 has the place value of tenths and the last 4 has the place value of hundredths.
and the first 4 is ten times the value of second 4.

Question 7.
Write the number of pounds of celery Henry’s family bought using number names and in expanded form.
Answer: The number name is 1.4 pounds
The expanded form is 14 × \(\frac{1}{10}\)

Explanation:
For Celery 1.402
0 is the rounding place, the digit is less than 5, leave the rounding digit alone.
Drop the digits to the right of the decimal point, that is 1.4
The rounding number is 1.4.

The number name is 1.4 pounds
The expanded form is 14 × \(\frac{1}{10}\)

Question 8.
The store where Henry’s family shops sold 103 times as many pounds of corn as Henry’s family bought.
Answer:263.68 pounds have sold.

Explanation:
For Corn 2.556
5 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 2.56
The rounding number is 2.56.

Given, Henry’s family shops sold 103 times as many pounds of corn as Henry’s family bought.
2.56 × 103 = 263.68

Part A
How many pounds of corn did the store sell? Write your answer in standard form and with number names.

Answer: The number form is twenty six thousand and three hundred and sixty eight.

Explanation:
Store has sold 263.68
The number form is twenty six thousand and three hundred and sixty eight.

Part B
Explain how you found your answer.
Answer:  detailed explanation is given below

Explanation:
For Corn 2.556
5 is the rounding place, the digit is 5 or greater, add 1 to the rounding digit.
Drop the digits to the right of the decimal point, that is 2.56
The rounding number is 2.56.

Given, Henry’s family shops sold 103 times as many pounds of corn as Henry’s family bought.
2.56 × 103 = 263.68