enVision Math Common Core Grade 5 Answer Key Topic 11 Understand Volume Concepts

Go through the enVision Math Common Core Grade 5 Answer Key Topic 11 Understand Volume Concepts regularly and improve your accuracy in solving questions.

enVision Math Common Core 5th Grade Answers Key Topic 11 Understand Volume Concepts

Essential Questions: What is the meaning of volume of a solid? How can the volume of a rectangular prism be found?

enVision STEM Project: Everyday Energy
Do Research Use the Internet and other sources to learn more about these five types of energy: electrical, light, mechanical, sound, and thermal. Make a table of the various types of energy you use every day. Include at least one example of how you use each type of energy.

Journal: Write a Report Include what you found. Also in your report:
• Draw a diagram of your classroom and label where and how 3 types of energy are used.
• Estimate how far your desk is from a light energy source and add this dimension to your sketch.
• Use your diagram to make up and solve problems involving measurements such as the volume of your classroom.

Review What You Know

A-Z Vocabulary

Choose the best term from the box. Write it on the blank.

• compensation
• partial products
• rectangle
• unit fraction

Question 1.
Adjusting a number to make a computation easier and balancing the adjustment by changing another number is called ____
Answer:

Adjusting a number to make a computation easier and balancing the adjustment by changing another number is called compensation

Question 2.
A fraction with a numerator of 1 is called a ____
Answer:

A fraction with a numerator of 1 is called a  unit fraction

Question 3.
A quadrilateral with 2 pairs of parallel sides that are the same length and 4 right angles is a ____
Answer:

A quadrilateral with 2 pairs of parallel sides that are the same length and 4 right angles is a rectangle

Area
Find the area of each figure.

Question 4.

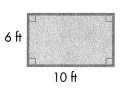
Answer:

From the figure,

Length = 10h

breadth =6h

Area of rectangle = Length x Breadth = 10h x 6h = 60h^2

Question 5.

Answer:

From the figure,

Length = 12cm

breadth = 8cm

Area of rectangle = Length x Breadth = 12cm x 8cm = 96cm^2

Operations

Find each product or quotient.

Question 6.
16 × 6
Answer:

96

Question 7.
3 × 42
Answer:

126

Question 8.
216 ÷ 3
Answer:

Question 9.
128 ÷ 4
Answer:

Question 10.
(5 × 6) × 3
Answer:

(5 × 6) × 3

(30) x 3

90

Question 11.
(6 × 6) × 6
Answer:

(6 × 6) × 6

(36) x 6

=196

Question 12.
Joanie has two 12-inch-long wood pieces and two 16-inch-long wood pieces. What is the combined length of the wood pieces?
A. 28 inches
B. 32 inches
C. 56 inches
D. 192 inches
Answer:

Given,

Number of 12 inch wood pieces = 2 = 12 x 2 = 24

Number of 16 inch wood pieces = 2 = 16 x 2 = 32

combined length of the wood pieces = 24 + 32 = 56

C. 56 inches is correct

Finding Area

Question 13.
Niko used square tiles to make a rectangle with 2 rows and 7 tiles in each row. Explain how you can find the area of the rectangle.
Answer:

Pick a Project

PROJECT 11A
How big are skyscrapers?
Project: Build a Skyscraper with Unit Cubes

PROJECT 11B
Why do cats climb into boxes?
Project: Design a Cat Tree

PROJECT 11C
Why are trucks useful for transporting packages?
Project: Model a Truck’s Capacity

3-ACT MATH PREVIEW

Math Modeling

Video

Fill ‘er Up

Before watching the video, think:
Ice is frozen below 32°F (or 0°C), but most picnics and cookouts happen when it’s warm out. The insulated walls of a cooler help keep ice from melting, which keeps my juice nice and cold!

Lesson 11.1 Model Volume

Activity

Solve & Share
Gina is building a rectangular prism out of sugar cubes for her art class project. She started by drawing a diagram of the rectangular prism that is 4 cubes high, 4 cubes long and 2 cubes wide. How many cubes does she use to make the prism? Solve this problem any way you choose.

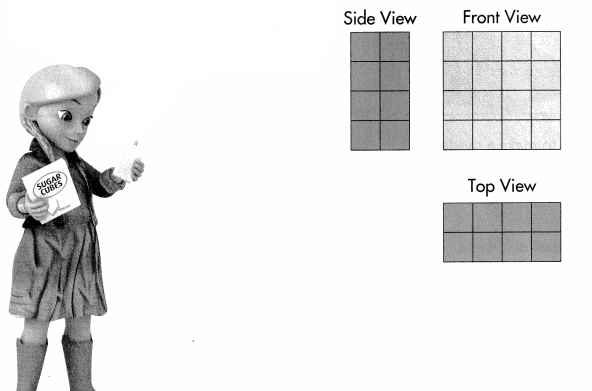
Use Appropriate Tools You can use cubes to build a rectangular prism and then draw a picture to show the different faces. Show your work!

Look Back! Gina decided to change her art project and build a rectangular prism that is 3 cubes long, 4 cubes wide, and 2 cubes high. Use the picture to determine the number of cubes she used.

Visual Learning Bridge

Essential Question How Can You Measure Space Inside a Solid Figure?

A.
Volume is the number of cubic units needed to pack a solid figure without gaps or overlaps. A cubic unit is the volume of a cube measuring 1 unit on each edge. What is the volume of this rectangular prism?

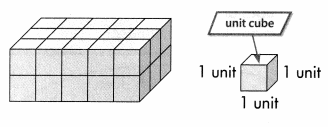
Each cube of a solid figure is 1 cubic unit.

B.
Use unit cubes to make a model.

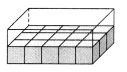
Count the number of cubes.
There are 15 unit cubes in the bottom layer. The volume of the bottom layer is 15 cubic units.

C.
There are two layers.

Multiply the volume of the bottom layer by 2.
The volume of the prism is 2 × 15 or 30 cubic units.

Convince Me! Reasoning in the picture below, how many unit cubes does it take to make the rectangular prism below without gaps or overlaps? How many 2-cube towers does it take to make the rectangular prism?

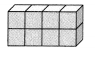
Guided Practice

Do You Understand?

Question 1.
Make a model of a rectangular prism with a bottom layer that is 3 cubes long by 3 cubes wide. Make a top layer that is the same as the bottom layer. Then draw a picture of your model. What is the volume?
Answer:

Each cube of a solid figure is 1 cubic unit.

There are 9 unit cubes in the bottom layer. The volume of the bottom layer is 9 cubic units.

Multiply the volume of the bottom layer by 2.

The volume of the prism is 2 × 9 or 18 cubic units.

Question 2.
A-Z Vocabulary What is the difference between a unit cube and a cubic unit?
Answer:

A unit cube, more formally a cube of side 1, is a cube whose sides are 1 unit long. The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units.

Do You Know How?

In 3 and 4, use unit cubes to make a model of each rectangular prism. Find the volume.

Question 3.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 4 unit cubes in the bottom layer. The volume of the bottom layer is 4 cubic units.

Multiply the volume of the bottom layer by 2.

The volume of the prism is 2 × 4 or 8 cubic units.

Question 4.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 12 unit cubes in the bottom layer. The volume of the bottom layer is 12 cubic units.

The volume of the prism is 12 × 1 or 12 cubic units.

Independent Practice

In 5-13, find the volume of each solid. Use unit cubes to help.

Question 5.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 9 unit cubes in the bottom layer. The volume of the bottom layer is 9 cubic units.

Multiply the volume of the bottom layer by 3.

The volume of the prism is 9 × 3 or 27 cubic units.

Question 6.

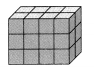
Answer:

Each cube of a solid figure is 1 cubic unit.

There are 8 unit cubes in the bottom layer. The volume of the bottom layer is 8 cubic units.

Multiply the volume of the bottom layer by 3.

The volume of the prism is 8 × 3 or 24 cubic units.

Question 7.

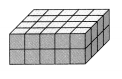
Answer:

Each cube of a solid figure is 1 cubic unit.

There are 20 unit cubes in the bottom layer. The volume of the bottom layer is 20 cubic units.

Multiply the volume of the bottom layer by 2.

The volume of the prism is 20 × 2 or 40 cubic units.

Question 8.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 8 unit cubes in the bottom layer. The volume of the bottom layer is 8 cubic units.

Multiply the volume of the bottom layer by 2.

The volume of the prism is 8 × 2 or 16 cubic units.

Question 9.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 2 unit cubes in the bottom layer. The volume of the bottom layer is 2 cubic units.

Multiply the volume of the bottom layer by 5.

The volume of the prism is 2 × 5 or 10 cubic units.

Question 10.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 6 unit cubes in the bottom layer. The volume of the bottom layer is 6 cubic units.

Multiply the volume of the bottom layer by 3.

The volume of the prism is 6 × 3 or 18 cubic units.

Question 11.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 12 unit cubes in the bottom layer. The volume of the bottom layer is 12 cubic units.

Multiply the volume of the bottom layer by 3.

The volume of the prism is 12 × 3 or 36 cubic units.

Question 12.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 12 unit cubes in the bottom layer. The volume of the bottom layer is 12 cubic units.

Multiply the volume of the bottom layer by 2.

The volume of the prism is 12 × 2 or 24 cubic units.

Question 13.

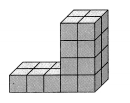
Answer:

Each cube of a solid figure is 1 cubic unit.

There are 10 unit cubes in the bottom layer. The volume of the bottom layer is 10 cubic units.

The remaining cubes are 4 x 3 or 12 and the volume is 12 cubic units

The volume of the prism is 10 + 12 or 22 cubic units.

Problem Solving

In 14-18, use the table.

Compare the volumes of the prisms. Write >, <, or = for each

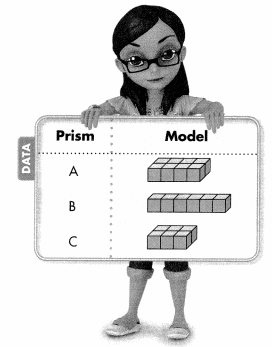
Question 14.
Prism A Prism B
Answer:

Prism A > Prism B

Question 15.
Prism B Prism C
Answer:

Prism B = Prism C

Question 16.
Prism C Prism A
Answer:

Prism C < Prism A

Question 17.
If you added another layer of unit cubes on top of Prism A, what would the volume of the new solid be in cubic units?
Answer:

Each cube of a solid figure is 1 cubic unit.

There are 8 unit cubes in the bottom layer. The volume of the bottom layer is 8 cubic units.

Multiply the volume of the bottom layer by 2.

The volume of the prism is 8 × 2 or 16 cubic units.

Question 18.
If you put Prism C on top of Prism A, what would the volume of the new solid be in cubic units?
Answer:

The volume of A is 16 cubic units

The volume of C is 6 cubic units

If you put Prism C on top of Prism A, Then the volume is 16 + 6 or 22 cubic units

Question 19.
Reasoning In an election, 471 people voted. Candidate B received \(\frac{2}{3}\) of the votes. How many votes did Candidate B receive?
Answer:

Number of votes voted = 471

Candidate B received 2/3 of the votes

Number of votes B received = 2/3 x 471 =314

Question 20.
Higher Order Thinking Ms. Kellson’s storage closet is 3 feet long, 3 feet wide, and 7 feet high. Can she fit 67 boxes that each have a volume of 1 cubic foot in her closet? Explain your answer.
Answer:

No.

Each cube of a solid figure is 1 cubic unit.

There are 9 unit cubes in the bottom layer. The volume of the bottom layer is 9 cubic units.

Multiply the volume of the bottom layer by 7.

The volume of the prism is 9 × 7 or 63 cubic units.

She can not fit 67 boxes that each have a volume of 1 cubic foot in her closet.

Assessment Practice

Question 21.
Natalie made the solid figures shown using unit cubes. Which statement about these models is true?

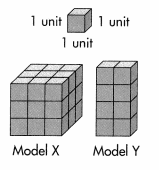
A. Model X and Model Y have the same volume.
B. The volume of Model X is 9 cubic units greater than the volume of Model Y.
C. The volume of Model X is 19 cubic units greater than the volume of Model Y.
D. The volume of Model X and Model Y combined is 45 cubic units.
Answer:

C. The volume of Model X is 19 cubic units greater than the volume of Model Y.

Visual Learning Bridge

Essential Question How Can You Use a Formula to Find Stor the Volume of a Rectangular Prism?

A.
Remember that volume is the number of cubic units (units”) needed to pack a solid figure without gaps or overlaps.
Find the volume of the rectangular prism if each cubic unit represents 1 cubic foot.

A formula is a rule that uses symbols to relate two or more quantities.

You can find the volume of a rectangular prism by counting cubes or using a formula.

B.
If the dimensions of a rectangular prism are given as length l, width w, and height h, then use this formula to find the volume V:

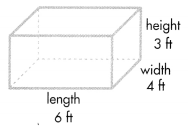
Volume = length × width × height
V = l × w × h
V = (6 × 4) × 3
V = 24 × 3
V = 72
The volume of the rectangular prism is 72 cubic feet or 72 ft³.

C.
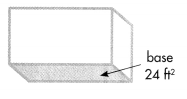
Another formula for the volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
V = 24 × 3
V = 72 ft³

Convince Me! Reasoning Give the dimensions of a different rectangular prism that also has a volume of 72 ft³. Explain how you decided.

Guided Practice

Do You Understand?

Question 1.
In the Example on page 462, could you first multiply the width by the height? Explain.
Answer:

Question 2.
A wooden block measures 5 centimeters tall, 3 centimeters wide, and 2 centimeters long. The area of the base is 6 centimeters. Draw a rectangular prism to show the block and label it. What is the volume of the block?
Answer:

Do You Know How?

In 3 and 4, find the volume of each rectangular prism.

Question 3.

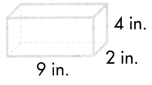
Answer:

Volume = length × width × height
V = l × w × h
V = (9 × 2) × 4
V = 18 × 4
V = 72
The volume of the rectangular prism is 72 cubic inch or 72 in³.

Question 4.

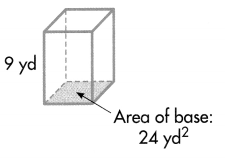
Answer:

The volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
V = 24 × 9
V = 216 yd³

Independent Practice

In 5-10, find the volume of each rectangular prism.

Question 5.

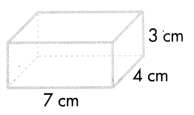
Answer:

Volume = length × width × height
V = l × w × h
V = (7 × 4) × 3
V = 28 × 3
V = 84

The volume of the rectangular prism is 84 cubic cm or 72 cm³.

Question 6.

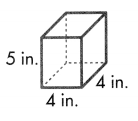
Answer:

Volume = length × width × height
V = l × w × h
V = (4 × 4) × 5
V = 16 × 5
V = 80
The volume of the rectangular prism is 80 cubic inch or 80 in³.

Question 7.

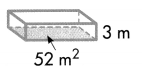
Answer:

The volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
V = 52 × 3
V = 156 m³

Question 8.

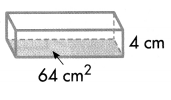
Answer:

The volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
V = 64 × 4
V = 256 cm³

Question 9.

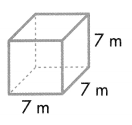
Answer:

Volume = length × width × height
V = l × w × h
V = (7 × 7) × 7
V = 49 × 7
V = 343
The volume of the rectangular prism is 343 cubic meter or 343 m³.

Question 10.

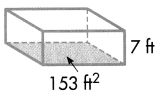
Answer:

The volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
V = 153 × 7
V = 1071 cm³

Problem Solving

Question 11.
The dictionary is 3 inches thick. What is the volume of the dictionary?

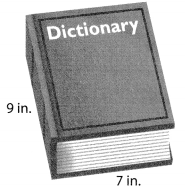
Answer:

Volume = length × width × height
V = l × w × h
V = (7 × 3) × 9
V = 21 × 9
V = 189
The volume of the rectangular prism is 189 cubic inch or 189 in³.

Question 7.

Question 12.
Higher Order Thinking Two ovens have measurements as shown. Which oven has a greater volume? How much greater is its volume? Show your work.

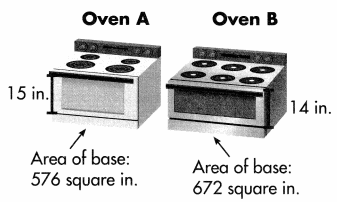
Answer:

The volume of a First oven is V = b × h, where b is the area of the base.
V = b × h.
V = 576 × 15
V = 8640 in³

The volume of a second oven is V = b × h, where b is the area of the base.
V = b × h.
V = 672 × 14
V = 9408 in³

The second oven has greater volume and 768 in³ greater than the first one.

Question 13.
The perimeter of an equilateral triangle is 51 feet. What is the length of one of its sides? Explain your work.
Answer:

The formula of the perimeter of an equilateral triangle is 3a, where a is the length of one side.

Given, The perimeter of an equilateral triangle is 51 feet

3a = 51

a = 51/3 = 17

Therefore, the length of one of its sides is 17 and all sides are equal.

Question 14.
Reasoning Harry is in line at the store. He has three items that cost $5.95, $4.25, and $1.05. Explain how Harry can add the cost of the items mentally before he pays for them.
Answer:

Given,

Harry has three items that cost $5.95, $4.25, and $1.05.

$5.95 approximately equals $6

$4.25  approximately equals $4

$1.05 approximately equals $1

Therefore, by approximation, Harry can add the cost of the items mentally before he pays for them.

$6 + $4 + $1 = $11. (approximately)

Assessment Practice

Question 15.
Choose all the Expressions that can be used to find the volume of this wooden box.

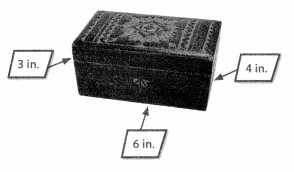
(6 × 4) < 3
(6 × 4) + 3
6 × 4
6 × (4 × 3)
24 × 3
Answer:

6 × 4

24 × 3

Lesson 11.3 Combine Volumes of Prisms

Activity

Solve & Share
Ariel is thinking of a three-dimensional figure that is made by combining two rectangular prisms. What is the volume of this three-dimensional figure? Solve this problem any way you choose.

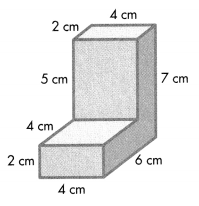
Use Structure You can find the volumes of the rectangular prisms that make up the solid figure. Show your work!

Look Back! How did you separate the solid into simpler rectangular prisms? Write the dimensions of each of the prisms.

Visual Learning Bridge

Essential Question How Can You Find the Volume of a Solid Figure question Composed of Two Rectangular Prisms?

A.
The shape and size of a storage building are shown in the figure. The building supervisor wants to find the volume to determine how much storage space is available. What is the volume of the building?

You can find the volume of this figure by finding the volume of two rectangular prisms that make up the figure.

B.
The building can be separated into two rectangular prisms as shown. Identify the measurements for the length, width, and height of each prism.

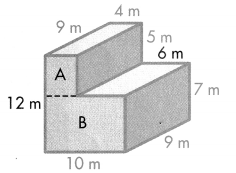
C.
Use the formula V = l × w × h to find the volume of each rectangular prism.

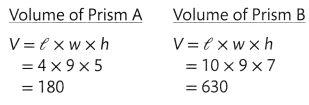
Add to find the total volume.
180 + 630 = 810
The volume of the storage building is 810 cubic meters.

Convince Me! Reasoning What is another way to divide the solid above into two rectangular prisms? What are the dimensions of each prism?

Guided Practice

Do You Understand?

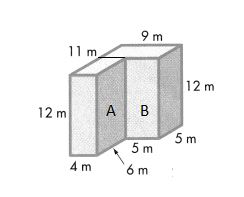
In 1 and 2, use the solid below. The dashed line separates it into two rectangular prisms, A and B.

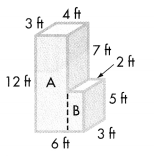
Question 1.
What are the length, width, and height of Prism A? What are the length, width, and height of Prism B?
Answer:

length, width, and height of Prism A are 4 ft, 3 ft, 12 ft respectively.

length, width, and height of Prism B are 3 ft, 2 ft, 5 ft respectively.

Question 2.
What is another way you could separate the shape into two rectangular prisms? What are each prism’s dimensions?
Answer:

Bisecting the figure horizontally, another way I could separate the shape into two rectangular prisms.

length, width, and height of Prism A are 4 ft, 3 ft, 7 ft respectively.

length, width, and height of Prism B are 6 ft, 3 ft, 5 ft respectively.

Do You Know How?

In 3 and 4, find the volume of each solid figure.

Question 3.

Answer:

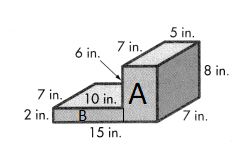
Volume = length × width × height
Volume of A = l × w × h
V = (5 × 7) × 8
V = 35 × 8
V = 280

The volume of the A is 280 cubic in or 280 in³.

Volume = length × width × height
Volume of B  = l × w × h
V = (10 × 7) × 2
V = 70 × 2
V = 140

The volume of the B is 140 cubic in or 140 in³.

Combined Volume  of Solid Figure is 280 in³ + 140 in³  = 420 in³ 

Question 4.

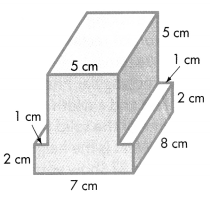
Answer:

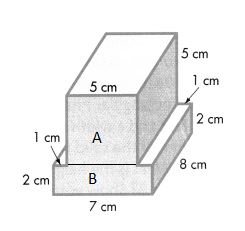
Volume = length × width × height
Volume of A = l × w × h
V = (5 × 8) × 5
V = 40 × 5
V = 200

The volume of the A is 200 cubic cm or 200 cm³.

Volume = length × width × height
Volume of B  = l × w × h
V = (7 × 8) × 2
V = 56 × 2
V = 112

The volume of the B is 112 cubic cm or 112 cm³.

Combined Volume  of Solid Figure is 200 cm³ + 112 cm³  = 312 in³

Independent Practice

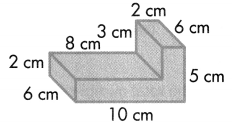
In 5-7, find the volume of each solid figure.

Question 5.

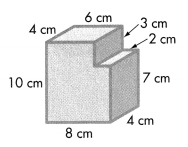
Answer:

Volume = length × width × height
Volume of A = l × w × h
V = (8 × 4) × 7
V = 32 × 7
V = 224

The volume of the A is 224 cubic cm or 224 cm³.

Volume = length × width × height
Volume of B  = l × w × h
V = (6 × 4) × 3
V = 24 × 3
V = 72

The volume of the B is 72 cubic cm or 72 cm³.

Combined Volume  of Solid Figure is 224 cm³ + 72 cm³  = 296 cm³

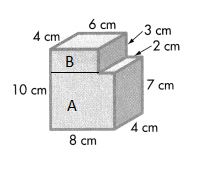
Question 6.

Answer:

Volume = length × width × height
Volume of A = l × w × h
V = (6 × 10) × 5
V = 60 × 5
V = 300

The volume of the A is 300 cubic ft or 300 ft³.

Volume = length × width × height
Volume of B = l × w × h
V = (6 × 2) × 4
V = 12 × 4
V = 48

The volume of the B is 48 cubic ft or 48 ft³.

Combined Volume  of Solid Figure is 300 ft³ + 48 ft³  = 348 ft³

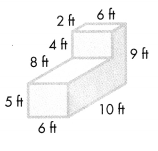
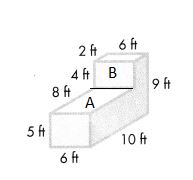
Question 7.

Answer:

Volume = length × width × height
Volume of A = l × w × h
V = (4 × 6) × 12
V = 24 × 12
V = 288

The volume of the A is 288 cubic m or 288 m³.

Volume = length × width × height
Volume of B  = l × w × h
V = (9 × 5) × 12
V = 45 × 12
V = 540

The volume of the B is 540 cubic m or 540 m³.

Combined Volume  of Solid Figure is 288 m³ + 540 m³  = 828 m³

Problem Solving

For 8-10, use the drawing of the solid figure.

Question 8.
How would you find the volume of the figure shown?
Answer:

Question 9.
Algebra Write two Expressions that can be added to find the volume of the solid figure.
Answer:

Volume = length × width × height
Volume of A = l × w × h
V = (5 × 4) × 10
V = 20 × 10
V = 200

The volume of the A is 200 cubic m or 200 m³.

Volume = length × width × height
Volume of B  = l × w × h
V = (5 × 2) × 7
V = 10 × 7
V = 70

The volume of the B is 70 cubic m or 70 m³.

Question 10.
What is the volume of the solid figure?
Answer:

Combined Volume  of Solid Figure is 200 m³ + 70 m³  = 270 m³

Question 11.
Higher Order Thinking A solid figure is separated into two rectangular prisms. The volume of Rectangular Prism A is 80 cubic feet. Rectangular Prism B has a length of 6 feet and a width of 5 feet. The total volume of the solid figure is 200 cubic feet. What is the height of Rectangular Prism B? Show your work.
Answer:

Question 12.
Model with Math The Peters family will drive 615 miles to reach their vacation destination. If they drive 389 miles the first day, how many miles will they drive the second day? Complete the bar diagram to help.

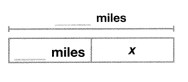
Answer:

Assessment Practice

Question 13.
A horizontal line separates the solid figure at the right into two rectangular prisms. Write an Expression for the volume of the solid figure.

Answer:

Volume of A  = length × width × height
V = l × w × h
V = (6 × 10) × 5
V = 60 × 5
V = 300

The volume of the rectangular prism is 300 cubic in or 300 in³.

Volume of B  = length × width × height
V = l × w × h
V = (10 × 10) × 2
V = 100 × 2
V = 200

The volume of the rectangular prism is 200 cubic in or 200 in³.

Total volume =  200 in³ + 300 in³  = 500 in³

Lesson 11.4 Solve Word Problems Using Volume

Activity

Solve & Share
A school has two wings, each of which is a rectangular prism. The school district is planning to install air conditioning in the school and needs to know its volume. What is the volume of the school? Solve this problem any way you choose.

Model with Math Write a multiplication Expression for the volume of each wing of the building.

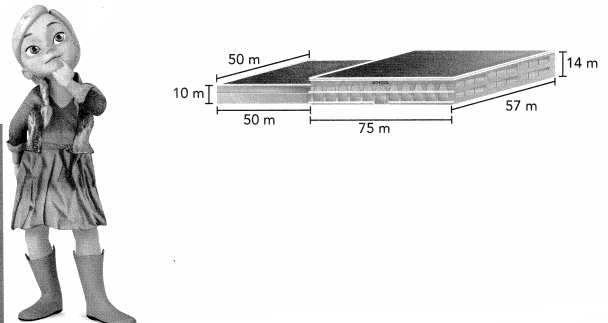
Look Back! Write a mathematical Expression that can be used to find the total volume of the school.

Visual Learning Bridge

Essential Question How Can You Use Volume Formulas to Solve Real-World Problems?

A.
The nature center has a large bird cage called an aviary. It consists of two sections, each shaped like a rectangular prism. There needs to be 10 cubic feet of space for each bird. How many birds can the nature center have in the aviary?

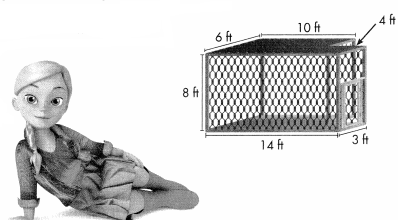
You can make sense of the problem by breaking it apart into simpler problems.

B.
Find the volume of each section. Use the formula V = l × w × h.
Small section:
V = 4 × 3 × 8 = 96
Large section:
V = 10 × 6 × 8 = 480
Add to find the total volume:
96 + 480 = 576
The combined volume is 576 cubic feet.

C.
Divide to find the number of birds that will fit.

576 ÷ 10 = 57.6
The nature center can put 57 birds in the aviary.

Convince Me! Critique Reasoning Tom solved the problem in a different way. First, he found the total area of the floor, and then he multiplied by the height. Does Tom’s method work? Explain.

Guided Practice

Do You Understand?

Question 1.
How can you find the volume of the china cabinet?

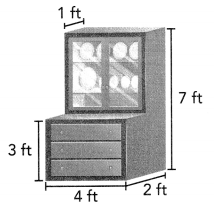
Question 2.
What is the height of the top section of the china cabinet? Explain.

Height of the top section of the china cabinet is 4 ft

Because, 7 ft – 3 ft = 4 ft

Question 3.
Find the volume of the china cabinet.
Answer:

Volume of china cabinet  = length × width × height
V = l × w × h
V = (4 × 1) × 4
V = 4 × 4
V = 16

The volume of the rectangular prism is 16 cubic ft or 16 ft³.

Do You Know How?

Question 4.
Find the volume of the building below.

Answer:

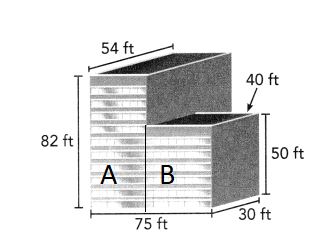
Volume of A = length × width × height
V = l × w × h
V = (35 × 54) × 82
V = 1890 × 82
V = 154,980

The volume of the rectangular prism is 154,980 cubic ft or 154,980 ft³.

Volume of B = length × width × height
V = l × w × h
V = (40 × 30) × 50
V = 1200 × 50
V = 60000

The volume of the rectangular prism is 60000 cubic ft or 60000 ft³

Therefore, Combined volume is  154,980 ft³ + 60000 ft³  = 214,980 ft³

Question 5.
The nature center has a fish tank shaped like a rectangular prism that measures 6 feet long by 4 feet wide by 4 feet high. It can be stocked safely with 3 small fish in each cubic foot of water. How many small fish can safely fit in the tank?
Answer:

Volume of rectangular prism  = length × width × height
V = l × w × h
V = (6 × 4) × 4
V = 24 × 4
V = 96

The volume of the rectangular prism is 96 cubic ft or 96 ft³.

If it can be stocked safely with 3 small fish in each cubic foot of water. Then 96/3 = 12

12 fish can be stocked safely with 3 small fish in each cubic foot of water.

Independent Practice

Question 6.
Sophie built a house out of building blocks. Find the volume of the house Sophie built.

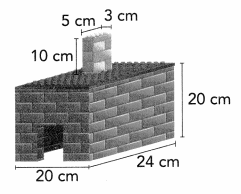
Answer:

Volume of A = length × width × height
V = l × w × h
V = (3 × 5) × 10
V = 15 × 10
V = 150

The volume of the rectangular prism is 150 cubic cm or 150 cm³.

Volume of B = length × width × height
V = l × w × h
V = (20 × 24) × 20
V = 480 × 20
V = 9600

The volume of the rectangular prism is 9600 cubic cm or 9600 cm³

Therefore, Combined volume is  150 cm³ + 9600 cm³  = 9750 cm³

Question 7.
How many cubic inches of concrete would it take to make these stairs?

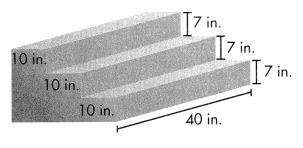
Answer:

Volume of first stair = length × width × height
V = l × w × h
V = (40 × 10) × 7
V = 400 × 7
V = 2800

The volume of the first stair is 2800 cubic in or 2800 in³.

Volume of Second stair = length × width × height
V = l × w × h
V = (40 × 10) × 14
V = 400 × 14
V = 5600

The volume of the second stair is 5600 cubic in or 5600 in³

Volume of third stair = length × width × height
V = l × w × h
V = (40 × 10) × 21
V = 400 × 21
V = 8400

The volume of the rectangular prism is 8400 cubic in or 8400 in³

Therefore, Combined volume is  2800 in³ + 5600 in³ + 8400 in³  = 16800 in³

16800 cubic inches of concrete it takes to make these stairs

Problem Solving

Question 8.
A floor plan of Angelica’s bedroom and closet is shown at the right. The height of the bedroom is 9 feet. The height of the closet is 7 feet. What is the total volume of the bedroom and the closet?

Answer:

Volume of bedroom = length × width × height
V = l × w × h
V = (14 × 12) × 9
V = 168 × 9
V = 1512

The volume of the second stair is 1512 cubic ft or 1512 ft³

Volume of  closet = length × width × height
V = l × w × h
V = (3 × 4) × 7
V = 12 × 7
V = 84

The volume of the rectangular prism is 84 cubic ft or 84 ft³

Therefore, Combined volume is  1512 ft³ + 84 ft³  = 11596 ft³

Question 9.
Critique Reasoning Does it make sense for Angelica to find the combined area of the bedroom floor and closet floor before finding the total volume? Explain your thinking.
Answer:

Yes. the total volume is sum of the bedroom and closet of Angelica room

Question 10.
Higher Order Thinking An office building surrounds a rectangular open air courtyard. What is the volume of the building? How did you find the answer?

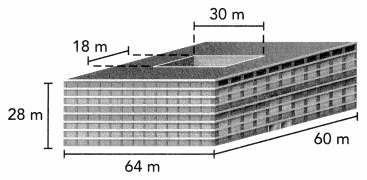
Answer:

Volume of building = length × width × height
V = l × w × h
V = (64 × 60) × 28
V = 3840 × 28
V = 107,520

The volume of the second stair is 107,520 cubic m or 107,520 m³

Volume of open air courtyard = length × width × height
V = l × w × h
V = (18 × 30) × 28
V = 540 × 28
V = 15120

The volume of the rectangular prism is 15120 cubic m or 15120 m³

Therefore, Total volume of building is  107,520 m³ – 15120 m³  = 92400 m³

Assessment Practice

Question 11.
Mrs. Bhatia’s closet consists of two sections, each shaped like a rectangular prism. She plans to buy mothballs to keep the moths away. She needs one box for every 32 cubic feet of space. How many boxes should she buy?
A. 6 boxes
B. 7 boxes
C. 8 boxes
D. 10 boxes

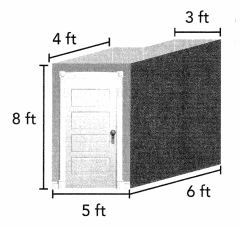
Answer:

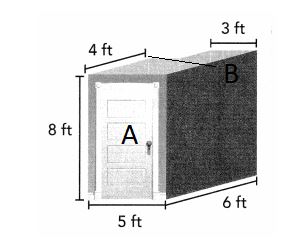
Volume of first section = length × width × height
V = l × w × h
V = (5 × 4) × 8
V = 20 × 8
V = 160

The volume of the first section is 160 cubic ft or 160 ft³

Volume of open second section = length × width × height
V = l × w × h
V = (3 × 2) × 8
V = 6 × 8
V = 48

The volume of the second section is 48 cubic ft or 48 ft³

Therefore, the total volume of the building is  160 ft³ + 48 ft³  = 208 ft³

If she needs one box for every 32 cubic feet of space. Then Number of boxes = 208 / 32 = 6.5

She needs 6 or 7 boxes.

Lesson 11.5 Use Appropriate Tools

Problem Solving

Solve & Share
A space station is being built from 24 cubic modules. The space station can be any shape but the modules must be placed together so that entire faces match up with each other. Choose a tool to create two different plans for the space station. Explain why you chose the tool you selected.

Thinking Habits
Be a good thinker! These questions can help you.
• Which tools can I use?
• Why should I use this tool to help me solve the problem?
• Is there a different tool I could use?
• Am I using the tool appropriately?

Look Back! Use Appropriate Tools How did you decide which tool to use?

Visual Learning Bridge

Glossory

Essential Question How Can You Use Appropriate Tools question to Solve Volume Problems?

A.
Jeremiah needs to build a display of boxes that is 4 feet tall.
The boxes he uses are cubes that measure 1 foot on each edge. His display needs to look like a pyramid, with just one box in the top layer.
How many boxes will Jeremiah need to make his display?

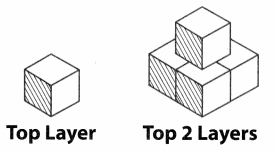
What do I need to do?
I need to choose an appropriate tool to solve this problem.

Here’s my thinking…

B.
How can I use appropriate tools strategically to help me solve this problem?
I can
• decide which tool is appropriate.
• use cubes to solve this problem.
• use the tool correctly.

C.
I could use grid paper, but I will use cubes because building a display will make it easier to count the cubes.
Each cube represents 1 box in the display. My display will have 4 layers because it needs to be 4 feet tall, and each box is 1 foot high.
The display has 1 + 4 + 9 + 16 = 30 cubes.

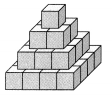
So, Jeremiah needs 30 boxes in all to make his display.

Convince Me! Use Appropriate Tools What tools other than cubes could you use to solve this problem? Explain.

Guided Practice

Use Appropriate Tools
A paint store manager is going to build a display with same-sized cubes. The display will look like a staircase with 5 steps. Each step in the display will be 6 cubes long. The store manager will build the staircase display with 1-foot plastic cubes.

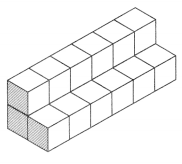
Question 1.
What tool might the manager use to be sure that there is enough space for the display? Explain.
Answer:

Question 2.
What is the volume of the display? Explain how you used tools to decide.
Answer:

Independent Practice

Use Appropriate Tools

Cindy plans to make a jewelry box shaped like a rectangular prism. She wants it to have a volume of 96 cubic inches.

Question 3.
How can you find possible dimensions of the box?
Answer:

Think about a tool you can use to help represent and solve the problem.

Question 4.
What could the dimensions of that jewelry box be?
Answer:

Question 5.
Can Cindy build the box so that it is twice as wide as it is tall?
Answer:

Question 6.
Cindy has some ribbon to decorate the jewelry box. What tool might help her decide how much of the jewelry box she can decorate?
Answer:

Problem Solving
Performance Task

Flower Planters
An architect is designing flower planters for a park. Each planter consists of a border of 1-foot concrete cubes surrounding a square opening. Each concrete cube weighs 120 pounds. The diagram below shows the top view of some of the planters.

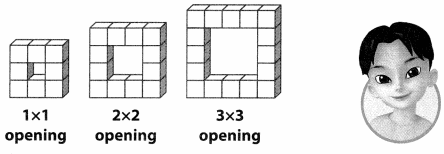
Remember to think about which tools make sense for these problems.

Question 7.
Use Structure What is the total volume of a planter that has a 6 × 6 opening?
Answer:

Question 8.
Use Structure What is the total volume of a planter that has an 8 × 8 opening?
Answer:

Question 9.
Use Appropriate Tools What will be the total volume of a planter that has a 12 × 12 opening? Can you determine this by just using paper and pencil? Explain.
Answer:

Question 10.
Model with Math Each concrete cube used to make the planters costs $3.00. What is the total cost of the cubes needed for two planters with 6 × 6 openings, two with 8 × 8 openings, and two with 12 × 12 openings? Write an Expression that represents the total cost.
Answer:

Topic 11 Fluency Practice

Activity

Find a Match

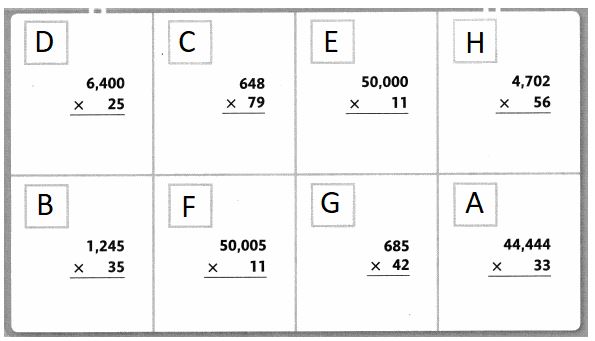
Work with a partner. Point to a clue. Read the clue.
Look below the clues to find a match. Write the clue letter in the box above the match.
Find a match for every clue.

Answer:

Topic 11 Vocabulary Review

Word List

Glossory

Understand Vocabulary

In 1-3, choose the best term from the Word List. Write it on the blank.
• area
• cubic unit
• formula
• rectangular prism
• unit cube
• volume

Question 1.
The number of same-size unit cubes that fill a solid figure without overlaps or gaps in the figure’s ____
Answer:

The number of same-size unit cubes that fill a solid figure without overlaps or gaps in the figure’s volume

Question 2.
A solid figure with 6 rectangular faces that are not all squares is a(n) ___
Answer:

A solid figure with 6 rectangular faces that are not all squares is a rectangular prism

Question 3.
A rule that uses symbols to relate two or more quantities is a(n) ___.
Answer:

A rule that uses symbols to relate two or more quantities is a formula

Question 4.
Cross out the Expression(s) below that do NOT represent the volume of the prism.

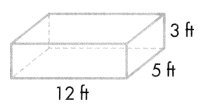
Answer:

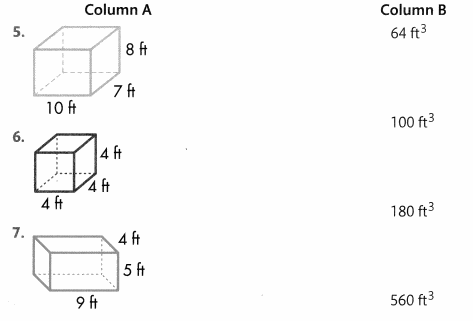
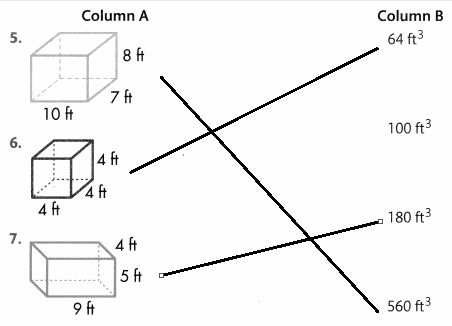
Draw a line from each three-dimensional figure in Column A to its volume in Column B.

Answer:

Question 8.
One box is 3 inches by 4 inches by 5 inches. A second box is 4 inches by 4 inches by 4 inches. Explain how to decide which box holds more.
Answer:

Volume of the first box is, V = 3 x 4 x 5 = 60 cubic inches.

Volume of the second box is, V = 4 x 4 x 4 = 64 cubic inches.

The second box holds more because it has more volume.

Topic 11 Reteaching

Set A
pages 457-460

Find the number of cubes needed to make this rectangular prism.

Multiply to find the total number of cubes.
3 × 5 × 3 = 45
The volume is 45 cubic units.

Remember, you can multiply the numbers in any order!

Remember that you can find the number of cubes in each layer and then multiply by the number of layers.

Find each volume. You may use cubes to help.

Question 1.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 14 unit cubes in the bottom layer. The volume of the bottom layer is 14 cubic units.

The volume of the prism is 14 × 2 or 28 cubic units.

Question 2.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 10 unit cubes in the bottom layer. The volume of the bottom layer is 10 cubic units.

The volume of the prism is 10 × 2 or 20 cubic units.

Question 3.

Answer:

Each cube of a solid figure is 1 cubic unit.

There are 12 unit cubes in the bottom layer. The volume of the bottom layer is 12 cubic units.

The volume of the prism is 12 × 6 or 72 cubic units.

Set B
pages 461-464
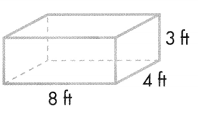
Find the volume of this rectangular prism.

Volume = length × width × height V=l×w×h
= 9 cm × 4 cm × 2 cm
V = 72 cubic centimeters or 72 cm³
The volume of the prism is 72 cm³.

Remember if you know the area of the base of a rectangular prism, use the formula V = b × h, where b is the area of the base.

Find each volume. You may use cubes to help.

Question 1.
Area of the base, b = 42 square meters and height = 3 meters
Answer:

The volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
V = 42 × 3
V = 126 m³

Question 2.
Area of the base = 75 square inches and height = 15 inches
Answer:

The volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
V = 75 × 15
V = 1125 in³

Question 3.

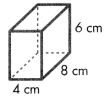
Answer:

Volume = length × width × height
Volume = l × w × h
V = (8 × 4) × 3
V = 32 × 3
V = 96

The volume of the B is 96 cubic ft or 70 ft³.

Set C
pages 465-468, 469-472

Some solid figures can be separated into two rectangular prisms.

Add the volume of each prism to find the total volume of the solid figure.
V = (4 × 4 × 5) + (10 × 4 × 5)
= 80 + 200
= 280
The volume of the solid figure is 280 cubic inches.

Remember to identify the length, width, and height of each prism, so that you can calculate the volume of each part.

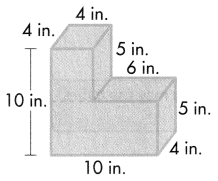
Question 1.
Find the volume.

Answer:

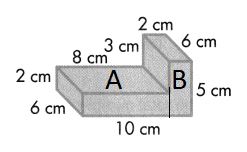
Volume = length × width × height
Volume of A = l × w × h
V = (10 × 6) × 2
V = 60 × 2
V = 120

The volume of the A is 120 cubic cm or 120 cm³.

Volume = length × width × height
Volume of B  = l × w × h
V = (2 × 6) × 3
V = 12 × 3
V = 36

The volume of the B is 36 cubic cm or 36 cm³.

Combined Volume  of Solid Figure is 120 cm³ + 36 cm³  = 156 cm³

Question 2.
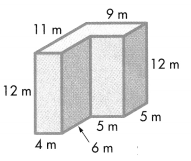
An office building has the dimensions shown. What is the volume of the building?

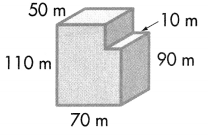
Answer:

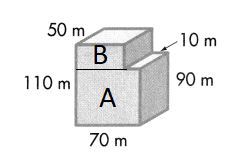
Volume = length × width × height
Volume of A = l × w × h
V = (70 × 50) × 90
V = 3500 × 90
V = 315,000

The volume of the A is 315,000 cubic m or 315,000 m³.

Volume = length × width × height
Volume of B  = l × w × h
V = (60 × 50) × 20
V = 3000 × 20
V = 60000

The volume of the B is 60000 cubic m or 60000 m³.

Combined Volume  of Solid Figure is 315,000 m³ + 60000 m³  = 375,000 m³

Set D
pages 473-476
Think about these questions to help you use appropriate tools strategically.

Thinking Habits
Molly used 1-inch cubes to build the structure shown. She left a 3-inch by 1-inch opening in both layers of the structure.
• Which tools can I use?
• Why should I use this tool to help me solve the problem?
• Is there a different tool I could use?
• Am I using the tool appropriately?

Remember that tools such as place-value blocks, cubes, and grid paper can help you solve problems involving volume.

Question 1.
What tools could you use to model the problem?
Answer:

cubes

Question 2.
What is the total volume of the structure?
Answer:

Total blocks in bottom layer = 5 x 3 =15

Height =2 ; total volume is 15 x 2 = 30.

blocks left = 3 x 1 x 2 = 6

Therefore, total volume = 30 – 6 = 24 cubic units

Topic 11 Assessment Practice

Question 1.
Julio used unit cubes to make a rectangular prism. What is the volume of the prism?

A. 18 cubic units
B. 72 cubic units
C. 54 cubic units
D. 108 cubic units
Answer:

B. 72 cubic units

Question 2.
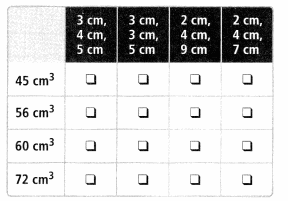
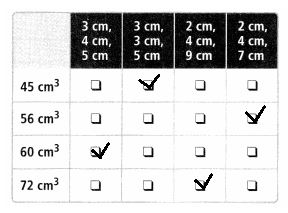
Select the possible dimensions for a prism with each given volume.

Answer:

Question 3.
A. A swimming pool is 50 meters long, 15 meters wide, and 3 meters deep. What is the volume of the pool?
A. 4,500 cubic meters
B. 2,250 cubic meters
C. 900 cubic meters
D. 750 cubic meters
B. After filling the pool for several minutes, the water is 1 meter deep. What is the volume of water in the pool?
Answer:

A.

Volume = length × width × depth
Volume of Swimming pool = l × w × h
V = (50 × 15) × 3
V = 750 × 3
V = 2250

The volume of the Swimming pool is 2250 cubic m or 2250 m³.

B.

Volume = length × width × depth
Volume of Swimming pool after filling the pool for several minutes, the water is 1 meter deep =
V = (50 × 15) × 4
V = 750 × 4
V = 3000

The volume of the Swimming pool is 3000 cubic m or 3000 m³.

Question 4.
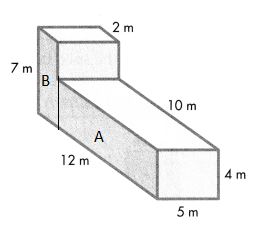
A small building has the dimensions shown.
A. Write an Expression for the total volume of the building.

B. What is the volume of the building?
Answer:

A.

Volume = length × width × height
Volume of A = l × w × h
V = (8 × 12) × 24
V = 96 × 24
V = 2304

The volume of the A is 2304 cubic ft or 2304 ft³.

Volume = length × width × height
Volume of B  = l × w × h
V = (32 × 12) × 16
V = 384 × 16
V = 6114

The volume of the B is 6114 cubic ft or 6114 ft³

B.

Combined Volume  of Solid Figure is 2304 ft³ + 6114 ft³  = 8418 ft³

Question 5.
A. Choose all the Expressions that could NOT be used to find the volume of the bale of hay.

100 × 40
(100 × 40) × 20
4,000 × 20
(100 × 40) + 20
(100 + 40) + 20
B. Another 10 cm of hay is added to the top of the bale. What is the volume of the bale of hay now?
Answer:

A.

(100 × 40) × 20
4,000 × 20

B.

Volume = length × width × height
Volume of bale of hay  = l × w × h
V = (100 × 40) × 30
V = 4000 × 30
V = 120000

The volume of the bale of hay is 120000 cubic cm or 120000 cm³

Question 6.
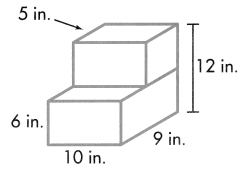
Madeline made the wooden steps shown. What is the volume of the steps?

A. 72 cubic inches
B. 540 cubic inches
C. 840 cubic inches
D. 1,080 cubic inches
Answer:

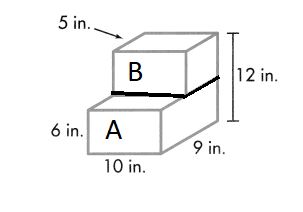
Volume = length × width × height
Volume of A = l × w × h
V = (10 × 9) × 6
V = 90 × 6
V = 540

The volume of the A is 540 cubic in or 540 in³.

Volume = length × width × height
Volume of B  = l × w × h
V = (10 × 5) × 6
V = 50 × 6
V = 300

The volume of the B is 300 cubic in or 300 in³

Combined Volume  of Solid Figure is 540 in³ + 300 in³  = 840 in³

Question 7.
A. What is the volume of the trunk shown?

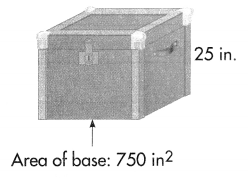
B. Which equation was used to find the volume of the trunk?
A. V = b × h
B. V = l × w × h
C. V = l × w
D. V = b × b × h
Answer:

A.

The volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
V = 750 × 25
V = 18750 in³

B.

Option A. V = b × h

Question 8.
For her science project, Jada wants to build a rectangular prism out of foam blocks. The prism should have a volume of 350 cubic inches and a height of 5 inches.
What does the area of the base of the prism need to be for the given volume and height? Give one pair of possible whole-number dimensions for the base.
Answer:

The volume of a rectangular prism is V = b × h, where b is the area of the base.
V = b × h.
350 = b × 5
b = 350/5 = 70

The area of the base of the prism needs to be for the given volume and height is 70 in²

Question 9.
Martin’s suitcase has a volume of 1,080 cubic inches. Lily’s suitcase measures 9 inches wide, 13 inches long, and 21 inches high. What is the combined volume of the two suitcases?
Answer:

The volume of the first suitcase is 1080 cubic in or 1080 in³.

Volume = length × width × height
Volume of Second suitcase is  = l × w × h
V = (9 × 13) × 21
V = 117 × 21
V = 2457

The volume of the second suitcase is 2457 cubic in or 2457 in³

The combined volume of both suitcases is 1080 in³ + 2457 in³  = 3537 in³

Question 10.
Select all the Expressions that can be used to find the volume of the box in cubic centimeters.

8 × 6
(4 × 8) × 6
32 × 6
46 × 8
(4 × 8) + 6
Answer:

(4 × 8) × 6
32 × 6

Topic 11 Performance Task

Sporting Goods
Hiroto works in a sporting goods store. 1. Hiroto stacks identical boxes of golf balls to form a rectangular prism. Each box is a cube.

Part A
How many boxes are in the Golf Ball Display?

Answer:

There are 84 boxes in the Golf Ball Display
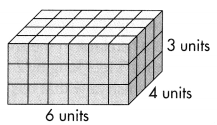
Part B
Explain how the number of boxes you found in Part A is the same as what you would find by using the formula V= l × w ×h.

Answer:

Each block has volume of 1 cubic unit.

Length = 7 boxes

Breadth = 4 boxes

Height = 3 boxes

Volume is length x breadth x height

V= l × w ×h = 7 x 4 x 3

v = 28 x 3 = 84 cubic units.

Part C
Hiroto needs to restack the boxes so the display is 2 layers high, less than 14 inches wide, and less than 30 inches long. The size of each box is shown in at the right. What is one way Hiroto can stack the boxes? Justify your answer.

Part D
What is the volume of the golf ball display in cubic inches? Explain how you solved.
Answer:

Question 2.
Hiroto builds two displays using rectangular foam blocks.
Part A
What is the volume of the foam block used for the Baseball Hats and Helmets Display? Explain how to solve using the formula V = b × h.

Part B
Hiroto used two blocks to build the Baseball Uniforms Display. What is the combined volume of the blocks? Explain how you solved.

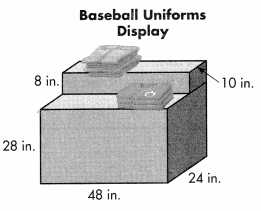
Part C
Explain how you knew which units to use for your answer to Part B.
Answer: