Go through the enVision Math Common Core Grade 5 Answer Key Topic 6 Use Models and Strategies to Divide Decimals regularly and improve your accuracy in solving questions.
enVision Math Common Core 5th Grade Answers Key Topic 6 Use Model Strategies to Divide Decimals

enVision STEM Project: States of Water
Do Research
Use the Internet or other sources to learn about the states of water. Find at least 5 examples of water in nature as a solid, as a liquid, and as a gas. At what temperature does liquid water change to ice? At what temperature does liquid water change to water vapor?
Journal: Write a Report Include what you found. Also in your report:
• Explain how liquid water changes to ice and to water vapor.
• At 23°F, 1 inch of rain equals 10 inches of snow. Convert 2 inches of rainfall to snowfall.
• Make up and solve division problems that involve decimals.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
• decimal
• dividend
• divisor
• quotient
Question 1.
_____ is the name for the answer to a division problem.
Answer:
Quotient is the name for the answer to a division problem.
Question 2.
A number that is being divided by another number is called the _____
Answer:
A number that is being divided by another number is called the dividend.
Whole Number Operations
Find each value.
Question 3.
9,007 – 3,128
Answer:
9,007 – 3,128 = 5,879
Explanation:
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. Subtraction of two whole numbers may not result in whole numbers. It can be an integer too. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Subtract 3,128 from 9,007 then the difference is 5,879.
Question 4.
725,864 + 39,798
Answer:
725,864 + 39,798 = 765,662
Explanation:
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. Two whole numbers if added or multiplied will give a whole number itself. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Perform addition operation on these two numbers 725,864 and 39,798 then the sum is 765,662.
Question 5.
35 × 17
Answer:
35 × 17 = 595
Explanation:
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. Two whole numbers if added or multiplied will give a whole number itself. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Perform multiplication operation on these two numbers 35 and 17 then the result is 595.
Question 6.
181 × 42
Answer:
181 × 42 = 7,602
Explanation:
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. Two whole numbers if added or multiplied will give a whole number itself. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Perform multiplication operation on these two numbers 181 and 42 then the result is 7,602.
Question 7.
768 ÷ 6
Answer:
768 ÷ 6 = 128
Explanation:
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. The inverse operation of multiplication is division. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Perform division operation on these two numbers 768 and 6. Here 768 is dividend and 6 is divisor then the quotient is 128.
Question 8.
506 ÷ 22
Answer:
506 ÷ 22 = 23
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. The inverse operation of multiplication is division. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Perform division operation on these two numbers 506 and 22. Here 506 is dividend and 22 is divisor then the quotient is 23.
Question 9.
6,357 ÷ 60
Answer:
6,357 ÷ 60 = 105.95
Explanation:
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. The inverse operation of multiplication is division. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Perform division operation on these two numbers 6357 and 60. Here 6,357 is dividend and 60 is divisor then the quotient is 105.95.
Question 10.
3,320 ÷ 89
Answer:
3,320 ÷ 89 = 37.30
Explanation:
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. The inverse operation of multiplication is division. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Perform division operation on these two numbers 3,320 and 89. Here 3,320 is dividend and 89 is divisor then the quotient is 37.30.
Question 11.
88,888 ÷ 20
Answer:
88,888 ÷ 20 = 4,444.4
Explanation:
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. The inverse operation of multiplication is division. Whole numbers are positive integers along with zero. They are all the natural numbers including zero. Perform division operation on these two numbers 88,888 and 20. Here 88,888 is dividend and 20 is divisor then the quotient is 4,444.4.
Rounding Decimals
Round each number to the place of the underlined digit.
Question 12.
0.34
Answer:
0.3
Explanation:
Rounding is a process to estimate a particular number in a context. To round a number look at the next digit in the right place, if the digit is less than 5, round down and if the digit is 5 or more than 5, round up. The number 0.34 is rounded to 0.3.
Question 13.
96.5
Answer:
97
Explanation:
Rounding is a process to estimate a particular number in a context. To round a number look at the next digit in the right place, if the digit is less than 5, round down and if the digit is 5 or more than 5, round up. The number 96.5 is rounded to 97.
Question 14.
81.27
Answer:
81.3
Explanation:
Rounding is a process to estimate a particular number in a context. To round a number look at the next digit in the right place, if the digit is less than 5, round down and if the digit is 5 or more than 5, round up. The number 81.27 is rounded to 81.3.
Question 15.
205.3
Answer:
205
Explanation:
Rounding is a process to estimate a particular number in a context. To round a number look at the next digit in the right place, if the digit is less than 5, round down and if the digit is 5 or more than 5, round up. The number 205.3 is rounded to 205.
Decimals
Question 16.
An insect measured 1.25 cm long. Which number is less than 1.25?
A. 1.35
B. 1.3
C. 1.26
D. 1.2
Answer:
Option D is correct.
Explanation:
An insect measured 1.25 cm long. We have to find out the number less than 1.25.
A. 1.35 is greater than 1.25. So option A is not correct.
B. 1.3 is greater than 1.25. So option B is not correct.
C. 1.26 is greater than 1.25 . So option C is not correct.
D. 1.2 is less than 1.25. So option D is correct.
Question 17.
Explain The grid in this model represents 1. What decimal does the shaded part represent? Explain.

Answer:
0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.04 = 0.64
The shaded part represents the decimal 0.64.
Explanation:
The above grid represents 1. In that grid 1 column is shaded. The shaded part decimal value is 0.1. The second column shaded part decimal value is 0.1. The third column shaded part decimal value is 0.1. The fourth column shaded part decimal value is 0.1. The fifth column shaded part decimal value is 0.1. The sixth column shaded part decimal value is 0.1. The seventh column shaded part decimal value is 0.04. By adding these columns decimal values the sum is 0.64.
Decimal Operations
Find each value.
Question 18.
23.7 – 11.82
Answer:

23.7 – 11.82 = 11.88
Explanation:
Four basic operations on decimals are addition, subtraction, multiplication and division. To add decimals numbers we follow this step.
Step 1: Write numbers under each other and line up vertically the decimal points.
Perform subtraction operation on these two numbers 23.7 and 11.82. Subtract 11.82 from 23.7 then the difference is 11.88.
Question 19.
66.8 + 3.64
Answer:

66.8 + 3.64 = 70.44
Explanation:
Four basic operations on decimals are addition, subtraction, multiplication and division. To add decimals numbers we follow this step.
Step 1: Write numbers under each other and line up vertically the decimal points.
Perform addition operation on these two numbers 66.8 and 3.64. Add 66.8 with 3.64 then the sum is 70.44.
Question 20.
9 × 1.4
Answer:
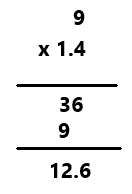
9 x 1. 4 = 12. 6
Explanation:
Four basic operations on decimals are addition, subtraction, multiplication and division. To add decimals numbers we follow this step.
Step 1: Write numbers under each other and line up vertically the decimal points.
Perform multiplication operation on these two numbers 9 and 1.4. Multiply 9 with 1.4 then the result is 12.6.
Question 21.
3.2 × 7.6
Answer:

3.2 x 7.6 = 24.32
Explanation:
Four basic operations on decimals are addition, subtraction, multiplication and division. To add decimals numbers we follow this step.
Step 1: Write numbers under each other and line up vertically the decimal points.
Perform multiplication operation on these two numbers 3.2 and 7.6. Multiply 3.2 with 7.6 then the result is 24.32.
Pick a Project
PROJECT 6A
Can you throw a dinner party?
Project: Plan a Party

PROJECT 6B
How much does it cost to run a company?
Project: Build a Company

PROJECT 6C
How do you organize food?
Project: Open Your Own Fruit Stand

PROJECT 6D
Would you like to build a house?
Project: Draw Plans for a Doll House

Lesson 6.1 Patterns for Dividing with Decimals
Activity
Solve & Share
An object is 279.4 centimeters wide. If you divide the object into 10 equal parts, how wide will each part be? Solve this problem any way you choose.
How can you use structure and the relationship between multiplication and division to help you?

Look Back! What do you notice about the width of the object and the width of each part?
Answer:
The width of the object is 279.4
279.4/10 = 27.94
The width of each part is 27.94
Explanation:
An object is 279.4 centimeters wide. If we divide the object into 10 equal parts. The wide of the each part is 27.94.
Multiplication and division are the reverse or opposite of each other in that when we divide, we break apart, and when we multiply, we put together.
Visual Learning Bridge
Essential Question How Can You Divide Question Decimals by Powers of 10?
A.
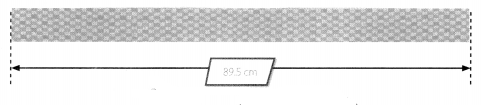
Shondra wants to cut a cloth into 10 strips. All the strips should be exactly the same size. You can use place value and what you know about whole numbers to divide decimals by powers of 10. How long will each strip be?
You can divide to find equal parts of a whole.

Remember that
10 = 10!

B.
Find 89.5 ÷ 10.
Place value is based on 10. The value of each place is \(\frac{1}{10}\) the value of the place to the left. Dividing by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left.
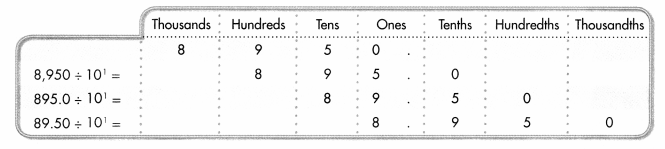
89.5 ÷ 101 = 8.95
Each cloth strip will be 8.95 cm long.
Convince Me! Use Structure Celinda thought of 89.5 in parts, 80 + 9 + 0.5, and divided each part: 80 ÷ 10 = 8; 9 ÷ 10 = \(\frac{9}{10}\) or 0.9; 0.5 ÷ 10 = 0.05. Then she added the parts to get 8.95. What do you notice?
Answer:
Celinda divided 89.5 into parts as 80 + 9 + 0.5, and divided each part 80 ÷ 10 = 8; 9 ÷ 10 = 0.9; 0.5 ÷ 10 = 0.05. Then she added the parts to get 8.95. I notice when we divide the number 89.5 with 10 then the result is 8.95 and dividing 89.5 into parts also we get same result as 8.95.
Guided Practice999
Do You Understand?
Question 1.
Suppose Shondra wanted to cut the cloth into 102 strips. How long would each strip be?
Answer:
89.5 ÷ 102
89.5 ÷ 100 = 0.895
Each cloth strip will be 0.895 cm long.
Explanation:
Shondra wanted to cut the cloth into 102 strips. Place value is based on 102. The value of each place is 1/100 the value of the place to the left. Dividing by 102 results in moving each digit two places to the right. This looks the same as moving the decimal point two places to the left. Each cloth strip will be 0.895 cm long.
Question 2.
Krista divides a number by 10. Then she divides the same number by 50. Which quotient is greater? How can you tell?
Answer:
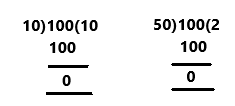
The quotient 10 is greater.
Explanation:
In the above image we can observe the quotient 10 and 2. Krista divides the number 100 by 10 then the quotient is 10. Then she divides the same number 100 by 50 then the quotient is 2. The quotient 10 is greater.
Do You Know How?
In 3-10, use mental math to find each quotient.
Question 3.
370.2 ÷ 102
Answer:
370.2 ÷ 102
370.2 ÷ 100 = 3.702
Explanation:
In the above division method the place value is based on 102. The value of each place is 1/100 the value of the place to the left. Dividing the number 370.2 by 102 results in moving each digit two places to the right. This looks the same as moving the decimal point two places to the left. The quotient for 370.2 ÷ 100 = 3.702.
Question 4.
126.4 ÷ 101
Answer:
126.4 ÷ 101
126.4 ÷ 10 = 12.64
Explanation:
In the above division method the place value is based on 101. The value of each place is 1/10 the value of the place to the left. Dividing the number 126.4 by 101 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 126.4 ÷ 10 = 12.64.
Question 5.
7.25 ÷ 10
Answer:
7.25 ÷ 10 = 0.725
Explanation:
In the above division method the place value is based on 10. The value of each place is 1/10 the value of the place to the left. Dividing the number 7.25 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 7.25 ÷ 10 = 0.725.
Question 6.
72.5 ÷ 103
Answer:
72.5 ÷ 103
72.5 ÷ 1000 = 0.0725
Explanation:
In the above division method the place value is based on 103. The value of each place is 1/1000 the value of the place to the left. Dividing the number 72.5 by 103 results in moving each digit three places to the right. This looks the same as moving the decimal point three places to the left. The quotient for 72.5 ÷ 1000 = 0.0725.
Question 7.
281.4 ÷ 100
Answer:
281.4 ÷ 100
281.4 ÷ 1 = 281.4
Explanation:
In the above division method the place value is based on 100. The value of each place is 1 the value of the place to the left. Dividing the number 281.4 by 1 results in moving each digit zero places to the right. This looks the same as moving the decimal point zero places to the left. The quotient for 281.4 ÷ 1 = 281.4.
Question 8.
2,810 ÷ 104
Answer:
2,810 ÷ 104
2,810 ÷ 10000 = 0.2810
Explanation:
In the above division method the place value is based on 104. The value of each place is 1/10000 the value of the place to the left. Dividing the number 2,810 by 104 results in moving each digit four places to the right. This looks the same as moving the decimal point four places to the left. The quotient for 2,810 ÷ 10000 = 0.2810.
Question 9.
3,642.4 ÷ 102
Answer:
3,642.4 ÷ 102
3,642.4 ÷ 100 = 36.424
Explanation:
In the above division method the place value is based on 102. The value of each place is 1/100 the value of the place to the left. Dividing the number 3,642.4 by 102 results in moving each digit two places to the right. This looks the same as moving the decimal point two places to the left. The quotient for 3,642.4 ÷ 100 = 36.424.
Question 10.
364.24 ÷ 101
Answer:
364.24 ÷ 101
364.24 ÷ 10 = 36.424
Explanation:
In the above division method the place value is based on 101. The value of each place is 1/10 the value of the place to the left. Dividing the number 364.24 by 101 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 364.24 ÷ 10 = 36.424.
Independent Practice
Leveled Practice in 11-25, find each quotient. Use mental math.
Question 11.
4,600 ÷ 10
460 ÷ 10
46 ÷ 10
4.6 ÷ 10
Answer:
4,600 ÷ 10 = 460
460 ÷ 10 = 46
46 ÷ 10 = 4.6
4.6 ÷ 10 = 0.46
Explanation:
In the above division method the place value is based on 10. The value of each place is 1/10 the value of the place to the left.
Dividing the number 4,600 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 4,600 ÷ 10 = 460.
Dividing the number 460 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 460 ÷ 10 = 46.
Dividing the number 46 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 46 ÷ 10 = 4.6.
Dividing the number 4.6 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 4.6 ÷ 10 = 0.46.
Question 12.
134.4 ÷ 103
134.4 ÷ 102
134.4 ÷ 101
134.4 ÷ 100
Answer:
134.4 ÷ 103
134.4 ÷ 1000 = 0.1344
134.4 ÷ 102
134.4 ÷ 100 = 1.344
134.4 ÷ 101
134.4 ÷ 10 = 13.44
134.4 ÷ 100
134.4 ÷ 1 = 134.4
Explanation:
Dividing the number 134.4 by 103 results in moving each digit three places to the right. This looks the same as moving the decimal point three places to the left. The quotient for 134.4 ÷ 1000 = 0.1344.
Dividing the number 134.4 by 102 results in moving each digit two places to the right. This looks the same as moving the decimal point two places to the left. The quotient for 134.4 ÷ 100 = 1.344.
Dividing the number 134.4 by 101 results in moving each digit one two place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 134.4 ÷ 10 = 13.44.
Dividing the number 134.4 by 100 results in moving each digit zero places to the right. This looks the same as moving the decimal point zero places to the left. The quotient for 134.4 ÷ 1 = 134.4.
Question 13.
98.6 ÷ 1
98.6 ÷ 100
98.6 ÷ 10
98.6 ÷ 1,000
Answer:
98.6 ÷ 1
98.6 ÷ 1 = 98.6
98.6 ÷ 100
98.6 ÷ 100 = 0.986
98.6 ÷ 10
98.6 ÷ 10 = 9.86
98.6 ÷ 1,000
98.6 ÷ 1,000 = 0.0986
Explanation:
Dividing the number 98.6 by 1 results the quotient for 98.6 ÷ 1 = 98.6.
Dividing the number 98.6 by 100 results in moving each digit two places to the right. This looks the same as moving the decimal point two places to the left. The quotient for 98.6 ÷ 100 = 0.986.
Dividing the number 98.6 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 98.6 ÷ 10 = 9.86.
Dividing the number 98.6 by 1000 results in moving each digit three places to the right. This looks the same as moving the decimal point three places to the left. The quotient for 98.6 ÷ 1,000 = 0.0986.
Question 14.
136.5 ÷ 10
Answer:
136.5 ÷ 10 = 13.65
Explanation:
In the above division method the place value is based on 10. The value of each place is 1/10 the value of the place to the left. Dividing the number 136.5 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 136.5 ÷ 10 = 13.65.
Question 15.
753 ÷ 100
Answer:
753 ÷ 100 = 7.53
Explanation:
In the above division method the place value is based on 100. The value of each place is 1/100 the value of the place to the left. Dividing the number 753 by 100 results in moving each digit two place to the right. This looks the same as moving the decimal point two places to the left. The quotient for 753 ÷ 100 = 7.53.
Question 16.
890.1 ÷ 100
Answer:
890.1 ÷ 1 = 890.1
Explanation:
In the above division method the place value is based on 100. Dividing the number 890.1 by 1 results in moving each digit zero places to the right. This looks the same as moving the decimal point zero places to the left. The quotient for 890.1 ÷ 1 = 890.1.
Question 17.
3.71 ÷ 102
Answer:
3.71 ÷ 100 = 0.0371
Explanation:
In the above division method the place value is based on 102. The value of each place is 1/100 the value of the place to the left. Dividing the number 3.71 by 102results in moving each digit two places to the right. This looks the same as moving the decimal point two places to the left. The quotient for 3.71 ÷ 100 = 0.0371.
Question 18.
8,100 ÷ 104
Answer:
8,100 ÷ 10000 = 0.81
Explanation:
In the above division method the place value is based on 104. The value of each place is 1/10000 the value of the place to the left. Dividing the number 8100 by 104 results in moving each digit four places to the right. This looks the same as moving the decimal point four places to the left. The quotient for 8,100 ÷ 10000 = 0.81.
Question 19.
864 ÷ 103
Answer:
864 ÷ 1000 = 0.864
Explanation:
In the above division method the place value is based on 103. The value of each place is 1/1000 the value of the place to the left. Dividing the number 864 by 103 results in moving each digit three places to the right. This looks the same as moving the decimal point three places to the left. The quotient for 864 ÷ 1000 = 0.864.
Question 20.
0.52 ÷ 101
Answer:
0.52 ÷ 10 = 0.052
Explanation:
In the above division method the place value is based on 101. The value of each place is 1/10 the value of the place to the left. Dividing the number 0.52 by 101 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 0.52 ÷ 10 = 0.052.
Question 21.
15.7 ÷ 1,000
Answer:
15.7 ÷ 1,000 = 0.157
Explanation:
In the above division method the place value is based on 1000. Dividing the number 15.7 by 1000 results in moving each digit three places to the right. This looks the same as moving the decimal point three places to the left. The quotient for 15.7 ÷ 1,000 = 0.157.
Question 22.
7,700 ÷ 102
Answer:
7,700 ÷ 100 = 77
Explanation:
In the above division method the place value is based on 100. Dividing the number 7,700 by 100 results in moving each digit two places to the right. This looks the same as moving the decimal point two places to the left. The quotient for 7,700 ÷ 100 = 77.
Question 23.
770 ÷ 102
Answer:
770 ÷ 100 = 7.7
Explanation:
In the above division method the place value is based on 102. The value of each place is 1/100 the value of the place to the left. Dividing the number 770 by 100 results in moving each digit two places to the right. This looks the same as moving the decimal point two places to the left. The quotient for 770 ÷ 100 = 7.7.
Question 24.
77 ÷ 101
Answer:
77 ÷ 10 = 7.7
Explanation:
In the above division method the place value is based on 101. The value of each place is 1/10 the value of the place to the left. Dividing the number 77 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 77 ÷ 10 = 7.7.
Question 25.
7.7 ÷ 101
Answer:
7.7 ÷ 10 = 0.77
Explanation:
In the above division method the place value is based on 101. The value of each place is 1/10 the value of the place to the left. Dividing the number 7.7 by 10 results in moving each digit one place to the right. This looks the same as moving the decimal point one place to the left. The quotient for 7.7 ÷ 10 = 0.77.
Problem Solving
For 26-28, use the table that shows the winning times at the Pacific Middle School swim meet.

Question 26.
What was the difference between the winning butterfly time and the winning backstroke time?
Answer:
The difference between the winning butterfly time and the winning backstroke time is 4.66 seconds.
Explanation:
The winning butterfly time is 58.49 seconds. The winning backstroke time is 53.83 seconds. Subtract the winning backstroke time from winning butterfly time then the difference is 4.66 seconds.
Question 27.
The winning time for the 100-yard freestyle was twice the time for the 50-yard freestyle. What was the winning time for the 100-yard freestyle?
Answer:
The winning time for the 100-yard freestyle is 44.34 seconds.
Explanation:
The winning time for the 100-yard freestyle was twice the time for the 50-yard freestyle. The winning time for 50-yard freestyle is 22.17 seconds. So add 22.17 seconds with 22.17 seconds then the sum is 44.34 seconds. The winning time for the 100-yard freestyle is 44. 34 seconds.
Question 28.
What was the difference between the winning 100-yard freestyle time and the winning butterfly time?
Answer:
The difference between the winning 100-yard freestyle time and the winning butterfly time is 14.15 seconds.
Explanation:
The winning 100-yard freestyle time is 44.34 seconds. The winning 100-yard butterfly time is 58.49 seconds. Subtract 100-yard freestyle winning time from 100-yard butterfly winning time then the difference is 14.15 seconds.
Question 29.
Reasoning A pickup truck carrying 103 identical bricks weighs 6,755 pounds. If the empty truck weighs 6,240 pounds, what is the weight of each brick? Explain how to solve the problem.
Answer:
Question 30.
Higher Order Thinking Katie noticed a pattern in the answers for each of the expressions below. What do you notice?

Answer:
14.6 x 0.1 = 1.46 14.6 ÷ 10 = 1.46
146 x 0.01 = 1.46 146 ÷ 100 = 1.46
146 x 0.001 = 0.146 146 ÷ 1,000 = 0.146
Explanation:
In first expressions I noticed that if we are multiplying 14.6 x 0.1 results the product as 1.46. When we are dividing 14.6 ÷ 10 results the quotient as 1.46.
In second expressions I noticed that if we are multiplying 146 x 0.01 results the product as 1.46. When we are dividing 146 ÷ 100 results the quotient as 1.46.
In third expressions I noticed that if we are multiplying 146 x 0.001 results the product as 0.146. When we are dividing 146 ÷ 1,000 results the quotient as 0.146.
Assessment Practice
Question 31.
Choose the equations in which n = 1,000 makes the equation true.
![]() 0 2.5 ÷ n = 0.025
0 2.5 ÷ n = 0.025
![]() 947.5 ÷ n = 0.9475
947.5 ÷ n = 0.9475
![]() 8,350 ÷ n = 8.35
8,350 ÷ n = 8.35
![]() 16.4 ÷ n = 0.0164
16.4 ÷ n = 0.0164
![]() 0.57 ÷ n = 0.0057
0.57 ÷ n = 0.0057
Answer:

Explanation:
If we put n = 1,000 in first equation 0.25 ÷ 1,000 = 0.0025. The First equation is not true.
If we put n = 1,000 in second equation 947.5 ÷ 1,000 = 0.9475. The Second equation is true.
If we put n = 1,000 in third equation 8,350 ÷ 1,000 = 8.35. The third equation is true.
If we put n = 1,000 in fourth equation 16.4 ÷ 1,000 = 0.0164. The fourth equation is true.
If we put n = 1,000 in fifth equation 0.57 ÷ 1,000 = 0.00057. The fifth equation is not true.
Question 32.
Choose the equations in which d = 102 makes the equation true.
![]() 386.2 ÷ d = 3.862
386.2 ÷ d = 3.862
![]() 4,963.6 ÷ d = 4.9636
4,963.6 ÷ d = 4.9636
![]() 0.6 ÷ d = 0.006
0.6 ÷ d = 0.006
![]() 5.8 ÷ d = 0.58
5.8 ÷ d = 0.58
![]() 15.3 ÷ d = 0.153
15.3 ÷ d = 0.153
Answer:

Explanation:
If we put d = 100 in first equation 386.2 ÷ 100 = 3.862. The First equation is true.
If we put d = 100 in second equation 4,963.6 ÷ 100 = 49.636. The Second equation is not true.
If we put d = 100 in third equation 0.6 ÷ 100 = 0.006. The third equation is true.
If we put d = 100 in fourth equation 5.8 ÷ 100 = 0.058. The fourth equation is not true.
If we put d = 100 in fifth equation 15.3 ÷ 100 = 0.153. The fifth equation is true.
Lesson 6.2 Estimate Decimal Quotients
Activity
Slove&Share
A 135.8-foot piece of construction material needs to be cut into pieces that are each 16 feet long. About how many pieces can be cut? Solve this problem any way you choose.

Answer:
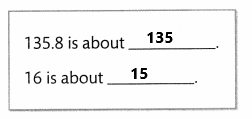
135 ÷ 15 = 9
The construction material can be cut into 9 pieces.
Explanation:
A 135.8-foot piece of construction material is about 135. We need to cut the material into pieces that are each 16 feet long. The 16 pieces material is rounded to 15. Apply division method to solve the problem. Divide 135 with 15 then the result is 9. The construction material can be cut into 9 pieces.
You can use reasoning to estimate decimal quotients.

Look Back! Reasoning Can you find a different way to estimate the answer for the problem above? Explain.
Visual Learning Bridge
Essential Question
How Can You Use Estimation to Find Quotients?
A.
Diego borrowed money from his parents to purchase a video gaming system for $473.89 (including tax). About how much are his monthly payments to his parents if he wants to pay this off in one year?

You can use division to find equal groups.

B.
One Way
Estimate $473.89 ÷ 12. Use rounding.
Round to the nearest ten: 473.89 rounds to 470; 12 rounds to 10
$473.89 ÷ 12 is about $470 ÷ 10 = $47.
Each monthly payment will be about $47.
C.
Another Way
Estimate $473.89 ÷ 12. Use compatible numbers.
Look for compatible numbers.
$473.89 ÷ 12 is close to $480 ÷ 12 = $40.
You know 48 ÷ 12 = 4.

Each monthly payment will be about $40.
Convince Me! Construct Arguments in the example above, which estimate is closer to the exact answer? Tell how you decided.
Answer:
We use compatible numbers to make the problem easier to solve in our head by rounding each number to the nearest ten, twenty, fifty or hundred. But if we make the numbers compatible and round up to the nearest hundred or ten spot, 300 and 350 are much easier to compute in our heads.
Guided Practice
Do You Understand?
Question 1.
Number Sense Leo is estimating 53.1 ÷ 8.4. Do you think he should use 53 ÷ 8 or 54 ÷ 9 to estimate? Why?
Answer:
Estimate 53.1 ÷ 8.4. Use compatible numbers.
Look for compatible numbers.
53.1 ÷ 8.4 is close to 54 ÷ 9 = 6.
53 ÷ 8 is not easy to find and 54 ÷ 9 is easy to find because 54 is multiple of 9.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 53.1 ÷ 8.4 is closes to 54 ÷ 9. The actual dividend 53.1 is compatible to 54. Perform division operation 54 ÷ 9 = 6. The Estimated quotient is 6. Here 54 is multiple of 9 so we can easily find out the quotient. 53 ÷ 8 = 6.625 so it is difficult to find.
Question 2.
Is each quotient greater than or less than 1?
A. 0.2 ÷ 4
B. 1.35 ÷ 0.6
Answer:
A. 0.2 ÷ 4 = 0.05
0.05 < 1
B. 1.35 ÷ 0.6 = 2.25
2.25 > 1
Explanation:
A. Divide 0.2 by 4 then the quotient is 0.05. 0.05 is less than 1.
B. Divide 1.35 by 0.6 then the quotient is 2.25. 2.25 is greater than 1.
How do you know?
In 3-8, estimate each quotient. Use rounding or compatible numbers.
Question 3.
42 ÷ 6.8
Answer:
Estimate 42 ÷ 6.8. Use compatible numbers.
Look for compatible numbers.
42 ÷ 6.8 is closes to 42 ÷ 7 = 6.
The Estimated quotient is 6.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 42 ÷ 6.8 is closes to 42 ÷ 7. The actual divisor 6.8 is compatible to 7. Perform division operation 42 ÷ 7 = 6. The Estimated quotient is 6.
Question 4.
102 ÷ 9.6
Answer:
Estimate 102 ÷ 9.6. Use rounding.
Round to the nearest ten: 102 rounds to 100; 9.6 rounds to 10
102 ÷ 9.6 is about 100 ÷ 10 = 10.
Explanation:
Rounding means replacing a number with an approximate value. In the above division method 102 ÷ 9.6. Round the numbers to the nearest ten or hundreds. Here 102 is rounded to 100 and 9.6 is rounded to 10. Now perform division operation on 100 ÷ 10 = 10. The estimated quotient is 10.
Question 5.
48.9 ÷ 4
Answer:
Estimate 48.9 ÷ 4. Use compatible numbers.
Look for compatible numbers.
48.9 ÷ 4 is closes to 50 ÷ 5 = 10.
The Estimated quotient is 10.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 48.9 ÷ 4 is closes to 50 ÷ 5. The actual dividend is 48.9 is compatible to 50. The actual divisor 4 is compatible to 5. Perform division operation 50 ÷ 5 =10. The Estimated quotient is 10.
Question 6.
72.59 ÷ 7
Answer:
Estimate 72.59 ÷ 7. Use rounding.
Round to the nearest ten: 72.59 rounds to 70; 7 rounds to 10
72.59 ÷ 7 is about 70 ÷ 10 = 7.
Explanation:
Rounding means replacing a number with an approximate value. In the above division method 72.59 ÷ 7. Round the numbers to the nearest ten or hundreds. Here 72.59 is rounded to 70 and 7 is rounded to 10. Now perform division operation on 70 ÷ 10 = 7. The estimated quotient is 7.
Question 7.
15.4 ÷ 1.9
Answer:
Estimate 15.4 ÷ 1.9. Use compatible numbers.
Look for compatible numbers.
15.4 ÷ 1.9 is closes to 16 ÷ 2 = 8.
The Estimated quotient is 8.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 15.4 ÷ 1.9 is closes to 16 ÷ 2. The actual dividend is 15.4 is compatible to 16. The actual divisor 1.9 is compatible to 2. Perform division operation 16 ÷ 2 =8. The Estimated quotient is 8.
Question 8.
44.07 ÷ 6.3
Answer:
Estimate 44.07 ÷ 6.3. Use compatible numbers.
Look for compatible numbers.
44.07 ÷ 6.3 is closes to 42 ÷ 6 = 7.
The Estimated quotient is 7.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 44.07 ÷ 6.3 is closes to 42 ÷ 6. The actual dividend is 44.07 is compatible to 42. The actual divisor 6.3 is compatible to 6. Perform division operation 42 ÷ 6 =7. The Estimated quotient is 7.
Independent Practice
Leveled Practice In 9 and 10, complete the work to estimate each quotient.
Question 9.

Answer:
Estimate 64.5 ÷ 12.3. Use rounding.
Round to the nearest ten: 64.5 rounds to 65 ; 12.3 rounds to 10
64.5 ÷ 12.3 is about 65 ÷ 10 = 6.5.
Explanation:
Rounding means replacing a number with an approximate value. In the above division method 64.5 ÷ 12.3. Round the numbers to the nearest ten or hundreds. Here 64.5 is rounded to 65 and 12.3 is rounded to 10. Now perform division operation on 65 ÷ 10 = 6.5. The estimated quotient is 6.5.
Question 10.
Estimate 64.5 ÷ 12.3 using compatible numbers.
65 ÷ 10 = _____
Answer:
Estimate 64.5 ÷ 12.3. Use compatible numbers.
Look for compatible numbers.
64.5 ÷ 12.3 is closes to 65 ÷ 10 = 6.5.
The Estimated quotient is 6.5.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 64.5 ÷ 12.3 is closes to 65 ÷ 10. The actual dividend is 64.5 is compatible to 65. The actual divisor 12.3 is compatible to 10. Perform division operation 65 ÷ 10 =6.5. The Estimated quotient is 6.5.
In 11-19, estimate each quotient.
Question 11.
7 ÷ 0.85
Answer:
Estimate 7 ÷ 0.85. Use compatible numbers.
Look for compatible numbers.
7 ÷ 0.85 is closes to 7 ÷ 1 = 7.
The Estimated quotient is 7.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 7 ÷ 0.85 is closes to 7 ÷ 1. The actual divisor 0.85 is compatible to 1. Perform division operation 7 ÷ 1 = 7. The Estimated quotient is 7.
Question 12.
9.6 ÷ 0.91
Answer:
Estimate 9.6 ÷ 0.91. Use compatible numbers.
Look for compatible numbers.
9.6 ÷ 0.91 is closes to 10 ÷ 1 = 10.
The Estimated quotient is 10.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 9.6 ÷ 0.91 is closes to 10 ÷ 1. The actual dividend 9.6 is compatible to 10.The actual divisor 0.91 is compatible to 1. Perform division operation 10 ÷ 1 = 10. The Estimated quotient is 10.
Question 13.
17.7 ÷ 3.2
Answer:
Estimate 17.7 ÷ 3.2. Use compatible numbers.
Look for compatible numbers.
17.7 ÷ 3.2 is closes to 18 ÷ 3 = 6.
The Estimated quotient is 6.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 17.7 ÷ 3.2 is closes to 18 ÷ 3. The actual dividend 17.7 is compatible to 18.The actual divisor 3.2 is compatible to 3. Perform division operation 18 ÷ 3 = 6. The Estimated quotient is 6.
Question 14.
91.02 ÷ 4.9
Answer:
Estimate 91.02 ÷ 4.9. Use compatible numbers.
Look for compatible numbers.
91.02 ÷ 4.9 is closes to 90 ÷ 5 = 18.
The Estimated quotient is 18.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 91.02 ÷ 4.9 is closes to 90 ÷ 5. The actual dividend 91.02 is compatible to 90.The actual divisor 4.9 is compatible to 5. Perform division operation 90 ÷ 5 = 18. The Estimated quotient is 18.
Question 15.
45.64 ÷ 6.87
Answer:
Estimate 45.64 ÷ 6.87. Use compatible numbers.
Look for compatible numbers.
45.64 ÷ 6.87 is closes to 49 ÷ 7 = 7.
The Estimated quotient is 7.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 45.64 ÷ 6.87 is closes to 49 ÷ 7. The actual dividend 45.64 is compatible to 49.The actual divisor 6.87 is compatible to 7. Perform division operation 49 ÷ 7 = 7. The Estimated quotient is 7.
Question 16.
821.22 ÷ 79.4
Answer:
Estimate 821.22 ÷ 79.4. Use rounding.
Round to the nearest ten: 821.22 rounds to 800 ; 79.4 rounds to 80
821.22 ÷ 79.4 is about 800 ÷ 80 = 10.
Explanation:
Rounding means replacing a number with an approximate value. In the above division method 821.22 ÷ 79.4. Round the numbers to the nearest ten or hundreds. Here 821.22 is rounded to 800 and 79.4 is rounded to 80. Now perform division operation on 800 ÷ 80 = 10. The estimated quotient is 10.
Question 17.
22.5 ÷ 3
Answer:
Estimate 22.5 ÷ 3. Use compatible numbers.
Look for compatible numbers.
22.5 ÷ 3 is closes to 24 ÷ 3 = 8.
The Estimated quotient is 8.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 22.5 ÷ 3 is closes to 24 ÷ 3. The actual dividend 22.5 is compatible to 24. Perform division operation 24 ÷ 3 = 8. The Estimated quotient is 8.
Question 18.
15.66 ÷ 9.3
Answer:
Estimate 15.66 ÷ 9.3. Use rounding.
Round to the nearest ten: 15.66 rounds to 20 ; 9.3 rounds to 10.
15.66 ÷ 9.3 is about 20 ÷ 10 = 2.
Explanation:
Rounding means replacing a number with an approximate value. In the above division method 15.66 ÷ 9.3. Round the numbers to the nearest ten or hundreds. Here 15.66 is rounded to 20 and 9.3 is rounded to 10. Now perform division operation on 20 ÷ 10 = 2. The estimated quotient is 2.
Question 19.
156.3 ÷ 14.5
Answer:
Estimate 156.3 ÷ 14.5. Use rounding.
Round to the nearest ten: 156.3 rounds to 160 ; 14.5 rounds to 20.
156.3 ÷ 14.5 is about 160 ÷ 20 = 8.
Explanation:
Rounding means replacing a number with an approximate value. In the above division method 156.3 ÷ 14.5. Round the numbers to the nearest ten or hundreds. Here 156.3 is rounded to 160 and 14.5 is rounded to 20. Now perform division operation on 160 ÷ 20 = 8. The estimated quotient is 8.
Problem Solving
Question 20.
Luci’s mother gave her $7.50 to buy 8 spiral notebooks. With tax, the cost of each notebook is $1.05. Does Luci have enough money? Use compatible numbers and estimation to help you decide.
Answer:
Question 21.
Critique Reasoning Kerri said that the quotient of 4.2 ÷ 5 is about 8 tenths because 4.2 ÷ 5 is close to 40 tenths ÷ 5. Do you agree with Kerri’s reasoning? Explain.
Answer:
Question 22.
Higher Order Thinking Write a decimal division problem that has an estimated quotient of 4. Explain how to get that estimate.
Answer:
Question 23.
Lia’s car averages 14.5 miles per gallon while Roman’s car averages 28.5 miles per gallon. Use estimation to find how many times as many miles per gallon Roman’s car gets compared to Lia’s car.
Answer:
In 24-26, use the table.

Question 24.
enVision® STEM Which sample from the experiment had the least mass? Which had the lowest temperature?
Answer:
In the above table we can observe Sample 3 had the least mass 0.058 g from the experiment. Sample 1 had the lowest temperature as 37.57°C.
Question 25.
Sample 3 was used in another experiment. A temperature of 82.14°C was recorded. How many degrees did the temperature change?
Answer:
In the above table we can observe sample 3 had the temperature 75.50°C. Sample 3 was used in another experiment. A temperature of 82.14°C was recorded. The difference of these two temperatures are 6.64°C
Question 26.
What is the difference in mass between Sample 1 and Sample 2?
Answer:
Sample 1 has the mass 0.98 g.
Sample 2 has the mass 0.58 g.
The difference in mass between Sample 1 and Sample 2 is 0.4.
Assessment Practice
Question 27.
Mauricio scored a total of 34.42 points in five gymnastic events. Which equation shows the best way to estimate Mauricio’s score for each event?
A. 35 ÷ 5 = 7
B. 35 ÷ 7 = 5
C. 30 ÷ 10 = 3
D. 40 ÷ 10 = 4
Answer:
Option A 35 ÷ 5 = 7 is correct.
35 ÷ 5 = 7 is the best way to estimate Mauricio’s score for each event.
Explanation:
Mauricio scored a total of 34.42 points in five gymnastic events. Use compatible method. In the above options option A is correct. The equation 34.42 ÷ 5 is closes to 35 ÷ 5. The actual dividend 34.42 is compatible to 35. Perform division operation 35 ÷ 5 = 7. The Estimated score for each event is 8.
Question 28.
Terry paid $117.50 for 18 identical flash drives. Which is the best estimate for the cost of each flash drive?
A. $6
B. $10
C. $12
D. $60
Answer:
Option A $6 is correct.
$117.50 ÷ 18
$120 ÷ 20 = $6.
The estimated cost of each flash drive is 6.
Explanation:
Terry paid $117.50 for 18 identical flash drives. Use rounding method. Rounding means replacing a number with an approximate value. In the above division method $117.50 ÷ 18. Round the numbers to the nearest ten or hundreds. Here $117.50 is rounded to $120 and 18 is rounded to 20. Now perform division operation on $120 ÷ 20 = $6. The estimated cost of each flash drive is $6.
Lesson 6.3 Use Models to Divide by a 1-Digit Whole Number
Activity
Solve&Share
Chris paid $3.60 for 3 colored pens. Each pen costs the same amount. How much did each pen cost? Solve this problem any way you choose.
You can use appropriate tools such as drawings, money, or place-value blocks to help you divide. Show your work!

Answer:
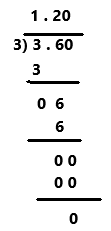
Each pen cost is $1.20.
Explanation:
Chris paid $3.60 for 3 colored pens. Each pen costs the same amount. Divide $3.60 with 3 colored pens then the quotient is $1.20. Each pen cost is $1.20.
Look Back! Without dividing, how do you know that the answer to the problem above must be greater than 1?
Answer:
The answer to the above problem must be greater than 1. Because each pen costs the same amount. we can clearly see that Chris paid $3.60 for 3 colored pens. So we can say without dividing method the answer to the above problem is greater than 1
Visual Learning Bridge
Essential Question How Can You Use Models to Find a Decimal Quotient?
A.
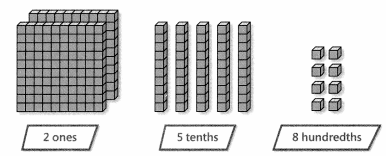
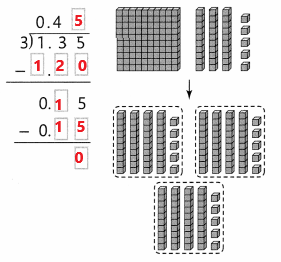
Three friends received $2.58 for aluminum cans they recycled. They decided to share the money equally. How much will each friend get?
You can use place value blocks. Let a 100 square = $1.00, a tenth bar = $0.10, and a hundredth cube = $0.01.

Find 2.58 ÷ 3.
B.
There are not enough ones to put 1 in each group, so regroup the 2 ones into 20 tenths. You can see that there are 25 tenths in 2.58. Divide the 25 tenths into 3 equal groups.

C.
Trade the one extra tenth for 10 hundredths to get 18 hundredths. Divide the 18 hundredths into 3 equal groups. Each group gets 6 hundredths.
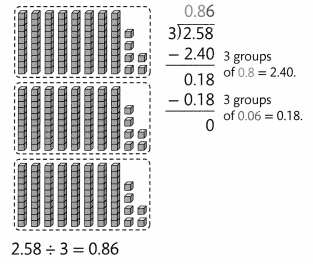
Each of the 3 friends will get $0.86.
Convince Me! Reasoning The next week, 4 friends got $8.24 for the cans they collected. How much money will each friend get? Estimate using compatible numbers and then use a strategy to find the answer.
Guided Practice
Do You Understand?
Question 1.
What is a reasonable estimate for 8.24 ÷ 4? Explain.
Answer:
Estimate $8.24 ÷ 4. Use compatible numbers.
Look for compatible numbers.
$8.24 ÷ 4 is closes to $8 ÷ 4 = $2.
The Estimated quotient is $2.
Each friend get $2.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. The next week, 4 friends got $8.24 for the cans they collected. In the above division problem $8.24 ÷ 4 is closes to 8 ÷ 4. The actual dividend 8.24 is compatible to 8. Perform division operation 8 ÷ 4 = 2. The Estimated quotient is 2. Each friend get $2.
Question 2.
How is dividing a decimal by a whole number similar to dividing a whole number by a whole number? Explain.
Answer:
Do You Know How?
Question 3.
Use models to help you divide 2.16 ÷ 4. Complete the division calculation.

Answer:

2.16 ÷ 4 = 0.54.
Explanation:
In the above image we can observe the division of 2.16 ÷ 4 = 0.54. There are not enough ones to put 1 in each group, so regroup the 2 ones into 20 tenths. Divide 20 tenths into 4 equal groups. Each group gets 5 tenths. Four groups of 0.5 = 2.0.
Trade the one extra tenth for 10 hundredths to get 16 hundredths. Divide the 16 hundredths into 4 equal groups. Each group gets 4 hundredths. Four groups of 0.04 = 0.16.
Independent Practice
Leveled Practice In 4-9, divide. Use or draw models to help.
Question 4.

Answer:
1.35 ÷ 3 = 0.45
Explanation:
In the above image we can observe the division of 1.35 ÷ 3 = 0.45. There are not enough ones to put 1 in each group, so regroup the 1 ones into 10 tenths. We can see that there are 13 tenths in 1.35. Divide the 13 tenths into 3 equal groups. Each group gets 4 tenths. Three groups of 0.4 = 1.2.
Trade the one extra tenth for 10 hundredths to get 15 hundredths. Divide the 15 hundredths into 3 equal groups. Each group gets 5 hundredths. Three groups of 0.05 = 0.15.
Question 5.
Answer:
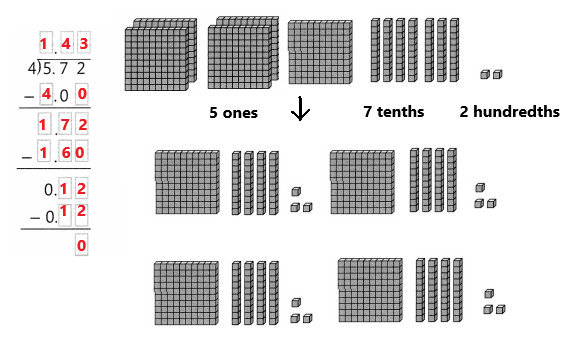
5.72 ÷ 4 = 1.43
Explanation:
In the above image we can observe the division of 5.72 ÷ 4 = 1.43. There are enough ones to put 1 in each group, and extra ones is regrouped. Divide the 5 ones into 4 equal groups. Each group gets 1 ones. Four groups of 1 = 4. Regroup of the 1 ones into 10 tenths. We can see that there are 17 tenths in 5.72. Divide the 17 tenths into 4 equal groups. Each group gets 4 tenths. Four groups of 0.4 = 1.6.
Trade the one extra tenth for 10 hundredths to get 12 hundredths. Divide the 12 hundredths into 4 equal groups. Each group gets 3 hundredths. Four groups of 0.03 = 0.12.
Question 6.
2.38 ÷ 7
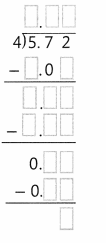
Answer:
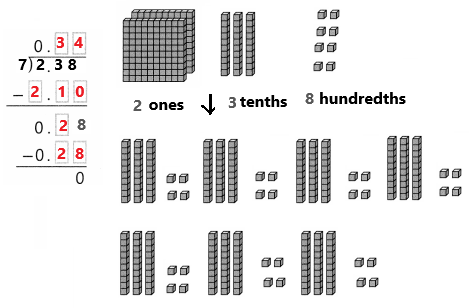
2.38 ÷ 7 = 0.34.
Explanation:
In the above image we can observe the division of 2.38 ÷ 7 = 0.34. There are not enough ones to put 1 in each group, so regroup the 2 ones into 20 tenths. We can see that there are 23 tenths in 2.38. Divide the 23 tenths into 7 equal groups. Each group gets 3 tenths. Seven groups of 0.3 = 2.1.
Trade the two extra tenth for 20 hundredths to get 28 hundredths. Divide the 28 hundredths into 7 equal groups. Each group gets 4 hundredths. Seven groups of 0.04 = 0.28.
Question 7.
4.71 ÷ 3
Answer:
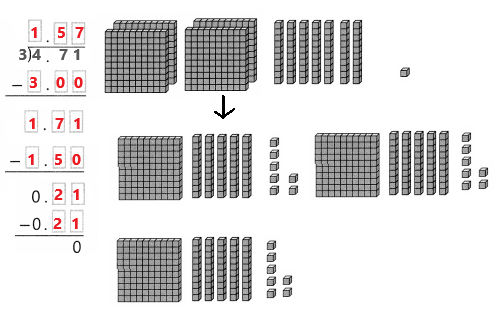
4.71 ÷ 3 = 1.57.
Explanation:
In the above image we can observe the division of 4.71 ÷ 3 = 1.57. There are enough ones to put 1 in each group, and extra ones is regrouped. Divide the 3 ones into 3 equal groups. Each group gets 1 ones. Three groups of 1 = 3. Regroup of the 1 ones into 10 tenths. We can see that there are 17 tenths in 4.71. Divide the 17 tenths into 3 equal groups. Each group gets 5 tenths. Three groups of 0.5 = 1.5.
Trade the two extra tenth for 20 hundredths to get 21 hundredths. Divide the 21 hundredths into 3 equal groups. Each group gets 7 hundredths. Three groups of 0.07 = 0.21.
Question 8.
1.76 ÷ 8
Answer:
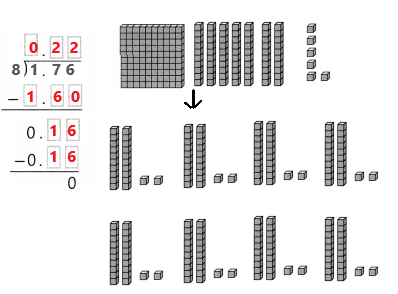
1.76 ÷ 8 = 0.22.
Explanation:
In the above image we can observe the division of 1.76 ÷ 8 = 0.22. There are not enough ones to put 1 in each group, so regroup the 1 ones into 10 tenths. We can see that there are 17 tenths in 1.76. Divide the 17 tenths into 8 equal groups. Each group gets 2 tenths. Eight groups of 0.2 = 1.6.
Trade the one extra tenth for 10 hundredths to get 16 hundredths. Divide the 16 hundredths into 8 equal groups. Each group gets 2 hundredths. Eight groups of 0.02 = 0.16.
Question 9.
5.36 ÷ 2
Answer:
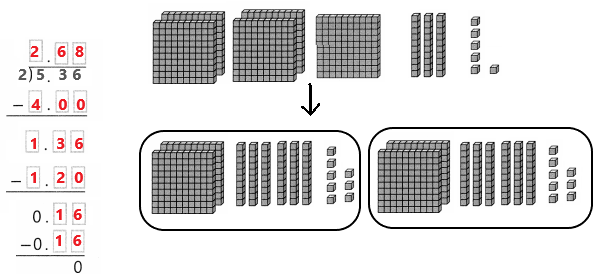
5.36 ÷ 2 = 2.68.
Explanation:
In the above image we can observe the division of 5.36 ÷ 2 = 2.68. There are enough ones to put 2 in each group, and extra ones is regrouped. Divide the 5 ones into 2 equal groups. Each group gets 2 ones. Two groups of 2 = 4. Regroup of the 1 ones into 10 tenths. We can see that there are 13 tenths in 5.36. Divide the 13 tenths into 2 equal groups. Each group gets 6 tenths. Two groups of 0.6 = 1.2.
Trade the one extra tenth for 10 hundredths to get 16 hundredths. Divide the 16 hundredths into 2 equal groups. Each group gets 8 hundredths. Two groups of 0.08 = 0.16.
Problem Solving
Question 10.
Reasoning Alan is modeling 2.65 ÷ 5. How should he exchange the place-value blocks so he can make 5 equal shares?
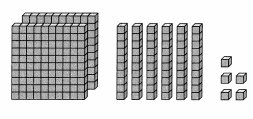
Answer:
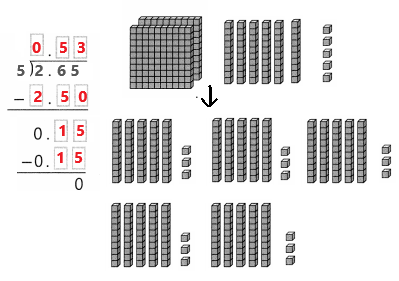
2.65 ÷ 5 = 0.53
Explanation:
In the above image we can observe the division of 2.65 ÷ 5 = 0.53. There are not enough ones to put 1 in each group, so regroup the 2 ones into 20 tenths. We can see that there are 26 tenths in 2.65. Divide the 26 tenths into 5 equal groups. Each group gets 5 tenths. Five groups of 0.5 = 2.5.
Trade the one extra tenth for 10 hundredths to get 15 hundredths. Divide the 15 hundredths into 5 equal groups. Each group gets 3 hundredths. Five groups of 0.03 = 0.15.
Question 11.
Algebra Abby wants to know the value of n in the equation 7.913 × n = 791.3. What value for n makes the equation true?
Answer:
7.913 × n = 791.3
7.913 × 100 = 791.3
If n= 100 makes the equation true.
Question 12.
To find 5.16 ÷ 6, should you divide the ones first or the tenths first? Why?
Answer:

First we have to divide the ones first.
5.16 ÷ 6 = 0.86
Explanation:
In the above image we can observe the division of 5.16 ÷ 6 = 0.86. There are not enough ones to put 1 in each group, so regroup the 5 ones into 50 tenths. We can see that there are 51 tenths in 5.16. Divide the 51 tenths into 6 equal groups. Each group gets 8 tenths. Six groups of 0.8 = 4.8.
Trade the one extra tenth for 10 hundredths to get 36 hundredths. Divide the 36 hundredths into 6 equal groups. Each group gets 6 hundredths. Six groups of 0.06 = 0.36.
Question 13.
There are 264 children going on a field trip. Are 5 buses enough if each bus holds 52 children? Tell how you decided.
Answer:
264 ÷ 5 = 52.8
5 buses are not enough to hold 52 children in each bus.
Explanation:
There are 264 children going on a field trip. Divide 264 by 5 then the quotient is 52.8. 5 buses are not enough to hold 52 children in each bus.
Question 14.
Higher Order Thinking Ginny earned $49.50 for 6 hours of gardening and $38.60 for 4 hours of babysitting. For which job did she earn more money per hour? How much more per hour did she earn? Explain how you found the answers.
Think about what information in the problem you need to compare.

Answer:
Ginny earned $49.50 for 6 hours of gardening.
$49.50 ÷ 6 = $8.25.
Ginny earns $8.25 per hour.
Ginny earned $38.60 for 4 hours of babysitting.
$38.60 ÷ 4 = $9.65.
Ginny earns $9.65 per hour.
$9.65 – $8.25 = $1.4.
She earns more $1.4 per hour.
Explanation:
Ginny earned $49.50 for 6 hours of gardening. Perform division operation on $49.50 ÷ 6 = $8.25. Ginny earns $8.25 per hour. Ginny earned $38.60 for 4 hours of babysitting. Perform division operation on $38.60 ÷ 4 = $9.65. Ginny earns $9.65 per hour. Now we have to calculate how much more money she is earning. Subtract
$9.65 – $8.25 = $1.4. She earns more $1.4 per hour.
Assessment Practice
Question 15.
Tia drew the model below for 1.35 ÷ 3.

Part A
Explain the mistake Tia made.
Answer:
1.35 ÷ 3 = 0.45.
Explanation:
In the above image we can observe the 4 groups. Tia made a mistake of drawing the model above. She has to draw 3 groups. She drew one extra group of 4 tenths and 5 hundredths.
Part B
Draw the correct model and find the quotient.
Answer:
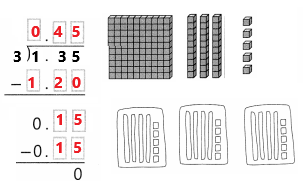
1.35 ÷ 3 = 0.45.
The quotient is 0.45.
Explanation:
In the above image we can observe the division of 1.35 ÷ 3 = 0.45. There are not enough ones to put 1 in each group, so regroup the 1 ones into 10 tenths. We can see that there are 13 tenths in 1.35. Divide the 13 tenths into 3 equal groups. Each group gets 4 tenths. Three groups of 0.4 = 1.2.
Trade the one extra tenth for 10 hundredths to get 15 hundredths. Divide the 15 hundredths into 3 equal groups. Each group gets 5 hundredths. Three groups of 0.05 = 0.15.
Lesson 6.4 Divide by a 2-Digit Whole Number
Activity
Solve&Share
Stan has a rectangular piece of carpet with an area of 23.4 square meters. The piece of carpet is 13 meters long. What is the width of the piece of carpet? Solve this problem any way you choose.
Model with Math You can write an equation to model the problem.

Look Back! How could you estimate the width of the piece of carpet?
Answer:
23.4 ÷ 13 = ?
23.4 ÷ 13 = 1.8
The width of the piece of carpet is 1.8 meters.
Explanation:
Stan has a rectangular piece of carpet with an area of 23.4 square meters. The piece of carpet is 13 meters long. Perform division operation 23.4 ÷ 13 = 1.8. The width of the piece of carpet is 1.8 meters.
Visual Learning Bridge
Essential Question How Do You Divide Decimals Question by 2-Digit Numbers?
A.
Erin’s garden has an area of 84.8 square feet. She knows the length is 16 feet. What is the width of Erin’s garden? How can you solve 84.8 ÷ 16 = w?

You can use what you know about dividing whole numbers to help.

B.
The total area is 84.8. The pieces of the model represent the areas for the partial quotients.

Convince Me! Reasoning How could Amy use estimation to make sure the decimal point is in the correct place in the quotient?
Guided Practice
Do You Understand?
In 1 and 2, use the example on the previous page.
Question 1.
Where is 5.3 shown in the diagram?
Answer:
Question 2.
How can you check that the quotient 5.3 is reasonable? Explain.
Answer:
Do You Know How?
In 3 and 4, complete the division problem.
Question 3.
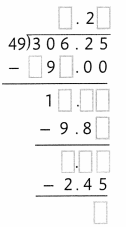
Answer:
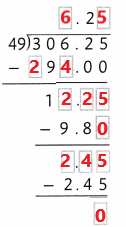
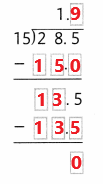
306.25 ÷ 49 = 6.25
Explanation:
In the above image we can observe the division operation 306.25 ÷ 49 = 6.25. The nearest possible multiple value of 49 is 294(49 x 6). Subtract 294 from 306.25 so as to get the remainder 12.25. 49 cannot be a multiple of 12.25 and so we have kept a decimal in the quotient and now 49 has the least possible multiple value of 9.8(49 x 0.2) near to 12.25. After subtracting 9.8 from 12.25, we are now having 6.2 as quotient and 2.45 as remainder. Now the possible multiple value of 49 near to 2.45 is 2.45 itself(49 x 0.05 = 2.45). Now the remainder is zero and the final quotient is 6.25.
Question 4.

Answer:
28.5 ÷ 15 = 1.9
Explanation:
In the above image we can observe the division operation 28.5 ÷ 15 = 1.9. The nearest possible multiple value of 15 is 15(15 x 1). Subtract 15 from 28.5 so as to get the remainder 13.5. 15 cannot be a multiple of 13.5 and so we have kept a decimal in the quotient and now the possible multiple value of 15 near to 13.5 is 13.5 itself(15 x 0.9 = 13.5). Now the remainder is zero and the final quotient is 1.9.
Independent Practice
Leveled Practice In 5-6, find each quotient and label the model.
Question 5.
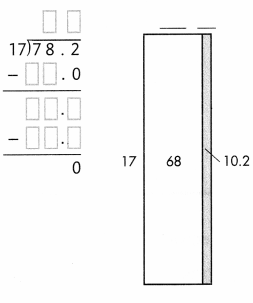
Answer:
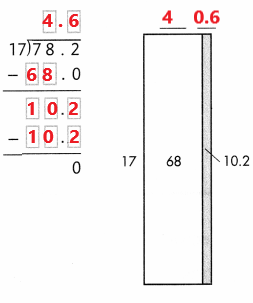
78.2 ÷ 17 = 4.6
Explanation:
In the above image we can observe the division operation 78.2 ÷ 17 = 4.6. The nearest possible multiple value of 17 is 68(17 x 4). Subtract 68 from 78.2 so as to get the remainder 10.2. 17 cannot be a multiple of 10.2 and so we have kept a decimal in the quotient and now the possible multiple value of 17 near to 10.2 is 10.2 itself(17 x 0.6 = 10.2). Now the remainder is zero and the final quotient is 4.6.
Question 6.
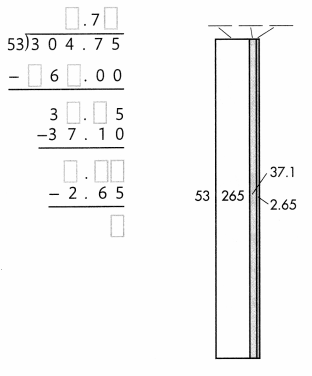
Answer:
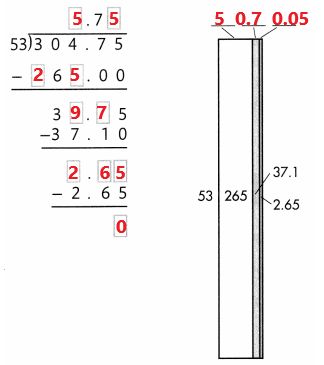
304.75 ÷ 53 = 5.75
Explanation:
In the above image we can observe the division operation 304.75÷ 53 = 5.75. The nearest possible multiple value of 53 is 265(53 x 5). Subtract 265 from 304.75 so as to get he remainder 39.75. 53 cannot be a multiple of 39.75 and so we have kept a decimal in the quotient and now 53 has the least possible multiple value of 37.10(53 x 0.7) near to 39.75. After subtracting 37.10 from 39.75, we are now having 5.7 as quotient and 2.65 as remainder. Now the possible multiple value of 53 near to 2.65 is 2.65 itself(53 x 0.05 = 2.65). Now the remainder is zero and the final quotient is 5.75.
In 7-10, find each quotient.
Question 7.
![]()
Answer:

91.8 ÷ 27 = 3.4
The quotient is 3.4
Explanation:
In the above image we can observe the division operation 91.8 ÷ 27 = 3.4. The nearest possible multiple value of 27 is 81(27 x 3). Subtract 81 from 91.8 so as to get the remainder as 10.8. 27 cannot be a multiple of 10.8 and so we have kept a decimal in the quotient and now the possible multiple value of 27 near to 10.8 is 10.8 itself(27 x 0.4 = 10.8). Now the remainder is zero and the final quotient is 3.4.
Question 8.
![]()
Answer:

3.9 ÷ 15 = 0.26
The quotient is 0.26
Explanation:
In the above image we can observe the division operation 3.9 ÷ 15 = 0.26. 15 cannot be a multiple of 3.9 so we have kept a decimal in the quotient and now 15 has the least possible multiple value of 3.0(15 x 0.2) near to 3.9. Subtract 3.0 from 3.9 then the remainder is 0.9. Now the possible multiple value of 15 near to 0.9 is 0.9 itself(15 x 0.06 = 0.9). Now the remainder is zero and the final quotient is 0.26.
Question 9.
![]()
Answer:

39.6 ÷ 12 = 3.3
The quotient is 3.3
Explanation:
In the above image we can observe the division operation 39.6 ÷ 12 = 3.3. The nearest possible multiple value of 12 is 36(12 x 3). Subtract 36 from 39.6 so as to get the remainder as 3.6. 12 cannot be a multiple of 3.6 and so we have kept a decimal in the quotient and now the possible multiple value of 12 near to 3.6 is 3.6 itself(12 x 0.3 = 3.6). Now the remainder is zero and the final quotient is 3.3.
Question 10.
![]()
Answer:

247.5 ÷ 50 = 4.95
Explanation:
In the above image we can observe the division operation 247.5 ÷ 50 = 4.95. The nearest possible multiple value of 50 is 200(50 x 4). Subtract 200 from 247.5 so as to get the remainder 47.5. 50 cannot be a multiple of 47.5 and so we have kept a decimal in the quotient and now 50 has the least possible multiple value of 45.0(50 x 0.9) near to 47.5. After subtracting 45.0 from 47.5, we are now having 4.9 as quotient and 2.5 as remainder. Now the possible multiple value of 50 near to 2.5 is 2.5 itself(50 x 0.05 = 2.5). Now the remainder is zero and the final quotient is 4.95.
Problem Solving
Question 11.
Sharon pays $98.75 for twenty-five 14-ounce boxes of Yummy Flakes cereal. How much does one box of cereal cost?
Answer:
Question 12.
Javier bought a new TV for $479.76. He will make equal payments each month for 2 years. How can Javier use compatible numbers to estimate each payment?
Answer:
Estimate $479.76 ÷ 24. Use compatible numbers.
Look for compatible numbers.
$479.76 ÷ 24 is closes to $480 ÷ 24 = $20.
The Estimated quotient is $20.
Javier pays each month $20.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. Javier bought a new TV for $479.76. He will make equal payments each month for 2 years. 2years means 24 months. In the above division problem $479.76 ÷ 24 is closes to 480 ÷ 24. The actual dividend $479.76 is compatible to 480. Perform division operation 480 ÷ 24 = 20. The Estimated quotient is 20. Javier pays each month $20.
Question 13.
Higher Order Thinking The area of the rectangular flower bed shown is 20.4 square meters. How many meters of edging are needed to go around the flower bed? Explain.

Answer:
Question 14.
Make Sense and Persevere Ms. Wang is shopping for a new refrigerator. Brand A costs $569 and uses 635 kilowatt-hours per year. Brand B costs $647 and uses 582 kilowatt-hours per year. If electricity costs $0.18 per kilowatt-hour, how much would Ms. Wang save on electricity per year by buying Brand B?
Answer:
Question 15.
Pat is driving from Seattle to Los Angeles. The distance is 1,135 miles. For the first 250 miles, it costs Pat $0.29 a mile to drive. After that, her driving cost is $0.16 a mile. What is Pat’s total driving cost?
Answer:
Assessment Practice
Question 16.
Which is equal to 27.3 divided by 13?
A. 0.21
B. 2.01
C. 2.1
D. 21
Answer:

27.3 ÷ 13 = 2.1
Option C is correct.
Explanation:
Divide 27.3 by 13 then the quotient is 2.1. So option C is correct.
Question 17.
Which is equal to 73.5 divided by 21?
A. 0.35
B. 3.05
C. 3.5
D. 30.5
Answer:

73.5 ÷ 21 = 3.5
Option C is correct.
Explanation:
Divide 73.5 by 21 the quotient is 3.5. So option C is correct.
Lesson 6.5 Divide by a Decimal
Activity
Solve & Share
Aaron buys erasers for his pencils. Each eraser costs $0.20. The total cost is $1.20. How many erasers does Aaron buy? Solve this problem any way you choose.
You can model the problem using hundredth grids or other drawings. Show your work!

Look Back! Reasoning How do you know your answer makes sense?
Answer:
$1.20 ÷ ? = $0.20
$1.20 ÷ 6 = $0.20
Aaron buys 6 erasers for his pencils.
Explanation:
Aaron buys erasers for his pencils. Each eraser costs $0.20. The total cost is $1.20. Divide $1.20 by $0.20 then the answer is 6. Aaron buys 6 erasers for his pencils.
Visual Learning Bridge
Essential Question How Can You Divide a Preston Decimal by a Decimal?
A.
Michelle purchases several bottles of water. Before tax is added, the total cost is $3.60 and the cost of each bottle is $1.20. How many bottles did she buy?
Divide $3.60 by $1.20.

You can use what you know about division with whole numbers to find how many groups of $1.20 are in $3.60.

B.
One Way
Think: $3.60 is the same as 36 dimes. $1.20 is the same as 12 dimes.
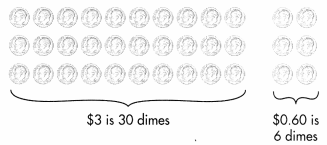
How many 12s are in 36?
She bought 3 bottles.
C.
Another Way
Think multiplication:
To find 3.60 ÷ 1.20, use the relationship between multiplication and division.
1.20 × ? = 3.60
Writing this another way:
120 hundredths ×? = 360 hundredths
? = 3
She bought 3 bottles.
Convince Me! Construct Arguments Is 3.6 ÷ 1.2 equal to, less than, or greater than 36 ÷ 12? Explain.
Guided Practice
Do You Understand?
Question 1.
How is dividing by a decimal like dividing by a whole number?
Answer:
Question 2.
How can you use multiplication to find 2.8 ÷ 0.7?
Answer:
Do You Know How?
In 3-6, use what you know about decimal division and mental math to find each quotient.
Question 3.
2 ÷ 0.5
Answer:
To find 2 ÷ 0.5, use the relationship between multiplication and division.
0.5 × ? = 2
? = 4
2 ÷ 0.5 = 4
The quotient is 4.
Explanation:
Multiply the divisor 0.5 with 4 then the product is 2. Divide the dividend 2 with the divisor 0.5 then the quotient is 4.
Question 4.
1.25 ÷ 0.25
Answer:
To find 1.25 ÷ 0.25, use the relationship between multiplication and division.
0.25 × ? = 1.25
? = 5
1.25 ÷ 0.25 = 5
The quotient is 5.
Explanation:
Multiply the divisor 0.25 with 5 then the product is 1.25. Divide the dividend 1.25 with the divisor 0.25 then the quotient is 5.
Question 5.
2.1 ÷ 0.7
Answer:
To find 2.1 ÷ 0.7, use the relationship between multiplication and division.
0.7 × ? = 2.1
? = 3
2.1 ÷ 0.7 = 3
The quotient is 3.
Explanation:
Multiply the divisor 0.7 with 3 then the product is 1.25. Divide the dividend 2.1 with the divisor 0.7 then the quotient is 3.
Question 6.
6.6 ÷ 0.3
Answer:
To find 6.6 ÷ 0.3, use the relationship between multiplication and division.
0.3 × ? = 6.6
? = 3
6.6 ÷ 0.3 = 22
The quotient is 22.
Explanation:
Multiply the divisor 0.3 with 22 then the product is 6.6. Divide the dividend 6.6 with the divisor 0.3 then the quotient is 22.
Think about how the dividend, divisor, and quotient are related.

Independent Practice
In 7-10, use what you know about multiplication, division, place value, and partial quotients to divide.
Question 7.
2.56 ÷ 0.04
Answer:
To find 2.56 ÷ 0.04, use the relationship between multiplication and division.
0.04 × ? = 2.56
Writing this another way:
4 hundredths × ? = 256 hundredths
? = 64
2.56 ÷ 0.04 = 64
Explanation:
We have to use the relationship between multiplication and division. Multiply the divisor 0.04 with 64 then the product is 2.56. By dividing 2.56 with 0.04 then the quotient is 64.
Question 8.
25.6 ÷ 0.4
Answer:
To find 25.6 ÷ 0.4, use the relationship between multiplication and division.
0.4 × ? = 25.6
Writing this another way:
4 tenths × ? = 256 tenths
? = 64
25.6 ÷ 0.4 = 64
Explanation:
We have to use the relationship between multiplication and division. Multiply the divisor 0.4 with 64 then the product is 25.6. By dividing 25.6 with 0.4 then the quotient is 64.
Question 9.
256 ÷ 4
Answer:
To find 256 ÷ 4, use the relationship between multiplication and division.
4 × ? = 256
Writing this another way:
4 ones × ? = 256 ones
? = 64
256 ÷ 4 = 64
Explanation:
We have to use the relationship between multiplication and division. Multiply the divisor 4 with 64 then the product is 256. By dividing 256 with 4 then the quotient is 64.
Question 10.
Describe the relationship among Problems 7, 8, and 9.
Answer:
The relationship among problems 7, 8, and 9. The quotient is same in all problems. In problem 7 hundredths place value is used. In problem 8 tenths place value is used. In problem 9 ones place value is used.
In 11-18, find each quotient.
Question 11.
![]()
Answer:

4.75 ÷ 0.25 = 19
The quotient is 19.
Explanation:
In this division operation 4.75 ÷ 0.25. The dividend is 4.75 and the divisor is 0.25. By dividing dividend 4.75 with the divisor 0.25 then the quotient is 19.
Question 12.
![]()
Answer:

4.56 ÷ 0.04 = 114
The quotient is 114.
Explanation:
In this division operation 4.56 ÷ 0.04. The dividend is 4.56 and the divisor is 0.04. By dividing dividend 4.56 with the divisor 0.04 then the quotient is 114.
Question 13.
![]()
Answer:
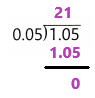
1.05 ÷ 0.05 = 21
The quotient is 21.
Explanation:
In this division operation 1.05 ÷ 0.05. The dividend is 1.05 and the divisor is 0.05. By dividing dividend 1.05 with the divisor 0.05 then the quotient is 21.
Question 14.
![]()
Answer:

182.8 ÷ 0.1 = 1828
The quotient is 1828.
Explanation:
In this division operation 182.8 ÷ 0.1. The dividend is 182.8 and the divisor is 0.1. By dividing dividend 182.8 with the divisor 0.1 then the quotient is 1828.
Question 15.
![]()
Answer:
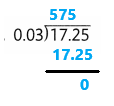
17.25 ÷ 0.03 = 575
The quotient is 575.
Explanation:
In this division operation 17.25 ÷ 0.03. The dividend is 17.25 and the divisor is 0.03. By dividing dividend 17.25 with the divisor 0.03 then the quotient is 575.
Question 16.
![]()
Answer:
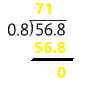
5.68 ÷ 0.8 = 71
The quotient is 71.
Explanation:
In this division operation 5.68 ÷ 0.8. The dividend is 5.68 and the divisor is 0.8. By dividing dividend 5.68 with the divisor 0.8 then the quotient is 71.
Question 17.
![]()
Answer:
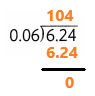
6.24 ÷ 0.06 = 104
The quotient is 104.
Explanation:
In this division operation 6.24 ÷ 0.06. The dividend is 6.24 and the divisor is 0.06. By dividing dividend 6.24 with the divisor 0.06 then the quotient is 104.
Question 18.
![]()
Answer:

27.5 ÷ 2.5 = 11
The quotient is 11
Explanation:
In this division operation 27.5 ÷ 2.5. The dividend is 27.5 and the divisor is 2.5. By dividing dividend 27.5 with the divisor 2.5 then the quotient is 11.
Problem Solving
Question 19.
Make up a money story for the equation 3.75 ÷ 0.25 = 15.
Answer:
Question 20.
Carol bought 5 pork chops and 3 steaks. Each pork chop weighed 0.32 pound and each steak weighed 0.8 pound. How many pounds of meat did Carol buy in all?
Answer:
Question 21.
Tim estimates that 60 ÷ 5.7 is about 10. Will the actual quotient be greater than or less than 10? Explain.
Answer:
Estimate 60 ÷ 5.7. Use compatible numbers.
Look for compatible numbers.
60 ÷ 5.7 is close to 60 ÷ 6 = 10.
Tim estimates that 60 ÷ 5.7 is about 10.
60 ÷ 5.7 = 10.53
The actual quotient is 10.53.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 60 ÷ 5.7 is closes to 60 ÷ 10. The actual divisor 5.7 is compatible to 6. Perform division operation 60 ÷ 6 = 10. The Estimated quotient is 10. The actual quotient is 10.53. The actual quotient is greater than 10.
Question 22.
Dex estimates that 4,989 ÷ 0.89 is about 500. Is his estimate reasonable? Why or why not?
Answer:
Estimate 4,989 ÷ 0.89. Use compatible numbers.
Look for compatible numbers.
4,989 ÷ 0.89 is close to 4,990 ÷ 1 = 4,990.
Dex estimates that 4,989 ÷ 0.89 is about 500.
His Estimation is not reasonable.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 4,989 ÷ 0.89 is closes to 4,990 ÷ 1. The actual dividend 4,989 is compatible to 4,990. The actual divisor 0.89 is compatible to 1. Perform division operation 4,990 ÷ 1 = 4,990. The Estimated quotient is 4,990. His Estimation is not reasonable.
Question 23.
Higher Order Thinking Susan solves 1.4 ÷ 0.2 using the diagram at the right. Is her reasoning correct? Explain her thinking.

Answer:
Question 24.
Use Structure The same dividend is divided by 0.1 and 0.01. How do the quotients compare? Explain your thinking.
Answer:
Question 25.
A-Z Vocabulary Give three examples of a power of 10. Explain why one of your examples is a power of 10.
Answer:
Assessment Practice
Question 26.
Select the expressions that have a quotient of 4.
![]() 2.8 ÷ 0.7
2.8 ÷ 0.7
![]() 0.28 ÷ 7
0.28 ÷ 7
![]() 2.8 ÷ 0.07
2.8 ÷ 0.07
![]() 0.28 ÷ 0.07
0.28 ÷ 0.07
Answer:

Explanation:
In the above image we can observe the expressions that have a quotient of 4. Option 1 and option 4 is correct.
1. When 2.8 is divided by 0.7 then the quotient is 4. So option 1 is correct.
2. When 0.28 is divided by 7 then the quotient is 0.04. So option 2 is not correct.
3. When 2.8 is divided by 0.07 then the quotient is 40. So option 3 is not correct.
4. When 0.28 is divided by 0.07 then the quotient is 4. So option 4 is correct.
Question 27.
Select the expressions that have a quotient of 9.
![]() 1.35 ÷ 1.5
1.35 ÷ 1.5
![]() 1.35 ÷ 0.15
1.35 ÷ 0.15
![]() 13.5 ÷ 1.5
13.5 ÷ 1.5
![]() 13.5 ÷ 0.15
13.5 ÷ 0.15
Answer:

Explanation:
In the above image we can observe the expressions that have a quotient of 9. Option 2 and option 3 is correct.
1. When 1.35 is divided by 1.5 then the quotient is 0.9. So option 1 is not correct.
2. When 1.35 is divided by 0.15 then the quotient is 9. So option 2 is correct.
3. When 13.5 is divided by 1.5 then the quotient is 9. So option 3 is correct.
4. When 13.5 is divided by 0.15 then the quotient is 90. So option 4 is not correct.
Lesson 6.6 Reasoning
Activity
Problem Solving
Reasoning
Solve & Share
Aaron has three slabs of beeswax. He plans to melt them and use all of the wax to form 36 candles. If all the candles are the same size and weight, how much will each candle weigh? Use reasoning to decide.

Thinking Habits
Be a good thinker! These questions can help you.
• What do the numbers and symbols in the problem mean?
• How are the numbers or quantities related?
• How can I represent a word problem using pictures, numbers, or equations?
Look Back! Reasoning Suppose Aaron wants each candle to weigh 0.5 pound. How many candles could he make with the beeswax?
Visual Learning Bridge
Essential Question How Can You Use Reasoning to Solve Problems?
A.
Ms. Watson is mixing mint green paint for her art class. She combines full bottles of blue, yellow, and white paint. How many 8-fluid ounce jars can she fill? Use reasoning to decide.

What do I need to do to solve this problem?
I need to add the three quantities of paint. Then I need to divide the sum by the capacity of a jar.
B.
How can I use reasoning to solve this problem?
I can
• identify the quantities I know
• draw a bar diagram to show relationships.
• give the answer using the correct unit.
Here’s my thinking…

C.
Use bar diagrams to show how the quantities are related.
First, find the sum of the three quantities of paint in the mixture.

Then, divide 93.6 by 8 to find the 11.7 number of jars that can be filled.

Ms. Watson can fill 11 jars. The 12th jar will be only partially filled.
Convince Me! Reasoning Ms. Watson is mixing 34.6 fluid Ounces of red paint and 18.2 fluid ounces of yellow paint to make orange paint. How many 12-fluid Ounce jars can she fill? Use reasoning to decide.
Guided Practice
Reasoning
Miranda mixed 34.5 fluid Ounces of blue paint, 40.5 fluid ounces of red paint, and 2 fluid Ounces of black paint to make purple paint. She poured the same amount of the purple paint into each of 14 jars. How much paint did she pour in each jar?
Use reasoning to decide how the quantities in the problem are related.

Question 1.
Explain what each of the quantities in the problem means.
Answer:
Question 2.
Describe one way to solve the problem.
Answer:
Question 3.
What is the solution to the problem? Explain.
Answer:
Independent Practice
Reasoning
Sue made chicken soup by combining the entire can of soup shown with a full can of water. How many 10-fluid Ounce bowls can she fill with the soup? How much soup will be left over?

Question 4.
Explain what each of the quantities in the problem means.
Answer:
Question 5.
Describe one way to solve the problem.
Answer:
Question 6.
What is the solution to the problem? Explain.
Answer:
Problem Solving
Performance Task
Cooking Competition
Lucas’s cooking class is having a cooking competition. There are 6 teams. Each student brought supplies that will be shared equally among the teams. The table shows the supplies Lucas brought. If the supplies are shared equally among the teams, how much of each supply will each team get?

Question 7.
Make Sense and Persevere Do you need all of the information given above to solve the problem? Explain.
Answer:
Question 8.
Reasoning Describe how to solve the problem.
Answer:
Use reasoning to think about what the quantities in the table represent.

Question 9.
Model with Math Write equations to represent how much of each supply each team will get.
Answer:
Question 10.
Be Precise What is the solution to the problem? Explain.
Answer:
Question 11.
Critique Reasoning Lucas says that to find the total cost of the rice, you should multiply 3.5 by $1.89. Do you agree? Explain.
Answer:
Topic 6 Fluency Practice
Activity
Follow the path
Solve each problem. Follow products that are multiples of 20 to shade a path from START to FINISH. You can only move up, down, right, or left.


Answer:
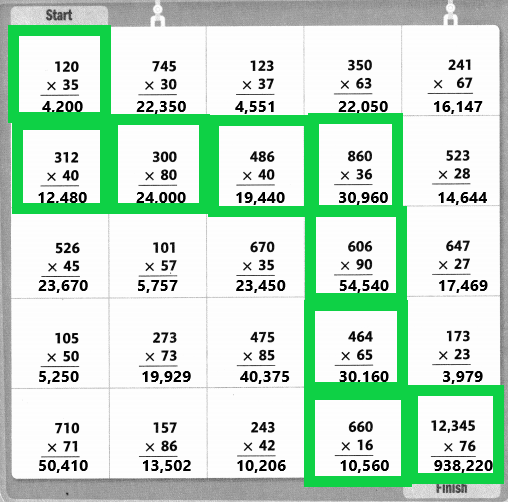
In the above image we can observe some multiplication problems. Products that are multiples of 20 to shade a path from START to FINISH. The products that are shaded with green color are multiples of 20.
Topic 6 Vocabulary Review
Glossary
Understand Vocabulary
Write always, sometimes, or never.
Word List
• estimate
• exponent
• hundredths
• power
• quotient
• rounding
• tenths
• thousandths
Question 1.
A digit in the hundredths place has \(\frac{1}{10}\) the value of the same digit in the tenths place. ______
Answer:
A digit in the hundredths place has \(\frac{1}{10}\) the value of the same digit in the tenths place. Sometimes.
Question 2.
The answer to a division problem is less than the divisor. ______
Answer:
The answer to a division problem is less than the divisor. Sometimes
Question 3.
A whole number divided by a decimal number is a whole number. ____
Answer:
A whole number divided by a decimal number is a whole number. Sometimes
Question 4.
Dividing by 103 moves the decimal point in the dividend three places to the left. ____
Answer:
Dividing by 103 moves the decimal point in the dividend three places to the left. Always
Question 5.
Multiplying the dividend and the divisor by the same power of 10 changes the quotient. ____
Answer:
Multiplying the dividend and the divisor by the same power of 10 changes the quotient. Never
Question 6.
The answer to a division problem is greater than the divisor. ______
Answer:
The answer to a division problem is greater than the divisor. Sometimes
Write T for true or F for false.
_____ Question 7.
3.65 ÷ 5.2 < 1
Answer: _____
3.65 ÷ 5.2 < 1
0.70 < 1
True
Explanation:
Perform division operation on 3.65 ÷ 5.2 = 0.70. The quotient is 0.70. The quotient 0.70 is less than 1. So the above expression is True.
Question 8.
48 ÷ 0.6 = 0.8
Answer:
48 ÷ 0.6 = 0.8
48 ÷ 0.6 = 80
The answer for above division operation is not correct. So the answer is False.
Explanation:
Perform division operation on 48 ÷ 0.6 = 80. The quotient is 80. In the above division operation the quotient is 0.8. So the above expression is False.
_____ Question 9.
2.42 ÷ 2.1 > 1.
Answer:
2.42 ÷ 2.1 > 1.
1.15 > 1
The answer for above division operation is 1.15 is greater than 1. So the answer is True.
Explanation:
Perform division operation on 2.42 ÷ 2.1 = 1.15. The quotient is 1.15. The quotient 1.15 is greater than 1. So the above expression is True.
_____ Question 10.
4.9 ÷ 0.8 < 4.9
Answer:
4.9 ÷ 0.8 < 4.9
6.125 < 4.9
The answer for above division operation is 6.125 is not less than 4.9. So the answer is False.
Explanation:
Perform division operation on 4.9 ÷ 0.8 = 6.125. The quotient is 6.125. The quotient 6.125 is not less than 4.9. So the above expression is False.
Use Vocabulary in Writing
Question 11.
Mary says the digits in the quotient of 381.109 0.86 are 4 4 315, but she doesn’t know where to place the decimal point. How can Mary use number sense to place the decimal point? Use at least three terms from the Word List in your answer.
Answer:
Topic 6 Reteaching
Set A
pages 229-232
Find 340.5 ÷ 100.
Dividing by 10, or 101, means moving the decimal point one place to the left.
Dividing by 100, or 102, means moving the decimal point two places to the left.
Dividing by 1,000, or 103, means moving the decimal point three places to the left.
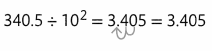
Remember that when dividing decimals by a power of 10, you may need to use one or more zeros as placeholders.
Use mental math to find each quotient.
Question 1.
34.6 ÷ 101
Answer:
34.6 ÷ 101
34.6 ÷ 10 = 3.46
The quotient is 3.46.
Explanation:
Dividing by 10, or 101, means moving the decimal point one place to the left. Move the dividend decimal point 34.6 one place to the left then the result is 3.46. The quotient is 3.46.
Question 2.
6,483 ÷ 102
Answer:
6,483 ÷ 102
6,483 ÷ 100 = 64.83
The quotient is 64.83.
Explanation:
Dividing by 100, or 102, means moving the decimal point two places to the left. Move the dividend decimal point 6,483 two places to the left then the result is 64.83. The quotient is 64.83.
Question 3.
148.3 ÷ 100
Answer:
148.3 ÷ 100 = 1.483
The quotient is 1.483.
Explanation:
Dividing by 100, or 102, means moving the decimal point two places to the left. Move the dividend decimal point 148.3 two places to the left then the result is 1.483. The quotient is 1.483.
Question 4.
29.9 ÷ 101
Answer:
29.9 ÷ 101
29.9 ÷ 10 = 2.99
The quotient is 2.99
Explanation:
Dividing by 10, or 101, means moving the decimal point one place to the left. Move the dividend decimal point 29.9 one place to the left then the result is 2.99. The quotient is 2.99.
Question 5.
70.7 ÷ 10
Answer:
70.7 ÷ 10 = 7.07
The quotient is 7.07.
Explanation:
Dividing by 10, or 101, means moving the decimal point one place to the left. Move the dividend decimal point 70.7 one place to the left then the result is 7.07. The quotient is 7.07.
Question 6.
5,913 ÷ 103
Answer:
5,913 ÷ 103
5,913 ÷ 1000 = 5.913
The quotient is 5.913.
Explanation:
Dividing by 1,000, or 103, means moving the decimal point three places to the left. Move the dividend decimal point 5,913 three place to the left then the result is 5.913. The quotient is 5.913.
Set B
pages 233-236
Estimate 27.3 ÷ 7.1. Use compatible numbers.
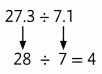
So, 27.3 ÷ 7.1 is about 4.
Estimate 42.5 ÷ 11. Use rounding.
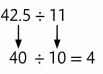
So, 42.5 ÷ 11 is about 4.
Remember that compatible numbers are numbers that are easy to compute in your head.
Write a number sentence that shows a way to estimate each quotient.
Question 1.
26.2 ÷ 5
Answer:
Estimate 26.2 ÷ 5. Use compatible numbers.
Look for compatible numbers.
26.2 ÷ 5 is closes to 25 ÷ 5 = 5.
So, 26.2 ÷ 5 is about 5.
The Estimated quotient is 5.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 26.2 ÷ 5 is closes to 25 ÷ 5. The actual dividend 26.2 is compatible to 25. Perform division operation 25 ÷ 5 = 5. The Estimated quotient is 5.
Question 2.
49.6 ÷ 7.8
Answer:
Estimate 49.6 ÷ 7.8. Use compatible numbers.
Look for compatible numbers.
49.6 ÷ 7.8 is closes to 49 ÷ 7 = 7.
So, 49.6 ÷ 7.8 is about 7.
The Estimated quotient is 7.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 49.6 ÷ 7.8 is closes to 49÷ 7. The actual dividend 49 is compatible to 25. The actual divisor 7.8 is compatible to 7. Perform division operation 25 ÷ 5 = 5. The Estimated quotient is 7.
Question 3.
121 ÷ 12.75
Answer:
Estimate 121 ÷ 12.75. Use compatible numbers.
Look for compatible numbers.
121 ÷ 12.75 is closes to 120 ÷ 12 = 10.
So, 121 ÷ 12.75 is about 10.
The Estimated quotient is 10.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 121 ÷ 12.75 is closes to 120 ÷ 12. The actual dividend 121 is compatible to 120. The actual divisor 12.75 is compatible to 12. Perform division operation 120 ÷ 12 = 10. The Estimated quotient is 10.
Question 4.
32.41 ÷ 10.9
Answer:
Estimate 32.41 ÷ 10.9. Use rounding.
Round to the nearest ten: 32 rounds to 30; 10.9 rounds to 10.
32.41 ÷ 10.9 is about 30 ÷ 10 = 3.
Explanation:
Rounding means replacing a number with an approximate value. In the above division method 32.41 ÷ 10.9. Round the numbers to the nearest ten or hundreds. Here 32.41 is rounded to 30 and 10.9 is rounded to 10. Now perform division operation on 30 ÷ 10 = 3. The estimated quotient is 3.
Question 5.
82.4 ÷ 3.7
Answer:
Estimate 82.4 ÷ 3.7. Use compatible numbers.
Look for compatible numbers.
82.4 ÷ 3.7 is closes to 80 ÷ 4 = 20.
So, 82.4 ÷ 3.7 is about 20.
The Estimated quotient is 20.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 82.4 ÷ 3.7 is closes to 80 ÷ 4. The actual dividend 82.4 is compatible to 80. The actual divisor 3.7 is compatible to 4. Perform division operation 80 ÷ 4 = 20. The Estimated quotient is 20.
Question 6.
28.5 ÷ 0.94
Answer:
Estimate 28.5 ÷ 0.94. Use compatible numbers.
Look for compatible numbers.
28.5 ÷ 0.94 is closes to 30 ÷ 1 = 30.
So, 28.5 ÷ 0.94 is about 30.
The Estimated quotient is 30.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 28.5 ÷ 0.94 is closes to 30 ÷ 1. The actual dividend 28.5 is compatible to 30. The actual divisor 0.94 is compatible to 1. Perform division operation 30 ÷ 1 = 30. The Estimated quotient is 30.
Set C
pages 237-240
Find 1.14 ÷ 3.
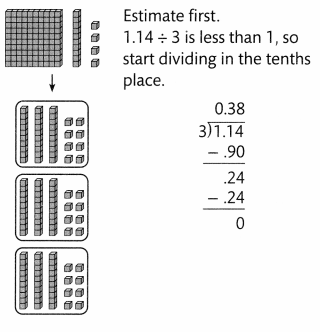
Remember to use estimation to check the placement of the decimal point in the quotient. Divide. Use models to help.
Question 1.
6.58 ÷ 7
Answer:
6.58 ÷ 7 = 0.94
Explanation:
In the above image we can observe the division of 6.58 ÷ 7 = 0.94. There are not enough ones to put 1 in each group, so regroup the 6 ones into 60 tenths. Divide 65 tenths into 7 equal groups. Each group gets 9 tenths. Seven groups of 0.9 = 6.3.
Trade the two extra tenth for 20 hundredths to get 28 hundredths. Divide the 28 hundredths into 7 equal groups. Each group gets 4 hundredths. Seven groups of 0.04 = 0.28.
Question 2.
156 ÷ 8
Answer:

156 ÷ 8 = 19.5
Explanation:
In the above image we can observe the division of 156 ÷ 8 = 19.5. There are enough ones to put 1 in each group, and extra ones is regrouped. Divide the 156 ones into 8 equal groups. Each group gets 19 ones. Eight groups of 19 = 152. Regroup of the 4 ones into 40 tenths. Divide the 40 tenths into 8 equal groups. Each group gets 5 tenths. Eight groups of 0.5 = 4.
Question 3.
34.2 ÷ 3
Answer:

34.2 ÷ 3 = 11.4
Explanation:
In the above image we can observe the division of 34.2 ÷ 3 = 11.4. There are enough ones to put 1 in each group, and extra ones is regrouped. Divide the 34 ones into 3 equal groups. Each group gets 11 ones. Three groups of 11 = 33. Regroup of the 1 one into 10 tenths. Divide the 12 tenths into 3 equal groups. Each group gets 4 tenths. Three groups of 0.4 = 1.2.
Question 4.
5.84 ÷ 4
Answer:
5.84 ÷ 4 = 1.46
Explanation:
In the above image we can observe the division of 5.84 ÷ 4 = 1.46. There are enough ones to put 1 in each group, and extra ones is regrouped. Divide the 5 ones into 4 equal groups. Each group gets 1 ones. Four groups of 1 = 4. Regroup of the 1 ones into 10 tenths. We can see that there are 18 tenths in 5.84. Divide the 18 tenths into 4 equal groups. Each group gets 4 tenths. Four groups of 0.4 = 1.6.
Trade the one extra tenth for 10 hundredths to get 24 hundredths. Divide the 24 hundredths into 4 equal groups. Each group gets 6 hundredths. Four groups of 0.06 = 0.24.
Question 5.
Michelle pays $66.85 for a costume pattern and 8 yards of fabric. The costume pattern costs $4.85. How much does each yard of the fabric cost?
Answer:
Set D
pages 241-244
Find 94.5 ÷ 15.
Estimate first
94.5 ÷ 15 is close to 100 ÷ 20 = 5, so start dividing with the ones place.
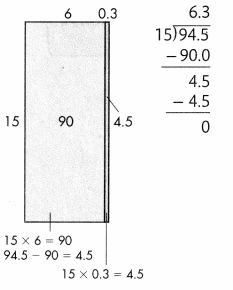
So, 94.5 ÷ 15 = 6.3
Remember that you can check your calculation by multiplying the quotient by the divisor.
Find each quotient.
Question 1.
91.2 ÷ 16
Answer:
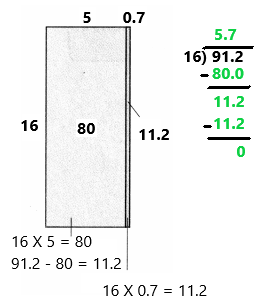
91.2 ÷ 16 = 5.7
Explanation:
In the above image we can observe the division operation 91.2 ÷ 16 = 5.7. The nearest possible multiple value of 16 is 80(16 x 5). Subtract 80 from 91.2 so as to get the remainder 11.2. 16 cannot be a multiple of 11.2 and so we have kept a decimal in the quotient and now the possible multiple value of 16 near to 11.2 is 11.2 itself(16 x 0.7 = 11.2). Now the remainder is zero and the final quotient is 5.7.
Question 2.
361.5 ÷ 15
Answer:
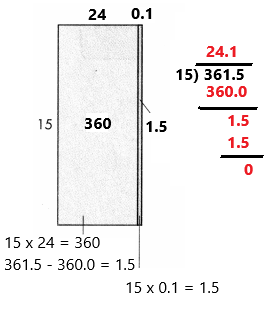
361.5 ÷ 15 = 24.1
Explanation:
In the above image we can observe the division operation 361.5 ÷ 15 = 24.1. The nearest possible multiple value of 15 is 360(15 x 24). Subtract 360 from 361.5 so as to get the remainder 1.5. 15 cannot be a multiple of 1.5 and so we have kept a decimal in the quotient and now the possible multiple value of 15 near to 1.5 is 1.5 itself(15 x 0.1 = 1.5). Now the remainder is zero and the final quotient is 24.1.
Question 3.
29.04 ÷ 22
Answer:
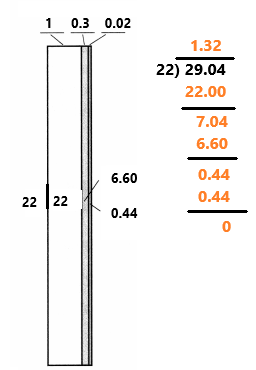
29.04 ÷ 22 = 1.32
Explanation:
In the above image we can observe the division operation 29.04 ÷ 22 = 1.32. The nearest possible multiple value of 22 is 22(22 x 1). Subtract 22 from 29.04 so as to get the remainder 7.04. 22 cannot be a multiple of 7.04 and so we have kept a decimal in the quotient and now 22 has the least possible multiple value of 6.60(22 x 0.3) near to 7.04. After subtracting 6.6 from 7.04, we are now having 1.3 as quotient and 0.44as remainder. Now the possible multiple value of 22 near to 0.44 is 0.44 itself(22 x 0.02 = 0.44). Now the remainder is zero and the final quotient is 1.32.
Question 4.
144 ÷ 45
Answer:

144 ÷ 45 = 3.2
Explanation:
In the above image we can observe the division operation 144 ÷ 45= 3.2. The nearest possible multiple value of 45 is 135(45 x 3). Subtract 135 from 144 so as to get the remainder 9. 45 cannot be a multiple of 9 and so we have kept a decimal in the quotient and now the possible multiple value of 45 near to 9.0 is 9.0 itself(45 x 0.2 = 9.0). Now the remainder is zero and the final quotient is 3.2.
Question 5.
A 12-ounce bottle of shampoo costs $4.20. A 16-ounce bottle costs $6.88. Which shampoo costs less per ounce? How do you know?
Answer:
A 12-ounce bottle of shampoo costs $4.20.
$4.20 ÷ 12 = $0.35.
A 16-ounce bottle costs $6.88.
$6.88 ÷ 16 = $0.43
12- ounce bottle shampoo costs less per ounce is $0.35.
Explanation:
A 12-ounce bottle of shampoo costs $4.20. Divide $4.20 ÷ 12 = $0.35. A 16-ounce bottle costs $6.88. Divide $6.88 ÷ 16 = $0.43. Compare these 12- ounce and 16- ounce bottle of shampoos. The 12-ounce bottle shampoo costs less per ounce is $0.35.
Set E
pages 245-248
Find 4.8 ÷ 0.6.
48 tenths ÷ 6 tenths
6 tenths × ? = 48 tenths
? = 8
So, 4.8 ÷ 6 = 8
Remember to use estimation Dates to check the quotient for reasonableness.
Question 1.
6.4 ÷ 3.2
Answer:
6.4 ÷ 3.2
3.2 x 2 = 6.4
6.4 ÷ 3.2 = 2
The quotient is 2.
Explanation:
Multiply 3.2 with 2 then the product is 6.4. Dividing 6.4 by 3.2 then the quotient is 2.
Question 2.
6.4 ÷ 0.32
Answer:
0.32 x 20 = 6.4
6.4 ÷ 0.32 = 20
The quotient is 20.
Explanation:
Multiply 0.32 with 20 then the product is 6.4. Dividing 6.4 by 0.32 then the quotient is 20.
Question 3.
9.6 ÷ 0.8
Answer:
12 x 8 = 96
12 x 0.8 = 9.6
9.6 ÷ 0.8 = 12
The quotient is 12.
Explanation:
Multiply 0.8 with 12 then the product is 9.6. Dividing 9.6 by 0.8 then the quotient is 12.
Question 4.
0.96 ÷ 0.08
Answer:
12 x 8 = 96
12 x 0.08 = 0.96
0.96 ÷ 0.08 = 12
The quotient is 12.
Explanation:
Multiply 0.08 with 12 then the product is 0.96. Dividing 0.96 by 0.08 then the quotient is 12.
Question 5.
41.8 ÷ 2.2
Answer:
19 x 2.2 = 41.8
41.8 ÷ 2.2 = 19
The quotient is 19.
Explanation:
Multiply 2.2 with 19 then the product is 41.8. Dividing 41.8 by 2.2 then the quotient is 19.
Question 6.
4.18 ÷ 0.22
Answer:
0.22 x 19 = 4.18
4.18 ÷ 0.22 = 19
The quotient is 19.
Explanation:
Multiply 0.22 with 19 then the product is 4.18. Dividing 4.18 by 0.22 then the quotient is 19.
Question 7.
81.4 ÷ 7.4
Answer:
11 x 7.4 = 81.4
81.4 ÷ 7.4 = 11
The quotient is 11.
Explanation:
Multiply 7.4 with 11 then the product is 81.4. Dividing 81.4 by 7.4 then the quotient is 11.
Question 8.
814 ÷ 74
Answer:
814 ÷ 74 = 11
The quotient is 11.
Explanation:
By Dividing 814 by 74 then the quotient is 11.
Question 9.
9.6 ÷ 0.03
Answer:
9.6 ÷ 0.03 = 320
The quotient is 320.
Explanation:
By Dividing 9.6 by 0.03 then the quotient is 320.
Question 10.
9.6 ÷ 0.3
Answer:
9.6 ÷ 0.3 = 32
The quotient is 32.
Explanation:
By Dividing 9.6 by 0.3 then the quotient is 32.
Set F
pages 249-252
Think about these questions to help you reason abstractly and quantitatively.
Thinking Habits
• What do the numbers and symbols in the problem mean?
• How are the numbers or quantities related?
• How can I represent a word problem using pictures, numbers, or equations?

Zoey has a goal of saving $750 for a vacation. Her vacation will last 6 days. She wants to save the same amount each week for 12 weeks to reach her goal. How much should she save each week?
Which quantities do you need to solve the problem?
The savings goal is $750; Zoey will save for 12 weeks.
Will Zoey need to save more than or less than $80 each week? Explain your reasoning.
Less than; 12 × $80 = $960, but she only needs to save $750.
How much should she save each week? Write an equation to represent the problem.
$62.50; $750 :12 = $62.50
Remember to check the reasonableness of a solution by making sure your calculations are correct, and that you answered all of the questions that were asked.
lan uses 4 feet of ribbon to wrap each package. How many packages can he wrap with 5.6 yards of ribbon?
Remember there are 3 feet in a yard.

Question 1.
Describe one way to solve the problem.
Answer:
Question 2.
What is the solution to the problem? Show your work.
Answer:
A bushel of apples weighs about 42 pounds. There are 4 pecks in a bushel. It takes 2 pounds of apples to make one pie. How many pies can you make with one peck of apples?
Question 3.
How are the numbers in the problem related?
Answer:
Question 4.
Describe one way to solve the problem.
Answer:
Question 5.
Solve the problem. Show your work.
Answer:
Topic 6 Assessment Practice
Question 1.
Mr. Dodd filled the gas tank on his lawn mower with 3.8 gallons of gas. He mowed his yard 10 times on the same tank of gas. He used the same amount of gas each time. How much gas did he use each time? Write an equation to show your work. Explain how the decimal point moves.
Answer:
Question 2.
Kimberly scored a total of 35.08 points in four events for her gymnastic competition. If she scored the same number of points in each event, how many points did she score in each? Write an equation to show your work.
Answer:
35.08 points ÷ 4 = 8.77 points.
She scored 8.77 points in each event.
Explanation:
Kimberly scored a total of 35.08 points in four events for her gymnastic competition. If she scored the same number of points in each event. Divide 35.08 by 4 then the quotient is 8.77. She scored 8.77 points in each event.
Question 3.
Choose the correct quotient for each expression. Use number sense and estimation to help.
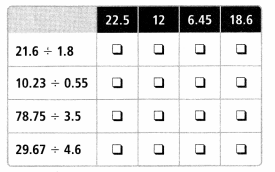
Answer:
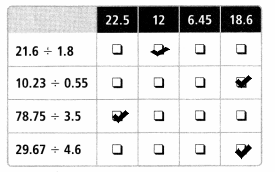
Explanation:
Perform division operation on 21.6 ÷ 1.8 = 12. The quotient is 12. Put a tick mark below the number 12.
Perform division operation on 10.23 ÷ 0.55 = 18.6. The quotient is 18.6. Put a tick mark below the number 18.6.
Perform division operation on 78.75 ÷ 3.5 = 22.5. The quotient is 22.5. Put a tick mark below the number 22.5.
Perform division operation on 29.67 ÷ 4.6 = 18.6. The quotient is 18.6. Put a tick mark below the number 18.6.
Question 4.
What is the value of the missing exponent in the equation?
![]()
A. 1
B. 2
C. 3
D. 4
Answer:

80.5 ÷ 102 = 0.805
The missing exponent in the equation is 2.
Question 5.
The chef at a restaurant bought 37 pounds of salad for $46.25. How much did she pay for each pound of salad?
A. 0.125
B. $1.25
C. $1.3
D. $12.50
Answer:

$46.25 ÷ 37 = $1.25
She pays $1.25 for each pound of salad.
Explanation:
The chef at a restaurant bought 37 pounds of salad for $46.25. Divide $46.25 by 37 pounds then the quotient is $1.25. She pays $1.25 for each pound of salad.
Question 6.
Kathleen spent $231 on concert tickets for herself and 11 friends. Each ticket cost the same amount.
A. Estimate the cost of each ticket. Write an equation to show your work.
B. Find the exact cost of each ticket. Compare your answer to your estimate to check for reasonableness.
Answer:
A. $231 ÷ 12 = ?
Estimate $231 ÷ 12 closes to 230 ÷ 12 = $19.16.
The estimated cost of each ticket is $19.16.
Explanation:
Kathleen spent $231 on concert tickets for herself and 11 friends. Each ticket cost the same amount. Divide 230 by 12 then the quotient is $19.16. The estimated cost of each ticket is $19.16.
B. $231 ÷ 12 = $19.25
The actual cost of each ticket is $19.25.
Explanation:
The estimated cost of each ticket is $19.16 and the actual cost of each ticket is $19.25. Both estimated answer and actual answer are reasonable.
Question 7.
Select all of the following equations that are true when 12.5 is used. Use number sense to help.
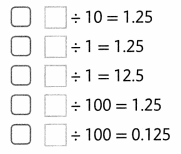
Answer:

Explanation:
In the above image we can observe the equations that are true when 12.5 is used. Option 1 and option 3, option 5 is correct.
1. When 12.5 is divided by 10 then the quotient is 1.25. So option 1 is correct.
2. When 12.5 is divided by 1 then the quotient is 12.5. So option 2 is not correct.
3. When 12.5 is divided by 1 then the quotient is 12.5. So option 3 is correct.
4. When 12.5 is divided by 100 then the quotient is 0.125. So option 4 is not correct.
5. When 12.5 is divided by 100 then the quotient is 0.125. So option 5 is correct.
Question 8.
Which division problem does the model Tess made represent?
A. 1.35 ÷ 3 = 0.45
B. 1.35 ÷ 3 = 0.54
C. 1.62 ÷ 3 = 0.45
D. 1.62 ÷ 3 = 0.54
Answer:
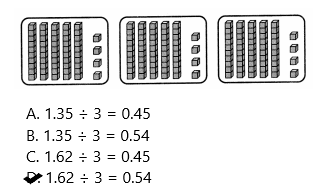
Option D 1.62 ÷ 3 = 0.54 is correct.
Explanation:
In the above image we can observe 5 tenths and 4 hundredths. By dividing 1.62 by 3 then the quotient is 0.54. The division problem answer option D represents the above image.
Question 9.
If 8 ounces of canned pumpkin has 82 calories, how many calories are in 1 ounce? Use your answer to find how many calories are in 6 ounces of pumpkin.
Answer:

10.25 calories are there in 1 ounce.
10.25 calories = 1 ounce
? calories = 6 ounces
10.25 calories x 6 ounces = 61.5 calories
61.5 calories are in 6 ounces of pumpkin.
Explanation:
8 ounces of canned pumpkin has 82 calories. Perform division operation on 82 ÷ 8 = 10.25. There are 10.25 calories in 1 ounce. We have to find out the how many calories are there in 6 ounces. Perform multiplication operation on these two numbers 10.25 calories and 6 ounces then the product is 61.5 calories. There are 61.5 calories in 6 ounces of pumpkin.
Question 10.
Use the equation 1.6 ÷ n = 0.016.
A. What value of n makes the equation true? Write your answer using an exponent.
B. Explain how you know your answer is correct.
Answer:
A. 1.6 ÷ n = 0.016.
1.6 ÷ 0.01 = 0.016.
1.6 ÷ 10-2 = 0.016.
The value n = 0.01 makes the equation true. The exponent form of 0.01 is 10-2 .
B. We can check the answer is correct or not by performing division operation on 0.016 ÷ 1.6 = 0.01.
Question 11.
Eileen bought 8 roses for $45.50. Which is the best way to estimate the cost of one rose?
A. $45 ÷ 5 = $9.00
B. $48 ÷ 8 = $6.00
C. $45 ÷ 10 = $0.45
D. $40 ÷ 8 = $0.50
Answer:
Option B $48 ÷ 8 = $6.00 is the best way to estimate the cost of one rose.
Estimate $45.50÷ 8. Use compatible numbers.
Look for compatible numbers.
$45.50÷ 8 is closes to $48 ÷ 8 = $6.
The Estimated cost of one rose is $6.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. Eileen bought 8 roses for $45.50. In the above division problem $45.50÷ 8 is closes to 48 ÷ 8. The actual dividend $45.50 is compatible to 48. Perform division operation $48 ÷ 8 = 6. The Estimated cost of one rose is $6.
Question 12.
Toby’s faucet dripped a total of 1.92 liters of water in 24 hours. The faucet dripped the same amount each hour.
A. Estimate how many liters his faucet dripped each hour. Write an equation to model your work.
B. Find the exact amount of water that dripped each hour.
C. Compare your estimate to your answer. Is your answer reasonable? Explain.
Answer:
A. 1.92 liters ÷ 24 = ?
Estimate 1.92 liters ÷ 24 closes to 2 liters ÷ 24 = 0.083 liters.
The estimated amount of water dripped each hour is 0.083 liters.
Explanation:
Toby’s faucet dripped a total of 1.92 liters of water in 24 hours. Divide 2liters by 24 then the result is 0.083 liters. The estimated amount of water dripped each hour is 0.083 liters.
B. 1.92 liters ÷ 24 = 0.08 liters.
The exact amount of water that dripped each hour is 0.08 liters.
Explanation:
Perform division operation on 1.92 liters by 24 hours. The quotient is 0.08 liters. The exact amount of water that dripped each hour is 0.08 liters.
c. The estimated amount of water dripped each hour is 0.083 liters.
The exact amount of water that dripped each hour is 0.08 liters. The answer is reasonable.
Topic 6 Assessment Practice
Question 13.
Choose the correct quotient for each expression.

Answer:
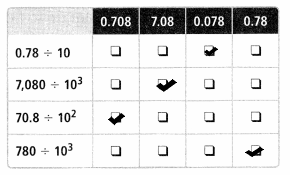
Explanation:
Perform division operation on 0.78 ÷ 10 = 0.078. The quotient is 0.078. Put a tick mark below the number 0.078.
Perform division operation on 7,080 ÷ 103 = 7.08. The quotient is 7.08. Put a tick mark below the number 7.08.
Perform division operation on 70.8 ÷ 102 = 0.708. The quotient is 0.708. Put a tick mark below the number 0.708.
Perform division operation on 780 ÷ 103 = 0.78. The quotient is 0.78. Put a tick mark below the number 0.78.
Question 14.
Diego is making a large mural. He draws a hexagon with a perimeter of 10.5 meters. Each side of the hexagon is the same length.
A. How many meters long is each side of Diego’s hexagon? Write an equation to model your work.
B. The total cost of the supplies to paint the mural is $38.70. Diego and 9 friends divide the total cost equally. How much does each person pay?
Answer:
Question 15.
Select all of the following equations that are true when 40.3 is used. Use number sense to help.
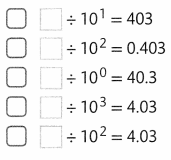
Answer:

Explanation:
In the above image we can observe the equations in option 2 and option 3 are true when 40.3 is used.
Perform division operation on 40.3 ÷ 102 = 0.403. The quotient is 0.403. So option 2 is correct.
Perform division operation on 40.3 ÷ 100 = 40.3. The quotient is 40.3. So option 3 is correct.
Question 16.
Lou’s Diner spent $12.80 on 8 pounds of potatoes. What was the cost of one pound of potatoes? What would be the total cost if the cost per pound remained the same and the diner bought 7 pounds? Show your work.
Answer:
$12.80 ÷ 8 pounds = $1.6
The cost of one pound of potatoes is $1.6.
? ÷ 7 pounds = $1.6
$1.6 x 7 pounds = $11.2
The total cost is $11.2. If the cost per pound remains same and the dinner bought 7 pounds.
Explanation:
Lou’s Diner spent $12.80 on 8 pounds of potatoes. Divide $12.80 ÷ 8 pounds = $1.6. The cost of one pound of potatoes is $1.6. If the cost per pound remains same and the dinner bought 7 pounds. Multiply $1.6 x 7 pounds = $11.2. The total cost is $11.2.
Question 17.
How many quarters are there in $30? Solve the equation 30 ÷ 0.25 to help you.
A. 12 quarters
B. 20 quarters
C. 120 quarters
D. 200 quarters
Answer:
30 ÷ 0.25 = 120
There are 120 quarters in $30.
Option C is correct.
Explanation:
Perform division operation on 30 ÷ 0.25 = 120 . Here the dividend is 30 and the divisor is 0.25. By dividing the dividend with divisor then the quotient is 120. There are 120 quarters in $30. So option C is correct.
Question 18.
When solving 6.1 ÷ 102, how is the decimal point moved?
A. 1 place to the right
B. 1 place to the left
C. 2 places to the right
D. 2 places to the left
Answer:
6.1 ÷ 102 = 0.061
Option D is correct .
Explanation:
Perform division operation on 6.1 ÷ 102 = 0.061 . Here the divisor is 102 which is 100. So the decimal point is moved two places to the left. The quotient is 0.061. So option D is correct.
Question 19.
A group of 5 friends bought a bag of grapes to share equally. If the bag of grapes weighs 11.25 pounds, how much is each person’s share? How many friends could share the grapes if each person’s share was 1.25 pounds? Write an equation to model your work.
Answer:
11.25 pounds ÷ 5 = 2.25 pounds.
Each person share is 2.25 pounds.
11.25 pounds ÷ ? = 1.25 pounds.
11.25 pounds ÷ 9 = 1.25 pounds.
9 friends can share the grapes if each person’s share was 1.25 pounds.
Explanation:
A group of 5 friends bought a bag of grapes to share equally. The bag of grapes weighs 11.25 pounds. Perform division operation on 11.25 pounds ÷ 5 = 2.25 pounds. Each person share is 2.25 pounds.
Divide 11.25 pounds ÷ 1.25 pounds = 9. Nine friends can share the grapes if each person’s share was 1.25 pounds.
Question 20.
When dividing 560.9 by 100, how should the decimal point be moved?
Answer:
560.9 ÷ 100 = 5.609
Explanation:
Dividing by 100, or 102, means moving the decimal point two places to the left. Move the dividend decimal point 560.9 two places to the left then the result is 5.609. The quotient is 5.609.
Question 21.
June says that there should be a decimal point in the quotient below after the 4. Is she correct? Use number sense to explain your answer. 43.94 ÷ 5.2 = 845
Answer:
43.94 ÷ 5.2 = 8.45
She is not correct. The decimal should be placed after 8.
Explanation:
June says that there should be a decimal point in the quotient after the 4. She is not correct because we have to place the decimal point after 8.
Question 22.
Three coworkers decided to buy fruit to share at lunchtime. Antonio spent $1.47 on bananas. Laura spent $2.88 on apples. Suzanne spent $2.85 on oranges.
A. Complete the bar diagram to find out how much they spent in all on fruit.
Answer:

They spent $7.2 in all on fruit.
Explanation:
Three coworkers decided to buy fruit to share at lunchtime. Antonio spent $1.47 on bananas. Laura spent $2.88 on apples. Suzanne spent $2.85 on oranges. Add all fruit costs. Add $1.47 with $2.88 and $2.85 then the sum is $7.2. They spent $7.2 in all on fruit.
B. They evenly divided the cost of the 3 types of fruit. How much did each person pay? Complete the bar diagram to help you.
Answer:
Each person has to pay $2.4 for fruits.
Explanation:
The three coworkers evenly divided the cost of the 3 types of fruit. The total cost of three fruits is $7.2. Divide $7.2 by 3 then the quotient is $2.4. Each person has to pay $2.4 for fruits.
C. If Laura bought 2.1 pounds of apples, is the price per pound of apples greater than or less than $1? How can you tell?
Answer:
Topic 6 Performance Task
Cooking Competition
Lydia is organizing a cooking competition at her school. She ordered some basic supplies to share among the teams that are competing. The teams will be bringing other ingredients as well.
Use the list at the right to answer the questions.
Question 1.
If 10 of the teams divide the olive oil equally, how much will each team receive? Write an equation to model your work.

Answer:
5.4 liters ÷ 10 = 0.54 liters.
Each team receives 0.54 liters.
Explanation:
10 of the teams divide the olive oil equally. Here we have total 5.4 liters of olive oil. Perform division operation on 5.4 liters ÷ 10 = 0.54 liters. Each team receives 0.54 liters.
Question 2.
Eight teams agree to share the flour equally.
Part A
About how many grams of flour will each team get? Use compatible numbers to estimate. Write an equation to show how you estimated.
Answer:
738.4 grams ÷ 8 = ?.
Estimate 738.4 grams ÷ 8. Use compatible numbers.
Look for compatible numbers.
738.4 ÷ 8 is closes to 738 ÷ 8 = 92.25 grams.
The Estimated quotient is 92.25.
Each team get 92.25 grams of flour.
Explanation:
Compatible numbers are pairs of numbers that are easy to add, subtract, multiply, or divide mentally. When using estimation to approximate a calculation, replace actual numbers with compatible numbers. In the above division problem 738.4 grams ÷ 8 is closes to 738 ÷ 8. The actual dividend738.4 is compatible to 738. Perform division operation 738 ÷ 8 = 92.25. The Estimated quotient is 92.25. Each team get 92.25 grams of flour.
Part B
Find the actual amount of flour each team will receive. Show your work.
Answer:
738.4 grams ÷ 8 = 92.3 grams.
Each team will receive 92.3 grams of flour.
Explanation:
Perform division operation on 738.4 grams ÷ 8 = 92.3 grams. Each team will receive the actual amount of flour is 92.3 grams.
Question 3.
Several teams agree to share the salt equally. Each team will be given 7.3 grams of salt. How many teams agree to share the salt? Write a division equation to model the problem. Then write an equivalent equation using whole numbers.
Answer:
87.6 grams ÷ ? = 7.3 grams.
87.6 grams ÷ 12 = 7.3 grams.
12 teams agree to share the salt.
Explanation:
Several teams agree to share the salt equally. Each team will be given 7.3 grams of salt. The division equation is 87.6 grams ÷ ? = 7.3 grams. Divide 87.6 with 7.3 then the answer is 12. 12 teams agree to share the salt.
Question 4.
Malcolm calculated how many liters of milk each team would get if 6 teams shared the milk equally. His work is shown at the right, but he forgot to place the decimal point in the quotient. Where should he place the decimal point? Explain.
Answer:

8.25 liters ÷ 6 = 1.375 liters.
Malcolm has to place the decimal point before 3 and after 1.
Each team get 1.375 liters of milk.
Explanation:
Malcolm calculated how many liters of milk each team would get if 6 teams shared the milk equally. His work is shown above, but he forgot to place the decimal point in the quotient. He has to place the decimal point before 3 and after 1. Each team get 1.375 liters of milk.
Question 5.
Lydia decides to provide cheddar cheese for the competition. She buys 4.2 kilograms for $39.90.
Part A
She estimates the cost of 1 kilogram of cheese to be $1. Is her estimate reasonable? Explain.
Answer:
4.2 kilograms ÷ $39.90 = ?
Estimate 4.2 ÷ $40 = $0.105
The cost of 1 kilogram of cheese to be $0.105. Her Estimation is not reasonable.
Explanation:
Lydia decides to provide cheddar cheese for the competition. She buys 4.2 kilograms for $39.90. Perform division operation on 4.2 ÷ $40 = $0.105. The cost of 1 kilogram of cheese to be $0.105. Her Estimation is not reasonable.
Part B
To find the actual cost of 1 kilogram of cheese, Lydia needs to divide $39.90 by 4.2. How can she change the division problem to an equivalent problem using whole numbers? Write and solve the equivalent problem..
Part C
If 7 teams share the cheese equally, how much cheese will each team get?
Answer:
4.2 kilograms ÷ 7 = 0.6 kilograms.
Each team get 0.6 kilograms of cheese equally.
Explanation:
The cheese we have is 4.2 kilograms. Seven teams takes the cheese equally. perform division operation on 4.2 kilograms ÷ 7 = 0.6 kilograms. Each team get 0.6 kilograms of cheese equally.

