Go through the enVision Math Common Core Grade 6 Answer Key Topic 3 Numeric And Algebraic Expressions regularly and improve your accuracy in solving questions.
Envision Math Common Core 6th Grade Answers Key Topic 3 Numeric And Algebraic Expressions
?Topic essential Question What are expressions and how they can be written and evaluated?
Answer:
Expressions are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
To evaluate an algebraic expression means to find the value of the expression when the variable is replaced by a given number. To evaluate an expression, we substitute the given number for the variable in the expression and then simplify the expression using the order of operations.
TOPIC 3 enVision STEM Project
Did You Know?
There are more than 600,000 bridges in the United States.

Your Task: Design a Bridge
Suppose the proposed ma×imum weight limit for a new bridge in your community is 100,000 pounds. How many and what types of vehicles can be allowed to cross the bridge? How can the weight on the bridge be controlled? You and your classmates will begin the engineering design process to understand the problem, do necessary research, and brainstorm solutions.
Topic 3 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
composite number
formula
numerical expression
prime number

Question 1.
A ____ is a rule that uses symbols to relate two or more quantities.
Answer:
We know that,
A “Formula” is a rule that uses symbols to relate two or more quantities
Hence, from the above,
We can conclude that
The best term that is suitable for the given definition is: Formula
Question 2.
The number 12 is a ____ because it has more than two factors.
Answer:
We know that,
The number 12 is a “Composite number” because it has more than two factors.
Hence, from the above,
We can conclude that
The best term that is suitable for the given definition is: Composite number
Question 3.
A ___ is a mathematical phrase that includes numbers and at least one operation.
Answer:
We know that,
A “Numerical expression” is a mathematical phrase that includes numbers and at least one operation.
Hence, from the above,
We can conclude that
The best term that is suitable for the given definition is: Numerical expression
Perimeter and Area
Use the formulas P = 2l + 2w and A = l × w, where l is the length and w is the width, to find the perimeter, P, and the area, A, of each figure.
Question 4.
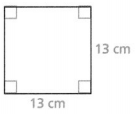
P = ___
A = ____
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The length of a rectangle (L) is: 13 cm
The width of a rectangle (W) is: 13 cm
Now,
We know that,
The perimeter of a rectangle (P) is: 2 (L + W)
The area of a rectangle (A) is: Length × Width
So,
P = 2 × (13 + 13)
= 2 ×26
= 52 cm
A = 13 × 13
= 169 cm²
Hence, from the above,
We can conclude that
The perimeter of the given rectangle is: 52 cm
The area of the given rectangle is: 169 cm²
Question 5.

P = ___
A = ____
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The length of a rectangle (L) is 5 in.
The width of a rectangle (W) is 21 in.
Now,
We know that,
The perimeter of a rectangle (P) is: 2 (L + W)
The area of a rectangle (A) is: Length × Width
So,
P = 2 × (21 + 5)
= 2 ×26
= 52 in.
A = 21 × 5
= 105 in.²
Hence, from the above,
We can conclude that
The perimeter of the given rectangle is 52 in.
The area of the given rectangle is 105 in.²
Question 6.
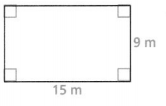
P = ___
A = ____
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The length of a rectangle (L) is 9 m
The width of a rectangle (W) is 15 m
Now,
We know that,
The perimeter of a rectangle (P) is: 2 (L + W)
The area of a rectangle (A) is: Length × Width
So,
P = 2 × (9 + 15)
= 2 ×24
= 48 m
A = 9 × 15
= 135 m²
Hence, from the above,
We can conclude that
The perimeter of the given rectangle is 48 m
The area of the given rectangle is 135 m²
Multiples
Write the first five multiples of each number.
Question 7.
8
Answer:
The given number is: 8
Now,
We know that,
A multiple is a number that can be divided by another number a certain number of times without a remainder
Hence, from the above,
We can conclude that
The first 5 multiples of 8 are: 8, 16, 24, 32, and 40
Question 8.
9
Answer:
The given number is: 9
Now,
We know that,
A multiple is a number that can be divided by another number a certain number of times without a remainder
Hence, from the above,
We can conclude that
The first 5 multiples of 9 are: 9, 18, 27, 36, and 45
Question 9.
10
Answer:
The given number is: 10
Now,
We know that,
A multiple is a number that can be divided by another number a certain number of times without a remainder
Hence, from the above,
We can conclude that
The first 5 multiples of 10 are: 10, 20, 30, 40, and 50
Question 10.
6
Answer:
The given number is: 6
Now,
We know that,
A multiple is a number that can be divided by another number a certain number of times without a remainder
Hence, from the above,
We can conclude that
The first 5 multiples of 6 are: 6, 12, 18, 24, and 30
Question 11.
4
Answer:
The given number is: 4
Now,
We know that,
A multiple is a number that can be divided by another number a certain number of times without a remainder
Hence, from the above,
We can conclude that
The first 5 multiples of 4 are: 4, 8, 12, 16, and 20
Question 12.
3
Answer:
The given number is: 3
Now,
We know that,
A multiple is a number that can be divided by another number a certain number of times without a remainder
Hence, from the above,
We can conclude that
The first 5 multiples of 3 are: 3, 6, 9, 12, and 15
Factors
Question 13.
How can you find the factors of 12 and 15? Explain.
Answer:
The given numbers are: 12 and 15
Now,
We know that,
A factor is a number that divides into another number exactly and without leaving a remainder
Hence, from the above,
We can conclude that
The factors of 12 are: 1, 2, 3, 4, 6, and 12
The factors of 15 are: 1, 3, 5, and 15
Operations
Question 14.
How are the terms difference, sum, quotient, and product alike?
Answer:
Sum:
The sum is the result of adding two or more numbers.
Product:
The product of two or more numbers is the result of multiplying these numbers.
Quotient:
The quotient of two numbers is the result of the division of these numbers
Difference:
The word difference is the result of subtracting one number from another
Language Development
Write terms and phrases related to Numeric expressions and Algebraic expressions in the Venn diagram.
In the box below, draw pictures to represent the terms and phrases in the overlap section of your diagram.
Topic 3 PICK A PROJECT
PROJECT 3A
What is the most inspiring poem you have read?
PROJECT: WRITE AN ALGEBRAIC POEM

PROJECT 3B
What equipment do you need to play your favorite sport?
PROJECT: PLAN A TEAM PURCHASE

PROJECT 3C
Where is the most interesting place you have gone swimming?
PROJECT: DESIGN A POOL PATIO

PROJECT 3D
In what ways have you seen exponents used in the real world?
PROJECT: CALCULATE WITH exPONENTS

Lesson 3.1 Understand and Represent exponents
Solve & Discuss It!
ACTIVITY
Fold a sheet of paper in half. Record the number of sections you see when it is unfolded. Continue folding the paper in half 4 more times. Record the number of sections each time. Describe any patterns you see.

Answer:
It is given that
Fold a sheet of paper in half. Record the number of sections you see when it is unfolded. Continue folding the paper in half 4 more times.
Now,
The given figure is:

Now,
From the given figure,
We can observe that,
When we fold a sheet of paper in half, there are 2 sections when we unfold the sheet of paper
So,
The number of sections when we fold the paper 4 more times in half = (The number of times a sheet of paper folded) × (The number of sections present when a sheet of paper is unfolded)
= 4 × 2
= 8 sections
Hence, from the above,
We can conclude that
The number of sections when we fold the paper 4 more times in half is: 8 sections
Look for Relationships How are the number of sections related to the number of folds?
Answer:
The figure from the above problem is:

Now,
When we observe the above figure,
We can say that
The number of sections present when we folded a paper in half is: 2 sections
So,
The number of sections = 2 × (The number of folds)
Hence, from the above,
We can conclude that
The relationship between the number of sections and the number of folds is:
The number of sections = 2 × (The number of folds)
Focus on math practices
Use Structure How many sections will there be after 6 folds? 7 folds?
Answer:
From the above problem,
We know that,
The number of sections = 2 × (The number of folds)
So,
The number of sections when there are 6 folds = 2 × 6
= 12 sections
The number of sections when there are 7 folds = 2 × 7
= 14 sections
Hence, from the above,
We can conclude that
The number of sections when there are 6 folds is: 12 sections
The number of sections when there are 7 folds is: 14 sections
VISUAL LEARNING
? Essential Question How can you write and evaluate numbers with exponents?
Answer:
You can use the “Order of operations” to evaluate the expressions containing exponents.
First, evaluate anything in Parentheses or grouping symbols.
Next, look for Exponents, followed by Multiplication and Division (reading from left to right)
Lastly, addition and subtraction (again, reading from left to right)
Example 1
The expression 2 × 2 × 2 represents the number of cells after 1 hour if there is 1 cell at the start. How can you write this expression using exponents? How many cells will there be after 1 hour?
Reasoning Repeated multiplication can be represented in more than one way.
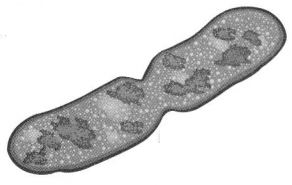
Some bacteria cells divide every 20 minutes to make 2 cells.
You can use an exponent to write the repeated multiplication of a number.
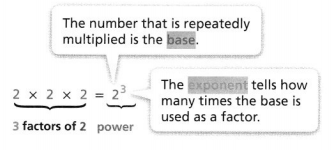
A number that can be written using exponents is called a power.
You can use repeated multiplication to evaluate or find the value of power.
Multiply the first two factors, 2 × 2 = 4.

There will be 8 cells after 1 hour.
Try It!
There are 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 bacteria cells after 3 hours. Write the repeated multiplication as power and then evaluate.
Answer:
It is given that
There are 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 bacteria cells after 3 hours
Now,
We know that,
The number that is repeatedly multiplied is the “Base”
The “Exponent” tells us how many times the base is used as a factor
A number that can be written using “Exponents” is called a “Power”
So,
The representation of the given repeated multiplication in the form of power is: 29
So,
29 = 25 × 24
= 32 × 16
= 512 cells
Hence, from the above,
We can conclude that
There are 512 bacteria cells present after 3 hours

Convince Me! Why can you represent the number of cells after two hours as power 26?
Answer:
From Example 1,
It is given that
The number of bacteria cells present in 1 hour is: 23
Now,
We know that,
am × an = am + n
So,
The number of bacteria cells present in 2 hours = 23 × 23
= 26 bacteria cells
Hence, from the above,
We can conclude that
We can represent the number of cells after 2 hours as 2
Try It!
Evaluate (\(\frac{1}{3}\))³?
Answer:
The given expression is: (\(\frac{1}{3}\))³
So,
(\(\frac{1}{3}\))³
= \(\frac{1}{3}\) × \(\frac{1}{3}\) × \(\frac{1}{3}\)
= \(\frac{1 × 1}{3 × 3}\) × \(\frac{1}{3}\)
= \(\frac{1}{9}\) × \(\frac{1}{3}\)
= \(\frac{1 × 1}{9 × 3}\)
= \(\frac{1}{27}\)
Hence, from the above,
We can conclude that
(\(\frac{1}{3}\))³ = \(\frac{1}{27}\)
Try It!
Rafael calculated the foil as 1.8 × 104 units thick. Evaluate Rafael’s expression.
Answer:
It is given that
Rafael calculated the foil as 1.8 × 104 units thick.
Now,
We know that,
104 = 102 × 102
= 100 × 100
= 10,000
So,
1.8 × 104 = 18,000
Hence, from the above,
We can conclude that
Rafael calculated the foil as 18,000 units thick
KEY CONCEPT
You can represent a repeated multiplication expression using an exponent.
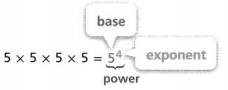
You can evaluate a power using repeated multiplication.
54 = 5 × 5 × 5 × 5 = 625
Do You Understand?
Question 1.
? Essential Question How can you write and evaluate numbers with exponents?
Answer:
You can use the “Order of operations” to evaluate the expressions containing exponents.
First, evaluate anything in Parentheses or grouping symbols.
Next, look for Exponents, followed by Multiplication and Division (reading from left to right)
Lastly, addition and subtraction (again, reading from left to right)
Question 2.
Look for Relationships How many times is 4 used as a factor in the expression 45? Write the numerical expression as repeated multiplication.
Answer:
The given expression is: 45
Now,
We know that,
The “Exponent” tells how many times the base is used as a factor
So,
In the given expression,
4 is used 5 times as a factor
So,
The representation of the given expression in the form of a repeated multiplication is:
4 × 4 × 4 × 4 × 4
Hence, from the above,
We can conclude that
4 is used 5 times as a factor
The representation of the given expression in the form of a repeated multiplication is:
4 × 4 × 4 × 4 × 4
Question 3.
Be Precise What is a power that has the same value as 18? Explain.
Answer:
The given expression is: 18
Now,
We know that,
The value of 1 raised to an exponent of any whole number is always equal to 1
So,
The power that has the same value as the given expression is: 1n
Where,
n = 0, 1, 2,…..
Hence, from the above,
We can conclude that
The power that has the same value as the given expression is: 1n
Where,
n = 0, 1, 2,…..
Question 4.
Construct Arguments Does 2.5 × 100 equal 0, 1, 2.5, or 25? Justify your answer.
Answer:
The given expression is: 2.5 × 100
Now,
We know that,
Any nonzero number raised to an exponent of zero has a value of 1
So,
2.5 × 100 = 2.5 × 1
= 2.5
Hence, from the above,
We can conclude that
The value of the given expression is: 2.5
Question 5.
Model with Math
How would you write (\(\frac{1}{2}\))3 as repeated multiplication?
Answer:
The given expression is: (\(\frac{1}{2}\))3
Now,
We know that,
The number that is repeatedly multiplied is the “Base”
The “Exponent” tells how many times the base is used as a factor
So,
The representation of the given expression as a repeated multiplication is:
\(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\)
Hence, from the above,
We can conclude that
The representation of the given expression as a repeated multiplication is:
\(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\)
Do You Know How?
Question 6.
Write 81 as a repeated multiplication of 3s. Then write it as a power.
Answer:
The given number is: 81
Now,
We know that,
81 = 9 × 9
= 3 × 3 × 3 × 3
Now,
We know that,
The number that is repeatedly multiplied is the “Base”
The “Exponent” tells how many times the base is used as a factor
So,
The representation of 81 in the form of power is:
81 = 34
Hence, from the above,
We can conclude that
The representation of 81 as a repeated multiplication is:
81 = 3 × 3 × 3 × 3
The representation of 81 as power is:
81 = 34
Question 7.
Write 125 as a repeated multiplication of 5s. Then write it as a power.
Answer:
The given number is: 125
Now,
We know that,
125 = 25 × 5
= 5 × 5 × 5
Now,
We know that,
The number that is repeatedly multiplied is the “Base”
The “Exponent” tells how many times the base is used as a factor
So,
The representation of 125 in the form of power is:
125 = 53
Hence, from the above,
We can conclude that
The representation of 125 as a repeated multiplication is:
125 = 5 × 5 × 5
The representation of 125 as power is:
125 = 53
Question 8.
What is 0.75 × 0.75 × 0.75 × 0.75 × 0.75 written as a power?
Answer:
The given expression is: 0.75 × 0.75 × 0.75 × 0.75 × 0.75
Now,
We know that,
The number that is repeatedly multiplied is the “Base”
The “Exponent” tells how many times the base is used as a factor
So,
The representation of 0.75 × 0.75 × 0.75 × 0.75 × 0.75 in the form of power is:
0.75 × 0.75 × 0.75 × 0.75 × 0.75 = 0.755
Hence, from the above,
We can conclude that
The representation of 0.75 × 0.75 × 0.75 × 0.75 × 0.75 as power is:
0.75 × 0.75 × 0.75 × 0.75 × 0.75 = 0.755
Question 9.
What is \(\frac{3}{8}\) × \(\frac{3}{8}\) × \(\frac{3}{8}\) written as a power?
Answer:
The given expression is: \(\frac{3}{8}\) × \(\frac{3}{8}\) × \(\frac{3}{8}\)
Now,
We know that,
The number that is repeatedly multiplied is the “Base”
The “Exponent” tells how many times the base is used as a factor
So,
The representation of \(\frac{3}{8}\) × \(\frac{3}{8}\) × \(\frac{3}{8}\) in the form of power is:
\(\frac{3}{8}\) × \(\frac{3}{8}\) × \(\frac{3}{8}\) = (\(\frac{3}{8}\))3
Hence, from the above,
We can conclude that
The representation of \(\frac{3}{8}\) × \(\frac{3}{8}\) × \(\frac{3}{8}\) as power is:
\(\frac{3}{8}\) × \(\frac{3}{8}\) × \(\frac{3}{8}\) = (\(\frac{3}{8}\))3
In 10-13, evaluate each power.
Question 10.
(\(\frac{1}{6}\))2
Answer:
The given expression is: (\(\frac{1}{6}\))2
So,
(\(\frac{1}{6}\))2
= \(\frac{1}{6}\) × \(\frac{1}{6}\)
= \(\frac{1 × 1}{6 × 6}\)
= \(\frac{1}{36}\)
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{1}{36}\)
Question 11.
450
Answer:
The given expression is: 450
Now,
We know that,
Any nonzero number raised to an exponent of zero has a value of 1
So,
450 = 1
Hence, from the above,
We can conclude that
The value of the given expression is: 1
Question 12.
0.15
Answer:
The given given expression is: 0.15
So,
0.15
= 0.1 × 0.1 ×0.1 × 0.1 × 0.1
= 0.00001
Hence, from the above,
We can conclude that
The value of the given expression is: 0.00001
Question 13.
73
Answer:
The given expression is: 73
So,
73
= 7 × 7 × 7
= 49 × 7
= 343
Hence, from the above,
We can conclude that
The value of the given expression is: 343
In 14-16, evaluate each expression.
Question 14.
4.5 × 104
Answer:
The given expression is: 4.5 × 104
Now,
We know that,
104 = 10,000
So,
4.5 × 104
= 45 × 103
= 45,000
Hence, from the above,
We can conclude that
The value of the given expression is: 45,000
Question 15.
0.6 × 106
Answer:
The given expression is: 0.6 × 106
Now,
We know that,
106 = 10,00,000
So,
0.6 × 106
= 6 × 105
= 6,00,000
Hence, from the above,
We can conclude that
The value of the given expression is: 6,00,000
Question 16.
3.4 × 100
Answer:
The given expression is: 3.4 × 100
Now,
We know that,
Any nonzero value raised to an exponent of zero has a value of 1
So,
100 = 1
So,
3.4 × 100
= 3.4 × 1
= 3.4
Hence, from the above,
We can conclude that
The value of the given expression is: 3.4
Practice & Problem Solving
Scan for Multimedia
In 17-20, write the exponent for each expression.
Question 17.
9 × 9 × 9 × 9
Answer:
The given expression is: 9 × 9 × 9 × 9
Now,
We know that,
The “Exponent” tells how many times the base is used as a factor
So,
From the given expression,
We can observe that
9 is repeated 4 times
Hence, from the above,
We can conclude that
The exponent for the given expression is: 4
Question 18.
1.29
Answer:
The given expression is: 1.29
Now,
We know that,
The “Exponent” tells how many times the base is used as a factor
So,
From the given expression,
We can observe that
1.2 is repeated 9 times
Hence, from the above,
We can conclude that
The exponent for the given expression is: 9
Question 19.
\(\frac{1}{6}\) × \(\frac{1}{6}\) × \(\frac{1}{6}\)
Answer:
The given expression is: \(\frac{1}{6}\) × \(\frac{1}{6}\) × \(\frac{1}{6}\)
Now,
We know that,
The “Exponent” tells how many times the base is used as a factor
So,
From the given expression,
We can observe that
\(\frac{1}{6}\) is repeated 3 times
Hence, from the above,
We can conclude that
The exponent for the given expression is: 3
Question 20.
7
Answer:
The given expression is: 7
Now,
We know that,
The “Exponent” tells how many times the base is used as a factor
So,
From the given expression,
We can observe that
7 is repeated 1 time
Hence, from the above,
We can conclude that
The exponent for the given expression is: 1
Leveled Practice In 21-26, evaluate each power or expression.
Question 21.
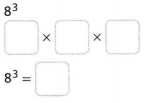
Answer:
The given expression is: 83
So,
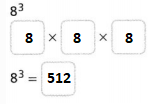
Hence, from the above,
We can conclude that
The value of the given expression is: 512
Question 22.
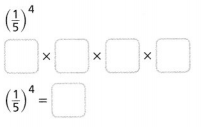
Answer:
The given expression is: (\(\frac{1}{5}\))4
So,
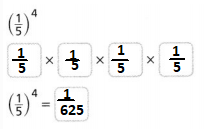
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{1}{625}\)
Question 23.
0.62
Answer:
The given expression is 0.6²
So,
0.6² = 0.6 × 0.6
= 0.36
Hence, from the above,
We can conclude that
The value of the given expression is: 0.36
Question 24.
(\(\frac{1}{4}\))2
Answer:
The given expression is: (\(\frac{1}{4}\))²
So,
(\(\frac{1}{4}\))² = \(\frac{1}{4}\) × \(\frac{1}{4}\)
= \(\frac{1 × 1}{4 × 4}\)
= \(\frac{1}{16}\)
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{1}{16}\)

Question 25.
580
Answer:
The given expression is: 580
Now,
We know that,
Any nonzero value raised to an exponent of zero has a value of 1
So,
580 = 1
Hence, from the above,
We can conclude that
The value of the given expression is: 1
Question 26.
6.2 × 103
Answer:
The given expression is: 6.2 × 103
So,
6.2 × 103 = 62 ×102
= 62 × 100
= 6,200
Hence, from the above,
We can conclude that
The value of the given expression is: 6,200
Question 27.
A company rents two storage units. Both units are cube-shaped. What is the difference in the volume between the two storage units? Note that the volume of a cube is s3, where s is the side length. Explain.

Answer:
It is given that
A company rents two storage units. Both units are cube-shaped
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The side length of the first storage unit is: 6.5 ft
The side length of the second storage unit is: 6 ft
Now,
We know that,
The volume of a cube = (Side)³
So,
The difference in volume between the two storage units = (The volume of the first storage unit) – (The volume of the second storage unit)
= (6.5)³ – 6³
= 274.625 – 216
= 58.63 ft³
Hence, from the above,
We can conclude that
The difference in volume between the two storage units is: 58.63 ft³
Question 28.
Jia is tiling a floor. The floor is a square with a side length of 12 feet. Jia wants the tiles to be squares with a side length of 2 feet. How many tiles does Jia need to cover the entire floor? Note that the area of a square is s2, where s is the side length. Explain.
Answer:
It is given that
Jia is tiling a floor. The floor is a square with a side length of 12 feet. Jia wants the tiles to be squares with a side length of 2 feet.
Now,
We know that,
The area of a square = (Side)²
So,
The area of the square floor = (The sidelength of the square floor)²
= 12²
= 144 feet²
So,
The area of the square tiles = (The sidelength of the square tiles)²
= 2²
= 4 feet²
Now,
The number of tiles Jia needed to cover the entire floor = (The area of the square floor) ÷ (The area of the square tiles)
= \(\frac{144}{4}\)
= 36 tiles
Hence, from the above,
We can conclude that
The number of tiles Jia needed to cover the entire floor is: 36 tiles
Question 29.
A marine biologist studies the population of seals in a research area. How many seals are in the research area?

Answer:
It is given that
A marine biologist studies the population of seals in a research area
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The population of Seals is: 3.27 × 10²
Now,
We know that,
10² = 10 × 10
= 100
So,
3.27 × 10² = 32.7 × 10
= 327 Seals
Hence, from the above,
We can conclude that
The number of Seals that are present in the research area is: 327 Seals
Question 30.
Higher-Order Thinking Zach invested $50 and tripled his money in two years. Kayla also invested $50, and after two years the amount was equal to 50 to the third power. Who had more money after two years? Explain.
Answer:
It is given that
Zach invested $50 and tripled his money in two years. Kayla also invested $50, and after two years the amount was equal to 50 to the third power
So,
According to the given information,
The amount of money invested by Zach in two years = $50 × 3
= $150
The amount of money invested by Kayla in two years = ($50)³
= $1,25,000
So,
From the above values,
We can say that
$1,25,000 > $150
Hence, from the above,
We can conclude that
Kayla had more money after two years
Question 31.
Malik read that the land area of Alaska is about 5.7 × 105 square miles. About how many square miles is the land area of Alaska?
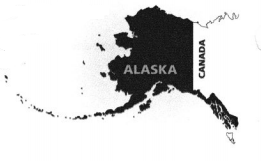
Answer:
It is given that
Malik read that the land area of Alaska is about 5.7 × 105 square miles.
Now,
We know that,
105 = 1,00,000
104 = 10,000
So,
5.7 × 105 = 57 × 104
= 57 × 10,000
= 57,000 square miles
Hence, from the above,
We can conclude that
The land area of Alaska is about 57,000 square miles

Question 32.
Explain why the expressions 100, 14, and 1 × 1.00 have the same value.
Answer:
The given expressions are: 100, 14, 1 × 1.04
Now,
We know that,
Any nonzero value that has raised to an exponent of zero has a value of 1
Any value of 1 that is raised to an exponent that contained a whole number has always a value of 1
Hence, from the above,
We can conclude that
The given expressions have the same value since some expressions have raised to an exponent of zero and some expressions have the value of 1 that is to an exponent of any whole number
Question 33.
Solve the equation 0.33 = n.
Answer:
The given equation is:
0.3³ = n
So,
By using the repeated multiplication,
n = 0.3 × 0.3 × 0.3
n = 0.09 × 0.3
n = 0.027
Hence, from the above,
We can conclude that
The value of “n” for the given equation is: 0.027
Question 34.
Construct Arguments The same digits are used for the expressions 25 and 52. Explain how to compare the values of the expressions.
Answer:
It is given that
The same digits are used for the expressions 25 and 52
Now,
We know that,
The number that is repeatedly multiplied is the “Base”
The “Exponent” tells how many times the base is used as a factor
So,
25 = 2 × 2 × 2 × 2 × 2
= 4 × 4 × 2
= 16 × 2
= 32
So,
52 = 5 ×5
= 25
So,
From the obtained values,
32 > 25
Hence, from the above,
We can conclude that 25 is greater than 52
Question 35.
Critique Reasoning Kristen was asked to write each of the numbers in the expression 80,000 × 25 using exponents. Her response was (8 × 103) × 52. Was Kristen’s response correct? Explain.
Answer:
It is given that
Kristen was asked to write each of the numbers in the expression 80,000 × 25 using exponents. Her response was (8 × 103) × 52
Now,
The given expression is: 80,000 × 25
Now,
80,000 × 25 = 8 × 10,000 × 25
= 2³ × 10,000 × 5²
Now,
We know that,
10,000 = 104
So,
80,000 × 25 = 23 × 4 × 52
= (8 × 104) × 52
Hence, from the above,
We can conclude that
Kristen’s response was not correct
Question 36.
Consider the equation 1,000,000 = 106. Why is 10 used as the base to write 106?
Answer:
The given equation is: 1,000,000 = 106
Now,
We know that,
In base-10, each digit of a number can have an integer value ranging from 0 to 9 (10 possibilities) depending on its position. The places or positions of the numbers are based on powers of 10. Each number position is 10 times the value to the right of it, hence the term base-10
Hence, from the above,
We can conclude that
We used 10 as the base to write 106 because of the position and the possibilities
Question 37.
Isabella saved 2 nickels today. If she doubles the number of nickels she saves each day, how many days, including today, will it take her to save more than 500 nickels?
Answer:
It is given that
Isabella saved 2 nickels today and she doubles the number of nickels she saves each day,
So,
The number of nickels she saved today is: 2
The number of nickels she saved the second day is 4 (or) 2²
The number of nickels she saved the third day is 8 (or) 2³
So,
The pattern for the number of nickels she saves each day will be like
2, 2², 2³, …..
Now,
The number of days it will take for her to save more than 500 nickels is: 28
Hence, from the above,
We can conclude that
The number of days she will take to save more than 500 nickels each day is about 8 days
Assessment Practice
Question 38.
Select all expressions equivalent to 5 × 5 × 5 × 5.
![]() 51 × 54
51 × 54
![]() 54
54
![]() 52 × 52
52 × 52
![]() 45
45
![]() 4(51)
4(51)
Answer:
The given expression is: 5 × 5 × 5 × 5
Now,
The representation of the given expression in the form of an exponent is:
5 × 5 × 5 × 5 = 5² × 5²
= 54
Hence, from the above,
We can conclude that
All the expressions equivalent to 5 × 5 × 5 × 5 are:

Question 39.
Which expression is equivalent to \(\frac{1}{36}\)?
A. \(\frac{1}{3}\) × \(\frac{1}{6}\)
B. \(\frac{1}{4}\) × (\(\frac{1}{3}\))3
C. (\(\frac{1}{2}\))2 × (\(\frac{1}{3}\))2
D. \(\frac{1}{2}\) × \(\frac{1}{3}\) × \(\frac{1}{3}\) × \(\frac{1}{3}\)
Answer:
The given expression is: \(\frac{1}{36}\)
Now,
The representation of the givene xpression in various forms is:
\(\frac{1}{36}\) = (\(\frac{1}{6}\))²
= \(\frac{1}{9}\) × \(\frac{1}{4}\)
= (\(\frac{1}{3}\))² × (\(\frac{1}{2}\))²
Hence, from the above,
We can conclude that
The expression is equivalent to \(\frac{1}{36}\) is:
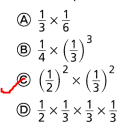
Lesson 3.2 Find Greatest Common Factor and Least Common Multiple
Solve & Discuss It!
ACTIVITY
Mark sets the dinner table every 2 days and dries the dishes every 3 days. If he sets the table on Day 2 and dries the dishes on Day 3, on what day would Mark first perform both chores on the same day?

Answer:
It is given that
Mark sets the dinner table every 2 days and dries the dishes every 3 days and he sets the table on Day 2 and dries the dishes on Day 3
Now,
To find the days that Mark would perform both chores on the same day,
Find the common multiplies of 2 and 3
So,
The common multiples of 2 and 3 are: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60….
Hence, from the above,
We can conclude that
The days that Mark would perform both chores on the same day must be the multiple of 6
Look for Relationships What is the relationship between the chores that Mark does each day?

Answer:
The completed list of days and chores is:
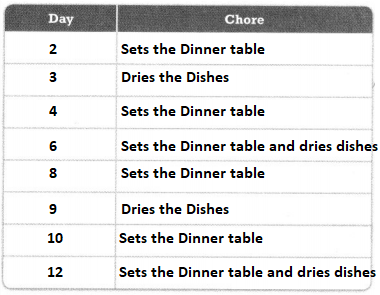
Now,
From the above list,
We can observe that
For every day that is multiple of 2,
Mark sets the dinner table
For every day that is multiple of 3,
Mark dries the dishes
For every day that is both the multiple of 2 and 3,
Mark sets the dinner table and dries the dishes
Hence, from the above,
We can conclude that
The relationship between the chores Mark does each day is:
a. For every day that is multiple of 2,
Mark sets the dinner table
b. For every day that is multiple of 3,
Mark dries the dishes
c. For every day that is both the multiple of 2 and 3,
Mark sets the dinner table and dries the dishes
Focus on math practices
Generalize on what day will Mark do both chores on the same day again? How can you find on which days Mark does both chores without making a list?
Answer:
From the above problem,
We can observe that
The days that Mark would perform both chores on the same day must be the multiple of 6 i.e., the common multiple of both 2 and 3
Hence, from the above,
We can conclude that
The days that Mark would perform both chores on the same day must be the multiple of 6 i.e., the common multiple of both 2 and 3
VISUAL LEARNING
? Essential Question How can you write the prime factorization and find the greatest common factor and least common multiple of two numbers?
Answer:
The steps to Write Prime Factorization of Composite Numbers are:
a. Put a prime factor on the outside left and the result or quotient (the number of times it divides evenly) underneath.
b. Divide the quotient (the number underneath) by another prime number and keep doing this until the bottom number is a prime
Examples:

The steps to find the GCF of a set of numbers, using prime factorization are:
a. List the prime factors of each number.
b. Circle every common prime factor i.e., every prime factor that’s a factor of every number in the set.
c. Multiply all the circled numbers. The result is the GCF.
The steps to find the LCM using the prime factorization method are:
a. Find the prime factorization of each number.
b. Write each number as a product of primes, matching primes vertically when possible.
c. Bring down the primes in each column.
d. Multiply the factors to get the LCM.
Try It!
Find the prime factorization of 56. Start with the least prime factor.

Answer:
The given number is: 56
Now,
By using the Prime factorization method,
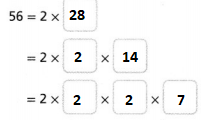
So,

Hence, from the above,
We can conclude that
The prime factorization of 56 is: 2³ × 7
Convince Me! A number is greater than 2 and it has 2 as a factor. Is the number prime or composite? Explain.
Answer:
It is given that
A number is greater than 2 and it has 2 as a factor
Now,
We know that,
2 is both prime and composite. The definition of prime is a number whose two factors are one and itself. If it has two, it must be composite, because that is not one or itself
Now,
According to the given information,
One of the numbers that are greater than 2 and have 2 as a factor will be: 4
Now,
We know that,
4 has more than 2 factors
Hence, from the above,
We can conclude that
A number that is greater than 2 and has 2 as a factor is a “Composite number”
Try It!
Keesha has 24 beads to add equally to each bag. Can she still make 6 bags and have no supplies left over? Explain.
Answer:
It is given that
Keesha has 24 beads to add equally to each bag.
Now,
The GCF of 24 and 6 is:

Now,
We can say that
The highest number of bags Keesha can make is: 6 bags
Hence, from the above,
We can conclude that
Keesha can still make 6 bags and have no supplies leftover
Try It!
Use the GCF and the Distributive Property to find the sum of 12 and 36.
Answer:
The given numbers are: 12 and 36
Now,
Step 1:
The GCF of 12 and 36 is:

Step 2:
Write 12 and 36 as a product using the GCF as a factor
Now,
By using the Distributive Property,
12 + 36 = (12 × 1) + (12 × 3)
= 12 × (1 + 3)
= 12 × 4
= 48
Hence, from the above,
We can conclude that
The sum of 12 and 36 is: 48
Try It!
Grant also buys bottled water and juice pouches for the picnic. There are 12 bottles of water in each case and 10 juice pouches in each box. Grant wants to buy the least amount but still have as many bottles of water as juice pouches. How many of each should he buy? Explain.
Answer:
It is given that
Grant also buys bottled water and juice pouches for the picnic. There are 12 bottles of water in each case and 10 juice pouches in each box. Grant wants to buy the least amount but still have as many bottles of water as juice pouches
Now,
To find the number of bottles and juice pouches Grant bought,
Find the LCM of 12 and 10
Now,
The LCM of 12 and 10 is:

So,
The number of bottles Grant should buy = \(\frac{60}{12}\)
= 5 bottles
The number of juice pouches Grant should buy = \(\frac{60}{10}\)
= 6 juice pouches
Hence, from the above,
We can conclude that
The number of bottles Grant should buy is: 5 bottles
The number of juice pouches Grant should buy is: 6 juice pouches
KEY CONCEPT
The greatest common factor (GCF) of two numbers is the greatest number that is a factor of both numbers.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
2 and 4 are common factors of 12 and 40. 4 is the greatest common factor.
The GCF of 12 and 40 is 4.
The least common multiple (LCM) of two numbers is the least multiple, not including zero, common to both numbers. Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48 …
Multiples of 9: 9, 18, 27, 36, 45, 54 …
18 and 36 are common multiples of 6 and 9.
18 is the least common multiple.
The LCM of 6 and 9 is 18.
Do You Understand?
Question 1.
? Essential Question How can you write the prime factorization and find the greatest common factor and the least common multiple of two numbers?
Answer:
The steps to Write Prime Factorization of Composite Numbers are:
a. Put a prime factor on the outside left and the result or quotient (the number of times it divides evenly) underneath.
b. Divide the quotient (the number underneath) by another prime number and keep doing this until the bottom number is a prime
Examples:

The steps to find the GCF of a set of numbers, using prime factorization are:
a. List the prime factors of each number.
b. Circle every common prime factor i.e., every prime factor that’s a factor of every number in the set.
c. Multiply all the circled numbers. The result is the GCF.
The steps to find the LCM using the prime factorization method are:
a. Find the prime factorization of each number.
b. Write each number as a product of primes, matching primes vertically when possible.
c. Bring down the primes in each column.
d. Multiply the factors to get the LCM.
Question 2.
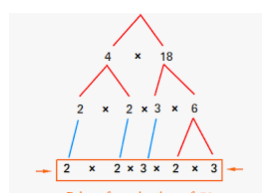
What are two different ways in which you can use prime factorization to find the prime factors of a number?
Answer:
There are two common ways to perform prime factorization. The first is called the “Prime Factor Tree”, and the second is known as the “Upside-Down Division”
An example of the Prime Factor Tree method is:
An example of the Upside Down Division method is:
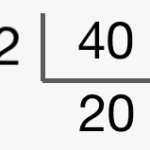
Question 3.
Generalize Why is the GCF of two prime numbers always 1?
Answer:
GCF stands for Greatest Common Factor. Since 1 is a factor of every number, any two or more numbers have a GCF, because even if the numbers are prime, or if they don’t share any prime factors, then the GCF will be 1. If they do share any prime factors, then the GCF will be the product of those shared prime factors.
Question 4.
Construct Arguments In example 4, Grant finds applesauce that comes in packages of 8, but now he finds juice bottles in only packages of 3. Will the LCM change? Explain.
Answer:
It is given that
In example 4, Grant finds applesauce that comes in packages of 8, but now he finds juice bottles in only packages of 3
Now,
In Example 4,
We can observe that
Grant should buy 8 packages of juice bottles and 6 packages of applesauce
Now,
From the given information,
We can observe that
Instead of 6 packages of applesauce, there are only 3 packages of applesauce now
Now,
We know that,
Since 3 and 6 are multiples, the LCM will be the same as in Example 4
Hence, from the above,
We can conclude that
The LCM will not change
Question 5.
Critique Reasoning Sarah says that you can find the LCM of any two whole numbers by multiplying them together. Provide a counterexample to show that Sarah’s statement is incorrect.
Answer:
We know that,
“LCM” means the “Lowest Common Multiple”
Now,
To find the LCM of the two whole numbers means finding the least common multiple of the two whole numbers
Example:
Find the LCM of 30 and 40
Now,
30 × 40 = 1,200
But,
1,200 is not the LCM of 30 and 40
Now,
The LCM of 30 and 40 are:

Hence, from the above,
We can conclude that
Sarah’s statement is incorrect
Do You Know How?
In 6-8, write the prime factorization of each number. If the number is prime, write prime.
Question 6.
33
Answer:
The given number is: 33
So,
The representation of the factors for the given number using the prime factorization method is:

Hence, from the above,
We can conclude that
The factors for the given number using the Prime factorization method is:
33 = 3 × 11
Question 7.
32
Answer:
The given number is: 32
So,
The representation of the factors for the given number using the prime factorization method is:

Hence, from the above,
We can conclude that
The factors for the given number using the Prime factorization method is:
32 = 2 × 2 × 2 × 2 × 2
Question 8.
19
Answer:
The given number is: 19
Now,
We know that,
19 has the factors of 1 and itself
Hence, from the above,
We can conclude that the given number is a prime number
In 9-11, find the GCF for each pair of numbers.
Question 9.
18, 36
Answer:
The given numbers are: 18, 36
Now,

Hence, from the above,
We can conclude that
The GCF of 18 and 36 is: 18
Question 10.
22, 55
Answer:
The given numbers are: 22, 55
Now,

Hence, from the above,
We can conclude that
The GCF of 22 and 55 is: 11
Question 11.
100, 48
Answer:
The given numbers are: 100, 48
Now,

Hence, from the above,
We can conclude that
The GCF of 100 and 48 is: 4
In 12-14, find the LCM for each pair of numbers.
Question 12.
2, 5
Answer:
The given numbers are: 2, 5
Now,

Hence, from the above,
We can conclude that
The LCM of 2 and 5 is: 10
Question 13.
8, 12
Answer:
The given numbers are: 8, 12
Now,

Hence, from the above,
We can conclude that
The LCM of 8 and 12 is: 24
Question 14.
8, 10
Answer:
The given numbers are: 8, 10
Now,

Hence, from the above,
We can conclude that
The LCM of 8 and 10 is: 40
Practice & Problem Solving
Leveled Practice
In 15-18, find the prime factorization of each number. If it is prime, write prime.
Question 15.
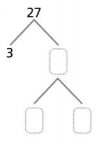
Answer:
The given number is: 27
Now,
The representation of the factors for the given number using the Prime factorization method is:
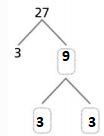
Hence, from the above,
We can conclude that
The factors of 27 by using the Prime Factorization method is: 3 × 3 × 3
Question 16.
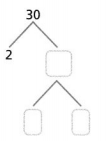
Answer:
The given number is: 30
Now,
The representation of the factors for the given number using the Prime factorization method is:
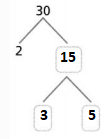
Hence, from the above,
We can conclude that
The factors of 30 by using the Prime Factorization method is: 2 × 3 × 5
Question 17.
26
Answer:
The given number is: 26
Now,
The representation of the factors for the given number using the Prime factorization method is:

Hence, from the above,
We can conclude that
The factors of 26 by using the Prime Factorization method is: 2 × 13
Question 18.
47
Answer:
The given number is: 47
Now,
We know that,
47 has factors of 1 and only itself
Hence, from the above,
We can conclude that
47 is a prime number
In 19-21, find the GCF for each pair of numbers.
Question 19.
21, 49
Answer:
The given numbers are: 21, 49
Now,

Hence, from the above,
We can conclude that GCF of 21, 49 is: 7
Question 20.
8, 52
Answer:
The given numbers are: 8, 52
Now,

Hence, from the above,
We can conclude that GCF of 8, 52 is: 4
Question 21.
32, 81
Answer:
The given numbers are: 32, 81
Now,

Hence, from the above,
We can conclude that GCF of 32, 81 is: 1
In 22-24, use the GCF and the Distributive Property to find each sum.
Question 22.
30 + 66
Answer:
The given expression is: 30 + 66
Now,
Step 1: Find the GCF of 30 and 66
So,

So,
The GCF of 30 and 66 is: 6
Step 2: Write each number as a product using GCF as a factor
So,
30 + 66 = (6 × 5) + (6 × 11)
= 6 × (5 + 11)
= 6 × 16
= 96
Hence, from the above,
We can conclude that
The sum of 30 and 66 is: 96
Question 23.
34 + 51
Answer:
The given expression is: 34 + 51
Now,
Step 1: Find the GCF of 34 and 51
So,

So,
The GCF of 34 and 51 is: 17
Step 2: Write each number as a product using GCF as a factor
So,
34 + 51 = (17 × 2) + (17 × 3)
= 17 × (2 + 3)
= 17 × 5
= 85
Hence, from the above,
We can conclude that
The sum of 34 and 51 is: 85
Question 24.
15 + 36
Answer:
The given expression is: 15 + 36
Now,
Step 1: Find the GCF of 15 and 36
So,

So,
The GCF of 15 and 36 is: 3
Step 2: Write each number as a product using GCF as a factor
So,
15 + 36 = (3 × 5) + (3 × 12)
= 3 × (5 + 12)
= 3 × 17
= 51
Hence, from the above,
We can conclude that
The sum of 15 and 36 is: 51
In 25-27, find the LCM for each pair of numbers.
Question 25.
12, 11
Answer:
The given numbers are: 12, 11
Now,

Hence, from the above,
We can conclude that
The LCM of 12 and 11 is: 132
Question 26.
4, 12
Answer:
The given numbers are: 4, 12
Now,

Hence, from the above,
We can conclude that
The LCM of 4 and 12 is: 12
Question 27.
5, 8
Answer:
The given numbers are: 5, 8
Now,

Hence, from the above,
We can conclude that
The LCM of 5 and 8 is: 40
Question 28.
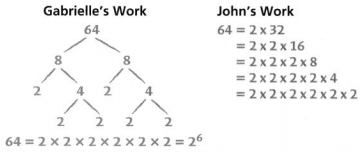
Critique Reasoning Gabrielle and John each wrote the prime factorization of 64. Analyze their work and explain any errors.
Answer:
It is given that
Gabrielle and John each wrote the prime factorization of 64
Now,
According to Gabrielle,
The factors of 64 by using the Prime factorization method is:
So,
The representation of factors of 64 using the Prime factorization method is:
64 = 2 × 2 × 2 × 2 ×2 × 2 = 26
Now,
According to John,
The factors of 64 are:
64 = 2 × 32
= 2 × 2 ×16
= 2 × 2 × 2 × 8
= 2 × 2 × 2 × 2 × 4
= 2 × 2 × 2 × 2 × 2 × 2
Hence, from the above,
We can conclude that
There are no errors in Gabriel’s and John’s work
Question 29.
To celebrate its grand opening, a store is giving customers gift certificates. Which customer is the first to get two gift certificates?
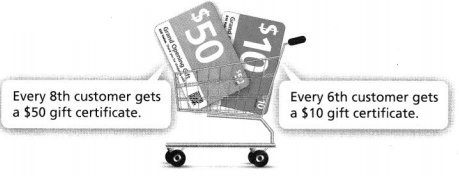
Answer:
It is given that
To celebrate its grand opening, a store is giving customers gift certificates.
Now,
The given figure is:

Now,
To find the customer who is the first that will get two gift certificates,
Find the LCM of 6 and 8
Now,

Hence, from the above,
We can conclude that
The 24th customer is the first to get the two gift certificates
Question 30.
A Model with Math
The Venn diagram at the right shows the factors of 24 and 40.
a. What is the meaning of each of the three shaded regions?
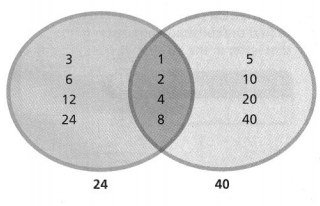
Answer:
The given numbers are: 24 and 40
Now,
The given Venn diagram is:

Now,
From the given Venn diagram,
We can observe that
The left side region of the Venn diagram shows: The factors of 24
The right side region of the Venn diagram shows: The factors of 40
The midle region of the Venn diagram shows: The common factors of 24 and 40
Hence, from the above,
We can conclude that
The meaning of the shaded regions is:
The left side region of the Venn diagram shows: The factors of 24
The right side region of the Venn diagram shows: The factors of 40
The midle region of the Venn diagram shows: The common factors of 24 and 40
b. Explain how you use the Venn diagram to find the GCF of 24 and 40. What is the GCF of 24 and 40?
Answer:
The given Venn diagram is:

Now,
We know that,
The GCF of the two numbers can be find out by identifying the highest factor in the common factors of a and b
So,
In he given Venn diagram,
The middle region represents the common factors of 24 and 40
In the common factors of 24 and 40, 8 is the highest factor
Hence, from the above,
We can conclude that
The GCF of 24 and 40 is: 8
Question 31.
Reasoning You have 50 blueberry scones and 75 cranberry scones. You want to make as many identical bags as possible. Each bag should have an equal number of blueberry scones and an equal number of cranberry scones. What is the greatest number of bags you can fill? Explain.
Answer:
It is given that
You have 50 blueberry scones and 75 cranberry scones. You want to make as many identical bags as possible. Each bag should have an equal number of blueberry scones and an equal number of cranberry scones
Now,
To find the greatest number of bags that you can fill an equal number of blueberry scones and cranberry scones,
Find the GCF of 50 and 75
Now,

Hence, from the above,
We can conclude that
The greatest number of blueberry scones bags and cranberry scones bags that you can fill is: 25 bags
Question 32.
Make Sense and Persevere The prime factorizations of A and B are shown. Find the value of n that needs to be listed as a prime factor of B so that the greatest common factor (GCF) of A and B is 9.
Prime factorization of A: 3 × 3 × 3
Prime factorization of B: 2 × 2 × 3 × n
Answer:
It is given that
The prime factorizations of A and B are shown and the greatest common factor (GCF) of A and B is 9.
Now,
The given prime factorizations of A and B are:
Prime factorization of A: 3 × 3 × 3
Prime factorization of B: 2 × 2 × 3 × n
Now,
To make GCF of A and B to be 9,
The numbers must be 27 and 36
Now,
27 = 3 × 3 × 3
36 = 2 × 2 × 3 × 3
So,
The missing number is: 3
Hence, from the above,
We can conclude that
The value of n is: 3
Question 33.
Higher-Order Thinking Gena has 28 trading cards, Sam has 91 trading cards, and Tiffany has 49 trading cards. Use the GCF and the Distributive Property to find the total number of trading cards Gena, Sam, and Tiffany, have.
Answer:
It is given that
Gena has 28 trading cards, Sam has 91 trading cards, and Tiffany has 49 trading cards.
Now,
To find the total number of trading cards Gena, Sam, and Tiffany have, the following steps that used to solve are:
Step 1: Find the GCF of 28, 91, and 49
So,

So,
The GCF of 28, 91, and 49 is: 7
Step 2: Write each number as a product using the GCF as a factor
So,
28 + 91 + 49 = (7 × 4) + (7 × 13) + (7 × 7)
= 7 × (4 + 13 + 7)
= 7 × 24
= 168 trading cards
Hence, from the above,
We can conclude that
The total number of trading cards Gena, Sam, and Tiffany have is: 168 trading cards
Question 34.
Periodical cicada species emerge in large numbers from their larval stage at different yearly intervals. What is the GCF of the years?
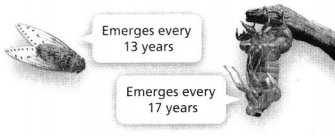
Answer:
It is given that
Periodical cicada species emerge in large numbers from their larval stage at different yearly intervals.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The two years are: 13 years and 17 years
Now,
The GCF of 13 and 17 is:
Hence, from the above,
We can conclude that
The GCF of the given years is: 1
Question 35.
People are waiting in line for a theater premiere. Every 5th person in line will receive a free theater ticket. Every 6th person will receive a gift card for $40. Which person is the first to receive both prizes?
Answer:
It is given that
People are waiting in line for a theater premiere. Every 5th person in line will receive a free theater ticket. Every 6th person will receive a gift card for $40
Now,
To find the person who is the first to receive both prizes,
Find the LCM of 5 and 6
Now,

Hence, from the above,
We can conclude that
The 30th person is the first to receive both prizes
Question 36.
Two volunteer groups plant trees. Group A plants the trees in clusters of 3. Group B plants the trees in clusters of 10. Both groups plant the same number of trees. What is the least number of clusters that Group B plants?
Answer:
It is given that
Two volunteer groups plant trees. Group A plants the trees in clusters of 3. Group B plants the trees in clusters of 10. Both groups plant the same number of trees
Now,
To find the least number of clusters that Group B plants,
Find the LCM of 3 and 10
Now,

Hence, from the above,
We can conclude that
The least number of clusters that Group B plants is: 30 clusters
Question 37.
Find the LCM of the two numbers. Then use the LCM to find the corresponding letter in the key. Write that letter in the box. What word did you decode?
Answer:
The given data is:

Now,
a.
The LCM of 2 and 3 is:

So,
The LCM of 2 and 3 is: 6
The letter that corresponds to the LCM of 2 and 3 is: F
b.
The LCM of 3 and 7 is:
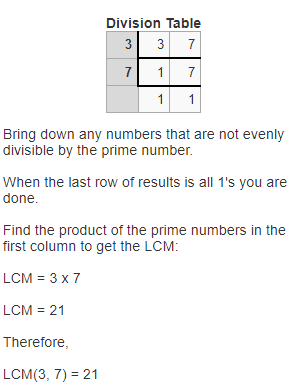
So,
The LCM of 3 and 7 is: 21
The letter that corresponds to the LCM of 3 and 7 is: U
c.
The LCM of 2 and 7 is:
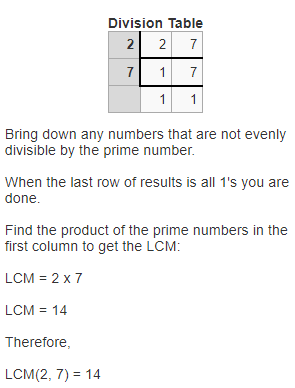
So,
The LCM of 2 and 7 is: 14
The letter that corresponds to the LCM of 2 and 7 is: N
So,
The word did you decode is: FUN
Hence, from the above,
We can conclude that
The word you decoded is: FUN
Question 38.
Rami has swimming lessons every 3 days and guitar lessons every 8 days. If he has both lessons on the first day of the month, in how many days will Rami have both lessons on the same day again?
Answer:
It is given that
Rami has swimming lessons every 3 days and guitar lessons every 8 days and he has both lessons on the first day of the month
Now,
To find the number of days will Rami have both lessons on the same day again,
Find the LCM of 3 and 8
Now,

Hence, from the above,
We can conclude that
In 24 days, Rami will have both lessons on the same day again
Question 39.
A number is between 58 and 68. It has prime factors of 2, 3, and 5. What is the number?
Answer:
It is given that
A number is between 58 and 68. It has prime factors of 2, 3, and 5
Now,
Let the number that has the given prime factors be x
Now,
If x has the prime factor of 5, then it must be a multiple of 5
So,
The multiples of 5 between 58 and 68 are: 60, 65
Now,
The factors of 65 using the Prime Factorization method are:
65 = 5 × 13
The factors of 60 using the Prime Factorization method are:
60 = 2 × 30
= 2 × 2 × 15
= 2 × 2 × 3 × 5
So,
60 has the prime factors of 2, 3, and 5 as given
Hence, from the above,
We can conclude that
The number that is between 58 and 68 and has the prime factors 2, 3, and 5 is: 60
Question 40.
A college offers shuttle service from Dickson Hall or Lot B to its campus quad. Both shuttles first depart their locations at 9:10 A.M. They run from each location to campus and back at the intervals shown. When is the next time both shuttles will depart for the campus at the same time? Explain.

Answer:
It is given that
A college offers shuttle service from Dickson Hall or Lot B to its campus quad. Both shuttles first depart their locations at 9:10 A.M. They run from each location to campus and back at the intervals shown.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The shuttle departs every 10 minutes from Lot B
The shuttle departs every 12 minutes from Dickson Hall
Now,
To find the next time both shuttles will depart for the campus at the same time,
Find the LCM of 10 and 12
Now,

Now,
We know that,
1 hour = 60 minutes
So,
The next time both shuttles will depart from the campus at the same time = (The first time both shuttles departed from the campus at the same time) + 1 hour
= 9:10 A.M + 1 hour
= 10:10 A.M
Hence, from the above,
We can conclude that
The next time both shuttles will depart from the campus at the same time is: 10:10 A.M
Assessment Practice
Question 41.
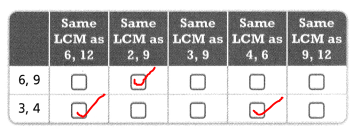
Match each pair of numbers with the pair(s) of numbers that have the same LCM.

Answer:
The given pairs of numbers are: (6, 9), (3, 4), (6, 12), (2, 9), (3, 9), (4, 6), and (9, 12)
Now,
The LCMs of the given pairs of numbers are:
The LCM of 6 and 9 is: 18
The LCM of 3 and 4 is: 12
The LCM of 6 and 12 is: 12
The LCM of 2 and 9 is: 18
The LCM of 3 and 9 is: 9
The LCM of 4 and 6 is: 12
The LCM of 9 and 12 is: 36
Hence, from the above,
We can conclude that
The matched pair of numbers with the pair of numbers that has the same LCM is:
Question 42.
Which expression is equivalent to 48 + 60?
A. 12(4 + 5)
B. 12(8 + 5)
C. 6(6 + 10)
D. 6(8 + 12)
Answer:
The given expression is: 48 + 60
Now,
Step 1: Find the GCF of 48 and 60
So,

Step 2: Write each number as a product by using the GCF as a factor
So,
48 + 60 = (12 × 4) + (12 × 5)
= 12 × (4 + 5)
Hence, from the above,
We can conclude that
The expression that is equivalent to 48 + 60 is:

Lesson 3.3 Write and Evaluate Numerical expressions
Solve & Discuss It!
ACTIVITY
An airline company charges additional fees for bags that do not meet the weight and size limits. For one flight, fees were charged for a total of 50 bags that were over the weight limit and 6 oversized bags. Find the total amount of fees collected for that flight.

Look for Relationships You can use the order of operations to evaluate numerical expressions.
Answer:
It is given that
An airline company charges additional fees for bags that do not meet the weight and size limits. For one flight, fees were charged for a total of 50 bags that were over the weight limit and 6 oversized bags.
Now,
The given figure is:

So,
The total amount of fees collected for the given flight = (The total number of overweight bags) × (The extra fees for each overweight bag) + (The total number of oversized bags) × (The extra fees for each oversized bag)
= (50 × $49) + (6 × $75)
Now,

Hence, from the above,
We can conclude that
The total amount of fees collected for the given flight is: $2900
Focus on math practices
A Model with Math
Tamara was charged for two bags that were over the weight limit and another bag that was over the size limit. Write and evaluate a numerical expression to find the additional fees Tamara was charged for her bags.
Answer:
It is given that
Tamara was charged for two bags that were over the weight limit and another bag that was over the size limit.
Now,
The given figure is:

So,
The total additional fees Tamara charged for her bags = (The total number of overweight bags) × (The extra fees for each overweight bag) + (The total number of oversized bags) × (The extra fee for each oversized bag)
= (2 × $49) + (1 × $75)
Now,
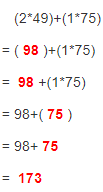
Hence, from the above,
We can conclude that
The total additional fees Tamara charged for her bags is: $173
VISUAL LEARNING
? Essential Question How do you write and evaluate numerical expressions?
Answer:
We write a numerical expression by using numbers and mathematical operators which are addition, subtraction, multiplication, and division.
Example:
The expression of the mathematical statement “4 added to 2”, will be 2+4.
To evaluate a numerical expression means to find the value of the expression by using the order of operations. To evaluate an expression, we follow the rules of the order of operations in the expression and then simplify the expression using the order of operations.
Scan for Multimedia
Try It!
Evaluate the numerical expression at the right.
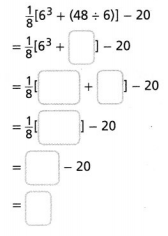
Answer:
The given numerical expression is: \(\frac{1}{8}\) [6³ + (48 ÷ 6)] – 20
Now,
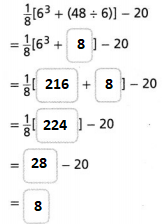
Hence, from the above,
We can conclude that
The value of the given numerical expression is: 8
Convince Me! Why is it important to follow the order of operations?
Answer:
The order of operations is a rule that tells you the right order in which to solve different parts of a math problem. Subtraction, multiplication, and division are all examples of operations. The order of operations is important because it guarantees that people can all read and solve a problem in the same way
Try It!
A. Evaluate the numerical expression: 3.22 – [(9 × 4) + 9] × (\(\frac{1}{3}\))2?
Answer:
The given numerical expression is: 3.22 – [(9 × 4) + 9] × (\(\frac{1}{3}\))2
Now,
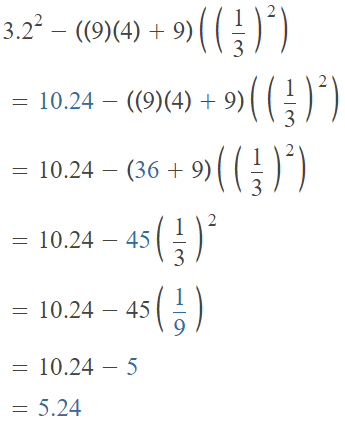
Hence, from the above,
We can conclude that
The value of the given numerical expression is: 5.24
B. Insert grouping symbols so that the numerical expression has a value of 80.
6 + 12 × (\(\frac{2}{3}\))2 × 3 + 7
Answer:
The given expression is:
6 + 12 × (\(\frac{2}{3}\))2 × 3 + 7
Now,
It is given that
The value of the given expression is: 80
Now,
Case 1:
6 + 12 × (\(\frac{2}{3}\))² × (3 + 7)
= 6 + 12 × \(\frac{4}{9}\) × 10
= 6 + \(\frac{160}{3}\)
= 6 + 53
= 59
Case 2:
(6 + 12) × (\(\frac{2}{3}\))² × (3 + 7)
= 18 × \(\frac{4}{9}\) × 10
= 2 × 4 ×10
= 8 × 10
= 80
Hence, from the above,
We can conclude that
The complete numerical expression with inserted grouping symbols and has a value of 80 is:
(6 + 12) × (\(\frac{2}{3}\))² × (3 + 7)
KEY CONCEPT
The order of operations is a set of rules used to evaluate expressions that include more than one operation.
Order of Operations
1 Evaluate inside grouping symbols,
such as parentheses or brackets.
2 Evaluate powers.
3 Multiply or divide from left to right.
4 Add or subtract from left to right.
Do You Understand?
Question 1.
? Essential Question How do you write and evaluate numerical expressions?
Answer:
We write a numerical expression by using numbers and mathematical operators which are addition, subtraction, multiplication, and division.
Example:
The expression of the mathematical statement “4 added to 2”, will be 2+4.
To evaluate a numerical expression means to find the value of the expression by using the order of operations. To evaluate an expression, we follow the rules of the order of operations in the expression and then simplify the expression using the order of operations.
Question 2.
Make Sense and Persevere Explain why grouping symbols can change the value of a numerical expression. Then insert grouping symbols to show four different values for the following expression. 80 ÷ 8 × 5 + 4
Answer:
We know that,
“Grouping symbols” are used in math to show a part of a math expression or equation that must be solved first, before any other calculations are done. The part between the two grouping symbols is treated like one number. Operations inside grouping symbols can be done before any other operations in order to simplify the problem
The position of grouping symbols decide the single value of the numerical expression based on the order of operations
Now,
The given expression is: 80 ÷ 8 × 5 + 4
Case 1:
The given expression with the grouping symbols is: (80 ÷ 8) × 5 + 4
So,
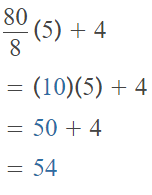
Case 2:
The given expression with the grouping symbols is: 80 ÷ (8 × 5) + 4
So,
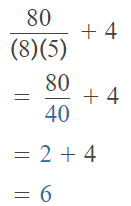
Case 3:
The given expression with the grouping symbols is: 80 ÷ 8 × (5 + 4)
So,
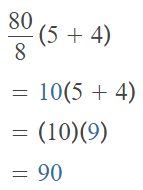
Case 4:
The given expression with the grouping symbols is: 80 ÷ (8 × (5 + 4))
So,
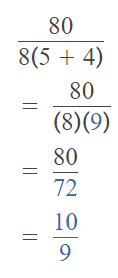
Question 3.
In the expression (21 – 3) × (7 + 2) ÷ (12 – 4), what operation should you perform last? Explain.
Answer:
The given expression is:
(21 – 3) × (7 + 2) ÷ (12 – 4)
To decide the order of operation,
We will follow BODMAS RULE
Where,
B – Brackets (or) Grouping symbols
O – Of
D – Division
M – Multiplication
A – Addition
S – Subtraction
Hence, from the above,
We can conclude that
The operation you should perform last for the given expression is: Multiplication
Question 4.
Critique Reasoning Charles says that 2 × 3 – 2 is 4, and Seth says that 2 × 3 – 2 is 2. Who is correct? Explain.
Answer:
It is given that
Charles says that 2 × 3 – 2 is 4, and Seth says that 2 × 3 – 2 is 2.
Now,
We know that,
To decide the order of operation,
We will follow BODMAS RULE
Where,
B – Brackets (or) Grouping symbols
O – Of
D – Division
M – Multiplication
A – Addition
S – Subtraction
So,
According to Charles:
The expression is: 2 × 3 – 2
So,
(2 × 3) – 2
= 6 – 2
= 4
According to Seth:
The expression is: 2 × 3 – 2
So,
2 × (3 – 2)
= 2 × 1
= 2
Hence, from the above,
We can conclude that
Charles is correct since he followed the order of operations correctly
Do You Know How?
In 5-9, evaluate each expression.
Question 5.
52 + (6.7 – 3.1)
Answer:
The given expression is: 52 + (6.7 – 3.1)
So,
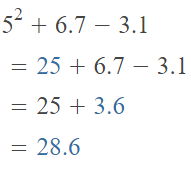
Hence, from the above,
We can conclude that
The value of the given expression is: 28.6
Question 6.
(8.2 + 5.3) ÷ 5
Answer:
The given expression is: (8.2 + 5.3) ÷ 5
So,
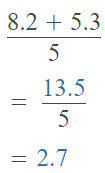
Hence, from the above,
We can conclude that
The value of the given expression is: 2.7
Question 7.
(1.5 – 0.52) ÷ [(3 + 2) × 2]
Answer:
The given expression is: (1.5 – 0.52) ÷ [(3 + 2) × 2]
So,
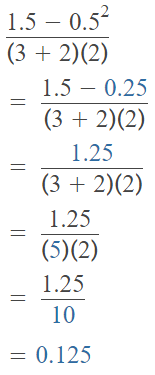
Hence, from the above,
We can conclude that
The value of the given expression is: 0.125
Question 8.
36.8 ÷ [11.5 – (2.5 × 3)]2
Answer;
The given expression is: 36.8 ÷ [11.5 – (2.5 × 3)]2
So,
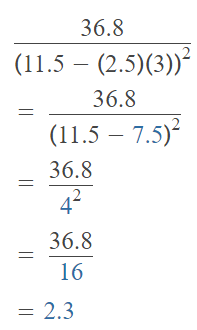
Hence, from the above,
We can conclude that
The value of the given expression is: 2.3
Question 9.
6 + 4 × 5 ÷ 2 – 8 × 1.5
Answer:
The given expression is: 6 + 4 × 5 ÷ 2 – 8 × 1.5
So,
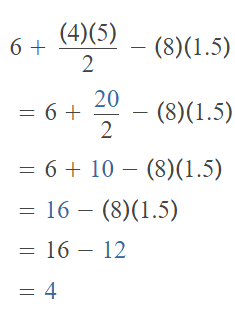
Hence, from the above,
We can conclude that
The value of the given expression is: 4
In 10-12, insert grouping symbols so that the expression has the given value.
Question 10.
12 × 32 + 36 Target value: 540
Answer:
The given expression is: 12 × 32 + 36
Now,
It is given that
The value of the given expression is: 540
Now,
Case 1:
12 × 32 + 36
= (12 × 32 ) + 36
= (12 × 9) + 36
= 108 + 36
= 144
Case 2:
12 × 3² + 36
= 12 × (3² + 36)
= 12 × (9 + 36)
= 12 × 45
= 540
Hence, from the above,
We can conclude that
The representation of the given expression with the grouping values and a target value of 540 is:
12 × (3² + 36)
Question 11.
32 ÷ 23 – 4 Target value: 8
Answer:
The given expression is: 32 ÷ 23 – 4
Now,
It is given that
The value of the given expression is: 8
Now,
Case 1:
32 ÷ 2³ – 4
= (32 ÷ 2³) – 4
= (32 ÷ 8) – 4
= 4 – 4
= 0
Case 2:
32 ÷ 2³ – 4
= 32 ÷ (2³ – 4)
= 32 ÷ (8 – 4)
= 32 ÷4
= 8
Hence, from the above,
We can conclude that
The representation of the given expression with the grouping values and a target value of 8 is:
32 ÷ (2³ – 4)
Question 12.
2.32 + 9 × 4 ÷ 2 Target value: 28.58
Answer:
The given expression is: 2.32 + 9 × 4 ÷ 2
Now,
It is given that
The value of the given expression is: 28.58
Now,
Case 1:
2.32 + 9 × 4 ÷ 2
= 2.32 + (9 × 4) ÷ 2
= 2.32 + (36) ÷ 2
= 2.32 + 18
= 23.29
Case 2:
2.32 + 9 × 4 ÷ 2
= (2.32 + 9 × 4) ÷ 2
= (5.29 + 36) ÷ 2
= 20.64
Case 3:
2.32 + 9 × 4 ÷ 2
= (2.32 + 9) × (4 ÷ 2)
= 14.29 × 2
= 28.58
Hence, from the above,
We can conclude that
The representation of the given expression with the grouping values and a target value of 28.58 is:
(2.32 + 9) × (4 ÷ 2)
Practice & Problem Solving
Leveled Practice
In 13-18, use the order of operations to evaluate.
Question 13.
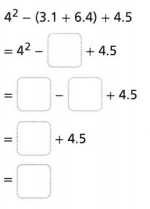
Answer:
The given expression is: 4² – (3.1 + 6.4) + 4.5
So,
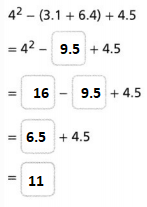
Hence, from the above,
We can conclude that
The value of the given expression is: 11
Question 14.
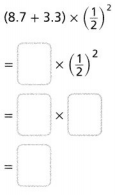
Answer:
The given expression is: (8.7 + 3.3) × (\(\frac{1}{2}\))²
So,
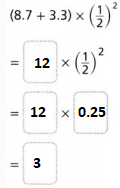
Hence, from the above,
We can conclude that
The value of the given expression is: 3
Question 15.
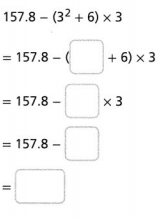
Answer:
The given expression is: 157.8 – (3² + 6) × 3
So,
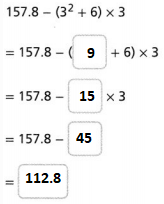
Hence, from the above,
We can conclude that
The value of the given expression is: 112.8
Question 16.
4.3 + (8.4 – 5.1)
Answer:
The given expression is: 4.3 + (8.4 – 5.1)
So,
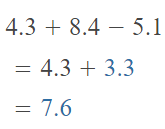
Hence, from the above,
We can conclude that
The value of the given expression is: 7.6
Question 17.
1.25 × 4 + 3 × 2 ÷ (\(\frac{1}{2}\))3
Answer:
The given expression is: 1.25 × 4 + 3 × 2 ÷ (\(\frac{1}{2}\))3
So,
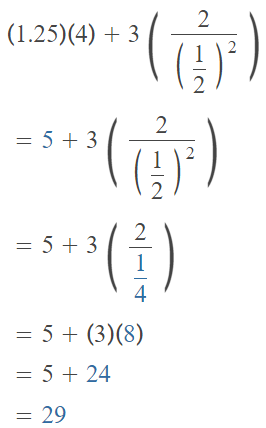
Hence, from the above,
We can conclude that
The value of the given expression is: 29
Question 18.
[23 × (152 ÷ 8)] – 52
Answer:
The given expression is: [23 × (152 ÷ 8)] – 52
So,
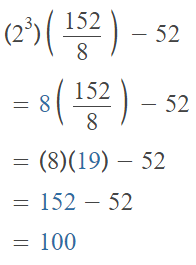
Hence, from the above,
We can conclude that
The value of the given expression is: 100
In 19-21, insert grouping symbols so that the expression has the given value.
Question 19.
Target value: 32
2 × 9 + 7
Answer:
The given expression is: 2 × 9 + 7
Now,
It is given that
The value of the given expression is: 32
Now,
Case 1:
2 × 9 + 7
= (2 × 9) + 7
= 18 + 7
= 25
Case 2:
2 × 9 + 7
= 2 × (9 + 7)
= 2 × 16
= 32
Hence, from the above,
We can conclude that
The representation of the given expression with the grouping values and a target value of 32 is:
2 × (9 + 7)
Question 20.
Target value: 6
\(\frac{1}{3}\) × 21 – 3
Answer:
The given expression is: \(\frac{1}{3}\) × 21 – 3
Now,
It is given that
The value of the given expression is: 6
Now,
Case 1:
\(\frac{1}{3}\) × 21 – 3
= (\(\frac{1}{3}\) × 21) – 3
= 7 – 3
= 4
Case 2:
\(\frac{1}{3}\) × 21 – 3
= \(\frac{1}{3}\) × (21 – 3)
= \(\frac{1}{3}\) × 18
= 6
Hence, from the above,
We can conclude that
The representation of the given expression with the grouping values and a target value of 6 is:
\(\frac{1}{3}\) × (21 – 3)
Question 21.
Target value: 43
2.5 + 5 × 6 – 2
Answer:
The given expression is: 2.5 + 5 × 6 – 2
Now,
It is given that
The value of the given expression is: 43
Now,
Case 1:
2.5 + 5 × 6 – 2
= (2.5 + 5) × (6 – 2)
= 7.5 × 4
= 30
Case 2:
2.5 + 5 × 6 – 2
= [(2.5 + 5) × 6] – 2
= (7.5 × 6) – 2
= 45 – 2
= 43
Hence, from the above,
We can conclude that
The representation of the given expression with the grouping values and a target value of 43 is:
[(2.5 + 5) × 6] – 2
Question 22.
Cory bought some baseball equipment. He used a coupon for \(\frac{1}{2}\) off the price of the bat and glove. Write and evaluate a numerical expression to find the total cost of the bat, the glove, and

Answer:
It is given that
Cory bought some baseball equipment. He used a coupon for \(\frac{1}{2}\) off the price of the bat and glove
Now,
The given figure is:

Now,
From the given information,
The new cost of the bat will become \(\frac{1}{2}\) of the old price of the bat
The new cost of the glove will become \(\frac{1}{2}\) of the old price of the glove
So,
The total cost of the bat, the glove and 3 baseballs = (The new cost of the bat) + (The new cost of the glove) + (3 × The cost of the baseball)
= \(\frac{$69}{2}\) + \(\frac{$75}{2}\) + (3 × $5.50)
= \(\frac{1}{2}\) (69 + 75) + (3 × $5.50)
= \(\frac{$144}{2}\) + $16.50
= $72 + $16.50
= $88.50
Hence, from the above,
We can conclude that
The total cost of the bat, the glove, and 3 baseballs is: $88.50
Question 23.
Make Sense and Persevere Write a numerical expression, with at least three operations, that has the same value as the following expression. Justify your answer.
5 + (8 – 4) ÷ 2 + 3
Answer:
The given expression is: 5 + (8 – 4) ÷ 2 + 3
Now,
So,
The value of the given expression is: 10
Now,
The expression that has the same value as the given expression and has at least 3 operations is:
(5 × 2) + 4 – (36 ÷ 9)
Question 24.
Use Structure How do you know which part of the numerical expression to evaluate first? Explain.
(26 + 2.5) – [(8.3 × 3) + (13 – 0.25)]
Answer:
The given expression is:
(26 + 2.5) – [(8.3 × 3) + (13 – 0.25)]
Now,
To solve an expression,
We will use the order of operations using the BODMAS rule and solve the part of the expression that involves more operations in it
So,
In the given expression,
We have to first evaluate [(8.3 × 3) + (13 – 0.25)]
Hence, from the above,
We can conclude that
By using the order of operations using the BODMAS rule and the part of the expression that involves more operations in it,
We have to first evaluate [(8.3 × 3) + (13 – 0.25)]
Question 25.
Construct Arguments Evan says that the value of the numerical expression 0.22 + 12 ÷ (1.5 × 4) is 32.04. Do you agree? Explain.
Answer:
The given expression is: 0.22 + 12 ÷ (1.5 × 4)
So,
But,
For the given expression,
It is given that the value is: 32.04
But,
We got the value of the expression as 2.04
Hence, from the above,
We can conclude that
We can not agree with Evan
Question 26.
The width of the rectangular drawing is one-third the length plus 3 inches. What is the perimeter of the drawing? Write and evaluate an expression to solve the problem.

Answer:
It is given that
The width of the rectangular drawing is one-third the length plus 3 inches.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The length of the rectangular drawing is 12 in.
Now,
According to the given information,
The width of the rectangular drawing = (The length of the rectangular drawing ÷ 3) + 3
= \(\frac{12}{3}\) + 3
= 4 + 3
= 7 in.
Now,
We know that,
The perimeter of a rectangle = 2 × (Length + Width)
So,
The perimeter of a rectangular drawing = 2 × (12 + 7)
= 2 × 19
= 38 in.
Hence, from the above,
We can conclude that
The perimeter of the rectangular drawing is 38 in.
Question 27.
Higher-Order Thinking Frederick evaluates the numerical expression [(53.7 + 37.2) – (33 + 3.8)] – 8.6 and records the answer as 51.5. Lana evaluates the numerical expression 53.7 + 37.2 – 33 + 3.8 – 8.6 and records the answer as 59.1. The expressions have the same numbers and operations. Explain how Frederick and Lana can both be correct.
Answer:
It is given that
Frederick evaluates the numerical expression [(53.7 + 37.2) – (33 + 3.8)] – 8.6 and records the answer as 51.5. Lana evaluates the numerical expression 53.7 + 37.2 – 33 + 3.8 – 8.6 and records the answer as 59.1. The expressions have the same numbers and operations
Now,
According to Fredrick:
The given expression is: [(53.7 + 37.2) – (33 + 3.8)] – 8.6
So,
Now,
According to Lana:
The given expression is: 53.7 + 37.2 – 33 + 3.8 – 8.6
So,
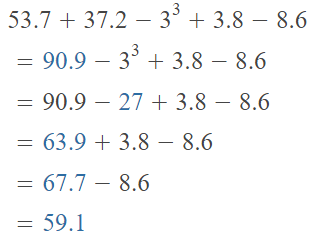
Now,
From both answers,
We can observe that
Even though the operations and the numbers are the same, the only difference between the expressions is the grouping symbols
Hence, from the above,
We can conclude that
Both Fredrick and Lana are correct and the only difference between their expressions is the grouping of symbols
Question 28.
Model with Math
Lillian went to the gift shop on the boardwalk and bought four bags of dyed seashells at $3.99 each. She had a coupon for $1 off. Her mom paid for half of the remaining cost. Write and evaluate a numerical expression to find how much Lillian paid toward the purchase of the seashells.
Answer:
It is given that
Lillian went to the gift shop on the boardwalk and bought four bags of dyed seashells at $3.99 each. She had a coupon for $1 off. Her mom paid for half of the remaining cost.
Now,
The cost of 4 bags of dyed seashells = 4 × (The cost of each bag of dyed seashells)
= 4 × $3.99
= $15.96
Now,
It is given that
She had a coupon for $1 off
So,
The amount Lilian paid to purchase 4 bags of dyed seashells = $15.96 – $1
= $14.96
Now,
It is given that
Lilian’s mom paid for half of the remaining cost
So,
The amount Lilian’s mom paid = \(\frac{$14.96}{2}\)
= $7.48
So,
The total amount Lilian paid toward the purchase of the seashells = $14.96 – $7.48
= $7.48
Hence, from the above,
We can conclude that
The total amount Lilian paid toward the purchase of the seashells is: $7.48
Question 29.
In an ecosystem, some animals get energy by eating plants. Write and evaluate an expression to find how many pounds of plants a herd of 18 elk can eat in one week.

Answer:
It is given that
In an ecosystem, some animals get energy by eating plants
Now,
The given figure is:

Now,
We know that,
1 week = 7 days
So,
The number of pounds of plants a herd of 18 elk can eat in one week = (The number of elks) × (The number of pounds of plants an elk eats each day) × (The number of days in a week)
= (18 × 20 × 7) pounds
= (126 × 20) pounds
= 2,520 pounds
Hence, from the above,
We can conclude that
The number of pounds of plants a herd of 18 elk can eat in one week is: 2,520 pounds
Assessment Practice
Question 30.
Select all expressions that are equivalent to 24 ÷ [(3.2 × 0.8) + 1.44].
![]() 24 ÷ [(4 × 0.64) + 1.44]
24 ÷ [(4 × 0.64) + 1.44]
![]() 16 ÷ [(22 × 0.64) + (0.72 × 2)]
16 ÷ [(22 × 0.64) + (0.72 × 2)]
![]() 8 ÷ [(3.2 × 0.8) + (0.48 × 3)]
8 ÷ [(3.2 × 0.8) + (0.48 × 3)]
![]() 24 ÷ [2.56 + (0.48 × 4)]
24 ÷ [2.56 + (0.48 × 4)]
![]() 42 ÷ [2.56 + (0.48 × 4)]
42 ÷ [2.56 + (0.48 × 4)]
Answer:
The given expression is: 24 ÷ [(3.2 × 0.8) + 1.44]
So,
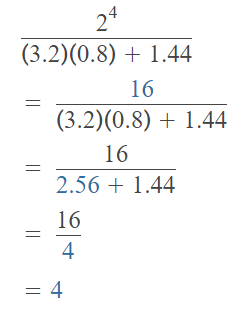
Now,
The given expressions and its values are:
A. 24 ÷ [(4 × 0.64) + 1.44] = 4
B. 16 ÷ [(22 × 0.64) + (0.72 × 2)] = 4
C. 8 ÷ [(3.2 × 0.8) + (0.48 × 3)] = 2
D. 24 ÷ [2.56 + (0.48 × 4)] = 3.57
E. 4² ÷ [2.56 + (0.48 × 4)] = 3.57
Hence, from the above,
We can conclude that
All expressions that are equivalent to 24 ÷ [(3.2 × 0.8) + 1.44] are:

Question 31.
Which value is equivalent to the expression 18.9 × [(2 × 2.7) – 4.6] – 22?
A. 1,112
B. 111.2
C. 11.12
D. 1.112
Answer:
The given expression is: 18.9 × [(2 × 2.7) – 4.6] – 22
So,
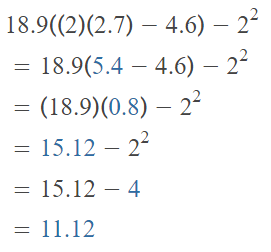
Hence, from the above,
We can conclude that
The value is equivalent to the expression 18.9 × [(2 × 2.7) – 4.6] – 2² is:

Topic 3 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary Describe the relationship between the base and the exponent in 43. Lesson 3-1
Answer:
The given expression is: 4³
Now,
From the given expression,
We can observe that
“4” is called the “Base”
“3” is called the “Exponent”
Now,
We know that,
The number that is repeatedly multiplied is the “Base”
The “Exponent” tells how many times the Base is used as a factor
Hence, from the above,
We can conclude that
“4” is the number that is repeatedly multiplied
“3” is the number that tells how many times “4” is used as a factor
Question 2.
What is the GCF of 14 and 42? Lesson 3.2
Answer:
The given numbers are: 14 and 42
Now,

Hence, from the above,
We can conclude that
The GCF of 14 and 42 is: 14
Question 3.
Which pair of numbers has a GCF of 5? Lesson 3.2
A. 15 and 30
B. 5 and 21
C. 45 and 9
D. 20 and 55
Answer:
The given numbers are:
A) 15 and 30 – GCF is 15
B) 5 and 21 – GCF is 1
C) 45 and 9 – GCF is 9
D) 20 and 55 – GCF is 5
Hence, from the above,
We can conclude that
The pair of numbers that has a GCF of 5 is:

Question 4.
What is the LCM of 12 and 9? Lesson 3.2
Answer:
The given numbers are: 12 and 9
So,

Hence, from the above,
We can conclude that
The LCM of 12 and 9 is: 36
Question 5.
Evaluate the numerical expression. Lesson 3.3
0.52 × (20 – 22 × 3) × (\(\frac{2}{5}\) × 25)
Answer:
The given numerical expression is:
0.52 × (20 – 22 × 3) × (\(\frac{2}{5}\) × 25)
So,
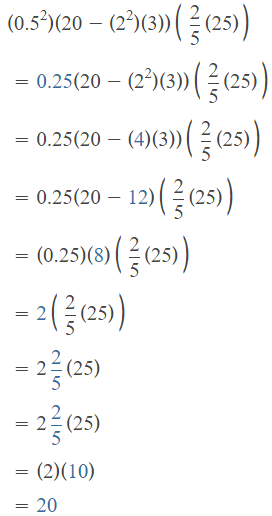
Hence, from the above,
We can conclude that
The value of the given numerical expression is: 20
Question 6.
Select all the expressions that are equal to (\(\frac{2}{3}\))2? Lesson 3.1
![]() \(\frac{4}{9}\)
\(\frac{4}{9}\)
![]() \(\frac{4}{3}\)
\(\frac{4}{3}\)
![]() \(\frac{1}{3}\) × \(\frac{1}{3}\)
\(\frac{1}{3}\) × \(\frac{1}{3}\)
![]() \(\frac{1}{9}\) × 4
\(\frac{1}{9}\) × 4
![]() \(\frac{2}{3}\) × \(\frac{2}{3}\)
\(\frac{2}{3}\) × \(\frac{2}{3}\)
Answer:
The given expression is: (\(\frac{2}{3}\))²
So,
(\(\frac{2}{3}\))²
= \(\frac{2}{3}\) × \(\frac{2}{3}\)
= \(\frac{2 × 2}{3 × 3}\)
= \(\frac{4}{9}\)
= 4 × \(\frac{1}{9}\)
Hence, from the baove,
We can conclude that
All the expressions that are equivalent to (\(\frac{2}{3}\))² are:
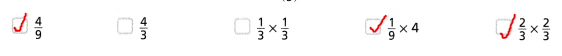
Question 7.
Liam bought 2 vintage movie posters, 2 rock posters, and 1 rap poster. He applied a $35 gift card to the total purchase and a \(\frac{1}{2}\)-off coupon to the rap poster. Write and evaluate a numerical expression to show how much Liam paid for the posters. Lesson 3.3
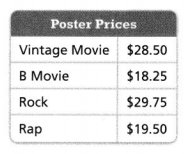
Answer:
It is given that
Liam bought 2 vintage movie posters, 2 rock posters, and 1 rap poster. He applied a $35 gift card to the total purchase and a \(\frac{1}{2}\)-off coupon to the rap poster
Now,
The given table is:

Now,
The amount Liam has to pay for the posters = (The number of vintage movie posters) × (The cost of each vintage movie poster) + (The number of rap posters) × (The cost of each rap poster) + (The number of rock posters) × (The cost of each rock poster)
= (2 × $28.50) + (1 × $19.50) + (2 × $29.75)
Now,
So,
The amount Liam has to pay for the posters is: $136
Now,
With a $35 gift coupon,
The amount Liam has to pay for the posters = $136 – $35
= $101
Now,
With the \(\frac{1}{2}\) off coupon of rap poster,
The total cost of rap poster = \(\frac{$19.50}{2}\)
= $9.75
So,
The amount Liam has to pay for the posters = $101 – $9.75
= $91.25
Hence, from the above,
We can conclude that
The amount of money Liam paid for the products is: $91.25
Question 8.
Eva counts up by 3s, while Jin counts up by 5s. What is the smallest number that they both say? Lesson 3-2
Answer:
It is given that
Eva counts up by 3s, while Jin counts up by 5s
Now,
To find the smallest number that both Evan and Jin can say,
Find the LCM of 3 and 5
Now,

Hence, from the above,
We can conclude that
The smallest number that both Eva and Jin can say is: 15
How well did you do on the mid-topic checkpoint? Fill in the stars. 
Topic 3 MID-TOPIC PERFORMANCE TASK
Monique and Raoul are helping teachers make gift bags and gather supplies for a student celebration day at Pineville Middle School.
PART A
Raoul has 72 wristbands and 96 movie passes to put in gift bags. The greatest common factor for the number of wristbands and the number of movie passes is equal to the number of gift bags Raoul needs to make. Find the number of gift bags Raoul needs to make. Then find how many wristbands and how many movies passes Raoul can put in each gift bag if he evenly distributes the items.
Answer:
It is given that
Monique and Raoul are helping teachers make gift bags and gather supplies for a student celebration day at Pineville Middle School.
Raoul has 72 wristbands and 96 movie passes to put in gift bags. The greatest common factor for the number of wristbands and the number of movie passes is equal to the number of gift bags Raoul needs to make.
Now,
According to the given information,
The number of gift bags Raoul needs to make = The GCF of the number of wristbands and the number of movies passes
So,

So,
The number of gift bags Raoul needs to make is: 24 gift bags
Now,
The number of wristbands = (The number of gift bags Raoul needs to make) ÷ 2
= \(\frac{24}{2}\)
= 12 wristbands
The number of movie tickets = (The number of gift bags Raoul needs to make) ÷ 2
= \(\frac{24}{2}\)
= 12 movie tickets
Hence, from the above,
We can conclude that
The number of gift bags Raoul needs to make is: 24 gift bags
The number of wristbands is: 12
The number of movie tickets is: 12
PART B
Monique wants to have an equal number of cups and napkins. What are the least number of packages of cups and the least number of packages of napkins Monique should buy to have an equal number of cups and napkins? Justify your answer.

Answer:
It is given that
Monique wants to have an equal number of cups and napkins
Now,
The given table is:

Now,
To find the least number of packages of cups and the least number of packages of napkins,
Find the LCM of the number of cups and napkins present in each package
So,
We have to find the LCM of 12 and 10 to find the least number of packages of cups and napkins
Now,

Hence, from the above,
We can conclude that
The least number of packages of cups and the least number of packages of napkins Monique should buy to have an equal number of cups and napkins is: 60
PART C
Which numerical expressions show the equal number of both cups and napkins that Monique will have in Part B? Select all that apply.
![]() 21 × 30
21 × 30
![]() 102 × 60
102 × 60
![]() 22 × 15
22 × 15
![]() 4600
4600
![]() 40 × 60
40 × 60
Answer:
From part B,
We can observe that
The least number of packages of cups and the least number of packages of napkins Monique should buy to have an equal number of cups and napkins is: 60
Hence, from the above,
We can conclude that
The numerical expressions that show the equal number of both cups and napkins that Monique will have in Part B are:
![]()
PART D
The teachers have $25 to buy supplies. Write and evaluate a numerical expression to show how much more money they will need to buy the cups and napkins.
Answer:
It is given that
The teachers have $25 to buy supplies
Now,
The given table is:

Now,
From the given table,
We can observe that
The total cost of cups and Napkins = (The number of cups per package) × (The cost of each cup) + (The number of Napkins per package) × (The cost of each Napkin)
= (12 × $3.80) + (10 × $4.25)
= $45.60 + $42.50
= $88.10
Now,
The amount of more money than the teachers need to buy cups and napkins = (The total cost of cups and Napkins) – (The amount of money the teachers have)
= $88.10 – $25
= $63.10
Hence, from the above,
We can conclude that
The more money the teachers will need to buy the cups and napkins is: $63.10
Lesson 3.4 Write Algebraic expressions
Explore It!
The table shows the number of games the Hornets won and the number of games the Lynx won.

A. What pattern do you see in the data in the table? Explain how the pattern relates to the number of games won.
Answer:
It is given that
The table shows the number of games the Hornets won and the number of games the Lynx won.
Now,
The given table is:

Now,
From the given table,
We can observe that
The number of games won by Lynx is 2 more than the number of games won by Hornets
Hence, from the above,
We can conclude that
The pattern that is related to the number of games won is:
The number of games won by Lynx = (The number of games won by Hornet) + 2
B. Look for Relationships Write numerical expressions to relate the number of games won by the Lynx to the number of games won by the Hornets.

Answer:
From part A,
We know that,
The number of games won by Lynx = (The number of games won by Hornet) + 2
Hence, from the above,
We can conclude that
The numerical expressions that relate the number of games won by the Lynx to the number of games won by the Hornets is:
C. Explain how to complete the table above for the Lynx if the Hornets won n games.
Answer:
From Part A,
We know that,
The number of games won by Lynx = (The number of games won by Hornet) + 2
Now,
It is given that
Hornets won n games
Hence, from the above,
We can conclude that
The number of games won by Lynx = n + 2
Where,
n is the number of games won by Hornets
Focus on math practices
Reasoning
Suppose the Lynx won g games. What mathematical expression could you write to show how many games the Hornets won? How is this expression related to the expression you wrote to find the number of games the Lynx won when the Hornets won n games? Explain.
Answer:
From Part A,
We know that,
The number of games won by Lynx = (The number of games won by Hornets) + 2
Now,
If Lynx won g games, then
The number of games won by Hornets = g – 2
Where,
g is the number of games won by Lynx
The expression when Hornets won n games is the same as the above expression as we replace the variable g with the variable n
VISUAL LEARNING
? Essential Question How can you write an algebraic expression?
Answer:
Algebraic expressions are useful because they represent the value of an expression for all of the values a variable can take on. Similarly, when we describe an expression in words that includes a variable, we are describing an algebraic expression, an expression with a variable
Try It!
Darius’s sister Rachel bought m mystery books for $6.50 each. Show three ways to write an algebraic expression that represents the total cost of the mystery books.
Answer:
It is given that
Darius’s sister Rachel bought m mystery books for $6.50 each
So,
The cost of m books bought by Rachel = (The total number of books) × (The cost of each book)
= m × $6.50
= $6.50m
Now,
The representation of the algebraic expression that represents the total cost of the mystery books in 3 ways is:
$6.50m (or) $6.50 × m (or) $6050(m)
Hence, from the above,
We can conclude that
The representation of the algebraic expression that represents the total cost of the mystery books in 3 ways is:
$6.50m (or) $6.50 × m (or) $6050(m)
Convince Me! How do you know that the expressions you wrote for the cost of the mystery books are algebraic expressions?
Answer:
We know that,
Algebraic expressions are combinations of variables, numbers, and at least one arithmetic operation.
For example,
2x+4y−9 is an algebraic expression.
Now,
When we observe the total cost of m mystery books,
We can observe that
m is a variable
Hence, from the above,”
We can conclude that
Since the expression that represents the total cost of the mystery books,
We can say that the expression that represents the total cost of the mystery books is an algebraic expression
Try It!
Write an algebraic expression that represents “8 minus the quantity b divided by 6.”
Answer:
The given algebraic expression in words is: 8 minus the quantity divided by 6
So,
The representation of the given algebraic expression that is in words into a symbolic form is:
(8 – b) ÷ 6 (or) \(\frac{8 – b}{6}\)
Hence, from the above,
We can conclude that
The representation of the given algebraic expression that is in words into a symbolic form is:
(8 – b) ÷ 6 (or) \(\frac{8 – b}{6}\)
Try It!
How many terms does the expression r ÷ 9 + 5.5 have? Explain.
Answer:
The given expression is: r ÷ 9 + 5.5
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
So,
The number of terms the given expression contains is: 2 terms
Hence, from the above,
We can conclude that
The number of terms the given expression contains is: 2 terms
KEY CONCEPT
A variable, written as a letter, represents a quantity that can change. You can use a variable to write an algebraic expression that has at least one operation.
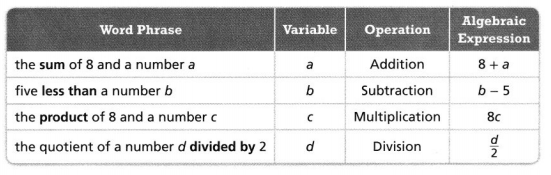
Do You Understand?
Question 1.
? Essential Question How can you write an algebraic expression?
Answer;
Algebraic expressions are useful because they represent the value of an expression for all of the values a variable can take on. Similarly, when we describe an expression in words that includes a variable, we are describing an algebraic expression, an expression with a variable
Question 2.
Be Precise Identify the variable and the operation in the algebraic expression \(\frac{6}{x}\)
Answer:
The given algebraic expression is: \(\frac{6}{x}\)
Now,
We know that,
A “Variable”, written as a letter, represents a quantity that can change
So,
In the given expression,
The variable is: x
The operation in the given algebraic expression is: Division
Hence, from the above,
We can conclude that
In the given expression,
The variable is: x
The operation in the given algebraic expression is: Division
Question 3.
Vocabulary Explain why 15 + \(\frac{1}{2}\)n is an algebraic expression.
Answer:
The given expression is: 15 + \(\frac{1}{2}\)n
Now,
We know that,
Algebraic expressions are useful because they represent the value of an expression for all of the values a variable can take on. Similarly, when we describe an expression in words that includes a variable, we are describing an algebraic expression, an expression with a variable
Hence, from the above,
We can conclude that
15 + \(\frac{1}{2}\)n is an algebraic expression
Question 4.
Reasoning Could you describe the expression 2(3 + 4) as a product of two factors? Explain.
Answer:
The given expression is: 2 (3 + 4)
Now,
By using the Distributive Property,
2 (3 + 4) = 2 × (3 + 4)
= (2 × 3) + (2 × 4)
Hence, from the above,
We can conclude that
The given expression could be described as a product of two factors
Question 5.
Which part of the expression 2(3 + 4) is the sum of two terms? Explain.
Answer:
The given expression is: 2 (3 + 4)
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
So,
In the given expression,
We can observe that
(3 + 4) contains two terms separated by an addition operation
Hence, from the above,
We can conclude that
In the given expression,
(3 + 4) is the sum of two terms
Do You Know How?
In 6 and 7, write an algebraic expression for each situation.
Question 6.
five less than y
Answer:
The given situation is: five less than y
Now,
We know that,
When we see the word “Less” in a situation, the operation that takes place in that situation must be “Subtraction”
Hence, from the above,
We can conclude that
The representation of the given situation into an algebraic expression is: y – 5
Question 7.
six times the quantity two x plus three y
Answer:
The given situation is: six times the quantity two x plus three y
Now,
We know that,
When we see the word “times the quantity” in a situation, the operation that takes place in that situation must be “Multiplication”
Hence, from the above,
We can conclude that
The representation of the given situation into an algebraic expression is: 6 (2x + 3y)
In 8-10, use the expression \(\frac{w}{4}\) + 12.5 – 7z.
8. How many terms does the expression have?
Answer:
The given expression is: \(\frac{w}{4}\) + 12.5 – 7z
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
Hence, from the above,
We can conclude that
The number of terms the given expression contains: 3 terms
Question 9.
Which term has a coefficient? Explain.
Answer:
The given expression is: \(\frac{w}{4}\) + 12.5 – 7z
Now,
We know that,
A “Coefficient” is the number that is multiplied by a variable
Hence, from the above,
We can conclude that
The term that has a coefficient in the given expression is: 7z
Question 10.
Which term is a constant numerical value?
Answer:
The given expression is: \(\frac{w}{4}\) + 12.5 – 7z
Now,
We know that,
A “Constant” is nothing but a numerical value
Hence, from the above,
We can conclude that
The term that is a constant numerical value in the given expression is: 12.5
Practice & Problem Solving
In 11-14, write an algebraic expression for each situation.
Question 11.
12 times a number g
Answer:
The given situation is: 12 times a number g
Now,
We know that,
When we see the word “times a number” in a situation, the operation that takes place in that situation must be “Multiplication”
Hence, from the above,
We can conclude that
The representation of the given situation into an algebraic expression is: 12 (g) (or) 12g
Question 12.
p pennies added to 22 pennies
Answer:
The given situation is: p pennies added to 22 pennis
Now,
We know that,
When we see the word “Add” in a situation, the operation that takes place in that situation must be “Addition”
Hence, from the above,
We can conclude that
The representation of the given situation into an algebraic expression is: p + 22
Question 13.
22 divided by a number s
Answer:
The given situation is: 22 divided by a number s
Now,
We know that,
When we see the word “Divide” in a situation, the operation that takes place in that situation must be “Division”
Hence, from the above,
We can conclude that
The representation of the given situation into an algebraic expression is: 22 ÷ s (or) \(\frac{22}{s}\)
Question 14.
12\(\frac{3}{4}\) less than the product of 7 and a number x
Answer:
The given situation is: 12\(\frac{3}{4}\) less than the product of 7 and a number x
Now,
We know that,
When we see the word “Less” and “Product” in a situation, the operation that takes place in that situation must be “Subtraction” and “Multiplication”
Hence, from the above,
We can conclude that
The representation of the given situation into an algebraic expression is: 7x – 12\(\frac{3}{4}\)
In 15-18, tell how many terms each expression has.
Question 15.
5 – g
Answer:
The given expression is: 5 – g
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
Hence, from the above,
We can conclude that
The number of terms the given expression contains is: 2 terms
Question 16.
3 + \(\frac{1}{2}\)b
Answer:
The given expression is: 3 + \(\frac{1}{2}\)b
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
Hence, from the above,
We can conclude that
The number of terms the given expression contains is: 2 terms
Question 17.
\(\frac{v}{3}\) + 2 • 5
Answer:
The given expression is: \(\frac{v}{3}\) + 2 • 5
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
Hence, from the above,
We can conclude that
The number of terms the given expression contains is: 2 terms
Question 18.
16.2 – (3 • 4) + (14 ÷ 2)
Answer:
The given expression is: 16.2 – (3 • 4) + (14 ÷ 2)
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
Hence, from the above,
We can conclude that
The number of terms the given expression contains is: 3 terms
In 19 and 20, use the expression 5.3t – (20 ÷ 4) + 11.
Question 19.
Which part of the expression is a quotient? Describe its parts.
Answer:
The given expression is: 5.3t – (20 ÷ 4) + 11
Now,
We know that,
The “Quotient” is only possible when there is a “Division” operation
Hence, from the above,
We can conclude that
The part of the expression that is a quotient is: 20 ÷ 4
Question 20.
Which part of the expression is a product of two factors? Describe its parts.
Answer:
The given expression is: 5.3t – (20 ÷ 4) + 11
Now,
We know that,
The “product” is possible when there are 2 numbers or a number and a variable
Hence, from the above,
We can conclude that
The part of the expression that is a product of two factors is: 5.3t
In 21 and 22, use the table at the right.
Question 21.
Model with Math
Write an expression to show how much longer the round-trip to San Diego is than the round-trip to San Jose. How many terms does the expression have?
Answer:
The given information is:
Now,
From the given table,
We can observe that
The distance of the round trip to San Jose is: 236 miles
The distance of the round trip to San Diego is: 1,012 miles
So,
The expression that shows how much longer the round-trip to San Diego is than the round-trip to San Jose
= (The distance of the round trip to San Diego) – (The distance of the round trip to San Jose)
= 1,012 – 236
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
So,
The number of terms in the above expression is: 2 terms
Hence, from the above,
We can conclude that
The expression that shows how much longer the round-trip to San Diego is than the round-trip to San Jose is: 1,012 – 236
The number of terms in the above expression is: 2 terms
Question 22.
Make Sense and Persevere Last month, a truck driver made 5 round-trips to Los Angeles and some round-trips to San Diego. Write an expression that shows how many miles he drove in all. Identify and describe the part of the expression that shows how many miles he drove and trips he made to San Diego.
Answer:
It is given that
Last month, a truck driver made 5 round-trips to Los Angeles and some round-trips to San Diego
Now,
The given information is:

Now,
From the above table,
We can observe that
The distance of the round trip to Los Angeles is: 770 miles
The distance of the round trip to San Diego is: 1,012 miles
Now,
Let the number of round trips to San Diego be: x
Let the number of miles the truck driver drove to Los Angeles be: p
Let the number of miles the truck driver drove to San Diego be: q
Now,
We know that,
The total distance traveled by the truck driver = (The number of round trips made to Los Angeles) × (The number of miles the truck driver drove to Los Angeles) + (The number of round trips to San Diego) × (The number of miles the truck driver drove to San Diego)
= 5p + xq
So,
The number of miles the truck driver drove is: 5p + xq
The number of trips the truck driver made to san Diego is: x
Hence, from the above,
We can conclude that
The number of miles the truck driver drove is: 5p + xq
The number of trips the truck driver made to san Diego is: x
Question 23.
Use the expression y ÷ 3(4 – 2) + 5.5 to complete the table. Identify the parts of the expression that correspond to the descriptions.

Answer:
The given expression is: y ÷ 3 (4 – 2) + 5.5
Now,
We know that,
A “Variable”, written as a letter, represents a quantity that can change
The symbol of Difference is: –
The symbol of Product is () (or) ×
Hence, from the above,
We can conclude that
The completed table with the corresponding descriptions is:
Question 24.
The floats in the Orlando Citrus parade may use as many citrus fruits as a small orchard produces in 6 years. If f is the number of citrus fruits a small orchard produces in 1 year, write an algebraic expression to represent the number of citrus fruits the floats in the parade may use.
Answer:
It is given that
The floats in the Orlando Citrus parade may use as many citrus fruits as a small orchard produces in 6 years and f is the number of citrus fruits a small orchard produces in 1 year
So,
The number of citrus fruits the floats in the parade may use in 6 years = 6 × (The number of citrus fruits a small orchard produces in 1 year)
= 6 × f
= 6f citrus fruits
Hence, from the above,
We can conclude that
The number of citrus fruits the floats in the parade may use in 6 years is: 6f citrus fruits
Question 25.
Critique Reasoning Anthony says that the expression abc has three terms because it uses three different variables. Critique Anthony’s reasoning and explain whether he is correct
Answer:
It is given that
Anthony says that the expression abc has three terms because it uses three different variables.
Now,
The given expression is: abc
Now,
We know that,
Each part of an expression that is separated by a plus sign or a minus sign is called a “Term”
Now,
From the given expression,
We can observe that
There are not any plus or minus signs
So,
The given expression is a single term
Hence, from the above,
We can conclude that
Anthony’s reasoning is incorrect
Question 26.
Yuri walked p poodles and b bulldogs on Monday. He walked the same number of poodles and bulldogs each day Tuesday through Friday as he did on Monday. Write an algebraic expression to represent how many total dogs were walked in this 5-day period.

Answer:
It is given that
Yuri walked p poodles and b bulldogs on Monday. He walked the same number of poodles and bulldogs each day Tuesday through Friday as he did on Monday
So,
The total dogs walked on Monday = (The number of poodles) + (The number of bulldogs)
= p + b
Now,
It is given that
The same number of dogs walked from Tuesday to Friday as on Monday
So,
The total number of dogs that were waked from Monday to Friday = (The number of days from Monday to Friday) × (The number of dogs walked on Monday)
= 5 × (p + b) dogs
Hence, from the above,
We can conclude that
The total number of dogs that were waked from Monday to Friday is: 5(p + b) dogs
Question 27.
Higher-Order Thinking Some students equally share 2 baskets of oranges. Each basket has 12 oranges. Write an algebraic expression to represent this situation. Then explain how you chose which variable and operations to use.
Answer:
It is given that
Some students equally share 2 baskets of oranges. Each basket has 12 oranges
Now,
Let the number of students be: x
Let the number of apples each student gets be: y
Now,
The total number of oranges in 2 baskets = 2(The number of baskets in each basket)
= 2 (12)
= 24 oranges
So,
The algebraic expression that represents the given situation is:
The number of apples each student gets = (The total number of apples in 2 baskets) ÷ (The number of students)
y = \(\frac{24}{x}\)
Hence, from the above,
We can conclude that
The algebraic expression that represents the given situation is:
y = \(\frac{24}{x}\)
Question 28.
Model with Math
The figure at the right is a regular octagon with side length s. Write two algebraic expressions that use different operations to represent the perimeter of the figure.

Answer:
It is given that
The figure at the right is a regular octagon with side length s.
Now,
The given figure is:

Now,
We know that,
The “Perimeter” of any figure is the sum of all the sides of the given figure
Now,
Let the perimeter of the regular Octagon be: P
So,
The perimeter of the given regular Octagon is:
P = s + s + s + s + s + s + s + s
P = 8 (s) = 8s
Hence, from the above,
We can conclude that
The two algebraic expressions that use different operations to represent the perimeter of the given figure is:
P = s + s + s + s + s + s + s + s
P = 8s
Assessment Practice
Question 29.
Which algebraic expression represents the phrase Four more than the product 3 times the number of c cats?
A. 4 + 3c
B. (4 + 3)c
C. 3 + 4c
D. 4 × 3 × c
Answer:
The given phrase is: Four more than the product 3 times the number of c cats
So,
The representation of the given phrase in the form of an algebraic expression is: 4 + 3c
Hence, from the above,
We can conclude that
The algebraic expression represents the phrase Four more than the product 3 times the number of c cats is:

Question 30.
Select all of the phrases that could be represented by the algebraic expression \(\frac{w}{4}\) – 4.
![]() four less than the quotient of a number w and four
four less than the quotient of a number w and four
![]() the difference between a number w and 4
the difference between a number w and 4
![]() four less than w divided by 4
four less than w divided by 4
![]() four less than a number w
four less than a number w
![]() the quotient of four and a number w
the quotient of four and a number w
Answer:
The given algebraic expression is: \(\frac{w}{4}\) – 4
So,
The representation of the given algebraic expression in the form of a phrase is:
a. 4 less than the quotient of w and 4
b. The difference between the quotient of w and 4 and 4
c. 4 less than w divided by 4
Hence, from the above,
We can conclude that
All of the phrases that could be represented by the algebraic expression \(\frac{w}{4}\) – 4. are:

Lesson 3.5 Evaluate Algebraic expressions
Solve & Discuss It!
A bike shop charges by the hour to rent a bike. Related items are rented for flat fees. Write an expression that represents how much it will cost to rent a bike and helmet for h hours. How much would it cost to rent a bike and a helmet for 3 hours?
Model with Math
You can write an algebraic expression with decimals in the same way you do with whole numbers.

Answer:
It is given that
A bike shop charges by the hour to rent a bike. Related items are rented for flat fees
Now,
The given table is:
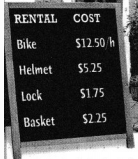
So,
The total cost of renting a bike and a helmet for h hours = (The cost of renting a bike per hour) × (The total number of hours) + The cost of a helmet
= $12.50 ×h + $5.25
So,
The total cost of renting a bike and a helmet for 3 hours = (The cost of renting a bike per hour) × (The total number of hours) + The cost of a helmet
= $12.50 ×3 + $5.25
= $37.50 + $5.25
= $42.75
Hence, from the above,
We can conclude that
The expression that represents the total cost to rent a bike and a helmet for h hours is:
The total cost of renting a bike and a helmet for h hours =$12.50 ×h + $5.25
The total cost of renting a bike and a helmet for 3 hours is: $42.75
Focus on math practices
Use Structure Write an expression that represents renting a bike, a lock, and a basket for h hours. What is the cost of renting this equipment for 4 hours?
Answer:
The given table is:

Now,
From the given table,
We can observe that
The cost to rent a bike, a lock, and a basket for h hours = (The cost of renting a bike per hour) × (The total number of hours) + The cost of renting a lock + The cost of renting a basket
= $12.50 × h + $1.75 + $2.25
= $12.50 × h + 4
Now,
The cost to rent a bike, a lock, and a basket for 4 hours = (The cost of renting a bike per hour) × (The total number of hours) + The cost of renting a lock + The cost of renting a basket
= $12.50 × 4 + $1.75 + $2.25
= $12.50 × 4 + $4
= $50 + $4
= $54
Hence, from the above,
We can conclude that
The expression that represents renting a bike, a lock, and a basket for h hours is:
The expression that represents renting a bike, a lock, and a basket for h hours = $12.50 × h + 4
The cost to rent a bike, a lock, and a basket for 4 hours is: $54
VISUAL LEARNING
? Essential Question How can you evaluate an algebraic expression?
Answer:
To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations.
Try It!
Evaluate the expression 50 – t when t equals 10, 20, or 25. Then complete the table to show the values.

Answer:
The given expression is: 50 – t
Where,
The value of t is: 10, 20, and 25
Now,
For t = 10, 20, and 25,
Hence, from the above,
We can conclude that
Convince Me! What does it mean to use substitution to evaluate an algebraic expression?
Answer:
To substitute the values of the numerals into an algebraic expression means to replace all numerals with their respective values (or numbers). Once the values of the numerals are substituted, the expression can be evaluated. While evaluating, the correct order of operations must be observed
Try It!
Evaluate the expression 3.4 + 12a ÷ 4 for a = 10.
Answer:
The given expression is 3.4 + 12a ÷ 4 for a = 10
Now,
For a = 10,
3.4 + 12a ÷4
= 3.4 + 12 (10) ÷ 4
= 3.4 + 120 ÷ 4
= 3.4 + 30
= 33.4
Hence, from the above,
We can conclude that
The value of the given expression is: 33.4
Try It!
Suppose Mr. Grant decides to buy square tiles that have side lengths of \(\frac{3}{4}\) foot. How many of these tiles will he need to buy?
Answer:
It is given that
Suppose Mr. Grant decides to buy square tiles that have side lengths of \(\frac{3}{4}\) foot
Now,
From Example 3,
It is given that
The expression to find the number of tiles Mr. Grant needs to buy is 27 ÷ s²
Where,
s is the sidelength
Now,
When s = \(\frac{3}{4}\) foot,
The number of tiles Mr.Grant needs to buy = 27 ÷ (\(\frac{3}{4}\))²
= 27 ÷ \(\frac{9}{16}\)
= 27 × \(\frac{16}{9}\)
= \(\frac{27 × 16}{9}\)
= 3 × 16
= 48 tiles
Hence, from the above,
We can conclude that
The number of tiles Mr.Grant needed to buy when the side length is \(\frac{3}{4}\) foot is: 48 tiles
KEY CONCEPT
To evaluate an expression, use substitution to replace a variable with its numerical value. Then use the order of operations to simplify.
Do You Understand?
Question 1.
? Essential Question How can you evaluate an algebraic expression?
Answer:
To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations
Question 2.
Construct Arguments Why is it important to use the order of operations to evaluate algebraic expressions?
Answer:
The order of operations is a rule that tells you the right order in which to solve different parts of a math problem. The order of operations is important because it guarantees that people can all read and solve a problem in the same way
Question 3.
How is evaluating an expression with fractions like evaluating an expression with whole numbers? How is it different?
Answer:
The fractions have the same denominators so you can start by adding the first two fractions. Add the fractions before adding the whole numbers. Then, take the sum and subtract the third fraction. Before evaluating the expression, rewrite the fractions with one common denominator
To evaluate an expression with a whole number, we substitute the given number for the variable in the expression and then simplify the expression using the order of operations. in the expression that involves fractions, first, we have to simplify the fractions into whole numbers and follow the order of operations to evaluate them
Question 4.
Reasoning Annalise earns $4 an hour walking pets in her neighborhood. She evaluates the expression 4h, where h represents the number of hours, to find the amount she earns. Can any number be substituted for h? Explain.
Answer:
It is given that
Annalise earns $4 an hour walking pets in her neighborhood. She evaluates the expression 4h, where h represents the number of hours, to find the amount she earns.
Now,
According to the given information,
The total amount of money earned by Annalise = $4h
Where,
h is the number of hours
Now,
We know that,
h will be any number i.e., either a whole number or a fraction
Hence, from the above,
We can conclude that
We can substitute any number for h
Do You Know How?
In 5-8, evaluate each expression for t = 8, w = \(\frac{1}{2}\), and x = 3.
Question 5.
3t – 8
Answer:
The givene xpression is: 3t – 8
Now,
For t = 8,
3t – 8
= 3 (8) – 8
= 24 – 8
= 16
Hence, from the baove,
We can conclude that
The value of the given expression is: 16
Question 6.
6w ÷ x + 9
Answer:
The given expression is: 6w ÷ x + 9
Now,
For w = \(\frac{1}{2}\), and x = 3,
6w ÷ x + 9
= 6 (\(\frac{1}{2}\)) ÷ 3 + 9
= \(\frac{6}{2}\) ÷ 3 + 9
= 3 ÷ 3 + 9
= 1 + 9
= 10
Hence, from the above,
We can conclude that
The value of the given expression is: 10
Question 7.
t2 – 12w ÷ ×
Answer:
The given expression is: t2 – 12w ÷ ×
Now,
For t = 8, w = \(\frac{1}{2}\), and x = 3,
t2 – 12w ÷ ×
= 82 – 12 (\(\frac{1}{2}\)) ÷ 3
= 64 – \(\frac{12}{2}\) ÷ 3
= 64 – 6 ÷ 3
= 64 – 2
= 62
Hence, from the above,
We can conclude that
The value of the given expression is: 62
Question 8.
5x – 2w + t
Answer:
The given expression is: 5x – 2w + t
Now,
For t = 8, w = \(\frac{1}{2}\), and x = 3,
5x – 2w + t
= 5 (3) – 2 (\(\frac{1}{2}\)) + 8
= 15 – \(\frac{2}{2}\) + 8
= 15 – 1 + 8
= 15 + 7
= 22
Hence, from the above,
We can conclude that
The value of the given expression is: 22
In 9-14, evaluate each expression for the value given.
Question 9.
z ÷ 4; z = 824
Answer:
The given expression is: z ÷ 4 with z = 824
Now,
For z = 824,
z ÷ 4
= 824 ÷ 4
= 206
Hence, from the above,
We can conclude that
The value of the given expression is: 206
Question 10.
6t ÷ 9 – 22; t = 60
Answer:
The given expression is: 6t ÷ 9 – 22 with t = 60
Now,
For t = 60,
6t ÷ 9 – 22
= 6 (60) ÷ 9 – 22
= 360 ÷ 9 – 22
= 40 – 22
= 18
Hence, from the above,
We can conclude that
The value of the given expression is: 18
Question 11.
r ÷ 2.4; r = 16.8
Answer:
The given expression is: r ÷2.4 with r = 16.8
Now,
For r = 16.8,
r ÷2.4
= 16.8 ÷ 2.4
= 7
Hence, from the above,
We can conclude that
The value of the given expression is: 7
Question 12.
9.85 × s; s = 4
Answer:
The given expression is: 9.85 × s with s = 4
Now,
For s = 4,
9.85 × s
= 9.85 × 4
= 39.40
Hence, from the above,
We can conclude that
The value of the given expression is: 39.40
Question 13.
x ÷ 12; x = \(\frac{2}{3}\)
Answer:
The given expression is: x ÷ 12, with x = \(\frac{2}{3}\)
Now,
For x = \(\frac{2}{3}\),
x ÷ 12
= \(\frac{2}{3}\) ÷ 12
= \(\frac{2}{3}\) × \(\frac{1}{12}\)
= \(\frac{2 ×1}{3 × 12}\)
= \(\frac{2}{36}\)
= \(\frac{1}{18}\)
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{1}{18}\)
Question 14.
\(\frac{3}{4}\) + 4y ÷ 3; y = 1\(\frac{1}{2}\)
Answer:
The given expression is: \(\frac{3}{4}\) + 4y ÷ 3 with y = 1\(\frac{1}{2}\)
Now,
For y = 1\(\frac{1}{2}\),
\(\frac{3}{4}\) + 4y ÷ 3
= \(\frac{3}{4}\) + 4 (1\(\frac{1}{2}\) ÷ 3
= \(\frac{3}{4}\) + 3 ÷ 3
= \(\frac{3}{4}\) + 1
= \(\frac{7}{4}\)
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{7}{4}\)
Practice & Problem Solving
Scan for Multimedia
In 15-17, evaluate each expression for w = 5, x = 3, y = 4, and z = 8.
Question 15.
9x
Answer:
The given expression is: 9x
Now,
For x = 3,
9x = 9 × 3
= 27
Hence, from the above,
We can conclude that
The value of the given expression is: 27
Question 16.
3y + 6 ÷ 2x
Answer:
The given expression is: 3y + 6 ÷ 2x
Now,
For x = 3, and y = 4,
3y + 6 ÷ 2x
= (3 × 4) + 6 ÷ (2 × 3)
= 12 + 6 ÷ 6
= 12 + 1
= 13
Hence, from the above,
We can conclude that
The value of the given expression is: 13
Question 17.
w2 + 2 + 48 ÷ 2z
Answer:
The given expression is: w2 + 2 + 48 ÷ 2z
Now,
For w = 5, and z = 8,
w2 + 2 + 48 ÷ 2z
= 5² + 2 + 48 ÷ (2 × 8)
= 25 + 2 + 48 ÷ 16
= 27 + 3
= 30
Hence, from the above,
We can conclude that
The value of the given expression is: 30
In 18-20, evaluate each expression for x = 1.8, x = 5, and x = 6.4.
Question 18.
x ÷ 4
Answer:
The given expression is: x ÷ 4
Now,
For x = 1.8
x ÷ 4 = 1.8 ÷ 4
= 0.45
Now,
For x = 5,
x ÷ 4 = 5 ÷ 4
= 1.25
Now,
For x = 6.4,
x ÷ 4 = 6.4 ÷ 4
= 1.6
Hence, from the above,
We can conclude that
The value of the given expression for x = 1.8 is: 0.45
The value of the given expression for x = 5 is: 1.25
The value of the given expression for x = 6.4 is: 1.6
Question 19.
x(3.35)
Answer:
The given expression is: x (3.35)
Now,
For x = 1.8,
x (3.35) = 1.8 (3.35)
= 6.03
Now,
For x = 5,
x (3.35) = 5 (3.35)
= 16.75
Now,
For x = 6.4,
x (3.35) = 6.4 (3.35)
= 21.44
Hence, from the above,
We can conclude that
The value of the given expression for x = 1.8 is: 6.03
The value of the given expression for x = 5 is: 16.75
The value of the given expression for x = 6.4 is: 21.44
Question 20.
2x + 3.1
Answer:
The given expression is: 2x + 3.1
Now,
For x = 1.8,
2x + 3.1 = (2 × 1.8) + 3.1
= 6.7
Now,
For x = 5,
2x + 3.1 = (2 × 5) + 3.1
= 10 + 3.1
= 13.1
Now,
For x = 6.4,
2x + 3.1 = (2 × 6.4) + 3.1
= 15.9
Hence, from the above,
We can conclude that
The value of the given expression for x = 1.8 is: 6.7
The value of the given expression for x = 5 is: 13.1
The value of the given expression for x = 6.4 is: 15.9
In 21-23, evaluate each expression for the value given.
Question 21.
j + \(\frac{3}{8}\); j = \(\frac{3}{4}\)
Answer:
The given expression is: j + \(\frac{3}{8}\)
Now,
For j = \(\frac{3}{4}\),
j + \(\frac{3{8}\)
= \(\frac{3}{8}\) + \(\frac{3}{4}\)
= \(\frac{3}{8}\) + \(\frac{6}{8}\)
= \(\frac{3 + 6}{8}\)
= \(\frac{9}{8}\)
Hence, from the baove,
We can conclude that
The value of the given expression is: \(\frac{9}{8}\)
Question 22.
8 – g ÷ \(\frac{7}{8}\); g = \(\frac{5}{6}\)
Answer:
The given expression is: 8 – g ÷ \(\frac{7}{8}\)
Now,
For g = \(\frac{5}{6}\),
8 – g ÷ \(\frac{7}{8}\)
= 8 – \(\frac{5}{6}\) ÷ \(\frac{7}{8}\)
= 8 – \(\frac{5}{6}\) × \(\frac{8}{7}\)
= 8 – \(\frac{5 × 8}{6 × 7}\)
= 8 – \(\frac{40}{42}\)
= 8 – \(\frac{20}{21}\)
= \(\frac{168 – 20}{21}\)
= \(\frac{148}{21}\)
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{148}{21}\)
Question 23.
3m ÷ \(\frac{2}{5}\); m = \(\frac{2}{3}\)
Answer:
The given expression is: 3m ÷ \(\frac{2}{5}\)
Now,
For m = \(\frac{2}{3}\),
3 × \(\frac{2}{3}\) ÷ \(\frac{2}{5}\)
= 2 ÷ \(\frac{2}{5}\)
= 2 × \(\frac{5}{2}\)
= 5
Hence, from the above,
We can conclude that
The value of the given expression is: 5
Question 24.
Evaluate the expression for the values of b.
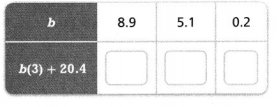
Answer:
The given expression is: b (3) + 20.4
Now,
For b = 8.9,
b (3) + 20.4
= 8.9 (3) + 20.4
= 47.1
Now,
For b = 5.1,
b (3) + 20.4
= 5.1 (3) + 20.4
= 35.7
Now,
For b = 0.2,
b (3) + 20.4
= 0.2 (3) + 20.4
= 21
Hence, from the above,
We can conclude that
The value of the given expression for the given values of b is:

Question 25.
Evaluate the expression for the values of j.
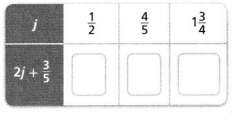
Answer:
The given expression is: 2j + \(\frac{3}{5}\)
Now,
For j = \(\frac{1}{2}\),
2j + \(\frac{3}{5}\)
= 2 (\(\frac{1}{2}\)) + \(\frac{3}{5}\)
= 1 + \(\frac{3}{5}\)
= \(\frac{8}{5}\)
= 1.6
Now,
For j = \(\frac{4}{5}\),
2j + \(\frac{3}{5}\)
= 2 (\(\frac{4}{5}\)) + \(\frac{3}{5}\)
= \(\frac{8}{5}\) + \(\frac{3}{5}\)
= \(\frac{11}{5}\)
= 2.2
For j = 1\(\frac{3}{4}\),
2j + \(\frac{3}{5}\)
= 2 (1\(\frac{3}{4}\)) + \(\frac{3}{5}\)
= \(\frac{14}{4}\) + \(\frac{3}{5}\)
= \(\frac{82}{20}\)
= 4.1
Hence, from the above,
We can conclude that
The value of the given expression for the values of j is:
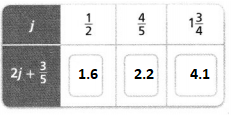
In 26-28, use the table at the right.
Question 26.
Model with Math
a. Ms. White wants to rent a small car for a week. It will cost the weekly fee plus $0.30 per mile driven. Let m= the number of miles Ms. White drives during the week. Write an expression that shows the amount she will pay for the car.

Answer:
It is given that
Ms. White wants to rent a small car for a week. It will cost the weekly fee plus $0.30 per mile driven. Let m= the number of miles Ms. White drives during the week.
Now,
The given table is:
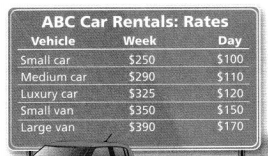
So,
The total amount Ms. White will pay for the car = (The rent of a small car for a week) + (The extra fee for a small car per mile during the week) × (The total number of miles)
= $250 + $0.30m
Hence, from the above,
We can conclude that
The expression that represents the total amount Ms. White will pay for the car is: $250 + $0.30m
b. Evaluate the expression you wrote to find how much Ms. White will pay if she drives 100 miles.
Answer:
From Part (a),
We can observe that
The expression that represents the total amount Ms. White will pay for the car is: $250 + $0.30m
Now,
When Ms. White drives for 100 miles,
The total amount Ms. White will pay for the car if she drives 100 miles = $250 + $0.30 (100)
= $250 + $30
= $280
Hence, from the above,
We can conclude that
The total amount Ms. White will pay for the car if she drives 100 miles is: $280
Question 27.
Mr. Black rents a lu×ury car for one week and a few days, d. He does not pay a per-mile fee. Evaluate the expression 325 + 120d to find how much Mr. Black will pay for an 11-day rental.
Answer:
It is given that
Mr. Black rents a lu×ury car for one week and a few days, d. He does not pay a per-mile fee.
Now,
The given table is:

Now,
According to the given information,
The expression that represents the total amount paid by Mr.Black for one week and a few days is: $325 + $120d
Where
d is the number of few days
Now,
For an 11-day rental,
The total amount paid by Mr.Black for one week and a few days = $325 + $120d
= $325 + $120 (11)
– $325 + $132
= $457
Hence, from the above,
We can conclude that
The total amount Mr.Black will pay for an 11-day rental is: $457
Question 28.
For any of the vehicles listed in the table, how many days can you rent the vehicle before it would be less expensive to rent for the week?
Answer:
The given list of vehicles is:

Now,
When we observe the list,
The least expensive rent is: $250 for a week
Now,
When we observe the rents for a day,
There are only 2 days’ rents that are less than the least expensive rent for a week
Hence, from the above,
We can conclude that
We can rent the vehicle for 2 days before it would be less expensive to rent for the week
In 29 and 30, use the table at the right.
Question 29.
Model with Math
Tamara is making a medium-length necklace. Write an expression that shows how much it will cost Tamara for the chain, pendant, and b beads that cost $0.25 each. Then find the total cost of the necklace if Tamara uses 30 beads.
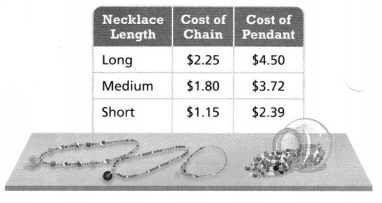
Answer:
It is given that
Tamara is making a medium-length necklace
Now,
The given table is:
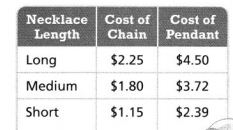
So,
The total cost of the medium-length necklace made by Tamara = (The cost of medium length necklace) + (The cost of medium length pendant) + (The cost of each bead) × (The total number of beads)
= $1.80 + $3.72 + $0.25b
= $5.52 + $0.25b
Now,
When there are 30 beads,
The total cost of the medium length necklace made by Tamara when there are 30 beads = $5.52 + $0.25b
= $5.52 + $0.25 (30)
= $13.02
Hence, from the above,
We can conclude that
The total cost of the medium-length necklace made by Tamara, when there are 30 beads, is: $13.02
Question 30.
Higher-Order Thinking Ronnie is making short and long necklaces with only one chain and one pendant per necklace. Write an expression that shows how much it will cost Ronnie to make s short necklaces and n long necklaces. Then find the cost for 3 short necklaces and 2 long necklaces.
Answer:
It is given that
Ronnie is making short and long necklaces with only one chain and one pendant per necklace.
Now,
The given table is:

Now,
The cost of a necklace made by Ronnie = [(The cost of a short-chain) + (The cost of a short pendant)] × (The number of short necklaces) + [(The cost of a long chain) + (The cost of a long pendant)] × (The number of long necklaces)
= ($1.15 + $2.39) × s + ($2.25 + $4.50) × n
= $3.54s + $6.75n
Where,
s is the number of short necklaces
n is the number of long necklaces
Now,
The cost of 3 short necklaces = $3.54s
= $3.54 × 3
= $10.62
Now,
The cost of 2 long necklaces = $6.75n
= 6.75 × 2
= $13.50
Hence, from the above,
We can conclude that
The expression that represents the cost of a necklace made by Ronnie is: $3.54s + $6.75n
The cost of 3 short necklaces is: $10.62
The cost of 2 long necklaces is: $13.50
Question 31.
Critique Reasoning Katrina says that the expression 5,432 + 4,564 + 13,908 = 61n can be evaluated by adding 5,432 + 4,564 + 13,908 and then dividing by the value of 61n. Do you agree? Explain.
Answer:
It is given that
Katrina says that the expression 5,432 + 4,564 + 13,908 = 61n can be evaluated by adding 5,432 + 4,564 + 13,908 and then dividing by the value of 61n.
Now,
The given expression is: 5,432 + 4,564 + 13,908 = 61n
Now,
We have to find the value of n in the given expression,
Now,
To find the value of n, the following steps have to be followed:
Step 1:
Add 5,432, 4,54, and 13,908
Step 2:
Divide the result that we obtained in step 1 by 61 to get the value of n
But,
According to the given information,
To find the value of the given expression, we have to divide the result that we obtained in step 1 by 61n
Hence, from the above,
We can conclude that
We can not agree with Katrina
Question 32.
The density, d, of an object can be found by using the formula d = \(\frac{m}{V}\), where m is the mass of the object and visits volume. What is the density of an object that has a mass of 73,430 kilograms and a volume of 7 m3?
Answer:
It is given that
The density, d, of an object can be found by using the formula d = \(\frac{m}{v}\), where m is the mass of the object and visits volume
Now,
The given expression is: d = \(\frac{m}{V}\)
Now,
For m = 73,430 Kilograms, and V = 7 m³,
d = \(\frac{73,430}{7}\)
d = 10,490 Kg / m³
Hence, from the above,
We can conclude that
The density of the given object for the given values of m and V is: 10,490 Kg / m³
Question 33.
The formula V = s3 can be used to find the volume of a cube. Use the formula to find the volume, V, of a cube-shaped bin with side length s of \(\frac{2}{3}\) yard.
Answer:
It is given that
The formula V = s3 can be used to find the volume of a cube.
Now,
The given side length of the cube is: \(\frac{2}{3}\) yard
So,
V = (\(\frac{2}{3}\))³
= \(\frac{2}{3}\) × \(\frac{2}{3}\) × \(\frac{2}{3}\)
= \(\frac{2 × 2 × 2}{3 × 3 × 3}\)
= \(\frac{8}{27}\) yard³
Hence, from the above,
We can conclude that
The volume of the cube-shaped bin with the given side length is: \(\frac{8}{27}\) yard³
Question 34.
Katie is evaluating the expression 15.75 ÷ p + 3p when p = 3.15. Explain each step that she should follow.
Answer:
It is given that
Katie is evaluating the expression 15.75 ÷ p + 3p when p = 3.15.
Now,
The given expression is: 15.75 ÷ p + 3p with p = 3.15
Now,
For p = 3.15,
15.75 ÷ p + 3p
= 15.75 ÷ 3.15 + 3 (3.15)
= 5 + 9.45
= 14.45
Hence, from the above,
We can conclude that
The value of the given expression is: 14.45
Assessment Practice
Question 35.
An equation is shown.
5x + (x ÷ 3) = 38.4
Which value of x makes the equation true?
A. x = 5.1
B. x = 5.2
C. x = 6.1
D. x = 7.2
Answer:
The given expression is:
5x + (x ÷ 3) = 38.4
Now,
5x + \(\frac{x}{3}\) = 38.4
\(\frac{16x}{3}\) = 38.4
16x = 38.4 (3)
16x = 115.2
x = \(\frac{115.2}{16}\)
x = 7.2
Hence, from the above,
We can conclude that
The value of x that makes the given equation true is:

3-Act Mathematical Modeling: The Field Trip
3-ACT MATH

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Make a prediction to answer this Main Question. Explain your prediction.

Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
Question 5.
Plot your prediction on the same number line.
Answer:
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.
Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
Reflect
Question 13.
Model with Math explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Critique Reasoning A classmate said your model works for any number of students and adults. Do you agree? Justify your reasoning or explain your classmate’s error.
Answer:
SEQUEL
Question 15.
Generalize Suppose the entire grade goes on the field trip: 283 students and 10 teachers. Each bus holds 72 people and costs $610 for transport. How much money is needed? Explain how you reused your model.

Answer:
Lesson 3.6 Generate Equivalent expressions
ACTIVITY
Explain It!
Juwon says all three expressions are equivalent.
A. Find the value of each expression for n = 1.

Answer:
It is given that
Juwon says all three expressions are equivalent.
Now,
For n = 1,
The value of each expression will be:

Hence, from the above,
We can conclude that

B. Find the value of each expression for n = 2.

Answer:
It is given that
Juwon says all three expressions are equivalent.
Now,
For n = 2,
The value of each expression will be:
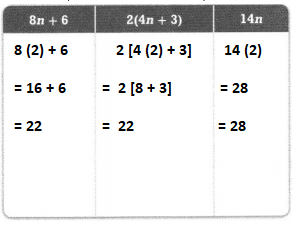
Hence, from the above,
We can conclude that

C. Critique Reasoning Do you agree with Juwon that all three expressions are equivalent? Explain.
Answer:
According to Juwon,
The expressions are:
a. 8n + 6
b. 2 (4n + 3)
c. 14n
Now,
From (a),
8n + 6 = 2 (4n + 3) ≠ 14n
Hence, from the above,
We can conclude that
We can not agree with Juwon that all the three expressions are equivalent
Focus on math practices
Generalize When a number is substituted for the same variable in two expressions, how many times must those two expressions have different values before you know they are not equivalent? Explain.
Answer:
When a number is substituted for the same variable in two expressions, those two expressions must have 2 different values before you know they are not equivalent
VISUAL LEARNING
? Essential Question How can you identify and write equivalent expressions?
Answer:
Combine any like terms on each side of the equation x-terms with x-terms and constants with constants. Arrange the terms in the same order, usually x-term before constants. If all of the terms in the two expressions are identical, then the two expressions are equivalent.
Try It!
Write an expression that is equivalent to 3y – 9.
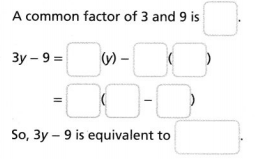
Answer:
The given expression is: 3y – 9
Now,

Hence, from the above,
We can conclude that
3y – 9 is equivalent to 3 (y – 3)
Convince Me! Why can you use properties of operations to write equivalent expressions?
Answer:
The properties of operations used to write equivalent expressions are:
a. Commutative Property of Addition: When adding, changing the order of the numbers does not change the sum.
b. Commutative Property of Multiplication
c. Associative Property of Addition
d. Associative Property of Multiplication
e. Distributive Property
Try It!
Which of the following expressions are equivalent? Explain.
![]()
Answer:
The given expressions are:
a. 10y + 5 b. 15y c. 5 (2y + 1)
Now,
10y + 5 = 5 (2y + 1)
Hence, from the above,
We can conclude that
10y + 5 and 5 (2y + 1) are equivalent expressions
Try It!
Are 2(x – 3) + 1 and 2x + 6 equivalent expressions? Use substitution to justify your work.
Answer:
The given expressions are: 2 (x – 3) + 1 and 2x + 6
Now,
2 (x – 3) + 1 = 2 (x) – 2 (3) + 1
= 2x – 6 + 1
= 2x – 5
So,
2x – 5 ≠ 2x + 6
Hence, from the above,
We can conclude that
2 (x – 3) + 1 and 2x + 6 are not equivalent expressions
KEY CONCEPT
Two algebraic expressions are equivalent if they have the same value when any number is substituted for the variable. You can use the properties of operations to write equivalent expressions.
Properties of Operations
1 Commutative Property
of Addition a + b = b + a
of Multiplication a × b = b × a
2 Associative Property
of Addition (a + b) + c = a + (b + c)
of Multiplication (a × b) × c = a × (b × c)
3 Distributive Property
across Addition a(b + c) = a(b) + a(c)
across Subtraction a(b – c) = a(b) – a(c)
Do You Understand?
Question 1.
? Essential Question How can you identify and write equivalent expressions?
Answer:
Combine any like terms on each side of the equation x-terms with x-terms and constants with constants. Arrange the terms in the same order, usually x-term before constants. If all of the terms in the two expressions are identical, then the two expressions are equivalent.
Question 2.
Use Structure which property of operations could you use to write an equivalent expression for y + \(\frac{1}{2}\)? Write the equivalent expression.
Answer:
The given expression is: y + \(\frac{1}{2}\)
Now,
To write the equivalent expression for the given expression,
We will use “Distributive Property of Addition”
Now,
y + \(\frac{1}{2}\)
= \(\frac{2 (y) + 1}{2}\)
= \(\frac{2y + 1}{2}\)
So,
The equivalent expression for the given expression is: \(\frac{2y + 1}{2}\)
Hence, from the above,
We can conclude that
The property of operation you could use to write y + \(\frac{1}{2}\) is: Distributive Property of Addition
The equivalent expression for y + \(\frac{1}{2}\) is: \(\frac{2y + 1}{2}\)
Question 3.
Generalize Are z3 and 3z equivalent expressions? Explain.
Answer:
The given expressions are: z³ and 3z
Now,
z³ = z × z × z
3z = z + z + z
Hence, from the above,
We can conclude that
z³ and 3z are not equivalent expressions
Question 4.
Are the expressions 3(y + 1) and 3y + 3 equivalent for y = 1? y = 2? y = 3?
Answer:
The given expressions are: 3 (y + 1) and 3y + 3
Now,
For y = 1,
3 (y + 1) = 3 (1 + 1)
= 3 (2) = 6
3y + 3 = 3 (1) + 3
= 3 + 3 = 6
Now,
For y = 2,
3 (y + 1) = 3 (2 + 1)
= 3 (3) = 9
3y + 3 = 3 (2) + 3
= 6 + 3 = 9
Now,
For y = 3,
3 (y + 1) = 3 (3 + 1)
= 3 (4) = 12
3y + 3 = 3 (3) + 3
= 9 + 3 = 12
So,
For y = 1, y = 2, and y = 3
3 (y + 1) = 3y + 3
Hence, from the above,
We can conclude that
3 (y + 1) is equivalent to 3y + 3 for y = 1, y = 2, and y = 3
Question 5.
Construct Arguments Are the expressions 3(y + 1) and 3y + 3 equivalent for any value of y? Explain.
Answer:
The given expressions are: 3 (y + 1) and 3y + 3
Now,
3 (y + 1) = 3 (y) + 3 (1)
= 3y + 3
So
3 (y + 1) = 3y + 3
Where,
y will be an integer or a whole number
Hence, from the above,
We can conclude that
The expressions 3 (y + 1) and 3y + 3 are equivalent for any value of y
Do You Know How?
In 6-8, use properties of operations to complete the equivalent expressions.
Question 6.
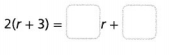
Answer:
The given expression is: 2 (r + 3)
Now,
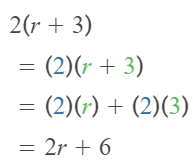
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 2r + 6
Question 7.
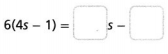
Answer:
The given expression is: 6 (4s – 1)
Now,
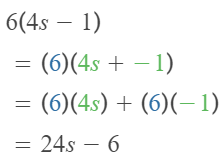
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is 24s – 6
Question 8.

Answer:
The given expression is: 8t + 2
Now,
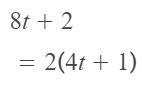
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 2 (4t + 1)
Question 9.
Complete the table below.

Answer:
The given expressions are:
a. 12x – 6 b. 3x + 3 c. 6 (2x – 1)
Now,
a.
For x = 1,
12x – 6 = 12 (1) – 6
= 12 – 6
= 6
For x = 2,
12x – 6 = 12 (2) – 6
= 24 – 6
= 18
For x = 3,
12x – 6 = 12 (3) – 6
= 36 – 6
= 30
b.
For x = 1,
3x + 3 = 3 (1) + 3
= 3 + 3
= 6
For x = 2,
3x + 3 = 3 (2) + 3
= 6 + 3
= 9
For x = 3,
3x + 3 = 3 (3) + 3
= 9 + 3
= 12
c.
For x = 1,
6 (2x – 1) = 6 [ 2 (1) – 1]
= 6
For x = 2,
6 (2x – 1) = 6 [2 (2) – 1]
= 18
For x = 3,
6 (2x – 1) = 6 [2 (3) – 1]
= 30
Hence, from the above,
We can conclude that
The completed table is:
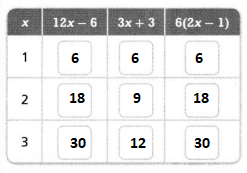
Question 10.
In exercise 9, which expressions in the table are equivalent?
Answer:
From Exercise 9,
The completed table is:

Now,
From the given table,
We can observe that
The values are the same for 12x – 6 and 6 (2x – 1) i.e.,
12x – 6 = 6 (2x – 1)
Hence, from the above,
We can conclude that
12x – 6 and 6 (2x – 1) are equivalent expressions
Practice & Problem Solving
Scan for Multimedia
Leveled Practice
In 11-20, write equivalent expressions.
Question 11.
![]()
Answer:
The given expression is: 3 (m + 3)
Now,
3 (m + 3) = 3 (m) + 3 (3)
= 3m + 9
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 3m + 9
Question 12.
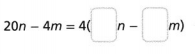
Answer:
The given expression is: 20n – 4m
Now,
20n – 4m = 4 (5n) – 4 (m)
= 4 (5n – m)
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 4 (5n – m)
Question 13.
3(x – 6)
Answer:
The given expression is: 3 (x – 6)
Now,
3 (x – 6) = 3 (x) – 3 (6)
= 3x – 18
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 3x – 18
Question 14.
2x + 10
Answer:
The given expression is: 2x + 10
Now,
2x + 10 = 2 (x) + 2 (5)
= 2 (x + 5)
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 2 (x + 5)
Question 15.
8(2y + \(\frac{1}{4}\))
Answer:
The given expression is: 8 (2y + \(\frac{1}{4}\))
Now,
8 (2y + \(\frac{1}{4}\)) = 8 (2y) + 8 (\(\frac{1}{4}\))
= 16y + 2
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 16y + 2
Question 16.
5.7 + (3z + 0.3)
Answer:
The given expression is: 5.7 + (3z + 0.3)
Now,
5.7 + (3z + 0.3) = 3z + (5.7 + 0.3)
= 3z + 6
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 3z + 6
Question 17.
5w – 15
Answer:
The give expression is: 5w – 15
Now,
5w – 15 = 5 (w) – 5 (3)
= 5 (w – 3)
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 5 (w – 3)
Question 18.
2x + 4y
Answer:
The given expression is: 2x + 4y
Now,
2x + 4y = 2 (x) + 2 (2y)
= 2 (x + 2y)
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 2 (x + 2y)
Question 19.
10(y2 + 2.45)
Answer:
The given expression is: 10 (y² + 2.45)
Now,
10 (y² + 2.45) = 10 (y²) + 10 (2.45)
= 10y² + 24.5
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 10y² + 24.5
Question 20.
\(\frac{3}{4}\) • (z3•4)
Answer:
The given expression is: \(\frac{3}{4}\) × (z³ × 4)
Now,
\(\frac{3}{4}\) × (z³ × 4) = z³ × \(\frac{3}{4}\) × 4
= 3z³
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 3z³
In 21-24, write the letters of the expressions that are equivalent to the given expression.
Question 21.
5(2x + 3)
a. 10x + 15
b. 5x + 15 + 5x
c. 10x + 8
Answer:
The given expression is: 5 (2x + 3)
Now,
5 (2x + 3) = 5 (2x) + 5 (3)
= 10x + 15
Hence, from the above,
We can conclude that
The expression that is equivalent to the given expression is:
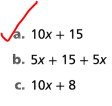
Question 22.
4x – 8
a. 2(2x – 6)
b. 2(2x – 4)
c. x – 8 + 3x
Answer:
The given expression is: 4x – 8
Now,
4x – 8 = 4 (x – 2)
= 3x + x – 8
= 2 (2x – 4)
Hence, from the above,
We can conclude that
The expressions that are equivalent to the given expression is:
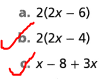
Question 23.
12x – 16
a. 9.6x – 16+ 2.4x
b. 3(3x – 5)
c. 4(3x – 4)
Answer:
The given expression is: 12x – 16
Now,
12x – 16 = 4 (3x – 4)
= 9.6x + 2.4x – 16
Hence, from the above,
We can conclude that
The expressions that are equivalent to the given expression is:
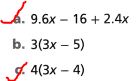
Question 24.
2(6x + \(\frac{1}{2}\))
a. 12x + 2
b. 12x + 1
c. 6x + \(\frac{1}{2}\) + 6x + \(\frac{1}{2}\)
Answer:
The given expression is: 2 (6x + \(\frac{1}{2}\))
Now,
2 (6x + \(\frac{1}{2}\))
= 6x + 6x + \(\frac{1}{2}\) + \(\frac{1}{2}\)
= 12x + 1
Hence, from the above,
We can conclude that
The expressions that are equivalent to the given expression is:
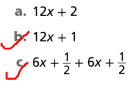
In 25-27, use the signs at the right.
Question 25.
Write an algebraic expression that represents each purchase.
a. Mr. Tonkery bought x number of soccer balls and 3 baseballs.
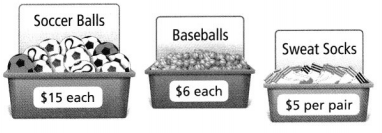
Answer:
It is given that
Mr. Tonkery bought x number of soccer balls and 3 baseballs.
Now,
The given figure is:

So,
The total purchase made by Mr. Tonkery = (The number of soccer balls) × (The cost of each soccer ball) + (The number of baseballs) × (The cost of each baseball)
= (x × $15) + (3 × $6)
= $15x + $18
Hence, from the above,
We can conclude that
The algebraic expression that represents Mr. Tonkery’s purchase is: $15x + $18
b. Dennis, Eddie, and Felix are on a baseball team. They each bought a baseball and x pairs of sweat socks.
Answer:
It is given that
Dennis, Eddie, and Felix are on a baseball team. They each bought a baseball and x pairs of sweat socks.
Now,
The given figure is:

So,
The total purchase made by Dennis, Eddie, and Felix = (The number of baseballs purchased by the three of them) × (The cost of each baseball) + (The number of sweat socs purchased by the three of them) × (The cost of each sweat socks)
= (3 × $6) + (3x × $5)
= $15x + $18
Hence, from the above,
We can conclude that
The algebraic expression that represents the total purchase made by Dennis, Eddie, and Felix is: $15x + $18
Question 26.
Make Sense and Persevere Suppose x has the same value in both of the expressions you wrote for exercise 25. Are the two expressions you wrote equivalent? Explain.
Answer:
It is given that
x has the same value in both of the expressions you wrote for exercise 25.
So,
From Part (a) and part (b) of Exercise 25,
$15x + $18 = $15x + $18
Hence, from the above,
We can conclude that
The two expressions in exercise 25’s part (a) and part (b) are equivalents
Question 27.
Critique Reasoning Wendy says that soccer balls cost 2\(\frac{1}{2}\) times as much as baseballs. Do you agree? Explain.
Answer:
It is given that
Wendy says that soccer balls cost 2\(\frac{1}{2}\) times as much as baseballs.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The cost of each soccer ball is: $15
The cost of each baseball is: $6
Now,
Let the number of times as soccer balls as many as base balls be x
So,
x × $6 = $15
x = \(\frac{15}{6}\)
x = \(\frac{5}{2}\)
x = 2\(\frac{1}{2}\)
Hence, from the above,
We can conclude that
We can agree with Wendy
Question 28.
Use Structure Write an algebraic expression to represent the area of the rectangular rug. Then use properties of operations to write an equivalent expression.
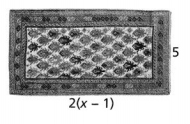
Answer:
The given figure is:

Now,
From the above figure,
We can observe that
The length of the rectangular rug is: 2 (x – 1)
The width of the rectangular rug is: 5
Now,
We know that,
The area of a rectangle = Length × Width
So,
The area of a rectangular rug = 2 (x – 1) × 5
= [2 (x) – 2 (1)] × 5
= (2x – 2) × 5
= 5 (2x) – 5 (2)
= 10x – 10
Hence from the above,
We can conclude that
The algebraic expression that represents the area of the given rectangular rug is: 10x – 10
Question 29.
Critique Reasoning Jamie says that the expressions 6x – 2x + 4 and 4(x + 1) are not equivalent because one expression has a term that is subtracted and the other does not. Do you agree? Explain.
Answer:
It is given that
Jamie says that the expressions 6x – 2x + 4 and 4(x + 1) are not equivalent because one expression has a term that is subtracted and the other does not.
Now,
The given expressions are: 6x – 2x + 4 and 4 (x + 1)
Now,
6x – 2x + 4 = 4x + 4
Now,
4 (x + 1) = 4 (x) + 4 (1)
= 4x + 4
So,
6x – 2x + 4 = 4x + 4
Hence, from the above,
We can conclude that
We can not agree with Jamie
Question 30.
Are the two expressions shown below equivalent? Explain.
4(n + 3) – (3 + n) and 3n + 9
Answer:
The given expressions are: 4 (n + 3) – (3 + n) and 3n + 9
Now,
4 (n + 3) – (3 + n) = 4 (n) + 4 (3) – 3 – n
= 4n + 12 – 3 – n
= 3n + 9
So,
4 (n + 3) – (3 + n) = 3n + 9
Hence, from the above,
We can conclude that
The given two expressions are equivalent expressions
Question 31.
Critique Reasoning Chris says that the expression 4n – 2 can be written as 2(2n – 1). Do you agree? Explain.
Answer:
It is given that
Chris says that the expression 4n – 2 can be written as 2(2n – 1)
Now,
The given expression is: 4n – 2
Now,
4n – 2 = 2 (2n – 1)
Hence, from the above,
We can conclude that
We can agree with Chris
Question 32.
Higher Order Thinking Write an expression that has only one term and is equivalent to the expression below.
(f • g2) + 5 – (g2 • f)
Answer:
The given expression is: (f × g²) + 5 – (g² ×f )
Now,
We know that,
According to the Associative Property of Multiplication,
a × b = b × a
So,
f × g² = g² × f
So,
(f × g²) + 5 – (g² ×f ) = 0 + 5
= 5
Hence, from the above,
We can conclude that
The expression that has only one term and is equivalent to the given expression is: 5
Question 33.
Construct Arguments A Florida college golf team with 14 members is planning an awards banquet. To find the total cost of the meals, the team uses the expression 5(g + 14), where g is the number of guests attending the banquet. A team member says that an equivalent expression is 5g + 14. Do you agree? Explain.
Answer:
It is given that
A Florida college golf team with 14 members is planning an awards banquet. To find the total cost of the meals, the team uses the expression 5(g + 14), where g is the number of guests attending the banquet. A team member says that an equivalent expression is 5g + 14
Now,
The given figure is:

Now,
The given expression is:
5 (g + 14) = 5 (g) + 5 (14)
= 5g + 70
So,
5 (g + 14) ≠ 5g + 14
Hence, from the above,
We can conclude that
We can not agree that the equivalent expression of 5 (g + 14) is 5g + 14
Assessment Practice
Question 34.
Select each expression that is equivalent to 8.5 + (2s + 0.5).
![]() (8.5 + 2s) + 0.5
(8.5 + 2s) + 0.5
![]() (8.5 + 0.5) + 2s
(8.5 + 0.5) + 2s
![]() 9 + 2
9 + 2
![]() 2(4.5 + s)
2(4.5 + s)
![]() 8.5(2s + 0.5)
8.5(2s + 0.5)
Answer:
The given epression is: 8.5 + (2s + 0.5)
Hence, from the above,
We can conclude that
The expressions that are equivalent to 8.5 + (2s + 0.5) are:

Question 35.
Select each expression that is equivalent to 5(n + 4).
![]() 5n + 4
5n + 4
![]() 5n + 20
5n + 20
![]() 15 + 5n + 5
15 + 5n + 5
![]() 5(n + 3) + 5
5(n + 3) + 5
![]() 5n + 54
5n + 54
Answer:
The given expression is: 5 (n + 4)
Hence, from the above,
We can conclude that
The expressions that are equivalent to 5 (n + 4) are:

Lesson 3.7 Simplify Algebraic expressions
Solve & Discuss It!
Write an expression equivalent to x + 5 + 2x + 2.

Make Sense and Persevere Use what you know about algebraic expressions and properties of operations to make sense of the problem.
Answer:
The given expression is: x + 5 + 2x + 2
Now,
We know that,
The terms that have the same variable are called “Like terms” and we use the Order of operations to write the equivalent expression
So,
x + 5 + 2x + 2 = (x + 2x) + (5 + 2)
= 3x + 7
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 3x + 7
Focus on math practices
Be Precise How do you know that the expression you wrote is equivalent to x + 5 + 2x + 2?
Answer:
The given expression is: x + 5 + 2x + 2
Now,
We know that,
The terms that have the same variable are called “Like terms” and we use the Order of operations to write the equivalent expression
Hence, from the above,
We can conclude that
We will use the Order of operations and “Like terms” to solve the given expression for its equivalent expression
VISUAL LEARNING
? Essential Question How can you simplify algebraic expressions?
Answer:
The steps to simplify the algebraic expressions are:
a. When simplifying mathematical expressions perform the operations in the following order: Parentheses and other Grouping Symbols.
b. Exponents.
c. Multiplication and Division.
d. Addition and Subtraction.
Try It!
Simplify the expression 4z – z + z – 2z.
4z – z + z – 2z
Answer:
The given expression is: 4z – z + z – 2z
Now,
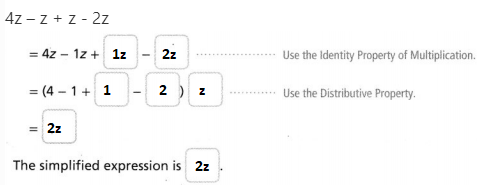
Hence, from the above,
We can conclude that
The value of the given expression is: 2z
Convince Me! How do you know that the expression 2x + 4y is not equivalent to 6xy?
Answer:
The given expressions are: 2x + 4y and 6xy
Now,
2x + 4y = 2 (x + 2y)
Now,
When we observe the two expressions,
2x + 4y contains “Addition” operation
6xy contains only the “Product” operation
So,
2x + 4y ≠ 6xy
Hence, from the above,
We can conclude that
2x + 4y is not equivalent to 6xy with the help of arithmetic symbols
Try It!
Park rangers add another section to the trail, represented by the expression in \(\frac{1}{2}\)n + n + \(\frac{1}{2}\). Write an expression for the new total length of the trail. Then write a simplified equivalent expression.
Answer:
It is given that
Park rangers add another section to the trail, represented by the expression in \(\frac{1}{2}\)n + n + \(\frac{1}{2}\)
Now,
The given figure is:
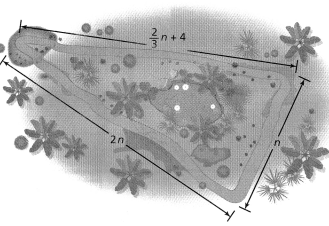
So,
The new total length of the trail = (The old total length of the trail that is present in Example 2) + \(\frac{1}{2}\) + n + \(\frac{1}{2}\)
= 3\(\frac{2}{3}\)n + 4 + \(\frac{1}{2}\)n + n + \(\frac{1}{2}\)
= \(\frac{11}{3}\)n + 4 + \(\frac{1}{2}\)n + n + \(\frac{1}{2}\)
= \(\frac{11}{3}\)n + \(\frac{3}{2}\)n + \(\frac{9}{2}\)
= \(\frac{31}{6}\)n + \(\frac{9}{2}\)
Hence, from the above,
We can conclude that
The simplified expression of the new total length of the trail is: \(\frac{31}{6}\)n + \(\frac{9}{2}\)
Try It!
Suppose Vanna increases her rate by 3.5 times and her expenses also increase by 3.5 times this summer. Write two equivalent expressions to represent how much she can earn mowing and raking grass.
Answer:
It is given that
Vanna increases her rate by 3.5 times and her expenses also increase by 3.5 times this summer.
Now,
The given figure is:

So,
The algebraic expression that represents the amount of money Vanna can earn from mowing and raking grass = 3.5 ($20.50x + $5.50x – $10)
Now,
By using the Distributive Property,
3.5 ($20.50x + $5.50x – $10)
= 3.5 ($26x – $10)
= 3.5 ($26x) – 3.5 ($10)
= $91x – $35
= 7 ($13x – $5)
Hence, from the above,
We can conclude that
The two equivalent expressions that represent the amount of money Vanna earned from mowing and raking grass is:
$91x – $35 (or) 7 ($13x – $5)
KEY CONCEPT
You can combine like terms to write equivalent expressions. Like terms have the same variable part.
2x + 6 + 5x + 4 ……… Identify like terms
= 2x + 5x + 6 + 4 ………… Commutative Property of Addition
= 7x + 10
2x + 6 + 5x + 4 = 7x + 10
Do You Understand?
Question 1.
? Essential Question How can you simplify algebraic expressions?
Answer:
The steps to simplify the algebraic expressions are:
a. When simplifying mathematical expressions perform the operations in the following order: Parentheses and other Grouping Symbols.
b. Exponents.
c. Multiplication and Division.
d. Addition and Subtraction.
Question 2.
Explain how you know which terms to combine when combining like terms.
Answer:
The terms that have identical variable parts (same variable(s) and same exponent(s)) are called “Like terms”. When simplifying using addition and subtraction, you combine “like terms” by keeping the “like term” and adding or subtracting the numerical coefficients
Question 3.
Construct Arguments Explain why the expression 2y – y can be written as y.
Answer:
The given expression is: 2y – y
Now,
By using the Order of operations,
2y – y = 2y – 1y
= y (2 – 1)
= y (1)
= y
Hence, from the above,
We can conclude that
2y – y can be written as y by using the Order of operations
Question 4.
Explain why the expressions \(\frac{1}{2}\)x + \(\frac{1}{2}\)x and x are equivalent.
Answer:
The given expression is: \(\frac{1}{2}\)x + \(\frac{1}{2}\)x
Now,
By using the order of Operations,
\(\frac{1}{2}\)x + \(\frac{1}{2}\)x
= \(\frac{x}{2}\) + \(\frac{x}{2}\)
= \(\frac{x + x}{2}\)
= \(\frac{2x}{2}\)
= \(\frac{x}{1}\)
= x
So,
\(\frac{1}{2}\)x + \(\frac{1}{2}\)x = x
Hence, from the above,
We can concldue that
\(\frac{1}{2}\)x + \(\frac{1}{2}\)x and x are equivalents by using the properties of addition in fraction and order of operations
Question 5.
Critique Reasoning Henry wrote 4z2 – z2 as 4. Are 4z2 – z2 and 4 equivalent expressions? Explain.
Answer:
The given expression is: 4z² – z²
Now,
By using the order of operations,
4z2 – z2
= 4z2 – 1z2
= z2 (4 – 1)
= z2 (3)
= 3z2
So,
4z2 – z2 ≠ 4
Hence, from the above,
We can conclude that
4z2 – z2 is not equivalent to 4
Do You Know How?
In 6-15, simplify each expression.
Question 6.
x + x + x + x
Answer:
The given expression is: x + x + x + x
Now,
By using the Order of Operations,
x + x + x + x
= 1x + 1x + 1x + 1x
= x (1 + 1 + 1 + 1)
= x (4)
= 4x
Hence, from the above,
We can conclude that
The value of the given expression is: 4x
Question 7.
4y – y
Answer:
The given expression is: 4y – y
Now,
By using the Order of Operations,
4y – y
= 4y – 1y
= y (4 – 1)
= y (3)
= 3y
Hence, from the above,
We can conclude that
The value of the given expression is: 3y
Question 8.
7y – 4.5 – 6y
Answer:
The given expression is: 7y – 4.5 – 6y
Now,
By using the Order of Operations,
7y – 4.5 – 6y
= (7y – 6y) – 4.5
= y – 4.5
Hence, from the above,
We can conclude that
The value of the given expression is: y – 4.5
Question 9.
4x + 2 – \(\frac{1}{2}\)x
Answer:
The given expression is: 4x + 2 – \(\frac{1}{2}\)x
Now,
By using the Order of Operations,
4x + 2 – \(\frac{1}{2}\)x
= (4x – \(\frac{1}{2}\)x) + 2
= \(\frac{8x – x}{2}\) + 2
= \(\frac{7x}{2}\) + 2
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{7x}{2}\) + 2
Question 10.
3 + 3y – 1 + y
Answer:
The given expression is: 3 + 3y – 1 + y
Now,
By using the Order of Operations,
3 + 3y – 1 + y
= (3 – 1) + (3y + y)
= 2 + 4y
= 4y + 2
Hence, from the above,
We can conclude that
The value of the given expression is: 4y + 2
Question 11.
x + 6x
Answer:
The given expression is: x + 6x
Now,
By using the Order of Operations,
x + 6x
= 1x + 6x
= x (1 + 6)
= x (7)
= 7x
Hence, from the above,
We can conclude that
The value of the given expression is: 7x
Question 12.
0.5w + 1.7w – 0.5
Answer:
The given expression is: 0.5w + 1.7w – 0.5
Now,
By using the Order of Operations,
0.5w + 1.7w – 0.5
= (0.5w + 1.7w) – 0.5
= w (0.5 + 1.7) – 0.5
= 2.2w – 0.5
Hence, from the above,
We can conclude that
The value of the given expression is: 2.2w – 0.5
Question 13.
12\(\frac{1}{3}\)b + 6\(\frac{2}{3}\) – 10\(\frac{2}{3}\)b
Answer:
The given expression is:
12\(\frac{1}{3}\)b + 6\(\frac{2}{3}\) – 10\(\frac{2}{3}\)b
Now,
Convert the given mixed numbers into fractions
So,
The given expression is: \(\frac{37}{3}\)b + \(\frac{20}{3}\) – \(\frac{32}{3}\)b
Now,
By using the Order of Operations,
\(\frac{37}{3}\)b + \(\frac{20}{3}\) – \(\frac{32}{3}\)b
= (\(\frac{37}{3}\)b – \(\frac{32}{3}\)b) + \(\frac{20}{3}\)
= b (\(\frac{37}{3}\) – \(\frac{32}{3}\)) + \(\frac{20}{3}\)
= \(\frac{5}{3}\)b + \(\frac{20}{3}\)
= \(\frac{1}{3}\) (5b + 20)
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{1}{3}\) (5b + 20)
Question 14.
\(\frac{3}{4}\)x + 2 + 3x – \(\frac{1}{2}\)
Answer:
The given expression is: \(\frac{3}{4}\)x + 2 + 3x – \(\frac{1}{2}\)
Now,
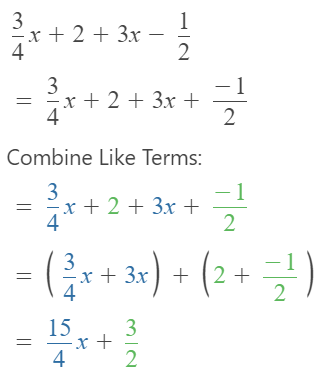
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{15}{4}\)x + \(\frac{3}{2}\)
Question 15.
3.2x + 6.5 – 2.4x – 4.4
Answer:
The given expression is: 3.2x + 6.5 – 2.4x – 4.4
Now,
By using the Order of Operations,
3.2x + 6.5 – 2.4x – 4.4
= (3.2x – 2.4x) + (6.5 – 4.4)
= x (3.2 – 2.4) + 2.1
= x (0.8) + 2.1
= 0.8x + 2.1
Hence, from the above,
We can conclude that
The value of the given expression is: 0.8x + 2.1
Practice & Problem Solving
Scan for Multimedia
Leveled Practice
In 16-26, combine like terms to simplify each expression.
Question 16.
Answer:
The given expression is: 2.1x² + 3 – 0.5x² – 1
Now,
2.1x² + 3 – 0.5x² – 1
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{8}{5}\)x² + 2
Question 17.
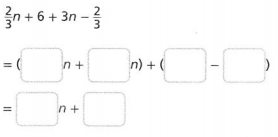
Answer:
The given expression is: \(\frac{2}{3}\)n + 6 +3n – \(\frac{2}{3}\)
Now,
\(\frac{2}{3}\)n + 6 +3n – \(\frac{2}{3}\)
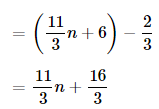
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{11}{3}\)n + \(\frac{16}{3}\)
Question 18.
5 + 3w + 3 – w
Answer:
The given expression is: 5 + 3w + 3 – w
Now,
5 + 3w + 3 – w
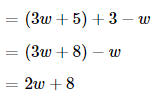
Hence, from the above,
We can conclude that
The value of the given expression is: 2w + 8
Question 19.
5w – 5w
Answer:
The given expression is: 5w – 5w
Now,
5w – 5w
= w (5 – 5)
= w (0)
= 0
Hence, from the above,
We can conclude that
The value of the given expression is: 0
Question 20.
2x + 5 + 3x + 6
Answer:
The givene xpression is: 2x + 5 + 3x + 6
Now,
2x + 5 + 3x + 6
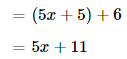
Hence, from the above,
We can conclude that
The value of the given expression is: 5x + 11
Question 21.
\(\frac{3}{4}\)z3 + 4 – \(\frac{1}{4}\)z3
Answer:
The given expression is: \(\frac{3}{4}\)z3 + 4 – \(\frac{1}{4}\)z3
Now,
\(\frac{3}{4}\)z3 + 4 – \(\frac{1}{4}\)z3
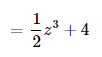
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{1}{2}\)z³ + 4
Question 22.
3.4m + 2.4m
Answer:
The given expression is: 3.4m + 2.4m
Now,
3.4m + 2.4m
= m (3.4 + 2.4)
= m (5.8)
= 5.8m
Hence, from the above,
We can conclude that
The value of the given expression is: 5.8m
Question 23.
4.2n + 5 – 3.2n
Answer:
The givene xpression is: 4.2n + 5 – 3.2n
Now,
4.2n + 5 – 3.2n
= (4.2n – 3.2n) + 5
= n (4.2 – 3.2) + 5
= n (1) + 5
= n + 5
Hence, from the above,
We can conclude that
The value of the given expression is: n + 5
Question 24.
q5 + q5 + q5
Answer:
The given expression is: q5 + q5 + q5
Now,
q5 + q5 + q5
= q5 (1 + 1 + 1)
= q5 (3)
= 3q5
Hence, from the above,
We can conclude that
The value of the given expression is: 3q5
Question 25.
3x + \(\frac{1}{4}\) + 2y + \(\frac{1}{4}\) + 7x – y
Answer:
The given expression is: 3x + \(\frac{1}{4}\) + 2y + \(\frac{1}{4}\) + 7x – y
Now,
3x + \(\frac{1}{4}\) + 2y + \(\frac{1}{4}\) + 7x – y
Hence, from the above,
We can conclude that
The value of the given expression is: 10x + y + \(\frac{1}{2}\)
Question 26.
1.5z2 + 4.5 + 6z – 0.3 – 3z + z2
Answer:
The given expression is: 1.5z2 + 4.5 + 6z – 0.3 – 3z + z2
Now,
1.5z2 + 4.5 + 6z – 0.3 – 3z + z2
Hence, from the above,
We can conclude that
The value of the given expression is: \(\frac{5}{2}\)z² + 3z + \(\frac{21}{5}\)
Question 27.
Use Structure Use the table at the right. Yolanda is planning a party that will take place in three rooms.
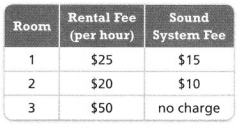
a. Write an expression that can be used to represent the total amount Yolanda will need to rent all three rooms and the sound system for t hours.
Answer:
It is given that
Yolanda is planning a party that will take place in three rooms.
Now,
The given table is:

So,
The amount of money Yolanda will need to rent all three rooms and the sound system for t hours =
(The total rental fee of the three rooms per hour) × (The total number of hours the three rooms are rented) + (The total fee of Sound system)
= ($25 + $20 + $50) × t + ($15 + $10)
= $95 × t + $25
= $95t + $25
Hence, from the above,
We can conclude that
The expression that can be used to represent the total amount Yolanda will need to rent all three rooms and the sound system for t hours is: $95t + $25
b. How can you use a property to write a simplified equivalent expression?
Answer:
The properties used to write a simplified equivalent expression are:
a. Commutative Property of Addition : When adding, changing the order of the numbers does not change the sum.
b. Commutative Property of Multiplication
c. Associative Property of Addition
d. Associative Property of Multiplication
e. Distributive Property
In 28-30, use the diagram at the right.
Question 28.
Write an algebraic expression for the perimeter of the swimming pool.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The swimming pool is in the form of a rectangle
Now,
From the given figure,
We can observe that
The length of the swimming pool is: 2y + 1
The width of the swimming pool is: y
Now,
We know that,
The perimeter of a recatngle = 2 × (Length + Width)
So,
The perimeter of the given swimming pool = 2 × (Length of the swimming pool + Width of the swimming pool)
= 2 × (2y + 1 + y)
= 2 × (3y + 1)
= 2 (3y + 1)
Hence,f rom the above,
We can conclude that
The algebraic expression that represents the perimeter of the swimming pool is: 2 (3y + 1)
Question 29.
Use Structure Write a new expression equivalent to the expression you wrote for exercise 28.
Answer:
From Exercise 28,
We know that,
The algebraic expression that represents the perimeter of the swimming pool is: 2 (3y + 1)
Now,
The given expression is: 2 (3y + 1)
Now,
2 (3y + 1)
= 2 (3y) + 2 (1)
= 6y + 2
Hence, from the above,
We can conclude that
The new expression that is equivalent to the expression you wrote for Exercise 28 is: 6y + 2
Question 30.
Justify that the two expressions are equivalent.
Answer:
From Exercise 28 and 29
We know that,
The expressions are: 2 (3y + 1) and 6y + 2
Now,
2 (3y + 1) = 2 (3y) + 2 (1)
= 6y + 2
So,
2 (3y + 1) = 6y + 2
Hence, from the above,
We can conclude that
The two expressions that are from Exercise 28 and Exercise 29 are equivalent expressions
Question 31.
Rodney rewrote the expression \(\frac{1}{2}\)(2x + 7) as x + 3\(\frac{1}{2}\). Which property of operations did Rodney use?
Answer:
It is given that
Rodney rewrote the expression \(\frac{1}{2}\)(2x + 7) as x + 3\(\frac{1}{2}\).
Now,
The given expression is: \(\frac{1}{2}\) (2x + 7)
Now,
By using the Distributive Property,
\(\frac{1}{2}\) (2x + 7)
= \(\frac{1}{2}\) (2x) + \(\frac{1}{2}\) (7)
= \(\frac{2x}{2}\) + \(\frac{7}{2}\)
= x + \(\frac{7}{2}\)
= x + 3\(\frac{1}{2}\)
Hence, from the above,
We can conclude that
Rodney used “Distributive Property” to solve the given expression
Question 32.
Construct Arguments Annie said that she simplified the expression 6.5(x + 0.5x + 1) by writing the equivalent expression 6.5x + 3.25x + 6.5. Do you agree? Explain.
Answer:
It is given that
Annie said that she simplified the expression 6.5(x + 0.5x + 1) by writing the equivalent expression 6.5x + 3.25x + 6.5
Now,
The given expression is: 6.5 (x + 0.5x + 1)
Now,
By using the Distributive Property,
6.5 (x + 0.5x + 1)
= 6.5 (x) + 6.5 (0.5x) + 6.5 (1)
= 6.5x + 3.25x + 6.5
Hence,from the above,
We can conclude that
We can agree with Annie
Question 33.
Critique Reasoning Thea said that the expressions 4x – 3x + 2 and x + 2 are equivalent. Is Thea correct? Explain.
Answer:
It is given that
Thea said that the expressions 4x – 3x + 2 and x + 2 are equivalent.
Now,
The given expression is: 4x – 3x + 2
Now,
4x – 3x + 2
= (4x – 3x) + 2
= x + 2
So,
4x – 3x + 2 = x + 2
Hence, from the above,
We can conclude that
Thea is correct
Question 34.
Higher Order Thinking Write an equivalent expression for the expression shown below.
\(\frac{a}{3}\) + \(\frac{a}{3}\) + \(\frac{a}{3}\)
Answer:
The given expression is:
\(\frac{a}{3}\) + \(\frac{a}{3}\) + \(\frac{a}{3}\)
Now,
\(\frac{a}{3}\) + \(\frac{a}{3}\) + \(\frac{a}{3}\)
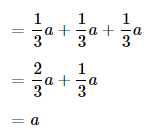
Hence, from the above,
We can conclude that
The value of the given expression is: a
Assessment Practice
Question 35.
Select all expressions that are equivalent to 8x + 3 + 5x – 2x.
![]() 13x + 3 – 2x
13x + 3 – 2x
![]() 11x + 3x
11x + 3x
![]() 11 + 3x
11 + 3x
![]() 14x
14x
![]() 11x + 3
11x + 3
Answer:
The given expression is: 8x + 3 + 5x – 2x
Now,
By using the Order of Operations,
8x + 3 + 5x – 2x
= (8x + 5x) + 3 – 2x
= 13x + 3 – 2x
= (13x – 2x) + 3
= 11x + 3
Hence, from the above,
We can conclude that
All expressions that are equivalent to 8x + 3 + 5x – 2x are:

Question 36.
Select which expression is equivalent to or NOT equivalent to the given expression.

Answer:
The givene xpression is: 2x + 7 + 6x – x
Now,
By using the Order of Operations,
2x + 7 + 6x – x
= (2x + 6x – x) + 7
= (8x – x) + 7
= 7x + 7
= 7 + 7x
Hence, from the above,
We can conclude that
The expression is equivalent to or not equivalent to the given expression is:

Topic 3 Review
? Topic Essential Question
What are expressions and how can they be written and evaluated?
Answer:
Expressions are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
To evaluate an algebraic expression means to find the value of the expression when the variable is replaced by a given number. To evaluate an expression, we substitute the given number for the variable in the expression and then simplify the expression using the order of operations.
Vocabulary Review
Complete each definition with a vocabulary word.
Vocabulary
algebraic expression
factor tree
coefficient
like terms
exponent
variable
Question 1.
A(n) ____ tells the number of times the base is used as a factor.
Answer:
We know that,
An “Exponent” tells the number of times the base is used as a factor.
Hence, from the above,
We can conclude that
The term that is suitable for the given definition is: Exponent
Question 2.
A letter or symbol that represents an unknown quantity is a(n) _____
Answer:
We know that,
A letter or symbol that represents an unknown quantity is a “variable”
Hence, from the above,
We can conclude that
The term that is suitable for the given definition is: Variable
Question 3.
A diagram that shows the prime factors of a composite number is a(n) ____
Answer:
We know that,
A diagram that shows the prime factors of a composite number is a “factor tree”
Hence, from the above,
We can conclude that
The term that is suitable for the given definition is: Factor tree
Draw a line from each pair of numbers in Column A to the least common multiple (LCM) of the numbers in Column B.

Answer:
The given pair of numbers are: (9, 6), (9, 12), and (8, 7)
So,
The LCM of (9, 6) is: 18
The LCM of (9, 12) is: 36
The LCM of (8, 7) is: 56
Hence, from the above,
We can conclude that
The matched pairs of Column A and Column B are:

Question 7.
Look at the variables in each expression below. Write Y if the terms of each expression are like terms. Write N if they are NOT like terms.
a. 3a + 3z
b. \(\frac{x}{3}\) + \(\frac{x}{4}\)
c. 4j – j + 3.8j
Answer:
The given expressions are:
a. 3a + 3z
b. \(\frac{x}{3}\) + \(\frac{x}{4}\)
c. 4j – j + 3.8j
Now,
We know that,
“Like terms” are terms whose variables (and their exponents such as the 2 in x2) are the same. In other words, terms that are “like” each other
Hence, from the above,
We can conclude that
The representation of Y and N for the given expressions are:
a. 3a + 3z – N
b. \(\frac{x}{3}\) + \(\frac{x}{4}\) – Y
c. 4j – j + 3.8j – Y
Use Vocabulary in Writing
Explain one way to simplify the expression 4(3q – q). Use vocabulary words in your explanation.
Answer:
The given algebraic expression is: 4 (3q – q)
Now,
When we observe the given expression,
In 3q, “3” is the coefficient
3q and q are the like terms
Now,
4 (3q – q) = 4 (3q – 1q)
= 4q (3 – 1)
= 4q (2)
= 8q
Hence, from the above,
We can conclude that
The value of the given expression is: 8q
Concepts and Skills Review
LESSON 3.1 Understand and Represent exponents
Quick Review
An exponent is a way to show repeated multiplication.
Example
Use an exponent to write the expression 6 × 6 × 6. Then evaluate the expression.
6 is used as a factor 3 times.
6 is the base and 3 is the exponent.
6 × 6 × 6 = 63 = 216
Find 60
A number with an exponent of 0 is always equal to 1.
60 = 1
Practice
Write each expression using an exponent.
Question 1.
8 × 8 × 8 × 8 × 8 × 8 × 8
Answer:
The given repeated multiplication is: 8 × 8 × 8 × 8 × 8 × 8 × 8
Now,
We know that,
An “Exponent” tells the number of times the base i.e., the given number is used as afactor
So,
8 × 8 × 8 × 8 × 8 × 8 × 8 = 87
Hence, from the above,
We can conclude that
The representation of the given expression using an exponent is: 87
Question 2.
4
Answer:
The given repeated multiplication is: 4
Now,
We know that,
An “Exponent” tells the number of times the base i.e., the given number is used as afactor
So,
4 = 41
Hence, from the above,
We can conclude that
The representation of the given expression using an exponent is: 41
Question 3.
10 × 10 × 10 × 10
Answer:
The given repeated multiplication is: 10 × 10 × 10 × 10
Now,
We know that,
An “Exponent” tells the number of times the base i.e., the given number is used as afactor
So,
10 × 10 × 10 × 10 = 104
Hence, from the above,
We can conclude that
The representation of the given expression using an exponent is: 104
Evaluate each expression.
Question 4.
92
Answer:
The given expression is: 9²
Now,
We know that,
An “Exponent” tells the number of times the base is used as a factor
So,
9² = 9 × 9
= 81
Hence, from the above,
We can conclude that
The value of the given expression is: 81
Question 5.
991
Answer:
The given expression is: 991
Now,
We know that,
An “Exponent” tells the number of times the base is used as a factor
So,
991 = 99
Hence, from the above,
We can conclude that
The value of the given expression is: 99
Question 6.
3,1050
Answer:
The given expression is: 3,1050
Now,
We know that,
An “Exponent” tells the number of times the base is used as a factor
Any nonzero number raised to an exponent of zero has always a value of 1
So,
3,1050 = 1
Hence, from the above,
We can conclude that
The value of the given expression is: 1
Question 7.
222
Answer:
The given expression is: 222
Now,
We know that,
An “Exponent” tells the number of times the base is used as a factor
So,
222 = 22 × 22
= 484
Hence, from the above,
We can conclude that
The value of the given expression is: 484
Question 8.
27
Answer:
The given expression is: 27
Now,
We know that,
An “Exponent” tells the number of times the base is used as a factor
So,
27 = 2 × 2 × 2 × 2 × 2 × 2 × 2
= 128
Hence, from the above,
We can conclude that
The value of the given expression is: 128
Question 9.
34
Answer:
The given expression is: 34
Now,
We know that,
An “Exponent” tells the number of times the base is used as a factor
So,
34 = 3 × 3 × 3 × 3
= 81
Hence, from the above,
We can conclude that
The value of the given expression is: 81
LESSON 3.2 Find Greatest Common Factor and Least Common Multiple
Quick Review
You can use prime factorization to find the greatest common factor and the least common multiple of two numbers.
Example
Find the greatest common factor (GCF) and the least common multiple (LCM) of 12 and 6.
List the prime factors of both numbers.

Practice
Find the GCF for each pair of numbers. Use the GCF and the Distributive Property to find the sum of each pair of numbers.
Question 1.
30, 100
Answer:
The given numbers are: 30, 100
Now,

Hence, from the above,
We can conclude that
The GCF of the given numbers is: 10
Question 2.
8, 52
Answer:
The given numbers are: 8, 52
Now,

Hence, from the above,
We can conclude that
The GCF of the given numbers is: 4
Question 3.
28, 42
Answer:
The given numbers are: 28, 42
Now,

Hence, from the above,
We can conclude that
The GCF of the given numbers is: 14
Question 4.
37, 67
Answer:
The given numbers are: 37, 67
Now,

Hence, from the above,
We can conclude that
The GCF of the given numbers is: 1
Question 5.
12, 24
Answer:
The given numbers are: 12, 24
Now,

Hence, from the above,
We can conclude that
The GCF of the given numbers is: 12
Question 6.
8, 12
Answer:
The given numbers are: 8, 12
Now,
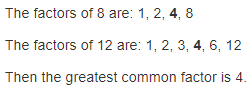
Hence, from the above,
We can conclude that
The GCF of the given numbers is: 4
Find the LCM for each pair of numbers.
Question 7.
4, 9
Answer:
The given numbers are: 4, 9
Now,

Hence, from the above,
We can conclude that
The LCM of the given numbers is: 36
Question 8.
3, 6
Answer:
The given numbers are: 3, 6
Now,
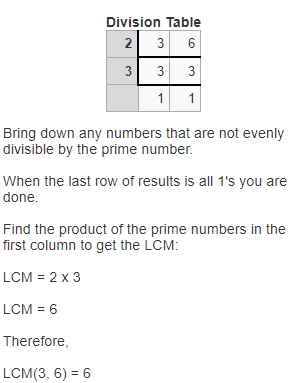
Hence, from the above,
We can conclude that
The LCM of the given numbers is: 6
Question 9.
8, 10
Answer:
The given numbers are: 8, 10
Now,

Hence, from the above,
We can conclude that
The LCM of the given numbers is: 40
Question 10.
3, 5
Answer:
The given numbers are: 3, 5
Now,

Hence, from the above,
We can conclude that
The LCM of the given numbers is: 15
Question 11.
12, 5
Answer:
The given numbers are: 12, 5
Now,

Hence, from the above,
We can conclude that
The LCM of the given numbers is: 60
Question 12.
4, 11
Answer:
The given numbers are: 4, 11
Now,

Hence, from the above,
We can conclude that
The LCM of the given numbers is: 44
LESSON 3.3 Write and Evaluate Numerical expressions
Quick Review
Use the order of operations to evaluate numerical expressions.
Example
Evaluate the expression 32 + 2[(21 – 9) ÷ 4].

Practice
Evaluate each expression.
Question 1.
80 – 42 ÷ 8
Answer:
The given expression is: 80 – 42 ÷ 8
Now,
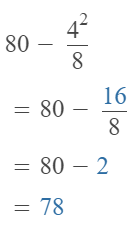
Hence, from the above,
We can conclude that
The value of the given expression is: 78
Question 2.
92.3 – (3.2 ÷ 0.4) × 23
Answer:
The given expression is: 92.3 – (3.2 ÷ 0.4) × 23
Now,
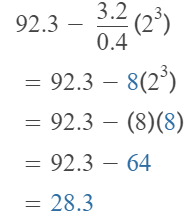
Hence, from the above,
We can conclude that
The value of the given expression is: 28.3
Question 3.
[(23 × 2.5) ÷ \(\frac{1}{2}\)] + 120
Answer:
The given expression is: [(23 × 2.5) ÷ \(\frac{1}{2}\)] + 120
Now,
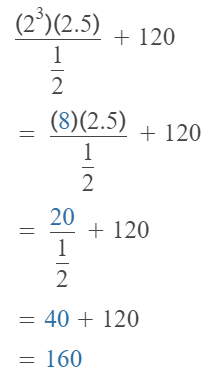
Hence, from the above,
We can conclude that
The value of the given expression is: 160
Question 4.
[20 + (2.5 × 3)] – 33
Answer:
The given expression is: [20 + (2.5 × 3)] – 33
Now,
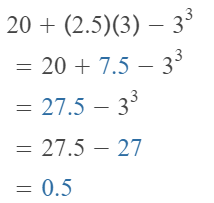
Hence, from the above,
We can conclude that
The value of the given expression is: 0.5
Question 5.
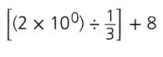
Answer:
The given expression is: [(2 × 100 ) ÷ \(\frac{1}{3}\)] + 8
Now,
Hence, from the above,
We can conclude that
The value of the given expression is: 14
LESSONS 3.4 AND 3.5 Write and Evaluate Algebraic expressions
Quick Review
An algebraic expression can be written to represent a situation with an unknown quantity. Use a variable to represent the unknown quantity. An algebraic expression can be evaluated by substituting a value for the variable and performing the operations.
Example
Write an algebraic expression for 9 times the difference of 12 and a divided by 2. Then evaluate the expression for a = 4.
9 times the difference of 12 and a divided by 2″ is represented by 9 × (12 – a) ÷ 2.

Practice
Write an algebraic expression to represent each situation.
Question 1.
22 less than 5 times a number f
Answer:
The given situation is: 22 less than 5 times a number f
Now,
We know that,
The term “Less than” represents the subtraction
The term”many times” (or) “times” represents the multiplication
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an algebraic expression is: 5f – 22
Question 2.
48 times a number of game markers, g
Answer:
The given situation is: 48 times a number of game markers, g
Now,
We know that,
The term”many times” (or) “times” represents the multiplication
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an algebraic expression is: 48g
Question 3.
A number of eggs, e, divided by 12
Answer:
The given situation is: A number of eggs, e, divided by 12
Now,
We know that,
The term”Division” (or) “Divide” represents the division
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an algebraic expression is: \(\frac{e}{12}\)
Question 4.
3 times the sum of m and 7
Answer:
The given situation is: 3 times the sum of m and 7
Now,
We know that,
The term”many times” (or) “times” represents the multiplication
The term “Sum” (or) “Add” represents the addition
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an algebraic expression is: 3 (m + 7)
Evaluate each expression for n = 7, x = 4, y = 8, and z = 1.
Question 5.
12x – 7
Answer:
The given expression is: 12x – 7
Now,
For x = 4,
12x – 7 = 12 (4) – 7
= 48 – 7
= 41
Hence, from the above,
We can conclude that
The value of the given expression is: 41
Question 6.
x2 ÷ y
Answer:
The given expression is: x² ÷ y
Now,
For x = 4, and y = 8,
x² ÷ y = 4² ÷ 8
= 16 ÷ 8
= 2
Hence, from the above,
We can conclude that
The value of the given expression is: 2
Question 7.
5z + 3n – z3
Answer:
The given expression is: 5z + 3n – z3
Now,
For z = 1, and n = 7,
5z + 3n – z3 = 5 (1) + 3 (7) – 13
= 5 + 21 – 1
= 25
Hence, from the above,
We can conclude that
The value of the given expression is: 25
Question 8.
y2 ÷ 2x + 3n – z
Answer:
The given expression is: y2 ÷ 2x + 3n – z
Now,
For x = 4, n = 7, z = 1, and y = 8,
y2 ÷ 2x + 3n – z = 8² ÷ 2 (4) + 3 (7) – 1
= 64 ÷ 8 + 21 – 1
= 8 + 20
= 28
Hence, from the above,
We can conclude that
The value of the given expression is: 28
LESSON 3.6 Generate Equivalent expressions
Quick Review
Equivalent expressions are expressions that have the same value. The properties of operations and substitution can be used to write and identify equivalent expressions.
Example
Are the expressions 5x + 20, 5(x + 4), and x + 4 equivalent?
For algebraic expressions to be equivalent, each expression must name the same value no matter what value is substituted for the variable.
Use the Distributive Property to write
5x + 20 as 5(x + 4).
5x + 20 = 5 • x + 5 • 4
= 5(x + 4)
Properties of operations cannot be used to write 5x + 20 or 5(x + 4) as x + 4.
5x + 20 and 5(x + 4) are equivalent expressions.
Practice
Complete the table. Then circle the expressions that are equivalent.
Question 1.
Answer:
The given expressions are:
a. 5 (2.2y + 1) – 3 b. 11y + 5 – y c. 11y + 2
Now,
a.
For y = 1,
5 (2.2y + 1) – 3 = 5 (2.2 + 1) – 3
= 13
For y = 2,
5 (2.2y + 1) = 5 (2.2 (2) + 1) – 3
= 24
For y = 3,
5 (2.2y + 1) – 3 = 5 (2.2 (3) + 1) – 3
= 35
Now,
b.
For y = 1,
11y + 5 – y = 11 + 5 – 1
= 15
For y = 2,
11y + 5 – y = 22 + 5 – 2
= 25
For y = 3,
11y + 5 – y = 33 + 5 – 3
= 35
Now,
c.
For y = 1,
11y + 2 = 11 + 2
= 13
For y = 2,
11y + 2 = 22 + 2
= 24
For y = 3,
11y + 2 = 33 + 2
= 35
Hence, from the above,
We can conclude that
The completed table and the expressions (Circled in the table) that are equivalent is:

In 2-4, write Yes or No to indicate whether the expressions are equivalent.
Question 2.
10x – 3 + 2x – 5 and 4(3x – 2)
Answer:
The given expressions are: 10x – 3 + 2x – 5 and 4(3x – 2)
Now,
10x – 3 + 2x – 5 = (10x + 2x) – (3 + 5)
= 12x – 8
= 4 (3x – 2)
So,
10x – 3 + 2x – 5 = 4 (3x – 2)
Hence, from the above,
We can conclude that
We can indicate YES since the given expressions are equivalent
Question 3.
3y + 3 and 9(y + \(\frac{1}{3}\))
Answer:
The given expressions are: 3y + 3 and 9(y + \(\frac{1}{3}\))
Now,
9(y + \(\frac{1}{3}\)) = 9 (y) + 9 (\(\frac{1}{3}\))
= 9y + 3
So,
3y + 3 ≠ 9y + 3
Hence, from the above,
We can conclude that
We can indicate NO since the given expressions are not equivalent
Question 4.
6(3x + 1) and 9x + 6 + 9x
Answer:
The given expressions are: 6(3x + 1) and 9x + 6 + 9x
Now,
9x + 6 + 9x = (9x + 9x) + 6
= 18x + 6
= 6 (3x + 1)
So,
6 (3x + 1) = 9x + 6 + 9x
Hence, from the above,
We can conclude that
We can indicate YES since the given expressions are equivalent
In 5-7, use properties of operations to complete the equivalent expressions.
Question 5.
2(x + 4) and ___x + ____
Answer:
The given expression is: 2 (x + 4)
Now,
By using the Distributive Property,
2 (x + 4) = 2 (x) + 2 (4)
= 2x + 8
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 2x + 8
Question 6.
5x – 45 and 5(___ – ___ )
Answer:
The given expression is: 5x – 45
Now,
By using the Distributive Property,
5x – 45 = 5 (x – 9)
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 5 (x – 9)
Question 7.
3(x + 7) and ___ ×+ ____
Answer:
The given expression is: 3 (x + 7)
Now,
By using the Distributive Property,
3 (x + 7) = 3 (x) + 3 (7)
= 3x + 21
Hence, from the above,
We can conclude that
The equivalent expression for the given expression is: 3x + 21
LESSON 3.7 Simplify Algebraic expressions
Quick Review
Combine like terms to simplify algebraic expressions.
Example
Simplify the expression 3x + 7 + 6x.

Practice
Simplify each expression.
Question 1.
9y + 4 – 6y
Answer:
The given expression is: 9y + 4 – 6y
Now,
9y + 4 – 6y
= (9y – 6y) + 4
= 5y + 4
Hence, from the above,
We can conclude that
The value of the given expression is: 5y + 4
Question 2.
3x + 5 + 7x
Answer:
The given expression is: 3x + 5 + 7x
Now,
3x + 5 + 7x
= (3x + 7x) + 5
= 10x + 5
= 5 (2x + 1)
Hence, from the above,
We can conclude that
The value of the given expression is: 5 (2x + 1)
Question 3.
8x + 13 – 3x + 9
Answer:
The given expression is: 8x + 13 – 3x + 9
Now,
8x + 13 – 3x + 9
= (8x – 3x) + (13 + 9)
= 5x + 22
Hence, from the above,
We can conclude that
The value of the given expression is: 5x + 22
Question 4.
y2 + 3y2
Answer:
The given expression is: y² + 3y²
Now,
y² + 3y²
= y² (1 + 3)
= y² (4)
= 4y²
Hence, from the above,
We can conclude that
The value of the given expression is: 4y²
Question 5.
4x + 15 – 3x + 10
Answer:
The given expression is: 4x + 15 – 3x + 10
Now,
4x + 15 – 3x + 10
= (4x – 3x) + (15 + 10)
= x + 25
Hence, from the above,
We can conclude that
The value of the given expression is: x + 25
Question 6.
10x + 2x – 12x
Answer:
The given expression is: 10x + 2x – 12x
Now,
10x + 2x – 12x
= x (10 + 2 – 12)
= x (12 – 12)
= x (0)
= 0
Hence, from the above,
We can conclude that
The value of the given expression is: 0
Topic 3 Fluency Practice
Crisscrossed

