Go through the enVision Math Common Core Grade 6 Answer Key Topic 4 Represent And Solve Equations And Inequalities regularly and improve your accuracy in solving questions.
Envision Math Common Core 6th Grade Answers Key Topic 4 Represent And Solve Equations And Inequalities
?Topic Essential Question What procedures can be used to write and solve equations and inequalities?
Answer:
The three methods most commonly used to solve systems of equation are substitution, and elimination. Substitution and elimination are simple methods that can effectively solve most systems of two equations in a few straightforward steps
The steps to solve an inequality are:
a. Add the same number to both sides.
b. Subtract the same number from both sides.
c. Multiply both sides by the same positive number.
d. Divide both sides by the same positive number.
e. Multiply both sides by the same negative number and reverse the sign
3-ACT MATH

Checking a Bag
A large plane flying across the ocean can weigh almost 1 million pounds! The heavier an airplane is, the more fuel it needs for a flight. The cost of fuel has led many airlines to add a weight restriction on luggage.
If you were to fly somewhere, what would you bring? What would you leave at home to minimize the weight of your luggage? Packing light is important, not only to avoid a fee but also to do your part to conserve fuel. Think about this during the 3-Act Mathematical Modeling lesson.

Topic 4 EnVision STEM Project
Did You Know?
The design of a bridge depends on factors such as the distance the bridge will cover, the expected number of vehicles that will cross the bridge daily, and the geographic conditions.
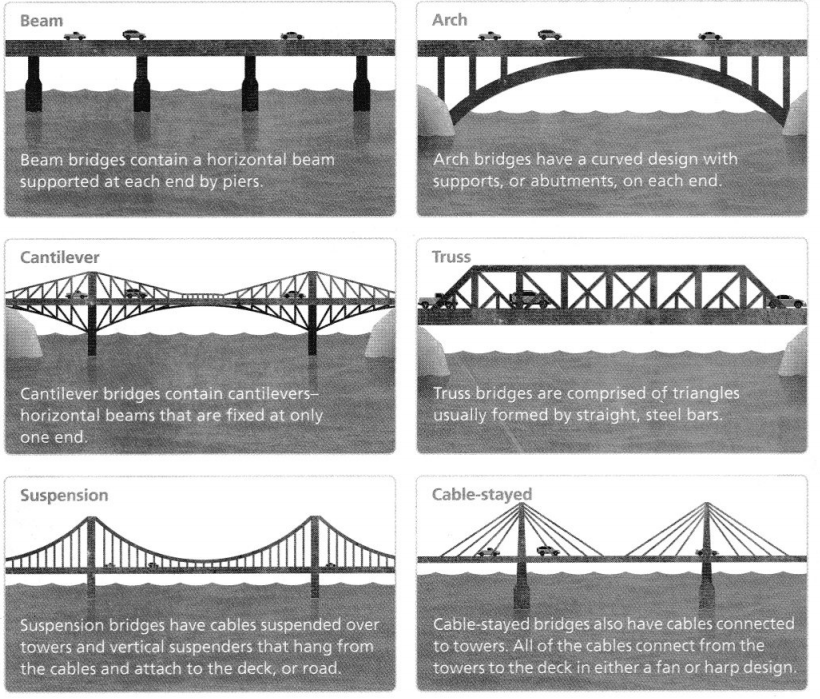
Your Task: Design a Bridge
Now that you have defined the problem, identified the criteria and constraints, and performed some data collection, it is time to focus on the solution. You and your classmates will continue to be engineers as you brainstorm solutions and develop prototypes for your bridge.
Topic 4 Get Ready!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
- algebraic expression
- coefficient equation
- evaluate
- variable
Question 1.
In 6x, x is a(n) _________ .
Answer:
We know that,
In 6x,
“6” is called as “Coefficient”
“x” is called as “Variable”
Hence, from the above,
We can conclude that
The best term that is suitable for the given statement is: Variable
Question 2.
x + 5 is an example of a(n) __________
Answer:
We know that,
The expressions are of 2 types. They are:
a. Numeric Expressions – The expression that contains only numbers and arithmetic symbols
Ex: 6 + 2 – 5
b. Algebraic expressions – The expression that contains variables, numbers,and arithmetic symbols
Ex: x + 2 – 5 + y
So,
x + 5 is an example of “Algebraic expression”
Hence, from the above,
We can conclude that
The best term that is suitable for the given statement is: Algebraic expression
Question 3.
__________ an expression to find its value.
Answer:
We know that,
“Evaluate” an expression to find its value
Hence, from the above,
We can conclude that
The best term that is suitable for the given statement is: Evaluate
Question 4.
The expressions on each side of the equal sign in a(n) __________ are equal.
Answer:
We know that,
The expressions on each side of the equal sign in an “Equation” are equal
Hence, from the above,
We can conclude that
The best term that is suitable for the given statement is: Equation
Equality
Tell whether the equation is true or false.
Question 5.
6 + 2 = 2 + 6
Answer:
The given equation is:
6 + 2 = 2 + 6
Now,
We know that,
According to the Commutative Property of Addition,
a + b = b + a
Hence, from the above,
We can conclude that
The given equation is: True
Question 6.
2.5 – 1 = 1 – 2.5
Answer:
The given equation is:
2.5 – 1 = 1 – 2.5
Now,
We know that,
According to the Commutative Property,
a – b ≠ b – a
Hence, from the above,
We can conclude that
The given equation is: False
Question 7.
\(\frac{1}{2}\) × 3= 3 × \(\frac{1}{2}\)
Answer:
The given equation is:
\(\frac{1}{2}\) × 3 = 3 × \(\frac{1}{2}\)
Now,
We know that,
According to the Commutative Property of Multiplication,
a × b = b × a
Hence, from the above,
We can conclude that
The given equation is: True
Question 8.
\(\frac{3}{4} \div 5=\frac{3}{4} \times \frac{1}{5}\)
Answer:
The given equation is:
\(\frac{3}{4}\) ÷ 5 = \(\frac{3}{4}\) × \(\frac{1}{5}\)
Now,
We know that,
When any number is present after the “Division” symbol, then it will turn into its reciprocal when it is converted into “Multiplication” and vice-versa
So,
÷ 5 will convert into × \(\frac{1}{5}\)
Hence, from the above,
We can conclude that
The given equation is: True
Question 9.
\(5 \div \frac{1}{3}=\frac{5}{3}\)
Answer:
The given equation is:
5 ÷ \(\frac{1}{3}\) = \(\frac{5}{3}\)
Now,
We know that,
When any number is present after the “Division” symbol, then it will turn into its reciprocal when it is converted into “Multiplication” and vice-versa
So,
÷ \(\frac{1}{3}\) will be converted into × 3
Hence, from the above,
We can conclude that
The given equation is: False
Question 10.
\(\frac{2}{3} \times 5=\frac{10}{15}\)
Answer:
The given equation is:
\(\frac{2}{3}\) × 5 = \(\frac{10}{15}\)
Now,
\(\frac{2}{3}\) × 5
= \(\frac{2 × 5}{3}\)
= \(\frac{10}{3}\)
Hence, from the above,
We can conclude that
The given equation is: False
Expressions
Evaluate each expression.
Question 11.
x – 2 for x = 8
Answer:
The given expression is: x – 2
Now,
For x = 8,
x – 2 = 8 – 2
= 6
Hence, from the above,
We can conclude that
The value of the given expression is: 6
Question 12.
2b for b = 9
Answer:
The given expression is: 2b
Now,
For b = 9,
2b = 2 × b
= 2 × 9
= 18
Hence, from the above,
We can conclude that
The value of the given expression is: 18
Question 13.
3\(\frac{3}{4}\) + y for y = \(\frac{5}{6}\)
Answer:
The given expression is: 3\(\frac{3}{4}\) + y
Now,
For y = \(\frac{5}{6}\),
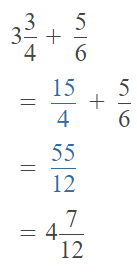
Hence, from the above,
We can conclude that
The value of the given expression is: 4\(\frac{7}{12}\)
Question 14.
\(\frac{15}{x}\) for x = 3
Answer:
The given expression is: \(\frac{15}{x}\)
Now,
For x = 3,
\(\frac{15}{x}\) = \(\frac{15}{3}\)
= 5
Hence, from the above,
We can conclude that
The value of the given expression is: 5
Question 15.
5.6t for t = 0.7
Answer:
The given expression is: 5.6t
Now,
For t = 0.7,
5.6t = 5.6 × t
= 5.6 × 0.7
= 3.92
Hence, from the above,
We can conclude that
The value of the given expression is: 3.92
Question 16.
4x for x = \(\frac{1}{2}\)
Answer:
The given expression is: 4x
Now,
For x = \(\frac{1}{2}\),
4x = 4 × \(\frac{1}{2}\)
= \(\frac{4}{2}\)
= 2
Hence, from the above,
We can conclude that
The value of the given expression is: 2
Order of Operations
Question 17.
Explain the order in which you should compute the operations in the expression below. Then evaluate the expression.
[(33 ÷ 3) + 1] – 22
Answer:
The given expression is: [(33 ÷ 3) + 1] – 2²
Now,
We know that,
We will follow the order of operations by uisng the BODMAS rule
Where,
B – Brackets
O – Of
D – Division
M – Multiplication
A – Addition
S – Subtraction
So,
In the given expression,
The order of expressions we have to compute from the first to the last is:
a. 33 ÷ 3
b. [(33 ÷ 3) + 1]
c. 2²
d. [(33 ÷ 3) + 1] – 2²
So,
[(33 ÷ 3) + 1] – 2²
= [11 + 1] – 2²
= 12 – 4
= 8
Hence, from the above,
We can conclude that
The value of the given expression is: 8
Graphing in the Coordinate Plane
Question 18.
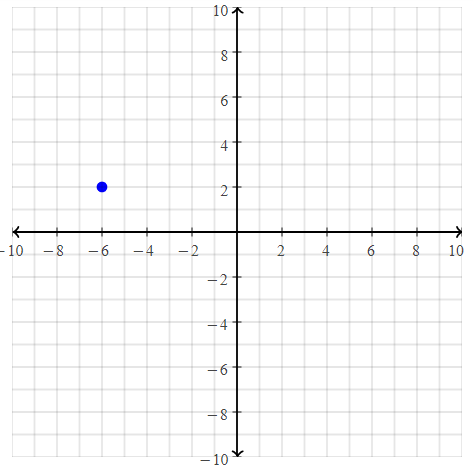
Describe how to plot point A(-6, 2) on a coordinate plane.
Answer:
The given point is: A (-6, 2)
Now,
When we observe the given point,
The x-coordinate of point A is negative and the y-coordinate of point A is positive
So,
For point A,
The x-coordinate is at the left side of the coordinate plane and the y-coordinate is at the top side of the coordinate plane
Hence,
The representation of A (-6, 2) in the coordinate plane is:
Language Development
Use the graphic organizer to help you understand new vocabulary terms.

Answer:

Pick A Project
PROJECT 4A
If you were going to try a new exercise, what would it be? Why?
PROJECT: ANALYZE AN EXERCISE ROUTINE

PROJECT 4B
What is the most interesting book you have read?
PROJECT: WRITE AND ILLUSTRATE A CHILDREN’S BOOK

PROJECT 4C
If you were a carpenter what sorts of things would you build?
PROJECT: MAKE A MODEL OF A STAIRCASE

PROJECT 4D
What skills would you need if you wanted to move as slowly as a snail?
PROJECT: PLAN A RACE

Lesson 4.1 Understand Equations and Solutions
Solve & Discuss It!
Unit cubes are placed on a pan balance. There are 3 cubes on one pan and 9 cubes on the other pan. What can you do to make the pans balance?
Model with Math
A pan balance can be used to represent the relationship between two quantities. You can write an equation with a variable to show this relationship.
I can… determine if a value for a variable makes an equation true.

Answer:
It is given that
Unit cubes are placed on a pan balance. There are 3 cubes on one pan and 9 cubes on the other pan.
Now,
Let the number of cubes on one pan that has to be added as to make the pan balance be: x
Let the number of cubes on other pan that has to be added as to make the pan balance be: y
So,
The number of cubes present on one pan = x + 3
The number of cubes present on other pan = y + 9
So,
To make the given pans balanced,
x + 3 = y + 9
Hence, from the above,
We can conclude that
The equation that makes the pans balances is:
x + 3 = y + 9
Focus on math practices
Use Structure Suppose that you added 10 cubes to the pan with 3 cubes and then added 4 cubes to the pan with 9 cubes. Would the pans balance? Write an equation to show this relationship.
Answer:
It is given that
you added 10 cubes to the pan with 3 cubes and then added 4 cubes to the pan with 9 cubes
So,
The number of cubes present on one pan = 10 + 3 = 13 cubes
The number of cubes present on other pan = 9 + 4 = 13 cubes
So,
The number of cubes present on both pans are the same
Hence, from the above,
We can conclude that
The pans are balanced
Essential Question
How can you determine whether a given number makes an equation true?
Answer:
We can check if the given solution to an expression is actually the solution the expression by replacing the variables in the equation with the given solution and solving the equation. If LHS = RHS with the given solution, the solution is correct. If not, it’s incorrect.
Try It!
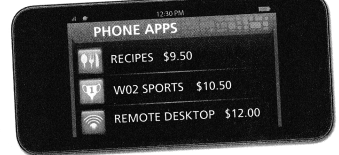
Tracy received a $21.00 gift card for phone apps. She has used $9.00 of the value and wants to buy one more app from the list above to use up the balance. Complete the bar diagram and use the equation $21.00 = x + $9.00 to determine which app she should buy.
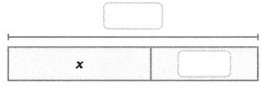
The solution is _________, so Tracy should buy the _________ app.
Answer:
It is given that
Tracy received a $21.00 gift card for phone apps. She has used $9.00 of the value and wants to buy one more app from the list above to use up the balance
Now,
The given figure is:
Now,
Let x be the cost of the another app that Tracy wanted to buy
So,
According to the given information,
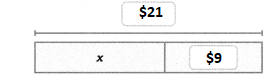
The equation that represents the used up balance is:
$9 + $x = $21
Now,
The representation of the above equation in the form of a bar diagram is:
So,
$x = $21 – $9
$x = $12
So,
![]()
Hence, from the above,
We can conclude that
Tracy should buy the “Remote Desktop” app with her balance of $12
Convince Me! What do you notice about the expression on the left side of an equation compared to the expression on the right side when a value is substituted for the variable? How do you know which value is a solution?
Answer:
When we observe the expression that is present on the left side of an equation and the expression that is present on the right side of an equation when a value is substituted for the variable,
We can say that
The left hand side of the equation = The right hand side of the equation
Now,
The solution for the equation is the value we substituted for a “Variable”
Try It!
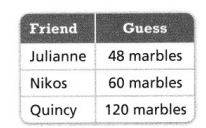
Anthony has a total of y marbles and 4 boxes. He puts 13 marbles in each box and has none left over. Which of his friends, if any, correctly guessed how many marbles Anthony has in all? Use the equation y ÷ 4 = 13.
Substitute each guess for y and evaluate.

Try y = 48: _______ ÷ 4 = _______
Try y = 60: _______ ÷ 4 = _______
Try y = 120: _______ ÷ 4 = _______
Of Anthony’s three friends, _______ correctly guessed the number of marbles he has in all.
No solution is given in the set of values.
Anthony has _______ marbles in all.
Answer:
It is given that
Anthony has a total of y marbles and 4 boxes. He puts 13 marbles in each box and has none left over.
Now,
The representation of the given situation in the form of a bar diagram is:

Now,
The given table is:
Now,
To find whether any friend of Anthony guesses correctly or not,
Substitute the values of marbles below

So,

Now,
The given equation that represents the number of marbles Anthony has is:
y ÷ 4 = 13
y = 13 × 4
y = 52 marbles
So,
![]()
Hence, from the above,
We can conclude that
The number of marbles Anthony has in all is: 52 marbles
KEY CONCEPT
A solution of an equation is a value for the variable that makes the equation true. Substitute values from a given set for the variable and evaluate. x – 4 = 12 x = 9, 16

Do You Understand?
Question 1.
Essential Question How can you determine whether a given number makes an equation true?
Answer:
We can check if the given solution to an expression is actually the solution the expression by replacing the variables in the equation with the given solution and solving the equation. If LHS = RHS with the given solution, the solution is correct. If not, it’s incorrect.
Question 2.
When is an equation true?
Answer:
To make a true equation, check your math to make sure that the values on each side of the equals sign are the same. Ensure that the numerical values on both sides of the “=” sign are the same to make a true equation
Question 3.
Reasoning Ben says that n = 5 is the solution of the equation 7n = 45. How can you check whether Ben is correct?
Answer:
It is given that
Ben says that n = 5 is the solution of the equation 7n = 45
Now,
The given equation is:
7n = 45
Now,
substitute the given value of n in the given equation
So,
For the given equation,
If LHS = RHS, then
Ben is correct
If LHS ≠ RHS, then
Ben is not correct
Question 4.
A pan balance has 3 cubes on one pan and 11 cubes on the other pan. Lucy thinks she should add 7, 8, 9, or 10 cubes to make the pans balance. How can you use the equation 3 + C = 11 to find the number of cubes Lucy should add?
Answer:
It is given that
A pan balance has 3 cubes on one pan and 11 cubes on the other pan. Lucy thinks she should add 7, 8, 9, or 10 cubes to make the pans balance.
Now,
According to the given information,
The number of cubes on one pan = 3 cubes
The number of cubes on other pan = 11 cubes
Now,
It is given that
Lucy wants to add the extra cubes with 3 cubes
So,
The number of cubes in the second pan is constant
Now,
Let the number of extra cubes on one pan to be added so that the pan should be balanced be: C
So,
3 + C = 11
So,
C = 11 – 3
C = 9 cubes
So,
Lucy should add 9 cubes to make the pans balance
Hence, from the above,
We can conclude that
Lucy should add 9 cubes on one pan to make both the pans balance
Do You Know How?
In 5-8, substitute each given value of the variable to find which, if any, is a solution of the equation.
Question 5.
d + 9 = 35; d = 16, 22, 26, 36
Answer:
The given equation is:
d + 9 = 35
Now,
For d = 16,
16 + 9 = 35
25 ≠ 35
For d = 22,
22 + 9 = 35
31 ≠ 35
For d = 26,
26 + 9 = 35
35 = 35
For d = 36,
36 + 9 = 35
45 ≠ 35
Hence, from the above,
We can conclude that
d = 26 is a solution to the given equation
Question 6.
14n = 35; n = 2, 3, 3.5, 4
Answer:
The given equation is:
14n = 35
Now,
For n = 2,
14 (2) = 35
28 ≠ 35
For n = 3,
14 (3) = 35
42 ≠ 35
For n = 3.5,
14 (3.5) = 35
49 ≠ 35
For n = 4,
14 (4) = 35
56 ≠ 35
Hence, from the above,
We can conclude that
The given values of n are not any solutions for the given equation
Question 7.
13.4 – g = 8.1; g = 4.3, 5.3, 5.5, 6.5
Answer:
The given equation is:
13.4 – g = 8.1
Now,
For g = 4.3,
13.4 – 4.3 = 8.1
9.1 ≠ 8.1
For g = 5.3,
13.4 – 5.3 = 8.1
8.1 = 8.1
For g = 5.5,
13.4 – 5.5 = 8.1
7.9 ≠ 8.1
For g = 6.5,
13.4 – 6.5 = 8.1
6.9 ≠ 8.1
Hence, from the above,
We can conclude that
g = 5.3 is a solution to the given equation
Question 8.
4 = 36 ÷ m; m = 4, 6, 8, 9
Answer:
The given equation is:
4 = 36 ÷ m
Now,
For m = 4,
4 = 36 ÷ 4
4 ≠ 9
For m = 6,
4 = 36 ÷ 6
4 ≠ 6
For m = 8,
4 = 36 ÷ 8
4 ≠ 4.5
For m = 9,
4 = 36 ÷ 9
4 = 4
Hence, from the above,
We can conclude that
m = 9 is a solution to the given equation
In 9-12, tell whether each equation is true or false for n = 8.
Question 9.
n = 54 – 36
Answer:
The given equation is:
n = 54 – 36
Now,
n = 54 – 36
= 18
So,
8 ≠ 18
Hence, from the above,
We can conclude that
The given equation is False for n = 8
Question 10.
5n = 40
Answer:
The given equation is:
5n = 40
Now,
5n = 40
n = \(\frac{40}{5}\)
= 8
So,
8 = 8
Hence, from the above,
We can conclude that
The given equation is True for n = 8
Question 11.
152 ÷ n = 21
Answer:
The given equation is:
152 ÷ n = 21
Now,
152 ÷ n = 21
n = \(\frac{152}{21}\)
= 0.7
So,
0.7 ≠ 8
Hence, from the above,
We can conclude that
The given equation is False for n = 8
Question 12.
n + 46 = 54
Answer:
The given equation is:
n + 46 = 54
Now,
n + 46 = 54
n = 54 – 46
= 8
So,
8 = 8
Hence, from the above,
We can conclude that
The given equation is True for n = 8
Practice & Problem Solving
In 13-16, tell which given value, if any, is a solution of the equation.
Question 13.
t – 2.1 = 0 t = 2.1, 2.4, 2.6, 2.8
Answer:
The given equation is:
t – 2.1 = 0
Now,
t – 2.1 = 0
Now,
Add with 2.1 on both sides
So,
t – 2.1 + 2.1 = 0 + 2.1
t = 2.1
Hence, from the above,
We can conclude that
t = 2.1 is the solution for the given equation
Question 14.
49 = 7r r = 3, 6, 7, 9
Answer:
The given equation is:
49 = 7r
Now,
49 = 7r
Divide by 7 on both sides
So,
\(\frac{49}{7}\) = \(\frac{7r}{7}\)
7 = r
Hence, from the above,
We can conclude that
r = 7 is the solution for the given equation
Question 15.
$4.10 = $6.25 – y y = $2.15, $2.95, $3.05, $3.15
Answer:
The given equation is:
$4.10 = $6.25 – y
Now,
$4.10 = $6.25 – y
y = $6.25 – $4.10
y = $2.15
Hence, from the above,
We can conclude that
y = $2.15 is the solution for the given equation
Question 16.
24 ÷ h = 6 h = 1, 3, 6, 8
Answer:
The given equation is:
24 ÷ h = 6
Now,
24 ÷ h = 6
h = \(\frac{24}{6}\)
h = 4
Hence, from the above,
We can conclude that
There is not any solution from the given values for the given equation
Question 17.
In the past, Marcie’s father rode his bike 108 miles in 7.5 hours. Her mother rode the same distance in 8 hours. Marcie plans to ride her bike 108 miles at a steady rate of 18 mph for y hours. Will she match her father’s or mother’s time? Use the equation 108 ÷ y = 18 to justify your answer.
Answer:
It is given that
In the past, Marcie’s father rode his bike 108 miles in 7.5 hours. Her mother rode the same distance in 8 hours. Marcie plans to ride her bike 108 miles at a steady rate of 18 mph for y hours.
Now,
We know that,
Speed = \(\frac{Distance}{Time}\)
Time = \(\frac{Distance}{Speed}\)
So,
According to the given information,
The time took for Marcie to ride her bike at a steady rate (t) = (The distance rode by Marcie) ÷ (The speed of Marcie’s bike)
= 108 ÷ 18
= 6 hours
Now,
From the given information,
The time took for Marcie’s father to ride his bike is: 7.5 hours
The time took for Marcie’s mother to ride her bike is: 8 hours
So,
6 ≠ 7.5 ≠ 8
Hence, from the above,
We can conclude that
Marcie will not match her father’s or mother’s time
Question 18.
Write if b = 6 is a solution or is not a solution of each equation.
a. 8b = 48
b. 11 – b = 6
c. b + 3 = 9
d. 54 ÷ b = 9
Answer:
The given expression sare:
a. 8b = 48
b. 11 – b = 6
c. b + 3 = 9
d. 54 ÷ b = 9
Now,
a.
For b = 6,
8 (6) = 48
48 = 48
b.
For b = 6,
11 – 6 = 6
5 ≠ 6
c.
For b = 6,
6 + 3 = 9
9 = 9
d.
For b = 6,
54 ÷ 6 = 9
9 = 9
Hence, from the above,
We can conclude that
The equations that have a solution b = 6 are:
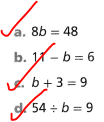
Question 19.
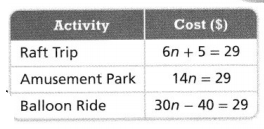
A group of 4 friends is planning a fun day trip. The equations in the table represent the number of people n who can participate in each activity for $29.

Which activity should the friends choose if they want to spend exactly $29?
Answer:
It is given that
A group of 4 friends is planning a fun day trip. The equations in the table represent the number of people n who can participate in each activity for $29.
Now,
The given table is:
Now,
For the friends to choose an activity so as they spend exactly $29,
The solutions of the variables should satisfy their own equations
Now,
a. For the Raft Trip activity:
The given equation is:
6n + 5 = 29
6n = 29 – 5
6n = 24
n = \(\frac{24}{6}\)
n = 4
Verification:
6 (4) + 5 = 29
24 + 5 = 29
29 = 29
b. For the Amusement park Trip activity:
The given equation is:
14n = 29
n = \(\frac{29}{14}\)
n = 2.07
n ≅ 2
Verification:
14 (2) = 29
28 ≠ 29
c. For the Balloon Ride activity:
30n – 40 = 29
30n = 20 + 49
30n = 69
n = \(\frac{69}{30}\)
n = \(\frac{23}{10}\)
n = 2.3
n ≅ 2
Verification:
30 (2) – 40 = 29
60 – 40 = 29
20 ≠ 29
Hence, from the above,
We can conclude that
The activity the friends should choose if they want to spend exactly $29 is: Raft Trip
Question 20.
There are 27 pennies on one pan of a pan balance and 18 pennies on the other. To make the pans balance, Hillary thinks 5 pennies should be added to the higher pan. Sean thinks 8 pennies should be added, and Rachel thinks 9 pennies should be added. Use the equation 27 = 18 + p to determine who is correct.
Answer:
It is given that
There are 27 pennies on one pan of a pan balance and 18 pennies on the other. To make the pans balance, Hillary thinks 5 pennies should be added to the higher pan. Sean thinks 8 pennies should be added, and Rachel thinks 9 pennies should be added
Now,
Let the nuber of pennies added be: p
Now,
The given equation in the problem that represents the situation is:
27 = 18 + p
So,
On the basis of the given information,
According to Hillary, p = 5
According to Sean, p = 8
According to Rachel, p = 9
Now,
For p = 5,
27 = 18 + p
27 = 18 + 5
27 ≠ 23
Now,
For p = 8,
27 = 18 + p
27 = 18 + 8
27 ≠ 26
Now,
For p = 9,
27 = 18 + p
27 = 18 + 9
27 = 27
Hence, from the above,
We can conclude that
Rachel is correct
Question 21.
Construct Arguments Gerard spent $5.12 for a drink and a sandwich. His drink cost $1.30. Did he have a ham sandwich for $3.54, a tuna sandwich for $3.82, or a turkey sandwich for $3.92? Use the equation s + 1.30 = 5.12 to justify your answer.
Answer:
It is given that
Gerard spent $5.12 for a drink and a sandwich. His drink cost $1.30
Now,
Let the cost of sandwich be: $s
So,
According to the given information,
$5.12 = s + $1.30
Subtract $1.30 on both sides
So,
$5.12 – $1.30 = s + $1.30 – $1.30
s = $3.82
Now,
According to the given information,
The cost of tuna sandwich is: $3.82
Hence, from the above,
We can conclude that
Gerard will have a tuna sandwich
Question 22.
Higher Order Thinking Write an equation that has a solution of 12. Show how you know that 12 is the solution.
Answer:
Let the equation that has a solution of 12 be:
6x = 72
Now,
We know that,
To find whether the solution is correct or not, substitute the solution in the place of the variable present in that equation and if LHS = RHS, then that solution is true for the equation
So,
The equation is: 6x = 72
Now,
Substitute 12 in place of x
So,
6 (12) = 72
Hence,
72 = 72
Question 23.
Gina’s family is driving 255 miles to visit Tallahassee. After driving for a while, they pass a sign that reads “Tallahassee: 124 miles.” Substitute the values m = 111, 121, 131, and 141 in the equation 255 – m = 124 to find the number of miles the family has already driven.
Answer:
It is given that
Gina’s family is driving 255 miles to visit Tallahassee. After driving for a while, they pass a sign that reads “Tallahassee: 124 miles.”
Now,
The given equation to represent the number of miles the Gina’s family has already driven is:
255 – m = 124 with m = 111, 121, 131, and 141
Now,
For m = 111,
255 – m = 124
255 – 111 = 124
144 ≠ 124
Now,,
For m = 121,
255 – m = 124
255 – 121 = 124
134 ≠ 124
Now,
For m = 131,
255 – m = 124
255 – 131 = 124
124 = 124
Now,
For m = 141,
255 – m = 124
255 – 141 = 124
114 ≠ 124
Hence, from the above,
We can conclude that
The number of miles the Gina’s family has already driven is: 131 miles
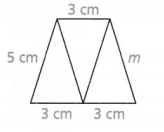
Question 24.
Lisa is making a quilt that uses a pattern of triangles like the one shown. Write an equation that represents the missing side length if the perimeter is 19 centimeters
Answer:
It is given that
Lisa is making a quilt that uses a pattern of triangles like the one shown
Now,
The given figure is:

Now,
We know that,
The “Perimeter” of a figure is the sum of all the side lengths of a figure
So,
For the given figure,
Perimeter = 5 + (3 + 3) + m + 3
19 = 5 + 6 + m + 3
19 = 14 + m
m = 19 – 14
m = 5 cm
Hence, from the above,
We can conclude that
The missing side length is: 5 cm
Question 25.
Alisa’s family planted 7 palm trees in their yard. The park down the street has 147 palm trees. Alisa guessed that the park has either 11 or 31 times as many palm trees as her yard has. Is either of Alisa’s guesses correct? Use the equation 7n = 147 to justify your answer.
Answer:
It is given that
Alisa’s family planted 7 palm trees in their yard. The park down the street has 147 palm trees. Alisa guessed that the park has either 11 or 31 times as many palm trees as her yard has.
Now,
The equation that represents the given information that is given in the problem is:
7n = 147
So,
n = \(\frac{147}{7}\)
n = 21 palm trees
But,
According to the given information,
Alisa had guessed that the park has either 11 or 31 times as many palm trees as her yard has
Hence, from the above,
We can conclude that
Alisa’s guesses are not correct
Assessment Practice
Question 26.
Trish has $26.00 to spend at a craft store. She buys fabric that costs $18.62. She also wants to buy knitting needles for $7.32, silk flowers for $7.38, or oil paints for $8.48.
Use the equation $18.62 + c = $26.00, where c is the item cost, to find the most expensive item Trish can buy Explain how you found your answer.
Answer:
It is given that
Trish has $26.00 to spend at a craft store. She buys fabric that costs $18.62. She also wants to buy knitting needles for $7.32, silk flowers for $7.38, or oil paints for $8.48.
Now,
The equation that represents the given information and is mentioned in the problem is:
$18.62 + c = $26.00
So,
c = $26.00 – $18.62
c = $7.38
So,
Trish can buy silk flowers with her balance
Hence, from the above,
We can conclude that
The most expensive item Trish can buy with the remaining amount of money is: Silk flowers
Lesson 4.2 Apply Properties of Equality
Solve & Discuss It!
Start with the equation 4 + 8 = 12 and complete each computation listed below. Do each computation individually. Which of the computations keeps the equation true? Explain.
I can… use the properties of equality to write equivalent equations.

Answer:
The given equation is:
4 + 8 = 12
Now,
We know that,
The equation will be true only when the equations’s
LHS = RHS
Now,
The completed table with the individual computations and the result as “True” and “False” is:

Hence, from the above,
We can conclude that
The computations that keep the equation true are:
a. Add 5 to both sides of the equation
b. Subtract 4 from both sides of the equation
Reasoning
How can you determine whether an equation is true?
Answer:
From above,
The completed table is:

Now,
We know that,
According to the Properties of Equality,
In an equation,
The operation we performed with the given number on the left side of the equation will be as the same as the operation we performed with the same number on the right side of the equation
So,
From the completed table,
Only 2 computations follows the “Properties of equality”
Hence, from the above,
We can conclude that
We can determine the equation by using the “Properties of equality”
Focus on math practices
Use Structure Complete the equation 7 + ☐ = 10 – ☐ by filling in the missing numbers. Describe at least two other operations with numbers that you can do to each side of the completed equation to keep it true.
Answer:
Let the missing number on the left side and right side of the given equation be: x
Now,
We know that,
According to the Properties of Equality,
In an equation,
The operation we performed with the given number on the left side of the equation will be as the same as the operation we performed with the same number on the right side of the equation
So,
7 + x = 10 – x
x + x = 10 – 7
2x = 3
x = \(\frac{3}{2}\)
x = 1.5
Hence, from the above,
We can conclude that
The completed equation is:
![]()
Essential Question
How can you use the properties of equality to write equivalent equations?
Answer:
Just as you can add or subtract the same exact quantity on both sides of an equation, you can also multiply both sides of an equation by the same quantity to write an equivalent equation.
Try It!
If 5y = 25, which property of equality was used to keep the equation 5y – 7 = 25 – 7 equal?
Answer:
The given equation is:
5y = 25
Now,
We know that,
The “Subtraction Property of equality” states that when you subtract the same amount from both sides of an equation, the two sides of the equation stay equal
So,
According to the above property,
5y = 25 changed into 5y – 7 = 25 – 7
Hence, from the above,
We can conclude that
The “Subtraction Property of Equality” was used to keep the equation 5y – 7 = 25 – 7 equal
Convince Me! What other properties of equality could you apply to keep the equation 5y = 25 equal? Give an example of each.
The given equation is:
5y = 25
Now,
We know that,
We can use any “Property of Equality” like “Addition Property of equality”, “Subtraction Property of equality” , “Multiplication Property of equality”, and “Division Property of equality” to keep the given equation true
Hence, from the above,
We can conclude that
The other properties of equality you could apply to keep the equation 5y = 25 equal are:
a. Addition Property of equality
b. Multiplication Property of equality
c. Division Property of equality
Try It!
A. A scale balances with four blue x-blocks on one side and 36 green blocks on the other side. Complete the equation to balance the scale with only one blue x-block.
4 • x = 36
(4 • x) ÷ ☐ = 36 ÷ ☐
x = 9
Answer:
It is given that
A scale balances with four blue x-blocks on one side and 36 green blocks on the other side.
Now,
According to the given information,
To balance the equation with only one blue x-block,
Divide the both sides of the given equation by 4 so that only one blue x rock will be present
So,
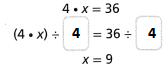
Hence, from the above,
We can conclude that
The number of blue x-rocks are: 9 blue x-rocks
B. If 25 + d = 36, does 25 + d – 25 = 36 – 20? Explain.
Answer:
The given equations are: 25 + d = 36 and 25 + d – 25 = 36 – 20
Now,
We know that,
The “Subtraction Property of equality” states that when you subtract the same amount from both sides of an equation, the two sides of the equation stay equal
So,
For 25+ d = 36,
According to the given second equation,
25 + d – 25 = 36 – 25
Hence, from the above,
We can conclude that
If 25 +d = 36, then 25 + d – 25 = 36 – 25
KEY CONCEPT
You can use the properties of equality to write equivalent equations.
Addition Property of Equality
7 + 3 = 10
(7 + 3) + a = 10 + a
Add the same amount to each side to keep the equation balanced.
Subtraction Property of Equality
7 + 3 = 10
(7 + 3) – a = 10 – a
Subtract the same amount from each side to keep the equation balanced.
Multiplication Property of Equality
7 + 3 = 10
(7 + 3) × a = 10 × a
Multiply each side of the equation by the same amount to keep the equation balanced.
Division Property of Equality
7+ 3 = 10
(7 + 3) ÷ a = 10 ÷ a
Divide each side of the equation by the same non-zero amount to keep the equation balanced.
Do You Understand?
Question 1.
Essential Question How can you use the properties of equality to write equivalent equations?
Answer:
Just as you can add or subtract the same exact quantity on both sides of an equation, you can also multiply both sides of an equation by the same quantity to write an equivalent equation.
Question 2.
A pan balance shows 7 + 5 = 12. If 4 units are removed from one side, what needs to be done to the other side to keep the pans balanced?
Answer:
It is given that
A pan balance shows 7 + 5 = 12. and 4 units are removed from one side
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
So,
To keeps the pans balanced, we have to remove 4 from the other side also
Hence, from the above,
We can conclude that
We have to remove 4 from other side also to keep the pans balanced
Question 3.
If one side of the equation 23 + 43 = 66 is multiplied by 3, what needs to be done to the other side of the equation to keep the sides equal?
Answer:
It is given that
One side of the equation 23 + 43 = 66 is multiplied by 3
Now,
We know that,
According to the “Multiplication Property of Equality”,
Multiply the same amount from each side to keep the equation balanced.
So,
To keeps the pans balanced, we have to multiply 3 to the other side also
Hence, from the above,
We can conclude that
We have to multiply 3 to the other side also to keep the pans balanced
Question 4.
Reasoning If one side of the equation x + 5 = 8 has 9 added to it and the other side has (4 + 5) added to it, will the equation stay equal?
Answer:
It is given that
One side of the equation x + 5 = 8 has 9 added to it and the other side has (4 + 5) added to it
Now,
We know that,
According to the “Addition Property of Equality”,
Add the same amount from each side to keep the equation balanced.
Now,
We know that,
4 + 5 = 9
So,
The equation stays equal
Hence, from the above,
We can conclude that
The equation will stay equal even we added (4 + 5) to the other side of the equation
Do You Know How?
In 5 and 6, answer yes or no and explain why or why not.
Question 5.
If 23 + 37 = 60, does 23 + 37 + 9 = 60 + 9?
Answer:
The given equations are:
23 + 37 = 60 and 23 + 37 + 9 = 60 + 9
Now,
We know that,
According to the “Addition Property of Equality”,
Add the same amount from each side to keep the equation balanced.
So,
From the above equation,
We can observe that
9 is added to both sides
Hence, from the above,
We can conclude that
The given equation is true
Question 6.
If 16 + 1 = 17, does (16 + 1) – 1 = 17 – 2?
Answer:
The given equations are:
16 + 1 = 17 and (16 + 1) – 1 = 17 – 2
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
So,
From the above equation,
We can observe that
1 is subtracted from one side and 2 is subtracted from the other side
Hence, from the above,
We can conclude that
The given equation is false
Question 7.
Apply the Multiplication Property of Equality to write an equation equivalent to 7n = 28.
Answer:
The given equation is:
7n = 28
Now,
We know that,
According to the “Multiplication Property of Equality”,
Multiply the same amount from each side to keep the equation balanced.
Now,
Let the number be multiplied on both sides of the equation be 2
So,
According the Multiplication Property of Equality,
7n × 2 = 28 × 2
Hence, from the above,
We can conclude that
According to the Multiplication Property of equation,
The equation that is equivalent to the given equation is:
7n × 2 = 28 × 2
Question 8.
Critique Reasoning Tomas says that if one side of the equation 6m = 9 is divided by 2 and the other side is divided by 3, the equation will stay equal because the result will be 3m = 3. Is Tomas correct? Explain.
Answer:
It is given that
Tomas says that one side of the equation 6m = 9 is divided by 2 and the other side is divided by 3
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount from each side to keep the equation balanced.
So,
We have to divide the both sides of the equation by either only 2 or only 2 but not with 2 on one side and with 3 on other side
Hence,f rom the above,
We can conclude that
Tomas is not correct
Practice & Problem Solving
In 9-12, tell which property of equality was used.
Question 9.
5m + 4 = 19
5m + 4 – 3 = 19 – 3
Answer:
The given equations are:
5m + 4 = 19
5m + 4 – 3 = 19 – 3
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
So,
From the given equation,
We can observe that
We subtracted 3 on both sides
Hence, from the above,
We can conclude that
“Subtraction Property of Equality” was used for the given equation
Question 10.
3t = 20
3t ÷ 2 = 20 ÷ 2
Answer:
The given equations are:
3t = 20
3t ÷ 2 = 20 ÷ 2
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount at each side to keep the equation balanced.
So,
From the given equation,
We can observe that
We divided by 2 on both sides
Hence, from the above,
We can conclude that
“Division Property of Equality” was used for the given equation
Question 11.
\(\frac{n}{6}\) = 9
\(\left(\frac{n}{6}\right)\) × 5 = 9 × 5
Answer:
The given equations are:
\(\frac{n}{6}\) = 9
\(\frac{n}{6}\) × 5 = 9 × 5
Now,
We know that,
According to the “Multiplication Property of Equality”,
Multiply the same amount at each side to keep the equation balanced.
So,
From the given equation,
We can observe that
We multiplied 5 on both sides
Hence, from the above,
We can conclude that
“Multiplication Property of Equality” was used for the given equation
Question 12.
5b – 6 = 14
(5b – 6) + 2 = 14 + 2
Answer:
The given equations are:
5b – 6 = 14
(5b – 6) + 2 = 14 + 2
Now,
We know that,
According to the “Addition Property of Equality”,
Add the same amount at each side to keep the equation balanced.
So,
From the given equation,
We can observe that
We added 2 on both sides
Hence, from the above,
We can conclude that
“Addition Property of Equality” was used for the given equation
Question 13.
If r + 9 = 42, does r + 9 – 9 = 42 + 9? Why or why not?
Answer:
The given equations are:
r + 9 = 42
r + 9 – 9 = 42 + 9
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
So,
From the given equation,
We can observe that
We subtracted 9 from one side and added 9 at the other side
Hence, from the above,
We can conclude that
r + 9 = 42 is not the equivalent of r + 9 – 9 = 42 + 9
Question 14.
If 6s = 24, does 6s ÷ 6 = 24 ÷ 6? Why or why not?
Answer:
The given equations are:
6s = 24
6s ÷ 6 = 24 ÷ 6
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount at each side to keep the equation balanced.
So,
From the given equation,
We can observe that
We divided with 6 on both sides
Hence, from the above,
We can conclude that
6s = 24 is the equivalent of 6s ÷ 6 = 24 ÷ 6
Question 15.
This scale was balanced. Find the number to add that makes the scale become balanced again. Then complete the equation to make it true.

Answer:
It is given that
This scale was balanced
Now,
The given figure is:

Now,
From the given figure,
We can observe that
To make the scale balanced again,
We have to add some quantity to 12 on the left side of the pan
Now,
Let the some quantity that is added on the left side of the pan be x
So,
To make the scale balanced,
12 + x = 2 + 7+ 3 + 16
So,
12 + x = 28
Subtract with 12 on both sides
12 + x – 12 = 28 – 12
x = 28 – 12
x = 16
Hence, from the above,
We can conclude that
The completed equation so that the equation is true is:
![]()
Question 16.
This scale balanced with 3 green blocks on one side and 1 blue x-block on the other side. Find the number to multiply by that makes the scale balance. Then complete the equation to make it true.

Answer:
It is given that
This scale balanced with 3 green blocks on one side and 1 blue x-block on the other side
Now,
The given figure is:

Now,
From the given information,
The equation that represents the given situation is:
1x = 3
So,
x = 3
Now,
Multiply both sides with 5
So,
5 × x = 3 × 5
5x = 15
15 = 5x
Hence, from the above,
We can conclude that
The completed equation so that the equation will be true is:
![]()
Question 17.
You start with the equation 8x = 24. Your friend changes the equation as follows.
8x = 24 ÷ 4
How can you make your friend’s equation equivalent to the original equation?
Answer:
The given equations are:
8x = 24
8x = 24 ÷ 4
Now,
From the above equation,
We can observe that
Your friend wants to change the equation by dividing the equation by 4
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount at each side to keep the equation balanced.
So,
For the given equation,
We have to divide by 4 on both sides instead of only one side like your friend
So,
8x ÷ 4 = 24 ÷ 4
Hence, from the above,
We can conclude that
The representation of your friend’s equation equivalent to the original given equation is:
8x ÷ 4 = 24 ÷ 4
Question 18.
A scale balanced with 1 blue x-block and 20 green blocks on the left side and 40 green blocks on the right side. A student bumped into the scale and knocked some blocks off so that only 1 blue x-block and 3 green blocks remained on the left side. How many blocks do you need to remove from the right side to make the scale balance?
Answer:
It is given that
A scale balanced with 1 blue x-block and 20 green blocks on the left side and 40 green blocks on the right side. A student bumped into the scale and knocked some blocks off so that only 1 blue x-block and 3 green blocks remained on the left side
So,
According to the given information,
Now,
Before a student bumped into the scale,
The representation of the equation is:
1x blue rocks + 20 green rocks = 40 green rocks
x blue rocks + 20 green rocks = 40 green rocks
Now,
After a student bumped into the scale,
x blue rocks + 20 green rocks – 0 blue rocks – 17 green rocks = 40 green rocks – x
Where,
x is the variable to make the equation balanced
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
So,
x blue rocks + 20 green rocks – 0 blue rocks – 17 green rocks = 40 green rocks – 0 blue rocks – 17 green rocks
Hence, from the above,
We can conclude that
The number of blocks you needed to remove from the right side to make the scale balance is: 17 green rocks
Question 19.
Bobbie wrote y + 6 = 15. Then she wrote (y + 6) ÷ 3 = 15. Explain why the second equation is not equivalent to the first. What can Bobbie do to make the two equations equivalent?
Answer:
It is given that
Bobbie wrote y + 6 = 15. Then she wrote (y + 6) ÷ 3 = 15
Now,
The given equations are:
y + 6 = 15
(y + 6) ÷ 3 = 15
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount at each side to keep the equation balanced.
So,
From the given equation,
We can observe that
We have to divide by 3 on both sides
But,
According to the second equation,
It has been divided only on the left side
So,
(y + 6) ÷ 3 ≠ 15
Hence, from the above,
We can conclude that
Due to the “Division Property of Equality”,
(y + 6) ÷ 3 ≠ 15
Question 20.
Construct Arguments John wrote that 5 + 5 = 10. Then he wrote that 5 + 5 + n = 10 + n. Are the equations John wrote equivalent? Explain.
Answer:
It is given that
John wrote that 5 + 5 = 10. Then he wrote that 5 + 5 + n = 10 + n
Now,
The given equations are:
5 + 5 = 10
5 + 5 + n = 10 + n
Now,
We know that,
According to the “Addition Property of Equality”,
Add the same amount at each side to keep the equation balanced.
So,
From the given equation,
We can observe that
John added n at both sides
So,
5 + 5 = 10 is equivalent to 5 + 5 + n = 10 + n
Hence, from the above,
We can conclude that
Due to the Addition Property of Equality,
5 + 5 = 10 is equivalent to 5 + 5 + n = 10 + n
Question 21.
Reasoning Scientists often use a pan balance to measure mass when doing experiments. The equation 4 + 3 – 1 = 7 – 1 represents a scientist taking away one unit of mass from each side of a pan balance. Construct an argument to explain how the scientist knows that the pans are still in balance.
Answer:
It is given that
Scientists often use a pan balance to measure mass when doing experiments. The equation 4 + 3 – 1 = 7 – 1 represents a scientist taking away one unit of mass from each side of a pan balance.
Now,
The given expression is:
4 + 3 – 1 = 7 – 1
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
So,
From the given equation,
We can observe that
1 is subtracted from both sides of the equation
So,
The pans are still in balance according to “Subtraction Property of Equality”
Hence, from the above,
We can conclude that
The pans are still in balance according to “Subtraction Property of Equality”
Question 22.
Bryce wrote the equation n – 3 = 4. Lexi used a property of equality to write an equivalent equation. Write an equation Lexi could have written. Explain how you know the equations are equivalent.
Answer:
It is given that
Bryce wrote the equation n – 3 = 4. Lexi used a property of equality to write an equivalent equation
Now,
The given equation is:
n – 3 = 4
Now,
We know that,
According to the “Addition Property of Equality”,
Add the same amount at each side to keep the equation balanced.
So,
n – 3 + 3 = 4 + 3
n = 7
So,
The equivalent equation of the given equation is: n = 7
Hence, from the above,
We can conclude that
The equation Lexi could have written is: n = 7
The equation swritten by Bryce and Lexi are equivalent by using the “Additie Property of Equality”
Question 23.
Higher Order Thinking Emil has $1 and a quarter. Jade has 5 quarters. If Emil gives Jade $1 and Jade gives Emil 4 quarters, will they each still have the same amount of money? Explain.

Answer:
It is given that
Emil has $1 and a quarter. Jade has 5 quarters and Emil gives Jade $1 and Jade gives Emil 4 quarters
Now,
We know that,
1 Quarter = $0.25
Now,
The amount of money Emil contains = $1 + $0.25
= $1.25
The amount of money Jade contains = 5 × $0.25
= $1.25
Now,
If Emil gives Jade $1, then
The amount of money Jade contains = $1.25 + $1
= $2.25
The remaining amount of money Emil contains = $1.25 – $1
= $0.25
If Jade gives 4 Quarters to Emil, then
The amount of money Emil contains = $0.25 + 4 × $0.25
= $0.25 + $1
= $1.25
Hence, from the above,
We can conclude that
Emil and Jade each still have the same amount of money
Question 24.
Vocabulary If 7w = 49, which property of equality was used to find the equivalent equation 7w ÷ 7 = 49 ÷ 7?
Answer:
The given equations are:
7w = 49
7w ÷ 7 = 49 ÷ 7
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount at each side to keep the equation balanced.
So,
From the given equation,
We can observe that
7 is divided on both sides
Hence, from the above,
We can conclude that
“Division Property of Equality” was used to find the equivalent equation of the given equation 7w ÷ 7 = 49 ÷ 7
Question 25.
You start with the equation 12b = 24. What step should you take to find the quantity that equals 4b?
Answer:
The given equation is:
12b = 24
Now,
It is given that
After using the “Equality Property”, we have to make 12b as 4b
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount at each side to keep the equation balanced.
So,
Divide the given equation by 3 on both sides
So,
\(\frac{12b}{3}\) = \(\frac{24}{3}\)
4b = 8
Hence, from the above,
We can conclude that
To find the quantity “4b”,
We have to use “Division Property of Equality” for the given equation
Assessment Practice
Question 26.
Which equation is equivalent to n + 4 = 11?.
A. (n + 4) × 2 = 11
B. (n + 4) × 2 = 11 ÷ 2
C. (n + 4) × 2 = 11 × 4
D (n + 4) × 2 = 11 × 2
Answer:
The given equation is:
n + 4 = 11
Now.
We know that,
According to the “Properties of Equality”,
The operation we are doing at the left side will be the same as the operation we are doing at the right side
Hence, from the above,
We can conclude that
The equation that is equivalent to n + 4 = 11 is:

Question 27.
Which of the equations is NOT equivalent to 8p = 12? Select all that apply.
☐ 8p ÷ 8 = 12 ÷ 8
☐ 8p ÷ 8 = 12 ÷ 12
☐ 8p + 4 = 12 + 4
☐ 8p – 2 = 12 – 2
☐ 8p × 8 = 12 × 12
Answer:
The given equation is:
8p = 12
Now.
We know that,
According to the “Properties of Equality”,
The operation we are doing at the left side will be the same as the operation we are doing at the right side
Hence, from the above,
We can conclude that
The equations that are not equivalent to 8p = 12 are:

Lesson 4.3 Write and Solve Addition and Subtraction Equations
Solve & Discuss It!
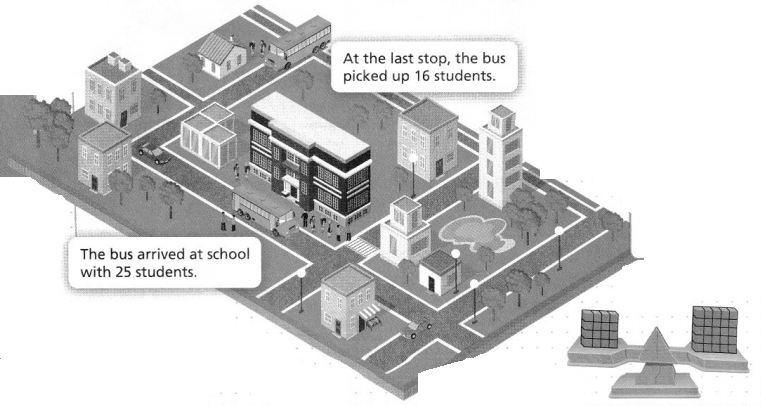
A group of students were on a school bus. How many students were on the bus before the last stop?
I can… write and solve an addition or subtraction equation.
Use Appropriate Tools
You use a pan balance to help solve for the unknown.
Answer:
It is given that
A group of students were on a school bus
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The total number of students arrived at school = (The total number of students present on the bus before the last stop) + (The total number of students present on the bus at the last stop)
Now,
Let the total number of students present on the bus before the last stop be x
So,
25 = x + 16
x = 25 – 16
x = 9 students
Hence, from the above,
We can conclude that
The total number of students present on the bus before the last stop is: 9 students
Focus on math practices
Reasoning How does using cubes on the pan balance demonstrate the Addition and Subtraction Properties of Equality?
Answer:
In the pan balance,
The cubes represent the variables
Remember that the pans must be in a balanced position and it is represented by “=”
Ex:
In a pan balance,
At one side, 3x cubes are present
At other side, 2x cubes are present
So,
The balanced pan will be:
3x = 2x
Ex:
In a pan balance,
At one side, 10x cubes are added
At other side, 25x cubes are added and later, 6x quantities are removed
So,
The balance pan will be:
10x = 25x – 6x
Essential Question
How can you write and solve an addition or subtraction equation?
Answer:
a.
To write a proper addition equation, you have an equals sign. One side shows you the total. The other side shows you what things are being added together. You can have a variable on either side of the equation
b.
When we write a subtraction equation, we use two symbols: – and =. The minus sign (-) means one thing is being subtracted from another
Try It!
Cabrini had some markers. After she bought 12 more markers, she had 16. How many markers did Cabrini have at the start?
Let n represent the number of markers Cabrini had at the start.
Solve the addition equation.
n + 12 = 16
n + 12 ___ = 16 ____
n = _____
Cabrini had ______ markers at the start.
Answer:
It is given that
Cabrini had some markers. After she bought 12 more markers, she had 16
Now,
Let the number of markers Cabrini had before she bought more markers be: x
So,
According to the given information,
The equation will be:
x + 12 = 16
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
So,
Subtract 12 from both sides in the given equation
So,
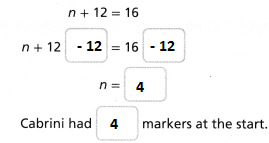
Hence, from the above,
We can conclude that
Cabrini had 4 markers at the start
Convince Me! Which property of equality is used to solve the equation n + 12 = 16? Could one of the other properties of equality have also been used? Explain.
The given equation is:
n + 12 = 16
Now,
To solve the above equation,
The property of equality we used is “Subtraction Property of Equality”
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
Now,
We know that,
If we observe the above equation,
We can say that,
We can use other “Properties of Equality” like “Addition Property of Equality”, “Multiplication Property of Equality”, and “Division Property of Equality”
Hence, from the above,
We can conclude that
We used “Subtraction Property of Equality” to solve the given equation n + 12 = 16
The other properties of equality can also be used to solve the given equation n + 12 = 16
Try It!
Vivian read 14 fewer pages than she was assigned to read. She read 60 pages. Write and solve an equation to find how many pages, p, Vivian was assigned to read.
Answer:
It is given that
Vivian read 14 fewer pages than she was assigned to read. She read 60 pages.
Now,
Let the number of pages Vivian was assigned to read be: x pages
Now,
According to the given information,
The equation that represents the given situation is:
x – 14 = 60
Now,
We know that,
According to the “Addition Property of Equality”,
Add the same amount at each side to keep the equation balanced.
So,
Add 14 on both sides to the given equation
So,
x – 14 + 14 = 60 + 14
x = 74 pages
Hence, from the above,
We can conclude that
The number of pages Vivian was assigned to read is: 74 pages
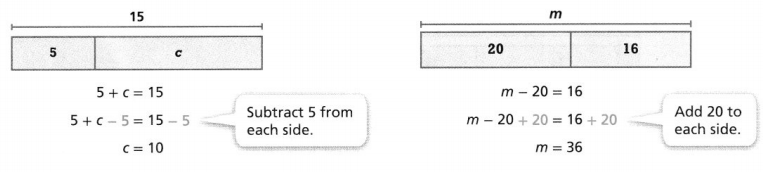
KEY CONCEPT
You can use inverse relationships and the properties of equality to solve equations.
Do You Understand?
Question 1.
Essential Question How can you write and solve an addition or subtraction equation?
Answer:
a.
To write a proper addition equation, you have an equals sign. One side shows you the total. The other side shows you what things are being added together. You can have a variable on either side of the equation
b.
When we write a subtraction equation, we use two symbols: – and =. The minus sign (-) means one thing is being subtracted from another
Question 2.
Explain how you can use the inverse relationship of addition and subtraction to solve the equation n + 7 = 25.
Answer:
The given equation is:
n + 7 = 25
Now,
We know that,
Addition and subtraction are inverse operations because one operation can “undo” the other operation
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
Now,
subtract 7 from both sides
So,
n + 7 – 7 = 25 – 7
n = 18
Hence, from the above,
We can conclude that
The value of n for the given equation is: 18
Question 3.
Model with Math Clare had t seashells. After she bought 8 more seashells, she had 24 seashells. Write and solve an equation to find the number of seashells Clare started with.
Answer:
It is given that
Clare had t seashells. After she bought 8 more seashells, she had 24 seashells.
So,
The number of seashells = (The number of seashells Clare had at the start) + (The number of seashells she bought after the start)
24 = t + 8
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
Now,
subtract 8 from both sides
So,
24 – 8 = t + 8 – 8
t = 16 seashells
Hence, from the above,
We can conclude that
The number of seashells Clare had at the start is: 16 seashells
Question 4.
Model with Math The outside temperature dropped 20°F from the time Arianna ate breakfast until the time she ate dinner. When she ate dinner the temperature was 35°F. Write and solve an equation to find the outside temperature t when Arianna ate breakfast.
Answer:
It is given that
The outside temperature dropped 20°F from the time Arianna ate breakfast until the time she ate dinner. When she ate dinner the temperature was 35°F
So,
The outside temperature from the time Arianna ate breakfast until the time she ate dinner = (The outside temperature when Arianna ate breakfast) + (The outside temperature when Arianna ate dinner)
20° F = x° F + 35° F
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from each side to keep the equation balanced.
Now,
subtract 35° F from both sides
So,
20° F – 35° F = x° F + 35° F – 35° F
x° F = – 15° F
Hence, from above,
We can conclude that
The outside temperature when Arianna ate breakfast is: -15° F
Do You Know How?
In 5-10, solve each equation.
Question 5.
24 + m = 49
Answer:
The given equation is:
24 + m = 49
Now,
Subtract with 24 on both sides
So,
24 + m – 24 = 49 – 24
m = 25
Hence, from the above,
We can conclude that
The value of m is: 25
Question 6.
12 = y – 11
Answer:
The given equation is:
12 = y – 11
Now,
Add 11 on both sides
So,
12 + 11 = y – 11 + 11
y = 23
Hence, from the above,
We can conclude that
The value of y is: 23
Question 7.
22 = 13 + a
Answer:
The givene quation is:
22 = 13 + a
Now,
Subtract 13 on both sides
So,
22 – 13 = 13 + a – 13
a = 9
Hence, from the above,
We can conclude that
The value of a is: 9
Question 8.
t – 40 = 3
Answer:
The given equation is:
t – 40 = 3
Now,
Add 40 on both sides
So,
t – 40 + 40 = 3 + 40
t = 43
Hence, from the above,
We can conclude that
The value of t is: 43
Question 9.
d + 11 = 15
Answer:
The given equation is:
d + 11 = 15
Now,
Subtract 11 on both sides
So,
d + 11 – 11 = 15 – 11
d = 4
Hence, from the above,
We can conclude that
The value of d is: 4
Question 10.
32 = s – 19
Answer:
The given equation is:
32 = s – 19
Now,
Add 19 on both sides
So,
32 + 19 = s – 19 + 19
s = 51
Hence, from the above,
We can conclude that
The value of s is: 51
Practice & Problem Solving
Leveled Practice
In 11-16, solve each equation.
Question 11.
y – 12 = 89
y – 12 + _____ = 89 + 12
y = ______
Answer:
The given equation is:
y – 12 = 89
Now,
Add 12 on both sides
So,
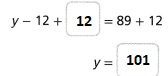
Hence, from the above,
We can conclude that
The value of y is: 101
Question 12.
80 + r = 160
80 + r – ______ = 160 – ______
r = ______
Answer:
The given equation is:
80 + r = 160
Now,
Subtract 80 on both sides
So,
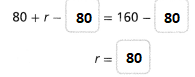
Hence, from the above,
We can conclude that
The value of r is: 80
Question 13.
60 = x – 16
60 + ______ = x – 16 + ______
______ = x
Answer:
The given equation is:
60 = x – 16
Now,
Add 16 on both sides
So,
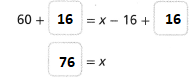
Hence, from the above,
We can conclude that
The value of x is: 76
Question 14.
20 = y + 12
Answer:
The givene quation is:
20 = y + 12
Now,
Subtract 12 on both sides
So,
20 – 12 = y + 12 – 12
y = 8
Hence, from the above,
We can conclude that
The value of y is: 8
Question 15.
x + 2 = 19
Answer:
The given equation is:
x + 2 = 19
Now,
Subtract 2 on both sides
So,
x + 2 – 2 = 19 – 2
x = 17
Hence, from the above,
We can conclude that
The value of x is: 17
Question 16.
z – 313 = 176
Answer:
The given equation is:
z – 313 = 176
Now,
Add 313 on both sides
So,
z – 313 + 313 = 176 + 313
z = 489
Hence, from the above,
We can conclude that
The value of z is: 489
Question 17.
You have some baseball trading cards. You give 21 baseball cards to a friend and have 9 left for yourself. How many baseball cards were in your original deck? Write and solve an equation to find t, the number of baseball cards in your original deck.
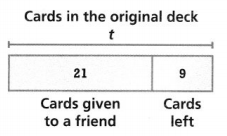
Answer:
It is given that
You have some baseball trading cards. You give 21 baseball cards to a friend and have 9 left for yourself
Now,
The representation of the given information in the form of a bar diagram is:

Now,
From the given bar diagram,
We can observe that
(The total number of baseball trading cards) – (The number of baseball cards you have given to your friend) = (The number of baseball cards you have left)
So,
t – 21 = 9
Now,
Add 21 on both sides
So,
t – 21 + 21 = 9 + 21
t = 30
Hence, from the above,
We can conclude that
The total number of baseball trading cards in your original deck is: 30 cards
Question 18.
Model with Math Joy added 26 new contacts to her phone list. She now has a total of 100 contacts. Let c represent how many contacts Joy had on her phone list before she updated it. Write an equation and solve for c.
Answer:
It is given that
Joy added 26 new contacts to her phone list. She now has a total of 100 contacts. Let c represent how many contacts Joy had on her phone list before she updated it
Now,
According to the given information,
The representation of the equation for the given information is:
c + 26 = 100
Now,
Subtract 26 on both sides
So,
c + 26 – 26 = 100 – 26
c = 84 contacts
Hence, from the above,
We can conclude that
The number of contacts Joy had on her phone list before she updated is: 84 contacts
Question 19.
Reasoning Jeremy bought a sandwich and a drink that cost him $7. His drink cost $1.75. Solve the equation 7 = s + 1.75 to find s, the cost of Jeremy’s sandwich.
Answer:
It is given that
Jeremy bought a sandwich and a drink that cost him $7. His drink cost $1.75
Now,
Let s be the cost of Jeremy’s sandwich
So,
According to the given information,
The total cost pf a sandwich and a drink that Jeremy bought = (The cost of Jeremy’s sandwich) + (The cost of Jeremy’s drink)
$7 = s + $1.75
Now,
subtract $1.75 on both sides
So,
$7 – $1.75 = s + $1.25 – $1.25
s = $5.25
Hence, from the baove,
We can conclude that
The cost of Jeremy’s sandwich is: $5.25
Question 20.
A triathlon is about 51 Kilometers. One participant completed two of the three legs of the race and traveled 42 Kilometers. Solve the equation 42 + d = 51 for the distance, d, of the third leg of the race.

Answer:
It is given that
A triathlon is about 51 Kilometers. One participant completed two of the three legs of the race and traveled 42 Kilometers
Now,
The representation of the given information in the form of a bar diagram is:

Now,
The representation of the equation that represents the given information ad as given in the problem is:
42 + d = 51
Where,
d is the Distance of the third leg
Now,
Subtract 41 from both sides
So,
42 + d – 42 = 51 – 42
d = 9 Kilometers
Hence, from the above,
We can conclude that
The distance of the third leg of the race is: 9 Kilometers
Question 21.
What operation should be used to solve the equation 153 = 9 + 45? Solve the equation.
Answer:
The given equation is:
153 = 9 + 45
Now,
When we observe the equation,
There is “Addition” operation taking place in the given equation
Now,
We have to subtract the required number
Hence, from the above,
We can conclude that
The operation we should be used to solve the given equation 153 = 9 + 45 is: Subtraction
Question 22.
Higher Order Thinking In the equation 6 + 3y = 4y + 2 the variable y represents the same value. Is y = 2, 3, 4, or 5 the solution of this equation? Explain.
Answer:
It is given that
In the equation 6 + 3y = 4y + 2 the variable y represents the same value
Now,
The given equation is:
6 + 3y = 4y + 2
Now,
For y = 2:
6 + 3y = 4y + 2
6 + 3 (2) = 4 (2) + 2
6 + 6 = 8 + 2
12 ≠ 10
For y = 3:
6 + 3y = 4y + 2
6 + 3 (3) = 4 (3) + 2
6 + 9 = 12 + 2
15 ≠ 14
For y = 4;
6 + 3y = 4y + 2
6 + 3 (4) + 4 (4) + 2
6 + 12 = 16 + 2
18 = 18
For y = 5:
6 + 3y = 4y + 2
6 + 3 (5) = 4 (5) + 2
6 + 15 = 20 + 2
21 ≠ 22
Hence, from the above,
We can conclude that
y = 4 is the solution for the given equation
Question 23.
A traffic helicopter descends to hover 477 meters above the ground. Let h be the original height of the helicopter. What is a subtraction equation that represents the problem? What was the original height of the helicopter?
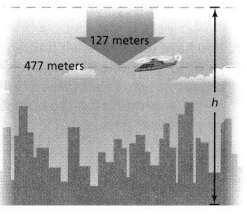
Answer:
It is given that
A traffic helicopter descends to hover 477 meters above the ground. Let h be the original height of the helicopter
Now,
The given figure is:

Now,
From the given figure,
We can observe that
(The original height of helicopter) + 127 m = 477 m
h – 127 = 477
Now,
Add 127 on both sides
So,
h + 127 – 127 = 477 + 127
h = 604 meters
Hence, from the above,
We can conclude that
The subtraction equation that represents the given problem is:
h – 127 = 477
The original height of the helicopter is: 604 meters
Question 24.
The drama club sold all the tickets for its annual production in three days. The club sold 143 tickets the first day and 295 tickets the second day. If the drama club sold 826 tickets, how many tickets were sold on the third day of sales? Solve the equation 438 + t = 826 for the number of tickets, t, sold on the third day of ticket sales.
Answer:
It is given that
The drama club sold all the tickets for its annual production in three days. The club sold 143 tickets the first day and 295 tickets the second day. If the drama club sold 826 tickets
So,
The total number of tickets sold by the drama club in two days = (The number of tickets sold on the first day) + (The number of tickets sold on the second day)
= 143 + 295
= 438 tickets
Now,
Let the number of tickets sold on third day be: t
So,
According to the given information,
The equation that represents the given information is:
438 + t = 826
Now,
Subtract 438 on both sides
So,
438 + t – 438 = 826 – 438
t = 388 tickets
Hence, from the above,
We can conclude that
The number of tickets sold on the third day of ticket sales is: 388 tickets
Question 25.
In a bag of mixed nuts, there are 35 almonds, 34 pecans, 32 walnuts, and p pistachios. The bag has a total of 134 nuts. Find the total number of almonds, pecans, and walnuts. Then write and solve an equation to find the number of pistachios in the bag.
Answer:
It is given that
In a bag of mixed nuts, there are 35 almonds, 34 pecans, 32 walnuts, and p pistachios. The bag has a total of 134 nuts
So,
The total number of almonds, pecans, and walnuts = 35 + 34 + 32
= 101
Now,
The total number of almonds, peacons, walnuts, and pistachios = (The total number of almond, pecans, and walnuts) + (The number of pistachios)
So,
134 = 101 + p
Now,
Subtract 101 on both sides
So,
134 – 101 = 101 + p – 101
p = 33
Hence, from the above,
We can conclude that
The number of pistachios in the bag is: 33 pistachios
Assessment Practice
Question 26.
Which equation has g = 6 as the solution?
A. g+ 2 = 10
B. 9- 1 = 10
C. 58 +9 = 60
D. 44 – g = 38
Answer:
The given equations are:
A. g+ 2 = 10
B. 9- 1 = 10
C. 58 +g = 60
D. 44 – g = 38
So,
A.
g + 2 = 10
g = 10 – 2
g = 8
B.
g – 1 = 10
g = 10 + 1
g = 11
C.
58 + g = 60
g = 60 – 58
g = 2
D.
44 – g = 38
g = 44- 38
g = 6
Hence, from the above,
We can conclude that
The equation that has g = 6 as the solution is:

Question 27.
Select all the equations that have the same solution as 36 = x + 32.
☐ 42 = 38 + x
☐ x + 15 = 19
☐ 18 = x – 2
☐ 36 = x – 32
☐ 52 – x = 46
Answer:
The given equation is:
36 = x + 32
So,
x = 36 – 32
x = 4
Now,
The given equations are:
A.
42 = 38 + x
x = 42 – 38
x = 4
B.
x + 15 = 19
x = 19 – 15
x = 4
C.
18 = x – 2
x = 18 + 2
x = 20
D.
36 = x – 32
x = 36 + 32
x = 68
E.
52 – x = 46
x = 52 – 46
x = 6
Hence, from the above,
We can conclude that
All the equations that have the same solution as 36 = x + 32 are:

Lesson 4.4 Write and Solve Multiplication and Division Equations
Solve & Discuss It!
A school group is planning a trip to New York City. There are 29 people going on the trip. They agreed to share the total cost of the trip equally. Let s equal each person’s share of the cost. What is each person’s share of the cost?
I can… write and solve a multiplication or division equation.
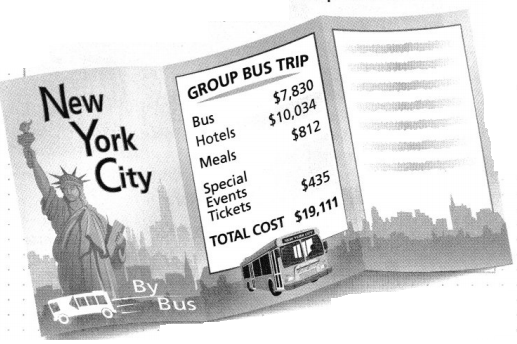
Answer:
It is given that
A school group is planning a trip to New York City. There are 29 people going on the trip. They agreed to share the total cost of the trip equally. Let s equal each person’s share of the cost
Now,
The given table is:
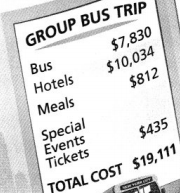
Now,
From the given table,
We can observe that
The total cost is: $19,111
So,
According to the given information,
(The total number of people going to a trip) × (The share of the cost of each person) = $19,111
29 × s = $19,111
s = \(\frac{$19,111}{29}\)
s = $659
Hence, from the above,
We can conclude that
Each person’s share of the cost is: $659
Generalize
How can you use what you know about dividing lesser numbers to write equations and solve problems involving greater numbers?
Answer:
Let a smaller faction be: \(\frac{a}{b}\)
Where,
a = 1, 2, ……… n
b = 1, 2, ……… n
Now,
When we divide lesser numbers say the lesser numbers only have 2 digits, then the quotient we will also get will be a small number
Now,
When we divide larger numbers say the larger numbers have 4 digits, then the quotient we will also get will be a large number with 3 (or) 4 digits
Focus on math practices
Construct Arguments Can you use the same strategy that you used above to find each person’s share of the hotel bill? Explain.
Answer:
Yes,
We can use the same strategy that you used above to find each person’s share of the hotel bill
Essential Question
How can you write and solve a multiplication or division equation?
Answer:
The steps to solve a multiplication or division problem is:
a. Always perform the same operation to both sides of the equation.
b. When you multiply or divide, you have to multiply and divide by the entire side of the equation.
c. Try to perform addition and subtraction first to get some multiple of x by itself on one side.
Try It!
Theresia picked the same number of tomatoes each day. In 4 days she picked 52 tomatoes. How many tomatoes did Theresia pick each day? Let n represent the number of tomatoes Theresia picked each day.
4n = 52
4n ÷ 4 = 52 ______
n = _______
Theresia picked _______ tomatoes each day.
Answer:
It is given that
Theresia picked the same number of tomatoes each day. In 4 days she picked 52 tomatoes
Now,
Let n represent the number of tomatoes Theresia picked each day.
So,
4 × (The number of tomatoes Theresia picked each day) = (The number of tomatoes Theresia picked in 4 days)
4 × n = 52
Now,
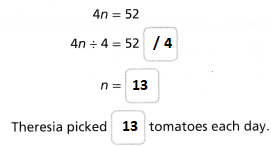
Hence, from the above,
We can conclude that
Theresia picked 13 tomatoes each day
Convince Me! Which property or equality can you use to solve Theresia’s equation? Explain.
Answer:
From the above problem,
The equation is:
4n = 52
Now,
To find the value of n (or) the number of tomatoes Theresia picked each day,
We have to use “Division Property of Equality”
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount to the equation to keep the equation balanced
Hence, from the above,
We can conclude that
We used the “Division Property of equality” to solve Theresia’s equation
Try It!
Meghann is reading a 630-page book. She reads 18 pages each day. Write and solve a division equation to find the number of days, d, it will take Meghann to finish her book.
Answer:
It is given that
Meghann is reading a 630-page book. She reads 18 pages each day
Now,
Let d be the number of days it will take Meghann to finish her book
Now,
(The number of pages Meghann reads each day) × (The number of days it will take Meghann to finish her book) = (The total number of pages in a book)
18 × d = 630
d = \(\frac{630}{18}\)
d = 35 days
Hence, from the above,
We can conclude that
It will take 35 days for Meghann to finish her 630-page book
KEY CONCEPT
You can multiply or divide both sides of an equation by the same number and it will remain balanced.

Do You Understand?
Question 1.
Essential Question How can you write and solve a multiplication or division equation?
Answer:
The steps to solve a multiplication or division problem is:
a. Always perform the same operation to both sides of the equation.
b. When you multiply or divide, you have to multiply and divide by the entire side of the equation.
c. Try to perform addition and subtraction first to get some multiple of x by itself on one side.
Question 2.
Which property of equality would you use to solve the equation 8n = 16?
Answer:
The given equation is:
8n = 16
Now,
Divide by 8 to find the value of n
So,
We have to use “Division Property of Equality”
Now,
We know that,
According to the “Division Property of Equality”,
Divide the same amount at each side to keep the equation balanced.
So,
\(\frac{8n}{8}\) = \(\frac{16}{8}\)
n = 2
Hence, from the above,
We can conclude that
You would use “Division Property of Equality” to solve the given equation 8n = 16
Question 3.
Which property of equality would you use to solve the equation a ÷ 9 = 2?
Answer:
The given equation is:
a ÷ 9 = 2
Now,
Multiply with 9 to find the value of ‘a’
So,
We have to use “Multiplication Property of Equality”
Now,
We know that,
According to the “Multiplication Property of Equality”,
Multiply the same amount at each side to keep the equation balanced.
So,
(a ÷ 9) × 9 = 2 × 9
a = 18
Hence, from the above,
We can conclude that
You would use “Multiplication Property of Equality” to solve the given equation a ÷ 9 = 2
Question 4.
There are 30 students in the drama club. They are carpooling in 5 vans to perform a play. They want each van to carry an equal number of students. Let s be the number of students in each van. Write and solve a multiplication equation to find the number of students in each van.
Answer:
It is given that
There are 30 students in the drama club. They are carpooling in 5 vans to perform a play. They want each van to carry an equal number of students.
Now,
Let s be the number of students in each van
So,
(The number of vans carpooling to perform a play) × (The number of students in each van) = (The total number of students in the drama club)
5 × s = 30
5s = 80
Now,
Divide by 5 on both sides
So,
\(\frac{5s}{5}\) = \(\frac{80}{5}\)
s = 16 students
Hence, from the above,
We can conclude that
The number of students in each van is: 16 students
Do You Know How?
In 5-8, explain how to solve each equation.
Question 5.
18m = 36
Answer:
The given equation is:
18m = 36
Now,
Divide the equation by 18 on both sides
So,
\(\frac{18m}{18}\) = \(\frac{36}{18}\)
m = 2
Hence, from the above,
We can conclude that
The value of m in the given equation is: 2
Question 6.
t ÷ 3 = 10
Answer:
The given equation is:
t ÷ 3 = 10
Now,
Multiply the equation with 3 on both sides
So,
(t ÷ 3) × 3 = 10 × 3
t = 30
Hence, from the above,
We can conclude that
The value of t in the given equation is: 30
Question 7.
12 = 2y
Answer:
The given equation is:
12 = 2y
Now,
Divide the equation by 2 on both sides
So,
\(\frac{12}{2}\) = \(\frac{2y}{2}\)
6 = y
y = 6
Hence, from the above,
We can conclude that
The value of y in the given equation is: 6
Question 8.
22 = a ÷ 5
Answer:
The given equation is:
22 = a ÷ 5
Now,
Multiply the equation with 5 on both sides
So,
22 × 5 = (a ÷ 5) × 5
a = 110
Hence, from the above,
We can conclude that
The value of a in the given equation is: 110
In 9-12, solve each equation.
Question 9.
23d = 2,392
Answer:
The given equation is:
23d = 2,392
Now,
Divide the given equation by 23 on both sides
So,
\(\frac{23d}{23}\) = \(\frac{2,392}{23}\)
d = 104
Hence, from the above,
We can conclude that
The value of d in the given equation is: 104
Question 10.
74f = 6,179
Answer:
The given equation is:
74f = 6,179
Now,
Divide the given equation by 74 on both sides
So,
\(\frac{74f}{74}\) = \(\frac{6,179}{74}\)
f = 83.5
Hence, from the above,
We can conclude that
The value of f in the given equation is: 83.5
Question 11.
y ÷ 11 = 987
Answer:
The given equation is:
y ÷ 11 = 987
Now,
Multiply the given equation with 11 on both sides
So,
(y ÷ 11) × 11 = 987 × 11
y = 10,857
Hence, from the above,
We can conclude that
The value of y in the given equation is: 10,857
Question 12.
r ÷ 187 = 9
Answer:
The given equation is:
r ÷ 187 = 9
Now,
Multiply the given equation with 187 on both sides
So,
(r ÷ 187) × 187 = 9 × 187
y = 1,683
Hence, from the above,
We can conclude that
The value of r in the given equation is: 1,683
Practice & Problem Solving
In 13-16, explain how to get the variable alone in each equation.
Question 13.
8y = 56
Answer:
The given equation is:
8y = 56
Now,
Divide the given equation with 8 on both sides
so,
\(\frac{8y}{8}\) = \(\frac{56}{8}\)
y = 7
Hence, from the above,
We can conclude that
The value of y for the given equation is: 7
Question 14.
t ÷ 15 = 3
Answer:
The given equation is:
t ÷ 15 = 3
Now,
Multiply the given equation with 15 on both sides
So,
(t ÷ 15) × 15 = 3 × 15
t = 45
Hence, from the above,
We can conclude that
The value of t for the given equation is: 45
Question 15.
u ÷ 8 = 12
Answer:
The given equation is:
u ÷ 8 = 12
Now,
Multiply the given equation with 8 on both sides
So,
(u ÷ 8) × 8 = 12 × 8
u = 96
Hence, from the above,
We can conclude that
The value of u for the given equation is: 96
Question 16.
31y = 310
Answer:
The given equation is:
31y = 310
Now,
Divide the given equation with 31 on both sides
so,
\(\frac{31y}{31}\) = \(\frac{310}{31}\)
y = 10
Hence, from the above,
We can conclude that
The value of y for the given equation is: 10
In 17-20, solve each equation.
Question 17.
d ÷ 2 = 108
Answer:
The given equation is:
d ÷ 2 = 108
Now,
Multiply the given equation with 2 on both sides
So,
(d ÷ 2) × 2 = 108 × 2
d = 216
Hence, from the above,
We can conclude that
The value of d for the given equation is: 216
Question 18.
7,200 = 800s
Answer:
The given equation is:
7,200 = 800s
Now,
Divide the given equation with 800 on both sides
so,
\(\frac{7,200}{800}\) = \(\frac{800s}{800}\)
9 = s
s = 9
Hence, from the above,
We can conclude that
The value of s for the given equation is: 9
Question 19.
x ÷ 3 = 294
Answer:
The given equation is:
x ÷ 3 = 294
Now,
Multiply the given equation with 3 on both sides
So,
(x ÷ 3) × 3 = 294 × 3
d = 882
Hence, from the above,
We can conclude that
The value of x for the given equation is: 882
Question 20.
99 = 3x
Answer:
The given equation is:
99 = 3x
Now,
Divide the given equation with 3 on both sides
so,
\(\frac{99}{3}\) = \(\frac{3x}{3}\)
33 = x
x = 33
Hence, from the above,
We can conclude that
The value of x for the given equation is: 33
In 21 and 22, write a division equation and a multiplication equation to represent each problem.
Question 21.
Lolo typed 1,125 words in 15 minutes. Let w represent the number of words typed each minute. If Lolo typed the same number of words each minute, how many words did she type in 1 minute?
Answer:
It is given that
Lolo typed 1,125 words in 15 minutes. Let w represent the number of words typed each minute. and Lolo typed the same number of words each minute
So,
(The number of minutes needed to type 1,125 words) × (The number of words Lolo typed each minute) = 1,125
15 ×w = 1,125
15w = 1,125
Now,
Divide by 15 on both sides
So,
\(\frac{15w}{15}\) = \(\frac{1,125}{15}\)
w = \(\frac{1,125}{15}\)
Hence, from the above,
We can conclude that
The representation of the multiplication equation and the division equation to represent the given situation is:
a. Multiplication equation: 15w = 1,125
b. Division equation: w = \(\frac{1,125}{15}\)
Question 22.
In 12 weeks Felipe earns $4,500 doing yard work. He earns the same amount each week. Let m stand for the amount earned each week. How much does Felipe make in 1 week?
Answer:
It is given that
In 12 weeks Felipe earns $4,500 doing yard work. He earns the same amount each week. Let m stand for the amount earned each week
So,
(The number of weeks needed to earn $4,500) × (The amount earned by Felipe each week) = $4,500
12 × m = $4,500
12m = $4,500
Now,
Divide by 12 on both sides
So,
\(\frac{12m}{12}\) = \(\frac{$4,500}{12}\)
m = \(\frac{$4,500}{12}\)
Hence, from the above,
We can conclude that
The representation of the multiplication equation and the division equation to represent the given situation is:
a. Multiplication equation: 12m = $4,500
b. Division equation: m = \(\frac{$4,500}{12}\)
Question 23.
Model with Math Abel has 3,330 toothpicks. He wants to use them all to make a floor mat with 18 equal rows. Use the bar diagram to write a division equation. Then solve the equation to find how many toothpicks Abel should use in each row.

Answer:
It is given that
Abel has 3,330 toothpicks. He wants to use them all to make a floor mat with 18 equal rows
Now,
The representation of the gven situation in the form of a bar diagram is:

Now,
Let the number of toothpicks Abel shoud use in each row be: t
Now,
From the given bar diagram,
We can observe that
(The total number of toothpicks) ÷ (The number of tooth picks Abel should use in each row) = (The total number of rows)
\(\frac{3,330}{t}\) = 18
t = \(\frac{3,330}{18}\)
t = 185 toothpicks
Hence, from the above,
We can conclude that
The number of toothpicks Abel should use in each row is: 185 toothpicks
Question 24.
Model with Math Emily took an airplane trip. Her plane flew an equal number of miles each hour. Let m stand for the miles flown each hour. Write an equation to represent one way you can find how many miles Emily’s plane flew each hour.

Answer:
It is given that
Emily took an airplane trip. Her plane flew an equal number of miles each hour. Let m stand for the miles flown each hour.
Now,
The given figure is:

Now,
From the figure,
We can observe that
The total distance airplane travels is: 2,184 miles in 12 hours
So,
(The time took for airplane to reach Emily’s destination) × (The number of miles Emily’s plane flew each hour) = (The total distance an airplane travels in 12 hours)
12 × m = 2,184
12m = 2,184
Now,
Divide by 12 on both sides
So,
m = \(\frac{2,184}{12}\)
m = 182 miles
Hence, from the above,
We can conclude that
The number of miles Emily’s plane flew each hour is: 182 miles
In 25 and 26, use the triangle.

Question 25.
The area of the isosceles triangle is 44 square centimeters. Use the equation \(\frac{1}{2}\)(8h) = 44 to find the height of the triangle.
Answer:
It is given that
The area of the isosceles triangle is 44 square centimeters
Now,
The given figure is:

Now,
We know that,
The area of an Isosceles triangle (A) = \(\frac{1}{2}\) × Base × Height
So,
Accoring to the given information,
\(\frac{1}{2}\) × 8 × h = 44
\(\frac{8h}{2}\) = 44
8h = 44 × 2
8h = 88
h = \(\frac{88}{8}\)
h = 11 cm
Hence, from the above,
We can conclude that
The height of the given triangle is: 11 cm
Question 26.
If the perimeter of the triangle is 32 centimeters, what is the length of each of the two sides? Write and solve an equation.
Answer:
It is given that
The perimeter of the triangle is 32 centimeters
Now,
The given figure is:

Now,
We know that,
In an Isosceles triangle, 2 sides lengths are the same
The “Perimeter” of any figure is the sum of all the side lengths in a given figure
Now,
Let x be the side length of the given triangle
So,
x + x + 8 = 32
2x + 8 = 32
2x = 32 – 8
2x = 24
x = \(\frac{24}{2}\)
x = 12 cm
Hence, from the above,
We can conclude that
The length of one side in the given triangle is: 12 cm
The length of the other side in the given triangle is: 12 cm
Question 27.
Kelsey and her 4 sisters spent an equal amount of time cleaning their home. Their parents added their times. They found that each of the 5 girls spent 3 hours cleaning. Let c be the total number of hours the girls spent cleaning. Write and solve a division equation to find the total number of hours the girls spent cleaning.
Answer:
It is given that
Kelsey and her 4 sisters spent an equal amount of time cleaning their home. Their parents added their times. They found that each of the 5 girls spent 3 hours cleaning. Let c be the total number of hours the girls spent cleaning.
So,
According to the given information,
(The total number of hours the girls spent cleaning) ÷ (The total number of girls) = (The time took each girl spent cleaning)
c ÷ 5 = 3
c = 3 × 5
c = 15 hours
Hence, from the above,
We can conclude that
The total number of hours the five girls spent cleaning is: 15 hours
Question 28.
Higher Order Thinking Veronica traveled 562 miles to Venice, Florida. She drove 85 miles every day. On the last day of her trip she only drove 52 miles. Write and solve an equation to find the number of days Veronica traveled. Explain each step of your problem-solving strategy.
Answer:
It is given that
Veronica traveled 562 miles to Venice, Florida. She drove 85 miles every day. On the last day of her trip she only drove 52 miles
Now,

Hence, from the above,
We can conclude that
The number of days Veronica traveled is: 7 days
Question 29.
Generalize A movie theater sells 11,550 tickets for 50 sold-out showings of the same movie. Write a division equation that you can use to find the number of people who bought tickets for each showing. Use what you know about dividing with larger numbers to solve the equation.

Answer:
It is given that
A movie theater sells 11,550 tickets for 50 sold-out showings of the same movie.
Now,
Let the number of people who bought tickets for each showing be: p
So,
According to the given information,
(The total number of tickets sold by a movie theater) ÷ (The number of people who bought tickets for each showing) = (The number of showings)
11,550 ÷ p = 50
p = \(\frac{11,550}{50}\)
p = 231 people
Hence, from the above,
We can conclude that
The number of people who bought tickets for each showing is: 231 people
Assessment Practice
Question 30.
In October, Calvin’s school used 4,920 pounds of sand to protect the building against flooding during different tropical storms. One bag contains 40 pounds of sand.
Which of the following equations can be used to find how many bags of sand, b, Calvin’s school used in October?
A. 4,920b = 40
B. b ÷ 40 = 4,920
C. 40b = 4,920
D. b ÷ 4,920 = 40
Answer:
It is given that
In October, Calvin’s school used 4,920 pounds of sand to protect the building against flooding during different tropical storms. One bag contains 40 pounds of sand.
Now,
Let b be the number of bags of sand
So,
According to the given information,
(The number of bags) × (The amount of sand in each bag) = (The total amount of sand)
40b = 4,920
\(\frac{4,920}{b}\) = 40
Hence, from the above,
We can conclude that
The equation that can be used to find how many bags of sand, b, Calvin’s school used in October is:

Lesson 4.5 Write and Solve Equations with Rational Numbers
Explore It!
The cost of T-shirts for four different soccer teams are shown below.
I can… write and solve equations that involve rational numbers.
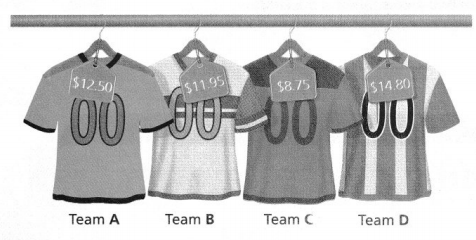
A. Lorna is on Team A. Ben is on another team. They paid a total of $21.25 for both team T-shirts. Write an equation represent the cost of Ben’s shirt
Answer:
It is given that
The cost of T-shirts for four different soccer teams are shown below.
Now,
The given figure is:

Now,
Let the cost of Ben’s shirt be: x
So,
According to the given information,
(The total cost of both T-shirts) = (The cost of Lorna’s shirt which is in Team A) + (The cost of Ben’s shirt)
$21.25 = $12.50 + x
So,
x = $21.25 – $12.50
x = $8.75
Hence, from the above,
We can conclude that
The cost of Ben’s shirt is: $8.75
B. Dario also plays soccer and he says that, based on the price of Ben’s T-shirt, Ben is on Team B. is Dario correct explain.
Answer:
It is given that
Dario said that based on the price of Ben’s T-shirt, Ben is on Team B
Now,
The given figure is:

Now,
We know that,
From Part A,
The cost of Ben’s T-shirt is: $8.75
Now,
From the given figure,
We can observe that
The T-shirt costs $8.75 that belongs to Team C
Hence, from the above,
We can conclude that
Dario is not correct
Focus on math practices
Generalize How is solving for unknowns involving money like solving for unknowns involving whole numbers?
We know that,
The representation of money is as the same as the rational numbers
So,
Whatever operations we are performing on the whole numbers, we can perform the same operations on the unknowns involving money
Essential Question
How can you write and solve equations involving rational numbers?
Answer:
Convert the rational number to decimals, then solve it as a decimal instead, (with the optional choice of re-converting it back to rational number).
Try It!
Suppose you cut the shorter piece of fruit snack from the example above into two pieces. The longer of the two pieces is 1\(\frac{3}{8}\) feet long. Complete the bar diagram to represent the equation. Then find the length of the shorter piece.
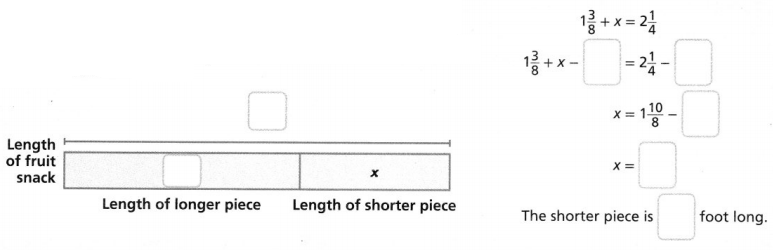
Answer:
It is given that
you cut the shorter piece of fruit snack from the example above into two pieces. The longer of the two pieces is 1\(\frac{3}{8}\) feet long.
Now,
From Example 1,
The length of the shorter piece is: 2\(\frac{1}{4}\) feet
Now,
The length of the longer piece in the given shorter piece is: 1\(\frac{3}{8}\) feet
Now,
Let the length of the shorter piece in the given shorter piece be: x
Now,
The representation of the given information in the form of a bar diagram is:
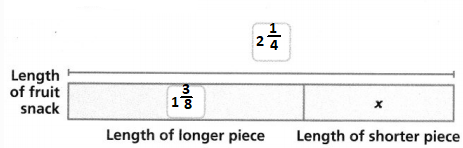
Now,
From the given diagram,
We can observe that
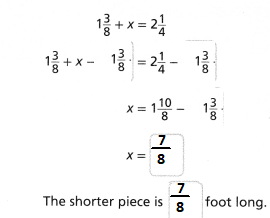
Hence, from the above,
We can conclude that
The shorter piece of the shorter piece is: \(\frac{7}{8}\) feet
Convince Me! How does the equation change if you know the length of the shorter piece is \(\frac{7}{8}\) foot and you want to know the length of the longer of the two pieces?
Answer:
If we know
The length of the shorter piece is: \(\frac{7}{8}\) foot
So,
The equation in the above problem will change into
\(\frac{7}{8}\) + x = 2\(\frac{1}{4}\)
Where,
x is the length of the other piece
Now,
x = 2\(\frac{1}{4}\) – \(\frac{7}{8}\)
x = 1\(\frac{3}{4}\) feet
So,
\(\frac{7}{8}\) < 1\(\frac{3}{4}\)
Hence, from the above,
We can conclude that
The length of the longer piece of the shorter piece is: 1\(\frac{3}{4}\) feet
Try It!
Solve \(\frac{5}{9}\)y = 25 for y.
Answer:
The given equation is:
\(\frac{5}{9}\)y = 25
Now,
Multiply with \(\frac{9}{5}\) on both sides
So,
\(\frac{5}{9}\) × \(\frac{9}{5}\)y = 25 × \(\frac{9}{5}\)
y = \(\frac{25 × 9}{5}\)
y = 45
Hence, from the above,
We can conclude that
The value of y for the given equation is: 45
Try It!
Molly also buys a bag of 8 apples for $3.60. Write and solve an equation to find how much Molly paid for each apple.
Answer:
It is given that
Molly also buys a bag of 8 apples for $3.60
So,
The cost of each apple = (The total cost of apples) ÷ (The total number of apples)
= \(\frac{$3.60}{8}\)
= $0.45
Hence, from the above,
We can conclude that
The cost of each apple is: $0.45
Try It!
Carmen spent $12.50 for a new notebook and a compass. The notebook cost $6.35. Write and solve an equation to find c, the cost of the compass.
Answer:
It is given that
Carmen spent $12.50 for a new notebook and a compass. The notebook cost $6.35
Now,
Let the cost of compass be c
So,
The total amount of money Carmen spent on a new notebook and a compass = (The cost of a compass) + (The cost of a new notebook)
$12.50 = c + $6.35
So,
c = $12.50 – $6.35
c = $6.15
Hence, from the above,
We can conclude that
The cost of a compass is: $6.15
KEY CONCEPT
You can solve equations using properties of equality and inverse relationships.

Do You Understand?
Question 1.
Essential Question How can you write and solve equations involving rational numbers?
Answer:
Convert the rational number to decimals, then solve it as a decimal instead, (with the optional choice of re-converting it back to rational number).
Question 2.
Construct Arguments Why are inverse relationships important for solving equations?
Answer:
Mathematically, Inverse operations are opposite operations. Addition is the opposite of subtraction; division is the opposite of multiplication, and so on. Inverse operations are used to solve simple algebraic equations to more difficult equations that involve exponents, logarithms, and trigonometry
Question 3.
Critique Reasoning Johnny says that he solved the equation x – 3.5 = 7.2 by adding 3.5 to the left side of the equation. Explain whether Johnny is correct.
Answer:
It is given that
Johnny says that he solved the equation x – 3.5 = 7.2 by adding 3.5 to the left side of the equation.
Now,
The given equation is:
x – 3.5 = 7.2
Now,
We know that,
According to the “Addition Property of Equality”,
Add the same amount on both sides to make the equation balanced
So,
For the given equation,
Add 3.5 on both sides
So,
x – 3.5 + 3.5 = 7.2 – 3.5
Hence, from the above,
We can conclude that
Johnny is not correct
Question 4.
Generalize When solving an equation involving a mixed number, such as y + \(\frac{3}{4}\) = 4\(\frac{1}{2}\), what do you need to do to the mixed number?
Answer:
The given equation is:
y + \(\frac{3}{4}\) = 4\(\frac{1}{2}\)
Now,
To solve the given equation,
We have to convert the mixed number into a proper fraction
Hence, from the above,
We can conclude that
We have to convert the given mixed number into a proper fraction
Question 5.
Construct Arguments How is solving an equation with fractions like solving an equation with whole numbers? How is it different?
Answer:
Solving an equation with a fraction isn’t much different than solving an equation full of whole numbers. You group the variable terms on one side, the constants on the other, and then simplify.
Do You Know How?
In 6-14, solve each equation.
Question 6.
t – \(\frac{2}{3}\) = 25\(\frac{3}{4}\)
Answer:
The given equation is:
t – \(\frac{2}{3}\) = 25\(\frac{3}{4}\)
Now,
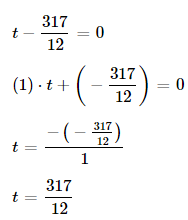
Hence, from the above,
We can conclude that
The value of t for the given expression is: \(\frac{317}{12}\)
Question 7.
\(\frac{f}{2}\) = \(\frac{5}{8}\)
Answer:
The given equation is:
\(\frac{f}{2}\) = \(\frac{5}{8}\)
Now,
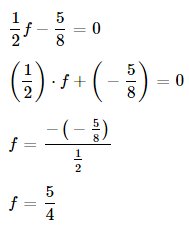
Hence, from the above,
We can conclude that
The value of f for the given equation is: \(\frac{5}{4}\)
Question 8.
13.27 = t – 24.45
Answer:
The given equation is:
13.27 = t – 24.45
Now,

Hence, from the above,
We can conclude that
The value of t for the given equation is: \(\frac{943}{25}\)
Question 9.
r ÷ 5.5 = 18.2
Answer:
The given equation is:
r ÷ 5.5 = 18.2
Now,
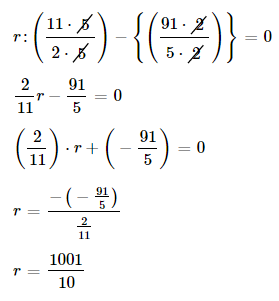
Hence, from the above,
We can conclude that
The value of r for the given equation is: \(\frac{1,001}{10}\)
Question 10.
\(\frac{7}{10}=x – [latex]\frac{3}{5}\)
Answer:
The given equation is:
\(\frac{7}{10}=x-[latex]\frac{3}{5}\)
Now,
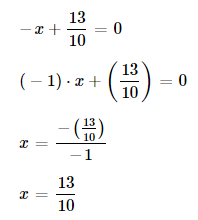
Hence, from the above,
We can conclude that
The value of x for the given equation is: \(\frac{13}{10}\)
Question 11.
1.8x = 40.14
Answer:
The given equation is:
1.8x = 40.14
Now,
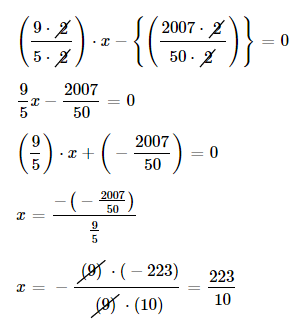
Hence, from the above,
We can conclude that
The value of x for the given equation is: \(\frac{223}{10}\)
Question 12.
17.3 + v = 22.32
Answer:
The given equation is:
17.3 + v = 22.32
Now,
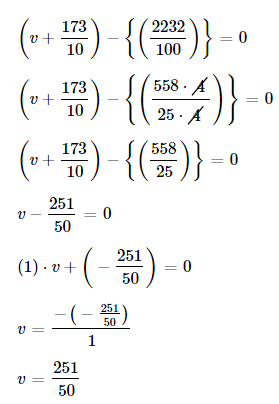
Hence, from the above,
We can conclude that
The value of v for the given equation is: \(\frac{251}{50}\)
Question 13.
9 = \(\frac{3}{8}\)y
Answer:
The given equation is:
9 = \(\frac{3}{8}\)y
Now,
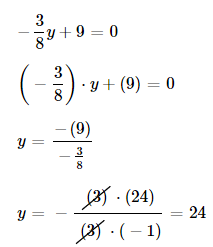
Hence, from the above,
We can conclude that
The value of y for the given equation is: 24
Question 14.
1\(\frac{3}{4}+z=2[latex]\frac{2}{3}\)
Answer:
The given equation is:
1\(\frac{3}{4}+z=2[latex]\frac{2}{3}\)
Now,
Convert the given mixed numbers into the fraction form
So,
1\(\frac{3}{4}\) = \(\frac{7}{4}\)
2\(\frac{2}{3}\) = \(\frac{8}{3}\)
Now,
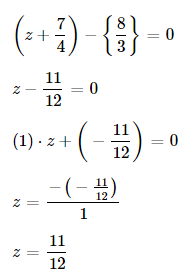
Hence, from the above,
We can conclude that
The value of y for the given equation is: \(\frac{11}{12}\)
Practice & Problem Solving
Leveled Practice
In 15-22, solve each equation.
Question 15.
w – 3.2 = 5.6
w – 3.2 + _____ = 5.6 + _____
w = _____
Answer:
The given equation is:
w – 3.2 = 5.6
Now,
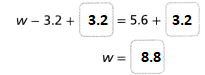
Hence, from the above,
We can conclude that
The value of w for the given equation is: 8.8
Question 16.
9.6 = 1.6y
9.6 ÷ _____ = 1.6y ÷ ______
_______ = y
Answer:
The given equation is:
9.6 = 1.6y
Now,

Hence, from the above,
We can conclude that
The value of y for the given equation is: 6
Question 17.
48.55 + k = 61.77
48.55 + k – _____ = 61.77 – _____
k = _____
Answer:
The given equation is:
48.55 + k = 61.77
Now,
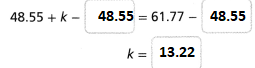
Hence, from the above,
We can conclude that
The value of k for the given equation is: 13.22
Question 18.
m ÷ 3.54 = 1.5
m ÷ 3.54 × _____ = 1.5 × _____
m = _____
Answer:
The given equation is:
m ÷ 3.54 = 1.5
Now,
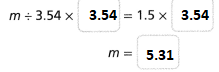
Hence, from the above,
We can conclude that
The value of m for the given equation is: 5.31
Question 19.
\(7 \frac{1}{9}=2 \frac{4}{5}+m\)
Answer:
The given equation is:
\(7 \frac{1}{9}=2 \frac{4}{5}+m\)
Now,
Convert the given mixed numbers into fractions
So,
7\(\frac{1}{9}\) = \(\frac{64}{9}\)
2\(\frac{4}{5}\) = \(\frac{14}{5}\)
Now,
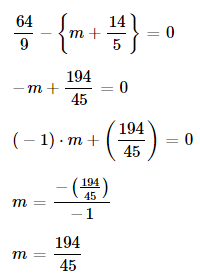
Hence, from the above,
We can conclude that
The value of m for the given equation is: \(\frac{194}{45}\)
Question 20.
\(a+3 \frac{1}{4}=5 \frac{2}{9}\)
Answer:
The given equation is:
\(a+3 \frac{1}{4}=5 \frac{2}{9}\)
Now,
Convert the given mixed numbers into the fractions
So,
3\(\frac{1}{4}\) = \(\frac{13}{4}\)
5\(\frac{2}{9}\) = \(\frac{47}{9}\)
Now,
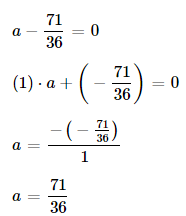
Hence, from the above,
We can conclude that
The value of a for the given equation is: \(\frac{71}{36}\)
Question 21.
\(\frac{1}{8}\) • y=4
Answer:
The given equation is:
\(\frac{1}{8}\) • y=4
Now,
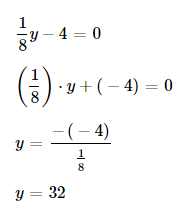
Hence, from the above,
We can conclude that
The value of y for the given equation is: 32
Question 22.
\(k-6 \frac{3}{8}=4 \frac{6}{7}\)
Answer:
The given equation is:
\(k-6 \frac{3}{8}=4 \frac{6}{7}\)
Now,
Convert the given mixed numbers into the fractions
So,
6\(\frac{3}{8}\) = \(\frac{51}{8}\)
4\(\frac{6}{7}\) = \(\frac{34}{7}\)
Now,
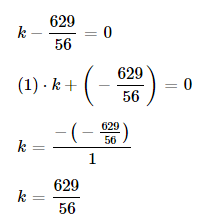
Hence, from the above,
We can conclude that
The value of k for the given equation is: \(\frac{629}{56}\)
Question 23.
Mr. Marlon buys these tickets for his family to visit the water park. The total cost is $210. Write and solve an equation to find the cost of each ticket.

Answer:
It is given that
Mr. Marlon buys these tickets for his family to visit the water park. The total cost is $210
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The number of tickets Mr. Marlon bought is: 4
Now,
The cost of each ticket = (The total cost of tickets) ÷ (The total number of people)
= \(\frac{210}{4}\)
= $ 52.50
Hence, from the above,
We can conclude that
The cost of each ticket is: $52.50
Question 24.
Higher Order Thinking Without solving, tell which equation below has a greater solution. Explain.
\(\frac{5}{8}\)m = 2\(\frac{3}{4}\)
\(\frac{5}{9}\)m = 2\(\frac{3}{4}\)
Answer:
The given equations are:
\(\frac{5}{8}\)m = 2\(\frac{3}{4}\)
\(\frac{5}{9}\)m = 2\(\frac{3}{4}\)
Now,
We know that,
In the given fraction,
The numerators are the same and to find whether which fraction is greater,
We can compare by using the denominators
If the denominator is a small number when the numerators are the same then the other denominator, then the fraction that contains the smallest value of denominator is the greater fraction
Now,
From the given fractions,
When we compare the denominators,
8 < 9
Hence, from the above,
We can conclude that
The equation which is greater is:
\(\frac{5}{8}\)m = 2\(\frac{3}{4}\)
Question 25.
Make Sense and Persevere A high school track team’s long jump record is 21 feet 2\(\frac{1}{4}\) inches. This year, Tim’s best long jump is 20 feet 9\(\frac{1}{2}\) inches. If long jumps are measured to the nearest quarter inch, how much farther must Tim jump to break the record?
Answer:
It is given that
A high school track team’s long jump record is 21 feet 2\(\frac{1}{4}\) inches. This year, Tim’s best long jump is 20 feet 9\(\frac{1}{2}\) inches
Now,
We know that,
1 foot = 12 inches
So,
21 feet 2\(\frac{1}{4}\) inches = (21 × 12) + 2\(\frac{1}{4}\) inches
= 252 + 2\(\frac{1}{4}\) inches
= 252 + 2.25 inches
= 254.25 inches
So,
20 feet 9\(\frac{1}{2}\) inches = (20 × 12) + 9\(\frac{1}{2}\) inches
= 240 + 9\(\frac{1}{2}\) inches
= 240 + 9.5 inches
= 249.5 inches
So,
The distance Tim has to cross to break the record = 254.25 – 249.5
= 4.75 inches
Hence, from the above,
We can conclude that
The distance Tim has to cross to break the record is: 4.75 inches
Question 26.
Make Sense and Persevere About how many gallons of fuel does it take to move the space shuttle 3 miles from its hangar to the Vehicle Assembly Building?
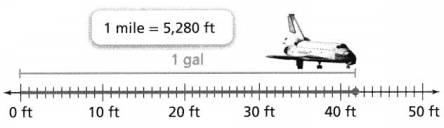
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
1 mile = 5,280 ft
It will take 1 gallon of fuel to move space shuttle 42 feet
Now,
The distance of 3 miles traveled by the space shuttle in fuel = (The number of feet required for 1 mile) × 3
= 3 × 5,280
= 15,840 feet
Now,
The number of gallons of fuel required to move the space shuttle 3 miles = (The total distance of 3 miles in feet) ÷ (The distance covered by 1 gallon of fuel)
= \(\frac{15,840}{42}\)
= 377 gallons
Hence, from the above,
We can conclude that
It will take 377 gallons of fuel to move the space shuttle 3 miles from its hangar to the Vehicle Assembly Building
Question 27.
Is the solution of b × \(\frac{5}{6}\) = 25 greater than or less than 25? How can you tell before computing?
Answer:
The given equation is:
b × \(\frac{5}{6}\) = 25
Now,
We know that,
When a multiplication is converted into a division, then the fraction after × or ÷ symbols will have to be reciprocal and vice-versa
So,
The reciprocal of \(\frac{5}{6}\) is: \(\frac{6}{5}\)
So,
b = 25 × \(\frac{6}{5}\)
Now,
We know that,
The value of \(\frac{6}{5}\) is greater than 1
So,
The solution for the given equation will also be greater than 25
Hence, from the above,
We can conclude that
The solution of b × \(\frac{5}{6}\) = 25 is greater than 25
Question 28.
What is the width of a rectangle with a length of \(\frac{3}{7}\) ft and an area of 2 ft2? Write an equation to show your work.
Answer:
It is given that
The area of a rectangle is: 2 ft²
The length of a rectangle is: \(\frac{3}{7}\) ft
Now,
Let the width of the rectangle be x
Now,
We know that,
The area of a rectangle = Length × Width
So,
2 = \(\frac{3}{7}\) × x
Now,
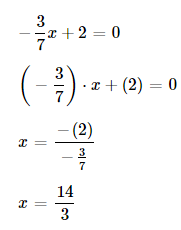
Hence, from the above,
We can conclude that
The width of the given rectangle is: \(\frac{14}{3}\) ft
Question 29.
Model with Math Helen is filling the pool shown for her little brother. She can carry 1\(\frac{7}{8}\) gallons of water each trip. Write and solve an equation to find how many trips Helen needs to make.

Answer:
It is given that
Helen is filling the pool shown for her little brother. She can carry 1\(\frac{7}{8}\) gallons of water each trip
Now,
The given figure is:

So,
The number of trips Helen needs to make = (The total amount of water held in the pool) ÷ (The amount of water Helen can carry each trip)
= 10\(\frac{1}{2}\) ÷ 1\(\frac{7}{8}\)
Now,
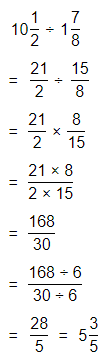
Hence, from the above,
We can conclude that
The number of trips Helen needs to make is about 6 trips
Question 30.
After the pool was full, Helen’s little brother and his friend splashed g gallons of water out of the pool. There are 7\(\frac{7}{8}\) gallons still left in the pool. Write and solve an equation to find how much water was splashed out of the pool.
Answer:
It is given that
After the pool was full, Helen’s little brother and his friend splashed g gallons of water out of the pool. There are 7\(\frac{7}{8}\) gallons still left in the pool
Now,
The given figure is:

Now,
Let the amount of water splashed from the pool be: g gallons
So,
(The total amount of water present in the pool) – (The amount of water splashed out of the pool) = (The amount of water still left in the pool)
10\(\frac{1}{2}\) – g = 7\(\frac{7}{8}\)
g = 10\(\frac{1}{2}\) – 7\(\frac{7}{8}\)
Now,
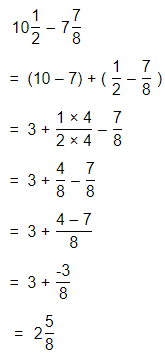
Hence, from the above,
We can conclude that
The amount of water that splashed out from the pool is: 2\(\frac{5}{8}\) gallons
Question 31.
Grace solved the equation 2\(\frac{1}{2}\)y = \(\frac{5}{8}\). Her steps for the solution are shown in the table but are all mixed up. Write her steps in the correct order on the right side of the table.
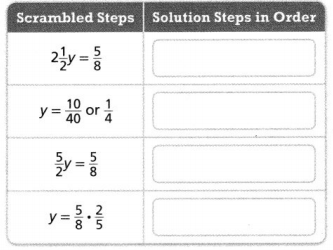
Answer:
It is given that
Grace solved the equation 2\(\frac{1}{2}\)y = \(\frac{5}{8}\). Her steps for the solution are shown in the table but are all mixed up.
Now,
The given equation is:
2\(\frac{1}{2}\)y = \(\frac{5}{8}\)
Now,
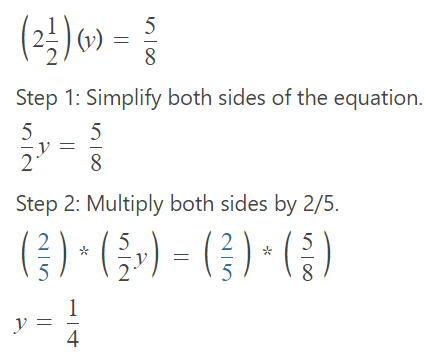
Hence,from the above,
We can conclude that
Her steps in the correct order on the right side of the table is:
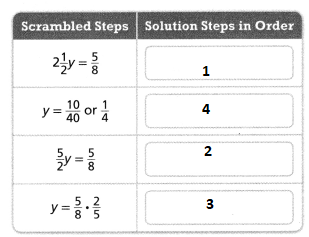
Question 32.
The scientific name for the little bumps on your tongue is fungiform papillae. Each bump can contain many taste buds. The number of taste buds a person has varies. There are three general classifications of taste: supertaster, medium taster, and non-taster. Suppose a supertaster has 8,640 taste buds. Solve the equation 4.5n = 8,640 to find the number of taste buds, n, a non-taster may have.

Answer:
It is given that
The scientific name for the little bumps on your tongue is fungiform papillae. Each bump can contain many taste buds. The number of taste buds a person has varies. There are three general classifications of taste: supertaster, medium taster, and non-taster. Suppose a supertaster has 8,640 taste buds
Now,
The given figure is:

The given equation according to the given information is:
4.5n = 8,640
Now,
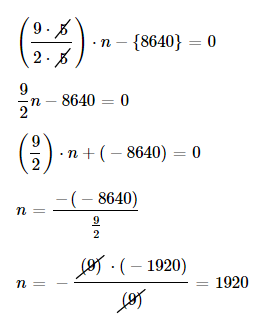
Hence, from the above,
We can conclude that
The number of taste buds a non-taster may have is: 1,920 taste buds
Question 33.
Model with Math In one study, the number of women classified as supertasters was 2.25 times the number of men classified as supertasters. Suppose 72 women were classified as supertasters. Write an equation that represents the number of men, m, who were classified as supertasters. Then solve the equation. How many men were classified as supertasters?
Answer:
It is given that
In one study, the number of women classified as supertasters was 2.25 times the number of men classified as supertasters. Suppose 72 women were classified as supertasters
Now,
From the given information,
The number of women who are supertasters = 2.25 × (The numberof men who are supertasters)
72 = 2.25 × (The number of men who are supertasters)
The number of men who are supertasters = \(\frac{72}{2.25}\)
= 32
Hence, from the above,
We can conclude that
The number of men who are classified as supertasters is: 32 men
Question 34.
Use Structure A fraction, f, multiplied by 5 equals \(\frac{1}{8}\). Write an algebraic sentence to show the equation. Then solve the equation and explain how you solved it.
Answer:
It is given that
A fraction, f, multiplied by 5 equals \(\frac{1}{8}\).
Now,
The representation of the given information in the form of an equation is:
f × 5 = \(\frac{1}{8}\)
5f = \(\frac{1}{8}\)
Now,
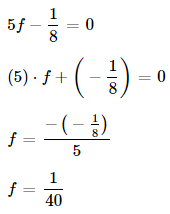
Hence, from the above,
We can conclude that
The value of f for the given equation is: \(\frac{1}{40}\)
Question 35.
Yelena needs to swim a total of 8 miles this week. So far, she swam 5\(\frac{3}{8}\) miles. Use the equation 5\(\frac{3}{8}\) + m = 8 to find how many more miles Yelena needs to swim.
Answer:
It is given that
Yelena needs to swim a total of 8 miles this week. So far, she swam 5\(\frac{3}{8}\) miles.
Now,
The givene quation according to the given information is:
5\(\frac{3}{8}\) + m = 8
Now,
Convert the given mixed number into a fraction
So,
\(\frac{43}{8}\) + m = 8
Now,
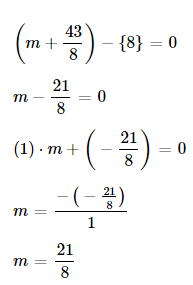
Hence, from the above,
We can conclude that
The number of miles Yelena needs to swim is: \(\frac{21}{8}\) miles
Question 36.
Can any equation that is written using addition be written as an equivalent equation using subtraction? Explain your reasoning and give an example containing decimals that shows your reasoning.
Answer:
Yes, any equation that is written using addition can be written as an equivalent equation using subtraction
Ex:
3.35 + y = 6.88
y = 6.88 – 3.35
y = 3.53
Now,
By using Subtraction:
Subtract any number let say 5 from both sides of 3.35 + y = 6.88
Now,
3.35 + y – 5 = 6.88 – 5
y – 1.65 = 1.88
y = 3.53
Question 37.
Critique Reasoning Oscar is 12 years old and his little sister is 6. Oscar uses a to represent his age. He says that he can use the expression a ÷ 2 to always know his sister’s age. Do you agree? Explain.
Answer:
It is given that
Oscar is 12 years old and his little sister is 6. Oscar uses a to represent his age. He says that he can use the expression a ÷ 2 to always know his sister’s age
Now,
Let the age of Oscar be: 18 years
Then,
The age of his sister will be: 8 – 6 = 12 years
So,
The relationship between the ages of Oscar and his sister is:
The age of Oscar = The age of his sister + 6
Hence, from the above,
We can conclude that
We can not agree with Oscar
Assessment Practice
Question 38.
Which value for y makes the equation 0.26y = 0.676 true?
A. y = 0.17576
B. y = 0.26
C. y = 2.6
D. y = 26
Answer:
The given equation is:
0.26y = 0.676
Now,
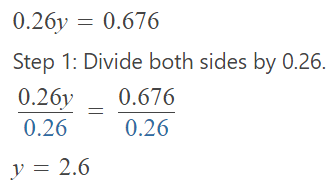
Hence, from the above,
We can conclude that
The value of y that makes the given equation true is:
Question 39.
Which value for x makes the equation 0.435 + x = 0.92 true?
A. x = 1.355
B. x = 0.595
C. x = 0.495
D. x = 0.485
Answer:
The given equation is:
0.435 + x = 0.92
Now,
x = 0.92 – 0.435
x = 0.485
Hence, from the above,
We can conclude that
The value of x that makes the givene quation true is:

Topic 4 Mid-Topic Checkpoint
Question 1.
Vocabulary Describe the relationship between equations and the properties of equality. Lessons 4-1 and 4-2
Answer:
The property of equality states that when we do arithmetic operations on both sides of an equation by the same number, the two sides remain equal and the property of equality is pplicable only on equations
In 2-4, write an equation for the situation. Then solve the equation.
Question 2.
A fraction f multiplied by 4 equals \(\frac{1}{2}\). Lesson 4-5
Answer:
The given situation is:
A fraction f multiplied by 4 equals \(\frac{1}{2}\)
Now,
The representation of the given situation in the form of an equation is:
4f = \(\frac{1}{2}\)
Now,
Divide the equation by 4 on both sides
So,
f = \(\frac{1}{2 × 4}\)
f = \(\frac{1}{8}\)
Hence, from the above,
We can conclude that
The value of f for the given equation is: \(\frac{1}{8}\)
Question 3.
When 832 is divided by n, the result is 16. Lesson 4-4
Answer:
The given situation is:
When 832 is divided by n, the result is 16
Now,
The representation of the given situation in the form of an equation is:
\(\frac{832}{n}\) = 16
Now,
Multiply the equation with n on both sides
So,
n = \(\frac{832}{16}\)
n = 52
Hence, from the above,
We can conclude that
The value of n for the given equation is: 52
Question 4.
When 10 is subtracted from x, the result is 6. Lesson 4-3
Answer:
The given situation is:
When 10 is subtracted from x, the result is 6.
Now,
The representation of the given situation in the form of an equation is:
x – 10 = 6
Now,
Add 10 on both sides for the equation
So,
x – 10 + 10 = 6 + 10
x = 16
Hence, from the above,
We can conclude that
The value of x for the given equation is: 16
Question 5.
Select all the equations that are equivalent to n-9 = 12. Lesson 4-2
☐ n – n – 9 = 12 – n
☐ n – 9 + 12 = 12 – 9
☐ n – 9 + 9 = 12 + 9
☐ n – 9 – n = 12 – n
☐ n – 9 + 9 = 12 – 12
Answer:
The given equation is: n – 9 = 12
Now,
We know that,
According to the “Property of Equality”,
We have to do the same arithmetic operation with the same number on both sides of the equation to keep the equation balanced
Hence, from the above,
We can conclude that
The equations that are equivalent to n – 9 = 12 are:
Question 6.
Select all the values ford that make the equation 9 = 18 ÷ d true. Lesson 4-1
☐ 2
☐ 0.5
☐ \(\frac{10}{5}\)
☐ 162
☐ \(\frac{1}{4}\)
Answer:
The given equation is:
9 = 18 ÷ d
Now,
Multiply with d on both sides fro the equation
So,
d = \(\frac{18}{9}\)
d = 2
Hence,f rom the above,
We can conclude that
The values of d that make the given equation true are:

Question 7.
The area, A, of a triangle is 15.3 square cm. Its base, b, is 4.5 cm. The formula for finding the area of a triangle is A = \(\frac{1}{2}\)bh. Write and solve an equation to find the height, h, of the triangle. Lessons 4-4 and 4-5
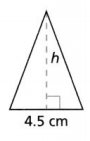
Answer:
It is given that
The area, A, of a triangle is 15.3 square cm. Its base, b, is 4.5 cm. The formula for finding the area of a triangle is A = \(\frac{1}{2}\)bh.
Now,
The given figure is:

Now,
According to the given formula in the given informatio,
15.3 = \(\frac{1}{2}\) × 4.5 × h
15.3 = 2.25 × h
h = \(\frac{15.3}{2.25}\)
h = 6.8 cm
Hence,f rom the above,
We can conclude that
The value of h of the given triangle is: 6.8 cm
Topic 4 Mid-Topic Performance Task
Ronald carved 3\(\frac{3}{8}\) feet of a totem pole. He says that the totem pole is \(\frac{3}{4}\) complete.

PART A
If h represents the height, in feet, of the finished totem pole, then \(\frac{3}{4}\)h = 3\(\frac{3}{8}\) represents this situation. Which equations show the use of a reciprocal to write an equivalent equation that can be used to solve for h? Select all that apply.

Answer:
It is given that
Ronald carved 3\(\frac{3}{8}\) feet of a totem pole. He says that the totem pole is \(\frac{3}{4}\) complete.
Now,
The given figure is:

Now,
If h represents the height, in feet, of the finished totem pole, then
\(\frac{3}{4}\)h = 3\(\frac{3}{8}\) represents this situation
Now,
We know that,
The term “Reciprocal” is applicable only for multiplication and division
Now,
We know that,
The reciprocal of \(\frac{3}{4}\) is: \(\frac{4}{3}\)
Now,
We know that,
According to the “Property of Equality”,
The arithmetic operation we performed on the left side of th equation with a number will have to be the same to the right side of the equation also
Hence, from the above,
We can conclude that
The equations that show the use of a reciprocal to write an equivalent equation that can be used to solve for h are:
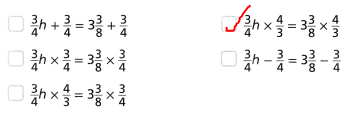
PART B
Use the equation in Part A to determine the height of the finished totem pole. Then write and solve an equation to find the height, s, of the section that has not been carved.
Answer:
From Part A,
The equation to determine the height h of the finished totem pole is:
\(\frac{3}{4}\)h = 3\(\frac{3}{8}\)
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The \(\frac{1}{4}\) of the section has not been carved
Now,
h = 3\(\frac{3}{8}\) × \(\frac{4}{3}\)
h = \(\frac{27}{8}\) × \(\frac{4}{3}\)
h = \(\frac{27 × 4}{8 × 3}\)
h = \(\frac{9}{2}\) ft
Now,
The height of the section that ahs not been carved (s) = \(\frac{h}{4}\)
= h × \(\frac{1}{4}\)
= \(\frac{9}{2}\) × \(\frac{1}{4}\)
= \(\frac{9}{8}\) ft
Hence, from the above,
We can conclude that
The height of the section that has not been carved is: \(\frac{9}{8}\) ft
PART C
Ronald spent $10.50 on tools and x dollars on the wood for the totem pole. His total cost for the totem pole is $19.35. The equation $10.50 + x = $19.35 represents this situation. What is the cost of the wood Ronald used?
Answer:
It is given that
Ronald spent $10.50 on tools and x dollars on the wood for the totem pole. His total cost for the totem pole is $19.35. The equation $10.50 + x = $19.35 represents this situation
Now,
The given equation that represents the given situation is:
$10.50 + x = $19.35
x = $19.35 – $10.50
x = $8.85
Hence, from the above,
We can conclude that
The cost of Wood Ronald used is: $8.85
PART D
To make the same totem pole with wood that costs y dollars, Ronald would have to spend a total of $35.19. Explain which property of equality Ronald could use to solve the equation $10.50 + y = $35.19 and why that property can be used. Then show how to use that property to solve for y.
Answer:
It is given that
To make the same totem pole with wood that costs y dollars, Ronald would have to spend a total of $35.19.
Now,
The given equation that is used to represent the given situation is:
$10.50 + y = $35.19
Now,
We know that,
According to the “Subtraction Property of Equality”,
Subtract the same amount from both sides to make the equation balanced
Now,
Subtract $10.50 from the given equation by using the “Subtraction Property of Equality”
So,
$10.50 + y – $10.50 = $35.19 – $10.50
y = $24.69
Hence, from the above,
We can conclude that
The cost of wood that is used to make the totem pole is: $24.69
Lesson 4.6 Understand and Write Inequalities
Solve & Discuss It!
The record time for the girls’ 50-meter freestyle swimming competition is 24.49 seconds. Camilla has been training and wants to break the record. What are some possible times Camilla would have to swim to break the current record?
I can… understand and write an inequality that describes a real-world situation.

Answer:
It is given that
The record time for the girls’ 50-meter freestyle swimming competition is 24.49 seconds. Camilla has been training and wants to break the record”
Now,
The given table is:

Now,
From the given table,
We can observe that
To break the record,
Camilia has to swim greater than the time it is taken for the girls’ 50-meter freestyle swimming competition
So,
The possible times Camilia would have to swim to break the current record is: 26.56 seconds, 25.14 seconds, and 25.32 seconds
Hence, from the above,
We can conclude that
The possible times Camilia would have to swim to break the current record is:
a. 26.56 seconds b. 25.14 seconds c. 25.32 seconds
Reasoning
How do Camilla’s possible times compare to 24.49 seconds?
Answer:
From the above Exercise,
We know that,
Camilia wants to break the record
So,
The possible times of Camilia must be greater than 24.49 seconds
Hence, from the above,
We can conclude that
Camilia’s possible times are greater than 24.49 seconds
Focus on math practices
Be Precise Fran won a blue ribbon for growing the heaviest pumpkin. It weighed 217 pounds. What could be the weights of other pumpkins in the contest? How could you show the weights of the other pumpkins using a mathematical statement? Explain.
Answer:
It is given that
Fran won a blue ribbon for growing the heaviest pumpkin. It weighed 217 pounds.
Now,
We know that,
The heaviest weight means there is no other weight greater than that weight
Now,
From the given information,
217 pounds is the heaviest weight
So,
Other weights other than 217 pounds are lesser
Now,
Let the weight of all the other pumpkins be x
So,
According to the given information,
The weights of all the pumpkins present in the contest have lesser weight than the heaviest pumpkin
So,
The mathematical representation of the above statement is:
x < 217 pounds
Hence, from the above,
We can conclude that
The representation of the give information in the form of a mathematical statement is:
The weights of all the pumpkins present in the contest have lesser weight than the heaviest pumpkin. i.e.,
x < 217 pounds
Essential Question
How can you write an inequality to describe a situation?
Answer:
The steps to write an inequality to describe a situation are:
a. Read through the entire problem.
b. Highlight the important information and key words that you need to solve the problem.
c. Identify your variables.
d. Write the equation or inequality.
e. Solve.
f. Write your answer in a complete sentence.
g. Check or justify your answer
Try It!
Use the number line to show some of the ages of people who do not need to be accompanied by an adult. Write an inequality to represent the ages of people, n, who do not need to be accompanied by an adult.
![]()
Answer:
Let the ages of the people who do not need to be accompanied by an adult be: n
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The people who are less than 8 years have to be accompanied by an adult
Now,
The representation of the people who do not need to be accompanied by an adult in the given number line is:

So,
The inequality that represents ages of people ,n, who do not need to be accompanied by an adult is:
n > 8 years
Hence, from the above,
We can conclude that
The inequality that represents ages of people ,n, who do not need to be accompanied by an adult is:
n > 8 years
Convince Me! How do you know to which group an 8-year-old belongs, those who must be accompanied by an adult or those who do not need to be accompanied by an adult? Explain.
Answer:
The given figure is:

Now,
Let the number of children who must be accompanied by an adult be: x
Let the number of children who do not need to be accompanied by an adult be: y
Now,
From the given figure,
We can observe that
The children under the age of 8 must be accompanied by an adult
So,
The representation of an inequality that represents the ages of the children who must be accompanied by an adult is:
x < 8
The representation of an inequality that represents the ages of the children who need not to be accompanied by an adult is:
y > 8
Hence, from the above,
We can conclude that
The representation of an inequality that represents the ages of the children who must be accompanied by an adult is:
x < 8
The representation of an inequality that represents the ages of the children who need not to be accompanied by an adult is:
y > 8
Try It!
Write an inequality to represent each situation.
a. Harry is taller than 60 inches.
Answer:
The given situation is:
Harry is taller than 60 inches.
Now,
Let h be the height of Harry
Hence, from the above,
We can conclude that
The representation of the inequality that represents the given situation is:
h > 60 inches
b. Sherry is not 4 years old.
Answer:
The given situation is:
Sherry is not 4 years old
Now,
Let a be the age of Sherry
Hence, from the above,
We can conclude that
The representation of the inequality that represents the given situation is:
a ≠ 4 years
c. Hank has at least $7.50.
Answer:
The given situation is:
Hank has at least $7.50
Now,
Let s be the amount of money Hank has
Hence, from the above,
We can conclude that
The representation of the inequality that represents the given situation is:
s ≥ $7.50
KEY CONCEPT
Inequality symbols can be used to describe situations that have more than one possible solution.
Do You Understand?
Question 1.
Essential Question How can you write an inequality to describe a situation?
Answer:
The steps to write an inequality to describe a situation are:
a. Read through the entire problem.
b. Highlight the important information and key words that you need to solve the problem.
c. Identify your variables.
d. Write the equation or inequality.
e. Solve.
f. Write your answer in a complete sentence.
g. Check or justify your answer
Question 2.
Generalize What is the difference between an equation with a variable and an inequality with a variable?
Answer:
An equation is a mathematical statement that shows the equal value of two expressions while an inequality is a mathematical statement that shows that an expression is lesser than or more than the other. An equation shows the equality of two variables while an inequality shows the inequality of two variables.
Question 3.
Would it be more efficient to use an inequality or to list all of the quantities less than 6? Explain.
Answer:
Without using “Inequalities”,
The qualities less than 6 are: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, and 5
By using the “Inequalities”,
The quantities less than 6 are: x < 6
Where,
x is the list of numbers that are less than 6
Question 4.
Generalize How are the symbols for greater than (>) and greater than or equal to (≥) related?
Answer:
“Greater than or equal to” and “less than or equal to” are just the applicable symbol with half an equal sign under it. For example, 4 or 3 ≥ 1 shows us a greater sign over half an equal sign, meaning that 4 or 3 are greater than or equal to 1. It works the other way, too
Do You Know How?
In 5-12, write an inequality for each situation.
Question 5.
A number, n, is greater than 22.
Answer:
The given situation is:
A number, n, is greater than 22.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
n > 22
Question 6.
The value, v, does not equal 2\(\frac{1}{2}\).
Answer:
The given situation is:
The value, v, does not equal 2\(\frac{1}{2}\).
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
v ≠ 2\(\frac{1}{2}\)
Question 7.
Sally’s age, a, is at most 15.
Answer:
The given situation is:
Sally’s age, a, is at most 15.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
a ≤ 15
Question 8.
The width of the picture, w, is shorter than 8.5 inches.
Answer:
The given situation is:
The width of the picture, w, is shorter than 8.5 inches.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
w < 8.5 inches
Question 9.
Steve’s height, h, is at least 48 inches.
Answer:
The given situation is:
Steve’s height, h, is at least 48 inches.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
h ≥ 48 inches
Question 10.
Vera’s baby brother’s age, b, is not 24 months.
Answer:
The given situation is:
Vera’s baby brother’s age, b, is not 24 months.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
b ≠ 24 months
Question 11.
The number of quarters, q, in the jar is less than 75.
Answer:
The given situation is:
The number of quarters, q, in the jar is less than 75.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
q < 75
Question 12.
The length of the fish a fisherman catches, f, must be at least 10 inches for him to keep it.
Answer:
The given situation is:
The length of the fish a fisherman catches, f, must be at least 10 inches for him to keep it
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
f ≥ 10 inches
Practice & Problem Solving
In 13-22, write an inequality for each situation.
Question 13.
Up to 12 people, p, can ride in the van.
Answer:
The given situation is:
Up to 12 people, p, can ride in the van.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
p ≤ 12 people
Question 14.
A number of days, d, of sunshine is not 28.
Answer:
The given situation is:
A number of days, d, of sunshine is not 28.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
d ≠ 28
Question 16.
The value, v, of the bracelet is less than $85.25.
Answer:
The given situation is:
The value, v, of the bracelet is less than $85.25.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
v < $85.25
Question 15.
The distance of the race, r, is farther than 6.2 miles.
Answer:
The given situation is:
The distance of the race, r, is farther than 6.2 miles.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
r > 6.2 miles
Question 17.
The number of people, p, that a restaurant can seat at one time is no more than 171.
Answer:
The given situation is:
The number of people, p, that a restaurant can seat at one time is no more than 171.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
p ≤ 171 people
Question 18.
The time, t, a customer has left on a parking meter is at least 25 minutes.
Answer:
The given situation is:
The time, t, a customer has left on a parking meter is at least 25 minutes.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
t ≥ 25 minutes
Question 19.
The bill, b, was less than $45.
Answer:
The given situation is:
The bill, b, was less than $45.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
b < $45
Question 20.
The girls live b blocks apart; they do not live 7\(\frac{1}{2}\) blocks apart.
Answer:
The given situation is:
The girls live b blocks apart; they do not live 7\(\frac{1}{2}\) blocks apart.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
b ≠ 7\(\frac{1}{2}\) blocks
Question 21.
The speed of the truck, s, must be no less than 34 miles per hour.
Answer:
The given situation is:
The speed of the truck, s, must be no less than 34 miles per hour.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
s ≤ 34 miles per hour
Question 22.
The number of baseball games, x, that Karen went to last year is more than 5.
Answer:
The given situation is:
The number of baseball games, x, that Karen went to last year is more than 5.
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
x ≤ 5 games
Question 23.
Mia is taller than Gage. If m represents Mia’s height and g represents Gage’s height, write an inequality that shows the relationship between their heights.
Answer:
It is given that
Mia is taller than Gage and m represents Mia’s height and g represents Gage’s height
Now,
According to the given information,
The representation of the inequality for the given situation is:
m > g
Hence, from the above,
We can conclude that
The representation of the inequality for the given situation is:
m > g
Question 24.
Taryn sold gift-wrapping paper for a school fund-raiser. She sold at least 15 rolls of paper. Write an inequality to represent the amount of money, d, she earned for the fund-raiser.

Answer:
It is given that
Taryn sold gift-wrapping paper for a school fund-raiser. She sold at least 15 rolls of paper
Now,
The given figure is:

Now,
Let the number of rolls of paper be: x
So,
The representation of the inequality for representing the rolls of paper is:
x ≥ 15 rolls
Now,
The amount of money, d, Taryn earned for the fundraiser = (The total number of rolls) × (The cost of each roll)
= 15 × $8
= $120
So,
The representation of the inequality for representing the amount of money Taryn earned for the fundraiser is:
d ≥ $120
Hence, from the above,
We can conclude that
The representation of the inequality for representing the amount of money Taryn earned for the fundraiser is:
d ≥ $120
Question 25.
A city in New England just experienced its greatest 1-day snowfall. Write an inequality to represent a snowfall that would beat this record.
Answer:
It is given that
A city in New England just experienced its greatest 1-day snowfall
Now,
The given figure is:

Now,
Let the snowfall that would beat the given record be: t
From the given figure,
We can observe that
The representation of the inequality to represent a snowfall that would beat the given record is:
t > 19.7 inches of snow
Question 26.
The first bookcase, a, in a library can hold 1 less book than the second bookcase. The second bookcase holds 2,492 books. Write an inequality to represent the number of books the first bookcase can hold.
Answer:
It is given that
The first bookcase, a, in a library can hold 1 less book than the second bookcase. The second bookcase holds 2,492 books
So,
The number of books the first bookcase can hold = (The number of books the second bookcase can hold) – 1
= 2,492 – 1
= 2,491 books
Now,
Let the number of books the first bookcase can hold be: x
Let the number of books the second bookcase can hold be: y
So,
From the above,
We can observe that
x < y
Hence, from the above,
We can conclude that
The number of books the first bookcase can hold < The number of books the second bookcase can hold
Question 27.
A certain airplane must carry no more than 134 passengers during a flight. Write an inequality to represent the number of passengers, p, that would NOT be allowed during this flight.
Answer:
It is given that
A certain airplane must carry no more than 134 passengers during a flight
Now,
Let p be the number of passengers during a flight
So,
The representation of the inequality to represent the number of passengers that would not be allowed during this flight is:
p > 134 passengers
Hence, from the above,
We can conclude that
The representation of the inequality to represent the number of passengers that would not be allowed during this flight is:
p > 134 passengers
Question 28.
Higher Order Thinking To ride a certain roller coaster, a rider must be at least 42 inches tall. To represent this situation, Elias wrote h > 42 and Nina wrote h > 42. Who is correct? Explain.

Answer:
It is given that
To ride a certain roller coaster, a rider must be at least 42 inches tall. To represent this situation, Elias wrote h > 42 and Nina wrote h > 42.
Now,
Let the height of the rider be: h inches
So,
The representation of the inequality that represents the height of a rider to ride a certain roller coaster is:
h ≥ 42
Hence, from the above,
We can conclude that
Elias is correct
Assessment Practice
Question 29.
Miguel earns extra money working two weekends with his dad. He is saving to buy a new bike that costs $140.
Heather says that Miguel needs to earn more than $6 for each hour that he works to have enough money to buy the bike. Her work is shown below. Write an inequality to explain why she is incorrect.
$140 ÷ 23 hours > $6.00 per hour
Miguel has to earn more than $6.00 per hour.
Answer:
It is given that
Miguel earns extra money working two weekends with his dad. He is saving to buy a new bike that costs $140.
Heather says that Miguel needs to earn more than $6 for each hour that he works to have enough money to buy the bike. Her work is shown below
Now,
The given figure is:
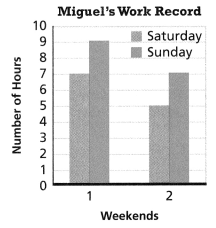
Now,
From the given figure,
We can observe that
Miguel’s work record in Weekend 1 is: 9 hours
Miguel’s work record in Weekend 2 is: 7 hours
So,
The total number of hours in 2 Weekends for Migul = 9 + 7
= 16 hours
So,
The amount of money Migul will earn per hour = (The amount of money Migul saved to buy a new bike) ÷ (The total number of hours in 2 Weekends for Migul)
= \(\frac{$140}{16}\)
= $8.75
Hence, from the above,
We can conclude that
The inequality that represents Migul’s work is:
W > $8.75 per hour
Lesson 4.7 Solve Inequalities
Solve & Discuss It!
Henry is thinking of a number that is less than 17. What number could he be thinking of?
I can… write and represent solutions of inequalities.

Answer:
It is given that
Henry is thinking of a number that is less than 17
Now,
Let x be the numbers less than 17
Where,
x may be an integer, decimal number (or) a whole number that is less than 17
So,
The representation of the inequality that represents the number that is less than 17 that Henry is thinking is:
x < 17
Hence, from the above,
We can conclude that
The representation of the inequality that represents the number that is less than 17 that Henry is thinking is:
x < 17
Use Appropriate Tools
How can you use a number line to show all the numbers that are less than 17?

Answer:
We know that,
The numebrs that are 17 will be an integer, decimal number or a Whole number
Now,
The whole numbers that are less than 17 are: 0, 1, 2, 3, …….. 16
Hence, from the above,
We can conclude that
The representation of the list of all the Whole numbers that are less than 17 in the given number line is:
![]()
Focus on math practices
Reasoning Could Henry be thinking of 17? Explain.
Answer:
No, Henry should not be thinking of 17 because it is clearly mentioned that Henry is thinking of a number that is less than 17
So,
The list of the numbers that Henry may be thinking is: 0, 1, 2, 3 ….. 16
Essential Question
How can you represent the solutions of an inequality?
Answer:
The rules for Solving Inequalities are:
a. Add the same number on both sides.
b. From both sides, subtract the same number.
c. By the same positive number, multiply both sides.
d. By the same positive number, divide both sides.
e. Multiply the same negative number on both sides and reverse the sign.
A closed, or shaded, circle is used to represent the inequalities greater than or equal to (≥) or less than or equal to (≤) . The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is not part of the solution
Try It!
Graph all of the solutions of x < 8.
To graph x < 8, draw a(n) ________ circle at 8 on the number line.
7 and 4 are two of the many possible solutions of the inequality.
Shade the solutions to the ________ of the ________ circle you drew at 8.
Answer:
The given inequality is: x < 8
Now,
The representation of the given inequality in the given number line is:

Now,


Hence, from the above,
We can conclude that
The solutions for the given inequality in the given number line is:

Convince Me! How does the graph of the inequality change when the less than sign is changed to a greater than sign? How does it stay the same?
Answer:
We know that multiplying or dividing an inequality by a negative number changes the direction of the inequality. In other words, a greater-than symbol becomes a less-than symbol, and vice versa
Now,
When the inequality has the symbol > (or) ≥, the numbers to the right of this inequality will become the solutions
When the inequality has the symbol < (or) ≤, the numbers to the left of this inequality will become the solutions
Try It!
There are no menu items on the children’s menu at the Flamingo Restaurant that cost more than $8.50. What are all the possible costs of the items on the children’s menu?

Answer:
It is given that
There are no menu items on the children’s menu at the Flamingo Restaurant that cost more than $8.50
Now,
Let c be the cost of the menu items on the children’s menu at the Flamingo Restaurant
So,
The representation of the inequality that represents the given situation is:
c < $8.50
Hence,
The representation of all the possible costs of the items on the children’s menu on the given number line is:

Try It!
Which athletes, if any, would qualify for the finals if the length of a jump that qualifies for the finals were at least 20\(\frac{1}{2}\) feet?
Answer:
It is given that
The length of a jump that qualifies for the finals were at least 20\(\frac{1}{2}\) feet
Now,
The given table is:
Now,
Let the length of a jump be: d feet
Now,
The representation of the given situation in teh form of an inequality is:
d ≥ 20\(\frac{1}{2}\) feet
Now,
From the given table,
We can observe that
The values that are greater than 20\(\frac{1}{2}\) feet are:
20\(\frac{1}{2}\) = 20\(\frac{1}{2}\)
20\(\frac{1}{2}\) > 22\(\frac{1}{3}\)
Hence, from the above,
We can conclude that
Amir and Ryan would qualify for the finals if the length of a jump that qualifies for the finals were at least 20\(\frac{1}{2}\) feet
KEY CONCEPT
An inequality uses these symbols: <, >, ≤ , or ≥ to compare two expressions.

Do You Understand?
Question 1.
Essential Question How can you represent the solutions of an inequality?
Answer:
The rules for Solving Inequalities are:
a. Add the same number on both sides.
b. From both sides, subtract the same number.
c. By the same positive number, multiply both sides.
d. By the same positive number, divide both sides.
e. Multiply the same negative number on both sides and reverse the sign.
A closed, or shaded, circle is used to represent the inequalities greater than or equal to (≥) or less than or equal to (≤) . The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is not part of the solution
Question 2.
In Example 1, why is 9 a solution of x > 5?
Answer:
The given equation is: x > 5
Now,
From the given equation,
We can observe that
Since x > 5,
The solutions to the given equation are all the numbers that are greater than 5
So,
The given equation will have infinitely many solutions that are greater than 5
Hence, from the above,
We can conclude that
9 is a solution of x > 5
Question 3.
Explain why 2 is NOT a solution of x > 5.
Answer:
The given equation is: x > 5
Now,
From the given equation,
We can observe that
Since x > 5,
The solutions to the given equation are all the numbers that are greater than 5
So,
The given equation will have infinitely many solutions that are greater than 5
Hence, from the above,
We can conclude that
2 is not a solution of x > 5
Question 4.
How many solutions does the inequality x > 12 have? Explain.
Answer:
The given equation is: x > 12
Now,
From the given equation,
We can observe that
Since x > 12,
The solutions to the given equation are all the numbers that are greater than 12
So,
The given equation will have infinitely many solutions that are greater than 12
Hence, from the above,
We can conclude that
x > 12 will have infinitely many solutions that are greater than 12
Question 5.
Generalize How do the graphs of the solutions of inequalities involving greater than (>) and greater than or equal to (≥) compare?
Answer:
A closed, or shaded, circle is used to represent the inequalities greater than or equal to (≥) or less than or equal to (≤) . The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is not part of the solution
Do You Know How?
In 6 and 7, write the inequality that each graph represents.
Question 6.
Answer:
The given number line is:
![]()
Now,
From the given number line,
We can observe that
There is an open circle on 14.
So,
14 will not be included and the selected numbers are to the left side of 14 in the given number line
So,
The representation of the inequality for the given number line is:
![]()
Hence, from the above,
We can conclude that
The representation of the inequality for the given number line is:
z < 14
Question 7.
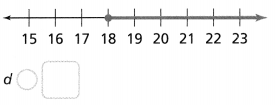
Answer:
The given number line is:
![]()
Now,
From the given number line,
We can observe that
There is a closed circle on 18.
So,
18 will be included and the selected numbers are to the right side of 18 in the given number line
So,
The representation of the inequality for the given number line is:
![]()
Hence, from the above,
We can conclude that
The representation of the inequality for the given number line is:
d ≥ 18
In 8-11, substitute each given value of the variable to find which, if any, is a solution of the inequality.
Question 8.
w < 8 w = 4.3, 5.3, 8.3, 9
Answer:
The given inequality is: w < 8
Now,
The given list of numbers are: 4.3, 5.3, 8.3, and 9
Now,
When we observe the given list of numbers,
4.3, and 5.3 are less than 8
Hence, from the above,
We can conclude that
The solutions for the given inequality are: 4.3, 5.3
Question 9.
t > 25 t = 24, 25, 25.1, 27
Answer:
The given inequality is: t > 25
Now,
The given list of numbers are: 24, 25, 25.1, and 27
Now,
When we observe the given list of numbers,
25.1 and 27 are greater the 25
Hence, from the above,
We can conclude that
The solutions for the given inequality are: 25.1, 27
Question 10.
g ≤ 4 g = 0, 4, 5, 6
Answer:
The given inequality is: g ≤ 4
Now,
The given list of numbers are: 0, 4, 5, and 6
Now,
When we observe the given list of numbers,
0 and 4 are less than or equal to 4
Hence, from the above,
We can conclude that
The solutions for the given inequality are: 0, 4
Question 11.
y ≥ 28 y = 4, 5, 6, 7
Answer:
The given inequality is: y ≥ 8
Now,
The given list of numbers are: 4, 5, 6, and 7
Now,
When we observe the given list of numbers,
The given list of numbers are less than 28
Hence, from the above,
We can conclude that
There are no solutions for the given inequality from the given list of numbers
Practice & Problem Solving
In 12-15, write the inequality that each graph represents.
Question 12.

Answer:
The given number line is:
![]()
Now,
From the given number line,
We can observe that
There is an open circle on 7.
So,
7 will not be included and the selected numbers are to the left side of 7 in the given number line
So,
The representation of the inequality for the given number line is:
![]()
Hence, from the above,
We can conclude that
The representation of the inequality for the given number line is:
y < 7
Question 13.
Answer:
The given number line is:
![]()
Now,
From the given number line,
We can observe that
There is an open circle on 0.
So,
0 will not be included and the selected numbers are to the right side of 0 in the given number line
So,
The representation of the inequality for the given number line is:
![]()
Hence, from the above,
We can conclude that
The representation of the inequality for the given number line is:
b > 0
Question 14.
Answer:
The given number line is:

Now,
From the given number line,
We can observe that
There is an open circle on 3.
So,
3 will not be included and the selected numbers are to the right side of 3 in the given number line
So,
The representation of the inequality for the given number line is:
![]()
Hence, from the above,
We can conclude that
The representation of the inequality for the given number line is:
x > 3
Question 15.
Answer:
The given number line is:
![]()
Now,
From the given number line,
We can observe that
There is a closed circle on 5.
So,
5 will be included and the selected numbers are to the left side of 5 in the given number line
So,
The representation of the inequality for the given number line is:
![]()
Hence, from the above,
We can conclude that
The representation of the inequality for the given number line is:
t ≤ 5
In 16-19, graph each inequality on a number line.
Question 16.
h ≥ 9

Answer:
The given inequality is: h ≥ 9
Hence, from the above,
We can conclude that
The representation of the given inequality on the number line is:
Question 17.
p < 3

Answer:
The given inequality is: p < 3
Hence, from the above,
We can conclude that
The representation of the given inequality on the number line is:
Question 18.
t ≤ 6

Answer:
The given inequality is: t ≤ 6
Hence, from the above,
We can conclude that
The representation of the given inequality on the number line is:
![]()
Question 19.
s > 1

Answer:
The given inequality is: s > 1
Hence, from the above,
We can conclude that
The representation of the given inequality on the number line is:

In 20-27, name three solutions of each inequality.
Question 20.
x > 10.5
Answer:
The given inequality is: x > 10.5
Now,
We know that,
If the inequality has a “>” symbol, then the values that are greater than the given number will be the solutions for the equation
Hence, from the above,
We can conclude that
The three solutions for the given inequality are: 11, 12, and 13
Question 21.
r < 19
Answer:
The given inequality is: r < 19
Now,
We know that,
If the inequality has a “<” symbol, then the values that are lesser than the given number will be the solutions for the equation
Hence, from the above,
We can conclude that
The three solutions for the given inequality are: 15, 16, and 17
Question 22.
y ≥ 200
Answer:
The given inequality is: y ≥ 200
Now,
We know that,
If the inequality has a “≥” symbol, then the values that are greater than or equal to the given number will be the solutions for the equation
Hence, from the above,
We can conclude that
The three solutions for the given inequality are: 200, 205, and 210
Question 23.
m ≤ 82
Answer:
The given inequality is: m ≤ 82
Now,
We know that,
If the inequality has a “≤” symbol, then the values that are lesser than or equal to the given number will be the solutions for the equation
Hence, from the above,
We can conclude that
The three solutions for the given inequality are: 75, 80, and 81
Question 24.
x ≥ 12
Answer:
The given inequality is: x ≥ 12
Now,
We know that,
If the inequality has a “≥” symbol, then the values that are greater than or equal to the given number will be the solutions for the equation
Hence, from the above,
We can conclude that
The three solutions for the given inequality are: 12, 13, and 14
Question 25.
q ≤ 3.5
Answer:
The given inequality is: q ≤ 3.5
Now,
We know that,
If the inequality has a “≤” symbol, then the values that are lesster than or equal to the given number will be the solutions for the equation
Hence, from the above,
We can conclude that
The three solutions for the given inequality are: 0, 1.5, and 3.5
Question 26.
v > 35
Answer:
The given inequality is: v > 35
Now,
We know that,
If the inequality has a “>” symbol, then the values that are greater than the given number will be the solutions for the equation
Hence, from the above,
We can conclude that
The three solutions for the given inequality are: 40, 45, and 50
Question 27.
m < 2.5
Answer:
The given inequality is: m < 2.5
Now,
We know that,
If the inequality has a “<” symbol, then the values that are lesser than the given number will be the solutions for the equation
Hence, from the above,
We can conclude that
The three solutions for the given inequality are: 0, 1, and 2
Question 28.
The inequality w ≤ 1,500 describes the maximum weight in pounds, w, allowed by law in a freight elevator. Is a total weight of either 1,505 pounds or 1,600 pounds allowed in a freight elevator? Explain.

Answer:
It is given that
The inequality w ≤ 1,500 describes the maximum weight in pounds, w, allowed by law in a freight elevator.
Now,
The given equation is: w ≤ 1,500
Now,
From the given inequality,
We can observe that
The solutions for the given inequality will be less than or equal to 1,500 but not greater than 1,500
So,
1,505 > 1,500 and 1,600 > 1,500
Hence, from the above,
We can conclude that
The total weight of either 1,505 pounds or 1,600 pounds will not be allowed in a freight elevator
Question 29.
Reasoning Graph the inequalities x > 2 and x < 2 on the same number line. What value, if any, is not a solution of either inequality? Explain.

Answer:
The given inequalities are: x > 2 and x < 2
Now,
The representation of x > 2 on the given number line is:

The representtaion of x < 2 on the given number line is:
![]()
Now,
When we observe the number lines of x > 2 and x < 2,
We can say that
2 is not a solution for either of the number lines
Hence, from the above,
We can conclude that
2 is not a solution of either inequality
Question 30.
Model with Math Death Valley is the hottest place in the United States. The highest temperature ever recorded there was 134°F. The lowest temperature recorded there was 15°F. Write two inequalities that would describe the temperature, in degrees Fahrenheit, in Death Valley at any time since temperatures have been recorded.
Answer:
It is given that
Death Valley is the hottest place in the United States. The highest temperature ever recorded there was 134°F. The lowest temperature recorded there was 15°F
Now,
Let the highest temperature recorded in the Death Valley be: H
Let the lowest temperature recorded in the Death Valley be: L
So,
The inequality that represents the highest temperature in °F in the Death Valley is: H < 134° F
The inequality that represents the lowest temperature in °F in the Death Valley is: L > 15° F
Hence, from the above,
We can conclude that
The two inequalities that describe the temperature in the Death Vally at any time since the temperatures have been recorded is:
The inequality that represents the highest temperature in °F in the Death Valley is: H < 134° F
The inequality that represents the lowest temperature in °F in the Death Valley is: L > 15° F
Question 31.
The number line below represents the solutions of the inequality x > 7. Is 7.1 a solution? Is 7.01 a solution? Explain.
Answer:
It is given that
The number line below represents the solutions of the inequality x > 7
Now,
The given number that represents the solution for the given inequality x > 7 is:

Now,
From the above number line,
We can observe that
The solutions for x > 7 will be all the numbers that are greater than 7 and will be infinite
So,
7.1 > 7 and 7.01 > 7
Hence, from the above,
We can conclude that
7.1 and 7.01 are the solutions of the given inequality x > 7
Question 32.
The temperature in a greenhouse should be 65 degrees or higher. Write an inequality to describe the allowable temperature in the greenhouse.
Answer:
It is given that
The temperature in a greenhouse should be 65 degrees or higher.
Now,
Let the temperature of the greenouse be: t
So,
The inequality that describes the allowable temperature in the greenhouse is:
t ≥ 65°
Hence, from the above,
We can conclude that
The inequality that describes the allowable temperature in the greenhouse is:
t ≥ 65°
Question 33.
Higher Order Thinking Francine received a gift card to buy cell phone apps. She says that the card’s value is enough to buy any of the apps shown at the right. Let v be the dollar value of the gift card. Write an inequality that best describes the value of the gift card.

Answer:
It is given that
Francine received a gift card to buy cell phone apps. She says that the card’s value is enough to buy any of the apps shown at the right. Let v be the dollar value of the gift card.
Now,
The given figure is:

Now,
When we observe the given figure,
We can say that
The maximum vaue of the given gift card is: $12
So,
The costs of the given apps should be less than $12
So,
The representation of the inequality that describes the value of the gift card is:
v ≤ $12
Hence, from the above,
We can conclude that
The representation of the inequality that describes the value of the gift card is:
v ≤ $12
Question 34.
The maximum load on a small plane is 400 pounds. Let w represent the weight on the plane. Write an inequality to describe the allowable weight on the plane.
Answer:
It is given that
The maximum load on a small plane is 400 pounds. Let w represent the weight on the plane
Now,
Since the maximum load is 400 pounds, the remaining weights will be less than or equal to 400 pounds
So,
The representation of the inequalty that describes teh allowable weight on the plane is:
w ≤ 400 pounds
Hence, from the above,
We can conclude that
The representation of the inequalty that describes teh allowable weight on the plane is:
w ≤ 400 pounds
Question 35.
Jillian is thinking of a whole number that is greater than 21. What numbers, if any, make the inequality n > 21 true for n = 0, 1, 2, 3, 4, …?
Answer:
It is given that
Jillian is thinking of a whole number that is greater than 21
Now,
The given inequality is: n > 21
Now,
We know that,
If any inequality has “>” symbol, then the solutions for that inequality will be greater than thenumber and the solutions will be infinite
So,
The solutions for the given inequality will be: 22, 23, 24,……..
Hence, from the above,
We can conclude that
The numbers that make the inequality n > 21 true are: 22, 23, 24, …..
Assessment Practice
Question 36.
Select all the given values of y that make the inequality 3y < 25 true.
☐ 6.5
☐ 7
☐ 8
☐ 8.5
☐ 9
Answer:
The given inequality is: 3y < 25
Now,
Divide the given nequality be 3 on both sides
So,
\(\frac{3y}{3}\) < \(\frac{25}{3}\)
y < 8.3
Hence, from the above,
We can conclude that
All the values of y that make the inequality 3y < 25 true are:

Question 37.
Tania started a graph to show the inequality y < 3.7. Finish labeling the number line and draw the graph.

Answer:
It is given that
Tania started a graph to show the inequality y < 3.7
Now,
The given inequality is: y < 3.7
Now,
The representation of the given number line and the solution for thegiven inequality is:

Hence, from the above,
We can conclude that
The completed number line and the solutions for y < 3.7 on the completed number line is:

3-ACT MATH
3-Act Mathematical Modeling: Checking a Bag

АСТ 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.

Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
Question 5.
Plot your prediction on the same number line.
Answer:
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
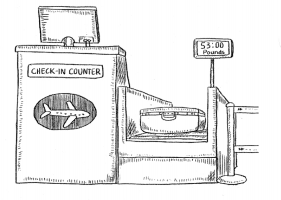
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? is it higher or lower than your prediction? Explain why.

Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?

Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
Reflect
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Was an equation or an inequality more useful to answer the Main Question? Explain.
Answer:
SEQUEL
Question 15.
Be Precise A different airline has a weight limit of 40 pounds for a checked bag. Explain how the answer would change for this airline.

Answer:
Lesson 4.8 Understand Dependent and Independent Variables
Explain It!
Max is shipping a present to his grandmother.
I can… identify dependent and independent variables.

A. What are three factors that will affect the weight of the box? What are three factors that will not affect the weight of the box?
Answer:
It is given that
Max is shipping a present to his grandmother.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The three factors that will affect the weight of the box is:
a. Size of the box
b. The material of the box
c. Contents inside the box
The three factors that will not affect the weight of the box is:
a. The color of the box
b. The shape of the box
c. The design of the box
B. How might the size of the box and the contents of the box affect the weight of the box?
Answer:
We know that,
When we increase the size of the box, the contents of the box will also increase in the box and also the weight of the box will increase
So,
The relationship between the size of the box and the contents of the box and the weight of the box is:
Size of the box ∝ Contents of the box ∝ Weight of the box
Focus on math practices
Model with Math Describe another situation in which changing one factor results in changes to another factor.
Answer:
The example of a situation in which changing one factor results in changes to another factor is:
The distance a car travels, d, is dependent on the speed, s, at which it travels. So, speed is the independent variable and distance is the dependent variable
So,
Here,
The distance a car travels, d, is dependent on the speed, s, at which it travels. So, speed is the independent variable and distance is the dependent variable
Essential Question
What does it mean for one variable to be dependent on another variable?
Answer:
A dependent variable is a variable whose value will change depending on the value of another variable, called the independent variable. In a scientific experiment, it is the variable being tested, and therefore, it is called the dependent variable
Try It!
A baker used a certain number of cups of batter, b, to make p pancakes. Which variable, p, pancakes or b, batter is the dependent variable? Explain.
Answer:
It is given that
A baker used a certain number of cups of batter, b, to make p pancakes
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
Now,
From the given situation,
We can observe that
The independent variable is: b
The dependent variable is: p
Hence, from the above,
We can conclude that
Pancakes (p) is the dependent variable
Convince Me! If the baker doubles the number of cups of batter used, b, what would you expect to happen to the number of pancakes made, p? Explain.
Answer:
It is given that
The baker doubles the number of cups of batter used, b
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
From the given situation,
We can observe that
If the baker doubles the number of cups of batter used, b, then the number of pancakes, p, would also be double in quantity
Hence, from the above,
We can conclude that
If the baker doubles the number of cups of batter used, b, then the number of pancakes, p, would also be double in quantity
Try It!
Jenna wants to rent a mountain bike by the week. Identify the independent variables that affect the total rental cost.
Answer:
It is given that
Jenna wants to rent a mountain bike by the week
Now,
From Example 3,
We can observe that
The dependent variables and independent present in Example 3 are:
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variables that affect the total rental cost for the given situation is:
a. Price per day (d)
b. Price per week (w)
c. Length of rental (l)
Hence, from the above,
We can conclude that
The independent variables that affect the total rental cost for the given situation is:
a. Price per day (d)
b. Price per week (w)
c. Length of rental (l)
KEY CONCEPT
A dependent variable changes in response to another variable, called an independent variable. An independent variable causes the change in a dependent variable. It is independent because its value is not affected by other variables.
The distance a car travels, d, is dependent on the speed, s, at which it travels. Speed is the independent variable, and distance is the dependent variable.
Do You Understand?
Question 1.
Essential Question What does it mean for one variable to be dependent on another variable?
Answer:
A dependent variable is a variable whose value will change depending on the value of another variable, called the independent variable. In a scientific experiment, it is the variable being tested, and therefore, it is called the dependent variable
Question 2.
Jake and Viola record the number of miles, m, they bike to help track the number of calories, s, they burn in an hour.

Critique Reasoning Viola says the number of calories, c, they burn is the dependent variable. Do you agree? Explain.
Answer:
It is given that
Jake and Viola record the number of miles, m, they bike to help track the number of calories, s, they burn in an hour.
Now,
From the given situation,
We can observe that
The number of calories they burn is dependent on the number of miles
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of miles
The dependent variable for the given situation is: Number of calories they burn
Hence, from the above,
We can conclude that
We can agree with Viola
Question 3.
Reasoning in the biking problem above, identify at least one other independent variable that could affect the dependent variable.
Answer:
The given situation from Exercise 2 is:

Now,
From the given situation,
We can observe that
The number of calories they burn is dependent on the number of miles
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of miles
The dependent variable for the given situation is: Number of calories they burn
Hence, from the above,
We can conclude that
The independent variable that could affect the dependent variale for the given situation is: Number of miles
Do You Know How?
In 4-11, identify the independent variable and the dependent variable.
Question 4.
The amount of money, m, earned if t raffle tickets are sold
Answer:
The given situation is:
The amount of money, m, earned if t raffle tickets are sold
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: traffic tickets, t
The dependent variable for the given situation is: Amount of oney, m
Hence, from the above,
We can conclude that
The independent variable for the given situation is: traffic tickets, t
The dependent variable for the given situation is: Amount of money, m
Question 5.
The number of hours, h, worked and the amount of money, m, earned
Answer:
The given situation is:
The number of hours, h, worked and the amount of money, m, earned
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of hours , h
The dependent variable for the given situation is: Amount of money, m
Hence, from the above,
We can conclude that
The independent variable for the given situation is: traffic tickets, t
The dependent variable for the given situation is: Amount of money, m
Question 6.
The number of shelves, s, in a bookcase and the number of books, b, the bookcase can hold
Answer:
The given situation is:
The number of shelves, s, in a bookcase and the number of books, b, the bookcase can hold
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of shelves, s
The dependent variable for the given situation is: Number of books, b, the bookcase can hold
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of shelves, s
The dependent variable for the given situation is: Number of books, b, the bookcase can hold
Question 7.
The number of pages, p, you read in your book in h hours
Answer:
The given situation is:
The number of pages, p, you read in your book in h hours
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of pages, p
The dependent variable for the given situation is: Number of hours, h
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of pages, p
The dependent variable for the given situation is: Number of hours, h
Question 8.
The number of gallons, g, of water a garden hose produces after running for m minutes
Answer:
The given situation is:
The number of gallons, g, of water a garden hose produces after running for m minutes
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of gallons, g, of water
The dependent variable for the given situation is: Number of minutes, m
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of gallons, g, of water
The dependent variable for the given situation is: Number of minutes, m
Question 9.
The number of peaches, y, a farmer harvests in x bushels
Answer:
The given situation is:
The number of peaches, y, a farmer harvests in x bushels
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of bushels, x
The dependent variable for the given situation is: Number of peaches, y
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of bushels, x
The dependent variable for the given situation is: Number of peaches, y
Question 10.
The number of hours, h, you spend driving at a speed of r miles per hour
Answer:
The given situation is:
The number of hours, h, you spend driving at a speed of r miles per hour
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of miles per hour, r
The dependent variable for the given situation is: Number of hours, h
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of miles per hour, r
The dependent variable for the given situation is: Number of hours, h
Question 11.
Name at least two independent variables that could result in a change in a monthly electric bill.
Answer:
The two independent variables that could result in a change in a monthly electric bill is:
a. Outside temperature and humidity
b. The frequency of the electrical appliances inside the house you use
Practice & Problem Solving
In 12-15, identify the independent variable and the dependent variable.
Question 12.
The pages, p, in a book and the weight, w, of the book
Answer:
The given situation is:
The pages, p, in a book and the weight, w, of the book
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of pages, p, in a book
The dependent variable for the given situation is: Weight, w, of the book
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of pages, p, in a book
The dependent variable for the given situation is: Weight, w, of the book
Question 13.
The number of hamburgers, h, sold and the dollar amount of sales, s, taken in
Answer:
The given situation is:
The number of hamburgers, h, sold and the dollar amount of sales, s, taken in
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of hamburgers, h, sold
The dependent variable for the given situation is: The amount of sales, s, taken in
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of hamburgers, h, sold
The dependent variable for the given situation is: The amount of sales, s, taken in
Question 14.
The pounds, p, of flour you buy and the number of bread loaves, b, you want to make
Answer:
The given situation is:
The pounds, p, of flour you buy and the number of bread loaves, b, you want to make
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: Number of pounds, p, of flour you buy
The dependent variable for the given situation is: Number of bread loaves, b, you want to make
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of pounds, p, of flour you buy
The dependent variable for the given situation is: Number of bread loaves, b, you want to make
Question 15.
The temperature, t, of water and the number of minutes, m, the water is in the freezer
Answer:
The given situation is:
The temperature, t, of water and the number of minutes, m, the water is in the freezer
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
So,
The independent variable for the given situation is: The temperature, t, of water
The dependent variable for the given situation is: Number of minutes, m, the water is in the freezer
Hence, from the above,
We can conclude that
The independent variable for the given situation is: The temperature, t, of water
The dependent variable for the given situation is: Number of minutes, m, the water is in the freezer
Question 16.
Write your own situation. Identify the independent and dependent variables.
Answer:
In an experiment in Psychology, on the impact of sleep deprivation on test performance,
a. Sleep deprivation would be the independent variable.
b. The dependent variable is the variable that is measured by the experimenter
Question 17.
Name at least two independent variables that could result in a change in the price of a basket of grapefruits.
Answer:
The independent variables that could result in a change in the price of a basket of grapefruits is:
a. The weight of grapefruits
b. The size of a basket
Question 18.
Critique Reasoning You spend c dollars for p identical pairs of pants. A friend claims that because c increases if you increase p, and p increases if you increase c, either corp could be the independent variable. Is your friend right or wrong? Explain.
Answer:
It is given that
You spend c dollars for p identical pairs of pants. A friend claims that because c increases if you increase p, and p increases if you increase c, either corp could be the independent variable.
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
Now,
From the given situation,
We can observe that
The independent variable for the given situation is: Identical pairs of pants, p
The dependent variable for the given situation is: Amount of money spent, c
Hence, from the above,
We can conclude that
Your friend is wrong
Question 19.
The number of oranges in a bag and the cost of the bag of oranges are related. What is the independent variable in this relationship? Explain.
Answer:
It is given that
The number of oranges in a bag and the cost of the bag of oranges are related
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
Now,
From the given situation,
We can observe that
The independent variable for the given situation is: Number of oranges
The dependent variable for the given situation is: The cost of oranges
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Number of oranges
Question 20.
The dependent variable g represents the growth of a plant. What variables can represent independent variables in this situation?

Answer:
It is given that
The dependent variable g represents the growth of a plant
Now,
We know that,
An “Independent variable” causes the dependent variable to change
A “Dependent variable” change in response to another variable
Now,
From the given figure,
We can observe that
The independent variable for the given situation is: The number of plants
Hence, from the above,
We can conclude that
The independent variable for the given situation is: The number of plants
In 21 and 22, use the table at the right.
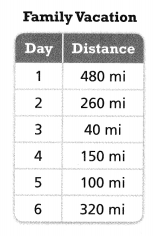
Question 21.
The table shows distances driven by the Williams family each day of their vacation. What is an independent variable that would affect the total distance they drove each day?
Answer:
It is given that
The table shows distances driven by the Williams family each day of their vacation
Now,
The given table is:

Now,
From the given table,
We can observe that
The independent variable that would affect the total distance is: Number of days
Hence, from the above,
We can conclude that
The independent variable that would affect the total distance is: Number of days
Question 22.
Name at least two dependent variables that could affect the amount of money the Williams family spends on meals during their vacation.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The independent variables that could affect the amount of money the Williams family spends on meals during their vacation is:
a. The number of items present during meals
b. The number of days
Hence, from the above,
We can conclude that
The independent variables that could affect the amount of money the Williams family spends on meals during their vacation is:
a. The number of items present during meals
b. The number of days
Question 23.
The cost of a salad at a restaurant depends on many factors. List at least two independent variables that could affect the cost of a salad.
Answer:
It is given that
The cost of a salad at a restaurant depends on many factors
So,
The independent variables that could affect the cost of a salad for the given situation is:
a. The amount of a salad
b. The type of restaurant
Hence, from the above,
We can conclude that
The independent variables that could affect the cost of a salad for the given situation is:
a. The amount of a salad
b. The type of restaurant
Question 24.
Julian drove from New York to Florida. List at least two independent variables that could affect the number of days Julian took to make the trip.
Answer:
It is given that
Julian drove from New York to Florida
So,
The independent variables that could affect the number of days Julian took to make the trip is:
a. The distance between New York and Florida
b. The number of hours she drove each day
Hence, from the above,
We can conclude that
The independent variables that could affect the number of days Julian took to make the trip is:
a. The distance between New York and Florida
b. The number of hours she drove each day
Question 25.
The number of incorrect answers and the score on a math test are related. What is the dependent variable in this relationship? Explain.
Answer:
It is given that
The number of incorrect answers and the score on a math test are related
Now,
From the given situation,
We can observe that
The dependent variable for the given situation is: The score on a math test
Hence, from the above,
We can conclude that
The dependent variable for the given situation is: The score on a math test
Question 26.
Higher Order Thinking Write a situation in which time, t, is an independent variable Then write a situation in which time, t, is a dependent variable.
Answer:
In the study of uniform motion, “Time” is an independent variable, denoted by t and represented on the horizontal axis, while position is a dependent variable, denoted by x and represented on the vertical axis.
“Time” is usually viewed as the independent variable for the simple reason that it doesn’t depend on anything else. Time simply ticks by at the same rate wherever you are (in non-relativistic context), independent of other variables so it doesn’t make sense to express time as a dependent variable
Assessment Practice
Question 27.
Jonas is concerned about the amount of water he uses to wash his laundry. He made a table to show the number of gallons of water used by different washing machines to complete a load of laundry.

PART A
Use variables to represent the independent and dependent quantities shown in the table.
Answer:
It is given that
Jonas is concerned about the amount of water he uses to wash his laundry. He made a table to show the number of gallons of water used by different washing machines to complete a load of laundry.
Now,
The given table is:

Now,
From the given table,
We can observe that
The independent variable for the given situation is: Type of Washing Machine
The dependent variable for the given situation is: Gallons of Water for a Washing Machine
Hence, from the above,
We can conclude that
The independent variable for the given situation is: Type of Washing Machine
The dependent variable for the given situation is: Gallons of Water for a Washing Machine
PART B
Use variables to represent the dependent variable and the independent variable in this sentence.
Jonas records the total cost of the water he uses and the number of gallons of water he uses.
Answer:
It is given that
Jonas records the total cost of the water he uses and the number of gallons of water he uses.
Now,
From the given sentence,
We can observe that
The independent variable for the given sentence is: Gallons of water
The dependent variable for the given sentence is: The total cost of water
Hence, from the above,
We can conclude that
The independent variable for the given sentence is: Gallons of water
The dependent variable for the given sentence is: The total cost of water
Lesson 4.9 Use Patterns to Write and Solve Equations
Solve & Discuss It!
The table below shows how many candles are in different numbers of boxes. Find a pattern that explains the relationship between the values of c and b. Use words and numbers to describe the pattern. How many candles will there be in 10 boxes?
I can… use patterns to write and solve equations with variables.

Answer:
It is given that
The table below shows how many candles are in different numbers of boxes.
Now,
The given table is:

Now,
From the given table,
We can observe that
The pattern that explains the relationship between the number of candles and the number of boxes is:
The number of boxes is one-fourth of the number of candles
Now,
The mathematical representation for the above pattern is:
The number of boxes = \(\frac{1}{4}\) × (The number of candles)
Now,
From the above relationship,
The number of candles present in 10 boxes is:
The number of boxes = \(\frac{1}{4}\) × (The number of candles)
10 = \(\frac{1}{4}\) × (The number of candles)
The number of candles = 10 × 4
The number of candles = 40
Hence, from the above,
We can conclude that
The pattern that explains the relationship between the number of candles and the number of boxes is:
The number of boxes is one-fourth of the number of candles
The number of candles present in 10 boxes is: 40 candles
Look for Relationships
How can you get from each value in the left column to its matching value in the right column?

Answer:
The given table is:

Now,
From the above Problem,
The mathematical representation for the pattern between the left column and the right column is:
The number of boxes = \(\frac{1}{4}\) × (The number of candles)
So,
The number of candles = 4 × (The number of boxes)
Hence, from the above,
We can conclude that
The relationship between each value in the left column to its matching value in the right column is:
The number of candles = 4 × (The number of boxes)
Focus on math practices
Use Structure Write a rule that explains how you get from the values in the right column of the table above to the values in the left column.
Answer:
The given table is:

Now,
The rule that explains the relationship between the values in the right column of the table to the values in the left column is:
The number of boxes = \(\frac{1}{4}\) × (The number of candles)
Essential Question
How can you use a pattern to write and solve an equation?
Answer:
Problems that are solved most easily by finding a pattern include those that ask students to extend a sequence of numbers or to make a prediction based on data. Finding a Pattern is an appropriate strategy to use to solve the problem. This is a pattern that is predictable and will be continuous
Try It!
The table shows the number of yards, y, that a professional bicyclist rides in s seconds. Find a pattern that relates the variables. If the cyclist maintains this speed, how far would the cyclist ride in 8 seconds?
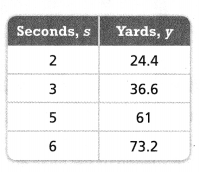
Answer:
It is given that
The table shows the number of yards, y, that a professional bicyclist rides in s seconds.
Now,
The given table is:

Now,
From the given table,
We can observe that
The relationship between the number of seconds, s, and the number of yards, y is:
12.2 × s = y
12.2s = y
Now,
The number of yards traveled by the cyclist in 8 seconds is:
12.2 × 8 = y
y = 97.6 yards
Hence, from the above,
We can conclude that
The relationship between the number of seconds, s, and the number of yards, y is:
12.2s = y
The number of yards traveled by the cyclist in 8 seconds is: 97.6 yards
Convince Me! How do you know that the equation you wrote describes the pattern in the table?
Answer:
The given table is:

Now,
From the above Problem,
The relationship (or) pattern between the number of seconds, s, and the number of yards, y is:
12.2s = y
Now,
Substitute 2, 3, 5 in the place of s
So,
y = 12.2 (2) = 24.4 yards
y = 12.2 (3) = 36.6 yards
y = 12.2 (5) = 61 yards
Hence, from the above,
We can conclude that
The equation that you wrote describes the pattern in the given table because the ratio between the number of seconds and the number of yards is constant
Try It!
If Ethan continues to pay $5 per week, how many more weeks will he need to pay his mother after 12 weeks? Explain.
Answer:
From Example 2,
It is given that
Ethan owes his mother $75 and he repays his mother a set amount of $5 each week
Now,
From Example 2,
The pattern for the given situation is: $75 – $5n
Where,
n is the number of weeks
Now,
For 12 weeks,
The amount Eathan owed to his mother = $75 – $5 (12)
= $75 – $60
= $15
Now,
We know that,
Eathan has to pay a set amount of $5 each week
So,
The number of weeks more Eathan has to pay $5 for his mother = \(\frac{$15}{$5}\)
= 3 weeks
Hence, from the above,
We can conclude that
The number of more weeks will ethan need to pay for his mother after 12 weeks is: 3 weeks
KEY CONCEPT
You can use patterns in a table to write an equation that relates the independent and dependent variables.

Do You Understand?
Question 1.
Essential Question How can you use a pattern to write and solve an equation?
Answer:
Problems that are solved most easily by finding a pattern include those that ask students to extend a sequence of numbers or to make a prediction based on data. Finding a Pattern is an appropriate strategy to use to solve the problem. This is a pattern that is predictable and will be continuous
Question 2.
Make Sense and Persevere How do you find a pattern that relates the values in a table?
Answer:
To determine the rule for a table, simply look at one pair of input/output numbers and figure out what number has been added, subtracted, multiplied, or divided by it. Then, make sure that pattern matches the rest of the numbers. Once you know the rule for a table, you can finish filling in the rest of it
Question 3.
Reasoning In Example 2, what happens to the value of the dependent variable, a, the amount still owed, when the value of the independent variable, w, the number of weeks Ethan pays $5, is increased by 1?
Answer:
From Example 2,
It is given that
Ethan owes his mother $75 and he repays his mother a set amount of $5 each week
Now,
From Example 2,
The pattern for the given situation is: $75 – $5n
Where,
n is the number of weeks
Now,
It is given that
Ethan owes his mother $75 and he repays his mothe a set amount of $s each week for 13 weeks
Now,
For 13 weeks,
The amount Eathan owed to his mother = $75 – $5 (13)
= $75 – $65
= $10
Hence, from the baove,
We can conclude that
The amount Etan still owed to his mother after 13 weeks is: $10
Question 4.
Look for Relationships Use the pattern in the table below to write an equation.

Answer:
The given table is:

Now,
From the given table,
We can observe that
The pattern between the values of x and y is:
y = 5x + 2
Hence, from the above,
We can conclude that
The pattern in the given table to represent as an equation is:
y = 5x + 2
Do You Know How?
Question 5.
The table shows Brenda’s age, b, when Talia’s age, t, is 7, 9, and 10. Find the pattern and then write a rule and an equation that represents the pattern. Then find Brenda’s age when Talia is 12.

Answer:
It is given that
The table shows Brenda’s age, b, when Talia’s age, t, is 7, 9, and 10.
Now,
The given table is:

Now,
From the given table,
We can observe that
The pattern between Talia’s age and Brenda’s age is:
Brenda’s age = Talia’s age – 5
b = t – 5
So,
Brenda’s age when Talia’s age is 12 is:
b = 12 – 5
b = 7 years
Hence, from the above,
We can conclude that
The pattern between Talia’s age and Brenda’s age is:
Brenda’s age = Talia’s age – 5
Brenda’s age when Talia’s age is 12 is: 7 years
In 6 and 7, use the table below.
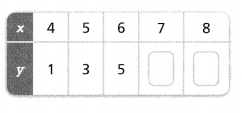
Question 6.
Use the equation y = 2x – 7 to complete the table.
Answer:
The given table is:

Now,
The given pattern (or) equation that represents the given table is:
y = 2x – 7
Now,
For x = 7,
y = 2 (7) – 7
= 14 – 7
= 7
For x = 8,
y = 2 (8) – 7
= 16 – 7
= 9
Hence, from the above,
We can conclude that
The completed table is:

Question 7.
State the rule for the pattern in words.
Answer:
The given pattern for the given table is:
y = 2x – 7
Now,
The given pattern in terms of words is:
The value of y is equal to the value of 7 less than the 2 times the value of x
Hence, from the above,
We can conclude that
The given pattern in terms of words is:
The value of y is equal to the value of 7 less than the 2 times the value of x
Practice & Problem Solving
In 8 and 9, write a rule and an equation that represents the pattern in each table.
Question 8.
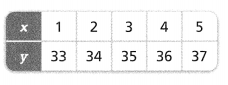
Answer:
The given table is:

Now,
From the given table,
We can observe that
The representation of the pattern for the given table in the form of an equation is:
y = x + 32
Hence, from the above,
We can conclude that
The equation that represents the pattern in the given table is:
y = x + 32
Question 9.
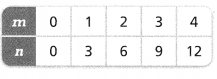
Answer:
The given table is:

Now,
From the given table,
We can observe that
The representation of the pattern for the given table in the form of an equation is:
n = 3m
Hence, from the above,
We can conclude that
The equation that represents the pattern in the given table is:
n = 3m
In 10 and 11, write a rule and an equation that represents the pattern in each table. Then complete the table.
Question 10.
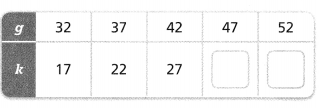
Answer:
The given table is:

Now,
From the given table,
We can observe that
The representation of the pattern for the given table in the form of an equation is:
k = g – 15
So,
The completed table by using the above pattern is:
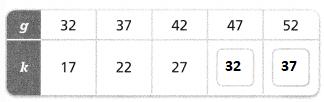
Hence, from the above,
We can conclude that
The equation that represents the pattern in the given table is:
k = g – 15
The completed table by using the above pattern is:

Question 11.

Answer:
The given table is:

Now,
From the given table,
We can observe that
The representation of the pattern for the given table in the form of an equation is:
y = \(\frac{x}{9}\)
So,
The completed table by using the above pattern is:
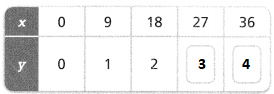
Hence, from the above,
We can conclude that
The equation that represents the pattern in the given table is:
y = \(\frac{x}{9}\)
The completed table by using the above pattern is:

Question 12.
To celebrate its 125th anniversary, a company produced 125 expensive teddy bears. These “125 Karat Teddy Bears” are made of gold thread and have diamonds for eyes. The table shows the approximate cost of different numbers of these bears. Write an equation that can be used to find c, the cost of n bears.
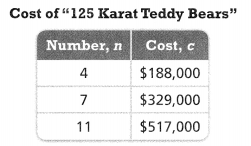
Answer:
It is given that
To celebrate its 125th anniversary, a company produced 125 expensive teddy bears. These “125 Karat Teddy Bears” are made of gold thread and have diamonds for eyes. The table shows the approximate cost of different numbers of these bears.
Now,
The given table is:

Now,
From the given table,
We can observe that
The pattern between the number of bears and the cost of bears is:
The cost of n Teddy bears = 47,000 × (n Teddy Bears)
So,
c = 47,000n
Hence, from the above,
We can conclude that
The equation that can be used to find c, the cost of n bears is:
c = 47,000n
Question 13.
Andrea attends the county fair. The fair charges for admission and for each ride is shown below.
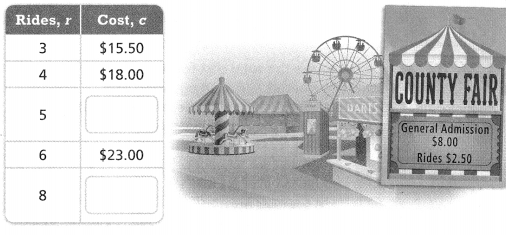
a. Use the pattern in the table to the find the cost for Andrea to ride 5 rides or 8 rides. Then write an equation for the pattern.
Answer:
It is given that
Andrea attends the county fair. The fair charges for admission and for each ride is shown
Now,
The given table is:
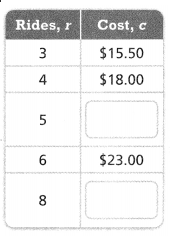
Now,
From the given table,
We can observe that
The pattern between the number of rides and the cost of rides is:
The cost of r rides = 2.5 × (Tne number of rides) + 8
So,
c = 2.5r + 8
Now,
The completed table by using the above pattern is:
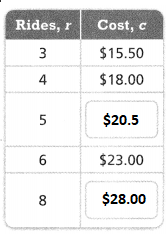
Hence, from the above,
We can conclude that
The pattern to find the cost for Andrea to ride 5 rides or 8rides is:
c = 2.5r + 8
The completed table by using the above pattern is:

b. Find the cost, c, for 12 rides.
Answer:
From Part (a),
The pattern to find the cost of r rides is:
c = 2.5r + 8
So,
The cost for 12 rides is:
c = 2.5 (12) + 8
c = $38
Hence, from the above,
We can conclude that
The cost for Andrea to ride 12 rides is: $38
In 14 and 15, write an equation that best describes the pattern in each table.
Question 14.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The pattern between w and z is:
z = w – 2
Hence, from the above,
We can conclude that
The equation that represents the pattern in the given table is:
z = w – 2
Question 15.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The pattern between x and y is:
y = 4x
Hence, from the above,
We can conclude that
The equation that represents the pattern in the given table is:
y = 4x
In 16-19, use the equation to complete each table.
Question 16.
t = 5d + 5
Answer:
The given equation is:
t = 5d + 5
Now,
The given table that is related to the given equation is:

Now,
For d = 3,
t = 5 (3) + 5
= 20
For d = 4,
t = 5 (4) + 5
= 25
So,
The completed table is:

Hence, from the above,
We can conclude that
The completed by using the given equation is:

Question 17.
y = \(\frac{1}{2}\)x – 1

Answer:
The given equation is:
y = \(\frac{1}{2}\)x – 1
Now,
The given table that is related to the given equation is:

Now,
For x = 8,
y = \(\frac{1}{2}\) (8) – 1
= 3
For x = 10,
y = \(\frac{1}{2}\) (10) – 1
= 4
So,
The completed table is:
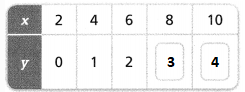
Hence, from the above,
We can conclude that
The completed by using the given equation is:

Question 18.
y = 2x + 1
Answer:
The given equation is:
y = 2x + 1
Now,
The given table that is related to the given equation is:

Now,
For x = 2,
y = 2 (2) + 1
= 5
For x = 3,
y = 2 (3) + 1
= 7
So,
The completed table is:
Hence, from the above,
We can conclude that
The completed by using the given equation is:

Question 19.
b = \(\frac{a}{2}\) – 2

Answer:
The given equation is:
b = \(\frac{a}{2}\) – 2
Now,
The given table that is related to the given equation is:

Now,
For a = 17,
b = \(\frac{17}{2}\) – 2
= 6.5
For a = 14,
b = \(\frac{14}{2}\) – 2
= 5
For a = 11,
b = \(\frac{11}{2}\) – 2
= 3.5
For a = 8,
b = \(\frac{8}{2}\) – 2
= 2
For a = 5,
b = \(\frac{5}{2}\) – 2
= 0.5
So,
The completed table is:
Hence, from the above,
We can conclude that
The completed by using the given equation is:

Question 20.
Higher Order Thinking Maya wrote the equation h= d+ 22 to represent the relationship shown in the table. Is this equation correct? Explain.
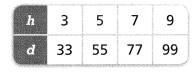
Answer:
It is given that
Maya wrote the equation h= d+ 22 to represent the relationship shown in the table.
Now,
The given table is:

Now,
From the given table,
We can observe that
The relationship between the values of h and d is:
d = 11h
So,
h = d + 22 and d = 11h are different relationships
Hence, from the above,
We can conclude that
h = d + 22 is not correct
Assessment Practice
Question 21.
The table below shows the total cost for the number of movie tickets purchased. Write an equation that represents the relationship between these two quantities. Use the equation to find the cost of 6 tickets.

Answer:
It is given that
The table below shows the total cost for the number of movie tickets purchased
Now,
The given table is:

Now,
From the given table,
We can purchase that
The relationship between the number of tickets and their cost is:
Cost of n tickets (c) = 8.75 × (Number of tickets)
So,
c = 8.75n
Where,
c is teh cost of n tickets
n is the number of tickets
Now,
The cost of 6 tickets by using the above pattern is:
c = 8.75 (6)
c = $52.5
Hence, from the above,
We can conclude that
The equation that represents the relationship between the number of tickets and their cost is:
c = 8.75n
The cost of 6 tickets by using the above equation is: $52.5
Lesson 4.10 Relate Tables, Graphs, and Equations
Solve & Discuss It!
Nancy walks 4 blocks to Maria’s house. Together, they continue the walk. The walk can be described as n = m + 4, where n is the number of blocks Nancy walks and m is the number of blocks Maria walks. Describe Nancy’s house how the equation, data table, and graph reflect the walk.
I can… analyze the relationship between dependent and independent variables in tables, graphs, and equations.
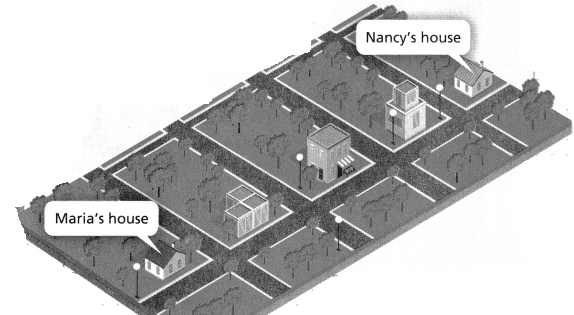
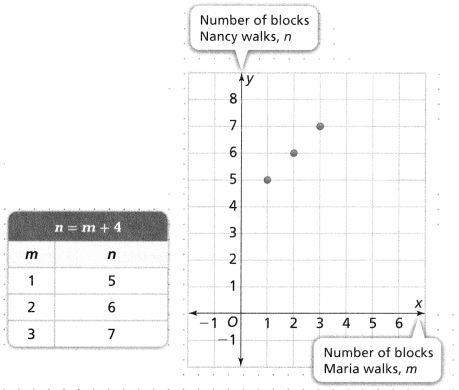
Answer:
It is given that
Nancy walks 4 blocks to Maria’s house. Together, they continue the walk. The walk can be described as n = m + 4, where n is the number of blocks Nancy walks and m is the number of blocks Maria walks.
Now,
The given equation that represents the given situation is:
n = m + 4
Where,
n is the number of blocks Nancy walks
m is the number of blocks Maria walks
Now,
From the given equation,
We can observe that
n is the output
m is the input
Now,
The given data table and the graph for the given situation is:

Now,
From the given data table,
We can observe that
m is the input
n is the output
We can take any value of input and calculate the value of output
Now,
From the given graph,
We can observe that
The graph can be drawn by taking the ordered pairs (m, n) and if we observe the graph, we can say that it is a straight line without passingthrough the origin
Look for Relationships How can you use the values in one row of the data table to describe the relationship shown in the equation, data table, and graph?

Answer:
From the above,
We know that,
The given equation that represents the given situation is:
n = m + 4
Where,
n is the number of blocks Nancy walks
m is the number of blocks Maria walks
Now,
From the given equation,
We can observe that
n is the output
m is the input
Now,
The given data table and the graph for the given situation is:

Now,
From the given data table,
We can observe that
m is the input
n is the output
We can take any value of input and calculate the value of output
Now,
From the given graph,
We can observe that
The graph can be drawn by taking the ordered pairs (m, n) and if we observe the graph, we can say that it is a straight line without passingthrough the origin
Focus on math practices
Model with Math Draw a line through the points on the graph. What ordered pair on the line includes m = 5? Explain what that ordered pair represents.
Answer:
The given data table is:

Now,
We know that,
The representation of the ordered pair is: (Input, Output)
Now,
From the given data table,
We can observe that
The ordered pairs are: (1, ), (2, 6), (3, 7)
So,
The representation of the ordered pairs in the coordinate plane is:
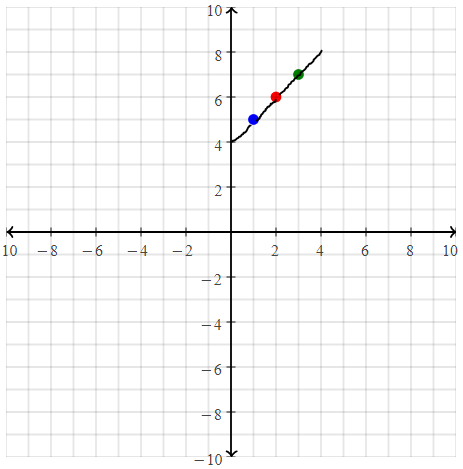
Now,
From the above,
We can observe that
The equation that represents the above situation is:
n = m + 4
Now,
For m = 5,
n = 5 + 4
= 9
So,
The ordered pair when m = 5 is: (5, 9)
The above ordered pair represents that
When Maria walks 5 blocks, Nncy walks 9 blocks
Hence, from the above,
We can conclude that
The ordered pair when m = 5 is: (5, 9)
The above ordered pair represents that
When Maria walks 5 blocks, Nancy walks 9 blocks
Essential Question
How can you analyze the relationship between dependent and independent variables using tables, graphs, and equations?
Answer:
In a graph, the X-axis runs horizontally (side to side) and the Y-axis runs vertically (up and down). Typically, the independent variable will be shown on the X axis and the dependent variable will be shown on the Y axis
In a table, the independent variable will be shown in the left side or the top of the column ans the dependent variable will be shown in the right side or the bottom of the column
In an equation, the independent variable will be shown at the right side of “=” and the dependent variable will be shown at the left side of “=”
Try It!
The booster club now raises $0.41 for each pom pom they sell. Complete the table and graph. Write and solve an equation to find how many pom poms they need to sell to raise $50.
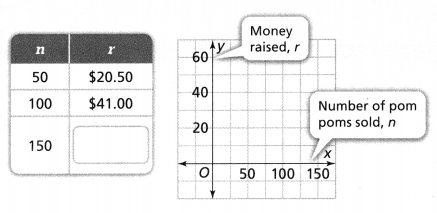
Answer:
It is given that
The booster club now raises $0.41 for each pom pom they sell.
Now,
From Example 1,
We can observe that
The representation of the equation that represents the amount of money raised to the number of pom poms sold is:
r = 0.45n
Where,
r is the amount of money raised
n is the number of pom poms
Now,
According to the given situation,
The representation of the equation that represents the amount of money raised to the number of pom poms sold is:
r = 0.41n
Now,
For n = 150,
r = 0.41 (150)
= 61.5
So,
The completed table is:

The representation of the graph in the coordinate plane according to the above table is:

Now,
For r = $50,
r = 0.41n
$50 = 0.41n
n = \(\frac{50}{0.41}\)
n = 121.95
n ≅ 122
Hence, from the above,
We can conclude that
The number of pom poms they needed to sell to raise $50 must be atleast 122 pom poms
Convince Me! How does finding three values for x and y help you represent the relationship between x and y?
Answer:
We know that,
In a graph,
The x-values represent on the horizontal axis and the y-values represent on the vertical axis
Now,
The representation of x and y values in a graph gives us the information that whether the equation is linear or not
Try It!
A company makes decorations for pens. All the supplies cost $5, and the company plans to sell the decorations for $2 apiece. Analyze the relationship between the number of decorations sold and the profit by completing the table and the graph. Use the table and the graph to write and solve an equation to find the number of decorations that must be sold for the company to make a $15 profit.
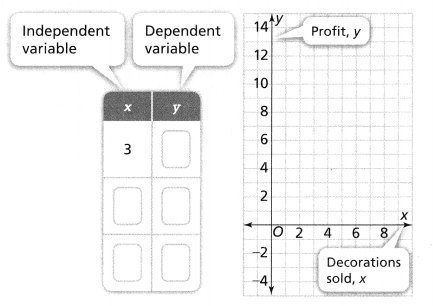
Answer:
It is given that
A company makes decorations for pens. All the supplies cost $5, and the company plans to sell the decorations for $2 apiece
Now,
Let the number of decorations be x
Let the profit be y
So,
The representation of the given situation in the form of an equation is:
Profit = $2 × (Number of decorations)
y = 2x
Now,
For x = 3,
y = 2 (3)
= 6
For x = 4,
y = 2 (4)
= 8
For x = 5,
y = 2 (5)
= 10
So,
The completed table for y = 2x is:
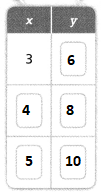
So,
The representation of the above table in the cordinate plane is:

Now,
The number of decorations that must be sold for the company to make a $15 profit is:
y = 2x
$15 = 2 (x)
x = \(\frac{15}{2}\)
x = 7.5
x ≅ 8
Hence, from the above,
We can conclude that
The number of decorations that must be sold for the company to make a profit of $15 should be about 8 decorations
KEY CONCEPT
You can analyze the relationship between independent and dependent variables in tables and graphs. You can relate tables and graphs to an equation.

Do You Understand?
Question 1.
Essential Question How can you analyze the relationship between dependent and independent variables using tables, graphs, and equations?
Answer:
In a graph, the X-axis runs horizontally (side to side) and the Y-axis runs vertically (up and down). Typically, the independent variable will be shown on the X axis and the dependent variable will be shown on the Y axis
In a table, the independent variable will be shown in the left side or the top of the column ans the dependent variable will be shown in the right side or the bottom of the column
In an equation, the independent variable will be shown at the right side of “=” and the dependent variable will be shown at the left side of “=”
Question 2.
Reasoning Using the relationship in Example 1, how many pom poms must the booster club sell to raise $75 for charity? Explain.
Answer:
From Example 1,
We know that,
The relationship between the amount of money raised and the number of pom poms sold is:
r = 0.45n
Where,
r is the amount of money raised
n is the number of pom poms sold
Now,
For r = $75,
75 = 0.45n
n = \(\frac{75}{0.45}\)
n = 166.66
n ≅ 167
Hence, from the above,
We can conclude that
The number of pom poms must booster club sell to raise $75 for charity should be at least 167 pom poms
Question 3.
Construct Arguments For every 4 bananas a grocery store sells, it sells 2 apples. Mary wrote the equation 4b × 2 = a, where b= the number of bananas sold and a = the number of apples sold. Does Mary’s equation correctly represent the relationship of bananas sold to apples sold? Explain.
Answer:
It is given that
For every 4 bananas a grocery store sells, it sells 2 apples. Mary wrote the equation 4b × 2 = a, where b= the number of bananas sold and a = the number of apples sold
Now,
According to the given information,
The representation of the given information in the form of an equation is:
4 × (The number of bananas) = 2 × (The number of apples)
So,
4b = 2a
4b × 2 = a and 4b = 2a are not the same
Hence, from the above,
We can conclude that
Mary’s equation does not correctly represent the relationship of bananas sold to apples sold
Do You Know How?
In 4-6, use the equation d = 4t.
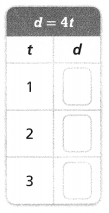
Question 4.
Complete the table.
d = distance t = time
Answer:
The given equation is: d = 4t
Now,
For t = 1,
d = 4 (1) = 4
For t = 2,
d = 4 (2) = 8
For t = 3,
d = 4 (3) = 12
So,
The completed table for the given equation is:
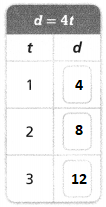
Hence, from the above,
We can conclude that
The completed table for d = 4t is:

Question 5.
Name four ordered pairs found on the line plotted using this equation.
Answer:
The given table is:

Now,
The representation of the given table in the coordinate plane is:
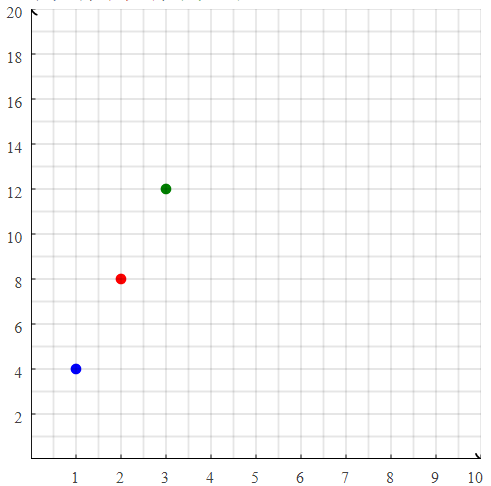
Hence, from the above,
We can conclude that
The ordered pairs found on the line plotted using the equation d = 4t are:
(1, 4), (2, 8), (3, 12)
Question 6.
Describe the relationship between the variables.
Answer:
The given equation is: d = 4t
Now,
From the given equation,
We can observe that
t is the independent variable (or) input
d is the dependent variable (or) output
Now,
From Question 5,
We can observe that
As the value of t increases, the value of d also increases
Hence, from the above,
We can conclude that
The relationship between the variables d and t in the equation d = 4t is:
As the value of t increases, the value of d also increases
In 7, complete the table and graph to show the relationship between the variables in the equation d = 5 + 5t.
Question 7.
d= distance
t = time
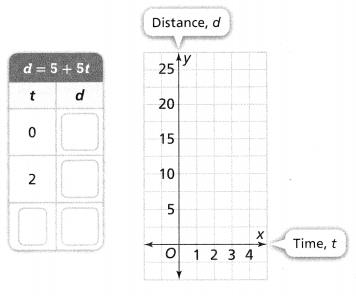
Answer:
The given equation is: d = 5 + 5t
Now,
For t = 0,
d = 5 + 0 = 5
For t = 2,
d = 5 + 5 (2)
= 5 + 10
= 15
For t = 4,
d = 5 + 5 (4)
= 5 + 20
= 25
So,
The completed table for the equation d = 5 + 5t is:
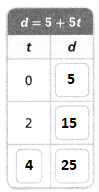
So,
The representation of the above table in the coordinate plane is:
Hence, from the above,
We can conclude that
The completed table and the graph to show the relationship between the variables in the equation d = 5 +5t are:


Practice & Problem Solving
In 8 and 9, complete the table and graph to show the relationship between the variables in each equation.
Question 8.
A rectangle is \(\frac{1}{2}\) inch longer than it is wide.
Let w = width.
Let l = length
Graph l = w + \(\frac{1}{2}\)

Answer:
It is given that
A rectangle is \(\frac{1}{2}\) inch longer than it is wide.
Now,
The given equation is:
l = w + \(\frac{1}{2}\)
Now,
For w = 1,
l = 1 + \(\frac{1}{2}\)
= 1 + 0.5
= 1.5
For w = 2,
l = 2 + \(\frac{1}{2}\)
= 2 + 0.5
= 2.5
For w = 3,
l = 3 + \(\frac{1}{2}\)
= 3 + 0.5
= 3.5
So,
The completed table for the equation l = w + \(\frac{1}{2}\) is:

So,
The representation of the above table in the coordinate plane is:

Hence, from the above,
We can conclude that
The completed table and the graph to show the relationship between the variables in the equation l = w + \(\frac{1}{2}\) are:


Question 9.
The sale price is $5 less than the regular price.
Let s = the sale price.
Let r = the regular price.
Graph s = r – 5.
Answer:
It is given that
The sale price is $5 less than the regular price.
Now,
The given equation is:
s = r – 5
Now,
For r = 10,
s = 10 – 5 = 5
For r = 20,
s = 20 – 5 = 15
For r = 30,
s = 30 – 5 = 25
So,
The completed table for the equation s = r – 5 is:
So,
The representation of the above table in the coordinate plane is:
Hence, from the above,
We can conclude that
The completed table and the graph to show the relationship between the variables in the equation l = w + \(\frac{1}{2}\) are:


Question 10.
The points (2, 4) and (-2, -4) are plotted on the coordinate plane using the equation y = a • x. How can you use the coordinates to find the value of a?
Answer:
It is given that
The points (2, 4) and (-2, -4) are plotted on the coordinate plane using the equation y = a • x
Now,
Compare the given points with (x, y)
Now,
The given equation is:
y = a . x
Now,
For (2, 4),
4 = a . 2
a = \(\frac{4}{2}\)
a = 2
Now,
For (-2, -4),
-4 = a . (-2)
4 = a . 2
a = \(\frac{4}{2}\)
a = 2
Hence, from the above,
We can conclude that
The value of a for the equation y = a . x is: 2
Question 11.
Without using a table or graph, identify three other points that a graph of the equation in Exercise 10 will pass through.
Answer:
From Question 10,
We know that,
The equation is: y = a . x
Now,
From Question 10,
We can observe that
The points that pss through y = a . x are: (2, 4), and (-2, -4)
Now,
For x = 3,
y = 2 . 3 = 6
For x = -3,
y = 2 . -3 = -6
For x = 4,
y = 2 . 4 = 8
Hence, from the above,
We can conclude that
The other three points that a graph of the equation y = a . x will pass through are: (3, 6), (-3, -6), and (4, 8)
Question 12.
Reasoning The Jackson family is planning a weekend vacation. They plan to rent a car from the ABC Car Rental Company. Let m represent the number of miles the family will drive. Let c represent the cost for renting a car. Write an equation that shows what the cost for renting a car will be.

Answer:
It is given that
The Jackson family is planning a weekend vacation. They plan to rent a car from the ABC Car Rental Company. Let m represent the number of miles the family will drive. Let c represent the cost for renting a car.
Now,
The given figure is:

Now,
According the given information,
The equation that represents the given situation is:
c = ($40 + $0.10)m
So,
c = $40.1m
Hence, from the above,
We can conclude that
The equation tht shows the cost for renting a car is:
c = $40.1m
In 13, write an equation. Complete the table and graph to solve the problem.
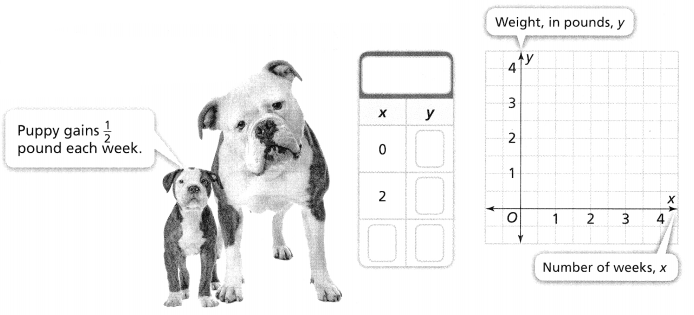
Question 13.
A puppy weighs 1 pound. What does the puppy weigh after 4 weeks?
Answer:
It is given that
A puppy weighs 1 pound and the puppy gains \(\frac{1}{2}\) each week
Now,
Let w be the number of weeks
Let p be the weight of the puppy
Now,
The completed table for the given information is:
Now,
The representation of the above table in the coordinate plane is:
Hence, from the above,
We can conclude that
The completed table and the completed graph for the given problem is:


Question 14.
Model with Math During a movie matinee, the film projector broke. The theater manager refunded the ticket price to everyone attending. Let n represent the number of people watching the movie. Let r represent the total amount of money refunded. Write an equation to represent the amount of money refunded.

Answer:
It is given that
During a movie matinee, the film projector broke. The theater manager refunded the ticket price to everyone attending. Let n represent the number of people watching the movie. Let r represent the total amount of money refunded.
Now,
The given figure is:

Now,
The amount of money collecting by selling the movie tickets = $5.00
Now,
The representation of the quation for the given information is:
The total amount of money refunded = $5 (The number of people watching the movie)
So,
r = 5n
Hence, from the above,
We can conclude that
The equation to represent the amount of money refunded is:
r = 5n
Question 15.
Higher Order Thinking Write an algebraic equation that matches the values shown in the table at the right. Explain how you solved the problem.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The pattern that describes the relationship between x and y is:
y = 3x + 5
Hence, from the above,
We can conclude that
The algebraic equation that matches the values shown in the table is:
y = 3x + 5
Assessment Practice
Question 16.
For every hour Sonia worked, she had made 2 seashell necklaces for her gift shop.

PART A
Write an equation that describes the relationship shown in the graph on the right.
Answer:
It is given that
For every hour Sonia worked, she had made 2 seashell necklaces for her gift shop.
Now,
The given graph that describes the given situation is:

Now,
From the given graph,
The representation of the quation that represents the given situation is:
The number of seashell necklaces = 2 × (Time in hours)
So,
n = 2h
Hence, from the above,
We can conclude that
The equation that describes the relationship shown in the graph is:
n = 2h
PART B
Describe the relationship between the variables in the graph and the equation.
Answer:
From Part A,
The equation that describes the relationship shown in the graph is:
n = 2h
Where,
n is the number of seashell necklaces
h is the number of hours
Now,
In the graph,
The x-axis represents the number of hours, h
The y-axis represents the number of seashell necklaces, n
Topic 4 Review
Topic Essential Question
What procedures can be used to write and solve equations and inequalities?
Answer:
The three methods most commonly used to solve systems of equation are substitution, and elimination. Substitution and elimination are simple methods that can effectively solve most systems of two equations in a few straightforward steps
The steps to solve an inequality are:
a. Add the same number to both sides.
b. Subtract the same number from both sides.
c. Multiply both sides by the same positive number.
d. Divide both sides by the same positive number.
e. Multiply both sides by the same negative number and reverse the sign
Vocabulary
Review Complete each definition with a vocabulary word.
Vocabulary
- dependent variable
- independent variable
- inequality
- equation
Question 1.
In the equation y = x + 9, the variable x is the ___________
Answer:
We know that,
In the equation y = x + 9,
x is called the “Independent variable”
Hence, from the above,
We can conclude that
The best term that is suitable for the given sentence is: Independent variable
Question 2.
A(n). __________ has an infinite number of solutions.
Answer:
We know that,
An “Inequality” has infinite number of solutions
Hence, from the above,
We can conclude that
The best term that is suitable for the given sentence is: Inequality
Question 3.
In the equation y = x -9, the variable y is the _________
Answer:
We know that,
In the equation y = x – 9,
y is called the “Dependent variable”
Hence, from the above,
We can conclude that
The best term that is suitable for the given sentence is: Dependent variable
Draw a line from each equation to the property of equality it illustrates.

Answer:
The equations that matched to the corresponding property of equality it illustrates is:

Use Vocabulary in Writing
Describe how to solve \(\frac{3}{7}\)n = 27. Use vocabulary words in your explanation.
Answer:
The given equation is:
\(\frac{3}{7}\)n = 27
Now,
From the given equation,
We can observe that
n is the variable
Now,
Multiply the given equation with \(\frac{7}{3}\) i.e., the reciprocal of \(\frac{3}{7}\) on both sides
So,
\(\frac{3}{7}\) × \(\frac{7}{3}\) × n = 27 × \(\frac{7}{3}\)
n = \(\frac{27 × 7}{3}\)
n = 9 × 7
n = 63
Hence, from the above,
We can conclude that
The value of n for the given equation is: 63
Concepts and Skills Review
Lesson 4.1 Understand Equations and Solutions
Quick Review
The solution of an equation makes the equation true. Substitute each of the given values into the equation for the variable to determine which value, if any, is a solution of the equation.
Example
Which value of x is a solution of the equation?
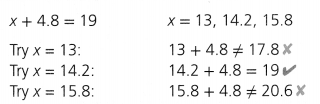
Practice
Tell which value of the variable, if any, is a solution of the equation.
Question 1.
d + 9 = 25
d = 6, 14, 16, 21
Answer:
The given equation is:
d + 9 = 25
Now,
For d = 6,
6 + 9 = 25
15 ≠ 25
For d = 14,
14 + 9 = 25
23 ≠ 25
For d = 16,
16 + 9 = 25
25 = 25
For d = 21,
21 + 9 = 25
30 ≠ 25
Hence, from the above,
We can conclude that
d = 16 is a solution of the givene quation
Question 2.
C – 8 = 25
C = 17, 28, 33, 35
Answer:
The givene quation is:
c – 8 = 25
Now,
For c = 17,
17 – 8 = 25
9 ≠ 25
For c = 28,
28 – 8 = 25
20 ≠ 25
For c = 33,
33 – 8 = 25
25 = 25
For c = 35,
35 – 8 = 25
27 ≠ 25
Hence, from the above,
We can conclude that
c = 33 is a solution of the given equation
Question 3.
2y = 30
y = 10, 12, 24, 36
Answer:
The given equation is:
2y = 30
Now,
Now,
For y = 10,
2 (10) = 30
20 ≠ 30
For y = 12,
2 (12) = 30
24 ≠30
For y = 24,
2 (24) = 30
48 ≠ 30
For y = 36,
2 (36) = 30
72 ≠ 30
Hence, from the above,
We can conclude that
The given equation does not have any solution from the given values of y
Question 4.
150 ÷ h = 50
h = 2, 3, 4, 5
Answer:
The given equation is:
150 ÷ h = 50
Now,
For h = 2,
150 ÷ 2 = 50
75 ≠ 50
For h = 3,
150 ÷ 3 = 50
50 = 50
For h = 4,
150 ÷ 4 = 50
37.5 ≠ 50
For h = 5,
150 ÷ 5 = 50
30 ≠ 50
Hence, from the above,
We can conclude that
h = 3 is a solution of the given equation
Question 5.
f – 13.2 = 28.9
f= 38.7, 42.2, 45.8, 51.4
Answer:
The given equation is:
f – 13.2 = 28.9
Now,
For f = 38.7,
38.7 – 13.2 = 28.9
25.5 ≠ 28.9
For f = 42.2,
42.2 – 13.2 = 28.9
29 ≠ 28.9
For f = 45.8,
45.8 – 13.2 = 28.9
32.6 ≠ 28.9
For f = 51.4,
51.4 – 13.2 = 28.9
38.2 ≠ 28.9
Hence, from the above,
We can conclude that
There are solutions for the given equation from the given values of f
Lesson 4.2 Apply Properties of Equality
Quick Review
The properties of equality allow you to apply the same operation with the same amount to both sides of an equation.
Example
The properties of equality are illustrated in the table.
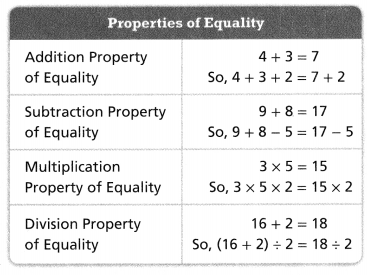
Practice
Question 1.
If 6+2 = 8, does 6 + 2 + 3 = 8+ 3? Why or why not?
Answer:
The given equations are:
6 + 2 = 8
6 + 2 + 3 = 8 + 3
Now,
According to “Addition Property of Equality”,
Add the same amount of number on both sides to make the equation balanced
So,
From the given equation,
We can observe that 3 is added on both sides
Hence, from the above,
We can conclude that
The given equations are the same by using the Addition Property of Equality
Question 2.
If 8 – 1 = 7, does 8 – 1 – 2 = 7 – 3? Why or why not?
Answer:
The given equations are:
8 – 1 = 7
8- 1 – 2 = 7 – 3
Now,
According to “Subtraction Property of Equality”,
Subtract the same amount of number from both sides to make the equation balanced
So,
From the given equation,
We can observe that
2 is subtracted from one side and 3 is subtracted from other side
Hence, from the above,
We can conclude that
The given equations are not the same by using the Subtraction Property of Equality
Question 3.
If 4 + 6 = 10, does (4 + 6) × 3 = 10 × 3? Why or why not?
Answer:
The given equations are:
4 + 6 = 10
(4 + 6) × 3 = 10 × 3
Now,
According to “Multiplication Property of Equality”,
Multiply the same amount of number on both sides to make the equation balanced
So,
From the given equation,
We can observe that 3 is multiplied on both sides
Hence, from the above,
We can conclude that
The given equations are the same by using the Multiplication Property of Equality
Question 4.
If 5 + 4 = 9, does (5 + 4) ÷ 3 = 9 ÷ 4? Why or why not?
Answer:
The given equations are:
5 + 4 = 9
(5 + 4) ÷ 3 = 9 ÷ 4
Now,
According to “Division Property of Equality”,
Divide the same amount of number on both sides to make the equation balanced
So,
From the given equation,
We can observe that
3 is divided on one side and 4 is divided on the other side
Hence, from the above,
We can conclude that
The given equations are not the same by using the Division Property of Equality
Lessons 4.3 AND 4.4 Write and Solve Addition, Subtraction, Multiplication, and Division Equations
Quick Review
Use the inverse relationship of addition and subtraction or multiplication and division to solve equations. To check, substitute your answer back into the original equation.
Example
23 + y = 57
23 + y – 23 = 57 – 23a
y = 34
a – 12 = 16
a – 12 + 12 = 16 + 12
a = 28
9z = 63
9z ÷ 9 = 63 ÷ 9
z = 7
c ÷ 4 = 24
c ÷ 4 × 4 = 24 × 4
c = 96
Practice
Solve for x.
Question 1.
8x = 64
Answer:
The given equation is:
8x = 64
Now,
Divide by 8 on both sides
So,
\(\frac{8x}{8}\) = \(\frac{64}{8}\)
x = 8
Hence, from the above,
We can conclude that
The value of x for the given equation is: 8
Question 2.
x + 2 = 11
Answer:
The given equation is:
x + 2 = 11
Now,
Subtract 2 on both sides
So,
x + 2 – 2 = 11 – 2
x = 9
Hence, from the above,
We can conclude that
The value of x for the given equation is: 9
Question 3.
x ÷ 20 = 120
Answer:
The given equation is:
x ÷ 20 = 120
Now,
Multiply with 20 on both sides
So,
(x ÷ 120) × 20 = 120 × 20
x = 2,400
Hence, from the above,
We can conclude that
The value of x for the given equation is: 2,400
Question 4.
x – 17 = 13
Answer:
The given equation is:
x – 17 = 13
Now,
Add 17 on both sides
So,
x – 17 + 17 = 13 + 17
x = 30
Hence, from the above,
We can conclude that
The value of x for the given equation is: 30
Question 5.
x ÷ 12 = 2
Answer:
The given equation is:
x ÷ 12 = 2
Now,
Multiply with 12 on both sides
So,
(x ÷ 12) × 12 = 2 × 12
x = 24
Hence, from the above,
We can conclude that
The value of x for the given equation is: 24
Question 6.
8 + x = 25
Answer:
The given equation is:
8 + x = 25
Now,
Subtract 8 on both sides
So,
8 + x – 8 = 25 – 8
x = 17
Hence, from the above,
We can conclude that
The value of x for the given equation is: 17
Question 7.
7x = 77
Answer:
The givene quation is:
7x = 77
Now,
Divide by 7 on both sides
So,
\(\frac{7x}{7}\) = \(\frac{77}{7}\)
x = 11
Hence, from the above,
We can conclude that
The value of x for the given equation is: 11
Question 8.
x – 236 = 450
Answer:
The given equation is:
x – 236 = 450
Now,
Add 236 on both sides
So,
x – 236 + 236 = 450 + 236
x = 686
Hence, from the above,
We can conclude that
The value of x for the given equation is: 686
Question 9.
26 = 13x
Answer:
The given equation is:
26 = 13x
Now,
Divide by 13 on both sides
So,
\(\frac{26}{13}\) = \(\frac{13x}{13}\)
2 = x
x = 2
Hence, from the above,
We can conclude that
The value of x for the given equation is: 2
Question 10.
x + 21.9 = 27.1
Answer:
The given equation is:
x + 21.9 = 27.1
Now,
Subtract 21.9 on both sides
So,
x + 21.9 – 21.9 = 27.1 – 21.9
x = 5.2
Hence, from the above,
We can conclude that
The value of x for the given equation is: 5.2
Question 11.
2,448 ÷ 48 = x
Answer:
The given equation is:
2,448 ÷ 48 = x
Now,
x = 2,448 ÷ 48
x = 51
Hence, from the above,
We can conclude that
The value of x for the given equation is: 51
Question 12.
x + 15 = 31
Answer:
The given equation is:
x + 15 = 31
Now,
Subtract with 15 on both sides
So,
x + 15 – 15 = 31 – 15
x = 16
Hence, from the above,
We can conclude that
The value of x for the given equation is: 16
Lesson 4.5 Write and Solve Equations with Rational Numbers
Quick Review
You can use inverse relationships and properties of equality to solve each equation.
Example
Solve w + 4\(\frac{1}{3}\) = 7.
Subtract 4\(\frac{1}{3}\) from both sides.
w + 4\(\frac{1}{3}\) – 4\(\frac{1}{3}\) = 7 – 4\(\frac{1}{3}\)
w = 2\(\frac{2}{3}\)
Solve \(\frac{3}{5}\)n = \(\frac{2}{3}\)
Multiply both sides by the reciprocal of \(\frac{3}{5}\).
\(\frac{5}{3} \times \frac{3}{5} n=\frac{5}{3} \times \frac{2}{3}\)
\(n=\frac{10}{9} \text { or } 1 \frac{1}{9}\)
Practice
In 1-8, solve for x.
Question 1.
x + 3\(\frac{5}{8}\) = 7\(\frac{1}{4}\)
Answer:
The given equation is:
x + 3\(\frac{5}{8}\) = 7\(\frac{1}{4}\)
Now,
x = 7\(\frac{1}{4}\) – 3\(\frac{5}{8}\)
So,
Hence, from the above,
We can conclude that
The value of x for the given equation is: 3\(\frac{5}{8}\)
Question 2.
x – \(\frac{4}{8}\) = 4\(\frac{1}{4}\)
Answer:
The given equation is:
x – \(\frac{4}{8}\) = 4\(\frac{1}{4}\)
Now,
x = 4\(\frac{1}{4}\) + \(\frac{4}{8}\)
So,
Hence, from the above,
We can conclude that
The value of x for the given equation is: 4\(\frac{3}{4}\)
Question 3.
x ÷ 15 = 8\(\frac{1}{3}\)
Answer:
The given equation is:
x ÷ 15 = 8\(\frac{1}{3}\)
Now,
x = 8\(\frac{1}{3}\) × 15
So,
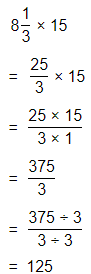
Hence, from the above,
We can conclude that
The value of x for the given equation is: 125
Question 4.
\(\frac{4}{2}\)x = 6
Answer:
The given equation is:
\(\frac{4}{2}\)x = 6
Now,
x = 6 × \(\frac{2}{4}\)
x = \(\frac{6 × 2}{4}\)
x = \(\frac{12}{4}\)
x = 3
Hence, from the above,
We can conclude that
The value of x for the given equation is: 3
Question 5.
\(\frac{x}{3}\) = 9
Answer:
The given equation is:
\(\frac{x}{3}\) = 9
Now,
x = 9 × 3
x = 27
Hence, from the above,
We can conclude that
The value of x for the given equation is: 27
Question 6.
14x = 73.5
Answer:
The given equation is:
14x = 73.5
Now,
x = \(\frac{73.5}{14}\)
x = 5.25
Hence, from the above,
We can conclude that
The value of x for the given equation is: 5.25
Question 7.
12x = 19.2
Answer:
The given equation is:
12x = 19.2
Now,
x = \(\frac{19.2}{12}\)
x = 1.6
Hence, from the above,
We can conclude that
The value of x for the given equation is: 1.6
Question 8.
17.9 – x = 12.8
Answer:
The given equation is:
17.9 – x = 12.8
Now,
x = 17.9 – 12.8
x = 5.1
Hence, from the above,
We can conclude that
The value of x for the given equation is: 5.1
Question 9.
Tomas buys a bag of 5 peaches for $3.55. Write and solve an equation to find how much money, m, Tomas paid for each peach.
Answer:
It is given that
Tomas buys a bag of 5 peaches for $3.55
Now,
The amount of money Tomas paid for each peach = (The amount of money Tomas paid for 5 peaches) ÷ (The number of peaches)
= \(\frac{$3.55}{5}\)
= $0.71
Hence, from the above,
We can conclude that
The amount of money Tomas paid for each peach is: $0.71
Question 10.
Krys has $1.54 and spends $0.76. Write and solve an equation to find how much money, m, Krys has left.
Answer:
It is given that
Krys has $1.54 and spends $0.76.
Now,
Let the amount of money Krys has left be x
So,
x = (The amount of money Krys has) – (The amount of money Krys spent)
x = $1.54 – $0.76
x = $0.78
Hence, from the above,
We can conclude that
The amount of money Krys has left is: $0.78
Lesson 4.6 Understand and Write Inequalities
Quick Review
An inequality is a mathematical sentence that contains < (less than), > (greater than), < (less than or equal to), 2 (greater than or equal to), or = (not equal to).
Example
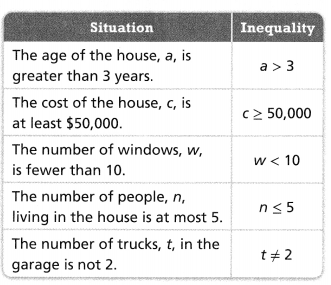
Practice
Write an inequality for each situation.
Question 1.
Up to 5 people, p, visited Mary today.
Answer:
The given situation is:
Up to 5 people, p, visited Mary today.
So,
The representation of the given situation in the form of an inequality is:
p ≤ 5
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
p ≤ 5
Question 2.
The value, v, of the hat is less than $9.
Answer:
The given situation is:
The value, v, of the hat is less than $9.
So,
The representation of the given situation in the form of an inequality is:
v < $9
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
v < $9
Question 3.
The number of guests, g, coming for dinner is not 8.
Answer:
The given situation is:
The number of guests, g, coming for dinner is not 8.
So,
The representation of the given situation in the form of an inequality is:
g ≠ 8
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
g ≠ 8
Question 4.
The distance of the race, d, is at least 6 miles.
Answer:
The given situation is:
The distance of the race, d, is at least 6 miles.
So,
The representation of the given situation in the form of an inequality is:
d ≥ 6 miles
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
d ≥ 6 miles
Question 5.
The time it takes to get to Grandma’s house, t, is longer than 2 hours.
Answer:
The given situation is:
The time it takes to get to Grandma’s house, t, is longer than 2 hours.
So,
The representation of the given situation in the form of an inequality is:
t > 2 hours
Hence, from the above,
We can conclude that
The representation of the given situation in the form of an inequality is:
t > 2 hours
Lesson 4.7 Solve Inequalities
Quick Review
To graph the solutions of an inequality on a number line, use an open circle for < or > and a closed circle for ≤ or ≥. If the values of the variable are less than the given number, shade to the left on the number line. If the values of the variable are greater than the given number, shade to the right on the number line.
Example
“Molly is less than 15 years old” is represented by the inequality x < 15. Write three ages that could represent Molly’s age.
To graph the inequality on a number line, draw an open circle at 15 and shade to the left of 15 because x is less than 15. Draw an arrow to show all numbers less than 15.

There are many solutions. Molly could be 10, 12, 14, or any age less than 15 years.
Practice
Write the inequality that each graph represents.
Question 1.
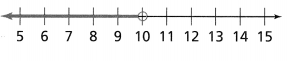
Answer:
The given number line is:

Now,
Let the solutions of the given number line be x
Now,
From the given number line,
We can observe that
There is an open circle on 10 and the list of numbers are on the left side of 10
So,
The representation of the given number line in the form of an inequality is:
x < 10
Hence, from the above,
We can conclude that
The representation of the given number line in the form of an inequality is:
x < 10
Question 2.

Answer:
The given number line is:

Now,
Let the solutions of the given number line be x
Now,
From the given number line,
We can observe that
There is an open circle on 5 and the list of numbers are on the right side of 5
So,
The representation of the given number line in the form of an inequality is:
x > 5
Hence, from the above,
We can conclude that
The representation of the given number line in the form of an inequality is:
x > 5
Question 3.
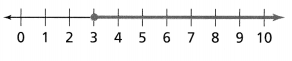
Answer:
The given number line is:

Now,
Let the solutions of the given number line be x
Now,
From the given number line,
We can observe that
There is a closed circle on 3 and the list of numbers are on the right side of 3
So,
The representation of the given number line in the form of an inequality is:
x ≥ 3
Hence, from the above,
We can conclude that
The representation of the given number line in the form of an inequality is:
x ≥ 3
Question 4.

Answer:
The given number line is:

Now,
Let the solutions of the given number line be x
Now,
From the given number line,
We can observe that
There is a closed circle on 7 and the list of numbers are on the left side of 7
So,
The representation of the given number line in the form of an inequality is:
x ≤ 7
Hence, from the above,
We can conclude that
The representation of the given number line in the form of an inequality is:
x ≤ 7
Lesson 4.8 Understand Dependent and Independent Variables
Quick Review
Think about how the values of variables affect each other.
To identify the dependent variable, ask yourself which variable depends on the other.
To identify the independent variable, ask yourself which variable causes the change.
Example
The spirit squad is washing cars. The equation m=2c represents the money they make, m, for washing c cars. Identify the dependent variable and the independent variable.
The amount of money the spirit squad makes depends on the number of cars they wash. The dependent variable is m.
The number of cars washed changes the amount of money made. The independent variable is c.
Practice
Identify the dependent variable and the independent variable in each situation.
Question 1.
The distance traveled, d, and the speed, s
Answer:
The given situation is:
The distance traveled, d, and the speed, s
Now,
To identify the “Dependent variable” ask yourself which variable depends on the other
To identify the “Independent variable”, ask yourself which variable causes the change
So,
The independent variable for the given situation is: d
The dependent variable for the given situation is: s
Hence, from the above,
We can conclude that
The independent variable for the given situation is: d
The dependent variable for the given situation is: s
Question 2.
The calories, c, in a snack and the amount of the snack, a
Answer:
The given situation is:
The calories, c, in a snack and the amount of the snack, a
Now,
To identify the “Dependent variable” ask yourself which variable depends on the other
To identify the “Independent variable”, ask yourself which variable causes the change
So,
The independent variable for the given situation is: c
The dependent variable for the given situation is: a
Hence, from the above,
We can conclude that
The independent variable for the given situation is: c
The dependent variable for the given situation is: a
Question 3.
The amount of money you have spent, s, and how much money you have left, m
Answer:
The given situation is:
The amount of money you have spent, s, and how much money you have left, m
Now,
To identify the “Dependent variable” ask yourself which variable depends on the other
To identify the “Independent variable”, ask yourself which variable causes the change
So,
The independent variable for the given situation is: s
The dependent variable for the given situation is: m
Hence, from the above,
We can conclude that
The independent variable for the given situation is: s
The dependent variable for the given situation is: m
Question 4.
The number of apple slices remaining, r, and the number of apple slices eaten, e
Answer:
The given situation is:
The number of apple slices remaining, r, and the number of apple slices eaten, e
Now,
To identify the “Dependent variable” ask yourself which variable depends on the other
To identify the “Independent variable”, ask yourself which variable causes the change
So,
The independent variable for the given situation is: e
The dependent variable for the given situation is: r
Hence, from the above,
We can conclude that
The independent variable for the given situation is: e
The dependent variable for the given situation is: r
Lesson 4.9 Use Patterns to Write and Solve Equations
Quick Review
Look for patterns between two related variables to find rules and write equations.
Example
Write a rule and an equation that represents the pattern. Then complete the table.
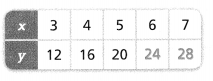
Find the rule and write an equation.
12 is 3 × 4
16 is 4 × 4
20 is 5 × 4
Rule: The value of y is 4 times the value of x.
Equation: y = 4x
Evaluate the equation for x = 6 and x = 7.
y = 4 × 6 = 24
y = 4 × 7 = 28
Practice
Question 1.
Find the pattern and then write a rule and an equation that represents the pattern. Then complete the table.

Answer:
The given table is:

Now,
From the given table,
We can observe that
The relationship (or) pattern between x and y is:
y = \(\frac{x}{2}\)
Now,
For x = 16,
y = \(\frac{16}{2}\)
y = 8
For x = 20,
y = \(\frac{20}{2}\)
y = 10
So,
The completed table by using the above relationship is:
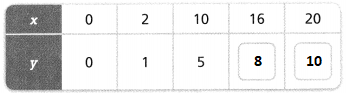
Hence, from the above,
We can conclude that
The completed table by using the above relationship is:

Question 2.
Use the equation to complete the table.
y = 6x + 1
Answer:
The given equation is:
y = 6x + 1
Now,
For x = 1,
y = 6 (1) + 1
= 7
For x = 2,
y = 6 (2) + 1
= 13
For x = 3,
y = 6 (3) + 1
= 19
For x = 4,
y = 6 (4) + 1
= 25
For x = 5,
y = 6 (5) + 1
= 31
So,
The completed table by uisng the above equation is:

Hence, from the above,
We can conclude that
The completed table by uisng the above equation is:

Lesson 4.10 Relate Tables, Graphs, and Equations
Quick Review
A table, equation, or graph can be used to analyze the relationship between dependent and independent variables. Ordered pairs that make an equation true can be used to graph the equation.
Example
Complete the table and graph to show the relationship between the variables in the equation t = s + 1.
A restaurant has a special that when you buy one sandwich you get a second sandwich for $1
Let s = price of one sandwich.
Let t = total price of two sandwiches.
Step 1
Make a table. Include at least three values.

Step 2
Graph each ordered pair on a coordinate plane. Then draw a line through the points.
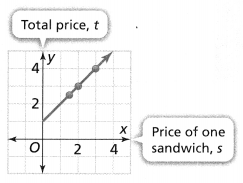
Practice
Question 1.
The cross country team practices by jogging on the town’s streets. The average jogging rate is 6 miles per hour. One member jogged for 3.5 hours one weekend. How many miles did the team member jog?
a. Complete the table to relate the number of miles to the number of hours jogged.
Answer:
It is given that
The cross country team practices by jogging on the town’s streets. The average jogging rate is 6 miles per hour. One member jogged for 3.5 hours one weekend.
So,
From the given situation,
We can observe that
The independent variable is: The number of hours the team member jogged
The dependent variable is: Number of miles the team member jogged
Now,
Let the dependent variable be y
Let the independent variable be y
So,
The relation between x and y from the given situation is:
y = 6x
Now,
The completed table by using the above equation is:
Hence, from the above,
We can conclude that
The completed table by using the above equation is:

b. Graph the ordered pairs on the coordinate plane.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The ordered pairs to draw in the coordinate plane is:
(1, 6), (2, 12), (3, 18)
Hence,
The representtaion of the given ordered pairs in the coordinate plane is:

c. Write an equation that describes the relationship. Then solve the problem.
Answer:
From part (a),
We know that,
The equation that describes the given situation is:
y = 6x
So,
The number of miles did the team member jog is:
y = 6x
= 6 (3.5)
= 21 miles
Hence, from the above,
We can conclude that
The number of miles did the team member jog is: 21 miles
Question 2.
Alex is making puppets for a show. He bought all the string needed for $125. It costs $18 for the remaining materials to make each puppet. What is the total cost to make 50 puppets?
Answer:
It is given that
Alex is making puppets for a show. He bought all the string needed for $125. It costs $18 for the remaining materials to make each puppet
So,
The total cost of the materials to make each puppet = $125 + $18
= $143
So,
The total cost to make 50 puppets = 50 × $143
= $7,150
Hence, from the above,
We can conclude that
The total cost to make 50 puppets = 50 × $143
= $7,150
Topic 4 Fluency Practice
Riddle Rearranging
Find each quotient. Then arrange the answers in order from least to greatest. The letters will spell out the answer to the riddle below.
I can… divide multi-digit numbers.

