Envision Math Common Core Grade 6 Answer Key Topic 7 Solve Area, Surface Area, And Volume Problems

Go through the enVision Math Common Core Grade 6 Answer Key Topic 7 Solve Area, Surface Area, And Volume Problems regularly and improve your accuracy in solving questions.

Envision Math Common Core 6th Grade Answers Key Topic 7 Solve Area, Surface Area, And Volume Problems

Topic 7 Essential Question

How can the areas of certain shapes be found? What are the meanings of surface area and volume and how can surface area and volume be found?

3-ACT MATH

That’s a Wrap
That’s a Wrap How you wrap a gift can say a lot about you. Some people conserve resources by reusing paper bags instead of purchasing wrapping paper. It may not look as nice at first, but you can unleash your crafty side and decorate the gift yourself.
No matter what you use to wrap a gift, you always need to consider the size of the object and how much paper you’ll need. Think about this during the 3-Act Mathematical Modeling lesson.

Topic 7 enVision STEM Project

Did You Know?
Food packaging is designed to identify products and to attract customers. Packaging also ensures food remains fresh and free from damage and contamination.

Common types of material used for packaging are paper, cardboard, glass, steel, and aluminum. The best material to use for packaging depends on the contents—for example, soup in a paper bag could be rather messy!

Manufacturers consider several factors when designing packaging, such as cost, amount of material used, and potential environmental impact. Steel food cans are the most recycled food package in the United States.

Packaging engineers consistently look for ways to innovate. Some food packaging is now selfopening, self-closing, or selfheating. Some packaging is biodegradable. Other advances include edible packaging.

Your Task: Pack It
Food packaging engineers consider many elements related to both form and function when designing packaging. How do engineers make decisions about package designs as they consider constraints, such as limited dimensions or materials? You and your classmates will use the engineering design process to explore and propose food packaging that satisfies certain criteria.

Topic 7 Get Ready!

Review What You Know!

Vocabulary
Choose the best term from the box to complete each definition.

• area
• parallelogram
• perpendicular
• polygon
• volume

Question 1.
A triangle is an example of a three-sided ___________

Answer:
A triangle is an example of a three-sided polygon.

Explanation:
In the above-given question,
given that,
A triangle is an example of a three-sided polygon.
for example:
equilateral triangle: all the sides are equal lengths, and all the internal angles are 60 degrees.
so a triangle is an example of a three-sided polygon.

Question 2.
________ lines form a right angle.

Answer:
Perpendicular lines form a right angle.

Explanation:
In the above-given question,
given that,
perpendicular lines form a right angle.
for example:
two lines that intersect and form right angles are called perpendicular lines.

Question 3.
__________ is the number of cubic units needed to fill a solid figure.

Answer:
Volume is the number of cubic units needed to fill a solid figure.

Explanation:
In the above-given question,
given that,
Volume is the number of cubic units needed to fill a solid figure.
for example:
A plane figure is a two-dimensional figure.
so volume is the number of cubic units needed to fill a solid figure.

Question 4.
__________ as opposite sides that are parallel and the same length.

Answer:
A parallelogram as opposite sides that are parallel and the same length.

Explanation:
In the above-given question,
given that,
A parallelogram has opposite sides that are parallel and the same length.
for example:
A rhombus is a parallelogram with sides that are all equal length.

Evaluate Expressions

Find the value of each expression when a = 12, b = 3, c = 4, and d = 9.
Question 5.
ac

Answer:
ac = 48.

Explanation:
In the above-given question,
given that,
a = 12, b = 3, c = 4, and d = 9.
ac = 12 x 4.
ac = 48.

Question 6.
\(\frac{1}{2}\)b

Answer:
3/2.

Explanation:
In the above-given question,
given that,
a = 12, b = 3, c = 4, and d = 9.
(1/2)b.
1/2 x 3.
3/2.

Question 7.
abd

Answer:
abd = 324.

Explanation:
In the above-given question,
given that,
a = 12, b = 3, c = 4, and d = 9.
abd = 12 x 3 x 9.
abd = 36 x 9.
abd = 324.

Question 8.
0.5a

Answer:
6.

Explanation:
In the above-given question,
given that,
a = 12, b = 3, c = 4, and d = 9.
0.5a = 0.5 x 12.
0.5a = 6.

Question 9.
\(\frac{3}{4}\)(ad)

Answer:
81.

Explanation:
In the above-given question,
given that,
a = 12, b = 3, c = 4, and d = 9.
(3/4)ad.
3/4 x 12 x 9.
3 x 3 x 9.
9 x 9 = 81.

Question 10.
ab + cd

Answer:
ab + cd = 72.

Explanation:
In the above-given question,
given that,
a = 12, b = 3, c = 4, and d = 9.
ab + cd.
12 x 3 + 4 x 9.
36 + 36.
72.

Multiplication

Find each product.
Question 11.
3.14 × 12

Answer:
3.14 x 12 = 37.68.

Explanation:
In the above-given question,
given that,
the numbers are 3.14 and 12.
find the product.
3.14 x 12.
37.68.

Question 12.
45.8 × 5

Answer:
45.8 x 5 = 229.

Explanation:
In the above-given question,
given that,
the numbers are 45.8 and 5.
find the product.
45.8 x 5.
229.

Question 13.
0.8 × 2.7

Answer:
2.16.

Explanation:
In the above-given question,
given that,
the numbers are 0.8 and 2.7.
find the product.
0.8 x 2.7.
2.16.

Question 14.
14 × 7.25 × 2.5

Answer:
14 x 7.25 x 2.5 = 253.75.

Explanation:
In the above-given question,
given that,
the numbers are 14, 7.25, and 2.5.
find the product.
14 x 7.25 x 2.5.
101.5 x 2.5.
253.75.

Question 15.
1\(\frac{1}{2}\) × \(\frac{1}{4}\)

Answer:
0.375.

Explanation:
In the above-given question,
given that,
the numbers are 3/2 and 1/4.
find the product.
3/2 x 1/4.
1.5 x 0.25.
0.375.

Question 16.
2\(\frac{1}{3}\) × 2\(\frac{1}{4}\) × 1\(\frac{3}{8}\)

Answer:
7.115.

Explanation:
In the above-given question,
given that,
the numbers are 7/3, 9/4, and 11/8.
find the product.
7/3 x 9/4 x 11/8.
2.3 x 2.25 x 1.375.
5.175 x 1.375.
7.115.

Geometry

Question 17.
How are parallelograms and rectangles similar and how are they different?

Answer:
The main difference between them is that a parallelogram has opposite sides that are equal.

Explanation:
In the above-given question,
given that,
the main difference between them is that a parallelogram has opposite sides equal.
while in a rectangle, the opposite sides are equal with all its adjacent sides being perpendicular to each.

Question 18.
How are the formulas for the area of a rectangle and the area of a triangle alike and different? Explain.

Answer:
Area of the rectangle = l x b.
area of the triangle = 1/2 x b x h.

Explanation:
In the above-given question,
given that,
the area of the rectangle = l x b.
where l = length and b = breadth.
the area of the triangle = 1/2 x b x h.
where b = base.
h = perpendicular height.

Language Development
Use the graphic organizer to help relate new vocabulary in this topic to terms you studied in previous topics.

Pick A Project

PROJECT 7A
If you could pick the shape of a building to live in, what shape would it be?
PROJECT: COMPARE CUBE-SHAPED BUILDINGS

PROJECT 7B
What are some ways you can use number cubes?
PROJECT: DRAW NETS OF NUMBER CUBES

PROJECT 7C
How far do you think a roll of wrapping paper reaches?
PROJECT: CALCULATE THE AMOUNT OF GIFT WRAP

PROJECT 7D
What sorts of music do you like?
PROJECT: WRITE A RAP BATTLE

Lesson 7.1 Find Areas of Parallelograms and Rhombuses

Solve & Discuss It!
Sofía drew the grid below and plotted the points A, B, C, and D. Connect point A to B, B to C, C to D, and D to A. Then find the area of the shape and explain how you found it. Using the same grid, move points B and C four units to the right. Connect the points to make a new parallelogram ABCD. What is the area of this shape?

I can… use what I know about areas of rectangles to find the areas of parallelograms and rhombuses.

Look for Relationships
What relationships do you see between rectangles and parallelograms?

Focus on math practices
Generalize How can you find the area of any parallelogram?

Answer:
Area of the parallelogram = b x h.

Explanation:
In the above-given question,
given that,
the area of the parallelogram = base x height.
area of the parallelogram = b x h.

Essential Question
How can you use the area formula of a rectangle to find the area formula of a parallelogram?

Try It!

Find the area of the parallelogram.

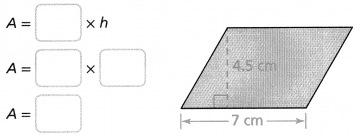
The area of the parallelogram is ________ cm².

Answer:
The area of the parallelogram = 31.5 sq cm.

Explanation:
In the above-given question,
given that,
area of the parallelogram = b x h.
area = 7 cm x 4.5 cm.
where b = base and h = height.
area = 31.5 sq cm.

Convince Me! Compare the area of this parallelogram to the area of a rectangle with a length of 7 cm and a width of 4.5 cm. Explain.

Answer:
Area = 15.75 sq cm.

Explanation:
In the above-given question,
given that,
area of the rectangle = 1/2( b x h).
area =1/2( 7 cm x 4.5 cm).
area = 1/2(31.5).
area = 15.75.

Try It!

a. Find the area of the rhombus.

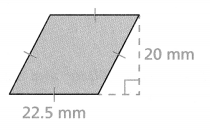
Answer:
Area of the rhombus = 21.25.

Explanation:
In the above-given question,
given that,
area of the rhombus = pq/2.
area = 22.5 + 20/2.
area = 42.5/2.
area = 21.25.

b. The area of the parallelogram is 65 ft². What is its height?

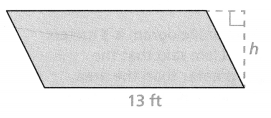
Answer:
The area of the parallelogram = 5 ft.

Explanation:
In the above-given question,
given that,
area = 65 sq ft.
area = b x h.
65 = 13 x h.
h = 65/13.
h = 5.
so the area of the parallelogram = 5 ft.

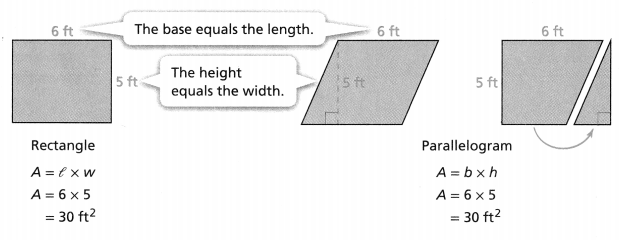
KEY CONCEPT
You can decompose a parallelogram and compose a rectangle to find the area of a parallelogram or a rhombus. The formula for the area of a rectangle, A = l × w, can be written as the formula A = b × h to find the area of a parallelogram or the area of a rhombus.

Do You Understand?
Question 1.
Essential Question How can you use the area formula of a rectangle to find the area formula of a parallelogram?

Answer:
The area of the rectangle = 30 sq ft.
The area of the parallelogram = 30 sq ft.

Explanation:
In the above-given question,
given that,
the area of the rectangle = l x w.
area = length x width.
for example:
area = 6 ft x 5 ft.
area = 30 sq ft.
the area of the parallelogram = b x h.
area = 6 ft x 5 ft.
area = 30 sq ft.

Question 2.
Ken combined a triangle and a trapezoid to make a parallelogram. If the area of the triangle is 12 in.² and the area of the trapezoid is 24 in.², what is the area of the parallelogram? Explain.

Answer:
The area of the parallelogram =

Explanation:
In the above-given question,
given that,
Ken combined a triangle and a trapezoid to make a parallelogram.
If the area of the triangle is 12 in.^{2and the area of the trapezoid is 24 in.2.}
area of the parallelogram = b x h.
area = 12 x 24.
area = 288 sq in.
so the area of the parallelogram = 288 sq in.

Question 3.
Critique Reasoning A parallelogram is 3 meters long and 7 meters high. Liam said that the parallelogram’s area is greater than the area of a rectangle with the same dimensions. Is he correct? Explain.

Answer:
Yes, he was correct.

Explanation:
In the above-given question,
given that,
A parallelogram is 3 meters long and 7 meters high.
area of the parallelogram = b x h.
area = 7 x 3.
area = 21.
so he was correct.

Do You Know How?
In 4-6, use a formula to find the area.
Question 4.

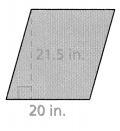
Answer:
The area of the parallelogram = 430.

Explanation:
In the above-given question,
given that,
the area of the parallelogram = b x h.
area = 20 x 21.5.
area = 430.
so the area of the parallelogram = 430.

Question 5.

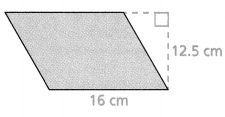
Answer:
The area of the parallelogram = 200.

Explanation:
In the above-given question,
given that,
the area of the parallelogram = b x h.
area = 16 x 12.5.
area = 200.
so the area of the parallelogram = 200.

Question 6.

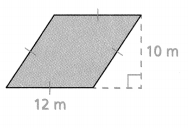
Answer:
The area of the parallelogram = 120.

Explanation:
In the above-given question,
given that,
the area of the parallelogram = b x h.
area = 12 x 10.
area = 120.
so the area of the parallelogram = 120.

Question 7.
A rhombus has an area of 440 m² and a base of 22 m. What is its height?

Answer:
The diagonal of the rhombus = 40.

Explanation:
In the above-given question,
given that,
A rhombus has an area of 440 sq m and a base of 22 m.
area of the rhombus = pq/2.
where p = diagonal and q = diagonal.
area = pq/2.
440 = px 22/2.
440 = 11p.
p = 440/11.
p = 40.

Practice & Problem Solving

Leveled Practice In 8–11, find the area of each parallelogram or rhombus.
Question 8.

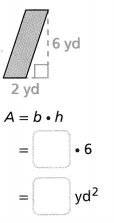
Answer:
The area of the parallelogram = 12 sq yd.

Explanation:
In the above-given question,
given that,
area of the quadrilateral = b x h.
where b = base and h = height.
area = 2 x 6.
area = 12 sq yd.

Question 9.

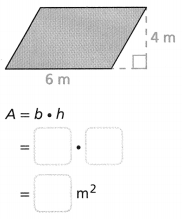
Answer:
Area = 24 sq m.

Explanation:
In the above-given question,
given that,
area of the parallelogram = b x h.
where b = base and h = height.
area = 6 x 4.
area = 24 sq m.

Question 10.

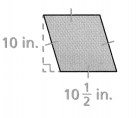
Answer:
The area of the rhombus = 52.5.

Explanation:
In the above-given question,
given that,
area of the rhombus = pq/2.
where p = diagonal and q = diagonal.
area = pq/2.
area = 10.5 x 10 /2.
area = 52.5.

Question 11.

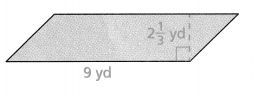
Answer:
Area = 20.7 sq yd.

Explanation:
In the above-given question,
given that,
area of the parallelogram = b x h.
where b = base and h = height.
area = 9 x 7/3.
area = 9 x 2.3.
area = 20.7 sq yd.

Question 12.
The area of the parallelogram is 132 in.². What is the height of the parallelogram?

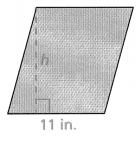
Answer:
height = 12 in.

Explanation:
In the above-given question,
given that,
area of the parallelogram = b x h.
where b = base and h = height.
132 = 11 x h.
h = 12  in.

Question 13.
The area of the rhombus is 52 m² What is the base of the rhombus?

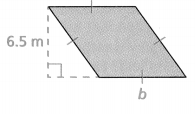
Answer:
The diagonal of the rhombus = 16.

Explanation:
In the above-given question,
given that,
A rhombus has an area of 52 sq m and a base of 6.5 m.
area of the rhombus = pq/2.
where p = diagonal and q = diagonal.
area = pq/2.
52 = px 6.5/2.
52 = 3.25p.
p = 52/3.25.
p = 16.

Question 14.
Micah and Jason made parallelogram-shaped stained glass windows with the same area. The height of Micah’s window is 9 inches, and its base is 10 inches. The height of Jason’s window is 6 inches. What is the base of Jason’s window?

Answer:
The base of Jason’s window = 15 in.

Explanation:
In the above-given question,
given that,
Micah and Jason made parallelogram-shaped stained glass windows with the same area.
The height of Micah’s window is 9 inches, and its base is 10 inches.
The height of Jason’s window is 6 inches.
area = b x h.
90 = b x 6.
b = 90/6.
b = 15.
so the base of Jason’s window = 15 in.

Question 15.
A rectangle has a length of 8 m and a width of 4.5 m. A parallelogram has a length of 6 m. The area of the parallelogram is twice the area of the rectangle. What is the height of the parallelogram?

Answer:
The height of the parallelogram = 3m.

Explanation:
In the above-given question,
given that,
A rectangle has a length of 8 m and a width of 4.5 m.
A parallelogram has a length of 6 m.
area of rectangle = 8 x 4.5.
area = 36.
area of parallelogram = 6 x h.
18 = 6 x h.
h = 18/6.
h = 3.

In 16 and 17, use the picture at the right.

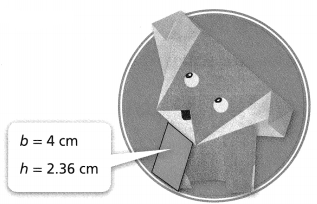
Question 16.
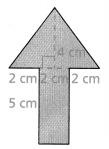
Hilary made an origami dog. What is the area of the parallelogram that is highlighted in the origami figure?

Answer:
The area of the parallelogram = 9.44 sq cm.

Explanation:
In the above-given question,
given that,
area of the parallelogram = b x h.
area = 4 cm x 2.36 cm.
b = base and h = height.
area = 9.44 sq cm.

Question 17.
A type of origami paper comes in 15 cm by 15 cm square sheets. Hilary used two sheets to make the origami dog. What is the total area of the origami paper that Hilary used to make the dog?

Answer:
The total area of the origami papaer = 225 sq cm.

Explanation:
In the above-given question,
given that,
A type of origami paper comes in 15 cm by 15 cm square sheets.
Hilary used two sheets to make the origami dog.
the total area of the origami paper = 15 x 15.
area = 225 sq cm.
so the total area of the origami paper = 225 sq cm.

Question 18.
Reasoning A rectangle and a parallelogram have the same base and the same height. How are their areas related? Provide an example to justify your answer.

Answer:
area = 1/2 x bh.

Explanation:
In the above-given question,
given that,
A rectangle and a parallelogram have the same base and the same height.
area of the rectangle = 1/2 b x h.
area = half of the base x height.
area of the parallelogram = l x w.
where l = length and w = weight.

Question 19.
Soshi’s rhombus has a base of 12 in. and a height of 10 in. Jack’s rhombus has base and height measures that are double those of Soshi’s rhombus. Compare the area of Jack’s rhombus to the area of Soshi’s rhombus. Explain.

Answer:
The area of Jack’s rhombus to the area of Soshi’s rhombus = 120.

Explanation:
In the above-given question,
given that,
Soshi’s rhombus has a base of 12 in. and a height of 10 in.
Jack’s rhombus has base and height measures that are double those of Soshi’s rhombus.
area = pq/2.
area = 12 x 10/2.
area = 120/2.
area = 60.
so the area of Jack’s rhombus to the area of Soshi’s rhombus = 120.

Question 20.
Higher Order Thinking The infield of a baseball diamond is in the shape of a rhombus. An infield cover with dimensions of 85 feet by 100 feet is used to protect the field during rainy weather. Will the cover protect the entire infield? Explain.

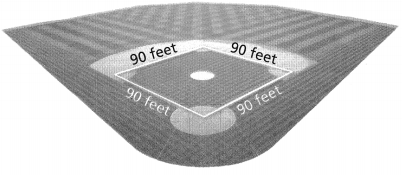
Answer:
The area of the rhombus = 90 ft.

Explanation:
In the above-given question,
given that,
The infield of a baseball diamond is in the shape of a rhombus.
An infield cover with dimensions of 85 feet by 100 feet is used to protect the field during rainy weather.
area of the rhombus = pq/2.
area = 90 x 90/2.
area = 180/2.
area = 90.
so the area of the rhombus = 90 ft.

Assessment Practice

Question 21.
The parking space shown at the right has an area of 209 ft². A custom truck has rectangular dimensions of 13.5 ft by 8.5 ft. Can the truck fit in the parking space? Justify your answer.

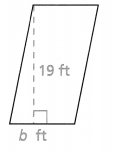
Answer:
Yes, the truck fits in the parking space.

Explanation:
In the above-given question,
given that,
The parking space shown at the right has an area of 209 ft^{2.
A custom truck has rectangular dimensions of 13.5 ft by 8.5 ft.
area of the parallelogram = b x h.
209 = b x 19.
b = 209/19.
b = 11.}
the rectangular dimensions of 13.5 ft by 8.5 ft.
area = 13.5 x 8.5 ft.
area = 114.75.

Lesson 7.2 Solve Triangle Area Problems

Solve & Discuss It!
Connect point A to B, B to C, C to D, and D to A. Then draw a diagonal line connecting opposite vertices in the figure and find the area of each triangle formed.
I can… find the areas of triangles.

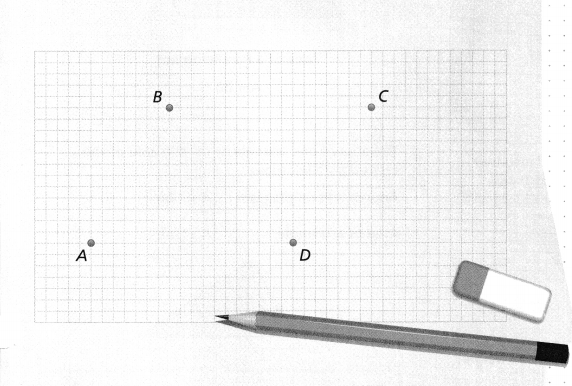
Use Structure
What relationships do you see between the area of the parallelogram and the areas of the triangles?

Focus on math practices
Generalize What is a rule for finding the area of any triangle?

Answer:
The area of the triangle = b x h/2.

Explanation:
In the above-given question,
given that,
the area of the triangle = b x h/2.
where b = base.
h = height.
so the area of the triangle = b x h/2.

Essential Question
How can you find the area of a triangle?

Try It!

Use the formula A = \(\frac{1}{2}\)bh to find the area of the triangle.

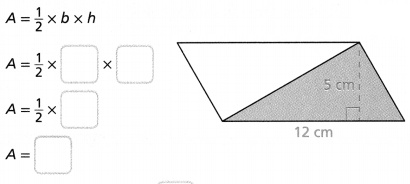
The area of the triangle is _________ cm²

Answer:
The area of the triangle = 30 sq cm.

Explanation:
In the above-given question,
given that,
area = 1/2 x b x h.
area = 1/2 x 12 x 5.
area = 1/2 x 60.
area = 30.
so the area of the triangle = 30 sq cm.

Convince Me! Two identical triangles form a parallelogram with a base of 8 inches and a height of 6 inches. What is the area of each triangle? Explain.

Try It!

Find the area of each triangle.
a.

Answer:
Area = 27 sq cm.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 9cm x 6cm.
area = 1/2 x 54.
area = 27 sq cm.

b.

Answer:
Area = 18 sq m.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 12m x 3m.
area = 1/2 x 36.
area = 18 sq m.

KEY CONCEPT
You can use the formula A = \(\frac{1}{2}\)bh to find the area of any triangle.

Do You Understand?
Question 1.
Essential Question How can you find the area of a triangle?

Answer:
The area of the triangle = 1/2bh.

Explanation:
In the above-given question,
given that,
to find the area of any triangle, we can use the formula.
area = 1/2 bh.
so the area of the triangle = 1/2bh.

Question 2.
Reasoning If you cut a rectangle into 2 identical triangles, what type of triangles will they be?

Answer:
The triangles formed are right-angled triangles.

Explanation:
In the above-given question,
given that,
the area of any triangle, we can use the formula.
area = 1/2 bh.
so the area of the triangle = 1/2bh.
the triangles formed are right-angled triangles.

Question 3.
Construct Arguments In Example 1, if the other diagonal were used to divide the parallelogram into two triangles, would the area of each of these triangles be half the area of the parallelogram? Explain.

Answer:
Yes, the area of each of these triangles is half the area of the parallelogram.

Explanation:
In the above-given question,
given that,
the area of the parallelogram = b x h.
where b = base.
h = height.
so the area of each of these triangles is half the area of the parallelogram.

Do You Know How?
In 4-6, find the area of each triangle.
Question 4.

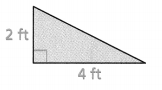
Answer:
Area = 4 sq ft.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 2ft x 4ft.
area = 1/2 x 8.
area = 4 sq ft.

Question 5.

Answer:
Area = 7.35 sq in.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 4.2 x 3.5.
area = 1/2 x 14.7.
area = 7.35 sq in.

Question 6.

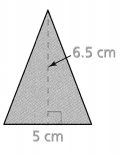
Answer:
Area = 16.25 sq cm.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 5 cm x 6.5 cm.
area = 1/2 x 32.5.
area = 16.25 sq cm.

Practice & Problem Solving

Leveled Practice In 7-12, find the area of each triangle.
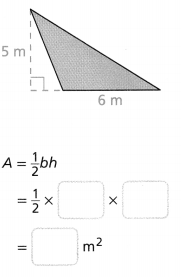
Question 7.

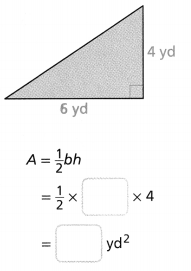
Answer:
Area = 12 sq yd.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 6 yd x 4 yd.
area = 1/2 x 24 sq yd.
area = 12 sq yd.

Question 8.

Answer:
Area = 15 sq m.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 6m x 5m.
area = 1/2 x 30.
area = 15 sq m.

Question 9.

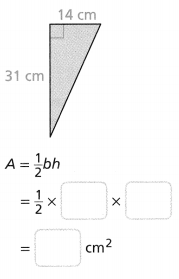
Answer:
Area = 91 sq cm.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 14 cm x 13 cm.
area = 1/2 x 182.
area = 91 sq cm.

Question 10.

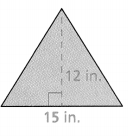
Answer:
Area = 90 sq in.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 15 in x 12 in.
area = 1/2 x 180.
area = 90 sq in.

Question 11.

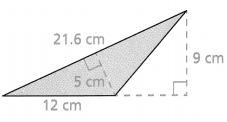
Answer:
Area = 54 sq cm.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 12 cm x 9 cm.
area = 1/2 x 108.
area = 54 sq cm.

Question 12.

Answer:
Area = 24 sq m.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
area = 1/2 x 8m x 6m.
area = 1/2 x 48.
area = 24 sq m.

Question 13.
The vertices of a triangle are A(0, 0), B(3, 8), and C(9, 0). What is the area of this triangle?

Answer:
The area of this triangle = -4.

Explanation:
In the above-given question,
given that,
the vertices of a triangle are A(0,0), B(3, 8), and C(9, 0).
x1 = 0, x2 = 3, x3 = 9.
y1 = 0, y2 = 8, y3 = 0.
area = 1/2[x1(y2-y3) + x2(y3 – y1) + x3(y1 – y2)].
area = 1/2[0(8) + 3(0) + 9(-8)].
arae = 1/2(-8).
area = -4.

Question 14.
Be Precise The base of a triangle is 2 ft. The height of the triangle is 15 in. What is the area of the triangle in square inches?

Answer:
Area of the triangle = 144 sq in.

Explanation:
In the above-given question,
given that,
The base of a triangle is 2 ft.
The height of the triangle is 15 in.
1 ft = 12 in.
2 ft = 24 in.
area = b x h.
area = 1/2 x 24 x 12.
area = 1/2(288).
area = 144 sq in.

Question 15.
Reasoning Ms. Lopez drew △ ABC, with a height of 6 inches and a base of 6 inches, and △RST, with a height of 4 inches and a base of 8 inches. Which triangle has the greater area? Use an area formula to justify your answer.

Answer:
Triangle ABC has the greater area.

Explanation:
In the above-given question,
given that,
Ms. Lopez drew △ ABC, with a height of 6 inches and a base of 6 inches, and △RST, with a height of 4 inches and a base of 8 inches.
area of the trianglee ABC = 1/2 x 6  x 6.
where b = base and h = height.
area = 1/2 x 36.
area = 18 sq in.
area of the triangle RST = 1/2 x 8 x 4.
area = 1/2 x 32.
area = 16 sq in.
so the triangle ABC has the greater area.

Question 16.
The dimensions of the sail for Erica’s sailboat are shown. Find the area of the sail.

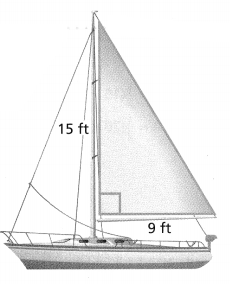
Answer:
Area of the sail = 67.5 sq ft.

Explanation:
In the above-given question,
given that,
area of the sail = 1/2 x b x h.
area = 1/2 x 9 x 15.
area = 1/2 x 135.
area = 67.5 sq ft.
so the area of the sail = 67.5 sq ft.

In 17 and 18, use the picture at the right.

Question 17.
Be Precise What is the area in square millimeters of the yellow triangle outlined on the origami figure at the right?

Answer:
Area = 2.64.

Explanation:
In the above-given question,
given that,
b = 3 cm.
h = 1.76 cm.
area = 1/2 x b x h.
area = 1/2 x 3 x 1.76.
area = 5.28/2.
area = 2.64.

Question 18.
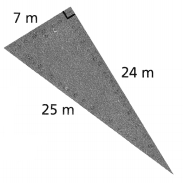
The nose of the origami dog is a right triangle with sides that are 2 cm, 3 cm, and 3.6 cm long. What is the area of this triangle?

Answer:
Area = 3 sq cm.

Explanation:
In the above-given question,
given that,
b = 3 cm.
h = 2 cm.
area = 1/2 x b x h.
area = 1/2 x 3 x 2.
area = 6/2.
area = 3 sq cm.

Question 19.
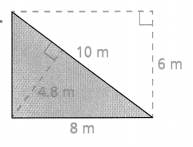
Michael is planting a garden in the shape of a right triangle. He wants 4 tickseed plants for each square meter of area. How many 25 m tickseed plants does Michael want in the garden?

Answer:
The 25 m tickseed plants does Michae want in the garden = 84.

Explanation:
In the above-given question,
given that,
Michael is planting a garden in the shape of a right triangle.
He wants 4 tickseed plants for each square meter of area.
area = 1/2 x b x h.
where b = base.
h = height.
area = 1/2 x 7 x 24.
area = 168/2.
area = 84.
so the 25 m tickseed plants does Michae want in the garden = 84.

Question 20.
Higher Order Thinking If you know the area and the height of a triangle, how can you find the base?
Answer:

Assessment Practice

Question 21.
Select all expressions that represent the area of the given triangle.

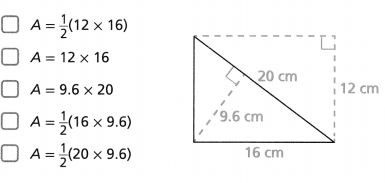
Answer:
Options A and E are correct.

Explanation:
In the above-given question,
given that,
area = 1/2 x 16 x 12.
where b = 16 cm.
height = 12 cm.
area = 1/2 x 192.
area = 96.
so options A and E are correct.

Lesson 7.3 Find Areas of Trapezoids and Kites

Explain It!
The European basketball key was changed from a trapezoid shape to a rectangle in 2010. The diagram shows the shape of the key before 2010 outlined in blue.

I can… find areas of trapezoids and kites.

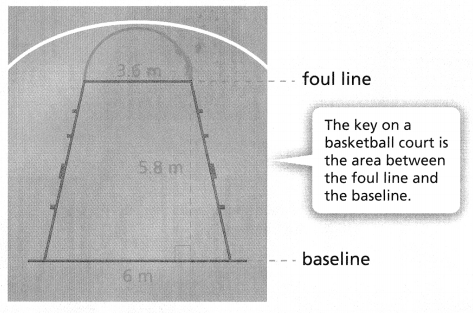
A. Construct Arguments Tim finds the area of the key by multiplying the base by the height. Does his strategy make sense?

Answer:
Yes.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
where b = base.
h = height.
area = 1/2 x 6 x 5.8.
area = 1/2 x 34.8.
area = 17.4.

B. Use Structure How could Tim find the area of the trapezoid by decomposing it into shapes he knows? What is the area of the key?
Answer:

Focus on math practices
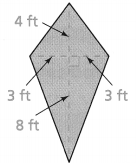
Use Structure How can you find the area of this kite? Explain.

Essential Question
How can you find the areas of trapezoids and kites?

Try It!

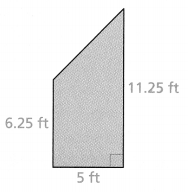
How would you decompose this trapezoid to find its area? Find the area of the trapezoid.

Answer:
The area of the trapezoid = 22.5 sq ft.

Explanation:
In the above-given question,
given that,
area of the trapezoid = 11.25 + 5 + 6.25.
area = 22.5.
so the area of the trapezoid = 22.5 sq ft.

Convince Me! How is finding the area of the trapezoid in Example 1 different from finding the area of the trapezoid in the Try It!?

Try It!

Find the area of the trapezoid and the area of the kite.
a.

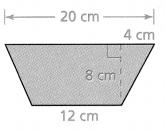
Answer:
Area of the trapezoid = 144 sq cm.

Explanation:
In the above-given question,
given that,
area = 24 cm + 24 cm + 96.
area = 48 cm + 96.
area = 144 sq cm.

b.

Answer:
Area of the kite = 72 sq in.

Explanation:
In the above-given question,
given that,
each triangle = 1/2 x 24 x 3.
triangle = 1/2 x 72.
triangle = 36 sq in.
Kite = 36 + 36.
kite = 72 sq in.

KEY CONCEPT
You can find the area of a trapezoid or a kite by decomposing the shapes into rectangles and triangles.

Do You Understand?
Question 1.
Essential Question How can you find the areas of trapezoids and kites?

Answer:
Area of the trapezoid = area of the triangle + area of the rectangle.
area of the kite = area of the triangle.

Explanation:
In the above-given question,
given that,
area of the trapezoid = area of the triangle + area of the rectangle.
area of the kite = area of the triangle.

Question 2.
Draw a line to divide the pasture in Example 1 into two triangles. What are the measures of the bases and the heights of the two triangles?
Answer:

Question 3.
Construct Arguments In Example 3, how could you use 4 triangles to find the kite’s area?
Answer:

Do You Know How?
In 4-6, find the area of each trapezoid or kite.
Question 4.

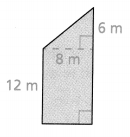
Answer:
Area of the kite = 16 sq m.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
where b = 2m and height = 8 m.
area = 1/2 x 2 x 8.
area = 16/2.
area = 8 sq m.
area of the kite = 8 + 8.
area = 16 sq m.

Question 5.

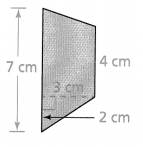
Answer:
Area of the kite = 6 sq cm.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
where b = 2cm and height = 3 cm.
area = 1/2 x 2 x 3.
area = 6/2.
area = 3 sq cm.
area of the kite = 3 + 3.
area = 6 sq cm.

Question 6.

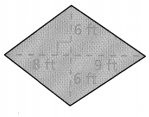
Answer:
Area of the kite = 90 sq ft.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 x b x h.
where b = 15 and height = 6 ft.
area = 1/2 x 15 x 6.
area = 90/2.
area = 45 sq ft.
area of the kite = 45 + 45.
area = 90 sq ft.

Practice & Problem Solving

Leveled Practice In 7-12, find the area of each trapezoid or kite.
Question 7.

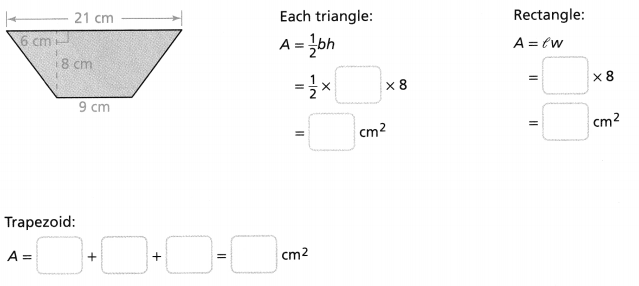
Answer:
Area of the trapezoid = 168 sq cm.

Explanation:
In the above-given question,
given that,
area of the trapezoid = area of each triangle + area of the rectangle.
area of the triangle = 1/2 x h x b.
area = 1/2 x 12 x 8.
area = 1/2 x 96.
area = 48.
area of the rectangle = l x w.
area = 9 x 8.
area = 72.
area of the trapezoid = 48 + 48 + 72.
area = 168 sq cm.

Question 8.

Answer:
Area of the trapezoid = 54 sq cm.

Explanation:
In the above-given question,
given that,
area of the trapezoid = area of each triangle + area of the rectangle.
area of the triangle = 1/2 x h x b.
area = 1/2 x 6 x 4.
area = 1/2 x 24.
area = 12.
area of the rectangle = l x w.
area = 5 x 6.
area = 30.
area of the trapezoid = 12 + 12 + 30.
area = 24 + 30 sq cm.
area = 54 sq cm.

Question 9.

Answer:
Area of the kite = 33 sq cm.

Explanation:
In the above-given question,
given that,
area of the kite = area of the triangle + area of the triangle.
area of the triangle = 1/2 x b x h.
where b = base and h = height.
area = 1/2 x 11 x 3.
area = 1/2 x 33.
area = 16.5.
area of the kite = 16.5 + 16.5.
area = 33.

Question 10.

Answer:
Area of the kite = 112 sq yd.

Explanation:
In the above-given question,
given that,
area of the kite = area of the triangle + area of the triangle.
area of the triangle = 1/2 x b x h.
where b = base and h = height.
area = 1/2 x 14 x 8.
area = 1/2 x 112.
area = 56.
area of the kite = 56 + 56.
area = 112 sq yd.

Question 11.
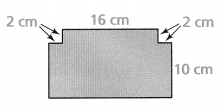
A sidewall of a building is shown below. What is the area of the wall?

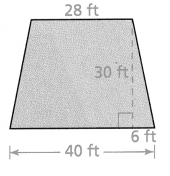
Answer:
Area of the trapezoid = 1020 sq ft.

Explanation:
In the above-given question,
given that,
area of the trapezoid = area of the triangle + area of the rectangle.
area of the triangle = 1/2 x b x h.
area = 1/2 x 6 x 30.
area = 180/2.
area = 90.
area of the rectangle = l x w.
area = 28 x 30.
area = 840.
area of the trapezoid = 90 + 90 + 840.
area = 180 + 840.
area = 1020.

Question 12.
Be Precise The window has the shape of a kite. How many square meters of glass were used to make the window?

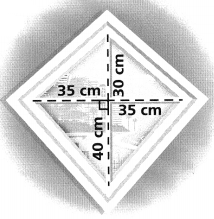
Answer:
The area of the Kite = 1225 sq cm.

Explanation:
In the above-given question,
given that,
area of the kite = area of the triangle.
area of the triangle = 1/2 x b x h.
area = 1/2 x 70 x 35.
area = 2450/2.
area = 1225.
area of the kite = 1225 + 1225.
area = 1225 sq cm.

Question 13.
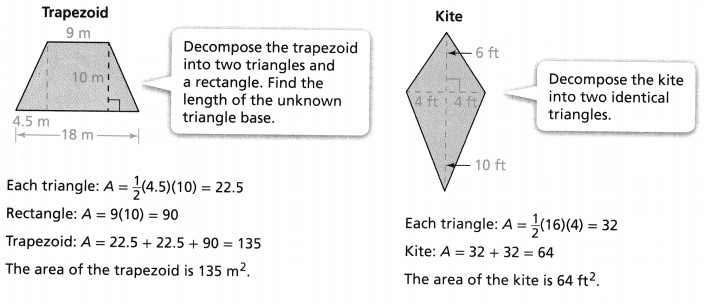
The area of the kite is 30 m². What is the value of x? Explain.

Answer:
The value of x = 6 m.

Explanation:
In the above-given question,
given that,
the area of the kite = 30 sq m.
area of the triangle = 1/2 x b x h.
30 = 1/2 x 10 x h.
30 = 5h.
h = 30/5.
h = 6.

Question 14.
Make Sense and Persevere Hunter drew two identical trapezoids and composed them to form a parallelogram. Use the area of the parallelogram to find the area of one trapezoid. Explain.

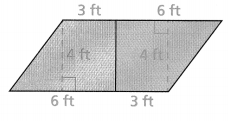
Answer:
The area of the trapezoid = 36 sq ft.

Explanation:
In the above-given question,
given that,
area of the parallelogram = b x h.
area = 9 x 4.
area = 36 sq ft.

Question 15.
Higher Order Thinking A craftsman wants to build this symmetrical fiddle. He needs to know the area of the face of the fiddle. How could he use the measurements shown to find the area? Use your strategy to find the area of the face of the fiddle.

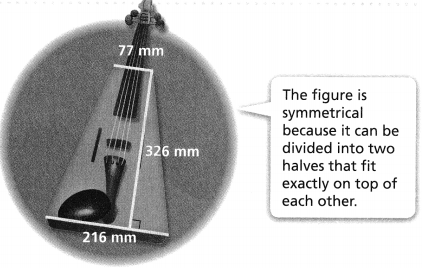
Answer:
The area of the fiddle = 35208 sq mm.

Explanation:
In the above-given question,
given that,
area of the fiddle = 1/2 x 326 x 216.
area = 1/2 x 70416.
area = 35208.
so the area of the fiddle = 35208 sq mm.

Assessment Practice

Question 16.
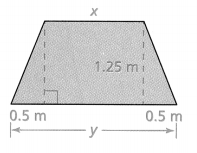
Marique is making a large table in the shape of a trapezoid. She needs to calculate the area of the table. The longest side of the table is twice as long as the table’s width. Find the area of the table by decomposing the trapezoid into familiar shapes. Show your work.

Answer:
The area of the trapezoid = 0.9375.

Explanation:
In the above-given question,
given that,
area of the trapezoid = area of the triangle + area of the rectangle.
area of the triangle = 1/2 x b x h.
area = 1/2 x 0.5 x 1.25.
area = 1/2 x 0.625.
area = 0.3125.
area of the rectangle = l x w.
area = 0.5 x 1.25.
area = 0.625.
area = 0.3125 + 0.625.
area = 0.9375.
so the area of the trapezoid = 0.9375.

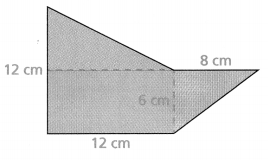
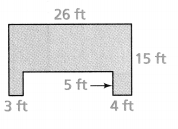
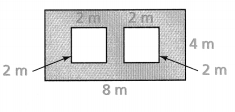
Lesson 7.4 Find Areas of Polygons

Solve & Discuss It!
Gabrielle wants to cover the floors of a room and a hallway in her dollhouse. She measured the room and hallway and sketched the floor plan below. How much felt does Gabrielle need?
I can… find the areas of polygons.

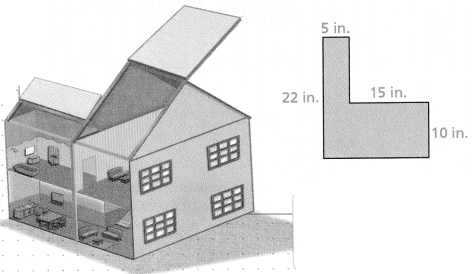
Answer:
Area of the polygon = 205 sq in.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the triangle + area of the triangle + area of the rectangle.
area = 1/2 x 15 x 10.
area = 1/2 x 150.
area = 75.
area = 1/2 x 22 x 5.
area = 1/2 x 110.
area = 55.
area of the polygon = 75 + 55 + 75.
area = 150 + 55.
area = 205.

Make Sense and Persevere
How can you decompose the sketch into regular shapes?

Focus on math practices
Make Sense and Persevere Show another way to find the area of the sketch.

Essential Question
How can you find the areas of polygons?

Try It!

Shari found the area of the patio by composing the shapes as shown at the right. How is Shari’s strategy different?

Answer:
Area of the polygon = 30 sq m.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the triangle + area of the triangle + area of the rectangle.
area = 1/2 x 3 x 2.
area = 1/2 x 6.
area = 3.
area = 1/2 x 2 x 3.
area = 1/2 x 6.
area = 3.
area of the polygon = 3 + 3 + 24.
area = 6 + 24.
area = 30.

Convince Me! How could you decompose the figure in the Try It! into two rectangles?

Try It!

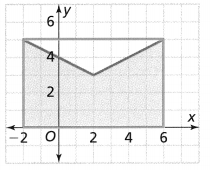
Find the area of the shaded region in square units.

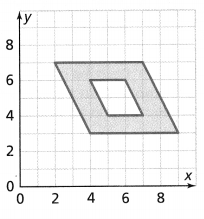
Answer:

KEY CONCEPT
There are many ways to find the area of a polygon. You can decompose or compose shapes, or you can use addition or subtraction, to calculate the area.
Use Addition

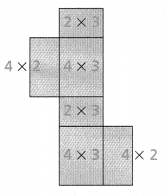
Blue triangle: A = \(\frac{1}{2}\)(12)(6) = 36
Green triangle: A = \(\frac{1}{2}\)(8)(6) = 24
Rectangle: A = (12)(6) = 72
36 + 24 + 72 = 132
The area of the polygon is 132 cm².

Use Subtraction

Draw a rectangle around the polygon.
Rectangle: A = 8 × 5 = 40
Triangle: A = \(\frac{1}{2}\) × 8 × 2 = 8
40 – 8 = 32
The area of the polygon is 32 square units.

Do You Understand?
Question 1.
Essential Question How can you find the areas of polygons?

Answer:
The area of the polygon = area of the triangle + area of the triangle + area of the rectangle.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the triangle + area of the triangle + area of the rectangle.
area of the triangle = 1/2 x b x h.
where b = base.
h = height.
area of the rectangle = l x w.
where l = length.
w = width.
so the area of the polygon = area of the triangle + area of the triangle + area of the rectangle.

Question 2.
Describe a way in which you can use subtraction to find the area of the shape in Exercise 4.
Answer:

Question 3.
Model with Math Describe how to break the floor plan in Example 3 into a trapezoid and a rectangle. Use coordinates to describe the line you can draw.
Answer:

Do You Know How?
In 4 and 5, find the area of each polygon.
Question 4.

Answer:
Area of the polygon = 280 sq in.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the small rectangle + area of the rectangle.
area of small rectangle = 8 x 10.
area = 80 sq in.
area of the rectangle = 20 x 10.
area = 200.
area of the polygon = 80 + 200.
area = 280 sq in.

Question 5.
A polygon with vertices at (6, 2), (9,5), (12, 2), (12, -4), and (6, -4)

Answer:

Practice & Problem Solving

In 6-9, find the area of each polygon or shaded region.
Question 6.

Answer:
Area of the polygon = 200 sq ft.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the small rectangle + area of the small rectangle + area of the big rectangle.
area of the small rectangle = 15 x 3.
area = 45.
area of the another small rectangle = 15 x 4.
area = 60.
area of the big rectangle = 19 x 5.
area = 95.
area of the polygon = 45 + 60 + 95.
area of the polygon = 200.

Question 7.

Answer:
Area of the polygon = 232 sq cm.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the small rectangle + area of the small rectangle + area of the big rectangle.
area of the small rectangle = 10 x 2.
area = 20.
area of the another small rectangle = 10 x 2.
area = 20.
area of the big rectangle = 16 x 12.
area = 192.
area of the polygon = 20 + 20 + 192.
area of the polygon = 232.

Question 8.

Answer:
Area of the polygon = 24 sq m.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the small rectangle + area of the small rectangle + area of the big rectangle.
area of the small rectangle = 2 x 2.
area = 4.
area of the another small rectangle = 2 x 2.
area = 4.
area of the big rectangle = 4 x 4.
area = 16.
area of the polygon = 16 + 4 + 4.
area of the polygon = 24.

Question 9.

Answer:
Area of the polygon = 76 sq cm.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the small triangle + area of the small triangle + area of the big rectangle.
area of the small triangle = 1/2(4 x 3).
area = 6 .
area of the another small rectangle = 1/2(3 x 4).
area = 6.
area of the big rectangle = 8 x 8.
area = 64.
area of the polygon = 64 + 6 + 6.
area of the polygon = 76.

In 10 and 11, find the area in square units of each polygon.
Question 10.

Answer:
Area of the polygon = 15 sq units.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the small triangle + area of the small triangle + area of the big triangle.
area of the small triangle = 1 x 3.
area = 3.
area of the another small triangle = 1 x 3.
area = 3.
area of the big rectangle = 3 x 3.
area = 9.
area of the polygon = 3 + 3 + 9.
area of the polygon = 15.

Question 11.

Answer:
Area of the polygon = 15 sq units.

Explanation:
In the above-given question,
given that,
area of the polygon = area of the small triangle + area of the small triangle + area of the big triangle.
area of the small triangle = 1 x 3.
area = 3.
area of the another small triangle = 1 x 3.
area = 3.
area of the big rectangle = 3 x 3.
area = 9.
area of the polygon = 3 + 3 + 9.
area of the polygon = 15.

Question 12.
Be Precise Diego is designing an exercise room. How many square feet of rubber flooring will he need to cover the floor? The product is sold in whole square yards. How many square yards should Diego buy? Explain.

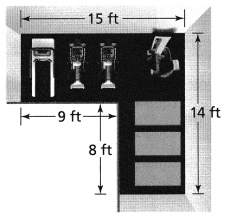
Answer:

In 13 and 14, use the diagram at the right.

Question 13.
David drew this diagram of a picture frame that he is going to make. Each square represents 1 square inch. What is the area of the picture frame?
Answer:

Question 14.
Use Structure How could you find the area of the picture frame without decomposing the frame into smaller shapes?
Answer:

Question 15.
Higher Order Thinking Isabella has three rectangular cards that are 4 inches by 5 inches. How can she arrange the cards, without overlapping, to make one larger polygon with the smallest possible perimeter? How will the area of the polygon compare to the combined area of the three cards?

Answer:

Assessment Practice

Question 16.
Select all expressions that can be used to find the area of the given polygon.

☐ (2 × 5) + (6 × 4)
☐ (5 × 2) + 2 • \(\frac{1}{2}\)(3 × 4)
☐ (6 × 5) – (3 × 4)
☐ ( 6× 9) – (3 × 4)
☐ (5 × 2) + \(\frac{1}{2}\)(2 + 2 + 2) × 4]

Answer:
Options A and E are correct.

Explanation:
In the above-given question,
given that,
(2 x 5) + (6 x 4).
10 + 24.
34.
so options A and E are correct.

Question 17.
What is the area of the polygon at the right?

A. 86 square units
B. 78 square units
C. 70 square units
D. 68 square units

Answer:
Option C is correct.

Explanation:
In the above-given question,
given that,
-5 x 8 = -40.
-5 x 6 = -30.
-40 + (-30).
70 square units.

Topic 7 Mid-Topic Checkpoint

Question 1.
Vocabulary How many pairs of opposite sides are parallel in a trapezoid? How is this different from a parallelogram? Lesson 7-3
Answer:

Question 2.
Calculate the area of each figure at the right. Which figure has the greatest area? Lessons 7-1, 7-2, and 7-3

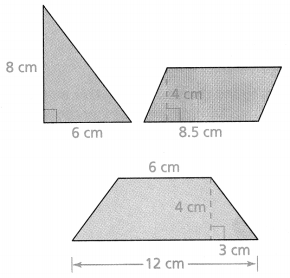
A. triangle
B. parallelogram
C. trapezoid

Answer:
Option C is correct.

Explanation:
In the above-given question,
given that,
the polygon are triangle, parallelogram, and trapezoid.
area of the triangle = l x b.
area = 6 x 8.
area = 48.
area of the parallelogram = 8.5 x 4.
area = 34.
area of trapezoid = 3 x 4 + 9 x 6.
area = 12 + 54.
area = 66.
so option C is correct.

Question 3.
An earring has the shape of a rhombus. The height is 5.2 mm and the area of the earring is 39 mm2. What is the length of each side of the earring? Lesson 7-1

Answer:
The length of each side of the earring = 7.5 mm.

Explanation:
In the above-given question,
given that,
An earring has the shape of a rhombus.
The height is 5.2 mm and the area of the earring is 39 mm2.
area = l x h.
39 = l x 5.2.
l = 39/5.2.
l = 7.5.
so the length of each side of the earring = 7.5 mm.

Question 4.
Shane wrapped the kite at the right with paper. How many square inches of paper did Shane use to cover the front and back? Lesson 7-3

Answer:
Area = 288 sq in.

Explanation:
In the above-given question,
given that,
Shane wrapped the kite at the right with paper.
area of the rhombus = area of each triangle + area of kite.
area of triangle = 1/2(32)(9).
area of triangle = 288/2.
area = 144.
area of kite = 144 + 144.
area = 288.

Question 5.
Explain one way to find the area of the polygon at the right. Then find the area in square units. Lesson 7-4

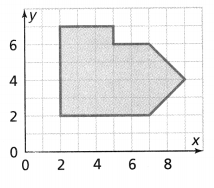
Answer:

Topic 7 Mid-Topic Performance Task

Kira hires a contractor to build a new deck in her backyard. A design for the deck is shown.

PART A
Kira found the area of the deck by decomposing it into two identical trapezoids. Describe another strategy you could use to find the area of the deck.

Answer:
The area of the deck = 204 sq ft.

Explanation:
In the above-given question,
given that,
area of trapezoid = area of the triangle + area of the rectangle.
area of triangle = 1/2(12)
area = 6.
area of rectangle = 16 x 12.
area = 192.
area of trapezoid = 6 + 6 + 192.
area = 12 + 192.
area = 204.

PART B
Which expression can you use to find the area of the deck? Select all that apply.
☐ (16 × 12) + 2(\(\frac{1}{2}\) × 12 × 5)
☐ (26 × 12) + 2(\(\frac{1}{2}\) × 12 × 5)
☐ (26 × 12) – 4(\(\frac{1}{2}\) × 6 × 5)
☐ (16 × 6) + 2(\(\frac{1}{2}\) × 6 × 5) + (16 × 6) + 2(\(\frac{1}{2}\) × 6 × 5)
☐ (16 × 12) + 2(\(\frac{1}{2}\) × 12 × 10)

Answer:
Option A is correct.

Explanation:
In the above-given question,
given that,
area of the deck = area of the triangle + area of the rectangle.
area = 1/2 x 12.
area = 6.
area of rectangle = 16 x 12.
area = 192.
area of trapezoid = 6 + 6 + 192.
area = 12 + 192.
area = 204.

PART C
A second design for Kira’s deck is shown at the right. Find the areas of the two deck designs. Which design will give Kira the deck with the greater area? Explain.

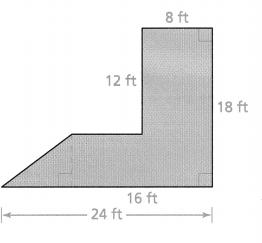
Answer:
Area = 216 sq ft.

Explanation:
In the above-given question,
given that,
A second design for Kira’s deck is shown at the right.
area of the polygon = area of the triangle + area of the rectangle.
area of triangle = 1/2(8)(6).
area = 1/2(48).
area = 24.
area of rectangle = 6 x 16.
area = 96.
area of up rectangle = 12 x 8.
area = 96.
area of polygon = 24 + 96 + 96.
area = 216 sqft.

Lesson 7.5 Represent Solid Figures Using Nets

Explore It!
Jamal is breaking down items for recycling and wonders what this box will look like when it is unfolded and flat.

I can… represent solid figures using nets.

A. How do the sides of the box help you think about what the unfolded box will look like?
Answer:

B. How can you use the grid to represent the unfolded box?

Answer:

Focus on math practices
Reasoning is there another way to represent the unfolded box on the grid? Explain.

Essential Question
How do you classify and represent solid figures?

Try It!

Classify this solid figure.

Answer:
The figure is Triangular pyramid.

Explanation:
In the above-given question,
given that,
the figure is triangular pyramid.
volume of triangular pyramid = 1/3 x B X H.
volume = 1/3 x 1/2 x BH.
volume = 1/6 Bh.

Convince Me! What attributes of a solid figure should you identify to classify it as a polyhedron?

Try It!

Identify the solid from its net.

Shape of polygonal faces: ___________
Shape of base(s): ___________
This is a net of a ___________.

Answer:
The figure is a polyhedron.

Explanation:
In the above-given question,
given that,
shape of polygonal faces = 3.
shape od base = 3.
this is a net of polyhedron.

KEY CONCEPT
You can use nets to represent solid figures.

Do You Understand?
Question 1.
Essential Question How do you classify and represent solid figures?

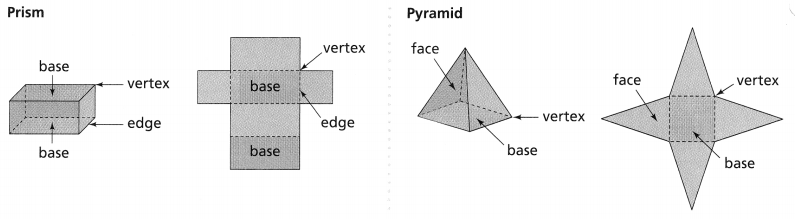
Answer:
The solid figures are prism and pyramids.

Explanation:
In the above-given question,
given that,
prism has more than one base.
pyramid has only one base.
prism does not have any face.
pyramid has its face.

Question 2.
Use Structure Explain the difference between a vertex and an edge.

Answer:
Vertex is the highest point or apex.
Edge is the outside area or a surface.

Explanation:
In the above-given question,
given that,
vertex is the highest point or top or apex.
edge is the outside area or a surface.

Question 3.
Be Precise Explain the difference between a pyramid and a prism.

Answer:
The solid figures are prism and pyramids.

Explanation:
In the above-given question,
given that,
prism has more than one base.
pyramid has only one base.
prism does not have any face.
pyramid has its face.

Question 4.
Describe the net of a triangular prism.
Answer:

Do You Know How?
In 5 and 6, classify the solid figures.
Question 5.

Answer:
The figure is Triangular pyramid.

Explanation:
In the above-given question,
given that,
the figure is triangular pymarid.
volume = 1/6 Bh.
where b = base.
h = height.
so the figure is triangular pyramid.

Question 6.

Answer:
The figure is rectangular prism.

Explanation:
In the above-given question,
given that,
the figure is a rectangular prism.
volume of prism = b x h.

In 7 and 8, identify each solid from its net.
Question 7.

Answer:
The figure is pyramid.

Explanation:
In the above-given question,
given that,
the net is pyramid.
pyramid has face, base, and vertex.
so the figure is pyramid.

Question 8.

Answer:

Question 9.
Draw a net of a rectangular prism that has a height of 2 units and bases that are 3 units long and 1 unit wide.

Answer:

Practice & Problem Solving

In 10-12, classify the solid figures.
Question 10.

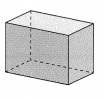
Answer:
The figure is rectangular prism.

Explanation:
In the above-given question,
given that,
the figure is a rectangular prism.
volume of prism = l x w x h.
where l = length.
w = width.
h = height.

Question 11.

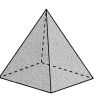
Answer:
The figure is Triangular pyramid.

Explanation:
In the above-given question,
given that,
the figure is triangular pymarid.
volume = 1/6 Bh.
where b = base.
h = height.
so the figure is triangular pyramid.

Question 12.

Answer:
The figure is a triangular pyramid.

Explanation:
In the above-given question,
given that,
the figure is a triangular pyramid.
volume = 1/3 x b x h.
b = base area.
h = height.

In 13-15, identify each solid from its net.
Question 13.

Answer:
The figure is pyramid.

Explanation:
In the above-given question,
given that,
the net is pyramid.
pyramid has face, base, and vertex.
so the figure is pyramid.

Question 14.

Answer:
Volume of the prism = 1/2bhl.

Explanation:
In the above-given question,
given that,
the figure is triangular prism.
volume of the prism = 1/2 x bhl.
where b = base.
h = height.
l = length.

Question 15.

Answer:
The figure is rectangular prism.

Explanation:
In the above-given question,
given that,
the figure is a rectangular prism.
volume of prism = l x w x h.
where l = length.
w = width.
h = height.

Question 16.
Ryan is going to draw a net of a rectangular prism. How many rectangles should there be in his drawing?

Answer:
The figure is rectangular prism.

Explanation:
In the above-given question,
given that,
the figure is a rectangular prism.
volume of prism = l x w x h.
where l = length.
w = width.
h = height.

Question 17.
Kayla is going to draw a net of a square pyramid. How many triangles should there be in her drawing?

Answer:
The formula of square pyramid = a x a x h/3.

Explanation:
In the above-given question,
given that,
the formula of square pyramid.
v = a x a x h/3.
where a = base edge.
h = height.

Question 18.
Make Sense and Persevere Zari folds the net below into a model of a solid figure. How many edges, faces, and vertices does the model have?

Answer:
The number of faces, edges, and vertices = 3.

Explanation:
In the above-given question,
given that,
the number of edges = 3.
the number of faces = 3.
the number of vertices = 3.

Question 19.
Critique Reasoning Tomas says that the net below can be folded to make a rectangular prism. Do you agree with Tomas? Explain.

Answer:

In 20-22, use the table at the right.

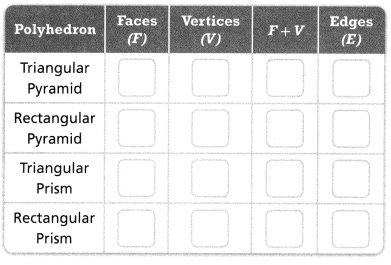
Question 20.
Look for Relationships The Swiss mathematician Leonhard Euler (OY-ler) and the French mathematician René Descartes (dã KART) both discovered a pattern in the numbers of edges, vertices, and faces of polyhedrons. Complete the table. Describe a pattern in the table.
Answer:

Question 21.
Higher Order Thinking Write an equation that relates the number of edges, E, to the number of faces, F, and vertices, V.
Answer:

Question 22.
Use the equation that you wrote in Exercise 21 to find the number of vertices of a cube, which has 12 edges and 6 faces.
Answer:

Question 23.
Corey bought the mailing tube shown at the right to mail a poster of the Gators Little League baseball team.

a. The mailing tube has the shape of which polyhedron?
Answer:

b. How many faces does the mailing tube have?
Answer:

c. When Corey bought the mailing tube, it was unfolded and looked like a net. What polygons would Corey have seen in the unfolded mailing tube?
Answer:

Assessment Practice

Question 24.
Draw a net of a square pyramid for which the base is 2 units long and the height of each triangular face is 5 units.

Answer:

3-ACT MATH

3-Act Mathematical Modeling: That’s a Wrap

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:

Question 2.
Write the Main Question you will answer.

Answer:

Question 3.
Construct Arguments Predict an answer to this Main Question Explain your prediction.
Answer:

Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:

Question 5.
Plot your prediction on the same number line.
Answer:

ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?

Answer:

Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:

Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.

Answer:

Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.
Answer:

ACT 3
Question 10.
Write the answer you saw in the video.
Answer:

Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?

Answer:

Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:

Reflect
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:

Question 14.
Look for Relationships Explain how the dimensions of the gift are related to the area of its net.
Answer:

SEQUEL
Question 15.
Critique Reasoning A classmate says that if all dimensions of the gift were doubled, you would need twice as many squares. Do you agree? Justify his reasoning or explain his error.

Answer:

Lesson 7.6 Find Surface Areas of Prisms

Solve & Discuss It!
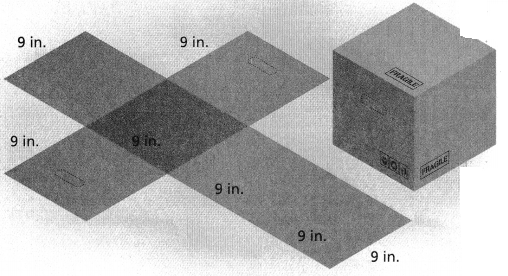
Marianne orders boxes to pack gifts. When they arrive, she finds flat pieces of cardboard as shown below. Marianne needs to cover each face of the boxes with green paper. What is the least amount of paper needed to cover each box? Explain.
I can… draw a net of a prism and use it to find the prism’s surface area

Make Sense and Persevere
What solid figure does this net represent?

Focus on math practices
Make Sense and Persevere Suppose Marianne has only one large sheet of green paper that is 15 inches by 30 inches. Is the area of this sheet of paper great enough to cover all of the faces of one box? Explain.

Essential Question
How can you find the surface area of a prism?

Try It!

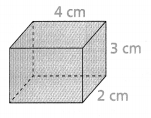
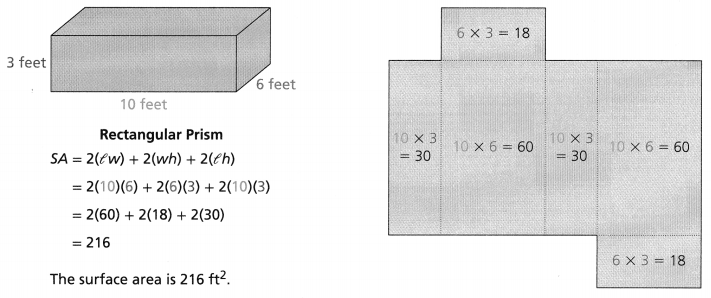
Use the net and the formula to find the surface area of the prism.
SA = 2(lw) + 2(wh) + 2(lh)

Answer:
Surface area = 52 sq cm.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
where l = length, w = width, and h = height.
surface area = 2(8) + 2(6) + 2(12).
surface area = 16 + 12 + 24.
surface area = 52 sq cm.

Convince Me! Why are tw, wh, and th each multiplied by 2 in the formula?

Try It!

Find the surface area of each prism.
a.

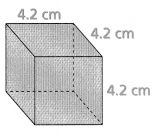
Answer:
Surface area = 52 sq cm.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
where l = length, w = width, and h = height.
surface area = 2(17.64) + 2(17.64) + 2(17.64).
surface area = 35.28 + 35.28 + 35.28.
surface area = 105.84 sq cm.

b.

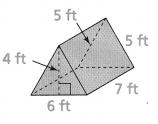
Answer:
Surface area = 214 sq ft.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
where l = length, w = width, and h = height.
surface area = 2(42) + 2(35) + 2(30).
surface area = 84 + 70 + 60.
surface area = 214 sq ft.

KEY CONCEPT
To find the surface area of a prism, use a net or a formula.

Do You Understand?
Question 1.
Essential Question How can you find the surface area of a prism?

Answer:
Area = 216.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(10)(6) + 2(6)(3) + 2(10)(3).
area = 2(60) + 2(18) + 2(30).
area = 120 + 36 + 60.
area = 216.

Question 2.
Construct Arguments Could you use the formula for the surface area of a rectangular prism to find the surface area of a cube? Explain.
Answer:

Question 3.
Look for Relationships Which faces of a rectangular prism always have the same area?
Answer:

Question 4.
Generalize What does it mean to find surface area?
Answer:

Do You Know How?
In 5-7, find the surface area of each prism.
Question 5.

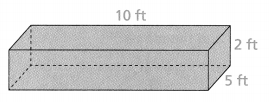
Answer:
Area = 160 sq ft.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(10)(5) + 2(5)(2) + 2(10)(2).
area = 2(50) + 2(10) + 2(20).
area = 100 + 20 + 40.
area = 160.

Question 6.

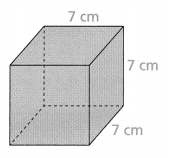
Answer:
Area = 294.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(7)(7) + 2(7)(7) + 2(7)(7).
area = 2(49) + 2(49) + 2(49).
area = 98 + 98 + 98.
area = 294.

Question 7.

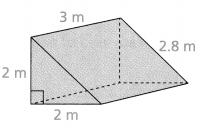
Answer:
Area = 30.4 sq m.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(2)(2.8) + 2(2.8)(2) + 2(2)(2).
area = 2(5.6) + 2(5.6) + 2(4).
area = 11.2 + 11.2 + 8.
area = 30.4.

Practice & Problem Solving

In 8-13, find the surface area of each prism.
Question 8.

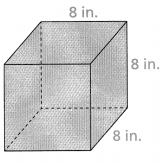
Answer:
Area = 384 sq in.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(8)(8) + 2(8)(8) + 2(8)(8).
area = 2(64) + 2(64) + 2(64).
area = 128 + 128 + 128.
area = 384.

Question 9.

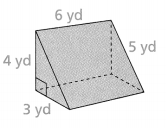
Answer:
Area = 114 sq yd.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(3)(5) + 2(5)(6) + 2(4)(3).
area = 2(15) + 2(30) + 2(12).
area = 30 + 60 + 24.
area = 114.

Question 10.

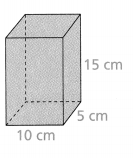
Answer:
Area = 550 sq cm.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(10)(5) + 2(5)(15) + 2(10)(15).
area = 2(50) + 2(75) + 2(150).
area = 100 + 150 + 300.
area = 550 sq cm.

Question 11.

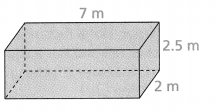
Answer:
Area = 73 sq m.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(7)(2) + 2(2.5)(2) + 2(7)(2.5).
area = 2(14) + 2(5) + 2(17.5).
area = 28 + 10 + 35.
area = 73 sq m.

Question 12.

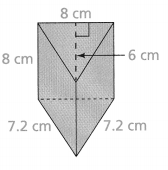
Answer:
Area = 358.4 sq cm.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(8)(7.2) + 2(7.2)(8) + 2(8)(8).
area = 2(57.6) + 2(57.6) + 2(64).
area = 115.2 + 115.2 + 128.
area = 358.4 sq cm.

Question 13.

Answer:
Area = 864 sq ft.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(12)(12) + 2(12)(12) + 2(12)(12).
area = 2(144) + 2(144) + 2(144).
area = 288 + 288 + 288.
area = 864 sq ft.

Question 14.
Critique Reasoning Jacob says that the surface: area of the cube is less than 1,000 cm². Do you agree with Jacob? Explain.

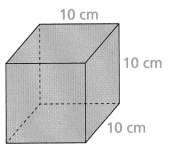
Answer:
Area = 216 sq cm.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(10)(6) + 2(6)(3) + 2(10)(3).
area = 2(60) + 2(18) + 2(30).
area = 120 + 36 + 60.
area = 216 sq cm.

Question 15.
You want to wrap a paperweight shaped like the triangular prism shown. How many square inches of wrapping paper do you need to completely cover the prism?

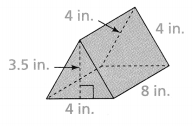
Answer:
Area = 128 sq in.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(4)(4) + 2(8)(4) + 2(4)(4).
area = 2(16) + 2(32) + 2(16).
area = 32 + 64 + 32.
area = 128 sq in.

Question 16.
Sasha has 2 blocks of clay shaped like the rectangular prism below. She joins them to form a rectangular prism with a length of 12 inches. What is the surface area of the larger prism?

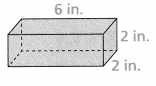
Answer:
Area = 56 sq in.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(6)(2) + 2(2)(2) + 2(6)(2).
area = 2(12) + 2(4) + 2(12).
area = 24 + 8 + 24.
area = 56 sq in.

Question 17.
A rectangular prism has a length of 12 cm, a height of 6 cm, and a width of 4 cm. Use the formula SA = 2(lw) + 2(wh) + 2(lh) to find the surface area of the rectangular prism.

Answer:
Area = 288 sq cm.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(12)(4) + 2(4)(6) + 2(12)(6).
area = 2(48) + 2(24) + 2(72).
area = 96 + 48 + 144.
area = 288 sq cm.

In 18 and 19, use the diagram of the birdhouse.

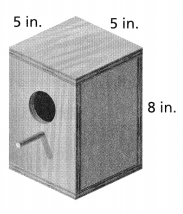
Answer:
Area = 210 sq in.

Explanation:
In the above-given question,
given that,
the surface area of the prism = 2(lw) + 2(wh) + 2(lh).
area = 2(5)(5) + 2(5)(8) + 2(5)(8).
area = 2(25) + 2(40) + 2(40).
area = 50 + 80 + 80.
area = 210.

Question 18.
Kali wants to build this birdhouse. She bought a 24-inch by 48-inch sheet of plywood. Does Kali have enough wood to make the birdhouse? Explain.

Answer:
Yes, kali has enough wood to make the birdhouse.

Explanation:
In the above-given question,
given that,
Kali wants to build this birdhouse.
She bought a 24-inch by 48-inch sheet of plywood.
24 x 48.
1152 sq in.
so kali has enough wood to make the birdhouse.

Question 19.
Reasoning kali decides to paint the birdhouse. She has a pint of paint that covers 32.5 ft² of surface. How can you tell that Kali has enough paint without calculating?

Answer:
Yes, kali has enough paint without calculating.

Explanation:
In the above-given question,
given that,
kali decides to paint the birdhouse.
She has a pint of paint that covers 32.5 ft² of the surface.
24 x 48.
1152 sq in.
so kali has enough paint without calculating.

Question 20.
Use the formula SA = 2lw + 2lh + 2wh to find the surface area for a rectangular prism with a length, l, of 2.3 inches; a width, w, of 1.1 inches; and a height, h, of 3 inches.

Answer:
Area = 25.92 sq in.

Explanation:
In the above-given question,
given that,
length = 2.3 in.
width = 1.1 in.
height = 3 in.
surface area for a rectangular prism = 2lw + 2lh + 2wh.
area = 2(2.3 x 1.2) + 2(2.3 x 3) + 2(1.1 x 3).
area = 2(2.76) + 2(6.9) + 2(3.3).
area = 5.52 + 13.8 + 6.6.
area = 25.92 sq in.

Question 21.
Make Sense and Persevere Justine wants to wrap a shipping box shaped like a rectangular prism. The box is 28 inches tall and has a square base with sides that each measure 2 inches. How much paper will Justine use?

Answer:
Justin uses 232 sq in of paper.

Explanation:
In the above-given question,
given that,
Justine wants to wrap a shipping box shaped like a rectangular prism.
The box is 28 inches tall and has a square base with sides that each measure 2 inches.
area = 2lw + 2wh + 2lh.
area = 2(2 x 2) + 2(2 x 28) + 2(2 x 28).
area = 2(4) + 2(56) + 2(56).
area = 8 + 112 + 112.
area = 232 sq in.
so Justin uses 232 sq in of paper.

Question 22.
Higher Order Thinking Margaret wants to cover a footrest in the shape of a rectangular prism with cotton fabric. The footrest is 18 inches by 12 inches by 10 inches. Margaret has 1 square yard of fabric. Can she completely cover the footrest? Explain.

Answer:
Yes, she completely covers the footrest.

Explanation:
In the above-given question,
given that,
Margaret wants to cover a footrest in the shape of a rectangular prism with cotton fabric.
The footrest is 18 inches by 12 inches by 10 inches.
Margaret has 1 square yard of fabric.
area = 2lw + 2wh + 2lh.
area = 2(18 x 12) + 2(12 x 10) + 2(18 x 10).
area = 2(216) + 2(120) + 2(180).
area = 432 + 240 + 360.
area = 1032 sq in.
1 square yd = 1296 sq in.
yes, she completely covers the footrest.

Question 23.
A cube has a surface area of 486 in.². Can the length of each side of the cube be 11 in.? Explain.

Answer:
No, the length of each side of the cube is 9 in.

Explanation:
In the above-given question,
given that,
A cube has a surface area of 486 sq.
the surface area of the cube = 6 a x a.
area = 6 x 9 x 9.
486 = 81 x 6.
no the length of each side of the cube is 9 in.

Assessment Practice

Question 24.
Using nets, find the surface area, in square feet, of a rectangular prism with a height of 2 feet, a length of 4.2 feet, and a width of 2.5 feet.

Answer:
Surface area = 47.8 sq ft.

Explanation:
In the above-given question,
given that,
rectangular prism with a height of 2 feet, a length of 4.2 feet, and a width of 2.5 feet.
surface area = 2lw + 2wh + 2lh.
area = 2(2 x 4.2) + 2(4.2 x 2.5) + 2(2 x 2.5).
area = 2(8.4) + 2(10.5) + 2(5).
area = 16.8 + 21 + 10.
area = 47.8 sq ft.

Question 25.
The surface area of a cube is 273.375 square feet. The net of the prism is shown.

What are the possible dimensions of the cube in feet?
A. 6, 6, 6
B. 6, 6.75, 6.75
C. 6.5, 6.5, 6.5
D. 6.75, 6.75, 6.75

Answer:
Option B is correct.

Explanation:
In the above-given question,
given that,
the surface area of the cube = 6a x a.
surface area = 6 x 6.75 x 6.75.
area = 6 x 45.5625.
area = 273.375 cubic feet.
so option B is correct.

Lesson 7.7 Find Surface Areas of Pyramids

Solve & Discuss It!
The fence in Marci’s front yard has decorative tops, in the shape of square pyramids, every 6 feet. Marci paints each face of each top a different color before attaching the tops to the fence. What is the total surface area that she paints on each decorative top?
I can… draw a net of a pyramid and use it to find the pyramid’s surface area.

Use Appropriate Tools
What tools can you use to help solve this problem?

Focus on math practices
Use Structure Suppose the side lengths of the square base of each decorative top are increased by 2 inches. What is the total surface area of each top?

Essential Question
How can you find the surface area of a pyramid?

Answer:
The surface area of the pyramid = A + 1/2 ps.

Explanation:
In the above-given question,
given that,
the surface area of the pyramid = A + 1/2 ps.
where A = area of the base.
p = perimeter of the base.
s = slant height.

Try It!

Find the surface area of the square pyramid. Draw a net to find the areas of the base and each face of the pyramid.

Answer:
The surface area of the square pyramid = 528 sq cm.

Explanation:
In the above-given question,
given that,
base edge = 6 cm.
height = 8 cm.
surface area of the square pyramid = axa + 2a square root of axa/4 + h x h.
area = 36 + 12 square root 36/4 + 64.
area = 48 6/2+   8.
area = 48 x 3 + 8.
area = 48 x 11.
area = 528 sq cm.

Convince Me! For the pyramid in the Try It!, what values would you use for B, n, and A in the formula SA = B + (nA)?

Try It!

Draw a net and find the surface area of the triangular pyramid. Find the area (T) of each equilateral triangle.

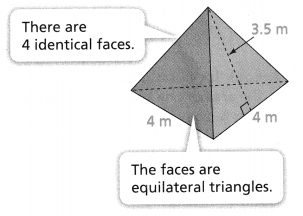
T = \(\frac{1}{2}\)bh
T = \(\frac{1}{2}\) _______ _______
= ________
The area of each equilateral triangle is __________ m².

Answer:
The area of each equilateral triangle is 7 sq m.

Explanation:
In the above-given question,
given that,
the area of each equilateral triangle is 1/2 x bh.
area = 1/2 x 4 x 3.5.
area = 2 x 3.5.
area = 7.
so area of each equilateral triangle is 7 sq m.

Find the surface area (SA) of the triangular pyramid.
SA = 4T
SA = ______ × T
SA = 4 × ________
= _______
The surface area of the triangular pyramid is ________ m²

Answer:
SA = 4T.

Explanation:
In the above-given question,
given that,
the surface area of the triangular pyramid is 4T.
SA = 4T.
SA is surface area.
4T = triangular pyramid.
4T = SA.

KEY CONCEPT
You can use a net to help find the surface area of a pyramid.

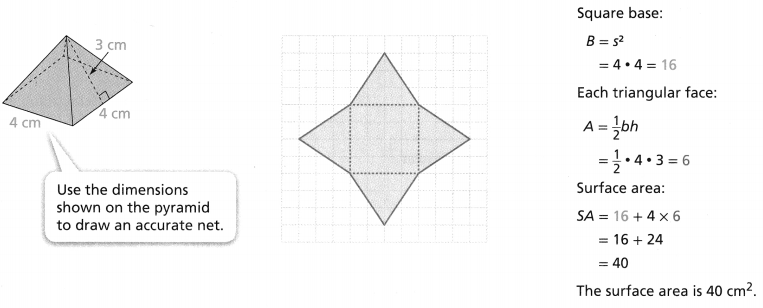
Do You Understand?
Question 1.
Essential Question How can you find the surface area of a pyramid?

Answer:
Surface area = 22 sq cm.

Explanation:
In the above-given question,
given that,
the surface area of a pyramid = SxS + 1/2bh.
side = 4 x 4.
side = 16.
surface area = 16 + 1/2bh.
area = 16 + 1/2 x 4 x 3.
area = 16 + 1/2 x 12.
area = 16 + 6.
area = 22 sq cm.

Question 2.
Look for Relationships How does finding the area of one face of a triangular pyramid that is made up of equilateral triangles help you find the surface area of the triangular pyramid?
Answer:

Question 3.
Make Sense and Persevere in the formula SA = 47, for the surface area of a triangular pyramid in which the faces are equilateral triangles, what does the variable T represent?

Answer:
Surface area = 47.

Explanation:
In the above-given question,
given that,
the surface area of the equilateral triangle = SxS + 1/2 bh.
area = 4 x 4 + 1/2 x 5 x 12.
area = 16 + 5 x 6.
area = 16 + 30.
area = 47.

Do You Know How?
Question 4.
Each side of the base of a square pyramid is 4 inches and the height of each triangular face is 3 inches. Draw a net for this pyramid and find its surface area.

Answer:
The surface area of the pyramid = 22 sq in.

Explanation:
In the above-given question,
given that,
Each side of the base of a square pyramid is 4 inches and the height of each triangular face is 3 inches.
surface area = sxs +1/2bh.
surface area = 4 x 4 + 1/2 3 x 4.
area = 16 + 6.
area = 22 sq in.

Question 5.
The faces of this triangular pyramid are equilateral triangles. Draw a net of the pyramid and use it to find the surface area.

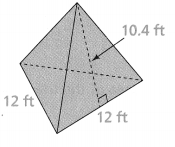
Answer:
The surface area of the pyramid = 204.4 sq ft.

Explanation:
In the above-given question,
given that,
bases = 12 ft and h = 10.4 ft.
surface area = sxs +1/2bh.
surface area = 12 x 12 + 1/2 12 x 10.4.
area = 144 +60.4.
area = 204.4 sq ft.

Practice & Problem Solving

Leveled Practice In 6 and 7, find the surface area of each pyramid. The faces of each triangular pyramid are equilateral triangles.
Question 6.

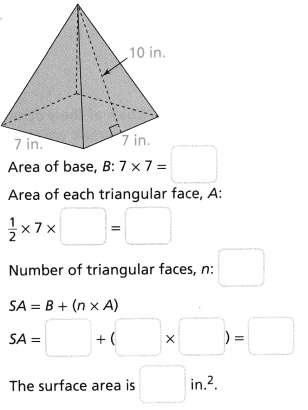
Answer:
The surface area is 84 sq.

Explanation:
In the above-given question,
given that,
Area of the base = 7 x 7.
area = 49.
surface area = 49 + 1/2 x 7 x 10.
area = 49 + 35.
area = 84.
so the surface area is 84 sq in.

Question 7.

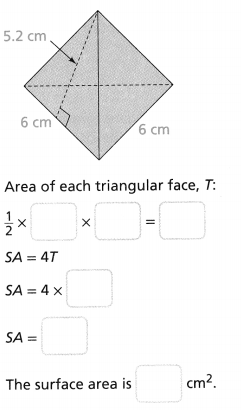
Answer:
The surface area is 51.2 sq cm.

Explanation:
In the above-given question,
given that,
Area of the base = 6 x 6.
area = 36.
surface area = 36 + 1/2 x 6 x 5.2.
area = 36 +15.2.
area = 51.2.
so the surface area is 51.2 sq cm.

Question 8.
Complete the net at the right to find the surface area of this triangular pyramid. The faces of the pyramid are equilateral triangles.

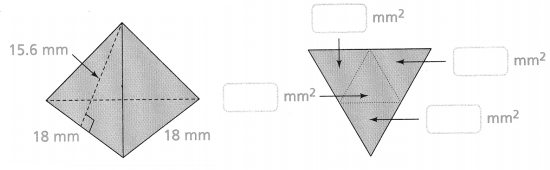
Answer:
The surface area is 459.6 sq mm.

Explanation:
In the above-given question,
given that,
Area of the base = 18 x 18.
area = 324.
surface area = 324 + 1/2 x 18 x 15.6.
area = 324 + 135.6.
area = 459.6.
so the surface area is 459.6 sq mm.

Question 9.
Simone is designing a piece of artwork in the shape of a square pyramid for a hotel. She wants to cover the pyramid with decorative glass. How many square feet of glass does Simone need to cover the entire pyramid?

Answer:
The surface area is 35 sq ft.

Explanation:
In the above-given question,
given that,
Area of the base = 5 x 5.
area = 25.
surface area = 25 + 1/2 x 5 x 4.
area = 25 +10.
area = 35.
so the surface area is 35 sq ft.

Question 10.
Critique Reasoning Kurt says that the surface area of this triangular pyramid with faces that are equilateral triangles is 173 cm2. Do you agree with Kurt? Explain.

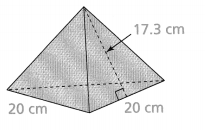
Answer:
The surface area is 570.3 sq cm.

Explanation:
In the above-given question,
given that,
Area of the base = 20 x 20.
area = 400.
surface area = 400 + 1/2 x 20 x 17.3.
area = 400 + 170.3.
area = 570.3.
so the surface area is 570.3 sq cm.

In 11 and 12, use the pyramid and net shown.

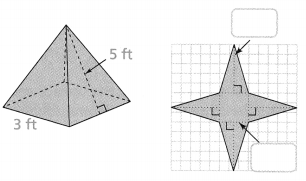
Question 11.
Model with Math Ken drew a square pyramid and its net to represent a doghouse that he is building. Complete the net by filling in the missing measures.

Answer:
The surface area is 16.5 sq ft.

Explanation:
In the above-given question,
given that,
Area of the base = 3 x 3.
area = 9.
surface area = 9 + 1/2 x 3 x 5.
area = 9 + 7.5.
area = 16.5.
so the surface area is 16.5 sq ft.

Question 12.
Use the net to find the amount of wood Ken needs to make the doghouse.
Answer:

Question 13.
The surface area of this square pyramid is 644 ft². Can the value of x be 20? Explain.

Answer:
The surface area is 336 sq ft.

Explanation:
In the above-given question,
given that,
Area of the base = 14 x 14.
area = 196.
surface area = 196 + 1/2 x 14 x 20.
area = 196 + 140.
area = 336.
so the surface area is 336 sq ft.

Question 14.
Construct Arguments Which of these pyramids do you think has the greater surface area? Explain.

• Square pyramid: The base is 10 cm by 10 cm and the triangular faces have a height of 8.66 cm.
• Triangular pyramid: All the faces are equilateral triangles with a base of 10 cm and a height of 8.66 cm.
  Answer:

Question 15.
Higher Order Thinking The base of a pyramid can be any polygon. How many faces does a pentagonal pyramid have? Describe the shapes of the faces.
Answer:

Question 16.
Vocabulary What is the term used to describe a point where three or more edges of a solid figure meet?
Answer:

Assessment Practice

Question 17.
Which net represents the pyramid with the greatest surface area?

Answer:

Lesson 7.8 Find Volume with Fractional Edge Lengths

Solve & Discuss It!
A rectangular prism has the dimensions shown. What is the volume of this rectangular prism?

I can… find the volume of a rectangular prism with fractional edge lengths.

Use Structure
How might filling the rectangular prism with layers of 3-inch cubes help you find the volume?

Focus on math practices
Look for Relationships You know how to use the formula V = \(\frac{1}{2}\)wh to find the volume of a rectangular prism. How might you use the formula to find the volume of the prism above?

Essential Question
How can you find the volume of a rectangular prism with fractional edge lengths?

Try It!

Find the volume of the rectangular prism built from \(\frac{1}{2}\)-inch cubes.

The bottom layer has _______ cubes. The prism is _______ cubes high. There are a total of _______ cubes in the prism. Each cube has a volume of _______ in³.
Volume of prism = _______ × _______ = _______ in³.

Answer:
Volume of prism =

Explanation:
In the above-given question,
given that,
the bottom layer has 5 cubes.
volume of the rectangular prism = 2(lw) + 2(wh) + 2(lh).
volume = 2(2.5 x 2.5) + 2(2.5 x 2.5) + 2(2.5 x 2.5).
volume = 2(
volume of prism =

Convince Me! Suppose that the length of the rectangular prism in the Try It! were 3\(\frac{1}{2}\) inches instead of 2\(\frac{1}{2}\) inches. How many cubes would there be in the prism? What would be the volume of the prism?

Try It!

Find the volume of each rectangular prism.
a.

Answer:
The volume of rectangular prism = 61 sq cm.

Explanation:
In the above-given question,
given that,
l = 3.2 cm, h = 4.5 cm, and w = 2.8 cm.
volume of rectangular prism = 2(lw) + 2(wh) + 2(lh).
volume = 2(3.2 x 2.8) + 2(2.8 x 4.5) + 2(3.2 x 4.5).
volume = 2(3.5) + 2(12.6) + 2(14.4).
volume = 7 + 25.2 + 28.8.
volume = 61 sq cm.

b.

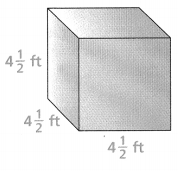
Answer:
The volume of rectangular prism = 121.5 sq ft.

Explanation:
In the above-given question,
given that,
l = 4.5 cm, h = 4.5 cm, and w = 4.5 cm.
volume of rectangular prism = 2(lw) + 2(wh) + 2(lh).
volume = 2(4.5 x 4.5) + 2(4.5 x 4.5) + 2(4.5 x 4.5).
volume = 2(20.25) + 2(20.25) + 2(20.25).
volume = 40.5 + 40.5 + 40.5.
volume = 121.5 sq ft.

KEY CONCEPT
You can find the volume of a rectangular prism with fractional edge lengths by determining the number of same-sized cubes with unit fraction edge lengths needed to completely fill the prism, then multiplying that number of cubes by the volume of each cube. You can also apply a formula.

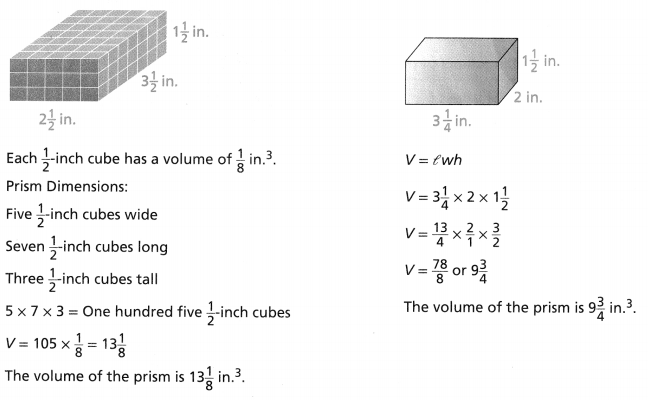
Do You Understand?
Question 1.
Essential Question How can you find the volume of a rectangular prism with fractional edge lengths?

Answer:
The volume of a rectangular prism = l x w x h.

Explanation:
In the above-given question,
given that,
the volume of a rectangular prism = l x w x h.
where l = length.
w = width.
h = height.

Question 2.
How is finding the volume of a rectangular prism with fractional edge lengths similar to finding the volume of a rectangular prism with whole number edge lengths?

Answer:
The volume of a rectangular prism = l x w x h.

Explanation:
In the above-given question,
given that,
the volume of a rectangular prism = l x w x h.
where l = length.
w = width.
h = height.

Question 3.
Construct Arguments How can you use the number of \(\frac{1}{2}\)-inch cubes in a rectangular prism to find the number of unit cubes in the rectangular prism?

Answer:
The volume of a rectangular prism = 0.125 sq in.

Explanation:
In the above-given question,
given that,
the volume of a rectangular prism = l x w x h.
where l = length.
w = width.
h = height.
volume = 0.5 x 0.5 x 0.5.
volume = 0.125 sq in.

Do You Know How?
In 4 and 5, tell how many of each size of cube can fill a 1-inch cube.
Question 4.
Edge = \(\frac{1}{3}\) inch

Answer:
Volume = 0.027 cubic in.

Explanation:
In the above-given question,
given that,
edge = 1/3 in.
volume = ax ax a.
volume = 0.3 x 0.3 x 0.3.
volume = 0.027 cubic in.

Question 5.
Edge = \(\frac{1}{4}\) inch

Answer:
Volume = 0.027 cubic in.

Explanation:
In the above-given question,
given that,
edge = 1/4 in.
volume = ax ax a.
volume = 0.25 x 0.25 x 0.25.
volume = 0.75 cubic in.

In 6-9, find the volume of each rectangular prism.
Question 6.

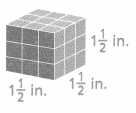
Answer:
Volume = 4.5 cubic in.

Explanation:
In the above-given question,
given that,
l = 3/2 in, w = 3/2 in, and h = 3/2 in.
volume = ax ax a.
volume = 1.5 x 1.5 x 1.5.
volume = 4.5 cubic in.

Question 7.

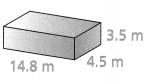
Answer:
Volume = 233.1 cubic m.

Explanation:
In the above-given question,
given that,
the volume of the rectangular prism = lwh.
length = 14.8 m.
width = 4.5 m.
height = 3.5 m.
volume = 14.8 x 4.5 x 3.5.
volume = 233.1 cubic m.

Question 8.

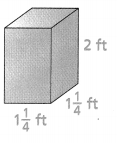
Answer:
Volume = 3.75 cubic ft.

Explanation:
In the above-given question,
given that,
the volume of the rectangular prism = lwh.
length = 1.25 ft.
width = 1.25 ft.
height = 2 ft.
volume = 1.25 x 1.25 x 1.25.
volume = 3.75 cubic ft.

Question 9.

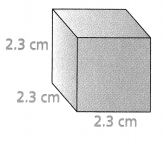
Answer:
Volume = 12.167 cubic cm.

Explanation:
In the above-given question,
given that,
the volume of the rectangular prism = lwh.
length = 2.3 cm.
width = 2.3 cm.
height = 2.3 cm.
volume = 2.3 x 2.3 x 2.3.
volume = 12.167 cubic cm.

Practice & Problem Solving

In 10-13, find the volume of each rectangular prism.
Question 10.

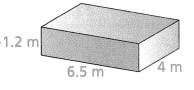
Answer:
Volume = 31.2 cubic m.

Explanation:
In the above-given question,
given that,
the volume of the rectangular prism = lwh.
length = 6.5 m.
width = 4 m.
height = 1.2 m.
volume = 6.5 x 4 x 1.2.
volume = 31.2 cubic m.

Question 11.

Answer:
Volume = 3.75 cubic yd.

Explanation:
In the above-given question,
given that,
the volume of the rectangular prism = lwh.
length = 2 yd.
width = 1.6 yd.
height = 5.3 yd.
volume = 2 x 1.6 x 5.3.
volume = 16.96 cubic yd.

Question 12.

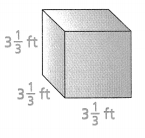
Answer:
Volume = 35.937 cubic ft.

Explanation:
In the above-given question,
given that,
the volume of the rectangular prism = lwh.
length = 3.3 ft.
width = 3.3 ft.
height =  3.3 ft.
volume = 3.3 x 3.3 x 3.3.
volume = 35.937 cubic ft.

Question 13.

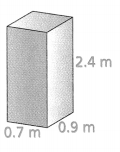
Answer:
Volume = 1.512 cubic m.

Explanation:
In the above-given question,
given that,
the volume of the rectangular prism = lwh.
length = 0.7 m.
width = 0.9 m.
height = 2.4 m.
volume = 0.7 x 0.9 x 2.4.
volume = 1.512 cubic m.

Question 14.
A clear box has the shape of a rectangular prism and is filled with sand. Find the volume of the box.

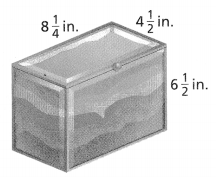
Answer:
Volume = 241.3 cubic in.

Explanation:
In the above-given question,
given that,
the volume of the rectangular prism = lwh.
length = 8.25 in.
width = 4.5 in.
height = 6.5 in.
volume = 8.25 x 4.5 x 6.5.
volume = 241.3 cubic in.

Question 15.
Use Structure A rectangular prism has a length of 2\(\frac{1}{2}\) yd, a width of 1\(\frac{1}{2}\) yd, and a height of 1\(\frac{1}{2}\) yd. You use cubes with fractional edge lengths of \(\frac{1}{2}\) yd to find the volume. How many cubes are tħere for each of the length, width, and height of the prism? What is the volume of the prism?

Answer:
The volume of the prism = 5.625 cubic yd.

Explanation:
In the above-given question,
given that,
A rectangular prism has a length of 2\(\frac{1}{2}\) yd, a width of 1\(\frac{1}{2}\) yd, and a height of 1\(\frac{1}{2}\) yd.
volume of the prism = l x w x h.
l = 2.5, w = 1.5, and h = 1.5.
volume = 2.5 x 1.5 x 1.5.
volume = 5.625 cubic yd.

Question 16.
A gift box has the shape of a cube. The length of each side is 10.5 cm. What is the volume of the gift box?

Answer:
The volume of the gift box = 31.5 cubic cm.

Explanation:
In the above-given question,
given that,
A gift box has the shape of a cube.
the length of each side is 10.5 cm.
volume = lx w x h.
volume = 10.5 x 10.5 x 10.5.
volume = 31.5.
so the volume of the gift box = 31.5 cubic cm.

Question 17.
A school locker has a length of 1 ft, a width of 18 in., and a height of 2\(\frac{1}{2}\) ft. What is the volume of the locker in cubic feet?

Answer:
The volume of rectangular prism = 45 cubic ft.

Explanation:
In the above-given question,
given that,
A school locker has a length of 1 ft, a width of 18 in, and a height of 2(1/2).
volume of the prism = l x w x h.
volume = 1 x 18 x 2.5.
volume = 45 cubic ft.

In 18 and 19, use the table.

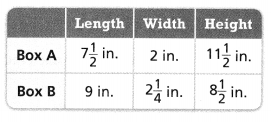
Question 18.
Use Structure Sandy has two boxes with the dimensions shown. She wants to use the box with the greater volume to ship a gift to her friend. Which box should Sandy use? Explain.

Answer:
Sandy ship a box B.

Explanation:
In the above-given question,
given that,
Sandy has two boxes with the dimensions shown.
the volume of the Box A = l x w x h.
volume = 7.5 x 2 x 11.5.
volume = 172.5 cubic ft.
volume = 172.5 cubic ft.
the volume of the Box B = l x w x h.
volume = 9 x 2.5 x 8.5.
volume = 191.25 cubic ft.

Question 19.
Sandy finds a third box, box C, that has a length of 8 inches, a width of 2\(\frac{3}{4}\) inches, and a height of 10\(\frac{1}{2}\) inches. If Sandy wants to use the box with the greatest volume, should she use box C? Explain.

Answer:
Sandy will ship box C.

Explanation:
In the above-given question,
given that,
Sandy finds a third box, box C, that has a length of 8 inches, a width of 2\(\frac{3}{4}\) inches, and a height of 10\(\frac{1}{2}\) inches.
volume = l x w x h.
volume = 8 x 11/4 x 21/2.
volume = 8 x 2.75 x 10.5.
volume = 231 cubic in.
Sandy will ship box C.

Question 20.
The volume of a large crate is 84 yd³. It is 2\(\frac{2}{3}\) yd wide and 4\(\frac{2}{3}\) yd high. What is the length of the crate?

Answer:
The length of the crate = 7.023.

Explanation:
In the above-given question,
given that,
The volume of a large crate is 84 yd³.
It is 2\(\frac{2}{3}\) yd wide and 4\(\frac{2}{3}\) yd high.
v = l x w x h.
84 = l x 8/3 x 14/3.
84 = l x 2.6 x 4.6.
84 = l x 11.96.
l = 84/11.96.
l = 7.023.
so the length of the crate = 7.023 sq yds.

Question 21.
Higher Order Thinking A box covers an area of 8\(\frac{3}{4}\) in.² when resting on its base. The volume of the box is 74\(\frac{3}{8}\) in.³. Can you find the surface area of the box? Explain.

Answer:
The surface area of the box = 74.375 cubic in.

Explanation:
In the above-given question,
given that,
A box covers an area of 8\(\frac{3}{4}\) in.² when resting on its base.
The volume of the box is 74\(\frac{3}{8}\) in.³
The surface area of the box = 595/8.
the surface area of the box = 74.375 cubics in.

Question 22.
Make Sense and Persevere A gold bar is similar in shape to a rectangular prism. A standard mint bar is approximately 7 in. × 3\(\frac{5}{8}\) in. × 1\(\frac{3}{4}\) in. If the value of gold is $1,313 per ounce, about how much is one gold bar worth? Use the formula w≈11.15n, where w is the weight in ounces and n is the volume in cubic inches, to find the weight in ounces. Explain how you found your answer.

Answer:

Assessment Practice

Question 23.
Which rectangular prism with the given dimensions has the same volume as the prism shown?

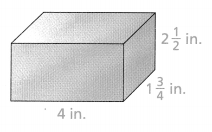
A. 1 in., 3.5 in., 4.25 in.
B. 1.25 in., 3.5 in., 4 in.
C. 1.75 in., 3 in., 3.5 in.
D. 2 in., 2.25 in., 4 in.

Answer:
Option C is correct.

Explanation:
In the above-given question,
given that,
volume of the rectangular prism = l x w x h.
volume = 4 x 7/4 x 5/2.
volume = 4 x 1.75 x 2.5.
volume = 17.5.
so option C is correct.

Topic 7 Review

Topic Essential Question
How can the areas of certain shapes be found? What are the meanings of surface area and volume and how can surface area and volume be found?

Vocabulary Review
Write the vocabulary term that best represents each item.
Vocabulary

• net
• rhombus
• trapezoid
• vertex
• volume

Question 1.
The measure of the space this solid figure occupies.

Answer:
The measure of the space this solid figure occupies is volume.

Explanation:
In the above-given question,
given that,
the measure of the space this solid figure occupies is volume.
the volume of the prism = l x w x h.
where l = length.
w = width.
h = height.

Question 2.

Answer:
The measure of the space this solid figure occupies is net.

Explanation:
In the above-given question,
given that,
the measure of the space this solid figure occupies is net.

Question 3.

Answer:
The figure is a rhombus.

Explanation:
In the above-given question,
given that,
the figure is a rhombus.
for example:
the volume of the rhombus = 12 ABH.
where a and b are diagonals of the rhombus.
h is the height of the prism.

Question 4.

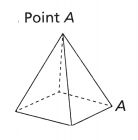
Answer:
The figure is a trapezoid.

Explanation:
In the above-given question,
given that,
the figure is a trapezoid.
area of the trapezoid = a+b/2 h.
where a = base.
b = base.
h = height.
so the figure is a trapezoid.

Use Vocabulary in Writing
Describe how to find the area of the quadrilateral. Use vocabulary words in your explanation.

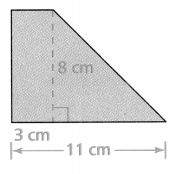
Answer:
Area = 44 sq cm.

Explanation:
In the above-given question,
given that,
area of the quadrilateral = 1/2 x diagonals length x (sum of the height of two triangles).
area = 1/2 x 11 x 8.
area = 44 sq cm.

Concepts and Skills Review

Lesson 7.1 Find Areas of Parallelograms and Rhombuses

Quick Review
You can use the formula A = bh to find the area of a parallelogram or a rhombus.

Example
Find the area of the parallelogram.

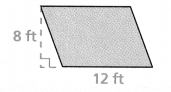
A = bh
A = 12 × 8
A = 96
The area of the parallelogram is 96 ft².

Practice
In 1-4, find the area of each parallelogram or rhombus.
Question 1.

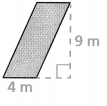
Answer:
Area = 36 sq m.

Explanation:
In the above-given question,
given that,
area of the parallelogram = bh.
where b = base and h = height.
area = 4 x 9.
area = 36 sq m.

Question 2.

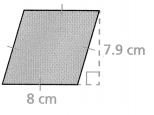
Answer:
Area = 63.2 sq cm.

Explanation:
In the above-given question,
given that,
area of the parallelogram = bh.
where b = base and h = height.
area = 8 x 7.9.
area = 63.2 sq cm.

Question 3.
Rhombus
b = 14 in.
h = 9 in.

Answer:
Area = 126 sq in.

Explanation:
In the above-given question,
given that,
area of the parallelogram = bh.
where b = base and h = height.
area = 14 x 9.
area = 126 sq in.

Question 4.
Parallelogram
b = 12 ft
h = 8.5 ft

Answer:
Area = 102 sq ft.

Explanation:
In the above-given question,
given that,
area of the parallelogram = bh.
where b = base and h = height.
area = 12 x 8.5.
area = 102 sq ft.

Question 5.
A rhombus has an area of 375 mm² and a base of 25 mm. What is its height?

Answer:
height = 15 sq mm.

Explanation:
In the above-given question,
given that,
area of the parallelogram = bh.
where b = base and h = height.
area = 375 sq mm.
base = 25 mm.
375 = 25h.
h = 375/25.
h = 15 sqmm.

Lesson 7.2 Solve Triangle Area Problems

Quick Review
You can use the formula A = \(\frac{1}{2}\)bh to find the area of any triangle.

Example
Find the area of the triangle.

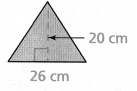
A = \(\frac{1}{2}\) × (26 × 20)
A = 260 cm²

Practice
Find the area of each triangle.
Question 1.

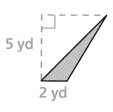
Answer:
Area of the triangle = 5 sq yd.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 bh.
area = 1/2 x 2 x 5.
area = 5.

Question 2.

Answer:
Area of the triangle = 24 sq ft.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 bh.
area = 1/2 x 8 x 6.
area = 4 x 6.
area = 24 sq ft.

Question 3.
b = 12.4 cm
h = 18 cm

Answer:
Area of the triangle = 111.6 sq cm.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 bh.
area = 1/2 x 12.4 x 18.
area = 12.4 x 9.
area = 111.6 sq cm.

Question 4.
b = 3.5 m
h = 6 m

Answer:
Area of the triangle = 10.5 sq m.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2 bh.
area = 1/2 x 3.5 x 6.
area = 3 x 3.5.
area = 10.5 sq m.

Lesson 7.3 Find Areas of Trapezoids and Kites

Quick Review
You can find the area of a trapezoid by decomposing it into a rectangle and one or more triangles. You can find the area of a kite by decomposing it into triangles.

Example
Find the area of the trapezoid and the kite.

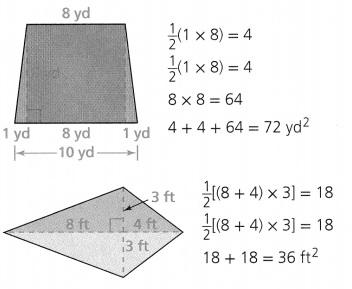
Practice
Find the area of each trapezoid or kite.
Question 1.

Answer:
Area of the trapezoid = 32.5 sq cm.

Explanation:
In the above-given question,
given that,
base = 5 cm.
h = 11 cm.
area of the triangle = 1/2(1 x 5).
area = 5/2 = 2.5.
area of the rectangle = 5 x 6.
area = 30.
area of the trapezoid = 2.5 + 30.
area = 32.5 sq cm.

Question 2.

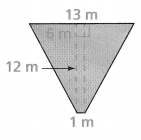
Answer:
Area of the trapezoid = 96 sq m.

Explanation:
In the above-given question,
given that,
area of the triangle = 1/2(7 x 12).
area = 42.
area of the rectangle = 1 x 12.
area = 12.
area of the trapezoid = 42 + 42 + 12.
area = 96 sq m.

Question 3.

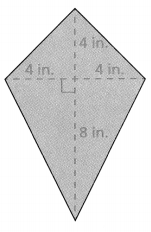
Answer:
Area = 48 sq in.

Explanation:
In the above-given question,
given that,
area of the kite = 1/2[(8 x 4) x 4].
area = 1/2[12] x 4.
area = 24.
area of the kite = 24 + 24.
area = 48 sq in.

Question 4.

Answer:
Area of the kite = 80 sq in.

Explanation:
In the above-given question,
given that,
area of the kite = 1/2[(10 x 4) x 2].
area = 1/2[40] x 2.
area = 20 x 2.
area = 40.
area of the kite = 40 + 40.
area = 80 sq in.

Lesson 7.4 Find Areas of Polygons

Quick Review
To find the area of a polygon, you can decompose or compose shapes, then use addition or subtraction to calculate the area.

Example
Find the area of the polygon.

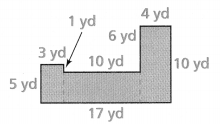
Area = (3 × 5) + (10 × 4) + (4 × 10)
= 15 + 40 + 40 = 95
The area of the polygon is 95 yd².

Practice
Question 1.
Find the area of the polygon.

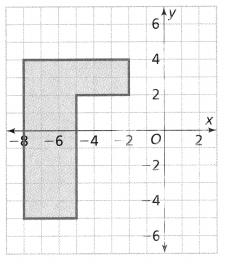
Answer:
Area of the polygon = -27.

Explanation:
In the above-given question,
given that,
the area of the polygon = (2 x -6) + (-3 x -5).
area of the polygon = (-12) + (-15).
area = -12 – 15.
area = -27.
so the area of the polygon = -27.

Lesson 7.5 Represent Solid Figures Using Nets

Quick Review
You can use nets to represent solid figures.

Example
Classify the solid figure and draw a net to represent it.

This figure has two congruent parallel bases, so it is a prism. The bases are rectangles, so it is a rectangular prism.
Net of rectangular prism:

Practice
In 1 and 2, classify the solid figures
Question 1.

Answer:
The figure name is a triangular pyramid.

Explanation:
In the above-given question,
given that,
the above figure is a triangular pyramid.
the surface area of triangular pyramid = 1/2(a x b) + 3/2(b x s).
where b = base.
s = side.

Question 2.

Answer:
The figure name is a triangular pyramid.

Explanation:
In the above-given question,
given that,
the above figure is a triangular pyramid.
the surface area of triangular pyramid = 1/2(a x b) + 3/2(b x s).
where b = base.
s = side.

Question 3.
Draw a net of the pyramid shown.

Answer:

In 4 and 5, identify each solid from its net.
Question 4.

Answer:
The net of the solid is a square pyramid.

Explanation:
In the above-given question,
given that,
the net of the solid is a square pyramid.
the formula of square pyramid = 1/3 x bxb x h.
where b = base, and h = height.
the figure is a square pyramid.

Question 5.

Answer:
The net of the solid is a rectangular pyramid.

Explanation:
In the above-given question,
given that,
the net of the solid is a rectangular pyramid.
the formula of rectangular pyramid = 1/3 x l x w x h.
where l = length, w = width, and h = height.
the figure is a rectangular pyramid.

Lesson 7.6 Find Surface Areas of Prisms

Quick Review
You can use a net or a formula to find the surface area of a prism.

Example
Find the surface area.

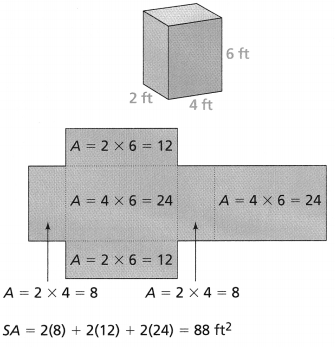
Practice
Find the surface area of each prism.
Question 1.

Answer:
The surface area of the rectangular prism = 126 cubic ft.

Explanation:
In the above-given question,
given that,
l = 6 ft, w = 3 ft, and h = 5 ft.
surface area of rectangular prism = 2(lw + lh + hw).
area = 2(6 x 3) + (6 x 5) + (5 x 3).
area = 2(18) + 30 + 15.
area = 2(63).
area = 126.

Question 2.

Answer:
The surface area of the triangular pyramid = 7168 cubic cm.

Explanation:
In the above-given question,
given that,
the surface area of the triangular prism = a x b x c x h.
where a = base side.
b = base side.
c = base side.
h = height.
surface area of the triangular prism = 8 x 16 x 8 x 7.
area = 7168 cubic cm.

Question 3.
Cube
s = 9.4 m

Answer:
Area = 530.16 sq m.

Explanation:
In the above-given question,
given that,
s = 9.4 m.
The surface area of a cube is 6a square.
area = 6 x 9.4 x 9.4.
area = 6 x 88.36.
area = 530.16 sq m.

Question 4.
Cube
s = 7 cm

Answer:
Area = 294 sq cm.

Explanation:
In the above-given question,
given that,
s = 9.4 m.
The surface area of a cube is 6a square.
area = 6 x 7 x 7.
area = 6 x 49.
area = 294 sq cm.

Question 5.
Rectangular prism
l = 12 in.
w = 7 in.
h = 3 in.

Answer:
The surface area of the rectangular prism = 282 cubics in.

Explanation:
In the above-given question,
given that,
l = 12 in, w = 7 in, and h = 3 in.
surface area of rectangular prism = 2(lw + lh + hw).
area = 2(12 x 7) + (7 x 3) + (12 x 3).
area = 2(84) + 21 + 36.
area = 2(141).
area = 282.

Question 6.
Rectangular prism
l = 5 cm
w = 6 cm
h = 7 cm

Answer:
The surface area of the rectangular prism = 214 cubics cm.

Explanation:
In the above-given question,
given that,
l = 5 cm, w = 6 cm, and h = 7 cm.
surface area of rectangular prism = 2(lw + lh + hw).
area = 2(5 x 6) + (7 x 6) + (5 x 7).
area = 2(30) + 42 + 35.
area = 2(107).
area = 214.

Lesson 7.7 Find Surface Areas of Pyramids

Quick Review
You can use a net or a formula to find the surface area of a pyramid.

Example
Find the surface area.
Area of one triangle:

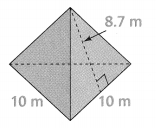
T = \(\frac{1}{2}\) × 10 × 8.7 = 43.5
SA = 4T
= 4 × 43.5
= 174
The surface area of the pyramid is 174 m².

Practice
In 1 and 2, find the surface area of each pyramid.
Question 1.

Answer:
The surface area of the pyramid = 10 sq in.

Explanation:
In the above-given question,
given that,
bases = 4 in.
height = 5 in.
surface area of the pyramid = 1/2 (p x s).
area = 1/2 (4 x 5).
area = 1/2(20).
area = 10 sq in.

Question 2.

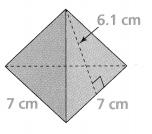
Answer:
The surface area of the pyramid = 21.35 sq cm.

Explanation:
In the above-given question,
given that,
bases = 7 cm.
height = 6.1 cm.
surface area of the pyramid = 1/2 (p x s).
area = 1/2 (7 x 6.1).
area = 1/2(42.7).
area = 21.35 sq cm.

Question 3.
Each side of the base of a square pyramid is 10 ft and the height of each triangular face is 7 ft. Find the surface area of the pyramid.

Answer:
The surface area of the pyramid = 607 sq ft.

Explanation:
In the above-given question,
given that,
Each side of the base of a square pyramid is 10 ft and the height of each triangular face is 7ft.
surface area of the pyramid = axa + 2a √axa/4 + h x h.
where a = base edge.
h = height.
area = 100+ 20 √100/4 + 49.
area = 120 √25 + 49.
area = 120 x 5 + 7.
area = 600 + 7.
area = 607.

Lesson 7.8 Find Volume with Fractional Edge Lengths

Quick Review
The volume of a rectangular prism is equal to the area of the base multiplied by the height.

Example
Find the volume of the rectangular prism.

STEP 1 Find the number of small \(\frac{1}{4}\)-in. cubes that will fill the prism.
14 small \(\frac{1}{4}\)-in. cubes 31in. fit along the 3\(\frac{1}{2}\) in. side.
12 small \(\frac{1}{4}\)-in. cubes fit along the 3 in. side.
15 small \(\frac{1}{4}\)-in. cubes fit along the 3\(\frac{3}{4}\) in. side.
14 • 12 • 15 = 2,520 small \(\frac{1}{4}\)-in. cubes fill the prism.

STEP 2
Find the volume of each small 7-in. cube.
V = lwh = \(\frac{1}{4}\) in. • \(\frac{1}{4}\) in. • \(\frac{1}{4}\) in. = \(\frac{1}{64}\) in.³

STEP 3
Find the volume of the prism.
2,520 • \(\frac{1}{64}\) in.³ = 39\(\frac{3}{8}\) in.³
You can also use a formula. .
V = lwh = 3\(\frac{1}{2}\) in. × 3 in. × 3\(\frac{3}{4}\) in. = 39\(\frac{3}{8}\) in.³

Practice
Find the volume of each rectangular prism.
Question 1.

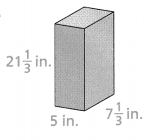
Answer:
Volume = 777.45 cubic in.

Explanation:
In the above-given question,
given that,
volume of rectangular prism = l x w x h.
where l = 5 in, w = 22/3 in, and h = 64/3 in.
v = 5 x 7.3 x 21.3.
v = 777.45 cubic in

Question 2.

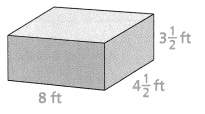
Answer:
Volume = 234 cubic ft.

Explanation:
In the above-given question,
given that,
volume of rectangular prism = l x w x h.
where l = 8 ft, w = 4.5 ft, and h = 6.5 ft.
v = 8 x 4.5 x 6.5.
v = 234 cubic ft.

Question 3.

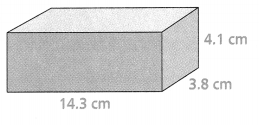
Answer:
Volume = 222.794 cubic cm.

Explanation:
In the above-given question,
given that,
volume of rectangular prism = l x w x h.
where l = 14.3 cm, w = 3.8 cm, and h = 4.1 cm.
v = 14.3 x 3.8 x 4.1.
v = 222.794 cubic cm.

Topic 7 Fluency Practice

Hidden Clue
For each ordered pair, simplify the two coordinates. Then locate and label the corresponding point on the graph. Draw line segments to connect the points in alphabetical order. Connect L to E to complete the picture, then use the completed picture to help answer the riddle below.
I can… multiply and divide multidigit decimals.

Answer:
A: (1.86, 2).
B: (2.4, 0.8).
C: (3.6, 1.25).
D: (5.4, 4.76).
E: (7.2, 8.2).
F: (13.6, 5).
G: (13.1, 8.8).
H: (11.8, 10.5).
I: (9.6, 12.7).
J: (6.4, 13.2).
K: (4.1, 13.2).
L: (1, 11.5).

Explanation:
In the above-given question,
given that,
multiply and divide the numbers.
A: (1.2 x 1.55, 2.7/1.35).
(1.86, 2).
B: (1.25 x 1.92, 0.48/0.6).
(2.4, 0.8).
C: (5.04/1.4, 0.5 x 2.5).
(3.6, 1.25).
D: (2.16 x 2.5, 11.9/2.5).
(5.4, 4.76).
E: (16.56/ 2.3, 5.125 x 1.6).
(7.2, 8.2).
F: (6.12/0.45, 6.25 x 0.8).
(13.6, 5).
G: (2.62 x 5, 12.32/1.4).
(13.1, 8.8).
H: (29.5 x 0.4, 3.675 /0.35).
(11.8, 10.5).
I: (12.48/1.3, 10.16 x 1.25)
(9.6, 12.7).
J: (20 x 0.32, 59.4/4.5).
(6.4, 13.2).
K: (7.79/1.9, 40 x 0.33).
(4.1, 13.2).
L: (25 x 0.04, 48.3/4.2).
(1, 11.5).