Go through the enVision Math Common Core Grade 8 Answer Key Topic 2 Analyze And Solve Linear Equations regularly and improve your accuracy in solving questions.
enVision Math Common Core 8th Grade Answers Key Topic 2 Analyze And Solve Linear Equations
Topic Essential Question
How can we analyze connections between linear equations, and use them to solve problems?
Answer:
One of the more obvious “connections” between linear equations is the presence of the same two variables (Generally, in most cases x and y) in these equations.
Assuming that your two equations are distinct (neither is merely a multiple of the other), we can use the “elimination by addition and subtraction” method or “Substitution method” to eliminate one variable, leaving us with an equation in one variable,
solve this 1-variable (x) equation, and then use the resulting value in the other equation to find the value of the other variable (y).
By doing this we find a unique solution (x, y) that satisfies both original equations.
Not only that but also this solution (x, y) will also satisfy both of the original linear equations.
3-ACT MATH

Powering Down
Do you know that feeling when you realize you left your charger at home? Uh-oh. It’s only a matter of time before your device runs out of power. Your battery percentage is dropping, but you still have so much left to do. Think about this during the 3-Act Mathematical Modeling lesson.

Topic 2 enVision STEM Project
Did You Know?
Demography is the study of changes, such as the number of births, deaths, or net migration, occurring in the human population over time.

Deaths Worldwide in 2015 (estimated)
Emigration is the act of leaving one’s country to settle elsewhere. In 2015, 244 million people, or 3.3% of the world’s population, lived outside their country of origin.

Immigration is the act of entering and settling in a foreign country. The United States has the largest immigrant population in the world.
Your Task: Modeling Population Growth

Human population numbers are in constant flux. Suppose a country has a population of 20 million people at the start of one year and during the year there are 600,000 births, 350,000 deaths, 100,000 immigrants, and 5,000 emigrants. You and your classmates will determine the total population at the end of the year and then model the expected change over a longer period.
Answer:
It is given that the population at the start of the year is 20 million people and during that year, there are 600,000 births, 350,000 deaths, 100,000 immigrants, and 5,000 emigrants
So,
The total population at the end of the year = (Total population at the start of the year) – ( Births + Deaths + Immigrants + Emigrants at that year)
= 20 million – (600,000 + 350,000 + 100,000 + 5,000)
= 20 million – 10.5 million
= 9.5 million
Change in Population = (Births + Immigration) – (Deaths + Emigration)
= (600,000 + 100,000) – (350,000 + 5,000)
= 700,000 – 355,000
= 345,000
Hence, from the above,
We can conclude that
The total population at the end of the year is: 9.5 million
The change in population at that year is: 345,000

Topic 2 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
inverse operations
like terms
proportion
variables
Question 1.
In an algebraic expression, __________ are terms that have the same variables raised to the same exponents.
Answer:
We know that,
In an algebraic expression, “Like terms” are terms that have the same variables raised to the same exponents.
Hence, from the above,
We can conclude that the best term that fits the given definition is: Like terms
Question 2.
Quantities that represent an unknown value are _________.
Answer:
We know that,
Quantities that represent an unknown value are “Variables”
Hence, from the above,
We can conclude that the best term that fits the given definition is: Variables
Question 3.
A _________ is a statement that two ratios are equal.
Answer:
We know that,
A “Proportion” is a statement that two ratios are equal.
Hence, from the above,
We can conclude that the best term that fits the given definition is: Proportion

Question 4.
Operations that “undo” each other are __________.
Answer:
We know that,
Operations that “undo” each other are ” Inverse Operations”
Hence, from the above,
We can conclude that the best term that fits the given definition is: Inverse Operations
Identify Like Terms
Complete the statements to identify the like terms in each expression.
Question 5.
4x + 7y – 62 + 6y – 9x
4x and ______ are like terms.
7y and _______ are like terms.
Answer:
The given expression is:
4x + 7y – 62 + 6y – 9x
We know that,
The “Like terms” are terms that have the same variables raised to the same exponents.
Hence, from the above,
We can conclude that
4x and 9x are like terms
7y and 6y are like terms
Question 6.
\(\frac{1}{2}\)s – (6u – 9u) + \(\frac{1}{10}\)s + 25
\(\frac{1}{2}\)s and _______ are like terms.
6u and _______ are like terms.
Answer:
The given expression is:
\(\frac{1}{2}\)s – (6u – 9u) + \(\frac{1}{10}\)s + 25
= \(\frac{1}{2}\)s + 9u – 6u + \(\frac{1}{10}\)s + 25
We know that,
The “Like terms” are terms that have the same variables raised to the same exponents.
Hence, from the above,
We can conclude that
\(\frac{1}{2}\)s and \(\frac{1}{10}\)s are like terms
6u and 9u are like terms
Solve One-Step Equations
Simplify each equation.
Question 7.
2x = 10
Answer:
The given expression is:
2x = 10
Divide by 2 into both sides
\(\frac{2}{2}\)x = \(\frac{10}{2}\)
x = 5
Hence, from the above,
We can conclude that the value of x is: 5
Question 8.
x + 3 = 12
Answer:
The given expression is:
x + 3 = 12
Subtract with 3 on both sides
x + 3 – 3 = 12 – 3
x = 9
Hence, from the above,
We can conclude that the vaue of x is: 9
Question 9.
x – 7 = 1
Answer:
The given expression is:
x – 7 = 1
Add with 7 on both sides
x – 7 + 7 = 1 + 7
x = 8
Hence, from the above,
We can conclude that the value of x is: 8
Simplify Fractions
Question 10.
Explain how to simplify the fraction \(\frac{12}{36}\).
Answer:
The given fraction is:
\(\frac{12}{36}\)
From the given fraction,
We can observe that the numerator and the denominator are the multiples of 12
So,
Divide the numerator by 12 and the denominator by 12
So,
\(\frac{12}{36}\) = \(\frac{1}{3}\)
Hence,
The simplified form of the given fraction is: \(\frac{1}{3}\)
Language Development
Fill in the Venn diagram to compare and contrast linear equations of the form y = mx and y = x + b.

In the box below, draw graphs to represent each form of the linear equations.
Topic 2 PICK A PROJECT
PROJECT 2A
If you had to escape from a locked room, how would you start?
PROJECT: DESIGN AN ESCAPE-ROOM ADVENTURE

PROJECT 2B
What animal would you most like to play with for an hour? Why?
PROJECT: PLAN A PET CAFÉ

PROJECT 2C
If you wrote a play, what would it be about?
PROJECT: WRITE A PLAY

PROJECT 2D
How many tiny steps does it take to cross a slackline?
PROJECT: GRAPH A WALKING PATTERN

Lesson 2.1 Combine Like Terms to solve Equations
Explore It!
A superintendent orders the new laptops shown below for two schools in her district. She receives a bill for $7,500.
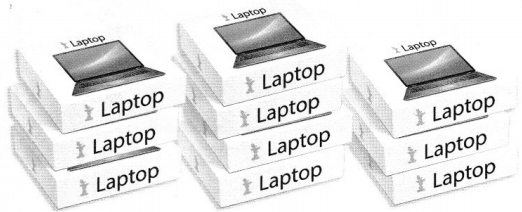
I can… solve equations that have like terms on one side.
A. Draw a representation to show the relationship between the number of laptops and the total cost.
Answer:
It is given that she receives a bill for $7,500
So,
The total cost of the laptops that are given in the above figure = $7,500
Now,
Let the cost of a laptop be $x
So,
$3x + $4x + $3x = $7,500
$10x = $7,500
Hence, from the above,
We can conclude that
The representation to show the relationship between the number of laptops and the total cost is:
$10x = $7,500
B. Use the representation to write an equation that can be used to determine the cost of one laptop.
Answer:
From part (a),
The representation to show the relationship between the number of laptops and the total cost is:
$10x = $7,500
Divide with 10 into both sides
So,
\(\frac{$10x}{10}\) = \(\frac{$7,500}{10}\)
$x = $750
Hence, from the above,
We can conclude that
The representation to write an equation that can be used to determine the cost of one laptop is:
$x = $750

Focus on math practices
Reasoning Why is it important to know that each laptop costs the same amount?
Answer:
From the given figure,
We can observe that all the laptops are of the same type
So,
Each laptop will cost the same amount since all the laptops are the same
Essential Question
How do you solve equations that contain like terms?
Answer:
We will solve the equations that contain like terms by rearranging the like terms on either the left side or the right side
Try It!
Selena spends $53.94 to buy a necklace and bracelet set for each of her friends. Each necklace costs $9.99, and each bracelet costs $7.99. How many necklace and bracelet sets, s, did Selena buy?
Selena buys necklace and bracelet sets for _________ friends.
_____ s + ______ s = 53.94
______ s = 53.94
s = ______
Answer:
Let each necklace and each bracelet be s
It is given that
The cost of each necklace is: $9.99
The cost of each bracelet is: $7.99
The total cost of a necklace and a bracelet is: $53.94
So,
$9.99s + $7.99s = $53.94
$17.98s = $53.94
$1798s = $5394
Divide by 1798 on both sides
\(\frac{$1798}{1798}\)s = \(\frac{$5394}{1798}\)
s = 3
Hence, from the above,
We can conclude that the number of necklace and bracelet sets that Selena buy is: 3
Convince Me!
Suppose the equation is 9.99s + 7.99s + 4.6 = 53.94. Can you combine the s terms and 4.6? Explain.
Answer:
The given equation is:
9.99s + 7.99s + 4.6 = 53.94
We know that,
We can only combine the terms only when they are the “Like terms”
So,
In the given equation,
9.99s and 7.99s are the like terms
53.94 and 4.6 are the like terms
Hence, from the above,
We can conclude that we can not combine the s terms and 4.6
Try It!
Nat’s grocery bill was $150, which included a 5% club discount. What was Nat’s bill before the discount? Write and solve an equation.
Answer:
It is given that Nat’s grocery bill was $150 which included a 5% club discount
Now,
Let x be Nat’s bill before the discount
So,
To find Nat’s bill before discount, we have to find the value of 5% of 150 and add its value from 150
We know that,
The value of the bill will always be less after discount when compared to the value of the bill before discount
Now,
Nat’s bill before the discount = (Nat’s bill which included a 5% club discount) + (Value of 5% of 150)
x = $150 + (\(\frac{5}{100}\) × 150)
x = $150 + \(\frac{5 × 150}{100}\)
x = $150 + \(\frac{750}{100}\)
x = $150 + $7.5
x = $157.5
Hence, from the above,
We can conclude that Nat’s bill before the discount is: $157.5
Try It!
Solve for d.
a. –\(\frac{1}{4}\)d – \(\frac{2}{5}\)d = 39
Answer:
The given expression is:
–\(\frac{1}{4}\)d – \(\frac{2}{5}\)d = 39
-d (\(\frac{1}{4}\) + \(\frac{2}{5}\)) = 39
-d (0.25 + 0.40) = 39
-d (0.65) = 39
-d = \(\frac{39}{0.65}\)
-d = \(\frac{39 × 100}{65}\)
-d = 60
d = -60
Hence, from the above,
We can conclude that the value of d is: -60
b. -9.760 – (-12.81d) = 8.54
Answer:
The given expression is:
-9.760 – (-12.81d) = 8.54
-9.760 + 12.81d = 8.54
Rearrange the like terms in the above equation
So,
12.81d = 8.54 + 9.760
12.81d = 18.3
Divide by 12.81 on both sides
So,
\(\frac{12.81d}{12.81}\) = \(\frac{18.3}{12.81}\)
d = 1.428
Hence, from the above,
We can conclude that the value of d is: 1.428
KEY CONCEPT
In an equation with variable terms on one side, you can combine like terms before using inverse operations and properties of equality to solve the equation.
0.8n + 0.6n = 42
1.4n = 42 → Combine like terms.
\(\frac{1.4 n}{1.4}=\frac{42}{1.4}\)
n = 30
Do You Understand?
Question 1.
Essential Question How do you solve equations that contain like terms?
Answer:
In the equations that contain “Like terms”,
First, arrange the like terms at one side i.e., either the left side or the right side and combine them and then solve the equation for the desired result
Question 2.
Look for Relationships How do you recognize when an equation has like terms?
Answer:
We know that,
“Like terms” are terms that have the same variables raised to the same exponents.
Hence,
When there are the same variables in the given equation, we can call that terms “Like terms” in the given equation
Question 3.
Make Sense and Persevere in the equation 0.755 – \(\frac{5}{8}\)s = 44, how do you combine the like terms?
Answer:
The given equation is:
0.755 – \(\frac{5}{8}\)s = 44
We know that,
“Like terms” are terms that have the same variables raised to the same exponents.
So,
In the given equation,
0.755 and 44 are the like terms
So,
\(\frac{5}{8}\)s = 0.755 + 44
\(\frac{5}{8}\)s = 44.755
Multiply with \(\frac{8}{5}\) on both sides
So,
\(\frac{5}{8}\)s × \(\frac{8}{5}\) = 44.755 × \(\frac{8}{5}\)
s = 71.608
Hence, from the above,
We can conclude that the value of s is: 71.608
Do You Know How?
Question 4.
Henry is following the recipe card to make a cake. He has 95 cups of flour. How many cakes can Henry make?

Answer:
It is given that Henry is following the recipe card to make a cake and he has 95 cups of flour
It is also given that
We need
2\(\frac{2}{3}\) cups of flour for the batter
\(\frac{1}{2}\) cup of flour for the topping
Now,
Let the number of cakes be x
So,
By using the flour for the batter and the topping, Henry can make x cakes
Now,
(2\(\frac{2}{3}\) + \(\frac{1}{2}\))x = 95
We know that,
2\(\frac{2}{3}\) = \(\frac{8}{3}\)
So,
(\(\frac{8}{3}\) + \(\frac{1}{2}\))x = 95
\(\frac{19}{6}\)x = 95
Multiply with \(\frac{6}{19}\) on both sides
So,
\(\frac{19}{6}\)x × \(\frac{6}{19}\) = 95 × \(\frac{6}{19}\)
x = \(\frac{95 × 6}{19}\)
x = 30
Hence, from the above,
We can conclude that the number of cakes made by Henry is: 30
Question 5.
A city has a population of 350,000. The population has decreased by 30% in the past ten years. What was the population of the city ten years ago?
Answer:
It is given that a city has a population of 350,000 and it has decreased by 30% in the past ten years
Now,
Let the population of the city ten years ago be: x
To find the population of the city ten years ago,
We have to find the value of 30% of 350,000 and add it to the 350,000
The reason is it is given that the population i.e., 350,000 decreased in the past ten years. So, the population will be more than 350,000 ten years ago
So,
The population of the city ten years ago = (The population of the city in the past ten years) + (The value of 30% of 350,000)
x = 350,000 + \(\frac{30}{100}\) × 350,000
x = 350,000 + \(\frac{30 × 350,000}{100}\)
x = 350,000 + 105,000
x = 455,000
Hence, from the above,
We can conclude that the population of the city ten years ago is: 455,000
Question 6.
Solve the equation –12.2z – 13.4z = -179.2.
Answer:
The given equation is:
-12.2z – 13.4z = -179.2
From the given equation,
We can observe that 12.2 and 13.4 are the like terms
So,
-z(12.2 + 13.4) = -179.2
z(12.2 + 13.4) = 179.2
z(25.6) = 179.2
Divide by 25.6 into both sides
So,
\(\frac{25.6}{25.6}\)z = \(\frac{179.2}{25.6}\)
z = 7
Hence, from the above,
We can conclude that the value of z is: 7
Practice & Problem Solving
Leveled Practice In 7 and 8, complete the steps to solve for x.
Question 7.
\(\frac{4}{5}\)x – \(\frac{1}{4}\)x = 11
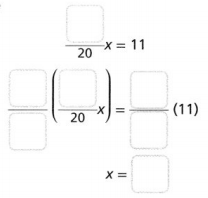
Answer:
The given equation is:
\(\frac{4}{5}\)x – \(\frac{1}{4}\)x = 11
x (\(\frac{4}{5}\) – \(\frac{1}{4}\)) = 11
x (\(\frac{16 – 5}{20}\)) = 11
\(\frac{11}{20}\)x = 11
Multiply with \(\frac{20}{11}\) on both sides
So,
\(\frac{20}{11}\) (\(\frac{11}{20}\)x) = 11 × \(\frac{20}{11}\)
x = \(\frac{11 × 20}{11}\)
x = 20
Hence, from the above,
We can conclude that the value of x is: 20
Question 8.
-0.65x + 0.45x = 5.4
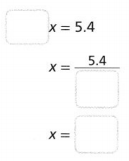
Answer:
The given equation is:
-0.65x + 0.45x = 5.4
So,
x (0.45 – 0.65) = 5.4
x (-0.20) =5.4
Divide by -0.20 into both sides
So,
\(\frac{-0.20}{-0.20}\)x = \(\frac{5.4}{-0.20}\)
x = -27
Hence, from the above,
We can conclude that the avlue of x is: -27
In 9-12, solve for x.
Question 9.
\(\frac{4}{9}\)x + \(\frac{1}{5}\)x = 87
Answer:
The given equation is:
\(\frac{4}{9}\)x + \(\frac{1}{5}\)x = 87
So,
x (\(\frac{4}{9}\) + \(\frac{1}{5}\)) = 87
x (\(\frac{20 + 9}{45}\)) = 87
\(\frac{29}{45}\)x = 87
Multiply with \(\frac{45}{29}\) on both sides
So,
\(\frac{45}{29}\) (\(\frac{29}{45}\)x) = 87 × \(\frac{45}{29}\)
x = \(\frac{87 × 45}{29}\)
x = 135
Hence, from the above,
We can conclude that the value of x is: 135

Question 10.
-3.8x – 5.9x = 223.1
Answer:
The given equation is:
-3.8x – 5.9x = 223.1
So,
-x (3.8 + 5.9) = 223.1
-x (9.7) =223.1
Divide by -9.7 into both sides
So,
\(\frac{-9.7}{-9.7}\)x = \(\frac{223.1}{-9.7}\)
x = -23
Hence, from the above,
We can conclude that the avlue of x is: -23
Question 11.
x + 0.15x = 3.45
Answer:
The givene quation is:
x + 0.15x = 3.45
So,
x (1 + 0.15) = 3.45
x (1.15) = 3.45
Divide be 1.15 into both sides
So,
\(\frac{1.15}{1.15}\)x = \(\frac{3.45}{1.15}\)
x = 3
Hence, from the above,
We can conclude that the value of x is: 3
Question 12.
–\(\frac{3}{5}\)x – \(\frac{7}{10}\) + \(\frac{1}{2}\)x = 56
Answer:
The given equation is:
–\(\frac{3}{5}\)x – \(\frac{7}{10}\) + \(\frac{1}{2}\)x = 56
x (\(\frac{1}{2}\) – \(\frac{3}{5}\)) – \(\frac{7}{10}\) = 56
x (\(\frac{5 – 6}{10}\)) – \(\frac{7}{10}\) = 56
–\(\frac{1}{10}\)x = 56 + \(\frac{7}{10}\)
–\(\frac{1}{10}\)x = \(\frac{560 + 7}{10}\)
Multiply with 10 on both sides
So,
–\(\frac{10}{10}\)x = \(\frac{567 × 10}{10}\)
-x = 567
x = -567
Hence, from the above,
We can conclude that the value of x is: -567
Question 13.
A contractor buys 8.2 square feet of sheet metal. She used 2.1 square feet so far and has $183 worth of sheet metal remaining. Write and solve an equation to find out how many sheets of metal costs per square foot.
Answer:
It is given that a contractor buys 8.2 square feet of sheet metal. She used 2.1 square feet so far and has $183 worth of sheet metal remaining.
So,
The remaining square feet of sheet metal = (Total square feet of sheet metal) – (The total square feet of sheet metal used so far)
The remaining square feet of sheet metal = 8.2 – 2.1
The remaining square feet of sheet metal = 6.1 square feet
Now,
It is given that there is$183 worth of sheet metal remaining
Now,
Let x be the number of sheet metals per square foot
So,
6.1x = $183
Divide by 6.1 into both sides
So,
\(\frac{6.1}{6.1}\)x = \(\frac{$183}{6.1}\)
x = 30
Hence, from the above,
We can conclude that the number of metal sheets per square foot is: 30
Question 14.
Make Sense and Persevere Clint prepares and sells trail mixes at his store. This week, he uses \(\frac{3}{8}\) his supply of raisins to make regular trail mix and \(\frac{1}{4}\) of his supply to make spicy trail mix. If Clint uses 20 pounds of raisins this week, how many pounds of raisins did he have at the beginning of the week?
Answer:
It is given that Clint prepares and sells trail mixes at his store and this week, he uses \(\frac{3}{8}\) his supply of raisins to make regular trail mix and \(\frac{1}{4}\) of his supply to make spicy trail mix.
So,
The total amount of raisins to make trail mix = (The supply of raisins to make regular mix) + (The supply of raisins to make spicy mix)
The total amount of raisins to make trail mix = \(\frac{3}{8}\) + \(\frac{1}{4}\)
The total amount of raisins to make trail mix = \(\frac{5}{8}\)
Now,
Let the number of pounds of raisins at the beginning of the week be x
So,
\(\frac{5}{8}\)x = 20
Multiply with \(\frac{8}{5}\) on both sides
So,
x = 20 × \(\frac{8}{5}\)
x = \(\frac{20 × 8}{5}\)
x = 32 pounds
Hence, from the above,
We can conclude that the number of pounds of raisins at the beginning of the week is: 32 pounds
Question 15.
Make Sense and Persevere A submarine descends to \(\frac{1}{6}\) of its maximum depth. Then it descends another \(\frac{2}{3}\) of its maximum depth. If it is now at 650 feet below sea level, what is its maximum depth?

Answer:
It is given that a submarine descends to \(\frac{1}{6}\) of its maximum depth and then it descends another \(\frac{2}{3}\) of its maximum depth and it is now at 650 feet below sea level
Now,
Let x be the maximum depth
So,
\(\frac{1}{6}\)x + \(\frac{2}{3}\)x = 650
\(\frac{1 + 4}{6}\)x = 650
\(\frac{5}{6}\)x = 650
Multiply with \(\frac{6}{5}\) on both sides
So,
x = 650 × \(\frac{6}{5}\)
x = \(\frac{650 × 6}{5}\)
x = 780 feet
Hence, from the above,
We can conclude that the maximum depth is: 780 feet
Question 16.
Model with Math Write an equation that can be represented by the bar diagram, then solve.

Answer:
The given bar diagram is:

So,
From the bar diagram,
The representation of the equation is:
-1.2y + (-4.2y) = -3.78
-1.2y – 4.2y = -3.78
– (1.2y + 4.2y) = -3.78
1.2y + 4.2y = 3.78
5.4y = 3.78
Divide by 5.4 into both sides
So,
\(\frac{5.4}{5.4}\)y = \(\frac{3.78}{5.4}\)
y = 0.7
Hence, from the above,
We can conclude that the value of y is: 0.7
Question 17.
Higher Order Thinking Solve \(\frac{2}{3}\)h – 156 = 3\(\frac{13}{24}\).
Answer:
The given equation is:
\(\frac{2}{3}\)h – 156 = 3\(\frac{13}{24}\)
We know that,
3\(\frac{13}{24}\) = \(\frac{85}{24}\)
So,
\(\frac{2}{3}\)h – 156 = \(\frac{85}{24}\)
\(\frac{2}{3}\)h = \(\frac{85}{24}\) + 156
0.666h = 3.541 + 156
0.666h = 159.541
Divide by 0.666 into both sides
So,
h = \(\frac{159.541}{0.666}\)
h = 239.552
Hence, from the above,
We can conclude that the value of ‘h’ is: 239.552
Question 18.
Model with Math Nathan bought one notebook and one binder for each of his college classes. The total cost of the notebooks and binders was $27.08. Draw a bar diagram to represent the situation. How many classes is Nathan taking?

Answer:
It is given that Nathan bought one notebook and one binder for each of his college classes. The total cost of the notebooks and binders was $27.08.
Now,
Let the number of notebooks and binders that Nathan bought be x
From the figure,
It is given that
The cost of 1 notebook is: $0.95
The cost of 1 binder is: $5.82
So,
The representation of the cost of total notebooks and binders in the form of the equation is:
$0.95x + $5.82x = $27.08
Hence,
The representation of the above equation in the form of a bar diagram is:

Assessment Practice
Question 19.
Construct Arguments Your friend incorrectly says the solution to the equation –\(\frac{3}{5}\)y – \(\frac{1}{7}\)y = 910 is y = 676. What error did your friend make?
A. Added –\(\frac{1}{7}\) to –\(\frac{3}{5}\)
B. Subtracted \(\frac{1}{7}\) from –\(\frac{3}{5}\)
C. Multiplied 910 by \(\frac{26}{35}\)
D. Multiplied 910 by \(\frac{35}{26}\)
Answer:
The given equation is:
–\(\frac{3}{5}\)y – \(\frac{1}{7}\)y = 910
-y (\(\frac{3}{5}\) + \(\frac{1}{7}\)) = 910
–\(\frac{26}{35}\)y = 910
Multiply with –\(\frac{35}{26}\) on both sides
So,
y = -910 × \(\frac{35}{26}\)
y = -1,225
Hence from the above,
We can conclude that the error your friend makes is:
Multiplied 910 by \(\frac{26}{35}\)
Question 20.
A 132-inch board is cut into two pieces. One piece is three times the length of the other. Find the length of the shorter piece.
PART A
Draw a bar diagram to represent the situation.
Answer:
It is given that a 132-inch board is cut into two pieces and one piece is 3 times the length of the other
Now,
Let the length of 1 piece be x inches
So,
The length of the other piece is: 3x inches
So,
The representation of the given situation in the form of an equation is:
3x + x = 132
Hence,
The representation of the above equation in the form of a bar diagram is:

PART B
Write and solve an equation to find the length of the shorter piece.
Answer:
From part (a),
The equation that represents the given situation is:
3x + x = 132
4x = 132
Divide by 4 into both sides
So,
x = \(\frac{132}{4}\)
x = 33 inches
Hence,from the above,
We can conclude that the length of the shorter piece is: 33 inches
Lesson 2.2 Solve Equations with Variables on Both Sides
Solve & Discuss It!
Jaxson and Bryon collected an equal amount of money during a car wash. They collected cash and checks as shown below. If each check is written for the same amount, x, what is the total amount of money collected by both boys? Explain.

I can… solve equations with variables on both sides of the equal sign.
Answer:
It is given that Jaxson and Bryon collected an equal amount of money during the car wash.
It is also given that they collected cash and checks and each check is written for the same amount x
So,
The amount earned by Jaxson = The amount earned by Bryon
Now,
From the given figure,
The amount earned by Jaxson = The amount earned by cash + The amount earned by checks
= 15 + 14x
The amount earned by Bryon = The amount earned by cash + The amount earned by checks
= 50 + 7x
So,
Now,
15 + 14x = 50 + 7x
Subtract with 7x on both sides
15 + 14x – 7x = 50 + 7x – 7x
15 + 7x = 50
Subtract with 15 on both sides
15 + 7x – 15 = 50 – 15
7x = 35
Divide by 7 on both sides
\(\frac{7}{7}\)x = \(\frac{35}{7}\)
x = 5
So,
The total amount of money collected by both boys = 15 +14x + 50 + 7x
= 21x + 65
= 21 (5) + 65
= 105 + 65
= $170
Hence, from the above,
We can conclude that the total amount earned by both the boys is: $170
Reasoning
How can you use an equation to show that expressions are equal?
Answer:
Combine any like terms on each side of the equation i.e., x-terms with x-terms and constants with constants. Arrange the terms in the same order, usually x-term before constants.
If all of the terms in the two expressions are identical, then the two expressions are equivalent.
Focus on math practices
Model with Math What expressions can you write to represent the amount of money collected by each boy? How can you use these expressions to write an equation?
Answer:
From the given figure,
We can observe that the two boys earned cash and checks
So,
The total amount earned by any boy = The amount earned due to cash + The amount earned due to checks
Now,
The amount earned by Jaxson = The amount earned by cash + The amount earned by checks
= 15 + 14x
The amount earned by Bryon = The amount earned by cash + The amount earned by checks
= 50 + 7x
Now,
It is given that the amount earned by both boys are equal
So,
The amount earned by Jaxson = The amount earned by Bryon
15 + 14x = 50 + 7x
Rearrange the like terms
14x – 7x = 50 – 15
7x = 35
Hence, from the above,
We can conclude that the representation of the amount collected by each boy in the form of the equation is:
7x = 35
Essential Question
How do you use inverse operations to solve equations with variables on both sides?
Answer:
The “Inverse operations” allow us to undo what has been done to the variable
Example:
Solve:
x+3=8
From the above equation,
We can observe that 3 has been added to the variable, x.
We know that,
The inverse of addition is subtraction
So,
By subtracting 3, We can undo the addition.
Now,
After 3 was added, the result was equal to 8.
We undo the addition, by subtracting 3 and see that, the starting amount was 5
Try It!
Class A was given a sunflower with a height of 8 centimeters that grows at a rate of 3\(\frac{1}{2}\) centimeters per week. Class B was given a sunflower with a height of 10 centimeters that grows at a rate of 3\(\frac{1}{4}\) centimeters per week. After how many weeks are the sunflowers the same height?
Let w= the number of weeks.
____ w + 8 = _____ w + 10
_____ w + 8 = 10
_____ w = _____
w = _____
The sunflowers are the same height after ________ weeks.
Answer:
It is given that
Class A was given a sunflower with a height of 8 centimeters that grows at a rate of 3\(\frac{1}{2}\) centimeters per week and class B was given a sunflower with a height of 10 centimeters that grows at a rate of 3\(\frac{1}{4}\) centimeters per week.
Now,
Let the number of weeks be w
So,
The height of a sunflower of class A after w weeks = 3\(\frac{1}{2}\)w + 8
We know that,
3\(\frac{1}{2}\) = \(\frac{7}{2}\)
So,
The height of a sunflower of class A after w weeks = \(\frac{7}{2}\)w + 8
Now,
The height of a sunflower of class B after w weeks = 3\(\frac{1}{4}\)w + 10
We know that,
3\(\frac{1}{4}\) = \(\frac{13}{4}\)
So,
The height of a sunflower of class A after w weeks = \(\frac{13}{4}\)w + 10
Now,
To make the height of a sunflower from both classes equal,
The height of sunflower of class A after w weeks = The height of sunflower of class B after w weeks
\(\frac{7}{2}\)w + 8 = \(\frac{13}{4}\)w + 10
Rearrange the like terms
\(\frac{7}{2}\)w – \(\frac{13}{4}\)w = 10 – 8
\(\frac{14 – 13}{4}\)w = 2
\(\frac{1}{4}\)w = 2
Multiply with 4 on both sides
\(\frac{4}{4}\)w = 2 (4)
w = 8 weeks
Hence, from the above,
We can conclude that after 8 weeks, the sunflowers of class A and class B are of the same height
Convince Me!
How can you check your work to make sure the value of the variable makes the equation true? Explain.
Answer:
To make a true equation, check your math to make sure that the values on each side of the equals sign are the same. Ensure that the numerical values on both sides of the “=” sign are the same to make a true equation.
Examples:
a) 9 = 9 is a true equation
b) 5 + 4 = 9 is a true equation
Try It!
Solve the equation 96 – 4.5y – 3.2y = 5.6y + 42.80.
Answer:
The given equation is:
96 – 4.5y – 3.2y = 5.6y + 42.80
Now,
Rearrange the like terms at one side i.e., y-terms to one side and the constant terms to other side
So,
-5.6y – 4.5y – 3.2y = 42.80 – 96
-13.3y = -53.2
13.3y = 53.2
Divide by 13.3 into both sides
So,
\(\frac{13.3}{13.3}\)y = \(\frac{53.2}{13.3}\)
y = 4
Hence, from the above,
We can conclude that the value of y is: 4
KEY CONCEPT
When two expressions represent equal quantities, they can be set equal to each other. Then you can use inverse operations and properties of equality to combine like terms and solve for the unknown.

3x + 15 = 4x + 12
3x – 3x + 15 = 4x – 3x + 12
15 = x + 12
15 – 12 = x + 12 – 12
3 = x
Do You Understand?
Question 1.
Essential Question How do you use inverse operations to solve equations with variables on both sides?
Answer:
The “Inverse operations” allow us to undo what has been done to the variable
Example:
Solve:
x+3=8
From the above equation,
We can observe that 3 has been added to the variable, x.
We know that,
The inverse of addition is subtraction
So,
By subtracting 3, We can undo the addition.
Now,
After 3 was added, the result was equal to 8.
We undo the addition, by subtracting 3 and see that, the starting amount was 5
Question 2.
Reasoning Why are inverse operations and properties of equality important when solving equations? Explain.
Answer:
An “Inverse operation” is two operations that undo each other
Ex: Addition and Subtraction or Multiplication and Division.
You can perform the same inverse operation on each side of an equivalent equation without changing the equality.
This gives us a couple of properties that hold true for all equations.
Question 3.
Model with Math Cynthia earns $680 in commissions and is paid $10.25 per hour. Javier earns $410 in commissions and is paid $12.50 per hour. What will you find if you solve for x in the equation 10.25x + 680 = 12.5x + 410?
Answer:
It is given that
Cynthia earns $680 in commissions and is paid $10.25 per hour. Javier earns $410 in commissions and is paid $12.50 per hour.
It is also given that
The representation of the given situation in the form of the equation is:
10.25x + 680 = 12.5x + 410
From the above equation,
We can observe that
10.25x is the amount paid to Cynthia per hour and x is the number of hours
Hence, from the above,
We can conclude that the variable x represents the “Number of hours”
Do You Know How?
Question 4.
Maria and Liam work in a banquet hall. Maria earns a 20% commission on her food sales. Liam earns a weekly salary of $625 plus a 10% commission on his food sales. What amount of food sales will result in Maria and Liam earning the same amount for the week?
Answer:
It is given that
Maria earns a 20% commission on her food sales. Liam earns a weekly salary of $625 plus a 10% commission on his food sales.
So,
To find the number of food sales that will result in Maria and Liam earning the same amount for the week,
20%x = $625 + 10%x
Where,
x is the number of food sales
So,
\(\frac{20}{100}\)x = $625 + \(\frac{10}{100}\)x
Rearrange the like terms
\(\frac{20 – 10}{100}\)x = $625
\(\frac{10}{100}\)x = $625
\(\frac{1}{10}\)x = $625
Multiply with 10 on both sides
So,
\(\frac{10}{10}\)x = $625 (10)
x = $6,250
Hence, from the above,
We can conclude that the number of food sales that will make the same amount in the week for Maria and Liam is: $6,250
Question 5.
Selma’s class is making care packages to give to victims of a natural disaster. Selma packs one box in 5 minutes and has already packed 12 boxes. Her friend Trudy packs one box in 7 minutes and has already packed 18 boxes. How many more minutes does each need to work in order to have packed the same number of boxes?
Answer:
It is given that
Selma’s class is making care packages to give to victims of a natural disaster. Selma packs one box in 5 minutes and has already packed 12 boxes. Her friend Trudy packs one box in 7 minutes and has already packed 18 boxes.
Now,
Let x be the number of more minutes that each has to work so that they have the same number of boxes
So,
To find the more minutes each need to work in order to have packed the same number of boxes,
\(\frac{x}{5}\) + 12 = \(\frac{x}{7}\) + 18
Rearrange the like terms
So,
\(\frac{x}{5}\) – \(\frac{x}{7}\) = 18 – 12
\(\frac{7x – 5x}{35}\) = 6
\(\frac{2x}{35}\) = 6
Divide by 35 into both sides
So,
2x = 6 (35)
Divide by 2 into both sides
So,
x = \(\frac{6 (35)}{2}\)
x = 3 (35)
x = 105 minutes
Hence, from the above,
We can conclude that the number of more minutes that each need to work so that the number of boxes becomes equal is: 105 minutes
Question 6.
Solve the equation –\(\frac{2}{5}\)x + 3 = \(\frac{2}{3}\)x + \(\frac{1}{3}\).
Answer:
The given equation is:
–\(\frac{2}{5}\)x + 3 = \(\frac{2}{3}\)x + \(\frac{1}{3}\)
Rearrange the like terms
So,
\(\frac{2}{3}\)x + \(\frac{2}{5}\)x = 3 – \(\frac{1}{3}\)
\(\frac{10 + 6}{15}\)x = \(\frac{9 – 1}{3}\)
\(\frac{16}{15}\)x = \(\frac{8}{3}\)
Multiply with \(\frac{15}{16}\) on both sides
x = \(\frac{8}{3}\) × \(\frac{15}{16}\)
x = \(\frac{8 × 15}{3 × 16}\)
x = \(\frac{5}{2}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{5}{2}\)
Question 7.
Solve the equation -2.6b + 4 = 0.9b – 17.
Answer:
The given equation is:
-2.6b + 4 = 0.9b – 17
Rearrange the like terms
So,
0.9b + 2.6b = 17 + 4
3.5b = 21
Divide by 3.5 into both sides
So,
\(\frac{3.5}{3.5}\)b = \(\frac{21}{3.5}\)
b = 6
Hence, from the above,
We can conclude that the value of b is: 6
Practice & Problem Solving
Leveled Practice In 8 and 9, solve each equation.
Question 8.
6 – 4x = 6x – 8x + 2
6 – 4x = ____ + 2
6 = _____ + 2
____ = _____
_______ = x
Answer:
The given equation is:
6 – 4x = 6x – 8x + 2
So,
6 – 4x = 2 – 2x
Rearrange the like terms
So,
4x – 2x = 6 – 2
2x = 4
Divide by 2 into both sides
So,
\(\frac{2}{2}\)x = \(\frac{4}{2}\)
x = 2
Hence, from the above,
We can conclude that the value of x is: 2
Question 9.
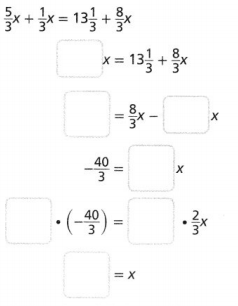
Answer:
The given equation is:
\(\frac{5}{3}\)x + \(\frac{1}{3}\)x = 13\(\frac{1}{3}\) + \(\frac{8}{3}\)x
Rearrange the like terms
So,
\(\frac{5 + 1}{3}\)x – \(\frac{8}{3}\)x = 13\(\frac{1}{3}\)
\(\frac{6 – 8}{3}\)x = 13\(\frac{1}{3}\)
–\(\frac{2}{3}\)x = \(\frac{40}{3}\)
Multiply with 3 on both sides
So,
-2x = 40
divide by -2 into both sides
So,
x = \(\frac{-40}{2}\)
x = -20
Hence, from the above,
We can conclude that the value of x is: -20
Question 10.
Two towns have accumulated different amounts of snow. In Town 1, the snow depth is increasing by 3\(\frac{1}{2}\) inches every hour. In Town 2, the snow depth is increasing by 2\(\frac{1}{4}\) inches every hour. In how many hours will the snowfalls of the towns be equal?
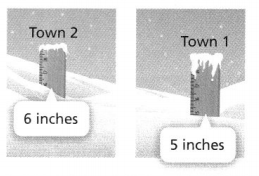
Answer:
It is given that
Two towns have accumulated different amounts of snow. In Town 1, the snow depth is increasing by 3\(\frac{1}{2}\) inches every hour. In Town 2, the snow depth is increasing by 2\(\frac{1}{4}\) inches every hour.
Now,
Let x be the number of hours
So,
To make the snowfalls of the two towns equal,
5 + 3\(\frac{1}{2}\)x = 6 + 2\(\frac{1}{4}\)x
We know that,
3\(\frac{1}{2}\) = \(\frac{7}{2}\)
2\(\frac{1}{4}\) = \(\frac{9}{4}\)
So,
\(\frac{7}{2}\)x – \(\frac{9}{4}\)x = 6 – 5
\(\frac{14 – 9}{4}\)x = 1
\(\frac{5}{4}\)x = 1
Multiply with \(\frac{4}{5}\) on both sides
So,
x = \(\frac{4}{5}\)
x = 0.8 hours
Hence, from the above,
We can conclude that after 0.8 hours, the snowfalls of the two towns will be equal
Question 11.
Solve the equation 5.3g + 9 = 2.3g + 15.
a. Find the value of g.
Answer:
The given equation is:
5.3g + 9 = 2.3g + 15
Rearrange the like terms
So,
5.3g – 2.3g = 15 – 9
3.0g = 6
Divide by 3 into both sides
\(\frac{3}{3}\)g = \(\frac{6}{3}\)
g = 2
Hence, from the above,
We can conclude that the value of g is: 2
b. Explain how you can check that the value · you found for g is correct. If your check does not work, does that mean that your result is incorrect? Explain.
Answer:
From part (a),
We get the value of g : 2
So,
Whether the value of g is correct or not, put it in the given equation
If LHS = RHS,
Then, your check is correct. Otherwise, your check is not correct
Now,
5.3g + 9 = 2.3g + 15
Put, g = 2
So,
5.3 (2) + 9 = 2.3 (2) + 15
10.6 + 9 = 4.6 + 15
19.6 = 19.6
Hence, from the above,
We can conclude that the check is correct
Question 12.
Solve the equation 6 – 6x = 5x – 9x – 2.
Answer:
The given equation is:
6 – 6x = 5x – 9x – 2
So,
6 – 6x = -4x – 2
Rearrange the like terms
So,
-4x + 6x = 6 + 2
2x = 8
Divide by 2 into both sides
So,
\(\frac{2}{2}\)x = \(\frac{8}{2}\)
x = 4
Hence, from the above,
We can conclude that the value of x is: 4
Question 13.
Model with Math The population of one town in Florida is 43,425. About 125 people move out of the town each month. Each month, 200 people on average move into town. A nearby town has a population of 45,000. It has no one moving in and an average of 150 people moving away every month. In about how many months will the population of the towns be equal? Write an equation that represents this situation and solve it.
Answer:
It is given that
The population of one town in Florida is 43,425. About 125 people move out of the town each month. Each month, 200 people on average move into town. A nearby town has a population of 45,000. It has no one moving in and an average of 150 people moving away every month.
Now,
Let the population that are moving in and moving out be x
We know that,
Moving in will be positive and Moving out will be negative
So,
The population of one town in Florida = 43,425 + 200x – 125x
The population of a nearby town = 45,000 – 150x
So,
To find out after how many months, they will be equal,
43,425 + 200x – 125x = 45,000 – 150x
43,425 + 75x = 45,000 – 150x
Rearrange the like terms
So,
150x + 75x = 45,000 – 43,425
225x = 1,575
Divide by 225 into both sides
\(\frac{225}{225}\)x = \(\frac{1,575}{225}\)
x = 7
Hence, from the above,
We can conclude that after 7 months, the population of the towns will be equal
Question 14.
Veronica is choosing between two health clubs After how many months will the total cost for each health club be the same?

Answer:
It is given that Veronica is choosing between two health clubs
Now,
Let x be the number of months so that the cost for the two health clubs will be the same
Now,
The total health cost of Yoga studio A = 22 + 24.50x
The total health cost of Yoga studio B = 47 + 18.25x
So,
To find out after how many months, the total cost for the two health clubs will be the same,
22 + 24.50x = 47 + 18.25x
Rearrange the like terms
So,
47 – 22 = 24.50x – 18.25x
25 = 6.25x
Divide by 25 into both sides
So,
\(\frac{25}{25}\) = \(\frac{6.25}{25}\)x
1 = 0.25x
\(\frac{x}{4}\) = 1
x = 4
Hence, from the above,
We can conclude that after 4 months, the total cost for the two health clubs will be the same
Question 15.
Higher-Order Thinking The price of Stock A at 9 A.M. was $12.73. Since then, the price has been increasing at the rate of $0.06 per hour. At noon, the price of Stock B was $13.48. It begins to decrease at the rate of $0.14 per hour. If the stocks continue to increase and decrease at the same rates, in how many hours will the prices of the stocks be the same?
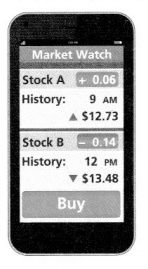
Answer:
It is given that
The price of Stock A at 9 A.M. was $12.73. Since then, the price has been increasing at the rate of $0.06 per hour. At noon, the price of Stock B was $13.48. It begins to decrease at the rate of $0.14 per hour.
Now,
Let x be the number of hours
So,
The price of stock A = $12.73 + $0.06x (Since it is increasing)
The price of stock B = $13.48 – $0.14x (Since it is decreasing)
Now,
To find out after how many hours, the prices will be the same,
$12.73 + $0.06x = $13.48 – $0.14x
Rearrange the like terms
So,
$13.48 – $12.73 = $0.14x + $0.06x
$0.75 = $0.2x
Divide by 0.2 into both sides
So,
x = \(\frac{0.75}{0.2}\)
x = 3.75
x = 3.60 + 0.15
x = 4 hours 15 minutes
Hence, from the above,
We can conclude that after 4 hours 15 minutes, the prices of the stocks will be equal
Assessment Practice
Question 16.
In an academic contest, correct answers earn 12 points and incorrect answers lose 5 points. In the final round, School A starts with 165 points and gives the same number of correct and incorrect answers. School B starts with 65 points and gives no incorrect answers and the same number of correct answers as School A. The game ends with the two schools tied.
PART A
Which equation models the scoring in the final round and the outcome of the contest?
A. 12x + 5x – 165 = -12x + 65
B. 12x – 5x + 165 = 12x + 65
C. 5x – 12x + 165 = 12x + 65
D. 12x – 5x – 165 = 12x + 65
Answer:
It is given that
In an academic contest, correct answers earn 12 points and incorrect answers lose 5 points. In the final round, School A starts with 165 points and gives the same number of correct and incorrect answers. School B starts with 65 points and gives no incorrect answers and the same number of correct answers as School A. The game ends with the two schools tied.
Now,
Let the number of answers be x
We know that,
The points earned for the correct answers will be positive whereas, for the negative answers, they will be negative
So,
For school A,
The number of answers is:
12x – 5x = -165
12x – 5x + 165 = 0
For school B,
The number of answers is:
12x + 0 = -65
12x + 65 = 0
Now,
It is given that the two schools are tied
So,
12x – 5x + 165 = 12x + 65
Hence, from the above,
We can conclude that option B matches the above-given situation
PART B
How many answers did each school get correct in the final round?
Answer:
From part (a),
The equation that models the scoring and outcome of the contest is:
12x – 5x + 165 = 12x + 65
Now,
Rearrange the terms
So,
12x – 12x – 5x = 65 – 165
-5x = -100
5x = 100
Divide by 5 into both sides
So,
\(\frac{5}{5}\)x = \(\frac{100}{5}\)
x = 20
Hence, from the above,
We can conclude that each school gets 20 correct answers in the final round
Lesson 2.3 Solve Multistep Equations
Solve & Discuss It!
A water tank fills through two pipes. Water flows through one pipe at a rate of 25,000 gallons an hour and through the other pipe at 45,000 gallons an hour. Water leaves the system at a rate of 60,000 gallons an hour.

I can… solve multistep equations and pairs of equations using more than one approach.
There are 3 of these tanks, and each tank holds 1 million gallons. Each tank is half full. Water is entering and leaving a tank at the maximum amounts. Determine the number of hours, x, it will take to fill all 3 tanks.
Answer:
It is given that
A water tank fills through two pipes. Water flows through one pipe at a rate of 25,000 gallons an hour and through the other pipe at 45,000 gallons an hour. Water leaves the system at a rate of 60,000 gallons an hour and there are 3 of these tanks, and each tank holds 1 million gallons. Each tank is half full. Water is entering and leaving a tank at the maximum amounts.
Now,
The capacity of each tank = \(\frac{1 million}{2}\) (Since the tank is half-full)
We know that,
1 million = 10 lakhs
So,
The capacity of each tank is: 5 Lakh gallons
So,
The capacity of 3 tanks = 5 Lakh gallons (3)
= 15 Lakh gallons
Now,
The rate of flow of each tank = (The rate of flow of inlet pipes) + (The rate of flow of outlet pipes)
We know that,
The rate of flow for the inlet pipe will be: Positive
The rate of flow for the outlet pipe will be: Negative
So,
The rate of flow of each tank = (45,000 + 25,000) – 60,000
= 70,000 – 60,000
= 10,000 gallons per hour
Since the three pipes are the same, the rate of flow will also be the same
So,
The rate of flow of three tanks = 10,000 (3)
= 30,000 gallons per hour
Now,
It is given that the number of hours is: x
So,
The number of hours took to fill all the three tanks = \(\frac{ The capacity of three tanks } { The rate of flow of the three tanks }\)
x = \(\frac{15,00,000}{30,000}\)
x = 50 hours
Hence, from the above,
We can conclude that the number of hours took to fill the three tanks is: 50 hours
Reasoning
Can you solve the problem in more than one way?
Answer:
Yes, we can solve the problem in more than one way
The first way:
First, calculate the capacity and the rate of flow of each tank and multiply both the quantities with 3 since it is for 3 tanks
So,
We will get the time took to fill the three tanks
The second way:
Calculate the capacity and the rate of the flow of each tank and also find the time taken to fill that tank and multiply the time taken by 3 to get the time taken to fill the three tanks
Focus on math practices
Use Structure What are two different ways to simplify the expression 4(3x + 7x + 5) so that it equals 40x – 20? Explain.
Answer:
The given expression is:
4 (3x + 7x + 5)
A)
The first way:
We know that,
The distributive property is:
a (b + c) = ab + ac
So,
4 (3x + 7x + 5)
= 4 (3x) + 4 (7x) + 4 (5)
= 12x + 28x + 20
= 40x + 20
B)
The second way:
4 (3x + 7x + 5)
First, simplify the expression in the brackets
So,
4 (3x + 7x + 5)
= 4 (10x + 5)
= 4 (10x) + 4(5)
= 40x + 20
Essential Question
How can you use the Distributive Property to solve multistep equations?
Answer:
Let A, B, and C be the three variables
Now,
We know that,
The Distributive Property of multiplication is:
A (B + C) = AB + AC
(A + B) C = AC + BC
(A + C) B = AB + BC
Try It!
Solve the equation 3(x – 5) – 5x = -25 + 6x.
3_____ + 3 ∙ ______ – 5x = – 25 + 6x
_____ – 5x = – 25 + 6x
______ x – 15 = – 25 + 6x
______ – 15 = -25 + _____ x
______ = _____ x ______
x = _____ or ______
Answer:
The given equation is:
3 (x – 5) – 5x = -25 + 6x
3 (x) – 3 (5) – 5x = -25 + 6x
3x – 15 – 5x = -25 + 6x
-15 – 2x = -25 + 6x
Rearrange the like terms
So,
-15 + 25 = 6x + 2x
8x = 10
Divide by 8 into both sides
x = \(\frac{10}{8}\)
x = \(\frac{5}{4}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{5}{4}\)
Convince Me!
Can you add x to -5x on the left side of the equation as the first step? Explain.
Answer:
No, we can’t add x to the -5x because from the given equation,
We are getting
3x – 5x
So,
We have to add 3x and not x to -5x
Try It!
Solve the equation -3(-7 – x) = \(\frac{1}{2}\)(x + 2).
Answer:
The given equation is:
-3 (-7 – x) = \(\frac{1}{2}\) (x + 2)
So,
-3 [-(x + 7)] = \(\frac{1}{2}\) (x + 2)
We know that,
– * – = +
So,
3 (x + 7) = \(\frac{1}{2}\) (x + 2)
Multiply with 2 on both sides
So,
6 (x + 7) = x + 2
6 (x) + 6 (7) = x + 2
6x + 42 = x + 2
Rearrange the like terms
6x – x = 2 – 42
5x = -40
Divide by 5 into both sides
So,
x = \(\frac{-40}{5}\)
x = -8
Hence, from the above,
We can conclude that the value of x is: -8
KEY CONCEPT
When solving multistep equations, sometimes you distribute first and then combine like terms.
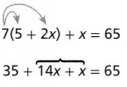
Sometimes you combine like terms first and then distribute.
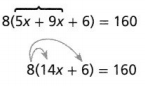
Do You Understand?
Question 1.
Essential Question How can you use the Distributive Property to solve multistep equations?
Answer:
Let A, B, and C be the three variables
Now,
We know that,
The Distributive Property of multiplication is:
A (B + C) = AB + AC
(A + B) C = AC + BC
(A + C) B = AB + BC
Question 2.
Reasoning What is the first step when solving the equation 3(3x – 5x) + 2 = -8?
Answer:
The given equation is:
3 (3x – 5x) + 2 = -8
Use the distributive property of multiplication
So,
3 (3x) – 3(5x) + 2 = -8 ——–> First step when solving the above equation
Question 3.
Use Structure How can you use the order of operations to explain why you cannot combine the variable terms before using the Distributive Property when solving the equation 7(x + 5) – x = 42?
Answer:
The given equation is:
7 (x + 5) – x = 42
To find the order of operations, We have to use the BODMAS rule
So,
From the above equation,
We will first solve the expression present in the brackets, then add, and then subtract
We know that,
We can do any operation only on the like terms
We know that,
The “Like terms” are the terms that have the same exponent
So,
For the above equation,
We can not combine the terms before using the distributive property
Now,
7 (x) + 7 (5) – x = 42
7x + 35 – x = 42
6x + 35 = 42
Subtract with 35 on both sides
6x = 42 – 35
6x = 7
Divide by 6 into both sides
So,
x = \(\frac{7}{6}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{7}{6}\)
Do You Know How?
Question 4.
Solve the equation 3x + 2 = x + 4(x + 2).
Answer:
The given equation is:
3x + 2 = x + 4 (x + 2)
3x + 2 = x + 4 (x) + 4 (2)
3x + 2 = x + 4x + 8
3x + 2 = 5x + 8
Rearrange the like terms
So,
5x – 3x = -8 + 2
2x = -6
Divide by 2 into both sides
So,
x = \(\frac{-6}{2}\)
x = -3
Hence, from the above,
We can conclude that the value of x is: -3
Question 5.
Solve the equation -3(x – 1) + 7x = 27.
Answer:
The given equation is:
-3 (x – 1) + 7x = 27
So,
-3 (x) + 3 (1) + 7x = 27
-3x + 3 + 7x = 27
4x + 3 = 27
Subtract with 3 on both sides
So,
4x = 27 – 3
4x = 24
Divide by 4 into both sides
So,
x = \(\frac{24}{4}\)
x = 6
Hence, from the above,
We can conclude that the value of x is: 6
Question 6.
Solve the equation \(\frac{1}{3}\)(x + 6) = \(\frac{1}{2}\)(x – 3).
Answer:
The given equation is:
\(\frac{1}{3}\)(x + 6) = \(\frac{1}{2}\)(x – 3)
Multiply with 6 on both sides so that we can make the fractions as integers (It is not compulsory to multiply with only 6. You can also multiply with any number that is multiple of both 2 and 3)
So,
\(\frac{6}{3}\) (x + 6) = \(\frac{6}{2}\) (x – 3)
2 (x + 6) = 3 (x – 3)
2 (x) + 2 (6) = 3 (x) – 3 (3)
2x + 12 = 3x – 9
Rearrange the like terms
So,
3x – 2x = 12 + 9
x = 21
Hence,f rom the above,
We can conclude that the value of x is: 21
Question 7.
Solve the equation 0.25(x + 4) – 3 = 28.
Answer:
The given equation is:
0.25 (x + 4) – 3 = 28
Add with 3 on both sides
So,
0.25 (x + 4) = 28 + 3
0.25 (x + 4) = 31
We know that,
0.25 = \(\frac{1}{4}\)
So,
\(\frac{x + 4}{4}\) = 31
Multiply with 4 on both sides
So,
x + 4 = 31 (4)
x + 4 = 124
Subtract with 4 on both sides
So,
x = 124 – 4
x = 120
Hence, from the above,
We can conclude that the value of x is: 120
Practice & Problem Solving
Leveled Practice In 8-10, find the value of x.
Question 8.
Lori bought sunglasses and flip-flops at a half-off sale. If she spent a total of $21 on the two items, what was the original price of the sunglasses?

The original price of the sunglasses was _________.
Answer:
It is given that
Lori bought sunglasses and flip-flops at a half-off sale. If she spent a total of $21 on the two items
Now,
Let x be the price of sunglasses
It is also given that
the price of flipflops is: $24
So,
\(\frac{1}{2}\) (x + $24) = $21
Multiply with 2 on both sides
So,
x + $24 = $21 (2)
x + $24 = $42
Subtract with $24 on both sides
So,
x = $42 – $24
x = $18
Hence, from the above,
We can conclude that the price of sunglasses is: $18
Question 9.
Use the Distributive Property to solve the equation 28 – (3x + 4) = 2(x + 6) + x.
28 – ______ x – _____ = 2x + _____ + x
24 – _____x = ______x + ______
24 – _____x = ______
_____ x = ______
x = ______
Answer:
The given equation is:
28 – (3x + 4) = 2 (x + 6) + x
By using the distributive property,
28 – 3x – 4 = 2 (x) + 2 (6) + x
24 – 3x = 2x + 12 + x
24 – 3x = 3x + 12
Rearrange the like terms
So,
3x + 3x = 24 – 12
6x = 12
Divide by 6 into both sides
So,
x = \(\frac{12}{6}\)
x = 2
Hence, from the above,
We can conclude that the value of x is: 2
Question 10.
Use the Distributive Property to solve the equation 3(x – 6) + 6 = 5x – 6.
x – _____ + 6 = 5x – ______
_____ x – _____ = 5x – _______
_____ x – _____ = _______
______ x = _______
x = ________
Answer:
The given equation is:
3 (x – 6) + 6 = 5x – 6
By using the Distributive property,
3 (x) – 3 (6) + 6 = 5x – 6
3x – 18 + 6 = 5x – 6
3x – 12 = 5x – 6
Rearrange the like terms
So,
5x – 3x = 6 – 12
2x = -6
x = \(\frac{-6}{2}\)
x = -3
Hence, from the above,
We can conclude that the value of x is: -3
Question 11.
What is the solution to -2.5(4x – 4) = -6?
Answer:
The given equation is:
-2.5 (4x – 4) = -6
So,
-2.5 (4x) + 2.5 (4) = -6
-10x + 10 = -6
Subtract with 10 on both sides
So,
-10x = -6 – 10
-10x = -16
10x = 16
Divide by 10 into both sides
So,
x = \(\frac{16}{10}\)
x = 1.6
Hence, from the above,
We can conclude that the solution of the given equation is: 1.6
Question 12.
What is the solution to the equation 3(x + 2) = 2(x + 5)?
Answer:
The given equation is:
3 (x + 2) = 2 (x + 5)
So,
3 (x) + 3 (2) = 2 (x) + 2 (5)
3x + 6 = 2x + 10
Rearrange the like terms
So,
3x – 2x = 10 – 6
x = 4
Hence, from the above,
We can conclude that the solution of the given equation is: 4
Question 13.
Solve the equation \(\frac{1}{6}\)(x – 5) = \(\frac{1}{2}\)(x + 6).
Answer:
The given equation is:
\(\frac{1}{6}\)(x – 5) = \(\frac{1}{2}\)(x + 6)
Multiply with 6 on both sides
So,
x – 5 = 3 (x + 6)
x – 5 = 3 (x) + 3 (6)
x – 5 = 3x + 18
Rearrange the like terms
So,
x – 3x = 18 + 5
-2x = 23
Divide by -2 into both sides
So,
x = –\(\frac{23}{2}\)
Hence, from the above,
We can conclude that the value of x for the given equation is: –\(\frac{23}{2}\)
Question 14.
Solve the equation 0.6(x + 2) = 0.55(2x + 3).
Answer:
The given equation is:
0.6 (x + 2) = 0.55 (2x + 3)
So,
0.6 (x) + 0.6 (2) = 0.55 (2x) + 0.55 (3)
0.6x + 1.2 = 1.10x + 1.65
Rearrange the like terms
So,
1.10x – 0.6x = 1.2 – 1.65
0.5x = -0.45
Divide by 0.5 into both sides
So,
x = \(\frac{-0.45}{0.5}\)
x = -0.9
Hence, from the above,
We can conclud ethat the value of x is: -0.9
Question 15.
Solve the equation 4x – 2(x – 2) = -9 + 5x – 8.
Answer:
The given equation is:
4x – 2 (x – 2) = -9 + 5x – 8
So,
4x – 2 (x) + 2 (2) = -9 + 5x – 8
4x – 2x + 4 = 5x – 17
2x + 4 = 5x – 17
Rearrange the like terms
So,
5x – 2x = 17 + 4
3x = 21
Divide by 3 into both sides
So,
x = \(\frac{21}{3}\)
x = 7
Hence, from the above,
We can conclude that the value of x is: 7
Question 16.
Use the Distributive Property to solve the equation 2(m + 2) = 22. Describe what it means to distribute the 2 to each term inside the parentheses.
Answer:
The given equation is:
2 (m + 2) = 22
We know that,
By using the distributive property of multiplication,
A (B + c) = AB + AC
So,
2 (m) + 2 (2) = 22
2m + 4 = 22
2m = 22 – 4
2m = 18
m = \(\frac{18}{2}\)
m = 9
Hence, from the above,
We can conclude that the value of m is: 9
Question 17.
What is Peter’s number?

Answer:
Let peter’s number be x
So,
According to the given statement,
-3 (x – 12) = -54
3 (x – 12) = 54
3x – 3 (12) = 54
3x – 36 = 54
3x = 36 + 54
3x = 90
x = \(\frac{90}{3}\)
x = 30
Hence, from the above,
We acn conclude that peter’s number is: 30
Question 18.
Higher Order Thinking Use the Distributive Property to solve the equation \(\frac{4x}{5}\) – x = \(\frac{x}{10}\) – \(\frac{9}{2}\)
Answer:
The given equation is:
\(\frac{4x}{5}\) – x = \(\frac{x}{10}\) – \(\frac{9}{2}\)
Rearrange the like terms
So,
\(\frac{4x}{5}\) – x – \(\frac{x}{10}\) = –\(\frac{9}{2}\)
\(\frac{7x}{10}\) – x = –\(\frac{9}{2}\)
–\(\frac{3x}{10}\) = –\(\frac{9}{2}\)
Multiplywith \(\frac{10}{3}\) on both sides
x = \(\frac{9 × 10}{2 × 3}\)
x = 15
Hence, from the above,
We can conclude that the value of x is: 15
Assessment Practice
Question 19.
How many solutions does the equation -2(x + 4) = -2(x + 4) – 6 have?
Answer:
The given equation is:
-2 (x + 4) = -2 (x + 4) – 6
So,
-2 (x) – 2 (4) = -2 (x) – 2 (4) – 6
-2x – 8 = -2x – 8 – 6
Rearrange the like terms
So,
-2x + 2x – 8 + 8 = -6
0 = -6
Hence, from the above,
We can conclude that there are no solutions for the given equation
Question 20.
Solve the equation 3(x + 4) = 2x + 4x – 6 for x.
Answer:
The given equation is:
3 (x + 4) = 2x + 4x – 6
So,
3 (x) + 3 (4) = 6x – 6
3x + 12 = 6x – 6
Rearrange the like terms
So,
6x – 3x = 12 + 6
3x = 18
x = \(\frac{18}{3}\)
x = 6
Hence, from the above,
We can conclude that the solution of the given equation is: 6
Lesson 2.4 Equations with No Solutions or Infinitely Many Solutions
Explore It!
The Great Karlo called twins Jasmine and James onto the stage. Jasmine, multiply your age by 3 and add 6. Then multiply this sum by 2. James, multiply your age by 2 and add 4. Then multiply this sum by 3. I predict you will both get the same number!

I can… determine the number of solutions an equation has.
A. Write expressions to represent Great Karlo’s instructions to each twin.
Answer:
It is given that
The Great Karlo called the twins Jasmine and James onto the stage. Jasmine, multiply your age by 3 and add 6. Then multiply this sum by 2. James, multiply your age by 2 and add 4. Then multiply this sum by 3.
Now,
Great Karlo’s instructions to Jasmine:
Let the age of Jasmine be x
Step 1:
Multiply your age by 3 and add 6
3x + 6
Step 2:
Multiply step 1 with 2
2 (3x +6)
So,
The expression representing the age of Jasmine is: 2 (3x + 6)
Great Karlo’s instructions to James
Let the age of James be x
Step 1:
Multiply your age by 2 and add 4
2x + 4
Step 2:
Multiply step 1 with 3
3 (2x +4)
So,
The expression representing the age of James is: 3 (2x + 4)
Hence, from the above,
We can conclude that the expressions that represent the Great Karlo’s instruction to each twin are:
For Jasmine —–> 2 (3x + 6)
For James ——-> 3 (2x + 4)
B. Choose 4 whole numbers for the twins’ age and test each expression. Make a table to show the numbers you tried and the results.
Answer:
It is given that the great Karlo predicted that the twins will get the same number
So,
2 (3x + 6) = 3 (2x + 4)
2 (3x) + 2 (6) = 3 (2x) + 3 (4)
6x + 12 = 6x + 12
Hence,
The table to show the numbers tried for Jasmine’s and James ages and the results are:
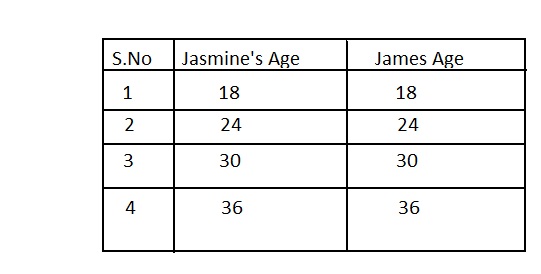
C. What do you notice about your results?
Answer:
From the table that is present in part (b),
We can observe that the ages of Jasmine and James are the same
Focus on math practices
Make Sense and Persevere Choose three more values and use them to evaluate each expression. What do you notice? Do you think this is true for all values? Explain.
Answer:
The table that represents three more values of Jasmine’s and James’ ages and its results are:
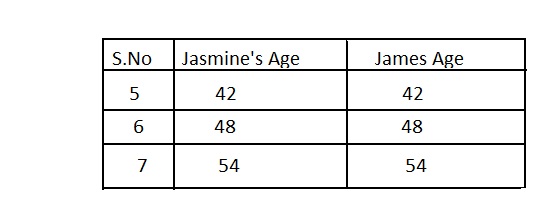
Hence, from the above table,
We can observe that the ages of Jasmine and James are the same
Hence, from the above,
We can conclude that for any type of the whole number, the ages of Jasmine and James are the same
Essential Question
Will a one-variable equation always have only one solution?
Answer:
Every linear equation that is a conditional equation has one solution. However, not every linear equation in one variable has a single solution. There are two other cases: no solution and the solution set of all real numbers
Try It!
How many solutions does the equation
3x + 15 = 2x + 10 + x + 5 have?
The equation has ______ solutions.
3x + 15 = 2x + 10 + x + 5
3x + 15 = _____ x + ______
3x – _____ + 15 = 3x – _____ + 15
______ = _______
Answer:
The given equation is:
3x + 15 = 2x + 10 + x + 5
So,
3x + 15 = 3x + 15
Subtract with 3x on both sides
So,
15 = 15
Hence, from the above,
We can conclude that the given equation has infinitely many solutions
Convince Me!
If the value of x is negative, would the equation still be true? Explain.
Answer:
For the given equation,
3x + 15 = 2x + 10 + x + 5,
The solutions are infinite i..e, for any value of x, the given equation will be true i.e., for both positive and negative values of x, the equation will be true
Hence, from the above,
We can conclude that the given equation would still be true even if the value of x is negative
Try It!
How many solutions does the equation 4x + 8 = 0.1x + 3 + 3.9x have? Explain.
Answer:
The given equation is:
4x + 8 = 0.1x + 3 + 3.9x
So,
4x + 8 = 4x + 3
Subtract with 4x on both sides
So,
8 = 3
Hence, from the above,
We can conclude that the given equation has no solutions
Try It!
Determine the number of solutions each equation has without solving. Explain your reasoning.
a. 3x + 1.5 = 2.5x + 4.7
Answer:
The give equation is:
3x + 1.5 = 2.5x + 4.7
Rearrange the like terms
So,
3x – 2.5x = 4.7 – 1.5
0.5x = 3.2
Divide by 0.5 into both sides
So,
x = \(\frac{3.2}{0.5}\)
x = 6.4
Hence, from the above,
We can conclude that the given equation ahs only 1 solution
b. 3(x + 2) = 3x – 6
Answer:
The given equation is:
3 (x + 2) = 3x – 6
So,
3 (x) + 3 (2) = 3x – 6
3x + 6 = 3x – 6
Subtract with 3x on both sides
So,
6 = -6
Hence, from the above,
We can conclude that the given equation has no solutions
c. 9x – 4 = 5x – 4 + 4x
Answer:
The given equation is:
9x – 4 = 5x – 4 + 4x
So,
9x – 4 = 9x – 4
Subtract with 9x on both sides
So,
-4 = -4
4 = 4
Hence, from the above,
We can conclude that the given equation has infinitely many solutions
KEY CONCEPT
A one-variable equation has infinitely many solutions when solving results in a true statement, such as 2 = 2.
A one-variable equation has one solution when solving results in one value for the variable, such as x = 2.
A one-variable equation has no solution when solving results in an untrue statement, such as 2 = 3.
Do You Understand?
Question 1.
Essential Question Will a one-variable equation always have only one solution?
Answer:
Every linear equation that is a conditional equation has one solution. However, not every linear equation in one variable has a single solution. There are two other cases: no solution and the solution set of all real numbers
Question 2.
Use Structure Kaylee writes the equation 6x + 12 = 2(3x + 6). Can you find the number of solutions this equation has without solving for x? Explain.
Answer:
The given equation is:
6x + 12 = 2 (3x + 6)
So,
6x + 2 = 2 (3x) + 2 (6)
6x + 12 = 6x + 12
Subtract with 12 on both sides
So,
12 = 12
Hence, from the above,
We can conclude that the given equation has infinitely many solutions
Question 3.
Construct Arguments The height of an experimental plant after x days can be represented by the formula 3(4x + 2). The height of a second plant can be represented by the formula 6(2x + 2). Is it possible that the two plants will ever be the same height? Explain.
Answer:
It is given that
The height of an experimental plant after x days can be represented by the formula 3(4x + 2). The height of a second plant can be represented by the formula 6(2x + 2)
So,
Now,
To find out whether the two plants will ever be the same height or not,
3 (4x + 2) = 6 (2x + 2)
So,
3 (4x) + 3 (2) = 6 (2x) + 6 (2)
12x + 6 = 12x + 12
Subtract with 12x on both sides
So,
6 = 12
So,
The given equation has no solution
Hence, from the above,
We can conclude that it is not possible the two plants will ever be the same height
Do You Know How?
Question 4.
How many solutions does the equation 3(2.4x + 4) = 4.1x + 7 + 3.1x have? Explain.
Answer:
The given equation is:
3 (2.4x + 4) = 4.1x + 7 + 3.1x
So,
3 (2.4x) + 3 (4) = 7.2x + 7
7.2x + 12 = 7.2x + 7
Subtract with 7.2x on both sides
So,
12 = 7
Hence, from the above,
We can conclude that the given equation has no solutions
Question 5.
How many solutions does the equation 7x + 3x – 8 = 2(5x – 4) have? Explain.
Answer:
The given equation is:
7x + 3x – 8 = 2 (5x – 4)
So,
10x – 8 = 2 (5x) – 2 (4)
10x – 8 = 10x – 8
Subtract with 10x on both sides
So,
-8 = -8
8 = 8
Hence, from the above,
We can conclude that the given equation has infinitely many solutions
Question 6.
Todd and Agnes are making desserts. Todd buys peaches and a carton of vanilla yogurt. Agnes buys apples and a jar of honey. They bought the same number of pieces of fruit. Is there a situation in which they pay the same amount for their purchases? Explain.

Answer:
It is given that
Todd and Agnes are making desserts. Todd buys peaches and a carton of vanilla yogurt. Agnes buys apples and a jar of honey. They bought the same number of pieces of fruit.
Now,
Let the number of pieces of fruit be x
So,
The amount purchased by Todd = $1.25x + $4
The amount purchased by Agnes = $1x + $6
Now,
To find whether they pay the same amount for purchase or not,
$1.25x + $4 = $1x + $6
Rearrange the like terms
So,
$1.25x – $1x = $6 – $4
$0.25x = $2
Divide by 0.25 into both sides
So,
x = \(\frac{2}{0.25}\)
x = 8
Hence, from the above,
We can conclude that if there are 8 fruits, then Todd and Agnes will pay the same amount for purchase
Practice & Problem Solving
Leveled Practice In 7 and 8, complete the equations to find the number of solutions.
Question 7.
Classify the equation 33x + 99 = 33x – 99 as having one solution, no solution, or infinitely many solutions.
33x + 99 = 33x – 99
33x – ______ + 99 = 33x – _____ – 99
99 ______ – 99
Since 99 is _______ equal to -99, the equation has _______ solution(s).
Answer:
The given equation is:
33x + 99 = 33x – 99
Subtract with 33x on both sides
So,
33x – 33x + 99 = 33x – 33x – 99
99 = -99
We know that,
99 ≠ -99
Hence, from the above,
We can conclude that there are no solutions for the given equation
Question 8.
Solve 4(4x + 3) = 19x + 9 – 3x + 3. Does the equation have one solution, no solution, or infinitely many solutions?
4(4x + 3) = 19x + 9 – 3x + 3
4 • ______ + 4 • ______ = 19x + 9 – 3x + 3
16x + 12 = _______ + _______
16x – ______ + 12 = 16x ______ + 12
12 _______ 12
Since 12 is ________ equal to 12, the equation has ________ solution(s).
Answer:
The given equation is:
4 (4x + 3) = 19x + 9 – 3x + 3
So,
4 (4x) + 4 (3) = 16x + 12
16x + 12 = 16x + 12
Subtract with 16x on both sides
So,
16x – 16x + 12 = 16x – 16x + 12
12 = 12
Hence, from the above,
We can conclude that the given equation has infinitely many solutions
Question 9.
Generalize What does it mean if an equation is equivalent to 0 = 0? Explain.
Answer:
If an equation is equivalent to 0 = 0, then
The equation is true for all the values of x
Hence,
That equation has infinitely many solutions
Question 10.
Solve 4x + x + 4 = 8x – 3x + 4. Does the equation have one solution, no solution, or infinitely many solutions? If one solution, write the solution. Explain.
Answer:
The given equation is:
4x + x + 4 = 8x – 3x + 4
So,
5x + 4 = 5x + 4
Subtract with x on both sides
So,
5x – 5x + 4 = 5x – 5x + 4
4 = 4
Hence, from the above,
We can conclude that the given equation has infinitely many solutions
Question 11.
Reasoning Two rival dry cleaners both advertise their prices. Let x equal the number of items dry cleaned. Store A’s prices are represented by the expression 15x – 2. Store B’s prices are represented by the expression 3(5x + 7). When do the two stores charge the same rate? Explain.
Answer:
It is given that
Two rival dry cleaners both advertise their prices. Let x equal the number of items dry cleaned. Store A’s prices are represented by the expression 15x – 2. Store B’s prices are represented by the expression 3(5x + 7)
So,
To find when the two stores charge the same rate,
15x – 2 = 3 (5x + 7)
So,
15x – 2 = 3 (5x) + 3 (7)
15x – 2 = 15x – 21
Subtract with 15x on both sides
So,
15x – 15x – 2 = 15x – 15x – 21
-2 = -21
2 = 21
So,
The equation has no solution
Hence, from the above,
We can conclude that the two stores will never charge the same rate
Question 12.
Reasoning How is solving an equation with no solution similar to solving an equation that has an infinite number of solutions?
Answer:
No solution would mean that there is no answer to the equation. It is impossible for the equation to be true no matter what value we assign to the variable. Infinite solutions would mean that any value for the variable would make the equation true.
Question 13.
Solve 0.9x + 5.1x – 7 = 2(2.5x – 3). How many solutions does the equation have?
Answer:
The given equation is:
0.9x + 5.1x – 7 = 2 (2.5x – 3)
So,
6.0x – 7 = 2 (2.5x) – 2 (3)
6x – 7 = 5x – 6
Rearrange the like terms
So,
6x – 5x = 7 – 6
x = 1
Hence, from the above,
We can conclude that the given equation has only 1 solution
Question 14.
Critique Reasoning Your friend solved the equation 4x + 12x – 6 = 4(4x + 7) and got x = 34.
What error did your friend make? What is the correct solution?
4x + 12x – 6 = 4 (4x + 7).
16x – 6 = 16x + 28
16x – 16x – 6 = 16x – 16x + 28
x – 6= 28
x – 6 + 6 = 28 + 6
x = 34
Answer:
The given equation is:
4x + 12x – 6 = 4 (4x + 7)
So,
16x – 6 = 4 (4x) + 4 (7)
16x – 6 = 16x + 28
Subtract with 16x on both sides
So,
16x – 16x – 6 = 16x – 16x + 28
-6 = 28
So,
From the above,
We can observe that after subtracting the given equation with 16x, there are no x terms.
So,
We can’t get the value of x but your friend takes variable x after subtracting 16x from the given equation even though there is no possibility for the x-term
Hence, from the above,
We can conclude that the correct solution for the given equation is: No solutions for the given equation
Question 15.
Solve 49x + 9 = 49x + 83.
a. Does the equation have one solution, no solution, or infinitely many solutions?
Answer:
The given equation is:
49x + 9 = 49x + 83
Subtract with 49x on both sides
So,
49x – 49x + 9 = 49x – 49x + 83
9 = 83
Hence, from the above,
We can conclude that the given equation has no solutions
b. Write two equations in one variable that have the same number of solutions as this equation.
Answer:
The two equations in one variable that have the same number of solutions as the equation that is present in part (a) are:
A) 10x + 8 = 10x – 25
B) 5 (3x + 10) = 15x + 40
Question 16.
Classify the equation 6(x + 2) = 5(x + 7) as having one solution, no solution, or infinitely many solutions.
Answer:
The given equation is:
6 (x + 2) = 5 (x + 7)
So,
6 (x) + 6 (2) = 5 (x) + 5 (7)
6x + 12 = 5x + 35
Rearrange the like terms
So,
6x – 5x = 35 – 12
x = 23
Hence, from the above,
We can conclude that the given equation has only 1 solution
Question 17.
Solve 6x + 14x + 5 = 5(4x + 1). Write a word problem that this equation, or any of its equivalent forms, represents.
Answer:
The given equation is:
6x + 14x + 5 = 5 (4x + 1)
So,
20x + 5 = 5 (4x) + 5 (1)
20x + 5 = 20x + 5
Subtract with 20x on both sides
So,
20x – 20x + 5 = 20x – 20x + 5
5 = 5
Hence, from the above,
We can conclude that the given equation is true for any value of x i..e, the given equation has infinitely many solutions
Question 18.
Classify the equation 170x – 1,000 = 30(5x – 30) as having one solution, no solution, or infinitely many solutions.
Answer:
The given equation is:
170x – 1,000 = 30 (5x – 30)
So,
170x – 1,000 = 30 (5x) – 30 (30)
170x – 1,000 = 150x – 900
Rearrange the like terms
So,
170x – 150x = 1,000 – 900
20x = 100
x= \(\frac{100}{20}\)
x = 5
Hence, from the above,
We can conclude that the given equation has only 1 solution
Question 19.
Higher Order Thinking Write one equation that has one solution, one equation that has no solution, and one equation that has infinitely many solutions.
Answer:
The example representation of the equation that has one solution is:
20x + 5 = 15x – 4
The example representation of the equation that has no solutions is:
3 (6x – 2) = 9 (2x – 4)
The example representation of the equation that has infinitely many solutions is:
4 (2x – 6) = 8 (x – 3)
Question 20.
Solve 4(4x – 2) + 1 = 16x – 7.
Answer:
The given equation is:
4 (4x – 2) + 1 = 16x – 7
So,
4 (4x) – 4 (2) + 1 = 16x – 7
16x – 8 + 1 = 16x – 7
16x – 7 = 16x – 7
Subtract with 16x on both sides
So,
16x – 16x – 7 = 16x – 16x – 7
-7 = -7
7 = 7
Hence, from the above,
We can conclude that the given equation is true for all the values of x i..e, the given equation has infinitely many solutions
Question 21.
Solve 6x + 26x – 10 = 8(4x + 10).
Answer:
The given equation is:
6x + 26x – 10 = 8 (4x + 10)
So,
32x – 10 = 8 (4x) + 8 (10)
32x – 10 = 32x + 80
Subtract with 32x on both sides
So,
32x – 32x – 10 = 32x – 32x + 80
-10 = 80
Hence, from the above,
We can conclude that the given equation has no solution
Question 22.
Classify the equation 64x – 16 = 16(4x – 1) as having one solution, no solution, or infinitely many solutions.
Answer:
The given equation is:
64x – 16 = 16 (4x – 1)
So,
64x – 16 = 16 (4x) – 16 (1)
64x – 16 = 64x – 16
Subtract with 64x on both sides
So,
64x – 64x – 16 = 64x – 64x – 16
– 16 = -16
16 = 16
Hence, from the above,
We can conclude that the given equation has infinitely many solutions
Question 23.
Classify the equation 5(2x + 3) = 3(3x + 12) as having one solution, no solution, or infinitely many solutions.
Answer:
The given equation is:
5 (2x + 3) = 3 (3x + 12)
So,
5 (2x) + 5 (3) = 3 (3x) + 3 (12)
10x + 15 = 9x + 36
Rearrange the like terms
So,
10x – 9x = 36 – 15
x = 21
Hence, from the above,
We can conclude that the given equation has only 1 solution
Assessment Practice
Question 24.
Which of the following best describes the solution to the equation 4(2x + 3) = 16x + 12 – 8x?
A. The equation has one solution.
B. The equation has infinitely many solutions.
C. The equation has no solution.
D. The equation has two solutions.
Answer:
The given equation is:
4 (2x + 3) = 16x + 12 – 8x
So,
4 (2x) + 4 (3) = 4x + 12
8x + 12 = 4x + 12
Rearrange the like terms
So,
8x – 4x = 12 – 12
4x = 0
x = 0
So,
The given equation has only 1 solution
Hence, from the above,
We can conclude that option A matches with the solution of the given equation
Question 25.
Which of the following statements are true about the equation 10x + 45x – 13 = 11(5x + 6)? Select all that apply.
☐ The operations that can be used to solve the equation are addition and multiplication.
☐ The operations that can be used to solve the equation are multiplication and division.
☐ The equation has infinitely many solutions.
☐ The equation has a solution of x = 53.
☐ The equation has no solution.
Answer:
Let the given options be named: A, B, C, D, and E
Now,
The given equation is:
10x + 45x – 13 = 11 (5x + 6)
So,
55x – 13 = 11 (5x) + 11 (6)
55x – 13 = 55x + 66
Subtract with 55x on both sides
So,
55x – 55x – 13 = 55x – 55x + 66
-13 = 26
Hence, from the above,
We can conclude that option A and option E matches with the situation for the given equation
Topic 2 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary How can you determine the number of solutions for an equation? Lesson 2-4
Answer:
A one-variable equation has infinitely many solutions when solving results in a true statement, such as 2 = 2.
A one-variable equation has one solution when solving results in one value for the variable, such as x = 2.
A one-variable equation has no solution when solving results in an untrue statement, such as 2 = 3.
Question 2.
Solve the equation –\(\frac{2}{3}\)d – \(\frac{1}{4}\)d = -22 for d. Lesson 2-1
Answer:
The given equation is:
–\(\frac{2}{3}\)d – \(\frac{1}{4}\)d = -22
So,
\(\frac{8 + 3}{12}\)d = 22
\(\frac{11}{12}\)d = 22
Multiply with \(\frac{12}{11}\) on both sides
So,
d = 22 × \(\frac{12}{11}\)
d = \(\frac{22 × 12}{11}\)
d = 24
Hence, from the above,
We can conclude that the value of d is: 24
Question 3.
Edy has $450 in her savings account. She deposits $40 each month. Juan has $975 in his checking account. He writes a check for $45.45 each month for his cell phone bill. He also writes a check for $19.55 each month for his water bill. After how many months will Edy and Juan have the same amount of money in their accounts? Lesson 2-2
Answer:
It is given that
Edy has $450 in her savings account. She deposits $40 each month. Juan has $975 in his checking account. He writes a check for $45.45 each month for his cell phone bill. He also writes a check for $19.55 each month for his water bill.
Now,
Let the number of months be x
So,
The amount of money in the account of Edy = $450 + $40x
The amount of money in the account of Juan = $975 – $45.45x – $19.55x
Now,
To find after how many months they will have the same amount of money in their accounts,
$450 + $40x = $975 – $45.45x – $19.55x
$450 + $40x = $975 – $65x
Rearrange the like terms
So,
$65x + $40x = $975 – $450
$105x = $525
Divide by 105 into both sides
So,
x = \(\frac{$25}{105}\)
x = 5 months
Hence, from the above,
We can conclude that after 5 months, Edy and Jian will have the same amount of money in their accounts
Question 4.
Which equation has infinitely many solutions? Lesson 2-4
A. \(\frac{3}{4}\)x + x – 5 = 10 + 2x
Answer:
The given equation is:
\(\frac{3}{4}\)x + x – 5 = 10 + 2x
\(\frac{3 + 4}{4}\)x – 5 = 10 + 2x
\(\frac{7}{4}\)x – 5 = 10 + 2x
Rearrange the like terms
So,
\(\frac{7}{4}\)x – 2x = 10 + 5
–\(\frac{1}{4}\)x = 15
Multiply with -4 on both sides
So,
x = -60
Hence, from the above,
We acn conclude that the given equation has only 1 solution
B. 3x – 2.7 = 2x + 2.7 + x
Answer:
The given equation is:
3x – 2.7 = 2x + x + 2.7
3x – 2.7 = 3x + 2.7
Subtract with 3x on both sides
So,
-2.7 = 2.7
Hence, from the above,
We can conclude that the given equation has no solutions
C. 9x + 4.5 – 2x = 2.3 +7x + 2.2
Answer:
The given equation is:
9x + 4.5 – 2x = 2.3 + 7x + 2.2
7x + 4.5 = 7x + 4.5
Subtract with 7x on both sides
So,
4.5 = 4.5
Hence, from the above,
We can conclude that the given equation has infinitely many solutions
D. \(\frac{1}{5}\) x – 7 = \(\frac{3}{4}\) + 2x – 25\(\frac{3}{4}\)
Answer:
The given equation is:
\(\frac{1}{5}\) x – 7 = \(\frac{3}{4}\) + 2x – 25\(\frac{3}{4}\)
We know that,
25\(\frac{3}{4}\) = \(\frac{103}{4}\)
So,
\(\frac{1}{5}\) x – 7 = \(\frac{3}{4}\) + 2x – \(\frac{103}{4}\)
Rearrange the like terms
So,
\(\frac{1}{5}\)x – 2x = 7 – \(\frac{103}{4}\)
–\(\frac{9}{5}\)x = –\(\frac{75}{4}\)
Multiply with –\(\frac{5}{9}\) on both sides
So,
x = \(\frac{75 × 5}{4 × 9}\)
x = \(\frac{125}{4}\)
Hence, from the above,
We can conclude that the given equation has only 1 solution
Question 5.
Solve the equation -4(x – 1) + 6x = 2(17 – x) for x. Lesson 2.3
Answer:
The given equation is:
-4 (x – 1) + 6x = 2 (17 – x)
So,
-4 (x) + 4 (1) + 6x = 2 (17) – 2 (x)
-4x + 4 + 6x = 34 – 2x
2x + 4 = 34 – 2x
Rearrange the like terms
So,
2x + 2x = 34 – 4
4x = 30
Divide by 4 on both sides
So,
x = \(\frac{30}{4}\)
x = \(\frac{15}{2}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{15}{2}\)
Question 6.
Hakeem subtracted 8 from a number, then multiplied the difference by \(\frac{4}{5}\). The result was 20. Write and solve an equation to find the number, x. Lesson 2-3
Answer:
It is given that
Hakeem subtracted 8 from a number, then multiplied the difference by \(\frac{4}{5}\). The result was 20.
Now,
Let the number be x
So,
According to Hakeem,
The expression that represents the given situation is:
\(\frac{4}{5}\) (x – 8) = 20
Multiply with \(\frac{5}{4}\) on both sides
So,
x – 8 = \(\frac{5 × 20}{4}\)
x – 8 = 25
Add with 8 on both sides
So,
x = 25 + 8
x = 34
Hence, from the baove,
We can conclude that Hakeem’s number is: 34
Topic 2 MID-TOPIC PERFORMANCE TASK
Hector is competing in a 42-mile bicycle race. He has already completed 18 miles of the race and is traveling at a constant speed of 12 miles per hour when Wanda starts the race. Wanda is traveling at a constant speed of 16 miles per hour.
PART A
Write and solve an equation to find when Wanda will catch up to Hector.
Answer:
It is given that
Hector is competing in a 42-mile bicycle race. He has already completed 18 miles of the race and is traveling at a constant speed of 12 miles per hour when Wanda starts the race. Wanda is traveling at a constant speed of 16 miles per hour.
Now,
Let the time be x
We know that,
Speed = \(\frac{Distance} {Time}\)
So,
Time = \(\frac{Distance}{Speed}\)
Now,
Time taken by Hector to complete a bicycle race = \(\frac{42 – 18}{12}\)
x = \(\frac{24}{12}\)
x = 2 hours
Now,
Time taken by Wanda to complete the bicycle race = \(\frac{The total distance of race}{The speed traveled by Wanda}\)
x = \(\frac{42}{16}\)
x = \(\frac{21}{8}\) hours
x = 2.625 hours
Now,
The time that took Wanda to catch up to Hector = The time taken by Wanda to complete the race – The tie taken by Hector to complete the race
= 2.625 – 2
= 0.625
= 0.625 (60 minutes)
= 37.5 minutes
Hence, from the above,
We can conclude that Wanda will catch up to Hector after 37.5 minutes of Hector completing the race
PART B
Will Wanda catch up to Hector before the race is complete? Explain.
Answer:
From part (a),
The time taken by Hector to complete the race is: 2 hours
The time taken by Wanda to complete the race is: 2.625 hours
So,
From the above times,
We can observe that the race is completed at 2 hours
Hence, from the above,
We can conclude that Wanda can’t catch up to Hector before the race is complete
PART C
At what constant speed could Wanda travel to catch up with Hector at the finish line? Explain.
Answer:
We know that,
Speed = \(\frac{Distance}{Time}\)
So,
The speed at which Wanda travel to catch up to Hector = \(\frac{The distance of the race}{The time taken by Hector to complete the race}\)
= \(\frac{42}{2}\)
= 21 miles per hour
Hence, from the above,
We can conclude that at 21 miles per hour speed, Wanda could catch up to Hector
3-Act Mathematical Modeling: Powering Down
3-ACT MATH

АСТ 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
After watching the video,
The first question that comes to mind is:
what will be the battery percentage you should have to complete your work?
Question 2.
Write the Main Question you will answer.

Answer:
The main question you will answer is:
what will be the battery percentage you should have to complete your work?
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.
Answer:
The answer to the main question is: 100%
Reason for the prediction:
We don’t know how much work has left. So, it is better to have a battery percentage of 100%
Question 4.
On the number line below, write a time that is too early to be the answer. Write a time that is too late.

Answer:
The time that is too early to be the answer for the above problem is: 5 minutes
The time that is too late to be the answer for the above problem is: Greater than the time that battery percentage is 100%
Question 5.
Plot your prediction on the same number line.
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?

Answer:
The information in this situation that would be helpful to know is:
A) The time is taken for battery percentage to be full
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math
Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it earlier or later than your prediction? Explain why.

Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
Act 3
Reflect
Question 13.
Model with Math
Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Look for Relationships What pattern did you notice in the situation? How did you use that pattern?
Answer:
SEQUEL
Question 15.
Be Precise After 35 minutes, he started charging his phone. 21 minutes later, the battery is at 23%. Explain how you would determine when the phone will be charged to 100%.
Answer:
Lesson 2.5 Compare Proportional Relationships
Solve & Discuss It!
Mei Li is going apple picking. She is choosing between two places. The cost of a crate of apples at each place is shown.
Where should Mei Li go to pick her apples? Explain.

Answer:
It is given that Mei Li is going apple picking. She is choosing between two places.
So,
In Annie’s Apple Orchard,
The cost of 20lb of apples is: $7.25
In Franklin’s fruit Orchard,
The cost of 12lb of apples is: $5
We know that,
Where the cost of 1lb of apples is low, Mei Li will go there to buy the apples
Now,
In Annie’s Apple Orchard,
The cost of 1lb of apples = \(\frac{$7.25}{20}\)
= $0.3625
In Franklin’s fruit Orchard,
The cost of 1lb of apples = \(\frac{$5}{12}\)
= $0.4166
So,
The cost of 1lb of apples in Annie’s Orchard < The cost f 1lb of apples in Franklin’s fruit Orchard
Hence, from the above,
We can conclude that Mei Li should go to pick apples from Annie’s Apple Orchard
Construct Arguments
What information provided can be used to support your answer?
Answer:
From the given figure,
The information provided that can be used to support your answer is:
The weight of the apples is inversely proportional to the price of the apples
So,
In Annie’s Apple Orchard, the weight of the apples is high when compared to the weight of the apples in franklin’s fruit Orchard
Hence,
The price of the apples is low in Annie’s Apple Orchard when compared to Franklin’s fruit Orchard
Focus on math practices
Model with Math Which representation did you use to compare prices? Explain why.
Answer:
The relation that is used to compare the prices of apples is:
Weight of the apples ∝ \(\frac{1}{Price of the apples}\)
? Essential Question
How can you compare proportional relationships represented in different ways?
Answer:
To compare proportional relationships represented in different ways, find the unit rate, or the constant of proportionality, for each representation.
Try It!
The graph represents the rate at which Marlo makes origami birds for a craft fair. The equation y = 2.5x represents the number of birds, y, Josh makes in x minutes. Who makes birds at a faster rate?
Answer:
It is given that
The graph represents the rate at which Marlo makes origami birds for a craft fair. The equation y = 2.5x represents the number of birds, y, Josh makes in x minutes.
So,
The rate that birds made by Josh = \(\frac{y}{x}\)
= 2.5
Now,
From the graph,
The rate that birds made by Marlo = \(\frac{Time taken to make birds by Marlo}{The number of birds}\)
= \(\frac{40}{8}\) (Here, we can take any value that is present in the graph. For example,\(\frac{20}{4}\), \(\frac{10}{2}\) etc., )
= 5
So,
The rate that birds made by Marlo > The rate that birds made by Josh
Hence, from the above,
We can conclude that Marlo makes birds at a faster rate
Convince Me!
If you were to graph the data for Josh and Marlo on the same coordinate plane, how would the two lines compare?
Answer:
When we graph the data for Josh and Marlo on the same coordinate plane,
We can observe that the two graphs will be the lines that are parallel to each other and the rate of change of Marlo will be greater than the rate of change of Josh
Try It!
The distance covered by the fastest high-speed train in Japan traveling at maximum speed is represented on the graph. The fastest high-speed train in the United States traveling at maximum speed covers 600 kilometers in 2\(\frac{1}{2}\) hours. Which train has a greater maximum speed? Explain.

Answer:
It is given that
The distance covered by the fastest high-speed train in Japan traveling at maximum speed is represented on the graph. The fastest high-speed train in the United States traveling at maximum speed covers 600 kilometers in 2\(\frac{1}{2}\) hours.
Now,
We know that,
Speed = \(\frac{Distance}{Time}\)
So,
The speed of the fastest high-speed train in the United states = 600 / \(\frac{5}{2}\)
We know that,
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
So,
The speed of the fastest high-speed train in the United states = \(\frac{600 × 2}{5}\)
= 240 kilometers per hour
Now,
From the given graph,
The speed of the fastest high-speed train in Japan = \(\frac{The difference between any two distances from the graph}{The difference between the values of the time that corresponds to the taken value of distances}\)
= \(\frac{1000 – 650}{3 – 2}\)
= 350 kilometers per hour
So,
The speed of the fastest high-speed train in Japan > The speed of the fastest high-speed train in the United States
Hence, from the above,
We can conclude that the fastest high-speed train in Japan has a maximum speed
KEY CONCEPT
To compare proportional relationships represented in different ways, find the unit rate, or the constant of proportionality, for each representation.
The representations below show the rental cost per hour for canoes at three different shops.

Do You Understand?
Question 1.
?Essential Question How can you compare proportional relationships represented in different ways?
Answer:
To compare proportional relationships represented in different ways, find the unit rate, or the constant of proportionality, for each representation.
Question 2.
How can you find the unit rate or constant of proportionality for a relationship represented in a graph?
Answer:
In a graph,
The unit rate or constant of proportionality for a relationship is represented by:
\(\frac{The value of y}{The value of x}\) or \(\frac{The difference between any 2 values of y}{The difference between the values of x that is corresponded to the values of x}\)
Question 3.
Generalize Why can you use the constant of proportionality with any representation?
Answer:
We can use the constant of proportionality to find the rate of change between the physical quantities that have a proportional relationship
Ex:
Speed Vs Distance, Speed Vs Time, etc
Do You Know How?
Question 4.
Amanda babysits and Petra does yard work on weekends. The graph relating Amanda’s earnings to the number of hours she babysits passes through the points (0, 0) and (4, 24). The table below relates Petra’s earnings to the number of hours she does yard work.

Who earns more per hour?
Answer:
It is given that
Amanda babysits and Petra does yard work on weekends. The graph relating Amanda’s earnings to the number of hours she babysits passes through the points (0, 0) and (4, 24). The table below relates Petra’s earnings to the number of hours she does yard work.
Now,
The Earnings per hour of Amanda = \(\frac{24 – 0}{4 – 0}\)
= \(\frac{24}{4}\)
= 6
The Earnings per hour of Petra = \(\frac{15}{3}\)
= 5
So,
The Earnings per hour of Amanda > The Earnings per hour of Petra
Hence, from the above,
We can conclude that Amanda earns more
Question 5.
Milo pays $3 per pound for dog food at Pat’s Pet Palace. The graph below represents the cost per pound of food at Mark’s Mutt Market. At which store will Milo pay a lower price per pound for dog food?
Answer:
It is given that
Milo pays $3 per pound for dog food at Pat’s Pet Palace. The graph below represents the cost per pound of food at Mark’s Mutt Market.
So,
Now,
The cost per pound of food at Mark’s Mutt Market = \(\frac{Any value of cost from the given graph}{The value of weight that corresponds to the selected cost}\)
= \(\frac{5}{1}\)
= $5
So,
The cost per pound of food at Pat’s Pet Palace < The cost per pound of food at Mark’s Mutt Market
Hence, from the above,
We can conclude that at Pat’s Pet Palace, Milo will pay a lower price per pound for dog food
Practice & Problem Solving
Leveled Practice For 6 and 7, complete the information to compare the rates.
Question 6.
Sam and Bobby want to know who cycled faster. The table shows the total miles Sam traveled over time. The graph shows the same relationship for Bobby. Who cycled faster.
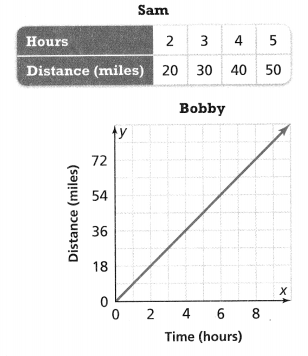
![]()
Find the unit rate (constant of proportionality) for Bobby.
Use (![]() ) and (
) and (![]() ) to find the constant of proportionality.
) to find the constant of proportionality.
The unit rate (constant of proportionality) is ![]()
So ![]() cycled faster.
cycled faster.
Answer:
It is given that
Sam and Bobby want to know who cycled faster. The table shows the total miles Sam traveled over time. The graph shows the same relationship for Bobby.
We know that,
Speed = \(\frac{Distance}{Time}\)
So,
For Sam, from the table,
Speed = \(\frac{20}{2}\) miles per hour
= 10 miles per hour
Now,
For Bobby, from the graph,
Speed = \(\frac{Any value of the distance from the graph}{The value of time that corresponds to the distance that we have taken}\)
= \(\frac{72}{8}\)
= 9 miles per hour
So,
The speed of Sam > The speed of Bobby
Hence, from the above,
We can conclude that Sam cycled faster
Question 7.
Model with Math The equation y = 15x can be used to determine the amount of money, y, Pauli’s Pizzeria makes by selling x pizzas. The graph shows the money Leo’s Pizzeria takes in for different numbers of pizzas sold. Which pizzeria makes more money per pizza?

Pauli’s Pizzeria takes in ![]() per pizza.
per pizza.
Leo’s Pizzeria takes in ![]() per pizza.
per pizza.
![]() ‘s Pizzeria takes in more money per pizza.
‘s Pizzeria takes in more money per pizza.
Answer:
It is given that
The equation y = 15x can be used to determine the amount of money, y, Pauli’s Pizzeria makes by selling x pizzas. The graph shows the money Leo’s Pizzeria takes in for different numbers of pizzas sold
So,
The money earned by Pauli’s Pizzeria = \(\frac{y}{x}\)
= 15 (From the given equation y = 15x)
Now,
From the given graph,
The money earned by Leo’s Pizzeria = \(\frac{Any value of the amount made from the graph}{The value of pizzas sold that corresponds to the value of the amount that we have considered}\)
= \(\frac{96}{8}\)
= 12
So,
The money earned by Pauli’s Pizzeria > The money earned by Leo’s Pizzeria
Hence, from the above,
We can conclude that Pauli’s Pizzeria takes in more money per pizza
Question 8.
The graph shows the amount of savings over time in Eliana’s account. Lana, meanwhile, puts $50 each week into her savings account. If they both begin with $0, who is saving at the greater rate?
Answer:
It is given that
The graph shows the amount of savings over time in Eliana’s account. Lana, meanwhile, puts $50 each week into her savings account
So,
The amount of savings over time in Lana’s account = \(\frac{Any value of total savings in the graph}{The corresponding value of time to that savings amount}\)
= \(\frac{94}{2}\)
= $47
So,
The amount of savings over time in Elina’s account > The amount of savings over time in Lana’s account
Hence, from the above,
We can conclude that Elina is saving money at a greater rate
Question 9.
Make Sense and Persevere Beth, Manuel, and Petra are collecting sponsors for a walk-a-thon. The equation y = 20x represents the amount of money Beth raises for walking x miles. The table shows the relationship between the number of miles Manuel walks and the amount of money he will raise. Petra will earn $15 for each mile that she walks.
a. In order to compare the proportional relationships, what quantities should you use to find the unit rate?
Answer:
In order to compare the proportional relationships,
The quantities you should use to find the unit rate is:
A) The number of miles walked
B) The amount of money raised for the corresponding number of miles
b. Compare the amount of money raised per mile by the three people.

Answer:
It is given that
Beth, Manuel, and Petra are collecting sponsors for a walk-a-thon. The equation y = 20x represents the amount of money Beth raises for walking x miles. The table shows the relationship between the number of miles Manuel walks and the amount of money he will raise. Petra will earn $15 for each mile that she walks.
So,
The amount of money raised by Beth = \(\frac{y}{x}\)
= $20 (From the equation y = 20x)
Now,
The amount of money raised by Manuel = \(\frac{Any value of the money raised in the table}{The number of miles walked that corresponds to the value of money raised}\)
= \(\frac{$45}{3}\)
= $15
So,
The amount of money raised by Beth > The amount of money raised by Manuel = The amount of money raised by Petra
Hence, from the above,
We can conclude that Beth raised more amount of money when compared to Manuel and Petra
Question 10.
Higher-Order Thinking Winston compares the heights of two plants to see which plant grows more per day. The table shows the height of Plant 1, in centimeters, over 5 days. The graph shows the height of Plant 2, in centimeters, over 10 days. Winston says that since Plant 1 grows 6 cm per day and Plant 2 grows 4 cm per day, Plant 1 grows more per day.
a. Do you agree with Winston? Explain your response.
Answer:
It is given that
Winston compares the heights of two plants to see which plant grows more per day. The table shows the height of Plant 1, in centimeters, over 5 days. The graph shows the height of Plant 2, in centimeters, over 10 days. Winston says that since Plant 1 grows 6 cm per day and Plant 2 grows 4 cm per day, Plant 1 grows more per day.
So,
From the given information,
The height growth of plant 1 > The height growth of plant 2
Hence, from the above,
You can agree with Winston
b. What errors might Winston have made?
Answer:
For plant 1,
The height growth per day = \(\frac{Any value of height}{The value of days correspond to the value of height}\)
= \(\frac{6}{2}\)
= 3 cm
For plant 2,
The height growth per day = \(\frac{Any value of height}{The value of days correspond to the value of height}\)
= \(\frac{4}{2}\)
= 2 cm
But,
It is given that
Winston says that Plant 1 grows 6 cm per day and Plant 2 grows 4 cm per day
But according to the calculation,
Plant 1 grows 3 cm per day and plant 2 grows 2 cm per day
So,
The calculation of the height growth of the plants are the errors made by Winston
Assessment Practice
Question 11.
Ashton, Alexa, and Clara want to know who types the fastest. The equation y = 39x models the rate at which Ashton can type, where y is the number of words typed and x is the time in minutes. The table shows the relationship between words typed and minutes for Alexa. The graph shows the same relationship for Clara. Who types the fastest?
Answer:
It is given that
Ashton, Alexa, and Clara want to know who types the fastest. The equation y = 39x models the rate at which Ashton can type, where y is the number of words typed and x is the time in minutes. The table shows the relationship between words typed and minutes for Alexa. The graph shows the same relationship for Clara.
So,
The rate at which Ashton can type = \(\frac{y}{x}\)
= 39 words per minute (From the equation y = 39x)
The rate at which Alexa can type = \(\frac{Any value of the words typed from the table}{The value of minds corresponds to the words typed}\)
= \(\frac{78}{2}\)
= 39 words per minute
The rate at which Clara can type = \(\frac{Any value of the words typed from the graph}{The value of minds corresponds to the words typed}\)
= \(\frac{78}{2}\)
= 39 words per minute
So,
The rate at which Ashton can type = The rate at which Alexa can type = the rate at which Clara can type
Hence, from the above,
We can conclude that no one is the fastest
Lesson 2.6 Connect Proportional Relationships and Slope
ACTIVITY
Solve & Discuss It!
In the fall, Rashida earns money as a soccer referee for her town’s under-10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall. How can Rashida determine how much she will earn refereeing soccer games this fall?

Answer:
It is given that
In the fall, Rashida earns money as a soccer referee for her town’s under-10 soccer league. So far, she has worked 5 games and has been paid $98.50. She will work a total of 14 games this fall.
So,
The amount of money paid for 1 game = \(\frac{The amount of money paid for 5 games}{5}\)
= \(\frac{$98.50}{5}\)
= $19.70
So,
The amount of money paid for 14 games to Rashida = (The total number of games) × (The amount of money paid for 1 game)
= 14 × $19.70
= $275.80
Hence, from the above,
We can conclude that by finding out the money paid to a game for Rashida, Rashida can find total money earned by refereeing soccer games in the fall
Look for Relationships
How is the number of games Rashida works related to her earnings?
Answer:
From the above,
We can observe that Rashida earns more money by refereeing more soccer games
Hence, from the above,
We can conclude that
The number of games Rashida works ∝ The earnings of Rashida
Focus on math practices
Reasoning: How would Rashida’s earnings change if she were paid by the hour instead of by the game?
Answer:
Rashida’s earnings would increase if she were paid by the hour instead of by the game
Example:
From the above,
We can observe that
The money earned by Rashida per game = $17.90
But, if a game will continue for 2 hours and the amount of money that is per game will also be applicable to this situation, then
The amount of money earned by Rashida for this game = $17.90 × 2 = $35.80
Hence, from the above,
We can conclude that Rashida can earn more if she were paid by the hour instead of by the game
? Essential Question
What is the slope?
Answer:
The slope of a line is a measure of its steepness. Mathematically, the slope is calculated as “rise over run” (change in y divided by change in x).
The representation of the slope mathematically is:
Slope = \(\frac{Rise}{Run}\)
Try It!
Jack graphs how far he plans to bike over a 3-day charity ride. Find the slope of the line.

Answer:
It is given that Jack graphs how far he plans to bike over a 3-day charity ride
Now,
From the given graph,
The given points are: (3, 90), and (2, 60)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{y2 – y1}{x2 – x1}\)
So,
The slope of the line = \(\frac{60 – 90}{2 – 3}\)
= 30
Hence, from the above,
We can conclude that the slope of the line is: 30
Convince Me!
How do the unit rate and constant of proportionality relate to the slope of a line?
Answer:
The relative steepness of the line is called slope. The slope of a graph is the same as the constant of proportionality of the equation. A line with a steeper slope has a larger value for k.
Try It!
The graph shows the proportions of red and blue food coloring that Taylor mixes to make the purple frosting. What is the slope of the line? Tell what it means in the problem situation.
Answer:
It is given that
The graph shows the proportions of red and blue food coloring that Taylor mixes to make the purple frosting.
Now,
From the given graph,
The given points are: (50, 70), and (25, 35)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{y2 – y1}{x2 – x1}\)
So,
The slope of the line = \(\frac{70 – 35}{50 – 25}\)
= \(\frac{35}{25}\)
= \(\frac{7}{5}\)
Hence, from the above,
We can conclude that
For every 7 parts of red food coloring, we have to mix 5 parts of blue food coloring to make the purple frosting
KEY CONCEPT
Slope is the measure of the steepness of a line. It represents the ratio of the rise (that is, the vertical distance) to the run (the horizontal distance) between two points on the line. In proportional relationships, slope is the same as the unit rate and constant of proportionality.
Do You Understand?
Question 1.
? Essential Question
What is the slope?
Answer:
The slope of a line is a measure of its steepness. Mathematically, the slope is calculated as “rise over run” (change in y divided by change in x).
The representation of the slope mathematically is:
Slope = \(\frac{y2 – y1}{x2 – x1}\) (or) Sloe = \(\frac{Rise}{Run}\)
Question 2.
Reasoning How is the slope related to a unit rate?
Answer:
The slope is the unit rate, which is the coefficient of x. For a table, the change in y divided by the change in x is the unit rate or slope.
Question 3.
Look for Relationships Why is the slope between any two points on a straight line always the same?
Answer:
The ratio of the rise over run describes the slope of all straight lines. This ratio is constant between any two points along a straight line, which means that the slope of a straight line is constant, too, no matter where it is measured along the line.
Do You Know How?
Question 4.
What is the slope of the line?
Answer:
The given graph is:

We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{ Any value of y}{The value of x that corresponds to the taken value of y}\)
= \(\frac{Price ($)}{Grapes (lb)}\)
So,
The slope of the line = \(\frac{6}{2}\)
= 3
Hence, from the above,
We can conclude that the slope of the line is: 3
Question 5.
The scale of a model airplane is shown in the graph.
a. Find the slope of the line using \(\frac{y2 – y1}{x2 – x1}\)
Answer:
The given graph is:

Now,
From the given graph,
The given points are: (6, 10), and (3, 5)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{y2 – y1}{x2 – x1}\)
So,
The slope of the line = \(\frac{5 – 10}{3 – 6}\)
= \(\frac{5}{3}\)
Hence, from the above,
We can conclude that the slope of the line is: \(\frac{5}{3}\)
b. What does the slope mean in the problem situation?
Answer:
From part (a),
The slope is: \(\frac{5}{3}\)
So,
From the above slope,
We can conclude that for every 3 cm, the model airplane can fly 5 feet
Practice & Problem Solving
Leveled Practice in 6 and 7, find the slope of each line.
Question 6.
The graph shows the number of soda bottles a machine can make over time. Use the two points shown to find the number of soda bottles the machine can make per minute.
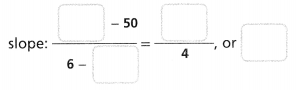
The machine ![]() can make soda bottles each minute.
can make soda bottles each minute.
Answer:
It is given that
The graph shows the number of soda bottles a machine can make over time
Now,
The given graph is:

Now,
From the given graph,
The given points are: (6, 150), and (2, 50)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{y2 – y1}{x2 – x1}\)
So,
The slope of the line = \(\frac{50 – 150}{2 – 6}\)
= \(\frac{100}{4}\)
= 25
Hence, from the above,
We can conclude that the machine can make 25 soda bottles each minute
Question 7.
Find the slope of the line.

Answer:
The given graph is:

We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{ Any value of y}{The value of x that corresponds to the taken value of y}\)
= \(\frac{Items}{Time in min}\)
So,
The slope of the line = \(\frac{50}{10}\)
= 5
Hence, from the above,
We can conclude that the slope of the line is: 5
Question 8.
Reasoning How can you find the slope of the line that passes through the points (0,0) and (2, 4)? Explain.
Answer:
The given points are: (0, 0), and (2, 4)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{y2 – y1}{x2 – x1}\)
So,
The slope of the line = \(\frac{4 – 0}{2 – 0}\)
= \(\frac{4}{2}\)
= 2
Hence, from the above,
We can conclude that the slope of the line is: 2
Question 9.
The points (2.1, -4.2) and (2.5, -5) form a proportional relationship. What is the slope of the line that passes through these two points?
Answer:
It is given that the points (2.1, -4.2) and (2.5, -5) form a proportional relationship
Now,
The given points are: (2.1, -4.2), and (2.5, -5)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{y2 – y1}{x2 – x1}\)
So,
The slope of the line = \(\frac{-5 + 4.2}{2.5 – 2.1}\)
= \(\frac{-0.8}{0.4}\)
= -2
Hence, from the above,
We can conclude that the slope of the line that passes through the given points is: -2
Question 10.
Find the slope of the line.
Answer:
The given graph is:

Now,
From the graph,
We can observe that
The given points are: (-3, 7), and (-1, 2)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{y2 – y1}{x2 – x1}\)
So,
The slope of the line = \(\frac{2 – 7}{-1 + 3}\)
= \(\frac{-5}{2}\)
= –\(\frac{5}{2}\)
Hence, from the above,
We can conclude that the slope of the line that passes through the given points is: –\(\frac{5}{2}\)
Question 11.
The graph shows the number of Calories Natalia burned while running.
a. What is the slope of the line?

Answer:
The given graph is:

We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{ Any value of y}{The value of x that corresponds to the taken value of y}\)
= \(\frac{Calories}{Time in min}\)
So,
The slope of the line = \(\frac{70}{7}\)
= 10
Hence, from the above,
We can conclude that the slope of the line is: 10
b. What does the slope tell you?
Answer:
From part (a),
We can observe that
The slope of the line is: 10
So,
From the given slope,
We can conclude that Natalia burns 10 calories per minute while running
Question 12.
Critique Reasoning A question on a test provides this graph and asks students to find the speed at which the car travels. Anna incorrectly says that the speed of the car is \(\frac{1}{64}\) mile per hour.
a. What is the speed of the car?
Answer:
The given graph is:

We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{ Any value of y}{The value of x that corresponds to the taken value of y}\)
= \(\frac{Distance in miles}{Time in hours}\)
So,
The slope of the line = \(\frac{256}{4}\)
= 64
Hence, from the above,
We can conclude that the speed of the car is: 64 miles per hour
b. What error might Anna have made?
Answer:
From part (a),
We can observe that the speed of the car is: 64 miles per hour
Bt,
According to Anna,
The speed of the car is: \(\frac{1}{64}\) miles per hour
So,
The error made by Anna is that she takes the slope in the form of \(\frac{x}{y}\) but the actual form of the slope is \(\frac{y}{x}\)
Question 13.
Higher-Order Thinking You use a garden hose to fill a wading pool. If the water level rises 11 centimeters every 5 minutes and you record the data point of (10, y), what is the value of y? Use slope to justify your answer.

Answer:
It is given that
You use a garden hose to fill a wading pool. If the water level rises 11 centimeters every 5 minutes and you record the data point of (10, y)
We know that,
Slope = \(\frac{Rise}{Run}\)
So,
From the given information,
We can write the slope as:
Slope = \(\frac{11}{5}\)
Now,
Compare the given point with (x, y)
So,
The slope of the line = \(\frac{y}{x}\)
= \(\frac{y}{10}\)
So,
\(\frac{y}{10}\) = \(\frac{11}{5}\)
Multiply with 10 on both sides
So,
y = \(\frac{11 × 10}{5}\)
y = 22
Hence, from the above,
We can conclude that the value of y is: 22
Assessment Practice
Question 14.
The points (15, 21) and (25, 35) form a proportional relationship.
a. Find the slope of the line that passes through these points.
Answer:
It is given that the points (15, 21) and (25, 35) form a proportional relationship.
Now,
The given points are: (15, 21), and (25, 35)
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope = \(\frac{Rise}{Run}\) = \(\frac{y2 – y1}{x2 – x1}\)
So,
The slope of the line = \(\frac{35 – 21}{25 – 15}\)
= \(\frac{14}{10}\)
= \(\frac{7}{5}\)
Hence, from the above,
We can conclude that the slope of the line that passes through the given points is: \(\frac{7}{5}\)
b. Which graph represents this relationship?
Answer:
We know that,
The representation of the equation when two points form a proportionate relationship is:
y = kx
and the line have to pass through the origin i.e., (0, 0)
So,
From the given graphs,
The graphs B and C have the possibility to become the graph of the given points
Now,
We know that,
Slope = \(\frac{Rise}{Run}\)
From graph B,
Slope = \(\frac{42}{30}\)
= \(\frac{7}{5}\)
From graph C,
Slope = \(\frac{30}{42}\)
= \(\frac{5}{7}\)
Hence, from the above,
We can conclude that the graph B represents the given relationship
Lesson 2.7 Analyze Linear Equations: y = mx
ACTIVITY
Explore It!
A group of college students developed a solar-powered car and entered it in a race. The car travels at a constant speed of 100 meters per 4 seconds.

A. What representation can show the distance the car will travel over time?
Answer:
It is given that
A group of college students developed a solar-powered car and entered it in a race. The car travels at a constant speed of 100 meters per 4 seconds.
We know that,
Speed = \(\frac{Distance}{Time}\)
It is given that speed is constant
So,
Distance ∝ Time
So,
The greater the distance, the greater the time
Hence, from the above,
We can conclude that
The representation that can show the distance the car will travel over time is:
Distance ∝ Time
B. What expression can show the distance the car will travel over time?
Answer:
From part (a),
We can observe that
Distance ∝ Time (Since the speed is constant)
Hence,
The expression that can show the distance the car will travel over time is:
Distance = k (Time)
Where,
k is a constant
C. Compare the representation and the expression. Which shows the distance traveled over time more clearly? Explain.
Answer:
From part (a),
The representation that can show the distance traveled over time is:
Distance ∝ Time
The expression that can show the distance traveled over time is:
Distance = k (Time)
Now,
From the representation and the expression,
We can observe that the expression shows the distance traveled over time more clearly because for any value of distance and time, the value of the expression is constant
Hence, from the above,
We can conclude that the expression shows the distance traveled over time more clearly
Focus on math practices
Be Precise How would the representation or expression change if the speed was converted to miles per minute?
Answer:
From part (a),
The representation is:
Distance ∝ Time
The expression is:
Distance = k (Time)
Now,
Even if the speed was converted to miles per minute, there will be no change in the representation and the expression because miles per minute is a unit of speed and it won’t affect the overall situation of the representation and the expression
? Essential Question
How does slope relate to the equation for a proportional relationship?
Answer:
The steepness of the slope for directly proportional relationships increases as the value of the constant m (y = mx) increases.
Try It!
Write an equation to describe the relationship shown in the graph.
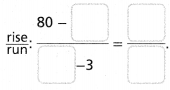 . The equation of the line is y =
. The equation of the line is y = ![]() x.
x.
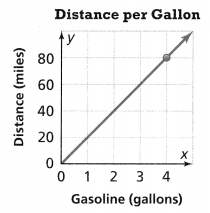
Answer:
The given graph is:

Now,
From the given graph,
The points are: (3, 60), and (4, 80) [We can take any 2 ordered pairs from the graph like (0, 0), and (1, 20); (2, 40), and (3, 60), etc]
Now,
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope can be represented as “m”
So,
m = \(\frac{y2 – y1}{x2 – x1}\)
So,
m = \(\frac{80 – 60}{4 – 3}\)
= \(\frac{20}{1}\)
= 20
We know that,
The equation of the line is:
y = mx
Hence, from the above,
We can conclude that
The equation of the line is: y = 20x
Convince Me!
How do the equations y = mx and y = kx compare?
Answer:
We can compare y = kx to the slope-intercept form of a line, y = mx + b. We can see that y = kx is a linear equation with slope k and y-intercept 0. This tells us that the graph of a direct variation is a line that passes through the origin, point (0,0).
Try It!
a. Write the equation of the line.
Answer:
The given graph is:

Now,
From the given graph,
The points are: (10, 4), and (-10, -4)
Now,
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope can be represented as “m”
So,
m = \(\frac{y2 – y1}{x2 – x1}\)
So,
m = \(\frac{-4 – 4}{-10 – 10}\)
= \(\frac{-8}{-20}\)
= \(\frac{2}{5}\)
We know that,
The equation of the line is:
y = mx
So,
y = \(\frac{2}{5}\)x
Multiply with 5 on both sides
So,
5y = 2x
Hence, from the above,
We can conclude that
The equation of the line is: 5y = 2x
b. Graph the line y = -3x.

Answer:
The given equation is:
y = -3x
Hence,
The representation of the given equation in the coordinate plane is:
KEY CONCEPT
The equation for a proportional relationship is y = mx where m represents the slope of the line.
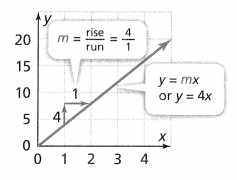
Do You Understand?
Question 1.
Essential Question How does slope relate to the equation for a proportional relationship?
Answer:
The steepness of the slope for directly proportional relationships increases as the value of the constant m (y = mx) increases.
Question 2.
Look for Relationships What do the graphs of lines in the form y = mx have in common? How might they differ?
Answer:
The graphs of lines in the form y = mx are all straight lines that pass through the origin
Question 3.
Use Structure The table below shows the distance a train traveled over time. How can you determine the equation that represents this relationship?
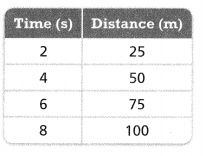
Answer:
It is given that
The table below shows the distance a train traveled over time.
Now,
Verify whether \(\frac{Distance}{Time}\) is constant or not
Now,
From the given table,
For 25 m and 2s,
\(\frac{Distance}{Time}\) = \(\frac{25}{2}\)
For 50m and 4s,
\(\frac{Distance}{Time}\) = \(\frac{50}{4}\) = \(\frac{25}{2}\)
Since,
\(\frac{Distance}{Time}\) is constant
Speed is also constant
So,
The representation of the equation that describes the given relationship is:
Distance = k (Time)
So,
y = mx [ Compare the above equation with y = mx ]
Where
m is a constant slope
So,
y = \(\frac{25}{2}\)x
2y = 25x
Hence, from the above,
We can conclude that the representation of the equation that represents the given situation is: 2y = 25x
Do You Know How?
Question 4.
The relationship between a hiker’s elevation and time is shown in the graph.
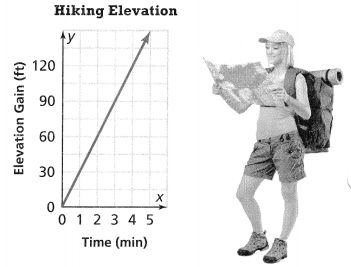
a. Find the constant of proportionality of the line. Then find the slope of the line.
Answer:
It is given that
The relationship between a hiker’s elevation and time is shown in the graph.
Now,
We know that,
The constant of proportionality and the slope are the same
So,
Slope of the line (m) = \(\frac{y}{x}\)
So,
From the given graph,
\(\frac{y}{x}\) = \(\frac{120}{4}\)
= 30
So,
m = 30
Hence, from the above,
We can conclude that the slope of the line is: 30
b. Write the equation of the line.
Answer:
We know that,
The equation of the line is:
y = mx
From part (a),
m = 30
Hence, from the above,
We can conclude that the equation of the line is: y = 30x
Question 5.
Graph the equation y = –\(\frac{1}{2}\)x.
Answer:
The given equation is:
y = –\(\frac{1}{2}\)x
Hence,
The representation of the given equation in the coordinate plane is:
Practice & Problem Solving
Question 6.
Leveled Practice Resting heart rate is a measure of how fast the heart beats when a person is not performing physical activity. The graph shows the number of heartbeats over time for a given person.
a. Use two sets of coordinates to write an equation to describe the relationship.
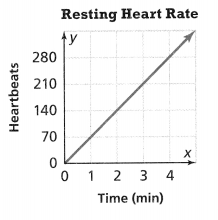
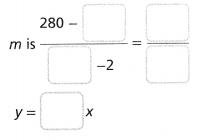
Answer:
It is given that
Resting heart rate is a measure of how fast the heart beats when a person is not performing physical activity. The graph shows the number of heartbeats over time for a given person.
Now,
From the given graph,
The points are: (3, 210), and (4, 280)
Now,
Compare the given points with (x1, y1), and (x2, y2)
We know that,
Slope can be represented as “m”
So,
m = \(\frac{y2 – y1}{x2 – x1}\)
So,
m = \(\frac{280 – 210}{4 – 3}\)
= \(\frac{70}{1}\)
= 70
We know that,
The equation of the line is:
y = mx
Hence, from the above,
We can conclude that
The equation of the line that describes the given situation is: y = 70x
b. Interpret the equation in words.
The heart’s resting heart rate is ![]() beats each minute.
beats each minute.
Answer:
From part (a),
The equation of the line that describes the given situation is: y = 70x
Hence, from the above,
We can conclude that the heart’s resting heart rate is 70 beats each minute
Question 7.
Model with Math The graph relates the number of gallons of white paint to the number of gallons of red paint Jess used to make the perfect pink. Write an equation that describes the relationship.
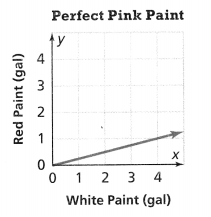
Answer:
It is given that
The graph relates the number of gallons of white paint to the number of gallons of red paint Jess used to make the perfect pink.
Now,
The given graph is:

Now,
Slope of the given line (m) = \(\frac{y}{x}\)
m = \(\frac{4}{1}\)
m = 4
We know that,
The equation of the line is:
y = mx
Hence, from the above,
We can conclude that the equation of the line that represents the given situation is: y = 4x
Question 8.
Critique Reasoning Franco made this graph to show the equation y = -x. Is the graph correct? Explain.

Answer:
The given graph is:

Now,
We know that,
Slope of the line (m) = \(\frac{y}{x}\)
m = \(\frac{4}{4}\)
m = 1
We know that,
The equation of the line is:
y = mx
So,
The equation of the line is:
y = x
But,
Franco made this graph to show the equation y = -x
Hence, from the above,
We can conclude that the graph of Franco is not correct
Question 9.
The graph shows a proportional relationship between the variables x and y.
a. Write an equation to model the relationship.
b. Reasoning Explain how you know if an equation or a graph represents a proportional relationship.

Answer:
a.
The given graph is:

We know that,
The slope of the line (m) = \(\frac{y}{x}\)
= \(\frac{96}{8}\)
= 12
We know that,
The equation of the line is:
y = mx
So,
The equation of the line to the given relationship is:
y = 12x
Hence, from the above,
We can conclude that the equation of the line that represents the given situation is: y = 12x
b.
If the relationship between two quantities is a proportional relationship, this relationship can be represented by the graph of a straight line through the origin with a slope equal to the unit rate. For each point (x, y) on the graph, ž is equal to k, where k is the unit rate.
Question 10.
Model with Math Graph the equation y = -5x on the coordinate plane.
Answer:
The given equation is:
y = -5x
Hence,
The representation of the given equation in the coordinate plane is:
Question 11.
Graph the equation y = \(\frac{3}{5}\)x on the coordinate plane.
Answer:
The given equation is:
y = \(\frac{3}{5}\)x
Hence,
The representation of the given equation in the coordinate plane is:
Question 12.
Higher-Order Thinking A movie theater sends out a coupon for 70% off the price of a ticket.
a. Write an equation for the situation, where y is the price of the ticket with the coupon and x is the original price.
Answer:
It is given that
A movie theater sends out a coupon for 70% off the price of a ticket.
So,
The proportionality constant of the given situation = \(\frac{70}{100}\)
= \(\frac{7}{10}\)
We know that,
Proportionality constant = Slope
So,
Slope (m) = \(\frac{7}{10}\)
We know that,
The equation of the line is:
y = mx
So,
y = \(\frac{7}{10}\)
10y = 7x
Hence, from the above,
We can conclude that the equation of the line for the given situation is: 10y = 7x
b. Graph the equation and explain why the line should only be in the first quadrant.
Answer:
From part (a),
The equation of the line is:
10y = 7x
So,
The representation of the given equation in the coordinate plane is:
From the graph,
We can observe that
The graph should only be in 1st quadrant because the values of x and y are both positive
Assessment Practice
Question 13.
An equation and a graph of proportional relationships are shown. Which has the greater unit rate? y = \(\frac{47}{2}\)x
Answer:
The given graph is:

From the given graph,
Slope (m) = \(\frac{y}{x}\)
= \(\frac{282}{6}\)
= 47
Now,
The given equation is:
y = \(\frac{47}{2}\)x
So,
Slope (m) = \(\frac{y}{x}\)
= \(\frac{47}{2}\)
Now,
When we compare the rates or slopes,
47 > \(\frac{47}{2}\)
Hence, from the above,
We ca conclude that the unit rate of the graph is greater than the unit rate of the equation
Question 14.
Car X travels 186 miles in 3 hours.
PART A Write the equation of the line that describes the relationship between distance and time.
Answer:
It is given that car X travels 186 miles in 3 hours.
Now,
We know that,
Speed = \(\frac{Distance}{Time}\)
We know that,
The equation of the line is:
y = mx
Where,
m = \(\frac{Distance}{Time}\)
So,
The equation of the line is:
y = \(\frac{186}{3}\)x
y = 62x
Hence, from the above,
We can conclude that the equation of the line that descries the relationship between distance and time is:
y = 62x
PART B Which graph represents the relationship between distance and time for Car X?
Answer:
From part (a),
The equation of the line that describes the relationship between distance and time is:
y = 62x
Where,
62 —-> The value of \(\frac{y}{x}\) (or) m
So,
From the above graphs,
We can observe that,
m = 62 is possible from graphs C and D
But,
We know that,
The equation y = mx passes through the origin
Hence, from the above,
We can conclude that the graph C represents the relationship between distance and time for car X
Lesson 2.8 Understand the y-Intercept of a Line
Solve and Discuss It!
Eight-year-old Alex is learning to ride a horse. The trainer says that a horse ages 5 years for every 2 human years. The horse is now 50 years old in human years. How can you determine the age of the horse, in human years, when Alex was born?

Answer:
It is given that
Eight-year-old Alex is learning to ride a horse. The trainer says that a horse ages 5 years for every 2 human years. The horse is now 50 years old in human years.
So,
When Alex is 8 years old,
The age of the horse in human years is: 50 years
Now,
For every 2 human years, the horse ages 5 years
So,
So,
For Alex,
The number of times his age increases = \(\frac{8}{2}\)
= 4 times
So,
The increase in the age of the horse when Alex is 8 years old = 5 × 4 = 20 years
So,
The age of the horse when Alex born = The present age of the horse – The increased age of the horse
= 50 – 20
= 30 years
Hence, from the above,
We can conclude that the age of the horse when Alex is born is: 30 years
Focus on math practices
Use Structure A veterinarian says that cat ages 8 years for every 2 human years. If a cat is now 64 years old in cat years, how old is the cat in human years?
Answer:
It is given that
A veterinarian says that a cat ages 8 years for every 2 human years.
Now,
Let the age of the cat in human years be x
So,
\(\frac{The age of the cat in cat years}{The age of the cat in human years}\) = \(\frac{The increase of the age of the cat for the increase of human years}{The increase of the age of human for the increase of human years}\)
\(\frac{64}{x}\) = \(\frac{8}{2}\)
Divide by 64 into both sides
So,
\(\frac{64}{x × 64}\) = \(\frac{8}{2 × 64}\)
\(\frac{1}{x}\) = \(\frac{1}{16}\)
x = 16 years
Hence, from the above,
We can conclude that the age of cat in human years is: 16 years
? Essential Question
What is the y-intercept and what does it indicate?
Answer:
The slope and y-intercept values indicate characteristics of the relationship between the two variables x and y. The slope indicates the rate of change in y per unit change in x. The y-intercept indicates the y-value when the x-value is 0.
Try It!
Prices for a different bowling alley are shown in the graph. How much does this bowling alley charge for shoe rental? The line crosses the y-axis as ![]()
The y-intercept is ![]()

Answer:
It is given that
The prices for a different bowling alley are shown in the graph
So,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
So,
From the given graph,
The given line crosses the y-axis at (0, 3)
We know that,
The y-intercept is the value of y when the value of x is 0
Hence, from the above,
We can conclude that
The given passes through (0, 3)
The y-intercept is: 3
Convince Me!
In these examples, why does the y-intercept represent the cost to rent bowling shoes?
Answer:
In this example,
From the slope,
We can determine the cost of each game
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept and that y-intercept is the cost to rent bowling shoes because the cost won’t ever be zero
Try It!
What is the y-intercept of each graph? Explain.

Answer:
Let the given graphs be named as graph A and graph B respectively
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
So,
From graph A,
The y-intercept is: (0, 2)
From graph B,
The y-intercept is: (0, -0.5)
KEY CONCEPT
The y-intercept is the y-coordinate of the point on a graph where the line crosses the y-axis.
When the line crosses through the origin, the y-intercept is 0.
When the line crosses above the origin, the y-intercept is positive.
When the line crosses below the origin, the y-intercept is negative.
Do You Understand?
Question 1.
? Essential Question What is the y-intercept and what does it indicate?
Answer:
The slope and y-intercept values indicate characteristics of the relationship between the two variables x and y. The slope indicates the rate of change in y per unit change in x. The y-intercept indicates the y-value when the x-value is 0.
Question 2.
Look for Relationships Chelsea graphs a proportional relationship. Bradyn graphs a line that passes through the origin. What do you know about the y-intercept of each student’s graph? Explain your answer.
Answer:
It is given that
Chelsea graphs a proportional relationship. Bradyn graphs a line that passes through the origin
So,
From the given situation,
We can observe that
The graph of Chelsea may pass through the origin or may not pass through the origin i.e., the y-intercept may be zero, positive, or negative
The graph of Braydon passes through the origin i.e., the y-intercept is zero
Question 3.
Generalize When the y-intercept is positive, where does the line cross the y-axis on the graph? When it is negative?
Answer:
When the y-intercept is positive, the line crosses above the origin,
When the y-intercept is negative, the line crosses below the origin
Do You Know How?
Question 4.
What is the y-intercept shown in the graph?
Answer:
The given graph is:

From the given graph,
We can observe that the line passes through the origin
Hence, from the above,
We can conclude that the value of the y-intercept is: 0
Question 5.
The graph shows the relationship between the remaining time of a movie and the amount of time since Kelly hit “play.” What is the y-intercept of the graph and what does it represent?
Answer:
It is given that
The graph shows the relationship between the remaining time of a movie and the amount of time since Kelly hit “play.”
Now,
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
So,
From the graph,
We can observe that the line crosses the y-axis at (0, 1.8)
Hence, from the above,
We can conclude that the y-intercept of the graph is: 1.8
The y-intercept represents the remaining time of a movie in the given situation
Practice & Problem Solving
Question 6.
Leveled Practice Find the y-intercept of the line. The y-intercept is the point where the graph crosses the ![]() -axis.
-axis.
The line crosses the y-axis at the point 
The y-intercept is ![]()
Answer:
The given graph is:

Now,
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
So,
From the graph,
We can observe that
The line crosses the y-axis at the point (0, 7)
Hence, from the above,
We can conclude that
The y-intercept is the point where the graph crosses the y-axis
The y-intercept for the given graph is: 8
Question 7.
Find the y-intercept of the graph.
Answer:
The given graph is:

Now,
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
So,
From the graph,
We can observe that
The line crosses the y-axis at the point (0, -4)
Hence, from the above,
We can conclude that
The y-intercept for the given graph is: -4
Question 8.
Find the y-intercept of the graph.
Answer:
The given graph is:

Now,
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
Now,
From the graph,
We can observe that
The equation of the line is:
y = kx
From the above equation,
We can say that the line passes through the origin
So,
The line crosses the y-axis at the point (0, 0)
Hence, from the above,
We can conclude that
The y-intercept of the given graph is: 0
Question 9.
The graph represents the height y, in meters, of a hot air balloon x minutes after beginning to descend. How high was the balloon when it began its descent?
Answer:
It is given that
The graph represents the height y, in meters, of a hot air balloon x minutes after beginning to descend
Now,
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
So,
From the graph,
We can observe that the line crosses the y-axis at (0, 80)
The y-intercept of the graph gives us information about the height of the balloon when it began its descent
Hence, from the above,
We can conclude that the height of the balloon when it began its descent is: 80 m
Question 10.
Model with Math The graph represents the amount of gasoline in a canister after Joshua begins to fill it at a gas station pump. What is the y-intercept of the graph and what does it represent?
Answer:
It is given that
The graph represents the amount of gasoline in a canister after Joshua begins to fill it at a gas station pump.
Now,
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
Now,
From the graph,
We can observe that the line passes through the origin
So,
The line crosses the y-axis at the point (0, 0)
Hence, from the above,
We can conclude that
The y-intercept of the given graph is: 0
The y-intercept of the given graph represents the amount of gas in gallons at the starting time
Question 11.
The line models the temperature on a certain winter day since sunrise.
a. What is the y-intercept of the line?
Answer:
It is given that
The line models the temperature on a certain winter day since sunrise.
Now,
We know that,
y-coordinate of the point where the line crosses the y-axis is the y-intercept
So,
From the graph,
We can observe that the line crosses the y-axis at (0, 4)
Hence, from the above,
We can conclude that the y-intercept of the given line is: 4
b. What does the y-intercept represent?
Answer:
The y-intercept of the graph gives us information about the starting temperature on a certain winter day at sunrise
Question 12.
Higher-Order Thinking Your friend incorrectly makes this graph as an example of a line with a y-intercept of 3.
a. Explain your friend’s possible error.
The given graph is:

Now,
From the given graph,
We can observe that the line crosses the y-axis at: (0, 4)
So,
The y-intercept of the graph is: 4
But,
Your friend incorrectly makes this graph as an example of a line with a y-intercept of 3.
Hence, from the above,
We can conclude that the y-intercept of the given graph is 4 but not 3
b. Draw a line on the graph that does represent a y-intercept of 3.
Answer:
Let the equation with the y-intercept of 3 is:
y = x + 3
Hence,
The representation of the graph that does represent a y-intercept of 3 in the coordinate plane is:
Assessment Practice
Question 13.
For each graph, draw a line through the point such that the values of the x-intercept and y-intercept are additive inverses.
Answer:
Let the graphs be named as graph A and graph B respectively
Now,
The given graphs are:

So,
From graph A,
We can observe that the x-intercept is 3 and the y-intercept is 3
We know that,
The “Additive inverse” of a number ‘a’ is the number that, when added to ‘a’, yields zero. This number is also known as the opposite (number), sign change, and negation.
So,
The additive inverses of the x-intercept and y-intercept are: (-3, -3)
From graph B,
We can observe that the x-intercept is -3 and the y-intercept is -3
We know that,
The “Additive inverse” of a number ‘a’ is the number that, when added to ‘a’, yields zero. This number is also known as the opposite (number), sign change, and negation.
So,
The additive inverses of the x-intercept and y-intercept are: (3, 3)
Hence,
The representation of the additive inverses of the x and y-intercepts in the coordinate plane is:
Question 14.
Which statements describe the graph of a proportional relationship? Select all that apply.
![]() The y-intercept is always at the point (0, 1).
The y-intercept is always at the point (0, 1).
![]() The line always crosses the y-axis at (0, 0).
The line always crosses the y-axis at (0, 0).
![]() The y-intercept is 0.
The y-intercept is 0.
![]() The y-intercept is 1.
The y-intercept is 1.
![]() The line does NOT cross the y-axis.
The line does NOT cross the y-axis.
Answer:
Let the options be named as A, B, C, D, and E respectively
Now,
We know that,
The representation of the proportional relationship is:
y = kx
So,
From the equation,
We can say that the equation passes through the origin and the y-intercept is 0
Hence, from the above,
We can conclude that options B and C describes the proportional relationship
Lesson 2.9 Analyze Linear Equations: y = mx + b
ACTIVITY
Explain It!
Xiu and Jon take the tram from the base camp to the mountain summit. After about six and a half minutes in the tram, Jon says, “Cool! We are a mile above sea level.” Xiu says, “We passed the one-mile mark a couple of minutes ago.”

A. Construct an argument to defend Xiu’s statement.
B. What mistake could Jon have made? Explain.
Answer:
Focus on math practices
Reasoning Can you use the equation y = mx to represent the path of the tram? Is there a proportional relationship between x and y? Explain.
? Essential Question
What is the equation of a line for a nonproportional relationship?
Answer:
Linear equations can be written in the form y = mx + b. When b ≠ 0, the relationship between x and y is nonproportional.
Try It!
Write a linear equation in slope-intercept form for the graph shown.
The y-intercept of the line is ![]()

Answer:
The given graph is:

From the given graph,
We can observe that,
The points are: (8, 8), and (4, 5)
Compare the given points with (x1, y1), (x2, y2)
We know that,
The y-intercept of the line is the point that crosses the y-axis
So,
From the given graph,
The y-intercept is: 2
We know that,
The linear equation in the slope-intercept form is:
y = mx + c
Where,
m is the slope
c is the y-intercept
Now,
m = \(\frac{y2 – y1}{x2 – x1}\)
= \(\frac{5 – 8}{4 – 8}\)
= \(\frac{3}{4}\)
So,
The linear equation in the slope-intercept form is:
y = \(\frac{3}{4}\)x + 2
y = \(\frac{3x + 8}{4}\)
4y = 3x + 8
Hence, from the above,
We can conclude that the linear equation in the slope-intercept form is:
4y = 3x + 8
Convince Me!
What two values do you need to know to write an equation of a line, and how are they used to represent a line?
Answer:
To write an equation of a line in the slope-intercept form,
The two values you need to know are:
A) Slope of a line and it is represented as “m”
B) The y-intercept of a line and is represented as “c”
KEY CONCEPT
The equation of a line that represents a nonproportional relationship can be written in slope-intercept form, y = mx + b, where m is the slope of the line and b is the y-intercept.
Do You Understand?
Question 1.
? Essential Question What is the equation of a line for a nonproportional relationship?
Answer:
Linear equations can be written in the form y = mx + b. When b ≠ 0, the relationship between x and y is nonproportional.
Question 2.
Use Structure The donations by a restaurant to a certain charity, y, will be two-fifths of its profits, x, plus $50. How can you determine the equation in slope-intercept form that shows the relationship between x and y without graphing the line?
Answer:
It is given that
The donations by a restaurant to a certain charity, y, will be two-fifths of its profits, x, plus $50.
So,
Donations to a certain charity by a restaurant = The part of the profits of a restaurant + $50
y = \(\frac{2}{5}\)x + $50
Compare the above equation with
y = mx + c
Where,
m is the slope of a line
c is the y-intercept of a line
So,
When we compare the equation,
The slope of a line is (m): \(\frac{2}{5}\)
The y-intercept of a line is (c) : $50
Question 3.
Be Precise Priya will graph a line with the equation y = \(\frac{3}{4}\)x – 4. She wants to know what the line will look like before she graphs the line. Describe the line Priya will draw, including the quadrants the line will pass through.
Answer:
It is given that
Priya will graph a line with the equation y = \(\frac{3}{4}\)x – 4. She wants to know what the line will look like before she graphs the line.
Now,
Compare the given equation with
y = mx + c
Where,
m is the slope of the line
c is the y-intercept
So,
By comparing,
We get,
m = \(\frac{3}{4}\)
c = -4
Now,
From the y-intercept,
We can say that the y-intercept lies below the origin i.e., in the 3rd quadrant
From the slope of the line,
We can say that the value of m lies in the 1st quadrant
Hence, from the above,
We can conclude that the line drawn by Priya will be in the 4th quadrant for the above values of c and m
Do You Know How?
Question 4.
Chrissie says the equation of the line shown on the graph is y = \(\frac{1}{2}\)x – 5. George says that the equation of the line is y = \(\frac{1}{2}\)x + 5. Which student is correct? Explain.

Answer:
It is given that
Chrissie says the equation of the line shown on the graph is y = \(\frac{1}{2}\)x – 5. George says that the equation of the line is y = \(\frac{1}{2}\)x + 5.
Now,
The given graph is

From the given graph,
The y-intercept is: 5
Now,
When we observe the given two equations,
The slope is the same and the y-intercepts are different and the correct y-intercept must be 5
Hence, from the above,
We can conclude that George is correct
Question 5.
Fara wants to rent a tent for an outdoor celebration. The cost of the tent is $500 per hour, plus an additional $100 set-up fee.
a. Draw a line to show the relationship between the number of hours the tent is rented, x, and the total cost of the tent, y.
Answer:
It is given that
Fara wants to rent a tent for an outdoor celebration. The cost of the tent is $500 per hour, plus an additional $100 set-up fee.
Now,
The total cost of the rent = The cost of the rent per hour + Additional set-up fee
So,
y = 500x + 100
Hence,
The representation of the above equation in the coordinate plane is:
b. What is the equation of the line in slope-intercept form?
Answer:
We know that,
The total cost of the rent = The cost of the rent per hour + Additional set-up fee
So,
y = 500x + 100
Where,
x is the number of hours
The above equation is in the form of
y = mx + c
Which is the slope-intercept form of the equation
Hence, from the above,
We can conclude that the equation of the line in the slope-intercept form is:
y = 500x + 100
Practice & Problem Solving
Question 6.
Leveled Practice What is the graph of the equation y = 2x + 4?
The y-intercept is ![]() , which means the line crosses the y-axis at the point (
, which means the line crosses the y-axis at the point (![]() ). Plot this point.
). Plot this point.
The slope of the line is positive, so it goes ![]() from left to right.
from left to right.
Start at the y-intercept. Move up ![]() , and then move right
, and then move right ![]()
You are now at the point (![]() ). Plot this point. Draw a line to connect the two points.
). Plot this point. Draw a line to connect the two points.
Answer:
The given equation is:
y = 2x + 4
So,
The representation of the given equation in the coordinate plane is:

Compare the given equation with
y = mx + c
Wher,
m is the slope of a line
c is the y-intercept of a line
So,
The y-intercept of the given graph is 4 which means the line crosses the y-axis at the point (0, 4)
The slope of the line is positive, so it goes up from left to right.
Start at the y-intercept. Move up 2 units, and then move right 2 units
So,
You are now at the point (3, 10).
Question 7.
Write an equation for the line in slope-intercept form.
Answer:
The given graph is:

We know that,
The equation of the line in the slope-intercept form is:
y = mx + c
Now,
From the given graph,
We can observe that the y-intercept is: -3
Now,
The given points from the graph to find the slope are: (-2, -2), and (4, -5)
Now,
SLope (m) = \(\frac{-5 – (-2)}{4 – (-2)}\)
m = \(\frac{-3}{6}\)
m = –\(\frac{1}{2}\)
So,
The equation of the line in the slope-intercept form is:
y = –\(\frac{1}{2}\)x – 3
Hence, from the above,
We can conclude that the equation of the line in the slope-intercept form is:
y = –\(\frac{1}{2}\)x – 3
Question 8.
Write an equation for the line in slope-intercept form.

Answer:
The given graph is:

We know that,
The equation of the line in the slope-intercept form is:
y = mx + c
Now,
From the given graph,
We can observe that the y-intercept is: 4
Now,
The given points from the graph to find the slope are: (1, 1), and (0, 4)
Now,
SLope (m) = \(\frac{4 – 1}{0 – 1}\)
m = \(\frac{3}{-1}\)
m = -3
So,
The equation of the line in the slope-intercept form is:
y = -3x + 4
Hence, from the above,
We can conclude that the equation of the line in the slope-intercept form is:
y = -3x + 4
Question 9.
The line models the cost of renting a kayak. Write an equation in slope-intercept form for the line, where x is the number of hours the kayak is rented and y is the total cost of renting the kayak.
Answer:
It is given that
The line models the cost of renting a kayak
where,
x is the number of hours the kayak is rented and y is the total cost of renting the kayak.
Nw,
The given graph is:

From the given graph,
We can observe that
The y-intercept of the graph is: 5
We know that,
The equation of the line in the slope-intercept form is:
y = mx + c
Where,
m is the slope
c is the y-intercept
Now,
From the given graph,
The points to find the graph are: (3, 40), and (2, 30)
So,
Slope (m) = \(\frac{30 – 40}{2 – 3}\)
= 10
So,
The equation of the line in the slope-intercept form is:
y = mx + c
So,
y = 10x + 5
Hence, from the above,
We can conclude that
The equation of the line in the slope-intercept form is:
y = 10x + 5
Question 10.
Graph the equation y = 3x – 5.
Answer:
The given equation is:
y = 3x – 5
Hence,
The representation of the given equation in the coordinate plane is:
Question 11.
Amy began with $25 in her bank account and spent $5 each day. The line shows the amount of money in her bank account. She incorrectly wrote an equation for the line in slope-intercept form as y = -5x + 5.
a. What is the correct equation for the line in slope-intercept form?
Answer:
It is given that
Amy began with $25 in her bank account and spent $5 each day. The line shows the amount of money in her bank account
Now,
The given graph is:

From the given graph,
The y-intercept is: 25
We know that,
The equation of the line in the slope-intercept form is:
y = mx + c
Now,
The given points to find the slope are: (5, 0), and (1, 20)
So,
Slope (m) = \(\frac{20 – 0}{5 – 1}\)
= \(\frac{20}{5}\)
= 4
So,
The equation of the line in the slope-intercept form is:
y = 4x + 25
Hence, from the above,
We can conclude that the equation of the line in the slope-intercept form is:
y = 4x + 25
b. Critique Reasoning What mistake might Amy have made?
Answer:
Answer:
The mistakes might made by Amy are:
A) The value of y-intercept is 25 and the value of x-intercept is: 5
B) The slope is not negative as it moves down from top to bottom
Question 12.
Higher-Order Thinking The line represents the cost of ordering concert tickets online.
a. Write an equation for the line in slope-intercept form, where x is the number of tickets and y is the total cost.
Answer:
It is given that
The line represents the cost of ordering concert tickets online.
Now,
The given graph is:

From the given graph,
The y-intercept is: 10
We know that,
The equation of the line in the slope-intercept form is:
y = mx + c
Now,
The given points to find the slope are: (1, 33.25), and (0, 12.25)
So,
Slope (m) = \(\frac{12.25 – 33.25}{0 – 1}\)
= \(\frac{21}{1}\)
= 21
So,
The equation of the line in the slope-intercept form is:
y = 21x + 10
Hence, from the above,
We can conclude that the equation of the line in the slope-intercept form is:
y = 21x + 10
b. Explain how you can write an equation for this situation without using a graph.
Answer:
We know that,
The total cost of ordering concert tickets online = (The cost of 1 Ticket) × (The number of Tickets) + Processing fee
Let the number of tickets be x
Let the total cost of ordering concert tickets online be y
So,
y = 21x + 10
Hence, from the above,
We can conclude that the equation for this situation without using a graph is:
y = 21x + 10
c. Is this graph a good representation of the situation? Explain.
Answer:
Yes,
The given graph is good for the given situation because the equation of the line is the same for this situation with using the graph and without using the graph
Assessment Practice
Question 13.
What should you do first to graph the equation y = \(\frac{2}{5}\)x – 1?
A. Plot the point (0, 0).
B. Plot the point (2, 5).
C. Plot a point at the x-intercept.
D. Plot a point at the y-intercept.
Answer:
The given equation is:
y = \(\frac{2}{5}\)x – 1
Compare the above equation with
y = mx + c
Hence, from the above,
We can conclude that the first step to draw the graph for the given equation is:
Plot a point at the y-intercept
Question 14.
Write an equation for the line in slope-intercept form.
Answer:
The given graph is:

From the given graph,
We can observe that
The y-intercept of the graph is: 8
We know that,
The equation of the line in the slope-intercept form is:
y = mx + c
Where,
m is the slope
c is the y-intercept
Now,
From the given graph,
The points to find the graph are: (4, 0), and (0, 8)
So,
Slope (m) = \(\frac{8 – 0}{0 – 4}\)
= -2
So,
The equation of the line in the slope-intercept form is:
y = mx + c
So,
y = -2x + 8
Hence, from the above,
We can conclude that
The equation of the line in the slope-intercept form is:
y = -2x + 8
TOPIC 2 REVIEW
? Topic Essential Question
How can you analyze connections between linear equations and use them to solve problems?
Answer:
Assuming that your two equations are distinct (neither is merely a multiple of the other), we can use the “elimination by addition and subtraction” method or substitution method to eliminate one variable, leaving us with an equation in one variable, solve this 1-variable (Ex: in x) equation, and then use the resulting value in the other
Vocabulary Review
Complete each definition and provide an example of each vocabulary word.


Question 1.
The change in y divided by the change in x is the ____
Answer:
The change in y divided by the change in x is defined as the “Slope of a line”
Example:
Slope = \(\frac{y}{x}\)
= \(\frac{2}{5}\)
Question 2.
The point on the graph where the line crosses the y-axis is the ____ of a line.
Answer:
The point on the graph where the line crosses the y-axis is the “y-intercept” of a line. In the y-intercept, the value of x is 0
Example:
The point on the graph where the line crosses the y-axis is at (0, 2)
So,
The y-intercept is: 2
Question 3.
The ____ of a line is y = mx + b. The variable m in the equation stands for the __. The variable b in the equation stands for the ___
Answer:
The “Slope-intercept form” of a line is
y = mx + b
The variable m in the equation stands for the x-intercept.
The variable b in the equation stands for the y-intercept
Use Vocabulary in Writing
Paddle boats rent for a fee of $25, plus an additional $12 per hour. What equation, in y = mx + b form, represents the cost to rent a paddle boat for x hours? Explain how you write the equation. Use vocabulary words in your explanation.
Answer:
It is given that
Paddleboats rent for a fee of $25, plus an additional $12 per hour.
Where,
x represents the cost to rent a paddleboat for x hours
Now,
The total cost to rent a paddleboat = The cost of a paddleboat per hour + $12
y = $25x + $12
Hence, from the above,
We can conclude that the equation of the line for this situation is:
y = $25x + $12
Concepts and Skills Review
LESSON 2.1 Combine Like Terms to Solve Equations
Quick Review
You can use variables to represent unknown quantities. To solve an equation, collect like terms to get one variable on one side of the equation. Then use inverse operations and properties of equality to solve the equation.
Practice
Solve each equation for x.
Question 1.
2x + 6x = 1,000
Answer:
The given equation is:
2x + 6x = 1,000
So,
8x = 1,000
Divide by 8 into both sides
x = \(\frac{1,000}{8}\)
x = 125
Hence, from the above,
We can conclude that the value of x is: 125
Question 2.
2\(\frac{1}{4}\)x + 2\(\frac{1}{2}\)x = 44
Answer:
The given equation is:
2\(\frac{1}{4}\)x + 2\(\frac{1}{2}\)x = 44
We know that,
2\(\frac{1}{4}\) = \(\frac{9}{4}\)
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
So,
\(\frac{9}{4}\)x + \(\frac{5}{2}\)x = 44
\(\frac{19}{4}\)x = 44
Multiply with \(\frac{4}{19}\) on both sides
So,
x = 44 × \(\frac{4}{19}\)
x = \(\frac{88}{19}\)
Hence, from the above,
We can conclude that the value of x is: \(\frac{88}{19}\)
Question 3.
-2.3x – 4.2x = -66.3
Answer:
The given equation is:
-2.3x – 4.2x = -66.3
So,
-6.5x = -66.3
6.5x = 66.3
Divide by 6.5 into both sides
So,
x = \(\frac{66.3}{6.5}\)
x = \(\frac{51}{5}\)
x = 10.2
Hence, from the above,
We can conclude that the value of x is: 10.2
Question 4.
Javier bought a microwave for $105. The cost was 30% off the original price. What was the price of the microwave before the sale?
Answer:
It is given that
Javier bought a microwave for $105. The cost was 30% off the original price
So,
The price of the microwave before the sale = The price of the microwave + 30% of the price of the microwave
= $105 + \(\frac{30}{100}\) ($105)
= $105 (\(\frac{130}{100}\))
= \(\frac{13650}{100}\)
= $136.5
Hence, from the above,
We can conclude that the price of the microwave before the sale is: $136.5
LESSON 2.2 Solve Equations with Variables on Both Sides
Quick Review
If two quantities represent equal amounts and have the same variables, you can set the expressions equal to each other. Collect all the variables on one side of the equation and all the constants on the other side. Then use inverse operations and properties of equality to solve the equation.
Practice
Solve each equation for x.
Question 1.
3x + 9x = 6x + 42
Answer:
The given equation is:
3x + 9x = 6x + 42
12x = 6x + 42
Rearrange the like terms
So,
12x – 6x = 42
6x = 42
So,
x = \(\frac{42}{6}\)
x = 7
Hence, from the above,
We can conclude that the value of x is: 7
Question 2.
\(\frac{4}{3}\)x + \(\frac{2}{3}\)x = \(\frac{1}{3}\)x + 5
Answer:
The given equation is:
\(\frac{4}{3}\)x + \(\frac{2}{3}\)x = \(\frac{1}{3}\)x + 5
So,
\(\frac{6}{3}\)x = \(\frac{1}{3}\)x + 5
\(\frac{6}{3}\)x – \(\frac{1}{3}[latex]x = 5
[latex]\frac{5}{3}\)x = 5
Multiply with \(\frac{3}{5}\) on both sides
So,
x = 5 × \(\frac{3}{5}\)
x = 3
Hence, from the above,
We can conclude that the value of x is: 3
Question 3.
9x – 5x + 18 = 2x + 34
Answer:
The given equation is:
9x – 5x + 18 = 2x + 34
So,
4x + 18 = 2x + 34
Rearrange the like terms
So,
4x – 2x = 34 – 18
2x = 16
Divide by 2 into both sides
So,
x = \(\frac{16}{2}\)
x = 8
Hence, from the above,
We can conclude that the value of x is: 8
Question 4.
Megan has $50 and saves $5.50 each week. Connor has $18.50 and saves $7.75 each week. After how many weeks will Megan and Connor have saved the same amount?
Answer:
It is given that
Megan has $50 and saves $5.50 each week. Connor has $18.50 and saves $7.75 each week.
Now,
Let x be the number of weeks
So,
The money saved by Megan = $50 + $5.50x
The money saved by Connor = $18.50 + $7.75x
So,
To find out after how many weeks Megan and Connor have saved the same amount,
$50 + $5.50x = $18.50 + $7.75x
Rearrange the like terms
So,
$50 – $18.50 = $7.75x – $5.50x
$31.05 = $2.25x
Divide by 2.25 into both sides
So,
x = \(\frac{31.05}{2.25}\)
x = 13.8
x = 14 weeks 1 day
x ≅ 14 weeks
Hence, from the above,
We can conclude that after approximately 14 weeks, Megan and Connor have saved the same amount
LESSON 2.3 Solve Multistep Equations
Quick Review
When solving multistep equations, sometimes the Distributive Property is used before you collect like terms. Sometimes like terms are collected, and then you use the Distributive Property.
Practice Solve each equation for x.
Question 1.
4(x + 4) + 2x = 52
Answer:
The given equation is:
4 (x + 4) + 2x = 52
So,
4 (x) + 4 (4) + 2x = 52
4x + 16 + 2x = 52
6x + 16 = 52
Rearrange the like terms
So,
6x = 52 – 16
6x = 36
x = \(\frac{36}{6}\)
x = 6
Hence, from the above,
We can conclude that the value of x is: 6
Question 2.
8(2x + 3x + 2) = -4x + 148
Answer:
The given equation is:
8 (2x + 3x + 2) = -4x + 148
So,
8 (5x + 2) = -4x + 148
8 (5x) + 8 (2) = -4x + 148
40x + 16 = -4x + 148
Rearrange the like terms
So,
40x + 4x = 148 – 16
44x = 132
x = \(\frac{132}{4}\)
x = 3
Hence, from the above,
We can conclude that the value of x is: 3
Question 3.
Justin bought a calculator and a binder that were both 15% off the original price. The original price of the binder was $6.20. Justin spent a total of $107.27. What was the original price of the calculator?
Answer:
It is given that
Justin bought a calculator and a binder that were both 15% off the original price. The original price of the binder was $6.20. Justin spent a total of $107.27.
So,
Total spent money of Justin = The original price of binder + The original price of a calculator
Let the original price of the calculator be x
So,
$6.20 + 30% of $6.20 + x + 30% of x = $107.27
$6.20 + \(\frac{3}{10}\) ($6.20) + x + \(\frac{3}{10}\) of x = $107.27
$6.20 + 1.86 + 1.3x = $107.27
$8.06 + 1.3x = $107.27
1.3x = $107.27 – $8.06
1.3x = 99.21
x = \(\frac{99.21}{1.3}\)
x = 76.31
Hence, from the above,
We can conclude that the original price of the calculator is: $76.31
LESSON 2.4 Equations with No Solutions or Infinitely Many Solutions
Quick Review
When solving an equation results in a statement that is always true, there are infinitely many solutions. When solving an equation produces a false statement, there are no solutions. When solving an equation gives one value for a variable, there is one solution.
Practice
How many solutions does each equation have?
Question 1.
x + 5.5 + 8 = 5x – 13.5 – 4x
Answer:
The given equation is:
x + 5.5 + 8 = 5x – 13.5 – 4x
So,
x + 13.5 = x – 13.5
Subtract with x on both sides
So,
13.5 = -13.5
Hence, from the above,
we can conclude that there are no solutions for the given equation
Question 2.
4(\(\frac{1}{2}\)x + 3) = 3x + 12 – x
Answer:
The given equation is:
4(\(\frac{1}{2}\)x + 3) = 3x + 12 – x
So,
4 × \(\frac{1}{2}\)x + 4 (3) = 3x + 12 – x
2x + 12 = 2x + 12
Subtract with 2x on both sides
So,
12 = 12
Hence, from the above,
We can conclude that there are infinitely many solutions for the given equation
Question 3.
2(6x + 9 – 3x) = 5x + 21
Answer:
The given equation is:
2 (6x + 9 – 3x) = 5x + 21
So,
2 (3x + 9) = 5x + 21
2 (3x) + 2 (9) = 5x + 21
6x + 18 = 5x + 21
Rearrange the like terms
So,
6x – 5x = 21 – 18
x = 3
Hence, from the above,
We can conclude that there is only 1 solution for the given equation
Question 4.
The weight of Abe’s dog can be found using the expression 2(x + 3), where x is the number of weeks. The weight of Karen’s dog can be found using the expression 3(x + 1), where x is the number of weeks. Will the dogs ever be the same weight? Explain.
Answer:
It is given that
The weight of Abe’s dog can be found using the expression 2(x + 3), where x is the number of weeks. The weight of Karen’s dog can be found using the expression 3(x + 1), where x is the number of weeks.
Now,
To find out whether the weight of the dogs will be the same or not,
2 (2x + 3) = 3 (3x + 1)
So,
2 (2x) + 2 (3) = 3 (3x) + 3 (1)
4x + 6 = 9x + 3
Rearrange the like terms
So,
9x – 4x = 6 – 3
5x = 3
x = \(\frac{3}{5}\)
So,
There is only 1 solution for the given equation
Hence, from the above,
We can conclude that the weights of the dogs will be the same
LESSON 2.5 Compare Proportional Relationships
Quick Review
To compare proportional relationships, compare the rate of change or find the unit rate.
Practice
Question 1.
Two trains are traveling at a constant rate. Find the rate of each train. Which train is traveling at the faster rate?

Answer:
We know that,
Unit rate = \(\frac{y}{x}\)
We know that,
Speed = \(\frac{Distance}{Time}\)
Now,
For Train A,
Unit rate = \(\frac{A value of Distance}{The value of time that corresponds to the Distance}\)
= \(\frac{50}{2}\)
= 25 miles per hour
For Train B,
Unit rate = \(\frac{y}{x}\)
= \(\frac{20}{1}\)
= 20 miles per hour
So,
Unit rate of Train A > Unit rate of Train B
Hence, from the above,
We can conclude that Train A is the fastest
Question 2.
A 16-ounce bottle of water from Store A. costs $1.28. The cost in dollars, y, of a bottle of water from Store B is represented by the equation y = 0.07x, where x is the number of ounces. What is the cost per ounce of water at each store? Which store’s bottle of water costs less per ounce?
Answer:
It is given that
A 16-ounce bottle of water from Store A. costs $1.28. The cost in dollars, y, of a bottle of water from Store B is represented by the equation y = 0.07x, where x is the number of ounces.
So,
The cost per ounce of water of store A = \(\frac{The cost of a 16-ounce bottle of water}{16}\)
= \(\frac{$1.28}{16}\)
= $0.08
The cost per ounce of water of store B = \(\frac{y}{x}\)
= $0.07
So,
The cost per ounce of water of store A > The cost per ounce of water of store B
Hence, from the above,
We can conclude that the cost per ounce of water of store B costs less per ounce
LESSON 2.6 Connect Proportional Relationships and Slope
Quick Review
The slope of a line in a proportional relationship is the same as the unit rate and the constant of proportionality.
Practice
Question 1.
The graph shows the proportions of blue paint and yellow paint that Briana mixes to make green paint. What is the slope of the line? Tell what it means in the problem situation.

Answer:
It is given that
The graph shows the proportions of blue paint and yellow paint that Briana mixes to make green paint.
Now,
The given graph is:

So,
From the graph,
The slope of the given line = \(\frac{y}{x}\)
= \(\frac{5}{6}\)
Hence, from the above slope of the line,
We can conclude that for 5 parts of yellow paint, we have to mix 6 parts of blue paint to make green paint
LESSON 2.7 Analyze Linear Equations: y = mx
Quick Review
A proportional relationship can be represented by an equation in the form y = mx, where m is the slope.
Practice
A mixture of nuts contains 1 cup of walnuts for every 3 cups of peanuts.
Question 1.
Write a linear equation that represents the relationship between peanuts, x, and walnuts, y.
Answer:
It is given that
A mixture of nuts contains 1 cup of walnuts for every 3 cups of peanuts.
We know that,
Slope (m) = \(\frac{y}{x}\)
m = \(\frac{1}{3}\)
We know that,
The linear equation that represents the relationship between peanuts and walnuts is:
y = mx
So,
y = \(\frac{1}{3}\)x
x = 3y
Hence, from the above,
We can conclude that the linear equation that represents the relationship between peanuts and walnuts is:
x = 3y
Question 2.
Graph the line.

Answer:
The linear equation that represents the relationship between peanuts and walnuts is:
x = 3y
Hence,
The representation of the linear equation in the coordinate plane is:
LESSON 2.8 Understand the y-Intercept of a Line
Quick Review
The y-intercept is the y-coordinate of the point where a line crosses the y-axis. The y-intercept of a proportional relationship is 0.
Practice
The equation y = 5 +0.5x represents the cost of getting a car wash and using the vacuum for x minutes.
Question 1.
What is the y-intercept?
Answer:
We know that,
The equation of the line in the y-intercept form is:
y = mx + c
Where,
m is the slope
c is the y-intercept
Now,
The given equation is:
y = 5 + 0.5x
Hence, from the above,
We can conclude that the y-intercept is: 5
Question 2.
What does the y-intercept represent?
Answer:
The y-intercept in the given situation represents that the initial cost of getting a car wash using the Vaccum
LESSON 2.9 Analyze Linear Equations: y = mx + b
Quick Review
An equation in the form y = mx + b, where b=0, has a slope of m and a y-intercept of b. This form is called the slope-intercept form. There is not a proportional relationship between x and y in these cases.
Practice
Question 1.
Graph the line with the equation y = \(\frac{1}{2}\)x – 1.
Answer:
The given equation is:
y = \(\frac{1}{2}\)x – 1
Hence,
The representation of the given equation in the coordinate plane is:
Question 2.
What is the equation of the line?
Answer:
The given graph is:

From the given graph,
We can observe that
The y-intercept is: 3
Now,
We know that,
The equation of the line in the slope-intercept form is:
y = mx + c
Now,
To find the slope,
The points are: (0, 3), and (3, 0)
So,
Slope (m) = \(\frac{0 – 3}{3 – 0}\)
= \(\frac{-3}{3}\)
= -1
Hence, from the above,
We can conclude that the equation of the line in the slope-intercept form is:
y = -x + 3
Topic 2 Fluency Practice
Pathfinder
Each block below shows an equation and a possible solution. Shade a path from START to FINISH. Follow the equations that are solved correctly. You can only move up, down, right, or left.