Envision Math 5th Grade Textbook Answer Key Topic 18 Reteaching
Reteaching
Set A, pages 402-404
What ordered pair names Point A?
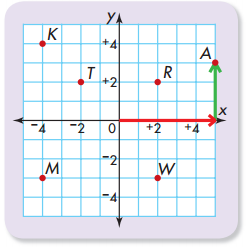
Start at the origin. The x-coordinate is the distance to the right or left along the x-axis. The y-coordinate is the distance up or down along the y-axis. Point A is at (+5, +3).
Remember to name a point on a coordinate grid, first find the x-coordinate. Then find the y-coordinate. Write the coordinates in (x, y) order.
Question 1.
Which point is located at (–4, –3)?
Answer:
Question 2.
Which point is located at (+2, +2)?
Answer:
Question 3.
Which point is located at (–4, +4)?
Answer:
Question 4.
What ordered pair names Point T?
Answer:
Question 5.
What ordered pair names Point W?
Answer:
Question 6.
What is the new ordered pair if Point A is moved to the left 5 spaces?
Answer:
Set B, pages 406-408
Make a line graph for the data.
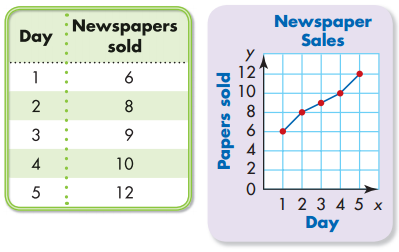
Use grid paper to draw a coordinate grid. Label the axes.
Number each axis with a consistent scale.
Plot the ordered pairs and connect the points.
Remember that line graphs show data that change over time.
Question 1.
Make a line graph for the data
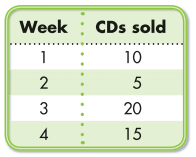
Answer:
Question 2.
Describe the trend.
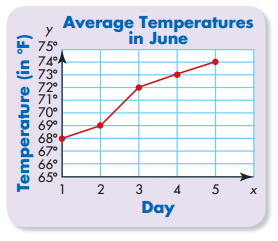
Answer:
Set C, pages 410–411
Graph the equation y = x + 2.
Choose values for x and find the values for y.

y = x + 2
0 = -2 + 2
2 = 0 + 2
5 = 3 + 2
Use grid paper to draw a coordinate grid.
Label and number the axes.
Plot the ordered pairs and connect the points.
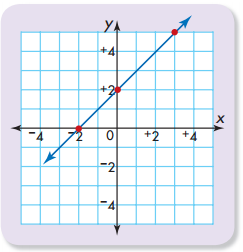
Remember to choose at least three values for x. The values for x and y must satisfy the equation.
Make a table of values for each equation. Then graph the equations on a coordinate grid.
Question 1.
y = x – 4
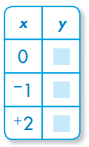
Answer:
Question 2.
y = 3x
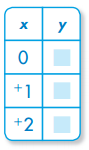
Answer:
Question 3.
y = x + 5
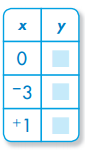
Answer:
Question 4.
y = x
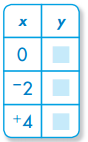
Answer:
Set D, pages 412-413
Franco worked on his science fair project for 35 minutes. Then he spent 20 minutes working on math homework. After that, Franco spent 45 minutes on the computer. If he logged off the computer at 8:10 P.M., what time did Franco begin working on his science fair project?
You can draw a picture to help you work backward. Use an inverse operation for each change.
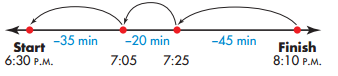
Remember that addition and subtraction have an inverse relationship.
Question 1.
Barb has 3\(\frac{1}{4}\) ft of ribbon left over. She used 2\(\frac{1}{4}\) ft to wrap a gift and \(\frac{3}{4}\) ft to decorate a picture frame. She then used 1\(\frac{3}{4}\) ft for hair ribbons. How many feet of ribbon did Barb start with?
Answer:
