Envision Math 5th Grade Textbook Answer Key Topic 19.8 Writing Probability as a Fraction
Writing Probability as a Fraction
What is the probability of an event?
Answer:
Reuben writes each letter of his name on a separate piece of paper and puts them in a bag. He chooses one piece of paper from the bag without looking.

The probability of an event is a number that describes the chance the event will occur.
Another Example
What is the probability of two events happening together?
Answer:
Eva puts the letters of her name into a bag and chooses a letter out of the bag without looking. She puts the letter back into the bag and chooses again without looking. What is the probability that Eva chooses an A both times?
Draw a tree diagram.
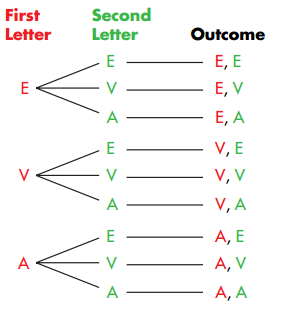
Find the probability.
Answer:
There are a total of 9 possible outcomes when the two letters are chosen and the first is replaced. One of the outcomes is favorable because only one of the outcomes has an A both times.
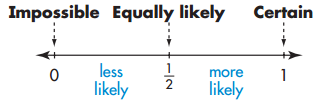
The probabilty of any event ranges from 0 to 1.
P(A, A) = \(\frac{1}{9}\)
The probability that Eva chooses an A both times is \(\frac{1}{9}\) .
Explain It
Question 1.
Use the tree diagram above to find the probability of choosing the same letter twice. Hint: Look for pairs of outcomes with the same letter.
Answer:
Question 2.
If an event has a probability of \(\frac{3}{4}\), is it less likely, more likely, equally likely, impossible, or certain to occur?
Answer:
Probability of an event = \(\frac{\text { number of favorable outcomes }}{\text { total number of possible outcomes }}\)
What is the probability that Reuben will choose the letter B?
There is 1 favorable outcome out of 6 possible outcomes, R, E, U, B, E, or N. The outcomes are equally likely (have the same chance of occurring). The probability of choosing the letter B can be written as P(B).
P(B) = \(\frac{1}{6}\)
The probability that Reuben chooses a B out of the bag is \(\frac{1}{6}\).
What is the probability that Reuben will choose the letter E?
There are 2 favorable outcomes out of 6 possible outcomes (since E appears twice).
P(E) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
The probability that Reuben chooses an E out of the bag is \(\frac{1}{3}\) or P(E) = \(\frac{1}{3}\).
Guided Practice
Do you know HOW?
For 1 through 4, use the spinner shown
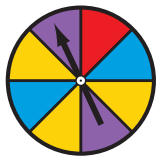
Question 1.
Find P(blue).
Answer:
Question 2.
Find P(yellow).
Answer:
Question 3.
Find P(red).
Answer:
Question 4.
Find P(green).
Answer:
Do you UNDERSTAND?
Question 5.
Writing to Explain
In the example above, is it likely, unlikely, impossible, or certain that Reuben draws a B?
Answer:
Question 6.
What is the probability that Reuben will NOT draw an R?
Answer:
Independent Practice
Question 7.
Write each letter of your first name on a separate small sheet of paper. Put each piece into a box. Do an experiment where you pick one letter and replace it each time. Do this 10 times. Record the number of times you pick each letter, and then write the probability as a fraction.
Answer:
For 8 through 12, suppose you toss a quarter and a penny.

Question 8.
Make a tree diagram to show the possible outcomes.
Answer:
Question 9.
Find P(one head).
Answer:
Question 10.
Find P(two heads).
Answer:
Question 11.
Find P(quarter heads, penny tails)
Answer:
Question 12.
Find P(no heads)
Answer:
Question 13.
When a number cube is tossed, there are 6 possible outcomes (1,2, 3, 4, 5, or 6). If the cube is tossed twice and the outcomes are added, the possible sums are from 2 through 12.
Answer:
Copy the table and give the probability of each sum.

Question 14.
Which sum (or sums) has the greatest probability of occurring?
Answer:
Question 15.
Which sum (or sums) has the least probability of occurring?
Answer:
Problem Solving
Question 16.
Geometry
Kendra tosses a colored cube. Half of the sides of the cube are red, \(\frac{1}{3}\) of the sides are blue, and one side is green. What is the probability that the cube will land on a color other than red when tossed?
Answer:
Question 17.
Mrs. Pierre bought 150 pencils to give to her students. She has three classes with 27, 25, and 23 students each. She wants every student to get the same number of pencils. How many pencils should she give to each student?
Answer:
Question 18.
Think About the Process
Jorge put colored cards into a bag. Two of the cards were green, three were red, one was orange, two were blue, and two were purple. Jorge wants to find the probability that he will pull an orange card from the bag. What step does Jorge take to determine the number of possible outcomes?
A. Count the number of orange cards.
B. Count the number of different colored cards.
C. Count the total number of cards in the bag.
D. Count the number of cards that are not orange.
Answer:
Question 19.
Carlita buys 3 beanbag throws for $1.00. What is the probability she will toss one beanbag through a hole in the top row of this game? Assume Carlita always throws a beanbag into a hole.

Answer:
Question 20.
How many parts of each color should there be to make sure that it is equally likely this spinner will land on each of 3 different colors?

Answer:
Algebra Connection
Which Equation is True?
Answer:
Remember that an equation is a number sentence that uses an equal sign to show that two expressions are equal. Both of the following are equations.
8 + 2 = 10
x + 25 = 100
The first equation is true. You don’t know if an algebraic equation is true or false until you replace the variable with a number.
If x = 75, then x + 25 = 100 is a true equation.
Example:
If m = 25, which equation is true?
2 + m = 30
m – 20 = 5
In the first equation, if you replace m with 25, the result is 2 + 25 = 30. This equation is false.
In the second equation if you replace m with 25, the result is 25 – 20 = 5. This equation is true.
Decide which equation is true for each replacement of the variable.
Question 1.
If x = 20, which equation is true?
Answer:
Question 2.
If y = 100, which equation is true? y – 80 = 180 or y ÷ 2 = 50
Answer:
Question 3.
If x = 50, which equation is true? x + 50 = 75 or \(\frac{x}{10}\) = 5
Answer:
Question 4.
If x = 80, which equation is true? 40x = 3,200 or \(\frac{x}{4}\) = 2
Answer:
Question 5.
If z = 200, which equation is true? 200 – x = 200 or x + 100 = 300
Answer:
Question 6.
If x = 70, which equation is true? 6x = 420 or x + 7 = 63
Answer:
Question 7.
If x = 0, which equation is true? 50x = 50 x + 7 = 7
Answer:
Question 8.
If x = 1, which equation is true? 40x = 40 or 40 + x = 40
Answer:
Question 9.
If a teacher has 32 students and divides them into teams of 4, which equation could be used to find how many students will be on each team? Let x represent the number of students on each team.
\(\frac{32}{4}\) = x
4 + x = 32
\(\frac{32}{x}\) = 4
4 × 32 = x
Answer:
