Envision Math Grade 5 Answer Key Topic 19.9 Problem Solving

Envision Math 5th Grade Textbook Answer Key Topic 19.9 Problem Solving

Problem Solving

Solve a Simpler Problem
Owen needs to read 2 books from a list of 6 books. How many different combinations of books are possible?

Answer:
Follow these steps to solve a simpler problem.

1. Break apart or change the problem into one that is simpler.
2. Solve the simpler problem.
3. Use the answers to the simpler problem to solve the original problem.

Guided Practice

Do you know HOW?
Question 1.
Draw a picture to show the number of combinations of pairs for 5 books.
Answer:

Question 2.
Think of extending the table at the top to find the number of pairs with 7 books. What number would you add to 15 to find the number of pairs? How many pairs would there be for 7 books?
Answer:

Do you UNDERSTAND?
Question 3.
Writing to Explain Is it easier to use the table or to draw a picture as the number of books increases?
Answer:

Question 4.
Write a Problem Write a real-world problem that can be solved by solving a simpler problem.
Answer:

Independent Practice

Solve each problem.
Question 5.
Continue the pattern in the book problem above. How many pairs of books would there be for 8 books? 9 books? 10 books?
Answer:

Question 6.
Find the number of degrees in a hexagon. HINT: Divide the hexagon into triangles.

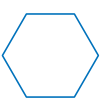
a. How many triangles are formed?
b. How many degrees are in each triangle?
c. What is the total number of degrees in the hexagon?
Answer:

Question 7.
Using the same strategy in Problem 6, what is the total number of degrees in a pentagon? An octagon?
Answer:

Use letters to represent the books.

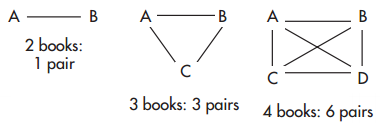
Look for a pattern.
Find the pattern. Continue the pattern to 6 books.

There are 15 different possible pairs.

Question 8.
Juanita tossed 3 number cubes, and these digits came up.

If each of the numbers 2, 1 and 4 is used only once to form a 3-digit number, which shows all the possible 3-digit numbers?
A. 214, 421, 142
B. 214, 124, 412, 421
C. 214, 241, 142, 412, 124
D. 214, 241, 142, 124, 412, 421
Answer:

Question 9.
Jill has 3 colored vases to arrange on a shelf

Let B stand for blue, O for orange, and G for green. Which list shows all the possible arrangements of the vases?
A. BOG, OBG, GOB
B. BOG, OBG, GOB, GBO
C. BOG, OBG, GOB, GBO, OGB
D. BOG, OBG, GOB, GBO, OGB, BGO
Answer:

Question 10.
George was choosing his clothes for the next day. In his closet he had 2 ties, 5 shirts, 3 trousers, and 2 belts. How many different ways could George choose a tie, shirt, trousers, and belt?
Answer:

Question 11.
The McMillan family wanted to buy a new vehicle. They could choose a van or a car; a black, silver, or white exterior; and a tan or black interior. How many different vehicles can they buy?
Answer:

Question 12.
After seeing a movie, 2 friends stopped for frozen yogurt. Three flavors were available in small, medium, and large sizes. How many different combinations of flavors and sizes are possible?
Answer:

Question 13.
Algebra Draw a picture and write an equation to solve.
Niko had 17\(\frac{1}{3}\) ft of fencing. He uses 5\(\frac{2}{3}\) ft to finish a job. How many feet of fencing does Niko have now? Let f = feet of fencing left?
Answer: