Envision Math Grade 5 Answer Key Topic 20.2 Constructing Lines

Envision Math 5th Grade Textbook Answer Key Topic 20.2 Constructing Lines

Constructing Lines
How can you construct perpendicular and parallel lines?
Answer:
The rails of the track are parallel. The ties are perpendicular to the rails.

Construct a line perpendicular to $\overleftrightarrow{L N}$ and a line parallel to $\overleftrightarrow{L N}$.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 1$
Answer:

Another Example
How do you construct a line segment congruent to a given line segment?
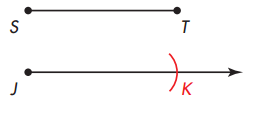
Without measuring with a ruler, draw $\overleftrightarrow{J K}$ congruent to $\overleftrightarrow{S T}$.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 2.1$
Step 1: Draw a ray. Label the endpoint J.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 2$
Step 2 : On $\overleftrightarrow{S T}$, with point S as the center, open the compass so that it lines
up with point T.
Then place the compass on the ray with point J as the center.
Without changing the compass setting, draw an arc that intersects the ray. Label the point of intersection K. $\overleftrightarrow{J K}$ is congruent to $\overleftrightarrow{S T}$.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 3$

Explain it
Question 1.
How is constructing a figure different from drawing a figure?
Answer:

Question 2.
In Step 2, could the ray be any length?
Answer:

Question 3.
Does a line segment need to be horizontal in order to construct another segment congruent to it?
Answer:

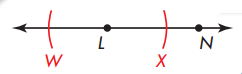
Draw a line with points L and N. With L as center, draw two arcs that intersect $\overleftrightarrow{L N}$. Label the points W and X.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 4$

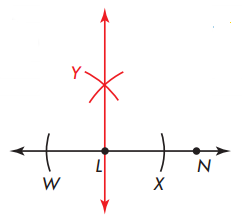
Set the compass wider. Using W and X as centers, draw arcs that intersect. Label the point Y. Draw $\overleftrightarrow{L Y}$
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 5$

Repeat Steps 1 and 2 at Y to find point Z.
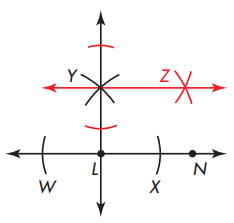
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 6$
$\overleftrightarrow{L Y}$ ⊥ $\overleftrightarrow{L N}$ and $\overleftrightarrow{L N}$ || $\overleftrightarrow{Y Z}$

Guided Practice

Do you know HOW?
Question 1.
Draw a line perpendicular to line CD. Copy $\overleftrightarrow{C D}$ on a separate sheet of paper and construct $\overleftrightarrow{T C}$ so that it is perpendicular to $\overleftrightarrow{C D}$.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 7$
Answer:

Question 2.
Draw as egment congruent to $\overline{E F}$. Copy $\overline{E F}$ on a separate sheet of paper. Then draw a ray labele d $\overleftrightarrow{M N}$. On that ray, construct $\overline{M P}$ so that $\overline{M P}$ is congruent to $\overline{E F}$.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 8$
Answer:

Do you UNDERSTAND?
Question 3.
Writing to Explain In Step 2 of the example above, why is it necessary to set the compass wider than the length of segment WL?
Answer:

Question 4.
Look at the line TC you constructed in Problem 1 that is perpendicular to line CD. Use point Tand construct a line perpendicular to line TC. How is that line related to line CD?
Answer:

Independent Practice

In 5 through 7, copy the figures on a separate sheet of paper and follow the directions.
Question 5.
Construct a line perpendicular to line XY.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 9$
Answer:

Question 6.
Construct a line perpendicular to line MN. Then construct a line through it that is parallel to line MN.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 10$
Answer:

Question 7.
Draw a line segment that is congruent to CD .
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 11$
Answer:

Problem Solving

Engineers are making plans to lay new railroad tracks between cities. In 8 and 9, use the information in the table.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 12$
Question 8.
If it costs $155 per mile to construct railroad tracks, how much would it cost to build tracks from San Francisco to Los Angeles?
Answer:

Question 9.
Estimation Railroad ties are set about 2 feet apart. About how many railroad ties are there between Eureka and Sacramento?
Answer:

Question 10.
If you are comparing two negative integers on a number line, how can you tell which one is greater?
Answer:

Question 11.
Four friends played golf. Their scores were +3, -1, *4, and ~4 in relation to par. The least score wins. Arrange the scores from best to worst.
Answer:

Question 12.
Algebra Ted has 15 trophies. This is 5 times as many as Harold has. How many trophies does Harold have? Write and solve an equation to answer the question.
Answer:

Question 13.
Writing to Explain Explain how perpendicular lines are similar to intersecting lines.
Answer:

Question 14.
Use the figure to tell whether the statements are true or false
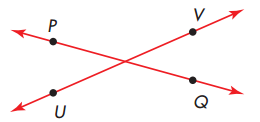
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 13$
a. $\overline{P Q}$ is parallel to $\overline{U V}$
b. $\overline{P Q}$ intersects $\overline{U V}$
c. $\overline{P Q}$ is perpendicular to $\overline{U V}$
Answer:

Question 15.
Estimation The gas tank in Shondra’s car can hold 18 gallons. Her car gets about 22 miles per gallon of gas. On a recent trip, Shondra used about 12 gallons of gas. Which is the best estimate of the distance Shondra drove?
A. 120 miles
B. 200 miles
C. 400 miles
D. 1,200 miles
Answer:

Stop and Practice

Find each difference. Simplify if possible.
Question 1.
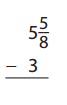
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 14$
Answer:

Question 2.
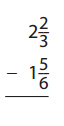
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 15$
Answer:

Question 3.
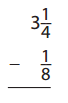
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 16$
Answer:

Question 4.
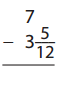
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 17$
Answer:

Question 5.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 18$
Answer:

Question 6.
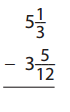
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 19$
Answer:

Question 7.
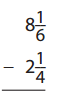
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 20$
Answer:

Question 8.
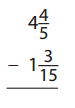
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 21$
Answer:

Find each difference. Simplify if possible.
Question 9.
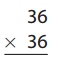
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 22$
Answer:

Question 10.
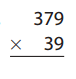
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 23$
Answer:

Question 11.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 24$
Answer:

Question 12.
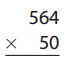
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 25$
Answer:

Question 13.
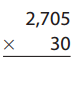
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 26$
Answer:

Question 14.
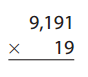
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 27$
Answer:

Question 15.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 28$
Answer:

Question 16.
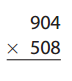
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 29$
Answer:

Question 17.
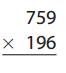
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 30$
Answer:

Question 18.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 31$
Answer:

Error Search Find each answer that is not correct. Write it correctly and explain the error.
Question 19.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 32$
Answer:

Question 20.
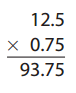
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 33$
Answer:

Question 21.
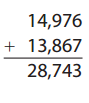
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 34$
Answer:

Question 22.
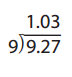
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 35$
Answer:

Question 23.
$Envision Math 5th Grade Answer Key Topic 20.2 Constructing Lines 36$
Answer:

Number Sense
Estimating and Reasoning Write whether each statement is true or false. Explain your reasoning.
Question 24.
The quotient of 1,546 ÷ 5 is less than 300.
Answer:

Question 25.
The product of 9.32 and 4.7 is less than 36.
Answer:

Question 26.
The difference of 6,631 and 3,021 is greater than 2,000 and less than 4,000.
Answer:

Question 27.
The sum of 43.04 + 21.56 is 0.04 more than 64.56.
Answer:

Question 28.
When x = -9, the expression x + +5 equals -14.
Answer:

Question 29.
The expression (4$\frac{5}{6}$ + 3$\frac{1}{2}$ – × $\frac{3}{4}$) × 0 equals 0.
Answer:

Envision Math Grade 5 Answer Key Topic 20.2 Constructing Lines

Envision Math 5th Grade Textbook Answer Key Topic 20.2 Constructing Lines

Leave a Reply Cancel reply