Envision Math Grade 6 Answer Key Topic 1.3 Exponents and Place Value

Envision Math 6th Grade Textbook Answer Key Topic 1.3 Exponents and Place Value

Exponents and Place Value

How can you write a number
using exponents?
Answer:
Each place in a place-value chart has a value that is 10 times as great as the place to its right. Use this pattern to write 1,000,000 as repeated multiplication.

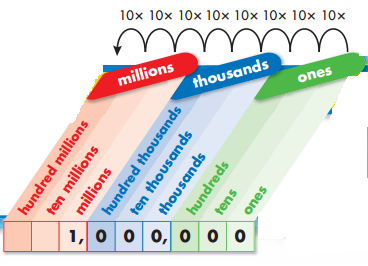
Another Example
How do you write the expanded form of a number using exponents?
Answer:
Standard form: 562,384
Expanded form: (5 × 100,000) + (6 × 10,000) + (2 × 1,000) + (3 × 100) + (8 × 10) + 4
Expanded form
using exponents: (5 × 10⁵) + (6 × 10⁴) + (2 × 10³) + (3 × 10²) + (8 × 10¹ ) + (4 × 10⁰)
Any number raised to the first power always equals that number. 10¹ = 10.

Explain It

Question 1.
How many times is 9 used as a factor in the exponent 98?
Answer:
8 times
Explanation:

Question 2.
Why does 3 × 100 = 3?
Answer:
10⁰ = 1, so 3 × 10⁰ = 3

Other Examples
Write each in exponential form.
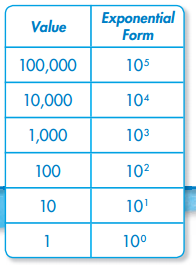
100,000 = 10⁵ 10 × 10 × 10 = 10³ 1 trillion = 10¹²
Evaluate numbers in exponential form.
5³ = 5 × 5 × 5 = 125 3⁴ = 3 × 3 × 3 × 3 = 81

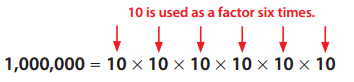
You can write the repeated multiplication of a number in exponential form.

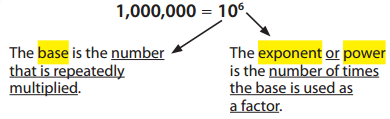
Each place in the place-value chart can be written using an exponent.

Guided Practice

Do you know HOW?
Question 1.
Write 10,000 as repeated multiplication.
Answer:
10,000 = 10 × 10 × 10 × 10
Explanation:

Question 2.
Write 7 × 7 × 7 × 7 in exponential form.
Answer:
7⁴
Explanation:

Question 3.
Write 37,169 in expanded form using exponents.
Answer:
(3 × 10⁴) + (7 × 10³) + (1 × 10²) + (6 × 10¹) + (9 × 10⁰)
Explanation:

Question 4.
Write 5³ in standard form.
Answer:
125
Explanation:

Do you UNDERSTAND?
Question 5.
In the example at the top, why was the number 10 used as the base to write 1,000,000 in exponential form?
Answer:
See margin.
Explanation:

Question 6.
Using the example, how many times would 10 be repeatedly multiplied to equal 100,000?
Answer:
5 times. 100,000 = 10 × 10 × 10 × 10 × 10 = 10
Explanation:

Question 7.
How many zeros are in 107 when it is written in standard form?
Answer:
7
Explanation:

Independent Practice

Leveled Practice What number is the base?
Question 8.
4⁹
Answer:
4
Explanation:

Question 9.
17⁹
Answer:
17
Explanation:

What number is the exponent?
Question 10.
31⁹
Answer:
9
Explanation:

Question 11.
2¹⁰⁰
Answer:
100
Explanation:

Write each in exponential form.
Question 12.
1,000
Answer:
10³
Explanation:

Question 13.
1,000,000,000
Answer:
10⁹
Explanation:

Question 14.
10 × 10 × 10 × 10 × 10
Answer:
10⁵
Explanation:

Write each number in expanded form using exponents.
Answer:
See margin
Explanation:

Question 15.
841
Answer:

Question 16.
5,832
Answer:

Question 17.
1,874,161
Answer:

Question 18.
22,600,000
Answer:

Evaluate 19 through 22.
Question 19.
6² = ☐
Answer:
36
Explanation:

Question 20.
10⁴ = ☐
Answer:
10,000
Explanation:

Question 21.
4³ = ☐
Answer:
64
Explanation:

Question 22.
2⁷ = ☐
Answer:
128
Explanation:

Problem Solving

Question 23.
The population of one U.S. state is approximately 33,871,648. What is this number in expanded form using exponents?
Answer:
See margin
Explanation:

Question 24.
Reasoning What number raised to both the first power and the second power equals 1?
Answer:
1; 1¹ = 1 and 1² = 1
Explanation:

Question 25.
Writing to Explain Explain how to compare 24 and 42.
Answer:
2⁴ = 2 × 2 × 2 × 2 = 16; 4² = 4 × 4 = 16; So 2⁴ = 4².
Explanation:

Question 26.
In Exercise 23, what is the place of the digit 7?
A. hundreds
B. thousands
C. ten thousands
D. millions
Answer:
C. ten thousands
Explanation:

Question 27.
Writing to Explain Kalesha was asked to write 80,808 in expanded form using exponents. Her response was (8 × 10²) + (8 × 10¹) + (8 × 10⁰). Explain where she made mistakes and write the correct response.
Answer:
See margin
Explanation:

Question 28.
Think About the Process You invest $1 in a mutual fund. Every 8 years, your money doubles. If you don’t add more money, which expression shows how much your investment is worth after 48 years?
A. 1 48
B. 1 × 2 × 2 × 2 × 2 × 2
C. 1 + 2 + 2 + 2 + 2 + 2 + 2
D. 1 × 2 × 2 × 2 × 2 × 2 × 2
Answer:
Explanation:
D. 1 × 2 × 2 × 2 × 2 × 2 × 2

Question 29.
Number Sense Using the map, write the population of the United States in expanded form using exponents.

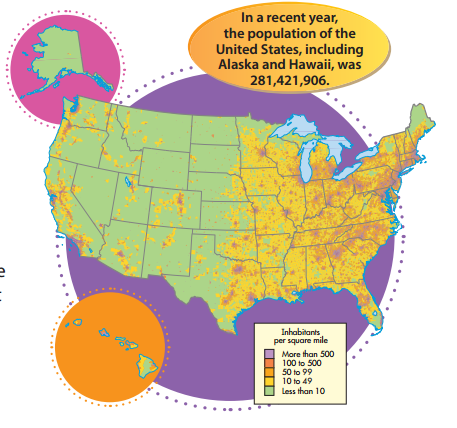
Answer:
See margin
Explanation:

Question 30.
In 1900, there were 76,803,887 people in the United States. How many more people were there in the United States in a recent year than in 1900?
Answer:
See margin
Explanation:

Algebra Connections

Solution Pairs
An equation is a mathematical sentence that uses an equals sign to show that two expressions are equal. Any values that make an equation true are solutions to the equation.

An inequality is a mathematical sentence that contains <, >, ≤, or ≥. Any value that makes the inequality true is a solution. You can graph the solutions of an inequality on a number line.

Example: Find two values for each variable that make the equation,
y = x + 3, true.
If x = 1, then y = 1 + 3 = 4 is true.
If x = 5, then y = 5 + 3 = 8 is true.
(1, 4) and (5, 8) are solution pairs.

Example: Graph three values that make the inequality, x > 3, true.
x = 3.1, x = 4, x = 5
Draw a number line. Plot three points that are greater than 3

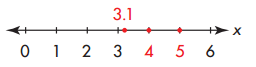
For 1 through 4, copy the table and find two values for each variable that make the equation true.
Question 1.
y = 4 + x
Answer:

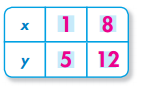
Explanation:

Question 2.
b = a – 2
Answer:

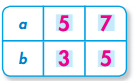
Explanation:

Question 3.
t = 3w
Answer:

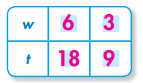
Explanation:

Question 4.
y = x ÷ 2
Answer:

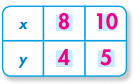
Explanation:

Question 5.
Copy the number line and graph 3 values that make the inequality, d ≥ 9, true.

Answer:
Any 3 points right of 9; or 9
Explanation:

Question 6.
Copy the number line and graph 3 values that make the inequality,\(\frac{x}{3}\) < 4, true.

Answer:
Any 3 points to left of 12
Explanation: