Envision Math Grade 6 Answer Key Topic 2 Reteaching

Envision Math 6th Grade Textbook Answer Key Topic 2 Reteaching

Reteaching

Set A, pages 28-29

Variables stand for unknown values.
The number sentence 24 + n means “the sum of 24 and a number.” The unknown number is a variable that is expressed by a letter, n.
Answer Terms
Addition → Sum
Subtraction → Difference
Multiplication → Product
Division → Quotient

Remember that you can use any letter as a variable that stands for an unknown value.

Write the phrases as algebraic expressions.
Question 1.
22 less forks than a number, f
Answer:

Question 2.
48 times a number of game markers, g
Answer:

Question 3.
a number of eggs, e, divided by 12
Answer:

Question 4.
3 times the number of milk cartons, m, used by the 6th grade class
Answer:

Set B, pages 30-31

The properties of operations help you evaluate expressions.

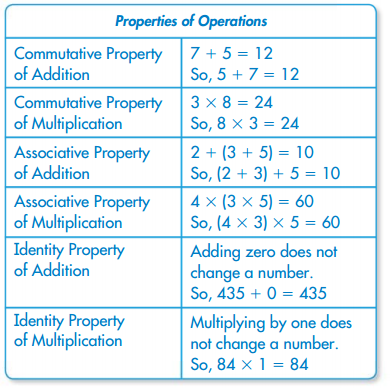
Evaluate the expression: 4 + 8 + 3 + 2
Following properties of operations:
4 + 8 + 3 + 2 = 4 + 3 + 8 + 2 = 7 + 10 = 17

Remember that when the properties of operations are not followed, numerical expressions are computed incorrectly.

Tell what properties are shown
Question 1.
3(4 × 32) = (3 × 4)32
Answer:

Question 2.
21 × 10 = 10 × 21
Answer:

Question 3.
9 + 8 + 4 = 8 + 4 + 9
Answer:

Question 4.
9 + 0 = 9
Answer:

Question 5.
6 × 8 = 8 × 6
Answer:

Question 6.
5 + 4 = 4 + 5
Answer:

Question 7.
6 × (4 × 3) = (6 × 4) × 3
Answer:

Question 8.
8 + (2 + 4) = (8 + 2) + 4
Answer:

Question 9.
9 + 6 = 6 + 9
Answer:

Question 10.
12 + 0 = 12
Answer:

Question 11.
425 × 1 = 425
Answer:

Question 12.
(8 × 5) × 4 = 4 × (5 × 8)
Answer:

Set C, pages 32–34

The order of operations helps you get the correct answer. The order of operations rules are:
Step 1: Compute inside parentheses.
Step 2: Evaluate terms with exponents.
Step 3: Multiply and divide from left to right.
Step 4: Add and subtract from left to right.

Evaluate 8 + 6 × 9 – 4 ÷ 2.
First, multiply and divide. 8 + 54 – 2
Then, add and subtract. 60

Remember that when the order of operations rules are followed, it helps you get the correct answer.

Use parentheses to make each sentence true.
Question 1.
9 + 8 – 2 × 7 + 1 = 1
Answer:

Question 2.
40 – 4 × 4² ÷ 2 = 8
Answer:

Question 3.
5 × 5 – 3 – 2 = 0
Answer:

Question 4.
8 + 12 ÷ 4 + 6 = 11
Answer:

Question 5.
9 + 8 ÷ 2 × 4 + 3² = 19
Answer:

Question 6.
6 × 2 – 1 + 5² = 31
Answer:

Question 7.
8 × 3 + 8 – 2² = 84
Answer:

Question 8.
50 – 3 × 6 + 2 + 4² = 42
Answer:

Set D, pages 36-37

Use the Distributive Property to evaluate mentally.
8(42)
Break the numbers apart to find numbers that
are easier to multiply mentally.
8(40 + 2)
Apply the Distributive Property.
8(40) + 8(2)
Multiply the separate sections. Add the products.
320 + 16 = 336

Remember that the Distributive Property says that multiplying a sum by a number is the same as multiplying each addend by the number and adding the products.

Use the Distributive Property to evaluate mentally.
Question 1.
5(41) + 5(9)
Answer:

Question 2.
3(45)
Answer:

Question 3.
4(23)
Answer:

Question 4.
9(32) + 9(8)
Answer:

Question 5.
3(27)
Answer:

Question 6.
6(7) + 6(23)
Answer:

Set E, pages 38-40

Find 4 × 18 × 25 using compatible numbers to compute mentally.
Look for compatible 4 × 18 × 25
numbers that are easy
to compute. 4 × 25 × 18
Then, do the remaining calculation. 100 × 18 = 1,800
So, 4 × 18 × 25 = 1,800.

Remember to find compatible numbers to make your mental math easier.

Compute mentally.
Question 1.
15 + 67 + 25
Answer:
107
Explanation:

Question 2.
463 – 333
Answer:
130
Explanation:

Question 3.
6 × 23 × 5
Answer:
690
Explanation:

Question 4.
250 × 6 × 4
Answer:
6,000
Explanation:

Question 5.
921 + 529
Answer:
1,450
Explanation:

Question 6.
297 – 100
Answer:
197
Explanation:

Question 7.
2 × 8 × 5
Answer:
80
Explanation:

Question 8.
20 × 16 × 5
Answer:
1,600
Explanation:

Set F, pages 42-43

Evaluate this expression for x = 2 and y = 3.
Question 1.
7x – 3y
Answer:
7(2) – 3(3) ← Use substitution.
14 – 9 = 5 ← Compute.

Question 2.
4x + 2y
Answer:
4(2) + 2(3) ← Use substitution.
8 + 6 = 14 ← Compute.

Question 3.
9x ÷ 3y
Answer:
9(2) ÷ 3(3) ← Use substitution.
18 ÷ 9 = 2 ← Compute.

Remember that using substitution means to replace the variables with the chosen values.

Evaluate each expression for x = 4 and y = 6.
Question 1.
12x – 7y
Answer:
6
Explanation:

Question 2.
3x + 18
Answer:
30
Explanation:

Question 3.
11 x + 4
Answer:
48
Explanation:

Question 4.
8x + 2y
Answer:
44
Explanation:

Question 5.
6x ÷ 2y
Answer:
2
Explanation:

Question 6.
8x – 5y
Answer:
2
Explanation:

Question 7.
7x – 4y
Answer:
4
Explanation:

Question 8.
4y – 9
Answer:
15
Explanation:

Question 9.
22y – 6
Answer:
126
Explanation:

Question 10.
9x – 3y
Answer:
18
Explanation:

Question 11.
4x ÷ (y – 2)
Answer:
4
Explanation:

Question 12.
10y – 8x
Answer:
28
Explanation:

Set G, pages 44–45

You can write an algebraic expression that explains an input/output relationship. If x is 4, how can you express 9?

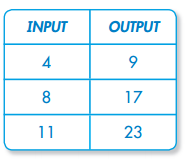
Try: 2x + 1 = 9
See if that works for the other input values.
2 × 8 + 1 = 17
2 × 11 + 1 = 23
Yes, it works!

Remember that input/ output tables can help you see patterns in expressions.

Use this input/ output table for 1 and 2.

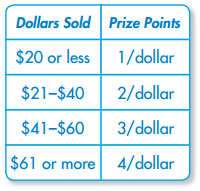
Question 1.
Students earn prize points for selling fundraising items. Write an algebraic expression that explains the relationship between input and output values for a student who sells between $41 and $60.
Answer:
3x
Explanation:

Question 2.
How many prize points would a student earn for selling $115 worth of items?
Answer:
4 × 115 = 460
Explanation:

Set H, pages 46-48

Making a table to organize your data helps to identify patterns and quickly find solutions. When making a table, include labels for the variable and the expression. Enter the values of x you want to find. Then solve the expression for each value.
Ginny is paid $12 a week for doing chores. She puts the money in her savings account. If she started out with $112, find out how much money she has in her account after x weeks.
Step 1: Identify the expression.
$112 + $12x
Step 2: Make a table.

Remember to choose labels based on the information to be found.

Write an equation for each problem. Then make a table to solve it.
Question 1.
Anna walks her dog 2 miles a day, 5 days a week. Find out how far Anna and her dog walked after x weeks.
Answer:
(2 × 5)x
Explanation:

Question 2.
Todd earns $500 a week, plus $50 every time he sells a computer. Find out how much money Todd earns per week when he sells x computers.
Answer:
500 + 50x
Explanation: