Go through the enVision Math Common Core Grade 5 Answer Key Topic 5 Use Models and Strategies to Divide Whole Numbers regularly and improve your accuracy in solving questions.
enVision Math Common Core 5th Grade Answers Key Topic 5 Use Models and Strategies to Divide Whole Numbers

Envision STEM Project: Average Temperature
Does Research Use a weather site from the Internet or another source of daily weather reports to find the average daily temperature for your city or town for every day of one month? The average daily temperature is the average temperature for a whole 24-hour period.
Journal: Write a Report that Includes what you found about daily temperatures. Also in your report:
• Find the average daily high temperature for the month. Which day had the greatest high temperature?
• Find the average daily low temperature for the month. Which day had the least low temperature?
• Makeup and solve division problems based on your data.
Review What You Know
VOC
• dividend
• quotient
• divisor
• remainder
Choose the best term from the box. Write it in the blank.
Question 1.
In the equation 80 ÷ 10 = 8, the number 80 is the ___.
Answer:
80 is called dividend
Question 2.
The number used to divide another number is the ___.
Answer:
The number used to divide another number is the Divisor
Question 3.
The result of dividing two numbers is the ___.
Answer:
The result of dividing two numbers is the quotient.
Multiplication and Division
Multiply or divide.
Question 4.
630 ÷ 9
Answer:
70
Question 5.
480 ÷ 6
Answer:
80
Question 6.
755 ÷ 5
Answer:
151
Question 7.
657 ÷ 9
Answer:
73
Question 8.
57 × 13
Answer:
741
Question 9.
71 × 109
Answer:
7739
Question 10.
For the state fair next month, 132 people volunteered to plan the fair’s activities. The volunteers formed 12 equal groups. How many volunteers were in each group?
Answer:
Number of volunteers = 132
Number of groups formed = 12
Now, the number of volunteers in each group =
132/12
= 11
Therefore, the number of volunteers in each group = 11
Question 11.
A town is holding a competition for various athletic games. Each community has 14 players. 112 communities are competing in the games. How many players are competing?
A. 1,676
B. 1,568
C. 126
D. 98
Answer:
1568
Estimate
Question 12.
A county has a goal to build 12,000 bus stop shelters in 48 months. If the county builds 215 bus shelters each month, will it reach its goal? Explain one way to estimate the answer.
Answer:
No
Explanation:
Because, if 215 bus shelters were built each month, in 48 months only 10320 bus shelters were built. 1680 bus shelters will remain.
215×48 = 10320.
12000-10320 = 1680.
Pick a Project
PROJECT 5A
How much does a field trip cost?
Project: Plan an Educational Field Trip

PROJECT 5B
How does an assembly line work?
Project: Design an Assembly Line for Toy Vehicles

PROJECT 5C
How do marathon runners get enough water?
Project: Position Water Stations

3-ACT MATH PREVIEW
Math Modeling
Flapjack Stack
Before watching the video, think:
Pancakes have been around for thousands of years and are popular all over the world. Some pancakes are made from potatoes and served with applesauce and sour cream. Other pancakes are sweet and served with blueberries and maple syrup.
Maybe I should plant a maple tree.

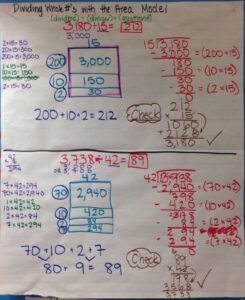
Lesson 5.1 Use Patterns and Mental Math to Divide
Solve & Share
A bakery sells muffins to local grocery stores in boxes that hold 20 muffins each. How many boxes are used if 60 muffins are sold? 600 muffins? 6,000 muffins? Solve this problem any way you choose.
Find the answer for 60 muffins. Then you can look for relationships to help find the answers for 600 and 6,000 muffins. Show your work!

Look Back! How can you use multiplication to help you divide 6,000 by 202?
Visual Learning Bridge
Essential Question How Can Patterns Help You Question Divide Multiples of 10?
A.
A jet carries 18,000 passengers in 90 trips. The plane is full for each trip. How many passengers does the plane hold?
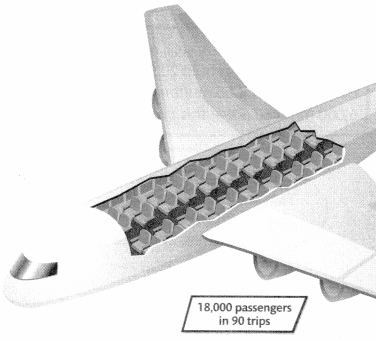
Find 18,000 ÷ 90, the number of passengers on each trip.

B.
Think of a basic fact to help you. 18 ÷ 9 = 2
Think about patterns in place value and multiples of 10:
180 ÷ 90 = 18 tens ÷ 9 tens = 2
1,800 ÷ 90 = 180 tens ÷ 9 tens = 20
18,000 ÷ 90 = 1,800 tens ÷ 9 tens = 200
So, the jet can hold 200 passengers.
C.
Or, use multiplication.
90 × 2 = 180
90 × 20 = 1,800
90 × 200 = 18,000
So 18,000 = 90 = 200
The jet can hold 200 passengers.
Think of multiplication to help you divide.

Convince Me! Look for Relationships If the jet above carried 10,000 people in 50 trips, how many people did it carry each trip? The jet carried the same number of people each trip.
What basic fact helped you find the answer?
Guided Practice
Do You Understand?
Question 1.
Why is 210 ÷ 30 the same as 21 tens ÷ 3 tens?
Answer:
Because 21 tens are 210
3 tens are 30
so, 210 ÷ 30 is the same as 21 tens ÷ 3 tens.

Question 2.
A jet carried 12,000 people in 40 trips. If the jet was full each trip, how many people did it carry for each trip?
Use a basic fact to help you.

Do You Know How?
Answer:
Given,
The jet carried 12,000 people in 40 trips.
12000 ÷ 40 = 300
Therefore, 300 people carried in each trip.
In 3-9, find each quotient. Use mental math.
Question 3.
210 ÷ 30 = 21 tens ÷ 3 tens = ____
Answer:
210 ÷ 30 = 21 tens ÷ 3 tens =
21 ÷ 3 = 7
Question 4.
480 ÷ 60 = 48 tens ÷ 6 tens = ___
Answer:
480 ÷ 60 = 48 tens ÷ 6 tens =
48 ÷ 6 = 8.
Question 5.
15,000 ÷ 30 = 1,500 tens ÷ 3 tens = ___
Answer:
15,000 ÷ 30 = 1,500 tens ÷ 3 tens =
1500 ÷ 3 = 500.
Question 6.
___ = 8,100 ÷ 90
Answer:
8,100 ÷ 90 =
810 ÷ 9 = 90.
Question 7.
2,800 ÷ 70 = ___
Answer:
2,800 ÷ 70 = 40
Question 8.
30,000 ÷ 50 = ___
Answer:
30,000 ÷ 50 =
3000 ÷ 5 = 600.
Question 9.
__= 1,800 ÷ 60
Answer:
1,800 ÷ 60 =
180 ÷ 6 = 30.
Independent Practice
Leveled Practice In 10-25, use mental math to find the missing numbers.
Question 10.
560 ÷ 70 = 56 tens ÷ 7 tens = ___
Answer:
560 ÷ 70 = 56 tens ÷ 7 tens =
56 ÷ 7 =
8.
Question 11.
360 ÷ 60 = 36 tens ÷ 6 tens = ___
Answer:
360 ÷ 60 = 36 tens ÷ 6 tens =
36 ÷ 6
= 6.
Question 12.
6,000 ÷ 50 = 600 tens ÷ 5 tens = ___
Answer:
6,000 ÷ 50 = 600 tens ÷ 5 tens =
600 ÷ 5
= 120.
Question 13.
24,000 ÷ 60 = 2,400 tens ÷ 6 tens = ___
Answer:
24,000 ÷ 60 = 2,400 tens ÷ 6 tens =
2400 ÷ 6 =
400.
Question 14.
___= 2,000 ÷ 20
Answer:
2,000 ÷ 20 =
200 ÷ 2 =
100.
Question 15.
6,300 ÷ 90 = ____
Answer:
630 ÷ 9 =
70.
Question 16.
___ ÷ 10 = 24
Answer:
___ ÷ 10 = 24
Let the number be x
x ÷ 10 = 24
x= 10×24 = 240
Therefore, number is 240.
Question 17.
21,000 ÷ ___ = 700
Answer:
21,000 ÷ ___ = 700
Let the number be x
21000 ÷ x = 700
x = 21000 ÷ 700
x= 30
Therefore, number is 30.
Question 18.
2,500 ÷ 50 = ___
Answer:
2,500 ÷ 50 =
250 ÷ 5 = 50.

Question 19.
72,000 ÷ ____ = 800
Answer:
72,000 ÷ ____ = 800
Let the number be x
72000 ÷ x = 800
x = 72000 ÷ 800
x = 90
Therefore, number is 90.
Question 20.
56,000 ÷ ___ = 800
Answer:
56,000 ÷ ___ = 800
Let the number be x
56,000 ÷ x = 800
x = 56,000 ÷ 800
x = 560 ÷ 8 = 70
Therefore, number is 70.
Question 21.
___ ÷ 10 = 100
Answer:
___ ÷ 10 = 100
Let the number be x
x ÷ 10 = 100
x = 10 x 100
x = 1000
Therefore, number is 1000.
Question 22.
45,000 ÷ 90 = ____
Answer:
45,000 ÷ 90 = ____
4500 ÷ 9 = 500.
Question 23.
___ = 42,000 ÷ 70
Answer:
___ = 42,000 ÷ 70
4200 ÷ 7 = 600.
Question 24.
64,000 ÷ ___ = 800
Answer:
64,000 ÷ ___ = 800
Let the number be x
64,000 ÷ x = 800
x = 64000 ÷ 800
x = 640 ÷ 8 = 80
Therefore, number is 80.
Question 25.
32,000 ÷ ___ = 400
Answer:
32,000 ÷ ___ = 400
Let the number be x
32,000 ÷ x = 400
x = 32000 ÷ 400
x = 320 ÷ 4 = 80
Therefore, the number is 80.
Problem Solving
Question 26.
The table shows the number of passengers who flew on airplane flights in or out of one airport. Each flight had the same number of passengers. How many passengers were on each flight?

Answer:
Given,
Total passengers = 27000
Number of flights = 90
Let the number of passengers were on each flight be x
Then,
x = 27000 ÷ 90
x = 2700 ÷ 9
x = 300
Therefore, the number of passengers were on each flight are 300.
Question 27.
Algebra A truck delivers 478 dozen eggs to stores in one day. Write and solve an equation to find n, the number of eggs the truck delivers in one day.
Answer:
1 dozen = 12 eggs
Number of dozens = 478
Equation = 478 x 12
n = 478 x 12
n = 5736 eggs
Therefore, the truck driver delivers 5736 eggs in one day.
Question 28.
Paula wants to divide 480 tomatoes equally among 80 baskets. How many tomatoes will Paula put in each basket?
Answer:
Number of Tomatoes = 480
Number of baskets = 80
Now,
= 480/80
= 6
Therefore, paul keeps 6 tomatoes in each basket.
Question 29.
Be Precise Ernesto measured the width of each of the three coins shown below.

What is the difference in width between the widest coin and the least wide coin?
Answer:
The width of the widest coin = 0.84 inch
The width of the least wide coin = 0.7 inch
Difference between them
= 0.84 – 0.7
= 0.14 inch
Therefore, the difference in width between the widest coin and the least wide coin = 0.14 inches.
Question 30.
Higher-Order Thinking A baker uses 30 grams of sea salt for each batch of bread. Sea salt comes in an 18-kilogram package or an 800-gram package. Which size package should the baker buy so that no sea salt is left after all of the batches are made? Explain.
1 kilogram equals 1,000 grams

Answer:
Salt for one batch of bread = 30 grams
For 800 grams package,
Now,
= 800/30
= 26 batches.
For 18 kg salt,
1 kg = 1000 grams
18 kg = 18 x 1000 = 18000
Now, 18000/30
= 600 batches.
For 18 kg divided by 30 then, 600 batches no salt will be left.
But in, 800 grams pack 26 batches are left
Therefore, The baker should use 18 kg so that no salt will be left.
Assessment Practice
Question 31.
Which is 2,400 divided by 80?
A. 3
B. 4
C. 30
D. 40
Answer:
2400 ÷ 80
240 ÷ 8 = 30
Therefore, C is the correct option.
Question 32.
Which expression has a quotient of 70?
A. 420 ÷ 60
B. 4,200 ÷ 6
C. 4,200 ÷ 60
D. 4,200 ÷ 600
Answer:
4,200 ÷ 60 = 420 ÷ 6 = 70
Therefore, C is correct option.
Lesson 5.2 Estimate Quotients with 2-Digit Divisors
Solve & Share
Kyle’s school needs to buy posters for a fundraiser. The school has a budget of $147. Each poster costs $13. About how many posters can his school buy? Solve this problem any way you choose.
You can find compatible numbers to estimate quotients. Show your work!

Look Back! Make Sense and Persevere What numbers are close to 147 and 13 that would be easy to divide using mental math?
Visual Learning Bridge.
Essential Question
How Can You Use Compatible Numbers to Estimate Quotients?
A.
Ella earned $159 by selling bracelets. Each bracelet was the same price. About how much did each bracelet cost?

You can use division to find the price.

You know the total amount earned and the number of bracelets.
B.
The question asks, “About how much?” So, an estimate is enough.
Use compatible numbers to estimate 159 ÷ 75.
Think: 159 is close to 160. Is there a number close to 75 that divides 160 evenly? Try 80.
160 ÷ 80 = 2
So, 160 and 80 are compatible numbers.
16 can be divided evenly by 8.

C.
Since 160 ÷ 80 = 2, 159 ÷ 75 is about 2.
Ella charged about $2 for each bracelet.
Use multiplication to check for reasonableness:
2 × 80 = 160.
Convince Me! Make Sense and Persevere Suppose Ella earned $230 selling the 75 bracelets. Estimate the price of each bracelet. What compatible numbers did you use?
Guided Practice
Do You Understand?
Question 1.
Ella has 425 more bracelets to sell. She wants to store these in bags that hold 20 bracelets each. She estimates she will need about 25 bags. Do you agree? Why or why not?
Answer:
Given,
Number of bracelets = 425
Number of bracelets in each = 20
Therefore, the Number of bags = 425 ÷ 20 = 21.25 which is approximately equal to 22.
Hence I agree with Ella because the number of bags is approximately equal to 25.
Do You Know How?
In 2-7, estimate using compatible numbers.
Question 2.
287 ÷ 42
Answer:
287 is approximately equal to 280
42 is approximately equal to 40
280 ÷ 40 = 7
Therefore, the estimation of 287 ÷ 42 is 7.
Question 3.
320 ÷ 11
Answer:
11 approximately equals 10
320 ÷ 10 = 32
Therefore, the estimation of 320 ÷ 11 is 32
Question 4.
208 ÷ 72
Answer:
208 approximately equals 210
72 approximately equals 70
210 ÷ 70 = 3
Therefore, the estimation of 208 ÷ 72 is 3
Question 5.
554 ÷ 62
Answer:
554 approximately equals 540
62 approximately equals 60
540 ÷ 60 = 9
Therefore, the estimation of 554 ÷ 62 is 9.
Question 6.
815 ÷ 23
Answer:
815 approximately equals 820
22 approximately eq820uals to 20
820 ÷ 20 = 41
Therefore, the estimation of 815 ÷ 23 is 41
Question 7.
2,491 ÷ 48
Answer:
2491 approximately equals 2500
48 approximately equals 50
2500 ÷ 50 = 50
Therefore, the estimation of 2,491 ÷ 48 is 50.
Independent Practice
Leveled Practice In 8-10, fill in the blanks to find each estimate.
Question 8.

Answer:
80
and the estimate is 5
Question 9.
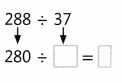
Answer:
40
and the estimate is 7
Question 10.
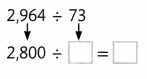
Answer:
70
and the estimate is 40
In 11-22, estimate using compatible numbers.
Question 11.
228 ÷ 19
Answer:
220 approximately equals 228
20 approximately equals 19
220 ÷ 20 = 11
Therefore, the estimation of 228 ÷ 19 is 11.
Question 12.
1,784 ÷ 64
Answer:
1800 approximately equals 1784
60 approximately equals 64
1800 ÷ 60 = 30
Therefore, the estimation of 1784 ÷ 64 is 30.
Question 13.
7,260 ÷ 83
Answer:
7200 approximately equals 7260
80 approximately equals 83
7200 ÷ 80 = 90
Therefore, the estimation of 7260 ÷ 83 is 90.
Question 14.
2,280 ÷ 12
Answer:
2400 approximately equals 2280
2400 ÷ 12 = 200
Therefore, the estimation of 2280 ÷ 12 is 20.
Question 15.
485 ÷ 92
Answer:
450 approximately equals 485
90 approximately equals 92
450 ÷ 90 = 5
Therefore, the estimation of 485 ÷ 92 is 5.
Question 16.
540 ÷ 61
Answer:
60 approximately equals 61
540 ÷ 60 = 9
Therefore, the estimation of 540 ÷ 61 is 9.
Question 17.
1,710 ÷ 32
Answer:
1800 approximately equals 1710
30 approximately equals 32
1800 ÷ 30 = 60
Therefore, the estimation of 1710 ÷ 32 is 60.
Question 18.
2,740 ÷ 67
Answer:
2800 approximately equals 2740
70 approximately equals 67
2800 ÷ 70 = 40
Therefore, the estimation of 2740 ÷ 67 is 40.
Question 19.
4,322 ÷ 81
Answer:
4400 approximately equals 4322
80 approximately equals 81
4400 ÷ 80 = 55
Therefore, the estimation of 4322 ÷ 81 is 55.
Question 20.
5,700 ÷ 58
Answer:
60 approximately equals 58
5700 ÷ 60 = 95
Therefore, the estimation of 5700 ÷ 60 is 95.
Question 21.
7,810 ÷ 44
Answer:
7875 approximately equals 7810
45 approximately equals 44
7875 ÷ 45 = 175
Therefore, the estimation of 7810 ÷ 44 is 175.
Question 22.
6,395 ÷ 84
Answer:
6400 approximately equals 6395
80 approximately equals 84
6400 ÷ 80 = 80
Therefore, the estimation of 6395 ÷ 84 is 80.
Problem Solving
Question 23.
A model with Math The sign shows the price of baseball caps for different pack sizes. Coach Lewis will buy the medium-size pack of caps. About how much will each cap cost? Write an equation to model the problem.

Answer:
Given,
Number of medium size caps = 32
Total cost = $270
30 approximately equals 32
Cost of each cap = $270 ÷ 30 = $9.
The cost of each cap approximately equals $9.
Question 24.
There are 91 days until the craft sale. Autumn needs to make 817 rings before the sale. She wants to make about the same number of rings each day. About how many rings should she make each day? Explain how Autumn can use compatible numbers to estimate.
Answer:
Number of days left = 91 which approximately equals 90
Number of rings to be made = 817 which approximately equals 810
Therefore, rings should she make each day are 810 ÷ 90 = 9
Approximately, she should make 9 rings each day.
Question 25.
Higher-Order Thinking A company purchased 3,128 bottles of water. Each department needs 55 bottles. Find compatible numbers to estimate the number of departments that can get the bottles they need. Explain.
Answer:
Given,
Number of bottles = 3128 which approximately equals 3080
Number of bottles each department need = 55
The number of departments that can get the bottles they need is 3080 ÷ 55 = 56
Therefore, the number of departments that can get the bottles they need is approximately equaled to 56.
Question 26.
Rita had $20. Then, she saved $5.85 each week for 8 weeks. How much money does she have now? Use the bar diagram to solve the problem. Show your work.
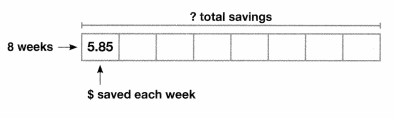
Answer:

Given, The amount Rita have = $20
The amount she saved = $5.85
Total number of weeks = 8
Now,
$5.85 x 8
= 44.64
Now, $44.64 + $20
= $66.80.
Assessment Practice
Question 27.
Lea bought 225 flowers and 12 vases. She put about the same number of flowers in each vase. Which is the best estimate for the number of flowers in each vase?
A. 40 flowers
B. 30 flowers
C. 20 flowers
D. 10 flowers
Answer:
C. 20 flowers
Question 28.
A school has 617 students. Each class has between 28 and 32 students. Which is the best estimate of the number of classes in the school?
A. 14 classes
B. 20 classes
C. 30 classes
D. 60 classes
Answer:
B. 20 classes
Lesson 5.3 Use Models and Properties to Divide with 2-Digit Divisors
Solve & Share
A parking lot has 270 parking spaces. Each row has 18 parking spaces. How many rows are in this parking lot? Solve this problem any way you choose.
You can use appropriate tools, such as grid paper, to solve the problem. Show your work!

Look Back! How can you use estimation to check that your answer to the problem above is reasonable?
Answer:
Total number of parking spaces = 270
Number of parking spaces in each row = 18
Therefore, the total number of parking rows = 270 ÷ 18 =15.
Visual Learning Bridge
Essential Question How Can You Use Area Models and Properties to Find Quotients?
A.
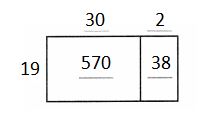
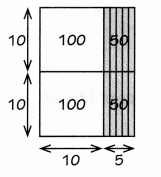
Emily has a rectangular garden with an area of 360 square feet. The length of her garden measures 20 feet. How many feet wide is her garden?
Think 20 × w = 360 or 360 ÷ 20 = w.

You can have w stand for the unknown side. Use place value and the Distributive Property to find the unknown side length.

B.
20 × 10 = 200 and 20 × 20 = 400, so, w is between 10 and 20. That is, W= 10 + ?
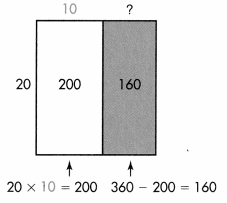
20 × ? = 160
C.
20 × 8 = 160
So w = 10 + 8 = 18.
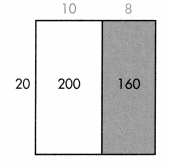
Multiply to check:
20 × 18 = 20 (10 + 8) = 200 + 160 = 360
So 360 ÷ 20 = 18.
The garden is 18 feet wide.
Convince Me! Make Sense and Persevere Use the diagram, place value, and the Distributive Property to find the quotient
408 ÷ 12. Hint: Find the value of x and solve.
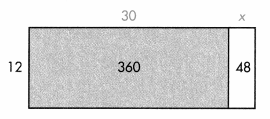
Answer:
12(30 + x) = 360+48
12(30 + x) = 408
30 + x = 408 ÷ 12
30 + x = 34
x = 34 – 30 = 4
Therefore value of x is 4.
Guided Practice
Do You Understand?
Question 1.
Write the missing numbers to find 154 ÷ 11.
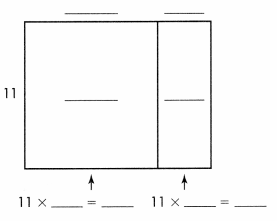
154 = 11 × __ + 11 × ___
= 11 × (___ + ___)
= 11 × ___
So, 154 ÷ 11 = ___
Answer:
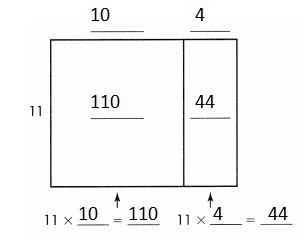
154 = 11 × 10 + 11 × 4
= 11 × (10 + 4)
= 11 × 14
So, 154 ÷ 11 = 14
Do You Know How?
Question 2.
Use the diagram to find 156 ÷ 12.
So, 156 ÷ 12 = ___
Answer:
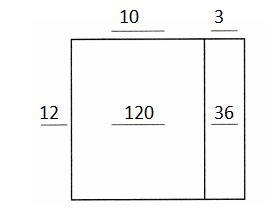
156 = 12 × 10 + 12 × 3
= 12 × (10 + 3)
= 12 × 13
So, 156 ÷ 12 = 13
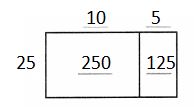
In 3 and 4, use grid paper or draw a picture to find each quotient.
Question 3.
682 ÷ 22
Answer:
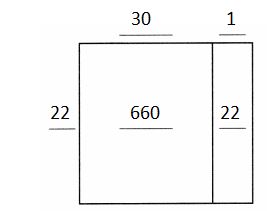
682 = 22 × 30 + 22 × 1
= 22 × (30 + 1)
= 22 × 31
So, 682 ÷ 22 = 31
Question 4.
143 ÷ 11
Answer:
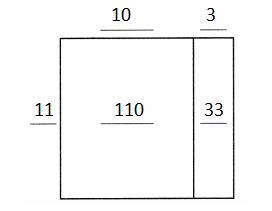
143 = 11 × 10 + 11 × 3
= 11 × (10 + 3)
= 11 × 13
So, 143 ÷ 11 = 13
Start by estimating how many tens will be in the quotient.

Independent Practice
Leveled Practice In 5-11, use grid paper or draw a picture to find each quotient.
Question 5.
Use the diagram to find 182 ÷ 13.
So, 182 ÷ 13 = ___

Answer:
Question 6.
342 ÷ 38
Answer:
Question 7.
720 ÷ 16
Answer:

Question 8.
608 ÷ 19
Answer:
Question 9.
752 ÷ 47
Answer:

Question 10.
375 ÷ 25
Answer:
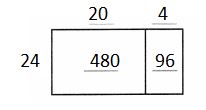
Question 11.
576 ÷ 24
Answer:
Problem Solving
Question 12.
Angelo is training for a long-distance bicycle ride. He travels 15 miles each hour. How many hours will it take him to ride 210 miles?
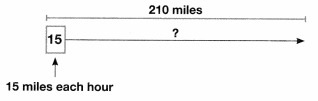
Answer:
Total Number of miles = 210
Number of miles each hour = 15
The number of hours it will take to ride 210 miles = 210 ÷ 15 = 14.
Question 13.
Higher-Order Thinking A rectangular doormat is 21 inches long and has an area of 714 square inches. Find its width. Will the doormat fit in an entryway that is 36 inches wide? Show your work.
Answer:
Given,
Total area = 714 square inches
Length = 21 inches
Then, length x width = area
21 x width = 714
width = 714 ÷ 21 = 34
Therefore, the Width of the doormat is 34 inches.
Yes, the doormat fits in an entryway that is 36 inches wide.
Question 14.
Use the map. How much longer is the distance from the library to the park to the train station than the distance from the library straight to the train station?
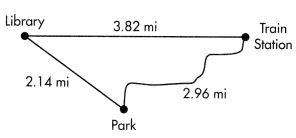
Answer:
Distance from the library to the park to the train station is 2.14 + 2.96 = 5.1 mi
Distance from the library straight to the train station is 3.82 mi
Difference = 5.1 – 3.82 = 1.28.
Question 15.
Algebra If you walk from the train station to the library, then to the park, and then back to the train station, how many miles would you walk in all? Write an equation to model your work.
Answer:
Distance from the library straight to the train station is 3.82 mi
Distance from the library to the park to the train station is 2.14 + 2.96 = 5.1 mi
Total distance = 3.82 + 5.1 = 8.92 mi
Question 16.
Make Sense and Persevere Explain how you can use the picture to show that 391 ÷ 23 = 17.
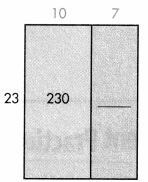
Answer:
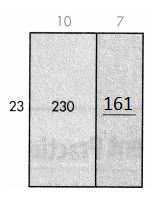
391 = 23 × 10 + 23 × 7
= 23 × (10 + 7)
= 23 × 17
So, 391 ÷ 23 = 17
Assessment Practice
Question 17.
There are 16 rows of chairs in the auditorium. Each row has the same number of chairs. There are 512 chairs in all. How many chairs are in each row?
A. 22 chairs
B. 30 chairs
C. 32 chairs
D. 33 chairs
Answer:
C. 32 chairs
Question 18.
A patio has an area of 286 square feet. If the length of the patio is 22 feet, what is the width?
A. 10 feet
B. 13 feet
C. 14 feet
D. 144 feet
Answer:
B. 13 feet
Lesson 5.4 Use Partial Quotients to Divide
Activity
Solve & Share
A hotel sets up tables for a conference for 156 people. If each table seats 12 people, how many tables will be needed? Solve this problem any way you choose.
You can use estimation to help solve this problem. Think about how many groups of 12 you can take away from 156. Show your work!

Look Back! Make Sense and Persevere How can you check that the answer to a division problem is correct?
Visual Learning Bridge
Essential Question How Can You Use Partial Quotients to Solve Division Problems?
A.
A theater has 375 seats arranged in rows with 15 seats in each row. How many rows are in this theater? Let r equal the number of rows. Think: 15 × r = 375 or 375 ÷ 15 = r.

An area model can help you find how many 15s are in 375.

B.
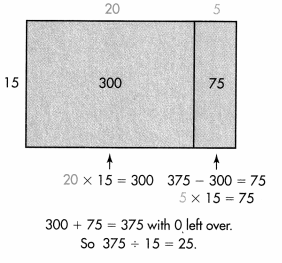
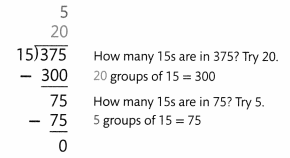
375 ÷ 15 = 25 because 15 × 25 = 375.
So, there are 25 rows and 0 additional seats in the theater.
Convince Me! Critique Reasoning Yimil’s solution to the problem above is shown on the right. Is his solution correct? Explain.

Guided Practice
Do You Understand?
Question 1.
Show one way of using partial quotients to find 233 ÷ 11.
Answer:
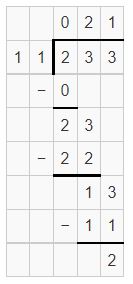
Partial quotients are 20,1
Question 2.
How can you use estimation to check that your answer to Problem 1 is correct?
Answer:
240 approximately equals 233
12 approximately equals 11
240 ÷ 12 = 20. It approximately equals 21.
Do You Know How?
In 3-6, use partial quotients to divide. Show your work.
Question 3.
![]()
Answer:
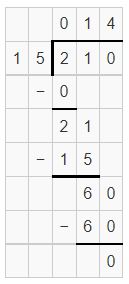
partial quotients are 10,4
Question 4.
![]()
Answer:

partial quotients are 20,2
Question 5.
![]()
Answer:
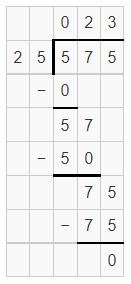
Question 6.
![]()
Answer:
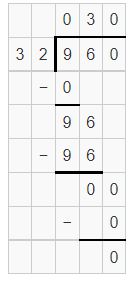
partial quotients are 30.
Independent Practice
Leveled Practice In 7-16, use partial quotients to divide. Show your work.
Question 7.

Answer:
Question 8.

Answer:
Question 9.
![]()
Answer:
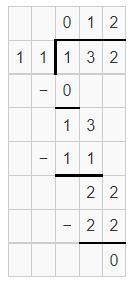
partial quotients are 10,2
Question 10.
![]()
Answer:

partial quotients are 40, and 5 leftover
Question 11.
![]()
Answer:

partial quotients are 10,9, and 0 leftover
Question 12.
![]()
Answer:
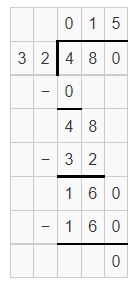
partial quotients are 10,5, and 0 leftover
Question 13.
![]()
Answer:
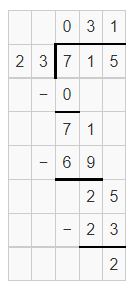
partial quotients are 30,1, and 2 leftover
Question 14.
![]()
Answer:
partial quotients are 20,2, and o left over
Question 15.
![]()
Answer:

partial quotients are 10,7, and 0 leftovers.
Question 16.
![]()
Answer:
partial quotients are 30,8, and 2 leftovers.
Problem Solving
Question 17.
A 969-acre wildlife preserve has 19 cheetahs. About how many acres does each cheetah have to itself, if each cheetah roams the same number of acres?
Answer:
Number of cheetahs = 19
Number of acres = 969
Number of acres does each cheetah have to itself = 969 ÷ 19 = 51
Question 18.
A factory produces 272 chairs in an 8-hour shift. If the factory produces the same number of chairs each hour, how many chairs does it produce in 30 minutes?
Answer:
Number of chairs = 272
Number of hours per shift = 8
Number of chairs in 1 hour = 272 ÷ 8 = 34
Therefore, the number of chairs it produces in 30 minutes = 34/ 2 = 17.
Question 19.
A cafeteria can seat 5 × 102 students. Each table has 2 × 101 seats. How many tables are in the cafeteria?
Answer:
Number of students in cafeteria = 500
Number of seats in a table = 20
Number of tables = 500 ÷ 20 = 25.
Question 20.
A model with Math Peter is driving 992 miles from Chicago to Dallas. His sister Anna is driving 1,068 miles from Phoenix to Dallas. Write and solve an equation to find how much farther Anna drives than Peter drives.
Answer:
Peter is driving 992 miles from Chicago to Dallas
His sister Anna is driving 1,068 miles from Phoenix to Dallas
Difference in Distance = 1068 – 992 = 78 miles.
Question 21.
Write a multiplication equation and a division equation that represent the model shown below.
Answer:
Question 22.
Higher-Order Thinking How can you use partial quotients to find 325 ÷ 13? Explain.
Answer:
Assessment Practice
Question 23.
Which expressions are equivalent to 35?
![]() 1,400 ÷ 4
1,400 ÷ 4
![]() 420 ÷ 12
420 ÷ 12
![]() 875 ÷ 25
875 ÷ 25
![]() 7,700 ÷ 22
7,700 ÷ 22
![]() 14,000 ÷ 40
14,000 ÷ 40
Answer:
420 ÷ 12 = 35
875 ÷ 25 = 35
Question 24.
Which expressions are equivalent to 22?
![]() 704 ÷ 32
704 ÷ 32
![]() 1,078 ÷ 49
1,078 ÷ 49
![]() 1,890 ÷ 30
1,890 ÷ 30
![]() 1,430 ÷ 65
1,430 ÷ 65
![]() 4,500 ÷ 50
4,500 ÷ 50
Answer:
704 ÷ 32
1,078 ÷ 49
1,430 ÷ 65
Lesson 5.5 Use Sharing to Divide: Two-Digit Divisors
Solve & Share
The Recycling Club has $294 to purchase one set of recycling bins for each of the 14 members. Each of the 14 sets of bins will be identical to the others and cost the same amount. What is the greatest amount they can spend on one set of bins? Use objects or draw pictures to help solve this problem. Explain how you found your answer.
Using appropriate tools like play money or place-value blocks can help you divide.

Look Back! Why can you use division to answer this question?
Visual Learning Bridge
Essential Question How Can You Record Division with a Two-Digit Divisor?
A.
Orchard workers have 258 grapefruit seedlings to plant in 12 equal rows. How many seedlings will be in each row?

Estimate: 258 ÷ 12 is close to 250 ÷ 10 = 25.
You can think about place-value and area models to solve the problem.

B.
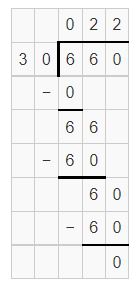
Regroup the blocks to fill the 12 rows.
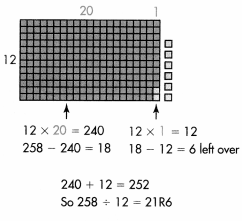
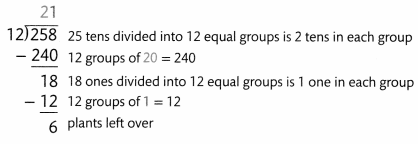
258 ÷ 12 = 21 R6 because 12 × 21 + 6 = 258.
There will be 21 seedlings in each row with 6 seedlings leftover.
Convince Me! Reasoning What does the remainder mean in the problem above?
Guided Practice
Do You Understand?
Question 1.
If the orchard has 200 seedlings and 12 are planted in each row, how many rows will be filled? Draw place-value blocks to show your answer.
Answer:
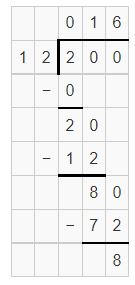

Question 2.
In Problem 1, what does the remainder represent?
Answer:
The remainder represents the remaining orchards after planting 12 in a row.
Do You Know How?
In 3 and 4, divide. Write the missing numbers.
Question 3.
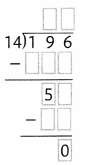
Answer:
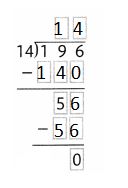
Question 4.
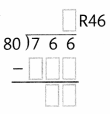
Answer:
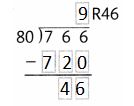
An estimate can help you decide if your answer is reasonable.

Independent Practice
Leveled Practice In 5-13, divide. Write the missing numbers.
Question 5.

Answer:

Question 6.

Answer:

Question 7.

Answer:
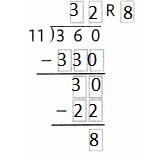
Question 8.
![]()
Answer:

Question 9.
![]()
Answer:

Question 10.
![]()
Answer:
Question 11.
![]()
Answer:
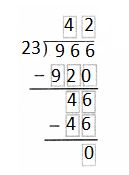
Question 12.
![]()
Answer:
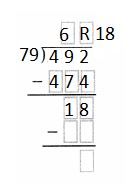
Question 13.
![]()
Answer:
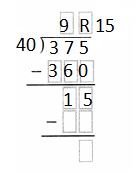
Problem Solving
Question 14.
Rita’s family is moving from Grand Junction to Dallas. The moving van averages 60 miles each hour. About how many hours does the van take to reach Dallas? Explain your work.

Answer:
Total miles = 980
Average speed = 60 miles each hour
Time it will take = 980 ÷ 60 = 16.33 hours
Question 15.
Due to construction delays on the trip from Little Rock to Chicago, a van driver averaged 48 miles each hour. About how long did that trip take?
Answer:
Total miles = 660
Number of miles each hour = 48
Time taken = 660 ÷ 48 = 13.75 hours
Question 16.
Higher-Order Thinking A scientist needs 72 milliliters of distilled water for each of 15 experiments. She has a bottle that contains 975 milliliters of distilled water. Is there enough water in the bottle for all 15 experiments? Explain.
Answer:
Total distilled water = 975 milliliters
Milliliters needed for experiments =72
Number of experiments can be done = 972 ÷ 72 = 13.5
Therefore, there is no enough water in the bottle for 15 experiments.
Question 17.
A model with Math The Port Lavaca fishing pier is 3,200 feet long. One person is fishing for every ten feet of length. Write and solve an equation to find how many people are fishing from the pier.
Answer:
Total length = 3200
One person fishing for every ten feet of length
Therefore, number of people = 3200 ÷ 10 = 320.
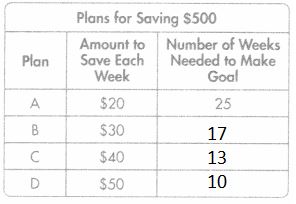
Question 18.
Todd made a table to show different plans he can use to save $500. Complete the table. Which plan can Todd use to save $500 in less than 16 weeks and have $20 extra? Explain how you found your answer.

Answer:
Assessment Practice
Question 19.
Find an expression that produces a quotient of 9 R15. Write the expression in the box.

Answer:
375 ÷ 40
Lesson 5.6 Use Sharing to Divide: Greater Dividends
Activity
Solve & Share
The city built a skate park that cost $3,240 and will be paid for over two years in equal monthly payments. How much is each monthly payment? Use objects or draw pictures to help solve this problem. Explain how you found your answer.
To make sense of the problem, you need to read carefully to find all the important information.

Look Back! Use Structure How did you use what you know about place value to find the answer to the problem?
Visual Learning Bridge
Essential Question
How Can You Record Division with a Two-Digit Divisor and a Four-Digit Dividend?
A.
Jake works at a flower shop. The shop just received a delivery of 1,830 roses. If the roses are distributed evenly among 15 coolers, how many roses should Jake put in each cooler?
You can use place-value and area models to solve the problem.


B.
There are not enough thousands to put one thousand in each group, so regroup the thousands into hundreds.
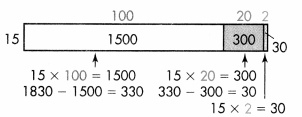
1,500 + 300 + 30 = 1,830
So 1,850 ÷ 15 = 122.

1,830 ÷ 15 = 122 because 15 × 122 = 1,830.
There should be 122 roses in each cooler with no roses left over.
Convince Me! Reasoning Why is 122 a reasonable answer for the problem?
Another Example
Divide 4,108 ÷ 85
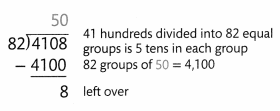
Think 41 hundred divided into 82 equal groups.

4,108 ÷ 82 = 50 R8 because 82 × 50 + 8 = 4,108.
Guided Practice
Do You Understand?
Question 1.
Use place-value blocks to model
3,710 ÷ 18.
Answer:
Do You Know How?
In 2-5, divide. Use place-value blocks to help.
Question 2.
4,632 ÷ 15
Answer:
Question 3.
3,332 ÷ 30
Answer:
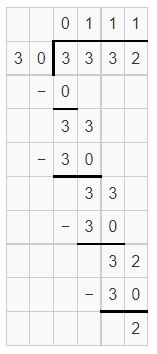
Question 4.
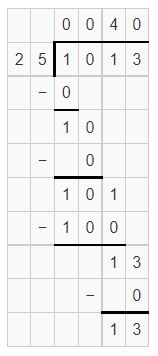
![]()
Answer:
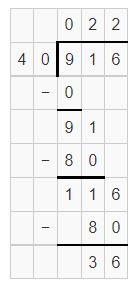
Question 5.
![]()
Answer:
Independent Practice
In 6, draw an area model for the division problem.
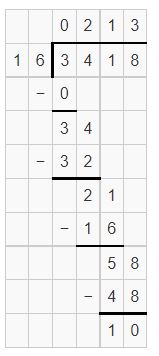
Question 6.
![]()
Answer:
In 7-12, divide. Use place-value blocks or area models to help.
Question 7.
7,905 ÷ 35
Answer:
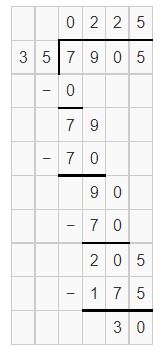
Question 8.
5,500 ÷ 90
Answer:
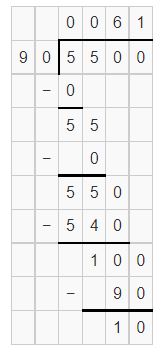
Question 9.
2,838 ÷ 11
Answer:

Question 10.
![]()
Answer:
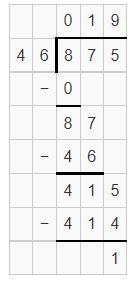
Question 11.
![]()
Answer:
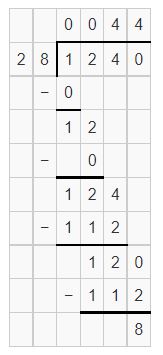
Question 12.
![]()
Answer:
Problem Solving
Question 13.
Number Sense The booster club picked 1,370 apples. They plan to sell bags of apples with 15 apples in each bag. How many bags can they make? Explain.
Answer:
Number of apples = 1370
Number of apples in each bag = 15
Number of bags= 1370 ÷ 15 =91.33 approximately equals to 91.
Question 14.
Mason teaches ice skating. He earns $24.50 per lesson. How much does he earn in 5 days if he gives 6 lessons per day?
Answer:
Money earned per lesson= $24.50
Number of lessons per day = 6
Total earned in a day = $24.50 x 6 = $147
In 5 days, she will earn = 147 x 5 = $735
Question 15.
Reasoning A delivery to the flower shop is recorded at the right. The shop makes centerpiece arrangements using 36 flowers that are all the same type. Will they be able to make at least 10 arrangements using each type of flower? At least 100 arrangements? Explain.

Answer:
Question 16.
Amelia and Ben have two different answers for 1,955 ÷ 85. Without dividing, how can you tell who might be correct? Amelia: 1,955 ÷ 85 = 23
Ben: 1,955 ÷ 85 = 203
Answer:
I can tell by estimating the values.
1955 approximately equals 2000
85 approximately equals 80
2000 ÷ 80 = 25 which is close to 23. so, amelia is correct
Question 17.
Higher-Order Thinking Estimate the quotient of 4,839 ÷ 15 to the nearest hundred. Explain how you found the estimate.
Answer:
4839 is close to 4800
Now, 4800 ÷15 = 320.
so, the estimation of the quotient of 4,839 ÷ 15 is close to 300.
Assessment Practice
Question 18.
Find 5,092 ÷ 38. How can you check the reasonableness of your answer?
Answer:
5,092 ÷ 38 = 134
I can check reasonableness by estimating the values
5000 close to 5092
40 is close to 38
5000 ÷ 40 = 125 which is close to 134.
Lesson 5.7 Choose a Strategy to Divide
Activity
Solve & Share
Choose a strategy to solve each problem. Explain your solutions.
Problem 1: Bob’s Citrus and Nursery sells cartons of citrus fruits. There are 24 oranges in each carton. They have 5,643 oranges to pack into cartons. How many cartons can they fill?
Problem 2: This year, 4,338 grapefruits have been harvested so far. Bob’s has 18 storage bins for grapefruits. If the grapefruits are distributed evenly among the 18 bins, how many grapefruits are in each bin?
The numbers and the situations in the problems can help you choose strategies. Show your work!

Look Back! Make Sense and Persevere How are your two strategies alike? How are they different?
Visual Learning Bridge
Essential Question
What Are Some Different Strategies I Can Use to Solve a Division Problem?
A.
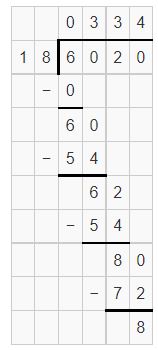
A company has three printers. The printer in Room 102 is for all of their 15 employees to use. If the available pages are distributed evenly among the employees, how many pages can each employee use?

Answer:
Number of pages available to print = 3720
Number of employees = 15
Number of pages can each employee use = 3720 ÷ 15 = 248
B.
You can first estimate.
3,720 ÷ 15 is between 3,000 ÷ 15 = 200 and 4,500 ÷ 15 = 300.
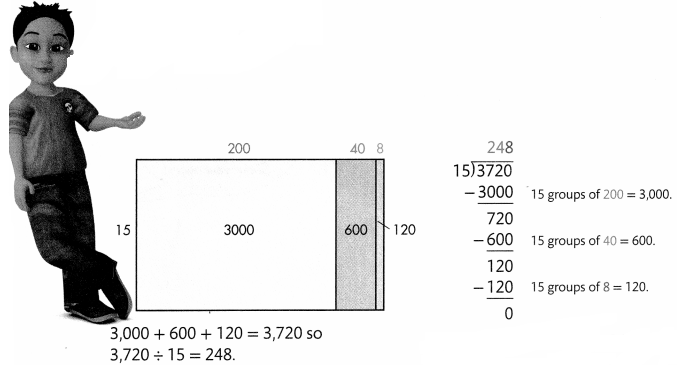
Each employee can print 248 pages.
Convince Me! Reasoning How can you check your answer?
Another Example
How many 32-page brochures can the 40 144 printers in Room 101 print?

The printer in Room 101 can print 144 brochures.
You need to find how many 32s are in 4,618. You can use division and show partial quotients. You can estimate 4,618 ÷ 32 using 4,500 ÷ 30 = 150.

Guided Practice
Do You Understand?
Question 1.
Can the remainder be greater than the divisor? Why or why not?
Answer:
No. the Remainder can not be greater than the divisor. If the remainder is greater than the divisor, the division is incomplete.
Do You Know How?
Question 2.
Estimate 452 ÷ 21.
Answer:
452 is close to 460
21 is close to 20
460 ÷ 20 = 23.
Question 3.
Divide.
![]()
Answer:
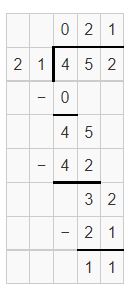
Yes, the answer is reasonable.
Remember to check that your answer is reasonable.

Independent Practice
In 4-11, estimate and then find the quotient. Use your estimate to check for reasonableness.
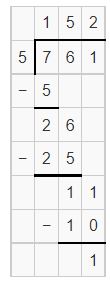
Question 4.
![]()
Answer:
Estimation is 400 ÷ 50 = 8
Yes, the estimation is reasonableness.
Question 5.
![]()
Answer:
Estimation is 640 ÷ 80 = 8
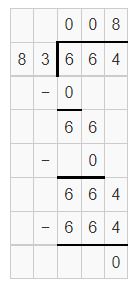
Yes, the estimation is reasonableness.
Question 6.
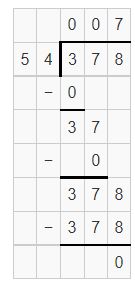
761 ÷ 5
Answer:
Estimation is 750 ÷ 5 = 150
Yes, the estimation is reasonableness.
Question 7.
510 ÷ 30
Answer:
Estimation is 510 ÷ 30 = 17
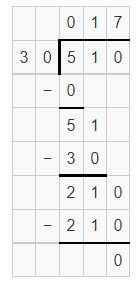
Yes, the estimation is reasonableness.
Question 8.
7,704 ÷ 24
Answer:
Estimation is 7,680 ÷ 24 = 320
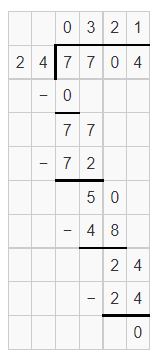
Yes, the estimation is reasonableness.
Question 9.
7,830 ÷ 33
Answer:
Estimation is 7821 ÷ 33 = 237
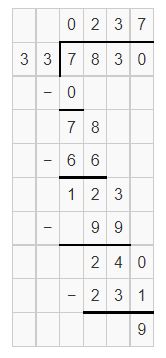
Yes, the estimation is reasonableness.
Question 10.
3,136 ÷ 64
Answer:
Estimation is 3,200 ÷ 64 = 50
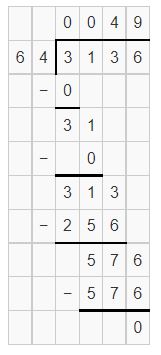
Yes, the estimation is reasonableness.
Question 11.
6,253 ÷ 71
Answer:
Estimation is 6,300 ÷ 70 = 90
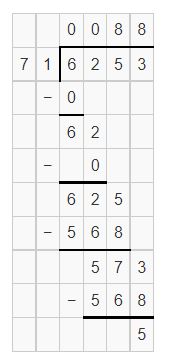
Yes, the estimation is reasonableness.
Problem Solving
For 12, use the table at right.
Question 12.
Make Sense and Persevere Bob’s sells tangelo gift cartons each December. Last year, they shipped a total of 3,300 tangelos. If each carton sells for $28, how much money did Bob’s earn from the tangelo gift cartons sold?

Answer:
Number of tangelos = 3300
Number of tangelos per carton = 12
Number of cartons = 3300 ÷ 12 = 275
Money earned = $28 x 275 = $7700.
Question 13.
Higher-Order Thinking A score is a group of 20 things. For example, a period of 20 years is called a score of years. The Statue of Liberty was dedicated in 1886. About how many scores of years ago was that?
Answer:
The score for every 20 years
The Statue of Liberty was dedicated in 1886.
1886 ÷ 20 = 94.3 approximately equals to 94.
Question 14.
At an automobile plant, each car is inspected by 34 different workers before it is shipped to a dealer. One day, workers performed 9,690 inspections. How many cars were shipped? Explain.
Answer:
workers performed 9,690 inspections
each car is inspected by 34 different workers
Therefore, number of cars were inspected = 9,690 ÷ 34 = 285
Assessment Practice
Question 15.
For which division problems is 46 the quotient? Write those division problems in the box.

Answer:

Lesson 5.8 Make Sense and Persevere
Problem Solving
Activity
Solve & Share
Write a word problem for the equation: 2,530 ÷ 23 = q
Solve your problem any way you choose.
Thinking Habits
Be a good thinker! These questions can help you.
• What information is provided?
• How are the quantities related to each other?
• What strategies do I know for solving this type of problem?
• What tools might help me?
• How can I check that my solution makes sense?
Look Back! Make Sense and Persevere Does your word problem ask you to find the equal number in each group, or the number of equal groups?
Visual Learning Bridge
Essential Question How Can You Make Sense of Problems and Persevere in Solving Them?
A.
For 3 months, a fifth-grade class raised money for charities. If the class divides the money equally among 32 different organizations, how many dollars will each organization receive, and how many dollars will be leftover?

You can make sense of the problem by answering these questions. How much money was raised in all?
How much should each organization get?

Here’s my thinking.

B.
How can I make sense of and solve the problem?
I can
• identify the quantities given.
• understand how the quantities are related.
• choose and implement an appropriate strategy.
• check to be sure my work and answer make sense.
C.
First, I can write an addition equation to find the total amount raised:
1,104 + 2,117 + 3,275 = 6,496
Next, I can write a division equation to model equal sharing:
6,496 ÷ 32 =
(6400 + 96) ÷ 32 =
(6400 ÷ 32) + (96 ÷ 32) =
200 + 3 = 203
So, each organization will receive $203.
Convince Me! Critique Reasoning Julio says that you can solve this problem by dividing each month’s total by 32 and then adding the three quotients together. Do you agree? Do you think his approach is easier or harder? Justify your answer.
Stuck? Try solving a simpler problem.

Guided Practice
Make Sense and Persevere
Dana starts with 875 stamps in her stamp collection. Her grandparents give her 332 stamps. Then, she buys 72 more. How many pages in her scrapbook can she fill?

Question 1.
What do you know?
Answer:
Dana starts with 875 stamps in her stamp collection.
Her grandparents give her 332 stamps.
Then, she buys 72 more
Question 2.
What are you trying to find?
Answer:
How many pages in her scrapbook can she fill?
Question 3.
How are the quantities related? What is the answer to the problem? Write equations to model your work.
Answer:
875 + 332 + 72 = 1279
Number of stamps in a page = 24
The number of pages in her scrapbook she can fill = 1279 ÷ 24 = 53.2 approximately equals 53.
Independent Practice
Make Sense and Persevere
Tanya is saving for a vacation. She wants to have at least $75 for each of the 12 days of her trip. If she saves $85 each month for 10 months, will she save enough money?
Question 4.
Use the strategy of mental math to find the total amount she will save. Then, write a division equation to see if she will save enough.
Answer:
Amount for 12 days = $75 x 12 = $900
Amount for 10 months = $85 x 10 = $850
She can not save enough money.
Question 5.
Jorge says he can solve this problem differently. He says that he can compare 85 × 10 and 75 × 12. Do you agree? Explain your thinking.
Answer:
Yes. I agree with Jorge. Because it is easy to estimate and compare both values of amounts.
Problem Solving
Performance Task
Pumpkin Patch Farms
The table shows the number of seeds the owners of Pumpkin Patch Farms received from different seed suppliers. Each of the pumpkins they harvest usually weighs between 10 and 12 pounds. There are 60 rows, and the farmers will plant the same number of seeds in each row. How many seeds will they plant in each row?
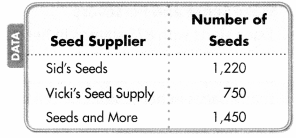
Question 6.
Make Sense and Persevere What do you know? What are you trying to find?
Answer:
Question 7.
Reasoning How are the quantities in the problem-related? What steps are needed to solve the problem?
Answer:
Question 8.
A model with Math Writes equations with variables to represent the steps needed to solve the problem.
Think about the problem-solving strategies to help you!

Question 9.
Be Precise Solve the equations and answer the question.
Answer:
Question 10.
Reasoning What strategy can you use to check that your answer makes sense?
Answer:
Topic 5 Fluency Practice Activity
Point & Tally
Work with a partner. Get paper and a pencil. Each partner chooses light blue or dark blue.
At the same time, Partner 1 and Partner 2 each point to one of their black numbers. Both partners find the product of the two numbers.
The partner who chose the color where the product appears gets a tally mark. Work until one partner has seven tally marks.

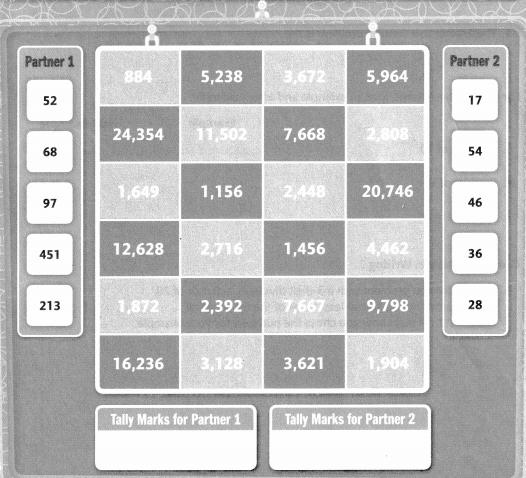
Topic 5 Vocabulary Review
Glossary
Understand Vocabulary
Word List
• compatible numbers
• dividend
• divisor
• estimate
• multiple
• product
• quotient
• remainder
Choose the best term from the Word List. Write it on the blank.
Question 1.
One way to estimate the answer to a division problem is to replace the divisor and dividend with ___
Answer:
Estimate and multiple
Question 2.
The part that is left when you divide into equal groups is called the ____
Answer:
remainder
Question 3.
To decide where to place the first digit of a quotient, ____ is the number of digits in the answer.
Answer:
The first digit of the quotient will be in the Hundreds Place, If the first digit is less than the divisor, If the first digit is greater than or equal to the divisor, the first digit of the quotient will be in the thousand’s place.
Question 4.
The answer to a division problem is the ______
Answer:
Remainder.
For each of these terms, give an example and a non-example.

Use Vocabulary in Writing
Question 8.
Write a division problem with a 3-digit dividend, a divisor of 20, and the remainder of 10. Use at least three of the terms in the Word List to explain how you chose the numbers for your example.
Answer:
Topic 5 Reteaching
Set A
pages 181-184
Find 32,000 ÷ 80 using mental math.
Use basic facts and place-value patterns to help.
32 ÷ 8 = 4
320 ÷ 80 = 4
3,200 ÷ 80 = 40
32,000 ÷ 80 = 400
Remember to look for a basic division fact in the numbers. Check your answer by multiplying. Find each quotient. Use mental math.
Question 1.
360 ÷ 40
Answer:
360 ÷ 40
36 ÷ 4 = 9.
Question 2.
270 ÷ 90
Answer:
270 ÷ 90
27 ÷ 9 = 3
Question 3.
2,100 ÷ 30
Answer:
2,100 ÷ 30
210 ÷ 3 = 70
Question 4.
4,800 ÷ 80
Answer:
4,800 ÷ 80
480 ÷ 8 = 60
Question 5.
72,000 ÷ 80
Answer:
72,000 ÷ 80
7200 ÷ 8 = 900
Question 6.
81,000 ÷ 90
Answer:
81,000 ÷ 90
8100 ÷ 9
900
Set B
pages 185-188
Estimate 364 ÷ 57.
Use compatible numbers and patterns to divide.
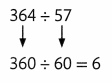
So, 364 ÷ 57 is about 6.
Remember that compatible numbers are numbers that are easy to compute mentally.
Estimate using compatible numbers.
Question 1.
168 ÷ 45
Answer:
168 ÷ 45
160 ÷ 40
4
Question 2.
525 ÷ 96
Answer:
525 ÷ 96
500 ÷ 100
5
Question 3.
379 ÷ 63
Answer:
379 ÷ 63
360 ÷ 60
6
Question 4.
234 ÷ 72
Answer:
234 ÷ 72
210 ÷ 70
3
Question 5.
$613 ÷ 93
Answer:
$613 ÷ 93
$630 ÷ 90
$7
Question 6.
$748 ÷ 92
Answer:
$748 ÷ 92
$720 ÷ 90
$8
Set C
pages 189-192
Find 195 ÷ 13.
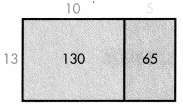
Draw a model to help you find 131 the number of tens and ones in the quotient.
1 ten + 5 ones = 15.
So, 195 ÷ 13 = 15
Remember to find the number of tens first, then find the number of ones.
Use a model to find each quotient.
Question 1.
180 ÷ 15
Answer:

Question 2.
154 ÷ 14
Answer:
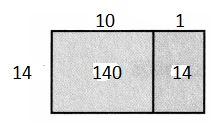
Question 3.
351 ÷ 27
Answer:
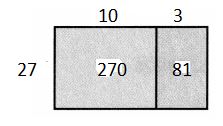
Question 4.
192 ÷ 16
Answer:

Question 5.
143 ÷ 11
Answer:
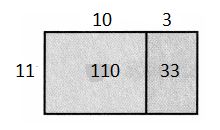
Question 6.
217 ÷ 31
Answer:
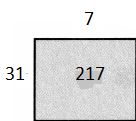
Question 7.
130 ÷ 26
Answer:
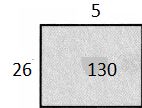
Question 8.
270 ÷ 18
Answer:
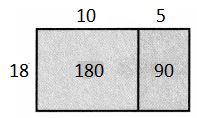
Set D
pages 193–196
Find 336 ÷ 21 using partial quotients.
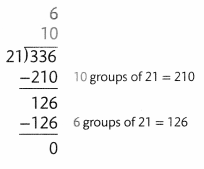
Add the partial quotients: 10 + 6 = 16. So, 336 = 21 = 16.
Remember to add the partial quotients to find the actual quotient.
Use partial quotients to divide.
Question 1.
![]()
Answer:
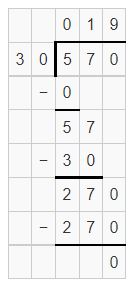
Partial quotients are 10, 9 and sum is 19
Question 2.
![]()
Answer:
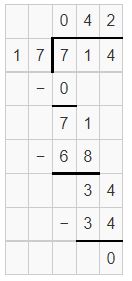
Partial quotients are 40,2 and sum is 42
Question 3.
![]()
Answer:
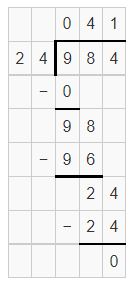
Partial quotients are 40,1 and sum is 41
Question 4.
![]()
Answer:
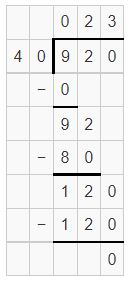
partial quotients are 20,3 and sum is 23.
Question 5.
![]()
Answer:
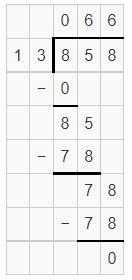
PArtial quotients are 60,6 and sum is 66.
Question 6.
![]()
Answer:
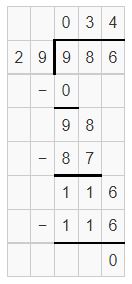
partial quotients are 30,4 and sum is 34.
Question 7.
![]()
Answer:

partial quotients are 20,8 and sum is 28
Question 8.
![]()
Answer:
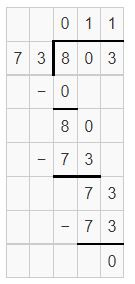
partial quotients are 10,1 and sum is 11.
Set E
pages 197-200
Find 461 ÷ 50.
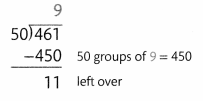
Remember that you can check your answer by multiplying the quotient by the divisor, and then adding any remainder.
Question 1.
![]()
Answer:
Question 2.
![]()
Answer:
Question 3.
![]()
Answer:
Question 4.
![]()
Answer:
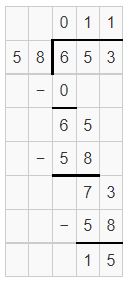
Question 5.
![]()
Answer:
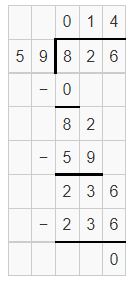
Question 6.
![]()
Answer:
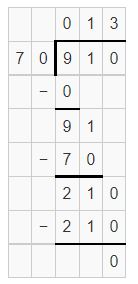
Question 7.
![]()
Answer:
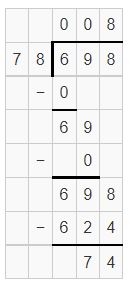
Question 8.
![]()
Answer:
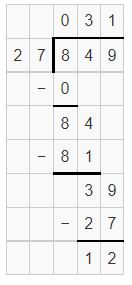
Question 9.
Ivan uses 30 craft sticks to make each toy cabin. He has a box of 342 craft sticks. How many toy cabins can Ivan make? How many sticks will be left?
Answer:
Set F
pages 201-204
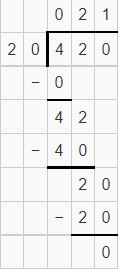
Find 3,657 ÷ 23.

Remember you can multiply the divisor by powers of 10 to estimate the quotient.
Divide. Use place-value blocks to help.
Question 1.
![]()
Answer:
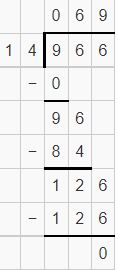
Question 2.
![]()
Answer:

Question 3.
![]()
Answer:
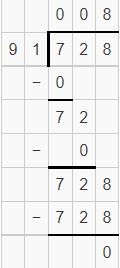
Question 4.
![]()
Answer:

Question 5.
![]()
Answer:
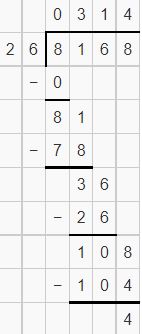
Question 6.
![]()
Answer:
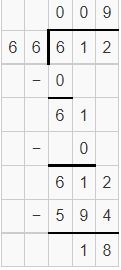
Question 7.
![]()
Answer:
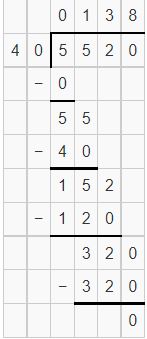
Question 8.
![]()
Answer:
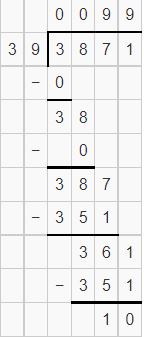
Set G
pages 205-208
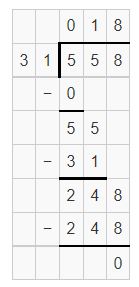
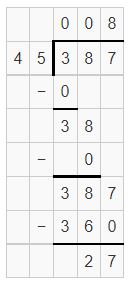
Find 789 ÷ 19.
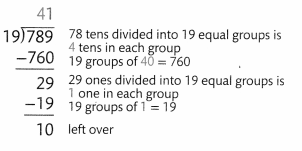
Remember that you can check your answer by multiplying the quotient by the divisor, and then adding any remainder.
Question 1.
![]()
Answer:
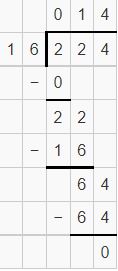
Question 2.
![]()
Answer:
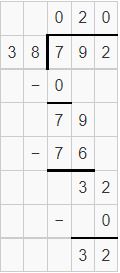
Question 3.
![]()
Answer:
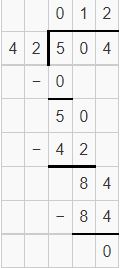
Question 4.
![]()
Answer:

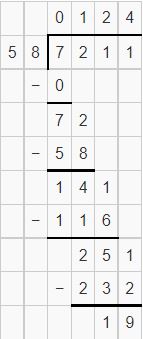
Question 5.
![]()
Answer:
Question 6.
![]()
Answer:
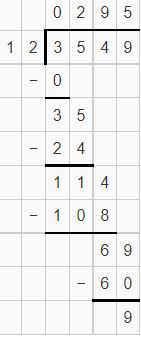
Question 7.
![]()
Answer:

Question 8.
![]()
Answer:
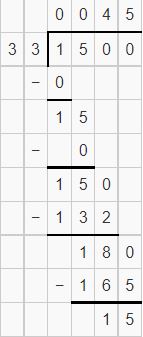
Question 9.
![]()
Answer:
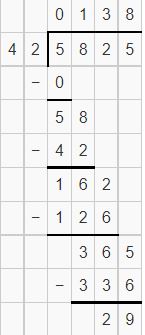
Question 10.
![]()
Answer:
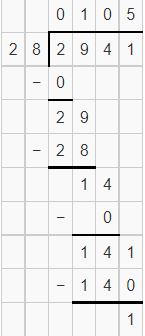
Set H
pages 209-212
Think about these questions to help you make sense and persevere in solving problems.
Thinking Habits
• What do I know?
• What do I need to find?
• What’s my plan for solving the problem?
• What else can I try if I get stuck?
• How can I check that my solution makes sense?

Selena is planning to visit her aunt in 5 weeks. She has saved $365 but thinks the trip will cost $500. She plans to save the same amount each week so she has $500 for the trip. How much does she need to save each week?
I can write an equation to find how much more money Selena needs:
500 – 365 = 135
Then divide the amount she needs by 5 weeks: 135 ÷ 5 = 27
Selena needs to save $27 each week.
My answer is reasonable because 365 + 27 + 27 + 27 + 27 + 27 = 500.
Remember to think about what steps are needed to solve each problem. Solve. Show your work.
Question 1.
The football coach spent a total of $890 including $50 in tax for 35 shirts for the team. Each shirt cost the same amount. What was the price of one shirt before tax was added?
Answer:
Total cost = $890 including tax
Total cost before tax added = $890 – $50 = $840
Total number of shirts = 35
Therefore, Price of one shirt = $840 ÷ 35 = $24
Question 2.
A gymnast practices 6 days each week. She practices the same number of hours each day. If she practices a total of 120 hours in a 4-week period, how many hours each day does she practice?
Answer:
Number of days in the 4-week period = 4×7 = 28
But, she practices only 6 days, Therefore, 6 days in a 4-week period = 6×4 = 24
Total number of hours in 4-week period = 120
Therefore, the number of hours each day she practices = 120 ÷ 24 =5.
Question 3.
Nathan works the same number of hours each day, 5 days each week. He earns $12 per hour. Last week he earned $420. How many hours did he work each day last week? Write equations to model your work.
Answer:
Total earned = $420
Number of days in each week = 5
Total earned in each day = $420 ÷ 5 = $84
Total earned per hour = $12
Therefore, the number of hours he works each day = $84 ÷$12 = 7.
Question 4.
A high-rise apartment building has 15 floors with 26 apartments on each floor. There are 3 kinds of apartments in the building: 1-, 2-, and 3-bedroom. The building has the same number of each kind of apartment. How many of each kind of apartment is in the building? Show your work.
Answer:
The number of floors = 15
The number of Apartments = 26
Now, 15 x 26 = 390 Apartments.
Given that, There are three kinds of apartments
= 390/3
= 130
Therefore, there are 130 apartments in the building.
Topic 5 Assessment Practice
Question 1.
Select all of the following equations the number 60 will make true.
![]() 420 ÷
420 ÷ ![]() = 70
= 70
![]() 1,800 ÷
1,800 ÷ ![]() = 300
= 300
![]() 5,400 ÷
5,400 ÷ ![]() = 90
= 90
![]() 2,400 ÷
2,400 ÷ ![]() = 40
= 40
![]() 500 ÷
500 ÷ ![]() = 10
= 10
Answer:
![]() 5,400 ÷
5,400 ÷ ![]() = 90
= 90
![]() 2,400 ÷
2,400 ÷ ![]() = 40
= 40
Question 2.
Which of the following is the best estimate of 487 ÷ 67?
A. 80
B. 70
C. 10
D. 7
Answer:
B. 70
Question 3.
The carnival committee has purchased 985 small prizes. The prizes are to be divided equally among the 20 game booths. A. In what place will the first digit of the quotient be?
B. How many prizes will each booth have?
C. How many prizes will be left?
Answer:
A. The first digit of the quotient be in Ten’s place.
B. 985 /20 = 49 as Quotient
Therefore, each booth have 49 prizes in each booth
C. 985 /20 = 5 as remainder
Therefore, 5 prizes will be left.
Question 4.
A rectangular living room has an area of 425 square feet. The width of the room is 17 feet.
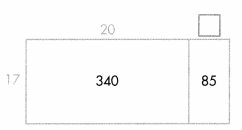
Write a number in the box to show the missing dimension. What is the length of the room?
____ feet
Answer:
Given, The Area of the living room = 425 square feet.
Now, 85/17 = 5
Therefore, the length of the room = 20 + 5 = 25 feet.
Question 5.
A. Divide.
2,700 ÷ 30 = ____
B. Select all the expressions that are equal to 2,700 ÷ 30.
![]() 270 ÷ 3
270 ÷ 3
![]() 270 tens ÷ 3 tens
270 tens ÷ 3 tens
![]() 2,700 ÷ 3 tens
2,700 ÷ 3 tens
![]() 2,700 ÷ 3
2,700 ÷ 3
![]() 2,700 tens ÷ 30
2,700 tens ÷ 30
Answer:
A. 90
B.![]() 270 ÷ 3
270 ÷ 3
![]() 270 tens ÷ 3 tens
270 tens ÷ 3 tens
![]() 2,700 ÷ 3 tens
2,700 ÷ 3 tens
Question 6.
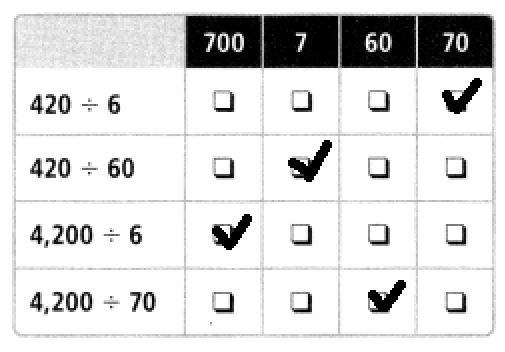
Select the quotient for each expression.

Answer:
Question 7.
Use the table.

A. Using Plan B, how many weeks will it take Althea to reach her savings goal? Write the missing number in the table.
B. Show how you found your answer to A.
Answer:
Althea’s plans for savings = $384
It approximately equals $390
Amount to save each week = $30 according to plan B
Therefore, Number of weeks needed = $390 ÷ $30 = 13

Question 8.
Five Star Farm purchased 2,400 apple trees. If 80 trees can be planted on each acre of land, how many acres will be needed to plant all the trees?
A. Identify which expression represents the problem.
A. 2,400 × 80
B. 80 × 2,400
C. 80 ÷ 2,400
D. 2,400 ÷ 80
B. How many acres will be needed to plant all the trees?
Answer:
A.
D. 2,400 ÷ 80
B.
Total number of apple trees = 2400
Number of trees planted on each acre land = 80
Number of acres needed to plant all the trees = 2400 ÷ 80 = 30
Question 9.
Mrs. Reiss has 264 crayons for her art class of 22 students. How many crayons will each student get if the crayons are divided equally? Use the model.
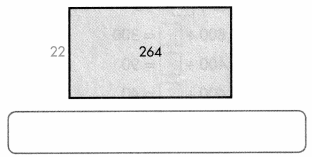
Answer:
Number of students = 22
Number of Crayons = 264
Now,
264/22
= 12
Therefore, Each Student gets 12 crayons.
Question 10.
Select all the expressions that have the value of 9.
![]() 270 ÷ 3
270 ÷ 3
![]() 250 ÷ 25
250 ÷ 25
![]() 270 ÷ 30
270 ÷ 30
![]() 207 ÷ 23
207 ÷ 23
![]() 189 ÷ 21
189 ÷ 21
Answer:
- 270 ÷ 3
- 270 ÷ 30
- 207 ÷ 23
- 189 ÷ 21
Question 11.
Kari wants to find 3,277 ÷ 29.
A. Without doing the division, which number will the quotient be closest to?
A. 1
B. 10
C. 100
D. 1,000
B. What is the exact quotient?
Answer:
A.
The quotient be closest to 100
B. The exact quotient =
3,277 ÷ 29.
= 113
Question 12.
The cost to rent a lodge for a family reunion is $975. If 65 people attend and pay the same price, how much does each person pay?
A. Which of the following expressions represents the problem?
A. 975 + 65
B. 975 ÷ 65
C. 975 × 65
D. 975 ÷ 2
B. How much does each person pay?
A. $16
B. $15
C. $14
D. $13
Answer:
$975 ÷ 65
= $15
Therefore, Each person pays $15.
Question 13.
Shady Rivers summer camp has 188 campers this week. If there are 22 campers to each cabin, what is the least number of cabins needed?
A. 7 cabins
B. 8 cabins
C. 9 cabins
D. 10 cabins
Answer:
188/22
= 8 cabins.
Question 14.
The area of a rectangular banquet hall is 7,400 square feet. The length of one side of the hall is 82 feet. Explain how you can use compatible numbers to estimate the width of the hall.
Answer:
Given,
The area of the rectangle = 7,400 square feet.
The length of one side = 82 feet.
We know that, The area of the rectangle =
Area = length x width
7400 = 82 x n
n = 7400/82
= 90.2 feet
Therefore, the width of the rectangular banquet hall = 90.2 feet.
Question 15.
The cost of renting a bus is $1,344. Tony wants to find how much each person will pay if 32 people ride the bus and share the cost equally. Fill in the partial quotients that are missing from Tony’s work below.
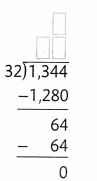
Answer:
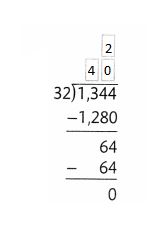
Question 16.
Jessie made 312 mini energy bars. She puts 24 bars in each bag. She plans to sell each bag for $6.
A. Write two equations with variables that Jessie can use to find the amount of money she will earn if she sells all of the bags.
B. How much will she earn if she sells all of the bags?
Answer:
Question 17.
Select all of the following equations the number 40 will make true.
![]() 280 ÷
280 ÷ ![]() = 7
= 7
![]() 800 ÷
800 ÷ ![]() = 20
= 20
![]() 4,000 ÷
4,000 ÷ ![]() = 10
= 10
![]() 3,200 ÷
3,200 ÷ ![]() = 80
= 80
![]() 800 ÷
800 ÷ ![]() = 200
= 200
Answer:
- 280 ÷ 40 = 7
- 800 ÷ 40 = 20
- 3200 ÷ 40 = 80
Question 18.
Select the quotient for each expression.
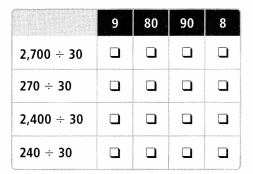
Answer:
- 2700 ÷ 30 = 90
- 270 ÷ 30 = 9
- 2400 ÷ 30 = 80
- 240 ÷ 30 = 8
Question 19.
Charles burns 4,350 calories hiking 15 miles of the Appalachian Trail. How many calories does he burn each mile?
A. Identify which expression represents the problem.
A. 4,350 ÷ 15
B. 4,350 × 15
C. 4,350 – 15
D. 4,350 ÷ 10
B. How many calories does he burn each mile?
Answer:
A. 4,350 ÷ 15
B. In each mile he burns 290 calories.
Question 20.
Find the quotient 432 ÷ 48.
Answer:
432 ÷ 48 = 9
Question 21.
Which partial quotients could be added to find 465 ÷ 15?
A. 20 and 1
B. 30 and 1
C. 30 and 9
D. 30 and 10
Answer:
B. 30 + 1
465 ÷ 15 = 31
30 + 1 = 31
Question 22.
The table shows the number of students going on field trips. For each trip, one adult is needed for every 15 students.

How many adults are needed to go on the seventh-grade trip?
Answer:
Given,
Number of students in seventh grade = 225
Condition is one adult is needed for every 15 students.
Number of adults are needed to go on the seventh-grade trip = 225 ÷ 15 = 15
Therefore, the number of adults are needed to go on the seventh-grade trip is 15.
Topic 5 Performance Task
School Supplies
A store had a sale on school supplies in August. The store manager recorded how many of several types of items were sold. Each of the same types of item costs the same amount. Use the information in the table to answer the questions.

Question 1.
Backpack sales totaled $1,200. How much did each backpack cost? Write an equation to model your work.
Answer:
Given,
Total sales = $1200
Total number of backpacks = 60
cost of each backpack = $1200 ÷ 60 = $120 ÷ 6 = $20.
Therefore, the cost of each backpack is $20.
Question 2.
The store sold 71 packages of pens. Use compatible numbers to estimate how many pens were in each package. Show your work.
Answer:
Given,
Number of packages = 71
Number of pens sold = 568
number of pens in each package is 568 ÷ 71 = 8
Therefore, the number of pens in each package is 8
Question 3.
There were 16 pencils in each box. Olivia wants to find how many boxes of pencils were sold.
Part A
When Olivia divides 784 by 16, in which place should she write the first digit of the quotient? Tell how you know without dividing.
Part B
How many boxes of pencils were sold?
Answer:
Number of pencils sold = 784
Number of pencils in each box = 16
Number of boxes of pencils sold = 784 ÷ 16 = 49
Therefore, the number of boxes of pencils sold is 49.
Question 4.
The store manager has ordered the calculators shown, but the shipment has been delayed.
Part A

If all the calculators ordered are sold, the total sales would be $2,014. Was the number of calculators ordered less than or greater than 100? How do you know without dividing?
Part B
How many calculators were ordered? Write an equation to model your work.
Answer:
Given,
Total sales = $2,014
Cost for each calculator = $19
Therefore number of calculators = $2,014 ÷ $19 = 106
So, the number of calculators ordered was 106 and it is greater than 100.
we can say it not by diving. 19 x 100 = 1900 and the total sales given is $2014. So it must be greater than 100.
Question 5.
The manager wants to order 408 more notebooks. The notebooks are shipped in packages of 12. He used partial quotients to find the number of packages to order. His work is shown on the right. Is his solution correct? Explain.
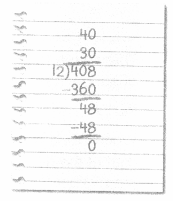
Answer:
No. The model to find the number of packages to order is not correct.
Explanation:
408 ÷ 12 = 34
But his work shown at right is showing the value is 40
So, it is not correct and the correct value is 34.
Question 6.
An additional 40 packages of paper were ordered at a total cost of $520. How much did each package of paper cost? Write an equation to model your work.
Answer:
Each package of paper cost $13
Because,
$520 ÷ 40
$52 ÷ 4 = $13.

