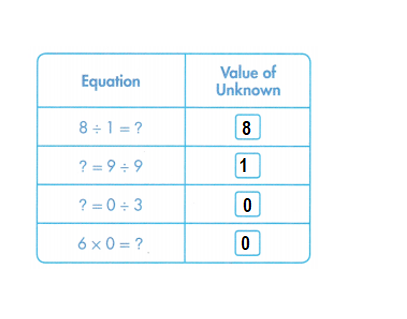
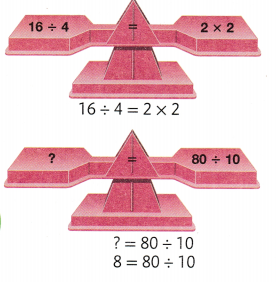
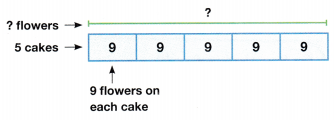
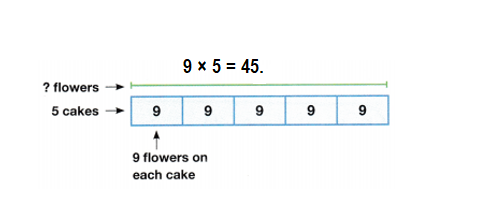
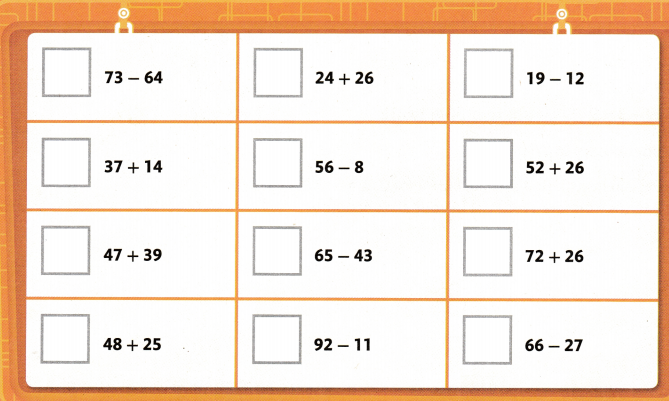
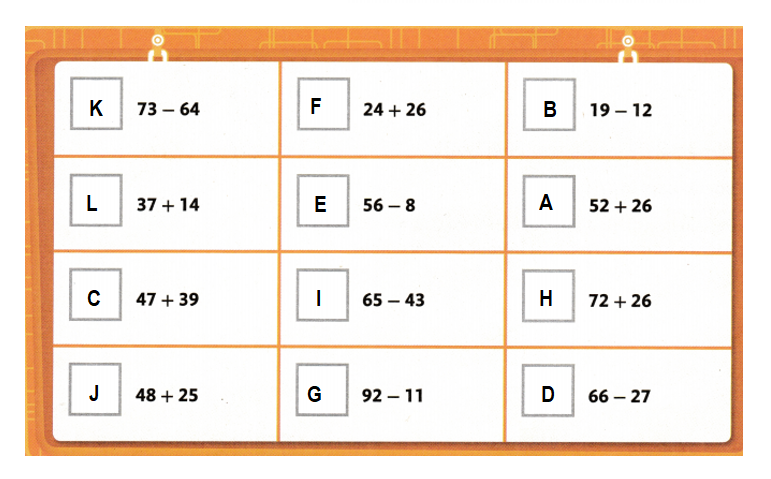
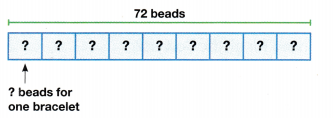
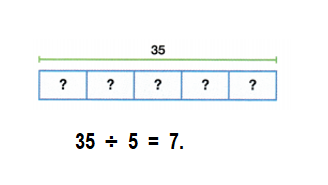
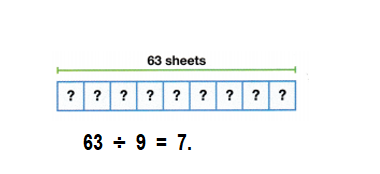
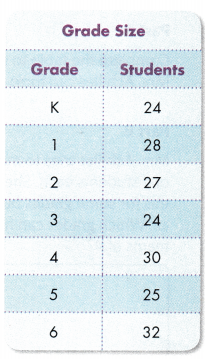
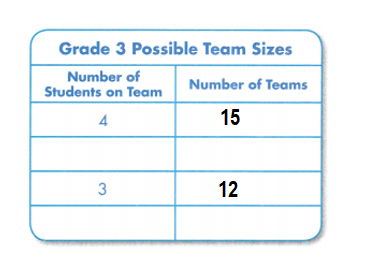
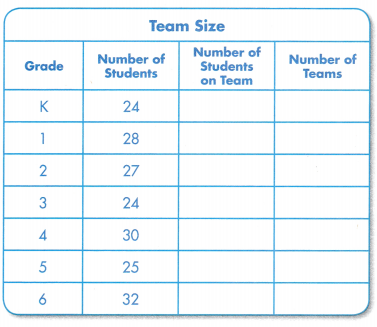
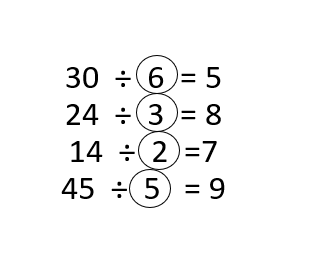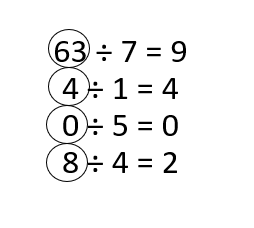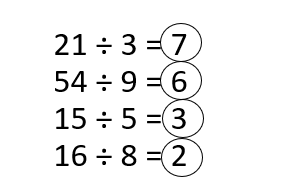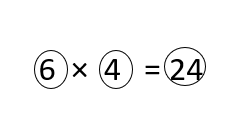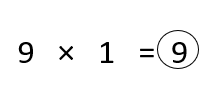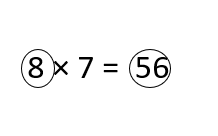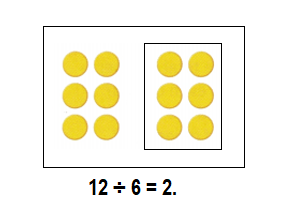Students must prepare with enVision Math Common Core 2nd Grade Solutions to get a good knowledge of the concept. You can find various ways to practice enVision Math 2.0 Grade 2 Questions. Also, we have given the assessment practice, reteaching, vocabulary review, and so on for the better practice of the students. You can easily clear all doubts by downloading enVision Math Answer Key. Students need not to pay a single penny to use this enVision Math Common Core 2nd Grade Answers.
Get volume-wise and topic-wise enVision Math Answer Key Common Core Grade 2 Volume 1 & Volume 2 Pdf from the quick links available and complete your assignments with ease.
enVision Math Common Core Grade 2 Answers | enVision Math Common Core 2nd Grade Textbook Answer Key
Chapter-wise quick links are provided here where you can get all the concepts questions with answers. Open each and every link to read out every chapter to improve your skills. Stand out by getting a good score by clearing all assessments on your own. When you are stuck while solving the assessments, then have a look at the topic. Get the solution for all the questions of enVision Math Common Core Grade 2 Textbook on this website. Check an effective preparation plan and prepare well for the test.
Along with the chapter-wise links, we have also given the features of this enVision Math Common Core 2nd Grade Solutions in the following sections. Download enVision Math Common Core Grade 2 Answers PDF for free of cost to know the tricks and steps to solve the 2nd grade maths problems.
enVision Math Common Core Grade 2 Volume 1 Answer Key | enVision Math Common Core 2nd Grade Volume 1 Answers
- Topic 1 Fluently Add and Subtract Within 20
- Topic 2 Work with Equal Groups
- Topic 3 Add Within 100 Using Strategies
- Topic 4 Fluently Add Within 100
- Topic 5 Subtract Within 100 Using Strategies
- Topic 6 Fluently Subtract Within 100
- Topic 7 More Solving Problems Involving Addition and Subtraction
- Topic 8 Work with Time and Money
enVision Math Common Core 2nd Grade Volume 2 Answer Key | enVision Math Common Core Grade 2 Volume 2 Answers
- Topic 9 Numbers to 1,000
- Topic 10 Add Within 1,000 Using Models and Strategies
- Topic 11 Subtract Within 1,000 Using Models and Strategies
- Topic 12 Measuring Length
- Topic 13 Shapes and Their Attributes
- Topic 14 More Addition, Subtraction, and Length
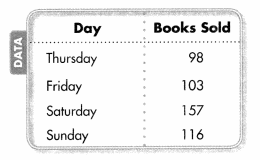
- Topic 15 Graphs and Data
Features of Elementary School Common Core Math Answer Key
The following are the important perks on enVision maths 2.0 grade 2 volume 1 and 2 solutions for learners.
- This enVision Maths Common Core Grade 2 Answers is a great supplement for the topics of volume 1 and volume 2 in the common core maths textbook.
- Answer key enVision 2.0 Grade 2 PDF covers the concepts of volume 1 and volume 2 in a comprehensive manner.
- Practice enVision Math Common Core Grade 2 Answer Key and solve exercise problems at the end of the chapter to enhance skills.
- The step by step solution for each question si helpful to assess your performance.
Summary
Hope that the data given on our page about enVision Math 2.0 Grade 2 Answer Key is useful to clear your doubts & queries. For any feedback on the same, you can always write us such that we can get back to you. Stay tuned to our website to avail the latest updates on grade-wise enVision Math Solutions at your fingertips.















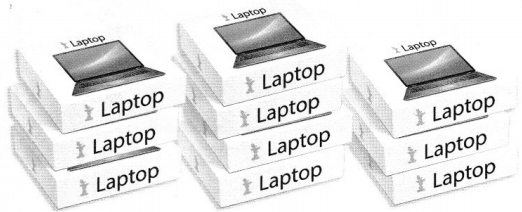

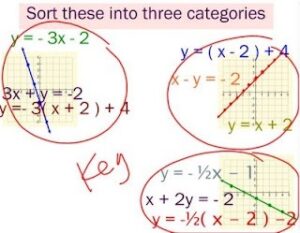














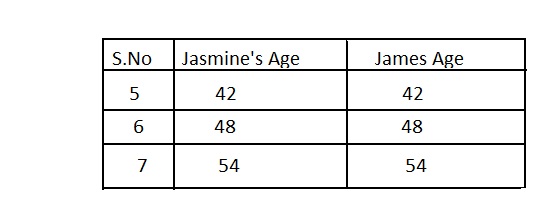








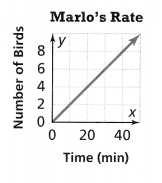



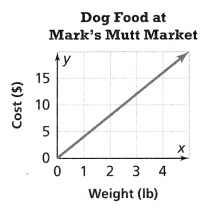
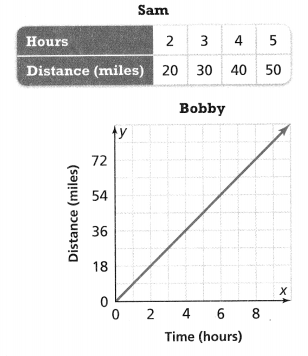

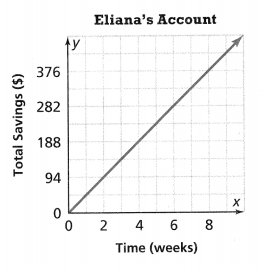

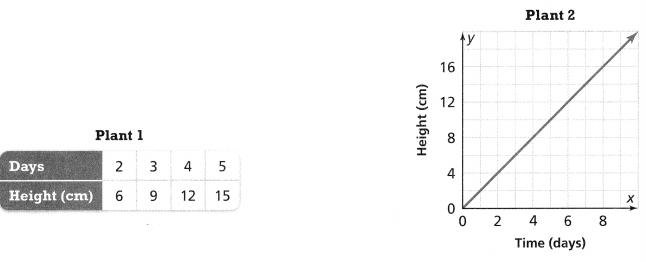
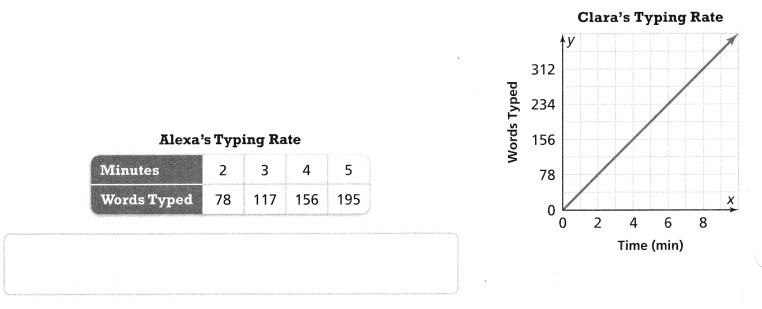

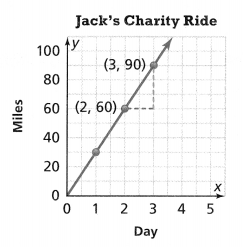

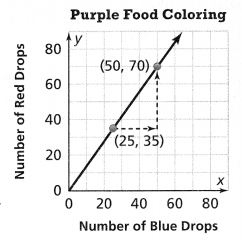
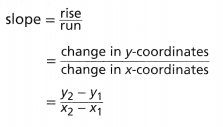
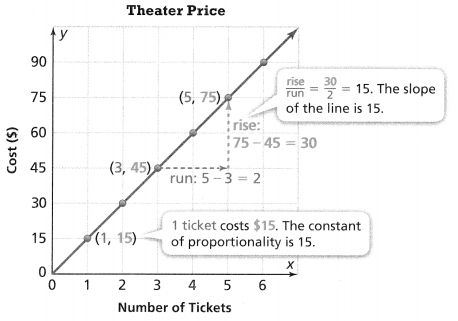
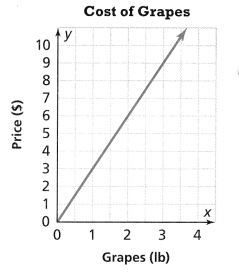
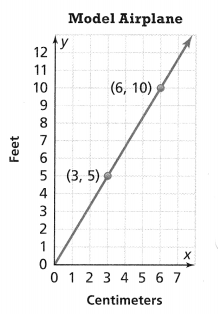
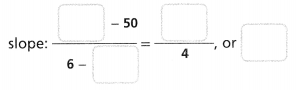
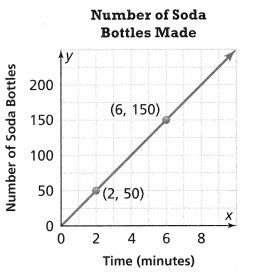

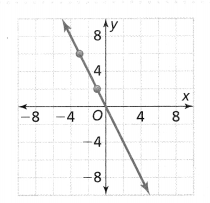

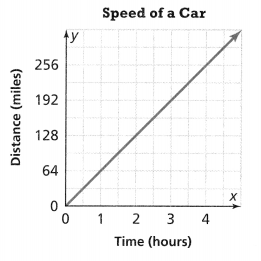

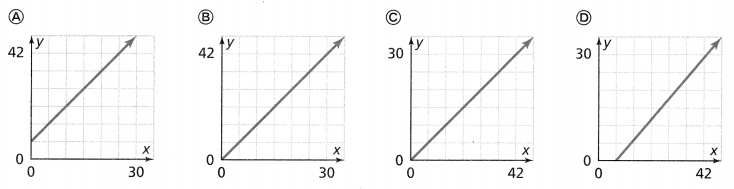

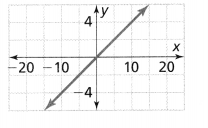
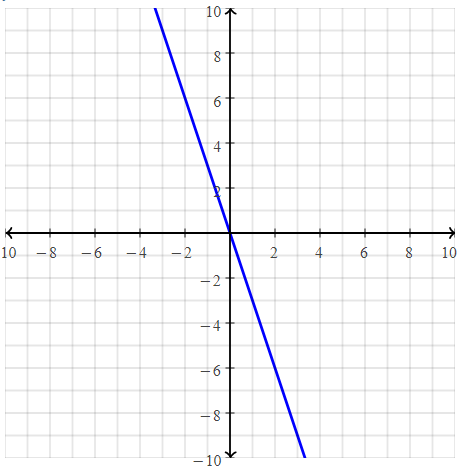
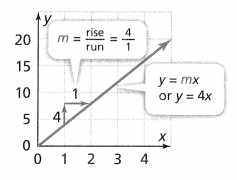
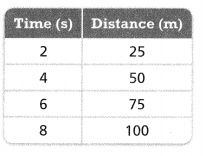
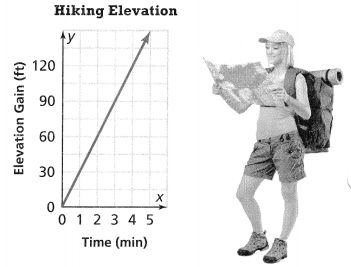
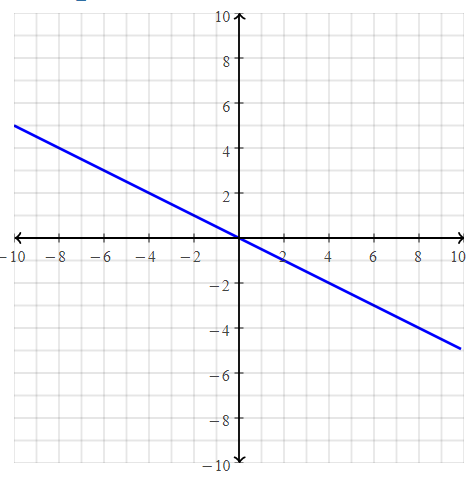
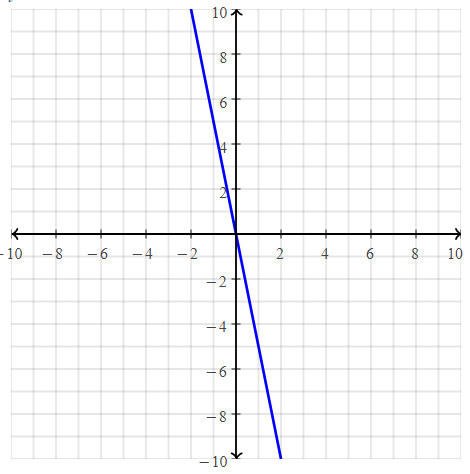
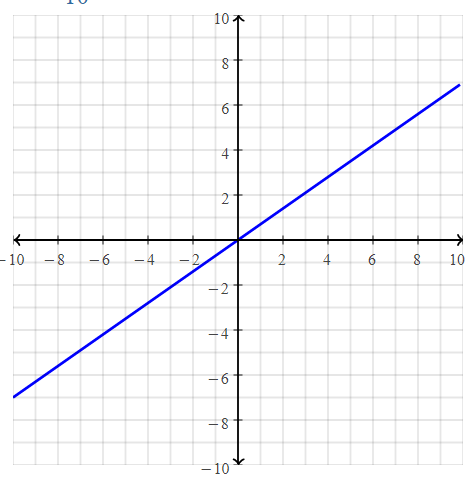
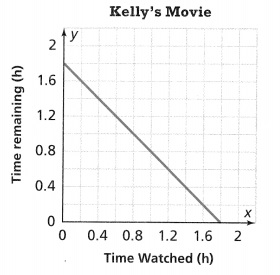
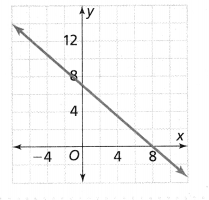
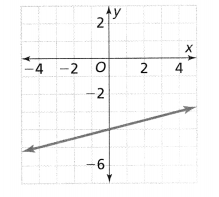
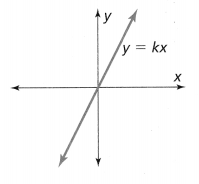
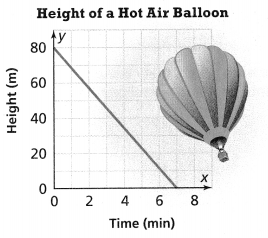
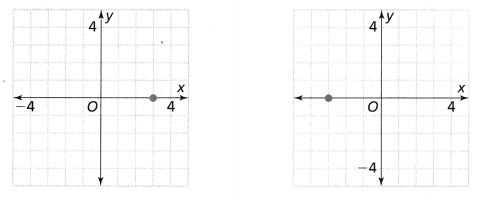
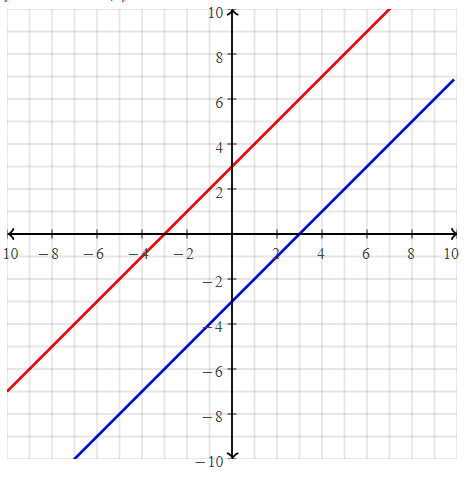
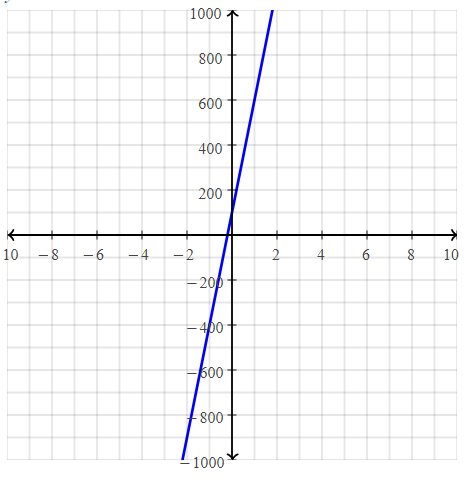
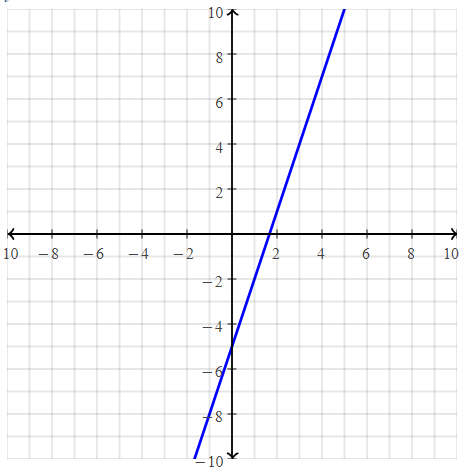
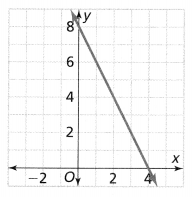
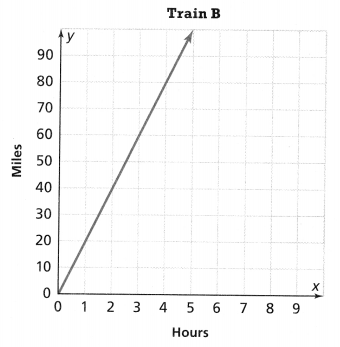
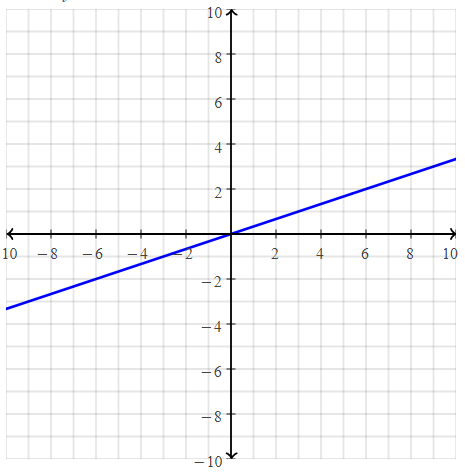
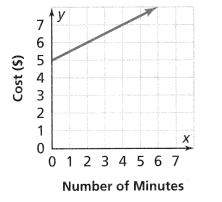
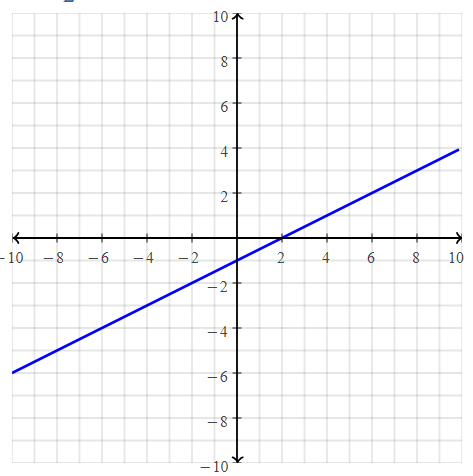
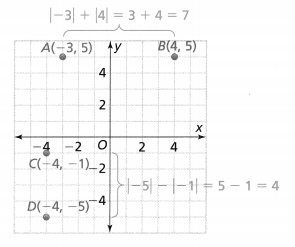
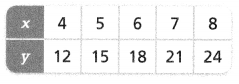
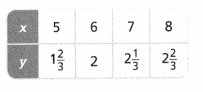
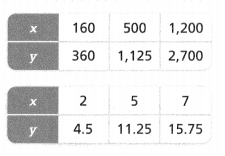
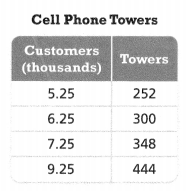
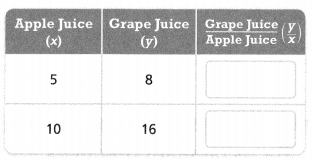
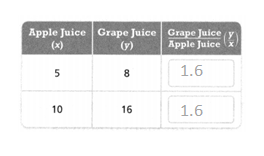
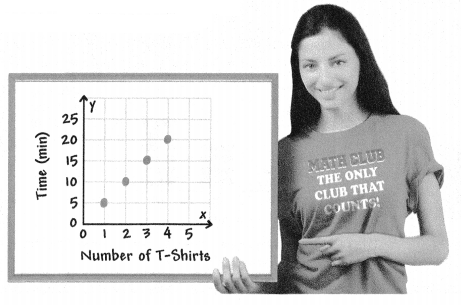
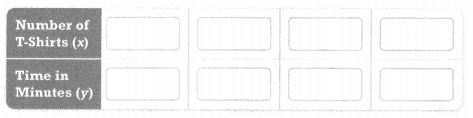
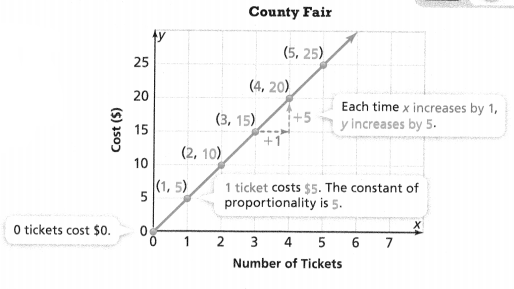
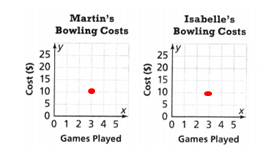
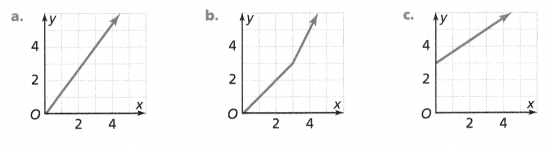
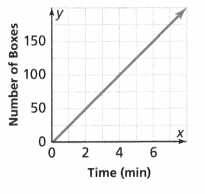
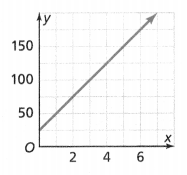
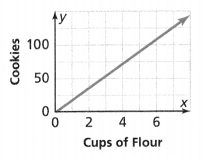
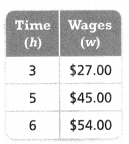
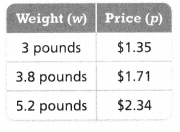
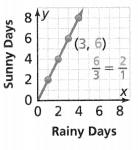
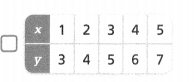
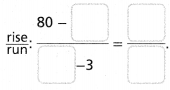 . The equation of the line is y =
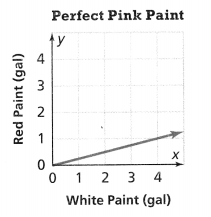
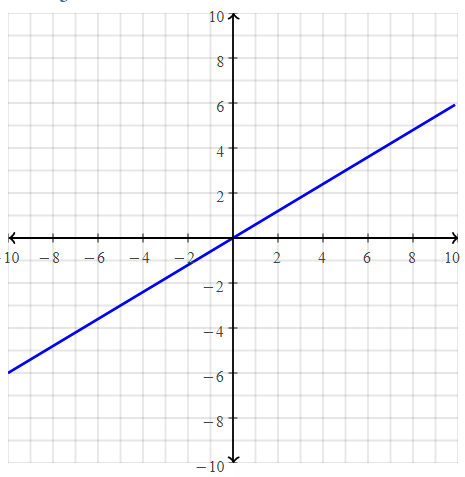
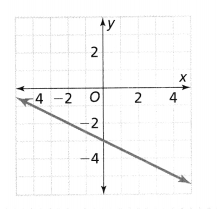
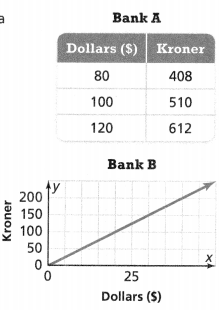
. The equation of the line is y = 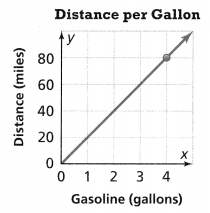

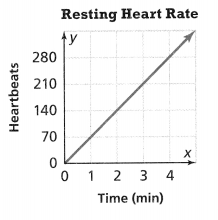
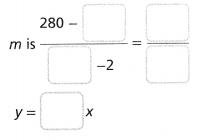





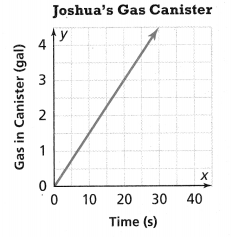
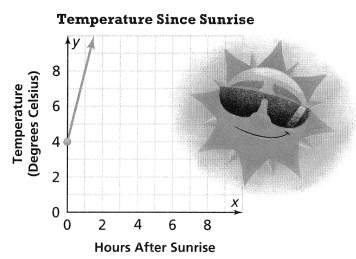
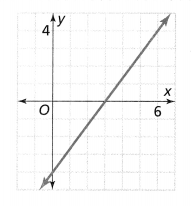
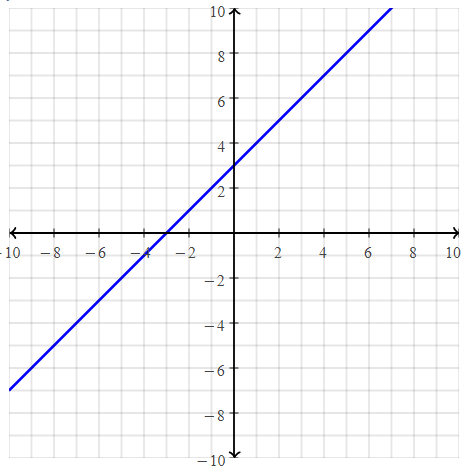


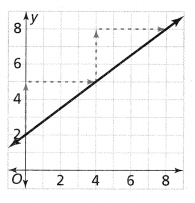













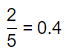
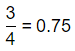
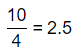
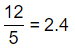

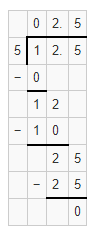
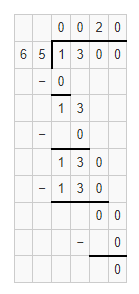
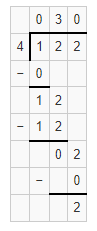
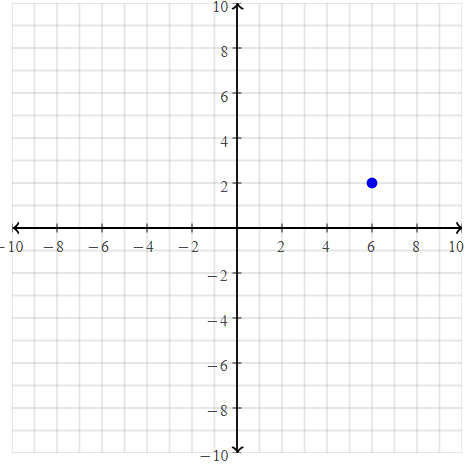
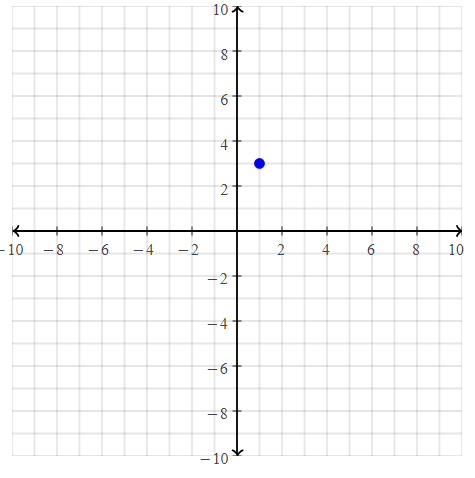

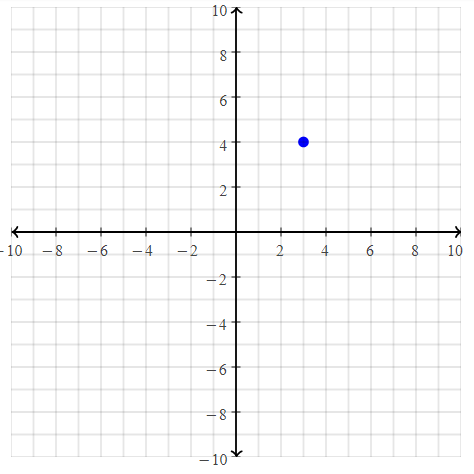
















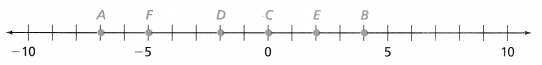


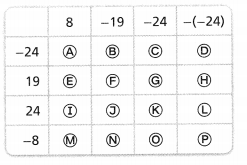


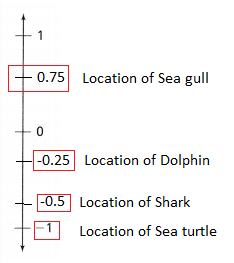

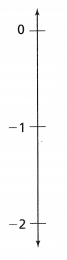
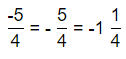
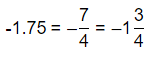
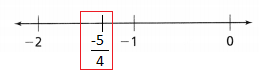
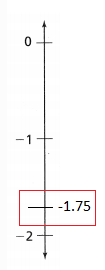
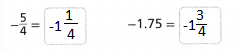
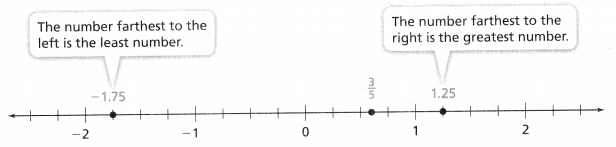
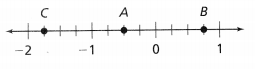

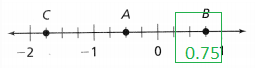
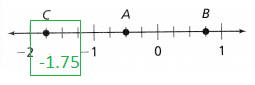

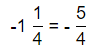
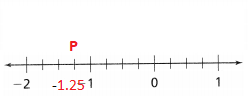








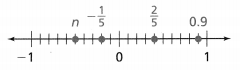
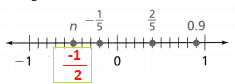
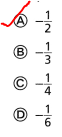









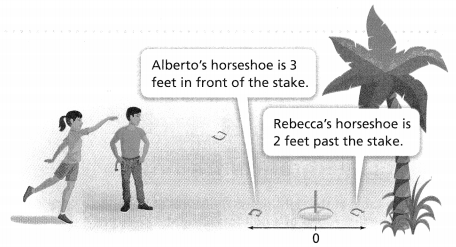






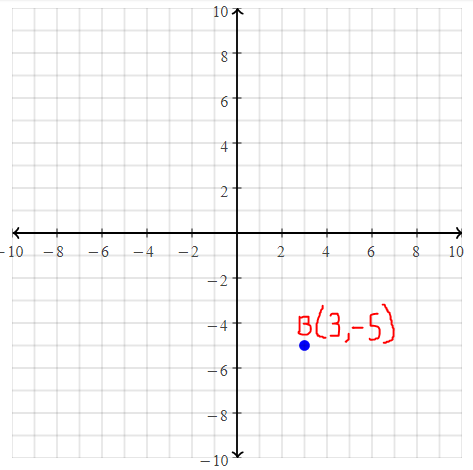
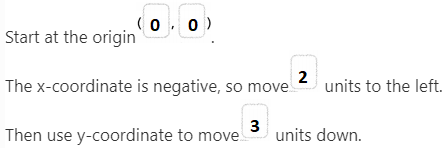

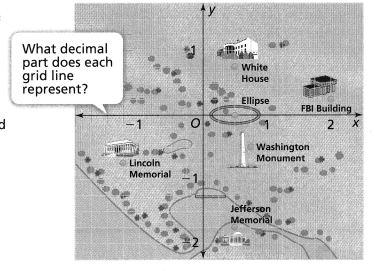
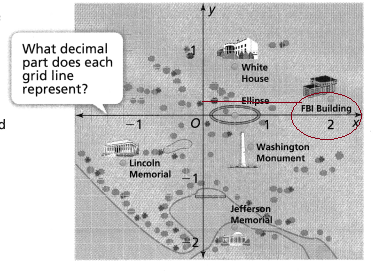
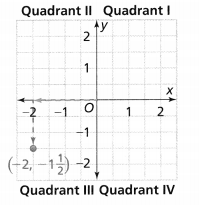
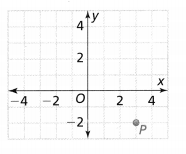
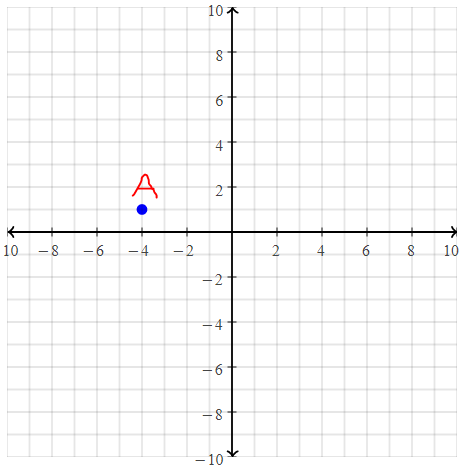
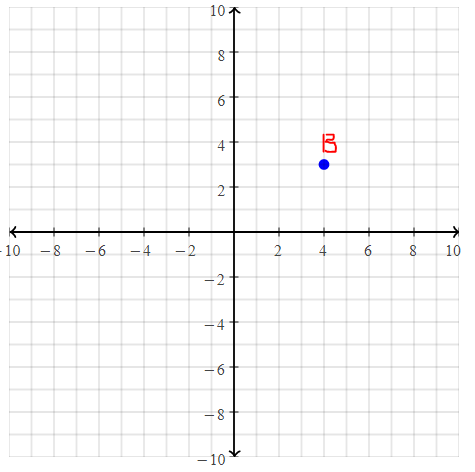
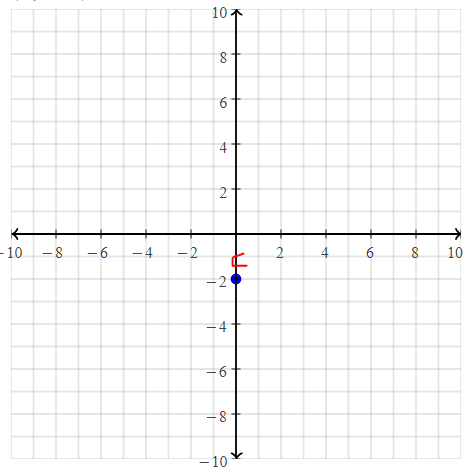
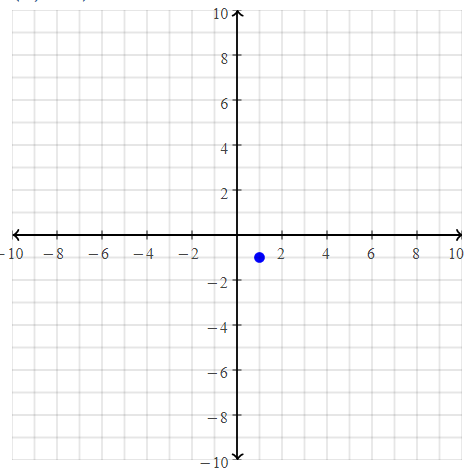
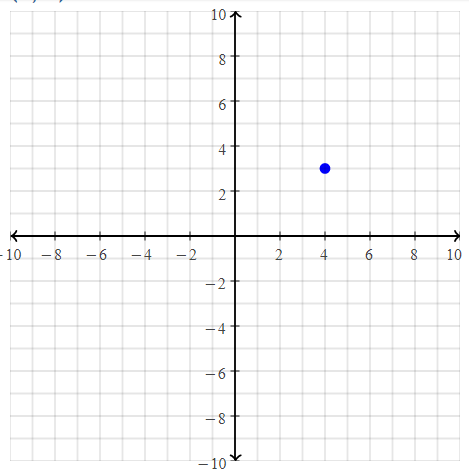
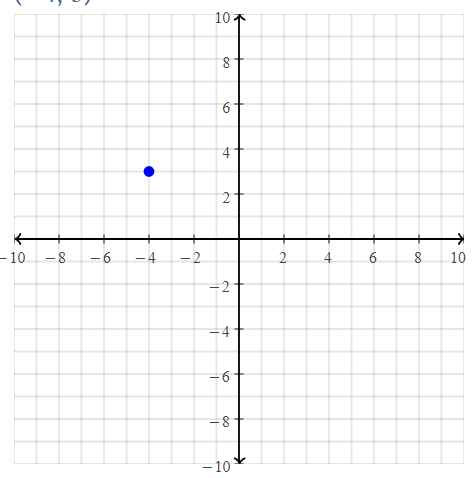
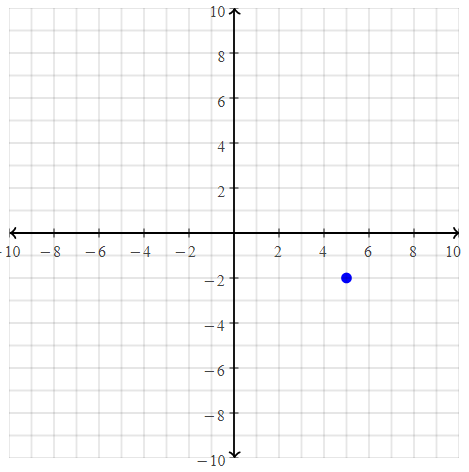
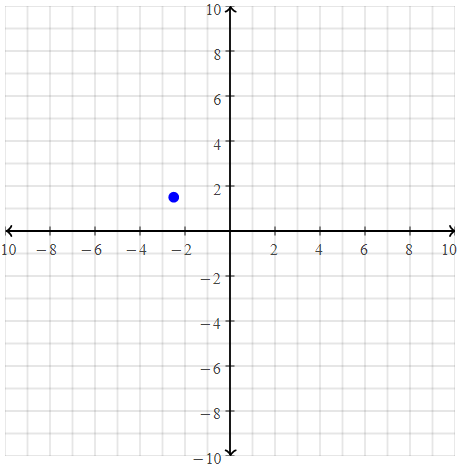
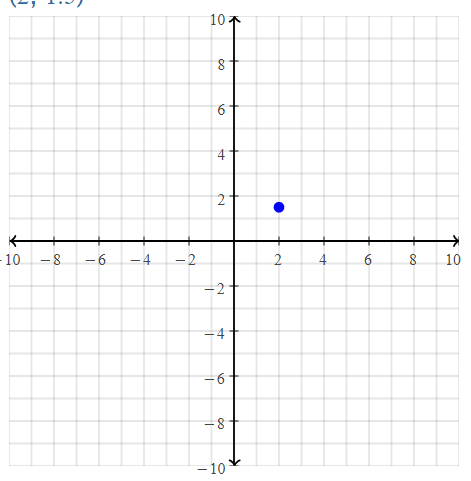
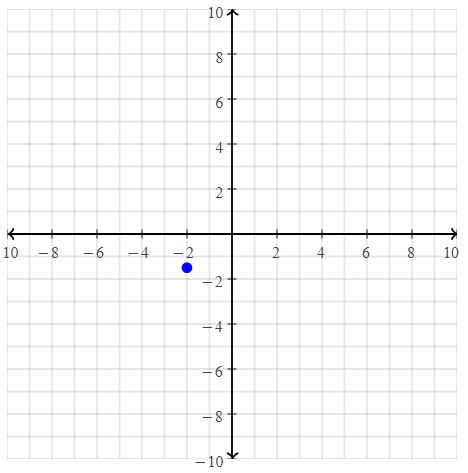
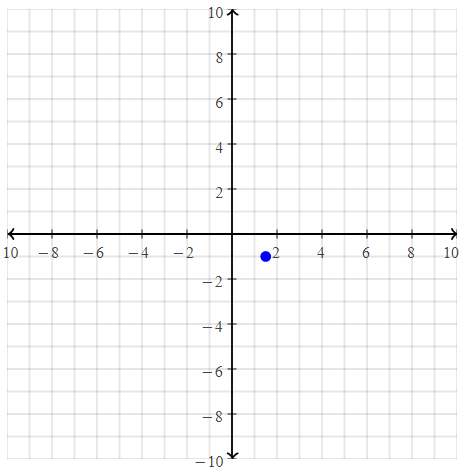
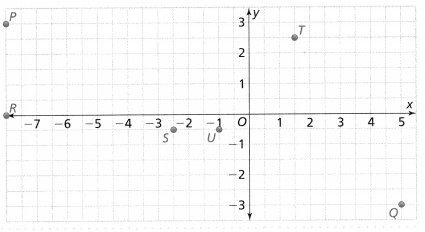


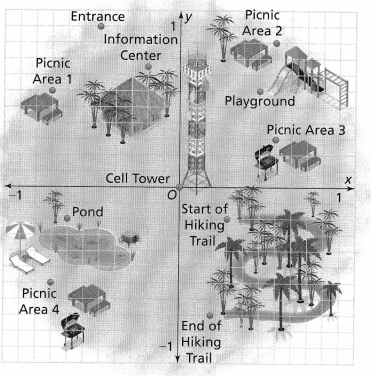
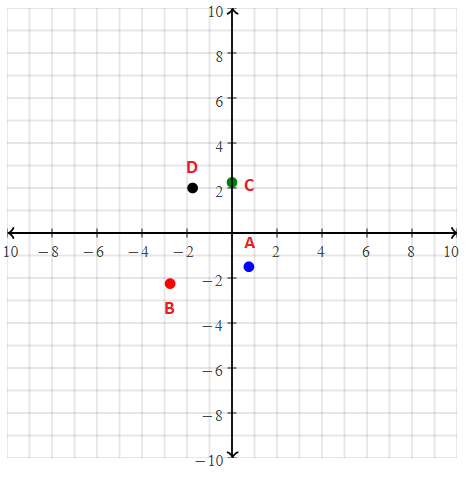




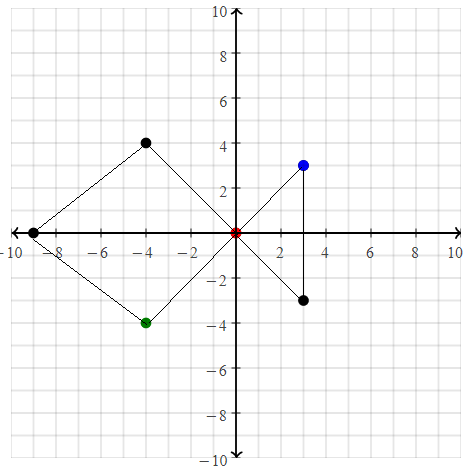


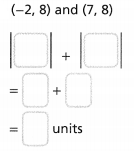
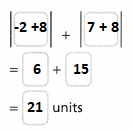
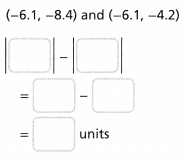
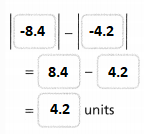
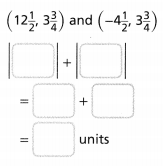
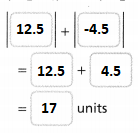
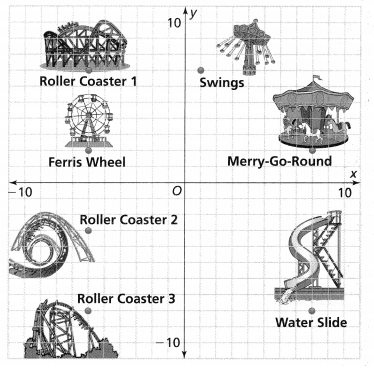

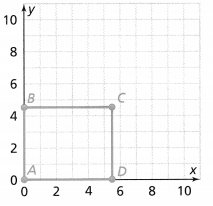

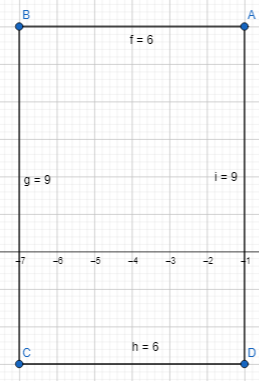

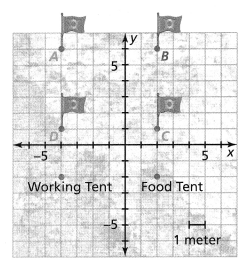

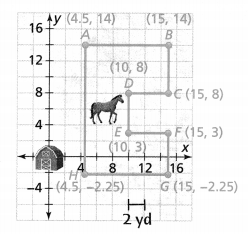

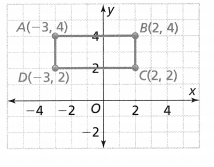

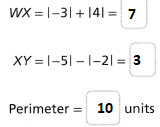
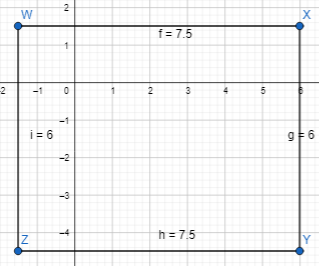
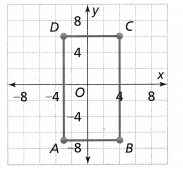

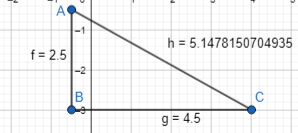





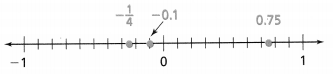


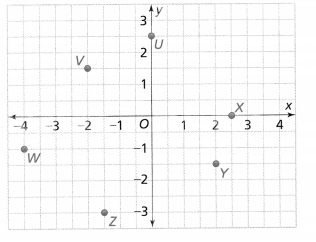
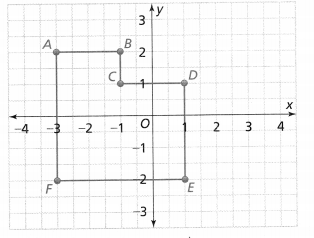
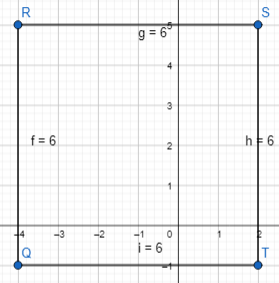




















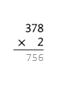
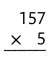
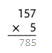
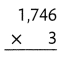
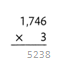
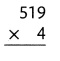
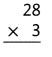
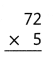
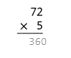
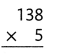
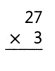

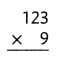
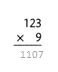
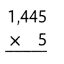
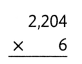
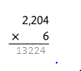












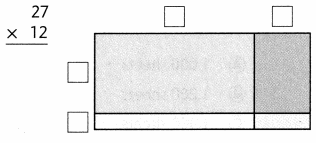

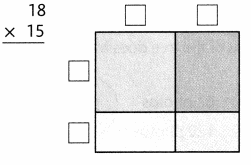
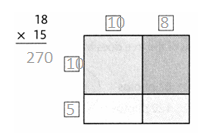


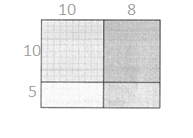


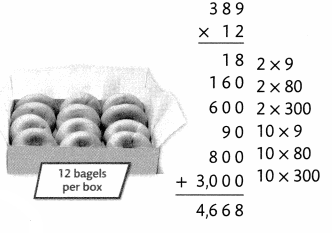

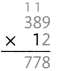

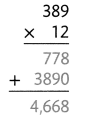
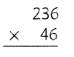
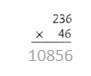
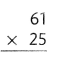
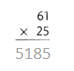
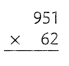
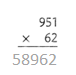
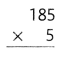
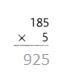

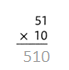
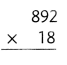

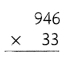

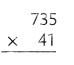
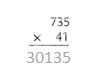
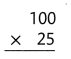
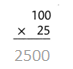
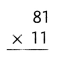
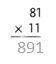
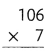
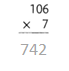
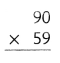
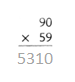
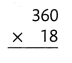
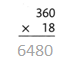
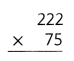

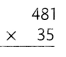
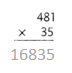
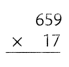
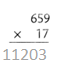

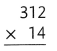




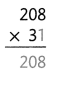
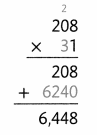
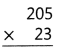
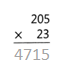

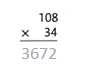
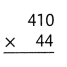
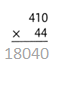
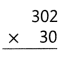

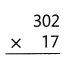
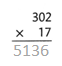
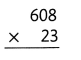
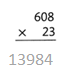
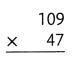

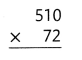
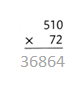
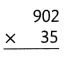
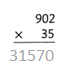
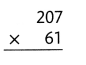
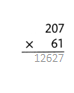
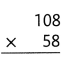
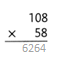





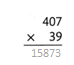

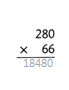

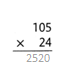
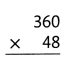
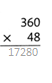







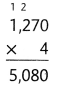
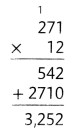

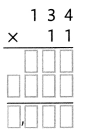
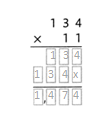

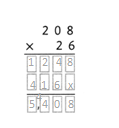

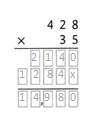


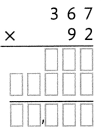
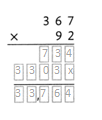
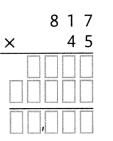
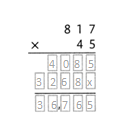
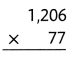

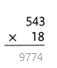
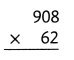
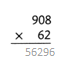
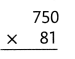
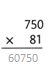

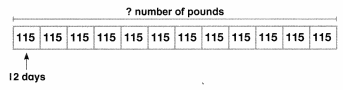
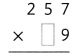






























































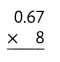
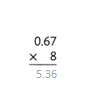

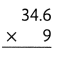
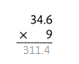
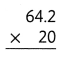
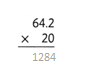
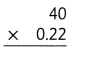

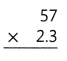
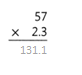



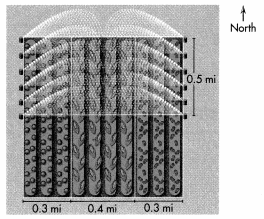
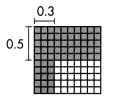










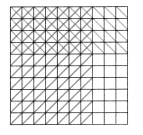

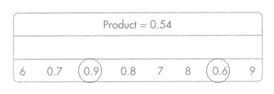

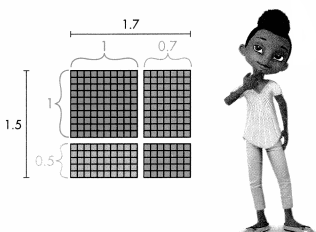
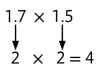

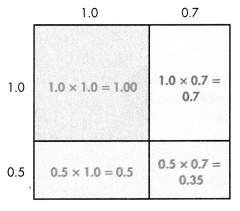
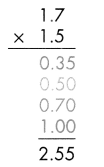
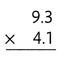
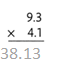
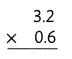

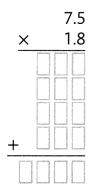
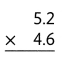
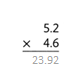


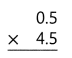
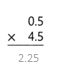
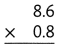








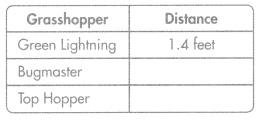


















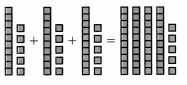






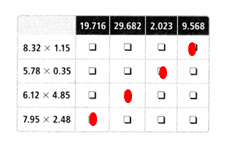

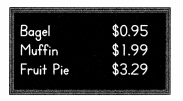
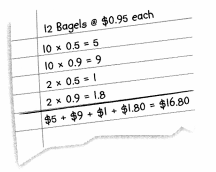






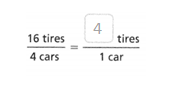
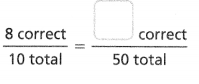


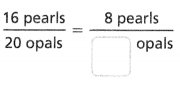
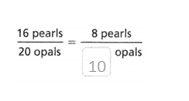
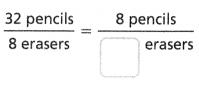
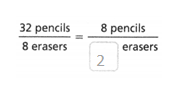

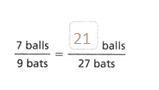







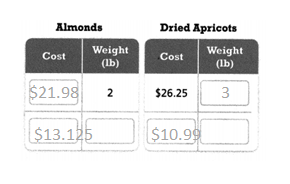

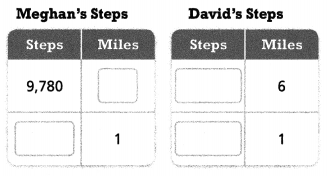


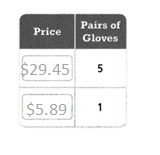




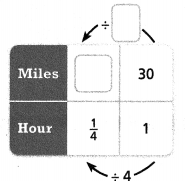





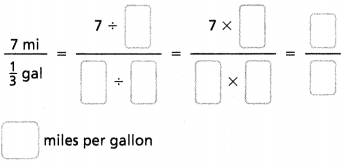
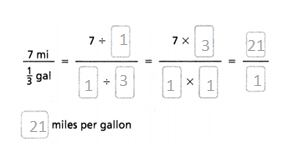
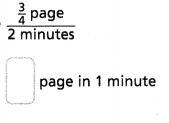

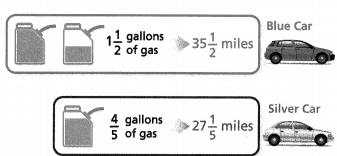
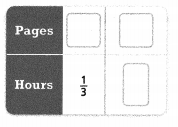
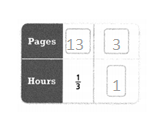

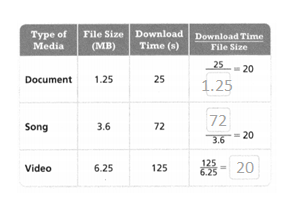
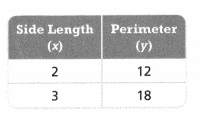
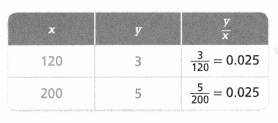
















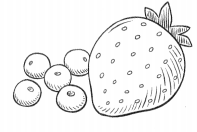


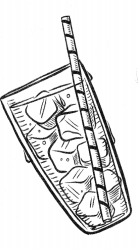

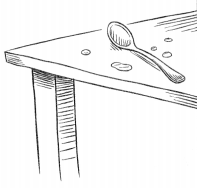
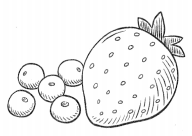









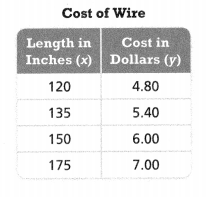





























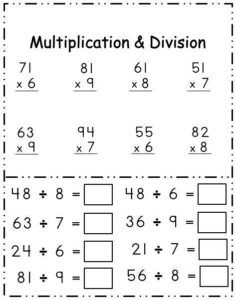








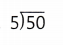 = 10.
= 10.
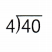

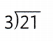



 = 4.
= 4.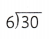
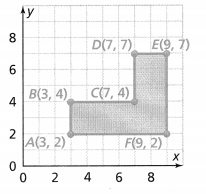
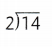 = 7.
= 7.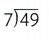 = 7.
= 7.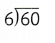 = 10.
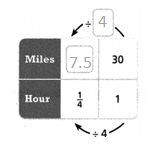
= 10.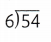 = 9.
= 9.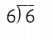 = 1.
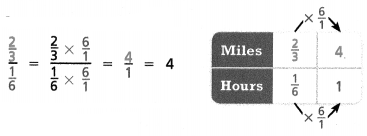
= 1.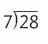 = 4.
= 4.


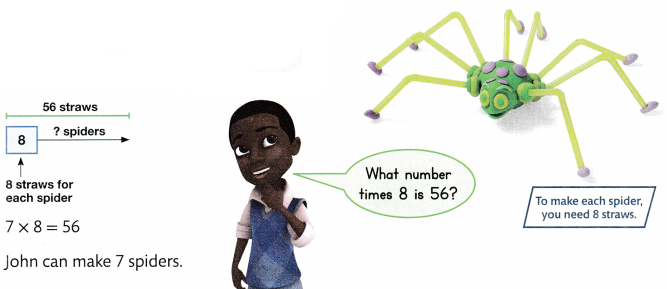

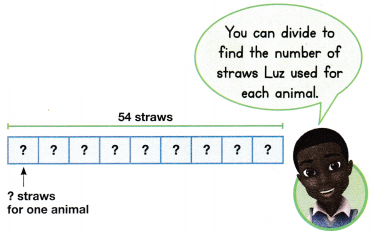
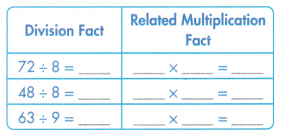
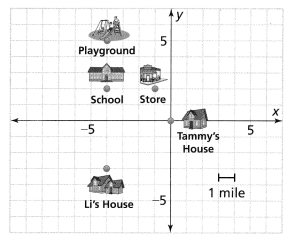
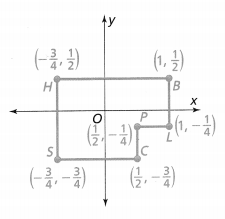
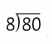 = 10.
= 10.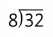 = 4.
= 4.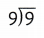 = 1.
= 1.






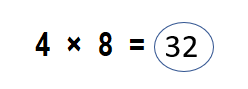







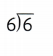

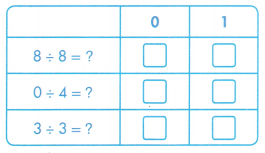
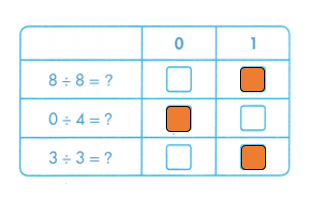
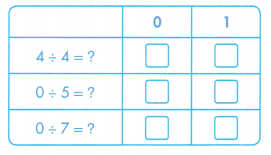


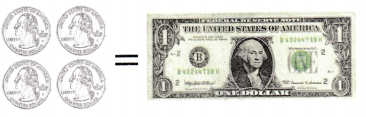

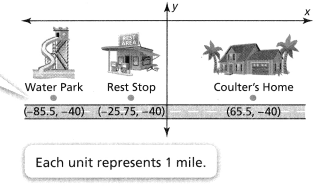
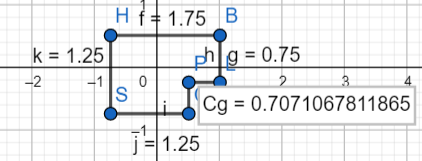
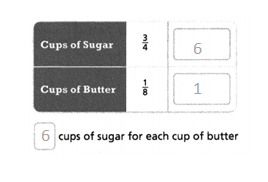
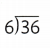 = 6.
= 6.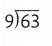 = 7.
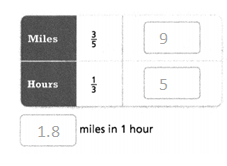
= 7.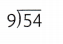 = 6.
= 6.