Envision Math 6th Grade Textbook Answer Key Topic 2.7 Using Expressions to Describe Patterns
Using Expressions to Describe Patterns
How can you write expressions to describe patterns?
Answer:
Delvin saves a part of everything he earns. The table at the right shows Delvin’s savings pattern.
The INPUT column shows the money he has earned.
The OUTPUT column shows the money he has saved.
Question.
Write an expression to describe the pattern.
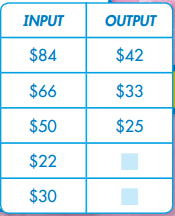
Answer:
Guided Practice
Do you know HOW?
Use the input/output table for 1 and 2.

Question 1.
If the input number is 8, what is the output number?
Answer:
11
Explanation:
Question 2.
Write an algebraic expression that describes the output pattern.
Answer:
x + 3
Explanation:

Do you UNDERSTAND?
Question 3.
Suppose that Delvin earned $36 mowing lawns. What input and output entries would you add to his table?
Answer:
IN: $36; OUT: $18
Explanation:
Question 4.
Reasonableness Is it reasonable for an output to be greater than the input in the table above? Explain.
Answer:
See margin.
Explanation:
Question 5.
What is the algebraic expression that describes the output pattern for the table above if the input is x?
Answer:
\(\frac{1}{2}\)x.
Explanation:
Independent Practice
Use this table for 6 and 7.

Question 6.
What is the cost of 4 lb, 5 lb, and 10 lb of apples?
Answer:
Question 7.
Write an algebraic expression that describes the output pattern if the input is a variable a.
Answer:
2a
Explanation:
Use this table for 8 and 9.
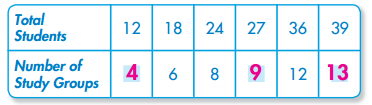
Question 8.
Copy and complete the table.
Answer:

Question 9.
Write an algebraic expression that describes the relationship between the input and output values.
Answer:
x ÷ 3
Explanation:
An input/output table is a table of related values. Identify the pattern.
What is the relationship between the values?
\(\frac{1}{2}\) (84) = 42 → 42 is half of 84
\(\frac{1}{2}\) (66) = 33 → 33 is half of 66
\(\frac{1}{2}\) (50) = 25 → 25 is half of 50.
The pattern is: \(\frac{1}{2}\) (INPUT) = OUTPUT
Let x= INPUT.
So, the pattern is \(\frac{1}{2}\) x.
Use the pattern to find the missing values.
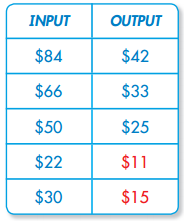
\(\frac{1}{2}\) (22) = 11
\(\frac{1}{2}\) (30) = 15
Problem Solving
Use the input/output table at right for 10 and 11.
Question 10.
Hazem keeps \(\frac{1}{3}\) of the tips he earns. Also, he gets $1 each night to reimburse his parking fee. This information is shown in the input/output table. Write an algebraic expression that describes the output pattern if the input is the variable k.
Answer:
(k ÷ 3) + 1 or \(\frac{1}{3}\) k + 1
Explanation:
Question 11.
How much money would Hazem keep in a night if he takes in $36 in tips?
Answer:
$13
Explanation:
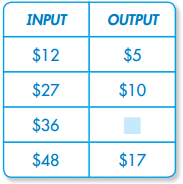
Use the input/output table at right for 12 and 13.

Question 12.
Ms. Windsor’s classroom has a tile floor. The students are making stars to put in the center of 4-tile groups. This input/ output chart shows the pattern. Write an algebraic expression that describes the output pattern if the input is the variable t.
Answer:
t ÷ 4
Explanation:
Question 13.
Writing to Explain There are 30 rows with 24 tiles in each row on a floor. Explain how to find the number of stars needed to complete the pattern for the floor.
Answer:
See margin.
Explanation:
Use the table at right for 14.
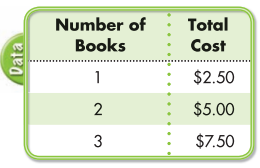
Question 14.
Think About the Process Which algebraic expression shows the cost of a chosen number of books b?
A. b + $2.50
B. $2.50b
C. $b – $2.50
D. b + $2.50
Answer:
B. $2.50b
