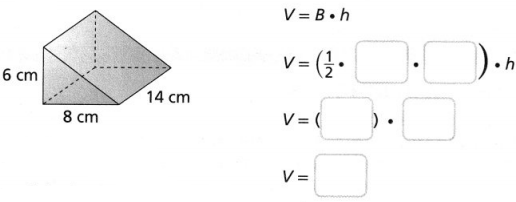
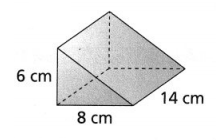
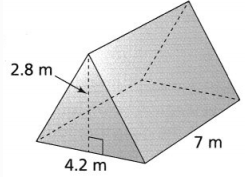
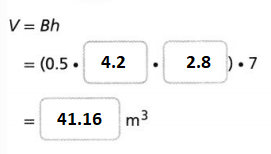
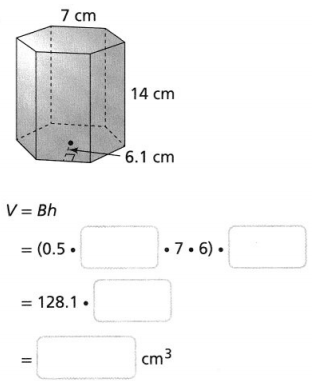
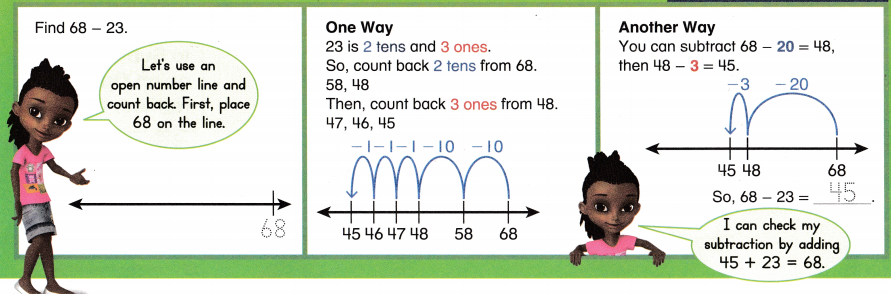
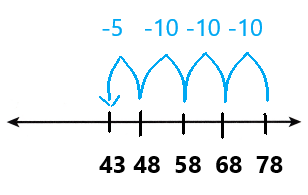
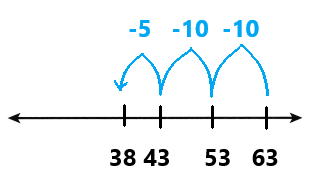
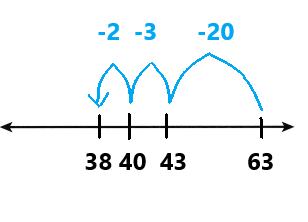
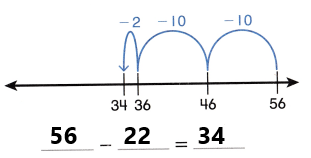
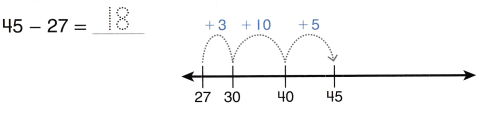
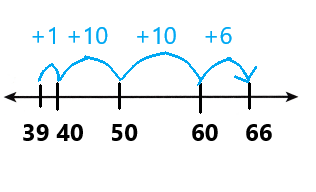
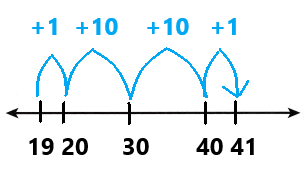
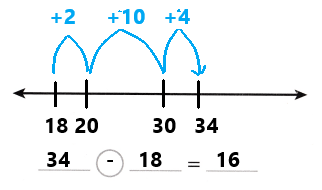
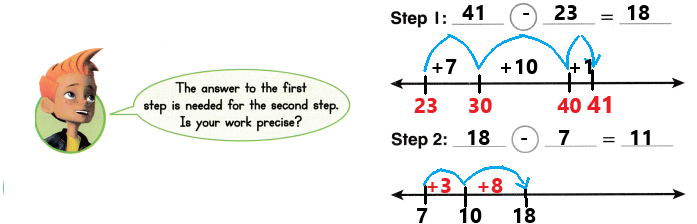
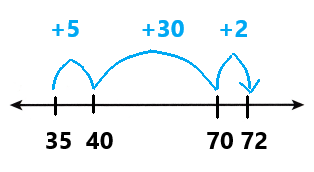
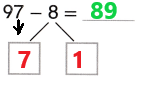
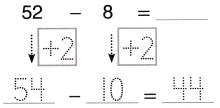
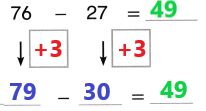
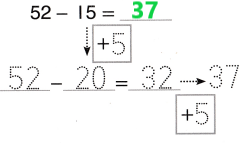
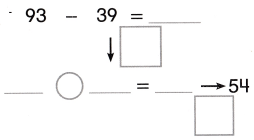
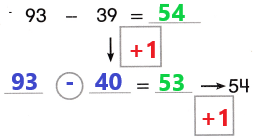
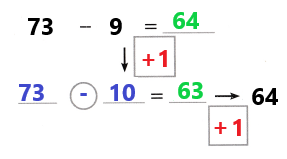
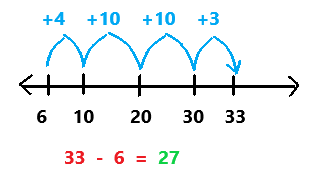
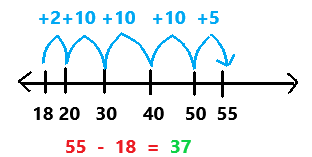
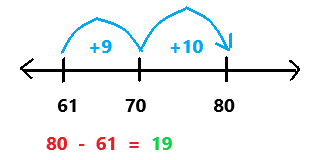
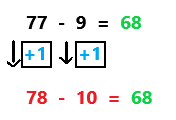
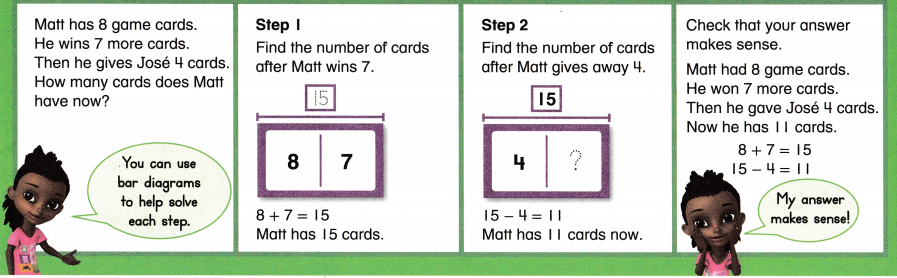
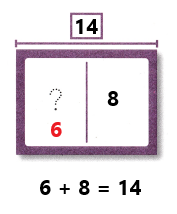
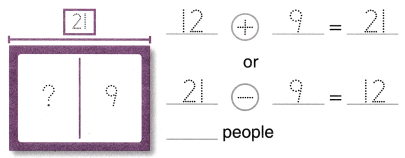
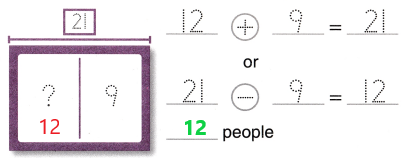
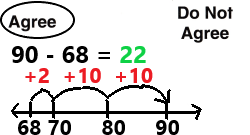
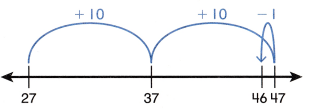
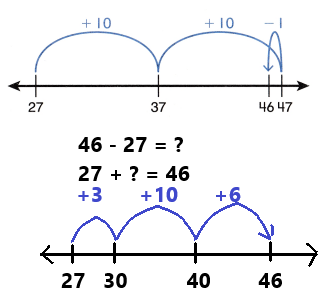
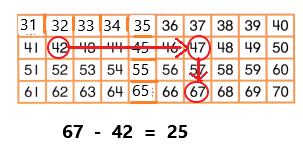
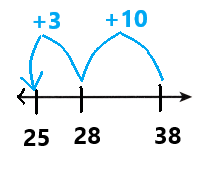
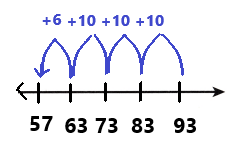
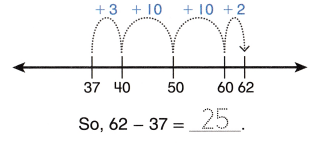
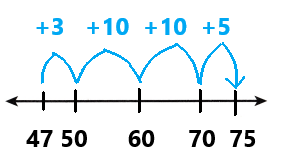
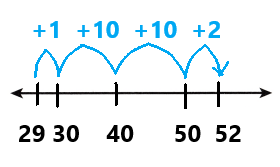
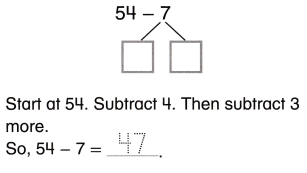
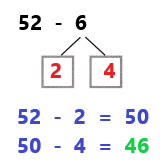
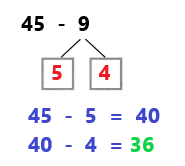
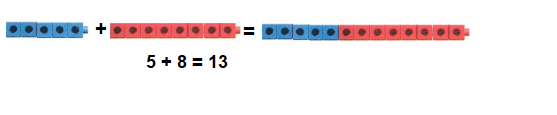
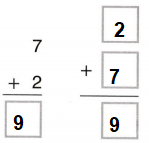
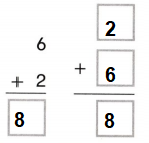
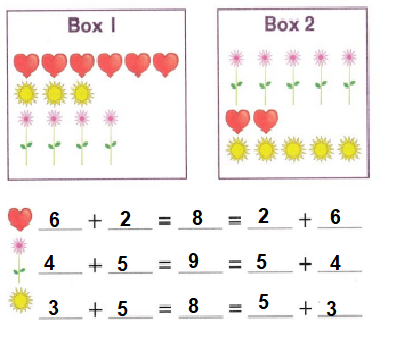
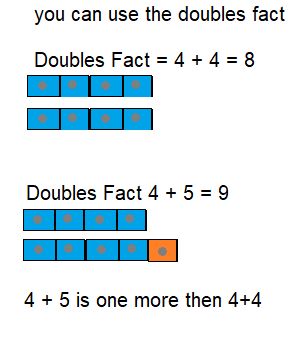
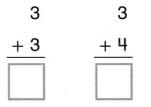
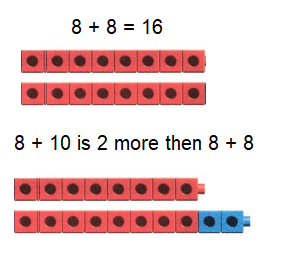
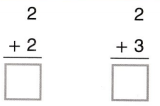
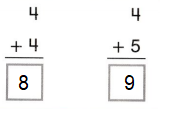
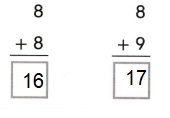
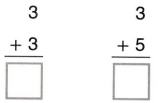
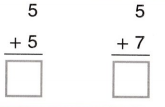
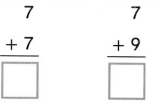
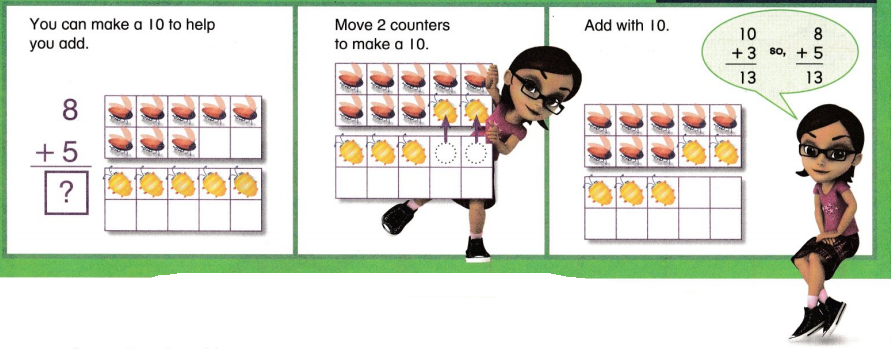
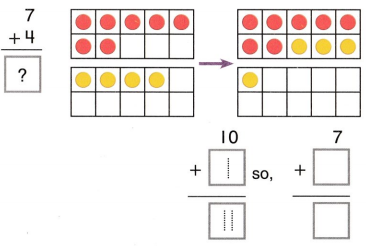
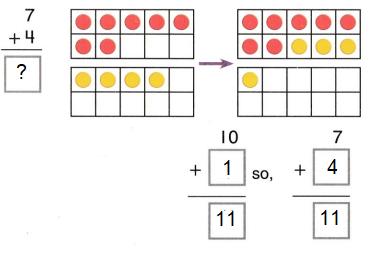
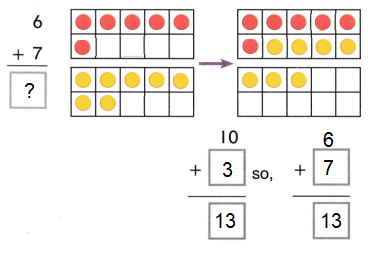
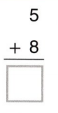
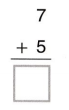
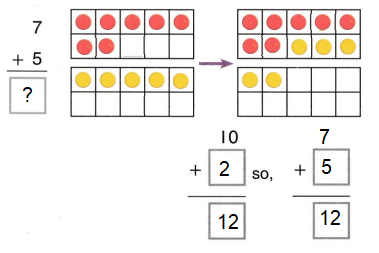
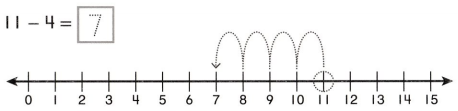
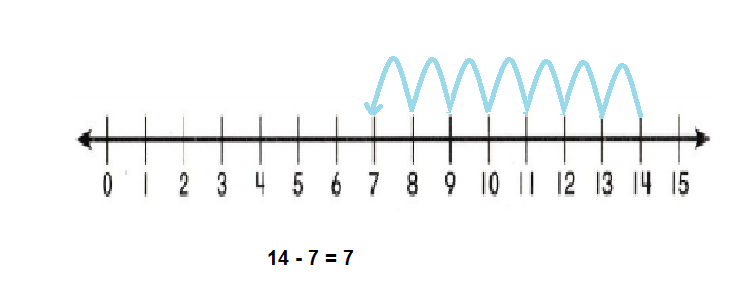
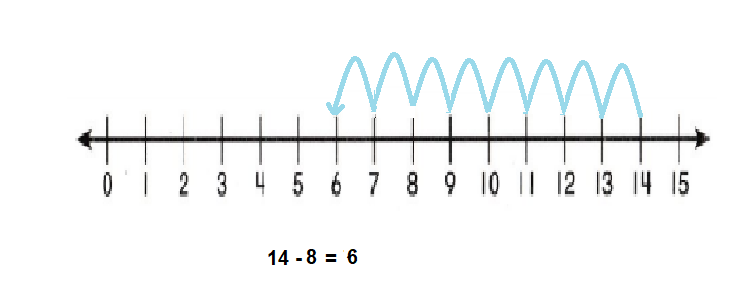
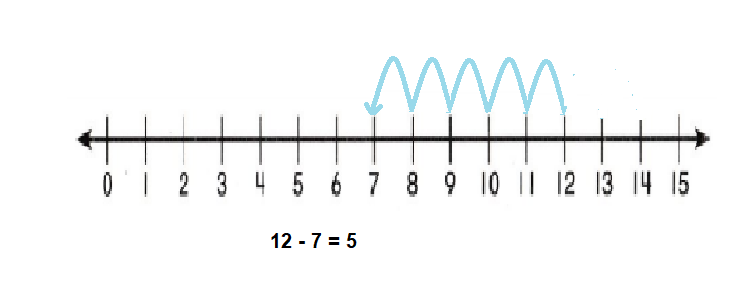
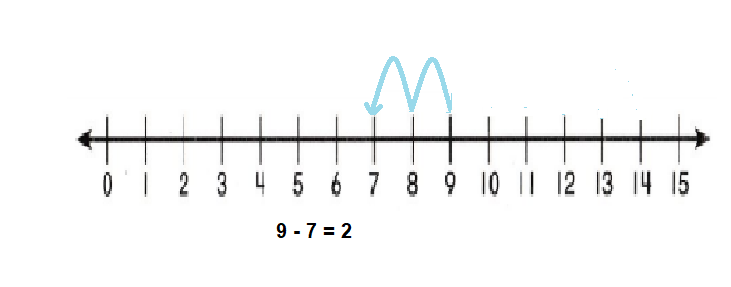
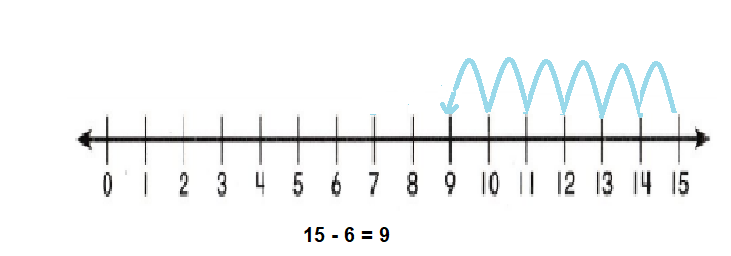
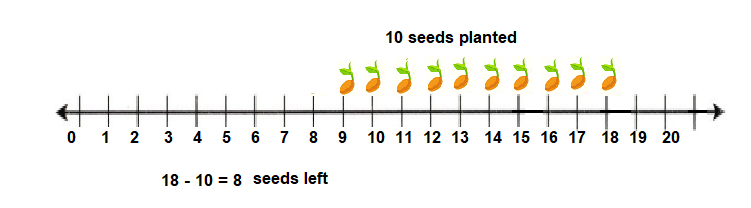
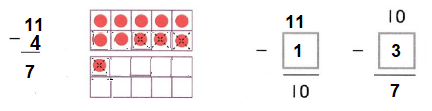
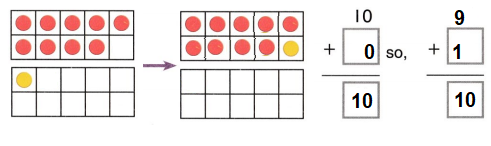
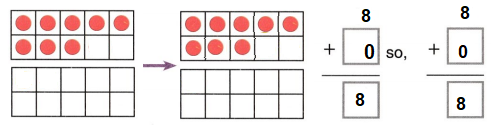
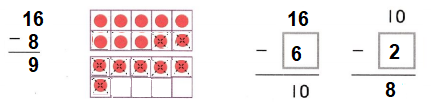
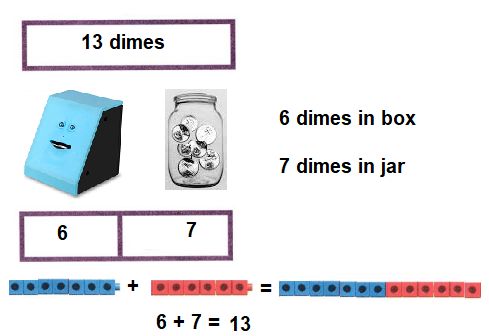
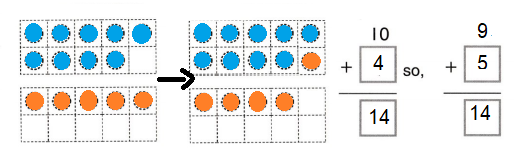
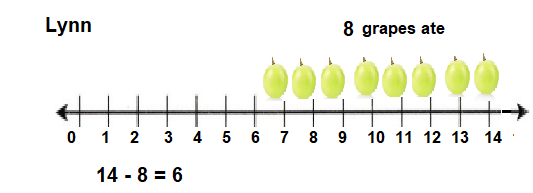
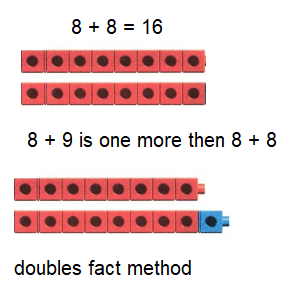
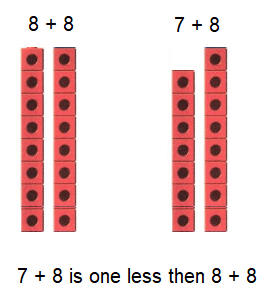
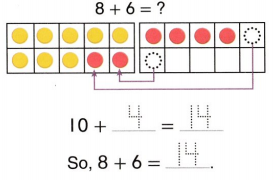
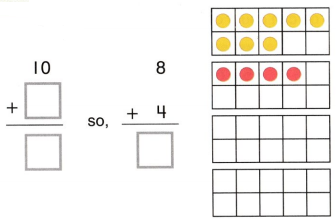
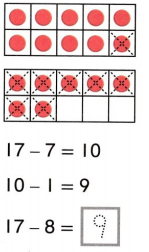
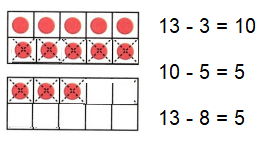
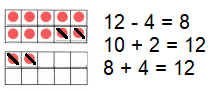
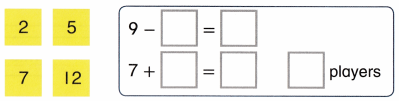
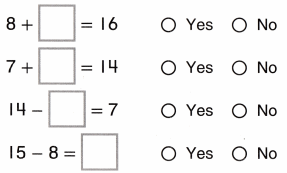
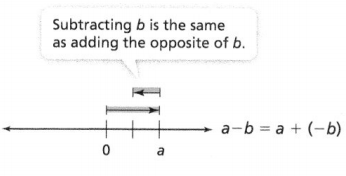
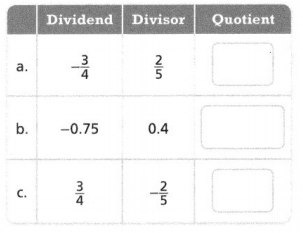
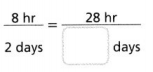
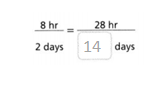
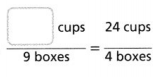
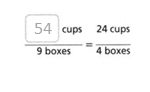
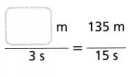
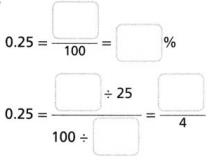
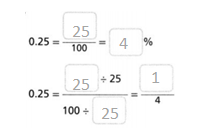
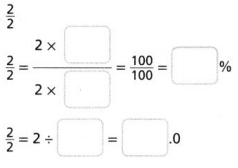
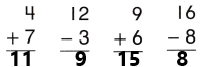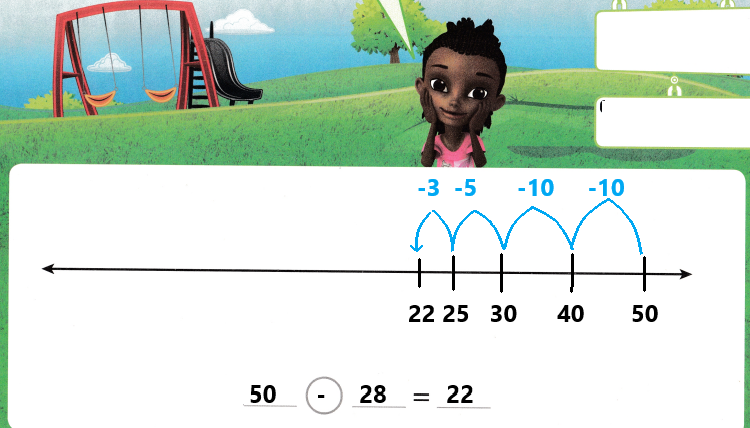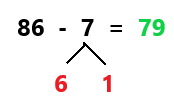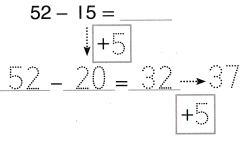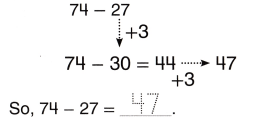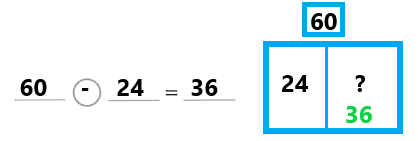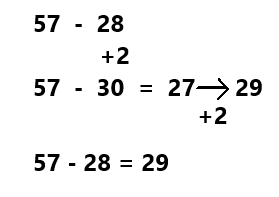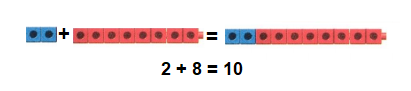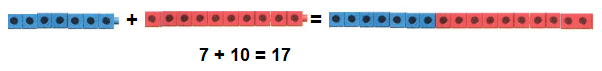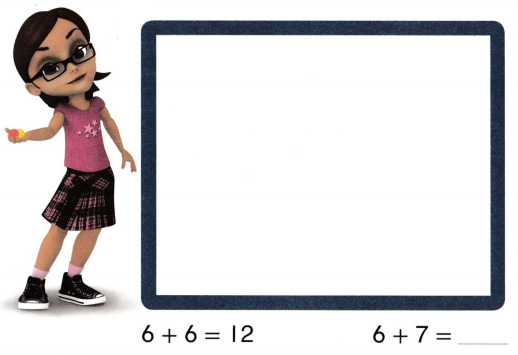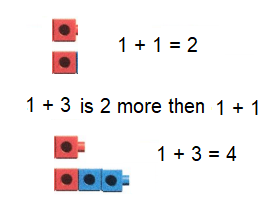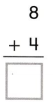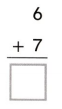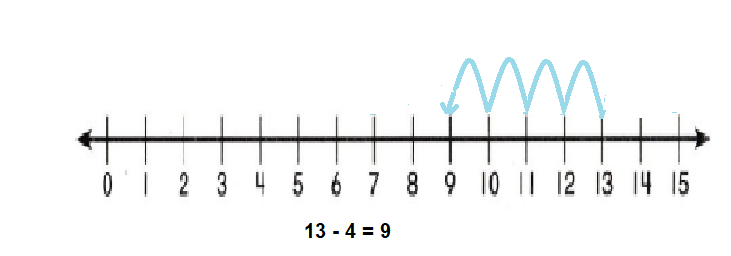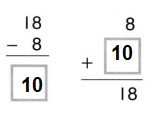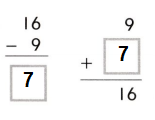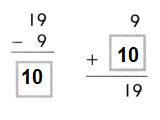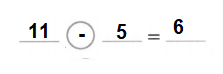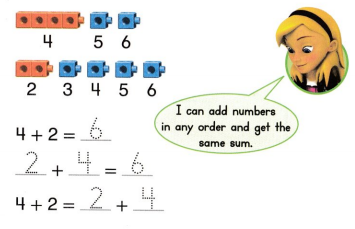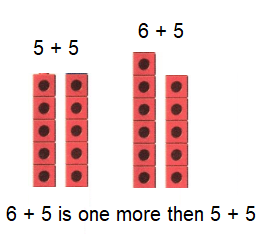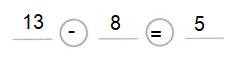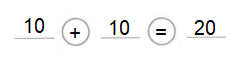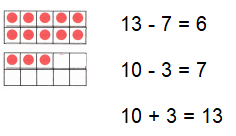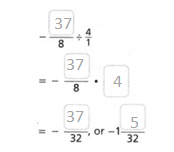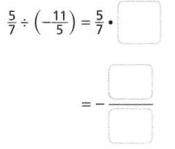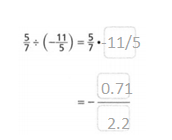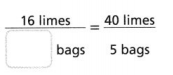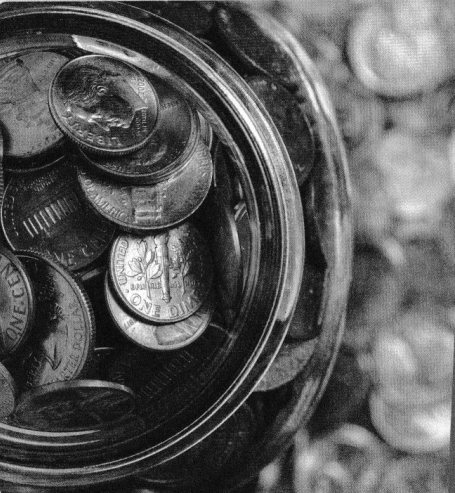Go through the enVision Math Common Core Grade 3 Answer Key Topic 8 Use Strategies and Properties to Add and Subtract regularly and improve your accuracy in solving questions.
enVision Math Common Core 2nd Grade Answers Key Topic 8 Use Strategies and Properties to Add and Subtract
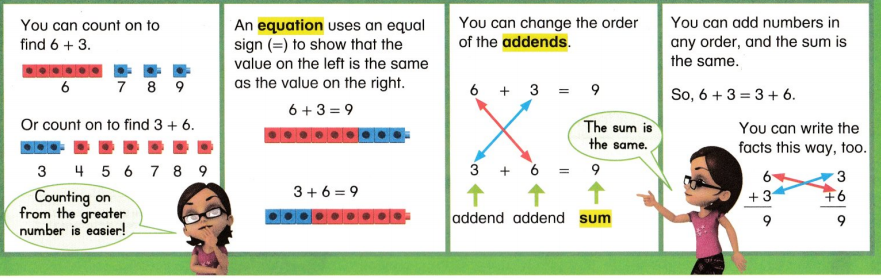
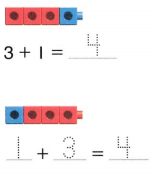
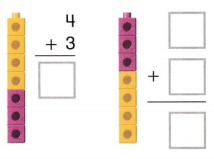
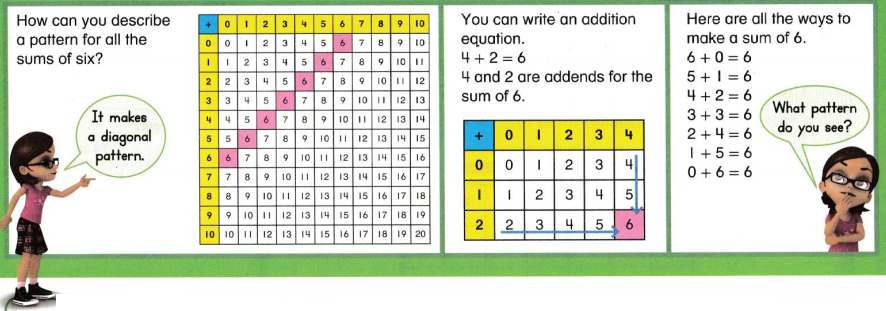
Essential Question: How can sums and differences be estimated and found mentally?

EnVision STEM Project: Traits and the Environment
Do Research Use the Internet or other sources to find out how the environment can influence plants or animals. Describe a trait in an animal or plant that can change due to the environment.
Journal: Write a Report Include what you found. Also in your report:
- Make a table that includes the plant or animal, the trait, and changes in the environment. Record any related data about the environment, such as temperature or rainfall.
- Include information about why the trait is useful.
- Write and solve addition problems using your data. Use estimation to check for reasonableness.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
• difference
• equation
• number line
• sum
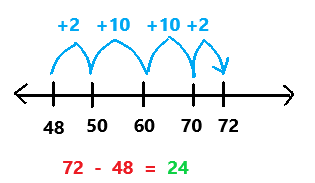
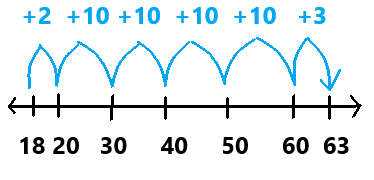
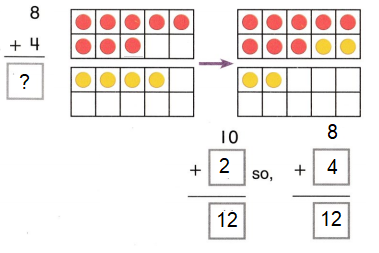
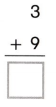
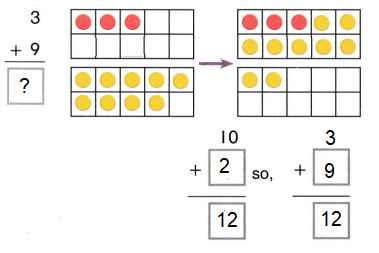
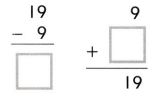
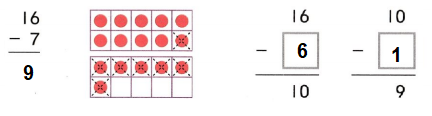
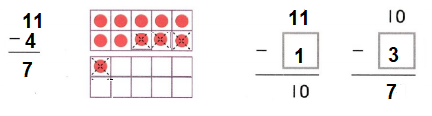
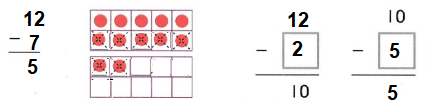
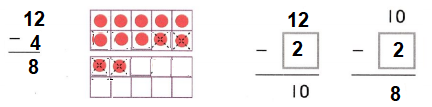
Question 1.
The amount that is left after you subtract is the ___.
Answer: The amount that is left after you subtract is the difference.
Question 2.
A line that shows numbers in order from left to right is a(n) ___.
Answer: A line that shows numbers in order from left to right is a number line
Question 3.
The total when you add is the ___.
Answer: The total when you add is the sum.

Question 4.
Both sides of a(n) ___ are equal.
Answer: Both sides of an equation are equal.
Addition and Subtraction Strategies
Find the sum or difference. Show your work.
Question 5.
32 + 58
Answer:
32 + 58
(30 + 2) + (50 +8) = 90
Question 6.
27 + 46
Answer:
27 + 46 = 73
(20 + 7) + (40 + 6) = 73
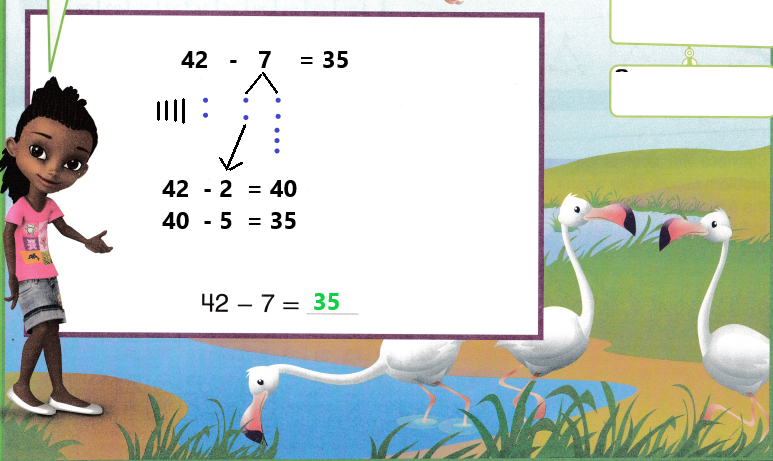
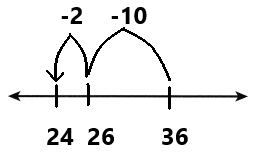
Question 7.
73 – 52
Answer:
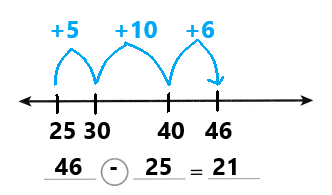
73 – 52 = 21
(70 + 3) – ( 50 + 2) = 21
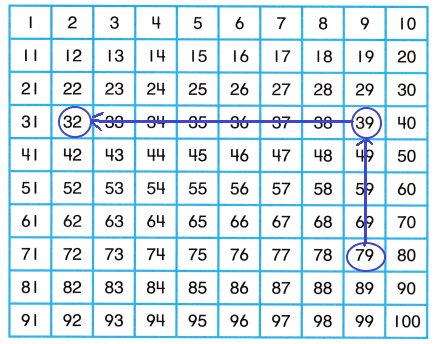
Question 8.
63 +16
Answer:
63 + 16 = 79
(60 + 3) + (10 + 6) = 79
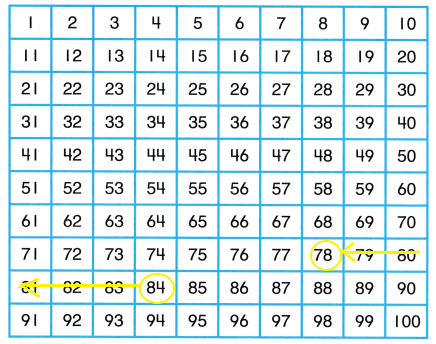
Question 9.
88 – 28
Answer:
88 – 28 = 60
(80 + 8) – (20 + 8) = 60
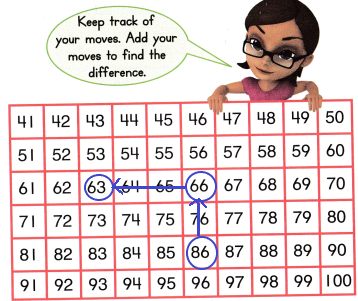
Question 10.
76 – 49
Answer:
76 – 49 = 27
(70 + 6) – (40 + 9) = 27
Numerical Expressions
Question 11.
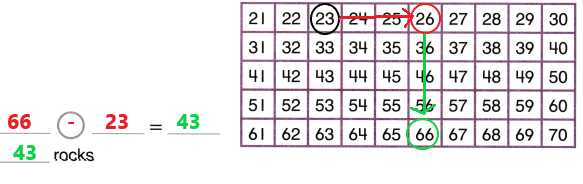
Atif puts 45 rocks in a display box. He has 54 rocks in all. Which expression can be used to find how many rocks are not in the display box?
A. 45 + 54
B. 45 + 45
C. 54 – 45
D. 54 – 54
Answer:
Option C is the correct answer because
Total rocks = 54
Atif puts in a display box = 45
Then total rocks – Atif puts in a display box = rocks are not in a display box.
Counting Money no
Question 12.
Tony has the coins shown at the right. Does he have enough money to buy a toy car that costs 86¢? Explain.

Answer:
No, because the sum of all cents is not enough to buy a toy car.
Pick a Project
PROJECT 8A
How much citrus is grown in Florida?
Project: Plan a Citrus Grove

PROJECT 8B
Would you like to travel across the country?
Project: Create and Perform Skits

PROJECT 8C
How can you add and subtract large numbers without a calculator?
Project: Make a Mental Math Game

PROJECT 8D
How many people live in our country?
Project: Design a Class Census and Give an Estimation Test

Lesson 8.1 Addition Properties
Activity
Solve & Share
Olivia arranges cups of buttons on three trays. She records the number of buttons on each cup. Which tray has the most buttons? Use place-value blocks or drawings to help solve the problem.

Are you making the same calculations more than once? How can you use structure to help solve the problem?

Look Back! Olivia pours all the buttons on Tray A into a bowl. She then divides the buttons equally into 8 cups. How many buttons are in each cup? Explain.

Visual Learning Bridge
Essential Question
What Are Some Properties of Addition?
A.
You can use properties of addition to join groups.
Parentheses show what to do first.

Associative (Grouping) Property of Addition: You can group addends in any way and the sum will be the same.

В.
Commutative (Order) Property of Addition: You can add numbers in any order and the sum will be the same.
57 + 35 = 35 + 57
C.
Identity (Zero) Property of Addition: The sum of zero and any number is that same number.

39 + 0 = 39
Convince Me!
Use Structure Pick one of the properties above. Explain how you can use a number line to show an example of that property.
Guided Practice
Do You Understand?
Question 1.
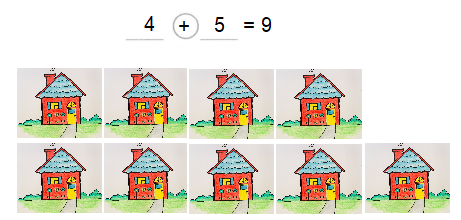
Ralph says he can rewrite (4 + 5) + 21 as 9 + 21. Do you agree? Why or why not?
Answer:
Yes I agree
because 4 + 5 = 9
So, In place of 4 + 5, we can write has 9
Question 2.
What property is shown with this equation? How do you know?
65 + (18 + 38) = (18 + 38) + 65
Answer:
This equation is in the form of Associative property. This property allows us to change the groupings of addition or multiplication and keep the same value.
Do You Know How?
In 3 and 4, identify each property.
Question 3.
4 + (15 + 26) = (4 + 15) + 26
Answer:
The equation is in the form of Associative property.
Associative property allows us to change groupings of addition or multiplication and keeps the same value.
Question 4.
17 + 0 = 17
Answer:
This equation is in the form of the Identity property of addition.
The identity property of 1 says that any number multiplied by 1 keeps its identity.
In 5-7, write each missing number.
Question 5.
__ + 90 = 90
Answer:
0 + 90 = 90
Question 6.
42 + 23 = 23 + __
Answer:
42 + 23 = 23 + 42
Question 7.
(2 + __) + 36 = 2 + (23 + 36).
Answer:
(2 + 23) + 36 = 2 + (23 + 36)
Independent Practice
In 8-11, identify each property.
Question 8.
19 + 13 = 13 + 19
Answer:
The equation is in the form of
a + b = b + a
It is a commutative property.
Commutative property states that the change in the order of numbers in the addition or multiplication operation does not change the sum or the product.
Question 9.
18 + 0 = 18
Answer:
It is a identity property.
The identity property of 1 says that any number multiplied by 1 keeps its identity.
Question 10.
16 + (14 + 13) = (16 + 14) + 13
Answer:
The equation is in the form of Associative property.This allows us to change groupings of addition or multiplication and keep the same value.
Question 11.
(39 + 12) + 8 = (12 + 39) + 8
Answer:
The equation is in the form of the commutative property.
Commutative property states that the change in the order of numbers in an addition or multiplication and keeps the same value.
In 12-19, write each missing number.
Question 12.
25 + 62 = __ + 25
Answer:
25 + 62 = 62 + 25
Thus the missing number is 62.
Question 13.
(22 + 32) + 25 = ___ + (22 + 32)
Answer:
(22 + 32) + 25 = 25 + (22 + 32)
Thus the missing number is 25.
Question 14.
23 + __ + 11 = 23 + 11
Answer:
23 + 0 + 11 = 23 + 11
Thus the missing number 0.
Question 15.
10 + (45 + 13) = (__ + 45) + 13
Answer:
10 + ( 45 + 13 ) = (10 + 45) + 13
Thus the missing number is 10.
Question 16.
(__ + 0) + 14 = 7 + 14
Answer:
(7 + 0) + 14 = 7 + 14
Thus the missing number is 7.
Question 17.
(12 + 2) + 20 = ___+ 20
Answer:
(12 + 2) + 20 = 14 + 20
Thus the missing number is 14.
Question 18.
34 + (2 + 28) = (___ + 28) + 34
Answer:
34 + (2 + 28) = ( 2 + 28 ) + 34
Thus the missing number is 2.
Question 19.
(50 + 30) + __ = 50 + (30 + 20)
Answer:
(50 + 30) + 20 = 50 + (30 + 20)
Thus the missing number is 20.
Problem Solving
Question 20.
Make Sense and Persevere Gino packs his blue and green pencils into boxes. He puts 8 pencils in each box. How many boxes does Gino use?

Answer:
Blue pencils = 23
Green pencils =17
Gino puts pencils in each box = 8
Blue pencils + Green pencils = 40
Therefore 40 ÷ 5 = 5
Gino uses 5 boxes.
Question 21.
Group the addends below in a different way to get the same sum. Write the new equation.
(42 + 14) + 6 = 62
Answer:
New equation is (6+ 14) + 42 = 62
Question 22.
Vocabulary How is the Commutative Property of Addition like the Commutative Property of Multiplication?
Answer:
The commutative property states that the numbers on which we operate can be moved from their position without making any difference to the answer.
The property holds for addition and multiplication.
Question 23.
enVision® STEM A lionfish has 13 spines on its back, 2 more spines near its stomach, and 3 more near its tail. Using a property of add isition, write two different equations to find how many spines a lionfish has. What property did you use?
Answer:
Lionfish has spines on its back = 13
More spines near it’s stomach = 2
More near it’s tail = 3
To find the total spines on lionfish we are using two different properties of addition.
1. Associative property of addition
(13 + 2) + 3 = 13 + (2 + 3)
2. Commutative property of addition
13 + 2 + 3 = 3 + 2 + 13
Total spines on lionfish = 18
Question 24.
Higher Order Thinking Barry says he can subtract numbers in any order and the difference will stay the same. Is Barry correct? Give an example to support your answer.
Answer: No
3 – 2 = 1
2 – 3 = -1
By this example, we can say that the subtraction of numbers in any order will not be the same.
Assessment Practice
Question 25.
Use place value to find the sum of 33 +42 + 17.
A. 89
B. 90
C. 91
D. 92
Answer:
D is the answer because
33 + 42 + 17 = 92

Question 26.
Use properties of operations to find the sum of 22 + 30 + 28.
A. 80
B. 70
C. 60
D. 50
Answer:
To find the sum of 22 + 30 + 28 we are using commutative property.
We write the as
22 + 28 + 30; 30 + 28 + 30,
From this equation, we can calculate 22,28 in an easy way.
Lesson 8.2 Algebra: Addition Patterns
Activity
Solve & Share
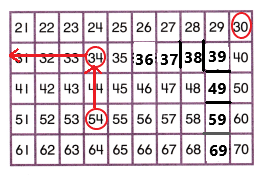
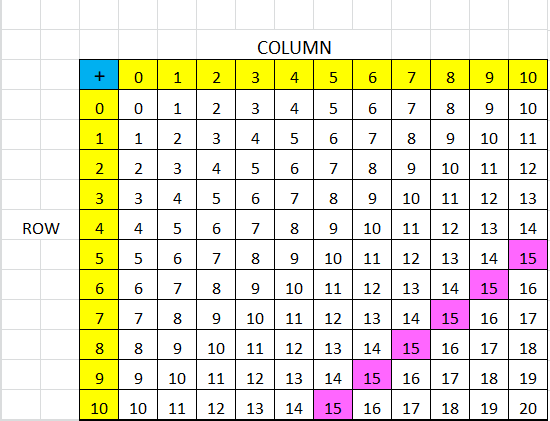
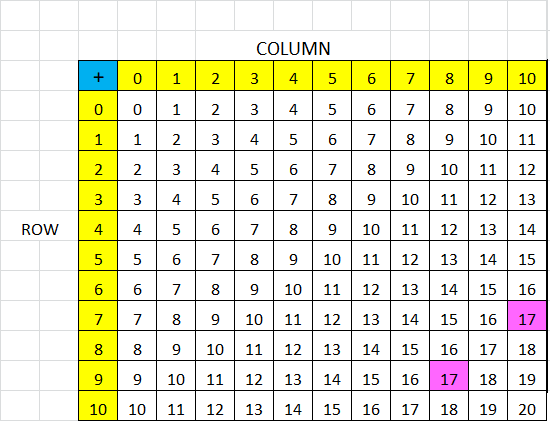
Shade three sums that are next to each other on the addition table. Add the first and third sums you shaded. Find a pattern using that total and the second sum you shaded. How are the total and the second sum related? Is this true for other sets of three sums next to each other?
You can look for relationships in the addition table. The numbers in the shaded column and shaded row are addends. The other numbers are the sums.

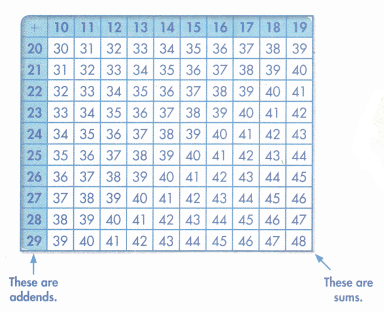
Look Back! Explain how you can test to see if the relationship among the three sums that are next to each other is a pattern.
Essential Question How Can You Find Addition Patterns?
Visual Learning Bridge
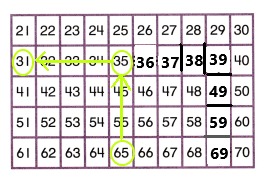
A.
Helen found the sum of the purple numbers in the red square. Then she found the sum of the green numbers. The sums form a pattern. Find the sums and describe the pattern.
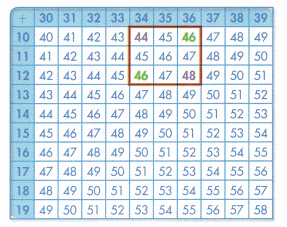
You can use a variety of strategies to find the sums!

B.
Use the Associative Property.
44 + 48 = 44 + (2 + 46)
= (44 + 2) + 46
= 46 + 46
C.
Use mental math.
44 +48 = (44 + 2) + (48 – 2)
= 46 +46
44 +48 = 46 + 46
The sum of the purple numbers is equal to the sum of the green numbers. That’s a pattern!

D.
Use the Commutative and Associative Properties.
44 + 48 = (10 + 34) + (12 + 36)
46 + 46 = (12 + 34) + (10 + 36)
Use the properties to rearrange the addends.
(10 + 34) + (12 + 36) = (10 + 34) + (12 + 36)
The sum of the purple numbers is 92.
The sum of the green numbers is 92.
The sums are double the middle number in the red square. That is another pattern.
Convince Me!
Generalize The red square above is 3 squares tall by 3 squares wide. Sebastian says there are other size squares in the addition table that have patterns. Describe a different-size square and its patterns.
Guided Practice
Do You Understand?
Question 1.
Are the sums of any two sets of diagonal corner numbers in a 3-by-3 square in a standard addition table always equal? Explain.
Answer: Yes
Do You Know How?
Question 2.
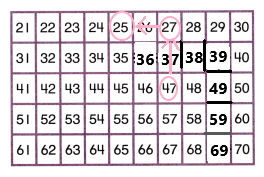
Look at the addition table in Box A on the previous page. Why do the numbers going down to the right on the diagonal increase by 2? Explain.
Answer: In the box A the numbers from left to right is sequence numbers so, in the diagonal box the numbers are going from down to right.
Independent Practice
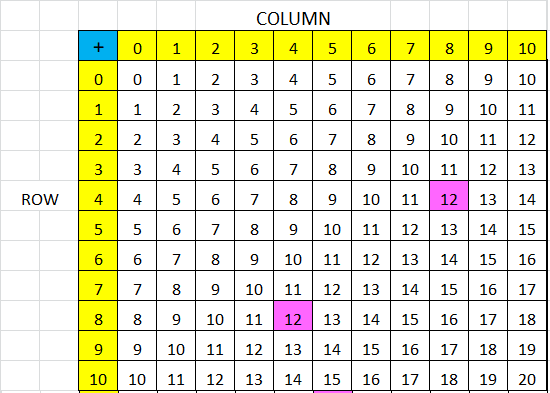
In 3 and 4, use the table at the right.
Question 3.
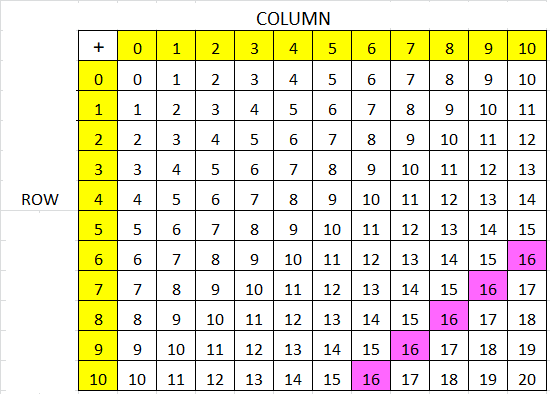
Look at the sums that are shaded the same color. Describe a pattern shown by these pairs of sums. Explain why this pattern is true.

Answer:
Question 4.
Find other pairs of sums with a similar pattern. Shade them on the table. Explain why you chose those sums.
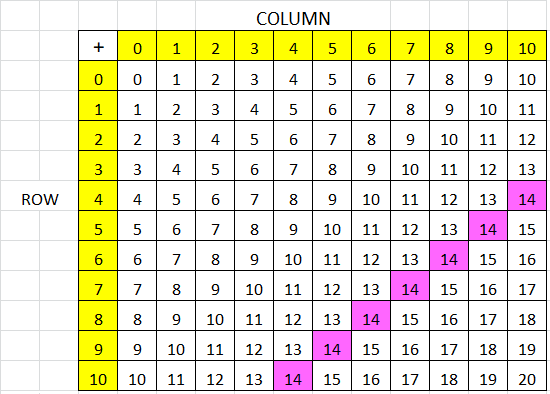
In 5 and 6, use the table at the right.
Question 5.
Shade the table to show a pattern you see. Describe your pattern.
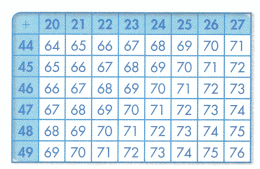
Answer:
Question 6.
Explain why your pattern is true.
Answer:
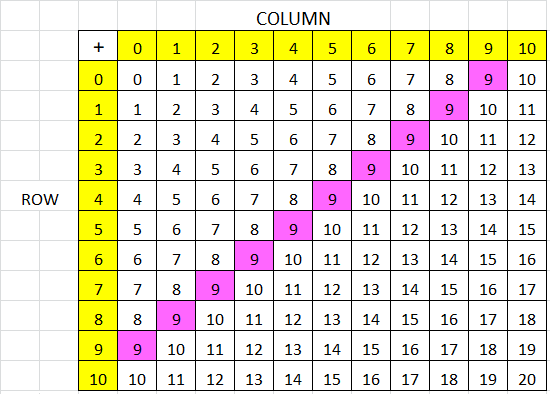
Problem Solving
Question 7.
Look for Relationships Greg drew a rectangle on the addition table at the right. He colored the corners. Find the sum of the green corners. Find the sum of the orange corners. What pattern do you notice?
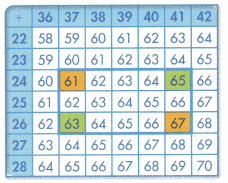
Answer:
Question 8.
Draw another rectangle on the addition table. See if Greg’s pattern is true for this rectangle.
Answer:
Question 9.
Explain why Greg’s pattern works.
Answer:
Question 10.
Which multiplication fact does the number line show? Write a related division fact.

Answer:
multiple of 5.
Question 11.
Higher Order Thinking Pierre made an addition table. He skip counted by 3 for the addends. Find and describe a pattern in Pierre’s table.
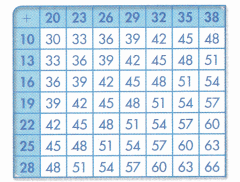
Answer:
Assessment Practice
Question 12.
Look at the shaded cells the addition table below.

Which pattern and property of operations are shown in the shaded cells?
A. Each orange sum is equal to zero plus the other addend; The Identity Property of Addition
B. Each green sum is 10 greater than one of its addends; The Identity Property of Addition
C. Each green sum is ten greater than the sum before; The Associative Property of Addition
D. There are no patterns or properties.
Answer:
Lesson 8.3 Mental Math: Addition
Activity
Solve & Share
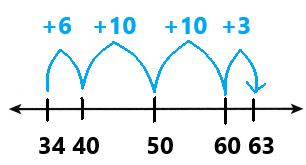
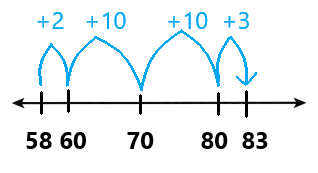
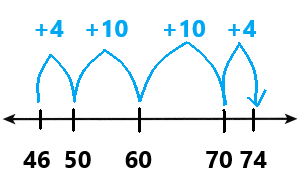
A school store sold 436 pencils last week and 7 packages that each had 4 pencils today. Use mental math to find how many pencils were sold in all. Explain how you found your answer.
You can use structure by examining the quantities in the problem.

Look Back! What is another way you can find the sum of 436 pencils plus 7 packages of 4 pencils each using mental math?
Visual Learning Bridge
Essential Question
How Can You Add with Question Mental Math?
A.
Dr. Gomez recorded the number of Northern Right Whales, Atlantic Spotted Dolphins, and Western Atlantic Harbor Seals she saw off the coast of Florida in two different years. How many whales did Dr. Gomez see during the two years?

You can use an open number line, mental math strategies, and properties of operations to solve this problem.

B.
One Way Find 325 + 114. Use the adding on strategy.
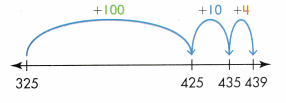
Start at 325. Break apart 114.
Add 100 to 325.
Add 10 to 425.
Add 4 to 435.
325 + 114 = 439
Dr. Gomez saw 439 whales.
C.
Another Way
Find 325 + 114. Use the make ten strategy. Break apart
114. 114 = 5 + 100 + 9
Add 5 to 325 to make ten.
325 + 5 = 330
Then, add 100.
330 + 100 = 430
Break 114 apart to find a number that makes a ten when added to 325.

Finally, add 9.
430 + 9 = 439
325 + 114 = 439
Dr. Gomez saw 439 whales.
Convince Me!
Model with Math Show two ways to find the total number of dolphins seen.
Guided Practice
Do You Understand?
Question 1.
Compare the One Way and on the previous page. How are they the same? How are they different?
Question 2.
Use mental math to find how many animals Dr. Gomez saw during Year 2. Show your work.
Answer:
Dr.Gomez saw whales in second year = 114
Dr.Gomez saw Dolphins in second year = 171
Dr. Gomez saw seals in second year = 212
Total number of animals that Dr.Gomez saw during second year is
114 + 171 +212
100 + 10 + 4 + 100 + 70 + 1 + 200 + 10 + 2
400 + 90 + 5 + 2
400 + 90 + 7
400 + 97 = 497
Do You Know How?
Question 3.
Use the make ten strategy to add 738 + 126.
126 = 2 + 24 + 100
738 + ___ = 740
740 + __ = 764
764 + __ = 864
So, 738 + 126 = ___.
Answer:
126 = 2 + 24 + 100
738 + 2 = 740
740 + 24 = 764
764 + 100 = 864
So, 738 + 126 = 864
Question 4.
Use the adding strategy to add 325 + 212.
212 = 200 + 10 + 2
325 + 200 = ___
525 + 10 = ___
___ + 2 = 537
So, 325 + 212 = __.
Answer:
212 = 200 + 10 + 2
325 + 200 = 525
525 + 10 = 535
535 + 2 = 537
So, 325 + 212 = 537
Independent Practice
In 5-12, find each sum using mental math or an open number line.
Question 5.
252 +44
Answer:
To find the sum here we are using mental math.
252 + 44
200 + 50 + 2 + 40 + 4
200 + 90 + 6
200 + 96 = 296
Question 6.
236 + 243
Answer:
To find the sum here we are using mental math.
236 + 243
200 + 30 + 6 + 200 +40 + 3
400 + 70 + 9
400 + 79 = 479
Question 7.
651 + 150
Answer:
To find the sum here we are using mental math.
651 + 150
600+ 50 + 1 +100 + 50
700 + 100 + 1
600 + 1 = 601
Question 8.
378 + 542
Answer:
To find the sum here we are using mental math.
378 + 542
300 + 70 + 8 + 500 + 40 + 2
800 + 110 + 10
800 + 120 = 920
Question 9.
473 + 198
Answer:
To find the sum here we are using mental math.
473 + 198
400 + 70 + 3 + 100 + 90 + 8
500 + 160 + 11
500 + 171 = 671
Question 10.
319 + 339
Answer:
To find the sum here we are using mental math.
319 + 339
300 + 10 + 9 + 300 + 30 + 9
600 + 40 + 18
600 + 58 = 658
Question 11.
208 + 511
Answer:
To find the sum here we are using mental math.
208 + 511
200 + 8 + 500 + 10 + 10 + 1
700 + 18 + 10 +1
710 + 19 = 729
Question 12.
523 + 169
Answer:
To find the sum here we are using mental math.
523 + 169
500 + 20 + 3 + 100 + 60 + 9
600 + 80 + 12
600 + 92 = 692
Problem Solving
Question 13.
Higher Order Thinking Maxine earns $8 each hour that she works as a cashier. She starts with $233. Today she cashiers for 6 hours. How much does she have at the end of the day? Explain how you found your answer.
Answer:
Given,
Maxine earns $8 each hour that she works as a cashier.
She starts with $233. Today she cashiers for 6 hours.
6 × $8 = $48
$233 + $48 = $281
Therefore Maxine have $281 at the end of the day.
Question 14.
Lauren sorted the 4 solids into 2 groups. Use mathematical terms to explain how she sorted the solids.

Answer:
Question 15.
The Rodriguez family drives 229 miles on Friday and 172 miles on Saturday. Explain how you can use the adding on strategy to find the total number of miles the Rodriguez family drives.
Answer:
Rodriguez family drives on Friday = 229 miles
Rodriguez family drives on Saturday = 172
Total number of miles that Rodriguez family drives = 229 + 172
200 + 20 + 9 + 100 + 70 + 2
300 + 90 + 11
300 + 101 = 401
Question 16.
Critique Reasoning Bill added 438 + 107. He recorded his reasoning below. Critique Bill’s reasoning. Are there any errors? If so, explain the errors.
Find 438 + 107.
I’ll think of 7 as 2 + 5.
438 + 2 = 440
440 + 7 = 447
447 + 100 = 547
So, 438 + 107 is 547.
Answer:
Above equation has an error, In place of adding 7 with 440 we want to add 5 then it is correct.
Assessment Practice
Question 17.
Find 153 + 121. Break apart 121 by place value, and then use the adding on strategy. Select numbers to complete the equations.

Answer:

Question 18.
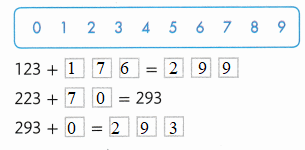
Find 123 + 176. Break apart 176 by place value, and then use the adding on strategy. Select numbers to complete the equations.
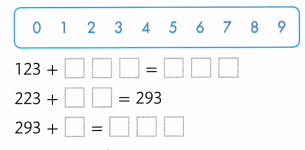
Answer:
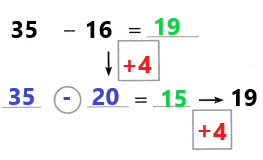
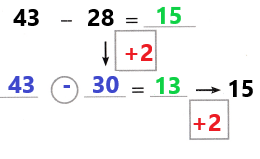
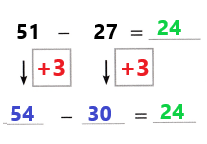
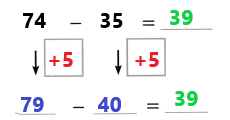
Lesson 8.4 Mental Math: Subtraction
Activity
Solve & Share
Peyton wants to buy one item that costs $425 and another item that costs $210. If she gets the discount shown on the sign below, what is the sale price? Explain how you can use mental math to find your answer.

Even when you use mental math, you can still show your work! You can construct arguments using mental math.

Look Back! What is another way you can use mental math to solve the problem?
Visual Learning Bridge
Essential Question
How Can You Subtract with Mental Math?
A.
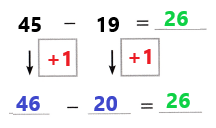
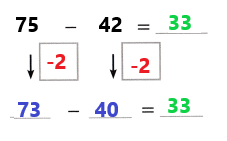
A store is having a sale on jackets. A jacket is on sale for $197 less than the original price. What is the sale price?

You can use mental math and the relationship between addition and subtraction to solve this problem.

The difference is the answer when subtracting two numbers.
B.
One Way
Count Back on the Number Line Find 352 – 197.
To subtract 197 on an open number line, you can subtract 200, and then add 3.
352 – 200 = 152
152 + 3 = 155

So, 352 – 197 = 155. The sale price is $155.
C.
Another Way
Count Up on the Number Line
Find 352 – 197.
To find 352 – 197, you can think addition: 197 + ? = 352
197 + 3 = 200
200 + 100 = 300
300 + 52 = 352
Addition and subtraction are inverse operations.
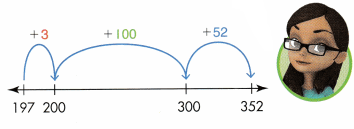
3+ 100 + 52 = 155
197 + 155 = 352, so 352 – 197 = 155.
The sale price is $155.
Convince Me! Construct Arguments Which of the two ways above would you use to solve 762 – 252? Explain.
Another Example!
You can make a simpler problem to find 352 – 197.
Add 3 to both numbers.
352 + 3 = 355 and 197 + 3 = 200.
Then you have 355 – 200.
So, 355 – 200 = 155 and 352 – 197 = 155.
If you get stuck using one strategy, another strategy may be easier!

Guided Practice
Do You Understand?
Question 1.
In the One Way example on the previous page, why do you add 3 to 152 instead of subtracting 3 from 152?
Answer: We have to add or subtract the same numbers for making the correct answer.
Question 2.
Suppose a computer costs $573. If you buy it today, it costs $498. What is the discount? Show your work.
Answer:
Given,
Suppose a computer costs $573. If you buy it today, it costs $498.
$573 – $498 = $92
Thus the discount is $92.
Do You Know How?
In 3-6, solve using mental math.
Question 3.
846 – 18
848 – 20 =___
Answer:
846 – 18
848 – 20
800 + 40 + 8 – 20
800 + 48 – 20
848 – 20 = 828
Question 4.
534 – 99
535 – 100 = __
Answer:
534 – 99
535 – 100
500 + 30 + 5 – 100
500 + 35 – 100
535 – 100 = 435
Question 5.
873 – 216
877 – 220 = ___
Answer:
873 – 216
877 – 220
800 + 70 + 7 – 200 + 20
800 + 77 – 220
877 – 220 = 657
Question 6.
782 – 347
785 – 350 = ___
Answer:
782 – 347
785 – 350
700 + 80 + 5 – 300 + 50
700 + 85 – 350
785 – 350 = 435
Question 7.
Find 400 – 138 using the make ten strategy
138 + __ = 140
140 + ___ = 200
200 + __ = 400
___ + __ + ___ = ___
Answer:
138 + 2 = 140
140 + 60 = 200
200 + 200 = 400
2 + 60 + 200 = 262
Independent Practice
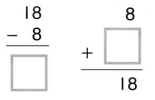
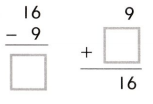
In 8-15, use an open number line or the think addition strategy to find each difference.
Question 8.
128 – 19
Answer: 109
Question 9.
887 – 18
Answer: 869
Question 10.
339 – 117
Answer: 222
Question 11.
468 – 224
Answer: 244
Question 12.
784 – 515
Answer: 269
Question 13.
354 – 297
Answer: 57
Question 14.
853 – 339
Answer: 514
Question 15.
638 – 372
Answer: 266
Problem Solving
Question 16.
Sarah has $350. How much money will she have after buying the computer at the sale price?

Answer:
Given,
Sarah has $350.
$350 – $58 = $292
Question 17.
Model with Math Jessica has an array with 9 columns. There are 36 counters in the array. How many rows does her array have? Show how to represent the problem and find the answer.
Answer:
Given,
Jessica has an array with 9 columns.
There are 36 counters in the array.
9 × 4 = 36
Thus there are 4 rows and 9 columns.
Question 18.
Of the students at Paul’s school, 270 are girls and 298 are boys. There are 354 students at Alice’s school. How many more students are there at Paul’s school than at Alice’s school?
Answer:
Girls at Paul’s school = 270
Boys at Paul’s school = 298
Students at Alice’s school = 354
Students at Paul’s school = 568
568 – 354 = 214
Paul’s school has 214 students more than Alice’s school students.
Question 19.
Higher Order Thinking To find 357 – 216, Tom added 4 to each number and then subtracted. Saul added 3 to each number and then subtracted. Will both ways work to find the correct answer? Explain.
Answer:
To find 357 – 216, Tom added 4 to each number and then subtracted.
357+4 = 361
216 + 4 = 220
361 – 220 = 141
Saul added 3 to each number and then subtracted.
357+3 = 360
216 + 3 = 219
360 – 219 = 141
Assessment Practice
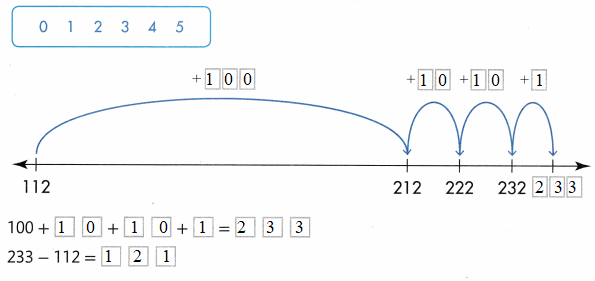
Question 20.
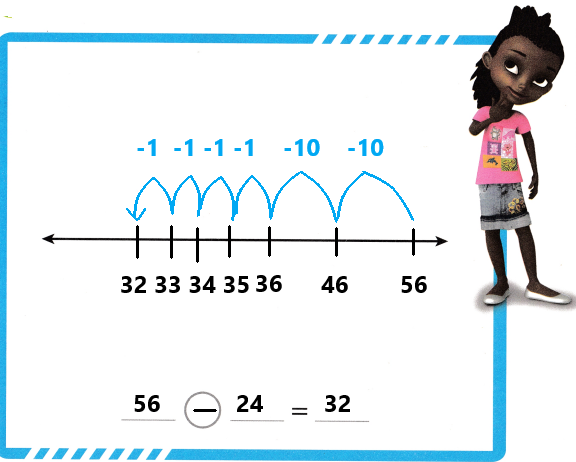
Use the relationship between addition and subtraction to find 233 – 112. Select numbers from the box to complete the work on the open number line and the equations.
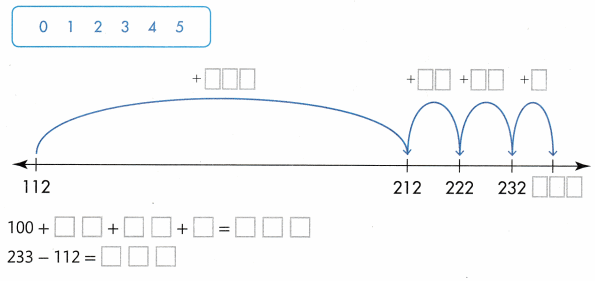
Answer:
Lesson 8.5 Round Whole Numbers
Activity
Solve & Share
Think about ways to find numbers that tell about how much or about how many. Derek has 277 stickers. What number can you use to describe about how many stickers Derek has? Explain how you decided.
Think about whether you need to be precise.

Look Back! Derek gets 3 more packages of 10 stickers. About how many stickers does Derek have now?
Essential Question
How Can You Round Numbers?
Visual Learning Bridge
A.
About how many rocks does Tito have? Round 394 to the nearest ten.
Place value is the value of the place a digit has in a number. Think about the place value of the digits in 394.

When you round to the nearest ten, you are finding the closest multiple of ten for a given number.


B.
You can use place-value understanding and a number line to round to the nearest ten.
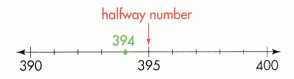
394 is closer to 390 than 400, so 394 rounds to 390.
Tito has about 390 rocks.
C.
About how many rocks does Donna have? Round 350 to the nearest hundred.
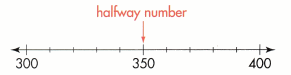
If a number is halfway between, round to the greater number
350 is halfway between 300 and 400, so 350 rounds to 400.
Donna has about 400 rocks.
Convince Me! Make Sense and Persevere Susan says, “I am thinking of a number that has a four in the hundreds place and a two in the ones place. When you round it to the nearest hundred, it is 500.” What number could Susan be thinking of? What other numbers could be Susan’s number?
Another Example
About how many rocks does Carl have? Round 345 to the nearest ten and hundred.
Round to the nearest ten.
345 is halfway between 340 and 350, so 345 rounds to 350.
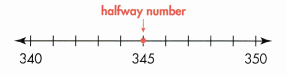
Round to the nearest hundred.
345 is closer to 300 than 400, so 345 rounds to 300.

Guided Practice
Do You Understand?
Question 1.
What number is halfway between 200 and 300?
Answer:
The halfway between 200 and 300 is 250.
Question 2.
Sheri rounds 678 to 680. What place does she round to?
Answer:
Here the digits in the one’s place is 8 in 678, now round to the nearest multiple of 10 which is greater than the number.
Given,
Sheri rounds 678 to 680.
The nearest ten to 678 is 680.
Question 3.
Tito adds one more rock to his collection on the previous page. About how many rocks does he have now, rounded to the nearest ten? Rounded to the nearest hundred? Explain.
Answer:
Do You Know How?
In 4-6, round to the nearest ten.
Question 4.
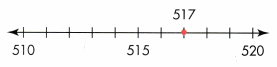
Answer: 517 to the nearest ten is 520.
Question 5.
149
Answer:
Here the digits in the one’s place of 149 is 9 , now round to the nearest multiple of 10 which is greater than the number.
149 to the nearest ten is 150.
Question 6.
732
Answer:
Here the digits in the one’s place of 732 is 2, now round to the nearest multiple of 10
732 to the nearest ten is 730.
In 7-9, round to the nearest hundred.
Question 7.
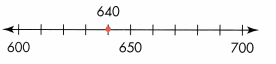
Answer:
When rounding to the nearest hundred, look at the ten’s digit. If the numbers is 0,1,2,3,4 you will round to previous hundred.
640 to the nearest hundred is 600.
Question 8.
305
Answer:
When rounding to the nearest hundred, look at the ten’s digit. If the numbers is 0,1,2,3,4 you will round to the previous hundred.
305 to the nearest hundred is 300.
Question 9.
166
Answer:
When rounding to the nearest hundred , look at the ten’s digit.If the numbers is 5,6,7,8,9 you will round to the next hundred.
166 to the nearest hundred is 200.
Independent Practice
In 10-12, round to the nearest ten.
Question 10.
88
Answer:
Here the digits in the one’s place of 88 is 8 , now round to the nearest multiple of 10 which is greater than the number.
88 to the nearest ten is 90.
Question 11.
531
Answer:
Here the digits in the one’s place of 531 is 1, now round to the nearest multiple of 10 which is less than the number.
531 to the nearest ten is 530.
Question 12.
855
Answer:
Here the digits in the one’s place of 855 is 5, now round to the nearest multiple of 10 which is greater than the number.
855 to the nearest ten is 860.
In 13-15, round to the nearest hundred.
Question 13.
428
Answer:
When rounding to the nearest hundred, look at the ten’s digit of the number.If the numbers are 0,1,2,3,4, you will round down to the previous hundred.
428 to the nearest hundred is 400.
Question 14.
699
Answer:
When rounding to the nearest hundred look at the ten’s digit of the given number.If the digits are 5,7,8,9 you will round to the previous hundred.
699 to the nearest hundred is 700.
Question 15.
750
Answer: when rounding to the nearest hundred, look at the ten’s digit of the number. If the digits are 5,6,7,8,9 you will round to the next hundred.
750 to the nearest hundred is 700. or 800.
Problem Solving
Question 16.
The Leaning Tower of Pisa in Italy has 294 steps. To the nearest ten, about how many steps are there? To the nearest hundred, about how many steps are there?

Answer:
Given,
The Leaning Tower of Pisa in Italy has 294 steps.
294 to the nearest ten is 290.
294 to the nearest hundred is 300.
Thus there are about 300 steps.
Question 17.
Critique Reasoning Zoe says 247 rounded to the nearest hundred is 300 because 247 rounds to 250 and 250 rounds to 300. Is Zoe correct? Explain.
Answer:
Zoe says 247 rounded to the nearest hundred is 300 because 247 rounds to 250 and 250 rounds to 300.
247 rounded to the nearest hundred is 200.
So, Zoe is not correct.
Question 18.
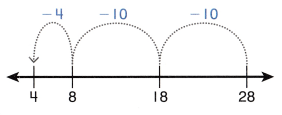
Use the number line to show a number that rounds to 200 when it is rounded to the nearest ten.
![]()
Answer:
Question 19.
Name the least number of coins you can use to show $0.47. What are the coins?
Answer:
Question 20.
Suppose you are rounding to the nearest hundred. What is the greatest number that rounds to 600? What is the least number that rounds to 600?
Answer:
The greatest number that round 600 to the nearest 100 would be 600 + 50 – 1 = 649. It won’t be 650 because of 650 rounds to 700.
Question 21.
Higher Order Thinking A 3-digit number has the digits 2,5, and 7. To the nearest hundred, it rounds to 800. What is the number? Show how you found the answer.
Answer:
For the number to be rounded off to 800, it needs to be either 750 or above or 850 and below.
With the given numbers, we can only have the following combinations:
257~300
275~300
527~500
572~600
725~700
752~800
And hence, 752 is the only combination of numbers that fits.
Question 22.
Emil says, “I am thinking of a number that is greater than 142, rounds to 100 when rounded to the nearest hundred, and has a 5 in the ones place.” What is Emil’s number?
What else can you try if you get stuck?

Answer: 542
Assessment Practice
Question 23.
Select all the numbers that will equal $100 when rounded to the nearest hundred.
![]() $10
$10
![]() $110
$110
![]() $ 89
$ 89
![]() $150
$150
![]() $91
$91
Answer:
$110, $89, $91 are rounded to the nearest hundred.
Question 24.
Select all the numbers that will equal 70 when rounded to the nearest ten.
![]() 62
62
![]() 75
75
![]() 72
72
![]() 83
83
![]() 73
73
Answer:
The number 70 rounded to the nearest ten is 75, 72, 73.
Lesson 8.6 Estimate Sums
Activity
Solve & Share
Look at the table below. Is the mass of a female and male sun bear together more or less than the mass of one female black bear? Without finding an exact answer, explain how you can decide.
 You can use symbols, numbers, and words to be precise in your explanation.
You can use symbols, numbers, and words to be precise in your explanation.
Look Back! Why is an exact answer not needed to solve the problem?
Essential Question
How Can You Estimate Sums?
Visual Learning Bridge
A.
Do the two pandas together weigh more than 500 pounds?
Estimate 255 + 329.

You can estimate to find about how much the two pandas weigh.

B.
One Way
Round to the nearest hundred.
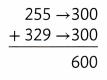
255 + 329 is about 600.
600 > 500
The pandas together weigh more than 500 pounds.
C.
Another Way
Use compatible numbers.

Compatible numbers are numbers that are close to the addends, but easy to add mentally
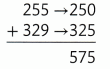
255 + 329 is about 575 and 575 > 500.
The total weight is more than 500 pounds.
Convince Me! Be Precise Sandy said, “Just look at the numbers. 200 and 300 is 500. The pandas weigh over 500 pounds because one panda weighs 255 pounds and the other weighs 329 pounds.” What do you think she means? Use numbers, words, or symbols to explain.
Another Example!
Suppose one panda ate 166 pounds of bamboo in a week and another ate 158 pounds. About how many pounds of bamboo did the two pandas eat?

You can estimate 166 + 158 by rounding to the nearest ten.
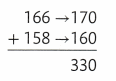
The pandas ate about 330 pounds of bamboo in a week.
Guided Practice
Do You Understand?
Question 1.
Two addends are rounded to greater numbers. Is the estimate greater than or less than the actual sum?
Answer:
Question 2.
Mary and Todd estimate 143 + 286. They have different answers. Can they both be correct? Explain why or why not.
Answer:
Mary and Todd has only one answer that is 143 + 286 = 429
Do You Know How?
Round to the nearest ten to estimate.
Question 3.
218 + 466 ___+___= ___
Answer:
Here the digit in the one’s place of 218 is 8, now round to the nearest multiple of 10 which is greater than the ten.
218 round to the nearest ten to estimate is 220.
The digit in the one’s place of 466 is 6, now round to the nearest multiple of ten which is greater than the number.
466 round to the nearest ten to estimate is 470
220 + 470 = 690
Question 4.
108 + 223 ___ + ___ = ____
Answer:
Here the digit in the one’s place of 108 is 8, now round to the nearest multiple of 10 which is greater than the number.
108 round to the nearest ten to estimate is 110.
The digit in the one’s place of 223 is 3, now round to the nearest multiple of 10 which is less than the number.
223 round to the nearest ten to estimate is 220.
110 + 220 = 330
Round to the nearest hundred to estimate.
Question 5.
514 + 258 ___ + ___ = ____
Answer:
Here the digit in the one’s place of 514 is 4, now round to the nearest multiple of 10 which is less than the number.
514 round to the nearest hundred to estimate is 500.
The digit in the one’s place of 258 is round to the nearest ten which is greater than the number.
258 round to the nearest hundred to estimate is 300.
500 + 300 = 800
Question 6.
198 + 426 ___ + ___ = ____
Answer:
Here the digit in the one’s place of 198 is 8,now round to the nearest multiple of ten which is greater than the number.
198 round to the nearest hundred to estimate is 200.
The digit in the one’s place of 426 is 6, now round to the nearest multiple of 10 which is greater than the number.
426 round to the nearest hundred to estimate is 400.
200 + 400 = 600
Independent Practice
In 7-10, round to the nearest ten to estimate.
Question 7.
138 + 435
Answer:
Here the digit in the one’s place of 138 is 8, now round to the nearest multiple of ten which is greater than the number.
138 round to the nearest ten to estimate is 140.
The digit in the one’s place of 435 is 5 now round to the nearest multiple of ten which is greater than the number.
435 round to the nearest ten to estimate is 440.
140 + 440 = 580
Question 8.
563 + 289
Answer:
Here the digit in the one’s place of 563 is 5 now round to the nearest multiple of ten which is less than the number.
563 round to the nearest ten to estimate is 560.
The digit in the one’s place of 289 is 9 now round to the nearest multiple of ten which is greater than the number.
289 round to the nearest ten to estimate is 290
560 + 290 = 850
Question 9
644 + 172
Answer:
Here the digit in the one’s place of 644 is 4 now round to the nearest multiple of ten which is less than the number.
644 round to the nearest ten to estimate is 640.
The digit in the one’s place of 172 is 2, now round to the nearest multiple of ten which is less than the number.
172 round to the nearest ten to estimate is 170
640 + 170 = 810
Question 10.
376 + 295
Answer:
Here the digit in the one’s place of the number 376 is 6 now round to the nearest ten which is greater than the number.
376 round to the nearest ten to estimate is 380.
The digit in the one’s place of 295 is 5 now round to the nearest multiple of ten which is greater than the number.
295 round to the nearest ten to estimate is 300
380 + 300 = 680
In 11-14, round to the nearest hundred to estimate.
Question 11.
403 + 179
Answer:
When rounding to the nearest hundred look at the ten’s digit of the number which the number is 0,1,2,3,4 you will round to the previous hundred.
403 round to the nearest hundred to estimate is 400.
Here the ten’s place of the 179 is 7 you will round to the next hundred.
179 round to the nearest hundred to estimate is 200.
400 + 200 = 600
Question 12.
462 + 251
Answer:
Here the ten’s place of the number is 462 is 6 you will round to the previous hundred.
462 round to the nearest hundred to estimate is 500.
Here the ten’s place of the number 251 is 5 you will round to the next hundred.
251 round to the nearest hundred to estimate is 300.
500 + 300 = 800
Question 13.
274 + 443
Answer:
Here the digit in the ten’s place of 274 is 7 you will round to the next hundred.
274 round to the nearest hundred to estimate is 300.
The digit in the ten’s of 443 is 4 you will round to the previous hundred.
443 round to the nearest hundred to estimate is 400.
300 + 400 = 700
Question 14.
539 + 399
Answer:
The digit in the ten’s place of 539 is 3 you will round to the previous hundred.
539 round to the nearest hundred to estimate is 500.
The digit in the ten’s place of 399 is 9 you will round to the next hundred.
399 round to the nearest hundred to estimate is 400.
500 + 400 = 900
In 15-18, use compatible numbers to estimate.
Question 15.
175 + 126
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply or division mentally.
Here 170 and 130 are the compatible numbers to the 175 and 126.
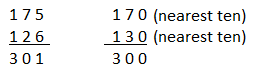
Question 16.
167 + 27
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply or division mentally.
Here 170 and 30 are the compatible number for 167 and 27.
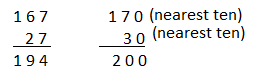
Question 17.
108 + 379
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply or division mentally.
Here 110 and 380 are the compatible numbers for 108 and 379.
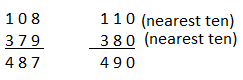
Question 18.
145 + 394
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply or division mentally.
Here 150 and 390 are the compatible numbers for 145 and 394.
Problem Solving
Use the table to answer 19 and 20.
Question 19.
Ms. Tyler drove from Albany to Boston, and then from Boston to Baltimore. To the nearest ten miles, about how many miles did she drive in all?
Answer:

Question 20.
Ms. Tyler drove from Boston to New York City and back again. To the nearest hundred miles, about how many miles did she drive?
Answer:
Given,
Ms. Tyler drives from Boston to New York City = 211
Ms.Tyler drives back to nearest hundred miles to Boston = 211 – 100
= 111
How many miles did she drive equals to 211 + 111 = 322
Question 21.
Reasoning Jen has $236. Dan has $289. Do Jen and Dan have more than $600 in all? Estimate to solve. Explain.
Answer:
Jen has $236
Don has $286
Jen and Don has 236 + 289 = 525
No, They did have more than $600
Question 22.
Ralph has 75¢. How much more money does he need to buy a pencil for 90¢? Complete the diagram.
Answer:
Ralph has 75 cents.
He need to buy a pencil for 90 cents.
Ralph need to buy a pencil = 90 cents – 75 cents =15 cents
Question 23.
Higher Order Thinking Susan drove 247 miles on Wednesday morning. Then she drove 119 miles on Wednesday afternoon. On Thursday, Susan drove 326 miles. About how far did Susan drive in all? Explain the method you used to estimate.
Remember that you learned different estimation strategies.

Assessment Practice
Question 24.
Round to the nearest 10 to estimate the sums.

Answer:
273 round to the nearest ten to estimate is 270
616 round to the nearest ten to estimate is 620
270 + 620 = 890
542 round to the nearest ten to estimate is 540
338 round to the nearest ten to estimate is 340
540 + 340 = 880
435 round to the nearest ten to estimate is 440
441 round to the nearest ten to estimate is 440
440 – 440 = 0
Question 25.
Round to the nearest 100 to estimate the sums.

Answer:
173 round to the nearest hundred to estimate is 200
139 round to the nearest hundred to estimate is 100
200 – 100 = 100
155 round to the nearest hundred to estimate is 200
177 round to the nearest hundred to estimate is 200
200 – 200 = 0
289 round to the nearest hundred to estimate is 300
18 round to the nearest hundred to estimate is 0
300 – 0 = 300
Lesson 8.7 Estimate Differences
Activity
Solve & Share
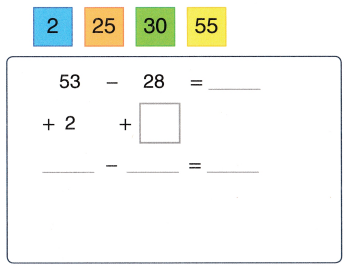
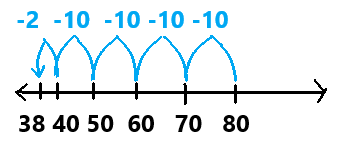
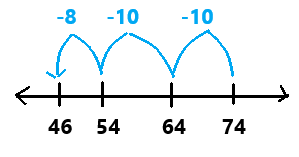
Sara collected 220 cans on Monday, 80 cans on Tuesday, and 7 cartons with 8 cans each on Wednesday to recycle. Pierre collected 112 cans. About how many more cans did Sara collect than Pierre?
You can make sense and persevere. What is a good strategy for solving this problem?

Look Back! Which strategy gives an estimate that is closest to the exact answer? How did you decide?
Essential Question
How Can You Estimate Differences?
A.
All of the tickets for a concert were sold. So far, 126 people have arrived at the concert. About how many people who have tickets have not arrived?
Estimate 493 – 126 by rounding.
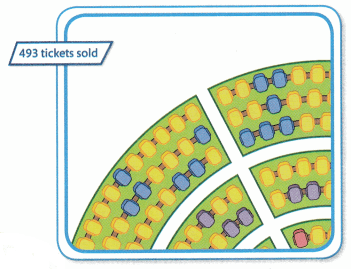
You can estimate to find about how many.

B.
One Way
Round each number to the nearest hundred and subtract.
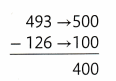
About 400 people have not yet arrived.
C.
Another Way
Round each number to the nearest ten and subtract.
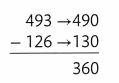
About 360 people have not yet arrived.
Convince Me! Model with Math Suppose 179 people have arrived at the concert. Estimate how many people have not arrived.
Another Example!
You can use compatible numbers to estimate differences.
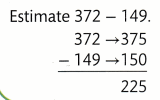
375 and 150 are compatible numbers for 372 and 149.

Guided Practice
Do You Understand?
Question 1.
Does rounding to the nearest ten or nearest hundred give an estimate closer to the exact answer for 295 – 153?
Answer:
Here the digit of the one’s place of 295 is 5 now round to the nearest multiple of ten which is greater than the number.
295 round to the nearest ten to estimate is 290
The digit in the one’s place of 153 is3 now round to the nearest multiple of ten which is less than the number.
153 round to the nearest ten to estimate is 140
290 – 140 =150
Question 2.
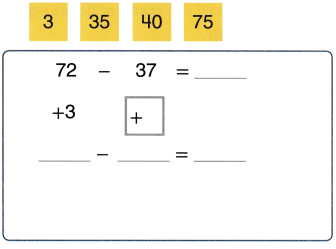
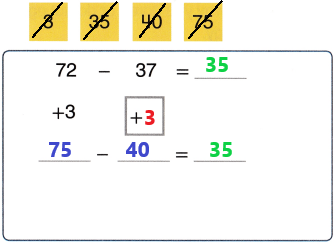
A theater sells 408 tickets. Two hundred seventy-three people arrive. About how many more people are expected to arrive? Use compatible numbers. Show your work.
Answer:
Given,
A theater sells tickets = 408
People arrive to theater = 253
Expected people to arrive = 408 – 253 = 155
The compatible numbers for 408 and 253 is 410 and 250
410 – 250 = 150
Do You Know How?
In 3-6, estimate. Use rounding or compatible numbers. Tell how you made each estimate.
Question 3.
321 – 182
Answer:
Compatible numbers are pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 321 and 182 is 320 and 180.
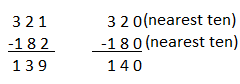
Question 4.
655 – 189
Answer:
Compatible numbers are pair of numbers that are easy to add, subtract, multiply or division mentally.
The compatible numbers for 655 and 189 is 660 and 190
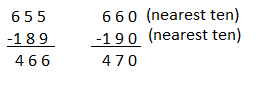
Question 5.
763 – 471
Answer:
Compatible numbers are pair of numbers that are easy to add, subtract multiply, and division mentally.
The compatible numbers for 763 and 471 are 760 and 470.
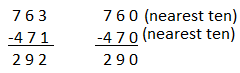
Question 6.
816 – 297
Answer:
Compatible numbers are pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 816 and 297 are 820 and 300.

Independent Practice
In 7-10, round to the nearest hundred to estimate.
Question 7.
286 – 189
Answer:
When rounding to the nearest hundred look at the ten’s place.The ten’s place of 286 is 8 now round to the next hundred.
286 round to the nearest hundred to estimate is 300.
The ten’s place of the number 189 is 8 now round to the next hundred
189 round to the nearest hundred to estimate is 200.
300 – 200 = 100
Question 8.
461 – 216
Answer:
When rounding to the nearest hundred look at the ten’s place.The ten’s place of the number 461 is 6 now round to the next hundred.
461 round to the nearest hundred to estimate is 500.
The ten’s place of the number 216 is 1 now round to the previous hundred.
216 round to the nearest hundred to estimate is 200.
500 – 200 = 300
Question 9.
891 – 686
Answer:
When rounding to the nearest hundred look at the ten’s place of the number 891 is 9 now round to the next hundred.
891 round to the nearest hundred to estimate is 900.
The ten’s place of the number 686 is 8 now round to the next hundred.
686 round to the nearest hundred to estimate is 700.
900 – 700 = 200
Question 10.
724 – 175
Answer:
When rounding to the nearest hundred look at the ten’s place of the number 724 is 2 now round to the previous hundred.
724 round to the nearest hundred to estimate is 600.
The ten’s place of the number 175 is 7 now round to the next hundred.
175 round to the nearest hundred to estimate is 200
600 – 200 = 400
In 11-14, round to the nearest ten to estimate.
Question 11.
766 – 492
Answer:
Here the digit of the one’s place of the number 766 is 6 now round to the nearest ten which is greater than the number.
766 round to the nearest ten to estimate is 770.
The one’s place of the number 492 is 2 now round to the nearest ten which is less than the number.
492 round to the nearest ten to estimate is 500.
770 – 500 = 270
Question 12.
649 – 487
Answer:
Here the digit of the one’s place of the number 649 is 9 now round to the nearest hundred which is greater than the number.
649 round to the nearest ten to estimate is 650.
The one’s place of the number 487 is 7 now round to the nearest hundred which is greater than the number.
487 round to the nearest ten to estimate is 490.
650 – 490 = 169
Question 13.
241 – 117
Answer:
Here the digit in the one’s place of the number 241 is 1 now round to the nearest hundred which is less than the number.
241 round to the nearest ten to estimate is 240.
The one’s place of the number 117 is 7 now round to the nearest hundred which is greater than the number.
117 round to the nearest ten to estimate is 120.
240 – 120 = 120
Question 14.
994 – 679
Answer:
Here the digit of the one’s place of the number 994 is 4 now round to the nearest hundred which is less than the number.
994 round to the nearest ten to estimate is 1000.
The digit in the one’s place of the number 679 is 9 which is greater than the number.
679 round to the nearest ten to estimate is 680.
1000 – 680 = 320
In 15-18, use compatible numbers to estimate.
Question 15.
760 – 265
Answer:
Compatible numbers are pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 760 and 265 are 760 and 270.

Question 16.
355 – 177
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally
Compatible numbers for 355 and 177 is 360 and 180.

Question 17.
481 – 105
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 481 and 105 is 480 and 110.
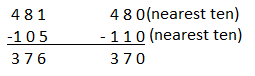
Question 18.
794 – 556
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 794 and 556 are 800 and 560.
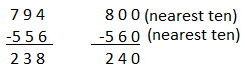
Problem Solving
Question 19.
The Grand Concert Hall sold 100 more tickets on Sunday than on Friday. On what day did it sell about 150 tickets more than it sold on Sunday?
Use estimation strategies to help find your answers.
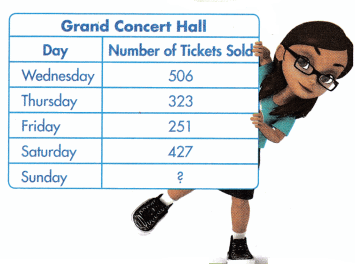
Question 20.
Model with Math Find the total number of tickets sold on Thursday and Friday. Explain what math you used.
Answer:
Number of tickets sold on Thursday = 323
Number of tickets sold on Friday = 251
Total number of tickets sold on Thursday and Friday equal to
321 + 251
300 + 20 + 1 + 200 + 50 +1
500 + 70 + 2
500 + 72 = 572
Question 21.
Algebra Anna and Joe write reports for their science class. Anna’s report is 827 words long. Joe’s report is 679 words long. Round each report length to the nearest ten and estimate how many more words Anna’s report is. Then write an equation that shows exactly how many more words Anna’s report is.
Answer:
Anna report is 827 long words.
Joe’s report is 679 long words.
827 round to the nearest ten to estimate is 830
679 round to the nearest ten to estimate is 680
830 – 680 = 150
Anna report is 150 long words more than Joe’s long report
Question 22.
Higher Order Thinking One week Mrs. Runyan earned $486, and the next week she earned $254. If Mrs. Runyan’s goal was to earn $545, by about how much did she exceed her goal? Show how you used estimation to find your answer.
Answers:
Mrs Runyan earned in one week = $486
Mrs Runyan earned in next week = $254
Total she earned in two weeks = $ 486 + $255
=$740
But she goal to earn is $545
She exceed her goal = $740 – $545
She exceed her goal is $ 195
Question 23.
About how many inches longer was a Brachiosaurus than a Tyrannosaurus rex?
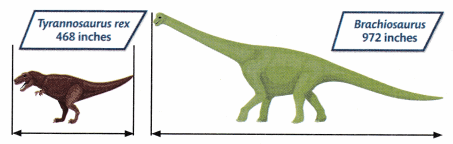
Answer:
Brachiosaurus length = 972 inches.
Tyrannosaurus length = 468 inches.
972 – 468 = 504
Brachiosaurus length is 504 longer than Tyrannosaurus length.
Assessment Practice
Question 24.
Estimate 753 – 221 by rounding each number to the nearest ten.
A. 540
B. 530
C. 520
D. 510
Answer:
753 round to the nearest ten to estimate is 750.
221 round to the nearest ten to estimate is 220
750 – 220 = 530
Thus the correct answer is option B.
Question 25.
Estimate 812 – 369 by rounding each number to the nearest hundred.
A. 500
B. 400
C. 300
D. 200
Answer:
812 round to the nearest hundred to estimate is 810.
369 round to the nearest hundred to estimate is 370.
810 – 370 = 440
440 to the nearest hundred is 400.
Thus the correct answer is option B.
Lesson 8.8 Model with Math
Activity
Solve & Share
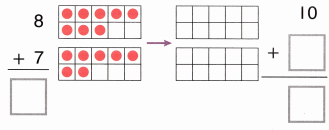
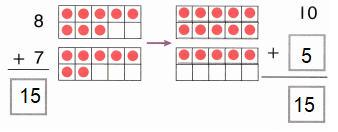
A pond has 458 rosy red minnows, 212 white cloud minnows, and 277 goldfish. How many more minnows than goldfish live in the pond?
Thinking Habits
Be a good thinker! These questions can help you.
• How can I use math I know to help solve this problem?
• How can I use pictures, objects, or an equation to represent the problem?
• How can I use numbers, words, and symbols to solve the problem?

Look Back! Model with Math Explain what math you used to solve this problem.
Essential Question How Can You Model With math?
A.
David has $583 to spend on soccer uniforms. He buys this soccer jersey and 2 soccer shorts. How much money does David spend?
What math do I need to use to solve the problem?

I need to show what I know and then choose the needed operations.
B. How can I model with math? I can
- apply math I know to solve the problem.
- use a bar diagram and equations to represent the problem.
- use an unknown to represent the number I am trying to find.
Here’s my thinking…

C.
I will use a bar diagram and an equation.
The hidden question is: How much does David spend on shorts?

$35 + $35 = ?
$35 + $35 = $70. The shorts cost $70.
So I need to find the total including the jersey.

$70+ $109 = ?
$70 + $109 = $179. David spends $179.
Convince Me! Model with Math How does the bar diagram help you model with math?
Guided Practice
Model with Math
Harris’s office building has 126 windows. Morgan’s bank has 146 windows. Devon’s bank has 110 windows. How many more windows do the banks have altogether than the office building?
One way you can model math is by using bar diagrams to represent each step of a two-step problem.
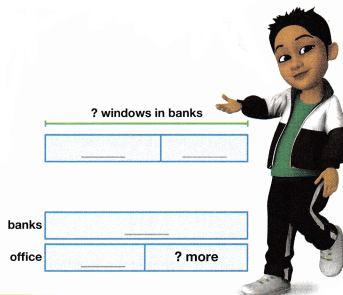
Question 1.
What is the hidden question you need to answer before you can solve the problem?
Answer:
How many windows do the banks have in all?
Question 2.
Solve the problem. Complete the bar diagrams. Show the equations you used.
Answer:
Morgan’s bank has 146 windows.
Devon’s bank has 110 windows.
Morgan’s and Devon’s office has 146 + 110 = 256 windows
Another office windows = 256 -126=130
Independent Practice
Model with Math
Regina’s bakery made 304 pies in January. Her bakery made 34 fewer pies in February. How many pies did her bakery make in both months?
Question 3.
What is the hidden question you need to answer before you can solve the problem?

Answer:
How many pies did the bakery make in February?
Question 4.
Solve the problem. Complete the bar diagrams. Show the equations you used.
Answer:
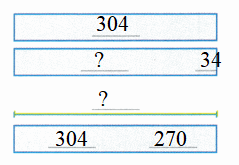
304 – 34 = ?
304 – 34 = 270
304 + 270 = ?
304 + 270 = 574
Question 5.
How would your equations change if the bakery made 34 more pies in February than in January?
Answer:
I would add 304 + 34 = ? instead of subtracting 304 – 34 = ? to find the number of pies baked in February.
Problem Solving
Performance Task
Skyscraper Heights
The Empire State Building in New York is 159 meters taller than the Republic Plaza in Denver. The John Hancock Building in Chicago is 122 meters taller than the Republic Plaza. The Empire State Building is 712 miles away from the Hancock Building. The Hancock Building is 920 miles away from the Republic Plaza. Manuel wants to know how tall the Hancock Building is. Answer Exercises 6-9 to solve the problem.

Answer:
Question 6.
Critique Reasoning Tom said to solve the problem, you should add 159 to the height of the Empire State Building. Do you agree? Explain why or why not.
Answer:
Question 7.
Model with Math What is the hidden question you need to solve in this problem? How can you represent the hidden question?
Answer:
Question 8.
Model with Math Solve the problem. Show the equations you used.
Answer:
Question 9.
Use Appropriate Tools Which tool would you use to represent and explain how to solve the problem: counters, cubes, or place-value blocks? Explain.
Model with math means you apply math you have learned to solve problems.

Answer:
Topic 8 Fluency Practice
Activity
Find a Match
Work with a partner. Point to a clue. Read the clue. Look below the clues to find a match. Write the clue letter in the box next to the match. Find a match for every clue. Once you find the matches, write the fact families for each of the facts.
Clues
A The missing number is 9.
B The missing number is 10.
C The missing number is 3.
D The missing number is 6.
E The missing number is 7.
F The missing number is 4.
G The missing number is 8.
H The missing number is 5.
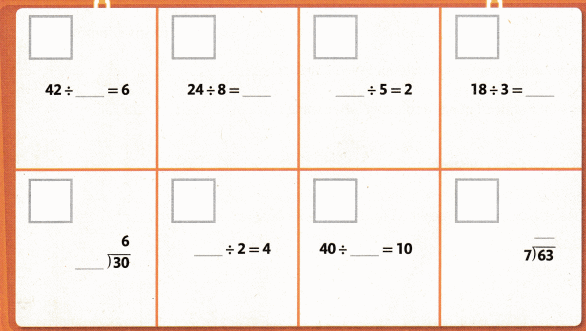
Answer:

Topic 8 Vocabulary Review
Glossary
Understand Vocabulary
Circle the property of addition shown in the following examples.
Word List
• Associative Property of Addition
• Commutative Property of Addition
• compatible numbers
• estimate
• Identity Property of Addition
• inverse operations
• mental math
• place value
• round
Question 1.
17 + 14 = 14 + 17
Associative Property Commutative Property Identity Property
Answer: Associative property.
Question 2.
93 + 0 = 93
Associative Property Commutative Property Identity Property
Answer: Identity property.
Question 3.
8 + (5 + 9) = (8 + 5) + 9
Associative Property Commutative Property Identity Property
Answer: Commutative property.
Question 4.
65 + 0 = 0 + 65
Associative Property Commutative Property Identity Property
Answer: Identity property.
Choose the best term from the box. Write it in the blank.
Question 5.
You ___ when you use the nearest multiple of ten or a hundred.
Answer: You Estimate sum and differences in the number when you use the nearest multiple of ten or a hundred.
Question 6.
Addition and subtraction are ___
Answer:
Addition and subtraction are the arithmetic operations.
Question 7.
___ is the value given to the place a digit has in a number.
Answer: Place value is the value given to the place a digit has in a number.
Question 8.
Numbers that are easy to compute mentally are ___
Answer: Numbers that are easy to compute mentally are mental math.
Question 9.
You do not need pencil and paper when using ___
Answer: You do not need pencil and paper when using mental math.
Use Vocabulary in Writing
Question 10.
Jim found that 123 + 284 is about 400. Explain what Jim did. Use at least 3 terms from the Word List in your answer.
Answer: Jim used rounding numbers to add the given numbers.
Topic 8 Vocabulary Reteaching
Set A
pages 289-292
You can use properties of addition to help solve addition problems.
The Commutative Property of Addition
12 + ![]() = 15 + 12
= 15 + 12
You can order addends in any way, and the sum will be the same.
12 + 15 = 15 + 12
The Associative Property of Addition
3 + (7 + 8) = (3 + ![]() ) + 8
) + 8
You can group addends in any way, and the sum will be the same.
3 + (7 + 8) = (3 + 7) + 8
The Identity Property of Addition
30 + ![]() = 30
= 30
The sum of any number and zero is that same number.
30 + 0 = 30
Remember that both sides of the equal sign must have the same value.
In 1-6, write each missing number.
Question 1.
18 + __ = 18
Answer:
18 + 0 = 18
Question 2.
14 + (16 + 15) = (___ +16) + 15
Answer:
14 + ( 16 + 15) = ( 14 + 16) + 15
Question 3.
___ + 13 = 13 + 17
Answer:
17 + 13 = 13 + 17
Question 4.
28 + (__ + 22) = 28 + (22 + 25)
Answer:
28 + (25 + 22) = 28 + ( 22 + 25 )
Question 5.
62 + 21 + 0 = 62 + ___
Answer:
62 + 21 + 0 = 62 + 21
Question 6.
___ + (26 + 78) = (31 + 26) + 78
Answer:
31 + (26 + 78) = (31 + 26) + 78
Question 7.
Use 78 and 34 to write an equation that shows the Commutative Property of Addition.
Answer:
78 + 34 = 34 + 78
Set B
pages 293-296
You can find patterns using an addition table.
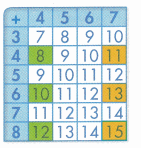
The green sums increase by 2 down the column and are even numbers.
The yellow sums increase by 2 down the column and are odd numbers.
Use examples to make generalizations!

Remember that properties can help you understand patterns.
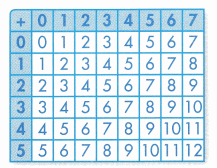
Question 1.
Find the doubles-plus-2 facts. What pattern do you notice about the sums?
Answer:
Question 2.
Explain why your pattern works.
Answer:
Set C
pages 297-300
Use mental math to find 374 + 238.
Break apart 238: 200 + 30+ 8.
Add hundreds, tens, and ones.
374 + 200 = 574
574 + 30 = 604
604 + 8 = 612
So, 374 + 238 = 612.
Remember that you can break apart addends when finding sums mentally.
Question 1.
302 + 56
Answer:
Using mental math
300 + 2 + 50 + 6
300 + 50 + 8
300 + 58 = 358
Question 2.
463 + 418
Answer:
Using mental math
463 + 418
400 + 60 + 3 + 400 + 10 + 8
800 + 70 + 11
800 + 81 = 881
Question 3.
222 + 725
Answer:
Using mental math
222 + 725
200 + 20 + 2 + 700 + 20 + 5
900 + 40 + 7
900 + 47 = 947
Question 4.
689 + 115
Answer:
Using mental math
689 + 115
600 + 80 + 9 + 100 + 10 + 5
700 + 90 + 14
700 + 104 = 804
Set D
pages 301-304
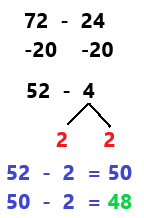
Think addition to find 400 – 168.
Count on.
168 + 2 = 170
170 + 30 = 200
200 + 200 = 400
2 +30 + 200 = 232
So, 400 – 168 = 232.
Remember that you can count on when subtracting mentally.
Question 1.
523 – 163
Answer:
Using mental math
523 – 163
500 + 20 + 3 – 100 + 60 + 3
400 – 40 = 360
Question 2.
847 – 372
Answer:
Using mental math
847 – 372
800 + 40 + 7 – 300 + 70 + 2
500 – 30 – 5
500 – 25 = 575
Question 3.
768 – 259
Answer:
Using mental math
768 – 259
700 + 60 + 8 – 200 + 50 + 9
500 + 10 – 1
500 + 9 = 509
Question 4.
282 – 125
Answer:
Using mental math
282 – 125
200 + 80 + 2 – 100 + 20 + 5
100 + 60 – 3
100 + 57 = 157
Set E
pages 305-308
You can use a number line to round.
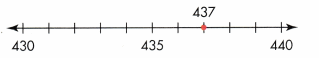
Nearest ten: 437 rounds to 440.
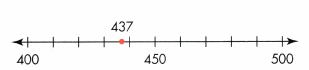
Nearest hundred: 437 rounds to 400.
Think about place value when you round.

Remember that if a number is halfway between, round to the greater number.
Question 1.
Round 374 to the nearest ten and the nearest hundred.
Answer:
374 round to the nearest ten to estimate is 370.
374 round to the nearest hundred to estimate is 400.
Question 2.
Round 848 to the nearest ten and the nearest hundred.
Answer:
842 round to the nearest ten to estimate is 850.
842 round to the nearest hundred to estimate is 800.
Question 3.
Mark’s family traveled 565 miles. Rounded to the nearest ten, about how many miles did they travel?
Answer:
Mark’s family traveled 565 miles
565 round to the nearest ten to estimate is 570.
Mark’s family traveled 570 miles.
Question 4.
Sara collected 345 shells. Rounded to the nearest hundred, about how many shells did she collect?
Answer:
Set F
pages 309-312
Estimate 478 + 112.
Round each addend to the nearest ten.
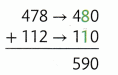
Round each addend to the nearest hundred.
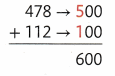
Use compatible numbers.
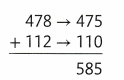
Remember that compatible numbers are numbers close to the actual numbers and are easier to add mentally.
Round to the nearest hundred.
Question 1.
367 + 319
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
Compatible numbers for 367 and 319 is 400 and 300.
Question 2.
737 + 127
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally,
The compatible numbers for 737 and 127 is 700 and 100
Round to the nearest ten.
Question 3.
298 + 542
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
Compatible numbers for 298 and 542 is 300 and 540.
Question 4.
459 + 85
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 459 and 85 is 460 and 90
Use compatible numbers.
Question 5.
372 + 173
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 372 and 173 is 370 and 170
Question 6.
208 + 164
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 208 and 164 is 210 and 160
Question 7.
Will rounding to the nearest ten or the nearest hundred give a closer estimate of 314 + 247? Explain your answer.
Answer:
314 + 247 = 561
314 round to the nearest ten to estimate is 310
247 round to the nearest ten to estimate is 250
310 +250 = 560
Set G
pages 313-316
Estimate 486 – 177.
Round each number to the nearest hundred.
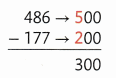
Round to the nearest hundred.
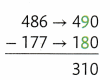
Use compatible numbers.
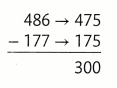
Remember that an estimate is close to the actual answer.
Question 1.
527 – 341
Answer:
Question 2.
872 – 184
Answer:
Round to the nearest ten.
Question 3.
387 – 298
Answer:
Here the digit in the one’s place of the number 387 is 7 now round to the nearest ten which is greater than the number.
387 round to the nearest ten is 390
The digit in the one’s place of the number 298 is 8 now round to the nearest ten which is greater than the number.
287 round to the nearest ten is 290
390 – 290 = 100
Question 4.
659 – 271
Answer:
Here the digit in the one’s place of the number 659 is 9 now round to the nearest ten which is greater than the number.
659 round to the nearest ten is 660
The digit in the one’s place of the number 271 is 1 which is less than the number.
271 is round to the nearest ten to 270
660 – 270 = 390
Use compatible numbers.
Question 5.
472 – 228
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
The compatible numbers for 472 and 228 is 470 and 230
Question 6.
911 – 347
Answer:
Compatible numbers are the pair of numbers that are easy to add, subtract, multiply and division mentally.
Compatible numbers for 911 and 347 is 910 and 350
Question 7.
Will rounding to the nearest ten or the nearest hundred give a closer estimate of 848 – 231? Explain your answer.
Answer:
848 -231 = 617
848 round to the nearest hundred to estimate is 800
231 round to the nearest hundred to estimate is 200
800 – 200 = 600
Set H
pages 317-320
Think about these questions to help you model with math.
Thinking Habits
• How can I use math I know to help solve this problem?
• How can I use pictures, objects, or an equation to represent the problem?
• How can I use numbers, words, and symbols to solve the problem?

Remember to apply the math you know to solve problems.
Elena has $265. She buys a jacket that costs $107 and a sweater that costs $69. How much money does Elena have left?
Question 1.
What is the hidden question you need to answer before you can solve the problem?
Answer:
Question 2.
Solve the problem. Draw bar diagrams to represent the problem. Show the equations you used.
Answer:
Toni read 131 pages on Monday, 56 pages on Tuesday, and some pages on Wednesday. She read 289 pages in all. How many pages did Toni read on Wednesday?
Ans:
Toni read pages on Monday = 131
Toni read pages on Tuesday = 56
Toni read pages on Wednesday = 289 – 131 + 56 = 102
Question 1.
What is the hidden question you need to answer before you can solve the problem?
Answer:
Question 2.
Solve the problem. Use equations to represent your work.
Answer:
Topic 8 Assessment Practice
Question 1.
What is the sum of 243, 132, and 157?
Answer:
243 + 132 + 157 = 532
Question 2.
Find a reasonable estimate for the sum of 171 and 69. Select all that apply.
![]() 175 + 70 = 245
175 + 70 = 245
![]() 100 + 60 = 160
100 + 60 = 160
![]() 170 + 70 = 240
170 + 70 = 240
![]() 175 + 75 = 250
175 + 75 = 250
![]() 130 + 70 = 200
130 + 70 = 200
Answer:
For the sum of 171 and 69 is we will appy 175 + 70 = 245 in the equation we are using the compatible numbers
170 + 70 = 240 in this equation we are using the nearest ten.
Question 3.
Subtract 382 – 148 mentally. Which of the following should you do first to find the difference?
A. Add 2 to 148 and add 2 to 382.
B. Add 2 to 148 and subtract 2 from to 382.
C. Subtract 8 from 148 and subtract 2 from 382.
D. Subtract 12 from 382 and add 12 to 148.
Answer:
To find the difference first to subtract 12 from 382 and add 12 to 148.
Question 4.
Estimate the difference of 765 and 333. Explain your estimate.
Answer:
The difference of 765 and 333 is
765 – 333 = 432
Our estimate is to Subtract the lowest value from the highest value.
Question 5.
Look at the sums in the shaded column. Look at the addends. What pattern do you see? Explain why this pattern is always true.
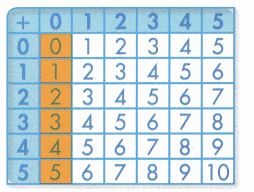
Answer:
Question 6.
Use mental math to add 332 and 154. Which of these shows how to break apart the numbers into hundreds, tens, and ones?
A. Break 332 into 320 + 12. Break 154 into 125 + 29.
B. Break 332 into 100+ 230 + 2. Break 154 into 100 + 52 + 2.
C. Break 332 into 300 + 16 + 16. Break 154 into 100 + 27 + 27.
D. Break 332 into 300 + 30+ 2. Break 154 into 100 + 50 + 4.
Answer:
D is the correct answer .
Question 7.
Use mental math to find 634 – 528.
Answer:
634 – 528
600 + 30 + 4 – 500 + 20 + 8
100 +10 – 4
110 – 4 = 106
Question 8.
Select all the equations that are true.
![]() 32 + 56 + 10 = 10 + 56 + 32
32 + 56 + 10 = 10 + 56 + 32
![]() (49 + 28) + 5 = 49 + (28 + 5)
(49 + 28) + 5 = 49 + (28 + 5)
![]() 56 + 890 = 890 + 56
56 + 890 = 890 + 56
![]() 82 + 0 = 82
82 + 0 = 82
![]() 45+ 27 = 27 + 35
45+ 27 = 27 + 35
Answer:
Yes all the equations are true they are in the associative property, commutative property and identity property.
Question 9.
Look at the table.
Write the letters A, B, C, and D above the number line to show each number rounded to the nearest ten.

Answer:
Question 10.
Use the subtraction work shown.
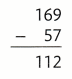
Which strategy shows a way to check the work using inverse operations?
A. Subtract 57 from 169.
B. Add 57 and 112.
C. Add 112 and 169.
D. Add 169 and 57.
Answer:
Inverse means reverse operation
Inverse operation is the Add 169 and 57
Question 11.
Estimate the sum of 405 and 385 by rounding to the nearest hundred. Explain your estimate.
Answer:
The sum of 405 + 385 = 790
When rounding to the nearest hundred look at the ten’s place of the number. The ten’s place of the 790 is 9 now round to the next hundred.
790 round to the nearest hundred to estimate is 800.
Question 12.
What addition equation can be used to check the answer for 456 – 342 = 114? Draw a bar diagram to show how the numbers in this problem are related.
Answer:
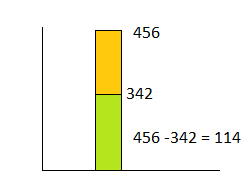
Question 13.
Find the sum of 350, 62, and 199.
A. Draw a bar diagram that represents the problem.
B. What is the first step you would do to solve this problem using mental math?
Answer:

The sum of 350 + 62 + 199 = 611
Question 14.
Subtract 341 – 97 mentally. First add 3 to 97 to get 100. What should the next step be? What is the difference?
A. Add 6 to 341. The difference is 247.
B. Add 200 to 100. The difference is 100.
C. Subtract 3 from 341. The difference is 238.
D. Add 3 to 341. The difference is 244.
Answer: The next step is Subtract 3 from 341. The difference is 238.
Question 15.
Round each number on the left to the nearest hundred. Select the appropriate answer.

Answer
668 round to the nearest hundred to estimate is 700.
404 round to the nearest hundred to estimate is 400.
649 round to the nearest hundred to estimate is 600.
489 round to the nearest hundred to estimate is 500.
Question 16.
Explain how to use mental math to find 620 – 278.
Answer:
Using the mental math
620 – 278
600 + 20 – 200 + 70 + 8
600 + 20 – 200 + 78
600 + 20 – 278
620 – 278 = 332
Question 17.
How can you check the answer for 693 – 231 = 462?
A. Subtract 639 – 300 = 339.
B. Subtract 462 – 231 = 231.
C. Add 693 + 231 = 924.
D. Add 462 + 231 = 693.
Answer:
The correct answer is D.
693 – 231 = 462
462 + 231 = 693
Question 18.
Consider the sum of 123, 201, and 387.
A. Estimate the sum by rounding to the nearest ten. Explain your estimate.
B. What is the difference between the exact sum of 123, 201, and 387 and your estimate? Explain your answer.
Answer:
The sum of 123 + 201 + 387 = 711
A. 711 round to the nearest ten to estimate is 710
B. The difference between the exact sum and the estimate sum is 711 – 710 is 1.
Question 19.
Consider the equation 360 = __ + 84.
Use a bar diagram to represent the equation. Then solve for the unknown value.
Answer:
360 = 276 + 84
Topic 8 Performance Task
Vacation Trip
Mia is planning a vacation in Orlando, FL.
The Mia’s Route table shows her route and the miles she will drive.
Use the Mia’s Route table to answer Questions 1-3.
Question 1.
Round each distance to the nearest ten to show about how many miles Mia will drive on each part of her trip.
Memphis, TN, to Birmingham, AL:
Birmingham, AL, to Gainesville, FL:
Gainesville, FL, to Orlando, FL:
Answer:
Mia’s drive from Memphis,TN, to Birmingham, AL is 237 miles.
237 is round to the nearest ten is to estimate is 240.
Mia’s drives from Memphis, TN, to Birmingham, AL is 240 miles.
Mia’s drive from Birmingham, AL to Gainesville, FL is 422
422 round to the nearest ten to estimate is 420
Mia’s drive from Birmingham, AL to Gainesville, FL is 420 miles.
Mia’s drive from Gainesville, FL to Orlando, FL is 183 miles.
183 round to the nearest ten to estimate is 180.
Mia’s drive from Gainesville, FL to Orlando, FL is 180 miles.
Question 2.
Use mental math to find the actual number of miles Mia will drive to reach Gainesville. Show your work.
Answer:
Mia’s started a drive from Memphis, TN to Birmingham, AL is 237 miles.
From Birmingham, AL to Gainesville, FL is 422 miles.
Mia’s drive to reach Gainesville is 237 + 422
By using mental math
237 +422
200 + 30 + 7 + 400 + 20 + 2
600 + 50 + 9
600 + 59 = 659
Question 3.
Mia says, “Birmingham is 185 miles closer to Memphis than to Gainesville.” Her brother says, “No, it is 175 miles closer.” Use mental math to decide who is correct. Show your work.
Answer:
Birmingham to Memphis is 237 miles.
Birmingham to Gainesville is 422 miles.
Mia’s says the correct
422 – 237
400 + 20 + 2 – 200 + 30 + 7
200 – 10 – 5
200 – 15 = 185
Mia has to book a hotel and buy theme park tickets. The Hotel Prices and Theme Park Prices tables show the total prices for Mia’s stay. The Mia’s Options list shows two plans that Mia can choose from.

Question 4.
Mia has $600 to spend on a hotel and tickets.
Part A
Which option does Mia have enough money for? Explain using estimation.
Part B
Create a new option for Mia. Fill out the table with a hotel and a theme park. Explain why Mia has enough money for this plan.

Question 5.
One theme park has a special offer. For each ticket Mia buys, she gets another ticket free. Shade the squares in the table at the right to show this pattern. Explain why the pattern is true.
Answer:




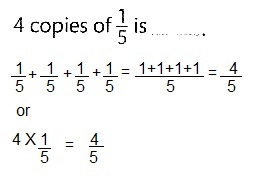
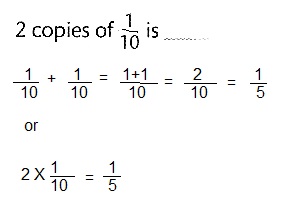
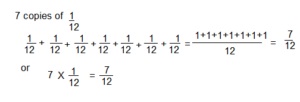
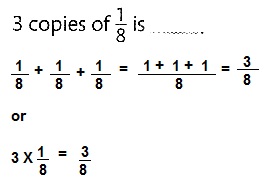































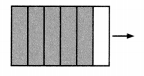
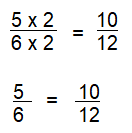
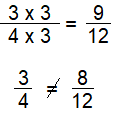
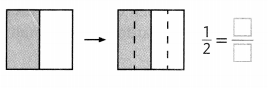
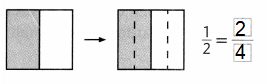
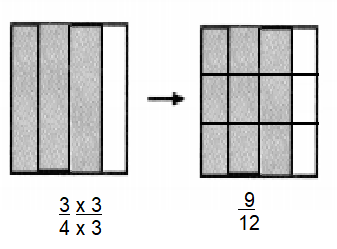
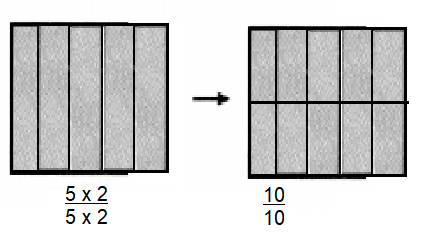
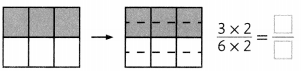
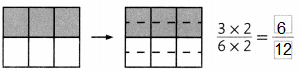

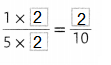
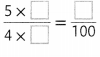
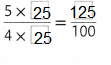
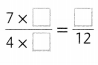
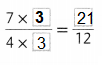
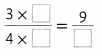
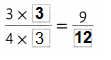

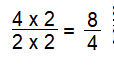

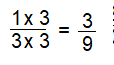


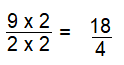
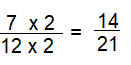

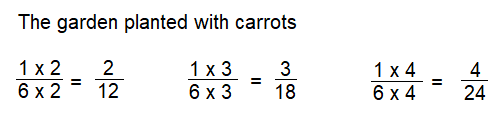
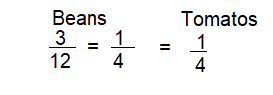
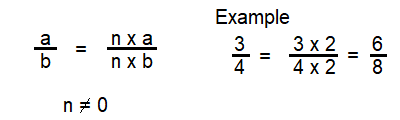

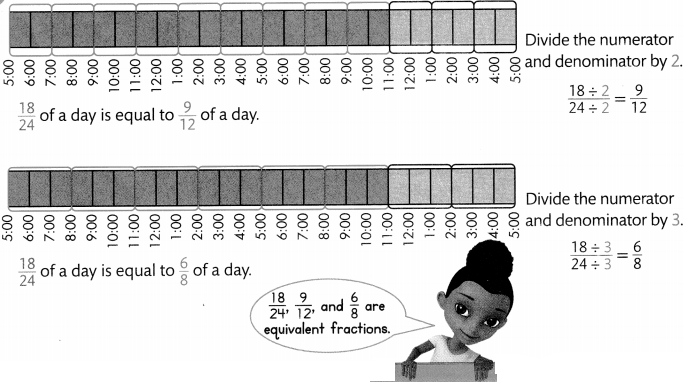

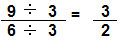
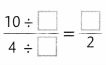
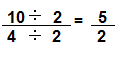

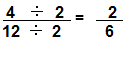
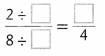

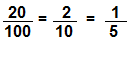
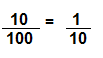
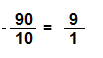
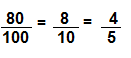
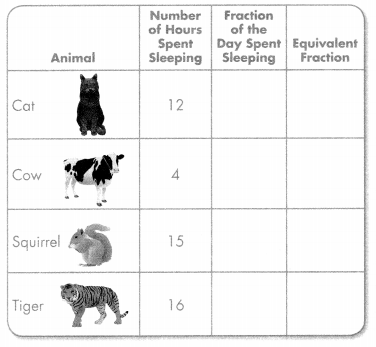

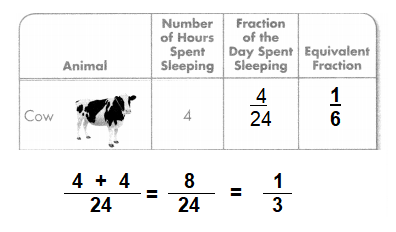




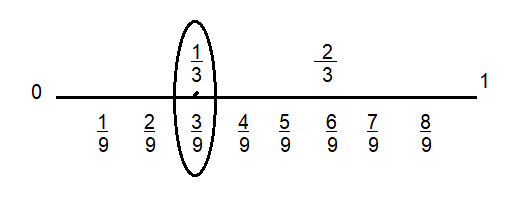
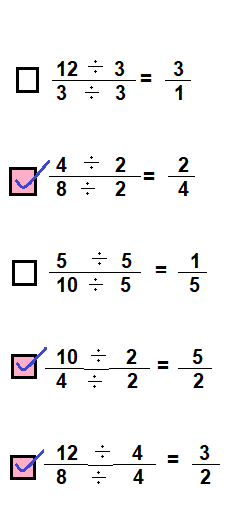



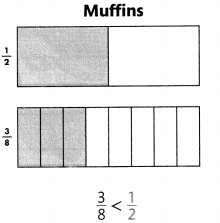

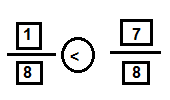

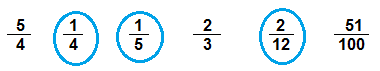
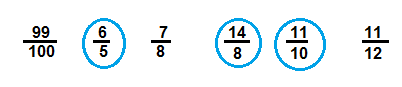

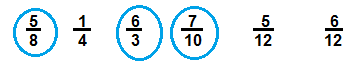












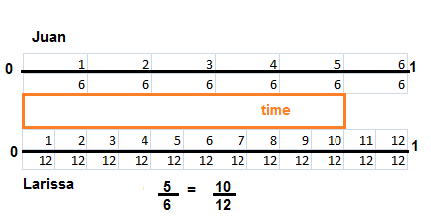

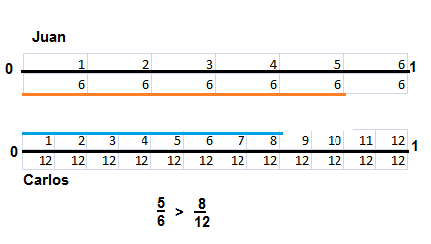
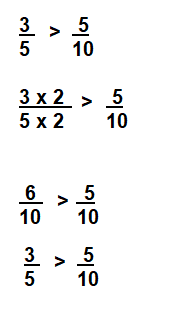
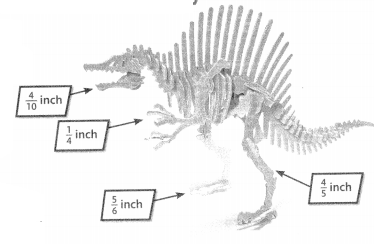
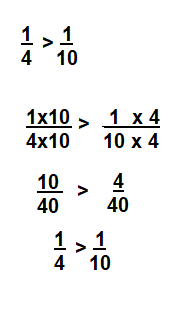
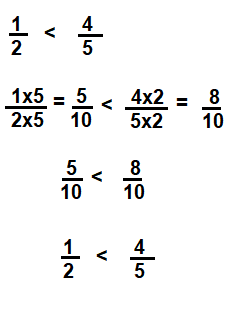
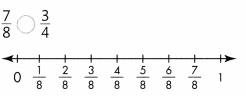
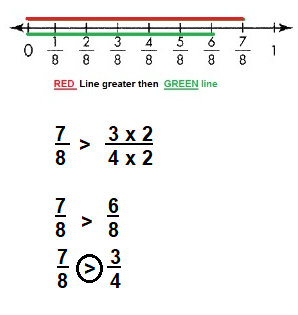
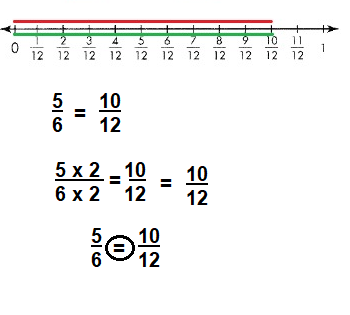
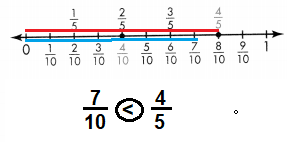
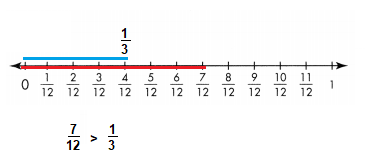
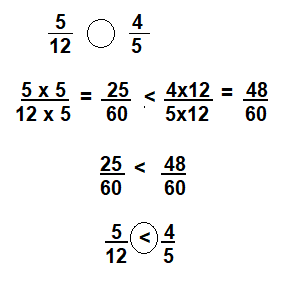
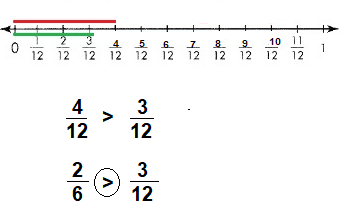

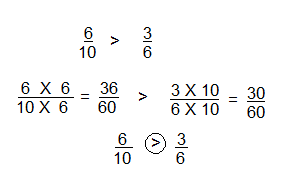

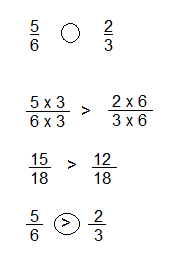
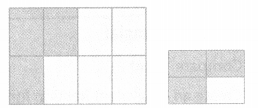














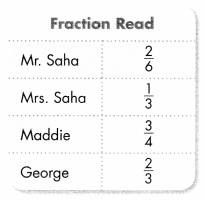

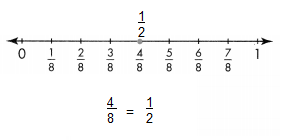
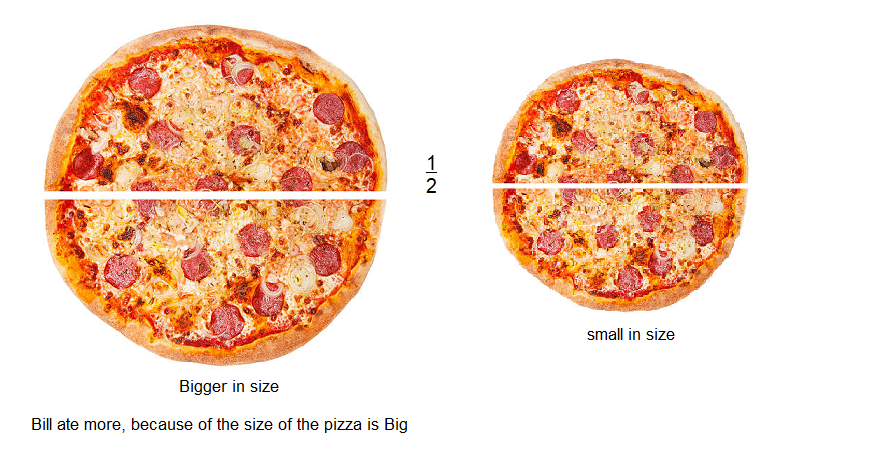
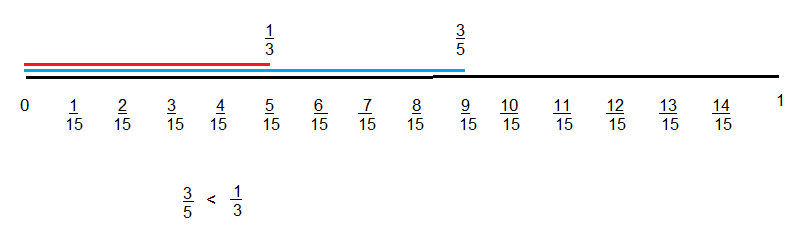





























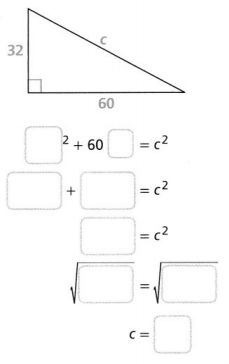
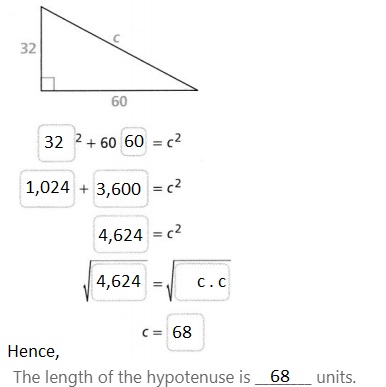
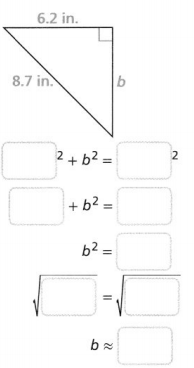
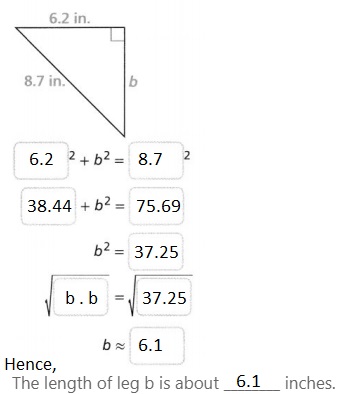
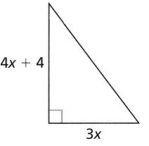
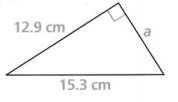
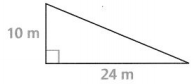



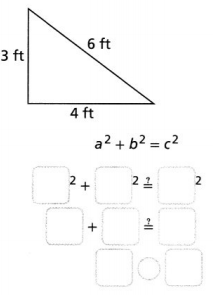
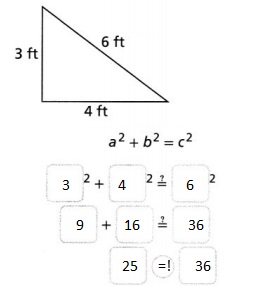

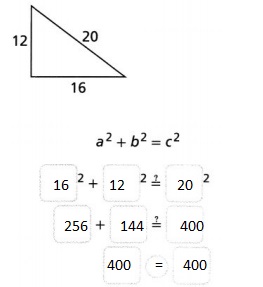

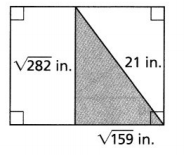




























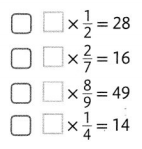














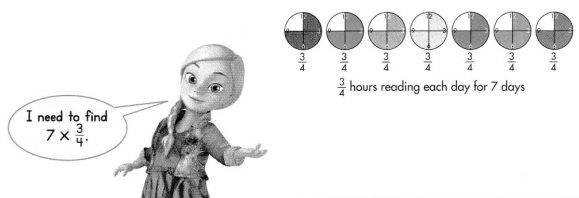
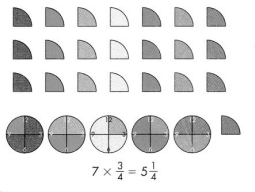


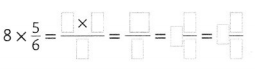






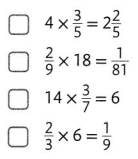
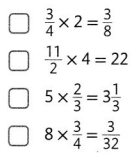
























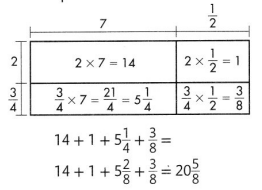

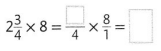
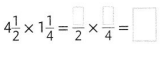

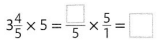
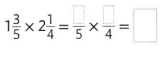

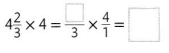


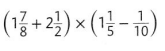
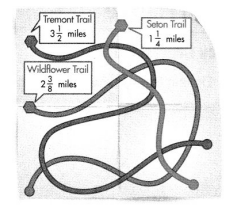
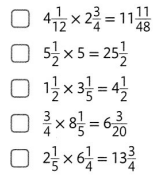

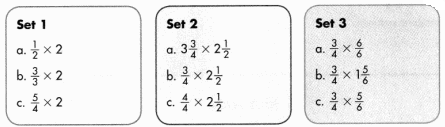

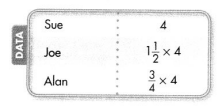

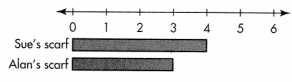

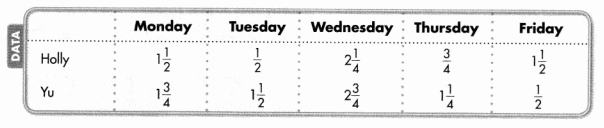

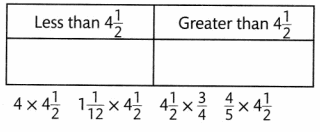

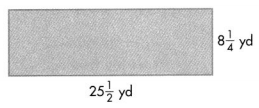













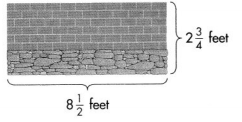





















































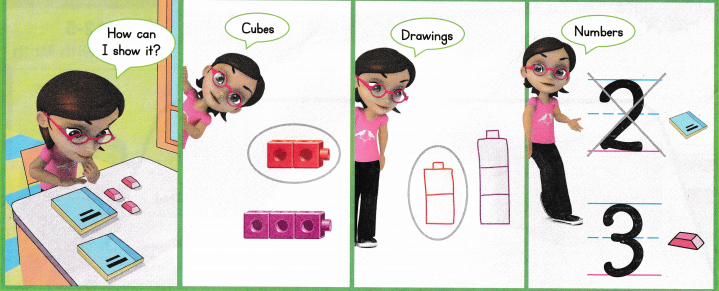












































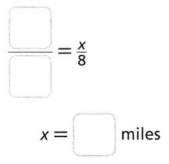
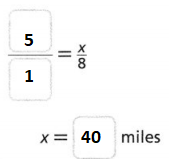
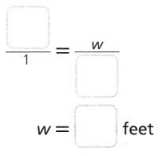






 Scale: 1 cm = 2 feet
Scale: 1 cm = 2 feet