Go through the enVision Math Common Core Grade 6 Answer Key Topic 6 Understand And Use Percent regularly and improve your accuracy in solving questions.
enVision Math Common Core 6th Grade Answers Key Topic 6 Understand And Use Percent
Topic 6 Essential Question
What is the meaning of percent? How can percent be estimated and found?
Answer:
A percent is a rate that compares a part to a whole.
The percent can be estimated to be 100.
Explanation:
In the above-given question,
given that,
A percent is a rate that compares a part to a whole.
the percent can be estimated to be 100.
the whole is 100%.
3-ACT MATH

Ace the Test
Numbers, percents, letters-teachers use grades as a language to help explain language to help explain how you are doing in class. When you know how your grade is determined, it is easier to understand your teacher’s expectations. Think about this during the 3-Act Mathematical Modeling lesson.

Topic 6 enVision STEM Project
Did You Know?
Extinction normally occurs at a rate of about one to five species per year. The earth is now losing species at 1,000 to 10,000 times that rate, with dozens going extinct every day.

There are 1,373 species of birds identified as threatened.

Polar Bears need ice floes to rest when they travel long distances to find food or migrate. Due to melting ice, the population will likely decrease by more than 30% in the next three generations.

Scientists estimate that the population of nearly 17,000 eastern lowland gorillas has declined by more than 50%.

Conservation efforts helped the total number of black rhinos to grow from 2,410 to 4,880 in 15 years.
According to the Chinese government, the population of wild giant pandas has reached 1,864, up from 1,596 at last count.
In 100 years, the number of the world’s tigers declined from 100,000 to 3,200.

Your Task: Engineering to Prevent Extinction
Engineers help to prevent extinction with both direct and indirect solutions. Materials engineers develop wood alternatives. Mechanical and chemical engineers produce clean energy. You and your classmates will research threatened species and identify ways that engineers can help to prevent the extinction of these species.

Topic 6 Get Ready!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
- decimal
- fraction
- ratio
- term
Question 1.
A _________ can be written as x to y, x:y, or \(\frac{x}{y}\).
Answer:
A ratio can be written as x to y, x:y, or \(\frac{x}{y}\).
Explanation:
In the above-given question,
given that,
A ratio can be written as x to y, x:y, or \(\frac{x}{y}\).
for example:
A ratio is a comparison of two numbers by division.
the ratio of x to y can be written as x to y.
x: y, x/y.

Question 2.
The number 2.25 is a ________
Answer:
The number 2.25 is a decimal.
Explanation:
In the above-given question,
given that,
the number 2.25 is a decimal.
for example:
17.591 in this 1 is in the tens place, 7 is in one’s places.
Question 3.
A number that can be used to describe a part of a whole is a ________.
Answer:
A number that can be used to describe a part of a whole is a fraction.
Explanation:
In the above-given question,
given that,
A number that can be used to describe a part of a whole is a fraction.
for example:
1/6 is one-sixth.
Rates
Write an equivalent rate.
Question 4.
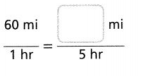
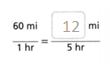
Answer:
The equivalent rate is 12 miles.
Explanation:
In the above-given question,
given that,
1 hr = 60 miles.
5 hours = 12 miles.
12 x 5 = 60.
so the equivalent rate is 12 miles.
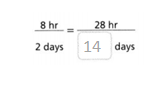
Question 5.
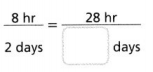
Answer:
The missing number of days is 14.
Explanation:
In the above-given question,
given that,
The missing number of days is 14.
2 x 4 = 8.
1 x 14 = 28.
Question 6.
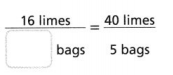
Answer:
The missing number of bags = 2.
Explanation:
In the above-given question,
given that,
the number of missing bags = 2.
2 x 8 = 16.
5 x 8 = 40.
so the number of missing bags = 2.

Question 7.
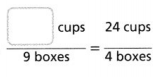
Answer:
The number of missing cups = 54.
Explanation:
In the above-given question,
given that,
the missing number of cups is 54.
4 x 6 = 24.
9 x 6 = 54.
so the number of missing cups = 54.
Question 8.
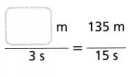
Answer:
The number of missing seconds = 27 m.
Explanation:
In the above-given question,
given that,
15 x 9 = 135.
3 x 9 = 27.
so the missing number of seconds = 27 m.

Question 9.

Answer:
The missing number of dollars = $24.
Explanation:
In the above-given question,
given that,
36 lb = 9 lb.
9 x 4 = 36lb.
6 x 4 = 24$.
so the missing number of dollars = $24.
Decimal Computation
Find each product or quotient.
Question 10.
21 ÷ 0.05
Answer:
The quotient is 420.
Explanation:
In the above-given question,
given that,
the two numbers are 21 and 0.05.
divide the numbers.
21 / 0.05 = 420.
So the quotient is 420.
Question 11.
18 × 1.25
Answer:
The product is 22.5.
Explanation:
In the above-given question,
given that,
the two numbers are 21 and 0.05.
multiply the numbers.
18 x 1.25 = 22.5.
So the product is 22.5.
Question 12.
10.2 ÷ 1.2
Answer:
The quotient is 8.5.
Explanation:
In the above-given question,
given that,
the two numbers are 10.2 and 1.2.
divide the numbers.
10.2 / 1.2 = 8.5.
So the quotient is 8.5.
Question 13.
150 × 0.625
Answer:
The product is 93.75.
Explanation:
In the above-given question,
given that,
the two numbers are 150 and 0.625.
multiply the numbers.
150 x 0.625 = 93.75.
So the product is 93.75.
Question 14.
4 ÷ 100
Answer:
The quotient is 0.04.
Explanation:
In the above-given question,
given that,
the two numbers are 4 and 100.
divide the numbers.
4 / 100 = 0.04.
So the quotient is 0.04.
Question 15.
0.25 × 0.1
Answer:
The product is 0.025.
Explanation:
In the above-given question,
given that,
the two numbers are 0.25 and 0.1.
multiply the numbers.
0.25 x 0.1 = 0.025.
So the product is 0.025.
Equivalent Ratios
Write three equivalent ratios for each ratio.
Question 16.
\(\frac{8}{12}\)
Answer:
The three equivalent ratios are 4/6, and 2/3.
Explanation:
In the above-given question,
given that,
the ratio is 8/12.
8/12 = 4/6.
4/6 = 2/3.
so the equivalent ratios are 4/6, and 2/3.
Question 17.
\(\frac{15}{35}\)
Answer:
The equivalent ratio is 3/7.
Explanation:
In the above-given question,
given that,
the ratio is 15/35.
15/35 = 3/7.
so the equivalent ratio is 3/7.
Question 18.
\(\frac{30}{48}\)
Answer:
The three equivalent ratios are 10/18, and 5/9.
Explanation:
In the above-given question,
given that,
the ratio is 30/48.
30/48 = 10/18.
10/18 = 5/9.
so the equivalent ratios are 10/18, and 5/9.

Question 19.
What are two ways to find an equivalent ratio for \(\frac{10}{25}\)?
Answer:
The two ways are 5 x 2 = 10, 2 x 5 = 10, and 5 x 5 = 25.
Explanation:
In the above-given question,
given that,
the two ways to find an equivalent ratio is 10/25.
10/25 = 2/5.
5 x 2 = 10.
5 x 5 = 25.
Language Development
Fill in the cluster diagram using key phrases, sentences, illustrations, or examples related to percents.

Pick A Project
PROJECT 6A
How would you describe your favorite work of art?
PROJECT: BUILD A MOSAIC

PROJECT 6B
If you had a jar of coins, what could you buy?
PROJECT: ESTIMATE PERCENTS
PROJECT 6C
How does advertising make you want to buy something?
PROJECT: DESIGN FLYERS

PROJECT 6D
Which do you think grows faster-a koala or a panda bear?
PROJECT: MAKE A GROWTH CHART

Lesson 6.1 Understand Percent
Explain It!
Tom made a vegetable pizza and a pepperoni pizza. He cut the vegetable pizza into 5 equal slices and the pepperoni pizza into 10 equal slices. Tom’s friends ate 2 slices of vegetable pizza and 4 slices of pepperoni pizza.
I can… represent and find the percent of a whole.
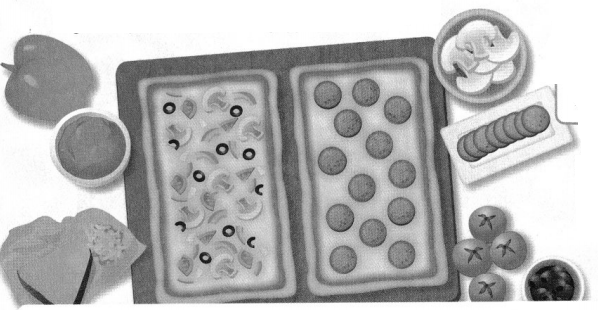
A. Draw lines on each rectangle to represent the equal slices into which each pizza was cut.
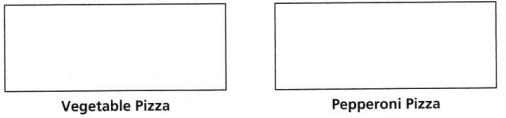
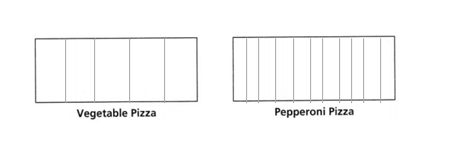
Answer:
The number of lines on vegetable pizza is 5.
the number of lines on pepperoni pizza is 10.
Explanation:
In the above-given question,
given that,
Tom made a vegetable pizza and a pepperoni pizza.
He cut the vegetable pizza into 5 equal slices and the pepperoni pizza into 10 equal slices.
5/10 = 1/2.
so the number of lines on vegetable pizza is 5.
the number of lines on pepperoni pizza is 10.
B. Construct Arguments Tom says his friends ate the same amount of vegetable pizza as pepperoni pizza. How could that be true?
Answer:
Yes, Tom was correct.
Explanation:
In the above-given question,
given that,
Tom made a vegetable pizza and a pepperoni pizza.
He cut the vegetable pizza into 5 equal slices and the pepperoni pizza into 10 equal slices.
5/10 = 1/2.
so the number of lines on vegetable pizza is 5.
the number of lines on pepperoni pizza is 10.
so Tom was correct.
Focus on math practices
Model with Math What if Tom’s friends ate 6 of the pepperoni pizza? How could you use the rectangles above to find an equal amount of vegetable pizza?
Answer:
The equal amount of vegetable pizza = 3.
Explanation:
In the above-given question,
given that,
Tom’s friends ate 6 of the pepperoni pizza.
vegetable pizza and pepperoni pizza are in the ratio is 1: 2.
so the equal amount of vegetable pizza = 3.
KEY CONCEPT
A percent is a rate that compares a part to a whole. The second term in the rate is always 100. The whole is 100%.
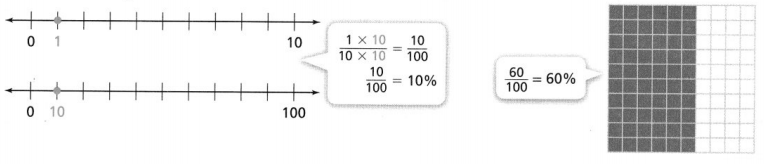
Do You Understand?
Question 1.
Essential Question How can you represent a rate with 100 as the whole?
Answer:
I will represent the whole as 100%.
Explanation:
In the above-given question,
given that,
A percent is a rate that compares a part to a whole.
The second term in the rate is always 100.
the whole is 100%.
Question 2.
When writing a percent as a fraction, what number do you write as the whole, or denominator?
Answer:
The percentage can be converted into a fraction by removing the %symbol and then writing the value in the form of a fraction with a 100 in the denominator.
Explanation:
In the above-given question,
given that,
The percent to a fraction is the conversion of percentage values to a fraction.
As per the percent to fraction steps, the percentage can be converted into a fraction by removing the % symbol and then writing the value in the form of a fraction with a 100 in the denominator.
Question 3.
Why are tenths, fifths, fourths, and halves easy to express as percents?
Answer:
1/10 = 0.1.
1/5 = 0.2.
1/4 = 0.25.
1/2 = 0.5.
Explanation:
In the above-given question,
given that,
tenths, fifths, fourths, and halves express as percents.
tenths = 1/10 = 0.1.
fifths = 1/5 = 0.2.
fourths = 1/4 = 0.25.
halves = 1/2 = 0.5.
Question 4.
Why is the grid in Example 1 a good way to represent a percent?
Answer:
Question 5.
Look for Relationships If CD in Example 3 represents 100%, is the length of a line segment that is 300% longer or shorter than 4 inches? Explain.
Answer:
Do You Know How?
In 6 and 7, write the percent of each figure that is shaded.
Question 6.
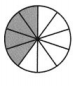
Answer:
The percent of the figure = 40%.
Explanation:
In the above-given question,
given that,
the above figure is divided into 10 equal parts.
out of 10 parts 4 parts are shaded.
4/10 = 0.4%.
so the percent of the figure = 40%.
Question 7.

Answer:
The percent of the figure = 7%.
Explanation:
In the above-given question,
given that,
the above figure is divided into 100 equal parts.
out of 100 parts 7 parts are shaded.
7/100 = 0.07.
so the percent of the figure = 7%.
In 8-10, find the percent.

Question 8.
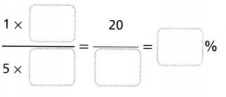
Answer:
The percent is 5%.
Explanation:
In the above-given question,
given that,
1 x 20 = 20.
5 x 4 = 20.
20 / 4 = 5.
so the percent is 5%.
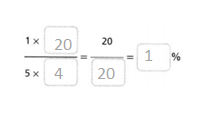
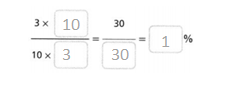
Question 9.
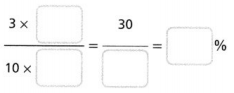
Answer:
The percent is 1%.
Explanation:
In the above-given question,
given that,
3 x 10 = 30.
10 x 3 = 30.
30/30 = 1%.
so the percent is 1%.
Question 10.
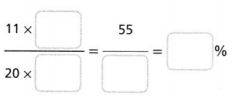
Answer:
The percent is 55.
Explanation:
In the above-given question,
given that,
11 x 5 = 55.
20 x 4 = 100.
55/100 = 55%.
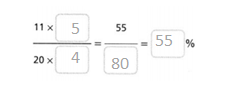
Question 11.
Find the percent of the line segment that point D represents in Example 2.
Answer:
Practice & Problem Solving
In 12 and 13, shade each model to represent the percent.
Question 12.
14%

Answer:
The percent is 14%.
Explanation:
In the above-given question,
given that,
the 14 percent.
the above figure is divided into 100 parts.
so we have to shade the 14 boxes.
Question 13.
20%
![]()
Answer:
The percent is 20%.
Explanation:
In the above-given question,
given that,
there are 5 boxes.
20% of the boxes are filled.
one box is shaded.
In 14 and 15, use \(\overline{A B}\).

Question 14.
If \(\overline{A B}\) represents 50%, what is the length of a line segment that is 100%?
Answer:
The length of the line segment that is 100% is 6 in.
Explanation:
In the above-given question,
given that,
the length of the segment is 3 in if it is 50%.
the length of the segment is 6 in if it is 100%.
3 + 3 = 6.
so the length of the line segment that is 100% is 6 in.
Question 15.
If \(\overline{A B}\) is 300%, what is the length of a line segment that is 100%?
Answer:
The length of a line segment that is 100% is 1in.
Explanation:
In the above-given question,
given that,
\(\overline{A B}\) is 300%.
the total length of the line segment is 3 in.
so the length of a line segment that is 100% is 1 in.
Question 16.
Your friend shows you a coin collection. In it, \(\frac{45}{50}\) of the coins are quarters. What percent of the coins are quarters?
Answer:
The percent of the coins are quarters is 0.25.
Explanation:
In the above-given question,
given that,
\(\frac{45}{50}\) of the coins are quarters.
45/50 = 9/10.
so the percent of the coins are quarters is 0.25.
Question 17.
Use Structure In a race, 19 out of 50 runners finished in fewer than 30 minutes. What percent of the runners finished in fewer than 30 minutes? Write an equivalent fraction to find the percent.
Answer:
The equivalent fraction is 9.5%.
Explanation:
In the above-given question,
given that,
19 out of 50 runners finished in fewer than 30 minutes.
19/50 = 9.5.
so the equivalent fraction is 9.5%.
Question 18.
A basketball player made 63 out of 100 attempted free throws. What percent of free throws did the player make?
Answer:
The percent of free throws did the player make = 63%.
Explanation:
In the above-given question,
given that,
A basketball player made 63 out of 100 attempted free throws.
63/100 = 63%.
so the percent of free throws did the player make = 63%.
Question 19.
Harry kept a weather journal for September. The sun was shining on 4 out of every 5 days. On what percent of the days was the sun not shining?

Answer:
The number of days was the sun not shining = 8%.
Explanation:
In the above-given question,
given that,
Harry kept a weather journal for September.
The sun was shining on 4 out of every 5 days.
4/5 = 0.8.
8/100 = 0.08.
so the number of days was the sun not shining = 8%.
In 20 and 21, use the line segment.

Question 20.
What percent of the line segment is 6 inches long?
Answer:
The line segment is 6 inches long is 100%.
Explanation:
In the above-given question,
given that,
the line segment is divided into 6 parts.
one part is equal to 1 inch.
6 parts = 6 inches.
so the line segment is 6 inches long is 100%.
Question 21.
What percent of the line segment does point C represent?
Answer:
The percent of the line segment does point C represents is 50%.
Explanation:
In the above-given question,
given that,
the line segment is divided into 6 parts.
one part is equal to 1 inch.
6 parts = 6 inches.
so the percent of the line segment does point C represents is 50%.

Question 22.
Critique Reasoning Kyle solved 18 of 24 puzzles in a puzzle book. He says that he can use an equivalent fraction to find the percent of puzzles in the book that he solved. How can he do that? What is the percent?
Answer:
The equivalent fractions are 3/4 and 6/8.
Explanation:
In the above-given question,
given that,
Kyle solved 18 of 24 puzzles in a puzzle book.
18/24 = 3/4.
18/24 = 6/8.
so the equivalent fractions are 3/4 and 6/8.
Question 23.
Reasoning Twenty of the students in Hannah’s class, or 80% of the class, voted to have pizza for lunch every Wednesday. How many students are in Hannah’s class?
Answer:
The number of students is in Hannah’s class = 25 students.
Explanation:
In the above-given question,
given that,
Twenty of the students in Hannah’s class, or 80% of the class, voted to have pizza for lunch every Wednesday.
20/100 = 1/5.
so the number of students is in Hannah’s class = 25 students.
Question 24.
According to a survey of workers, \(\frac{2}{20}\) of the workers walk to work, \(\frac{1}{20}\) bike, \(\frac{4}{20}\) carpool, and \(\frac{13}{20}\) drive alone. What percent of the workers walk or bike to work?
Answer:
The percent of the workers walk or bike to work = 30 %.
Explanation:
In the above-given question,
given that,
According to a survey of workers, \(\frac{2}{20}\) of the workers walk to work,
\(\frac{1}{20}\) bike,
\(\frac{4}{20}\) carpool,
\(\frac{13}{20}\) drive alone.
2/20 = 1/10.
1/20 + 1/10 = 1/30.
Question 25.
Higher Order Thinking From Monday through Friday, James works in the library on 2 days and in the cafeteria on another day. On Saturday and Sunday, James washes cars 50% of the days. How many days does James work in a week? What percent of the days from Monday through Friday does he work?
Answer:
The percent of the days from Monday through Friday does he work = 80%.
Explanation:
In the above-given question,
given that,
From Monday through Friday, James works in the library on 2 days and in the cafeteria on another day.
On Saturday and Sunday, James washes cars 50% of the day.
2 + 1 = 3.
3 + 2 = 5.
so the percent of the days from Monday through Friday does he work = 80%.
Assessment Practice
Question 26.
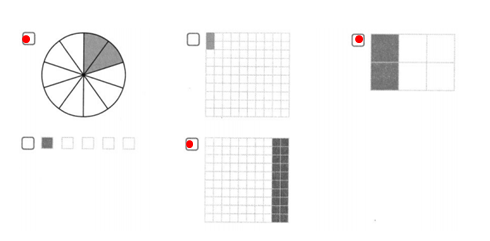
Select all the figures that are shaded to represent 20% of the whole.
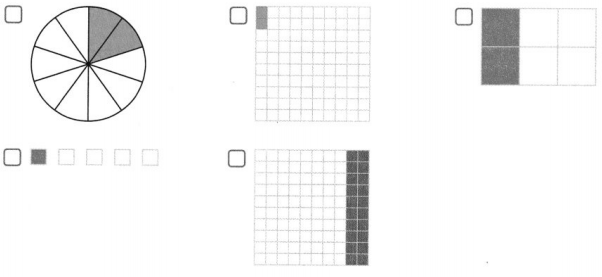
Answer:
Options 1, 3, and 5 are correct.
Explanation:
In the above-given question,
given that,
the figures that are shaded to 20% as a whole is:
in the 1st figure, the circle is divided into 10 parts.
20% of the figure is shaded.
in the 3rd figure, there are 5 boxes.
1 box is filled is 20%.
so options 1, 3, and 5 are correct.
Lesson 6.2 Relate Fractions, Decimals, and Percents
Solve & Discuss It!
The grid is shaded with blue, orange, and yellow. What part of the grid is shaded blue? What part is shaded orange? What part of the grid is shaded?
I can… write equivalent values as fractions, decimals, or percents.

Use Structure
Look for patterns in the grid to help count parts that are shaded in blue and in orange.
Focus on math practices
Reasoning Write the part of the grid that is shaded yellow as a decimal and a percent. How are the decimal and the percent alike and how are they different?
Essential Question
How are fractions, decimals, and percents related?
Try It!
Ana spends 0.45 of her homework time reading. What is 0.45 as a percent? Explain.
Answer:
The percent is 45.
Explanation:
In the above-given question,
given that,
Ana spends 0.45 of her homework time reading.
0.45 can be written as a percent is 45.
so the percent is 45.
Convince Me! What relationship do you see when comparing the equivalent fraction and percent?
Try It!
Isabel spends \(\frac{3}{8}\) of her homework time on reading. What is \(\frac{3}{8}\) as a decimal and as a percent?
Answer:
3/8 = 0.375 and 0.00375%
Explanation:
In the above-given question,
given that,
Isabel spends \(\frac{3}{8}\) of her homework time on reading..
3/8 = 0.375.
3/8 = 0.00375%.
KEY CONCEPT
You can use division and equivalent ratios to express fractions, decimals, and percents in equivalent forms.
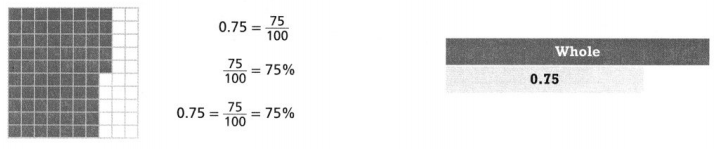
Do You Understand?
Question 1.
Essential Question How are fractions, decimals, and percents related?
Answer:
Fractions, decimals, and percents are related.
Explanation:
In the above-given question,
given that,
0.75 = 75/100.
75/100 = 75%.
0.75 = 75/100 = 75%.
so the fractions, decimals, and percents are related.
Question 2.
Why do you use a denominator of 100 when you write a percent as a fraction?
Answer:
We can use a denominator of 100 when we write a percent as a fraction.
Explanation:
In the above-given question,
given that,
we can use a denominator of 100 when we write a percent as a fraction.
for example:
75/100 = 0.75.
0.75 = 75%.
Question 3.
Look for Relationships How do you use the digits in a hundredths decimal to write a percent?
Answer:
Question 4.
How do you write a fraction with a denominator of 20 as a decimal?
Answer:
The fraction with a denominator of 20 as a decimal is 0.05.
Explanation:
In the above-given question,
given that,
5/100 = 20.
5/100 = 0.05.
so the fraction with a denominator of 20 as a decimal is 0.05.
Do You Know How?
In 5-7, write each number in equivalent forms using the two other forms of notation: fraction, decimal, or percent.
Question 5.
27%
Answer:
Fraction = 27/100.
decimal = 0.27.
percent = 27%.
Explanation:
In the above-given question,
given that,
the decimal is 0.27.
The fraction is 27/100.
the percent is 27%.
Question 6.
0.91
Answer:
Fraction = 91/100.
decimal = 0.91.
percent = 91%.
Explanation:
In the above-given question,
given that,
the decimal is 0.91.
The fraction is 91/100.
the percent is 91%.
Question 7.
\(\frac{6}{100}\)
Answer:
Fraction = 6/100.
decimal = 0.06.
percent = 6%.
Explanation:
In the above-given question,
given that,
the decimal is 0.06.
The fraction is 6/100.
the percent is 6%.
Question 8.
Greek yogurt has 25% of the calcium that most people need in a day. What is 25% as a decimal?

Answer:
The decimal is 0.25.
Explanation:
In the above-given question,
given that,
Greek yogurt has 25% of the calcium that most people need in a day.
25%.
so the decimal is 0.25.
Question 9.
Linda received \(\frac{4}{5}\) of the votes in the election for student council president. What percent of the votes did Linda receive?
Answer:
The percent of the votes did Linda receive = 80%.
Explanation:
In the above-given question,
given that,
Linda received \(\frac{4}{5}\) of the votes in the election for student council president.
4/5 = 0.8.
80% = 80/100.
8/10 = 0.8.
so the percent of the votes did Linda receive = 80%.
Practice & Problem Solving
Leveled Practice in 10-15, write each number in equivalent forms using the two other forms of notation: fraction, decimal, or percent.
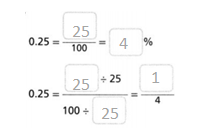
Question 10.
0.25
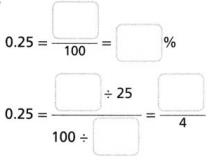
Answer:
0.25 = 25/100 = 25%.
Explanation:
In the above-given question,
given that,
0.25 = 25/100.
25/100 = 25%.
25/25 = 1.
100/25 = 4.
Question 11.
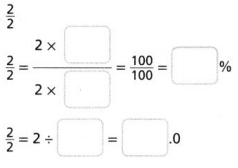
Answer:
2/2 = 2 x 50/ 2 x 50 = 100/100 = 1%.
Explanation:
In the above-given question,
given that,
2/2 = 2x 50 = 100.
100/100 = 1%.
2/2 = 2/1 = 2%.
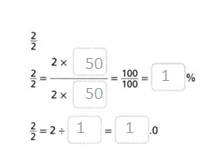
Question 12.
7%
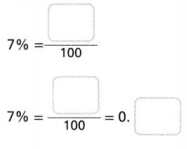
Answer:
7% = 7/100.
Explanation:
In the above-given question,
given that,
7 percent = 7%.
7% = 7/100.
7/100 = 0.07.

Question 13.
38%
Answer:
38% = 0.38.
Explanation:
In the above-given question,
given that,
38 percent = 38%.
38% = 38/100.
38/100 = 0.38.
Question 14.
\(\frac{7}{8}\)
Answer:
7/8 = 0.875.
Explanation:
In the above-given question,
given that,
7/8 = 0.875.
0.875 = 875/100.
875/100 = 87.5.
Question 15.
0.04
Answer:
0.04 = 4%.
Explanation:
In the above-given question,
given that,
0.04 = 4%.
4% = 4/100.
4/100 = 0.04.
Question 16.
Devon answered 23 out of 25 problems on a math test correctly. What percent of the problems did Devon answer correctly?

Answer:
The percent of the problems did Devon answer = 92%.
Explanation:
In the above-given question,
given that,
Devon answered 23 out of 25 problems on a math test correctly.
23/25 = 0.92.
92/100 = 0.92.
0.92 = 92%.
Question 17.
Reasoning How could you write \(\frac{4}{8}\) as a percent without dividing?
Answer:
4/8 = 0.5.
Explanation:
In the above-given question,
given that,
4/8 = 0.5.
5/10 = 0.5.
5/100 = 0.05.
4/8 = 0.5%.
In 18-21, use the circle graph.
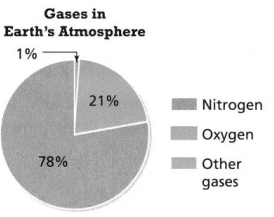
Question 18.
Many chemical elements, can be found in Earth’s atmosphere. What fraction of Earth’s atmosphere is made up of nitrogen?
Answer:
Nitrogen is made up of 78%.
Explanation:
In the above-given question,
given that,
Many chemical elements, can be found in Earth’s atmosphere.
nitrogen is made up of 78%.
oxygen is made up of 21%.
other gases are made up of 1%.
Question 19.
How much of Earth’s atmosphere is made up of oxygen? Write the part as a decimal.
Answer:
The Earth’s atmosphere is made up of oxygen is 0.21.
Explanation:
In the above-given question,
given that,
The Earth’s atmosphere is made up of oxygen.
21% = 21/100.
21/100 = 0.21.
so the Earth’s atmosphere is made up of oxygen is 0.21.
Question 20.
What percent of gases in Earth’s atmosphere does the whole circle graph represent?
Answer:
The percent of gases in Earth’s atmosphere does the whole circle graph represents is 1%.
Explanation:
In the above-given question,
given that,
Nitrogen gas = 78%.
oxygen gas = 21%.
the percent of gases in Earth’s atmosphere does the whole circle graph represents is 1%.
Question 21.
What fraction of the gases in Earth’s atmosphere are gases other than nitrogen and oxygen?
Answer:
The fraction of the gases in the Earth’s atmosphere is gases other than nitrogen and oxygen = 1/100.
Explanation:
In the above-given question,
given that,
Many chemical elements, can be found in Earth’s atmosphere.
nitrogen is made up of 78%.
oxygen is made up of 21%.
the fraction of the gases in the earth’s atmosphere = 1/100.
1/100 = 0.01.
Question 22.
Look for Relationships All T-shirts in a store are on sale as shown. Is this markdown greater than or less than a markdown of off the original price? Explain.

Answer:
The original price = 25%.
Explanation:
In the above-given question,
given that,
All T-shirts in a store are on sale as shown.
100 – 25 = 75%.
so the original price = 25%.
Question 23.
Critique Reasoning Enrollment at Jacksonville Middle School increased by 3% this year. Sofia says that the increase, written as a decimal, is 0.3. Is Sofia correct? Explain.
Answer:
No, Sofia is correct.
Explanation:
In the above-given question,
given that,
Enrollment at Jacksonville Middle School increased by 3% this year.
3% = 3/100.
3/100 = 0.03.
so Sofia is correct.
Question 24.
Generalize What are the attributes of fractions that are equivalent to 100%?
Answer:
The attributes of fractions that are equivalent to 100% = 1000/100.
Explanation:
In the above-given question,
given that,
the fractions are 1000/100.
1000/100 = 100.
so the attributes of fractions that are equivalent to 100% = 100.
Question 25.
The cost of building a new library is 0.85 of the cost of remodeling the old library. What is the cost as a percent?
Answer:
The cost as a percent = 85%.
Explanation:
In the above-given question,
given that,
The cost of building a new library is 0.85 of the cost of remodeling the old library.
0.85 = 85/100.
85/100 = 85%.
so the cost as a percent = 85%.
Question 26.
Nine out of every 20 people walking out of a movie theater say that they would recommend the movie to a friend. What percent of the people would recommend the movie to a friend?
Answer:
The percent of the people who would recommend the movie to a friend = 45%.
Explanation:
In the above-given question,
given that,
Nine out of every 20 people walking out of a movie theater say that they would recommend the movie to a friend.
9/20 = 0.45.
45/100 = 0.45.
so the percent of the people who would recommend the movie to a friend = 45%.
Question 27.
Higher Order Thinking Ms. Rose bought a package of sea life stickers. Out of every 10 stickers, 4 are starfish. If there are 60 stickers in the package, what fraction of the stickers are starfish? What percent of the stickers in the package are starfish?

Answer:
The percent of the stickers in the package is starfish = 24%.
Explanation:
In the above-given question,
given that,
Ms. Rose bought a package of sea life stickers.
Out of every 10 stickers, 4 are starfish.
10/4 = 5/2.
for 60 there are 24 starfish.
so the percent of the stickers in the package is starfish = 24%.
Assessment Practice
Question 28.
\(\frac{3}{4}\) can be represented as a percent. Select all the fractions and decimals that are also equivalent to this percent.
☐ \(\frac{51}{68}\)
☐ 0.34
☐ \(\frac{36}{50}\)
☐ 0.75
☐ \(\frac{39}{52}\)
Answer:
Options A, D, and E are correct.
Explanation:
In the above-given question,
given that,
3/4 = 0.75.
51/68 = 0.75.
39/52 = 0.75.
so options A, D, and E are correct.
Question 29.
There are 110 sixth-grade students in a Florida middle school. 40% of the students enjoy playing video games on the weekends. Using the percent as a rate per 100, how many students enjoy playing video games?
Answer:
The number of students who enjoy playing video games = 4%.
Explanation:
In the above-given question,
given that,
There are 110 sixth-grade students in a Florida middle school.
40% of the students enjoy playing video games on the weekends.
40/100 = 0.4.
so the number of students who enjoy playing video games = 4%.
Lesson 6.3 Represent Percents Greater Than 100 or Less Than 1
Solve & Discuss It!
Marci, Bobby, and Max began their homework at the same time. Marci finished her homework in 60 minutes. Bobby finished his homework in 50% of the time it took Marci to finish. Max finished his homework in 150% of Marci’s time. How long did each of them work?
I can… write percents that are greater than 100 or less than 1.

Model with Math
How can you use a model to represent a part that is greater than a whole?
Focus on math practices
Reasoning Did Max spend more time or less time on his homework than Marci? Explain.
Essential Question
How can you write a percent greater than 100 or less than 1 as a fraction and as a decimal?
Try It!
The area of a new movie theater is 225% of the area of the old theater. What is 225% as a fraction and as a decimal?
Answer:
Fraction = 225/100.
Decimal = 2.25.
Explanation:
In the above-given question,
given that,
the area of a new movie theater is 225% of the area of the old theater.
225% = 225/100.
225/100 = 2.25.
so fraction = 225/100.
decimal = 2.25.
Convince Me! How would you write 1.75 as a percent? Give an example in which you would use a percent that is greater than 100.
Answer:
Percent = 175/100.
The percent that is greater than 100 is 175.
Explanation:
In the above-given question,
given that,
175/100 = 1.75.
175 is greater than 100.
Try It!
Write each percent as a fraction and as a decimal.
a. \(\frac{2}{5}\)%
Answer:
2/5 = 0.4.
0.4% = 0.004.
Explanation:
In the above-given question,
given that,
2/5 % = 0.4%.
0.4% = 0.004.
b. 0.3%
Answer:
0.003.
Explanation:
In the above-given question,
given that,
0.3% = 3/100.
3/100 = 0.003.
KEY CONCEPT
You can express percents greater than 100 or less than 1 in equivalent forms.

Do You Understand?
Question 1.
Essential Question How can you write a percent greater than 100 or less than 1 as a fraction and as a decimal?
Answer:
The percent greater than 100 or less than 1 is 275%.
Explanation:
In the above-given question,
given that,
The percent greater than 100 or less than 1 is 275%.
275% = 275/100.
275/100 = 11/4.
275% = 11/4 = 2.75.
so the percent greater than 100 or less than 1 is 275%.
Question 2.
Reasoning Explain why \(\frac{3}{4}\) is less than 100%.
Answer:
3/4 = 0.75.
Explanation:
In the above-given question,
given that,
3/4 = 0.75.
75/100 = 0.75.
75% is less than 100%.
so 3/4 is less than 100%.
Question 3.
Reasoning Why is the numerator greater than the denominator in a fraction that is equivalent to a percent greater than 100?
Answer:
Question 4.
Explain the difference between \(\frac{1}{2}\) and \(\frac{1}{2}\)%.
Answer:
The difference between 1/2 and 1/2% is 0.5.
Explanation:
In the above-given question,
+given that,
1/2 = 0.5.
1/2 = 0.5%.
0.5/100 = 0.005.
0.5 is greater than 0.005.
Do You Know How?
In 5–7, write each percent as a fraction and as a decimal.
Question 5.
150%
Answer:
Fraction = 150/100.
decimal = 1.5.
Explanation:
In the above-given question,
given that,
the percent is 150%.
fraction = 150/100.
150/100 = 1.5.
decimal = 1.5.
Question 6.
\(\frac{3}{10}\)%
Answer:
3/10% = 0.003.
Explanation:
In the above-given question,
given that,
the percent is 3/10%.
3/10 = 0.3.
0.3% = 0.3/100.
0.3/100 = 0.003.
Question 7.
0.24%
Answer:
Fraction = 24/100.
Decimal = 0.24.
Explanation:
In the above-given question,
given that,
the percent is 0.24%.
fraction is 24/100.
Decimal = 0.24.
Question 8.
Kelly saved \(\frac{4}{5}\)% of her allowance. What is this percent expressed as a fraction and as a decimal?
Answer:
The percent expressed as a fraction and as a decimal = 0.8/100 and 0.008.
Explanation:
In the above-given question,
given that,
Kelly saved \(\frac{4}{5}\)% of her allowance.
the percent is 4/5%.
4/5% = 0.8%.
0.8% = 0.8/100.
0.8/100 = 0.008.
Question 9.
Mrs. Sanchez sold her house for 250% of the amount she paid for it. What is this percent expressed as a fraction and as a decimal?
Answer:
The percent expressed as a fraction and as a decimal is 250/100 and 2.5.
Explanation:
In the above-given question,
given that,
Mrs. Sanchez sold her house for 250% of the amount she paid for it.
250/100 = 25/10.
25/10 = 2.5.
so the percent expressed as a fraction and as a decimal is 250/100 and 2.5.
Practice & Problem Solving
Leveled Practice in 10-15, write each percent as a fraction and as a decimal.
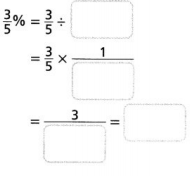
Question 10.
Answer:
3/5% = 0.006.
Explanation:
In the above-given question,
given that,
3/5% = 3/5 / 100.
3/5 x 1/100.
3/500 = 0.006.

Question 11.
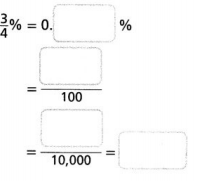
Answer:
3/4% = 0.75%.
Explanation:
In the above-given question,
given that,
3/4% = 3/4 / 100.
0.75/100 = 0.0075.
3/4% = 0.0075.
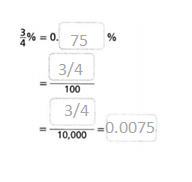
Question 12.
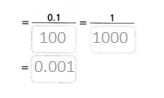
0.1% = 0.1 ÷ 100
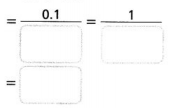
Answer:
0.1% = 0.1 / 100.
Explanation:
In the above-given question,
given that,
0.1% = 0.1 / 100.
0.1 / 100 = 0.001.
1/1000 = 0.001.
Question 13.
0.4% = 0.4 ÷ 100
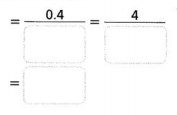
Answer:
0.4% = 0.4 / 100.
Explanation:
In the above-given question,
given that,
0.4% = 0.4 / 100.
0.4/100 = 4/10.
4/10 = 0.4.

Question 14.
322%
Answer:
322% = 322/100.
Explanation:
In the above-given question,
given that,
322% = 322/100.
322/100 = 3.22.
322% = 3.22.
Question 15.
210%
Answer:
210% = 2.10.
Explanation:
In the above-given question,
given that,
210% = 210/100.
210/100 = 2.10.
210% = 2.10.
Question 16.
Reasoning Use the art at the right. How do you express the length of the Queen Mary 2 as it compares to the height of the Washington Monument as a fraction and as a decimal?

Answer:
The height of the Washington Monument is = 2.
Explanation:
In the above-given question,
given that,
the length of the Queen Mary 2 as it compares to the height of the Washington Monument.
200% = 200/100.
200/100 = 2.
so the height of the Washington Monument is 2.
Question 17.
About \(\frac{7}{10}\)% of the passengers on a cruise ship swam in the ship’s pool on the first day of the cruise. How would you express this number as a decimal and as a percent?
Answer:
The number can be written as a decimal and as a percent = 0.007 and 7/10%.
Explanation:
In the above-given question,
given that,
About \(\frac{7}{10}\)% of the passengers on a cruise ship swam in the ship’s pool on the first day of the cruise.
7/10% = 7/1000.
7/1000 = 0.007.
so the number can be written as a decimal and as a percent = 0.007.
Question 18.
The fastest boat can reach speeds more than 710% as fast as the Queen Mary 2. How would you express this number as a fraction and as a decimal?
Answer:
The number as a fraction and as a decimal is 710/100 and 7.1.
Explanation:
In the above-given question,
given that,
The fastest boat can reach speeds more than 710% as fast as the Queen Mary 2.
710% = 710/100.
710/100 = 71/10.
71/10 = 7.1.
so the number as a fraction and as a decimal is 710/100 and 7.1.
Question 19.
The weight of the Washington Monument is about 105% as much as the Queen Mary 2. Write this percent as a fraction and as a decimal.
Answer:
The number can be written as a fraction and as a decimal = 1.5.
Explanation:
In the above-given question,
given that,
The weight of the Washington Monument is about 105% as much as the Queen Mary 2.
105% = 105/100.
105/100 = 15/10.
15/10 = 1.5.
so the number can be written as a fraction and as a decimal = 1.5.
Question 20.
Students set a goal for the number of cans to collect for the canned food drive. They reached 120% of their goal. What is 120% expressed as a fraction and as a decimal?

Answer:
The fraction is 120/100 and 1.2.
Explanation:
In the above-given question,
given that,
Students set a goal for the number of cans to collect for the canned food drive.
120/100 = 12/10.
12/10 = 1.2.
so the fraction is 120/100 and 1.2.
Question 21.
Use Structure Popcorn sales at a Saturday afternoon matinee were 108% of the sales at the 8:00 showing of the movie. Calvin expressed 108% as 10.8. Is Calvin correct? Explain.
Answer:
No, Calvin was not correct.
Explanation:
In the above-given question,
given that,
Popcorn sales at a Saturday afternoon matinee were 108% of the sales at the 8:00 showing of the movie.
108% = 108/100.
18/10 = 1.8.
so Calvin was not correct.
Question 22.
Construct Arguments There are 350% more students enrolled in Spanish class than Latin class. How does expressing 350% as a decimal prove that more than 3 times as many students are enrolled in Spanish class as are enrolled in Latin class?
Answer:
350% = 350/100.
Explanation:
In the above-given question,
given that,
There are 350% more students enrolled in Spanish classes than in Latin classes.
350% = 350/100.
350/100 = 35/10.
35/10 = 3.5.
Question 23.
Critique Reasoning Free round-trip tickets to Orlando, Florida were given to 0.4% of the people staying at a hotel. Larry says that tickets were given to 40 of the people at the hotel. What did Larry do wrong when he calculated 0.4% as a fraction? What is the correct fraction?
Answer:
Larry was correct.
Explanation:
In the above-given question,
given that,
Free round-trip tickets to Orlando, Florida were given to 0.4% of the people staying at a hotel.
Larry says that tickets were given to 40 of the people at the hotel.
40/100 = 0.4.
so Larry was correct.
Question 24.
The unemployment rate decreased by \(\frac{1}{10}\)% in one month. Write \(\frac{1}{10}\)% as a fraction and as a decimal.
Answer:
The unemployment rate decreased by 1/10/100 and 0.001.
Explanation:
In the above-given question,
given that,
The unemployment rate decreased by \(\frac{1}{10}\)% in one month.
1/10% = 1/10/100.
1/10 x 1/100 = 1/1000.
1/1000 = 0.001.
sp the unemployment rate decreased by 1/10/100 and 0.001.
Question 25.
Higher Order Thinking A photo of a mosquito in a science book is magnified to 635% of the mosquito’s actual size. If the mosquito is 16 millimeters long, what is the length of the mosquito in the picture?

Answer:
The length of the mosquito in the picture = 6.35 mm.
Explanation:
In the above-given question,
given that,
A photo of a mosquito in a science book is magnified to 635% of the mosquito’s actual size.
If the mosquito is 16 mm long.
635% = 635/100.
635/100 = 6.35.
so the actual length of the mosquito in the picture = 6.35 mm.
Assessment Practice
Question 26.
At a Florida zoo, one adult female panther weighs 100 pounds. An adult male panther at the same zoo weighs 159% of the female panther’s weight. What is the weight of the adult male panther? Show your work.
Answer:
The weight of the adult male panther = 1.59.
Explanation:
In the above-given question,
given that,
At a Florida zoo, one adult female panther weighs 100 pounds.
An adult male panther at the same zoo weighs 159% of the female panther’s weight.
159/100 = 1.59.
so the weight of the adult male panther = 1.59.
Question 27.
The results of a survey show that 0.32% of the people in the survey have never sent a text message. Select all the fractions and decimals that can be expressed as 0.32%.
☐ \(\frac{32}{100}\)
☐ \(\frac{2}{625}\)
☐ 0.0032
☐ \(\frac{8}{2,500}\)
☐ 0.032
Answer:
Options A, B, C, and D are correct.
Explanation:
In the above-given question,
given that,
0.32% = 0.32/100.
2/625 = 0.0032.
8/2500 = 0.0032.
so options A, B, C, and D are correct.
Topic 6 Mid-Topic Checkpoint
Question 1.
Vocabulary Explain how fractions, decimals, and percents are related. Lesson 6-2
Answer:
Percent is a ratio that can be written as a fraction, and a fraction can be written as a decimal.
Explanation:
In the above-given question,
given that,
percent is a ratio that can be written as a fraction, and a fraction can be written as a decimal.
covert the fraction first to a decimal, then move the decimal point 2 places to the right and add the % symbol.
for example:
3/4 is a fraction.
0.75 is a decimal.
75% is a percent.
Question 2.
Sarai is mixing a solution. She pours all the liquid from a full small beaker into a large beaker. The liquid fills the large beaker to 15% of its capacity. If the small beaker holds 300 ml, how much does the large beaker hold? Lessons 6-1 and 6-3
Answer:
The large beaker can hold = 0.05 ml.
Explanation:
In the above-given question,
given that,
Sarai is mixing a solution.
She pours all the liquid from a full small beaker into a large beaker.
The liquid fills the large beaker to 15% of its capacity.
15/300 = 0.05.
so the large beaker can hold = 0.05 ml.
Question 3.
The Murphy family is on a road trip. On the first day, they traveled 30% of their total distance. On the second day, they traveled another of the total distance. What fraction of the total distance do they have left after the second day? What percent? Lesson 6-2
Answer:
The fraction of the total distance do they have left after the second day = 3/10.
Explanation:
In the above-given question,
given that,
The Murphy family is on a road trip.
On the first day, they traveled 30% of their total distance.
On the second day, they traveled another of the total distance.
30% = 30/100.
30/100 = 3/10.
3/10 = 0.3.
so the fraction of the total distance do they have left after the second day = 3/10.
Question 4.
Complete the table. Lessons 6-2 and 6-3

Answer:
70% = 70/100 = 0.7.
125% = 125/100 = 1.25.
55% = 11/20 = 0.55.
0.2% = 0.2/100 = 0.002.
Explanation:
In the above-given question,
given that,
the percents, decimals, and fractions are given.
70% = 70/100 = 0.7.
125% = 125/100 = 1.25.
55% = 11/20 = 0.55.
0.2% = 0.2/100 = 0.002.
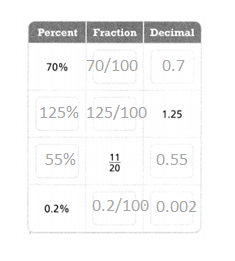
Question 5.
A basketball player made 17 out of 20 free throws at practice. What percent of the free throws did the player miss? Lesson 6-1
Answer:
The percent of the free throws did the player miss = 85%.
Explanation:
In the above-given question,
given that,
A basketball player made 17 out of 20 free throws at practice.
17/20 = 0.85.
85/100 = 0.85.
so the percent of the free throws did the player miss = 85%.
Question 6.
A section of rope 5 inches long represents 20% of the length of the entire rope. How long is the rope? Lesson 6-1
Answer:
The length of the rope = 25 in.
Explanation:
In the above-given question,
given that,
A section of rope 5 inches long represents 20% of the length of the entire rope.
5/20%.
5/ 20/100.
500/20 = 50/2.
50/2 = 25.
so the length of the rope is 25 in.
Topic 6 Mid-Topic Performance Task
The students in Mr. Anderson’s class conducted a survey of 1,000 people. They asked each person to name his or her favorite color. The results are shown in the table.
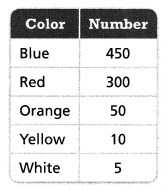
PART A
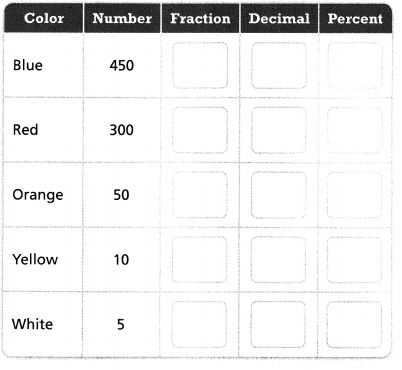
Complete the table to write each result as a fraction, a decimal, and a percent.
Answer:
Fraction = 450/815, Decimal = 0.55, and Percent = 55%.
Fraction = 300/815, Decimal = 0.36, and Percent = 36%.
Fraction = 50/815, Decimal = 0.06, and percent = 6%.
Fraction = 10/815, Decimal = 0.01, and percent = 1%.
Fraction = 5/815, Decimal = 0.006, percent = 0.6%.
Explanation:
In the above-given question,
given that,
the number of the color is shown in the table.
450/815 = 0.55 = 55%.
300/815 = 0.36 = 36%.
50/815 = 0.06 = 6%.
10/815 = 0.01 = 1%.
5/815 = 0.006 = 0.6%.
PART B
Green was chosen by 18% of the people. Which number is equivalent to 18%? Select all that apply.
☐ \(\frac{18}{1,000}\)
☐ 0.18
☐ \(\frac{9}{5}\)
☐ \(\frac{18}{100}\)
☐ 0.018
Answer:
Option B and D are correct.
Explanation:
In the above-given question,
given that,
The number is equivalent to 18%.
18/100 = 0.18.
so options B and D are correct.
PART C
Cecilia noticed that not all of the survey responses were recorded in the table. What percent of the responses were not recorded in the table? Explain.
Answer:
The percent of the responses was not recorded in the table = 200%.
Explanation:
In the above-given question,
given that,
Cecilia noticed that not all of the survey responses were recorded in the table.
The students in Mr. Anderson’s class conducted a survey of 1,000 people.
5/1000 = 1/200.
so the percent of the responses were not recorded in the table = 200%.
Lesson 6.4 Estimate to Find Percent
Explore It!
Sarah wants to score 78% on her next test. She knows that the test will have 40 questions.
I can.. estimate the percent of a number using equivalent fractions, rounding, or compatible numbers.

A. How can Sarah represent the situation to help her determine how many questions she needs to answer correctly?

Answer:
She needs to answer correctly = 31 questions.
Explanation:
In the above-given question,
given that,
Sarah wants to score 78% on her next test.
She knows that the test will have 40 questions.
78/100 x 40.
78/100 = 0.78.
0.78 x 40 = 31.2.
312/10 = 31.2.
so Sarah needs to answer correctly = 31 questions.
B. How could you use the model to help solve the problem?
Answer:
Focus on math practices
Use Structure on her last test, Sarah answered 82% of 60 questions correctly. About how many questions did Sarah answer correctly? Use estimation.
Answer:
Sarah answer correctly = 49 questions.
Explanation:
In the above-given question,
given that,
Sarah answered 82% of the 60 questions correctly.
82/100 = 0.82.
0.82 x 60 = 49.2.
so Sarah answer correctly = 49 questions.
Essential Question
How can you estimate to find the percent of a number?
Try It!
Suppose the graph shows eye colors among 120 students in sixth grade. About how many sixth grade students would have green eyes? Explain how you can use estimation to find the answer.
Answer:
The number of students who would have green eyes = 1.2.
Explanation:
In the above-given question,
given that,
the graph shows eye colors among 120 students in sixth grade.
120/100 = 12/10.
12/10 = 1.2.
so the number of students who would have green eyes = 1.2.
Convince Me! How does understanding fraction equivalents help you estimate how many students in sixth grade have green eyes?
Try It!
Students in another survey were asked whether they plan to attend summer camp. Out of the 56 students in the survey, 44% said yes. Use rounding and compatible numbers to estimate how many students plan to attend summer camp.
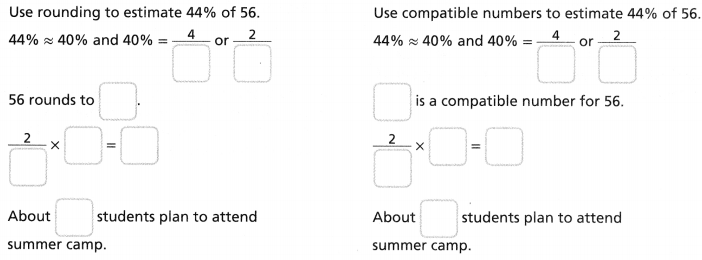
Answer:
4/10 = 2/5.
Explanation:
In the above-given question,
given that,
we are rounding 44% to estimate 40%.
40/100 = 4/10.
4/10 = 2/5.
56 rounds to 55.
2/5 x 55 = 22.
About 22 students plan to attend summer camp.

KEY CONCEPT
Fraction equivalents, rounding, or compatible numbers can be used to estimate the percent of a number.

Do You Understand?
Question 1.
Essential Question How can you estimate to find the percent of a number?
Answer:
We can estimate the percent of a number to the nearest number.
Explanation:
In the above-given question,
given that,
we can estimate the percent of a number to the nearest number.
for example:
8% is approximately equal to 10%.
10/100 = 1/10.
1/10 = 0.1.
Question 2.
Is there more than one fraction you could use to estimate 27% of 200? Explain.
Answer:
Yes, there is more than one fraction.
Explanation:
In the above-given question,
given that,
27% of 200.
27% is approximately equal to 25%.
25/100 x 200.
1/4 x 200 = 50.
Question 3.
What compatible number could you use to estimate 75% of 35? Why is this number compatible with 75%?
Answer:
75% of 35 = 26.25.
Explanation:
In the above-given question,
given that,
75% of 35.
75/100 = 0.75.
0.75 = 3/4.
3/4 x 35 = 26.25.
Question 4.
Use Structure Out of 195 students, 9% have hazel eyes. How can you estimate the number of students with hazel eyes?
Answer:
The number of students with hazel eyes = 18.
Explanation:
In the above-given question,
given that,
out of 195 students, 9% have hazel eyes.
9% = 9/100.
9/100 = 0.09.
195 is approximately equal to 200.
0.09 x 200 = 18.
so the number of students with hazel eyes = 18.
Do You Know How?
In 5-8, estimate the percent of each number.
Question 5.
47% of 77
47% ≈ ______ 77 ≈ ________
______ of ______ = ________
Answer:
47% of 77 = 40.
Explanation:
In the above-given question,
given that,
47% of 77.
47% ≈ 50%.
77%≈ 80.
50/100 = 5/10.
5/10 = 1/2.
1/2 x 80 = 40.
Question 6.
18% of 48
18% ≈ ______ 48 ≈ ________
______ of ______ = ________
Answer:
18% of 48 = 10.
Explanation:
In the above-given question,
given that,
18% of 48.
18% ≈ 20%.
48%≈ 50.
20/100 = 2/10.
2/10 = 1/5.
1/5 x 50 = 10.
Question 7.
73% of 800
Answer:
73% of 800 = 600.
Explanation:
In the above-given question,
given that,
73% of 800.
73% ≈ 75%.
75/100 = 0.75.
800 x 0.75 = 600.
Question 8.
31% of 94
Answer:
31% of 94 = 28.5.
Explanation:
In the above-given question,
given that,
31% of 94.
31% ≈ 30%.
94 ≈ 95.
30/100 = 3/10.
3/10 = 0.3.
3/10 x 95 = 28.5.
Question 9.
Tara sent party invitations to 98 people. Eighty two percent of the people said they will come to the party. About how many people said they will come to the party? Explain.
Answer:
The number of people who said they will come to the party = 85.
Explanation:
In the above-given question,
given that,
Tara sent party invitations to 98 people.
Eighty-two percent of the people said they will come to the party.
98 x 82/100.
98 is equal to 100.
85/100 = 0.85.
0.85 x 100 = 85.
Practice & Problem Solving
Leveled Practice in 10-15, estimate the percent of each number.
Question 10.
74% of 63
74% ≈ ______ 63 ≈ ________
______ of ______ = ________
Answer:
74% of 63 = 50.
Explanation:
In the above-given question,
given that,
74% of 63.
74% ≈ 75%.
63%≈ 65.
75/100 = 0.75.
0.75 x 65 = 50.
Question 11.
8% of 576
8% ≈ ______ 576 ≈ ________
______ of ______ = ________
Answer:
8% of 576 = 58.
Explanation:
In the above-given question,
given that,
8% of 576.
8% = 10.
10/100 = 1/10.
1/10 = 0.1.
576 = 580.
0.1 x 580 = 58.
Question 12.
34% of 55
Answer:
34% of 55 = 20.
Explanation:
In the above-given question,
given that,
34% of 55.
34% = 35.
35/100 = 0.35.
0.35 x 55 = 20.
Question 13.
27% of 284
Answer:
27% of 284 = 85.5.
Explanation:
In the above-given question,
given that,
27% of 284.
27% = 30.
30/100 = 3/10.
3/10 = 0.3.
284 = 285.
0.3 x 285 = 85.5.
Question 14.
65% of 89
Answer:
65% of 89 = 65.
Explanation:
In the above-given question,
given that,
65% of 89.
65% = 65.
65/100 = 0.65.
89 = 100.
0.65 x 100 = 65.
Question 15.
4% of 802
Answer:
4% of 802 = 32.2.
Explanation:
In the above-given question,
given that,
4% of 802.
4% = 5.
4/100 = 0.04.
802 = 805.
805 x 0.04 = 32.2.
Question 16.
There are about 320 million residents in the United States. If 38% of them live in the South, estimate how many live in other areas of the United States.

Answer:
The number of people who live in other areas of the united states = 121.6.
Explanation:
In the above-given question,
given that,
There are about 320 million residents in the United States.
38% of the U.S. population lives in this region.
38/100 x 320.
0.38 x 320.
121.6.
so the number of people who live in other areas of the united states = 121.6.
Question 17.
Lisa and Bill made 60 magnets for a craft fair. They sold 55% of the magnets. Lisa says that they sold about 30 magnets. Bill says that they sold about 36 magnets. Could they both be correct? Explain.
Answer:
No, both of them are not correct.
Explanation:
In the above-given question,
given that,
Lisa and Bill made 60 magnets for a craft fair.
They sold 55% of the magnets.
Lisa says that they sold about 30 magnets.
Bill says that they sold about 36 magnets.
55% of 60.
55/100 x 60.
0.55 x 60 = 33
Question 18.
Make Sense and Persevere Roland has 180 coins in his collection. Approximately 67% of the coins are quarters. About how much money does Roland have in quarters? Explain.
Answer:
The money does Ronald has in quarters = 120.6.
Explanation:
In the above-given question,
given that,
Roland has 180 coins in his collection.
Approximately 67% of the coins are quartered.
67% of 180.
67/100 x 180.
0.67 x 180 = 120.6.
Question 19.
Out of 9,799 whistles that a company manufactured, some were rejected for shipment to stores because they did not pass the quality control standards of the company. Estimate the number of whistles that did not pass.

Answer:
The number of whistles that did not pass = 1861.81.
Explanation:
In the above-given question,
given that,
Out of 9,799 whistles that a company manufactured, some were rejected for shipment to stores because they did not pass the quality control standards of the company.
19% of 9799.
19/100 x 9799.
0.19 x 9799 = 1861.81.
so the number of whistles that did not pass = 1861.81.
Question 20.
There are 8,249 people registered to vote in the town of Mayfield. About how many people voted in the election? Explain

Answer:
The number of people who voted in the election = 6104.
Explanation:
In the above-given question,
given that,
There are 8,249 people registered to vote in the town of Mayfield.
voter turnout reaches 74%.
74% of 8249.
74/100 x 8249.
0.74 x 8249 = 6104.26.
so the number of people voted in the election = 6104.
Question 21.
Higher Order Thinking Lea spent 25% of x hours at her part-time job. What is x if 25% of x is about 30 hours? Explain how you estimated and which property of equality you used to find x.
Answer:
The property of equality = 7.5.
Explanation:
In the above-given question,
given that,
Lea spent 25% of x hours at her part-time job.
25% of 30 hours.
25/100 x 30.
0.25 x 30 = 7.5.
so the property of equality = 7.5.
Question 22.
Reasoning Vanessa scored 78% on a test with 120 questions. What benchmark fraction would you use to estimate the number of questions that Vanessa answered correctly? Explain.
Answer:
The number of questions that Vanessa answered correctly = 93.6.
Explanation:
In the above-given question,
given that,
Vanessa scored 78% on a test with 120 questions.
78% of 120.
78/100 x 120.
0.78 x 120 = 93.6.
so the number of questions that Vanessa answered correctly = 93.6.
Question 23.
Jason has saved 41% of what he needs to buy a skateboard. About how much has Jason saved? Explain.

Answer:
The amount has Jason saved = 29.93.
Explanation:
In the above-given question,
given that,
Jason has saved 41% of what he needs to buy a skateboard.
41% of $73.
41/100 x $73.
0.41 x $73 = 29.93.
so the amount has Jason saved = 29.93.
Assessment Practice
Question 24.
There were 240 shoppers at an electronics store on opening day. The specials that day allowed 25% of shoppers to receive a free set of earbuds and 20% of shoppers to receive $10 off their first purchase.
PART A
Use an equivalent fraction to determine how many shoppers received a free set of earbuds. Show your work.
Answer:
The number of shoppers who received a free set of earbuds = 600 and $2.
Explanation:
In the above-given question,
given that,
There were 240 shoppers at an electronics store on opening day.
The specials that day allowed 25% of shoppers to receive a free set of earbuds and 20% of shoppers to receive $10 off.
250% of 240.
250/100 x 240.
25/10 x 240.
2.5 x 240 = 600.
20% of $10.
20/100 x $10.
1/5 x $10.
0.2 x $10 = $2.
PART B
Use an equivalent fraction to determine how many shoppers received $10 off their first purchase. Show your work.
Answer:
The equivalent fraction that a number of shoppers received $10 off their first purchase = $2.
Explanation:
In the above-given question,
given that,
The specials that day allowed 25% of shoppers to receive a free set of earbuds and 20% of shoppers to receive $10 off.
20% of $10.
20/100 x $10.
1/5 x $10.
0.2 x $10 = $2.
so the equivalent fraction that a number of shoppers received $10 off their first purchase = $2.
Lesson 6.5 Find the percent of a Number
Solve & Discuss It!
Lauren bought a jacket that was on sale for 60% off. She paid 40% of the original price of $75. How much did Lauren pay for the jacket?
I can… solve problems involving percents.

Model with Math
How can you use a model to represent problems involving percents?
Answer:
The amount did Lauren pay for the jacket = $30.
Explanation:
In the above-given question,
giving that,
Lauren bought a jacket that was on sale for 60% off.
She paid 40% of the original price of $75.
40% of $75.
40/100 x $75.
0.4 x $75.
$30.
so the amount did Lauren pay for the jacket = $30.
Focus on math practices
Generalize When finding the percent of a number, how can you tell whether your answer is reasonable? Will the answer be greater than or less than the original amount? Explain.
Essential Question
How can you find percents?
Try It!
Suppose 68% of the students attending the field trip were boys. How can you use the double number line diagram above to find the number of boys and to check whether your answer is reasonable?
Answer:
The number of boys = 86.
Explanation:
In the above-given question,
given that,
Suppose 68% of the students attending the field trip were boys.
68/100 = 0.86.
so the number of boys = 86.
Convince Me! In finding the percent of a number, when might you want to use the fraction form of the percent instead of the decimal form?
Try It!
What is 0.8% of 35?
Answer:
0.8% of 35 = 0.28.
Explanation:
In the above-given question,
given that,
0.8% of 35.
0.8/100 x 35.
0.008 x 35 = 0.28.
Try It!
What percent of 120 is 72?
Answer:
The percent of 120 is 86.4.
Explanation:
In the above-given question,
given that,
x of 120 is 72.
72/100 x 120.
0.72 x 120 = 86.4.
so the percent of 120 is 86.4.
KEY CONCEPT
Percent equations have a part, a whole, and a percent. You can use the equation to solve for the part, the whole, or the percent.
Find the Part
What is 12% of 6.75?
x = 0.12 • 6.75
x = 0.81
12% of 6.75 is 0.81.
Find the Percent:
What percent of 6.75 is 0.81?
p • 6.75 = 0.81
6.75p = 0.81
\(\frac{6.75 p}{6.75}=\frac{0.81}{6.75}\)
p = 0.12 or 12%
12% of 6.75 is 0.81.
Do You Understand?
Question 1.
Essential Question How can you find percents?
Answer:
Percent equations have a part, a whole, and a percent.
Explanation:
In the above-given question,
given that,
Percent equations have a part, a whole, and a percent.
for example:
p x 6.75 = 0.81.
12% of 6.75 is 0.81.
Question 2.
Describe the equation you use to find the unknown part in a percent problem.
Answer:
Question 3.
Describe the equation you use to find the percent value in a percent problem.
Answer:
Question 4.
Be Precise in the expression 34% of 60, what operation does the word “of” mean?
Answer:
34% of 60 = 20.4.
Explanation:
In the above-given question,
given that,
34% of 60.
34/100 x 60.
0.34 x 60 = 20.4.
34% of 60 = 20.4.
Question 5.
Use Appropriate Tools How can you use a calculator to find what percent of 180 is 108?
Answer:
194.4.
Explanation:
In the above-given question,
given that,
180/100 x 108.
18/10 x 108.
1.8 x 108.
194.4.
Do You Know How?
In 6 and 7, find the part.
Question 6.
What is 26% of 50?
Answer:
26% of 50 is 12.
Explanation:
In the above-given question,
given that,
26% of 50.
26/100 x 50.
0.26 x 50.
12.
so 26% of 50 is 12.
Question 7.
What is 2.1% of 60?
Answer:
2.1% of 60 = 1.26.
Explanation:
In the above-given question,
given that,
2.1% of 60.
2.1/100 x 60.
0.021 x 60.
1.26.
2.1% of 60 = 1.26.
In 8 and 9, find the percent.
Question 8.
What percent of 315 is 126?
Answer:
The percent of 315 is 126 = 396.9.
Explanation:
In the above-given question,
given that,
315% of 126.
315/100 x 126.
3.15 x 126.
396.9.
so the percent of 315 is 126 = 396.9.
Question 9.
What percent of 120 is 28.8?
Answer:
The percent of 120 is 28.8 = 34.56.
Explanation:
In the above-given question,
given that,
120/100 x 28.8.
12/10 x 28.8.
1.2 x 28.8.
34.56.
so the percent of 120 is 28.8 = 34.56.
Question 10.
An electronics company has 450 employees. The company plans to increase its staff by 30%. How many new employees will the company hire?
Answer:
The number of new employees will the company hire = 135.
Explanation:
In the above-given question,
given that,
An electronics company has 450 employees.
The company plans to increase its staff by 30%.
30% of 450.
30/100 x 450.
3/10 x 450.
0.3 x 450.
135.
so the number of new employees will the company hire = 135.
Question 11.
The original price of a computer game is $45. The price is marked down by $18. What percent of the original price is the markdown?
Answer:
The percent of the original price is the markdown is $27.
Explanation:
In the above-given question,
given that,
The original price of a computer game is $45.
The price is marked down by $18.
$45 – $18 = $27.
so the percent of the original price is the markdown is $27.
Practice & Problem Solving
Leveled Practice In 12-17, find each part or percent.
Question 12.
What is 5% of 210?
x = ______ × 210
x = ______
Answer:
5% of 210 = 10.5.
Explanation:
In the above-given question,
given that,
5% of 210.
5/100 x 210.
0.05 x 210 = 10.5.
5% of 210 = 10.5.
Question 13.
What is 8.2% of 500?
x = _____ × 500
x = _______
Answer:
8.2% of 500 = 41.
Explanation:
In the above-given question,
given that,
8.2% of 500.
8.2/100 x 500.
0.082 x 500.
41.
8.2% of 500 = 41.
Question 14.
What percent of 32 is 5.6?
p • 32 = _______
32 p = _______
\(\frac{32 p}{32}=\frac{ }{32}\)
p = _______ = _______%
Answer:
p = 0.00175.
Explanation:
In the above-given question,
given that,
p x 32 = 5.6%.
32p = 5.6%.
5.6/100 = 32p.
0.056 = 32p.
p = 0.056/32.
p = 0.00175.
Question 15.
What is 35% of 10?
Answer:
35% of 10 is 3.5.
Explanation:
In the above-given question,
given that,
35% of 10.
35/100 x 10.
0.35 x 10.
3.5.
so 35% of 10 is 3.5.
Question 16.
What percent of 75 is 33?
Answer:
24.75 percent of 75 is 33.
Explanation:
In the above-given question,
given that,
x of 75 is 33.
75/100 x 33.
0.75 x 33.
24.75.
Question 17.
What is 2.25% of 24?
Answer:
2.25% of 24 = 0.54.
Explanation:
In the above-given question,
given that,
2.25% of 24.
2.25/100 x 24.
0.0225 x 24.
0.54.
2.25% of 24 = 0.54.
Question 18.
The meal tax at a restaurant is 5.5%. What is the meal tax on a dinner that costs $24?

Answer:
The meal tax on dinner costs $24.
Explanation:
In the above-given question,
given that,
The meal tax at a restaurant is 5.5%.
5.5% of $24.
5.5/100 x $24.
0.055 x 24.
$1.32.
so the meal tax on dinner costs $24.
Question 19.
An electronics store donated a percentage of every sale to charity. The total sales were $7,150, of which the store donated $429. What percent of $7,150 was donated to charity?
Answer:
The percent of the money was donated to charity = $6721.
Explanation:
In the above-given question,
given that,
An electronics store donated a percentage of every sale to charity.
The total sales were $7,150, of which the store donated $429.
$7150 – $429 = $6721.
so the percent of the money was donated to charity = $6721.
In 20-22, use the circle graph.
There are 180 cars in a parking lot. The colors of the cars are represented in the circle graph.
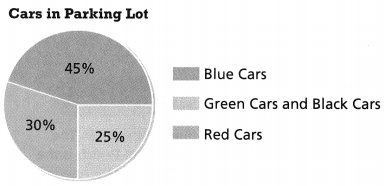
Question 20.
How many blue cars are there?
Answer:
The number of blue cars = 81.
Explanation:
In the above-given question,
given that,
There are 180 cars in a parking lot.
Blue cars = 45%.
Green cars and Black cars = 25%.
Red cars = 30%.
45% of 180.
45/100 x 180.
0.45 x 180.
so the number of blue cars = 81.
Question 21.
How many red cars are there?
Answer:
The number of red cars = 54.
Explanation:
In the above-given question,
given that,
There are 180 cars in a parking lot.
Blue cars = 45%.
Green cars and Black cars = 25%.
Red cars = 30%.
30% of 180.
30/100 x 180.
0.3 x 180.
so the number of red cars = 54.
Question 22.
Reasoning There are 27 more green cars than black cars in the parking lot. What percentage of the cars in the parking lot are green? What percent are black?
Answer:
The percent of cars that are black = 48.6%.
Explanation:
In the above-given question,
given that,
There are 27 more green cars than black cars in the parking lot.
27/100 x 180.
0.27 x 180.
48.6.
so the percent of cars that are black = 48.6%.
Question 23.
The bank contains pennies, nickels, dimes, and quarters. There are 4 more nickels than pennies. How much money does the bank contain?

Answer:
The money does the bank contains = 66%.
Explanation:
In the above-given question,
given that,
The bank contains pennies, nickels, dimes, and quarters.
There are 4 more nickels than pennies.
of the 50 coins, 10% are pennies and 42% are dimes.
10% + 42% + 14%.
66%.
so the money does the bank contains = 66%.
Question 24.
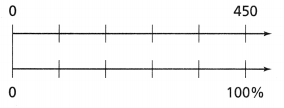
Model with Math How can you use the double number line diagram to find what percent of 450 is 270?
Answer:
The percent of 450 is 270 is 1215.
Explanation:
In the above-given question,
given that,
450% is 270.
450/100 x 270.
45/10 x 270.
4.5 x 270.
1215.
so the percent of 450 of 270 is 1215.
Question 25.
Make Sense and Persevere A movie complex is showing the same movie in three theaters. In theater A, 112 of the 160 seats are filled. In theater B, 84 seats are filled and 56 seats are empty. In theater C, 63 of the 180 seats are empty. Which theater has the greatest percent of its seats filled?
Answer:
The greatest percent of its seats filled = Theater A.
Explanation:
In the above-given question,
given that,
A movie complex is showing the same movie in three theaters.
In theater A, 112 of the 160 seats are filled. In theater B, 84 seats are filled and 56 seats are empty.
In theater C, 63 of the 180 seats are empty.
112/100 x 160.
1.12 x 160.
179.2.
84/100 x 56.
0.84 x 56.
47.04.
63/100 x 180.
0.63 x 180 = 113.4.
so the greatest percent of its seats filled = Theater A.
Question 26.
Higher Order Thinking Thomas has an album that holds 600 baseball cards. Each page of the album holds 6 cards. If 45% of the album is empty, how many pages are filled with baseball cards?
Answer:
The number of pages is filled with baseball cards = 1620.
Explanation:
In the above-given question,
given that,
Thomas has an album that holds 600 baseball cards.
Each page of the album holds 6 cards.
If 45% of the album is empty.
600 x 6 = 3600.
45/100 x 3600.
0.45 x 3600.
so the number of pages is filled with baseball cards = 1620.
Question 27.
Be Precise Miguel collected aluminum cans for recycling. He collected a total of 150 cans. How many of the cans Miguel collected were not soda cans?

Answer:
The number of cans Miguel collected were not soda cans = 87.
Explanation:
In the above-given question,
given that,
Miguel collected aluminum cans for recycling.
He collected a total of 150 cans.
58% of the cans collected were soda cans.
58% of 150.
58/100 x 150.
0.58 x 150.
87.
so the number of cans Miguel collected were not soda cans = 87.
Assessment Practice
Question 28.
Ava’s aquarium is 95% filled with water. The tank holds 1,120 gallons of water. Which is the remaining number of gallons of water needed to fill the aquarium to the top?
A. 1,120 gallons
B. 1,010 gallons
C. 101 gallons
D. 56 gallons
Answer:
Option B is correct.
Explanation:
In the above-given question,
given that,
Ava’s aquarium is 95% filled with water.
The tank holds 1,120 gallons of water.
95% of 1120.
95/100 x 1120.
0.95 x 1120.
1064.
so option B is correct.
Question 29.
Students set a goal of collecting 900 cans for the canned food drive. The number of cans they have collected so far is 82% of their goal. How many more cans do the students need to collect to reach their goal?
A. 162 cans
B. 180 cans
C. 720 cans
D. 738 cans
Answer:
Explanation:
In the above-given question,
given that,
Students set a goal of collecting 900 cans for the canned food drive.
The number of cans they have collected so far is 82% of their goal.
82% of 900.
82/100 x 900.
0.82 x 900 =
so option
Lesson 6.6 Find the whole Given a Part and the Percent
Solve & Discuss It!
A school soccer team won 80% of its matches. The team won 40 matches. How many matches did the soccer team play?
I can… find the whole amount when given a part and the percent.

Look for Relationships
How can you use a diagram to analyze the relationship between the quantities?
Focus on math practices
Model with Math Write an equation to find the total number of matches played by the soccer team. Let m represent the total number of matches.
Essential Question
How can you find the whole in a percent problem?
Try It!
Bree took another math test and scored 152 points, which was 95% of the total possible points on the test. What was the total number of possible points?
Answer:
The total number of possible points = 144.4.
Explanation:
In the above-given question,
given that,
Bree took another math test and scored 152 points, which was 95% of the total possible points on the test.
95% of 152.
95/100 x 152.
0.95 x 152.
144.4.
so the total number of possible points = 144.4.
Convince Me! How could you use a double number line diagram to check your answer?
Try It!
a. 300% of what number is 180?
Answer:
300% of 180 is 60.
Explanation:
In the above-given question,
given that,
300% of x is 180.
300%x x 180.
3x = 180.
x = 180/3.
x = 60.
300% of 180 is 60.
b. 0.3% of what number is 24?
Answer:
The value of x is 8000.
Explanation:
In the above-given question,
given that,
0.3% of x is 24.
0.3/100x = 24.
0.003x = 24.
x = 24/0.003.
x = 8000.
KEY CONCEPT
You can use a double number line diagram or an equation to find the whole when the percent and a part are known.
Use a diagram.
150% of 8 is 12.
Use an equation.
Let n = the whole.
150% • n = 12
\(\frac{1.5 n}{1.5}=\frac{12}{1.5}\)
n = 8
150% of 8 is 12.
Do You Understand?
Question 1.
Essential Question How can you find the whole in a percent problem?
Answer:
Question 2.
When you write an equation for a problem such as 300% of what number is 180, what do you use to represent the phrase ‘what number’?
Answer:
The number is 540.
Explanation:
In the above-given question,
given that,
300% of a number is 180.
300/100 x 180.
3 x 180 = 540.
so the number is 540.
Question 3.
When you find the whole in a percent problem in which the percent is greater than 100%, is the whole less than or greater than the part?
Answer:
1 is greater than the part.
Explanation:
In the above-given question,
given that,
the percent is greater than 100%.
100% = 100/100.
100/100 = 1.
so 1 is greater than the part.
Question 4.
Be Precise Tony participated in 6 races, or 10% of the events. Do the 6 races represent the part, the percent, or the whole? Tell what the others represent.
Answer:
The 6 races represent the whole.
Explanation:
In the above-given question,
given that,
Tony participated in 6 races or 10% of the events.
10/100 x 6.
0.1 x 6 = 0.6.
so the 6 races represent the whole.
Do You Know How?
Question 5.
40% of what number is 80?
Answer:
40% of x is 80 = 32.
Explanation:
In the above-given question,
given that,
40% of x is 80.
x = 40/100 x 80.
x = 0.4 x 80.
x = 32.
40% of x is 80 = 32.
Question 6.
300% of what number is 90?
Answer:
300% of x is 90 is 30.
Explanation:
In the above-given question,
given that,
300% of x is 90.
300/100 x x = 90.
3x = 90.
x = 30.
300% of x is 90 is 30.
Question 7.
70% of what number is 112?
Answer:
The number is 78.4.
Explanation:
In the above-given question,
given that,
70% of what number is 112.
70/100 x 112.
0.7 x 112.
78.4.
so 70% of the number is 112 is 78.4.
Question 8.
35% of what number is 28?
Answer:
The number is 78.4.
Explanation:
In the above-given question,
given that,
70% of what number is 112
70/100 x 112.
0.7 x 112.
78.4.
so the number is 78.4.
Question 9.
7.5% of what number is 15?
Answer:
The number is 200.
Explanation:
In the above-given question,
given that,
7.5% of x is 15.
7.5/100 x = 15.
0.075x = 15.
x = 15/0.075.
x = 200.
Practice & Problem Solving
Leveled Practice In 10-15, find each whole.
Question 10.
35% of what number is 91?
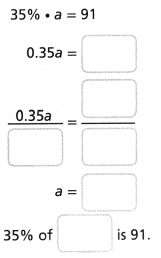
Answer:
35% of 260 is 91.
Explanation:
In the above-given question,
given that,
35% x a = 91.
35/100 x a = 91.
0.35a = 91.
a = 91/0.35.
a = 260.
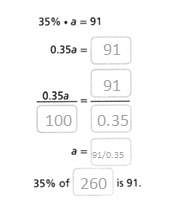
Question 11.
125% of what number is 45?

Answer:
125% of 36 is 45.
Explanation:
In the above-given question,
given that,
125% x n = 45.
1.25n = 45.
n = 45/1.25.
n = 36.
125% of 36 is 45.
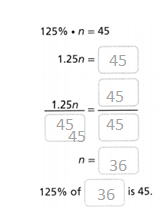
Question 12.
87.5% of what number is 49?
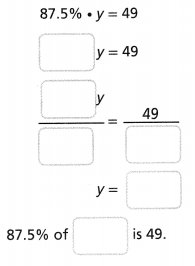
Answer:
87.5% of 56 is 49.
Explanation:
In the above-given question,
given that,
87.5% of y = 49.
87.5/100 y = 49.
0.875y = 49.
y = 49/0.875.
y = 56.
87.5% of y is 49.
Question 13.
700% of what number is 1,540?
Answer:
700% of 1540 is 220.
Explanation:
In the above-given question,
given that,
700% of x is 1540.
700/100x = 1540.
7x = 1540.
x = 1540/7.
x = 220.
700% of 1540 is 220.
Question 14.
0.7% of what number is 35?
Answer:
0.7% x is 5000.
Explanation:
In the above-given question,
given that,
0.7% of x is 35.
0.7/100 x x = 35.
0.007x = 35.
x = 35/0.007.
x = 5000.
0.7% x is 5000.
Question 15.
56% of what number is 14?
Answer:
56% of 25 is 14.
Explanation:
In the above-given question,
given that,
56% of x is 14.
56/100 x = 14.
0.56x = 14.
x = 14/0.56.
x = 25.
56% of x is 25.
In 16-18, use the list of state taxes.

Question 16.
Reasoning Otis had a salad for $4.50, a sandwich for $6.25, and a drink at his favorite restaurant. The tax for the entire meal was $0.54. What was the price of the drink?
Answer:
The price of the drink = $10.21.
Explanation:
In the above-given question,
given that,
Otis had a salad for $4.50, a sandwich for $6.25, and a drink at his favorite restaurant.
The tax for the entire meal was $0.54.
4.50 + 6.25 = 10.75.
10.75 – 0.54 = 10.21.
so the price of the drink = $10.21.
Question 17.
Jill paid a sales tax of $1.40 when she bought a vest. What was the price of the vest not including the tax?
Answer:
The price of the vest not including the tax = $9.35.
Explanation:
In the above-given question,
given that,
Jill paid a sales tax of $1.40 when she bought a vest.
$10.75 – $1.40.
$9.35.
so the price of the vest not including the tax = $9.35.
Question 18.
Rachel paid $46 in tax for the money she earned as a camp counselor. How much money did Rachel earn?
Answer:
The money did Rachel earn is $35.75.
Explanation:
In the above-given question,
given that,
Rachel paid $46 in tax for the money she earned as a camp counselor.
$10.25 – $46 =
35.75.
so the money did Rachel earn is $35.75.
Question 19.
A restaurant wants to study how well its salads sell. The circle graph shows the sales of salads during the past few days. If 5 of the salads sold were Caesar salads, how many total salads did the restaurant sell?
Answer:
The total salads did the restaurant sell = 1.
Explanation:
In the above-given question,
given that,
A restaurant wants to study how well its salads sell.
The circle graph shows the sales of salads during the past few days.
if 5 of the salads sold were caesar salads.
20% is caesar salads.
20/100 x 5.
2/10 x 5.
0.2 x 5 = 1.
so the total salads did the restaurant sell = 1.
Question 20.
Make Sense and Persevere Sydney completed 60% of the math problems assigned for homework. She has 4 more problems to finish. How many math problems were assigned for homework?
Answer:
The number of math problems was assigned for homework = 2.4.
Explanation:
In the above-given question,
given that,
Sydney completed 60% of the math problems assigned for homework.
She has 4 more problems to finish.
60% of 4.
60/100 x 4.
0.6 x 4 = 2.4.
so the number of math problems was assigned for homework = 2.4.
Question 21.
Reasoning Carrie gave her hair stylist a $4.20 tip. The tip was 15% of the cost of the haircut. Write an equation to find h, the cost of the haircut.
Answer:
The cost of the haircut = $28.
Explanation:
In the above-given question,
given that,
Carrie gave her hairstylist a $4.20 tip.
The tip was 15% of the cost of the haircut.
15% of h is $4.20.
15/100 x h = $4.20.
h = $4.20/0.15.
h = $28.
Question 22.
Use Structure Solve each of the number sentences and describe the pattern. 80% of what number is 80? 60% of what number is 60? 127% of what number is 127?
Answer:
The number is 100.
Explanation:
In the above-given question,
given that,
80% of x is 80.
80/100 x = 80.
0.8x = 80.
x = 80/0.8.
x = 100.
60/100 x = 60.
0.6x = 60.
x = 60/0.6.
x = 100.
127% of x is 127.
127/100 x = 127.
1.27 x = 127.
x = 127/1.27.
x = 100.
so the number is 100.
Question 23.
Higher Order Thinking An hour before show time, only 105 people have arrived for a concert. According to ticket sales, 95% of the people have yet to arrive. How many tickets were sold for the concert? Explain.

Answer:
The number of tickets was sold for the concert = 99.75.
Explanation:
In the above-given question,
given that,
only 105 people have arrived for a concert.
According to ticket sales, 95% of the people have yet to arrive.
95% of 105.
95/100 x 105.
0.95 x 105.
99.75.
so the number of tickets was sold for the concert = 99.75.
Question 24.
Nineteen students named lacrosse as their favorite sport. Explain how to use the circle graph to find the total number of students surveyed.
Answer:
The total number of students surveyed = 38.
Explanation:
In the above-given question,
given that,
Nineteen students named lacrosse as their favorite sport.
the number of students who selected Lacrosse is 38%.
38% of 100.
38/100 x 100.
38.
so the total number of students surveyed = 38.
Assessment Practice
Question 25.
People use water to cook, clean, and drink every day. It is estimated that 16.8% of the water used each day is for cleaning. If a family uses 67.2 gallons of water per day for cleaning, how many total gallons do they use per day? Explain.
Answer:
The total gallons of water do they use per day = 11.2896 gallons.
Explanation:
In the above-given question,
given that,
People use water to cook, clean, and drink every day.
It is estimated that 16.8% of the water used each day is for cleaning.
If a family uses 67.2 gallons of water per day for cleaning.
16.8% of 67.2.
16.8/100 x 67.2.
0.168 x 67.2.
11.2896.
so the total gallons of water do they use per day = 11.2896 gallons.
Question 26.
Martha has a budget for groceries, fuel, and utilities. She spent 20% of her budget on groceries. If Martha spent $42.00 on groceries, how much is her budget?
Answer:
The budget is $8.4.
Explanation:
In the above-given question,
given that,
Martha has a budget for groceries, fuel, and utilities.
She spent 20% of her budget on groceries.
If Martha spent $42.00 on groceries.
20% of $42.
20/100 x $42.
0.2 x $42.
$8.4.
so the budget is $8.4.
3-ACT MATH
3-Act Mathematical Modeling: Ace the Test

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Predict an answer to this Main Question.
Answer:
Question 4.
Construct Arguments Explain how you arrived at your prediction.
Answer:
АСТ 2
Question 5.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 6.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.

Answer:
Question 7.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 8.
What is your answer to the Main Question? Does it differ from your prediction? Explain.

Answer:
ACT 3
Question 9.
Write the answer you saw in the video.

Answer:
Question 10.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 11.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
Reflect
Question 12.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 13.
Be Precise Why are percents more useful in this situation than the number of correct answers?
Answer:
SEOUEL
Question 14.
Reasoning Suppose each test has 3 additional questions, and she gets 2 of them correct. How will that affect the answer?

Answer:
Topic 6 Review
Essential Question
What is the meaning of percent? How can percent be estimated and found?
Vocabulary Review
Complete each definition with a vocabulary word.
Vocabulary
- compatible numbers
- fraction
- percent
- ratio
Question 1.
A ratio of a quantity to 100 is a __________
Answer:
A ratio of a quantity to 100 is a percent.
Explanation:
In the above-given question,
given that,
A ratio of a quantity to 100 is a percent.
for example:
70% is 70/100.
70/100 = 0.7.
Question 2.
A __________ compares two numbers or the number of items in two groups.
Answer:
A ratio compares two numbers or the numbers of items in two groups.
Explanation:
In the above-given question,
given that,
A ratio compares two numbers or the numbers of items in two groups.
for example:
the ratio of two numbers a and b can be written as a to b is a:b.
Question 3.
________ are numbers that are easier to compute mentally.
Answer:
Compatible numbers are numbers that are easier to compute mentally.
Explanation:
In the above-given question,
given that,
Compatible numbers are numbers that are easier to compute mentally.
for example:
560 + 7 = 80.
56 and 7 are compatible.
Draw a line to match each fraction, decimal, or percent in Column A to the equivalent value in Column B. Column A

Answer:
D, C, A, and B.
Explanation:
In the above-given question,
given that,
40/50 = 0.8, 80% = 0.8.
13% = 0.13.
1.75 = 1(3/4) = 7/4 = 1.75.
155% = 155/100 = 1.55.
1(11/20) = 31/20 = 1.55.
Use Vocabulary in Writing
Out of 230 students surveyed, 11% chose gymnastics as their favorite sport. Explain how you can estimate the number of students who chose gymnastics. Use vocabulary words in your explanation.
Answer:
The number of students who chose gymnastics = 25.3.
Explanation:
In the above-given question,
given that,
Out of 230 students surveyed, 11% chose gymnastics as their favorite sport.
11% of 230.
11/100 x 230.
0.11 x 230.
25.3.
so the number of students who chose gymnastics = 25.3.
Concept and Skills Review
Lesson 6.1 Understand Percent
Quick Review
A percent is a rate that compares a part to 100. The word percent means “of a hundred.”
Example
Write the percent represented by the shaded part of the grid.

\(\frac{54}{100}\) parts shaded = 54%
Practice
In 1 and 2, write the percent of each figure that is shaded.
Question 1.

Answer:
The percent is 21%.
Explanation:
In the above-given question,
given that,
there are 100 boxes.
21 boxes are filled.
21/100 x 100.
21%.
so the percent is 21%.
Question 2.

Answer:
The percent is 70%.
Explanation:
In the above-given question,
given that,
10 boxes are there.
7 boxes are filled.
70/100 x 100.
70%.
so the percent is 70%.
In 3 and 4, write each ratio as a percent.
Question 3.
14 losses in 50 games
Answer:
The percent is 7.
Explanation:
In the above-given question,
given that,
14 losses in 50 games.
14/100 x 50.
0.14 x 50 = 7.
so the percent is 7.
Question 4.
\(\frac{4}{5}\) of the students ride a bus.
Answer:
The number of students who ride a bus = 0.8.
Explanation:
In the above-given question,
given that,
4/5 = 0.8.
the number of students who rides a bus = 0.8.
Question 5.
If \(\overline{A B}\) represents 25%, what is the length of a line segment that is 100%?
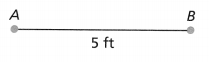
Answer:
The length of the line segment is 1.25 ft.
Explanation:
In the above-given question,
given that,
25% of 5.
25/100 x 5.
0.25 x 5.
1.25.
so the length of the line segment is 1.25 ft.
Lesson 6.2 Relate Fractions, Decimals, and Percents
Quick Review
Fractions, decimals, and percents are three ways to show parts of a whole. You can write a percent as a fraction with 100 as the denominator. Then you can write that fraction as a decimal.
Example
Write 35% as a fraction and a decimal.
35% = \(\frac{35}{100}\) or \(\frac{7}{20}\)
\(\frac{35}{100}\) = 0.35
Practice
In 1-6, write each number using the two other forms of notation: fraction, decimal, or percent.
Question 1.
0.16
Answer:
Fraction: 16/100.
decimal: 0.16.
Percent: 16%.
Explanation:
In the above-given question,
given that,
the number is 0.16.
16/100 = 0.16.
16% = 16/100.
Question 2.
\(\frac{63}{100}\)
Answer:
Fraction: 63/100.
decimal: 0.63.
Percent: 63%.
Explanation:
In the above-given question,
given that,
the number is 63/100.
63/100 = 0.63.
63% = 63/100.
Question 3.
27%
Answer:
Fraction: 27/100.
decimal: 0.27.
Percent: 27%.
Explanation:
In the above-given question,
given that,
the number is 27%.
27/100 = 0.27.
27% = 27/100.
Question 4.
\(\frac{7}{8}\)
Answer:
Fraction: 875/100.
decimal: 0.875.
Percent: 875%.
Explanation:
In the above-given question,
given that,
the number is 7/8.
7/8 = 0.875.
875/100 = 8.75.
875% = 875/100.
Question 5.
0.55
Answer:
Fraction: 55/100.
decimal: 0.55.
Percent: 55%.
Explanation:
In the above-given question,
given that,
the number is 0.55.
55/100 = 0.55.
55% = 55/100.
Question 6.
7%
Answer:
Fraction: 7/100.
decimal: 0.07.
Percent: 7%.
Explanation:
In the above-given question,
given that,
the number is 7%.
7/100 = 0.07.
7% = 7/100.
Question 7.
One piece of wheat bread contains 2 g of fiber or 8% of the amount of fiber that most people need in a day. What is 8% as a decimal and as a fraction?
Answer:
Decimal = 0.16.
Fraction = 8/100.
Explanation:
In the above-given question,
given that,
One piece of wheat bread contains 2 g of fiber or 8% of the amount of fiber that most people need in a day.
8% of 2.
8/100 x 2.
0.08 x 2.
0.16.
8% as a decimal = 0.16.
fraction = 8/100.
Lesson 6.3 Represent Percents Greater Than 100 or Less Than 1
Quick Review
Percents less than 1% are less than \(\frac{1}{100}\), and percents greater than 100% are more than one whole. You can express percents greater than 100 or less than 1 in equivalent forms.
Example
Write 221% as a fraction and as a decimal.
Fraction: \(\frac{221}{100}\)
Decimal: \(\frac{221}{100}\) = 221 ÷ 100 = 2.21
Write 1% as a fraction and as a decimal.
Fraction: \(\frac{1}{4} \%=\frac{1}{4} \div 100\)
\(=\frac{1}{4} \times \frac{1}{100}=\frac{1}{400}\)
Decimal: \(\frac{1}{4} \%=0.25 \%\)
= \(\frac{0.25}{100}\)
= \(\frac{25}{10,000}\)
= 0.0025
Practice
In 1-6, write each percent as a fraction and as a decimal.
Question 1.
140%
Answer:
Fraction: 140/100.
decimal: 1.4.
Explanation:
In the above-given question,
given that,
140%.
140/100 = 140%.
140/100 = 1.4.
Question 2.
\(\frac{7}{10}\)%
Answer:
Fraction: 0.7/100.
decimal: 0.007.
Explanation:
In the above-given question,
given that,
7/10%.
0.7/100.
0.007.
Question 3.
375%
Answer:
Fraction: 375/100.
decimal: 3.75.
Explanation:
In the above-given question,
given that,
375%.
375/100 = 375.
375% = 3.75.
Question 4.
0.33%
Answer:
Fraction: 33/100.
decimal: 0.0033.
Explanation:
In the above-given question,
given that,
0.33%.
0.33/100.
0.0033.
Question 5.
0.5%
Answer:
Fraction: 0.5/100.
decimal: 0.005.
Explanation:
In the above-given question,
given that,
0.5%.
0.5/100.
0.005.
Question 6.
250%
Answer:
Fraction: 250/100.
decimal: 2.5.
Explanation:
In the above-given question,
given that,
250%.
250/100.
2.5.
Question 7.
The radius of the planet Saturn is 945% of the radius of Earth. What is 945% expressed as a fraction and as a decimal?
Answer:
Fraction = 945/100.
decimal = 9.45.
Explanation:
In the above-given question,
given that,
The radius of the planet Saturn is 945% of the radius of Earth.
945% = 945/100.
945/100 = 9.45.
Lesson 6.4 Estimate to Find Percent
Quick Review
Fraction equivalents, rounding, or compatible numbers can be used to estimate the percent of a number
Example
Estimate 24% of 83.
24% ≈ 25% and 25% = \(\frac{1}{4}\)
83 rounds to 80.
\(\frac{1}{4}\) × 80 = 20
24% of 83 is about 20.
Practice
In 1-6, estimate the percent of each number.
Question 1.
22% of 96
Answer:
22% of 96 = 19.
Explanation:
In the above-given question,
given that,
22% is equal to 20%.
96 round to 95.
20% of 100.
20/100 x 95.
0.2 x 95.
19.
so 22% of 96 = 19.
Question 2.
38% of 58
Answer:
38% of 58 = 24.
Explanation:
In the above-given question,
given that,
38% is equal to 40%.
58 is round to 60.
40/100 x 60.
0.4 x 60 = 24.
so 38% of 58 = 24.
Question 3.
9% of 89
Answer:
9% of 89 = 9.
Explanation:
In the above-given question,
given that,
9% of 89.
9% is equal to 10.
89 =90.
10% of 90.
10/100 x 90.
0.1 x 90 = 9.
so 9% of 89 = 9.
Question 4.
76% of 41
Answer:
76% of 41 = 9.
Explanation:
In the above-given question,
given that,
76% of 41.
76% is equal to 80.
41 is rounded to 40.
80/100 x 40.
0.8 x 40 = 32.
so 76% of 41 = 9.
Question 5.
48% of 71
Answer:
48% of 71 = 35.
Explanation:
In the above-given question,
given that,
48% of 71.
48% is equal to 50.
71 is rounded to 70.
50/100 x 70.
0.5 x 70 = 35.
Question 6.
27% of 62
Answer:
27% of 62 = 18.
Explanation:
In the above-given question,
given that,
27% of 62.
27% is equal to 30.
62 is rounded to 60.
30/100 x 60.
0.3 x 60.
18.
so 27% of 62 = 18.
Question 7.
Joanna wants to buy a backpack that costs $37.98. The sales tax rate is 8.75%. Estimate the amount of sales tax that Joanna will pay.
Answer:
The amount of sales tax that Joanna will pay = 3.32.
Explanation:
In the above-given question,
given that,
Joanna wants to buy a backpack that costs $37.98.
The sales tax rate is 8.75%.
8.75% x $37.98.
8.75/100 x 37.98.
0.0875 x 37.98.
3.3232.
so the amount of sales tax that Joanna will pay = 3.32.
Lesson 6.5 Find the Percent of a Number
Quick Review
Percent equations have a percent value, a whole, and a part.
Example
What is 16% of 73.5?
Let x = the unknown part.
x = 0.16 • 73.5
Write 16% as a decimal.
x = 11.76
16% of 73.5 is 11.76.
What percent of 22 is 9.35?
Let p = the percent value.
p • 22 = 9.35
\(\frac{22 p}{22}=\frac{9.35}{22}\)
p = 0.425 = 42.5%
42.5% of 22 is 9.35.
Practice
Find each part or percent.
Question 1.
9% of 124
Answer:
9% of 124 = 11.16.
Explanation:
In the above-given question,
given that,
9/100 x 124.
0.09 x 124.
11.16.
9% of 124 = 11.16.
Question 2.
What percent of 20 is 3?
Answer:
15 percent of 20 is 3.
Explanation:
In the above-given question,
given that,
p x 20 = 3.
p = 3/20.
p = 0.15.
15/100 = 0.15.
Question 3.
24% of 35
Answer:
24% of 35 = 8.4.
Explanation:
In the above-given question,
given that,
24/100 x 35.
0.24 x 35.
8.4.
24% of 35 = 8.4.
Question 4.
What percent of 110 is 71.5?
Answer:
65 percent of 110 is 71.5.
Explanation:
In the above-given question,
given that,
p x 110 = 71.5.
110p = 71.5.
p = 71.5/110.
p = 0.65.
65/100 = 0.65.
Question 5.
43% of 82
Answer:
43% of 82 = 35.26.
Explanation:
In the above-given question,
given that,
43/100 x 82.
0.43 x 82.
35.26.
43% of 82 = 35.26.
Question 6.
What percent of 30 is 24?
Answer:
8 percent of 30 is 24.
Explanation:
In the above-given question,
given that,
px 30 = 24.
30p = 24.
p = 24/30.
p = 0.8.
Question 7.
On Tuesday, 620 students attended a middle school. A survey showed that 341 students brought lunch to school that day. What percent of the students brought their lunches?
Answer:
The percent of students who brought their lunches = 2114.2.
Explanation:
In the above-given question,
given that,
On Tuesday, 620 students attended a middle school.
A survey showed that 341 students brought lunch to school that day.
341/100 x 620.
3.41 x 620 = 2114.2.
so the percent of students brought their lunches = 2114.2.
Lesson 6.6 Find the Whole Given a part and the Percent
Quick Review
You can use an equation or a double number line diagram to find the whole when given the part and the percent.
Example
80% of what number is 96?
Let n = the whole. Write an equation, rename the percent as a decimal, and solve for n.
80% • N = 96
0.8n = 96
\(\frac{0.8 n}{0.8}=\frac{96}{0.8}\)
n = 120
80% of 120 is 96.
Practice
Find each whole.
Question 1.
140% of what number is 308?
Answer:
140% of 220 is 308.
Explanation:
In the above-given question,
given that,
140% of n = 308.
140/100 . n = 308.
1.4 n = 308.
n = 308/1.4.
n = 220.
140% of 220 is 308.
Question 2.
62% of what number is 186?
Answer:
62% of 300 is 186.
Explanation:
In the above-given question,
given that,
62% of n = 186.
62/100. n = 186.
0.62n = 186.
n = 186/0.62.
n = 300.
Question 3.
80% of what number is 120?
Answer:
80% of 150 is 120.
Explanation:
In the above-given question,
given that,
80% of n = 120.
80/100. n = 120.
0.8n = 120.
n = 120/0.8.
n = 150.
Question 4.
40% of what number is 10?
Answer:
40% of 25 is 10.
Explanation:
In the above-given question,
given that,
40% of n = 10.
40/100. n = 10.
0.4n = 10.
n = 10/0.4.
n = 25.
Question 5.
Desmond paid 8.5% sales tax when he bought a new phone. The sales tax was $12.75. What was the total cost of the phone, including tax?
Answer:
The total cost of the phone, including tax, is $150.
Explanation:
In the above-given question,
given that,
Desmond paid 8.5% sales tax when he bought a new phone.
The sales tax was $12.75.
8.5% n = $12.75.
8.5/100 = $12.75.
0.085n = $12.75.
n = $12.75/0.085.
n = $150.
so the total cost of the phone, including tax, is $150.
Topic 6 Fluency Practice
Crisscrossed
Find each quotient. Write your answers in the cross-number puzzle below. Each digit of your answer goes in its own box.
I can… divide multidigit numbers.

ACROSS
A. 94,070 = 46
C. 3,828 = 22
E. 46,680 ÷ 15
F. 61,065 ÷ 45
J. 5,136 ÷ 214
K. 9,840 ÷ 48
L. 2,407 ÷ 29
N. 67,870 ÷ 55
Q. 9,114 ÷ 62
R. 8,268 ÷ 12
T. 80,120 ÷ 20
DOWN
A. 7,644 ÷ 28
B. 22,016 ÷ 43
D. 49,980 ÷ 12
G. 67,704 ÷ 13
H. 10,582 ÷143
K. 4,148 ÷ 17
M. 10,062 ÷ 26
P. 63,860 ÷ 31
Q. 4,508 ÷ 23
S. 7,238 ÷ 77
