Go through the enVision Math Common Core Grade 3 Answer Key Topic 5 Fluently Multiply and Divide within 100 regularly and improve your accuracy in solving questions.
enVision Math Common Core 3rd Grade Answers Key Topic 5 Fluently Multiply and Divide within 100
Essential Question:
What are strategies to solve multiplication and division facts?

enVision STEM Project: Weather Information
Do Research Use the Internet or other sources to find the weather in different places on Earth. Find the weather at different times of day. Write down the temperature for each place. Also write down any conditions such as rain or snow.
Journal: Write a Report Include what you found. Also in your report:
- Tell how many places you checked.
- Tell how many times you checked the weather in one day.
- Write a multiplication or division story using your information. Then find an answer for your story.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- dividend
- divisor
- product
- quotient
- factor
Question 1.
The answer to a division problem is the _________.
Answer:
The answer to a division problem is the ___quotient___.
Explanation:
The answer to a division problem is the quotient.
Question 2.
A ________ is the answer to a multiplication problem.
Answer:
A _product_______ is the answer to a multiplication problem.
Explanation:
A product is the answer to a multiplication problem.
Question 3.
The _________ is the number in a division problem that is divided into equal groups.
Answer:
The __dividend_______ is the number in a division problem that is divided into equal groups.
Explanation:
The dividend is the number in a division problem that is divided into equal groups.
Question 4.
Multiply a factor by a ___________ to solve a multiplication problem.
Answer:
Multiply a factor by a ____factor_______ to solve a multiplication problem.
Explanation:
Multiply a factor by a factor to solve a multiplication problem.
Multiplication
Question 5.
6 × 2 = _______
Answer:
6 × 2 = ___12____.
Explanation:
6 × 2 = 12.
Question 6.
5 × 1 = _________
Answer:
5 × 1 = ___5______.
Explanation:
5 × 1 = 5.
Question 7.
4 × 10 = ________
Answer:
4 × 10 = __40______.
Explanation:
4 × 10 = 40.
Question 8.
7 × 5 = _______
Answer:
7 × 5 = ___35____.
Explanation:
7 × 5 = 35.
Question 9.
4 × 4 = _______
Answer:
4 × 4 = __16_____.
Explanation:
4 × 4 = 16.
Question 10.
9 × 3 = _______
Answer:
9 × 3 = __27_____.
Explanation:
9 × 3 = 27.
Question 11.
The oranges in a store are in 7 rows and 8 columns. How many oranges are there?
Answer:
Total number of oranges in all = 56.
Explanation:
Number of rows of oranges = 7.
Number of columns of oranges = 8.
Total number of oranges in all = Number of rows of oranges × Number of columns of oranges
= 7 × 8
= 56.
Division
Question 12.
60 ÷ 6 = ______
Answer:
60 ÷ 6 = _10_____.
Explanation:
60 ÷ 6 = 10.
Question 13.
25 ÷ 5 = _______
Answer:
25 ÷ 5 = __5_____.
Explanation:
25 ÷ 5 = 5.
Question 14.
12 ÷ 3 = _______
Answer:
12 ÷ 3 = ___4____.
Explanation:
12 ÷ 3 = 4.
Question 15.
30 ÷ 6 = _______
Answer:
30 ÷ 6 = __6_____.
Explanation:
30 ÷ 6 = 6.
Question 16.
14 ÷ 2 = _______
Answer:
14 ÷ 2 = ___7____.
Explanation:
14 ÷ 2 = 7.
Question 17.
9 ÷ 3 = _______
Answer:
9 ÷ 3 = ___3____.
Explanation:
9 ÷ 3 = 3.
Question 18.
If 28 stamps are arranged into an array with 4 columns, how many rows are there?
Answer:
Number of rows of stamps arranged in array = 7.
Explanation:
Total number of stamps arranged in array = 28.
Number of columns of stamps arranged in array = 4.
Number of rows of stamps arranged in array = Total number of stamps arranged in array ÷ Number of columns of stamps arranged in array
= 28 ÷ 4
= 7.
The Distributive Property
Question 19.
Explain how to use 2s facts to find 4 × 9.
Answer:
4 × 9 = (2 × 9) + (2 × 9) = 36.
Explanation:
4 × 9 = (2 × 9) + (2 × 9)
4 × 9 = 18 + 18
4 × 9 = 36.
Pick a Project
PROJECT 5A
How many books are in a library?
Project: Design a Library

Answer:

Explanation:
The word “library” seems to be used in so many different aspects now, from the brick-and-mortar public library to the digital library. Public libraries—and indeed, all libraries–are changing and dynamic places where librarians help people find the best source of information whether it’s a book, a web site, or database entry.
PROJECT 5B
How would you use number cubes?
Project: Make a Multiplication Game

Answer:
Place each token on the “Start” space. Have one student roll the dice, then move his token the same number of places he rolled. Have the student multiply the number on the game space with the number shown on the dice. If the student answers the multiplication problem correctly, he earns a point. If he answers incorrectly, the next player can steal the point by answering the problem.
Explanation:
When you multiply a whole number (not a fraction) by itself, and then by itself again the result is a cube number.
For example 3 x 3 x 3 = 27.
PROJECT 5C
Would you rather ride a bike or a “trike”?
Project: Create a Bike Chart

Answer:

Explanation:
Cycle sport is competitive physical activity using bicycles. There are several categories of bicycle racing including road bicycle racing, cyclo-cross, mountain bike racing, track cycling, BMX, and cycle speedway.
3-ACT MATH PREVIEW
Math Modeling
The Cheese Sticks

Lesson 5.1 Patterns for Multiplication Facts
Solve & Share
Max found 6 × 8 = 48. He noticed that (6 × 4) + (6 × 4) also equals 48. Use the multiplication table to find two other facts whose sum is 48. Use facts that have a 6 or 8 as a factor. What pattern do you see?
I can … use structure and properties to explain patterns for multiplication facts.
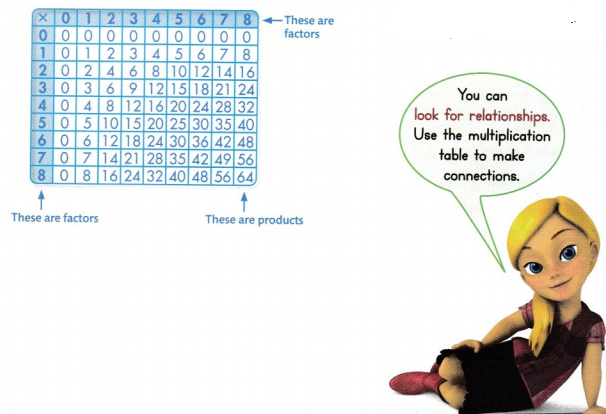
Look Back! How can a multiplication table help you find products that equal 48 when added together?
Answer:
Multiplication table can help in finding products that are equal 48 when added together are by finding the factors of 48 and later adding them, which is easy.
Explanation:
Multiplication table helps in easy way to find factors required for the given number.
Essential Question
How Can You Explain Patterns on in the Multiplication Chart?
Answer:
Factors of 48:
2 × 24 = 48.
3 × 16 = 48.
4 × 12 = 48.
6 × 8 = 48.
Explanation:

?? + ?? = 48.
Factors of 48:
2 × 24 = 48.
3 × 16 = 48.
4 × 12 = 48.
6 × 8 = 48.
Visual Learning Bridge
Yolanda noticed that 4 × 6 is double 2 × 6. How can you explain this?
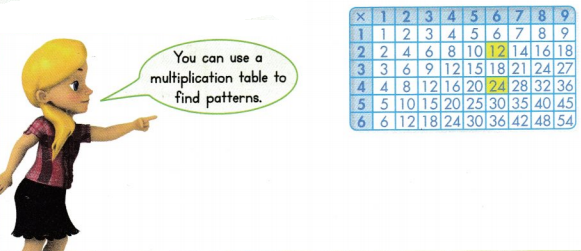
4 is the double of 2.
So, 4 × 6 is double 2× 6.
You can use the Distributive Property of Multiplication to explain.
4×6= (2 × 6) + (2 × 6)
4 × 6 = 12 + 12
4 × 6= 24
Look at the highlighted rows.
The product of any number multiplied by 4 will be double the product of that number multiplied by 2.

Convince Me! Look for Relationships Look at the highlighted rows of numbers multiplied by 2 or 4. What pattern do you see across the rows?
Answer:
The highlighted rows of numbers multiplied by 2 or 4 shows they are the multiples of the 2 and 4 numbers.
Explanation:
The highlighted rows of numbers multiplied by 2 or 4 shows the pattern of difference of 2 and 4 between them. They are the multiples of the 2 and 4 numbers.
Guided Practice
Do You Understand?
Question 1.
How are 3 × 7 and 6 × 7 related?
Answer:
6 × 7 is double of 3 × 7.
Explanation:
6 × 7 = (3 × 7) + (3 × 7)
6 × 7 = 21 + 21
6 × 7 = 42.
Question 2.
In the table on the previous page, is the pattern that Yolanda found also true for factors that are multiplied by 3 and 6? Explain.
Answer:
No, in the table on the previous page, is the pattern that Yolanda found also true for factors that are multiplied by 3 and 6.
Explanation:
No, in the table on the previous page, is the pattern that Yolanda found also true for factors that are multiplied by 3 and 6. They are the multiples of 2 and 4 not 3 and 6.
Do You Know How?
In 3 and 4, use the multiplication table shown below.
Question 3.
What pattern do you see in the columns and rows that have 0 as a factor?
Answer:
The pattern seen in the columns and rows that have 0 as a factor is crossed.
Explanation:
The pattern seen in the columns and rows that have 0 as a factor is crossed. Zero multiplied by any factor, the result is zero.
Question 4.
Use a property to explain why this pattern is true.
Answer:
8 × 0 = (4 × 0) + (4 × 0)
8 × 0 = 0 + 0
8 × 0 = 0.
Explanation:
Distributive property can be used.
8 × 0 = (4 × 0) + (4 × 0)
8 × 0 = 0 + 0
8 × 0 = 0.
Independent Practice
In 5-8, use the multiplication table shown at the right.

Question 5.
Look at the shaded products. What pattern do you see?
Answer:
Shaded products shows the pattern of 8 difference from 0 to 8, 8 to 14, later 4 difference from 14 to18, later 2 difference from18 to 20, and reverse from 20 to 0.
Explanation:
Shaded products shows the pattern of 8 difference from 0 to 8, 8 to 14, later 4 difference from 14 to18, later 2 difference from18 to 20, and reverse from 20 to 0. Its not content change of pattern noticed.
Question 6.
Write the equation for each shaded product.
Answer:
(0 × 0) + (0 × 0) = 0 + 0 = 0.
(2 × 2) + (2 × 2) = 4 + 4 = 8.
(2 × 4) + (2 × 3) = 8 + 6 = 14.
(2 × 5) + (2 × 4) = 10 + 8 =18.
(2 × 5) + (2 × 5) = 10 + 10 = 20
Explanation:
shaded product:
(0 × 0) + (0 × 0) = 0 + 0 = 0.
(2 × 2) + (2 × 2) = 4 + 4 = 8.
(2 × 4) + (2 × 3) = 8 + 6 = 14.
(2 × 5) + (2 × 4) = 10 + 8 =18.
(2 × 5) + (2 × 5) = 10 + 10 = 20
Question 7.
Look at the factors you wrote. Use a property to explain why the pattern for the products is true.
Answer:
0 = (0 × 0) + (0 × 0) = 0 + 0
8 = (2 × 4) = (2 × 2) + (2 × 2) = 4 + 4.
14 = (2 × 7) = (2 × 4) + (2 × 3) = 8 + 6.
18 = (2 × 9) = (2 × 5) + (2 × 4) = 10 + 8.
20 = (2 × 10) = (2 × 5) + (2 × 5) = 10 + 10.
Distributive property:
0 = (0 × 0) + (0 × 0) = 0 + 0
8 = (2 × 4) = (2 × 2) + (2 × 2) = 4 + 4.
14 = (2 × 7) = (2 × 4) + (2 × 3) = 8 + 6.
18 = (2 × 9) = (2 × 5) + (2 × 4) = 10 + 8.
20 = (2 × 10) = (2 × 5) + (2 × 5) = 10 + 10.
Question 8.
Shade a line in the multiplication table to show how this pattern is true for other products.
Answer:

Explanation:
shaded numbers are 8,14,16,20. The numbers are shaded.
8 = 2 × 4.
14 = 2 × 7.
18 = 2 × 9.
Problem Solving
Question 9.
enVision® STEM How many arms do 9 starfish have if …
a. each starfish has 6 arms? Write a multiplication equation to solve.
Answer:
Total number of arms 9 star fishes have = Number of arms each star fish has × Number of star fishes
= 6 × 9
= 54.
Explanation:
Number of arms each star fish has = 6.
Number of star fishes = 9.
Total number of arms 9 star fishes have = Number of arms each star fish has × Number of star fishes
= 6 × 9
= 54.
b. each starfish has 7 arms? Write a multiplication equation to solve.

Answer:
Total number of arms 9 star fishes have = Number of arms each star fish has × Number of star fishes
= 7 × 9
= 63.
Explanation:
Number of arms each star fish has = 7.
Number of star fishes = 9.
Total number of arms 9 star fishes have = Number of arms each star fish has × Number of star fishes
= 7 × 9
= 63.
Question 10.
Higher Order Thinking Karen found a pattern on the multiplication table. What pattern did she find? Explain why it is true.
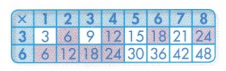
Answer:
The pattern she found is the difference of 6 in between every number highlighted on the multiplication table.
Explanation:
The pattern she found is the multiples of 6 number on the multiplication table.
Question 11.
Write the fact family for each fact: 2 × 0, 2 × 1, 2 × 2, 2 × 3, 2 × 4, 2 × 5, 2 × 6, 2 × 7, 2 × 8, 2 × 9, and 2 × 10.
Answer:
2 × 0 = 0. => 0 × 2 = 0.
2 × 1 = 2. => 1 × 2 = 2.
2 × 2 = 4. => 2 × 2 = 4.
2 × 3 = 6. => 3 × 2 = 6.
2 × 4 = 8. => 4 × 2 = 8.
2 × 5 = 10. => 5 × 2 = 10.
2 × 6 = 12. => 6 × 2 = 12.
2 × 7 = 14. => 7 × 2 = 14.
2 × 8 = 16. => 8 × 2 = 16.
2 × 9 = 18. => 9 × 2 = 18.
2 × 10 = 20. => 2 × 2 = 4.
Explanation:
Fact family:
2 × 0 = 0. => 0 × 2 = 0.
2 × 1 = 2. => 1 × 2 = 2.
2 × 2 = 4. => 2 × 2 = 4.
2 × 3 = 6. => 3 × 2 = 6.
2 × 4 = 8. => 4 × 2 = 8.
2 × 5 = 10. => 5 × 2 = 10.
2 × 6 = 12. => 6 × 2 = 12.
2 × 7 = 14. => 7 × 2 = 14.
2 × 8 = 16. => 8 × 2 = 16.
2 × 9 = 18. => 9 × 2 = 18.
2 × 10 = 20. => 2 × 2 = 4.
Question 12.
Be Precise Describe a pattern you see in the 9s row of the multiplication table.
Answer:
The pattern noticed is they are the multiples of 9 number in the 9s row of the multiplication table.
Explanation:

Assessment Practice
Question 13.
One row and 1 column are shaded in the multiplication table below.
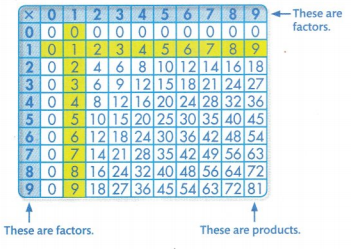
What pattern and property of operations is shown in the shaded row and column?
A. The products are all equal to the factor that is multiplied by 1; The Identity Property of Multiplication
B. The products in the shaded row are equivalent to the products in the shaded column; The Zero Property of Multiplication
C. Each product is 1 greater than the product before; The Distributive Property
D. There are no patterns or properties.
Answer:
A. The products are all equal to the factor that is multiplied by 1; The Identity Property of Multiplication is the pattern and property of operations is shown in the shaded row and column:
Explanation:
The pattern and property of operations is shown in the shaded row and column:
A. The products are all equal to the factor that is multiplied by 1; The Identity Property of Multiplication
Lesson 5.2 Use a Table to Multiply and Divide
Solve & Share
Find 18 ÷ 3 any way you choose.
I can … use reasoning and the relationship between multiplication and division to find basic facts.

Look Back! Describe another way you can find 18 ÷ 3.
Answer:
Another way:
18 ÷ 6 = 3.
6 × 3 = 18.
Explanation:
Another way:
18 ÷ 3 = 6.
18 ÷ 6 = 3.
6 × 3 = 18.
Essential Question
How Can You Use a Multiplication to Table to Solve Division Problems?
Answer:
We can use a Multiplication to Table to Solve Division Problems by using the factors.
For Example:
2 × 5 = 10.
10 ÷ 2 = 5.
Explanation:
We use the multiplication tables of the smaller. Number to get the answer to a division problem quickly. For Example:
2 × 5 = 10.
10 ÷ 2 = 5.
Visual Learning Bridge
Write a missing factor equation and then use the multiplication table to find 15 ÷ 3.

15 ÷ 3= ?
3 × ? = 15
3 times what number equals 15?
Step 1 You know one factor is 3. Find the 3 in the first column of this multiplication table.
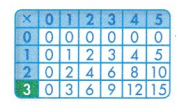
Step 2 You know the product is 15. Follow the row the 3 is in until you come to 15.
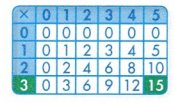
Step 3 Look straight up to the top of that column of the table. The number on the top of the column is 5. The missing factor is 5.
3 × 5 = 15
15 ÷ 3 = 5
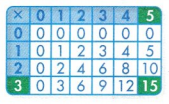
Convince Me! Reasoning Write a missing factor equation and use the multiplication table above to solve each division problem.
6 ÷ 3 = ?
12 ÷ 3 = ?
9 ÷ 3 = ?
Answer:
6 ÷ 3 = 2.
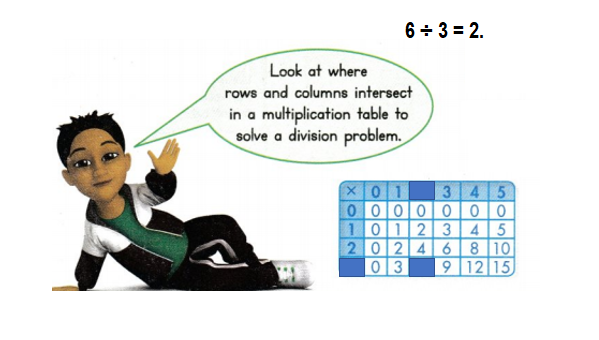
12 ÷ 3 = 4.

9 ÷ 3 = 3.
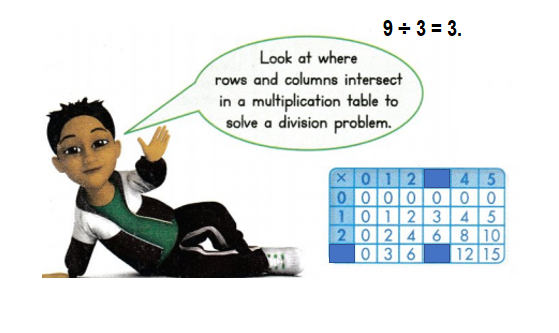
Explanation:
6 ÷ 3 = ?
=> 6 ÷ 3 = 2.
12 ÷ 3 = ?
=> 12 ÷ 3 = 4.
9 ÷ 3 = ?
=> 9 ÷ 3 = 3.
Another Example!
How can you find the missing numbers in the table?

Guided Practice
Do You Understand?
Question 1.
Explain how to use a multiplication table to solve a missing factor equation.
Answer:
Way you can find the missing factor in a multiplication:
Equation is using a repeated addition let’s take a look at this multiplication equation four times something equals 24.
24 ÷ 4 = ??
=> 24 ÷ 4 = 6.
Explanation:
Equation is using a repeated addition let’s take a look at this multiplication equation four times something equals 24.
24 ÷ 4 = ??
=> 24 ÷ 4 = 6.
Do You Know How?
In 2-5, find the value that makes the equation correct. Use a multiplication table to help.
Question 2.
24 ÷ 6 = _______
24 = 6 × _______
Answer:
24 ÷ 6 = ___4____.
24 = 6 × ___4____.
Explanation:
24 ÷ 6 = 4.
24 = 6 × 4.
Question 3.
63 ÷ 9 = _______
9 × _____ = 63
Answer:
63 ÷ 9 = __7_____.
9 × _7____ = 63.
Explanation:
63 ÷ 9 = 7.
9 × 7 = 63.
Question 4.
25 ÷ 5 = ______
5 × ______ = 25
Answer:
25 ÷ 5 = __5____.
5 × __5____ = 25.
Explanation:
25 ÷ 5 = 5.
5 × 5 = 25.
Question 5.
42 ÷ 7 = _______
42 = 7 × _______
Answer:
42 ÷ 7 = ___6____.
42 = 7 × __6_____.
Explanation:
42 ÷ 7 = 6.
42 = 7 × 6.
Independent Practice
In 6 and 7, find the missing factors and products.
Question 6.
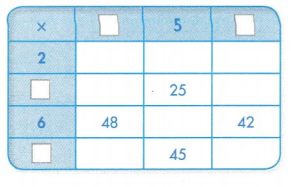
Answer:
5 × ? = 25.
6 × ? = 48.
6 × ? = 42.
? × 5 = 45.
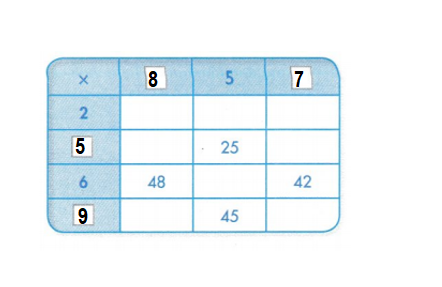
Explanation:
5 × ? = 25.
=> 5 × 5 = 25.
6 × ? = 48.
=> 6 × 8 = 48.
6 × ? = 42.
=> 6 × 7 = 42.
? × 5 = 45.
=> 9 × 5 = 45.
Question 7.

Answer:
4 × ? = 12.
? × 9 = 54.
3 × ? = 6.
? × 9 = 72.
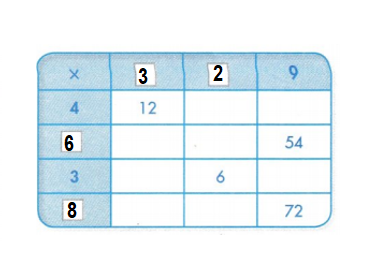
Explanation:
4 × ? = 12.
=> 4 × 3 = 12.
? × 9 = 54.
=> 6 × 9 = 54.
3 × ? = 6.
=> 3 × 2 = 6.
? × 9 = 72.
=> 8 × 9 = 72.
Problem Solving

Question 8.
Some members of the Bird Club used a tally chart to record how many different birds they each saw one day. Fill in the blanks below to make the sentence correct. _________ saw 4 more birds than ________.
Answer:
__Miss. Simmons_______ saw 4 more birds than ___Ms. Chester_____.
Explanation:
Number of birds Ms. Chester saw = 7.
Number of birds Mr. Dobbs saw = 4.
Number of birds Miss. Simmons saw = 11.
Number of birds Mr. Molina saw = 0.
Difference:
Number of birds Miss. Simmons saw – Number of birds Ms. Chester saw
= 11 – 7
= 4.
Question 9.
Complete the chart to show that Mr. Molina saw 5 fewer birds than Mr. Dobbs and Miss Simmons combined.
Answer:
Mr. Molina saw 15 fewer birds than Mr. Dobbs and Miss Simmons combined.
Explanation:
Number of birds Ms. Chester saw = 7.
Number of birds Mr. Dobbs saw = 4.
Number of birds Miss. Simmons saw = 11.
Number of birds Mr. Molina saw = 0.
Number of birds Mr. Dobbs and Miss Simmons combined = Number of birds Miss. Simmons saw + Number of birds Mr. Dobbs saw
= 11 + 4
= 15.
Question 10.
Critique Reasoning Bill used a multiplication table to find the value of 12 = 6. His answer was 3. Do you agree? Why or why not?
Answer:
Bill is wrong because 12 = 6 when the answer is 2 not 3.
=> 12 ÷ 2 = 6.
Explanation:
12 = 6.
=> 12 ÷ 2 = 6.
Question 11.
Write the fact family for each fact: 5 × 0, 5 × 1, 5 × 2, 5 × 3, 5 × 4, 5 × 5, 5 × 6, 5 × 7, 5 × 8, 5 × 9, and 5 × 10.
Answer:
Fact family:
5 × 0 = 0.
= 0 × 5 = 0.
5 × 1 = 5.
=> 1 × 5 = 5.
5 × 2 = 10.
=> 2 × 5 = 10.
5 × 3 = 15.
=> 3 × 5 = 15.
5 × 4 = 20.
=> 4 × 5 = 20.
5 × 5 = 25.
=> 5 × 5 = 25.
5 × 6 = 30.
=> 6 × 5 = 30.
5 × 7 = 35.
=> 7 × 5 = 35.
5 × 8 = 40.
=> 8 × 5 = 40.
5 × 9 = 45.
=> 9 × 5 = 45.
5 × 10 = 50.
=> 10 × 5 = 50.
Explanation:
5 × 0 = 0.
= 0 × 5 = 0.
5 × 1 = 5.
=> 1 × 5 = 5.
5 × 2 = 10.
=> 2 × 5 = 10.
5 × 3 = 15.
=> 3 × 5 = 15.
5 × 4 = 20.
=> 4 × 5 = 20.
5 × 5 = 25.
=> 5 × 5 = 25.
5 × 6 = 30.
=> 6 × 5 = 30.
5 × 7 = 35.
=> 7 × 5 = 35.
5 × 8 = 40.
=> 8 × 5 = 40.
5 × 9 = 45.
=> 9 × 5 = 45.
5 × 10 = 50.
=> 10 × 5 = 50.
Question 12.
Higher Order Thinking Brit uses a multiplication table to multiply 2 different factors. She notices that the product is in the same column as the number 35. What is one of the factors in Brit’s multiplication problem? Explain your answer.

Answer:
One of the factors in Brit’s multiplication problem:
7 × 5 = 35.
Explanation:
One of the factors in Brit’s multiplication problem:
7 × 5 = 35.
Assessment Practice
Question 13.
Use the relationship between multiplication and division to find the missing number in 21 ÷ ☐ = 7.
A. 1
B. 3
C. 7
D. 9
Answer:
21 ÷ 3 = 7.
B. 3
Explanation:
21 ÷ ☐ = 7.
=> 21 ÷ ?? = 7.
=> 21 ÷ 3 = 7.
Lesson 5.3 Use Strategies to Multiply
Solve & Share
Alfredo has 6 bags of oranges. Each bag contains 7 oranges. How many oranges does Alfredo have? Show 2 ways to find this answer.
I can … use different strategies to solve multiplication problems.

Look Back! How do strategies such as skip counting, using known facts, and making arrays help you solve multiplication facts?
Answer:
Strategies such as skip counting, using known facts, and making arrays helps solve multiplication facts by easy calculations and easy in finding the solution for the problem.
Explanation:
Strategies such as skip counting, using known facts, and making arrays helps solve multiplication facts by easy calculations and easy in finding the solution for the problem.
Essential Question
How Do You Use Strategies Question to Multiply?
Answer:
Strategies help us use what we do know (easier multiplication facts or addition facts) to solve any problem.
Explanation:
Strategies help us use what we do know (easier multiplication facts or addition facts) to understand the problem and solve the problem.
Visual Learning Bridge
A scientist on a boat is studying hammerhead sharks. The length of 6 hammerhead sharks lined up nose to tail without gaps is equal to the length of the boat. How long is the boat?
Drawings, skip counting, tools, and properties of operations are strategies you can use to multiply equal groups.

One Way
Use a bar diagram to find 6 × 5.
6 × 5 means 6 groups of 5. Skip count by 5s.
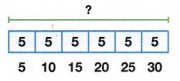
So, 6 × 5= 30.
The boat is 30 yards long.
Another Way
Use counters and properties to find 6 × 5.
The Distributive Property says you can break the problem into smaller parts. Use 2s facts and 4s facts to help.
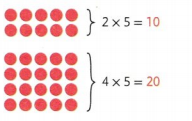
Then add the two products: 10 + 20 = 30.
The boat is 30 yards long.
Convince Me! Use Structure How can knowing the product of 5 × 6 help you solve 6 × 5?
Answer:
5 × 6 = 30.
6 × 5 = 30.
Both the products value is same.
Explanation:
5 × 6 = (2 × 6) + (3 × 6) = 12 + 18 = 30.
6 × 5 = (4 × 5) + ( 2 × 5) = 20 + 10 = 30.
Guided Practice
Do You Understand?
Question 1.
What two known facts can you use to find 3 × 5?
Answer:
3 × 5 = (1 × 5) + (2 × 5) = 5 + 10 = 15.
Explanation:
3 × 5 = (1 × 5) + (2 × 5)
3 × 5 = 5 + 10
3 × 5 = 15.
Question 2.
How could knowing 7 × 5 = 35 help you find 9 × 5?
Answer:
9 × 5 = (7 × 5) + (2 × 5) = 35 + 10 = 45.
Explanation:
7 × 5 = 35 helps to find 9 × 5.
9 × 5 = (7 × 5) + (2 × 5)
9 × 5 = 35 + 10
9 × 5 = 45.
Do You Know How?
In 3-8, multiply.
Question 3.
6 × 4 = _______
Answer:
6 × 4 = __24._____
Explanation:
6 × 4 = (3 × 4) + (3 × 4)
6 × 4 = 12 + 12
6 × 4 = 24.
Question 4.
______ = 4 × 5
Answer:
__20____ = 4 × 5.
Explanation:
4 × 5 = (2 × 5) + (2 × 5)
4 × 5 = 10 + 10
4 × 5 = 20.
Question 5.
9 × 3 = _______
Answer:
9 × 3 = __27_____.
Explanation:
9 × 3 = (6 ×3) + (3 × 3)
9 × 3 = 18 + 9
9 × 3 = 27.
Question 6.
3 × 2 = ________
Answer:
3 × 2 = ____6____.
Explanation:
3 × 2 = (1 × 2) + (2× 2)
3 × 2 = 2 + 4
3 × 2 = 6.
Question 7.
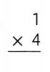
Answer:
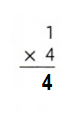
Explanation:
1 × 4 = 4.
Question 8.
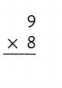
Answer:
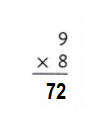
Explanation:
9 × 8 = (5 × 8) + (4 × 8)
9 × 8 = 40 + 32
9 × 8 = 72.
Independent Practice
In 9-25, use strategies to find the product.
Question 9.
_____ = 5 × 5
Answer:
__25___ = 5 × 5.
Explanation:
5 × 5 = (3 × 5) + (2 × 5)
5 × 5 = 15 + 10
5 × 5 = 25.
Question 10.
9 × 2 = _______
Answer:
9 × 2 = ___18____.
Explanation:
9 × 2 = (7 × 2) + (2 × 2)
9 × 2 = 14 + 4
9 × 2 = 18.
Question 11.
______ = 5 × 9
Answer:
__45____ = 5 × 9.
Explanation:
5 × 9 = (3 × 9) + (2 × 9)
5 × 9 = 27 + 18
5 × 9 = 45.
Question 12.
8 × 7 = _______
Answer:
8 × 7 = __56_____.
Explanation:
8 × 7 = (4 × 7) + (4 × 7)
8 × 7 = 28 + 28
8 × 7 = 56.
Question 13.
_____ = 3 × 6
Answer:
__18___ = 3 × 6.
Explanation:
3 × 6 = (1 × 6) + (2 × 6)
3 × 6 = 6 + 12
3 × 6 = 18.
Question 14.
8 × 4 = _______
Answer:
8 × 4 = ___32____.
Explanation:
8 × 4 = (4 × 4) + (4 × 4)
8 × 4 = 16 + 16
8 × 4 = 32.
Question 15.
![]()
Answer:
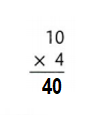
Explanation:
10 × 4 = (5 × 4) + (5 × 4)
10 × 4 = 20 + 20
10 × 4 = 40.
Question 16.
![]()
Answer:
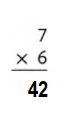
Explanation:
7 × 6 = ( 4 × 6) + ( 3 × 6)
7 × 6 = 24 + 18
7 × 6 = 42.
Question 17.

Answer:
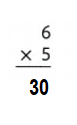
Explanation:
6 × 5 = (3 × 5) + (3 × 5)
6 × 5 = 15 + 15
6 × 5 = 30.
Question 18.
![]()
Answer:
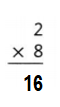
Explanation:
2 × 8 = (1 × 8) + (1 × 8)
2 × 8 = 8 + 8
2 × 8 = 16.
Question 19.
![]()
Answer:
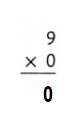
Explanation:
9 × 0 = (5 × 0) + (4 × 0)
9 × 0 = 0 + 0
9 × 0 = 0.
Question 20.
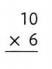
Answer:
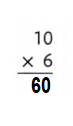
Explanation:
10 × 6 = (5 × 6) + (5 × 6)
10 × 6 = 30 + 30
10 × 6 = 60.
Question 21.
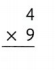
Answer:
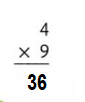
Explanation:
4 × 9 = (2 × 9) + (2 × 9)
4 × 9 = 18 + 18
4 × 9 = 6.
Question 22.
![]()
Answer:
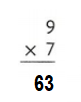
Explanation:
9 × 7 = ( 6 × 7) + ( 3 × 7)
9 × 7 = 42 + 21
9 × 7 = 63.
Question 23.
What is 4 × 6? _______
Answer:
4 × 6 = 24.
Explanation:
4 × 6 = (2 × 6) + (2 × 6)
4 × 6 = 12 + 12
4 × 6 = 24.
Question 24.
What is 5 × 8?_______.
Answer:
5 × 8 = 40.
Explanation:
5 × 8 = (3 × 8) + (2 × 8)
5 × 8 = 24 + 16
5 × 8 = 40.
Question 25.
What is 10 × 1? _________
Answer:
10 × 1 = 10.
Explanation:
10 × 1 = (6 × 1) + ( 4 × 1)
10 × 1 = 6 + 4
10 × 1 = 10.
Problem Solving
In 26 and 27, use the pictures below.
Question 26.
Dr. Marks is studying 3 blacktip sharks and 4 tiger sharks. What is the total length of the 7 sharks? Show your strategy.

Answer:
Total length of the 7 sharks = 22 square yards long.
Explanation:
Number of blacktip sharks Dr. Marks is studying = 3.
Number of tiger sharks Dr. Marks is studying = 4.
Length of the each blacktip shark = 2 yards long.
Length of the each tiger shark = 4 yards long.
Total length of the 7 sharks = (Length of the blacktip shark × Number of blacktip sharks Dr. Marks is studying) + ( Length of the each tiger shark × Number of tiger sharks Dr. Marks is studying)
= (2 × 3) + ( 4 × 4)
= 6 + 16
= 22 square yards long.
Question 27.
Critique Reasoning Kent reasons that the total length of 4 blacktip sharks can be found using addition. Is his reasoning correct? Explain.

Answer:
Yes, his reasoning is correct, we can find the total length of 4 blacktip sharks can be found using addition.
Explanation:
Length of the each blacktip shark = 2 yards long.
Total length of 4 blacktip sharks = Length of the each blacktip shark + Length of the each blacktip shark + Length of the each blacktip shark + Length of the each blacktip shark
= 2 + 2 + 2 + 2
= 4 + 2 + 2
= 6 + 2
= 8 square yards long.
Question 28.
Write the fact family for each fact: 3 × 0, 3 × 1, 3 × 2, 3 × 3, 3 × 4, 3 × 5, 3 × 6, 3 × 7, 3 × 8, 3 × 9, and 3 × 10.
Answer:
Fact family:
3 × 0 = 0.
=> 0 × 3 = 0.
3 × 1 = 3.
=> 1 × 3 = 3.
3 × 2 = 6.
=> 2 × 3 = 6.
3 × 3 = 9.
=> 3 × 3 = 9.
3 × 4 = 12.
=> 3 × 4 = 12.
3 × 5 = 15.
=> 5 × 3 = 15.
3 × 6 = 18.
=> 6 × 3 = 18.
3 × 7 = 21.
=> 7 × 3 = 21.
3 × 8 = 24.
=> 8 × 3 = 24.
3 × 9 = 27.
=> 9 × 3 = 27.
3 × 10 = 30.
= 10 × 3 = 30.
Explanation:
3 × 0 = 0.
=> 0 × 3 = 0.
3 × 1 = 3.
=> 1 × 3 = 3.
3 × 2 = 6.
=> 2 × 3 = 6.
3 × 3 = 9.
=> 3 × 3 = 9.
3 × 4 = 12.
=> 3 × 4 = 12.
3 × 5 = 15.
=> 5 × 3 = 15.
3 × 6 = 18.
=> 6 × 3 = 18.
3 × 7 = 21.
=> 7 × 3 = 21.
3 × 8 = 24.
=> 8 × 3 = 24.
3 × 9 = 27.
=> 9 × 3 = 27.
3 × 10 = 30.
= 10 × 3 = 30.
Question 29.
Higher Order Thinking Show how you can use known facts to find 11 × 9. Explain how you chose the known facts.
Answer:
11 × 9 = (6 × 9) + (5 × 9) = 66 + 33 = 99.
Explanation:
11 × 9 = (6 × 9) + (5 × 9)
11 × 9 = 66 + 33
11 × 9 = 99.
Assessment Practice
Question 30.
Which shows one way you could use properties of operations to find 7 × 2?
A. (5 × 2) + (2 × 2)
B. (7 + 2) + (7 + 2)
C. (7 × 2) × 2
D. 7 × (2 × 2)
Answer:
A. (5 × 2) + (2 × 2) is one way you could use properties of operations to find 7 × 2.
Explanation:
7 × 2 = (5 × 2) + (2 × 2)
7 × 2 = 10 + 4
7 × 2 = 14.
Question 31.
Which multiplication equation could you use to help find 40 ÷ 8 = ☐?
A. 55 = 25
B. 8 × 8 = 64
C. 1 × 8 = 8
D. 8 × 5 = 40
Answer:
D. 8 × 5 = 40 multiplication equation could you use to help find 40 ÷ 8 = ☐.
Explanation:
40 ÷ 8 = ??
40 ÷ 8 = 5.
=> 8 × 5 = 40.
Lesson 5.4 Solve Word Problems: Multiplication and Division Facts
Solve & Share
At the Fall Fest parade, members of the Cat Lovers Club and the Dog Lovers Club will march in equal rows. There will be 6 members in each row. How many rows of dog lovers will march in the parade? How many total cat lovers will march in the parade? Complete the table.
I can … use strategies to solve word problems that involve multiplication and division.

Look Back! What operations did you use to solve the problem? Explain your reasoning.
Answer:
Operations used to solve the problem are multiplication and division.
Number of rows of dog lovers in the parade = 4.
Number of members of cat lovers in the parade = 30.
Explanation:
Number of members in each row = 6.
Number of dog lovers in the parade = 24.
Number of rows of dog lovers in the parade = Number of dog lovers in the parade ÷ Number of members in each row
= 24 ÷ 6
= 4.
Number of members in each row = 6.
Number of rows of cat lovers given = 5.
Number of members of cat lovers in the parade = Number of rows of cat lovers given × Number of members in each row
= 5 × 6
= 30.

Essential Question
How Can You Solve Word Problems Using Multiplication and Division?
Answer:
We can solve Word Problems Using Multiplication and Division by using a repeated method of finding what is asked, by using the data given and finding the correct solution of the problem.
Explanation:
We can solve Word Problems Using Multiplication and Division by using a repeated method step-by-step of finding what is asked, by using the data given and finding the correct solution of the problem.
Visual Learning Bridge
Gina has 45 hats. She is packing them by putting 9 hats in each of several boxes. How many boxes will she fill?


One Way
Think: 45 divided by what number equals 9?
45 ÷ 5 = 9
There are 5 groups of 9 in 45.
Gina can divide 45 hats into 5 boxes of 9 hats each.
Another Way
You can use a related fact.
Think: 9 times what number equals 45?
9 × 5 = 45
So, 45 ÷ 9 = 5.
Gina can divide 45 hats into 5 boxes of 9 hats each.
Convince Me! Generalize Krys has 42 hats. She puts 6 hats in each of several boxes. Can you find how many boxes she needs using the same strategies as in the example above? Explain.
Answer:
Number of boxes she needs = 7.
Explanation:
Number of hats Krys has = 42.
Number of hats in each box she puts = 6.
Number of boxes she needs = Number of hats Krys has ÷ Number of hats in each box she puts
= 42 ÷ 6
= 7.
Guided Practice
Do You Understand?
Question 1.
Why can you use division to model the problem on the previous page?
Answer:
We can use division to model the problem on the previous page because according to given data, the required solution is only found by using division method.
Explanation:
We can use division to model the problem on the previous page because according to given data, the required solution is only found by using division method.
Number of boxes she needs = Number of hats Krys has ÷ Number of hats in each box she puts
Question 2.
Casey gives 27 stickers to 3 friends. She writes the equation 27 ÷ 3 = 9. What does the 9 represent in this problem?
Answer:
Number of stickers she gives to each friend = 9.
Explanation:
Number of stickers Casey gives = 27.
Number of friends she gives = 3.
Number of stickers she gives to each friend = Number of stickers Casey gives ÷ Number of friends she gives
= 27 ÷ 3
= 9.
Do You Know How?
In 3, represent the problem with an equation or a bar diagram. Then solve.
Question 3.
A checkerboard has 64 squares. It has 8 rows. How many columns does it have?
Answer:
Number of columns a checkerboard has = 8.
Explanation:
Number of squares a checkerboard has = 64 .
Number of rows a checkerboard has = 8.
Number of columns a checkerboard has = Number of squares a checkerboard has ÷ Number of rows a checkerboard has
= 64 ÷ 8
= 8.
Independent Practice
In 4 and 5, draw a bar diagram to represent the problem. Then solve.
Question 4.
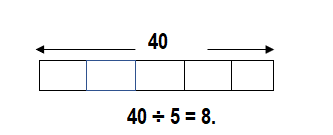
There are 5 pancakes in a stack. Elise makes 40 pancakes. How many stacks does Elise make?
Answer:
Number of stacks Elise makes = 8.
Explanation:
Number of pancakes in a stack = 5.
Number of pancakes Elise makes = 40.
Number of stacks Elise makes = Number of pancakes Elise makes ÷ Number of pancakes in a stack
= 40 ÷ 5
= 8.
Question 5.
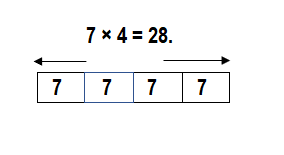
A park has 4 swing sets. Each of the sets has 7 swings. How many swings are in the park?
Answer:
Number of swings are in the park = 28.
Explanation:
Number of swing sets a park has = 4.
Number of swings in each set = 7.
Number of swings are in the park = Number of swing sets a park has × Number of swings in each set
= 4 × 7
= 28.
In 6 and 7, write an equation with an unknown to represent the problem. Then solve.
Question 6.
Mrs. Jameson plants 30 tulips in rows. Each row has 6 tulips. How many rows did Mrs. Jameson plant?
Answer:
Number of rows Mrs. Jameson plants = 5.
Explanation:
Number of tulips in rows Mrs. Jameson plants = 30.
Number of tulips in each row = 6.
Number of rows Mrs. Jameson plants = Number of tulips in rows Mrs. Jameson plants ÷ Number of tulips in each row
= 30 ÷ 6
= 5.
Question 7.
Bonnie buys 6 paperback books every month. She buys 2 hardcover books every month. How many books does she buy in 4 months?
Answer:
Total number of books she buys in 4 months = 32.
Explanation:
Number of paperback books every month Bonnie buys = 6.
Number of hardcover books every month Bonnie buys = 2.
Total number of books she buys in 4 months = 4 ( Number of paperback books every month Bonnie buys + Number of hardcover books every month Bonnie buys)
= 4 ( 6 + 2)
= 4 × 8
= 32.
Problem Solving
Question 8.
Jodie has 24 flowers in her garden. She wants to give an equal number of flowers to 4 families in her neighborhood. How many flowers will each family get? Complete the bar diagram and write an equation to help solve this problem.
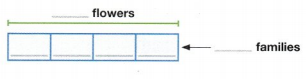
Answer:
Number of flowers each family gets = 6.
Explanation:
Number of flowers in her garden Jodie has = 24.
Number of families she want to give flowers equally = 4.
Number of flowers each family gets = Number of flowers in her garden Jodie has ÷ Number of families she want to give flowers equally
= 24 ÷ 4
= 6.
Question 9.
Model with Math Casey has 2 sisters. He gave each sister 2 pages of stickers. Each page had 9 stickers on it. How many stickers did Casey give in all? Explain what math you used to solve.
Answer:
Total number of stickers Casey give in all = 18.
Math used to solve the problem is multiplication.
Explanation:
Number of stickers Model with Math Casey has = 2.
Number of pages of stickers he gave each sister = 2.
Number of stickers each page has = 9.
Total number of stickers Casey give in all = Number of pages of stickers he gave each sister × Number of stickers each page has
= 2 × 9
= 18.
Question 10.
Write the fact family for each fact: 6 × 0, 6 × 1, 6 × 2, 6 × 3, 6 × 4, 6 × 5, 6 × 6, 6 × 7, 6 × 8, 6 × 9, and 6 × 10.
Answer:
Fact family:
6 × 0 = 0.
=> 0 × 6 = 0.
6 × 1 = 6.
=> 1 × 6 = 6.
6 × 2 = 12.
=> 2 × 6 = 12.
6 × 3 = 18.
=> 3 × 6 = 18.
6 × 4 = 24.
=> 4 × 6 = 24.
6 × 5 = 30.
=> 5 × 6 = 30.
6 × 6 = 36.
=> 6 × 6 = 36.
6 × 7 = 42.
=> 7 × 6= 42.
6 × 8 = 48.
=> 8 × 6 = 48.
6 × 9 = 54.
=> 9 × 6 = 54.
6 × 10 = 60.
=> 10 × 6= 60.
Explanation:
6 × 0 = 0.
=> 0 × 6 = 0.
6 × 1 = 6.
=> 1 × 6 = 6.
6 × 2 = 12.
=> 2 × 6 = 12.
6 × 3 = 18.
=> 3 × 6 = 18.
6 × 4 = 24.
=> 4 × 6 = 24.
6 × 5 = 30.
=> 5 × 6 = 30.
6 × 6 = 36.
=> 6 × 6 = 36.
6 × 7 = 42.
=> 7 × 6= 42.
6 × 8 = 48.
=> 8 × 6 = 48.
6 × 9 = 54.
=> 9 × 6 = 54.
6 × 10 = 60.
=> 10 × 6= 60.
Question 11.
Higher Order Thinking Twenty-five students are working in groups on a science project. Each group can have either 2 or 3 students in it. What is the fewest number of groups there could be?

Answer:
Number of students in each group of 2 is the fewest number of groups than Number of students in each group of 3.
Explanation:
Number of students are working in groups on a science project = 25.
Number of students in each group = 2.
Number of groups = Number of students are working in groups on a science project × Number of students in each group
= 25 × 2
= 50.
Number of students are working in groups on a science project = 25.
Number of students in each group = 3.
Number of groups = Number of students are working in groups on a science project × Number of students in each group
= 25 × 3
= 75.
Assessment Practice
Question 12.
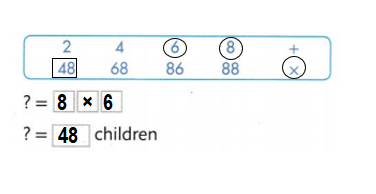
Eight vans are going to the zoo. There are 6 children in each van. How many children are going to the zoo?
Select numbers and an operation from the box to complete an equation that could be used to answer the problem. Then solve the equation.
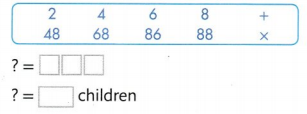
Answer:
Number of children going to the zoo = 48.
Explanation:
Number of vans going to the zoo = 8.
Number of children in each van = 6.
Number of children going to the zoo = Number of vans going to the zoo × Number of children in each van
= 8 × 6
= 48.
Question 13.
Ninety children are going to a museum. Nine children can ride in each minibus. How many minibuses are needed? Select numbers and an operation from the box to complete an equation that could be used to answer the problem. Then solve the equation.
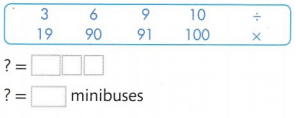
Answer:
Number of minibuses are needed = 10.
Explanation:
Number of children are going to a museum = 90.
Number of children can ride in each minibus = 9.
Number of minibuses are needed = Number of children are going to a museum ÷ Number of children can ride in each minibus
= 90 ÷ 9
= 10.

Lesson 5.5 Write Multiplication and Division Math Stories
Solve & Share
Write a real-world division story for 28 ÷ 4. Then write another real-world story that shows a different way to think about 28 ÷ 4.
I can … write and solve math stories for multiplication and division equations.

Look Back! Draw a bar diagram and write an equation to represent and solve one of your division stories.
Answer:
Number of students in each bus = Total number of students in a school ÷ Number of buses
= 28 ÷ 4
= 7.
Explanation:
Total number of students in a school = 28.
Number of buses = 4.
Number of students in each bus = Total number of students in a school ÷ Number of buses
= 28 ÷ 4
= 7.

Essential Question
How Can You Describe a Multiplication Fact?
Answer:
A multiplication fact is the answer to a multiplication calculation.
For example, in the sum 3 x 3 = 9, the multiplication fact is 9
Explanation:
The repeated addition of the same number is expressed by multiplication in short. Hence, repeated addition of 2 five times is equal to 2 multiplied by 5. Thus, 3 × 6 = 18 that 3 multiplied by 6 is equal to 18, or 3 into 6 is equal to 18, or product of 3 and 6 is 18. 3 × 6 = 18 is called a multiplication fact
Visual Learning Bridge
Write a multiplication story for 3 × 6.

Equal Groups
Randy has 3 packs of 6 buttons. How many buttons does he have?
3 × 6 = 18
Randy has 18 buttons.
An Array
Eliza planted 6 lilies in each of 3 rows. How many lilies did she plant?

3 × 6 = 18
Eliza planted 18 lilies.
Bar Diagram
A rabbit eats an equal amount of carrots each day for 3 days. If the rabbit eats 6 carrots each day, how many carrots does it eat in all?

3 × 6 = 18
The rabbit eats 18 carrots.
Convince Me! Reasoning Write a multiplication story for 3 × 10 = ☐.
Answer:
Number of buns he eats in all = Number of buns each day Rakesh eats × Number of buns he eats each day
= 3 × 10
= 30.
Explanation:
A Rakesh eats an equal amount of buns each day for 3 days. If the Rakesh eats 10 buns each day, how many buns does he eat in all?
Number of buns each day Rakesh eats = 3.
Number of buns he eats each day = 10.
Number of buns he eats in all = Number of buns each day Rakesh eats × Number of buns he eats each day
= 3 × 10
= 30.
Another Example!
Seth has 15 fluid ounces of juice. Write and solve division . You can write a division stories about Seth and his juice. Use the equation story about “How many are 15 ÷ 3 = ?.

How many in each group?
Seth has 15 fluid ounces of juice. He pours an equal amount of juice into 3 containers. How many fluid ounces of juice are in each container?
15 ÷ 3 = 5 fluid ounces How many groups are there?
How many groups are there?
Seth has 15 fluid ounces of juice. He wants to pour 3 fluid ounces of juice into each container. How many containers does Seth need?
15 ÷ 3 = 5 containers
Guided Practice
Do You Understand?
Question 1.
When you write a division story, what two pieces of information do you need to include?
Answer:
For writing any division story, the two pieces of information required are total number n each part about what the problem is mandatory.
Explanation:
For writing any division story, the two pieces of information required are total number n each part about what the problem is mandatory.
Do You Know How?
In 2 and 3, write a story for the equation. Then solve.
Question 2.
3 × 5 = ________
Answer:
Mimi has 15 container of fluid ounces of juice. She wants to pour 3 fluid ounces of juice into each container. How many containers does Mimi has ?
3 × 5 = __15______.
Explanation:
Mimi has 5 container of fluid ounces of juice. She wants to pour 3 fluid ounces of juice into each container. How many containers does Mimi has ?
Number of fluid ounces of juice Mimi wants to pour into each container = 3.
Number of container Mimi has = 5.
Number of fluid ounces of juice Mimi has = Number of fluid ounces of juice Mimi wants to pour into each container × Number of container Mimi has
= 3 × 5
= 15.
Question 3.
8 ÷ 4 = ________
Answer:
Mia has 8 books. She puts books equally into 4 boxes. How many books are in each box?
8 ÷ 4 = ___2_____.
Explanation:
Mia has 8 books. She puts books equally into 4 boxes. How many books are in each box?
Number of books Mia has = 8.
Number of boxes she puts the books = 4.
Number of books are in each box = Number of books Mia has ÷ Number of boxes she puts the books
= 8 ÷ 4
= 2.
Independent Practice
In 4-7, write a story for each equation. Then solve.
Question 4.
7 × 3 = _______
Answer:
Mimi has 5 container of fluid ounces of oil. She wants to pour 3 fluid ounces of oil into each container. How many containers does Mimi has ?
7 × 3 = __21_____.
Explanation:
Mimi has 5 container of fluid ounces of oil. She wants to pour 3 fluid ounces of oil into each container. How many containers does Mimi has ?
Number of fluid ounces of oil Mimi wants to pour into each container = 3.
Number of container Mimi has = 7.
Number of fluid ounces of oil Mimi has = Number of fluid ounces of oil Mimi wants to pour into each container × Number of container Mimi has
= 3 × 7
= 21.
Question 5.
5 × 5 = ________
Answer:
Moni has 5 packets of chocolates. She wants to put 5 packets of chocolates into each container. How many containers does Moni has ?
5 × 5 = ___25_____.
Explanation:
Moni has 5 packets of chocolates. She wants to put 5 packets of chocolates into each container. How many containers does Moni has ?
Number of packets of chocolates Moni wants to put into each container = 5.
Number of container Mimi has = 5.
Number of packets of chocolates Moni has = Number of packets of chocolates Moni wants to put into each container × Number of container Moni has
= 5 × 5
= 25..
Question 6.
18 ÷ 3 = ________
I will write about 18 __________
I will put them in 3 equal groups.
Answer:
18 ÷ 3 = ___6_____.
Explanation:
18 ÷ 3 = ___6_____.
I will write about 18 biscuits packets.
I will put them in 3 equal groups.
Each group 6.
Question 7.
14 ÷ ____ = 2
I will write about 14
I will put them in groups of 2.
Answer:
14 ÷ _7___ = 2.
Explanation:
14 ÷ _7___ = 2.
I will write about 14 students.
I will put them in groups of 2.
Students each group 7.
Problem Solving
Question 8.
Reasoning Write a multiplication story about these pencils. Write an equation for your story.

Answer:
Number of pencils kept in each group = Total number of pencils ÷ Number of groups equally they are kept
= 8 ÷ 2
= 4.
Explanation:
Total number of pencils = 8.
Number of groups equally they are kept = 2.
Number of pencils kept in each group = Total number of pencils ÷ Number of groups equally they are kept
= 8 ÷ 2
= 4.
Question 9.
Write the fact family for each fact: 8 × 0, 8 × 1, 8 × 2, 8 × 3, 8 × 4, 8 × 5, 8 × 6, 8 × 7, 8 × 8, 8 × 9, and 8 × 10.
Answer:
Fact family:
8 × 0 = 0.
=> 0 × 8 = 0.
8 × 1 = 8.
=> 1 × 8 = 8.
8 × 2 = 16.
=> 8 × 2 = 16.
8 × 3 = 24.
=> 3 × 8 = 24.
8 × 4 = 32.
=> 4 × 8 = 32.
8 × 5 = 40.
=> 5 × 8 = 40.
8 × 6 = 48.
=> 6 × 8 = 48.
8 × 7 = 56.
=> 7 × 8 = 56.
8 × 8 = 64.
=> 8 × 8 = 64.
8 × 9 = 72.
=> 9 × 8 = 72.
8 × 10 = 80.
=> 10 × 8= 80.
Explanation:
8 × 0 = 0.
=> 0 × 8 = 0.
8 × 1 = 8.
=> 1 × 8 = 8.
8 × 2 = 16.
=> 8 × 2 = 16.
8 × 3 = 24.
=> 3 × 8 = 24.
8 × 4 = 32.
=> 4 × 8 = 32.
8 × 5 = 40.
=> 5 × 8 = 40.
8 × 6 = 48.
=> 6 × 8 = 48.
8 × 7 = 56.
=> 7 × 8 = 56.
8 × 8 = 64.
=> 8 × 8 = 64.
8 × 9 = 72.
=> 9 × 8 = 72.
8 × 10 = 80.
=> 10 × 8= 80.
Question 10.
A soccer team traveled to a game in 4 vans. Each van held 6 players. Two of the players are goalkeepers. How many of the players are not goalkeepers?
Answer:
Number of players are not goalkeepers = 22.
Explanation:
Number of vans soccer team traveled to a game = 4.
Number of players in each van = 6.
Number of players are goalkeepers = 2.
Number of soccer team players traveled to a game = Number of vans soccer team traveled to a game × Number of players in each van
= 4 × 6
= 24.
Number of players are not goalkeepers = Number of soccer team players traveled to a game – Number of players are goalkeepers
= 24 – 2
= 2.
Question 11.
Higher Order Thinking A group of 9 monarch butterflies is getting ready to migrate. Write a multiplication story involving this group. Explain what fact you are using and find the product.

Answer:
Number of wings and legs monarch butterfly has = 90.
Multiplication fact is used to find the product.
Explanation:
Number of bright orange wings each monarch butterfly has = 4.
Number of legs each monarch butterfly has = 6.
Total number of monarch butterfly = 9.
Number of wings and legs monarch butterfly has = Total number of monarch butterfly (Number of bright orange wings each monarch butterfly has + Number of legs each monarch butterfly has)
= 9(4 + 6)
= 9 × 10
= 90.
Assessment Practice
Question 12.
Mary writes the following story for 72 ÷ 9 = ?.
There are 72 marbles separated into 9 equal groups. How many marbles are in each group? Select the correct answer for Mary’s story.
A. 7 marbles
B. 8 marbles
C. 9 marbles
D. 10 marbles
Answer:
Number of marbles in each group = 8.
B. 8 marbles.
Explanation:
Total number of marbles = 72.
Number of groups = 9.
Number of marbles in each group = Total number of marbles ÷ Number of groups
= 72 ÷ 9
= 8.
Question 13.
Chris writes the following story for 4 × 10 = ?.
There are 4 pieces of wood set end to end to make a ramp. Each piece is 10 inches long. How long is the ramp? Select the correct answer for Chris’s story.
A. 4 inches
B. 10 inches
C. 20 inches
D. 40 inches
Answer:
Length of the ramp = 40 inches.
D. 40 inches.
Explanation:
Number of pieces of wood set end to end to make a ramp = 4.
Length of each piece = 10 inches.
Length of the ramp = Number of pieces of wood set end to end to make a ramp × Length of each piece
= 10 × 4
= 40 inches.
Lesson 5.6 Problem Solving
Look For and Use Structure
Solve & Share
Jacob has started the pattern below. Fill in the blanks to make correct equations and continue the pattern. Explain your thinking.
I can … use the structure of multiplication and division to compare expressions.
6 × 1 = 3 × 2
6 × 2 = 3 × 4
6 × 3 = 3 × ☐
6 × = 3 × ☐
☐ × ☐ = ☐ × ☐
Thinking Habits
Be a good thinker! These questions can help you.
- What patterns can I see and describe?
- How can I use the patterns to solve the problem?
- Can I see expressions and objects in different ways?

Look Back! Use Structure Jacob starts this new pattern. Fill in the blank to make the equation true. What do you notice about this pattern compared to the pattern above?
3 × 2 = 6 × 1
3 × 4 = 6 × 2
3 × ☐ = 6 × 3
Answer:
3 × 6 = 6 × 3 = 18.
It is noticed that from from equation to other there is a difference of 6.
Explanation:
3 × 2 = 6 × 1
=> 3 × 2 = 6 × 1 = 6.
3 × 4 = 6 × 2
=> 3 × 4 = 6 × 2 = 12.
3 × ?? = 6 × 3
=> 3 × ?? = 6 × 3 = 18
=> 3 × 6 = 6 × 3 = 18.
Essential Question
How Can You Use the Structure of Mathematics?
Answer:
The Structure of Mathematics helps in understanding the problem in order to find the correct solution to the problem.
Explanation:
In mathematics, a structure is a set endowed with some additional features on the set. Often, the additional features are attached or related to the set, so as to provide it with some additional meaning or significance.
Visual Learning Bridge
How can you tell without computing whether the symbol >, <, or = should be placed in each circle below?
1. 4 × 5 × 2 ○ 4 × 3 × 5
2. 6 × 7 ○ 7 × 6

What do I need to do to complete the task?
I need to compare the expressions. Instead of doing any calculations, I will look at the values of the factors in each expression.
How can I make use of structure to solve this problem?
I can
- think about properties i know.
- look for patterns and use them as needed.
Here’s my thinking
Some factors in the expressions are the same and some are different. I will use this to help me compare.
1. I know that I can group factors in any way, so I can rewrite one expression.
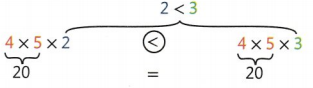
2. I see the factors are the same on both sides. I know this means the products are the same.
![]()
Convince Me! Use Structure Dario says, “I can find 9 × 0 < 3 × 1 without computing. I can think about properties that I know.” What could he mean?
Answer:
He could mean:
1. He know that he can group factors in any way, so he can rewrite one expression.
2. He sees the factors are the same on both sides. He knows this means the products are the same.
Explanation:
He could mean:
1. He know that he can group factors in any way, so he can rewrite one expression.
2. He sees the factors are the same on both sides. He knows this means the products are the same.
9 × 0 < 3 × 1
=> 9 × 0 = 0.
=> 3 × 1 = 3.
Hence, 9 × 0 < 3 × 1.
Guided Practice
Use Structure Hakeem and Nicole each have 48 stickers. Hakeem shared his stickers among 8 friends. Nicole shared her stickers among 6 friends. These expressions show how Hakeem and Nicole shared their stickers.

48 ÷ 8 ○ 48 ÷ 6
Question 1.
Look at the expressions. Explain how you can use what you see to compare without computing.
Answer:
48 ÷ 8 ○ 48 ÷ 6
=> 48 ÷ 8 < 48 ÷ 6.
We use this expression without computing in this way.
Explanation:
Total number of stickers Hakeem and Nicole each have = 48.
Number of Hakeem shared his stickers = 8.
Number of stickers each friend of Hakeem gets = Total number of stickers Hakeem and Nicole each have ÷ Number of Hakeem shared his stickers
= 48 ÷ 8
= 6.
Number of Nicole shared his stickers = 6.
Number of stickers each friend of Nicole gets = Total number of stickers Hakeem and Nicole each have ÷ Number of Nicole shared his stickers
= 48 ÷ 6
= 8.
Question 2.
Whose friends each received more stickers? Write the correct symbol >, <, or = in the circle above.
Answer:
Number of stickers each friend of Hakeem gets < Number of stickers each friend of Nicole gets
=> 6 < 8.
Explanation:
Number of stickers each friend of Hakeem gets = Total number of stickers Hakeem and Nicole each have ÷ Number of Hakeem shared his stickers
= 48 ÷ 8
= 6.
Number of stickers each friend of Nicole gets = Total number of stickers Hakeem and Nicole each have ÷ Number of Nicole shared his stickers
= 48 ÷ 6
= 8.
Independent Practice Use Structure Dan has saved $10 each week for 7 weeks. Misha has saved $7 each week for 9 weeks. These expressions show how they saved. 7 × $10 ○ 9 × $7
Answer:
Total amount Dan saved > Total amount Misha saved.
7 × $10 > 9 × $7.
Explanation:
Number of money Dan has saved each week = $10.
Number of weeks he saved = 7.
Total amount Dan saved = Number of money Dan has saved each week × Number of weeks he saved
= $10 × 7
= $70.
Number of money Misha has saved each week = $7.
Number of weeks she saved = 9.
Total amount Misha saved = Number of money Misha has saved each week × Number of weeks he saved
= $7 × 9
= $63.
Question 3. Look at the expressions. Explain how you can use what you see to compare without computing. Answer:
We can use what is seen to compare without computing is by this way: finding the total two sides and using the required symbol.
7 × $10 > 9 × $7.
Explanation:
7 × $10 ○ 9 × $7
=> $70 > $63.
Question 4. Who saved more money? Write the correct symbol >, <, or = in the circle above.
Answer:
Total amount Dan saved is more than the total amount Misha saved.
7 × $10 > 9 × $7.
Explanation:
Total amount Dan saved = $70.
Total amount Misha saved = $63.
7 × $10 > 9 × $7.
Question 5.
Can you use the same symbol you wrote in Exercise 4 to compare $10 × 7 and $7 × 9? Explain.
Answer:
Yes, we can the same symbol written in Exercise 4 to compare $10 × 7 and $7 × 9.
$10 × 7 > $7 × 9.
Explanation:
$10 × 7 and $7 × 9
$10 × 7 = $70.
$7 × 9 = $63.
Problem Solving
Performance Task
Selling Necklaces Trina wants to find the least expensive way to buy 24 necklaces. She wants to buy only the same type of packages. She has $48. The table shows the number of necklaces in a package and the cost of each package.
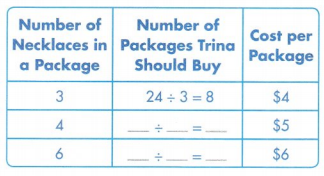
Question 6.
Model with Math Complete the table to find the number of packages Trina would need to buy.
Answer:

Explanation:
Number of packages Trina want to buy = 24.

Question 7.
Use Structure Trina can use 8 × $4 to find the cost of enough $4 packages. Write a similar expression that shows a way to find how much it costs Trina to buy enough $5 packages.
Answer:
Total cost needed to buy for Trina = $120.
Explanation:
Number of packages Trina want to buy = 24.
Cost of each package = $5.
Total cost needed to buy for Trina = Number of packages Trina want to buy × Cost of each package
= 24 × $5
= $120.
Write a similar expression that shows a way to find how much it costs Trina to buy enough $6 packages.

Answer:
Total cost needed to buy for Trina = $144.
Explanation:
Number of packages Trina want to buy = 24.
Cost of each package = $6.
Total cost needed to buy for Trina = Number of packages Trina want to buy × Cost of each package
= 24 × $6
= $144.
Question 8.
Make Sense and Persevere Compare the cost of buying the $5 packages to the $6 packages. Which package type costs less if Trina wants to buy 24 necklaces? Explain how to solve without computing.
Answer:
Total cost needed to buy enough $5 packages for Trina is less than the Total cost needed to buy enough $6 packages for Trina
$120 < $144.
Explanation:
Total cost needed to buy enough $5 packages for Trina = $120.
Total cost needed to buy enough $6 packages for Trina = $144.
=> $120 < $144.
Question 9.
Construct Arguments Compare the costs of buying the $4 packages to the $6 packages. Which package type costs less if Trina wants to buy 24 necklaces? Explain how to solve without computing.
Answer:
Total cost needed to buy enough $4 packages for Trina is less than the Total cost needed to buy enough $6 packages for Trina
$96< $144.
Explanation:
Number of packages Trina want to buy = 24.
Cost of each package = $4.
Total cost needed to buy for Trina = Number of packages Trina want to buy × Cost of each package
= 24 × $4
= $96.
Number of packages Trina want to buy = 24.
Cost of each package = $6.
Total cost needed to buy for Trina = Number of packages Trina want to buy × Cost of each package
= 24 × $6
= $144.
Topic 5 Fluency Practice Activity
Point & Tally
Find a partner. Get paper and a pencil. Each partner chooses a different color: light blue or dark blue.
Partner 1 and Partner 2 each point to a black number at the same time. Both partners multiply those numbers.
If the answer is on your color, you get a tally mark. Partners then write the remaining facts in the fact family. Work until one partner has seven tally marks.
I can … multiply and divide within 100.

Answer:
9 × 7 = 63.
5 × 4 = 20.
6 × 5 = 30.

Explanation:
9 × 7 = 63.
5 × 4 = 20.
6 × 5 = 30.
8 × 6 = 48.
4 × 9 = 36.
Three are correct , tally marks are three.
Topic 5 Vocabulary Review
Understand Vocabulary
For each of these terms, give an example and a non-example.
Word List
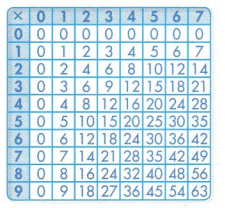
- column
- equation
- even
- fact family
- odd
- row

Write always, sometimes, or never.
Answer:

Explanation:

Question 5.
An even number can __________ be divided by 2 with none left over.
Answer:
An even number can ____300______ be divided by 2 with none left over.
Explanation:
An even number can be divided by 2 with none left over:
all multiples of 2 number.
Like : 4, 50, 100, 3060, so on….
Question 6.
A fact family _________ has odd numbers.
Answer:
A fact family ____odd_____ has odd numbers.
Explanation:
A fact family odd has odd numbers.
Question 7.
An array _________ has the same number of rows and columns.
Answer:
An array ___square______ has the same number of rows and columns.
Explanation:
An array square has the same number of rows and columns.
Question 8.
The product of an odd number times an odd number is ____________ an even number.
Answer:
The product of an odd number times an odd number is ____odd not________ an even number.
Explanation:
The product of an odd number times an odd number is odd not an even number.
Use Vocabulary in Writing
Question 9.
Explain the pattern in the green squares. Use at least 2 terms from the Word List in your explanation.

Answer:
The pattern in the green squares:
odd × odd = odd number.
Explanation:
The pattern in the green squares:
1 × 1 = 1.
1 × 3 = 3.
1 × 5 = 5.
3 × 1 = 3.
3 × 3 = 9.
3 × 5 = 15.
1 × 5 = 5.
3 × 5 = 15
5 × 5 = 25.
Topic 5 Reteaching
Set A pages 169-172
You can see patterns in a multiplication table.

Remember that properties can help to explain patterns.
In 1 and 2, use the multiplication table to answer the questions.
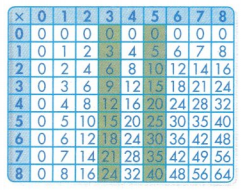
Question 1.
Find the column that has products that are the sum of the green shaded numbers in each row. Shade this column.
Answer:

Explanation:
Column shaded in purple color has the products that are the sum of the green shaded numbers in each row.
Question 2.
Explain why this pattern is true.
Answer:
Yes, the pattern is true because the sum of the two green color numbers is equal to the number shaded in the same column.
Explanation:
Numbers in green color:
1 + 6 = 7.
2 + 12 = 14.
Set B pages 173-176
Use a multiplication table to find 20 ÷ 4.

Find 4 in the first column of the table.
Follow the 4s row until you come to 20.
Then look to the top of that column to find the missing factor: 5. 20 ÷ 4 = 5.
Remember how multiplication and division are related
In 1-12, use the multiplication table to find each product or quotient.
Question 1.
2 × 7 = ______
Answer:
2 × 7 = __14____.
Explanation:
2 × 7 = 14. (product)
Question 2.
5 × 8 = ________
Answer:
5 × 8 = ___40_____.
Explanation:
5 × 8 = 40.(product)
Question 3.
2 × 10 = _______
Answer:
2 × 10 = ___20____.
Explanation:
2 × 10 = 20.(product)
Question 4.
5 × 4 = _______
Answer:
5 × 4 = __20_____.
Explanation:
5 × 4 = 20.(product)
Question 5.
3 × 5 = _____
Answer:
3 × 5 = __15___.
Explanation:
3 × 5 = 15.(product)
Question 6.
6 × 5 = _______
Answer:
6 × 5 = ___30____.
Explanation:
6 × 5 = 30.(product)
Question 7.
63 ÷ 9 = ______
Answer:
63 ÷ 9 = ___7___.(quotient)
Explanation:
63 ÷ 9 = 7.
Question 8.
56 ÷ 8 = _______
Answer:
56 ÷ 8 = __7_____.
Explanation:
56 ÷ 8 = 7.(quotient)
Question 9.
45 ÷ 9 = _______
Answer:
45 ÷ 9 = __5_____.
Explanation:
45 ÷ 9 = 5.(quotient)
Question 10.
40 ÷ 8 = _______
Answer:
40 ÷ 8 = ___5____.
Explanation:
40 ÷ 8 = 5.(quotient)
Question 11.
35 ÷ 7 = _______
Answer:
35 ÷ 7 = __5_____.
Explanation:
35 ÷ 7 = 5.(quotient)
Question 12.
36 ÷ 6 = ______
Answer:
36 ÷ 6 = ___6___.
Explanation:
36 ÷ 6 = 6.(quotient)
Set B, continued pages 173-176
You can use basic facts and properties to find missing numbers in a multiplication table.
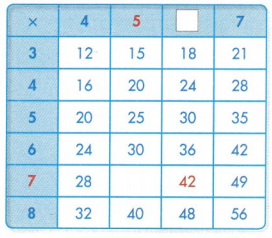
Use multiplication or division to find missing factors.
42 ÷ 7 = 6, so 7 × 6 = 42
Use strategies to find products.
3 × 5 = 15 4 × 5 = 20
5 × 5 = 25 6 × 5 = 30
So, 7 × 5 = 35
Remember that you can use strategies and reasoning to find missing numbers.
Use multiplication and division strategies to complete the multiplication table. Show your work.
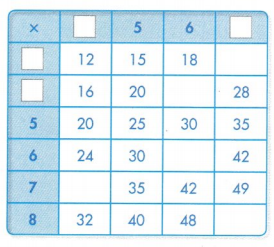
Answer:
Explanation:
? × ? = 12.
=> 3 × 4 = 12.
3 × ? = ??.
=> 3 × 7 = 21.
?? × 6 = 24.
=> 4 × 6 = 24.
6 × ?? = 24.
=> 6 × 4 = 24.
7 × ?? = 28.
=> 7 × 4 = 28.
8 × ?? = ??
=> 8 × 7 = 56.
Set C pages 177-180
Find 4 × 7.

You can use skip counting: 7, 14, 21, 28
You can use known facts:
2 × 7 = 14
4 × 7 = (2 × 7) + (2 × 7)
4 × 7 = 14 + 14 = 28
Remember that you can use patterns, known facts, or skip counting to find products.
In 1-8, use strategies to find the product.
Question 1.
5 × 9 = ________
Answer:
5 × 9 = ___45_____. (product)
Explanation:
5 × 9 = (3 × 9) + (2 × 9)
5 × 9 = 27 + 18
5 × 9 = 45.
Question 2.
8 × 10 = _______
Answer:
8 × 10 = __80_____. (product)
Explanation:
8 × 10 = (4 × 10) + (4 × 10)
8 × 10 = 40 + 40
8 × 10 = 80.
Question 3.
4 × 10 = ________
Answer:
4 × 10 = ___40_____.
Explanation:
4 × 10 = (3 × 10) + (1 × 10)
4 × 10 = 30 + 10
4 × 10 = 40.
Question 4.
9 × 8 = ________
Answer:
9 × 8 = ___72_____.
Explanation:
9 × 8 = (5 × 8) + (4 × 8)
9 × 8 = 40 + 32
9 × 8 = 72.
Question 5.
6 × 9 = _______
Answer:
6 × 9 = ___54____.
Explanation:
6 × 9 = (3 × 9) + (3 × 9)
6 × 9 = 27 + 27
6 × 9 = 54.
Question 6.
7 × 3 = _______
Answer:
7 × 3 = __21_____.
Explanation:
7 × 3 = (4 × 3) + (3 × 3)
7 × 3 = 12 + 9
7 × 3 = 21.
Question 7.
6 × 5 = ______
Answer:
6 × 5 = __30____.
Explanation:
6 × 5 = (3 × 5) + (3 × 5)
6 × 5 = 15 + 15
6 × 5 = 30.
Question 8.
4 × 9 = _______
Answer:
4 × 9 = ___36____.
Explanation:
4 × 9 = (2 × 9) + (2 × 9)
4 × 9 = 18 + 18
4 × 9 = 36.
Set D pages 181-184
You can solve word problems using multiplication and division.
Aaron has 49 books. His bookcase has 7 shelves. He wants to display an equal number of books on each shelf. How many books can Aaron put on each shelf?
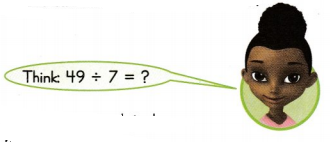
You can use a related multiplication fact:
7 × 7 = 49
49 ÷ 7 = 7
Aaron can put 7 books on each shelf.
Remember that multiplication and division use equal groups.
Solve each problem. Show your work.
Question 1.
Oksana’s dad has 36 batteries in his desk drawer. The batteries come in packs of 4. How many packs of batteries does he have?
Answer:
Number of packs of batteries he has = 9.
Explanation:
Number of batteries in his desk drawer Oksana’s dad has = 36.
Number of packs batteries came in = 4.
Number of packs of batteries he has = Number of batteries in his desk drawer Oksana’s dad has ÷ Number of packs batteries came in
= 36 ÷ 4
= 9.
Question 2.
Every time Lee wins the ring toss at the carnival, he gets 3 prize tickets. Lee needs to win the ring toss 9 times to have enough prize tickets for 1 toy. How many prize tickets does Lee need for 2 toys?
Answer:
Number of prize tickets Lee needs to win for 2 toys = 27.
Explanation:
Number of prize tickets Lee gets = 3.
Number of times Lee needs to win to get ring toss to have enough prize tickets for 1 toy = 9.
Number of prize tickets Lee needs to win for 2 toys = Number of prize tickets Lee gets × Number of times Lee needs to win to get ring toss to have enough prize tickets for 1 toy
= 3 × 9
= 27.
Set E pages 185–188
Write a multiplication story for 4 × 7.
You can think of multiplication as equal groups.
Tim has 4 bunches of flowers. Each bunch has 7 flowers. How many flowers does Tim have?

Tim has 28 flowers.
Remember that rows and columns can also represent multiplication.
Write a multiplication story for each equation. Then solve.
Question 1.
3 × 9 = _______
Answer:
Number of nuts Mia has = Number of packets of nuts Mia has × Number of nuts in each packet
=> 3 × 9 = ___27____.
Explanation:
Mia has 3 packets of nuts. Each packet has 9 nuts. How many nuts does Mia have?
Number of packets of nuts Mia has = 3.
Number of nuts in each packet = 9.
Number of nuts Mia has = Number of packets of nuts Mia has × Number of nuts in each packet
= 3 × 9
= 27.
Question 2.
5 × 6 = ________
Answer:
Number of oranges John has = Number of packets of oranges John has × Number of oranges in each packet
=> 5 × 6 = ___30___.
Explanation:
John has 5 packets of oranges. Each packet has 6 oranges. How many oranges does John have?
Number of packets of oranges John has = 5.
Number of oranges in each packet = 6.
Number of oranges John has = Number of packets of oranges John has × Number of oranges in each packet
= 5 × 6
= 30.
Set E, continued pages 185-188
Write a division story for 20 ÷ 5.
If 20 children form 5 equal teams, how many children are on each team?
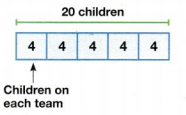
20 ÷ 5 = 4
There are 4 children on each team.
Remember that division stories can ask for the number in each group, or the number of equal groups.
Write a division story for each equation. Then solve.
Question 1.
60 ÷ 10 = _______
Answer:
Number of buses used = Number of students in the school ÷ Number of students in each bus
=> 60 ÷ 10 = 6.
Explanation:
In a school, there are 60 students. 10 Students go in each bus to picnic. How many buses are used for picnic.
Number of students in the school = 60.
Number of students in each bus = 10.
Number of buses used = Number of students in the school ÷ Number of students in each bus
= 60 ÷ 10
= 6.
Question 2.
32 ÷ 4 = _______
Answer:
Number of students in each bus = Number of students in the school ÷ Number of buses used
=> 32 ÷ 4 = 8.
Explanation:
In a school, there are 32 students. 4 buses are used to go the zoo. How many Students go in each bus to zoo.
Number of students in the school = 32.
Number of buses used = 4.
Number of students in each bus = Number of students in the school ÷ Number of buses used
= 32 ÷ 4
= 8.
Set F pages 189-192
Think about these questions to help you look for and make use of structure.
Thinking Habits
- What patterns can I see and describe?
- How can I use the patterns to solve the problem?
- Can I see expressions and objects in different ways?

Remember that properties can help you understand patterns.
Leroy earns $7 each hour that he works. He works for 8 hours. Rebecca earns $8 each hour that she works. She works for 7 hours. These expressions show the money they earned.
8 × $7 ○ 7 × $8
Question 1.
Look at the expressions. Explain how you can use what you see to compare without computing.
Answer:
Total amount earned by Leroy = $7 × 8 = $56.
Total amount earned by Rebecca = $8 × 7 = $56.
8 × $7 = 7 × $8
= $56.
Explanation:
Amount earned by Leroy for each hour = $7.
Number of hours Leroy works = 8.
Total amount earned by Leroy = Amount earned by Leroy for each hour × Number of hours Leroy works
= $7 × 8
= $56.
Amount earned by Rebecca for each hour = $8.
Number of hours Rebecca works = 7.
Total amount earned by Rebecca = Amount earned by Rebecca for each hour × Number of hours Rebecca works
= $8 × 7
= $56.
Question 2.
Who earned more money? Write the correct symbol >, <, or = in the circle above.
Answer:
Both the total amount earned by Leroy and the total amount earned by Rebecca are the same amount of $56.
=> 8 × $7 = 7 × $8
=> $56.
Explanation:
Total amount earned by Leroy = $7 × 8 = $56.
Total amount earned by Rebecca = $8 × 7 = $56.
Both Leroy and Rebecca earns the same amount $56.
Topic 5 Assessment Practice
Question 1.
Find 48 ÷ 6.
Answer:
48 ÷ 6= 8.
Explanation:
48 ÷ 6 = 8.
Question 2.
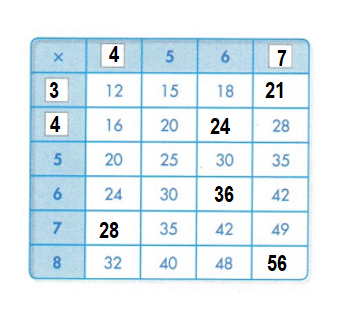
A. Fill in the missing factors and products in the multiplication table below.
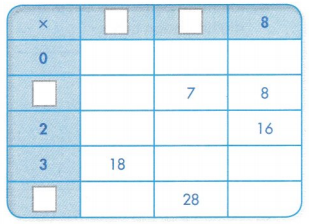
Answer:

Explanation:
0 × 6 = 0.
0 × 7 = 0.
0 × 8 = 0.
1 × 6 = 6.
2 × 6 = 12.
2 × 7 = 14.
3 × 7 = 21.
3 × 8 = 24.
4 × 6 = 24.
4 × 8 = 32.
B. What pattern do you see in the first row of products in the table? Explain why this pattern is true.
Answer:
The first row of products in the table is zero because number multiplied by zero, results in zero itself.
Explanation:
The first row of products in the table is zero because number multiplied by zero, results in zero itself.
0 × 6 = 0.
0 × 7 = 0.
0 × 8 = 0.
Question 3.
Find 45 ÷ 5. Draw a bar diagram to represent the problem.
Answer:
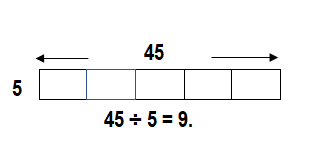
Explanation:
45 ÷ 5 = 9.
Question 4.
Find the product.
5 × 7
A. 28
B. 30
C. 35
D. 42
Answer:
5 × 7 = 35.
C. 35.
Explanation:
5 × 7 = (2 × 7) + (3 × 7)
5 × 7 = 14 + 21
5 × 7 = 35. (product)
Question 5.
Find the product.
6 × 3 = ☐
Answer:
6 × 3 = 18.
Explanation:
6 × 3 = (3 × 3) + (3 × 3)
6 × 3 = 9 + 9
6 × 3 = 18. (product)
Question 6.
Which of the following strategies can help you solve 4 × 6? Select all that apply.
☐ (6 × 6) + (6 × 6)
☐ (4 × 3) + (4 × 3)
☐ (5 × 5) + (4 × 1)
☐ (5 × 4) + (1 × 4)
☐ (2 × 4) + (2 × 6)
Answer:
(4 × 3) + (4 × 3) and (5 × 4) + (1 × 4) is applied strategy helps you to solve 4 × 6.
Explanation:
4 × 6 = (2 × 6) + (2 × 6)
4 × 6 = 12 + 12
4 × 6 = 24.
or
4 × 6 = (4 × 3) + (4 × 3)
4 × 6 = 12 + 12
4 × 6 = 24.
or
4 × 6 = (5 × 4) + (1 × 4)
4 × 6 = 20+ 4
4 × 6 = 24.
Question 7.
What number is missing from this multiplication table?

A. 8
B. 9
C. 11
D. 12
Answer:
D. 12
Explanation:
2 × 6 = 12.
Question 8.
Select the correct product or quotient for each equation.
Answer:
Explanation:
54 ÷ 6 = 9.
8 × 7 = 56.
49 ÷ 7 = 7.
6 × 6 = 36.
Question 9.
Some squares are shaded orange to show a pattern in the multiplication table.
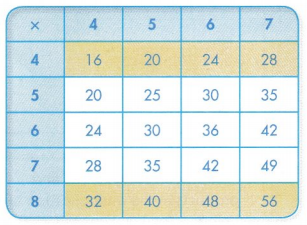
A. Identify a pattern shown in the multiplication table.
Answer:
Orange colored are the multiples of 4 number and 8 number shown in the multiplication table.
Explanation:
The pattern shown in the multiplication table orange colored are the multiples of 4 number and 8 number.
B. Explain why this pattern is true.
Answer:
This pattern is true because they show the multiples of 4, 5, 6, 7, and 8 numbers.
Explanation:
Multiplication table shows he multiples of 4, 5, 6, 7, and 8 numbers.
Question 10.
Divide.
70 ÷ 7
Answer:
70 ÷ 7 = 10.
Explanation:
70 ÷ 7 = 10.
Question 11.
Which division equation could be used to solve 8 × ? = 32?
A. 32 ÷ 7 = ?
B. 32 ÷ 2 = ?
C. 32 ÷ 8 = ?
D. 8 ÷ ? = 32
Answer:
8 × ? = 32
=> 8 × 4 = 32.
C. 32 ÷ 8 = ? division equation could be used to solve 8 × ? = 32
Explanation:
8 × ? = 32
=> ? = 32 ÷ 8
=> ? = 4.
Question 12.
Twelve can be evenly divided by which of the following numbers? Select all that apply.
☐ 9
☐ 3
☐ 5
☐ 4
☐ 7
Answer:
Twelve can be evenly divided by the 2, 3, 4, 6 numbers:
3 and 4 numbers are applied to divide 12 number evenly.
Explanation:
Twelve can be evenly divided by the following numbers:
12 ÷ 2 = 6.
12 ÷ 3 = 4.
12 ÷ 4 = 3.
12 ÷ 6 = 2.
Question 13.
What is the product of 9 and 3? Write an equation to solve the problem.
Answer:
Equation:
9 × 3 = 27.
Explanation:
Equation:
9 × 3 = 27. (product)
Question 14.
Look at these two expressions.
40 ÷ 4 40 ÷ 8
A. Explain how you can compare the expressions without computing.
Answer:
We can compare the expressions without computing like this finding the answer.
40 ÷ 4 > 40 ÷ 8.
Explanation:
40 ÷ 4 = 10.
40 ÷ 8 = 5.
B. Check your answer by computing both quotients.
Answer:
40 ÷ 4 = 10. (quotient)
40 ÷ 8 = 5. (quotient)
Explanation:
40 ÷ 4 = 10. (quotient)
40 ÷ 8 = 5. (quotient)
Question 15.
Which shows a way to solve 5 × 5?
A. Skip count 5 times by numbers that end in 5: 5, 15, 25, 35, 45
B. Use the Distributive Property: (4 × 5) + (1 × 5)
C. Look at a multiplication table: Find the 5s row. Go across until you find 5. The product is the number at the top of that column, 1.
D. Use repeated addition: 5 + 5 + 5 + 5
Answer:
B. Use the Distributive Property: (4 × 5) + (1 × 5)
Explanation:
5 × 5 = (4 × 5) + (1 × 5)
5 × 5 = 20 + 5
5 × 5 = 25.
Question 16.
Roberta is planting flowers in her garden. She plants 9 rows of flowers. There are 7 flowers in each row. How many flowers does does she plant in all? Write an equation to solve the problem.
Answer:
Number of flowers she plants in all = Number of rows of flowers Roberta plants × Number of flowers in each row
= 9 × 7
= 63.
Explanation:
Number of rows of flowers Roberta plants = 9.
Number of flowers in each row = 7.
Number of flowers she plants in all = Number of rows of flowers Roberta plants × Number of flowers in each row
= 9 × 7
= 63.
Question 17.
Multiply.
7 × 2
Answer:
7 × 2 = 24.
Explanation:
7 × 2 = (1 × 2) + (6 × 2)
7 × 2 = 2 + 12
7 × 2 = 14.
Question 18.
Look at the multiplication table below.
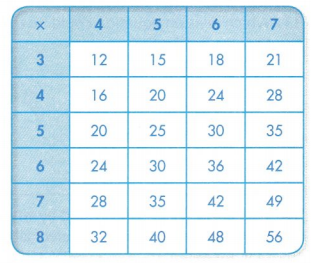
A. Shade the products in the 5s column of the table. What pattern do you see there?
Answer:
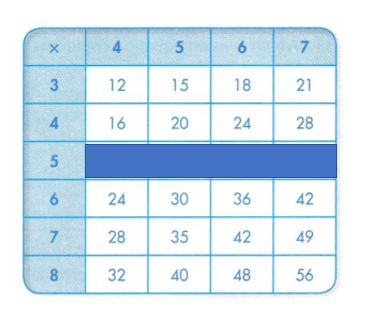
Explanation:
The products in the 5s column of the table are 20, 25, 30, 35.
5 × 4 = 20.
5 × 5 = 25.
5 × 6 = 30.
5 × 7 = 35.
B. Explain the pattern you found.
Answer:
The pattern found is difference is 5 in between the numbers and are the multiples of 5 number.
Explanation:
The pattern found is difference is 5 in between the numbers and they are multiples of 5 number.
Topic 5 Performance Task
Photograph Gallery Riley is setting up a display. She is hanging photographs on two walls. The photographs are hung in arrays. Riley has to decide how to arrange the photographs. She makes tables to decide which arrangement to use.
Question 1.
Use the Left Wall table to answer the questions.

Part A
Which arrangement on the left wall has the most photographs?
Answer:
Left wall B arrangement has the most photographs of 27.
Explanation:
Left wall arrangement :
A = Rows × Columns
= 3 × 7
= 21.
B = Rows × Columns
= 3 × 9
= 27.
C = Rows × Columns
= 7 × 2
= 14.
D = Rows × Columns
= 8 × 3
= 24.
Part B
Explain how Riley could find the answer to Part A without calculating the size of each arrangement.
Answer:
Riley could find the answer to Part A without calculating the size of each arrangement by checking the highest columns or rows size.
Explanation:
Riley could find the answer to Part A without calculating the size of each arrangement by checking the highest columns or rows size.
Use the Right Wall table to answer Exercises 2 and 3.
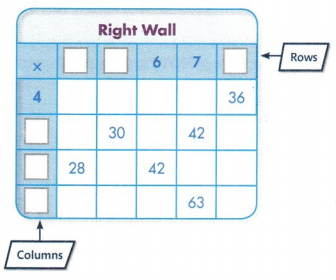
Question 2.
Fill in the missing columns, rows, and numbers of photographs so that Riley’s table is complete.
Answer:
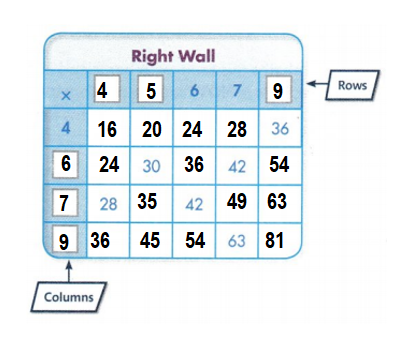
Explanation:
4 × ? = 36.
=> 4 × 9 = 36.
7 × ? = 42
=> 7 × 6 = 42.
6 × ? = 42.
=> 6 × 7 = 42.
7 × ? = 63.
=> 7 × 9 = 63.
6 × ? = 30.
=> 6 × 5 = 30.
4 × ? = ??
=> 4 × 4 = 16.
=> 6 × 4 = 24.
=> 6 × 6 = 36.
=> 6 × 9 = 54.
7 × 4 = 28.
=> 7 × 5 = 35.
=> 7 × 6 = 42.
=> 7 × 7 = 49.
=> 7 × 9 = 63.
9 × 4 = 36.
=> 9 × 5 = 45.
=> 9 × 6 = 54.
=> 9 × 7 = 63.
=> 9 × 9 = 81.
Question 3.
Riley has 42 on her table twice. Is this reasonable? Explain why or why not.
Answer:
Riley has 42 on her table twice and it is reasonable because rows and columns count is not same 6 × 7 = 42 and 7 × 6 = 42.
Explanation:

Rows × Columns
6 × 7 = 42.
7 × 6 = 42.
Use the Right Wall table to answer Exercises 4-6.
Question 4.
Some of the photographers were men, and some were women. Riley wants the number of photographs taken by men to be equal to the number of photographs taken by women. Shade the squares in the table to show the arrangements that let Riley do this. Explain what pattern you find.
Answer:
The pattern followed is doubling the numbers.

Explanation:
Riley wants the number of photographs taken by men to be equal to the number of photographs taken by women:
4 × 4 = 16.
6 × 6 = 36.
7 × 7 = 49.
9 × 9 = 81.
Question 5.
Riley shares this table with her friend Leo. Leo is working on a different project. He is NOT hanging photographs. For what project could Leo use the table? Explain what 7 × 4 means for Leo’s project.
Answer:
7 × 4 means for Leo’s project is 28 photographs .
Explanation:
7 × 4 = (3 × 4) + (4 × 4)
7 × 4 = 12 + 16
7 × 4 = 28.
Question 6.
Riley also shares this table with her mother. Riley’s mother is working on a different project. She is also NOT hanging photographs. For what project could Riley’s mother use the table? Explain what 30 ÷ 6 means for Riley’s mother’s project.
Answer:
30 ÷ 6 means for Riley’s mother’s project is 5 photographs.
Explanation:
30 ÷ 6 = 5Go through the enVision Math Common Core Grade 3 Answer Key Topic 5 Fluently Multiply and Divide within 100 regularly and improve your accuracy in solving questions..

