Go through the enVision Math Common Core Grade 3 Answer Key Topic 7 Represent and Interpret Data regularly and improve your accuracy in solving questions.
enVision Math Common Core 3rd Grade Answers Key Topic 7 Represent and Interpret Data
Essential Question:
How can data be represented, analyzed, and interpreted?

enVision STEM Project: Seasons
Do Research Use the Internet or other sources to find information about patterns of temperature in the different seasons where you live. Include information about the average monthly temperatures and the record low and high temperatures.
Journal: Write a Report Include what you found. Also in your report:
- For one week, record the daily high and low temperatures in the area where you live. Make a graph displaying this information.
- Find the difference between the highest and lowest daily temperatures from your graph.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
• equal groups
• multiples
• multiplication
• number line
Question 1.
_______ have the same number of items.
Answer:
_Equal Groups__ have the same number of items.
Question 2.
A ________ can be used to help compare numbers.
Answer:
A _multiples_ can be used to help compare numbers.
Question 3.
________ is used to find a total when joining equal groups.
Answer:
_Multiplication__ is used to find a total when joining equal groups.
Multiplication
In 4 and 5, complete the equation.
Question 4.
5 × 3 = _______
Answer:
5 × 3 = 15.
Explanation:
When we multiply 5 with 3 times we get 15.
When you add 5 three times we get 15.
5 + 5 + 5 = 15.
Question 5.
3 × _______ = 21
Answer:
3 × 7 = 21
Explanation:
Given
one multiple and the product.
one multiple = 3
Product = 21
To find the other multiple we divide product by multiple
21 ÷ 3 = 7
3 × 7 = 21.
Question 6.
Make a bar diagram to represent 4 × 6.
Answer:

Multiplication on the Number Line
Question 7.
Ed bought 2 bags of grapefruit. There are 6 grapefruit in each bag. How many grapefruit did he buy? Draw jumps on the number line to find the answer.

Answer:

Question 8.
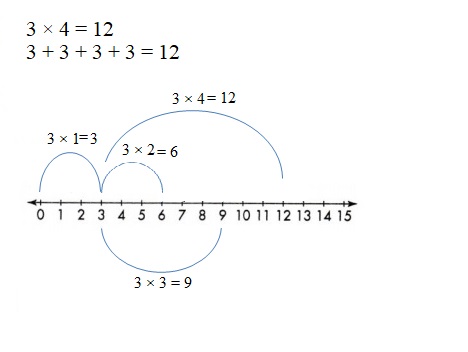
Show the multiplication fact 3 x 4 on the number line. Write the product.

Answer:
Finding Area
Question 9.
Find the area of the rectangle.
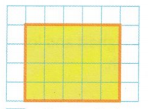
☐ = 1 square inch
Answer:
Number of squares = 4 × 5 = 20 squares.
Area = 20 square inches.
Pick a Project
PROJECT 7A
How is a book printed?
Project: Collect Data and Create Picture Graphs

PROJECT 7B
Would you like to live in a city?
Project: Make a Bar Graph About Cities and Towns

PROJECT 7C
What is your favorite animal?
Project: Develop a Picture Graph About Animals

3-ACT MATH PREVIEW
Math Modeling
Swings and Slides

+ `1
Solve & Share
Students in Jorge’s class took a survey of their favorite cereals and made this graph to show the results. Name at least three facts about the information in the graph.
I can … use picture graphs and bar graphs to answer questions about data sets.

Look Back! What do the two different symbols on the graph stand for?
Essential Question
How Can You Read Picture Graphs?
Visual Learning Bridge
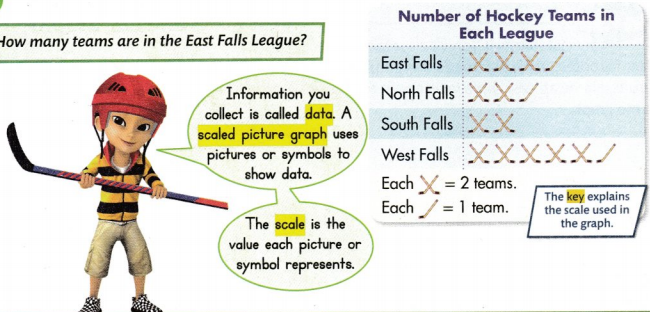
Use the key
Look at the data for East Falls League.
There are 3 ![]() and 1
and 1 ![]() .
.
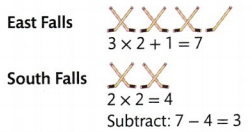
The 3 ![]() represent 3 × 2 = 6 teams.
represent 3 × 2 = 6 teams.
The 1 ![]() represents 1 × 1 = 1 team.
represents 1 × 1 = 1 team.
6 + 1 = 7
There are 7 teams in the East Falls League.
How many more teams does the East Falls League have than the South Falls League?
Use the picture graph to write equations and compare the two rows.
The East Falls League has 3 more teams than the South Falls League.
Convince Me! Be Precise Tell something about each league you can find out from the picture graph.

Another Example!
A scaled bar graph uses bars to represent and compare information. This bar graph shows the number of goals scored by different players on a hockey team. The scale shows the units used.
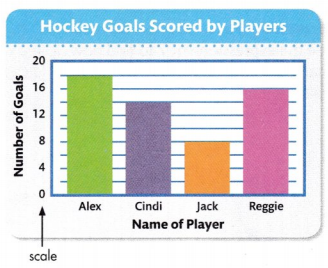
On this bar graph, each horizontal grid line represents two units. Every other grid line is labeled: 0, 4, 8, and so on. For example, the line halfway between 4 and 8 represents 6 goals.
Guided Practice
Do You Understand?
In 1 and 2, use the bar graph above.
Question 1.
How many goals in all did Alex and Reggie score?
Answer:

Number of goals Alex scored = 18 goals.
Number of goals Reggie scored = 16 goals.
Total number of goals both scored in all = 18 + 16 = 34 goals.
Do You Know How?
Question 2.
Explain how to find how many fewer goals Cindi scored than Alex.
Answer:
Number of goals Alex scored = 18 goals
Number of goals Cindi scored = 14 goals
Number of fewer goals Cindi scored than Alex = 18 – 14 = 4 goals.
Cindi scored 4 fewer goals than Alex.
Independent Practice
In 3-5, use the picture graph.
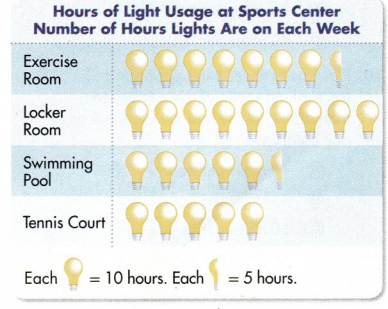
Question 3.
Which area has lights on for exactly 50 hours each week?
Answer:
full bulb = 10 hours Half bulb = 5 hours
Number of hours of light on each week in Exercise room = 7 full bulb and 1 half bulb
(7 × 10 hours) + (1 × 5 hours) = 70 + 5 = 75 hours.
Number of hours of light on each week in Locker room = 9 full bulbs
9 × 10 hours = 90 hours
Number of hours of light on each week in Swimming Pool = 5 full and 1 half
(5 × 10 hours) + (1 × 5 hours) = 50 + 5 = 55 hours.
Number of hours of light on each week in Tennis Court = 5 full
5 × 10 hours = 50 hours.
Tennis Court area has lights on for exactly 50 hours each week
Question 4.
What does the half bulb in the data for the exercise room represent?
Answer:
Half bulb in the data for exercise room represents 5 hours.
Question 5.
In one week, how many more hours are lights on in the exercise room than at the swimming pool?
Answer:
Number of hours of light on each week in Exercise room = 7 full bulb and 1 half bulb
(7 × 10 hours) + (1 × 5 hours) = 70 + 5 = 75 hours.
Number of hours of light on each week in Swimming Pool = 5 full and 1 half
(5 × 10 hours) + (1 × 5 hours) = 50 + 5 = 55 hours.
Number of more hours of light on in the exercise room than the swimming Pool = 75 hours – 55 hours = 20 hours.
20 hours of more light on in the exercise room than the swimming Pool
Problem Solving
In 6-8, use the picture graph.

Question 6.
Reasoning For which days can you use the expression 9 x 7 to find how many points were scored?
Answer:

From the data above
Number of points scored by a football team on October 3 = 9 × 7 = 63 points
Number of points scored by a football team on October 10 = 9 × 7 = 63 points
Number of points scored by a football team on October 17 = 6 × 7 = 42 points
Number of points scored by a football team on October 24 = 7 × 7 = 49 points
October 3 and October 10 days can use the expression 9 x 7 to find number of points scored.
On both the days the team scored 9 × 7 points = 63 points.
Question 7.
On which days did the football team score fewer than 50 points?
Answer:
Number of points scored by a football team on October 17 = 6 × 7 = 42 points
Number of points scored by a football team on October 24 = 7 × 7 = 49 points
On October 17 and October 24 the football team scored points fewer than 50.
Question 8.
Higher Order Thinking How many more points were scored on October 10 and 24 combined than on October 3 and 17?
Answer:
Number of points scored by a football team on October 3 = 9 × 7 = 63 points
Number of points scored by a football team on October 17 = 6 × 7 = 42 points
Number of points scored on October 3 and October 17 combined = 63 + 42 = 105 points.
Number of points scored by a football team on October 10 = 9 × 7 = 63 points
Number of points scored by a football team on October 24 = 7 × 7 = 49 points
Number of points scored on October 10 and October 24 combined =63 + 49 = 112 points.
Number of more points scored on October 10 and 24 combined than on October 3 and 17 combined = 112 – 105 = 7 points.
7 more points scored on October 10 and 24 combined than on October 3 and 17 combined.
Assessment Practice
In 9 and 10, use the bar graph at the right.
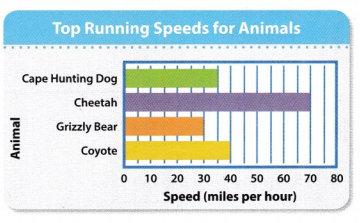
Question 9.
How many more miles per hour is the top running speed of the cheetah than of the Cape hunting dog?
A. 25 miles per hour
B. 30 miles per hour
C. 35 miles per hour
D. 40 miles per hour
Answer:

Given the Top running speeds of animals
mile per hour – mph
The running speed of Cape Hunting Dog = 35 mph
The running speed of Cheetah = 70 mph
The running speed of Grizzly Bear = 30 mph
The running speed of Coyote = 40 mph
The top running speed of the Cheetah more than of the Cape hunting dog = 70 mph – 35 mph
= 70 mph – 35 mph = 35 mph.
Answer B. 35 mph more miles per hour is the top running speed of the Cheetah than of the Cape hunting dog.
Question 10.
How many fewer miles per hour is the top running speed of the grizzly bear than of the coyote and the Cape hunting dog combined?

A. 40 miles per hour
B. 45 miles per hour
C. 50 miles per hour
D. 55 miles per hour
Answer:
The top running speed of Grizzly Bear = 30 mph
The top running speed of Coyote = 40 mph
The top running speed of Cape Hunting Dog = 35 mph
The top running speed of Coyote and Cape Hunting Dog combined = 40 mph + 35 mph = 75 mph
The top running speed of the grizzly bear fewer than of the coyote and the Cape hunting dog combined = 75 mph – 30 mph
= 75 mph – 30 mph
= 45 mph
Answer B. 45 mph is fewer miles per hour is the top running speed of the grizzly bear than of the coyote and the Cape hunting dog combined.
Lesson 7.2 Make Picture Graphs
Solve & Share
Mary is helping her teacher count school playground equipment. She records the data in a frequency table. Use the data in the table to complete the picture graph. Write two statements about your completed graph.
I can … make a picture graph to record information and answer questions about a data set.

Look Back! How did you know the number of symbols to draw for jump ropes?
Essential Question
How Do You Make a Picture Graph?
Visual Learning Bridge
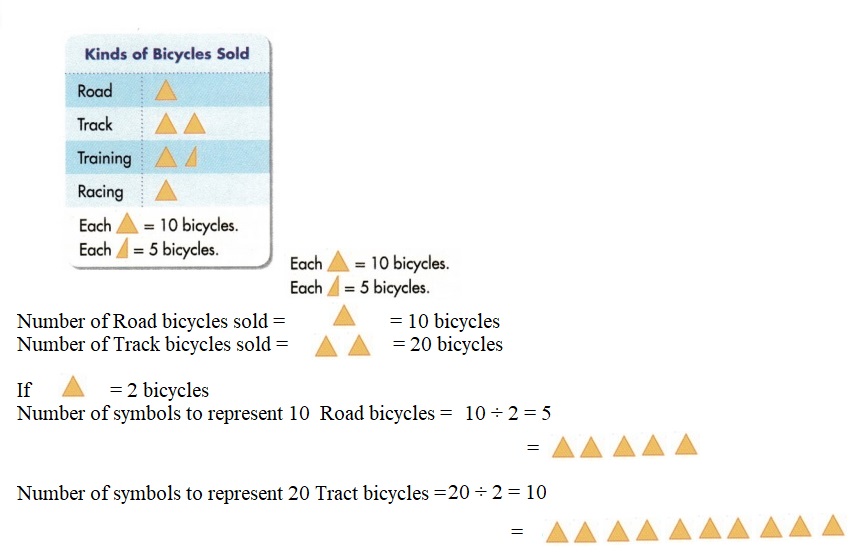
Sam recorded the number of each kind of bicycle a store sold during one month. He made a frequency table. Use the table to make a picture graph.
You can also collect data with a survey by asking people questions.
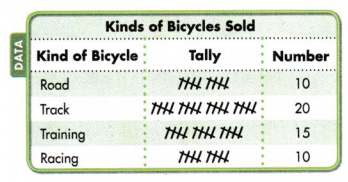
Write a title for the picture graph.
The title is “Kinds of Bicycles Sold.”
Choose a symbol for the key. Decide what each whole symbol and half-symbol will represent.
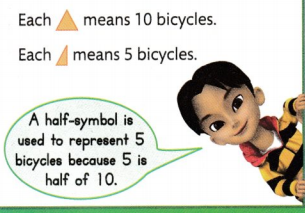
Set up the graph and list the kinds of bicycles. Decide how many symbols you need for each number of bicycles sold. Draw the symbols.
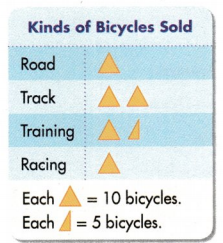
Convince Me! Model with Math Suppose 25 mountain bicycles were also sold. Draw symbols to show a row in the picture graph for mountain bicycles. Explain how you decided.
Guided Practice
Do You Understand?
In 1 and 2, use the picture graph on the previous page.
Question 1.
Explain the symbols that were used for the number of training bicycles sold.
Answer:

Question 2.
If the scale used in the key were ![]() = 2 bicycles, how many symbols would be used for the number of road bicycles sold? For the number of track bicycles sold?
= 2 bicycles, how many symbols would be used for the number of road bicycles sold? For the number of track bicycles sold?
Answer:
Do You Know How?
Question 3.
Use the table to complete the picture graph.

Answer:

Independent Practice
In 4-6, use the data in the chart.

Question 4.
Complete the picture graph.

Answer:
Question 5.
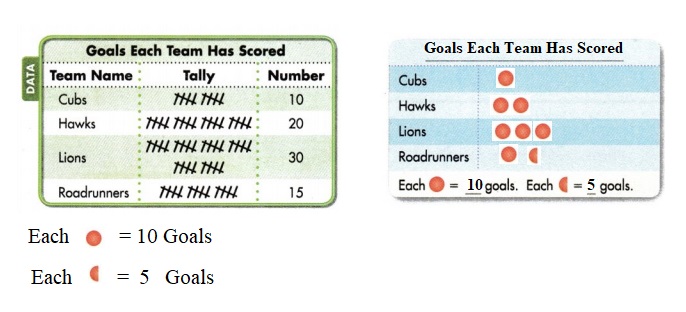
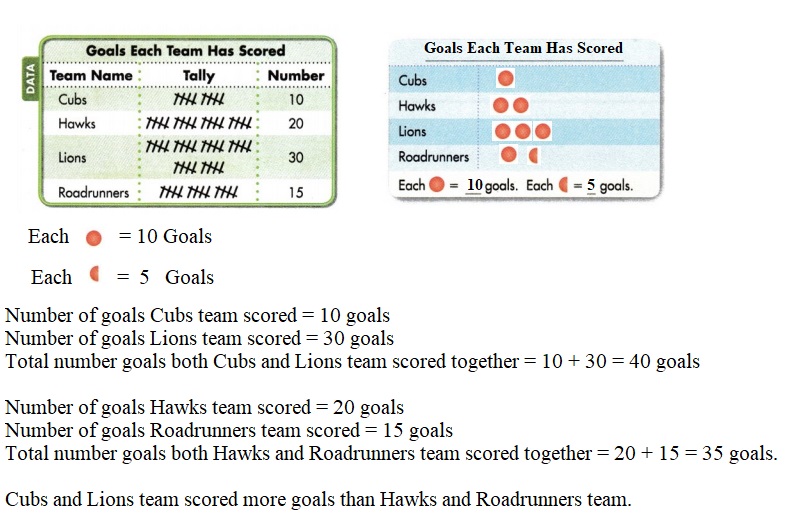
Which two teams scored more goals, the Cubs and the Lions or the Hawks and the Roadrunners?
Answer:
Question 6.
Explain how you decided the number of each symbol to draw to show the goals for the Roadrunners.
Answer:

Problem Solving
In 7-9, use the frequency table at the right.

Question 7.
Use Appropriate Tools Select and use appropriate tools to help make a picture graph to show the data in the table.
Answer:

Question 8.
What is the difference between the odd number and the sum of the even numbers in the table?
Answer:

Question 9.
Ask six students in your class which of the three vegetables is their favorite. Record the answers in your picture graph.
Answer:

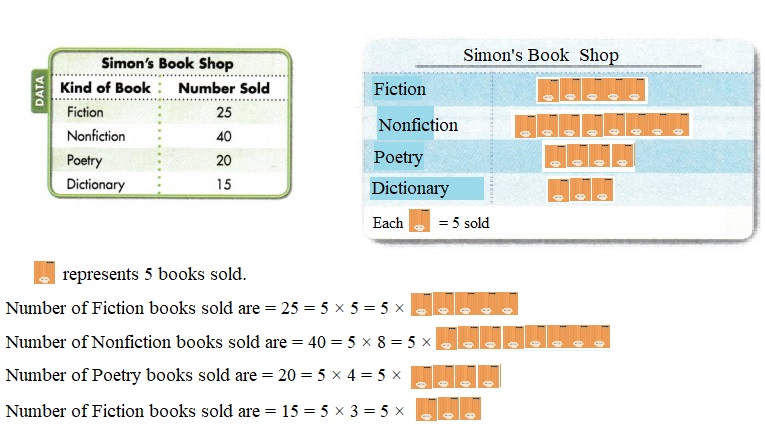
Question 10.
Higher Order Thinking Suppose you are going to make a picture graph to show the data in the Simon’s Book Shop table. Choose a symbol to stand for 5 books sold. Draw the row for fiction books sold. Justify your drawing.

Answer:
Assessment Practice
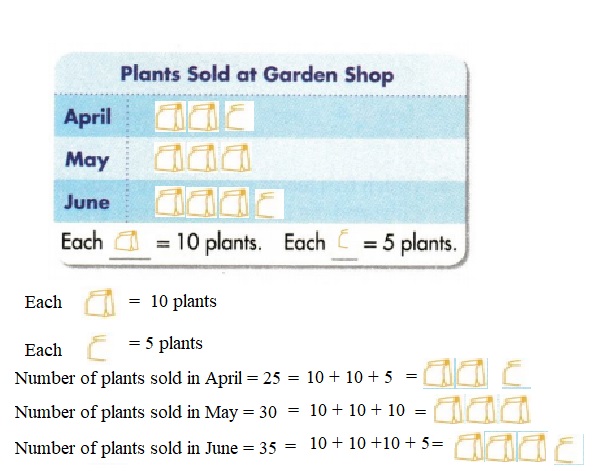
Question 11.
The Garden Shop sold 25 plants in April, 30 plants in May, and 35 plants in June. Complete the picture graph for this data. Choose the symbols you will use.

Answer:
Lesson 7.3 Make Bar Graphs
Solve & Share
Use the data in the table below to complete the bar graph. What conclusions can you make by analyzing the bar graph?
I can … make a bar graph to record information and answer questions about a data set.

Look Back! How can tools such as a ruler help you create a bar graph?
Essential Question
How Do You Make a Bar Graph?
Visual Learning Bridge
Greg made a table to show the amount of money he saved each month from tutoring. Use the data in the table to make a bar graph.

Write a title. Use the same title as in the table.
The title of this bar graph is
Amount Greg Saved Each Month.
Choose the scale. Decide how many units each grid line will represent.

Set up the graph with the scale, each month listed in the table, and labels. Draw a bar for each month.
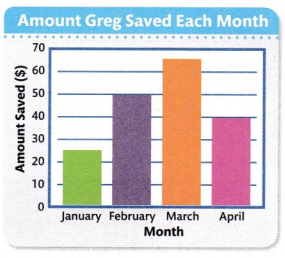
Convince Me! Be Precise Write new amounts for how much Greg saved in 4 later months. Consider the scale.

In May, Greg saved __________.
In June, Greg saved __________.
In July, Greg saved __________.
In August, Greg saved __________.
Draw bars on the graph to show your new data.
Guided Practice
Do You Understand?
In 1-3, use the bar graph on the previous page.
Question 1.
Explain why the bar for January ends between 20 and 30.
Answer:
The bar for January ends between 20 and 30 because in January Greg saved $25.
Since the grid line represents $10.
Half of $10 is = $10 ÷ 2 = $5
So, $25 is represented between 20 and 30.
Question 2.
Suppose Greg saved $35 in May. Between which grid lines would the bar for May end?
Answer:
$35 would be between the grid lines of 30 and 40.
Question 3.
How can you tell how much more Greg saved in February than in April?
Answer:
Total Amount Greg saved in February = $50
Total Amount Greg saved in April = $40
Difference of amount Greg saved in February and April = $50 – $40 = $10.
Greg saved $10 more in February than in April.
Do You Know How?
Question 4.
Use the table to complete the bar graph.

Answer:
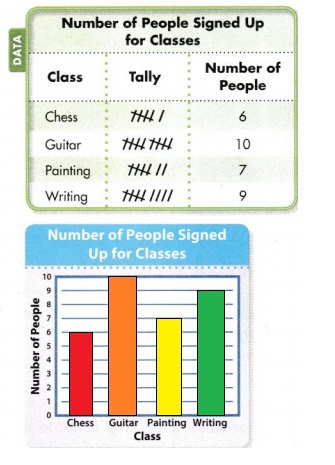
Explanation:
The bar graph has number of people who signed up for classes on one side and the classes on the other side.
Here Chess class is represented with Red color
Guitar class is represented with Orange color
Painting class is represented with Yellow color
Writing class is represented with Green color.
Independent Practice
In 5, use the table at the right.
Question 5.
Complete the bar graph to show the data.

Answer:

Deal Mart represented with Blue color
Jane’s represented with Purple color
Parker’s represented with Indigo blue color
Trends represented with Brown color.
Number of votes are represented on one side of the bar with 5 multiples.
Other side represents the stores.
Problem Solving
In 6-8, use the table at the right.

Question 6.
Make a bar graph to show the data.
Answer:
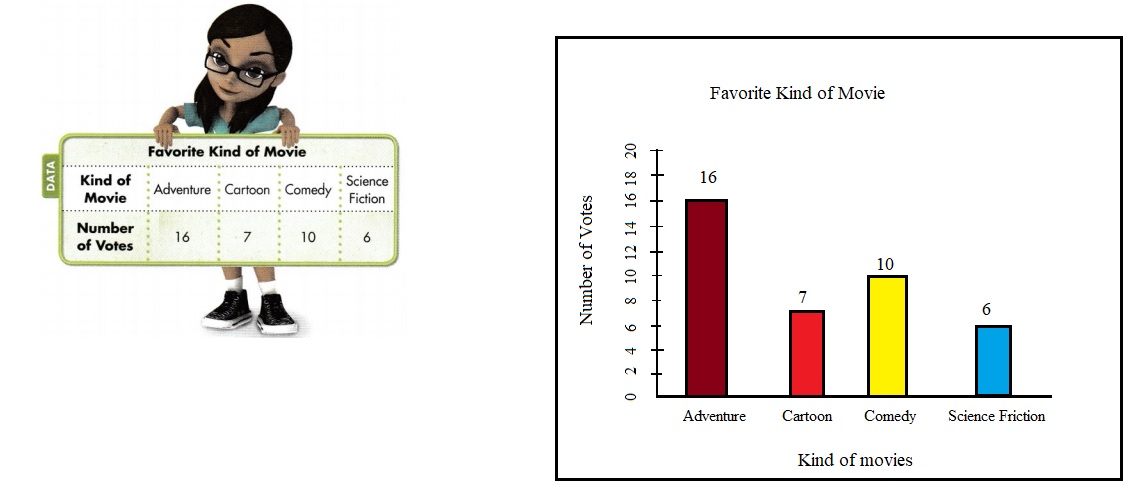
Question 7.
Construct Arguments Which two kinds of movies received about the same number of votes? Explain how to use your bar graph to find the answer.
Answer:
Cartoon and Science Friction movies received about same number of votes.
The bar graph represents the votes the kind of movies received.
The vertical side of the bar graph represents the number of votes received.
Votes are represented with 2 multiples.
The horizontal line represents the kind of movies.
Looking at the graph
Number of votes for Cartoon kind of movies = 7
Number of votes for Science Friction kind of movies = 6
They both received about the same number of votes.
Question 8.
Each movie ticket costs $8. Jo buys tickets for the number of people who voted for science fiction. How much change does she get from $50?
Answer:
Cost of each movie ticket = $8
Number of votes for science fiction movie = 6
Total amount Jo have = $50
Cost for 6 science fiction movie tickets = 6 × $8 = $48
The change Jo get for her $50 = $40 – $48 = $2
Jo get $2 change from $50.
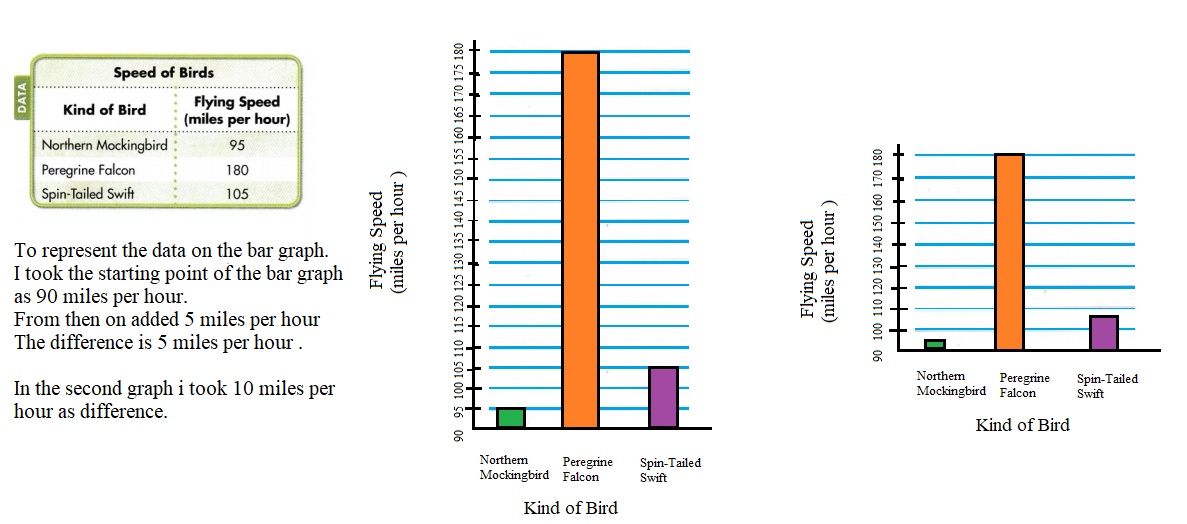
Question 9.
Higher Order Thinking Suppose you are going to make a bar graph to show the data in the table at the right. What scale would you choose? Explain.

Answer:
Assessment Practice
Question 10.
Tanji collected data on the colors of his friends’ shoes. Eight friends have black shoes. Five friends have blue shoes. Seven friends have white shoes. Use Tanji’s data to complete the bar graph.

Answer:

Lesson 7.4 Solve Word Problems Using Information in Graphs
Solve & Share
The students in Ms. Seymour’s class voted for their favorite kind of sandwich. How many more students voted for peanut butter than cheese? How many fewer students voted for tuna than peanut butter?
I can … use graphs and other tools to solve word problems.

Look Back! What is the scale for this graph? How do you know the number of votes a bar represents when it is between two lines on this graph?
Essential Question
How Can You Solve Problems Question Using Graphs?
Visual Learning Bridge
Angela wants Karli and Monique to have a total of 60 paper cranes. The bar graph shows how many paper cranes her friends already have. How many more paper cranes does Angela need to make for Karli and Monique to have 60 paper cranes in all?
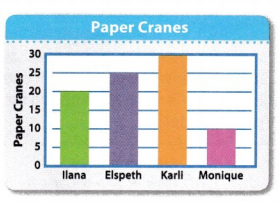
This problem has a hidden question!
Solve the hidden question.
How many paper cranes do Karli and Monique already have?
Use the scale to find how many paper cranes Karli and Monique each have. Then add.

Karli has 30 paper cranes. Monique has 10 paper cranes.
30 + 10 = 40
Together they have 40 paper cranes.
Solve the main question.
How many paper cranes does Angela need to make?
Subtract the number of cranes the friends already have from the total.
60 – 40 = 20
Angela needs to make 20 paper cranes.
Convince Me! Critique Reasoning Angela says, “I want llana and Elspeth to also have 60 cranes in all. I can subtract two times to find how many more cranes I need to make for them.” Is Angela correct? Explain.
Guided Practice
Do You Understand?
Question 1.
Look at the graph on the previous page. Explain whether you would add, subtract, multiply, or divide to find how many more paper cranes Karli already has than Monique.
Answer:

Number of Paper Cranes Karli has = 30
Number of Paper Cranes Monique has = 10
To find how many more paper cranes Karli has than Monique
we subtract Monique paper cranes from Karli’s paper cranes
30 – 10 = 20
Karli has 20 more paper cranes than Monique.
Question 2.
How does a bar graph help you compare data?
Answer:
A bar diagram makes it easy to compare sets of data between different groups at a glance. The graph represents categories on one axis and a discrete value in the other. The goal is to show the relationship between the two axes.
Do You Know How?
In 3, use the bar graph.
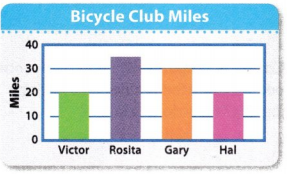
Question 3.
How many more miles did Hal and Victor ride together than Rosita?
Answer:
Number of miles Hal rode = 20 miles
Number of miles Victor rode = 20 miles
Total number of miles Hal and Victor rode together = 20 + 20 = 40 miles.
Number of miles Rosita rode = 35 miles
35 miles because it is represented between 30 and 40 miles bar line in the bar graph.
Number of more miles Hal and victor ride together than Rosita = 40 miles – 35 miles = 5 miles.
Independent Practice
In 4-6, use the picture graph at the right.
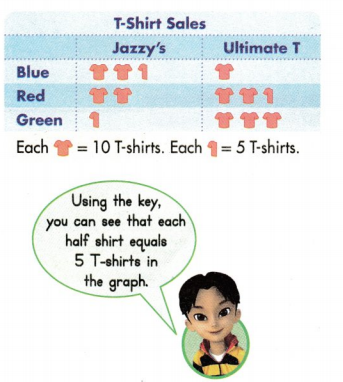
Question 4.
How many more red T-shirts were sold at Ultimate T than at Jazzy’s?
Answer:
You see
Full T-shirt = 10 T-shirts
Half T-shirt = 5 T-shirts
Number of red T-shirts sold at Ultimate T = 2 full T-shirts and 1 half T-shirt = 10+10+5 = 25 T-shirts
Number of red T-shirts sold at Jazzy’s =2 full T-shirts = 10 +10 =20 T-shirts
Number of more red T-shirts sold at Ultimate T than at Jazzy’s = 25 – 20 = 5 T-shirts.
Question 5.
How many fewer green T-shirts were sold at Jazzy’s than at Ultimate T?
Answer:
Full T-shirt = 10 T-shirts
Half T-shirt = 5 T-shirts
Number of green T-shirts sold at Ultimate T = 3 full T-shirts = 10 + 10 + 10 = 30 T-shirts
Number of green T-shirts sold at Jazzy’s = 1 half T-shirt = 5 T-shirt
Number of fewer green T-shirts were sold at Jazzy’s than at Ultimate T = 30 – 5 = 25 T-shirts.
25 fewer green T-shirts were sold at Jazzy’s than at Ultimate T.
Question 6.
How many more blue and red T-shirts combined were sold at Jazzy’s than green T-shirts were sold at Ultimate T?
Answer:
Number of Blue T-shirts sold at Jazzy’s = 2 full T-shirts and 1 half T-shirt = 10+10+5 = 25 T-shirts
Number of red T-shirts sold at Jazzy’s =2 full T-shirts = 10 +10 = 20 T-shirts
Total number of Blue and red T-shirts combined were sold at Jazzy’s = 25 + 20 = 45 T-shirts
Number of green T-shirts were sold at Ultimate T = 3 full T-shirts = 10 + 10 + 10 = 30 T-shirts
Number of more blue and red T-shirts combined were sold at Jazzy’s than green T-shirts were sold at Ultimate T =
= 45 – 30 = 15 T-shirts.
Problem Solving
In 7-9, use the bar graph at the right.

Question 7.
Number Sense How many people voted for their favorite type of exercise? How can you find the answer?
Answer:
Here three types of exercises are given
Jogging
Swimming
Gymnastics
Number of people voted for Jogging = 6
Number of people voted for Swimming = 14
Number of people voted for Gymnastics = 12
Total number of people who voted for their favorite exercises = 6 + 14 + 12 = 32.
32 people voted for their favorite exercises.
By adding the votes of all the exercises gives the answer to find people voted for their favorite exercise.
Question 8.
Construct Arguments How many more people voted for gymnastics than for jogging? How do you know?
Answer:
Number of people voted for Jogging = 6
Number of people voted for Gymnastics = 12
By subtracting votes of jogging from gymnastics
we find
Number of more people voted for gymnastics than for jogging = 12 – 6 = 6 votes.
6 more people voted for gymnastics than for jogging.
Question 9.
How many fewer people voted for swimming than for gymnastics and jogging combined?
Answer:
Number of people voted for Jogging = 6
Number of people voted for Gymnastics = 12
Total number of votes for gymnastics and jogging combined = 12 + 6 = 18 votes.
Number of people voted for Swimming = 14
Subtracting votes for Swimming from gymnastics and jogging combined
Number of fewer people voted for swimming than for gymnastics and jogging combined = 18 – 14 = 4
4 fewer people voted for swimming than for gymnastics and jogging combined.
Question 10.
Leslie delivers papers on weekdays and Saturdays. She delivers 6 papers each weekday and 16 papers on Saturday. How many papers does Leslie deliver during the entire week?
Answer:
A week has 7 days
5 weekdays
2 = weekends -Saturday and Sunday
Number of papers Leslie delivers on weekday = 6 each
Total number of papers she delivers on all weekdays = 6 × 5 = 30 papers
Number of papers Leslie delivers on Saturday = 16 papers
Total number of papers Leslie deliver during the entire week = 30 + 16 = 46 papers.
Leslie delivers 46 papers during the entire week.
Question 11.
Higher Order Thinking What kinds of comparisons can you make when you look at a bar graph or a picture graph?
Answer:
Fewer , more , difference, adding
Assessment Practice
Question 12.
Daryl made a bar graph to record the number of books read by each member of a reading club. How many fewer books did Alice read than Sandra and Daryl combined?
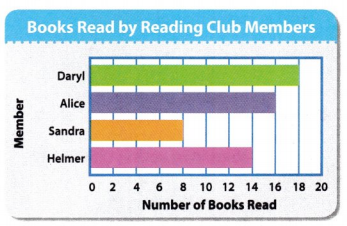
A 6 books
B. 8 books
C. 10 books
D. 12 books
Answer:
Number of books Alice read = 16 books
Number of books Sandra read = 8 books
Number of books Daryl read = 18 books
Total number of books Sandra and Daryl read combined = 18 + 8 = 26 books
Number of fewer books Alice read than Sandra and Daryl combined = 26 – 16 = 10 books.
Alice read 10 fewer books than Sandra and Daryl combined.
Lesson 7.5 Problem Solving
Precision
Solve & Share
Action books and mystery books cost $5 each. Biography books cost $10 each. A librarian has $100 to spend on new books. She collected some information about the kinds of books that students checked out to read last month.
I can … be precise when solving math problems.
Thinking Habits
Be a good thinker! These questions can help you.
- Am I using numbers, units, and symbols appropriately?
- Am I using the correct definitions?
- Am I calculating accurately?
- Is my answer clear?

Look Back! Be Precise How did you use words and symbols to explain your answer?
Essential Question
How Can You Be Precise When out Solving Math Problems?
Visual Learning Bridge
Bella has a bakery. She will use the bakery items at the right to make a gift basket worth $40. Bella wants the basket to have more than one of each bakery item. Show one way to make a gift basket.

What do I need to do to make a gift basket?
I need to be precise. I will decide how many of each item to put in a basket so the total is exactly $40.
Here’s my thinking…
How can I be precise in solving this problem?
I can
- correctly use the information given.
- calculate accurately.
- decide if my answer is clear and appropriate.
- use the correct units.
I will start with $40.
I know how many of each item is available.
3 wheat loaves × $4 = $12
$40 – $12 = $28
9 cinnamon buns × $2 = $18
$28 – $18 = $10
10 muffins × $1 = $10
$10 – $10 = $0
All calculations are correct. My gift basket has 3 wheat loaves, 9 cinnamon buns, and 10 muffins. The total is exactly $40.
Convince Me! Be Precise Is there another way to make a gift basket that totals exactly $40? Explain.
Guided Practice
Be Precise Use the graph on the previous page. Suppose Bella wanted to make a gift basket worth $25 instead. The gift basket must also have more wheat loaves than muffins. Show one way Bella can make the gift basket.

Question 1.
What given information will you use to solve?
Answer:

Given
Bella wants a gift basket worth of $25
She wants more wheat loaves than muffins.
Using the list of items in the Bakery and the cost of the items. I will calculate the cost of the items and compare with the basket worth.
Question 2.
Show and explain one way Bella can make the gift basket.
Answer:
Total worth of the gift basket = $25
Cost of Muffins = $1 each
Cost of Cinnamon Buns = $2 each
Cost of Wheat loaves = $4 each
Cost of 4 Wheat loaves = 4 × $ 4 = $16
Cost of the basket – cost of 4 Wheat loaves
= $25 – $16
= $9
Remaining Amount = $9
Cost of 3 Cinnamon Buns = 3 × $2 = $6
Remaining Amount – Cost of 3 Cinnamon Buns
= $9 – $6
= $3
Remaining Amount
Cost of 3 Muffins =3 × $1 = $3
Remaining Amount – Cost of 3 Muffins
= $3 – $3
= $0
The gift basket worth of $25 have 4 Wheat loaves , 3 Cinnamon Buns , 3 Muffins.
Independent Practice
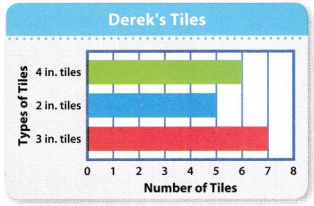
Be Precise Derek is making a tile pattern that will be 30 inches long. The graph shows how many of each length of tile Derek has. He wants to use more than one of each length of tile in his pattern. Show one way to make the pattern.
Question 3.
What given information will you use to solve?
Answer:
The length of the tile pattern = 30 inches
Type of tiles Derek have
3 in tile
2 in tile
4 in tile.
Number of tiles he have.
Number of 2 in tile he have = 5 tiles
Number of 3 in tile he have = 7 tiles
Number of 4 in tile he have = 6 tiles
Use these information to solve the problem.
Question 4.
Show and explain one way Derek can make the pattern.
Answer:
The length of the tile pattern = 30 inches
Type of tiles Derek have
3 in tile
2 in tile
4 in tile.
Number of tiles he have.
Number of 2 in tile he have = 5 tiles
Number of 3 in tile he have = 7 tiles
Number of 4 in tile he have = 6 tiles
To make the tile pattern he wants to use more than one of each length of tile in his pattern.
if we use 1 of each tile
length of all types of tiles = 2 inch + 3 inch + 4 inch = 9 inch
Total length of tile pattern = 30 inches
= 30 inches – 9 inches = 21 inches.
Now,
To make more 21 inches
2 time length of all tiles = 2 × 9 = 18 inches
= 18 inches +3 inch
= 21 inches
Total types of tiles needed for the 30 inch tile pattern = Three 4 in tiles + Four 3 inch tile + Three 2 inch tiles
=Three 4 in tiles + Four 3 inch tile + Three 2 inch tiles
=( 3 × 4) + (4 ×3) + (2 × 3)
= 12 + 12 + 6
= 30 inches.
Problem Solving
Performance Task
Picture Planning
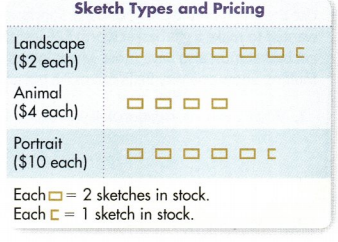
Marta has $50 to spend on sketches. She wants to display them in an array of 3 rows, with 4 sketches in each row. Marta wants to include each type of sketch at least two times in her array.
Question 5.
Reasoning How many sketches does Marta want?
Answer:
Marta wants a array of 3 rows.
Each row has 4 sketches in each row.
Number of sketches in the array = 3 × 4 = 12 sketches.
Marta wants 12 sketches.
Question 6.
Make Sense and Persevere What is a good plan for solving the problem?
Answer:
As Marta need 12 sketches. and she has $50 to spend on sketches.
There are three types of sketches and their cost
Portrait = $10 each
Animals = $4 each
Landscape =$2 each
She want each type at least two times in the array.
Calculating the cost of each sketches and plan the sketches in the array.
Question 7.
Be Precise Show one way Marta can buy sketches to make the array. Use math words and symbols to explain.
Be precise when analyzing the symbols, words, and numbers displayed in a picture graph.
Answer:
As Marta need 12 sketches.
At least 2 sketches of each type in the array
2 Portrait sketches = 2 × $10 = $20
2 Animal sketches = 2 × $4 = $8
2 Landscape sketches = 2 × $2 = $4
Total number of sketches = 2 + 2 + 2 = 6
6 more sketches remaining.
Adding all the costs
= $20 + $8 + $4 = $32
Total amount Marta has = $50
$50 – $32 = $18 remaining.
$18 remaining for 6 more sketches
we can add
=3 Animal sketch + 3 Landscape sketches
$18 = (3 × $4) + (3 × $2)
$18 = $12 + $6
$18 = $18.
Total number of sketches in the Marta’s array = 2 Portrait + 5 Animal + 5 Landscape
=(2 × $10) + (5 × $4) + (5 × $2 )
=$20 + $20 + $10
=$50.
Question 8.
Generalize Suppose Marta wants to make an array of 4 rows, with 3 sketches in each row. Would your answer still work? Explain.
Answer:
If Marta wants to make a array of 4 rows and 3 sketches in each row.
Total sketches = 4 × 3 = 12 sketches.
In both the cases the total sketches are same. So, the answer will work in this case as well.
Just the order of sketches changes.
Topic 7 Fluency Practice Activity
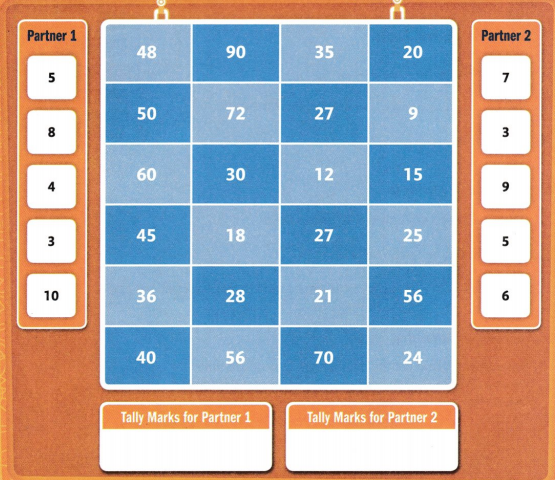
Point & Tall
Find a partner. Get paper and a pencil. Each partner chooses a different color: light blue or dark blue.
Partner 1 and Partner 2 each point to a black number at the same time. Both partners multiply those numbers.
If the answer is on your color, you get a tally mark. Partners then write the remaining facts in the fact family. Work until one partner has seven tally marks.
I can… multiply and divide within 100.
Topic 7 Vocabulary Review
Understand Vocabulary

Graph A
Word List
• data
• frequency table
• graph
• key
• scale
• scaled bar graph
• scaled picture graph
• survey
Complete each sentence with scaled picture graph, scaled bar graph, key, or scale.
Question 1.
The _________ in Graph A shows that each umbrella represents 2 days.
Answer:
The _Key__ in Graph A shows that each umbrella represents 2 days.
Question 2.
Graph A is a _________
Answer:
Graph A is a __Scaled picture graph___.
Question 3.
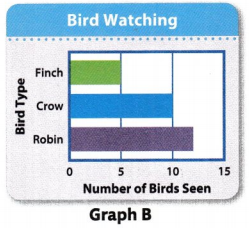
The ________ in Graph B increases by 5.
Answer:
The _Scale__ in Graph B increases by 5
Question 4.
Graph B is a _________.
Answer:
Graph B is a __scaled bar graph___.
Write T for True or F for False.
Question 5.
________ A survey is the only way to collect data.
Answer:
True A survey is the only way to collect data.
Question 6.
________ A scaled bar graph has a key.
Answer:
False A scaled bar graph has a key.
Question 7.
________ Data from a frequency table can be used to make a scaled bar graph.
Answer:
True Data from a frequency table can be used to make a scaled bar graph.
Use Vocabulary in Writing
Question 8.
Suppose you found out the number and type of pets your classmates have. Explain how you can display that information. Use at least 3 terms from the Word List in your answer.
Answer:
Given data
Number of pets
Type of pets.
I will be using a scaled bar graph with number of pets on one axis and type of pets on the other axis. The scale range and key depends on the data collected by the survey.
Topic 7 Reteaching
Set A pages 253-256
Picture graphs use pictures or parts of pictures to represent data.

Bar graphs use bars to represent data. You can use a scale to find how much a bar represents.
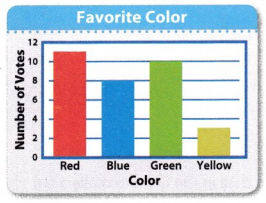
Each line in this bar graph represents 2 votes.
Remember to use a key or scale. The number of pictures in picture graphs and the lengths of bars in bar graphs help to compare data.
In 1-3, use the picture graph on the left.
Question 1.
How many more baseball caps are on sale than racing caps?
Answer:
1 full cap represents 10 caps
1 half cap represents 5 caps
Number of baseball caps on sale = 3 full + 1 half = 10+10+10+5= 35 caps
Number of Racing caps on sale = 2 full caps = 10 + 10 = 20 caps.
Subtracting racing caps from baseball caps
Number of more baseball caps are on sale than racing caps = 35 caps – 20 caps = 15 caps
There are 15 more baseball caps are on sale than racing caps.
Question 2.
How many more baseball caps are on sale than basketball and racing caps combined?
Answer:
Number of basketball caps on sale = 1 full cap = 10 caps
Number of Racing caps on sale = 2 full caps = 10 + 10 = 20 caps.
Total number of basketball and racing caps combined = 10 + 20 = 30 caps.
Number of baseball caps on sale = 3 full + 1 half = 10+10+10+5= 35 caps
Number of more baseball caps are on sale than basketball and racing caps combined = 35 caps – 30 caps = 5 caps.
There are 5 more baseball caps are on sale than basketball and racing caps combined.
Question 3.
How many fewer basketball caps are on sale than baseball caps?
Answer:
Number of basketball caps on sale = 1 full cap = 10 caps
Number of baseball caps on sale = 3 full + 1 half = 10+10+10+5= 35 caps.
Number of fewer basketball caps are on sale than baseball caps = 35 – 10 = 25 caps
There are 25 fewer basketball caps are on sale than baseball caps.
In 4-7, use the bar graph on the left.
Question 4.
Which color got the most votes? How many votes did that color get?
Answer:

Red color got the most votes.
11 people voted for red color.
Question 5.
How many fewer votes were for yellow than for green?
Answer:
Number of votes for yellow = 3 votes
Number of votes for green = 10 votes
Number of fewer votes for yellow than for green = 10 – 3 = 7 votes.
There are 7 fewer votes for yellow than for green.
Question 6.
How many more votes were for red than for blue?
Answer:
Number of votes for red = 11 votes
Number of votes for blue = 8 votes
Number of more votes to red than for blue = 11 – 8 = 3 votes.
There are 3 more votes for red than for blue.
Question 7.
What is the difference between the votes for red and the votes for blue and yellow combined?
Answer:
Number of votes for blue = 8 votes
Number of votes for yellow = 3 votes
Total number of votes for blue and yellow combined = 8 + 3 = 11 votes
Number of votes for red = 11 votes
The difference between the votes for red and the votes for blue and yellow combined = 11 – 11 = 0 votes.
There is 0 difference between the votes for red and the votes for blue and yellow combined.
Set B pages 257-264
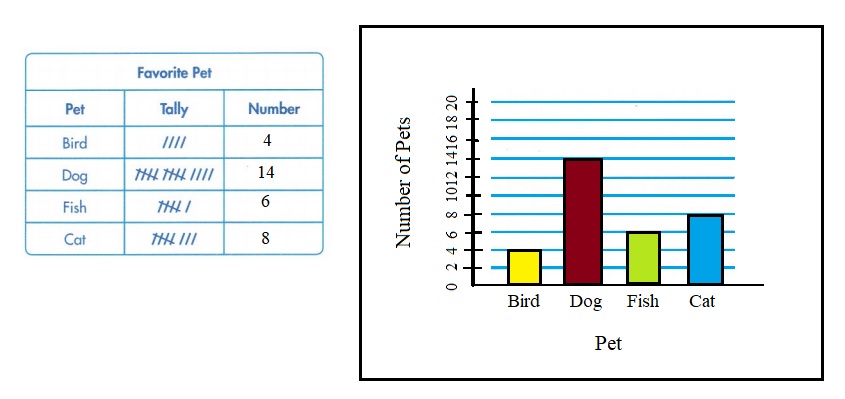
This frequency table shows data about the number of coins Mark has.
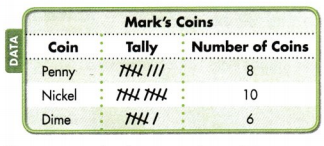
You can use the data to make a picture graph. Picture graphs include a title, symbol, and a key to show the scale.

In this picture graph, each symbol equals 2 coins. You also can use the data to make a bar graph.
1. Label the bottom and side of the graph.
2. Choose a scale.
3. Draw a bar for each type of coin.
4. Include a title.
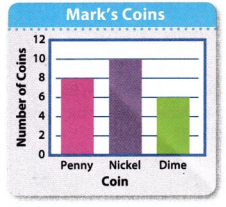
Remember that a frequency table includes tally marks or numbers. A picture graph uses pictures to show data.
In 1 and 2, use the frequency table below.
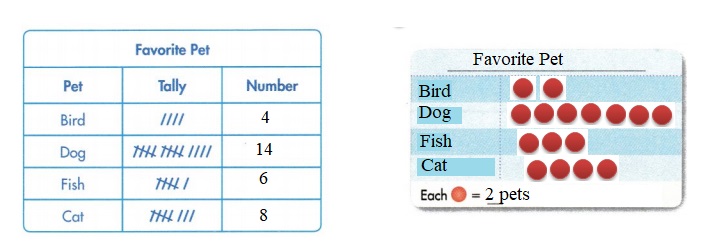
Dan’s class voted for their favorite pet. The results are shown in this frequency table.

Question 1.
Complete the frequency table.
Answer:

Question 2.
Use the data in the frequency table to make a picture graph.
Answer:
Question 3.
Use the data in the table to make a bar graph.
Answer:
Set C pages 265-268
You can use data from bar graphs or picture graphs to draw conclusions.
In a picture graph, Erica recorded the number of magazines she read. How many more magazines did she read in April and May combined than in June?

You can solve 2-step data problems.
There are 6 symbols for April and May.
There are 3 symbols for June.
6 – 3 = 3. There are 3 more symbols for April and May.
Each symbol represents 2 magazines. 3 × 2= 6. Erica read 6 more magazines in April and May than in June.
Remember you can use tables and graphs to make comparisons. Sometimes you need to find and answer hidden questions.
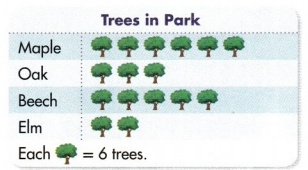
In 1-6, use the picture graph below.
Question 1.
How many more maple trees than elm trees are there?
Answer:
1 Tree symbol = 6 trees
Number of Maple trees = 6 Tree = 6 × 6 = 36 trees.
Number of elm trees = 2 Tree = 2 × 6 = 12 trees.
Number of more maple trees than elm trees = 36 – 12 = 24 trees.
There are 24 more maple trees than elm trees.
Question 2.
How many fewer beech trees are there than maple trees?
Answer:
Number of beech trees = 5 Tree = 5 × 6 trees = 30 trees
Number of Maple trees = 6 Tree = 6 × 6 trees = 36 trees.
Number of fewer beech trees are there than maple trees = 36 – 30 = 6 trees.
There are 6 fewer beech trees are there than maple trees.
Question 3.
How many trees are NOT maple trees?
Answer:
Number of elm trees = 2 Tree = 2 × 6 = 12 trees.
Number of beech trees = 5 Tree = 5 × 6 trees = 30 trees.
Number of Oak trees = 3 Tree = 3 × 6 trees = 18 trees.
Total number of trees which are NOT Maple trees = elm trees + beech trees + Oak trees
= 12 + 30 + 18
= 60 trees.
There are 60 trees which are NOT Maple trees.
Question 4.
How many more maple and beech trees combined are there than oak trees?
Answer:
Number of beech trees = 5 Tree = 5 × 6 trees = 30 trees.
Number of Maple trees = 6 Tree = 6 × 6 trees = 36 trees.
Total number of maple and beech trees combined = 36 + 30 = 66 trees.
Number of Oak trees = 3 Tree = 3 × 6 trees = 18 trees.
Number of more maple and beech trees combined are there than oak trees = 66 – 18 = 48 trees.
Question 5.
How many fewer oak trees are there than beech and elm trees combined?
Answer:
Number of beech trees = 5 Tree = 5 × 6 trees = 30 trees.
Number of elm trees = 2 Tree = 2 × 6 = 12 trees.
Total number of beech and elm trees combined = 30 + 12 = 42 trees.
Number of Oak trees = 3 Tree = 3 × 6 trees = 18 trees.
Number of fewer oak trees are there than beech and elm trees combined = 42 – 18 = 24 trees.
There are 24 fewer oak trees are there than beech and elm trees combined.
Question 6.
If the city wants to have 24 elm trees, how many more elm trees does it need to plant? Explain how to solve.
Answer:
Number of elm trees = 2 Tree = 2 × 6 = 12 trees.
Total number of elm trees city wants = 24 trees.
Number of more elm trees need to plant = 24 – 12 = 12 trees.
The city needs 12 more elm trees to plant. and
2 TREE to be added to the picture graph to make it 24 trees.
Set D pages 269-272
Think about these questions to help you attend to precision.
Thinking Habits
- Am I using numbers, units, and symbols appropriately?
- Am I using the correct definitions?
- Am I calculating accurately?
- Is my answer clear?

Remember to use words, numbers, and symbols to show your reasoning.
In 1 and 2, use the bar graph at the left to solve.
Jackie has $50 to spend on books. She has made a bar graph to show the number of each type of book the store has in stock. Jackie wants to buy at least 2 of each type of book. Show one way Jackie can spend $50 on books.
Action books cost $5.
Biographies cost $10.
Mysteries cost $5.
Question 1.
What given information will you use to solve the problem?
Answer:
From the bar graph we know
Types of books and the number of books.
Cost of each type of books in the store.
Total amount Jackie can spend on books = $50.
Question 2.
Show one way Jackie can spend $50 on books. Use math words and symbols to explain your thinking.
Answer:

Action books cost $5.
Biographies cost $10.
Mysteries cost $5.
Number of Action books = 4
Number of Mystery books = 5
Number of Biography books = 7
Total money Jackie have = $50
Given that Jackie wants to buy at least 2 of each type of book.
cost of 2 action books = 2 × $5 = $10
$50 – $10 = $40
Remaining money =$40
Cost of 2 Mystery books = 2 × $5 = $10
$40 – $10 = $30
Cost of 2 Biography books = 2 × $10 = $20
$30 – $20 = $10
Remaining money after buys 2 books of each type = $10.
Here are two probabilities
Jackie may buy 2 Action books or 2 Mystery books or 1 Action and 1 mystery book or 1 Biography book.
Here are the ways Jackie spend her $50 buying books.
4 Action books + 2 Mystery books + 2 Biography books = 20 + 10 + 20 = 50
2 Action books + 4 Mystery books + 2 Biography books = 10 + 20 + 20 = 50
3 Action books + 3 Mystery books + 2 Biography books = 15 + 15 + 20 = 50
2 Action books + 2 Mystery books + 3 Biography books = 10 + 10 + 30 = 50
Topic 7 Assessment Practice
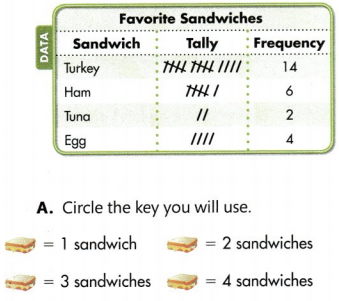
Question 1.
Use the data from the frequency table to make a picture graph.
Answer:

B. Draw a picture graph.
Answer:

Question 2.
Use the data from the picture graph you made in Question 1. How many students did NOT choose turkey as their favorite sandwich?
A. 10
B. 13
C. 12
D. 14
Answer:
There are 4 types of sandwiches.
Turkey, Ham, Tuna, Egg
Number of Ham sandwiches = 6
Number of Tuna sandwiches = 2
Number of Egg sandwiches = 4
Total number of sandwiches which are not Turkey = 6 + 2 + 4 = 12 sandwiches.
Question 3.
Jamie’s class made a picture graph to show how many hours they volunteered each week. In which week or weeks did the class volunteer 9 hours?

A. Week 1
B. Week 2
C. Week 3
D. Weeks 1 and 3
Answer:
1 full clock = 2 hours
1 half clock = 1 hour
Number of hours volunteered in week 1 = 5 full clock = 5 × 2 hours = 10 hours.
Number of hours volunteered in week 2 = 4 full and 1 half clock = (4 × 2 hours) + (1 × 1 hour) = 8 + 1 = 9 hours.
Number of hours volunteered in week 3 = 3 full and 1 half clock = (3 × 2 hours ) + (1 × 1 hour ) = 6 + 1 = 7 hours.
In Week 2 Jamie’s class volunteered 9 hours.
Question 4.
Look at the picture graph above. How many total hours did the class volunteer?
Answer:
Number of hours volunteered in week 1 = 5 full clock = 5 × 2 hours = 10 hours.
Number of hours volunteered in week 2 = 4 full and 1 half clock = (4 × 2 hours) + (1 × 1 hour) = 8 + 1 = 9 hours.
Number of hours volunteered in week 3 = 3 full and 1 half clock = (3 × 2 hours ) + (1 × 1 hour ) = 6 + 1 = 7 hours.
Total number of hours class volunteer = 10 hours + 9 hours + 7 hours = 26 hours.
Question 5.
How many more hours did the class volunteer in Weeks 2 and 3 combined than in Week 1?
Answer:
Number of hours volunteered in week 1 = 5 full clock = 5 × 2 hours = 10 hours.
Number of hours volunteered in week 2 = 4 full and 1 half clock = (4 × 2 hours) + (1 × 1 hour) = 8 + 1 = 9 hours.
Number of hours volunteered in week 3 = 3 full and 1 half clock = (3 × 2 hours ) + (1 × 1 hour ) = 6 + 1 = 7 hours.
Number of hours class volunteer in Weeks 2 and 3 combined = 9 hours + 7 hours = 16 hours.
Number of more hours the class volunteer in Weeks 2 and 3 combined than in Week 1 = 16 hours – 10 hours = 6 hours
The class volunteer in Weeks 2 and 3 combined than in Week 1
Question 6.
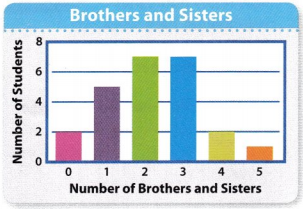
Mr. Thomas’s class made a bar graph of the number of brothers and sisters each student has. How many students in the class have 1 brother or sister?
A. 1
B. 2
C. 5
D. 7
Answer:
5 students have 1 brother or sister. The bar is represented with purple color.
Question 7.
Compare students with 3 brothers and sisters and students with O brothers and sisters. How many more students have 3 brothers and sisters?
________ more student(s)
Answer:
Number of students having 3 brothers and sisters = 7 students.
Number of students having 0 brothers and sisters = 2 students.
Number of more students have 3 brothers and sisters = 7 – 2 = 5 students.
5 more students have 3 brothers and sisters.
Question 8.
How many students in the class have 2 or more brothers and sisters?
Answer:
Number of students having 2 brother and sisters = 7 students
Number of students having 3 brothers and sisters = 7 students
Number of students having 4 brothers and sisters = 2 students
Number of students having 5 brothers and sisters = 1 students
Total number of students having 2 or more brothers and sisters = 7 + 7 + 2 + 1 = 17 students.
Question 9.
Beth is making a bar graph to compare how many marbles of each color she has. She has 25 blue marbles, 35 red marbles, 5 green marbles, and 15 yellow marbles. Which scale makes the most sense for Beth to use with her graph?
A. Each grid line equals 1 marble.
B. Each grid line equals 2 marbles.
C. Each grid line equals 5 marbles.
D. Each grid line equals 20 marbles.
Answer:
25 , 35, 5, 15 all these are in the multiples of 5. So, the grid line equals 5 marbles.
25 = 5 × 5 grid line
35 = 5 × 7 grid line
5 = 5 × 1 grid line
15 = 5 × 3 grid line
Question 10.
Use the information in Question 9 to make a bar graph of Beth’s marbles.

Answer:

Question 11.
Select all the statements that are true. Use the information from Question 9.
☐ Beth has more green and yellow marbles combined than blue ones.
☐ Beth has as many blue and yellow marbles combined as red ones.
☐ Beth has more red marbles than blue and green ones combined.
☐ Beth has fewer yellow marbles than blue and green ones combined.
☐ Beth has fewer red marbles than green and yellow ones combined.
Answer:
25 blue marbles, 35 red marbles, 5 green marbles, and 15 yellow marbles
1. Beth has more green and yellow marbles combined than blue ones.
Green and yellow = 5 + 15 = 20 , blue = 25
25 – 20 = 5 marbles.
5 fewer marbles.
False Beth has more green and yellow marbles combined than blue ones.
2. Beth has as many blue and yellow marbles combined as red ones
blue and yellow = 25 + 15 = 40 marbles , red = 35 marbles.
False Beth has as many blue and yellow marbles combined as red ones.
3. Beth has more red marbles than blue and green ones combined.
Red marbles = 35 marbles , blue and green combined = 25 + 5 = 30 marbles.
35 – 30 = 5 marbles
True Beth has 5 more red marbles than blue and green ones combined.
4 . Beth has fewer yellow marbles than blue and green ones combined.
blue and green combined = 25 + 5 = 30 marbles , yellow marbles = 15 marbles
30 – 15 = 15 marbles.
True Beth has 15 fewer yellow marbles than blue and green ones combined.
5. Beth has fewer red marbles than green and yellow ones combined.
green and yellow ones combined = 5 + 15 = 20 marbles , red marbles = 35 marbles.
35 – 20 = 15 marbles.
False .
Question 12.
The school had a fundraiser in the first part of the school year. In which month did the school make the most money?
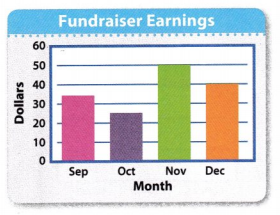
A. September
B. October
C. November
D. December
Answer:
Amount of fund raised in September = $35
Amount of fund raised in October = $25
Amount of fund raised in November = $50
Amount of fund raised in December = $40
The school make the most money in November of $50.
Question 13.
Look at the bar graph above. Suppose $45 was raised in January. Where would the bar end?
Answer:
If the money raised $45 in January it would end put between 40 and 50 grid line.
Question 14.
Did the school earn more money in September and October combined than in November? Explain.
Answer:
Amount of fund raised in September = $35
Amount of fund raised in October = $25
Total money earned in September and October combined = $35 +$25 = $60.
Amount of fund raised in November = $50
Amount of more money earned in September and October combined than in November = $60 – $50 = $10.
School earned $10 of more money earned in September and October combined than in November.
Question 15.
The frequency table below shows the time Kelly jumped rope during the week. Use the data to make a picture graph.
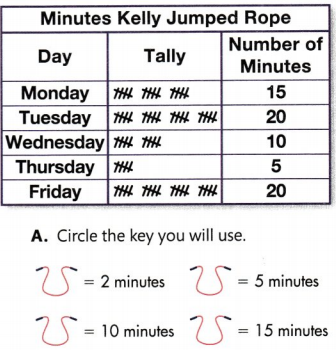
Answer:

B. Draw a picture graph.
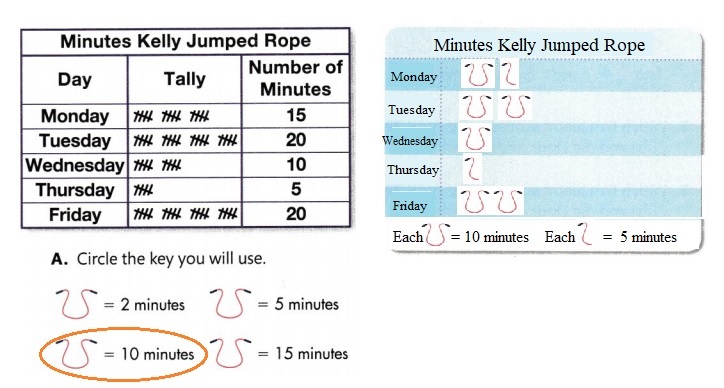
Answer:
Question 16.
Look at the picture graphs below. Which type of book was chosen by the same number of students in each class?

A. Adventure
B. Mystery
C. Nonfiction
D. Not here
Answer:
Full book = 2 students and Half book = 1 student
In Class A picture graph
Number of students choose Nonfiction types of books = 2 full and 1 half = (2 × 2) + 1 = 5 students.
In Class B picture graph
Number of Nonfiction types of books choose = 2 full and 1 half = (2 × 2) + 1 = 5 students.
Question 17.
How many students in Classes A and B chose mystery as their favorite type of book?
Answer:
Number of students in class A chose Mystery type of book = 5 Full = 5 × 2 = 10 students
Number of students in class B chose Mystery type of book = 4 full and 1 half = (4 × 2) + 1 = 8 + 1 = 9 students.
Total number of students in Classes A and B chose mystery as their favorite type of book = 10 + 9 = 19 students.
Question 18.
A. Ellie has $22 to spend on art supplies. She wants to buy at least one canvas, one tube of paint, and one brush. Which art supplies can she buy if she spends all of her money?

Answer:

She can buy 3 canvas , 2 tube of paint and 2 brushes.
B. Describe the given information and solve the problem. Explain your thinking and show the supplies she can buy on the bar graph.
Answer:

Topic 7 Performance Task
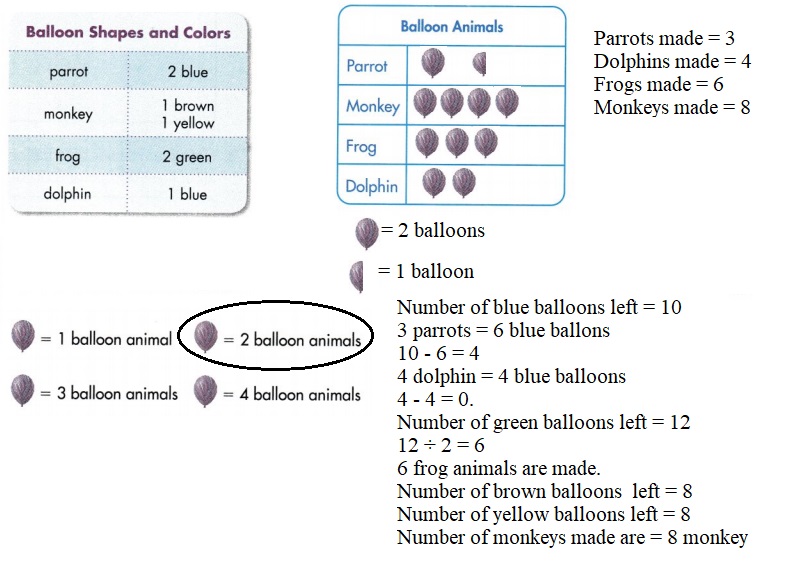
Twisting Balloons Miles twisted balloons into different animals at his daughter’s birthday party. The Balloons Used picture graph shows the different color balloons he used.
Use the Balloons Used picture graph to answer Questions 1 and 2.

Question 1.
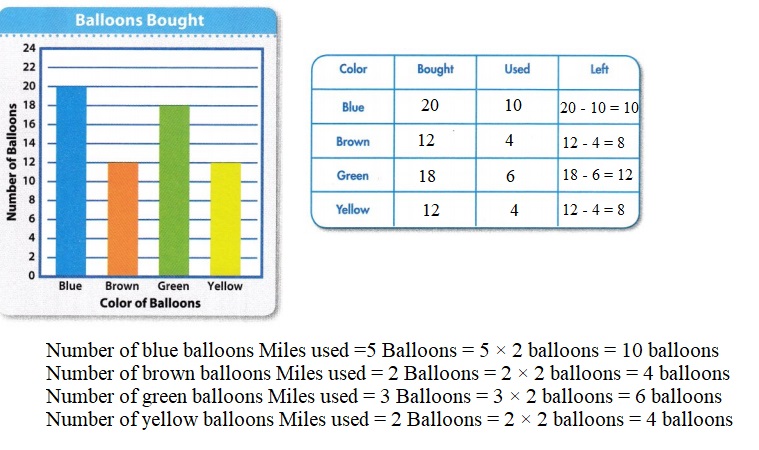
How many more green balloons than yellow balloons did Miles use? Explain.
Answer:
one Balloon = 2 balloons
Number of green balloons Miles used = 3 Balloons = 3 × 2 balloons = 6 balloons
Number of yellow balloons Miles used = 2 Balloons = 2 × 2 balloons = 4 balloons
Number of more green balloons Miles used than yellow balloons = 6 – 4 = 2 balloons.
Miles used 2 more green balloons than yellow balloons.
Question 2.
How many fewer blue balloons were used than all of the other colors combined? Explain.
Answer:
Number of blue balloons Miles used =5 Balloons = 5 × 2 balloons = 10 balloons
Number of brown balloons Miles used = 2 Balloons = 2 × 2 balloons = 4 balloons
Number of green balloons Miles used = 3 Balloons = 3 × 2 balloons = 6 balloons
Number of yellow balloons Miles used = 2 Balloons = 2 × 2 balloons = 4 balloons
Total number of green, yellow and brown balloons Miles used combined = 4 + 6 + 4 = 14 balloons.
Number of fewer blue balloons were used than all of the other colors combined = 14 – 10 = 4 balloons.
4 fewer blue balloons were used than all of the other colors combined.
Use the Balloons Used picture graph and the Balloons Bought bar graph to answer Question 3.
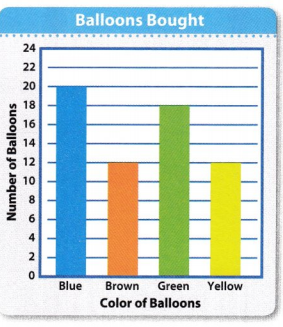
Question 3.
How many balloons does Miles have left? Complete the table below.
Answer:
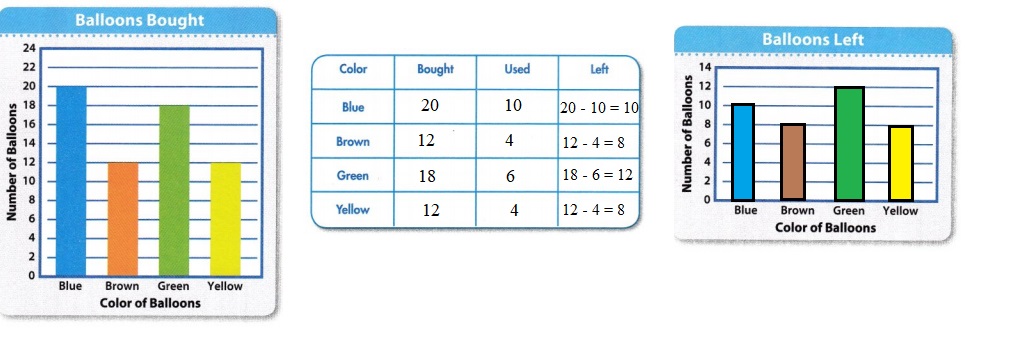
Use your response to Question 3 to answer Question 4.
Question 4.
Complete the bar graph to show how many balloons are left.
The Balloon Shapes and Colors table shows the number and color of balloons Miles needs to use to make each balloon animal. Use your response to Question 4 and the Balloon Shapes and Colors table to answer Question 5.

Answer:
Question 5.
Miles plans to use all of the balloons that are left and wants to make at least one of each balloon animal. Make a picture graph to show one way Miles can finish using the balloons.

Part A
Circle the key you will use.

Answer:

Part B
Complete the picture graph and explain how you solved the problem.

Answer: