Go through the enVision Math Common Core Grade 4 Answer Key Topic 12 Understand and Compare Decimals regularly and improve your accuracy in solving questions.
enVision Math Common Core 4th Grade Answers Key Topic 12 Understand and Compare Decimals
Essential Questions:
How can you write a fraction as a decimal? How can you locate points on a number line? How do you compare decimals?

enVision STEM Project: Energy and Decimals
Do Research Use the Internet or other sources to research other sports or games where players transfer energy to cause collisions in order to score points and win.
Journal: Write a Report Include what you found. Also in your report:
- Explain how the transfer of energy helps the player or team score.
- A game of curling is broken into ten rounds called ends. Suppose a team wins 6 of the 10 ends. Write a fraction with a denominator of 10 and an equivalent fraction with a denominator of 100. Then, write an equivalent decimal that represents the same value.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- hundredth
- tens
- place value
- tenth
Question 1.
A ________ is one of 10 equal parts of a whole, written as \(\frac{1}{10}\).
Answer: A tenth is one of 10 equal parts of a whole, written as \(\frac{1}{10}\).

Question 2.
__________ is the position of a digit in a number that is used to determine the value of the digit.
Answer: tens is the position of a digit in a number that is used to determine the value of the digit.
Question 3.
A __________ is one of 100 equal parts of a whole, written as \(\frac{1}{100}\).
Answer: A hundredth is one of 100 equal parts of a whole, written as \(\frac{1}{100}\).
Comparing Fractions
Write >, <, or = in the ![]() .
.
Question 4.
\(\frac{5}{100}\) ![]() \(\frac{5}{10}\)
\(\frac{5}{10}\)
Answer: \(\frac{5}{100}\) < \(\frac{5}{10}\)
Question 5.
\(\frac{1}{10}\) ![]() \(\frac{1}{100}\)
\(\frac{1}{100}\)
Answer: \(\frac{1}{10}\) > \(\frac{1}{100}\)
Question 6.
\(\frac{2}{10}\) ![]() \(\frac{20}{100}\)
\(\frac{20}{100}\)
Answer: \(\frac{2}{10}\) = \(\frac{20}{100}\)
Parts of a Whole
Complete each fraction to represent the shaded part of the whole.
Question 7.
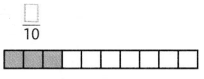
Answer: There are 10 blocks of which 3 are shaded. So, the fraction of the shaded part of the whole is \(\frac{3}{10}\)
Question 8.
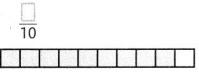
Answer: There are 10 blocks of which 0 are shaded. So, the fraction of the shaded part of the whole is 0.
Question 9.

Answer: There are 10 blocks of which 7 are shaded. So, the fraction of the shaded part of the whole is \(\frac{7}{10}\)
Shade the part of the whole that represents the fraction.
Question 10.

Answer:

Question 11.

Answer:

Question 12.

Answer:


Problem Solving
Question 13.
Reasoning Rob walked \(\frac{2}{10}\) block. Drew walked \(\frac{5}{10}\) block. Write a comparison for the distance Rob and Drew each walked.
Answer:
Given,
Rob walked \(\frac{2}{10}\) block.
Drew walked \(\frac{5}{10}\) block.
Drew walked more than Rob.
Pick a Project
PROJECT 12A
How much will it cost to visit a national park?
Project: Write a Travel Journal

PROJECT 12B
How do you know who won the event?
Project: Compare Olympic Racing Times

PROJECT 12C
Would you like to win an award for a presentation?
Project: Make a Presentation about Adding Fractions

PROJECT 12D
How did railroads help build Florida?
Project: Build a Miniature Railroad

Lesson 12.1 Fractions and Decimals
Solve & Share
According to a survey, 7 out of 10 pet owners have a dog. Represent this in a drawing.
I can … relate fractions and decimals.

Look Back! How many pet owners do NOT have a dog? Write your answer as a fraction.
Essential Question
How Can You Write a Fraction as a Decimal?
Visual Learning Bridge
On Kelsey Street, 6 out of 10 houses have swing sets. Write \(\frac{6}{10}\) as a decimal.
A decimal is another representation for a fraction and also names parts of wholes. A decimal is a number with one or more digits to the right of the decimal point.
Fractions with denominators of 10 and 100 may be written as decimals.
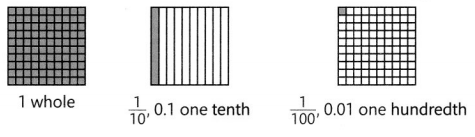
Sixth tenths or \(\frac{6}{10}\) of the houses have swing sets.
You can write \(\frac{6}{10}\) as a decimal by putting a 6 in tenths place. The tenths place is to the right of the decimal point.
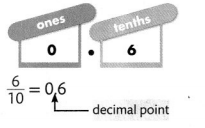
\(\frac{6}{10}\) and \(\frac{60}{100}\) are equivalent.
You can write \(\frac{60}{100}\) as a decimal by using tenths and hundredths places The hundredths place is to the right of tenths place.
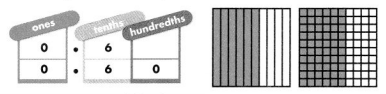
So, 0.6 or 0.60 of the houses have swing sets.
Convince Me! Reasoning in the Kelsey Street neighborhood, 75 out of 100 houses are two-story homes. Write \(\frac{75}{100}\) as a decimal. Shade the grid to show the equivalent fraction and decimal.

Another Example!
You can use grids to show how money relates to fractions and decimals.
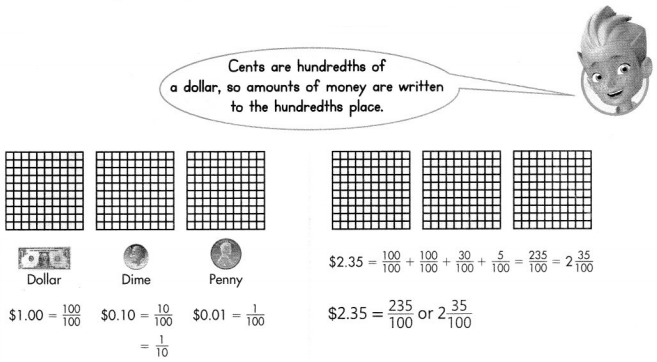
Guided Practice
Do You Understand?
Question 1.
How can you use grids to represent $4.71?
Answer:
Do You Know How?
Question 2.
Write a decimal and a fraction for the part of the grid that is shaded.

Answer: There are 10 blocks of which 5 are shaded and 5 are not shaded.
So, the decimal of the shaded part is 0.5
The fraction of the shaded part is \(\frac{5}{10}\)
Independent Practice
For 3-6, write a decimal and fraction for each diagram.
Question 3.

Answer: There are 100 blocks of which 4 are shaded and 96 are not shaded.
So, the decimal of the shaded part is 0.04
The fraction of the shaded part is \(\frac{4}{100}\)
Question 4.

Answer: There are 200 blocks of which 154 are shaded and 46 are not shaded.
So, the decimal of the shaded part is 0.77
The fraction of the shaded part is \(\frac{154}{200}\)
Question 5.

Answer: There are 100 blocks of which 39 are shaded and 61 are not shaded.
So, the decimal of the shaded part is 0.39
The fraction of the shaded part is \(\frac{39}{100}\)
Question 6.

Answer:
Problem Solving
Question 7.
The arena of the Colosseum in Rome was about \(\frac{15}{100}\) of the entire Colosseum. Write this amount as a decimal.

Answer:
Given,
The arena of the Colosseum in Rome was about \(\frac{15}{100}\) of the entire Colosseum.
The fraction \(\frac{15}{100}\) can be written as 0.15.
Question 8.
What fraction of the Colosseum was NOT the arena? Write and solve an equation.
Answer:
\(\frac{100}{100}\) – \(\frac{15}{100}\) = \(\frac{85}{100}\)
Question 9.
Vocabulary Write the vocabulary word that best completes the sentence:
Jelena says, “One dime is one ________ of a dollar.”
Answer:
Jelena says, “One dime is one tenth of a dollar.”
Question 10.
Number Sense About how much of the rectangle is shaded green? Write this amount as a fraction and as a decimal.

Answer: \(\frac{1}{10}\) or 0.1
Question 11.
Critique Reasoning Cher adds up the money in her piggy bank. She has a one-dollar bill and 3 dimes. Did Cher write the amount of money correctly? If not, what mistake did Cher make? $1.3
Answer:
Given,
Cher adds up the money in her piggy bank. She has a one-dollar bill and 3 dimes.
The amount of money is always written in hundredths. Cher should have written $1.30
Question 12.
Higher Order Thinking The diagram models the plants in a vegetable garden. Write a fraction and a decimal for each vegetable in the garden.

Answer:
Radishes: \(\frac{23}{100}\), 0.23
Carrots: \(\frac{35}{100}\), 0.35
Corn: \(\frac{15}{100}\), 0.15
Lettuce: \(\frac{27}{100}\), 0.27
Assessment Practice
Question 13.
Which decimal represents \(\frac{5}{100}\)?
A. 0.05
B. 0.5
C. 0.50
D. 0.95
Answer:
Given the fraction \(\frac{5}{100}\)
It can be written in the decimal form as 0.05.
Thus the correct answer is option A.
Question 14.
Which fraction and decimal represent twenty-nine hundredths?
A. 0.29 and \(\frac{29}{10}\)
B. 0.29 and \(\frac{100}{29}\)
C. 2.9 and \(\frac{29}{100}\)
D. 0.29 and \(\frac{29}{100}\)
Answer:
twenty-nine hundredths mean 29 of hundred.
The decimal form will be 0.29
The fraction form is \(\frac{29}{100}\).
Thus the correct answer is option D.
Lesson 12.2 Fractions and Decimals on the Number Line
Solve & Share
Name the fractions and/or decimals of each lettered point on the number lines. Tell how you decided.
I can … locate and describe fractions and decimals on number lines.

Look Back! Is the name for point B above different from the name for point B on the number line below? Explain.

Essential Question
How Can You Locate Points on a Number Line?
Visual Learning Bridge
In long-track speed skating, each lap is \(\frac{4}{10}\) kilometer. During practice, Elizabeth skated 3.75 kilometers. Draw a number line to show \(\frac{4}{10}\) and 3.75.
You can use a number line to locate and describe fractions and decimals.
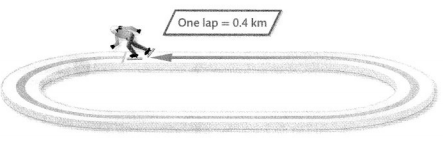
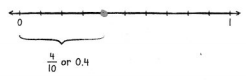
Locate \(\frac{4}{10}\) on a number line.
Draw a number line and divide the distance from 0 to 1 into 10 equal parts to show tenths.
The distance from 0 to 0.4 is four tenths the distance from 0 to 1.
Draw a point at \(\frac{4}{10}\)
Locate 3.75 on a number line.
You can show 3.75 on a number line divided into tenths by plotting a point halfway between 3.7 and 3.8.

You can use a second number line to show the interval between 3.7 and 3.8. The points on both number lines are at 3.75.
Convince Me! Be Precise Which decimal shown on the number line is not placed in the correct location? Explain.

Another Example!
Fractions and decimals can name the same points on a number line.
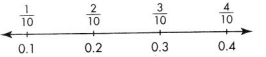
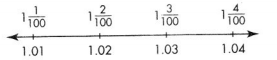
Mixed numbers and decimals can name the the same points on a number line.
Guided Practice
Do You Understand?
Question 1.
Locate\(\frac{45}{100}\) on the number line.

Answer:
Question 2.
Draw a number line to represent both the decimal and fraction for eight tenths.
Answer:
Do You Know How?
For 3-6, name the decimal and fraction for each point on the number line.
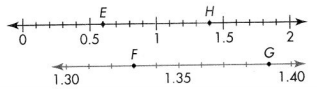
Question 3.
E
Answer:
The decimal at E point is 0.6.
The fraction at E point is 6/100.
Question 4.
H.
Answer:
The decimal at H point is 1.4.
The fraction at H point is 7/5.
Question 5.
F
Answer:
The decimal at F point is 1.33
The fraction at F point is 133/100.
Question 6.
G
Answer:
The decimal at G point is 1.39
The fraction at G point is 139/100
Independent Practice
For 7-8, label the number lines with the given fractions and decimals.
Question 7.
Represent the decimals and fractions from 3.08 to 3.13.

Answer:
Question 8.
Represent the fractions and decimals from \(\frac{4}{10}\) to 1.

Answer:
For 9-16, name the decimal and fraction for each point on the number line.
![]()
Question 9.
J
Answer:
The decimal at the point J is 4.66
The fraction at the point J is 233/50
Question 10.
K
Answer:
The decimal at the point K is 4.62
The fraction at the point K is 231/50.
Question 11.
L
Answer:
The decimal at the point L is 4.8
The fraction at the point L is 48/100.
Question 12.
M
Answer:
The decimal at the point M is 4.53
The fraction at the point M is 453/100.
Question 13.
N
Answer:
The decimal at the point N is 4.69
The fraction at the point N is 469/100.
Question 14.
O
Answer:
The decimal at the point 0 is 4.76
The fraction at the point 0 is 119/25.
Question 15.
P
Answer:
The decimal at the point P is 4.6
The fraction at the point P is 23/5.
Question 16.
Q
Answer:
The decimal at the point Q is 3.59
The fraction at the point Q is 359/100
Problem Solving
Question 17.
Write the five missing decimals on the number line.
![]()
Answer:
![]()
The five missing decimals on the number line are 0.4, 0.6, 0.8, 1.2, and 1.4.
The difference of the numbers in the number line is 0.2
Question 18.
Write the five missing fractions on the number line.

Answer:

The five missing fractions on the number line are 41/100, 43/100, 46/100, 47/100, and 50/100.
The difference of the fractions on the number line is 1/100.
Question 19.
Draw a number line to show 60 cents. Use the number line to write 60 cents as a fraction and as a decimal.
Answer:
Question 20.
Make Sense and Persevere Neil is learning about unusual units of volume. There are 2 pecks in 1 kenning. There are 2 kennings in 1 bushel. There are 8 bushels in 1 quarter. There are 5 quarters in 1 load. Write a number sentence to show how many pecks are in 1 load.
Answer:
Given that,
2 pecks in 1 kenning.
2 kinnings in 1 bushel.
8 bushels in 1 quarter.
5 quarters in 1 load.
Therefore 2 pecks in 1 load.
Question 21.
Draw a number line and plot a point at each number shown.
2\(\frac{71}{100}\) 2.6 2\(\frac{82}{100}\)
Answer:
Question 22.
Higher Order Thinking Use a number line to name two numbers that are the same distance apart as 3.2 and 3.8.
Answer: 0 and 0.6
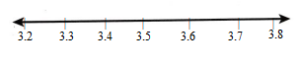
Assessment Practice
Question 23.
What decimals or fractions do the points on the number lines show? Choose the decimals and fractions from the box to label the number lines.
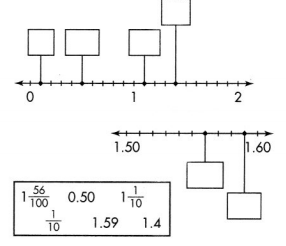
Answer:
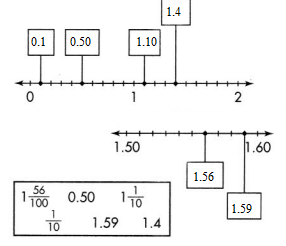
Question 24.
What decimals or fractions do the points on the number lines show? Choose the decimals and fractions from the box to label the number lines.
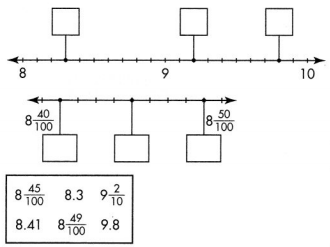
Answer:
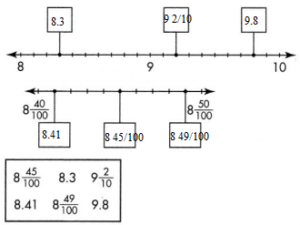
Lesson 12.3 Compare Decimals
Solve & Share
A penny made in 1982 weighs about 0.11 ounce. A penny made in 2013 weighs about 0.09 ounce. Which penny weighs more? Solve this problem any way you choose.
I can … compare decimals by reasoning about their size.

Look Back! Construct Arguments Simon and Danielle are eating oranges. Danielle says, “Because we each have 0.75 of an orange left, we have the same amount left to eat.” Do you agree with Danielle? Explain.
Essential Question
How Do You Compare Decimals?
Visual Learning Bridge
Donovan ran the 100-meter race in 10.11 seconds. Sal ran the same race in 10.09 seconds. Who had the faster time?
There is more than one way to compare decimals.

One Way
Use hundredths grids.
The whole numbers are the same. Compare the digits in the tenths place.
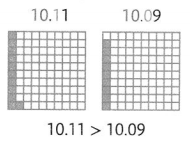
Sal had the faster time.
Another Way
Use place value.
The whole number parts are the same.
The decimal parts are both to the hundredths.
11 hundredths is greater than 9 hundredths.
10.11 >10.09
Sal had the faster time.
Another Way
Start at the left.
Compare each place value. Look for the first place where the digits are different.
10.11 10.09
1 tenth > 0 tenths
10.11 > 10.09
Sal had the faster time.
Convince Me! Reasoning Write four different digits in the blank spaces to make each comparison true. Explain your reasoning.
0. ______ 8 < 0.______ 0.5 _____ > 0.______ 9
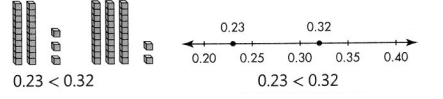
Another Example!
You can also use place-value blocks or number lines to compare.
Grids, place-value blocks, and number lines are all appropriate tools to use for comparing decimals. When using place-value blocks, let
the flat equal one whole.
Guided Practice
Do You Understand?
Question 1.
Cy says, “0.20 is greater than 0.2 because 20 is greater than 2.” Do you agree? Explain.
Answer: No 0.20 and 0.2 are equal in the decimal. Because 0 after 2 will remain the same and 0 before 2 will make a lot of change as it becomes hundredths.
Do You Know How?
For 2-5, write >, <, or = in each ![]() . Use an appropriate tool as needed to compare.
. Use an appropriate tool as needed to compare.
Question 2.
0.70 ![]() 0.57
0.57
Answer:
0.70 > 0.57
Question 3.
0.41 ![]() 0.14
0.14
Answer:
0.41 > 0.14
Question 4.
6.28 ![]() 7.31
7.31
Answer:
6.28 < 7.31
Question 5.
1.1 ![]() 1.10
1.10
Answer:
1.1 = 1.10
Independent Practice
Leveled Practice For 6-14, write >,<, or = in each ![]() . Use an appropriate tool as needed to compare.
. Use an appropriate tool as needed to compare.
Question 6.

Answer:
0.17 < 0.2
Question 7.
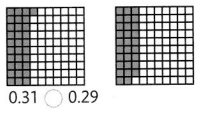
Answer:
0.31 > 0.29
Question 8.
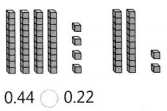
Answer:
0.44 > 0.22
Question 9.
0.1 ![]() 0.1 0
0.1 0
Answer:
0.1 = 0.10
Question 10.
$2.98 ![]() $2.56
$2.56
Answer:
$2.98 > $2.56
Question 11.
7.01 ![]() 7.1
7.1
Answer:
7.01 > 7.1
Question 12.
0.08 ![]() 0.7
0.7
Answer:
0.08 < 0.7
Question 13.
3.40 ![]() 3.4
3.4
Answer:
3.40 = 3.4
Question 14.
$21.50 ![]() $20.99
$20.99
Answer:
$21.50 > $20.99
For 15-20, write a decimal to make each comparison true.
Question 15.
______ < 0.23
Answer:
0.20 < 0.23
Question 16.
8.60 = _______
Answer:
8.60 = 8.60
Question 17.
______ > 4.42
Answer:
3.43 > 4.42
Question 18.
13.2 > ______
Answer:
13.2 > 12.4
Question 19.
5.2 < ______
Answer:
5.2 < 4.3
Question 20.
6.2 = ______
Answer:
6.2 = 6.2
Problem Solving
Question 21.
Use Appropriate Tools Maria timed how long it took her Venus Fly Trap to close. The first time it took 0.43 second to close. The second time took 0.6 second to close. Which was the faster time? Draw place-value blocks to show your comparison.
Answer:
Given that,
Maria took a time to her venus fly trap to close for first time = 0.43
Maria took a time to her venus fly trap to close for second time = 0.6
Second time was the faster time.
Question 22.
Fishing lures have different weights. Which lure weighs more?
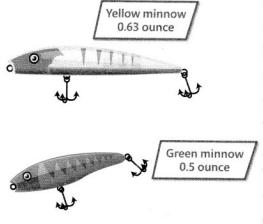
Answer:
Given that,
The weight of the yellow minnow fishing lures = 0.63
The weight of the green minnow fishing lures = 0.5
Yellow minnow fishing lures is more than green minnow fishing lures.
So, 0.63 > 0.5
Question 23.
Number Sense Ellen wants to give 100 toys to each of 9 charities. In one week, she collects 387 toys. The next week, she collects 515 toys. Has Ellen reached her goal? Use an estimate to explain.
Answer:
Given that,
Ellen wants to give 100 toys to each of 9 charities.
Total number of toys she collected in one week = 387
Total number of toys she collected in next week = 515
Total number of toys she collected = 387 + 515 = 902
100 toys to each of 9 charities = 9 × 100 = 900
So, she reached her goal.
Question 24.
Higher Order Thinking Tori has two different-sized water bottles. In the larger bottle, she has 0.81 liter of water. In the smaller bottle, she has 1.1 liters of water. Can you tell whether one bottle has more water? Explain.
Answer:
Given that,
In the longer bottle she has a water = 0.81 liter.
In the smaller bottle she has a water = 1.1 liter.
0.81 > 1.1
So, the smaller has more water.
Assessment Practice
Question 25.
Stanley found the weights of two minerals, quartz and garnet. The quartz weighed 3.76 ounces and the garnet weighed 3.68 ounces.
Explain how Stanley can use a tool to find which mineral weighed more.
Explain how Stanley can use place value to find which mineral weighed less.
Answer:
Given that,
The weight of a quartz = 3.76 ounces
The weight of a garnet = 3.68 ounces
Therefore 3.68 > 3.75
The weight of a quartz is more than the weight of a garnet
Using the place value
3.68 and 3.75
Ten’s place of a numbers are
6 < 7
The weight of a quartz is more.
Lesson 12.4 Add Fractions with Denominators of 10 and 100
Solve & Share
The mural is divided into 100 equal parts. Marilyn’s class painted io of the mural, and Cal’s class painted 20 of the mural. How much of the mural have the two classes painted? Solve this problem any way you choose.
I can … use equivalence to add fractions with denominators of 10 and 100.

You can use appropriate tools. Think about how you can use the grid to find how much of the mural the two classes painted. Show your work in the space above!
Look Back! How much of the mural remains to be painted? Write the amount as a decimal.
Essential Question
Hall How Can You Add Fractions with Denominators of 10 and 100?
Visual Learning Bridge
Steve and Jana collected money for an animal shelter. Steve collected \(\frac{4}{10}\) of their goal while Jana collected \(\frac{5}{100}\). How much of their goal did Jana and Steve collect?

Use like denominators to add fractions.
The red shows \(\frac{4}{10}\) of the goal, and the blue shows \(\frac{5}{100}\) of the goal.
The amount they collected can be written as to \(\frac{4}{10}\) + \(\frac{5}{100}\)
You can use equivalent fractions to write tenths as hundredths.
Rename \(\frac{4}{10}\) as an equivalent fraction with a denominator of 100.
Multiply the numerator and denominator by 10.
\(\frac{4 \times 10}{10 \times 10}=\frac{40}{100}\)
Add the numerators and write the sum over the like denominator.
\(\frac{40}{100}\) + \(\frac{5}{100}\) = \(\frac{45}{100}\)
Jana and Steve collected \(\frac{45}{100}\) of their goal.
Convince Me! Construct Arguments in the problem above, why is the denominator of the total 100 and not 200?
Guided Practice
Do You Understand?
Question 1.
Suppose Jana collected another \(\frac{25}{100}\) of their goal. What fraction of the goal have they now collected?
Answer:
Given that,
Jana collected money = \(\frac{5}{100}\).
Jana collected another \(\frac{25}{100}\).
Fraction of goal have they collected =
\(\frac{5}{100}\) + \(\frac{25}{100}\) =
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
\(\frac{5}{100}\) + \(\frac{25}{100}\) =\(\frac{30}{100}\)
Question 2.
Write a problem that represents the addition shown below, then solve.
Answer:
Do You Know How?
For 3-8, add the fractions.
Question 3.
\(\frac{3}{10}+\frac{4}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCM of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{3}{10}\) × \(\frac{10}{10}\)) + (\(\frac{4}{100}\) × \(\frac{1}{1}\))
\(\frac{30}{100}\) + \(\frac{4}{100}\) = \(\frac{34}{100}\)
Question 4.
\(\frac{71}{100}+\frac{5}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{71}{100}\) × \(\frac{1}{1}\)) + (\(\frac{5}{10}\) × \(\frac{10}{10}\))
\(\frac{71}{100}\) + \(\frac{50}{100}\) = \(\frac{121}{100}\)
Question 5.
\(\frac{4}{100}+\frac{38}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{4}{100}\) × \(\frac{1}{1}\)) + (\(\frac{38}{10}\) × \(\frac{10}{10}\))
\(\frac{4}{100}\) + \(\frac{380}{100}\) = \(\frac{384}{100}\)
Question 6.
\(\frac{90}{100}+\frac{1}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{90}{100}\) × \(\frac{1}{1}\)) + (\(\frac{1}{10}\) × \(\frac{10}{10}\))
\(\frac{90}{100}\) + \(\frac{10}{100}\) = \(\frac{100}{100}\) = 1
Question 7.
\(\frac{8}{10}+\frac{1}{10}+\frac{7}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{9}{10}\) × \(\frac{10}{10}\)) + (\(\frac{7}{100}\) × \(\frac{1}{1}\))
\(\frac{90}{100}\) + \(\frac{7}{100}\) = \(\frac{97}{100}\)
Question 8.
\(\frac{38}{100}+\frac{4}{10}+\frac{2}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{38}{100}\) × \(\frac{1}{1}\)) + (\(\frac{6}{10}\) × \(\frac{10}{10}\))
\(\frac{38}{100}\) + \(\frac{60}{100}\) = \(\frac{98}{100}\)
Independent Practice
Leveled Practice For 9-23, add the fractions.
Question 9.
\(\frac{21}{100}+\frac{2}{10}=\frac{21}{100}+\frac{ }{100}\)
Answer :
Given,
\(\frac{21}{100}+\frac{2}{10}=\frac{21}{100}+\frac{ }{100}\)
We have to find the missing number.
\(\frac{21}{100}+\frac{2}{10}\)
LCM of 10 and 100 is 100.
= \(\frac{21}{100}+\frac{20}{100}\) = \(\frac{41}{100}\)
So, the missing fraction is \(\frac{20}{100}\)
\(\frac{21}{100}+\frac{2}{10}=\frac{21}{100}+\frac{20}{100}\)
Question 10.
\(\frac{ }{10}+\frac{68}{100}=\frac{30}{100}+\frac{68}{100}\)
Answer:
Given,
\(\frac{ }{10}+\frac{68}{100}=\frac{30}{100}+\frac{68}{100}\)
We have to find the missing number.
LCM of 10 and 100 is 100.
\(\frac{30}{100}\) = \(\frac{3}{10}\)
So, the missing fraction is \(\frac{3}{10}\)
\(\frac{3}{10}+\frac{68}{100}=\frac{30}{100}+\frac{68}{100}\)
Question 11.
\(\frac{4}{10}+\frac{60}{100}=\frac{ }{10}+\frac{ }{10}\)
Answer:
Given,
\(\frac{4}{10}+\frac{60}{100}=\frac{ }{10}+\frac{ }{10}\)
We have to find the missing number.
LCM of 10 and 100 is 100.
\(\frac{60}{100}\) = \(\frac{6}{10}\)
\(\frac{4}{10}\) = \(\frac{4}{10}\)
So, the missing fraction is \(\frac{6}{10}\) and \(\frac{4}{10}\)
\(\frac{4}{10}+\frac{60}{100}=\frac{4}{10}+\frac{6}{10}\)
Question 12.
\(\frac{32}{100}+\frac{28}{100}+\frac{6}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{60}{100}\) × \(\frac{1}{1}\)) + (\(\frac{6}{10}\) × \(\frac{10}{10}\))
\(\frac{60}{100}\) + \(\frac{60}{100}\) = \(\frac{120}{100}\)
Question 13.
\(\frac{11}{10}+\frac{41}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{11}{10}\) × \(\frac{10}{10}\)) + (\(\frac{41}{100}\) × \(\frac{1}{1}\))
\(\frac{110}{100}\) + \(\frac{41}{100}\) = \(\frac{151}{100}\)
Question 14.
\(\frac{72}{100}+\frac{6}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{72}{100}\) × \(\frac{1}{1}\)) + (\(\frac{6}{10}\) × \(\frac{100}{100}\))
\(\frac{72}{100}\) + \(\frac{600}{100}\) = \(\frac{672}{100}\)
Question 15.
\(\frac{5}{10}+\frac{3}{10}+\frac{18}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{8}{10}\) × \(\frac{10}{10}\)) + (\(\frac{18}{100}\) × \(\frac{1}{1}\))
\(\frac{80}{100}\) + \(\frac{18}{100}\) = \(\frac{98}{100}\)
Question 16.
\(\frac{7}{100}+\frac{6}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{7}{100}\) × \(\frac{1}{1}\)) + (\(\frac{6}{10}\) × \(\frac{10}{10}\))
\(\frac{7}{100}\) + \(\frac{60}{100}\) = \(\frac{67}{100}\)
Question 17.
\(\frac{9}{10}+\frac{4}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{9}{10}\) × \(\frac{10}{10}\)) + (\(\frac{4}{100}\) × \(\frac{10}{10}\))
\(\frac{90}{100}\) + \(\frac{40}{100}\) = \(\frac{130}{100}\)
Question 18.
\(\frac{30}{100}+\frac{5}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{30}{100}\) × \(\frac{1}{1}\)) + (\(\frac{5}{10}\) × \(\frac{10}{10}\))
\(\frac{30}{100}\) + \(\frac{50}{100}\) = \(\frac{80}{100}\)
Question 19.
\(\frac{39}{100}+\frac{2}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{39}{100}\) × \(\frac{1}{1}\)) + (\(\frac{2}{10}\) × \(\frac{10}{10}\))
\(\frac{39}{100}\) + \(\frac{20}{100}\) = \(\frac{59}{100}\)
Question 20.
\(\frac{8}{10}+\frac{9}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{8}{10}\) × \(\frac{10}{10}\)) + (\(\frac{9}{100}\) × \(\frac{1}{1}\))
\(\frac{80}{100}\) + \(\frac{9}{100}\) = \(\frac{89}{100}\)
Question 21.
\(\frac{44}{100}+\frac{34}{100}+\frac{9}{10}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{78}{100}\) × \(\frac{1}{1}\)) + (\(\frac{9}{10}\) × \(\frac{10}{10}\))
\(\frac{78}{100}\) + \(\frac{90}{100}\) = \(\frac{168}{100}\)
Question 22.
\(\frac{70}{10}+\frac{33}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{70}{10}\) × \(\frac{10}{10}\)) + (\(\frac{33}{100}\) × \(\frac{1}{1}\))
\(\frac{700}{100}\) + \(\frac{33}{100}\) = \(\frac{733}{100}\)
Question 23.
\(\frac{28}{10}+\frac{72}{10}+\frac{84}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{100}{10}\) × \(\frac{10}{10}\)) + (\(\frac{84}{100}\) × \(\frac{1}{1}\))
\(\frac{1000}{100}\) + \(\frac{84}{100}\) = \(\frac{1084}{100}\)
Problem Solving
Question 24.
Algebra A mail carrier made a total of 100 deliveries in a day. \(\frac{76}{100}\) of the deliveries were letters, \(\frac{2}{10}\) were packages, and the rest were postcards. Write and solve an equation to find the fraction that represents how many of the deliveries were letters and packages.
Answer:
Given,
A mail carrier made a total of 100 deliveries in a day.
\(\frac{76}{100}\) of the deliveries were letters, \(\frac{2}{10}\) were packages, and the rest were postcards.
\(\frac{76}{100}\) + \(\frac{2}{10}\)
\(\frac{76}{100}\) + \(\frac{20}{100}\) = \(\frac{96}{100}\)
Question 25.
Make Sense and Persevere Balloons are sold in bags of 30. There are 5 giant balloons in each bag. How many giant balloons will you get if you buy 120 balloons? Explain.

Answer:
Given that,
Total number of balloons solids in bags = 30
Balloons in each bag = 5
If you buy 120 balloons how many bags do you have = 120/5 = 24
For 120 balloons 24 bags are filled.
Question 26.
Higher Order Thinking of the first 100 elements on the periodic table, \(\frac{13}{100}\) were discovered in ancient times, and \(\frac{21}{100}\) were discovered in the Middle Ages. Another \(\frac{5}{10}\) were discovered in the 1800s. What fraction of the first 100 elements was discovered after the 1800s? Explain.
Answer:
\(\frac{13}{100}\) were discovered in ancient times.\(\frac{21}{100}\) were discovered in the Middle Ages.
Another \(\frac{5}{10}\) discovered after 1800.
Find how many discovered after 1800 is
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{34}{100}\) × \(\frac{1}{1}\)) + (\(\frac{5}{10}\) × \(\frac{10}{10}\))
\(\frac{35}{100}\) + \(\frac{50}{100}\) = \(\frac{85}{100}\)
\(\frac{85}{100}\) are discovered after 1800.
Assessment Practice
Question 27.
Delia hiked \(\frac{7}{10}\) mile one day and \(\frac{67}{10}\) mile the next. She wanted to know how far she hiked in all. Her work is shown below.

Is Delia’s work correct? Explain.
Answer:
Delia hiked \(\frac{7}{10}\) mile one day
\(\frac{67}{10}\) mile the next.
She hiked in all is
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
L.C.M of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{7}{10}\) × \(\frac{10}{10}\)) + (\(\frac{67}{10}\) × \(\frac{10}{10}\))
\(\frac{70}{100}\) + \(\frac{670}{100}\) = \(\frac{737}{100}\)
Delia hiked in all =\(\frac{737}{100}\)
Lesson 12.5 Solve Word Problems involving Money
Solve & Share
A flash drive costs $24, including tax. A customer purchases 3 flash drives and pays the cashier $80. How much change should the cashier give back to the customer? Solve this problem any way you choose.
I can … use fractions or decimals to solve word problems involving money.

Look Back! Generalize How can you estimate and check if your solution is reasonable?
Essential Question
How Can You Solve Word Problems Involving Money?
Visual Learning Bridge
Marcus buys a toy airplane and a toy car. How much does Marcus spend? How much more does the toy airplane cost than the toy car?
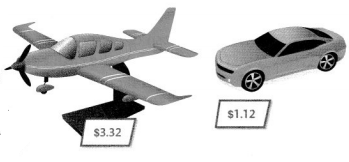
You can draw or use bills and coins to solve problems involving money.
Find $3.32 + $1.12.
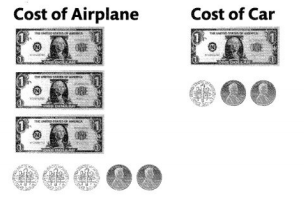
Add the bills, then count on to add each type of coin.
$4.00 + $0.40 + $0.04 = $4.44
Marcus spent $4.44.
Find $3.32 – $1.12.
Start with the cost of the airplane, then subtract the cost of the car.

Count the remaining bills and coins.
$2.00 + $0.20 = $2.20
The toy airplane costs $2.20 more than the toy car.
Convince Me! Use Structure in the examples above, how can you use place value to help add or subtract?
Another Example!
Find $6.33 ÷ 3. Draw or use bills and coins.
You can use multiplication or division to solve problems involving money.

Guided Practice
Do You Understand?
Question 1.
Write a fraction and a decimal to describe how the quantities are related.

Answer:
One coin = 1/10 of a dollar = $0.10
Three coins = 1/10 + 1/10 + 1/10 = $0.3
Question 2.
Write a fraction and a decimal to describe how the quantities are related.

Answer:
One coin = 1/100 of a dollar = $0.01
Three coins = 1/100 + 1/100 + 1/100 = $0.01
Do You Know How?
For 3, use the bills and coins to solve.
Question 3.
Marcus has $15.00. He buys a movie ticket for $11.25. How much money does Marcus have left?

Answer:
Given that,
Marcus has a total amount = $15.00
Marcus buy a movie ticket for $11.25
Marcus left amount = $15.00 – $11.25 = 3.75
Independent Practice
For 4-5, you may draw or use bills and coins to solve.
Question 4.
Sarah bought 3 wool scarves. The price of each scarf was $23.21. How much did 3 scarves cost?
Answer:
Given that,
Sarah bought wool scarves = 3
The price for each scarf= $23.21
Total amount for 3 scarves = $23.21 × 3 = 69.63
Question 5.
Carlos spends $14.38 on equipment. How much change should Carlos receive if he gives the clerk $20.00?
Answer:
Given that,
Carlos spends on equipment = $14.38
He give the clerk = $20.00
Carlos received tha change = $20.00 – $14.38 =$6.62
Problem Solving
Question 6.
Use Structure Leo went to lunch with his parents. The bill was $17.85. Complete the table to show two different combinations of coins and bills that can represent $17.85.
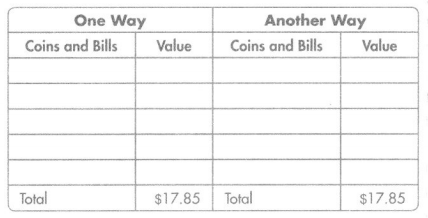
Answer:
Question 7.
Kenya purchases a new tablet for $109.78. She pays with six $20 bills. Show how you would estimate how much change Kenya should receive.
Answer:
Given that,
Kenya purchases a new tablet for $109.78
She pay with six $20 bills = 6 × 20 = 120
Kenya received change = $120 – $109.78 =$11.78
Question 8.
Algebra Marco paid $12 for 3 jump ropes. If each jump rope costs the same amount, how much does 1 jump rope cost? Write and solve an equation.
Answer:
Given that,
Algebra Marco paid $12 for 3 jump ropes.
For each jump = 12/3 = $4
For each jump cost = $4
Question 9.
Number Sense Jiang has a collection of 3,788 toy building bricks. He used 1,229 bricks to build a city. About how many bricks does Jiang have left? Explain how you estimated.
Answer:
Given that,
Jiang has a collection of toy building bricks = 3788
Jiang used bricks to build a city = 1229
Jiang has left = 3788 – 1229 = 2559
Question 10.
Higher Order Thinking Edward bought 7 concert tickets for himself and six friends for a total of $168. Each friend paid Edward back for his or her ticket. If one of Edward’s friends gave him a $50 bill, how much change should Edward return? Explain.
Answer:
Edward bought a concert tickets for himself and six friends for total = $168
Money for each ticket = 168/7 = $
24
Assessment Practice
Question 11.
Rajeev bought a skateboard for $37.74. How much change should Rajeev receive if he gave the cashier $40.00? You may draw or use bills and coins to solve.
A. $2.26
B. $2.74
C. $3.26
D. $3.74
Answer: $2.26
Explanation:
Given,
Rajeev bought a skateboard for $37.74.
Rajeev receive if he gave the cashier $40.00
40.00 – 37.74 = 2.26
Thus the correct answer is option A.
Question 12.
Genevieve bought a catcher’s mitt for $30.73 and a bat for $19.17. How much did Genevieve spend? You may draw or use bills and coins to solve.
A. $11.56
B. $49.17
C. $49.90
D. $50.73
Answer:
Given,
Genevieve bought a catcher’s mitt for $30.73 and a bat for $19.17.
30.73 + 19.17 = $49.90
Thus the correct answer is option C.
Lesson 12.6 Problem Solving
Look For and Use Structure
Solve & Share
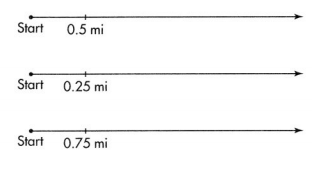
Three people hiked the same 1-mile trail. The distance for each hiker is represented in the drawings. Show about where the 1-mile mark should be on each drawing. Explain.
I can … use the structure of the place-value system to solve problems.
Thinking Habits
Be a good thinker! These questions can help you.
- What patterns can I see and describe?
- How can I use the patterns to solve the problem?
- Can I see expressions and objects in different ways?
Look Back! Look For Relationships The three drawings represent 0.5, 0.25, and 0.75 mile with equivalent lengths. How does this affect where 1-mile is located on each drawing?
Essential Question
How Can You Look for and Make Use Question of Structure to Solve Problems?
Visual Learning Bridge
Maps from two different ski resorts show a 1-mile cross-country ski trail for beginners. Show about where to mark 0.25, 0.5, and 0.75 mile on each trail.
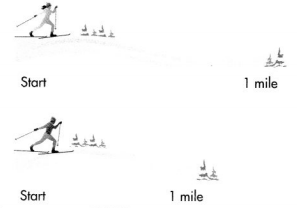
How can you determine where to mark the points on each drawing?
I need to analyze each drawing and decide about where the given decimals should be located on each.
How can I make use of structure to solve this problem?
I can
- break the problem into simpler parts.
- use what I know about decimal meanings to locate the points.
- use equivalent forms of numbers.
Here’s my thinking.
The size of a decimal depends on the size of the whole. The size of the whole is not the same for each drawing. Divide each whole in half to show 0.5 on each whole.
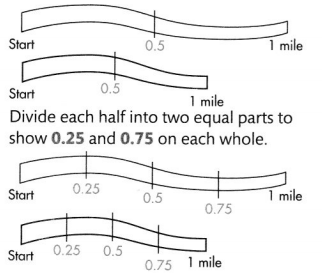
Convince Me! Use Structure Use the drawing of the trail shown. Where is the 1.5-mile mark on the trail? How did you decide?

Guided Practice
Use Structure
Margie painted 0.4 of her banner blue. Helena painted 0.5 of her banner blue.

Question 1.
Complete the drawings to show the whole, or 1, for each banner.
Answer:
Question 2.
Explain how you determined where to draw 1 whole for each banner.
Answer:
Question 3.
Do the drawings show 0.4 < 0.5? Explain.
Answer:
Independent Practice
Use Structure
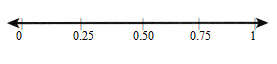
Kaitlin is making a map for the walk/run race. She wants the water stops to be at 0.5 mile, 0.3 mile, and 0.85 mile from the start.

Question 4.
Label 0.25, 0.5, 0.75 on the number line as a scale reference. Explain how you decided where to mark the number line.
Answer:
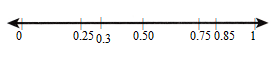
Question 5.
Estimate where 0.3 and 0.85 are located compared to the other points. Mark the points 0.3 and 0.85. Explain how you estimated.
Answer:
Problem Solving
Performance Task
Watching Savings Grow
Tomas deposits money in his savings account every month. If he continues to save $3.50 each month, how much money will he have at the end of 6 months? 12 months? Use the table and Exercises 6-11 to help solve.
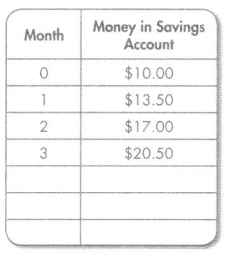
Question 6.
Reasoning What quantities are given in the problem and what do the numbers mean?
Answer:
Question 7.
Make Sense and Persevere What do you need to find?
Answer:
To find the total money in the savings account.
Question 8.
Use Structure What is the relationship between the amount of money Tomas will have in his savings account in the fourth month and the amount in the third month?

Answer:
Given that,
The amount of money Tomas will have in his savings account in the third month = $20.50
For each month he saves = $3.50
Total amount in the forth month = $20.50 + $3.50 = $24
Question 9.
Model with Math Write an expression that can be used to find the amount saved at the end of 6 months.
Answer:
For each month he save $3.50
For 6 months = $3.50 × 6 = $21.25
From the given table at 0 month he have $10 in her savings account.
So, for 6 months = $21.25 + $10 = $31.25
Question 10.
Model with Math Complete the table to find how much Tomas will have saved in 6 months.
Answer:
Question 11.
Be Precise Use the answers from the table to find how much money Tomas will have at the end of 12 months. Show your work.
Answer:
For each month he save $3.50
For 6 months = $3.50 × 12 = $42
From the given table at 0 month he have $10 in her savings account.
So, for 6 months = $42 + $10 = $52
Topic 12 Fluency Practice Activity
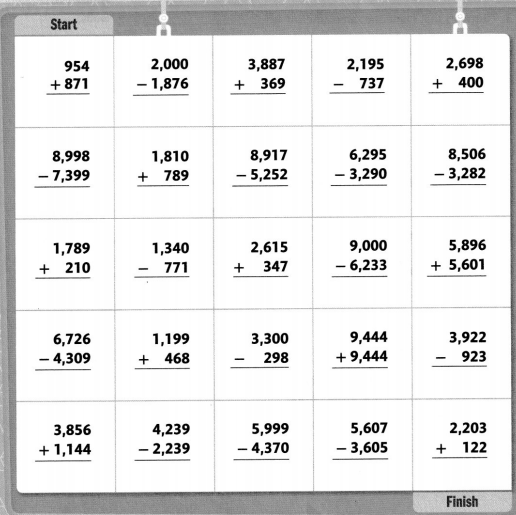
Follow the path
Shade a path from Start to finish. Follow the sums or differences that round to 2,000 when rounded to the nearest thousand. You can only move up, down, right, or left.
I can … add and subtract multi-digit whole numbers.
Topic 12 Vocabulary Review
Understand Vocabulary
Word List
- decimal
- decimal point
- equivalent
- fraction
- greater than symbol (>)
- hundredth
- less than symbol (<)
- tenth
Choose the best term from the box. Write it on the blank.
Question 1.
A dot used to separate dollars from cents or ones from tenths in a number is called a _________
Answer:
A dot used to separate dollars from cents or one’s from tenths in a number is called a one decimal point.
Question 2.
One part of 100 equal parts of a whole is called a ___________
Answer:
One part of 100 equal parts of a whole is called a one hundredth.
Question 3.
Numbers that name the same amount are __________
Answer:
Numbers that name the same amount are equivalent.
Question 4.
A symbol, such as \(\frac{2}{3}\), \(\frac{5}{1}\), or \(\frac{8}{5}\), used to name part of a whole, part of a set, or a location on a number line is called a __________
Answer: fraction
Question 5.
One out of ten equal parts of a whole is called a _________
Answer:
One out of ten equal parts of a whole is called a one hundredth.
For each of these terms, give an example and a non-example.

Answer:

Use Vocabulary in Writing
Question 9.
Krista wrote \(\frac{75}{100}\) and 0.75. Use at least 3 terms from the Word List to describe Krista’s work.
Answer:
Topic 12 Reteaching
Set A pages 445-448
The essay question on a 100-point test was worth 40 points. Write this part as a fraction and a decimal.
There are 100 points, so each point is \(\frac{1}{100}\).
\(\frac{40}{100}\) is 0.40.
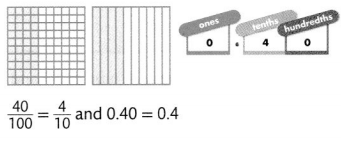
Remember that the name of a fraction can help you write it as a decimal.
Write a decimal and a fraction for each model.
Question 1.

Answer: 57/100
Question 2.

Answer: 7/10
Question 3.
Donnie has 4 dollars, 6 pennies, and 9 dimes. Write a decimal for the amount of money Donnie has.
Answer:
Set B pages 449-452
Locate 0.8 and 0.62 on a number line.
The distance from 0 to 0.8 is eight-tenths the distance from 0 to 1.
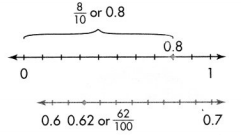
Draw a number line showing hundredths. 0.62 is between 0.6 and 0.7.
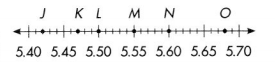
Name the decimal and fraction at each point.
Question 1.
K
Answer:
The decimal at the point K is 5.47
The fraction at the point K is 547/100.
Question 2.
M
Answer:
The decimal at the point M is 5.55
The fraction at the point M is 111/20
Question 3.
O
Answer:
The decimal at the point O is 5.68
The fraction at the point O is 144/25
Question 4.
N
Answer:
The decimal at the point N is 5.60
The fraction at the point N is 560/100.
Question 5.
L
Answer:
The decimal at the point L is 5.50
The fraction at the point L is 11/2
Question 6.
J
Answer:
The decimal at the point J is 5.42
The fraction at the point J is 542/100.
Set C pages 453-456
Compare 1.74 and 1.08.
The digits in the ones place are the same, so look at the digits after the decimal point to compare.
1.74 1.08
7 tenths > 0 tenths
1.74 > 1.08
Remember you can use tools such as place value blocks, number lines, or grids to compare decimal amounts.
Write >, <, or = in each ![]() .
.
Question 1.
$4.13 ![]() $4.32
$4.32
Answer:
The digits in the ones place are the same, so look at the digits after the decimal point to compare.
$4.13 and $4.32
1 tenths < 3 tenths
$4. 13 < $4.32
Question 2.
0.6 ![]() 0.60
0.60
Answer:
The digits in the ones place are the same, so look at the digits after the decimal point to compare.
0.6 and 0.60
0. 6 < 0.60
Question 3.
5.29 ![]() 52.9
52.9
Answer:
The digits in the ones place are the same, so look at the digits after the decimal point to compare.
5.29 and 52.9
5.29 < 52.9
Question 4.
12.91 ![]() 12.19
12.19
Answer:
The digits in the ones place are the same, so look at the digits after the decimal point to compare.
12.91and 12.19
12.91 > 12.19
Set D pages 457-460
Find \(\frac{9}{10}+\frac{49}{100}\)
Rewrite \(\frac{9}{10}\) as an equivalent fraction with a denominator of 100.
\(\frac{9 \times 10}{10 \times 10}=\frac{90}{100}\)
\(\frac{90}{100}+\frac{49}{100}=\frac{139}{100}\) or 1\(\frac{39}{100}\)
Remember to find equivalent fractions with like denominators to add.
Add. Use grids or place-value blocks as needed to help.
Question 1.
\(\frac{8}{10}+\frac{40}{100}\)
Answer:
Rewrite \(\frac{8}{10}\) as an equivalent fraction with a denominator of 100.
\(\frac{8 \times 10}{10 \times 10}=\frac{80}{100}\)
\(\frac{80}{100}+\frac{40}{100}=\frac{120}{100}\) or 1 \(\frac{1}{5}\)
Question 2.
\(\frac{24}{100}+\frac{6}{10}\)
Answer:
Rewrite \(\frac{6}{10}\) as an equivalent fraction with a denominator of 100.
\(\frac{6 \times 10}{10 \times 10}=\frac{60}{100}\)
\(\frac{24}{100}+\frac{60}{100}=\frac{84}{100}\)
Set E pages 461-464
Find $5.21 + $1.52.

Add the bills, then count on to add each type of coin.
$6.00 + $0.50 + $0.20 + $0.03 = $6.73
Remember to take away each type of bill and coin when subtracting money.
Question 1.
Chelsea had $71.18. She bought a new pair of glasses for $59.95. Can she buy a case that costs $12.95? Explain.
Answer:
Given that,
Chelsea had = $71.18
She bought a new pair of glasses = $59.95
Remaining money with Chelsea = $71.18 – $59. 95 = 12. 77
She buy a case for = $12.95
She can’t buy a case because she has only $12.77 but the cost of a case is $12.95.
Question 2.
Eddie bought 3 train tickets for $17.00 each. If he paid with three $20 bills, how much change did Eddie receive?
Answer:
Given
Eddie bought 1 train tickets = $17.00
For three tickets = $17.00 × 3 = $51
He paid bills = 3 × $20 = $60
Thus Eddie received money = $60 – $51 = $9
Set F pages 465-468
Think about these questions to help you look for and make use of structure.
Thinking Habits
- What patterns can I see and describe?
- How can I use the patterns to solve the problem?
- Can I see expressions and objects in different ways?

Remember you can use structure to break a problem into simpler parts.
Raven joined a walk-a-thon. The red dot shows how far Raven walked in one hour.
Question 1.
Complete the number line below.

Answer:

Question 2.
Estimate how far Raven walked in the first hour. Explain.
Answer: Raven walked 2 miles in one hour.
Topic 12 Assessment Practice
Question 1.
Which represent the decimal 0.7? Select all that apply.
☐ 0.07
☐ 7.00
☐ \(\frac{7}{10}\)
☐ \(\frac{70}{10}\)
☐ \(\frac{70}{100}\)
Answer:
☐ 0.07
☐ 7.00
![]() \(\frac{7}{10}\) can be written in the decimal as 0.7
\(\frac{7}{10}\) can be written in the decimal as 0.7
☐ \(\frac{70}{10}\)
![]() \(\frac{70}{100}\) can be written in the decimal as 0.7
\(\frac{70}{100}\) can be written in the decimal as 0.7
Question 2.
Select all the statements that correctly compare two numbers.
☐ 29.48 > 29.69
☐ 29.48 < 29.69 ☐ 15.36 > 15.39
☐ 16.99 < 17.99
☐ 21.30 = 21.03
Answer:
☐ 29.48 > 29.69
![]() 29.48 < 29.69 ☐ 15.36 > 15.39
29.48 < 29.69 ☐ 15.36 > 15.39
![]() 16.99 < 17.99
16.99 < 17.99
☐ 21.30 = 21.03
Question 3.
Lucy buys a puzzle for $3.89, a model airplane for $12.75, and a stuffed animal for $2.50. How much money did she spend in all? Draw or use bills and coins to solve.
A. $19.14
B. $19.00
C. $16.64
D. $16.00
Answer:
Given,
Lucy buys a puzzle for $3.89, a model airplane for $12.75, and a stuffed animal for $2.50.
$3.89 + $12.75 + $2.50 = $19.14
Therefore she spent $19.14 in all.
Thus the correct answer is option A.
Question 4.
Which point is incorrectly labeled? Explain.
![]()
Answer: C (4.9) is incorrectly labeled.
Question 5.
Catalina takes the money shown to the bookstore.

A. Does Catalina have enough for all three books? If not, how much more money does Catalina need? Explain. Draw or use bills and coins to solve.
Answer:
B. Catalina chooses to buy only 2 of the books. Choose two books for Catalina to buy, and then find how much money she will have left. Draw or use bills and coins to solve.
Answer:
Question 6.
Write a fraction and a decimal that represent the part of the grid that is green.

Answer: 63/100
There are 63 shaded blocks out of 100.
So, the fraction is \(\frac{63}{100}\)
Question 7.
Match each number on the left to its equivalent fraction.
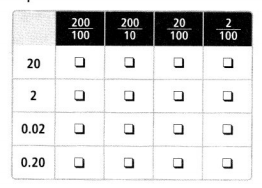
Answer:
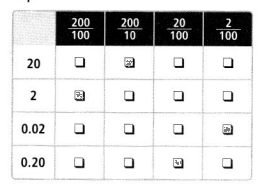
20 can be written as 20/100
2 can be written as 200/100 = 2
0.02 can be written in the fraction form as 2/100
0.20 can be written in the fraction form as 20/100 or 2/10.
Question 8.
Select all the statements that correctly compare two numbers.
☐ 7.27 > 74.7
☐ 1.24 < 1.42 ☐ 58.64 > 48.64
☐ 138.5 < 13.85 ☐ 12.56 > 12.65
Answer:
☐ 7.27 > 74.7
![]() 1.24 < 1.42
1.24 < 1.42 ![]() 58.64 > 48.64
58.64 > 48.64
☐ 138.5 < 13.85 ☐ 12.56 > 12.65
Question 9.
What fraction is equivalent to 0.4?
Answer:
The fraction is equivalent to 0.4 is \(\frac{4}{10}\)
Question 10.
Explain how to find the sum of
\(\frac{3}{10}+\frac{4}{100}\)
Answer:
The fractions have, unlike denominators. First, find the Least Common Denominator and rewrite the fractions with the common denominator.
LCM of 10 and 100 is 100.
Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCD. This is basically multiplying each fraction by 1.
(\(\frac{3}{10}\) × \(\frac{10}{10}\)) + (\(\frac{4}{100}\) × \(\frac{1}{1}\))
\(\frac{30}{100}\) + \(\frac{4}{100}\) = \(\frac{34}{100}\)
Question 11.
Use the table below.

Create a number line and plot the value of each letter.
Answer:
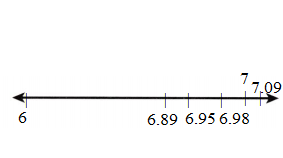
Question 12.
What decimal represents \(\frac{44}{100}\)?
Answer: The decimal that represents \(\frac{44}{100}\) is 0.44
Topic 12 Performance Task
Nature Club
The nature club at the school devoted a month to learning about different local birds. The Bird Traits photos show information about several birds they observed.

Question 1.
The club leader asked students to analyze and compare the measures from the Bird Traits photos.
Part A
Randall was asked to write the mass of a red-tailed hawk as a fraction. Label the mass on the number line and write the equivalent fraction.
Answer:
Part B
Melanie was assigned to compare the wingspans of the blue jay and the sandpiper. Which bird had a greater wingspan? Show the decimals on the grids, and write the comparison using symbols.

Answer:
Part C
Mila compared the wingspans of the red-tailed hawk and the great horned owl. Explain how to use place value to find the greater wingspan. Show the comparison using symbols.
Answer:
Question 2.
Gerald found the mass of a great horned owl and a sandpiper combined. Show how to write each mass as a fraction and then write and solve an addition equation.
Answer:
Given that mass of the great horned owl = 1.8
Mass of the sandpiper = 0.06
1.8 fraction is 18/10
0.06 fraction is 3/10
Mass of sandpiper and great horned owl is = 18/10 + 3/10 = 21/10.
Question 3.
The Blue Jay photo shows the wingspan of a blue jay Susannah observed.

Susannah said the wingspan of the blue jay was greater than the wingspan of the great horned owl since 1.4 > 1.3. Do you agree? Explain.
Answer:
Yes I will agree because the wingspan of the blue jay is 1.4
Wingspan of the great horned owl is 1.3
So the wingspan of the blue jay is greater than the wingspan of the great horned.
