Go through the enVision Math Common Core Grade 4 Answer Key Topic 7 Factors and Multiples regularly and improve your accuracy in solving questions.
enVision Math Common Core 4th Grade Answers Key Topic 7 Factors and Multiples
Essential Questions:
How can you use arrays or multiplication to find the factors of a number? How can you identify prime and composite numbers? How can you find multiples of a number?

enVision STEM Project: Analyzing the Animal Kingdom
Do Research As a defense against the cold, emperor penguins huddle together in large groups. Use the Internet or other sources to research how this helps them protect each other and their chicks.
Journal: Write a Report Include what you found. Also in your report:
- Suppose 64 penguins form a huddle to keep warm. Use a grid to draw all the possible arrays for 64.
- If a huddle of 72 penguins breaks apart, how many different ways can the penguins form equal groups? Is 72 prime or composite? Write the factor pairs of 72 to show all the ways the penguins can form equal groups.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- product
- dividend
- divisor
- quotient
Question 1.
The _________ is the answer to a division problem.
Answer:
The quotient is the answer to a division problem.
Question 2.
The number being divided is the ________.
Answer:
The number being divided is the dividend.
Question 3.
The _________ is the number that tells into how many groups something is being divided.
Answer:
The divisor is the number that tells into how many groups something is being divided.

Multiplication Find each product.
Question 4.
8 × 4
Answer:
8 × 4 = 32
32 is the product.
Question 5.
17 × 6
Answer:
17 × 6 = 102
102 is the product.
Question 6.
304 × 9
Answer:
304 × 9 = 2,735
2735 is the product.
Question 7.
555 × 5
Answer:
555 × 5 = 2775
2775 is the product.
Question 8.
22 × 26
Answer:
22 × 26 = 572
572 is the product.
Question 9.
33 × 11
Answer:
33 × 11 = 363
363 is the product.
Question 10.
56 × 70
Answer:
56 × 70 = 3920
3920 is the product.
Question 11.
36 × 91
Answer:
36 × 91 = 3,276
3276 is the product.
Question 12.
27 × 48
Answer:
27 × 48 = 1296
1296 is the product.

Question 13.
56 × 13
Answer:
56 × 13 = 728
728 is the product.
Question 14.
12 × 19
Answer:
12 × 19 = 228
228 is the product.
Question 15.
36 × 16
Answer:
36 × 16 = 576
576 is the product.
Division Find each quotient.
Question 16.
27 ÷ 3
Answer:
27 ÷ 3 = 9
9 is the quotient.
Question 17.
56 ÷ 8
Answer:
56 ÷ 8 = 7
7 is the quotient.
Question 18.
36 ÷ 4
Answer:
36 ÷ 4 = 9
9 is the quotient.
Question 19.
72 ÷ 9
Answer:
72 ÷ 9 = 8
8 is the quotient.
Question 20.
39 ÷ 3
Answer:
39 ÷ 3 = 13
13 is the quotient.
Question 21.
64 ÷ 4
Answer:
64 ÷ 4 = 16
16 is the quotient.

Question 22.
105 ÷ 5
Answer:
105 ÷ 5 = 21
21 is the quotient.
Question 23.
824 ÷ 4
Answer:
824 ÷ 4 = 206
206 is the quotient.
Question 24.
942 ÷ 3
Answer:
942 ÷ 3 = 314.33
314.33 is the quotient.
Question 5.
9,156 ÷ 3
Answer:
9156 ÷ 3 = 3052
3052 is the quotient.
Question 26.
2,156 ÷ 4
Answer:
2156 ÷ 4 = 539
539 is the quotient.
Question 27.
4,136 ÷ 8
Answer:
4136 ÷ 8 = 517
517 is the quotient.
Problem Solving
Question 28.
Model with Math Cecilia bought 2 sandwiches last week and 4 sandwiches this week. She spent a total of $42. If each sandwich costs the same amount, how much did Cecilia spend on each sandwich? Write and solve equations.
Answer:
Given that,
Total number of sandwich brought by Cecilia in last week = 2
Total number of sandwich brought by Cecilia in this week = 4
Total she spent money on sandwich = $42
Total number of sandwiches Cecilia brought in two weeks = 2 + 4 = 6
Money spent on one sandwich = $42/6 = 7
Pick a Project
PROJECT 7A
Where is Mammoth Cave National Park?
Project: Model a Campground

PROJECT 7B
How many people can fill a college basketball arena?
Project: Create a Basketball Arena

PROJECT 7C
How many arrays of potted plants do you see?
Project: Design a Plant Array for a Store Display

3-ACT MATH PREVIEW
Math Modeling
Can-Do Attitude

I can … model with math to solve a problem that involves estimating and using factors and multiples.
Lesson 7.1 Understand Factors
Solve & Share
Fourth graders at Ames School have 24 carpet squares. What are all the different ways they can organize the carpet squares into a rectangular array? Solve this problem any way you choose.
I can … find the factor pairs of a whole number

Look Back! Look for Relationships What patterns do you see in the arrays?
Essential Question
How Can You Use Arrays to Find the Factor Pairs of a Number?
Visual Learning Bridge
The music director is trying to find the best way to arrange the chairs for a performance. The chairs must be arranged in a rectangular array. How many different ways can the chairs be arranged into a rectangular array? Use grids to show all the ways the chairs can be arranged.

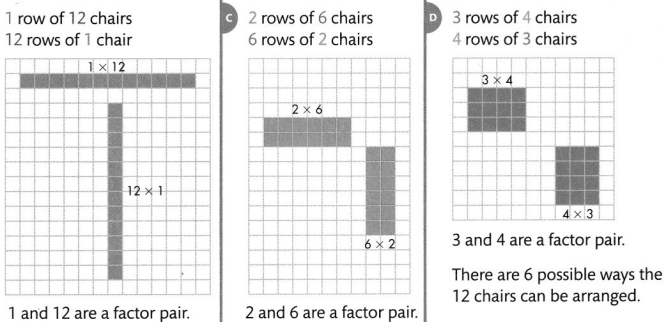
Convince Me! Critique Reasoning Blake says, “Greater numbers will always have more factors.” Do you agree? Explain.
Guided Practice
Do You Understand?
Question 1.
How are the lengths of the sides of the arrays shown on the grids on the previous page related to the factors of 12?
Answer:
Given that,
On the previous page, the length of the sides of the arrays on the grids are shown by rows and columns.
For the factor of 12
A factor divides exactly into a number , leaving no remainder is called a factors.
Rows and columns are arranged in
1 row of 12 chairs and 12 rows of 1 chair.
The factors of 12 are 1 and 12.
Question 2.
What are the lengths of the sides of the arrays that show how 5 chairs can be arranged?
Answer:
5 chairs can be arranged in
1 row of 5 chairs
5 rows of 1chairs
1 and 5 are the factors of 5.
Do You Know How?
For 3-4, find all of the factor pairs for each number. You can use grids to help.
Question 3.
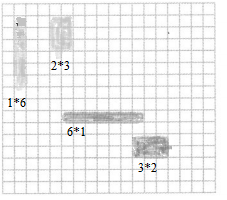
6
Answer:
A factor divides exactly into a number , leaving no remainder is called a factors.
The factors of 6 are 1, 2, 3 and 6
Factor pairs of 16 are
1 and 6
2 and 3
We can arrange the factor pairs on the grid paper be like
1 and 6 = 1 row of 6
2 and 3 = 2 rows of 3
We can also show in another away to arrange the factor pairs
6 rows of 1 and 3 rows of 2.
Question 4.
16
Answer:
A factor divides exactly into a number , leaving no remainder is called a factors.
The factors of 16 are 1, 2, 8 and 16
Factor pairs of 16 are
1 and 16
2 and 8
We can arrange the factor pairs on the grid paper be like
1 and 16 = 1 row of 16
2 and 8 = 2 rows of 8
We can also show in another away to arrange the factor pairs
16 rows of 1 and 8 rows of 2.

For 5-6, find the factors of each number.

Question 5.
45
Answer:
A factor divides exactly into a number, leaving no remainder is called factors. Factors of 35 are the 1, 3, 5, 9, 15 and 45
Question 6.
30
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
Factors of 30 are the 1, 2, 3, 5, 6, 10, 15 and 30
Independent Practice
For 7-8, use the grids to find all the possible arrays for each number. Use the arrays to help write the factors.
Question 7.

Answer:
Question 8.

Answer:
For 9-14, use grids to find the factor pair or pairs for each number.
Question 9.
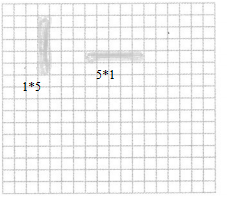
5
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
The factors of 5 are 1and 5
Factor pairs of 5 are
1 and 5
We can arrange the factor pairs on the grid paper be like
1 and 5 = 1 row of 5
We can also show in another away to arrange the factor pairs.
5 rows of 1
Question 10.
25
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
The factors of 25 are 1, 5 and 25
Factor pairs of 25 are
1 and 25
5 and 5
We can arrange the factor pairs on the grid paper be like
1 and 25 = 1 row of 25
5 and 5 = 5 rows of 5
We can also show in another away to arrange the factor pairs
25 rows of 1 and 5 rows of 5.
Question 11.
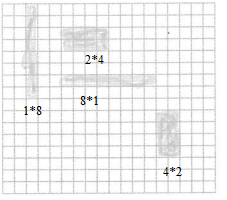
8
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
The factors of 8 are 1, 2, 4 and 8
Factor pairs of 8 are
1 and 8
2 and 4
We can arrange the factor pairs on the grid paper be like
1 and 8 = 1 row of 8
2 and 4 = 2 rows of 4
We can also show in another away to arrange the factor pairs
8 rows of 1 and 4 rows of 2.
Question 12.
36
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
The factors of 36 are 1, 2, 3, 4, 9, 12, 18 and 36
Factor pairs of 16 are
1 and 36
2 and 18
2 and 12
4 and 9
We can arrange the factor pairs on the grid paper be like
1 and 36 = 1 row of 36
2 and 18 = 2 rows of 18
3 and 12 = 3 rows of 12
4 and 9 = 4 rows of 9
We can also show in another away to arrange the factor pairs
36 rows of 1, 18 rows of 2, 12 rows of 3, and 9 rows of 4.
Question 13.
23
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
The factors of 23 are 1 and 23
Factor pairs of 23 are
1 and 23
We can arrange the factor pairs on the grid paper be like
1 and 16 = 1 row of 23
We can also show in another away to arrange the factor pairs
23 rows of 1.
Question 14.
27
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
The factors of 27 are 1, 3, 9 and 27
Factor pairs of 27 are
1 and 27
9 and 3
We can arrange the factor pairs on the grid paper be like
1 and 27 = 1 row of 27
9 and 3 = 9 rows of 3
We can also show in another way to arrange the factor pairs.
27 rows of 1 and 3 rows of 9.
Problem Solving
Question 15.
Reasoning Use the grid to find two numbers that have 2 and 3 as factors.

Answer:
Question 16.
The dwarf planet Pluto takes about 90,403 days to orbit the sun. Write this number in expanded form and using number names.
Answer:
Question 17.
David makes 17 dollars in an hour and works 25 hours each week. Linda makes ! 25 dollars in an hour and works 17 hours ! each week. How much do David and Linda make together each week? What property of multiplication does this represent?
Answer:
Given that,
Total number of dollars that David makes in an hour = 17
David works in a week = 25 hours
Total number of dollars that David makes in 25 hours = 25 × 17 =
Total number of dollars that Linda makes in an hour = 25
Linda works in a week = 17
Total number of dollars that Linda makes in 17 hours = 17 × 25
Total number of dollars with David and Linda = (25 × 17) + (17 + 25) = 850
The equation represents the Associative property of multiplication
Question 18.
What do you notice about the number of possible arrays and the number of factors of 22?
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
The factors of 22 are 1, 11 and 22
A number of factors of 22 are 3.
Question 19.
Higher Order Thinking Jane says 5 is a factor of every whole number that has a 5 in the one’s place. Fred says 5 is a factor of every whole number that has a 0 in the one’s place. Who is correct? Explain.
Answer:
Both Jane and Fred said was correct
If you divide a number with a 5 in the one’s place by 5 they divide evenly.
And if you do the same thing with any number with a 0 in the one’s place they divide evenly.
Assessment Practice
Question 20.
Which of the following are factors of both 18 and 42? Select all that apply.
☐ 1
☐ 3
☐ 4
☐ 6
☐ 14
Answer:
A factor divides exactly into a number, leaving no remainder is called factors.
The factors of both 18 and 42 are 1, 3 and 6
Question 21.
Which of the numbers below have 2, 3, and 4 as factors? Select all that apply.
☐ 86
☐ 72
☐ 36
☐ 32
☐ 24
Answer:
The numbers 72, 36, 32, and 24 have a factor of 2, 3, and 4.
Lesson 7.2 Factors
Solve & Share
Jared has 20 flowers. He wants to plant all of the flowers in equal rows in his garden. What are the different ways Jared can arrange the flowers in equal rows? Solve this problem any way you choose.
I can … use multiplication to find the factor pairs for a whole number.

Look Back! Make Sense and Persevere How can you check you have found all the different ways Jared can plant his flowers?
Essential Question
How Can You Use Multiplication to Find the Factors of a Number?
Visual Learning Bridge
Jean wants to arrange her action figures in equal-size groups. What are all the ways Jean can arrange her action figures?
Jean can think of all the factor pairs of 16. Factor pairs are two whole numbers that when multiplied give you
a certain product.

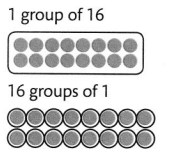
Jean can arrange 1 group of 16 figures or 16 groups of 1 figure.
1 × 16 = 16
16 × 1 = 16
So, 1 and 16 are factors of 16.
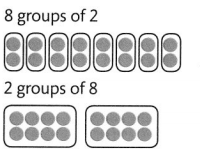
Jean can arrange 8 groups of 2 figures or 2 groups of 8 figures.
2 × 8 = 16
8 × 2 = 16
So, 2 and 8 are factors of 16.
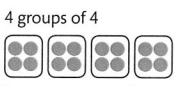
Jean can arrange 4 groups of 4 figures. 4 is a factor of 16.
4 × 4 = 16
The factor pairs for 16 are 1 and 16, 2 and 8, and 4 and 4.
Convince Me! Construct Arguments How do you know there are no other factors for 16 other than 1, 2, 4, 8, and 16? Explain.
Guided Practice
Do You Understand?
Question 1.
Jean bought 7 more action figures. What are the different equal-sized groups she can make now?
Answer:
Total number of action figures = 16
Total number of action figures that Jean brought = 7
Total number of figure at Jean = 16 + 7 = 23
Jean can arrange in two ways that are
1 group of 23 and 23 groups of 1
Question 2.
What factor besides 1 does every even number have?
Answer:
Any even number one factor is always 2 wheather one or many all the others be odd prime number.
Do You Know How?
For 3-6, write the factors of each number. Use counters to help.
Question 3.
2
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
Factors of 2 are the 1, 2
Question 4.
20
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
Factors of 20 are 1, 2, 4, 5, 10 and 20
Question 5.
28
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
Factors of 28 are 1, 2, 4, 7, 14 and 28
Question 6.
54
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
Factors of 54 are 1, 2, 3, 6, 9, 18, 27 and 50
Independent Practice
Leveled Practice For 7-12, write the factor pairs for each number.
Remember, the factors of a number always include 1 and the number.
Question 7.
34
______ and 34
2 and ______
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
Pair factors of 34 are
1 and 34
2 and 17
Question 8.
39
1 and ______
______ and 13
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
The factors of 39 are
1 and 39
3 and 13
Question 9.
61
1 and ______
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
The factors of 61 are
1 and 61
Question 10.
14
______ and ______
______ and ______
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
The factors of 14 are
1 and 14
2 and 17
Question 11.
22
______ and ______
______ and ______
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
Factors of 22 are
1 and 14
2 and 7
Question 12.
51
______ and ______
______ and ______
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
The factors of 51 are
1 and 51
3 and 17
For 13-21, write the factors of each number. Use counters to help as needed.
Question 13.
6
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 6 are 1, 2, 3 and 6
Question 14.
32
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 32 are 1, 2, 3, 4, 8, 16 and 32
Question 15.
83
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 83 are 1 and 83
Question 16.
11
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 11 are 1 and 11
Question 17.
49
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 49 are 1, 7 and 49
Question 18.
25
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 25 are 1, 5 and 25
Question 19.
30
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30
Question 20.
63
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 63 are 1, 3, 7, 9, 21 and 63
Question 21.
19
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 19 are 1 and 19
Problem Solving
Question 22.
Irene wants to list the factors for 88. She writes 2, 4, 8, 11, 22, 44, and 88. Is Irene correct? Explain.
Answer:
Given that,
The Irene write the list of factors for are
2, 4, 8, 11, 22, 44, and 88 all these are the factors of 88.
Yes, Irena is correct.
But we have one another factor that is 1.
Question 23.
enVision® STEM The roots of a plant are often the largest part of the plant. Winter rye can grow combined root tissue well over 984,000 feet in length. Write this number in expanded form.
Answer:
Question 24.
Model with Math A restaurant receives a shipment of 5,000 ketchup packets. In one week, they use 1,824 packets. The next week, they use 2,352 packets. Write and solve equations to find how many ketchup packets the restaurant has left.
Answer:
Given that,
The restaurant receives a shipment of ketchup packets = 5000
Total number of ketchup packets that the restaurant used in one week = 1824
Total number of ketchup packets that the restaurant used in next week = 2352
Total number of packets that the restaurant used in one week and next week = 1824 + 2352 = 4176
Question 25.
Any number that has 9 as a factor also has 3 as a factor. Why is this?
Answer:
Question 26.
Higher Order Thinking A mother manatee, pictured to the right, is three times as long as her baby manatee.
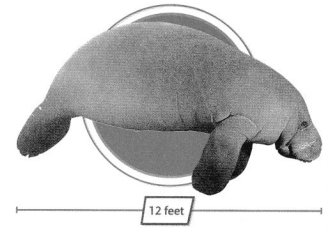
a. How long is her baby manatee? Write and solve an equation.
Answer:
b. If a blue whale is 9 times as long as the manatee shown, how much longer is a blue whale than the manatee? Write and solve equations:
Answer:
Given that,
The given manatee show length = 12 feets
The blue whale length = 9 times longer than the manatee.
Total length of the blue whale = 12 × 9 = 108 feets
Assessment Practice
Question 27.
Which number has 3 and 29 as one of its factor pairs?
A. 3
B. 17
C. 67
D. 87
Answer:
D is correct.
87 has the factor pair of 3 and 29.
Factor pair is a set of two factors which, when multiplied together give a particular product is called factor pairs.
Question 28.
A store manager wants to display 45 cans of soup in an array. Which of the following shows 3 ways the cans could be displayed?
A. 1 × 9, 9 × 5, 3 × 15
B. 15 × 3, 9 × 1, 5 × 9
C. 5 × 9, 3 × 15, 9 × 5
D. 45 × 1, 15 × 1, 9 × 1
Answer:
Given that,
The store manager wants to display 45 cans of soup in an array.
We want to arrange in 3 ways from the following
5 × 9, 3 × 15, 9 × 5
Option C is the correct
Lesson 7.3 Problem Solving
Repeated Reasoning
Solve & Share
A closet company sells wooden storage cubicles. Jane bought 24 cubicles. She wants to arrange them in a rectangular array. What are all of the different ways Jane can arrange them, using all of her cubicles? Explain how you know you found them all.
I can … use repeated reasoning to generalize how to solve similar problems.

Thinking Habits
Be a good thinker! These questions can help you.
- Are any calculations repeated?
- Can I generalize from examples?
- What shortcuts do I notice?

Look Back! Generalize Do you need to try all numbers from 1 to 24 to be sure you have all the factor pairs for 24? Explain.
Essential Question
How Can You Use Repeated Reasoning to Find All the Factors for a Number?
Visual Learning Bridge
A new city park is opening. The gardener needs to select 15 trees from a nursery and plant the trees in a rectangular array. What are all the different ways the gardener can plant the trees?

Can you look for a general method to solve this problem?
I can find all the possible factors of 15 that can be arranged in a rectangular array.
How can I make a generalization from repeated reasoning?
I can
- look for things that repeat in a problem.
- look for shortcuts.
- generalize from the example.
To find all of the factors of 15, I divide 15 by divisors starting with 1. Then I use the Commutative Property to write two multiplication equations.
1 × 15 = 15 and 15 × 1= 15
2 is not a factor
3 × 5 = 15 and 5 × 3 = 15
4 is not a factor
5 × 3 = 15 and 3 × 5 = 15
When factor pairs start repeating, you can make a general statement, or generalize, that all the factors of a number
are found.
I already found the factor paired with 5, 3 × 5 and 5 × 3.
The gardener has 4 different ways to plant the trees: 1 × 15, 15 × 1, 5 × 3, and 3 × 5 arrays.
Convince Me! Construct Arguments The diagram shows all the factor pairs of 24. Use the diagram to justify the conclusion that when factor pairs start repeating, you know you have found all the factors of a number.

Guided Practice
Generalize Ms. Maribel wants to arrange the 20 desks in her classroom into rows with the same number of desks in each row. She wants at least 2, but not more than 8 rows.

Question 1.
What are the factor pairs for 20? Explain how you know you have found them all.
Answer:
The factor pairs of 20 are
1 and 20
2 and 10
4 and 5
Factors are often given as pairs of numbers that multiply together to give the original numbers these are called factor pairs.
Question 2.
Find the ways Ms. Maribel can arrange the desks.
Answer:
Given that,
Total number of desks = 20
Ms. Maribel can arrange the desks in 3 ways that are
1 row of 20 desks
2 row of 10 desks
Independent Practice
Generalize Kevin invited 15 friends to his birthday party. They played a game where everyone had to separate into groups. Each group had the same number of children. The game could not be played with all 16 children in one group and each group had to have more than 1 child.
Question 3.
List the factor pairs of 16 and then find the different ways Kevin and his friends could divide into groups.
Answer:
Factors are often given as pairs of numbers that multiply together to give the original numbers these are called factor pairs.
The factor pairs of 16 are 1 and 16, 2 and 8 .
Kevin and his friends could divide the children’s groups into two ways that are
16 children in 1 group
8 Children in 2 groups
Question 4.
Why does 16 have an odd number of factors?
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 16 are 1, 2, 8 and 16
The total number of factors of 16 is 4
Then it is not an odd number of factors.
Question 5.
Can you stop checking for factor pairs when you find a pair that repeats? Explain.
Answer:
Yes, we can stop the factor pairs when we find the repeated factors.
We can write one factor only one time.
Problem Solving
Performance Task
Store Displays A pet store needs 3 displays with the products shown. The boxes of kitty litter need to be stacked with the same number of boxes in each row. There needs to be at least 3 rows with at least 3 boxes in each row. What are all the ways the boxes of kitty litter could be stacked?

Question 6.
Make Sense and Persevere What quantities are given in the problem and what do the numbers mean?

Answer:
Question 7.
Reasoning What are the factor pairs for 48?
Answer:
The factor pairs mean the pair of numbers that multiply together to give the original number is called factor pairs.
Factor pairs of 48 are
1 and 48
2 and 24
3 and 16
4 and 12
6 and 8
By multiplying these numbers we get 48.
Question 8.
Be Precise What are all the ways the boxes of kitty litter can be stacked with at least 3 rows with at least 3 boxes in each row?
Answer:
Here we can arrange the boxes of Kitty litter in different ways with atleast 3 rows with at least 3 boxes.
Total number of Kitty litter boxes = 48
First, we can arrange 48 boxes in 3 rows of 16 boxes.
Second, we can arrange in 4 rows of 12 boxes.
Third, we can arrange in 6 rows of 8 boxes.
Lesson 7.4 Prime and Composite Numbers
Solve & Share
Max has 2 red tiles, 3 blue tiles, 4 yellow tiles, and 8 green tiles. How many different rectangular arrays of each color can Max make? Explain how you know you found all the arrays. Solve this problem any way you choose.
I can … use factors to determine if a whole number is prime or composite.

Look Back! What do you notice about the factors of each number of color tiles and the number of arrays?
Essential Question
How Can You Identify Prime and Composite Numbers?
Visual Learning Bridge
The data table lists the factors for 2, 3, 4, 5, and 6. What do you notice about the factors for 5? What do you notice about the factors for 6?
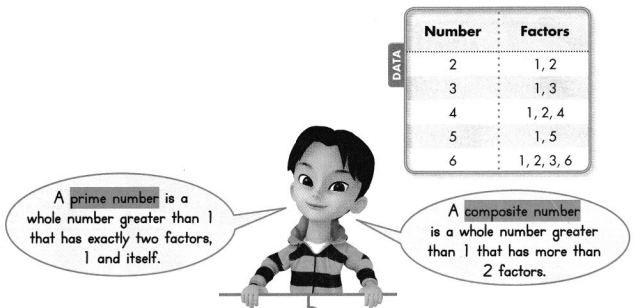
Prime Numbers
5 is a prime number.
It has only 2 factors, 1 and itself.
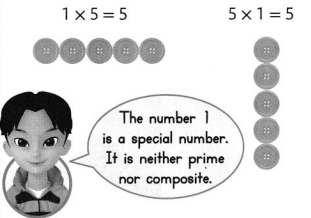
Composite Numbers
6 is a composite number.
The factors for 6 are 1, 2, 3, and 6.

Convince Me! Generalize Can a number be both prime and composite? Explain.
Guided Practice
Do You Understand?
Question 1.
What is the only even prime number?
Answer:
2 is the only even prime number.
2 has only two factors that are 1 and 2
The factors that are less than two factors are called prime numbers.
Question 2.
Write an odd number that is not prime. What makes it a composite number?
Answer:
49 is the odd number and it is not prime because it has more than 2 factors.
Factors of 49 are 1, 7 and 49
So, it is a composite number.
Question 3.
Roger has 47 cars. Can he group the cars in more than 2 ways?
Answer:
Given that,
Total number of cars at Roger = 47
We can arrange in two groups
17 cars in 1 group
1 group of 17 cars
Do You Know How?
For 4-9, tell whether each number is prime or composite.
Question 4.
32
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 32 are 1, 2, 4, 8, 16 and 32
32 is not a prime number because it has more than 2 factors.
The number that having more than two factors are called composite numbers.
So 32 is a composite number.
Question 5.
51
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 51 are 1, 3, 17 and 51
51 is not a prime number because it has more than 2 factors.
The number that having more than two factors are called composite numbers.
So, 51 is a composite number.
Question 6.
73
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 73 are 1 and 17 and
51 is a prime number because it has 2 factors.
The number that having more than two factors are called composite numbers.
So, 73 is not a composite number.
Question 7.
21
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 21 are 1, 3, 7 and 21
21 is not a prime number because it has more than 2 factors.
The number that having more than two factors are called composite numbers.
So, 21 is a composite number.
Question 8.
95
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 95 are 1, 5, 19 and 95
95 is not a prime number because it has more than 2 factors.
The number that having more than two factors are called composite numbers.
So, 95 is a composite number.
Question 9.
29
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 29 are 1 and 29
29 is a prime number because it has 2 factors.
The number that having more than two factors are called composite numbers.
So,29 is not a composite number.
A number is composite if it has more than 2 factors.
Independent Practice
Leveled Practice For 10-19, tell whether each number is prime or composite.
Question 10.

Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 7 are 1 and 7
7 is a prime number because it has 2 factors.
The number that having more than two factors are called composite numbers.
So, 7 is not a composite number.
Question 11.
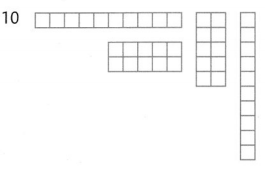
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 10 are 1, 2, 5 and 10
7 is a composite number because it has more than 2 factors.
Question 12.
12
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 12 are 1, 2, 3, 4, 6 and 12
The number 12 is a composite number because it has more than 2 factors.
Question 13.
97
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 97 are 1 and 97
The number 97 is a prime number because it has 2 factors.
The number that having more than two factors are called composite numbers.
So, 97 is not a composite number.
Question 14.
90
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 and 90
The number 90 is a composite number because it has more than 2 factors.
Question 15.
31
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 30 are 1 and 30
The number 30 is a prime number because it has 2 factors.
The number that having more than two factors are called composite numbers.
So, 30 is not a composite number.
Question 16.
11
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 11 are 1 and 11
The number 11 is a prime number because it has 2 factors.
The number that having more than two factors are called composite numbers.
So, 11 is not a composite number.
Question 17.
44
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 44 are 1, 2, 4, 11, 22 and 44
The number 44 is a composite number because it has more than 2 factors.
Question 18.
3
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 3 are 1 and 3
3 is a prime number because it has 2 factors.
The number that having more than two factors are called composite numbers.
So, 3 is not a composite number.
Question 19.
59
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 59 are 1 and 59
The number 59 is a prime number because it has 2 factors.
The number that having more than two factors are called composite numbers.
So, 59 is not a composite number.
Problem Solving
For 20-21, use the graph at the right.

Question 20.
Which type of flower received a prime number of votes?
Answer:
Total number of Daffodils flowers = 5
The factors of 5 are 1 and 5
The number 5 is a prime number because it has only two factors.
The Daffodils flowers received the prime number of votes.Question 21.
How many votes are represented by the picture graph?
Answer:
Given that,
Total number of Daffodils flowers = 2 and half
Total number of Daisies flowers = 3
Total number of Tulips flowers = 5
Each flower icon = 2 votes
Total number of flowers = 2 and half + 3 + 5 = 10 and half
10 and half flowers × 2 = 21
Total number of votes = 21Question 22.
Critique Reasoning Maria says every number in the nineties is composite. Jackie says 1 number in the nineties is prime. Who is correct? Explain your answer.
Answer:
Given that,
Maria says every number in the nineties is composite.
Jackie says 1 number in the nineties is prime.
Jackie said was correct 1 number in the nineties is prime that is 97.
The number 97 has 2 factors so it is a prime number.Question 23.
Critique Reasoning Greta says the product of two prime numbers must also be prime. Joan disagreed. Who is correct?
Answer:
The product of two prime numbers is a composite numbers
For example, 3 and 7 are the two prime numbers.
The product of 3 and 7 is 21
The factors of 21 are 1, 3, 7 and 21
21 is not a prime number it is a composite number.Question 24.
Janelle has 342 pennies, 62 nickels, and 12 dimes. If Janelle exchanges her coins for dollars, how many dollars will she have? How many cents will remain?
Answer:
Question 25.
Higher Order Thinking Why is 1 neither a prime number nor a composite number?
Answer:
A prime number is a whole number that only has two factors which are itself and one.
A composite number has a factor in addition to one and itself the number is neither prime nor composite.
Assessment Practice
Question 26.
Select all the groups of numbers that are prime.
☐ 17, 19, 53
☐ 37, 43, 79
☐ 52, 67, 99
☐ 63, 72, 83
☐ 59, 89, 97
Answer:
17, 19, 53
37, 43, 79
59, 89, 97 these set of groups having the prime numbers.
Question 27.
Select all the expressions with sums that are composite.
☐ 17 + 25
☐ 33 + 51
☐ 16 + 83
☐ 29 + 32
☐ 47 + 29
Answer:
17 + 25 = 42
33 + 51 = 84
16 + 83 = 99
47 + 29 = 76
The factors of 42 are 1, 2, 3,6, 7, 14, 21 and 42
The factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28 and 84
The factors of 99 are 1, 3, 9, 11, 33 and 99
The factors of 76 are 1, 2, 4, 19, 38 and 76
42, 84, 99, 76 are the composite number because the factors of all these numbers are
Lesson 7.5 Multiples
Solve & Share
There are 9 players on the golf practice range. If each player practices with the same number of golf balls, how many balls might be in play at the same time? Solve this problem any way you choose.
I can … use multiplication to find multiples of a number

Look Back! Can you show all of the answers to the problem? Explain.
Essential Question
How Can You Find Multiples of a Number?
Visual Learning Bridge
It takes 8 minutes for Car A to make one full turn on the Ferris wheel. If the Ferris wheel continues to turn at the same speed for the next hour, at what times during the hour will Car A return to the starting point?

Step 1
One full turn takes 8 minutes.
1 × 8 = 8
8 is a multiple of 1 and 8 because 1 × 8 = 8.
Car A is back at the starting point after another 8 minutes.
Step 2
Two full turns take 16 minutes.
2 × 8 = 16
Car A is back at the starting point after 8 minutes.
2 and 8 are factors of 16. 16 is a multiple of 2 and 8.
Step 3
Car A is at the starting point every 8 minutes after that:
3 × 8 = 24
4 × 8 = 32
5 × 8 = 40
6 × 8 = 48
7 × 8 = 56
During the hour, Car A returns to the starting point after 8, 16, 24, 32, 40, 48, and 56 minutes.
Convince Me! Reasoning What is the next multiple after 56? Explain why it is NOT used.
Another Example!
Factors are numbers that when multiplied together give a product. A whole number is a multiple of each of its factors.
Factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
24 is a multiple of 1, 2, 3, 4, 6, 8, 12, and 24.
Guided Practice
Do You Understand?
Question 1.
If the Ferris wheel in the example on the previous page turns at the same speed, will Car A return to the starting point at 75 minutes? Explain.
Answer:
Question 2.
Suppose the Ferris wheel speeds up so it makes one full turn every 6 minutes. When will Car A return to the starting point if the Ferris wheel continues to turn for one half hour?
Answer:
Do You Know How?
For 3-4, write five multiples of each number
Question 3.
2
Answer:
Five multiples of 2 are
2 × 1 = 2
2 × 2 = 4
2 × 3 = 6
2 × 4 = 8
2 × 5 = 10
Question 4.
9
Answer:
Five multiples of 9 are
9 × 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45
For 5-6, tell whether the first number is a multiple of the second number.
Question 5.
14, 2
Answer:
Multiple of a number is exactly divisible by the number.
14 is exactly divisible by 2.
So, 14 is not a multiple of 2.
Question 6.
3, 18
Answer:
Multiple of a number is exactly divisible by the number
3 is not exactly divisible by 18.
So, 3 is not a multiple of 6
Independent Practice
For 7-14, write five multiples of each number.
You can skip count to find multiples of numbers. Be Precise.
Question 7.
7
Answer:
Five multiples of 7 are
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35
The five numbers 7, 14, 21, 28 and 35 are multiples of 7
Question 8.
4
Answer:
Five multiples of 4
4 × 1 = 4
4 × 2 = 8
4 × 3 = 12
4 × 4 = 16
4 × 5 = 20
The five numbers 4, 8, 12, 16, and 20 are the multiples of 4.
Question 9.
6
Answer:
6 × 1 = 6
6 × 2 = 12
6 × 3 = 18
6 × 4 = 24
6 × 5 = 30
The five numbers 6, 12, 18, 24, and 30 are the multiples of 30
Question 10.
5.
Answer:
Five multiples of 5 are
5 × 1 = 5
5 × 2 = 10
5 × 3 = 15
5 × 4 = 20
5 × 5 = 25
The five numbers 5, 10, 15, 20 and 25 are the multiples of 5
Question 11.
11
Answer:
Five multiples of 11 are
11 × 1 = 11
11× 2 = 22
11 × 3 = 33
11 × 4 = 44
11 × 5 = 55
The first five numbers 11, 22, 33, 44 and 55 are the multiples of 11
Question 12.
1
Answer:
Five multiples of 1 are
1 × 1 = 1
1 × 2 = 2
1 × 3 = 3
1 × 4 = 4
1 × 5 = 5
The first five numbers 1, 2, 3, 4 and are the multiples of 1
Question 13.
20
Answer:
Five multiples of 20 are
20 × 1 = 20
20 × 2 = 40
20 × 3 = 60
20 × 4 = 80
20 × 5 = 100
The five numbers 20, 40, 60, 80 and 100 are the multiples of 20
Question 14.
15
Answer:
15 × 1 = 15
15 × 2 = 30
15 × 3 = 45
15 × 4 = 60
15 × 5 = 75
The five numbers 15, 30, 45, 60, and 75 are the multiples of 15
For 15-18, tell whether the first number is a multiple of the second number.
Question 15.
44, 6
Answer:
Multiple of a number is exactly divisible by the number.
44 is not exactly divisible by 6.
So, 44 is not a multiple of 6.
Question 16.
25, 5
Answer:
Multiple of a number is exactly divisible by the number.
25 is exactly divisible by 5.
So, 25 is a multiple of 5.
Question 17.
30, 6
Answer:
Multiple of a number is exactly divisible by the number.
30 is exactly divisible by 6.
So, 30 is a multiple of 6.
Problem Solving
Question 19.
Name all the numbers of which 45 is multiple.
Answer:
The numbers 45, 90, 135, 180 and 225 are the multiples of 45
Question 20.
Critique Reasoning Lindsay says all numbers that are multiples of 4 have 2 as a factor. Is Lindsay correct? Explain.
Answer:
Question 21.
Trisha bought bags of tennis balls. There are eight tennis balls in each bag. Could Trisha have 75 tennis balls? Explain.
Answer:
Given that,
Number of tennis ball in each bags at Trisha = 8
Expected tennis balls at Trisha = 75
How many Balls at Trisha = 75 ÷ 8
Question 22.
Higher Order Thinking Gerri says that if a number is a multiple of 9 it is also a multiple of 3. Do you agree? Explain.
Answer:
Multiple of 9 is also a multiple of 3
For example 27 ÷ 9 = 3
So, 27 is a multiple of 3 and 9.
Question 23.
Describe how 20,000 and 2,000 are related.
Answer:
Question 24.
Isabel wrote this mystery problem: The quotient is a multiple of 6. The dividend is a multiple of 9. The divisor is a factor of 12. Write one possible equation to Isabel’s mystery problem.
Answer:
Assessment Practice
Question 25.
Latifa and John played a game of multiples. Each player picks a number card and says a multiple of that number. Latifa picked a 9. Write all the multiples of 9 from the box.

Answer:

Multiples of 9 from the given numbers are 9, 12, and 33.
Question 26.
A roller-coaster ride completes a full loop every 3 minutes. Seth listed multiples of 1 3 to determine when the ride would be back at its starting point. Write all the multiples of 3 from the box.
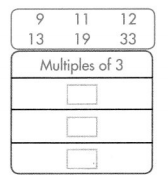
Answer:
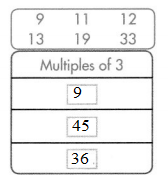
Multiples of 3 from the given numbers are 9, 45, and 36.
Topic 12 Fluency Practice Activity
Follow the Path
Shade a path from START to FINISH. Follow the sums and differences that are correct. You can only move up, down, right, or left.
I can … add and subtract multi-digit whole numbers.
Topic 7 Vocabulary Review
Understand Vocabulary
Word List
- array
- composite number
- factor
- factor pairs
- generalization
- multiple
- prime number
- whole number
Question 1.
Cross out the numbers that are NOT factors of 16.
1
2
3
4
8
Answer:
Question 2.
Cross out the numbers that are NOT multiples of 3.
3
6
9
13
23
Answer:
The numbers 13 and 23 are not the multiples of 3.
Question 3.
Cross out the numbers that are NOT whole numbers.
\(\frac{1}{4}\)
\(\frac{1}{2}\)
7
17\(\frac{1}{5}\)
6,219
Answer:
Question 4.
Cross out the numbers that are NOT factor pairs for 24.
1 and 24
2 and 12
3 and 6
4 and 8
4 and 6
Answer:
Label each example with a term from the Word List.
Question 5.
13 __________
Answer:
Question 6.
12 _____________
Answer:
Question 7.
![]() ____________
____________
Answer:
Question 8.
When factor pairs begin repeating, I have found all the pairs for a number.
Answer:
Use Vocabulary in Writing
Question 9.
Marisol says 23 is both a prime and a composite number because 2 and 3 are both prime. Use at least 3 terms from the Word List to explain the error in Marisol’s reasoning.
Answer:
23 is only a prime number it is not a composite number
The factors of 23 are 1 and 23
The factors that are more than two are composite numbers.
Here there are only 2 factors so it is called a prime number.
23 is a whole number.
Topic 7 Reteaching
Set A pages 261-264
Draw arrays to find all the factor pairs for 8.
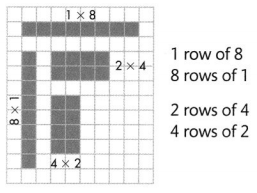
The factor pairs for 8 are 1 and 8, 2 and 4.
Remember that 1 is a factor of every number.
Use grid paper to find the factor pairs for each number.
Question 1.
26
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
Factors pairs of 26 are
1 and 26
2 and 13
Question 2.
9
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
Factor pairs of 9 are
1 and 9
3 and 3
Question 3.
37
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
Factor pairs of 37 are
37 and 1
1 and 37
Question 5.
19
Answer:
Factor pairs are the set of two factors that, when they are multiplied together to give a particular product is called factor pairs.
Factor pairs of 19 are
1 and 19
Set B pages 265-268
Find the factor pairs for 12.
1 and 12
2 and 6
3 and 4
The factors of 12 are 1, 2, 3, 4, 6, and 12.
Remember you can use counters or grids to make arrays and find the factors of a number.
Find the factors of each number.
Question 1.
45
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 45 are 1, 3, 5, 15 and 45
Question 2.
40
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 40 are 1, 2, 4, 5, 8, 10, 20 and 40
Question 3.
56
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 56 are 1, 2, 4, 7, 8, 14, 28 and 56
Question 4.
63
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 63 are 1, 3, 7, 9, 21 and 63
Set C pages 269-272
Think about these questions to help you use repeated reasoning.
Thinking Habits
- Are any calculations repeated?
- Can I generalize from examples?
- What shortcuts do I notice?

Remember to look for repeating factors when dividing to find the factor pairs of a number.
A valet has 34 cars to park in a rectangular array.
Question 1.
What are the different ways the valet could park the cars?
Answer:
Given that,
Total number of cars = 34
Factors of 34 are 1, 2, 17, and 34
The different ways the valet could park the cars are
1 and 34
34 and 1
2 and 17
17 and 2
Question 2.
How do you know when you can stop looking for factors of a number?
Answer:
Set D pages 273-276
Is 49 prime or composite?
To determine if 49 is prime or composite, find whether 49 has factors other than 1 and 49.
49 is composite because it is divisible by 7.
49 = 7 × 7

Remember you can use an array to determine if a number is prime or composite.
Tell whether each number is prime or composite.
Question 1.
13
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 13 are 1 and 13
The number that has only two factors is called a prime number.
So, The number 12 is a prime number.
So it is not a composite number.
Question 2.
25
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 25 are 1,5 and 25
The number that has more than two factors are called composite numbers.
So, The number 25 is composite number.
Question 3.
55
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 55 are 1,5, 11 and 55
The number that has more than two factors are called composite numbers.
So, The number 55 is a composite number.
Question 4.
2
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 2 are 1 and 2
The number that has only two factors is called a prime number.
So, The number 2 is a prime number.
Question 5.
29
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 25 are 1 and 29
The number that has only two factors is called a prime number.
So, The number 25 is a prime number.
Question 6.
23
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 23 are 1 and 23
The number that has only two factors is called a prime number.
So, The number 23 is a prime number.
Question 7.
64
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 64 are 1, 2, 4, 8, 16 32and 64
The number that has more than two factors are called composite numbers.
So, The number 64 is a composite number.
Question 8.
99
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 99 are 1, 3, 9, 11, 33 and 99
The number that has more than two factors are called composite numbers.
So, The number 99 is a composite number.
Question 9.
5
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 5 are 1 and 5
The number that has only two factors is called a prime number.
So, The number 5 is a prime number.
Question 10.
21
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
The factors of 21 are 1, 3, 7 and 21
The number that has more than two factors are called composite numbers.
So, The number 21 is a composite number.
Set E pages 277-280
Find five multiples of 7.
Use multiplication.
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35

Remember that to find multiples of a number, multiply the number by any whole number.
Find five multiples of each number.
Question 1.
3
Answer:
Five multiples of 3 are
3 × 1 = 3
3 × 2 = 6
3 × 3 = 9
3 × 4 = 12
3 × 5 = 15
Question 2.
6
Answer:
Five multiples of 6 are
6 × 1 = 6
6 × 2 = 12
6 × 3 = 18
6 × 4 = 24
6 × 5 = 25
Question 3.
4
Answer:
Five multiples of 4
4 × 1 = 4
4 × 2 = 8
4 × 3 = 12
4 × 4 = 16
4 × 5 = 20
Question 4.
9
Answer:
Five multiples of 9 are
9 × 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45
Five multiples of 9 are 9, 18, 27, 36 and 45
Tell whether the first number is a multiple of the second number.
Question 5.
22, 2
Answer:
Multiple of number is exactly divisible by the number.
Here 22 is exactly divisible by 2
So, 22 is a multiple of 2.
Question 6.
29, 3
Answer:
Multiple of number is exactly divisible by the number.
Here 29 is not exactly divisible by 3.
So, 29 is not a multiple of 3.
Question 7.
25, 5
Answer:
Multiple of number is exactly divisible by the number.
Here 25 is exactly divisible by 5.
So, 25 is a multiple of 5.
Question 8.
40, 8
Answer:
Multiple of number is exactly divisible by the number.
Here 40 is exactly divisible by 8.
So, 40 is a multiple of 8.
Topic 7 Assessment Practice
Question 1.
Courtney has 36 photos to arrange on a gallery wall.
A. How many arrays can Courtney make with the 36 photos? List all the possible arrays.
Answer:
Given that the total number of photos = 36
Factors of 36 are 1, 2, 3, 4, 9, 12, 18 and 36
The number of possible arrays are
1 and 36, 36 and 1
3 and 12, 12 and 3
2 and 18, 18 and 2
4 and 9, 9 and 4
The number of possible arrays is 8
B. How many factors are there for 36? Write them. What do you notice about the number of factors of 36 and the number of arrays Courtney can make with the photos?
Answer:
Given that the total number of photos = 36
Factors of 36 are 1, 2, 3, 4, 9, 12, 18 and 36
A number of factors of 36 are 8.
The number of possible arrays are
1 and 36, 36 and 1
3 and 12, 12 and 3
2 and 18, 18 and 2
4 and 9, 9 and 4
The number of possible arrays is 8.
C. Write all the factor pairs for 36. Is 36 prime or composite? Explain.
Answer:
The factor pairs of 36 are
1 and 36
2 and 18
3 and 12
4 and 9
The factors of 36 are 1, 2, 3, 4, 18, 12, 9 and 36
The number 36 is not a prime number it is a composite number because the factors of 36 are more than 2 so it is a composite number.
Question 2.
Determine whether the numbers in each list are factors or multiples of 16.
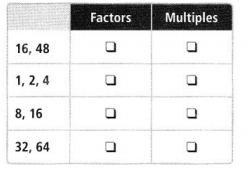
Answer:
Question 3.
Which statement is true?
A. The only factors of 3 are 3 and 1; therefore, 3 is prime.
B. The only factors of 4 are 4 and 1; therefore, 4 is prime.
C. The only factors of 5 are 5 and 1; therefore, 5 is composite.
D. The only factors of 8 are 8 and 1; therefore, 8 is composite.
Answer:
Question 4.
Determine if each number is prime or composite. Then write all the factors for each number. 19, 33
Answer:
The factors of 19 are 1 and 19
The number 19 is a prime number because it has only two factors.
The factors of 33 are 1, 11 and 33
The number 33 is a composite number because it has more than two factors .
Question 5.
Select all equations that have a dividend that is a multiple of 4 and a quotient that is a factor of 18.
☐ 8 ÷ 4 = 2
☐ 48 ÷ 8 = 6
☐ 18 ÷ 6 = 3
☐ 16 ÷ 4 = 4
☐ 36 ÷ 3 = 12
Answer:
Question 6.
Write 3 multiples and 3 factors for 24.
Answer:
3 factors of 24 are 1, 2, 3
3 multiple of 24 are
24 × 1 = 24
24 × 2 = 48
24 × 3 = 72
The numbers 24, 48, 72 are the multiples of 24
Question 7.
Write two multiples of 3 that have a factor of 7. Use equations to explain.
Answer:
Question 8.
Select all the true statements.
☐ 33 has more than two factors.
☐ All of the factors of 34 are even numbers.
☐ 35 has exactly two factors.
☐ 3 is a factor of 36.
☐ 37 is a prime number.
☐ 38 is a composite number.
Answer:
Question 9.
Martika says factors and multiples are related. Use the equation 6 × 7 = 42 to describe the relationship between factors and multiples.
Answer:
Question 10.
Which lists all the factors of 25 that are also prime?
A. 1, 25
B. 5
C. 1, 10, 25
D. 5, 25
Answer:
Question 11.
Carter lives on a street where all the house numbers are multiples of 6. Name two possible house numbers between 70 and 80. Explain.
Answer:
Question 12.
Write the factors of 30 that are also prime numbers.
Answer:
A factor divides exactly into a number leaving no remainder is called the factors.
Factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30
30 is not a prime number it is a composite number.
It has more than two factors .
Question 13.
Javier says all odd numbers greater than 2 and less than 20 are prime. Find an odd number greater than 2 and less than 20 that is NOT prime. Explain why the number is not prime.
Answer:
Topic 7 Performance Task
Arranging Cars to Sell Ms. Ortiz owns a car dealership. The dealership has the inventory of cars listed in the Ortiz Car Dealership table.

Question 1.
Ms. Ortiz wants to arrange all of the trucks in the front lot. She would like to have same number of trucks in each row.
Part A
How many different ways can the trucks be arranged in the front lot if the same number of trucks are parked in each row?
Answer:
Part B
What are all the ways the trucks can be arranged? Draw and label the different arrays.
Answer:
The trucks can be arranged in four different ways that are
Total number of trucks = 15
The factors of 15 are 1, 3, 5 and 15
Factor pairs of 15 are 1 and 15, 3 and 5
The trucks can be arranged in
1 row of 15 cars
3 rows of 5 cars
15 cars in 1 row
5 cars in 3 rows
Part C
Ms. Ortiz would like the arrangement to have more than 2 rows of trucks but less than 6 rows. What are the ways the trucks can be arranged? Explain.
Answer:
The trucks can be arranged in four different ways that are
Total number of trucks = 15
The factors of 15 are 1, 3, 5 and 15
Factor pairs of 15 are 1 and 15, 3 and 5
The trucks can be arranged in more than two rows and less than six rows
3 rows of 5 cars
5 cars in 3 rows
Question 2.
As Ms. Ortiz sells sedans, those sedans remaining are parked in different arrangements.
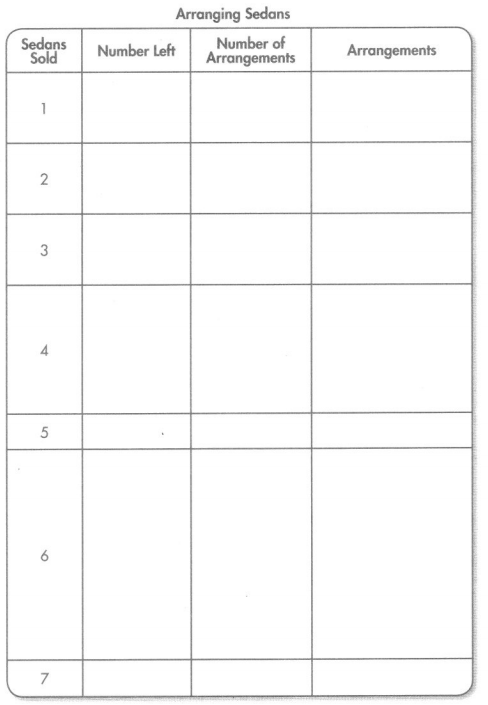
Complete the Arranging Sedans table to find the number of ways Ms. Ortiz can arrange each number of sedans in the front lot so there are at least 2 rows with the same number of sedans in each row and more than one sedan in each row.
Answer:
