enVision Math Common Core Grade 5 Answer Key Topic 12 Convert Measurements

Go through the enVision Math Common Core Grade 5 Answer Key Topic 12 Convert Measurements regularly and improve your accuracy in solving questions.

enVision Math Common Core 5th Grade Answers Key Topic 12 Convert Measurements

enVision STEM Project: Grand Canyon
Do Research Use the Internet and other sources to learn about the Grand Canyon and the Colorado River. Where is the Grand Canyon? How was it formed? What do the different rock layers tell us? Predict how you think the canyon dimensions will change in a million years.
Journal: Write a Report Include what you found. Also in your report:
• Describe the canyon’s dimensions.
• Describe the Colorado River’s dimensions.
• Define erosion.
• Make up and solve problems involving measurement units and conversions.

Review What You Know

A-Z Vocabulary

Choose the best term from the box. Write it on the blank.

• customary
• multiplication
• subtraction
• exponent
• metric

Question 1.
A meter is a unit of length in the ___ system of measurement.
Answer:

A meter is a unit of length in the Metric system of measurement.

Question 2.
A foot is a unit of length in the ____ system of measurement.
Answer:

A foot is a unit of length in the British imperial and United States customary system of measurement.

Question 3.
The division has an inverse relationship with _____
Answer:

The division has an inverse relationship with Multiplication.

Question 4.
A(n) ____ shows the number of times a base is used as a factor.

Answer:

An Exponent shows the number of times a base is used as a factor.

Multiplication

Find each product.

Question 5.
60 × 6
Answer:

60 × 6 = 360

Question 6.
24 × 10³
Answer:

24 × 10³  

= 24000

Question 7
16 × 7
Answer:

16 × 7 = 112

Question 8.
10² × 1.6
Answer:

10² × 1.6 = 160

Question 9.
100 × 34
Answer:

100 x 34 = 3400

Question 10.
10⁴ × 0.37
Answer:

10⁴ × 0.37 = 3700

Question 11.
46.102 × 10²
Answer:

46.102 × 10^{2 =} 

= 4702. 404

Question 12.
10¹ × 0.005
Answer:

0.05

Division
Find each quotient.

Question 13.
1,000 ÷ 100
Answer:

1,000 ÷ 100

Quotient = 10

Question 14.
176 ÷ 16
Answer:

176 ÷ 16

Quotient = 11

Question 15.
3,600 ÷ 60
Answer:

3,600 ÷ 60

Quotient = 60

Question 16.
120 ÷ 24
Answer:

120 ÷ 24

Quotient = 5

Measurement
Circle the more appropriate unit of measure for each item.

Question 17.
The capacity of a swimming pool: liters or milliliters
Answer: Liters

Question 18.

The length of an ear of corn: yards or inches
Answer: Yards

Question 19.
The mass of a gorilla: grams or kilograms
Answer: Kilograms

Question 20.
The weight of a tennis ball: ounces or pounds

Answer: Ounces

Question 21.

Would you use more centimeters or meters to measure the length of car? Explain.
Answer:

meters is more useful to measure the length of the car.

meters are used to measure the length of the car. Because centimeters are shorter than meters.

Pick a Project
PROJECT 12A
What makes a treehouse so cool?
Project: Build a Model of a Treehouse

PROJECT 12B
What would you weigh on Mars?
Project: Make a Mobile Display of the Solar System

PROJECT 12C
Have you ever heard of National Punch Day?
Project: Plan a Class Party

PROJECT 12D
What are the characteristics of Florida panthers?
Project: Design a Zoo Space for Florida Panther Cubs

Lesson 12.1 Convert Customary Units of Length

Activity

Solve & Share
William has a piece of wire that measures 1 yard long. He will use wire to fix several electrical outlets in his house. How many inches long is the wire? Solve this problem by using bar diagrams.

You can show the relationship between yards and inches in a bar diagram. Show your work!

Look Back! Generalize How can you convert inches to yards? Would you multiply or divide when converting from a smaller unit to a larger unit? Explain.

Visual Learning Bridge

Essential Question How Do You Change from One Leon Unit of Length to Another?

A.
Some frogs can jump 11\(\frac{1}{4}\) feet. What are some other ways to describe the same distance?

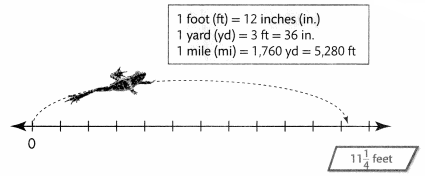
The table shows equivalent measures.

B.
To change larger units to smaller units, multiply.

You know 1 foot equals 12 inches.

You know 3 feet is equal to 1 yard.

C.
To change smaller units to larger units, divide.
Ed’s frog jumped 11 feet. How many yards is this?

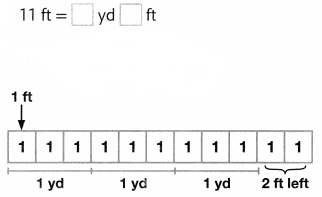
11 ÷ 3 = 3 R2 So, 11 feet = 3 yards, 2 feet.

Convince Me! Generalize In the example above, explain how you could use a mixed number to write 11 feet as an equivalent measure in yards.

Guided Practice

Do You Understand?

Question 1.
If you want to convert yards to feet, what operation would you use?
Answer:

To convert a yard measurement to a foot measurement, multiply the length by the conversion ratio. The length in feet is equal to the yards multiplied by 3.

Question 2.
If you want to convert feet to miles, what operation would you use?
Answer:

To convert a foot measurement to a mile measurement, divide the length by the conversion ratio.

Question 3.
What are some tools you could select to measure length? Explain when you would use them.
Answer:

The most common way to measure length is by using the scale on some sort of hand-held tool or implement, but you can also measure length — or distance — with radar, sonar, and laser beams.

Do You Know How?

In 4-8, convert each unit of length.

Question 4.
9 ft = ___ yd
Answer: 3

Question 5.
8 ft 7 in. = ___ in.
Answer:

103 inches

Question 6.
5\(\frac{1}{2}\) ft = __in.
Answer: 66 inches

Question 7.
288 in. = __ yd
Answer:

8 yards

Question 8.
219 in. = ___ ft ___ in. or. ___ ft
Answer:

18 feet 3 inches

18.25 ft

Independent Practice

In 9 and 10, complete the table to show equivalent measures.

Will the number in your answer be greater than or less than the number in the given measurement?

Question 9.

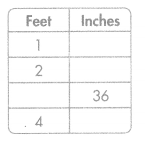
Answer:

1 feet = 12 inches

2 feet = 24 inches

3 feet = 36 inches

4 feet = 48 inches

Question 10.

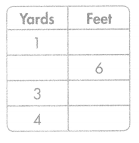
Answer:

1 yard = 3 feet

2 yard = 6 feet

3 yard = 9 feet

4 yard = 12 feet

In 11-16, convert each unit of length.

Question 11.
3 yd = ___ in.
Answer:

3 yd = 108 inches

Question 12.
324 ft =__ yd
Answer:

324 ft = 108 yd

Question 13.
2\(\frac{2}{3}\) mi = ___ ft
Answer:

2 2/3 miles = 14080 feet

Question 14.
56 ft = ___ yd ___ ft
Answer:

56 ft = 18 yd 2 ft

Question 15.
12\(\frac{1}{2}\)  = ___ in.
Answer:

12 1/2 feet = 150 inches

Question 16.
6 in. = ___ ft
Answer:

6 in = 0.5 feet

In 17-19, compare lengths. Write >,<, or = for each

Question 17.
100 ft 3 yd
Answer:

100 ft >3 yd

Question 18.
74 in. 2 yds 2 in.
Answer:

74 in = 2 yd 2 in

Question 19.
5,200 ft 145 in. 1 mi 40 in.
Answer:

5200 ft 145 in > 1 mi 40 in.

Problem Solving

Question 20.
Number Sense Which number would be greater, the height of a tree in feet or the height of the same tree in yards?
Answer:

1 feet = 30.48 centimeters

1 yard = 91.44 centimeters.

Question 21.
Reasoning The dimensions of the nation’s smallest post office are 8 feet 4 inches by 7 feet 3 inches. Why would you use the measurement 8 feet 4 inches instead of 7 feet 16 inches?

Answer:

16 inches = 1 foot 4 inches

1 foot is added to 7 inches

Therefore,

The measurement 8 feet 4 inches instead of 7 feet 16 inches

Question 22.
Roger earns $24 a week mowing lawns. He spends \(\frac{1}{6}\) of his earnings on lunch and \(\frac{2}{3}\) of his earnings on music. He saves the rest. How many dollars does Roger save? Tell me how you found the answer.
Answer:

Given that, Roger earns $24 a week

The amount he spends on his lunch = 1/6 of his earnings

Which means, 1/6 x 24 = 4

Also given, he spends 2/3 of his earnings on music

This means, 2/3 x 24 = 16

Total amount he spend = 16 + 4 = 20

Remaining amount = 24 – 20

= $4

Therefore, Roger saves 4 dollars.

Question 23.
Ariana has 144 peaches. She has to pack 9 boxes with an equal number of peaches. How many peaches should she pack in each box?

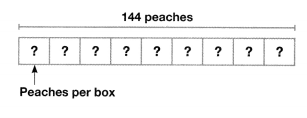
Answer:

Total number of peaches = 144

The number of boxes she has to pack  = 9

Now,

144/9 = 16

Therefore, Ariana has to pack 15 peaches in each box.

Question 24.
Higher-Order Thinking How do you convert 108 inches to yards?
Answer:

108 inches = 3 yards

1 inch = 0.02 yards

108 inches =

= 108 x 0.02

= 3 yards.

Question 25.
A-Z Vocabulary What is an appropriate customary unit to use when measuring the length of a driveway? Justify your answer.
Answer:

The most appropriate units are either feet, yards, or meters.

Assessment Practice

Question 26.
Select all of the measurements greater than 7 feet.
2 yards
2 yards 2 inches
2 yards 2 feet
3 yards
Answer:

c. 2 yards 2 feet

d. 3 yards.

Question 27.
Select all of the measurements less than 435 inches.
37 feet
36 feet 2 inches
12 yards 3 inches
12 feet 3 inches
Answer:

36 feet 2 inches

12 feet 3 inches

Lesson 12.2 Convert Customary Units of Capacity

Activity

Solve&Share

A recipe makes 16 cups of soup. How many quarts does the recipe make? Remember, there are 2 cups in a pint and 2 pints in a quart. Solve this problem any way you choose!

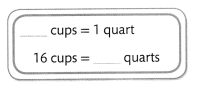
Given,

There are 16 cups of soup

4 cup =  1 quart

16 cups = 4 pints.

You can use reasoning to help you convert between different units.

Look Back! Is the number of cups greater than or less than the number of quarts? Why do you think that is?

Visual Learning Bridge

Essential Question How Do You Convert Customary stion Units of Capacity?

A.
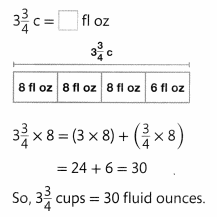
Sue is making punch. She needs 3\(\frac{3}{4}\) cups of orange juice and 5 pints of lemonade. How many fluid ounces of orange juice and how many quarts of lemonade does she need?

1 gallon (gal) = 4 quarts (qt)
1 quart = 2 pints (pt)
1 pint = 2 cups (c)
1 cup = 8 fluid Ounces (fl oz)

You can multiply or divide to convert one unit of capacity to a different one.

B.
To change a larger unit to a smaller unit, multiply.

C.
To change a smaller unit to a larger unit, divide.

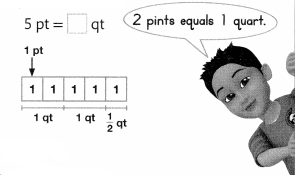
Find 5 ÷ 2.
5 ÷ 2 = \(\frac{5}{2}\) = 2\(\frac{1}{2}\)
So, 5 pints = 2\(\frac{1}{2}\) quarts.

Convince Me! Generalize When you convert from pints to quarts, why do you divide?

Guided Practice

Do You Understand?

Question 1.
Why would you change 4 gallons 5 quarts to 5 gallons 1 quart?
Answer:

Given, 4 gallons 5 quarts

4 quarts = 1 gallon

So, 4 gallons 5 quarts can also be written as 5 gallons 1 quart.

Question 2.
Why is \(\frac{1}{8}\) cup equal to 1 fluid ounce?
Answer:

1 cup = 8 fluid ounces

1/8 cup = 2 tablespoon  = 1 fluid ounce

Do You Know How?

In 3-8, convert each unit of capacity.

Question 3.
32c = __ gal
Answer:

2 gal

Question 4.
\(\frac{1}{4}\)qt = __ gal
Answer:

64 gal

Question 5.
48 qt = __ pt
Answer:

96 pt

Question 6.
6\(\frac{1}{8}\) qt = __ c
Answer:

1 qt = 4 cups

6 qt = 24 cups

1/8 qt = 0.5 cups

6 1/8 qt = 24.5 cups

Question 7.
73 qt 1 pt = __ pt
Answer: 147 pints

1 qt = 2 pints

73 qt= 73 x 2

= 146

146 pt + 1 pt

= 147 pints.

Question 8.
9 pt = __ qt__ pt or ___ qt
Answer:

1 qt = 2 pt

9 pt =

4 qt 1 pt

or

4.5 qt.

Independent Practice

You may need to convert more than once.

In 9-20, convert each unit of capacity.

Question 9.
10 pt = __ qt
Answer: 5 qt

Question 10.
48 fl oz = ___ c
Answer: 6 c

Question 11.
\(\frac{1}{2}\)c = __ pt
Answer: 0.25 pt

1  cup = 0.5 pt

So, 1/2 cup = 0.25 pt

Question 12.
9\(\frac{1}{4}\) pt = ___ c
Answer:

1 pt = 2 cups

9 pt = 9 x 2 = 18 cups

1/4 = 0.5 or 1/2 cups

Total = 18+0.5

= 18.5 cups

Question 13.
36 pt = ___ qt
Answer: 18 qt

1 pt = 0.5 qt

36 pt =

36 x 0.5

= 18 qt.

Question 14.
30 qt = __ gal __ qt
Answer:

1 quart = 0.25 gal

30 qt = 7 gal 2 qt

Question 15.
1qt = ____ gal
Answer:

1 qt = 0.25 gal

Question 16.
5 gal = ___ c
Answer:

1 gal = 16 cups

So, 5 gal = 5 x 16 = 80 cups.

Question 17.
1 gal 1c = ___ fl oz
Answer:

136 fl oz

1 gal = 16 c

16 c + 1 c = 17 c

1 c = 8 fl oz

17 c = 17 x 8 = 136 fl oz

Question 18.
7c = __ fl oz
Answer:

1 cup = 8 fl oz

7 c = 7 x 8

= 56 fl oz

Question 19.
72 pt = ___ gal
Answer: 9 gal

Question 20.
\(\frac{1}{3}\) pt = ___ c
Answer:

1/3 pt = 0.66 c

Question 21.
Complete the table to show equivalent measures.

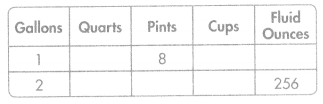
Answer:

1 gallon = 4 quarts = 8 pints = 16 cups = 128 fl oz

2 gallon = 8 quarts = 16 pints = 36 cups = 256 fl oz.

Problem Solving

For 22-24, use the aquarium.

Question 22.
The class aquarium holds 2 gallons of water. How many cups is this? How many fluid ounces is this?

Answer:

1 gallon = 16 cups

Which means, 2 gallon  = 2 x 16 = 32 cups

Therefore, there are 32 cups in 2 gallons

1 gallon = 128 fl oz

Which means, 2 gallons = 2 x 128 = 256 fl oz .

Therefore, 256 fl oz are there in 2 gallons.

Question 23.
Susan finds that 2 pints 1 cup of water have evaporated from the class aquarium. How many pints of water are left in the aquarium?
Answer:

The number of cups in aquarium = 32 cups

2 pints 1 cup = 5 cups

Now, 32 – 5 = 27 cups

1 cup = 0.5 pints

So, 27 cups = 13.5 pints

Therefore, 13.5 pints of water are left in the aquarium.

Question 24.
If all of the dimensions of the aquarium were doubled, what would be the volume of the new aquarium?
Answer:

Given,

the dimensions of the aquarium are doubles means

Volume = 20 in x 16 in x 18 in

= 4320 cubic inches.

Therefore, the volume of the new aquarium = 4320 cubic inches.

Question 25.
Carrie has 3 gallons of paint. Bryan has 10 quarts of paint. How many more pints of paint does Carrie have than Bryan?
Answer:

Given Carrie has 3 gallons of paint

3 gallons = 24 pints

Bryan has 10 quarts of paint

10 quarts = 20 pints

Now,

24 pints – 20 pints

= 4 pints

There are 4 more pints of paint Carrie has than Bryan.

Question 26.
Reasoning Lorelei filled her 5-gallon jug with water. How many times could she fill her 2-quart canteen with water from the jug? Explain.
Answer:

1 gallon = 4 quarts

5 gallons = 4 x 5 = 20 quarts

Now, 20/2 = 10

Therefore, she can fill the canteen by 10 times.

Question 27.
Higher-Order Thinking A recipe calls for 3 tablespoons of pineapple juice. A can of pineapple juice is 12 fluid ounces. How many teaspoons of juice are in the can?

Answer:

Given, a can of pineapple juice = 12 fluid ounces

1 fl oz = 2 tablespoon

Now, 12 fl oz = 24 tablespoons

The amount of pineapple juice recipe contains = 3 tablespoon

Now, 3  x 24 tablespoons = 72 teaspoon

Therefore, there are 72 teaspoons of pineapple are there in the can.

Assessment Practice

Question 28.
Choose all the measurements that are greater than 4 cups.
30 fluid ounces
2 pints
3 pints
1 quart
1 gallon
Answer:

1 gallon > 4 cups.

Question 29.
Choose all the statements that are true.
15 pt < 2 gal
1 gal < 5 qt
12 fl oz > 2c
2 qt 1 cup > 10 cups
20 pints = 10 quarts
Answer:

20 pints = 10 quarts

Lesson 12.3 Convert Customary Units of Weight

Activity

Solve & Share
Maria adopted 4 dogs. All together they eat 1\(\frac{3}{4}\) pound of food each day. One pound is equal to 16 ounces. How many ounces of food will the dogs eat in 5 days? Solve this problem any way you choose.

Answer:

1 pound = 16 ounces

1 3/4 pounds = 28 ounces

Number of days = 5

Now, 28 x 5

= 140 ounces

Therefore, the dogs can eat 140 ounces of food in 5 days.

A model with Math You can use drawings or equations to solve the problem. Show your work!

Look Back! Which is the larger unit of weight, an ounce or a pound? How can you use this relationship to find the number of ounces in 5 pounds?

Answer:

1 pound = 16 ounces

5 pounds = 5 x 16 = 80 ounces

Visual Learning Bridge

Essential Question How Can You Convert Units of Weight?

A.
An adult African elephant weighs about 5 tons. A baby African elephant weighs about 250 pounds. How many pounds does the adult elephant weigh? How can you convert 250 pounds to tons?

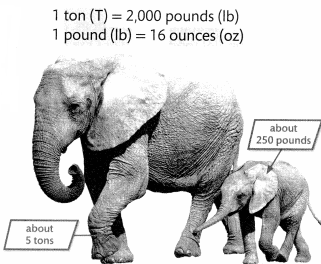
To convert from one unit of weight to another, you can use multiplication or division.

B.
To convert from larger units to smaller units, multiply.

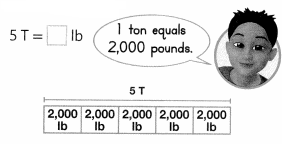
Find 5 × 2,000.
5 × 2,000 = 10,000
So, 5 tons = 10,000 pounds.

C.
To convert from smaller units to larger units, divide.

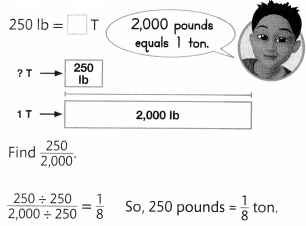
Convince Me! Generalize When you convert 16 pounds to ounces, do you multiply or divide? Explain.

To convert pounds to ounces we have to multiply.

16 pounds = 256 ounces

Guided Practice

Do You Understand?

Question 1.
Would it be best to measure the weight of an egg in tons, pounds, or ounces? Explain.
Answer:

Ounces are the best way to measure the weight of an egg.

Question 2.
What types of tools do people select to measure weight? Explain your example.
Answer:

A scale or a balance are the tools used to measure weight

A balance is used to determine an object’s mass.

A scale to measure ounces and pounds.

Do You Know How?

In 3-6, convert each unit of weight.

Question 3.
2,000 lb = __ T
Answer: 0.907 T

Question 4.
48 oz = ___ lb
Answer: 3 lb

Question 5.
6,500 lb = ___oz
Answer: 96000 oz

Question 6.
\(\frac{1}{2}\) lb = __ oz
Answer: 8 oz

In 7 and 8, compare. Write >, <, or = for each .

Question 7.
2T 45,000 lb
Answer:

2T < 45,000 lb

Question 8.
4 lb 64 oz
Answer:

4 lb = 64 oz

Independent Practice

In 9-14, convert each unit of weight.

Will your answer be greater than or less than the number you started with?

Question 9.
240 oz = __ lb
Answer: 15 lb

Question 10.
7\(\frac{1}{10}\)T = ___ lb
Answer: 14200lb

Question 11.
8 lb = ___ oz
Answer: 128 oz

Question 12.
4 oz = ___ lb
Answer: 0.25 lb

Question 13.
250 lb = ___ T
Answer: 0.113 T

Question 14.
1 T = ___ oz
Answer: 32,000 oz

In 15-17, compare. Write >, <, or = for each .

Question 15.
5,000 lb 3 T
Answer:

5,000 lb > 3 T

Question 16.
24 lb 124 oz
Answer:

24 lb > 124 oz

Question 17.
64,000 oz 2 T
Answer:

64,000 oz < 2 T

In 18 and 19, complete each table to show equivalent measures.

Question 18.

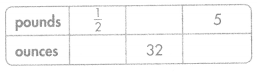
Answer:

1/2 lb = 8

2 lb = 32 oz

5 lb = 80 oz

Question 19.

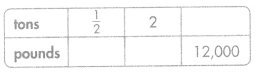
Answer:

1/2 t = 1000 pounds

2 pounds = 4000

6 tons = 12,000

Problem Solving

Question 20.
Be Precise The perimeter of the rectangular playground shown below is 160 feet. What is the area of the playground?

Answer:

Given, perimeter = 160 feet

We know that, perimeter = 2 (l + b )

160 = 2 ( 50 + b )

80 = 50 + b

b = 80 – 50

b = 30 feet

We know that area of rectangle = length x breadth

A = 80 x 30

= 2400 square feet

Therefore, Area = 2400 square feet.

Question 21.
enVision® STEM Humans exploring space have left behind bags of trash, bolts, gloves, and pieces of satellites. There are currently about 4,000,000 pounds of litter in orbit around Earth. Julia says that this amount using number names is four billion. Do you agree? Explain your thinking.
Answer:

No,  I do not agree because 4 billion > 4,000,000

In 22-25, use the table.

Question 22.
What would be the most appropriate unit to measure the combined weight of 4 horses?
Answer: Tons will be the most appropriate unit to measure the combined weight of 4 horses

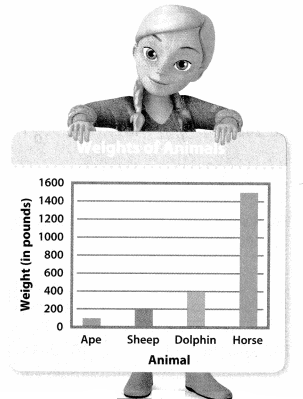
Question 23.
About how much would 4 horses weigh? Write the weight in two different ways.
Answer: The horses weigh 1500 pounds

1500 pounds = 0.75 tons

1500 pounds = 24000 ounces

Question 24.
How many more ounces do the sheep weigh than the ape?
Answer:

1600 ounces more the sheep weigh than the ape.

Question 25.
Higher-Order Thinking What is the difference in weight between the horse and the combined weight of the dolphin and the ape? Write your answer in tons.
Answer:

The  weight of 4 horses = 0.75 tons

The combined weight of dolphin and ape = 0.3 tons

Now, the difference between the weights =

= 0.75 – 0.3

= 0.45 tons

Therefore, the weight difference = 0.445 tons

Assessment Practice

Question 26.
Part A
The world’s heaviest lobster weighed 44 pounds 6 ounces. Write the lobster’s weight in ounces below.
44 lb 6 oz = ___ ounces

Answer:

44 lb 6 oz = 710 ounces
Part B
Describe the steps you took to find your answer.
Answer:

1 lb = 16 ounces

44 lb = 44 x 16

= 704 oz

704 oz + 6 oz

= 710 oz

Lesson 12.4 Convert Metric Units of Length

Activity

Solve & Share
Measure the length of your book in centimeters. Then measure it in millimeters. What do you notice about the two measurements?

1 cm = 10 mm

length of book = 25 cm

length of book = 250 mm

You can select appropriate units and tools to measure the length of objects!

Look Back! Use Structure How many meters long is your textbook? How do you know?

Visual Learning Bridge

Essential Question How Do You Convert Metric question Units of Length?

A.
The most commonly used metric units of length are the kilometer (km), meter (m), centimeter (cm), and millimeter (mm).
1 km = 10³ m = 1,000 m
1 m = 10² cm = 100 cm
1 m = 10³ mm = 1,000 mm
1 cm = 10 mm

Every metric unit is 10 times as great as the next smaller unit.

B.
The distance between two towns is 3 kilometers. How many meters apart are they?
3 km = __ m
To change from larger units to smaller units, multiply.
Find 3 × 10³.
3 km = 3,000 m
So, the towns are 3,000 meters apart.

One kilometer equals 1,000 meters.

To change from smaller units to larger units, divide.

C.
The distance between a kitchen and living room is 1,200 centimeters. How many meters apart are they?
1,200 cm = __ m
Find 1,200 ÷ 10²
1,200 cm = 12 m
So, the kitchen and the living room are 12 meters apart.

Convince Me! Critique Reasoning Elena says that 25 cm is equal to 250 mm. Do you agree? Why or why not?

Answer:

Yes, I agree because,

1 cm = 10 mm

Now,

25 cm = 25 x 10 = 250 mm

Guided Practice

Do You Understand?

Question 1.
To find the number of meters in six kilometers, why do you multiply 6 × 10³?
Answer: 6000 meters = 6 kilometers

Because, 1 km = 1000 m

6 km = 6 x 1000 = 6000m

Question 2.
Convert 12.5 centimeters to millimeters. Explain.
Answer:

12.5 cm = 125 mm

Explanation:

1 cm = 10 mm

12 cm = 120mm

0.5 cm = 5 mm

Total : 120 + 5 = 125 mm

Do You Know How?

In 3-6, convert each unit of length.

Question 3.
10³ cm = __ m
Answer: 1000 m

Question 4.
58 m = ___ mm
Answer: 58000 mm

Question 5.
1,000 mm = __ cm
Answer: 100 cm

Question 6.
3 km = ___ m
Answer: 3000 m

In 7 and 8, compare lengths. Write >,<, or = for each .

Question 7.
9,000 m 20 km
Answer:

9,000 m < 20 km

Question 8.
400 cm 4m
Answer:

400 cm = 4 m

Independent Practice

In 9-14, convert each unit of length.

Question 9.
7.5 cm = ___ mm
Answer: 75 mm

Question 10.
6m = __ сm
Answer: 600 cm

Question 11.
0.8 km = ___ cm
Answer: 80000 cm

Question 12.
17,000 m = ___ km
Answer: 17 km

Question 13.
48,000 mm = ___ m
Answer: 48 m

Question 14.
4 km = ___ m
Answer: 4000 m

In 15-20, compare lengths. Write >, <, or = for each .

Question 15.
25,365 cm 30 m
Answer:

25,365 cm > 30 m

Question 16.
3.6 km 3,600 m
Answer:

3.6 km = 3600

Question 17.
1,200 mm 12 m
Answer:

1200 mm< 12 m

Question 18.
52,800 cm 1 km
Answer:

52,800 cm <  1 km

Question 19.
7,500,000 m 750 km
Answer:

7,500,000 m > 750 km

Question 20.
800 m 799,999 mm
Answer:

800 m > 799,999 mm

In 21 and 22, complete each table.

Question 21.

Answer:

1 km = 1000 m

0.5 km = 500 m

0.1 km = 100 m

Question 22.

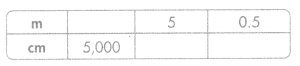
Answer:

50 m = 5,000 cm

5 m = 500 cm

0.5 m = 50 cm

Problem Solving

Question 23.
Number Sense Let x = the length of an object in meters and y = the length of the same object in millimeters. Which is a smaller number, x or y?
Answer: y

1 meter = 1000 mm

1 mm = 0.001 mm

Therefore, Y is smaller than x

Question 24.
Higher-Order Thinking How many millimeters are equal to one kilometer? Show your work.
Answer:

One kilometer is equal to 1000000 millimeters.

1 km = 1000000 mm

Question 25.
Reasoning Which fraction is greater: \(\frac{7}{8}\) or \(\frac{9}{12}\)? Explain how you know.
Answer:

7/8 >9/12

Explanation :

L.c.m of 8,12 = 24

Now,

7/8 x 3/3 = 21/24

9/12 x 2/2 = 18/24

21/24 > 18/24

Therefore,

7/8 >9/12

Question 26.
A week ago, Trudy bought the pencil shown. Now the pencil measures 12.7 centimeters.
How many centimeters of the pencil has been used?

Answer:

The original length of the pencil = 18 cm

The present length of pencil = 12.7 cm

Length difference = 18 – 12.7

= 5.3 cm

Therefore, the length of pencil used = 5.3 cm

How do you compare fractions?

Question 27.
enVision® STEM Mount St. Helens, located in Washington, erupted on May 18, 1980. Before the eruption, the volcano was 2.95 kilometers high. After the eruption, the volcano was 2.55 kilometers high. Use the bar diagram to find the difference in height of Mount St. Helens before and after the eruption. Convert the difference to meters.

Answer:

The original height of the volcano = 2.95 km

After the eruption, the height of the volcano = 2.55 km

Difference = 2.95 – 2.55

= 0.4 km

0.4 km = 400 meters.

Therefore, the difference in height of the volcano = 400 meters.

Assessment Practice

Question 28.
Eileen plants a tree that is 2 meters tall in her yard. Which of the following is equivalent to 2 meters?
A. 200 mm
B. 20 cm
C. 200 km
D. 2,000 mm
Answer:

B. 2 meters = 20 cm

Question 29.
Which of these number sentences is NOT true?
A. 600 cm = 6 m
B. 1 m < 9,000 mm
C. 900 mm = 9 cm
D. 10 km > 5,000 m
Answer:

B. 1 m < 9,000 mm

Lesson 12.5 Convert Metric Units of Capacity

Solve & Share
A pitcher holds 4 liters of water. How many milliliters does the pitcher hold? Solve this problem any way you choose.

You can convert metric units of capacity using multiplication or division. Show your work!

Answer:

1 liter = 1000000 milliliters

4 liters = 4 x 1000000 mL

= 4000000 mL

Look Back! Look for Relationships Juanita shares a one-liter bottle of water equally with 3 friends. How much water does each person get? Give your answer in liters and milliliters.

Visual Learning Bridge

Essential Question How Do You Convert Metric Units of Capacity?

A.
The most commonly used units of capacity in the metric system are the liter (L) and the milliliter (mL).

Can you find a liter or milliliter in the real world?

B.
Susan has 1.875 liters of water. How many milliliters is this?
1.875 L = __ mL
To change a larger unit to a smaller unit, multiply.
Find 1.875 × 10³.
1.875 × 10³ = 1,875
1.875 L = 1,875 mL
So, Susan has 1,875 milliliters of water.

C.
Jorge has 3,500 milliliters of water. How many liters is this?
3,500 mL = __ L
To change a smaller unit to a larger unit, divide.
Find 3,500 ÷ 10³.
3,500 ÷ 10³ = 3.5
3,500 mL = 3.5 L
So, Jorge has 3.5 liters of water.

Convince Me! Reasoning Order these measurements from greatest to least. Explain how you decided.

2,300 L >22L > 3000 mL > 2L > 500 mL

Guided Practice

Do You Understand?

Question 1.
Explain how you can convert milliliters to liters.
Answer:

1 milliliters = 0.001 liters

To convert milliliters to liters, we divide by 1000.

Question 2.
What types of tools would you select to measure capacity? Give an example and explain how that tool could be used.
Answer:

The most popular tool used to measure capacity is the measuring cup.

And also There are five basic units for measuring capacity in the U.S. customary measurement system. These are the fluid ounce, cup, pint, quart, and gallon.

Do You Know How?

In 3-8, convert each unit of capacity.

Question 3.
2.75 L = ___ mL
Answer: 2750 ml

Question 4.
3,000 mL = ___L
Answer: 3 L

Question 5.
5L = ___ mL
Answer: 5000 mL

Question 6.
250 mL = __ L
Answer: 0.25 L

Question 7.
0.027 L = __ mL
Answer: 27 ml

Question 8.
400 mL = __ L

Answer : 0.4 L

Independent Practice

In 9-20, convert each unit of capacity.

Question 9.
5,000 mL = ___ L
Answer:

5 L

Question 10.
45,000 mL = __ L
Answer:

45

Question 11.
4.27 L = __ mL
Answer:

4270 ml

Question 12.
13 L = ___ mL
Answer:

13000

Question 13.
3,700 mL = __ L
Answer:

3.7 L

Question 14.
0.35 L = __ mL
Answer:

350 ml

Question 15.
2,640 mL = ___ L
Answer:

2.64 L

Question 16.
314 mL = ___ L
Answer:

0.314 L

Question 17.
0.06 L = __ mL
Answer:

60

Question 18.
2,109 mL = ___ L
Answer:

0.0021

Question 19.
85 mL = __ L
Answer:

0.085 L

Question 20.
9.05 L = ___ mL
Answer:

9050

In 21 and 22, complete each table to show equivalent measures.

Question 21.

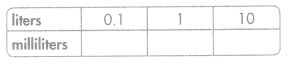
Answer:

0.1 L = 100 mL

1 L = 1000 mL

10 L = 10000 mL

Question 22.

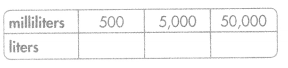
Answer:

500 mL = 0.5

5000 mL = 5

50,000 mL =50

Problem Solving

Question 23.
Reasoning Carla’s famous punch calls for 3 liters of mango juice. The only mango juice she can find is sold in 500-milliliter cartons. How many cartons of mango juice does Carla need to buy?
Answer:

Amount of Carla’s Famous punch = 3 liters

We know that 1 liter = 1000 milliliters

Also given, 500 mL = 1 Carton

Now, Number of cartons =

3000/ 500 = 6

Therefore, Carla needs to buy 6 cartons of mango juice.

Question 24.
Carla makes 6 liters of punch. She pours the punch into 800 ml bottles. How many bottles can she fill?
Answer:

6 liters of punch = 6000 milliliters

Now, 6000/800

=  7.5

Therefore, she can fill approximately 7.5 bottles.

Question 25.
Bobby filled the jug with water for soccer practice. If each player gets 250 milliliters of water, how many players will the water jug serve?

Answer:

The capacity of water jug =  5 liters

1 litre = 1000 millilitres

Now, 5 litres = 5000 millilitres

Now, 5000/ 250

= 20

Therefore, the water jug will serve 20 people.

Question 26.
Higher-Order Thinking One cubic centimeter will hold 1 milliliter of water. How many milliliters will the aquarium below hold? How many liters will it hold?

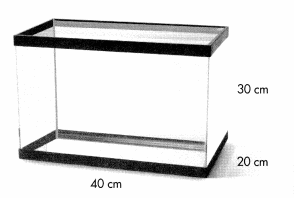
Answer:

Volume of the aquarium =

length x width x height

V =  40 x 20 x 30

V = 24000 cubic centimeters

We know that, 1 L = 1000 mL

Therefore, The aquarium holds 24 L .

Question 27.
Terry is buying juice. He needs 3 liters. A half-liter of juice costs $2.39. A 250-milliliter container of juice costs $1.69. What should Terry buy so he gets 3 liters at the lowest price? Explain.
Answer:

He needs 3 L.

A half-liter of juice costs $2.39.
A 250 mL container of juice costs $1.69.
One liter of juice in half-liter packs costs,

$2.39 x 2 = $4.78.
One liter of juice in 250 mL packs costs,

$1.69 x 4 = $6.76.
So, Terry should buy 6 half-liter packs of juice and spend
$2.39 x 6 = $9.56 to get 3 liters at the lowest price.

What steps do you need to do to solve this problem?

Assessment Practice

Question 28.
A birdbath holds 4 liters of water. How many milliliters of water does it hold?
A. 400 ml
B. 800 mL
C. 4,000 mL
D. 8,000 mL
Answer:

C. 4,000 mL

1 litre = 1000 milliliters

So, 4 litres = 4000 millilitres.

Question 29.
You are filling a 2-liter bottle with liquid from full 80-milliliter containers. How many containers will it take to fill the
A. 400
B. 250
C. 40
D. 25
Answer:

1 litre = 1000 millilitres

So, The number of  80 mL containers need are

2000/80

= 25

Therefore, 25 containers are required.

Lesson 12.6 Convert Metric Units of Mass

Activity

Solve & Share
In chemistry class, Rhonda measured 10 grams of a substance. How many milligrams is this? Solve this problem any way you choose.

Answer:

1 gram = 1000 mg

So,

10 grams = 10000 milligrams.

Look for Relationships You can use patterns to help you see a relationship between the units.

Look Back! How many kilograms did Rhonda measure? Write an equation to model your work.

Visual Learning Bridge

Essential Question How Do You Convert Metric Units of Mass?

A.
The three most commonly used units of mass are the milligram (mg), the gram (g), and the kilogram (kg).

Converting metric (units of mass is like converting other metric units.

B.
A whistle has a mass of about 5 grams. How many milligrams is this?
To change from a larger unit to a smaller unit, multiply.
Find 5 × 10³
5 × 10³ = 5 × 1,000 = 5,000
So, 5 g = 5,000 mg
So, a whistle has a mass of about 5,000 milligrams.

C.
How many kilograms is the whistle?
To change from a smaller unit to a larger unit, divide.
Find 5 ÷ 10³
5 ÷ 10³ = 5 ÷ 1,000 = 0.005
So, 5 g = 0.005 kg.
So, a whistle has a mass of about 0.005 kilograms.

Convince Me! Use Structure in the picture above, what is the football player’s mass in grams and in milligrams? How can you tell?

Guided Practice

Do You Understand?

Question 1.
A-Z Vocabulary How does the relationship between meters and millimeters help you understand the relationship between grams and milligrams?
Answer:

1 meter = 1000 millimeters.

1 Gram = 1000 milligrams.

Question 2.
Which has the greater mass: 1 kilogram or 137,000 milligrams? Explain how you made your comparison.
Answer:

137,000 is greater

Because, 1 kg = 1000000

Therefore, 137,000 is greater than 1 kg

Do You Know How?

In 3 and 4, convert each unit of mass.

Question 3.
9.25 g = ___ mg
Answer:

9250 mg

Question 4.
190 g = __ kg
Answer:

0.19 kg

In 5 and 6, compare. Write >,<, or = for each

Question 5.
7,000 mg 7,000 g
Answer:

7,000 mg < 7,000 g

Question 6.
10² kg 10⁴ g
Answer:

10² kg > 10⁴ g

Independent Practice

In 7-12, convert each unit of mass.

Question 7.
17,000 g = ___ kg
Answer:

17,000 = 17 kg

Question 8.
18 kg = ___ g
Answer:

18 kg = 18000 g

Question 9.
4,200 mg = ___ g
Answer: 4.2 g

Question 10.
0.276 g = ____ mg
Answer: 276 mg

Question 11.
4.08 kg = ___ g
Answer: 4080 g

Question 12.
43 mg = ___ g
Answer: 0.043 g

In 13-18, compare. Write >, <, or = for each

Question 13.
2,000 g 3 kg
Answer:

2000 g < 3 kg

Question 14.
4 kg 4,000 g
Answer:

4 kg = 4000 g

4 kg  = 4,000 g

Question 15.
10⁴ mg 13 g
Answer:

10⁴ mg < 13 g

Question 16.
7 kg 7,000 g
Answer:

7 kg < 7000 g

Question 17.
9,000 g 8 kg
Answer:

9000 g > 8 kg

Question 18.
8,000 g 5 kg
Answer:

8000 > 5 kg

In 19 and 20, complete each table.

Question 19.

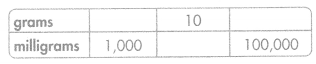
Answer:

1 grams = 1000 milligrams

10 grams = 10000 milligrams

100 grams = 100000 milligrams

Question 20.

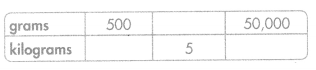
Answer:

500 grams = 0.5 kg

5000 grams = 5 kg

50000 grams = 50 kg

Problem Solving

Question 21.
Make Sense and Persevere Sheryl has a recipe for pasta with vegetables. The recipe calls for 130 grams of vegetables and twice as much pasta as vegetables. What is the total mass in grams of the recipe?
Answer:

Given,

The mass of vegetables = 130 grams

Also given, the mass of pasta is twice as vegetables

Which means, 130 x 2 = 260

Total mass = 260 + 130

= 390 grams

Therefore, the total mass of the recipe = 390 grams.

Question 22.
Terri is beginning a science experiment in the lab. The instructions call for 227 milligrams of potassium. Calculate the difference between this amount and 1 gram.
Answer:

We know that,

1 gram = 1000 milligrams

Given that, The weight of potassium = 227 milligrams

Now, The difference between the amount

= 1000 – 227

= 773 grams.

Therefore, the difference between the amount and 1 gram = 773 grams.

Question 23.
Number Sense One of the world’s heaviest hailstones weighed 2.2 pounds. Which is more appropriate to express its mass, 1 kilogram or 1 gram?
Answer:

2.2 pounds = 0.997 kg

2.2 pounds = 997. 9 grams

Therefore, 1 kilogram is more appropriate to express the mass.

Question 24.
Higher Order Thinking A cook has 6 onions that have a total mass of 900 grams and 8 apples that have a total mass of 1 kilogram. All onions are the same size, and all apples are the same size. Which has the greater mass, an onion or an apple? Explain.
Answer:

Given,

Number of onions = 6

Total mass = 900 grams

Weight of each onion = 900/6

= 150 grams.

Number of apples = 8

Total mass = 1 kg or 1000 grams

Weight of each apple = 1000/8

= 125 grams.

Therefore, Onion has a greater mass than apple.

In 25 and 26, use the given information and the picture.

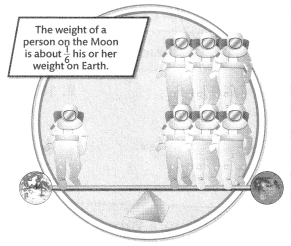
enVision® STEM If a man weighs 198 pounds on Earth, his mass on Earth is 90 kilograms.

Question 25.
What is this man’s weight on the Moon?
Answer:

Given,

The weight of the person on the moon is 1/6 weight on earth.

Also given, the mass on earth = 90 kgs

The weight of man’s weight on the moon =

90/6 =15 or 14.9 approx.

Question 26.
What is his mass in grams?
Answer:

1 kg = 1000 grams.

15 kg = 15000 grams

Assessment Practice

Question 27.
Write the following masses on the lines from least to greatest.

Answer:

5000 mg > 500 g > 50 kg

Question 28.
If you convert grams to milligrams, what operation would you use?
A. Addition
B. Subtraction
C. Multiplication
D. Division
Answer:

Multiplication.

Lesson 12.7 Convert Units of Time

Activity

Solve&Share
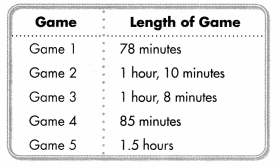
Emily played softball all weekend. She was wondering the difference in time between the shortest game and the longest game. Can you help her figure it out?

Select a common unit of time to help compare game times.

Look Back! Make Sense and Persevere Mateo saw a professional baseball game, which lasted 2\(\frac{1}{2}\) hours. How many minutes longer was the professional game than Emily’s Game 3? Explain.

Visual Learning Bridge

Essential Question How Do You Solve Problems that Involve Different Units of Time?

A.
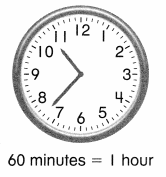
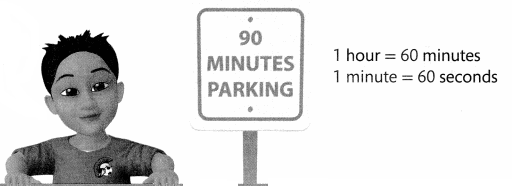
Kendall’s family is driving to the theater to see a 2-hour movie. Kendall notices this sign at the parking lot closest to the theater. Do you think they should park there?

You can convert one of these times so you are comparing like units.

B.
One Way:
Convert 2 hours to minutes. Then compare.
To change from larger units to smaller units, multiply.

Remember, 1 hour equals 60 minutes.

2 × 60 minutes = 120 minutes
120 minutes > 90 minutes, so Kendall’s family should not park in that lot.

C.
Another Way:
Convert 90 minutes to hours. Then compare.
To change from smaller units to larger units, divide.
90 ÷ 60 = \(\frac{90}{60}\) = 1\(\frac{1}{2}\) hours
1\(\frac{1}{2}\) hours < 2 hours, so Kendall’s family should not park in that lot.

Convince Me! Make Sense and Persevere explain how to convert 4 hours, 15 minutes to minutes.

Another example!
There is often more than one way to show converted units of time. Find the missing numbers.
Divide. Write the quotient with a remainder.
210 ÷ 60 = 3 R 30
So, 210 seconds = 3 minutes, 30 seconds

Remember, 1 minute equals 60 seconds.

210 seconds = ___ minutes
Divide. Write the quotient as a mixed number.
\(\frac{210}{60}\) = 3\(\frac{30}{60}\) = 3\(\frac{1}{2}\)
So, 210 seconds = 3\(\frac{1}{2}\) minutes

Guided Practices

Do You Understand?

Question 1.
Which is the longest time: 5 minutes, 25 seconds, or 315 seconds? Explain.
Answer:

5 hours 25 seconds

Explanation :

1 minute = 60 seconds

So, 5 minutes = 300 seconds

Now, 300 +25 = 325 seconds

Therefore, 325 seconds is longer than 315

Question 2.
How many minutes are in a quarter-hour? How do you know?
Answer:

Quarter hour = 15 minutes

We know that 15 minutes = quarter.

Do You Know How?

In 3-6, convert each time.

Question 3.
240 seconds = ___ minutes
Answer:

4 Minutes.

Question 4.
2 hours, 18 minutes = ___ minutes
Answer:

120 + 18

138 minutes

Question 5.
4\(\frac{1}{2}\) minutes ___ seconds
Answer:

4 minutes = 4 x 60 = 240 seconds

1/2 minute = 30 seconds

Now, 240 + 30 = 270 Seconds

Therefore, 4 1/2 Minute = 270 seconds.

Question 6.
80 minutes = ___ Seconds

Answer:

1 minute = 60 seconds

80 minutes = 80 x 60 = 480 seconds.

Independent Practice

In 7-10, convert each time.

Question 7.
6 hours = ___ minutes
Answer:

1 hour = 60 minutes

So, 6 hours = 6 x 60 =

= 360 minutes.

Question 8.
390 seconds = ___ minutes
Answer:

60 seconds = 1 minute

Now, 360 seconds = 6 minutes

30 seconds = 1/2 minute

390 seconds = 6 1/2 minutes.

Question 9.
208 minutes = ___hours, ___ minutes
Answer:

1 hour = 60 minutes

3 hours = 180 minutes And

208 – 180 = 28 minutes

Therefore, 208 minutes = 3 hours 28 minutes.

Question 10.
7 minutes, 12 seconds = ___ seconds

Answer:

1 minute = 60 seconds

7 minutes = 7 x 60 = 420 seconds

420 + 12 = 432 seconds .

Therefore, 7 minutes, 12 seconds = 432 seconds

In 11-12, compare. Write >, <, or = for each

Question 11.
330 minutes 7.5 hours
Answer:

330 minutes  < 7.5 hours

Question 12.
45 minutes \(\frac{3}{4}\) hour
Answer:

45 minutes  = 3/4  hour

Problem Solving

Question 13.
Brock spends 15 minutes walking to school and 15 minutes walking home each day. By the end of the school week (5 days) how many hours has Brock spent traveling between home and school?
Answer:

Given,

Brock spends 15 minutes walking to school

15 minutes walking home

Total = 15 + 15

= 30

Number of days = 5

Now, 5 x 30 = 150 minutes

1 hour = 60 minutes

150 minutes = 2.5 hours

Therefore, Brock spent 2.5 hours traveling between home and school

Question 14.
A television station shows commercials for 7\(\frac{1}{2}\) minutes each hour. How many 45-second commercials can it show per hour?
Answer:

1 minute  = 60 seconds

7 minutes = 60 x 7 = 420 seconds

420 + 30 = 450

450/45 = 10

Therefore, 10 45 second commercials it can show per hour.

Question 15.
Leslie is making these two recipes. Which takes longer to make, the strawberry bread or the spaghetti sauce? How many minutes longer?

Answer:

The time is taken to prepare spaghetti sauce is 1 hour 40 minutes

Also, the time taken to prepare strawberry bread is 1 hour 15 minutes

Therefore spaghetti sauce takes longer

Now,

1 hour 40 minutes – 1 hour 15 minutes

= 25 minutes

spaghetti sauce takes 25 minutes longer than strawberry bread.

Question 16.
Critique Reasoning The school day is 6 hours, 15 minutes long. Jenna says that it’s 6\(\frac{1}{4}\) hours. Henry says it’s 6.25 hours. Can they both be correct? Explain.
Answer:

Jenna is correct.

Given, the time of the school day = 6 hours 15 minutes long

1 hour = 60 minutes

1/4 hour = 15 minutes and 6 hours

Total: 6 1/4 hour

6.25 hours means 25 minutes more

But the school day is only 15 minutes long

Therefore, Jenna is correct.

Question 17.
Higher-Order Thinking How many seconds are there in 1 hour? In 10 hours? Explain.
Answer:

1 hour = 60 minutes

1 minute = 60 seconds

60 minutes = 60 x 60 = 3600 seconds

10 hours = 10 x 60 = 600 minutes

600 minutes = 600 x 600 = 36000 seconds.

Assessment Practice

Question 18.
Three hikers reported how long it took to hike a trail. Write the names of the hikers from fastest to slowest.
___ ____ _____

Answer:

Anita – First – 70 minutes

Brad – second – 75 minutes

Sanjay – Third – 90 minutes

Lesson 12.8 Solve Word Problems Using Measurement Conversions

Activity

Solve&Share
Amy wants to frame a poster that has a width of 8 inches and a length of 1 foot. What is the perimeter of the poster? Solve this problem any way you choose.

Make Sense and Persevere
You can use measurement conversions in real-world situations. Show your work!

Look Back! Which measurement did you convert? Can you find the perimeter by converting to the other unit of measurement?

Visual Learning Bridge

Essential Question How Can You Convert Units of Session Measurement to Solve a Problem?

A.
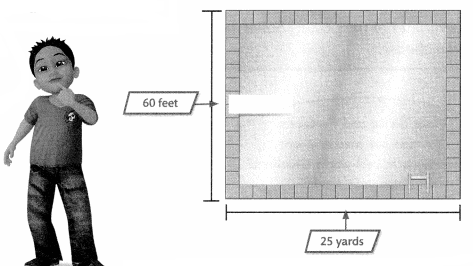
A city pool is in the shape of a rectangle with the dimensions shown. What is the perimeter of the pool?

You can convert one of the measures so that you are adding like units.

B.
What do you know?
The dimensions of the pool:
l = 25 yards
w = 60 feet
What are you asked to find?
The perimeter of the pool

You can use feet for perimeter.

C.
Convert 25 yards to feet so you can add like units.
1 yard = 3 feet
To change from larger units to smaller units, multiply.
25 × 3 feet = 75 feet
So, 25 yards = 75 feet.

D.
Substitute like measurements into the perimeter formula.
Perimeter = (2 × length) + (2 × width)
P = (2 × l) + (2 × w)
P = (2 × 75) + (2 × 60)
P = 150 + 120
P = 270 feet
The perimeter of the pool is 270 feet.

Convince Me! Be Precise If the width of the pool is increased by 3 feet, what would be the new perimeter of the pool? Explain.

length = 75 feet

width = 63 feet

Perimeter = 2 ( l+b)

2 (75+63)

2 ( 138 )

= 276 feet.

Guided Practice

Do You Understand?

Question 1.
In the example on the previous page, how could you find the perimeter by converting all measurements to yards?
Answer:

75 feet = 25 yards

60 feet = 20 yards

perimeter = 2 ( 25 + 20 )

= 2 ( 45)

perimeter = 90 feet

Question 2.
Write a real-world multiple-step problem that involves measurement.
Answer:

Multiple-step problem :

Robert had 16 marbles. His brother gave him 3 more bags of marbles. If each bag contained 5 marbles, how many marbles does Robert have now?

Do You Know How?

Question 3.
Stacia needs enough ribbon to wrap around the length (l) and height (h) of a box. If the length is 2 feet and the height is 4 inches, how much ribbon will she need?

Answer:

Given length = 2 feet

And height = 4 inches

Perimeter = 2 (l+b)

= 2 ( 2 + 4)

= 2 (6)

= 12 feet

1 feet = 12 inches

Now, 12 feet = 12 x 12

= 144 inches.

Question 4.
If ribbon is sold in whole number yards and costs $1.50 per yard, how much will it cost Stacia to buy the ribbon?
Answer:

144 x $1.05

= 151.2

Therefore it costs approx $151 to buy the ribbon.

Independent Practice

In 5-7, use conversions to solve each problem.

Edging means she will put bricks around the perimeter of the hexagon.

Question 5.
Becca wants to edge her hexagonal garden with brick. All sides are equal. The brick costs $6 per yard. What is the perimeter of the garden? How much will it cost to buy the edging she needs?
Answer:

The perimeter of the hexagon =

Number of sides = 6

Now, 12 x 6 = 72 feet

The perimeter of hexagon = 72 feet or 24 yards

Given, the cost of the brick = $6

Now, 24 x $6

= $144

Therefore, it costs $144 to buy the edging.

Question 6.
Isaac buys milk to make milkshakes for his friends. He buys 1 quart of milk and \(\frac{1}{2}\) gallon of milk. How many cups of milk does he buy?
Answer:

1 quart = 4 cups

1/2 gallon = 8 cups

Total = 4 + 8

= 12 cups

Therefore, he bought 12 cups of milk.

Question 7.
Maggie buys 1\(\frac{1}{2}\) pounds of walnuts, 8 ounces of pecans, and pound of almonds. How much do the nuts weigh in all?
Answer:

1 1/2 pounds of walnuts = 24 ounces

8 ounces of pecans

1 pound of walnuts = 16 ounces

Total : 24 + 8 + 16

= 48 ounces

Therefore, the nuts weigh 48 ounces

Problem Solving

Question 8.
Reasoning Matt’s family is thinking about buying a family pass to the city pool. The pass is $80 for a family of 4. Individual passes are $25 each. How much money can Matt’s family save by purchasing a family pass instead of 4 individual passes?
Answer:

Given, the amount of family pass = $80

Also given, the price of an individual pass = $25

Total number of family members = 4

Now, $25 x 4

= $100

So, $100 – $80

=$20

Therefore, Matt’s family saves $20 by purchasing a family pass instead of 4 individual passes

Question 9.
Marcia walked 900 meters on Friday. On Saturday, she walked 4 kilometers. On Sunday, she walked 3 kilometers, 600 meters. How many kilometers did Marcia walk over all three days?
Answer:

Given,

On Monday she walked 900 meters

On Tuesday she walked 4 kilometers

1 km = 1000 m

4 km = 4000 m

On Sunday, she walked 3 km,600 m

3 km =3000 m + 600 m

= 3600 m

Total : 900 + 4000 + 3600

= 8500 meters.

8500 meters = 8.5 kilometers

Therefore, Marica walked 8.5 kilometers.

Question 10.
Higher-Order Thinking

Raul wants to put wood shavings in his rabbit’s cage. The floor of the cage measures 1 yard wide by 5 feet long. One bag of shavings covers 10 square feet. How many bags will Raul have to buy to cover the floor of the cage? Explain.
Answer:

1.5 bags

Explanation:

Width = 1 yard = 3 feet

Length = 5 feet

Area of the floor = 5ft × 3ft = 15sqft

1 bag = 10sqft

x bag = 15sqft

x bags = (15 × 1)/10

= 1.5 bags

Therefore, Raul needs 1.5 bags.

Question 11.
Cheryl’s fish tank is 2 yards long by 24 inches wide by 3 feet high. What is the volume of Cheryl’s tank in cubic inches?

Answer:

Given,

length = 2 yards

2 yards = 72 inches

wide = 24 inches

Height = 3 feet

3 feet = 36 inches

Volume of the tank = length x width x height

Question 12.
Some statistics about a typical adult Royal antelope are shown in the data table.
a What is a typical Royal antelope’s tail length in millimeters?
b. How many centimeters high can a typical Royal antelope jump?
c. What is the mass of a typical Royal antelope in grams?

Answer:

a.

Given,

tail length =  6 cm

1 cm = 10 mm

6 cm = 6 x 10 = 60 mm

b.

Given, vertical leap = 2 meters

1 m = 1000 cm

Now, 2 meters = 2 x 1000 = 2000 cm

Therefore, it can jump 2000 cm

c.

2.4 kg = mass of antelope

1 kg = 1000 grams

2.4 kg = 2000 + 400

= 2400 grams.

Therefore, the mass of a typical Royal antelope in grams= 2400 grams

Assessment Practice

Question 13.
Joann wants to put a wallpaper border around her room. The border costs $3 per foot. The diagram shows Joann’s room. How much money will the border cost?
A. $120
B. $102
C. $84
D. $60

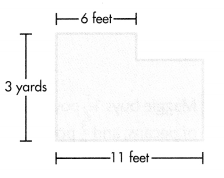
Answer:

Given,

The cost of border per foot = $3

Now, 11 x 3 = $33

3 yards = 9 feet

9 feet = 9 x 3 = $27

Total : $33 + $27

= $60

The border cost $60.

Lesson 12.9 Precision

Problem Solving

Solve & Share
Beth wants to make a picture frame like the one pictured below. She recorded the outside dimensions as 5 cm by 7 cm. Measure the outside dimensions of the frame in millimeters. Compare your measurements to Beth’s. Do you think her measurements are precise enough? Explain.

Thinking Habits
Think about these questions to help you attend to precision.
• Am I using numbers, units, and symbols appropriately?
• Am I using the correct definitions?
• Am I calculating accurately?
• Is my answer clear?

Look Back! Be Precise What is the difference between the perimeter based on the measurements Beth made and the perimeter based on the measurements you made? Explain how you found the answer.

Visual Learning Bridge

Essential Question How Can You Be Precise When Solving Math Problems?

A.
Chad and Rhoda are hanging a swing. Chad cut a piece of chain 6 feet 2 inches long. Rhoda cut a piece of chain 72 inches long. When they hung the swing, it was crooked.
Use precise language to explain why.

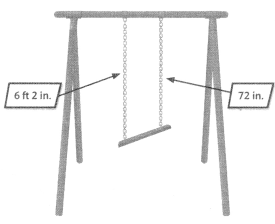
Be Precise means that you use appropriate math words, symbols, and units as well as accurate calculations when you solve problems.

B.
How can I be precise in solving this problem?
I can
• calculate accurately.
• give a clear answer.
• use the correct units.

Here’s my thinking.

C.
Convert 6 ft 2 inches to inches to see if Chad and Rhoda cut equal lengths of chain.
6 ft 2 in. = ___ in.
6 × 12 = 72, so 6ft = 72 in.
6 ft 2 in. = 72 +2 = 74 in.
Chad’s chain is 74 inches long, but Rhoda’s chain is only 72 inches long. Since Chad and Rhoda used unequal lengths of chain, the swing is crooked.

Convince Me! Be Precise What recommendations would you make to Chad and Rhoda so that the swing hangs level?

Guided Practice
Mary needs a board 4 feet 8 inches long. She cut a board 56 inches long.

Remember to be precise by converting measurements accurately.

Question 1.
What measurements are given? Are the same units used for each measurement? Explain.
Answer: No

The measurements are mentioned with different units.

Question 2.
Explain how you can convert one of the measurements so that both use the same unit.
Answer:

4 feet 8 inches can be converted into 56 inches as

1 foot = 12 inches

Now, 4 feet = 4 x 12 = 48 inches

48 + 8 = 56 inches.

Question 3.
Is the board Mary cut the right length? Give a clear and appropriate answer.
Answer:

Yes, mary cut the right length.

4 feet 8 inches can be shown as 56 inches

Therefore, mary cut the right length.

Independent Practice

Be Precise
Sean is making meat loaf. He used the amount of catsup shown in the measuring cup.

Question 4.
Are the units that Sean used to measure the catsup s the same as those given in the recipe? Explain.
Answer:

No, the units that Sean used to measure the catsup s the same as those given in the recipe.

Question 5.
How can you convert one of the measurements so that both use the same unit?
Answer:

1 fl oz = 0.125 cups

So, 6 fl oz = 0.75 cups.

Question 6.
Did Sean use the right amount of catsup? Give a clear and appropriate answer.
Answer:

No,

6 fl oz = 0.75 cups

0.75 cups = 3/4

But sean used 2/3 cup of catsup.

Problem Solving

Performance Task
Shipping a Package
A customer is using regular delivery to ship a package. Northside Shipping Company discovered that its old scale is not very accurate. It registers a weight that is 2 ounces too heavy. A new, accurate scale shows that the actual weight of the customer’s package is 2 pounds 11 ounces.

Question 7.
Make Sense and Persevere Which information do you need to determine the total shipping cost using either scale?
Answer:

We need the weight of the package and delivery charges to the total shipping cost using either scale

Question 8
Be Precise Why do you need to convert measurements to determine total shipping costs?
Answer:

Because To make the answer accurate we have to convert the measurements.

To be precise, you need to check that the words, numbers, symbols, and units you use are correct and that your calculations are accurate.

Question 9.
Model with Math Show how to convert the measurements you described in exercise 8.
Answer:

1 pound =16 ounces.

2 pounds 11 ounces = 43 ounces.

Question 10.
Be Precise What would the total cost be if the package is weighed on the new scale? What would the total cost be if the package is weighed on the old scale? Show your work.
Answer:

The weight on the new scale = $ 25. 95

The weight on the old scale = $27.15

Topic 12 Fluency Practice

Activity

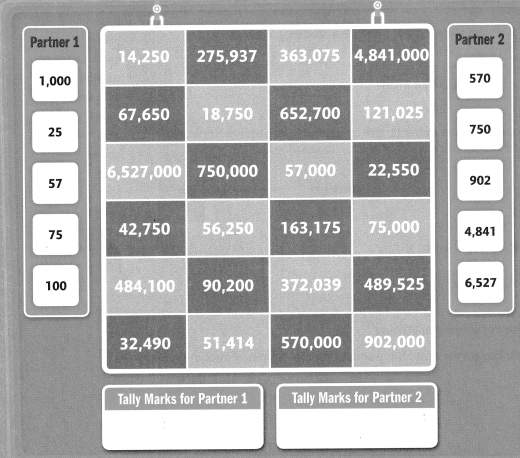
Point&Tally

Find a partner. Get paper and a pencil. Each partner chooses light blue or dark blue.
At the same time, Partner 1 and Partner 2 each point to one of their black numbers. Both partners find the product of the two numbers.
The partner who chose the color where the product appears gets a tally mark. Work until one partner has seven tally marks.

Topic 12 Vocabulary Review

Glossary

Word List

• capacity
• centimeter
• cup
• fluid ounce
• foot
• gallon
• gram
• inch
• kilogram
• kilometer
• liter
• mass
• meter
• mile
• milligram
• milliliter
• millimeter
• ounce
• pint
• pound
• quart
• ton
• weight
• yard

Understand Vocabulary

Choose the best term from the Word List. Write it on the blank.

Question 1.
One ___ is equivalent to twelve ___
Answer:

one foot is equivalent to 12 inches

Question 2.
The measure of the amount of matter in an object is known as ___
Answer: Mass

Question 3.
The volume of a container measured in liquid units is its ____
Answer: liters

Question 4.
There are 1,000 meters in one ____
Answer: kilometer

Question 5.
Finding how light or how heavy an object is means measuring its _____
Answer: Weight

Question 6.
There are 2 cups in one _____

Answer: Pint

For each of these objects, give an example and a non-example of a unit of measure that could be used to describe it.

Milk is measured in liters

person’s height is measured in feet

shoe’s length is measured in centimeters or inches

Use Vocabulary in Writing

Question 10.
Explain the relationship among the metric units of mass in the Word List.
Answer:

Length = meter, kilometer

Mass = gram, kilogram

volume = liter, milliliter.

Topic 12 Reteaching

Set A
pages 489-492, 517-520

Convert 3 yards to inches.
1 foot (ft) = 12 inches (in.)
1 yard (yd) = 3 ft = 36 in.
1 mile (mi) = 1,760 yd = 5,280 ft
1 yard = 36 inches. To change larger units to smaller units, multiply: 3 × 36 = 108.
So, 3 yards = 108 inches.

Remember to divide when changing smaller units to larger units.
Convert.

Question 1.
7 ft = ___ in.
Answer: 84 in

Question 2.
7,920 ft = ___ mi
Answer: 1 1/2 mi

Question 3.
Max wants to put a fence around his triangular garden. If each side is 6 yards, how many feet of fencing does Max need?
Answer:

Given, the side of the triangle = 6 yards

Perimeter = 6 x 6 x 6

= 18 yards

1yd/3 ft x 18/18

Now, 18/ 54

Therefore, Max have 54 feet of fencing.

Set B
pages 493-496
Convert 16 cups to pints.
2 cups = 1 pint. To change smaller units to larger units, divide: 16 ÷ 2 = 8.
So, 16 cups = 8 pints.

Remember that 1 gal = 4 qt, 1 qt = 2 pt, 1 pt = 2 c, and 1 c= 8 fl oz.

Convert.

Question 1.
36C = ___ gal
Answer: 2.25 gal

Question 2.
7 pt = __qt
Answer: 3.5 qt

Question 3.
1\(\frac{1}{2}[latex] gal = ___ fl oz
Answer:

1 1/2 gal = 192 fl oz

Question 4.
6 pt = ___ c
Answer:

1 pt = 2 cups

So, 6 pt = 6 x 2 = 12 cups.

Set C
pages 497-500
Convert 6 pounds to ounces. 1 pound = 16 ounces. To change larger units to smaller units, multiply: 6 × 16 = 96.
So, 6 pounds = 96 ounces.

Remember that 2,000 pounds = 1 ton.

Convert.

Question 1.
2[latex]\frac{3}{4}\) lb = __oz
Answer: 44 oz

Question 2.
56 oz = __ lb
Answer: 3 1/2 lb

Question 3.
4,000 lb = ___ T
Answer: 2 T

Question 4.
6\(\frac{1}{2}\)T = __ lb

Answer: 13,000 lb

Set D
pages 501-504
Convert 2 meters to centimeters.
1 km = 1,000 m
1 m= 100 cm
1 m = 1,000 mm
1 cm = 10 mm
1 meter = 100 centimeters. To change larger units to smaller units, multiply: 2 × 100 = 200.
So, 2 meters = 200 centimeters.

Remember to multiply or divide by a power of 10 to convert metric measurements.

Convert.

Question 1.
5.4 m = ___ cm
Answer: 540 cm

Question 2.
2.7 km = ___ m
Answer: 2700 m

Question 3.
0.02 km = __ cm
Answer: 20000 cm

Question 4.
0.025 m = ___ mm
Answer: 25mm

Question 5.
675 mm = ___ m
Answer: 0.675m

Question 6.
7,435 cm = ___ m
Answer: 74.35 m

Set E
pages 505-508
Convert 6,000 milliliters to liters.
1,000 milliliters = 1 liter. To change milliliters to larger units, divide: 6,000 ÷ 1,000 = 6.
So, 6,000 milliliters = 6 liters.

Remember that the most commonly used metric units of capacity are the liter and milliliter.

Convert.

Question 1.
6L = ___ mL
Answer: 6000

Question 2.
0.15 L = ___mL
Answer: 150

Question 3.
2,000 mL = __ L
Answer:  2

Question 4.
900 mL = ___ L
Answer: 9

Set F
pages 509-512
Convert 6 kilograms (kg) to grams (g).
1 kilogram = 1,000 grams. To change larger units to smaller units, multiply:
6 × 1,000 = 6,000.
So, 6 kg = 6,000 g.

Remember that to convert metric units, you can annex zeros and move the decimal point.

Convert.

Question 1.
30 kg = ___ g
Answer: 30000

Question 2.
3,000 mg = ___ g
Answer:  3

Question 3.
560 g = ___ kg
Answer: 56

Question 4.
0.17g = __mg
Answer: 170

Set G
pages 513-516
The choir concert is scheduled to last 90 minutes. The band concert is scheduled from 7:00-8:45. Which concert is scheduled to be longer? By how many minutes?
The choir concert will last 90 minutes = 1 hour, 30 minutes. The band concert will last 1 hour, 45 minutes. The band concert will be 15 minutes longer.

Remember to check if the units in the problem are the same.

Convert.

Question 1.
8 minutes = ___ seconds
Answer:

1 minute = 60 seconds

8 minutes = 8 x 60 = 480 seconds

Question 2.
86 minutes = ___ hour, ___ minutes
Answer:

1 hour = 60 minutes

86 minutes = 1 hour 26 minutes

Question 3.
A movie starts at 7:10 and ends at 9:03. How long does the movie last? __ hour, ___ minutes
Answer:

The movie lasts 1 hour 53 minutes

Set H
pages 521-524
Think about these questions to help you be precise in your work.

Thinking Habits
• Am I using numbers, units, and symbols appropriately?
• Am I using the correct definitions?
• Am I calculating accurately?
• Is my answer clear?

Remember that the problem might have more than one step.

Solve. Show your work.

Question 1.
Monica bought a 40-pound bag of dog food. Twice a day, she gives her dog 6 ounces of food. How many pounds of dog food will she use in 1 week? Explain.
Answer:

Given, The amount of dog food Monica bought = 40 pounds

40 pounds = 640 ounces

The amount of food Monica gives dog = 6 ounces

Twice = 6 x 2 = 12 oz

In one week = 12 x 7 = 84 oz

Therefore, Monica gives 84 oz of dog food will she use in 1 week

Topic 12 Assessment Practice

Question 1.
Which of the following are equivalent to 7 grams? Select all that apply.
0.007 kilogram
70 milligrams
7,000 kilograms
7,000 milligrams
0.007 milligram
Answer:

0.007 kilogram

7,000 milligrams

Question 2.
Justin’s garden is shown below.

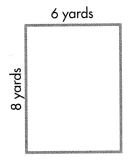
A. How can you convert the dimensions of Justin’s garden from yards to inches?
B. What is the perimeter of Justin’s garden in inches?
Answer:

A.

Given, Length = 8 yards

8 yards = 8 x 36 = 288 inches

6 yards = 6 x 36 = 216 inches.

B.

Perimeter = length x width

288 x 216 = P

62208 = Perimeter

Therefore, The perimeter of Justin’s Garden = 62208  inches.

Question 3.
Which of the following equations can be used to find how many kilograms are in 2,000 grams?
A. 1,000 ÷ 2,000 = 0.5 kilogram
B. 2,000 ÷ 1,000 = 2 kilograms
C. 2,000 × 1,000 = 2,000,000 kilograms
D. 2,000 × 100 = 200,000 kilograms
Answer:

2,000 ÷ 1,000 = 2 kilograms

Question 4.
A. 10 bales of cotton weigh approximately 5,000 pounds. How can you convert 5,000 pounds to tons?
B. Which comparison is true?
A. 5,000 pounds > 10,000 tons
B. 5,000 pounds = 3 tons
C. 5,000 pounds < 3 tons
D. 5,000 pounds > 3 tons
Answer:

A.

1 pound = 0.0005 tons

Now, 5000 pounds = 2.5 tons.

B.

5,000 pounds > 3 tons

Question 5.
Tyrell bought 4 liters of fruit punch for a party. He will serve the punch in glasses that can hold 200 milliliters. How many full glasses of fruit punch can he serve?
Answer:

1 litre = 1000 millilitres

Now, 4 litres = 4000 milliliters.

4000/200 = 20

Therefore, Tyrell can fill 20 glasses of fruit punch.

Question 6.
Select each equation that the number 103 will make true.
? km = 1 mm
? mm = 1 m
? cm = 1 m
?m = 1 km
? dm = 1 m
Answer:

1000000 km = 1 mm

1000 mm = 1 m

100 cm = 1 m

1000 m = 1 km

10 dm = 1m

Question 7.
Match each measurement on the left to its equivalent measurement.

Answer:

1 gallon = 4 quarts

1 cup = 8 fl oz

1 quart = 2 pints

1 pint = 2 cups.

Question 8.
Select all lengths that are equal to 6 feet 12 inches.
3 yd 1 ft
7 ft
7 ft 2 in.
2 yd 1 ft
1 yd 4 ft
Answer:

a. 7 feet

b. 2 yd 1 ft

c. 1 yd 4 ft

Question 9.
Write and solve an equation to find how many milliliters are in 3.4 liters.
Answer:

1 liter = 1000 milliliters

3.4 liters = 3400 milliliters.

Question 10.
Mason made 5 quarts of salsa. Which of the following can be used to find the number of cups of salsa Mason made?
A. 5 × 2 × 2
B. 5 × 4 × 4
C. 5 ÷ 2 ÷ 2
D. 5 × 4 ÷ 2
Answer:

1 quart = 4 cups

The answer is 5 x 2 x 2.

Question 11.
Alicia bought 5 pounds of potting soil. She wants to put 10 ounces of soil in each flower pot.
A. How can she convert 5 pounds to ounces?
B. How many flower pots can she fill?
Answer:

A.

1 pound = 16 ounces

So, 5 pounds = 5 x 16 = 80 ounces

B.

Now, 80/10 = 8

Therefore, she can make 8 flower pots.

Question 12.
The tail of a Boeing 747 is 63 feet 8 inches tall. How many inches tall is the tail?
Answer:

Given,

The length of tail = 63 feet

1 feet = 12 inches

Now, 63 x 12

= 756

Total = 756 + 8

= 764 inches

Question 13.
Write and solve an equation to convert 0.38 meters to centimeters.
Answer:

1 meter = 100 centimeters

Now, 0.38 meters = 38 cm.

Topic 12 Performance Task

Orange Juice
Heidi sells freshly-squeezed orange juice in Heidi’s Orange Juice cups.

Question 1.
Use the Information About Oranges. Answer the questions below to find how many pounds of oranges Heidi needs for her orange juice.
Part A
How many oranges does Heidi need to make one large orange juice? Show your work.

Part B
How many pounds of oranges does Heidi need to make one large orange juice? Show your work.

Answer:

2.5 cups = 20 fluid ounces.

20 fl oz = 1.5 pounds

Question 2.
Answer the following to find the area of Heidi’s Display Shelf.
Part A
What units can you use for the area? Explain.

Part B
What is the area of Heidi’s Display Shelf? Show your work.
Answer:

4 feet = 48 inches

Area = length x width

= 48 x 15

= 720 sq. inches

therefore, the area of hiedi’s shelf = 720 inches

Question 3.
The Orange Nutrition table shows nutrients in one medium-sized orange that weighs 5 ounces or 140 grams. All the nutrients in the orange are also in Heidi’s orange juice.

Part A
How many grams of potassium are in one large cup of Heidi’s orange juice? Explain how you solved.

Answer:

Given,

250 milligrams of potassium is there in the juice cup

1 milligram = 0.001

250 mg = 0.25 grams

therefore, there are 0.25 grams of potassium in orange juice.

Part B
How many milligrams of fiber is in one large cup of Heidi’s orange juice? Use an exponent when you explain the computation you used to solve.
Answer:

1 gram = 1000 milligrams

3.5 grams = 3500 milligrams

Therefore, there is 3500 mg of fiber.

Question 4.
Heidi also sells cartons of orange juice. Use the picture of Heidi’s Orange Juice Carton. Find the volume of the carton in cubic centimeters. Explain.

Answer:

The measurements of the carton are

10 cm, 50 mm = 5 cm, 0.2 m = 20 cm

Volume = l x w x h

= 50 x 5 x 20

= 500 Cubic centimeters

therefore, volume = 500 cubic centimeters.