Go through the enVision Math Common Core Grade 5 Answer Key Topic 15 Algebra: Analyze Patterns and Relationships regularly and improve your accuracy in solving questions.
enVision Math Common Core 5th Grade Answers Key Topic 15 Algebra: Analyze Patterns and Relationships
Essential Questions: How can number patterns be analyzed and graphed? How can number patterns and graphs be used to solve problems?

enVision STEM Project: Analyze Patterns
Do Research Use the Internet or other sources to find patterns in cities and buildings in other parts of the world.
Journal: Write a Report Include what you found. Also in your report:
• Describe types of patterns found in nature.
• Describe types of patterns found in cities.
• Make a graph to show relationships between some of the patterns you found.
Review What You Know
A-Z Vocabulary
Choose the best term from the Word List. Write it on the blank.
• equation
• Expression
• variable
• evaluate
• ordered pair
Question 1.
A numerical _____ is a mathematical phrase that has numbers and at least one operation.
Answer:
A numerical expression is a mathematical phrase that has numbers and at least one operation.
Explanation:
In the above-given question,
given that,
A numerical expression is a mathematical phrase that has numbers and at least one operation.
for example:
14 – 8 = 6.
21 – 5 + 2.
21 – 7 = 14.
Question 2.
A(n) _____ can be used to show the location of a point on the coordinate plane.
Answer:
A(n) ordered pair can be used to show the location of a point on the coordinate plane.
Explanation:
In the above-given question,
given that,
A(n) ordered pair can be used to show the location of a point on the coordinate plane.
for example:
(1, 3) is an ordered pair.
1 is on the x-axis.
3 is on the y-axis.
Question 3.
The letter n in $10 × n is called a(n) ___ and is a quantity that can change.
Answer:
The letter n in $10 x n is called a(n) variable and is a quantity that can change.
Explanation:
In the above-given question,
given that,
The letter n in $10 x n is called a(n) variable and is a quantity that can change.
for example:
A factor can be a number, variable, term, or a longer expression.
Expressions
Write a numerical Expression for each calculation.
Question 4.
Add 230 and 54, and then divide by 7.
Answer:
230 + 54 / 7.
Explanation:
In the above-given question,
given that,
Add 230 and 54, and then divide by 7.
230 + 54.
230 + 54 / 7.
284 / 7 = 40.5.
Question 5.
Subtract 37 from the product of 126 and 4.
Answer:
37 – 126 x 4 = 467.
Explanation:
In the above-given question,
given that,
Subtract 37 from the product of 126 and 4.
126 x 4 – 37.
504 – 37.
467.
Solve Equations
Solve each equation.
Question 6.
7,200 + x = 13,000
Answer:
X = 5800.
Explanation:
In the above-given question,
given that,
the equation is 7200 + x = 13000.
7200 + x = 13000.
13000 – 7200 = x.
x = 5800.
Question 7.
6,000 = 20 × g
Answer:
G = 300.
Explanation:
In the above-given question,
given that,
the equation is 6000 = 20 x g.
6000 = 20 x g.
g = 6000/ 20.
g = 300.
Question 8.
105 + 45 = w × 3
Answer:
W = 50.
Explanation:
In the above-given question,
given that,
the equation is 105 + 45 = w x 3.
150 = w x 3.
w = 150 / 3.
w = 50.
Question 9.
38 + 42 = 480 ÷ b
Answer:
B = 6.
Explanation:
In the above-given question,
given that,
the equation is 38 + 42 = 480 ÷ b.
80 = 480 / b.
b = 480 / 80.
b = 6.

Question 10.
Janine has 85 hockey cards in one book and 105 hockey cards in another book. The hockey cards come in packages of 5 cards. If Janine bought all of her hockey cards in packages, how many packages did she buy?
A. 21 packages
B. 38 packages
C. 190 packages
D. 195 packages
Answer:
Option D is correct.
Explanation:
In the above-given question,
given that,
Janine has 85 hockey cards in one book and 105 hockey cards in another book.
The hockey cards come in packages of 5 cards.
85 + 105 = 190.
190 + 5 = 195.
so option D is correct.
Evaluate Expressions
Question 11.
Explain how to evaluate the Expression 9 + (45 × 2) ÷ 10.
Answer:
9 + (45 x 2) / 10 = 18
Explanation:
In the above-given question,
given that,
9 + (45 x 2) / 10.
9 + (90) / 10.
9 + 9.
18.
9 + (45 x 2) / 10 = 18.
Pick a Project
PROJECT 15A
How are piano keys arranged on a keyboard?
Project: Learn More About Keyboards

PROJECT 15B
Why is it important to protect gopher tortoises?
Project: Use Information to Write Problems

PROJECT 15C
How can you use patterns to make art?
Project: Create a Work of String Art

3-ACT MATH PREVIEW
Math Modeling
Video
Speed Stacks

Before watching the video, think:
Stacking cups is a lot less messy when they’re empty.
Lesson 15.1 Numerical Patterns
Activity
Solve & Share
Emma has $100 in her savings account. Jorge has $50 in his savings account. They each put $10 in their accounts at the end of each week. Complete the tables to see how much each of them has saved after 5 weeks. What patterns do you notice?

Answer:
Emma has $150 and Jorge has $100 after 5 weeks.
Explanation:
In the above-given question,
given that,
Emma has $100 in her savings account.
Jorge has $50 in his savings account.
They each put $10 in their accounts at the end of each week.
100 + 10 = 110, 110 + 10 = 120, 120 + 10 = 130, 130 + 10 = 140, and 140 + 10 = 150.
50 + 10 = 60, 60 + 10 = 70, 70 + 10 = 80, 80 + 10 = 90, 90 + 10 = 100.
so Emma has $150 and Jorge has $100 after 5 weeks.
Look for Relationships to see what is alike and what is different in the two tables.

Answer:
Both of them saved an equal amount of money that is $50.
Explanation:
In the above-given question,
given that,
Emma has $100 in her savings account.
Jorge has $50 in his savings account.
They each put $10 in their accounts at the end of each week.
100 + 10 = 110, 110 + 10 = 120, 120 + 10 = 130, 130 + 10 = 140, and 140 + 10 = 150.
50 + 10 = 60, 60 + 10 = 70, 70 + 10 = 80, 80 + 10 = 90, 90 + 10 = 100.
so both of them saved an equal amount of money that is $50.
Look Back! If the savings patterns continue, will Jorge ever have as much saved as Emma? Explain.
Visual Learning Bridge
Essential Question How Can You Solve Problems Involving Numerical Patterns?
A.
Lindsey has a sage plant that is 3.5 inches tall. She also has a rosemary plant that is 5.2 inches tall. Both plants grow 1.5 inches taller each week. How tall will the plants be after 5 weeks? What is the relationship between the heights of the plants?
You can create tables to help identify relationships between corresponding terms in the number sequences.

B.
You can use the rule “add 1.5” to complete the tables.

Convince Me! Reasoning If the patterns continue, how can you tell that the rosemary plant will always be taller than the sage plant?
Guided Practice
Do You Understand?
Question 1.
Anthony says, “The pattern is that the sage plant is always 1.7 inches shorter than the rosemary plant.” Do you agree? Explain.
Answer:
Yes, I will agree.
Explanation:
In the above-given question,
given that,
Lindsey has a sage plant that is 3.5 inches tall.
She also has a rosemary plant that is 5.2 inches tall.
Both plants grow 1.5 inches taller each week.
5.2 – 3.5 = 1.7.
so I will agree.
Question 2.
How does making tables help you identify relationships between terms in patterns?
Answer:
The difference for every pattern is 1.7.
Explanation:
In the above-given question,
given that,
Lindsey has a sage plant that is 3.5 inches tall.
She also has a rosemary plant that is 5.2 inches tall.
Both plants grow 1.5 inches taller each week.
5.2 – 3.5 = 1.7.
so the difference for every pattern is 1.7.
Do You Know How?
Question 3.
If the plants continue to grow 1.5 inches each week, how tall will each plant be after 10 weeks?
Answer:
After 10 weeks each plant will be 18.5.
Explanation:
In the above-given question,
given that,
if the plants continue to grow 1.5 inches each week.
11 + 1.5 = 12.5.
12.5 + 1.5 = 14.0.
14.0 + 1.5 = 15.5.
15.5 + 1.5 = 17.0.
17.0 + 1.5 = 18.5.
Question 4.
If the plants continue to grow 1.5 inches each week, how tall will each plant be after 15 weeks?
Answer:
After 15 weeks each plant will be 26.0.
Explanation:
In the above-given question,
given that,
if the plants continue to grow 1.5 inches each week.
18.5 + 1.5 = 20.0.
20.0 + 1.5 = 21.5.
21.5 + 1.5 = 23.0.
23.0 + 1.5 = 24.5.
24.5 + 1.5 = 26.0.
Independent Practice
In 5-7, use the rule “add $0.50” to help you.
Question 5.
Tim and Jill each have a piggy bank. Tim starts with $1.25 in his bank and puts in $0.50 each week. Jill starts with $2.75 in her bank and also puts in $0.50 each week. Complete the table to show how much money each has saved after five weeks.
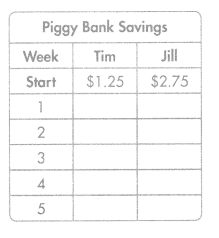
Answer:
Tim saved $3.75 and Jill saved $5.25.
Explanation:
In the above-given question,
given that,
Tim and Jill each have a piggy bank.
Tim starts with $1.25 in his bank and puts in $0.50 each week.
Jill starts with $2.75 in her bank and also puts in $0.50 each week.
1.25 + 0.50 = 1.75.
1.75 + 0.50 = 2.25.
2.25 + 0.50 = 2.75.
2.75 + 0.50 = 3.25.
3.25 + 0.50 = 3.75.
2.75 + 0.50 = 3.25.
3.25 + 0.50 = 3.75.
3.75 + 0.50 = 4.25.
4.25 + 0.50 = 4.75.
4.75 + 0.50 = 5.25.
Question 6.
What relationship do you notice between the amount Tim has saved and the amount Jill has saved each week?
Answer:
Tim has saved $3.75 and Jill saved $5.25.
Explanation:
In the above-given question,
given that,
Tim and Jill each have a piggy bank.
Tim starts with $1.25 in his bank and puts in $0.50 each week.
Jill starts with $2.75 in her bank and also puts in $0.50 each week.
1.25 + 0.50 = 1.75.
1.75 + 0.50 = 2.25.
2.25 + 0.50 = 2.75.
2.75 + 0.50 = 3.25.
3.25 + 0.50 = 3.75.
2.75 + 0.50 = 3.25.
3.25 + 0.50 = 3.75.
3.75 + 0.50 = 4.25.
4.25 + 0.50 = 4.75.
4.75 + 0.50 = 5.25.
Question 7.
If Tim and Jill continue saving in this way, how much will each have saved after 10 weeks? Explain how you decided.
Answer:
Tim saves $6.25 and Jill saves $7.75.
Explanation:
In the above-given question,
given that,
Tim and Jill each have a piggy bank.
Tim starts with $1.25 in his bank and puts in $0.50 each week.
Jill starts with $2.75 in her bank and also puts in $0.50 each week.
3.75 + 0.50 = 4.25.
4.25 + 0.50 = 4.75.
4.75 + 0.50 = 5.25.
5.25 + 0.50 = 5.75.
5.75 + 0.50 = 6.25.
5.25 + 0.50 = 5.75.
5.75 + 0.50 = 6.25.
6.25 + 0.50 = 6.75.
6.75 + 0.50 = 7.25.
7.25 + 0.50 = 7.75.
Problem Solving
For 8-10, use the table.
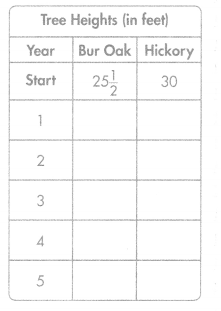
Question 8.
enVision® STEM Bur oak and hickory trees are deciduous, which means that they lose their leaves seasonally. A bur oak is 25\(\frac{1}{2}\) feet tall and grows 1\(\frac{1}{2}\) feet each year. A hickory is 30 feet tall and grows 1\(\frac{1}{2}\) feet each year. Complete the chart to show the heights of the two trees each year for five years.
Answer:
The heights of the two trees each year for five years = 32 and 37.5.
Explanation:
In the above-given question,
given that,
Bur oak and hickory trees are deciduous, which means that they lose their leaves seasonally.
A bur oak is 25\(\frac{1}{2}\) feet tall and grows 1\(\frac{1}{2}\) feet each year.
A hickory is 30 feet tall and grows 1\(\frac{1}{2}\) feet each year.
25(1/2) = 51/2 = 25.5.
3/2 = 1.5.
25.5 + 1.5 = 27.0.
27.0 + 1.5 = 28.5.
28.5 + 1.5 = 30.
30 + 1.5 = 31.5.
31.5 + 1.5 = 32.
30 + 1.5 = 31.5.
31.5 + 1.5 = 33.
33 + 1.5 = 34.5.
34.5 + 1.5 = 36.0.
36.0 + 1.5 = 37.5.
Question 9.
If each tree continues to grow 1\(\frac{1}{2}\) feet each year, how tall will each tree be after 15 years?
Answer:
The height of each tree after 15 years = 39.5 and 45.0.
Explanation:
In the above-given question,
given that,
A bur oak is 25\(\frac{1}{2}\) feet tall and grows 1\(\frac{1}{2}\) feet each year.
Hickory is 30 feet tall and grows 1\(\frac{1}{2}\) feet each year.
32 + 1.5 = 33.5.
33.5 + 1.5 = 35.0.
35.0 + 1.5 = 36.5.
36.5 + 1.5 = 38.0.
38.0 + 1.5 = 39.5.
37.5 + 1.5 = 39.0.
39.0 + 1.5 = 40.5.
40.5 + 1.5 = 42.0.
42.0 + 1.5 = 43.5.
43.5 + 1.5 = 45.0.
Question 10.
Higher Order Thinking What relationship do you notice between the height of the bur oak and the height of the hickory each year? Explain.
Answer:
Question 11.
Reasoning Each small square on the chessboard is the same size. The length of a side of a small square is 2 inches. What is the area of the chessboard? Explain.

Answer:
The area of the chessboard = 4 sq in.
Explanation:
In the above-given question,
given that,
Each small square on the chessboard is the same size.
The length of a side of a small square is 2 inches.
area of the square = side x side.
area of the square and area of the chessboard is the same.
area = s x s.
s = 2 inches.
area = 2 x 2.
area = 4 sq in.
so the area of the chessboard = 4 sq in.
Assessment Practice
Question 12.
Jessica has saved $50. She will add $25 to her savings each week. Ron has saved $40 and will add $25 to his savings each week. How much will each person have saved after 5 weeks?
A. Jessica: $275; Ron: $225
B. Jessica: $250; Ron: $240
C. Jessica: $175; Ron: $165
D. Jessica: $165; Ron: $175
Answer:
Option C is correct.
Explanation:
In the above-given question,
given that,
Jessica has saved $50.
She will add $25 to her savings each week.
Ron has saved $40 and will add $25 to his savings each week.
$50 + $25 = $75.
$25 x 5 = $125.
$125 + $50 = $175.
$40 + $25 = $65.
$65 + $100 = $165.
Question 13.
Which of the following statements are true?
![]() Jessica has always saved $25 more than Ron.
Jessica has always saved $25 more than Ron.
![]() Jessica has always saved $10 more than Ron.
Jessica has always saved $10 more than Ron.
![]() Ron has always saved $25 less than Jessica.
Ron has always saved $25 less than Jessica.
![]() Ron has always saved $10 less than Jessica
Ron has always saved $10 less than Jessica
Answer:
Option B is correct.
Explanation:
In the above-given question,
given that,
Jessica has saved $50.
She will add $25 to her savings each week.
Ron has saved $40 and will add $25 to his savings each week.
$175 – $165 = $10.
so option B is correct.
Lesson 15.2 More Numerical Patterns
Activity
Solve & Share
During summer vacation, Julie read 45 pages each day. Her brother Bret read 15 pages each day. Complete the tables to show how many pages each of them read after 5 days. What relationship do you notice between the terms in each pattern?
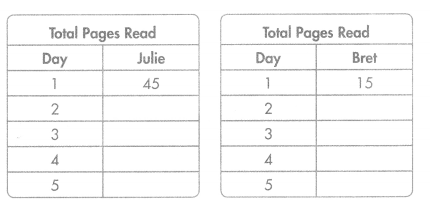
Find a rule to help you complete each table.

Answer:
The number of pages each of them read after 5 days = 105 and 75.
Explanation:
In the above-given question,
given that,
During summer vacation, Julie read 45 pages each day.
Her brother Bret read 15 pages each day.
45 + 15 = 60.
60 + 15 = 75.
75 + 15 = 90.
90 + 15 = 105.
105 + 15 = 125.
15 + 15 = 30.
30 + 15 = 45.
45 + 15 = 60.
60 + 15 = 75.
Look Back! Reasoning Explain why this relationship Exists between the terms.
Visual Learning Bridge
Essential Question
How Can You Identify Relationships Between Patterns?
A.
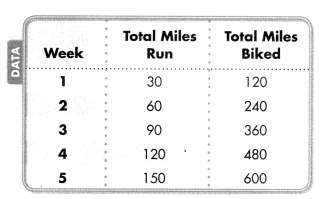
Jack is training for a race. Each week, he runs 30 miles and bikes 120 miles. He created a table to record his progress. How many total miles will he run and bike after 5 weeks? Can you identify any relationship between the miles run and the miles biked?
You can use the rules “add 30” and “add 120″ to help you complete the table.

B.
Since jack runs 30 miles each week, add 30 to find the nExt term for the total miles run. Add 120 to find each term in the pattern for the total number of miles biked.
C.
Compare the corresponding terms in the patterns:
30 × 4 = 120
60 × 4 = 240
90 × 4 = 360
120 × 4 = 480
150 × 4 = 600
So, the total number of miles biked is always 4 times the total number of miles run.
Convince Me! Generalize Do you think the relationship between the corresponding terms in the table Jack created will always be true? Explain.
Answer:
The relationship between the corresponding terms in the table Jack created will always be true.
Explanation:
In the above-given question,
given that,
Jack is training for a race.
Each week, he runs 30 miles and bikes 120 miles.
He created a table to record his progress.
30 × 4 = 120.
60 × 4 = 240.
90 × 4 = 360.
120 × 4 = 480.
150 × 4 = 600.
so the relationship between the corresponding terms in the table Jack created will always be true.
Guided Practice
Do You Understand?
In 1-3, use the table on page 598.
Question 1.
Neko says that the relationship between the terms is that the number of miles run is \(\frac{1}{4}\) the number of miles biked. Do you agree? Explain.
Answer:
Yes, it is true.
Explanation:
In the above-given question,
given that,
the number of miles run is 1/4 the number of miles biked.
Jack is training for a race.
Each week, he runs 30 miles and bikes 120 miles.
He created a table to record his progress.
30 × 4 = 120.
60 × 4 = 240.
90 × 4 = 360.
120 × 4 = 480.
150 × 4 = 600.
So it is true.
Question 2.
How many total miles will Jack have run and biked after 10 weeks? 15 weeks?
Answer:
The number of miles will Jack have run and biked after 10 weeks and 15 weeks = 1200 and 1800.
Explanation:
In the above-given question,
given that,
180 x 4 = 720.
210 x 4 = 840.
240 x 4 = 960.
270 x 4 = 1080.
300 x 4 = 1200.
330 x 4 = 1320.
360 x 4 = 1440.
390 x 4 = 1560.
420 x 4 = 1680.
450 x 4 = 1800.
so the number of miles Will Jack have run and biked after 10 weeks and 15 weeks = 1200 and 1800.
Question 3.
Miguel says that he can use multiplication to find the terms in the patterns. Do you agree? Explain.
Answer:
Yes, Miguel says that he can use multiplication to find the terms in the patterns.
Explanation:
In the above-given question,
given that,
180 x 4 = 720.
210 x 4 = 840.
240 x 4 = 960.
270 x 4 = 1080.
300 x 4 = 1200.
330 x 4 = 1320.
360 x 4 = 1440.
390 x 4 = 1560.
420 x 4 = 1680.
450 x 4 = 1800.
Independent Practice
In 4-6, use the rules “add 250” and “add 125” to help you.
Question 4.
Maria and Henry are each starting a savings account. Maria puts $250 into her account each month. Henry puts $125 into his account each month. How much money will each of them have saved after 6 months? Complete the table to solve.

Answer:
The money will each of them have saved after 6 months =
Explanation:
In the above-given question,
given that,
Maria and Henry are each starting a savings account.
Maria puts $250 into her account each month.
Henry puts $125 into his account each month.
Question 5.
What relationship do you notice between the total amount Maria has saved after each month and the total amount Henry has saved after each month?
Answer:
Question 6.
If Maria and Henry continue saving this way for a full year, how much more will Maria have saved than Henry?
Answer:
Problem Solving
Question 7.
Sheila and Patrick are making a table to compare gallons, quarts, and pints. Use the rule “add 4” to complete the column for the number of quarts. Then use the rule “add 8” to complete the column for the number of pints.
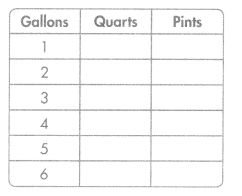
Answer:
Question 8.
Patrick has a 12-gallon fish tank at home. How many quarts of water will fill his fish tank? How many pints?
Answer:
Question 9.
Look for Relationships What relationship do you notice between the number of quarts and the number of pints?
Answer:
Question 10.
Higher Order Thinking At their family’s pizzeria, Dan makes 8 pizzas in the first hour they are open and 6 pizzas each hour after that. Susan makes 12 pizzas in the first hour and 6 pizzas each hour after that. If the pizzeria is open for 6 hours, how many pizzas will they make in all? Complete the table using the rule “add 6” to help you.
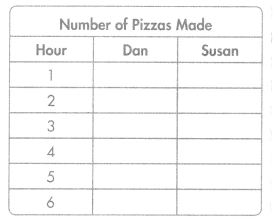
Answer:
Question 11.
Look for Relationships Compare the total number of pizzas made by each person after each hour. What relationship do you notice?
Answer:
Assessment Practice
Question 12.
Mike and Sarah are packing boxes at a factory. Mike packs 30 boxes each hour. Sarah packs 15 boxes each hour. How many boxes will each person have packed after an 8-hour shift?
A. Mike: 38 boxes; Sarah: 23 boxes
B. Mike: 86 boxes; Sarah: 71 boxes
C. Mike: 120 boxes; Sarah: 240 boxes
D. Mike: 240 boxes; Sarah: 120 boxes
Answer:
Question 13.
Which of the following are true statements about the number of boxes Mike and Sarah have packed after each hour?
![]() Mike has always packed a total of 15 more boxes than Sarah.
Mike has always packed a total of 15 more boxes than Sarah.
![]() Mike has always packed twice as many boxes as Sarah.
Mike has always packed twice as many boxes as Sarah.
![]() Sarah has always packed twice as many boxes as Mike.
Sarah has always packed twice as many boxes as Mike.
![]() Sarah has always packed half as many boxes as Mike.
Sarah has always packed half as many boxes as Mike.
Answer:
Lesson 15.3 Analyze and Graph Relationships
Activity
Solve & Share
A bakery can fit either 6 regular muffins or 4 jumbo muffins in each box. Each box will contain either regular or jumbo muffins. Complete the table to show how many of each muffin will fit in 2, 3, or 4 boxes. Then generate ordered pairs and graph them.

Find rules that describe the relationships between the number of boxes and the number of muffins.

Look Back! Look for Relationships The bakery can fit 12 mini-muffins in a box. How many mini-muffins will fit in 4 boxes? Without Extending the table, what relationship do you notice between the number of mini-muffins and the number of boxes?
Visual Learning Bridge
Essential Question How Can You Generate and Graph Numerical Patterns?
You can look for a relationship between the corresponding terms in the patterns.

A.
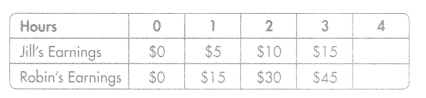
Jill earns $5 per hour babysitting. Robin earns $15 per hour teaching ice skating lessons. The girls made a table using the rule “Add 5” to show Jill’s earnings and the rule “Add 15” to show Robin’s earnings. Complete the table, compare their earnings, and graph the ordered pairs of the corresponding terms.
B.
Compare the numbers in Jill’s and Robin’s sequences.
Each sequence begins with zero. Then each term in Robin’s pattern is 3 times as great as the corresponding term in Jill’s pattern.
Generate ordered pairs from the total amount Jill and Robin have earned after each hour.
(0, 0), (5, 15), (10,30), (15,45), (20,60)
C.
Graph the ordered pairs.

Convince Me! Make Sense and Persevere What does the point (0,0) represent?
Guided Practice
Do You Understand?
Question 1.
In the Example on page 602, what ordered pair would you write for how much Jill and Robin have each earned after 5 hours?
Question 2.
Ben says that the relationship is that Jill earns \(\frac{1}{3}\) as much as Robin. Do you agree? Explain.
Answer:
Do You Know How?
Sam and Eric record the total number of miles they walk in one week. Sam walks 2 miles each day. Eric walks 4 miles each day.
Question 3.
What ordered pair represents the number of miles each has walked in all after 7 days?
Answer:
Question 4.
What relationship do you notice between the total number of miles Sam and Eric have each walked?
Answer:
Independent Practice
In 5-8, use the rule “add 4″ to help you.
Question 5.
Megan and Scott go fishing while at camp. Megan catches 3 fish in the first hour and 4 fish each hour after that. Scott catches 5 fish in the first hour and 4 fish each hour after that. Complete the table to show the total number of fish each has caught after each hour.
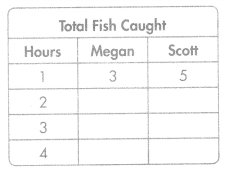
Answer:
Question 6.
What ordered pair represents the total number of fish they each caught after 4 hours?
Answer:
Question 7.
What relationship do you notice between the total number of fish each has caught after each hour?
Answer:
Question 8.
Graph the ordered pairs of the total number of fish each has caught after each hour.
Answer:
Question 9.
The pattern continues until Scott’s total is 29 fish. What ordered pair represents the total number of fish they each caught when Scott’s total is 29 fish?
Answer:
Problem Solving
In 10-12, use the rules “add 15″ and “add 10” to help you.
Question 10.
The Snack Shack made a table to track the amount of money from sales of frozen yogurt and fruit cups for four hours. What are the missing values in the table?

Answer:
Question 11.
Use Structure If sales continue in the same manner, what ordered pair would represent the money from sales of yogurt and fruit cups at 1 P.M.? Explain how you know.
Answer:
Question 12.
Graph the ordered pairs for the money from sales of yogurt and fruit cups from 9 A.M. to 1 P.M.
Answer:
Question 13.
A-Z Vocabulary Write two number sequences. Then, circle corresponding terms in the two sequences.
Answer:
Question 14.
Higher Order Thinking Pedro runs 2\(\frac{1}{2}\) miles each day for 5 days. Melissa runs 4 miles each day for 5 days. How many more miles will Melissa run in 5 days than Pedro? Make a table to help you.
Answer:
Assessment Practice
Question 15.
Every month, Leonard pays $240 for a car payment. He spends $60 each month for a gym membership. Write an ordered pair to represent how much Leonard spends in 12 months for car payments and the gym membership.
Answer:
Question 16.
What relationship do you notice between how much Leonard spends in 12 months on car payments and the gym membership?
Answer:
Lesson 15.4 Make Sense and Persevere
Activity
Solve & Share
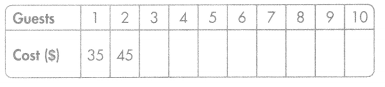
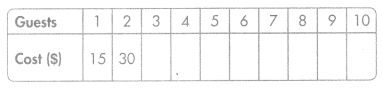
Val is planning a bowling-and-pizza party. Including herself, there will be no more than 10 guests. Val wonders which bowling alley offers the less Expensive party plan.
Complete the tables for Leonard’s Lanes and Southside Bowl. On the same grid, graph the ordered pairs in each table. Use a different color for the values in each table. Which bowling alley would be less Expensive? Explain how you know.
Leonard’s Lanes
Bowling and Pizza: $25 plus $10 per person
Southside Bowl
Bowling and Pizza: $15 per person Guests 1 2 3 4 5 6 7
Thinking Habits
Think about these questions to help you make sense and persevere.
• What do I need to find?
• What do I know?
• What else can I try if I get stuck?
• How can I check that my solution makes sense?
Look Back! Make Sense and Persevere How did the graph help you answer the question?
Visual Learning Bridge
Essential Question How Can You Make Sense of a Problem Question and Persevere in Solving It?
A.
Make Sense of the Problem
On Aiden’s farm, there are 12 acres of soybeans and 8 acres of corn. Aiden plans to replace his other crops with more acres of soybeans and corn. Will his farm ever have the same number of acres of soybeans and corn? Explain.

You can make sense of the problem by answering these questions. What do you know? What are you asked to find?

B.
How can I make sense of and solve this problem?
I can
• choose and implement an appropriate strategy.
• use ordered pairs to make graphs.
• identify and analyze patterns.
• check that my work and answer make sense.
Here’s my thinking…

C.
For each crop, I can write a rule, make a table, and plot the ordered pairs. Then I can see if the number of acres is ever the same.
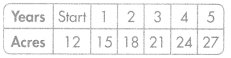
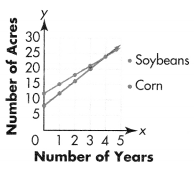
Soybeans
Rule: Start at 12 and add 3.
Corn
Rule: Start at 8 and add 4.
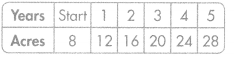
Where the lines intersect, at 4 years, Aiden’s farm has 24 acres of each crop.
Convince Me! Make Sense and Persevere How can you check your work? Does your answer make sense? Explain.
Guided Practice
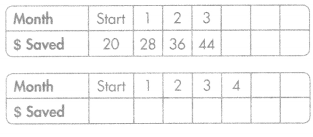
Mindy has already saved $20 and plans to save $8 each month. Georgette has no money saved yet but plans to save $5 each month. Will the girls ever have saved the same amount? Explain.
Question 1.
Write a rule and complete each table.
Rule: _______
Rule: _______
Answer:
Question 2.
On the same grid, graph the ordered pairs in each table.
Answer:
Question 3.
Explain whether the girls will ever have the same amount of money saved.
Answer:
Independent Practice
Make Sense and Persevere
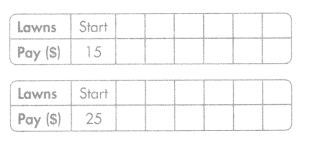
O’Brien’s Landscaping pays employees $15 plus $12 per lawn. Carter’s Landscaping pays $25 plus $10 per lawn. Which company pays more? Explain.
Question 4.
Write a rule and complete each table.
Rule: _______
Rule: _______
Answer:
Question 5.
On the grid, graph the ordered pairs in each table. Explain which company pays more.
Answer:
Problem Solving
Performance Task
Track-a-Thon
Jordan is running in a track-a-thon to raise money for charity. Who will make a larger donation, Aunt Meg or Grandma Diane? Explain.

Question 6.
Make Sense and Persevere How can you use tables and a graph to solve the problem?
Answer:
Question 7.
Use Appropriate Tools For each pledge, write a rule and complete the table.
Rule: ________

Rule: ________

When you make sense and persevere, you choose and implement an appropriate strategy

Question 8.
Use Appropriate Tools On the grid, graph the ordered pairs in each table.
Answer:
Question 9.
Reasoning Explain whose donation will be greater.
Answer:
Topic 15 Fluency Practice
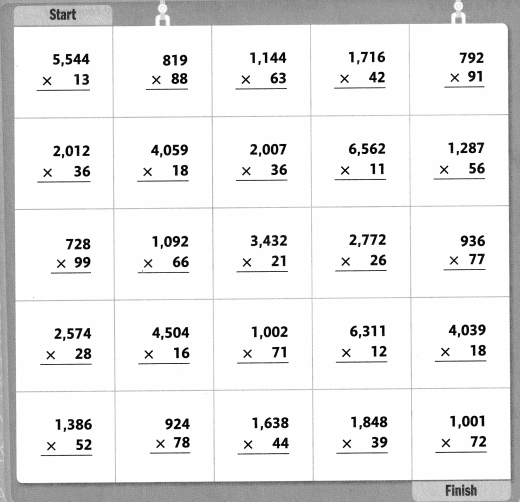
Activity
Follow the path
Solve each problem. Follow problems with an answer of 72,072 to shade a path from START to FINISH. You can only move up, down, right, or left.

Topic 15 Vocabulary Review
Glossory
Word List
• coordinate grid
• corresponding terms
• number sequence
• ordered pair • origin
• x-axis
• x-coordinate
• y-axis
• y-coordinate
Understand Vocabulary
Write always, sometimes, or never on each blank.
Question 1.
Corresponding terms are ____ in the same position in a pair of number sequences.
Answer:
Question 2.
An ordered pair can ____ be plotted on the origin of a coordinate grid.
Answer:
Question 3.
The origin is ____ any other location on a coordinate grid besides (0,0).
Answer:
Question 4.
Two number lines that form a coordinate grid _____ intersect at a right angle.
Answer:
Question 5.
The second number of an ordered pair ____ describes the distance to the right or left of the origin.
Answer:
In 6-8, use the lists of numbers below.
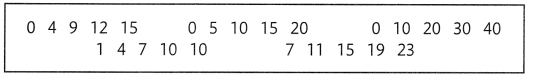

Use Vocabulary in Writing
Question 9.
Explain how to identify corresponding terms in two number sequences. Use terms from the Word List in your Explanation.
Answer:
Topic 15 ReTeaching
Set A pages 593-596
Maria has $4. She will save $10 each week. Stephen has $9 and will also save $10 each week.
Maria uses the rule “add 10” to create tables to see how much each will have saved after each week. What relationship do you notice between the corresponding terms?
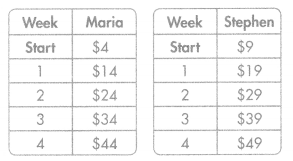
After each week, Stephen has $5 more saved than Maria. Or, Maria’s savings are always $5 less than Stephen’s savings.
Remember to compare corresponding terms to see if there is a relationship.
Question 1.
Two groups of students went hiking. After 1 hour, Group A hiked 1\(\frac{1}{2}\) miles and Group B hiked 2\(\frac{1}{2}\) miles. After that, each group hiked 2 miles each hour. Complete the tables to show how far each group had hiked after 3 hours.
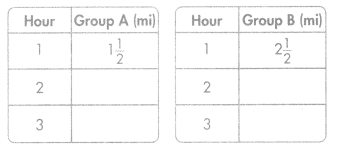
Answer:
Question 2.
What relationship do you notice between the corresponding terms?
Answer:
Set B
pages 597-600
Each week, Andre lifts weights twice and runs 4 times. Andre uses the rules “add 2” and “add 4” to complete the table. What relationship do you notice between the corresponding terms?
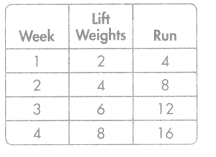
The number of times Andre went running is always 2 times the number of times he lifted weights.
Remember to use the rules to help you complete the tables.
Question 1.
A garden center sells 15 trees and 45 shrubs each day for one week. Complete the table to show how many trees and shrubs in all were sold in 4 days. Use the rules “add 15″ and “add “45” to help you.

Answer:
Question 2.
What is the relationship between the corresponding terms of the sequences?
Answer:
Set C
pages 601-604
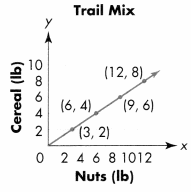
Kelly uses 3 pounds of nuts and 2 pounds of cereal to make each batch of trail mix. The chart shows how many total pounds of each she will need for 4 batches. Graph ordered pairs of the corresponding terms. What does the point (12, 8) represent?
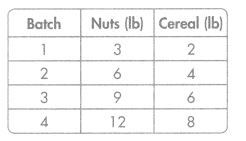
The chart and graph both represent the problem. The point (12,8) shows that when Kelly uses 12 pounds of nuts, she will use 8 pounds of cereal.
Remember to make ordered pairs from corresponding terms.
Question 1.
Lauren has $6 and saves $5 each week. Derrick has $3 and saves $5 each week. How much will each have saved after 4 weeks? Use the rule “add 5” to complete the table.

Answer:
Question 2.
What does the point (26, 23) represent?
Answer:
Question 3.
What is the relationship between the corresponding terms?
Answer:
Set D
pages 605-608
Think about these questions to help you make sense and persevere in solving problems.
Thinking Habits
• What do I need to find?
• What do I know?
• What else can I try if I get stuck?
• How can I check that my solution makes sense?

Remember that you can use patterns, tables, and graphs to represent and solve problems.
Question 1.
Sam starts with 5 stamps and buys 10 more each month. Pat starts with 9 stamps and buys 9 more each month. Complete the table using the rules “add 10” and “add 9”.
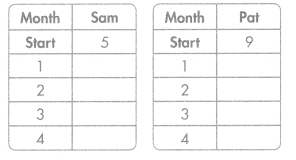
Answer:
Question 2.
Make a graph from the data in the tables. Will Sam ever have more stamps than Pat?
Answer:
Topic 15 Assessment Practice
Question 1.
Liz and Fareed each start a new savings account. Liz starts her account with $75. Fareed starts his account with $100. Each month, both save another $50.
A. Complete the table to show the total amount each has saved after each month. Use the rule “add 50”.
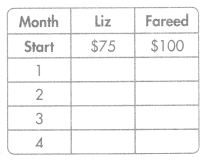
B. Select all the ordered pairs that represent amounts Liz and Fareed have each saved.
![]() (50, 75)
(50, 75)
![]() (75, 100)
(75, 100)
![]() (125, 150)
(125, 150)
![]() (150, 200)
(150, 200)
![]() (275, 300)
(275, 300)
C. Describe the relationship between the amount each person has saved after each month.
Answer:
Question 2.
There are 16 pawns and 2 kings in each chess set.
A. Complete the table to show how many pawns and kings in all are in different numbers of chess sets. Use the rules “add 16″ and “add 2”.
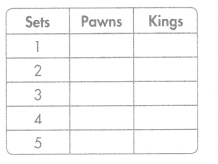
B. Use the total number of pawns and kings to form ordered pairs. Graph the ordered pairs below.
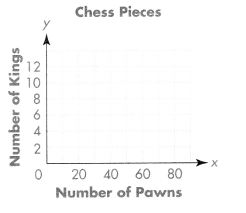
C. What would the ordered pair (96, 12) represent?
Answer:
Question 3.
Luis kept track of the heights of his basil and chive plants. His basil plant was 15\(\frac{1}{2}\)cm tall and grew 1\(\frac{1}{2}\) cm each week. His chive plant was 18\(\frac{1}{2}\) cm tall and grew \(\frac{1}{2}\) cm each week.
A. Complete the table to show the heights of each plant after each week. Use the rules “add 1\(\frac{1}{2}\)” and “add 1\(\frac{1}{2}\)“.
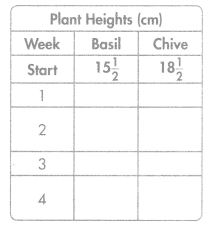
B. Will the basil plant ever be taller than the chive plant? If so, when?
C. How does the table in A help you answer the question in B?
Answer:
Question 4.
Bonnie’s Bakery makes 12 cakes and 36 muffins each hour.
A. Complete the table to show how many cakes and muffins in all the bakery has made after each hour. Use the rules “add 12” and “add 36”.
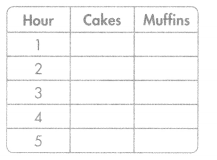
B. Miles says “the total number of muffins made is always 24 more than the total number of cakes made.” Do you agree? Explain your reasoning.
C. Bonnie wants to graph this information. What ordered pair represents the total number of each item made after 6 hours?
A. (36,12)
B. (18,42)
C. (60, 180)
D. (72, 216)
Answer:
Topic 15 Performance Task
Butterfly Patterns
Use the Butterflies picture to Explore patterns.
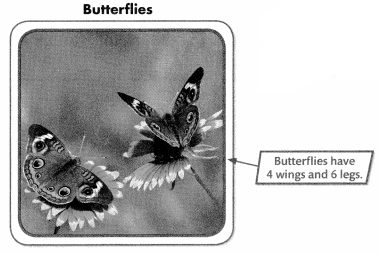
Question 1.
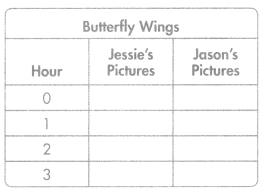
Jessie and Jason use their cell phones to take pictures of butterflies. Jessie had 3 pictures of butterflies stored in her cell phone and Jason had 1 picture in his. On Saturday, they each took a picture of 1 butterfly every hour.
Part A
How many butterfly wings are in each photo collection after 3 hours? Complete the table.
Part B
What is the relationship between the corresponding terms of the two patterns in Part A?
Part C
Write rules for the number of butterfly wings in Jessie’s pictures and in Jason’s pictures.
Answer:
Question 2.
Compare the number of wings to the number of legs in different numbers of butterflies.

Part A
Complete the table.
Part B
What is the relationship between the number of wings and the number of legs you found in Part A?
Answer:
Question 3.
Tomika has no pictures of butterflies in her cell phone, but Kyle has 3 pictures in his. On Saturday, Tomika takes 2 pictures of butterflies every hour and Kyle takes 1 picture every hour. Answer the following to find whether or not their collections of butterfly pictures will ever have the same number of wings.
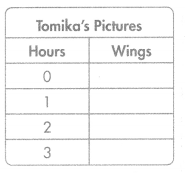
Part A
Write a rule and complete the Tomika’s Pictures table.
Part B
Write a rule and complete the Kyle’s Pictures table.
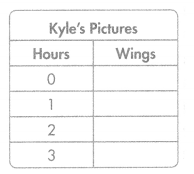
Part C
Graph the ordered pairs from Part A and Part B on the same coordinate grid and draw lines through each set.
Part D
Will Tomika and Kyle ever have the same number of wings in their pictures? Explain.

Answer:

