Envision Math Grade 6 Answer Key Topic 2.6 Evaluating Expressions

Envision Math 6th Grade Textbook Answer Key Topic 2.6 Evaluating Expressions

Evaluating Expressions

How can you evaluate an algebraic expression?
Answer:
Willie has one large case that holds 20 miniature racecars.
He also has 3 smaller cases with miniature racecars.

Question
The number of miniature cars Willie has can be expressed as 20 + 3x. How many miniature cars does he have if each smaller case holds 14 cars?
Answer:

Guided Practice

Do you know HOW?
Use substitution to evaluate.
Remember that substituting means to replace the variable with a value.
Question 1.
t – 8; t = 18
Answer:
18 – 8 = 10
Explanation:

Question 2.
6(w) + 9; w = 3
Answer:
(6 × 3) + 9 = 27
Explanation:

Question 3.
2x ÷4; x=12
Answer:
(2 × 12) + 4 = 6
Explanation:

Question 4.
3z + 4 2z; z = 5
Answer:
(3 × 5) + 4 –
Explanation:

Question 5.
p + (8r – 4); p = 9, r = 3
Answer:
(2 × 5) = 9
9 + (24 – 4) = 29
Explanation:

Do you UNDERSTAND?
Question 6.
Why is it important to use order of operations to evaluate algebraic expressions?
Answer:
See margin.
Explanation:

Question 7.
Suppose that Willie’s large case holds 36 cars, and the 3 small cases each hold 18 cars. Write an algebraic expression to represent the number of cars. Then, evaluate the expression for x = 18.
Answer:
36+ 3x; 36+ 3(18) = 90
Explanation:

Independent Practice

For 8 through 22, evaluate each expression for 3, 4, and 10.
Answer:
See margin.
Explanation:

Question 8.
9x
Answer:

Question 9.
3x + 6
Answer:

Question 10.
48 ÷ x
Answer:

Question 11.
x(0)
Answer:

Question 12.
1x
Answer:

Question 13.
x(4) ÷ 2
Answer:

Question 14.
x – 3
Answer:

Question 15.
x² + 1
Answer:

Question 16.
x ÷ x
Answer:

Question 17.
100 – x²
Answer:

Question 18.
3x + 4x
Answer:

Question 19.
2x + 7
Answer:

Question 20.
3x + 9
Answer:

Question 21.
5x + 6x
Answer:

Question 22.
x² – 1
Answer:

Question 23.
Evaluate the expression for the values of n.
Answer:

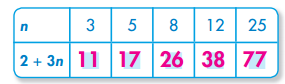
Explanation:

Question 24.
Evaluate the expression for the values k = 9, m = 5, n = 7.
2(k – 4) + 3m – n
Answer:
18
Explanation:

Evaluate 20 + 3x.
Evaluate means to find the value of an expression. To evaluate an algebraic expression, use substitution to replace the variable with a number.
If x equals the number of miniature cars in each smaller case, then evaluate for x = 14.
20 + 3(14)
20 + 42
62
Willie has 62 miniature racecars.

Suppose that the smaller cases each hold 10 miniature cars. How many cars would he have then?
20 + 3x
20 + 3(10)
50
Willie would have 50 cars.

Problem Solving

Use the table at right for 25 and 26.

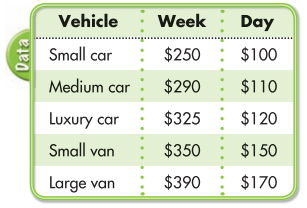
Question 25.
Corinne wants to rent a small white car. It will cost the weekly fee plus 304 per mile. Write an expression that shows the amount Corinne will owe for her car. Then solve for 100 miles.
Answer:
250 + .30x; $280.
Explanation:

Question 26.
Trey is renting a luxury car for a week and a few days. He does not have to pay a per-mile fee. Write an expression that shows the amount Trey will owe for his car. Then solve for an 11-day rental.
Answer:
325 + 120(x – 7); $805
Explanation:

Question 27.
Writing to Explain What operations are involved in the expressions 2x + 7 and 3x + 6?
Answer:
Multiplying and adding
Explanation:

Question 28.
San Juan Capistrano is about 700 miles from Eureka, CA. Joey and Paulo want to find how many miles they have to average per hour to make the trip in about 22 hours. They wrote the expression 700 ÷ x to help them figure it out. Which of the following numbers could they substitute for x?
A. 8
B. 17
C. 22
D. 29
Answer:
C. 22
Explanation:

Question 29.
Each year, cliff swallows travel 12,000 km from Goya, Argentina, to San Juan Capistrano, CA. The trip takes about 30 days. What is the average distance the swallows cover per day?
A. 200 \(\frac{\mathrm{km}}{\mathrm{day}}\)
B. 360 \(\frac{\mathrm{km}}{\mathrm{day}}\)
C. 400 \(\frac{\mathrm{km}}{\mathrm{day}}\)
D. 450 \(\frac{\mathrm{km}}{\mathrm{day}}\)
Answer:
C. 400 \(\frac{\mathrm{km}}{\mathrm{day}}\)