Category: Envision Math

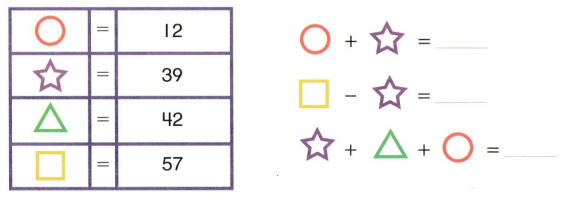
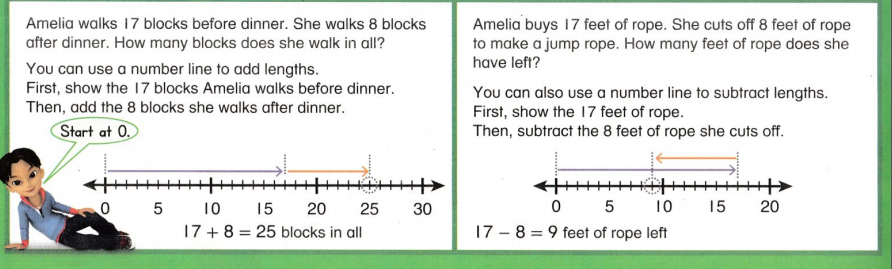
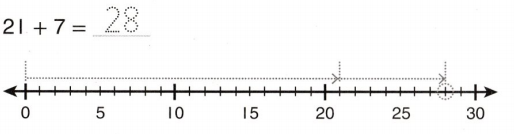
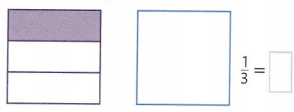
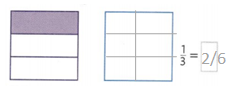
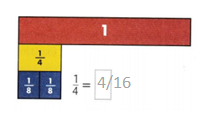
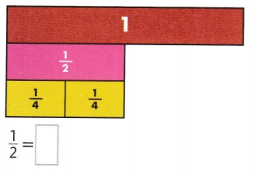
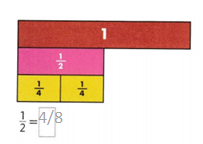
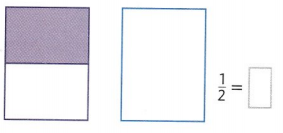
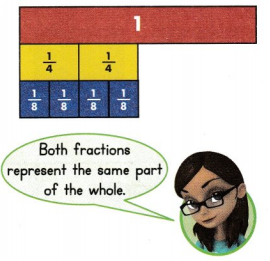
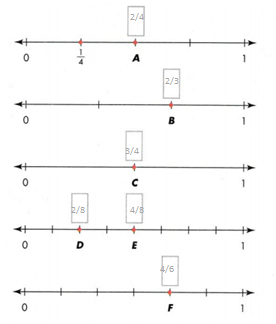
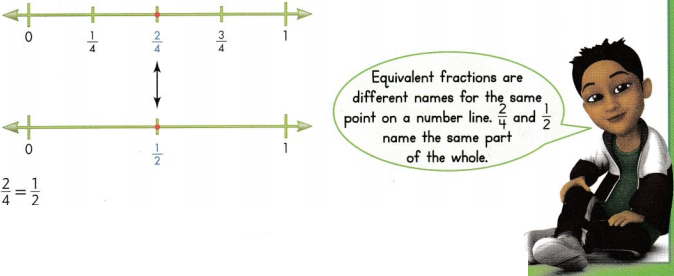
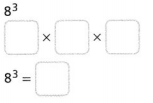
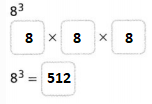
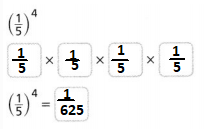
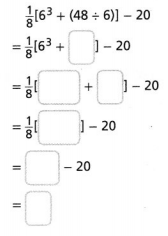
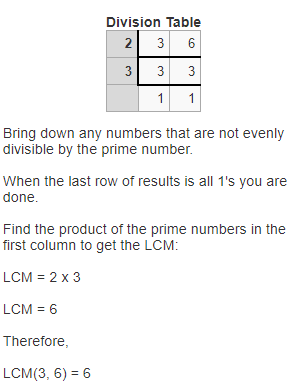
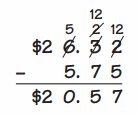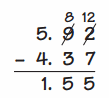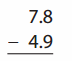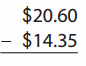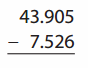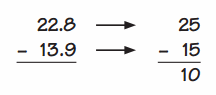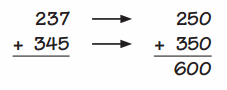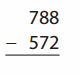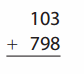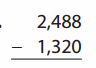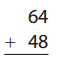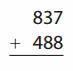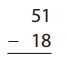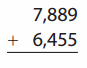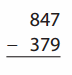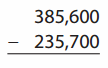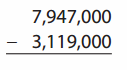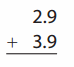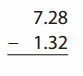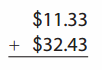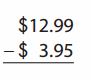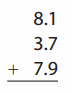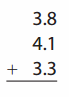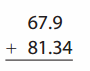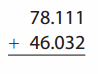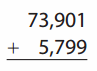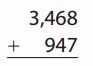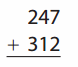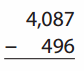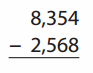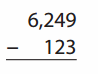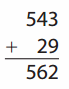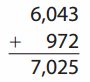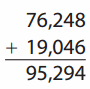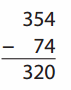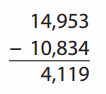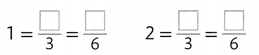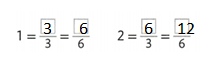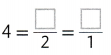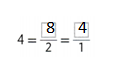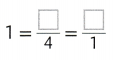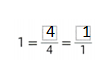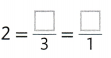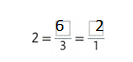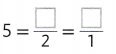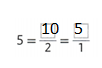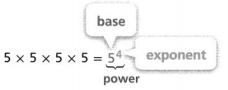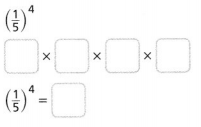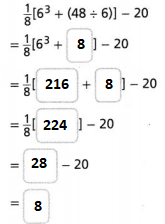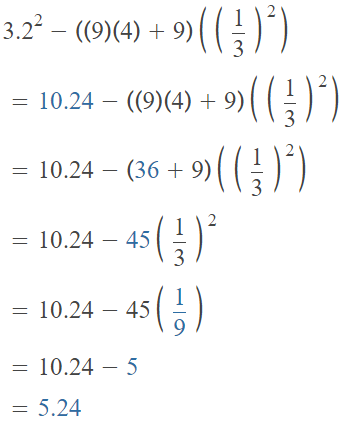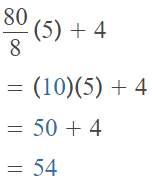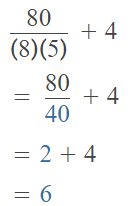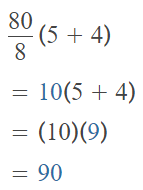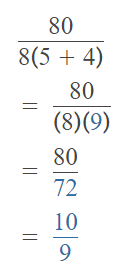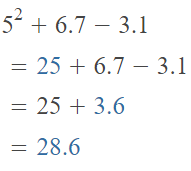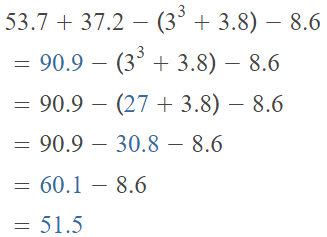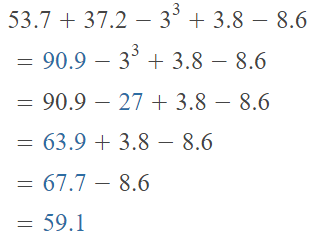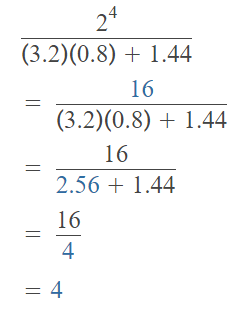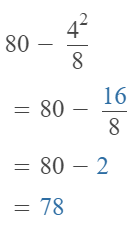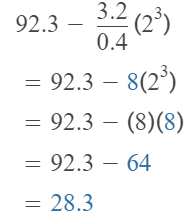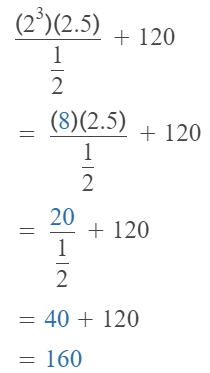Go through the enVision Math Common Core Grade 2 Answer Key Topic 3 Add Within 100 Using Strategies regularly and improve your accuracy in solving questions.

enVision Math Common Core 2nd Grade Answers Key Topic 3 Add Within 100 Using Strategies

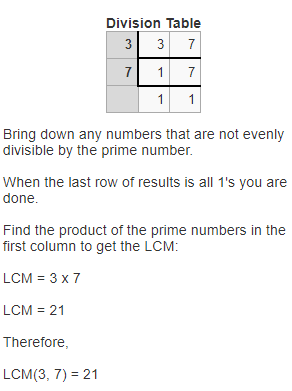
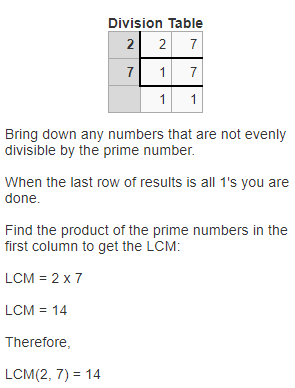
Essential Question:
What are strategies for adding numbers to 100?

enVision STEM Project: Earth Changes and Addition Strategies
Find Out Find and share books about how the Earth changes. Talk about changes that people can see, hear, and feel. Talk about changes that people cannot see happening.
Journal: Make a Book Show what you learn in a book. In your book, also:

• Write new science words you learn. Draw pictures that help show what the words mean.
• Write new math words you learn. Draw pictures that help show what the words mean.

Review What You Know

Vocabulary
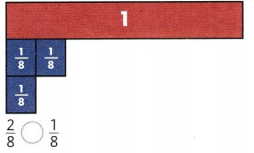
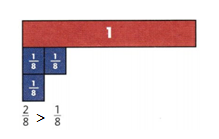
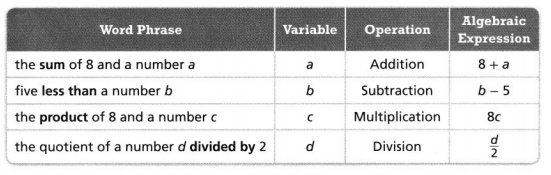
Question 1.
Draw a circle around each even number. Use cubes to help.
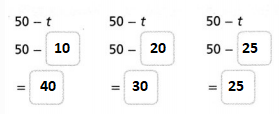
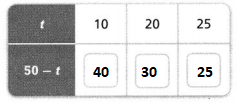
15
7
14
2
19
18
Answer:

In the given numbers 14, 2 and 18 are the even numbers.know draw a circle around the 14, 2 and 18.

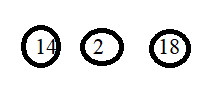
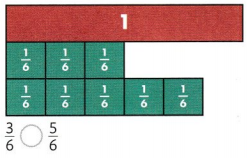
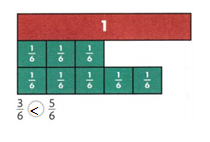
Question 2.
Draw a square around each odd number. Use cubes to help.
12
3
6
17
11
4
Answer:

In the given numbers 3,17 and 11 are the odd numbers. Know draw the square around the 3, 17 and 11.

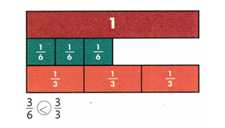
Question 3.
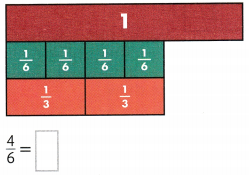
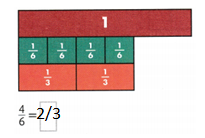
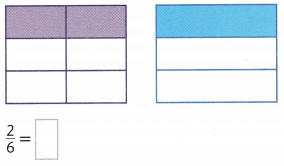
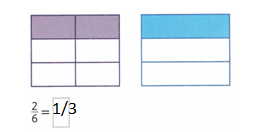
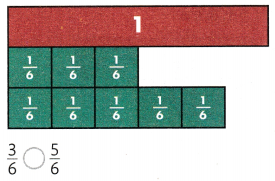
Complete the bar diagram to show the sum of 3 + 5.

Answer:

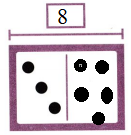
In the above diagram they have given a 3 dots on the left side. Know we want to draw 5 dots on the right side. By adding both sides of the dots wet get 3 + 5 = 8

Arrays

Write an equation to show the number of circles in each array.
Question 4.

By rows
_______ + _______ = _______
Answer:

Given,
Total number of rows = 2
Each row contains 4 circles.
4 + 4 = 8

Question 5.

By columns
_______ + _______ = _______
Answer:
Given that,
Total number of columns = 3
Each column contains 3 circles.
3 + 3 + 3 = 9

Math Story
Question 6.
Joe has 5 apples. He picks 3 more apples. How many apples does Joe have now?
_______ apples
Does Joe have an even or an odd number of apples?
_________ number
Answer:
Given that
Total number of apples at Joe = 5
Joe picks more apples = 3
Total number of apples near Joe = 5 + 3 =8
Joe has an even number of apples.

Pick a Project

PROJECT ЗА
How far would you travel to cheer for your team?
Project: Make a Map to the Game

PROJECT ЗB
What are some important things to do at the airport?
Project: Write a List of Air Travel Tasks

PROJECT 3C
How many Olympic Games have there been?
Project: Create an Olympics Poster

3-ACT MATH PREVIEW

Math Modeling
Piled Up

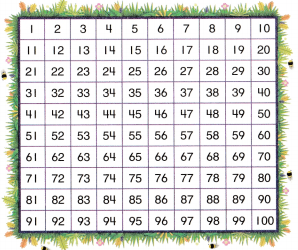
Lesson 3.1 Add Tens and Ones on a Hundred Chart

Solve & Share
How can you use the hundred chart to help you find 32 + 43? Explain.
Write an equation to show the sum.

I can … add within 100 using place-value strategies and properties of operations.

______ + _______ = ________

Visual Learning Bridge

Convince Me! Max says that to find 54 + 18 on a hundred chart, you can start at 54, move down 2 rows, and move back 2 spaces. Do you agree? Explain.

Guided Practice

Add using the hundred chart. Draw arrows on the chart if needed.

Question 1.
17 + 32 = ________
Answer:
We are using the hundred chart to find the sum of 17 + 32
In the hundred charts we start at 17 moves down to 3 rows and move front to 2 spaces then we get 49
17 + 32 = 49
Question 2.
28 + 21 = ________
Answer:
We are using the hundred chart to find the sum of 28 + 21
In the hundred charts we start at 28 move down to 2 rows and move front to 1 space then we get 49.
28 + 21 = 49
Question 3.
________ = 19 + 20
Answer: we are using a hundred charts to find the sum of 19 + 20
In the hundred charts we start at 19 moves down to 2 rows then we get 39.
39 = 19 + 20
Question 4.
18 + 8 = ________
Answer:
We are using the hundred chart to find the sum of 18 + 8
In the hundred charts, we start at 18 moves down to 1 row and back to 2 space then we get 26
18 + 8 = 26

Independent Practice

Add using the hundred chart.

Question 5.
33 + 9 = ________
Answer:
We are using the hundred chart to find the sum of 33 + 9
In the hundred charts we start at 33 down to 1 row and move back to 1 space then we get 42
33 + 9 = 42

Question 6.
________ = 12 + 73
Answer:
We are using the hundred chart to find the sum of 12 + 73
In the hundred charts we start at 12 down to 7 rows and move front to 3 Space we get 85
85 = 12 + 73
Question 7.
38 + 21 = ________
Answer:
We are using the hundred chart to find the sum of 38 + 21
In the hundred charts we start at 38 down to 2 rows and front to 1 space then we get 59
38 + 21 = 59
Question 8.
56 + 42 = ________
Answer:
We are using the hundred chart to find the sum of 56 + 42
In the hundred charts we start at 56 down to 4 rows and front to 2 spaces then we get 98
56 + 42 = 98
Question 9.
________ = 47 + 28
Answer:
We are using the hundred chart to find the sum of 47 + 28
In the hundred charts, we start at 47 down to 3 rows and back to  2 spaces then we get 75
75 = 47 + 28
Question 10.
39 + 17 = ________
Answer:
We are using the hundred chart to find the sum of 39 + 17
In the hundred charts, we start at 39 down to 2 rows and back to 3 spaces then we get 56
39 + 17 =56
Question 11.
________ = 61 + 19
Answer:
We are using the hundred chart to find the sum of 61 + 19
In the hundred charts, we start at 61 and down to 2 rows and back to 8 space then we get 89
89 = 61 + 19

Question 12.
Higher Order Thinking Write the digit that makes each equation true.

Answer:
7 + 83 = 90
The number 7 makes the equation true.
34 + 25 = 57
The digit 5 makes the equation true.
16 + 52 = 67
The digit 1 makes the equation true.
62 + 21 = 83
The digit 2 makes the equation true.
Problem Solving

Use Tools Use the hundred chart to solve the problems.

Question 13.
Sara has 48 buttons. Luis has 32 buttons. How many buttons do they have in all?
________ buttons
Answer:
Given that,
Total number of buttons at Sara = 48
Total number  buttons at Luis = 32
The total number of buttons at both of them have = 48 + 32
By using a hundred charts the sum of 48 + 32 is
In the hundred charts Start at 48 and down to 3 rows and front to 2 spaces then we get 80.
48 + 32 = 80
Question 14.
Mika had 70 buttons. Then she found 19 more buttons. How many buttons does Mika have now?
_______ buttons
Answer:
Given that,
Total number of buttons at Mika  = 70
She found more buttons = 19
Total number of buttons with Mike = 70 + 19
By using the hundred chart we find the sum of 70 + 19
In the hundred chart, we start at 70 then down to 2 rows and back to 1 space then we get
Question 15.
Higher Order Thinking Write the steps you take to add 43 and 39 on a hundred chart.
Answer:
We are using the hundred chart to find the sum of 43 and 39
In the hundred charts, we start at 43 and down to 4 rows and back to 1 space then we get 82
43 + 39 = 82
Question 16.
Assessment Practice which has a sum of 35? Choose all that apply.
☐ 15 + 20
☐ 16 + 19
☐ 20 + 15
☐ 30 + 15
Answer:
15 + 20 has a sum of 35.
16 + 19 has a sum of 35
20 + 15 has a sum 0f 35

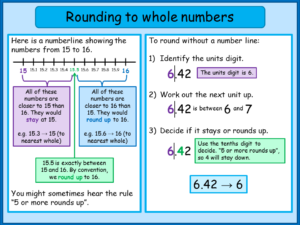
Lesson 3.2 Add Tens and Ones on an Open Number Line

Solve & Share
How can you use the open number line to find 35 + 24?
Write an equation to show the sum. Explain your work.

I can … use an open number line to add tens and ones within 100.

Visual Learning Bridge

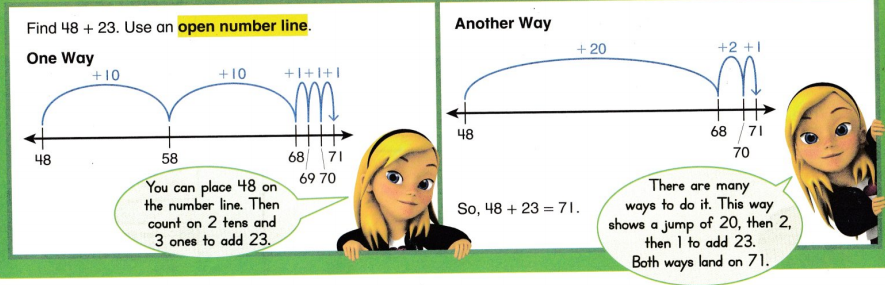
Convince Me! Explain how you can use an open number line to find 56 + 35.

Guided Practice

Use an open number line to find each sum.
Question 1.
59 + 24 = _________

Answer: 59 + 24 = 83
Question 2.
47 + 25 = _________

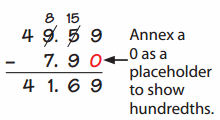
Answer:
First, draw a line.
Represent the numbers on the line.
The first number is 47 and counts by 20 then it gets 67 and hump 5 then we get 72.
Count the numbers and draw an arrow
47 + 25 = 72

Independent Practice

Use an open number line to find each sum.
Question 3.
34 + 15 = ________

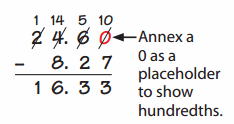
Answer:
First, draw the line.
Represent the numbers on the line.
The first number is 34 and counts by 10 then it gets 44 and 5 then we get 49.
Count the numbers and draw an arrow.
34 + 15 = 49

Question 4.
34 + 46 = ________

Answer:
34 + 46 = 80
First, draw the Line.
Represent the number on the line.
The first number is 34 and counts by 20 then it gets 54 and counts again 20 then it gets 74 and jump to 6 then it gets 80.
Count the numbers and draw an arrow

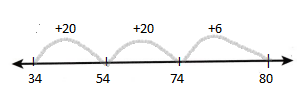
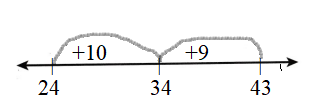
Question 5.
16 + 28 = _________

Answer:
16 + 28 =44
First, draw the Line.
Represent the number on the line.
The first number is 16and counts by 10 then it gets 26 and jumps to 2 then it gets 28.

Count the numbers and draw an arrow.
Question 6.
59 + 26 = ________

Answer: 59 + 26 = 85
First draw the Line.
Represent the number on the line.
The first number is 59 and counts by 20 then it gets 79 and jumps to 6 then it gets 85.
Count the numbers and draw an arrow.

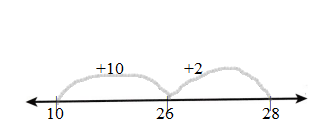
Question 7.
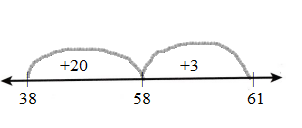
Number Sense Matt found 55 + 28 using the open number line below. Is his work correct? Explain.

Answer: 55 + 28 = 83

Problem Solving

Use the open number line to solve each problem below.
Question 8.
Reason There are 24 apples in a basket. There are 19 apples on a tray. How many apples are there in all?

_________ apples
Answer: Apples in a basket = 24
Apples in a tray = 19
Total number of apples = 24 + 19 = 43
Using the number line.
First, draw the Line.
Represent the number on the line.
The first number is 24 and counts by 10 then it gets 34 and jumps to 9 then it gets 43.
Count the numbers and draw an arrow.

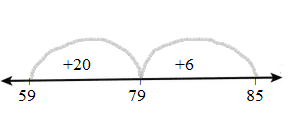
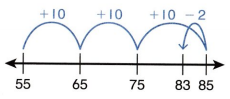
Question 19.
Reason Jamie has 27 more berries than Lisa. Lisa has 37 berries. How many berries does Jamie have?

_________ berries
Answer:
Lisa has berries = 37
Jamie has berries = 27 berries more than Lisa
Jamie has berries = 37 + 27 =64
First draw the Line.
Represent the number on the line.
The first number is 37 and counts by 20 then it gets 54  and jumps to 9 then it gets 80.
Count the numbers and draw an arrow.

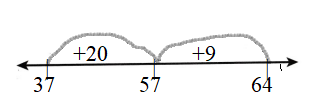
Question 10.

Higher Order Thinking Use two different number lines to show that 34 + 23 has the same value as 23 + 34.


Answer:
34 + 23 = 57
First, draw the Line.
Represent the number on the line.
The first number is 34 and counts by 20 then it gets 54 and jumps to 3 then it gets 57.
Count the numbers and draw an arrow.

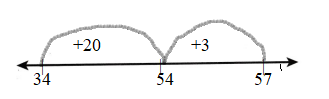
23 + 34 = 57
First, draw the Line.
Represent the number on the line.
The first number is 23 and counts by 30 then it gets 53 jumps to 3 then it gets 57.
Count the numbers and draw an arrow.

Question 11.
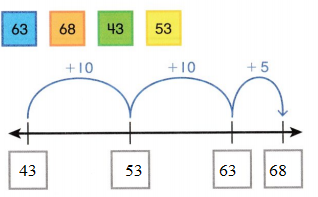
Assessment Practice Use the numbers on the cards. Write the missing numbers under the number line to show how to find the sum.

43 + 25 = _________
Answer:
43 + 25 = 68

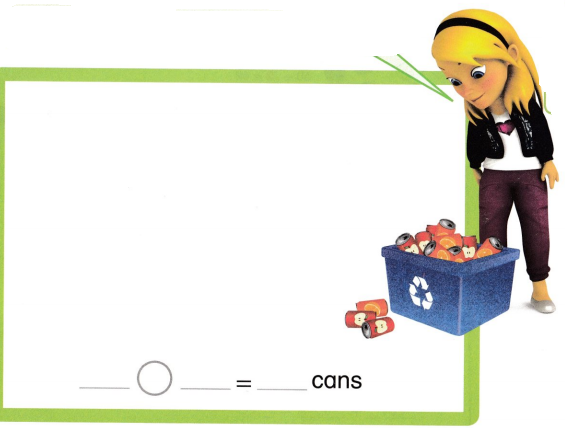
Lesson 3.3 Break Apart Numbers to Add

Solve & Share
Josh has 34 cans to recycle. Jill has 27 cans. How many cans do they have in all? Solve any way you choose. Use drawings and equations to explain your work.
I can … break apart numbers into tens and ones to find their sum.

Visual Learning Bridge

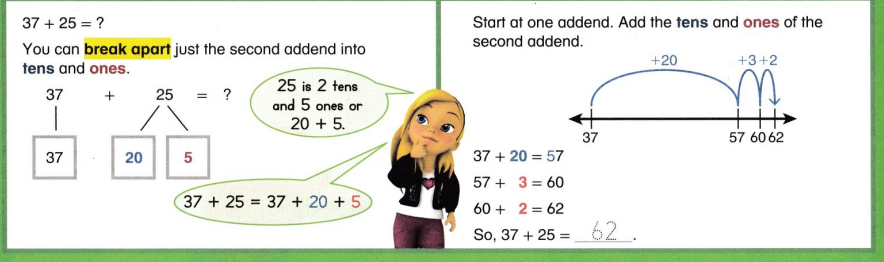
Convince Me! Explain how you can break apart 28 to find 33 + 28.

Guided Practice

Break apart the second addend to find the sum. Show your work. Use an open number line to help.
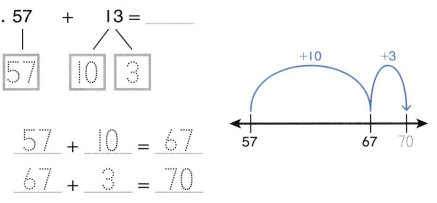
Question 1.

Independent Practice

Break apart the second addend to find the sum. Show your work. Draw an open number line to help.
Question 2.
42 + 16 = ________
Answer:
42 + 16 =
42 + 10 + 6
52 + 6 = 58
First draw the Line.
Represent the number on the line.
The first number is 42 and counts by 10 then it gets 52 and jumps to 6 then it gets 58.
Count the numbers and draw an arrow.

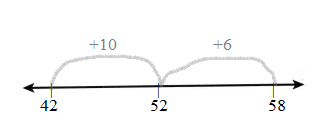
Question 3.
36 + 44 = ________
Answer:
36 + 44
36 + 40 + 4
76 + 4 = 80
First draw the Line.
Represent the number on the line.
The first number is 36 and counts by 20 then it gets 56 and counts again by 20 ten we get 76 and jump to 4 then it gets 80.
Count the numbers and draw an arrow.

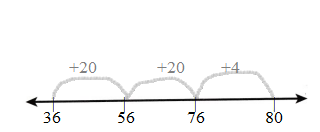
Question 4.
41 + 37 = ________
Answer:
41 + 37
41 + 30 + 7
71 + 7 = 78
First draw the Line.
Represent the number on the line.
The first number is 41 and counts by 30 then it gets 71 and jumps to 7 then it gets 78.
Count the numbers and draw an arrow.

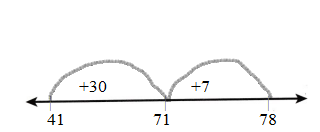
Question 5.
35 + 47 = ________
Answer:
35 + 47
35 + 40 + 7
75 + 7 = 82
First draw the Line.
Represent the number on the line.
The first number is 35 and counts by 40 then it gets 75 and jumps to 7 then it gets 82.
Count the numbers and draw an arrow.

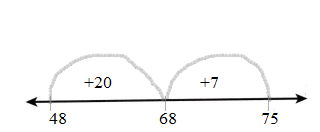
Question 6.
32 + 28 = ________
Answer:
32 + 28
32 + 20 + 8
52 + 8 = 60
First draw the Line.
Represent the number on the line.
The first number is 32 and counts by 20 then it gets 52 and jumps to 8 then it gets 60.
Count the numbers and draw an arrow.

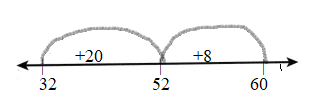
Question 17.
48 + 27 = ________
Answer:
48 + 27
48 + 20 + 7
68 + 7 = 75
First draw the Line.
Represent the number on the line.
The first number is 48 and counts by 20 then it gets 68 and jumps to 7 then it gets 75.
Count the numbers and draw an arrow

Question 8.
Number Sense Write the digit that makes each equation true.

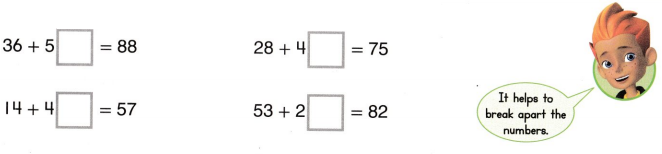
Answer:
36 + 52 = 88
Here the digit 2 makes the equation true.
28 + 47 = 75
Here the digit 7 makes the equation true.
14 + 43 = 57
Here the digit 3 makes the equation true.
53 + 29 = 82
Here the digit 9 makes the equation true.
Problem Solving

Solve each problem. Show your work.
Question 9.
Amir planted 35 trees. Juan planted 27 trees. How many trees did they plant in all?
________ trees
Answer:
Given that,
Total number of trees planted by Amir  = 35
Total number of trees planted by Juan = 27
Total number of  plants planted by Amir and Juan = 35 + 27 = 62
Question 10.
Carmen has 18 pennies. Patrick has 12 more pennies than Carmen. How many pennies does Patrick have?
________ pennies
Answer:
Given that,
Total number of pennies at Carmen  = 18
Total number of pennies at Patrick  more than Carmen = 12
Total number of pennies at Patrick = 18 + 12 = 30
Question 11.
Higher Order Thinking Use the numbers on the cards. Use each number once to write a true equation.

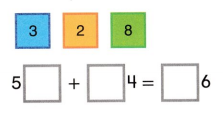
Answer:
The numbers on the card are 3, 2, 8
First, write the 2 in the first empty box then we get 52, and write the 3 in the second empty box then we get 34
By adding 52 and 34 we get 86. Write the 8 in the third box.
The true equation is
52 + 34 = 86

Question 12.
Assessment Practice which has a sum of 67? Choose all that apply.

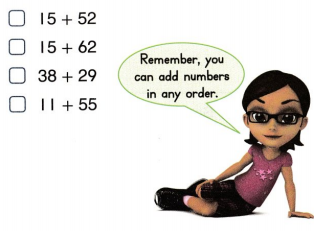
Answer:
15 + 52 = 67

Lesson 3.4 Add Using Compensation

Solve & Share
27 + 16 = ________
Draw counters on the ten frames to show each addend. Then show how you can move some counters to make it easier to find the sum. Explain your work.
I can … break apart addends and combine them in different ways to make numbers that are easy to add mentally.

Visual Learning Bridge

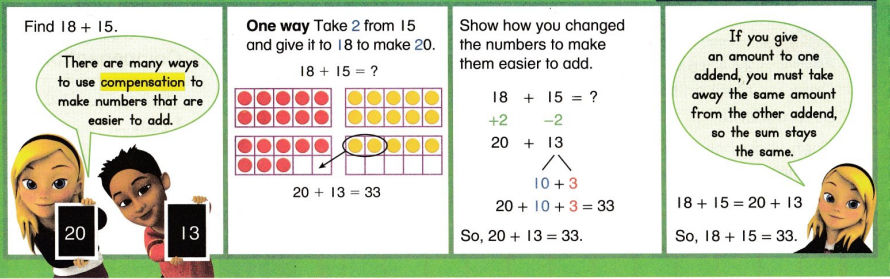
Convince Me! Solve.
19 + 26 = ☐
Explain how you can change the addends to make them easier to add.

Guided Practice

Use compensation to make numbers that are easier to add. Then solve. Show your work.
Question 1.
17 + 9 = ________

Question 2.
16 + 14 = __________

Answer:

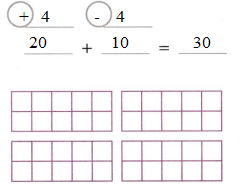
Independent Practice

Use compensation to make numbers that are easier to add. Then solve. Show your work.
Question 3.
33 + 19 = __________
Answer:
33 + (10 + 9)
(33 + 10) + 9
43 + 9 = 52
Question 4.
28 + 8 = __________
Answer:
28 + (2 + 6)
(28 + 2) + 6
30 + 6 = 36
Question 5.
27 + 36 = __________
Answer:
27  + ( 30 + 6)
(27 + 30) + 6
57 + 6 = 63
Question 6.
Number Sense Explain how you can use compensation to make numbers that are easy to add. Solve. Show your work.
28 + 37 =
______ + ______ =
Answer:
28 + 37 =
28 + ( 30 + 7)
(28 + 30) + 7
58 + 7 = 65
Question 7.
Higher Order Thinking Show two different ways you could use compensation to make numbers that are easy to add. Solve. Show your work.
17 + 26 =
Answer:
17 + 26
17 + (20 + 6)
(17 + 20) + 6
37 + 6 = 43

Problem Solving

Use compensation to make numbers that are easier to add. Then solve. Show your work.
Question 8.
Explain Bella said there is only one way to rewrite this problem to make the numbers easier to add. Is she correct? Explain. Then solve.
42 + 29 =
Answer:
42 + 29
42 + (20 + 9)
(42 + 20) + 9
62 + 9 = 71
Question 9.
Vocabulary Show two different ways to use compensation to find the sum. Then solve.
58 + 35 =
What number is close to 58 or 35?
Answer:
58 + 35
58 + (30 + 5)
(58 + 30) + 5
88 + 5 = 92
Question 10.
Higher Order Thinking Show two different ways to use compensation to find the sum. Then solve.
37 + 16 + 5 =
Answer:
37 + (10 + 6) + 5
(37 + 10) + 6 + 5
47 + 6 + 5
47 + 11
47 +(10 + 1)
(47 + 10) + 1
57 + 1= 58
Question 11.
Assessment Practice which is equal to 42 + 18? Choose all that apply.
☐ 58
☐ 40 + 20
☐ 40 + 10 + 8
☐ 50 + 10
Answer:
The equation 40 + 20 and 50 + 10 are equal to 42 + 18

Lesson 3.5 Practice Adding Using Strategies

Solve & Share
Tameka has 39 blocks. Kim has 43 blocks. How many blocks do they have in all? Choose any strategy. Solve. Show and explain your work.

I can … choose a strategy to help me add two-digit numbers.

_________ bolcks

Visual Learning Bridge

Convince Me! In 66 + 25 above, why was 4 added to 66 and then subtracted from 95?

Guided Practice

Find each sum. Use any strategy. Show your work.
Question 1.

Question 2.
67 + 26 = ___________
Answer:
67 + 26 =
67 + 20 + 6
87 + 6 = 93

Independent Practice

Find each sum. Use any strategy. Show your work.
Question 3.
33 + 52 = ___________
Answer:
33 + 52 =
33 + 50 + 2
73 + 2 = 75
Question 4.
27 + 6 = ___________
Answer:
27 + 6 = 33
Question 5.
___________ = 49 + 45
Answer:
49 + 45
49 + 40 + 5
89 + 5 = 94
Question 6.
57 + 12 = ___________
Answer:
57 + 12
57 + 10 + 2
67 + 2 = 69
Question 7.
___________ = 63 + 20
Answer:
66 + 20 = 86
Question 18.
14 + 58 = ___________
Answer:
14 + 58
14 + 50 + 8
64 + 8 = 72
Question 9.
45 + 55 = ___________
Answer:
45 + 55
45 + 50 + 5
95 + 5 = 100
Question 10.
87 + 9 = ___________
Answer:
87 + 9 = 96
Question 11.
19 + 61 = ___________
Answer:
19 + 61
19 + 60 + 1
79 + 1 = 80

Number Sense Write the digit that makes each equation true.
Question 12.
45 + 1☐ = 61
Answer:
45 + 16 = 61
The digit 6 makes the equation true.
Question 13.
84 = ☐8 + 56
Answer:
84 = 28 + 56
The digit 2 makes the equation true.
Question 14.
3☐ + 19 + 56
Answer:
30 + 19 + 56 = 105
The digit 0 makes the equation true

Problem Solving

Use the hundred chart to solve each problem. Be prepared to explain your work.

Question 15.
Reasoning Martin has 44 marbles. Carol has 39 marbles. Steve has 90 marbles. How many marbles do Martin and Carol have in all? Do they have more or fewer marbles than Steve?

_______ marbles
Circle:
more
fewer
Answer:
Given that,
Total number of marbles at Martin = 44
Total number of marbles at Carol = 39
Total number of marbles at Steve = 90
Total  number of marbles at Martin and Carol  = 44 + 39
Using a hundred charts find the sum of 44 + 39
In the hundred charts we start at 44 then down to 3 rows we get 74 and front to 4 space then we get 78
44 + 39 = 78
They both them have fewer marbles than Steve.
Question 16.
Higher Order Thinking José collected 32 leaves on Saturday. On Sunday, he collected 14 more leaves than he did on Saturday.
How many leaves did José collect in all?

________ leaves
Answer:
Given that
Total number of leaves Jose collected  on Saturday = 32
Total number of leaves Jose collected on Sunday = 14
Total number of leaves they collected = 32 + 14 = 46
Question 17.
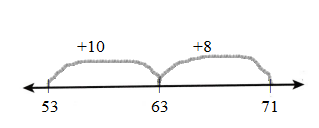
Lucita wants to use an open number line to find 53 + 18. Show how Lucita can use an open number line to find 53 + 18.

Answer:
53 + 18 = 71
First, draw the Line.
Represent the number on the line.
The first number is 53 and counts by 10 then it gets 63 and jumps to 8 then it gets 71.
Count the numbers and draw an arrow.

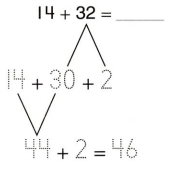
Question 18.
Assessment Practice Maria used a hundred chart to find a sum. She started at 68. Then she moved down 3 rows and back I space. Which number did she land on?
A. 88
B. 97
C. 98
D. 99
Answer:
Maria started at 68
She moved down to three rows is 98
And she back to 1 space then his number is 97

Lesson 3.6 Solve One-Step and Two-Step Problems

Solve & Share
The red team has 15 more points than the blue team. The blue team has 36 points. How many points does the red team have?
Choose any strategy. Solve. Explain your work.

I can … use drawings and equations to solve one-step and two-step problems.

Visual Learning Bridge

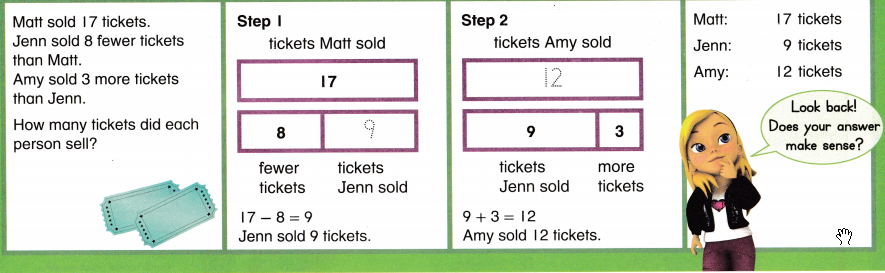
Convince Me! What steps did you take to find the number of tickets Amy sold? Explain.

Guided Practice

Solve the two-step problem. Show your work.
Question 1.
Steve read 15 books. Sam read 9 fewer books than Steve. Dixon read 8 more books than Sam. How many books did Sam read?

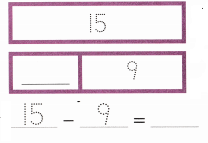
Sam read _______ books.

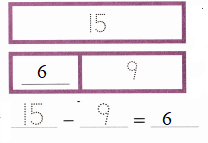
sam read 6 books.

How many books did Dixon read?

Dixon read _______ books.

Dixon read 14 books.

Independent Practice

Solve the problems below. Show your work.
Question 2.
Brian has 17 fewer marbles than Kyle. Brian has 21 marbles. How many marbles does Kyle have?
________ marbles
Answer:
Given that,
Total number of marbles at Brain = 21
The total number of marbles at Brain has  fewer than Kyle  = 17
Total number of marbles marbles at Kyle = 21 + 17 = 38
Question 3.
Clint catches 7 frogs. 3 frogs hop away. Then Clint catches 6 more frogs. How many frogs does Clint have now?
_________ frogs
Answer:
Given that,
Total number of frogs the Clint catches = 7
Total number of Frogs hop away = 3
Clint catches another more frogs = 6
Total number of frogs at Clint = 7 – 3 + 6 = 10
Question 4.
Erwin sees 23 birds in a tree. Then 18 more birds come. How many birds does Erwin see now?
_________ birds
Answer:
Given that,
Erwin sees the total number of birds in a tree = 23
More birds come on the tree = 18
Total number of birds that seen bye the Erwin  = 23 + 18 = 41
Question 5.
There are 31 bluefish in a pond. There are also 8 goldfish and 3 redfish in the pond. How many fish are in the pond?
________ fish
Answer:
Given that
Total number of Blue fishes in a pound = 31
Total number of Goldfishes in a pound = 8
Total number of Red fishes in a pound = 3
Total number of fishes in a pound = 31 + 8 + 3 = 42
Question 6.
Higher Order Thinking Mr. Leu buys 6 bananas. Then he buys 8 more bananas. He gives some bananas to Mr. Shen. Now Mr. Leu has 5 bananas. How many bananas did Mr. Leu give to Mr. Shen?
_________ bananas
Answer:
Given that,
Mr. Leu buys bananas = 6
He buys more bananas = 8
Total bananas at Mr. Leu = 6 + 8 = 14
Mr. Leu gave some bananas to the Mr. Shen
Mr. Leu left only 5 bananas
Mr. Leu gave to Mr. Shen = 14 – 5 = 9

Problem Solving

Solve the problems below. Show your work.
Question 7.
There are 21 more green crayons than blue crayons. There are 14 blue crayons. How many green crayons are there?
__________ green crayons
Answer:
Given that,
Total number of Blue crayons = 14
Green crayons are 21 more than blue crayons.
Total number of Green crayons = 14 + 21 = 35

Question 8.
Make Sense Dan swims 4 laps on Monday. He swims 5 laps on Tuesday. Then he swims 9 laps on Wednesday. How many laps does Dan swim in all?
_________ laps
Answer:
Given that,
Dan swims on Monday = 4 laps
Dan swims on Tuesday = 5 laps
Dan swims on Wednesday = 9 laps
Total number of laps that Don swim = 4 + 5 + 9 = 18

Question 9.
Higher Order Thinking Robert has 20 blueberries. He has 10 more blueberries than Janessa. He has 14 fewer blueberries than Amari. How many blueberries does Janessa have? How many blueberries does Amari have?
Janessa has ________ blueberries.
Amari has __________ blueberries.
Answer:
Given that,
A robot has 20 blueberries
He has 10 more blueberries than Janessa
Janessa has blueberries = 20 – 10 = 10
The robot has 14 blueberries fewer than Amari
Amari has total number of blueberries = 20 + 14 = 34

Question 10.
Assessment Practice Billy saw 19 animals at Grayson Zoo in the morning. He saw 17 more animals after lunch. How many animals did Billy see in all?
__________ animals
Answer:
Given that,
Billy saw animals at Grayson Zoo in the morning = 19
Billy saw animals at Grayson Zoo in the afternoon = 17
Total number of animals that Billy saw = 19 + 17

Lesson 3.7 Problem Solving

Construct Arguments
Solve & Share
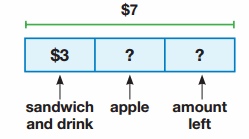
Carrie has 16 more red apples than green apples. She has 24 green apples. How many red apples are there?
Use any strategy to solve. Use pictures, numbers, or words to explain your thinking and work.

I can … use pictures, numbers, and words to explain why my thinking and work are correct.

Thinking Habits
Construct Arguments
How can I use math to explain why my work is correct?
Am I using numbers and symbols correctly?
Is my explanation clear?

Visual Learning Bridge

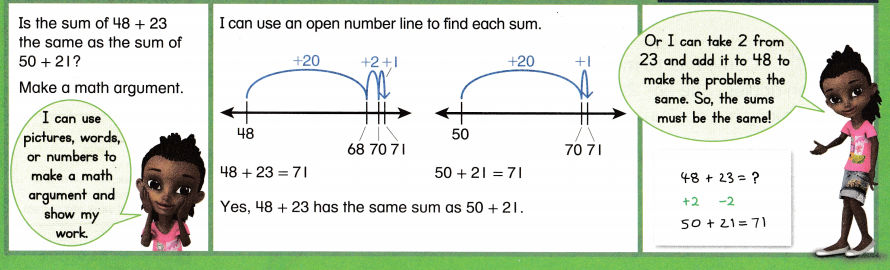
Convince Me! Are both math arguments above clear and complete? Explain.

Guided Practice

Solve. Use pictures, words, or numbers to make a math argument. Show your work.
Question 1.
There are 16 chickens in the yard. There are 19 chickens in the barn. There are 30 nesting boxes. Will all of the chickens have a nest? Explain.

Answer:
Given that,
Total number of Chickens in a yard = 16
Total number of Chickens in a barn = 19
Total number of Chickens in a nesting  = 30
Total number of chickens = 16 + 19 = 35
5 chickens have no nest

Independent Practice

Solve each problem. Use pictures, words, or numbers to make a math argument. Show your work.
Question 2.
Greg had 45 sports cards. Jamal gives him 26 more cards. How many sports cards does Greg have now?

_________ sports cards
Answer:
Given that,
Total number of sports cards at Grah  = 45
Jamal gives more cards to Grah = 26
Total number of sports cards at Grah = 45 + 26 = 71

Question 3.
Denise drew 8 stars with crayons. Then she drew 6 more stars. Trina drew 5 stars. How many fewer stars did Trina draw than Denise?
________ fewer stars
Answer:
Given that,
Denise draw stars with crayons = 8
She draws more stars = 6
Total number of stars drawn by Denise = 8 + 6 = 14
Trina draw a star = 5
14 – 5 = 9
Trina draw 9 fewer stars than Denise

Problem Solving

Performance Task
Bean Bag Toss Evan and Pam each throw two bean bags. Points are added for a score. Pam’s total score is 100. Which two numbers did Pam’s bean bags land on?

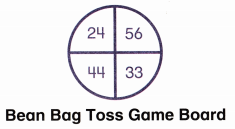
Question 4.
Make Sense What information is given? What do you need to find?
Answer:
In the above task, Pam and Evan play a bean bag toss game.
The score Pam’s is 100
The numbers that Pam’s bean bag lands on are 56 and 44.
By adding 56 and 44 we get 100.so, the beam bag lands on 56 and 44.
Question 5.
Explain Which numbers did Pam’s bags land on? Explain how you know.
Answer:
Given that,
Pam’s bags land on 56 and 44
The total score Pam’s is 100
By adding 56 and 44 we get 100
So, Pam’s bags are landed on 56 and 44.

Question 6.
Explain How could you use a hundred charts to solve the problem? Explain.

Answer:
using a hundred charts for example you went to find the sum of 10  + 15.
first, mark the 10 in the hundred charts and down to 1 row and back to 5 places then we get 15 has the answer.
This is the way to solve the problem using a hundred charts.

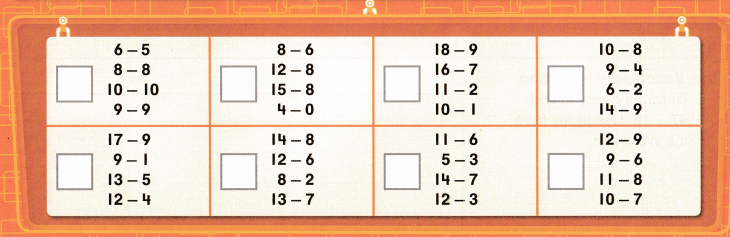
Topic 3 Fluency Practice Activity

Find & Match
Find a partner. Point to a clue. Read the clue.
Look below the clues to find a match. Write the clue letter in the box next to the match.
Find a match for every clue.
I can … subtract within 20.

Clues
A. Every difference equals 3.
B. Every difference is less than 2.
C. Every difference equals 11 – 5.
D. Exactly two differences are equal.
E. Every difference is greater than 8.
F. Exactly three differences are odd.
G. Every difference equals 16 – 8.
H. Exactly three differences are even.

Topic 3 Vocabulary Review

Understand Vocabulary
Word List

• bar diagram
• break apart
• compensation
• mental math
• ones
• open number line
• tens

Question 1.
Circle the numbers that have a 3 in the one’s place.
33
45
13
38
Answer:
In the above-given numbers, 33 and 13 has 3 in the one’s place then circle the 33 and 13.
Question 2.
Cross out the numbers that do NOT have an 8 in the tens place.
80
18
78
89
Answer:
In the above-given numbers, 18 and 78 do not have 8 in the ten’s place. Then cross out the 18 and 78.

Question 3.
Write an equation to show how to break apart 54 by place value.
Answer: 50 + 4
Question 4.
Use the open number line to find 38 + 23. Add the tens and then add the ones.

Answer:
38 + 23
38 + (20 + 3)
58 + 3 = 61
First draw the Line.
Represent the number on the line.
The first number is 38 and counts by 20 then it gets 54 and jumps to 3 then it gets 61.
Count the numbers and draw an arrow.

Use Vocabulary in Writing
Question 5.
Describe a way to find 47 + 18. Use terms from the Word List.
Answer:
47 + (10 + 8)
(47 + 10) + 8
57 + 8 = 65

Topic 3 Reteaching

Set A

You can use a hundred charts to help you add. Find 62 + 12.
Start at 62. Move down 1 row to add the 1 ten in 12.
Then move over 2 columns to add the 2 ones in 12.

Use a hundred charts to find each sum.
Question 1.
85 + 15 = _______
Answer:
Using the hundred chart the sum of 85 + 15 is
In the hundred charts, we start at the 85 then down to 1 row then we get 95, and move front to 5 space then we get 100.
85 + 15 = 100
Question 2.
60 + 23 = _________
Answer:
Using the hundred chart the sum of 60 + 23 is
In the hundred charts, we start at 60 and then move down to 2 rows then we get 80 and move front to 3 space then we get 83
60 + 23 = 83

Set B

You can use an open number line to find 49 + 32.

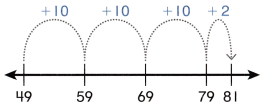
Place 49 on the number line. There are 3 tens in 32. So, count on by 10 three times. There are 2 ones in 32. So, count on 2 from 79.
So, 49 + 32 = 81

Use an open number line to find each sum.
Question 3.
35 + 13 = ________

Answer:
35 + 13 = 48
First, draw the Line.
Represent the number on the line.
The first number is 35 and counts by 10 then it gets 45  and jumps to 3 then it gets 48.
Count the numbers and draw an arrow.

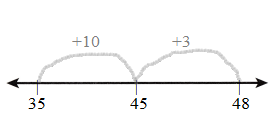
Question 4.
47 + 26 = _________

Answer:
47 + 26 = 73
First, draw the Line.
Represent the number on the line.
The first number is 47 and counts by 20 then it gets 67 and jumps to 6 then it gets 73.
Count the numbers and draw an arrow.

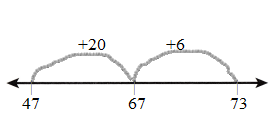
Set C

Find 55 + 17.
Break apart 17 into 10+ 7.

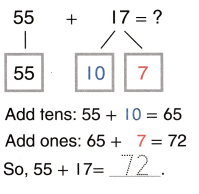
Break apart the second addend to find the sum. Show your work.
Question 5.
53 + 28 = _________
Answer:
53 + 28
53 + 20 + 8
73 + 8 = 81Question 6.
78 + 19 = _________
Answer:
78 + 19
78 + 10 + 9
88 + 9 = 97

Set D

Find 48 + 27.
48 is close to 50. So, take 2 from 27 and give it to 48 to make 50.
48 + 27 = ?

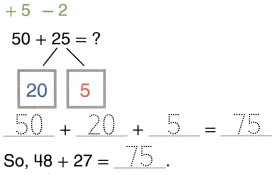
Use compensation to make numbers that are easier to add. Then solve. Show your work.
Question 7.
17 + 46 = ________
Answer:
17 + 46
17 + 40 + 6
57 + 6 = 63

Question 8.
29 + 57 = ________
Answer:
29 + 57
29 + 50 + 7
79 + 7 = 86

Set E

You can use different strategies and tools to find a sum.
You can:

• Use a hundred chart
• Use an open number line
• Break apart one addend
• Use compensation

Solve. Show your work.
Question 9.
Ted’s puzzle has 37 more pieces than his brother’s puzzle. His brother’s puzzle has 48 pieces. How many pieces does Ted’s puzzle have?
________ pieces
Answer:

Given that,
Ted’s puzzle has more pieces than her brother = 37
His brother puzzle has pieces = 48
Total number of pieces does Ted’s have = 48 + 37 = 85

Set F

Marla walks 12 blocks on Monday. On Tuesday, she walks 4 fewer blocks. How many blocks does Marla walk in all?
Blocks Marla walks on Tuesday:

Solve the two-step problem.
Question 10.
Wyatt has 16 crayons. He buys 24 new crayons. Then he finds 7 more crayons. How many crayons does Wyatt have now?

________ crayons
Answer:

Total number of crayon = 47

Set G

Thinking Habits
Construct Arguments
How can I use math to explain my work?
Am I using numbers and symbols correctly?
Is my explanation clear?

Solve the problem. Use words and numbers to make a math argument.
Question 11.
A second-grade class sets a goal to collect 70 cans. One week they collect 38 cans. The next week they collect 35 cans. Do they meet their goal?
Answer:
Given that,
A second-grade class set a goal to collect cans = 70
One week the second-grade class set collect cans = 38
Next week the second-grade class set collect cans = 35
Total number of cans they collected = 38 + 35 =73
Yes they meet their goal by collecting 73 cans out of 70

Topic 3 Assessment Practice

Question 1.
Which have a sum of 43? Choose all that apply.
☐ 33 + 10
☐ 28 + 13
☐ 10 + 33
☐ 19 + 24
☐ 10 + 21
Answer:
33 + 10 has a sum of 43
10 + 33 has a sum of 43
19 + 24 has a sum of 43
Question 2.
Terry has 63 crayons. She gets 25 more crayons. How many crayons does Terry have in all? Show your work.
________ crayons
Answer:
Given that,
Total number of crayons near Terry = 63
Tenny get more crayons = 25
Total number of crayons at Terry = 63 + 25 = 88
Question 3.
Which equation does this number line show?

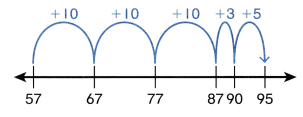
A. 57 + 28 = 85
B. 57 + 38 = 95
C. 57 + 33 = 90
D. 57 + 39 = 96
Answer:
57 + 38 = 95
Question 4.
Use the numbers on the cards. Write the missing numbers under the number line to show how to find the sum of 40 + 35.

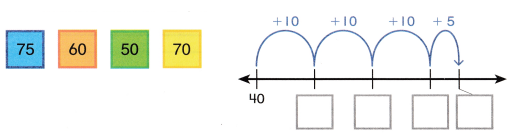
Answer:
Question 5.
Colin has 54 pennies and 28 nickels. How many coins does Colin have?
Break apart the second addend to solve. Show your work.
________ coins
Answer:
Given that,
Total number of pennies near Colin = 54
Total number of nickels near Colin = 28
Total number of coins near colin = 54 + 28
54 + (20 + 8)
(54 + 20) + 8
74 + 8 = 82

Question 6.
Show how to add 68 + 16 using the open number line.

68 + 16 = ___________
Answer:
68 + 16 = 84
First draw the Line.
Represent the number on the line.
The first number is 68 and counts by 10 then it gets 78 and jumps to 6 then it gets 84.
Count the numbers and draw an arrow.

Question 7.
Part A
Show how you can use an open number line to find 44 + 27.

44 + 27 = _________
Answer:
44 + 27 = 71
First draw the Line.
Represent the number on the line.
The first number is 44 and counts by 20 then it gets 64 and jumps to 7 then it gets 71.
Count the numbers and draw an arrow.

Part B
In words, tell how you used the open number line to find the sum.
Answer:
Suppose  we have a sum that is 14 + 13
Then draw a line and represent the numbers on a line and place a 14 on the line shift  10 from the 14 we get 24 then jump to 3 then we get 27.
The sum of 14 + 13 = 27.

Question 8.
Which have a sum of 70? Choose all that apply.
☐ 35 + 35
☐ 40 + 30
☐ 45 + 45
☐ 50 + 200
☐ 30 + 30
Answer:
35 + 35
40 + 30

Question 9.
Lisa has 18 markers. Adam has 22 markers. Will all of the markers fit in a box that can hold 38 markers?
Make a math argument. Explain.
Answer:
Given that,
Total number of markers near Lisa = 18
Total number of markers near Adam = 22
Total number of Markers fit in a box = 38
Total number of markers = 18 + 22 = 40
Total markers are not fit into a box.

Question 10.
Ted has 52 cards in a box. Tyrone has 48 more cards than Ted. How many cards does Tyrone have? Show your work to explain your thinking.
________ cards
Answer:
Given that
Ted has  cards in a box = 52
Tyrone has more card than Ted = 48
Total number of cards at Tyrone = 52 + 48 = 100
Question 11.
Which are equal to 47 + 25? Choose all that apply.
☐ 40 + 20 + 7 +5
☐ 40 + 20 + 12
☐ 50 + 12
☐ 50 + 22
Answer:
To find the sum of 47 + 25 we apply the 40 + 20 + 7 + 5

Question 12.
Emma has 46 rocks. She gets 25 more rocks from Gus. How many rocks does Emma have now?

________ rocks
Answer:
Given that,
Emma has rocks = 46
She get more rocks = 25
Total number of rocks at Emma = 46 + 25 = 71
Question 13.
Is each sum 64? Choose Yes or No.

Answer:

Question 14.
Break apart the second addend to find 56 + 38. Show your work.

56 + 38 = ________
Answer:
56 + 38
56 + 30 + 8
86 + 8 = 94

Question 15.
Write an equation to solve each part of the two-step problem.
Ken has 45 stamps. He uses 20 stamps. Then he buys 7 more stamps. How many stamps does he have now?

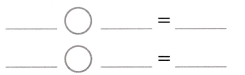
Ken has ________ stamps.
Answer:
Given that,
Ken has total number of stamps = 45
He used total number of stamps = 20
He buy another stamps = 7
Total number of stamps Ken have = 45 – 20 + 7
25 + 7 = 32

Question 16.
Show two different ways to find 28 + 49 using compensation.
Way 1
Way 2
Answer:
Way 1: 28 + 49 = 77
Way 2:  28 + 49
28 + 40 + 9
68 + 9 = 77

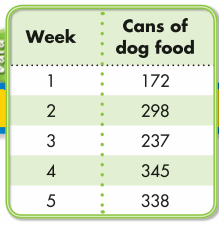
Topic 3 Performance Task

Popcorn Sales
A second-grade class is selling popcorn to help pay for a field trip.
This table shows how many boxes some students have sold.

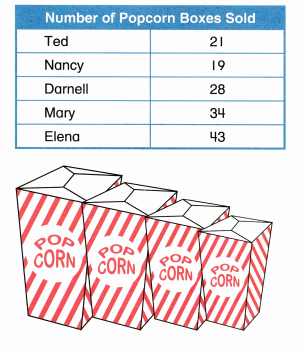
Question 1.
How many boxes of popcorn did Ted and Mary sell in all? Use the open number line to solve. Show your work.

_________ boxes
Answer:
Given that,
Number of popcorn did Ted sell = 21
Number of popcorn did Mary sell = 34
Total number of popcorn box sell = 21 + 34 = 55
First draw the Line.
Represent the number on the line.
The first number is 21and counts by 30 then it gets 51and jumps to 4 then it gets 80.
Count the numbers and draw an arrow.

Question 2.
James says that Mary and Nancy sold more boxes in all than Darnell and Ted sold in all. Do you agree with him?
Circle:
Yes
No
Explain your answer.
Answer:
Given that,
Total number of boxes sold by Mary = 34
Total number of boxes sold by Nancy = 19
Total number of boxes sold by Mary and Nancy = 34 + 19 = 43
Total number of boxes sold by Darnell = 28
Total number of boxes sold by Ted = 21
A total number of boxes sold by Darnell and Ted = 21 + 28 = 49
James said wrong that Mary and Nancy sold fewer boxes than Darnell and Ted.
Question 3.
Which two students sold a total of 55 boxes? Use any strategy to solve. Show your work.
Circle the names of the two students.

Question 4.
Nancy sold 18 fewer boxes than Lucas. How many boxes did Lucas sell?

Part A
Solve the problem. Show your work and explain your thinking.
________ boxes
Answer:
Given that,
Nancy sold fewer boxes than Lucas = 18
Total number of boxes that Nancy sold = 19
Total number of boxes that Lucas sold more than Nancy = 19 – 18 = 1

Part B
Look at the list of strategies on the left. To show that your answer in Part A is correct, use a different strategy to solve the problem.
Answer:

Go through the enVision Math Common Core Grade 2 Answer Key Topic 14 More Addition, Subtraction, and Length regularly and improve your accuracy in solving questions.

enVision Math Common Core 2nd Grade Answers Key Topic 14 More Addition, Subtraction, and Length

Essential Question:
How can you add and subtract lengths?

enVision STEM Project: Modeling Land, Water, and Length
Find Out Find and share books and other sources that show the shapes and kinds of land and water in an area. Draw a picture or make a model to show the land or water in an area.
Journal: Make a Book Show what you learn in a book. In your book, also:

• Draw a picture to show the shape of some land or water in your area.
• Make up a math story about lengths. Draw a picture to show how to solve the problem in your story.

Review What You Know

Vocabulary
Question 1.
Circle the measuring unit that is better to estimate the length of a room.
meter
centimeter
Answer: centimeter

Question 2.
Circle the number of feet in 1 yard.
2 feet
3 feet
4 feet
12 feet
Answer: 3 feet

Question 3.
The clock shows the time a math class begins. Circle a.m. or p.m.

Answer: 10 a.m.

Estimate
Question 4.
Estimate the length of the eraser in centimeters.

About _______ centimeter
Answer: 4 centimeter

Compare
Question 5.
A sidewalk is 632 yards long. A jogging trail is 640 yards long.
Use <, >, or = to compare the lengths.
632 640
Answer: 632 < 640

Rectangles
Question 6.
Label the 2 missing lengths of the sides of the rectangle.

Answer: The missing lengths are 3cm and 4 cm.
In the rectangle opposite sides are equal. So, the 2 missing lengths of the sides of a rectangle are 3cm and 4cm.

Pick a Project

PROJECT 14A
How tall are Ferris wheels?
Project: Write a Ferris Wheel Story

PROJECT 14B
How big are insects?
Project: Make Insect Drawings

PROJECT 14C
How can you measure if you do not have tools?
Project: Make a Measurement Poster

PROJECT 14D
How is some food grown?
Project: Draw a Garden Plan

Lesson 14.1 Add and Subtract with Measurements

Solve & Share
The ant crawled along the edge of this blue rectangle. Measure the total distance the ant crawled. Show your work and be ready to explain it.
I can … solve problems by adding or subtracting length measurements.

Visual Learning Bridge

Convince Me! Explain how to find the distance around a square park that is 2 miles long on each side.

Guided Practice

Decide if you need to add or subtract. Then write an equation to help solve each problem.
Question 1.
What is the distance around the baseball card?

Question 2.
What is the distance around the puzzle?

Distance around: _________ in.
Answer:
The puzzle has four sides one side is 12in and 15in.
The opposite side of 12in is also 12in and the opposite side of 15in is also 15in.
The total distance around the puzzle is 15 + 15 + 12 + 12 = 54
The distance around the puzzle is 54in.
Independent Practice

Decide if you need to add or subtract. Then write an equation to help solve each problem.
Question 3.
What is the distance around the door?

_________
Distance around: ________ ft
Answer:
The door has four sides one side is 3ft and 7ft.
The opposite side of 3ft is also 3ft and the opposite side of 7ft is also 7ft.
The total distance around the door is 3 + 3 + 7 + 7 = 20
The distance around the door is 20ft.

Question 4.
What is the distance around the cell phone?

___________
Distance around: _________ in.
Answer:
The cell has four sides one side is 4in and 2in.
The opposite side of 2in is also 2in and the opposite side of 4in is also 4in.
The total distance around the cell is 2 + 2 + 4 + 4 = 12
The distance around the cell is 12in.

Question 5.
How much longer is the red scarf than the blue scarf?

________ in. longer
Answer:
Given that,
The length of the red scarf is 60in.
The length of the blue scarf is 45in.
Red scarf – blue scarf = 60 – 45 = 15
The red scarf is 15in longer than a blue scarf.

Question 6.
Algebra What is the length of the shorter side of the rectangle?

Complete the equation to solve.
20+ _______ + 20 + _______ = 60
The shorter side is ________ centimetres.
Answer:
The Given that,
The length of the longer side of the  rectangle is 20cm
The other side of the longer side is also 20cm
But the given equation is
20 + 20 = 60
40 = 60
60 – 40 = 20
20 can be divided into 2 shorter sides so, one shorter side is 10 and another shorter side is 10.
The shorter side is 20 centimetres.

Problem Solving

Decide if you need to add or subtract. Then write an equation to help solve each problem.
Question 7.
Model Ashley’s sunflower is 70 inches tall. Kwame’s sunflower is 60 inches tall. How much taller is Ashley’s sunflower than Kwame’s sunflower?

_________ inches taller
Answer:
Given that,
The length of Ashley’s sunflower is 70 inches.
The length of Kwame’s sunflower is 60 inches.
70 – 60 = 10
Ashley’s sunflower is 10inches longer than Kwame’s sunflower.

Question 8.
Model Ben compares the length of a leaf and a plant. The leaf is 15 centimetres. The plant is 37 centimetres. How much shorter is the leaf than the plant?

__________ centimeters shorter
Answer:
Given that,
The total length of the leaf is 15 centimeters.
The total length of the plant is 37 centimeters.
37 – 15 = 22
The length of the leaf is 22 centimeters shorter than the length of the plant.

Question 9.
Higher Order Thinking Tyler threw a ball 42 feet and then 44 feet. Sanjay threw a ball 38 feet and then 49 feet. Who threw the longer distance in all? Show you work.
Answer:
Given that,
Tyler threw a ball is 42 feet and then 44 feet.
Tyler threw a ball in total = 42 + 44 = 86
Sanjay threw a ball is 38 feet and then 49 feet.
Sanjay threw a ball in total = 38 + 49 = 87
Sanjay threw a ball longer distance than Tyler.

Question 10.
Assessment Practice What is the distance around the placemat?

A. 28 in.
B. 39 in.
C. 56 in.
D. 66 in.
Answer:
The placemat has four sides one side is 121in and 17in.
The opposite side of 11in is also 11in and the opposite side of 17in is also 17in.
The total distance around the placemat is 11 + 11 + 17 + 17 = 56
The distance around the placemat is 56in.
C is the correct option.

Lesson 14.2 Find Unknown Measurements

Solve & Share
Julie and Steve each cut a piece of yarn. The total length of both pieces is 12 cm. Measure each piece of yarn. Circle Julie and Steve’s pieces. Then explain your thinking.
I can … add or subtract to solve problems about measurements.

Visual Learning Bridge

Convince Me! How does drawing a yardstick help you solve the problem above?

Guided Practice

Write an equation using a ? for the unknown number. Solve with a picture or another way.
Question 1.
A square stamp measures 2 centimeters in length. How many centimeters long are two stamps?

Anawer: 2+2 = 4

Question 2.
Stuart’s desk is 64 centimeters long. His dresser is 7 centimeters longer than his desk. How long is Stuart’s dresser?
________ cm
Answer:
Given that,
Stuart’s desk is 64 centimeters long. His dresser is 7 centimeters longer than his desk.
64 + 7 = 71 centimeters
Thus his dresser is 71 centimeter long.

Independent Practice

Write an equation using a ? for the unknown number. Solve with a picture or another way.
Question 3.
Filipe’s pencil box is 24 centimeters long. Joe’s pencil box is 3 centimeters shorter than Filipe’s. How long is Joe’s pencil box?
_________ cm
Answer:
Given that
Filipe’s pencil box is 24 centimeters long. Joe’s pencil box is 3 centimeters shorter than Filipe’s.
24 – 3 = 21 centimeters
Thus Joe’s pencil box is 21 centimeters.

Question 4.
Clark threw a red ball and a blue ball. He threw the red ball 17 feet. He threw the blue ball 7 feet farther. How far did Clark throw the blue ball?
__________ ft
Answer:
Given that,
Clark threw a red ball and a blue ball. He threw the red ball 17 feet.
He threw the blue ball 7 feet farther.
17 + 7 = 24 feet.Question 5.
en Vision® STEM Ashlie’s map shows where animals, land, and water are at a zoo. The distance around her map is 38 inches. What is the length of the missing side?

____________ inches
Answer: The length of the missing side in the given map is 11 in.

Problem Solving

Solve each problem.
Question 6.
Make Sense A brown puppy is 43 centimeters tall. A spotted puppy is 7 centimeters shorter than the brown puppy. A white puppy is 14 centimeters taller than the brown puppy. How tall is the spotted puppy? Think about what you need to find.
_______ cm

Answer:
Given that,
the brown puppy is 43 centimeters tall.
A spotted puppy is 7 centimeters shorter than a brown puppy.
A white puppy is 14 centimeters taller than the brown puppy.
43 – 7 = 36 centimeters
Thus spotted puppy is 36 centimeters tall.

Question 7.
Vocabulary Complete the sentences using the terms below.
foot
yard
inch
A paper clip is about 1 _______ long.
My math book is about 1 ________ long.
A baseball bat is about 1 ________ long.
Answer:
A paper clip is about 1 inch long.
My math book is about 1 foot long.
A baseball bat is about 1 yard long

Question 8.
Higher Order Thinking Jack jumped 15 inches. Tyler jumped I inch less than Jack and 2 inches more than Randy. Who jumped the farthest? How far did each person jump?
Answer:
Given that,
Jack jumped = 15 inches
Tyler jumped 1 inch less than jack
Tyler jumped = 14 inches
Randy jumped = 14 + 2 = 16
Randy jumped farthest.

Question 9.
Assessment Practice Kim was 48 inches tall in January. She grew 9 inches during the year. How tall is Kim at the end of the year? Write an equation with an unknown and then draw a picture to solve.
Answer:
Given that,
Kim was tall in January = 48 inches
Kim grew during the year = 9 inches
Total Kim tall at the end of the year = 48 + 9 = 57 inches

Lesson 14.3 Continue to Find Unknown Measurements

Solve & Share
Alex has a piece of ribbon that is 45 feet long. He cuts the ribbon. Now he has 39 feet of ribbon. How many feet of ribbon did Alex cut off? Draw a picture and write an equation to solve. Show your work.
I can … add and subtract to solve measurement problems by using drawings and equations.

Visual Learning Bridge

Convince Me! How does writing an equation help you solve the problem above?

Guided Practice

Write an equation using a ? for the unknown number. Solve with a picture or another way.
Question 1.
A plant was 15 inches tall. It grew and is now 22 inches tall. How many inches did the plant grow?

Answer: 15 + 7 = 22

Question 2.
Each bus is 10 meters long. Each boat is 7 meters long. What is the total length of two buses and two boats?
Answer:
Given that,
Total number of buses = 2
Length of each bus = 10
Total length of two buses = 2 × 10 = 20
Total number of boats = 2
Length of each boats = 7
Total length of two boats = 7 × 2 = 14
Therefore, total length of two buses and two boats = 20 + 14 = 34

Independent Practice

Write an equation using a ? for the unknown number. Solve with a picture or another way.
Question 3.
Brent’s rope is 49 inches long. He cuts off some of the rope and now it is 37 inches long. How much rope did Brent cut off?
Answer:
Given that,
The total length of Brent’s rope = 49 inches
He cut off some of the rope and now it is = 37 inches
Brent cut off rope = 49 – 37 = 12inches
Question 4.
Sue ran for some meters and stopped. Then she ran another 22 meters for a total of 61 meters in all. How many meters did she run at first?
Answer:
Given that,
Sue ran total meters in all = 61 meters
Sue ran some meters from 61 meters = 22 meters
Sue rum at first time  = 61 – 22 = 39

Question 5.
Algebra Solve each equation. Use the chart.

Answer:
Problem Solving

Solve each problem.
Question 6.
Make Sense The yellow boat is 15 feet shorter than the green boat. The green boat is 53 feet long. How long is the yellow boat? Think about what you are trying to find. Write an equation to solve. Show your work.
________ ft
Answer:
Given that,
The total length of Green boat = 53 feets
Length of the yellow boat is 15 feet shorter than green boat = 53 – 15 = 38 feets
Length of the yellow boat is 38 feets

Question 7.

Vocabulary Steve measured the length of his desk. It measured 2 units.
Circle the unit Steve used.
meter
foot
centimeter
inch
Lori measured the length of her cat. It measured 45 units.
Circle the unit Lori used.
centimeter
yard
inch
foot
Answer:
Steve used:
Meter
Lori used
Centimeter

Question 8.
Higher Order Thinking Lucy’s ribbon is I foot long. Kathleen’s ribbon is 15 inches long. Whose ribbon is longer and by how many inches? Explain your thinking.
Answer:
Given that,
Lucy’s ribbon = 1 foot long
1 foot = 12 inches
Kathleen’s ribbon = 15 inches
Kathleen’s ribbon is longer than Lucy’s ribbon.

Question 9.
Assessment Practice Mary’s water bottle is 25 cm long. Joey’s water bottle is 22 cm long. Ella’s water bottle is 17 cm long.
Which statements are correct? Choose all that apply.
☐ Mary’s bottle is 8 cm longer than Ella’s.
☐ Joey’s bottle is 6 cm longer than Ella’s.
☐ Joey’s bottle is 3 cm shorter than Mary’s.
☐ Ella’s bottle is 8 cm longer than Mary’s.
Answer: Mary’s bottle is 8 cm longer than Ella’s and Joey’s bottle is 3 cm shorter than Mary’s are correct.

Lesson 14.4 Add and Subtract on a Number Line

Solve & Share
Amelia walks 18 blocks on Monday and 5 blocks on Tuesday. How many blocks does she walk in all?
Use the number line to show how many blocks Amelia walks. Then write an equation to show your work.
I can … add and subtract on a number line.

Visual Learning Bridge

Convince Me! Explain how to add 14 inches and 11 inches using a number line.

Guided Practice

Use the number lines to add or subtract.
Question 1.

Question 2.
28 – 14 = _______

Answer:
Subtraction of 28 and 14 is
28 – 14 = 14

Independent Practice

Use the number lines to add or subtract.
Question 3.
80 – 35 = ________

Answer:
Subtraction of 80 and 35 is
80 – 35 = 45

Question 4.
19+ 63 = ________

Answer:
Addition of 19 and 63
19 + 63 = 82

Question 5.
Higher Order Thinking Use the number line to show 15 inches plus O inches. Explain your thinking.

Answer:
15 inches + 0 inches = 15 inches

Question 6.
Number Sense Show each number below as a length from 0 on the number line. Draw four separate arrows.

Answer:

Problem Solving

Use the number line to solve each problem.
Question 7.
Use Tools A football team gains 15 yards 1 on its first play. The team gains 12 yards on its second play. How many yards does the team gain in two plays?

__________ yards
Answer:

Given that,
A football team gains on its first play = 15 yards.
A football team gains on its second play =12 yards.
Food ball team gains in two plays = 15 + 12 = 27 yards.

Question 8.
Use Tools Mia buys 25 feet of board. She uses 16 feet of board for a sandbox. How many feet of board does she have left?

_________ feet
Answer:
Given that,
Total length of board Mia buy = 25 feets
She uses a board for sand box = 16 feets
How many feets of board she left = 25 – 16 = 9

Question 9.
Higher Order Thinking The runners on the track team ran 12 miles on Monday. On Tuesday, they ran 6 more miles than they ran on Monday. How many miles did they run in all on both days?

_________ miles
Answer:
Given that,
The runners on the track team ran on Monday = 12 miles
The runners on the track team ran on Tuesday = 6 more miles than Monday = 6miles + 12miles = 18miles
They ran in all on both days = 12 miles+ 18 miles = 30 miles

Question 10.
Assessment Practice Deb has two pencils. One pencil is 9 cm long and the other pencil is 13 cm long. What is the total length of both pencils?
Use the number line to show your work.

___________ centimeters
Answer:
Given that,
Deb has two pencils
The total length of one pencil = 9 centimeters
The total length of other pencils = 13 centimeters
Total length of both the pencils = 9 centimetres + 13 centimetres = 22 centimetres

Lesson 14.5 Problem Solving

Use Appropriate Tools
Solve & Share

Choose a tool to solve each part of the problem. Be ready to explain which tools you used and why.
Which line is longer? How much longer? Draw a line that is that length.
I can … choose the best tool to use to solve problems.

Thinking Habits Which of these tools can I use?
counters
paper and pencil cubes
place-value blocks
measuring tools
string
number line
technology
Am I using the tool correctly?

Visual Learning Bridge

Convince Me! Explain why counters are NOT the best tool to use to solve the problem above.

Guided Practice

Choose a tool to use to solve the problem. \ Show your work. Explain why you chose that tool and how you got your answer.
Question 1.
Sara cut 19 centimeters of ribbon into two pieces. One piece is 11 centimeters long. How long is the other piece?
Answer:
Given that,
Sara cut 19 centimeters of ribbon into two pieces.
The length of one piece = 11 centimetres
The length of other piece = 19 centimetres – 11 centimetres = 8 centimetres.
The length of other pieces = 8 centimeters.

Independent Practice

Solve each problem. Show your work.
Question 2.
Work with a partner. Measure each other’s arm from the shoulder to the tip of the index finger. Measure to the nearest inch. Whose arm is longer and by how much?
Choose a tool to use to solve the problem. Explain why you chose that tool and how you got your answer.
Answer:

Question 3.
Marcel jumped 39 centimeters high. Jamal jumped 48 centimeters high. How much higher did Jamal jump than Marcel?
Which tool would you NOT use to solve this problem? Explain.
Answer:
Given that,
Marcel jumped = 39 centimetres
Jamal jumped = 48 centimetres
Jamal jumped more than Marcel.

Place value box tool is not used for solving the problem.

Problem Solving

Performance Task
Sailboats Zak is measuring sailboats at the dock. Mr. Lee’s sailboat is 64 feet long. Ms. Flint’s sailboat is 25 feet shorter than Mr. Lee’s boat. Help Zak find the length of Ms. Flint’s boat.

Question 4.
Use Tools Which tool would you NOT use to solve this problem? Explain.
Answer:

Question 5.
Be Precise Will you add or subtract to solve the problem?
______________
Write an equation. Use ? for the unknown.
______________
What unit of measure will you use?
______________
Answer:

Question 6.
Explain What is the length of Ms. Flint’s boat? Did you use a tool to solve the problem? Explain.
Answer:
Given that,
The length of Ms. Flint’s boat = 25 feet shorter than Mr. Lee’s boat.
Mr. Lee’s boat = 65 feets.
Length of the Ms. Flint’s boat = 65

Topic 14 Fluency Practice

Follow the path
Color a path from Start to Finish. Follow the sums and differences that are odd numbers. You can only move up, down, right, or left.
I can … add and subtract within 100.

Topic 14 Vocabulary Review

Understand Vocabulary
Choose a term from the Word List to complete each sentence.
Word List
• centimeter (cm)
• foot (ft)
• height
• inch (in.)
• length
• mental math
• meter (m)
• yard (yd)

Question 1.
The length of your finger can best be measured in centimeters or ___________.
Answer:
The length of your finger can best be measured in centimetres or inches.

Question 2.
100 ________ equals 1 meter.
Answer:
100 centimetres equals to 1 meter.

Question 3.
__________ is how tall an object is from bottom to top.
Answer:
Height is how tall an object is from bottom to top.

Write T for true or F for false.
Question 4.
_______ 1 yard is 5 feet long.
Answer:
False

Question 5.
________ 12 inches is I foot long.
Answer:
True

Question 6.
________ A centimeter is longer than a meter.
Answer:
False

Question 7.
_________ You can do mental math in your head.
Answer:
False

Use Vocabulary in Writing
Question 8.
Tell how to find the total length of two pieces of string. One piece of string is 12 inches long. The other piece is 9 inches long. Use terms from the Word List.
Answer:
Given that,
The total length of one piece of string = 12 inches
The total length of other pieces of string = 9 inches
The total length of two pieces = 12 inches + 9 inches = 21 inches

Topic 14 Reteaching

Set A

What is the distance around the front of the bookcase?

Add the lengths. Write an equation.
4+ 3+ 4+ 3 = 14
Distance around: 14 feet

Write an equation to help solve.
Question 1.
What is the distance around the front of the crayon box?

Distance around: _________ cm
Answer:
Given that,
The crayon box has four sides
The length of the two sides is 12cm and 9cm.
The opposite side of 12 cm is also 12 cm.
The opposite side of 9cm is also 9 cm
Total distance around crayon box = 12 + 12 + 9 + 9 = 42 centimetres.

Set B

A kite string is 27 feet long. Some of the string is cut off. Now the kite string is 18 feet long. How many feet of kite string were cut off?
Write an equation and draw a picture.
27 – ? = 18 or 18+? = 27

Write an equation using a ? for the unknown number. Then draw a picture to solve.
Question 2.
A piece of yarn is 42 inches long. Mia cuts some of it off. It is now 26 inches long. How much yarn did Mia cut off?
Answer:
Given that,
A piece of yarn = 42 inches long
Mia cuts some of it and now it is = 26 inches
Mia cut off yarn = 42 – 26 = 16 inches

Set C

A book measures 10 inches long. Another book measures 13 inches long. What is the total length of both books?
You can show 10 + 13 on a number line.

Solve the problem using the number line.
Question 3.
One room in Jackie’s house is 15 feet long. Another room is 9 feet long. What is the total length of both rooms?

Answer:
Given that,
The length of one room in Jackie’s house = 15 feets
The length of other room in Jackie’s house = 9 feets
Total length of two rooms in Jackie’s house = 15 + 9 = 24 feets

Set D

Thinking Habits
Use Tools
Which of these tools can I use?
counters
paper and pencil cubes
place-value blocks
measuring tools
string
number line
technology
Am I using the tool correctly?

Choose a tool to solve the problem.
Question 4.
Damon’s shoelace is 45 inches long. His shoelace breaks. One piece is 28 inches long. How long is the other piece?
Explain your solution and why you chose the tool you used.
Answer:
Given that,
The total length of Damon’s shoelace = 45 inches long.
His shoelace breaks into two pieces and one-piece length = 28 inches
The length of other piece = 45 inches – 28 inches = 17 inches

Topic 14 Assessment Practice

Question 1.
A notebook has a length of 7 in. and a width of 5 in. What is the total distance around the notebook? Use the image below for help.

Distance around: _______ in.
Answer:
Given that,
The note book has a length of 7 inches and 5 inches
Total distance around the note book = 7 + + 7 + 5 + 5 = 24
Total distance around the note book = 24 inches.

Question 2.
Kate is 48 inches tall. Tom is 2 inches taller than Kate. James is 3 inches shorter than Tom.
How tall is James?
A. 45 inches
B. 47 inches
C. 50 inches
D. 53 inches
Answer:
Given that,
Kate is 48 inches tall.
Tom is 2 inches tall than Kate = 48 + 2 = 50 inches
James is 3 inches shorter than Tom = 50 – 3 = 47 inches
James has 47 inches tall.
Option B is correct.

Question 3.
Alexis has a rope that is 7 feet long. Mariah’s rope is 9 feet long. Sam’s rope is 3 feet longer than Mariah’s rope.
Use the measurements on the cards to complete each sentence.

Sam’s rope is ________ long.
Alexis’s rope is ________ shorter than Mariah’s rope.
Sam’s rope is _________ longer than Alexis’s rope.
Answer:
Sam’s rope is 12 feet long.
Alexis’s rope is 2 feets shorter than Mariah’s rope.
Sam’s rope is 5 feet longer than Alexis’s rope.

Question 4.

Joe rides his bike 18 miles. Then he rides 7 more miles.
Use the number line to find how far Joe rides. Then explain your work.

Answer:
Given that,
Joe rides his bike = 18 miles.
He rides 7 more miles = 18 + 7 = 25 miles
Joe rides in total = 25 inches.

Question 5.
Pat says that each unknown equals 25 cm. Do you agree? Choose Yes or No.

Answer:

Question 6.
Grace got a plant that was 34 cm tall. The plant grew and now it is 42 cm tall. How many centimeters did the plant grow?
A. 8 cm
B. 12 cm
C. 42 cm
D. 76 cm
Answer:
Given that,
Grace got a plant that was 34 centimeters long.
The plant grows up to 42 centimeters tall.
How much the plant grow = 42 – 34 = 8 centimetres.
Option A is correct

Question 7.
Claire rides her bike 26 miles on Saturday and Sunday. She rides 8 miles on Sunday. How many miles does she ride on Saturday?
Write an equation to show the unknown. Then use the number line to solve the problem.

Answer:
Given that,
Claire rides her bike on Saturday and Sunday = 26 miles
She rides on Sunday = 8 miles
She rides on Saturday = 26 – 8 = 18 miles

Question 8.
Chris had a string that is 18 cm long. He cut off 7 cm. How much string is left?
A. Which of these tools could you use to solve the problem? Choose all that apply.
☐ centimeter ruler
☐ paper and pencil
☐ measuring cup
☐ number line
☐ inch ruler
Answer:

B. Write an equation to show the unknown.
Then draw a number line to solve.
________ _______ = _________
________ cm
Answer:

Topic 14 Performance Task

Fishing Fun Jim and his family go on a fishing trip. They use a boat and fishing gear to help them catch fish.

Question 1.
Jim takes this fishing box with him. What is the distance around the front of the fishing box? Write an equation to help solve the problem.

Distance around: _________ centimeters
Answer:
Jim takes this fishing box with him.
The length of the fishing box = 31
The breath of the fishing box = 16
Distance around the front of the fishing box = 31 + 16 = 47 centimetres

Question 2.
Jim’s fishing pole is 38 inches long. Performance His dad’s fishing pole is 96 inches Task long. How much shorter is Jim’s pole than his dad’s pole? Part A
Write a subtraction equation that shows the problem.

Part B
Solve the problem.
__________ inches shorter
Answer:
Jim’s fishing pole = 38 inches
His dad’s fishing pole = 96 inches
96 – 38 = 58
Jim’s fishing pole is 58 inches shorter than his dad’s fishing pole.

Question 3.
Jim catches a fish 49 yards away from the shore. Later, he helps row the boat closer to the shore. Now he is 27 yards away from the shore. How many yards closer to shore is Jim now than when he caught the fish?
Part A
Write an addition equation that shows the problem.
Answer:

Part B
Solve the problem.
______ yards
Answer:

Question 4.
Jim catches a silver fish that is 12 inches long. His sister catches a green fish that is 27 inches long. What is the total length of both fish?
Use the number line to solve.

__________ inches
Answer:
Given that,
Jim catches a silver fish that is 12 inches long.
His sister catches a green fish that is 27 inches long.
The total length of two fishes = 12 + 27 = 39 inches.

Question 5.
Jim has 27 yards of fishing line. He gives 12 yards of line to a friend. How many yards of line does Jim have left?

Answer:
Given that,
Jim has 27 yards of fishing line.
He gives 12 yards of line to a friend.
Jim left the fishing line = 27 – 12 = 15 yards

Question 6.
Jim’s family meets a man with a big boat. A parking spot at the dock is 32 feet long. Will the man’s car and boat fit in the parking spot?

Part A
What do you need to find?
Answer:
A parking spot at the dock is 32 feets
Length of the big boat = 27 feets.
Length of the car = 7 feets.
There is a space between car and boat = 2 feets.
Total length of car and boat = 34 feets
Yes the car and boat fit in the parking spot.

Part B
What is the total length? Write an equation to solve.
Will the car and boat fit in the parking spot? Explain.
_____________
What tool did you use? _______________
Answer:

Go through the enVision Math Common Core Grade 3 Answer Key Topic 13 Fraction Equivalence and Comparison regularly and improve your accuracy in solving questions.

enVision Math Common Core 3rd Grade Answers Key Topic 13 Fraction Equivalence and Comparison

Essential Question:
What are different ways to compare fractions?

enVision STEM Project: Life Cycles
Do Research A frog egg hatches into a tadpole that lives in water. The tadpole will change and eventually become an adult frog. Use the Internet or another source to gather information about the life cycle of a frog and other animals.

Journal: Write a Report Include what you found. Also in your report:

• Tell about what is in a frog’s habitat to support changes the frog goes through in its life cycle.
• Compare the life cycles of the different animals you studied.
• For the animals you studied, make up and solve problems using fractions. Draw fraction strips to represent the fractions.

Review What You Know

Choose the best term from the box. Write it on the blank.

• <
• >
• numerator
• unit fraction

Vocabulary

Question 1.
The symbol ___________ means is greater than.

Answer:
The symbol > means greater than.

Explanation:
In the above-given question,
given that,
greater than symbol is used to compare numbers.
for example:
3 > 1.
so the symbol > is used for large numbers when compared with small numbers.

Question 2.
The symbol _________ means is less than.

Answer:
The symbol < means less than.

Explanation:
In the above-given question,
given that,
less than a symbol is used to compare numbers.
for example:
1 < 3.
so the symbol < is used for small numbers when compared with large numbers.

Question 3.
A ________ represents one equal part of a whole.

Answer:
The fraction represents one equal part of a whole.

Explanation:
In the above-given question,
given that,
a fraction represents one equal part of a whole.
for example:
3/4.
the whole part is 4.
the 3/4 of the portion is filled.
so the fraction represents one equal part of a whole.

Comparing Whole Numbers

Compare. Write <, >, or =.
Question 4.
48 30

Answer:
48 > 30.

Explanation:
In the above-given question,
given that,
the two numbers are 48 and 30.
30 is less than 48.
48 is greater than 30.
48 > 30.

Question 5.
6 6

Answer:
6 = 6.

Explanation:
In the above-given question,
given that,
the two numbers are 6 and 6.
6 is equal to 6.
6 = 6.

Question 6.
723 732

Answer:
723 < 732.

Explanation:
In the above-given question,
given that,
the two numbers are 723 and 732.
723 is less than 732.
732 is greater than 723.
723 < 732.

Question 7.
152 183

Answer:
152 < 183.

Explanation:
In the above-given question,
given that,
the two numbers are 152 and 183.
152 is less than 183.
183 is greater than 152.
152 < 183.

Question 8.
100 10

Answer:
100 > 10.

Explanation:
In the above-given question,
given that,
the two numbers are 100 and 10.
100 is greater than 10.
10 is less than 100.
100 > 10.

Question 9.
189 99

Answer:
189 > 99.

Explanation:
In the above-given question,
given that,
the two numbers are 189 and 99.
189 is greater than 99.
99 is less than 189.
189 > 99.

Question 10.
456 456

Answer:
456 = 456.

Explanation:
In the above-given question,
given that,
the two numbers are 456 and 456.
456 is equal to 456.
456 = 456.

Question 11.
123 223

Answer:
123 < 223.

Explanation:
In the above-given question,
given that,
the two numbers are 123 and 223.
123 is less than 223.
223 is greater than 123.
123 < 223.

Question 12.
421 399

Answer:
421 > 399.

Explanation:
In the above-given question,
given that,
the two numbers are 421 and 399.
421 is greater than 399.
399 is less than 421.
421 > 399.

Question 13.
158 185

Answer:
158 < 185.

Explanation:
In the above-given question,
given that,
the two numbers are 158 and 185.
158 is less than 185.
185 is greater than 158.
158 < 185.

Question 14.
117 117

Answer:
117 = 117.

Explanation:
In the above-given question,
given that,
the two numbers are 117 and 117.
117 is equal to 117.
117 = 117.

Question 15.
900 893

Answer:
900 > 893.

Explanation:
In the above-given question,
given that,
the two numbers are 900 and 893.
900 is greater than 893.
893 is less than 900.
900 > 893.

Identifying Fractions

For each shape, write the fraction that is shaded.
Question 16.

Answer:
The fraction is 4/8.

Explanation:
In the above-given question,
given that,
the figure contains 8 boxes.
4 boxes are filled.
4/8 portion of the boxes are filled.
4/8 = 1/2.
so half portion of the boxes is filled.

Question 17.

Answer:
The fraction is 1/6.

Explanation:
In the above-given question,
given that,
there are 6 boxes in the figure.
1 box is filled.
so 1/6 portion is filled.

Question 18.

Answer:
The fraction is 2/4.

Explanation:
In the above-given question,
given that,
the figure contains 4 boxes.
2 boxes are filled.
2/4 portion of the boxes are filled.
2/4 = 1/2.
so half portion of the boxes is filled.

Division

Divide.
Question 19.
30 ÷ 5

Answer:
The answer is 6.

Explanation:
In the above-given question,
given that,
the two numbers are 30 and 5.
5 x 6 = 30.
30 / 5 = 6.

Question 20.
72 ÷ 8

Answer:
72 / 8 = 9.

Explanation:
In the above-given question,
given that,
the two numbers are 72 and 8.
8 x 9 = 72.
72 / 8 = 9.

Question 21.
28 ÷ 4

Answer:
28 / 4 = 7.

Explanation:
In the above-given question,
given that,
the two numbers are 28 and 4.
4 x 7 = 28.
28 / 4 = 7.

Question 22.
48 ÷ 6

Answer:
48 / 6 = 8.

Explanation:
In the above-given question,
given that,
the two numbers are 48 and 6.
6 x 8 = 48.
48 / 6 = 8.

Question 23.
81 ÷ 9

Answer:
81 / 9 = 9.

Explanation:
In the above-given question,
given that,
the two numbers are 81 and 9.
9 x 9 = 81.
81 / 9 = 9.

Question 24.
45 ÷ 5

Answer:
45 / 5 = 9.

Explanation:
In the above-given question,
given that,
the two numbers are 45 and 5.
5 x 9 = 45.
45 / 5 = 9.

Question 25.
32 ÷ 8

Answer:
32 / 8 = 4.

Explanation:
In the above-given question,
given that,
the two numbers are 32 and 8.
8 x 4 = 32.
32 / 8 = 4.

Question 26.
42 ÷ 6

Answer:
42 / 6 = 7.

Explanation:
In the above-given question,
given that,
the two numbers are 42 and 6.
6 x 7 = 42.
42 / 6 = 7.

Question 27.
49 ÷ 7

Answer:
49 / 7 = 7.

Explanation:
In the above-given question,
given that,
the two numbers are 49 and 7.
7 x 7 = 49.
49 / 7 = 7.

Question 28.
How can you check if the answer to 40 ÷ 5 is 8?

Answer:
40 / 5 = 8.

Explanation:
In the above-given question,
given that,
the two numbers are 40 and 5.
40 / 5 = 8.
8 x 5 = 40.

Pick a Project

PROJECT 13A
Do you want to ride a horse?
Project: Design a Racetrack for Horses

PROJECT 13B
How deep do you have to dig before you reach water?
Project: Create a Picture of a Well

PROJECT 13C
How many coffee beans does it take to fill up a container?
Project: Plot Fractions on a Number Line

3-ACT MATH PREVIEW

Math Modeling
What’s the Beef?

Lesson 13.1 Equivalent Fractions: Use Models

Solve & Share
Gregor threw a softball of the length of the yard in front of his house. Find as many fractions as you can that name the same part of the length of the yard that Gregor threw the ball. Explain how you decided
I can … find equivalent fractions that name the same part of a whole.

Answer:
1/9, 2/9, 3/9, 4/9.

Explanation:
In the above-given question,
given that,
Gregor threw a softball off the length of the yard in front of his house.
Gregor threw the 1st ball at 1 yard.
1/9.
the length of the yard is 9.
Gregor threw the 2nd ball at 2 yards.
2/9.
Gregor threw the 3rd ball at 3 yards.
3/9.
Gregor threw the 4th ball at 4 yards.
4/9.
so the fractions are 1/9, 2/9, 3/9, and 4/9.

Look Back! How can fraction strips help you tell if a fraction with a denominator of 2, 3, or 6 would name the same part of a whole as \(\frac{3}{4}\)?

Answer:
2/4 and 6/4.

Explanation:
In the above-given question,
given that,
the denominators are 2, 3, and 6.
3/4 and 2/4 = 1/2.
6/4 = 3/2.

Essentials Question
How Can Different Fractions Name the Same Part of a Whole?

Visual Learning Bridge
The Chisholm Trail was used to drive cattle to market. Ross’s herd has walked \(\frac{1}{2}\) the distance to market. What is another way to name \(\frac{1}{2}\)?

\(\frac{1}{2}\) = \(\frac{}{}\) You can use fraction strips.

The fractions \(\frac{1}{2}\) and \(\frac{2}{4}\) represent the same part of the whole.
Two \(\frac{1}{4}\) strips are equal to \(\frac{1}{2}\), so \(\frac{1}{2}\) = \(\frac{2}{4}\).
Another name for \(\frac{1}{2}\) is \(\frac{2}{4}\).

You can find other equivalent fractions. Think about fractions that name the same part of the whole.

Four \(\frac{1}{8}\) strips are equal to \(\frac{1}{2}\), so \(\frac{1}{2}\) = \(\frac{4}{8}\).
Another name for \(\frac{1}{2}\) is \(\frac{4}{8}\)

Convince Me! Look for Relationships In the examples above, what pattern do you see in the fractions that are equivalent to \(\frac{1}{2}\)? What is another name for \(\frac{1}{2}\) that is not shown above?

Answer:
The other name is 4/8.

Explanation:
In the above-given question,
given that,
Four \(\frac{1}{8}\) strips are equal to \(\frac{1}{2}\).
\(\frac{1}{2}\) = \(\frac{4}{8}\).
\(\frac{1}{2}\) is \(\frac{4}{8}\).
so the other name is 4/8.

Another Example!
You can find an equivalent fraction for \(\frac{4}{6}\) using an area model.

Both area models have the same-sized whole. One is divided into sixths. The other shows thirds. The shaded parts show the same part of a whole. Because \(\frac{4}{6}\) = \(\frac{2}{3}\), another name for \(\frac{4}{6}\) is \(\frac{2}{3}\).

Guided Practice

Do You Understand?
Question 1.
Divide the second area model into sixths. Shade it to show a fraction equivalent to \(\frac{1}{3}\):

Answer:
1/3 = 2/6.

Explanation:
In the above-given question,
given that,
divide the second area model into sixths.
\(\frac{1}{3}\) = \(\frac{2}{6}\).
\(\frac{1}{3}\) is \(\frac{2}{6}\).
2/6 = 1/3.

Do You Know How?
Question 2.
Use the fraction strips to help find an equivalent fraction.

Answer:
1/4 = 4/16.

Explanation:
In the above-given question,
given that,
\(\frac{1}{4}\) = \(\frac{4}{16}\).
\(\frac{4}{16}\) is \(\frac{1}{4}\).
1/4 = 4/16.

Independent Practice

Question 3.
Use the fraction strips to help find an equivalent fraction.

Answer:
1/2 = 4/8.

Explanation:
In the above-given question,
given that,
1/4 + 1/4 = 1/2.
1/2 + 1/2 = 1.
4/8 = 1/2.

Question 4.
Divide the second area model into eighths. Shade it to show a fraction equivalent to \(\frac{1}{2}\).

Answer:
1/2 = 4/8.

Explanation:
In the above-given question,
given that,
divide the second area model into eights.
\(\frac{1}{2}\) = \(\frac{4}{8}\).
\(\frac{1}{2}\) is \(\frac{4}{8}\).
1/2 = 4/8.

In 5-8, find each equivalent fraction. Use fraction strips or draw area models to help.
Question 5.
\(\frac{3}{4}\) = \(\frac{}{8}\)

Answer:
\(\frac{3}{4}\) = \(\frac{6}{8}\).

Explanation:
In the above-given question,
given that,
divide the 1st area model into fourths.
divide the second area model into eights.
3/4 = 6/8.
6/8 = 3/4.

Question 6.
\(\frac{6}{6}\) = \(\frac{}{8}\)

Answer:
\(\frac{6}{6}\) = \(\frac{1}{8}\).

Explanation:
In the above-given question,
given that,
divide the 1st area model into sixths.
divide the second area model into eights.
6/6 = 1.
1/8 = 6/6.

Question 7.
\(\frac{2}{6}\) = \(\frac{}{3}\)

Answer:
\(\frac{2}{6}\) = \(\frac{1}{3}\).

Explanation:
In the above-given question,
given that,
divide the 1st area model into sixths.
divide the second area model into thirds.
2/6 = 1/3.
1/3 = 2/6.

Question 8.
\(\frac{4}{8}\) = \(\frac{}{2}\)

Answer:
\(\frac{4}{8}\) = \(\frac{1}{2}\).

Explanation:
In the above-given question,
given that,
divide the 1st area model into eigths.
divide the second area model into halfs.
4/8 = 1/2.
1/2 = 4/8.

Problem Solving

In 9 and 10, use the fraction strips at the right.

Question 9.
Marcy used fraction strips to show equivalent fractions. Complete the equation.
\(\frac{}{4}\) = ________

Answer:
\(\frac{1}{4}\) = \(\frac{2}{8}\).

Explanation:
In the above-given question,
given that,
divide the 1st area model into fourths.
divide the second area model into eights.
1/4 = 2/8.
2/8 = 1/4.

Question 10.
Rita says the fraction strips show fractions that are equivalent to \(\frac{1}{2}\). Explain what you could do to the diagram to see if she is correct.

Answer:
\(\frac{2}{4}\) = \(\frac{1}{2}\).

Explanation:
In the above-given question,
given that,
divide the 1st area model into fourths.
divide the second area model into halves.
2/4 = 1/2.
1/2 = 2/4.

Question 11.
Reasoning A band learns 4 to 6 new songs every month. What is a good estimate for the number of songs the band will learn in 8 months? Explain.

Answer:
The number of songs the band will learn in 8 months = 80 songs.

Explanation:
In the above-given question,
given that,
A band learns 4 to 6 new songs every month.
4 + 6 = 10.
10 x 8 = 80.
so the number of songs the band will learn in 8 months = 80 songs.

Question 12.
Three-eighths of a playground is covered by grass. What fraction of the playground is NOT covered by grass?

Answer:
The fraction of the playground is not covered by grass = 5/8.

Explanation:
In the above-given question,
given that,
three-eights of a playground is covered by grass.
8 – 3 = 5.
so the fraction of the playground is not covered by grass = 5/8.

Question 13.
Higher Order Thinking Aiden folded 2 strips of paper into eighths. He shaded a fraction equal to \(\frac{1}{4}\) on the first strip and a fraction equal to \(\frac{3}{4}\) on the second strip. Use eighths to show the fractions Aiden shaded on the pictures to the right. Which fraction of each strip did he shade?

Answer:
The fraction he shaded = 6/8.

Explanation:
In the above-given question,
given that,
Aiden folded 2 strips of paper into eighths.
2/8.
He shaded a fraction equal to \(\frac{1}{4}\) on the first strip.
1/4.
fraction equal to \(\frac{3}{4}\) on the second strip.
3/4.
he shaded the 6/8 portion of each strip.
6/8 = 3/4.

Assessment Practice

Question 14.
Which fractions are equivalent? Select all that apply.

Answer:
1/4 and 2/8.
3/4 and 6/8.
2/4 and 4/8.

Explanation:
In the above-given question,
given that,
there are three equivalent fractions.
the fractions are:
2/8 = 1/4.
6/8 = 3/4.
4/8 = 2/4.

Lesson 13.2 Equivalent Fractions: Use the Number Line

Solve & Share
The top number line shows a point at \(\frac{1}{4}\). Write the fraction for each of the points labeled A, B, C, D, E, and F. Which of these fractions show the same distance from 0 as \(\frac{1}{4}\)?
I can … use number lines to represent equivalent fractions.

Look Back! How can number lines show that two fractions are equivalent?

Answer:
The fractions are 1/2, 2/4, 3/4, 2/8, 4/8, and 4/6.

Explanation:
In the above-given question,
given that,
The number line A shows the fraction 1/2.
B shows the fraction 2/4.
C shows the fraction 3/4.
D shows the fraction 2/8.
E shows the fraction 4/8.
F shows the fraction 4/6.
2/4 = 1/2.
2/8 = 1/4.
4/8 = 1/2.
4/6 = 2/3.

Essential Question
How Can You Use Number Lines to Find Equivalent Fractions?

Visual Learning Bridge
The Circle W Ranch 1-mile trail has water for cattle at each \(\frac{1}{4}\) mile mark. The Big T Ranch 1-mile trail has water for cattle at the \(\frac{1}{2}\)-mile mark. What fractions name the points on the trails where there is water for cattle at the same distance from the start of each trail?

You can use number lines to find the fractions.

The fractions \(\frac{2}{4}\) and \(\frac{1}{2}\) name the same points on the trails where there is water for cattle. They are at the same distance from the start of the trails.

Convince Me! Model with Math lan paints \(\frac{6}{8}\) of a fence. Anna paints \(\frac{3}{4}\) of another fence of equal size and length. How can you show that lan and Anna have painted the same amount of each fence?

Answer:
Yes, both Anna and Lan have painted the same amount of each fence.

Explanation:
In the above-given question,
given that,
Lan paints \(\frac{6}{8}\) of a fence.
Anna paints \(\frac{3}{4}\) of another fence of equal size and length.
3/4 = 6/8.
2 x 3 = 6.
4 x 2 = 8.
so both Anna and Lan have painted the same amount of each fence.

Guided Practice

Do You Understand?
Question 1.
Complete the number line to show that \(\frac{2}{6}\) and \(\frac{1}{3}\) are equivalent fractions.

Answer:
2/6 = 1/3.

Explanation:
In the above-given question,
given that,
the fractions on the number line are:
1/6, 2/6, 3/6, 4/6, and 5/6.
2/6 = 1/3.
4/6 = 2/3.

Question 2.
Sheila compares \(\frac{4}{6}\) and \(\frac{4}{8}\) she discovers that the fractions are NOT equivalent. How does Sheila know?

Answer:
Yes, both fractions are not equivalent.

Explanation:
In the above-given question,
given that,
Sheila compares \(\frac{4}{6}\) and \(\frac{4}{8}\).
4/6 = 2/3.
2 x 2 = 4.
2 x 3 = 6.
4/8 = 2/4.
2 x 2 = 4.
4 x 2 = 8.
so 4/6 is not equal to 4/8.

Do You Know How?
In 3 and 4, find the missing equivalent fractions on the number line. Then write the equivalent fractions below.
Question 3.

Answer:
The missing equivalent fractions on the number line is 3/6.

Explanation:
In the above-given question,
given that,
the fractions on the number line are:
1/6, 2/6, 3/6, 4/6, 5/6, and 1.
3/6 = 1/2.
so the 3/6 and 1/2 are the equivalent fractions.

Question 4.

Answer:
6/8 = 3/4.

Explanation:
In the above-given question,
given that,
the fractions on the number line are:
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, and 7/8.
2/8 = 1/4.
4/8 = 1/2.
6/8 = 3/4.
2 x 3 = 6.
2 x 4 = 8.

Independent Practice

In 5-8, find the missing equivalent fractions on the number line. Then write the equivalent fractions below.
Question 5.

Answer:
The missing equivalent fractions on the number line are 2/8.

Explanation:
In the above-given question,
given that,
the fractions on the number line are 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, and 7/8.
2/8 = 1/4.
1 x 2 = 2.
4 x 2 = 8.
so the missing equivalent fraction is 2/8 = 1/4.

Question 6.

Answer:
The missing equivalent fractions on the number line are 4/6.

Explanation:
In the above-given question,
given that,
the fractions on the number line are 1/6, 2/6, 3/8, and 5/6.
2/6 = 1/3.
1 x 2 = 2.
3 x 2 = 6.
4/6 = 2/3.
2 x 2 = 4.
3 x 2 = 6.
so the missing equivalent fraction is 4/6 = 2/3.

Question 7.

Answer:
The missing equivalent fractions on the number line are 4/8.

Explanation:
In the above-given question,
given that,
the fractions on the number line are 1/8, 2/8, 3/8, 5/8, 6/8, and 7/8.
2/8 = 1/4.
1 x 2 = 2.
4 x 2 = 8.
4/8 = 2/4.
2 x 2 = 4.
4 x 2 = 8.
so the missing equivalent fraction is 4/8 = 2/4.

Question 8.

Answer:
The missing equivalent fractions on the number line are 6/6.

Explanation:
In the above-given question,
given that,
the fractions on the number line are 1/6, 2/6, 3/6, 4/6, and 5/6.
2/6 = 1/3.
1 x 2 = 2.
3 x 2 = 6.
4/6 = 2/3.
2 x 2 = 4.
3 x 2 = 6.
6/6 = 1.
1 x 6 = 6.
so the missing equivalent fraction is 6/6 = 1.

Problem Solving

Question 9.
Number Sense Bradley had 40 slices of pizza to share. How many pizzas did he have? Explain how you solved the problem.

Answer:
The number of pizzas did he have = 5.

Explanation:
In the above-given question,
given that,
Bradley had 40 slices of pizza to share.
each pizza was cut into 8 slices.
40/8 = 5.
5 x 8 = 40.
so the number of pizzas did he have = 5.

Question 10.
Ms. Owen has 15 magazines to share among 5 students for an art project. How many magazines will each student get? Use the bar diagram to write an equation that helps solve the problem.

Answer:
The number of magazines will each student get = 3.

Explanation:
In the above-given question,
given that,
Ms. Owen has 15 magazines to share among 5 students for an art project.
15 / 5 = 3.
3 + 3 + 3 + 3 + 3 = 15.
3 x 5 = 15.
so the number of magazines will each student get = 3.

Question 11.
Yonita has 28 different apps on her computer. Casey has 14 music apps and 20 game apps on his computer. How many more apps does Casey have than Yonita? Explain.

Answer:
The number of apps does Casey has more than Yonita = 6.

Explanation:
In the above-given question,
given that,
Yonita has 28 different apps on her computer.
Casey has 14 music apps and 20 game apps on his computer.
14 + 20 = 34.
34 – 28 = 6.
so the number of apps does Casey has more than Yonita = 6.

Question 12.
Construct Arguments How can you tell, just by looking at the fractions, that \(\frac{2}{4}\) and \(\frac{3}{4}\) are NOT equivalent? Construct an argument to explain.

Answer:
Yes, 2/4 and 3/4 are not equivalent fractions.

Explanation:
In the above-given question,
given that,
the fraction 2/4 = 1/2.
1 x 2 = 2.
2 x 2 = 4.
the fraction 3/4 is not an equivalent fraction.
so both the fractions are not equal.

Question 13.
Higher Order Thinking Fiona and Gabe each had the same length of rope. Fiona used \(\frac{2}{3}\) of her rope. Using sixths, what fraction of the length of rope will Gabe need to use to match the amount Fiona used? Draw a number line as part of your answer.

Answer:
The fraction of the rope Gabe used is 4/6.

Explanation:
In the above-given question,
given that,
Fiona and Gabe each had the same length of rope.
Fiona used \(\frac{2}{3}\) of her rope.
4/6 = 2/3.
2 x 2 = 4.
3 x 2 = 6.
so the fraction of rope Gabe used is 4/6.

Assessment Practice

Question 14.
Use the number line to find which fraction is equivalent to \(\frac{3}{6}\).

Answer:
Option A is the correct answer.

Explanation:
In the above-given question,
given that,
3/6 = 1/2.
1 x 3 = 3.
3 x 2 = 6.
1/2 = 3/6.
so option A is correct.

Question 15.
Use the number line to find which fraction is equivalent to \(\frac{4}{8}\).

Answer:
Option C is the correct answer.

Explanation:
In the above-given question,
given that,
4/8 = 2/4.
2 x 2 = 4.
4 x 2 = 8.
2/4 = 4/8.
so option C is correct.

Lesson 13.3 Use Models to Compare Fractions: Same Denominator

Solve & Share
Maria and Evan are both jogging a mile. Maria has jogged mile, and Evan has jogged mile. Show how far each has jogged. Use any model you choose. Who jogged farther? How do you know?
I can … compare fractions that refer to the same-sized whole and have the same denominator by comparing their numerators.

Look Back! Suppose Evan had jogged \(\frac{5}{8}\) mile instead of \(\frac{3}{8}\) mile. Now, who has jogged farther? Explain.

Answer:
Evan jogged farther than Maria.

Explanation:
In the above-given question,
given that,
Evan had jogged \(\frac{5}{8}\) mile instead of \(\frac{3}{8}\).
5/8 – 3/8 = 2/8.
so I think maria jogged very little when compared to Evan.
so Evan jogged farther than Maria.

Essential Question
How Can You Compare Fractions with the Same Denominator?

Visual Learning Bridge
Two banners with positive messages are the same size. One banner is \(\frac{4}{6}\) yellow, and the other banner is \(\frac{2}{6}\) yellow. Which is greater, \(\frac{4}{6}\) or \(\frac{2}{6}\)?

\(\frac{4}{6}\) is 4 of the unit fraction is \(\frac{1}{6}\).
\(\frac{2}{6}\) of the unit fraction \(\frac{1}{6}\).
So, \(\frac{4}{6}\) is greater than \(\frac{2}{6}\).

Record the comparison using symbols or words.
\(\frac{4}{6}\) > \(\frac{2}{6}\)
Four sixths is greater than two sixths.
If two fractions have the same denominator, the fraction with the greater numerator is the greater fraction.

Convince Me! Reasoning Write a number for each numerator to make each comparison true. Use a picture and words to explain how you decided.

Guided Practice

Do You Understand?
Question 1.
Explain how you can use fraction strips to show whether \(\frac{5}{6}\) or \(\frac{3}{6}\) of the same whole is greater.

Answer:
5/6 > 3/6.

Explanation:
In the above-given question,
given that,
the fractions are 5/6 and 3/6.
so 5/6 is greater than 3/6.
3/6 < 5/6.
5/6 > 3/6.

Question 2.
Which is greater, \(\frac{3}{4}\) or \(\frac{2}{4}\)? Draw \(\frac{1}{4}\)-strips to complete the diagram and answer the question.

Answer:
3/4 is greater than 2/4.

Explanation:
In the above-given question,
given that,
3/4 is greater than 2/4.
the whole is 4.
but one time it is divided into 3 parts.
it is divided into 2 parts.
so 3/4 > 2/4.

Do You Know How?
In 3 and 4, compare. Write <, >, or =. Use the fraction strips to help.
Question 3.

Answer:
2/8 > 1/8.

Explanation:
In the above-given question,
given that,
the fractions are 2/8 and 1/8.
1/8 + 1/8 = 2/8.
2/8 is greater than 1/8.
so 2/8 > 1/8.

Question 4.

Answer:
3/6 < 5/6.

Explanation:
In the above-given question,
given that,
the fractions are 3/6 and 5/6.
5/6 is divided into 5 parts.
1/6 + 1/6 + 1/6 = 3/6.
so 3/6 < 5/6.

Independent Practice

Leveled Practice In 5-14, compare. Write <, >, or =. Use or draw fraction strips to help. The fractions refer to the same whole.
Question 5.

Answer:
3/8 < 4/8.

Explanation:
In the above-given question,
given that,
the two fractions are 3/8 and 4/8.
1/8 + 1/8 + 1/8 = 3/8.
1/8 + 1/8 + 1/8 + 1/8 = 4/8.
so 3/8 < 4/8.

Question 6.

Answer:
3/4 = 3/4.

Explanation:
In the above-given question,
given that,
the two fractions are 3/4 and 3/4.
1/4 + 1/4 + 1/4 = 3/4.
3/4 = 3/4.
so both of them are equal.

Question 7.
\(\frac{6}{8}\) \(\frac{3}{8}\)

Answer:
6/8 > 3/8.

Explanation:
In the above-given question,
given that,
the two fractions are 6/8 and 3/8.
6/8 = 3/4.
2 x 3 = 6.
4 x 2 = 8.
1/8 + 1/8 + 1/8 = 3/8.
6/8 > 3/8.

Question 8.
\(\frac{5}{8}\) \(\frac{7}{8}\)

Answer:
5/8 < 7/8.

Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 7/8.
1/8 + 1/8 + 1/8  + 1/8 + 1/8 = 5/8.
1/8 x 7 = 7/8.
5/8 < 7/8.

Question 9.
\(\frac{1}{2}\) \(\frac{1}{2}\)

Answer:
1/2 = 1/2.

Explanation:
In the above-given question,
given that,
the two fractions are 1/2 and 1/2.
1/2 x 1 = 1/2.
1/2 x 1 =1/2.
so both of them are equal.

Question 10.
\(\frac{1}{3}\) \(\frac{2}{3}\)
Answer:

1/3 < 2/3.

Explanation:
In the above-given question,
given that,
the two fractions are 1/3 and 2/3.
1/3 x 1 = 1/3.
1/3 + 1/3 = 2/3.
1/3 < 2/3.

Question 11.
\(\frac{6}{6}\) \(\frac{3}{6}\)
Answer:

6/6 > 3/6.

Explanation:
In the above-given question,
given that,
the two fractions are 6/6 and 3/6.
1/6 + 1/6 + 1/6  + 1/6 + 1/6 + 1/6 = 6/6.
1/6 + 1/6 + 1/6 = 3/6.
6/6 > 3/6.

Question 12.
\(\frac{2}{8}\) \(\frac{3}{8}\)
Answer:

2/8 < 3/8.

Explanation:
In the above-given question,
given that,
the two fractions are 2/8 and 3/8.
1/8 + 1/8 = 2/8.
1/8 + 1/8 +1/8 = 3/8.
2/8 < 3/8.

Question 13.
\(\frac{3}{3}\) \(\frac{1}{3}\)
Answer:

3/3 > 1/3.

Explanation:
In the above-given question,
given that,
the two fractions are 3/3 and 1/3.
1/3 + 1/3 + 1/3  = 3/3.
1/3 x 1 = 1/3.
3/3 > 1/3.

Question 14.
\(\frac{1}{4}\) \(\frac{3}{4}\)
Answer:

1/4 < 3/4.

Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 3/4.
1/4 x 1 = 1/4.
1/4 +1/4 + 1/4  = 3/4.
1/4 < 3/4.

Problem Solving

In 15 and 16, use the pictures of the strips that have been partly shaded.

Question 15.
Compare. Write <, >, or =
The green strips show \(\frac{1}{6}\) \(\frac{2}{6}\)

Answer:
1/6 < 2/6.

Explanation:
In the above-given question,
given that,
the two fractions are 1/6 and 2/6.
1/6 x 1 = 1/6.
1/6 +1/6 = 2/6.
1/6 < 2/6.

Question 16.
Do the yellow strips show \(\frac{2}{4}\) > \(\frac{3}{4}\)? Explain.

Answer:
No, 2/4 < 3/4.

Explanation:
In the above-given question,
given that,
the two fractions are 2/4 and 3/4.
1/4 +1/4 = 2/4.
1/4 +1/4 + 1/4  = 3/4.
2/4 < 3/4.

Question 17.
Izzy and Henry have two different pizzas. Izzy ate \(\frac{3}{8}\) of her pizza. Henry ate \(\frac{3}{8}\) of his pizza. Izzy ate more pizza than Henry. How is this possible? Explain.

Answer:
No, it was not possible.

Explanation:
In the above-given question,
given that,
Izzy and Henry have two different pizzas.
Izzy ate \(\frac{3}{8}\) of her pizza.
Henry ate \(\frac{3}{8}\) of his pizza.
3/8 = 1/8 + 1/8 + 1/8.
3/8 x 1 = 3/8.
3/8 = 3/8.
so both of them ate the equal.

Question 18.
Generalize Two fractions are equal. They also have the same denominator. What must be true of the numerators of the fractions? Explain.

Answer:
Yes, the two fractions are equal.

Explanation:
In the above-given question,
given that,
Izzy and Henry have two different pizzas.
Izzy ate \(\frac{3}{8}\) of her pizza.
Henry ate \(\frac{3}{8}\) of his pizza.
3/8 = 1/8 + 1/8 + 1/8.
3/8 x 1 = 3/8.
3/8 = 3/8.
so both of them ate the equal.

Question 19.
Number Sense Mr. Domini had $814 in the bank on Wednesday. On Thursday, he withdrew $250, and on Friday, he withdrew $185. How much money did he have in the bank then?

Answer:
The money he has in the bank = $379.

Explanation:
In the above-given question,
given that,
Mr. Domini had $814 in the bank on Wednesday.
On Thursday, he withdrew $250.
On Friday, he withdrew $185.
250 + 185 = 435.
814 – 435 = 379.
so Mr. Domini had $814 in the bank on Wednesday.

Question 20.
Higher Order Thinking Tom’s parents let him choose whether to play his favorite board game for \(\frac{7}{8}\) hour or for \(\frac{8}{8}\) hour. Explain which amount of time you think Tom should choose and why.

Answer:
Tom should choose 8/8 hour.

Explanation:
In the above-given question,
given that,
Tom’s parents let him choose whether to play his favorite board game for 7/8 hours.
8/8 hour = 1.
7/8 x 1 = 7/8.
1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 = 8/8.
1 = 8/8.
so i think Tom should choose 1 hour.

Assessment Practice

Question 21.
Paul and Enrique each have equal-sized pizzas cut into 8 equal slices. Paul eats 3 slices. Enrique eats 2 slices. Select numbers and symbols from the box to write a comparison for the fraction of pizza Paul and Enrique have each eaten.

Answer:
Paul eats more slices than Enriques.

Explanation:
In the above-given question,
given that,
Paul and Enrique each have equal-sized pizzas cut into 8 equal slices.
Paul eats 3 slices.
Enrique eats 2 slices.
1/8 + 1/8 + 1/8 = 3/8.
1/8 + 1/8 = 2/8.
so paul eats more slices than Enriques.

Lesson 13.4 Use Models to Compare Fractions: Same Numerator

Solve & Share
Krista, Jamal, and Rafe each had 1 serving of vegetables. Krista ate \(\frac{2}{6}\), Jamal ate \(\frac{2}{3}\), and Rafe ate \(\frac{2}{8}\) of his serving. Arrange the fractions in order from least to greatest to show who ate the least and who ate the greatest amount of vegetables.
I can … compare fractions that refer to the same whole and have the same numerator by comparing their denominators.

Answer:
Rafe, Krista, and Jamal.

Explanation:
In the above-given question,
given that,
Krista, Jamal, and Rafe each had 1 serving of vegetables.
Krista ate \(\frac{2}{6}\), Jamal ate \(\frac{2}{3}\).
Rafe ate \(\frac{2}{8}\) of his serving.
2/6 = 1/6 + 1/6.
2/3 = 1/3 + 1/3.
2/8 = 1/8 + 1/8.
so Rafe ate least when compared to Krista and Jamal.
so the order from least to highest.
Rafe, Krista, and Jamal.

Look Back! Tamika ate \(\frac{2}{2}\) of a serving of vegetables. In order from least to greatest, arrange the fractions of a serving Krista, Jamal, Rafe, and Tamika each ate. Explain your reasoning.

Answer:
Rafe, Krista, Jamal, and Tamika.

Explanation:
In the above-given question,
given that,
Tamika ate \(\frac{2}{2}\) of a serving of vegetables.
2/2 = 1.
so Tamika at more than Rafe, Krista, and Jamal.

Essential Question
How Can You Compare Fractions with the Same Numerator?

Visual Learning Bridge
Claire bought 2 scarves as souvenirs from her visit to a Florida university. The scarves are the same size. One scarf is \(\frac{5}{6}\) orange, and the other scarf is \(\frac{5}{8}\) orange. Which is greater, \(\frac{5}{6}\) or \(\frac{5}{8}\)?

What You Show
Use fraction strips to reason about the size of \(\frac{5}{6}\) a compared to the size of \(\frac{5}{8}\).

There are 5 sixths. There are 5 eighths. The parts are different sizes.
The greater the denominator, the smaller each part will be.

What You Write
Describe the comparison using symbols or words.
\(\frac{5}{6}\) > \(\frac{5}{8}\)
Five sixths is greater than five eighths.
If two fractions have the same numerator, the fraction with the lesser denominator is the greater fraction.

Convince Me! Critique Reasoning Julia says \(\frac{1}{8}\) is greater than \(\frac{1}{4}\) because 8 is greater than 4. Critique Julia’s reasoning. Is she correct? Explain.

Answer:
Yes, Julia’s reasoning was correct.

Explanation:
In the above-given question,
given that,
Julia says \(\frac{1}{8}\) is greater than \(\frac{1}{4}\).
1/8 = 1 x 1/8.
1/4 = 1 x 1/4.
so Julia’s reasoning was correct.

Guided Practice

Do You Understand?
Question 1.
How can fraction strips help you reason about whether \(\frac{4}{6}\) or \(\frac{4}{8}\) of the same whole is greater?

Answer:
4/6 > 4/8.

Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 4/8.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
4/6 x 1 = 4/6.
4/8 x 1 = 4/8.
so 4/6 > 4/8.

Question 2.
Which is greater, \(\frac{1}{4}\) or \(\frac{1}{6}\)? Draw fraction strips to complete the diagram and answer the question.

Answer:
1/4 > 1/6.

Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 1/6.
1/4 x 1 = 1/4.
1/6 x 1 = 1/6.
1 is divided into 1/4 and 1/6.
1/4 > 1/6.

Do You Know How?
In 3 and 4, compare. Write <, >, or =. Use fraction strips to help.
Question 3.

Answer:
3/6 < 3/3.

Explanation:
In the above-given question,
given that,
the two fractions are 3/6 and 3/3.
3/6 = 1/6 + 1/6 + 1/6.
3/3 = 1.
so 3/6 < 3/3.

Question 4.

Answer:
4/6 < 4/8.

Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 4/8.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
so 4/6 = 1 x 4/6.
so 4/6 < 4/8.

Independent Practice

Leveled Practice In 5-14, compare. Write <, >, or =. Use or draw fraction strips to help. The fractions refer to the same whole.
Question 5.

Answer:
2/4 < 2/3.

Explanation:
In the above-given question,
given that,
the two fractions are 2/4 and 2/3.
2/4 = 1/4 + 1/4.
2/3 = 1/3 + 1/3.
so 2/4 < 2/3.

Question 6.

Answer:
4/4 > 4/6.

Explanation:
In the above-given question,
given that,
the two fractions are 4/4 and 4/6.
4/4 = 1.
1/6 + 1/6 + 1/6 + 1/6 = 4/6.
so 4/4 > 4/6.

Question 7.
\(\frac{2}{3}\) \(\frac{2}{2}\)

Answer:
2/3 > 2/2.

Explanation:
In the above-given question,
given that,
the two fractions are 2/3 and 2/2.
2/2 = 1.
1/3 + 1/3 = 2/3.
so 2/3 > 2/2.

Question 8.
\(\frac{4}{8}\) \(\frac{4}{8}\)

Answer:
4/8 = 4/8.

Explanation:
In the above-given question,
given that,
the two fractions are 4/8 and 4/8.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
4/8 x 1 = 4/8.
so 4/8 = 4/8.

Question 9.
\(\frac{5}{6}\) \(\frac{5}{8}\)

Answer:
5/6 > 5/8.

Explanation:
In the above-given question,
given that,
the two fractions are 5/6 and 5/8.
5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
so 5/6 > 5/8.

Question 10.
\(\frac{1}{4}\) \(\frac{1}{3}\)

Answer:
1/4 > 1/3.

Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 1/3.
1/4 = 1/4 x 1.
1/3 x 1 = 2/3.
so 1/4 > 1/3.

Question 11.
\(\frac{1}{3}\) \(\frac{1}{6}\)

Answer:
1/3 > 1/6.

Explanation:
In the above-given question,
given that,
the two fractions are 1/3 and 1/2.
1/3 = 1 x 1/3.
1/2 x 1 = 1/3.
so 1/3 > 1/6.

Question 12.
\(\frac{4}{6}\) \(\frac{4}{6}\)

Answer:
4/6 = 4/6.

Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 4/6.
4/6 = 1 x 4/6.
1/6 + 1/6 + 1/6 + 1/6 = 4/6.
so 4/6 = 4/6.

Question 13.
\(\frac{1}{8}\) \(\frac{1}{2}\)

Answer:
1/8 < 1/2.

Explanation:
In the above-given question,
given that,
the two fractions are 1/8 and 1/2.
1/8 = 1 x 1/8.
1/2 x 1 = 1/2.
so 1/8 < 1/2.

Question 14.
\(\frac{2}{6}\) \(\frac{2}{3}\)

Answer:
2/6 < 2/3.

Explanation:
In the above-given question,
given that,
the two fractions are 2/6 and 2/3.
2/6 = 1/6 + 1/6.
1/3 + 1/3 = 2/3.
so 2/6 < 2/3.

Problem Solving

Question 15.
James uses blue and white tiles to make the two designs shown here. James says that the total blue area in the top design is the same as the total blue area in the bottom design. Is he correct? Explain.

Answer:
Yes, James was correct.

Explanation:
In the above-given question,
given that,
James uses blue and white tiles to make the two designs.
James says that the total blue area in the top design is the same as the total blue area in the bottom design.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
1/8 x 4 = 4/8.
so James was correct.

Question 16.
Amy sold 8 large quilts and 1 baby quilt. How much money did she make from selling quilts?

Answer:
The money did she make from selling quilts = $520.

Explanation:
In the above-given question,
given that,
Amy sold 8 large quilts and 1 baby quilt.
60 x 8 = 480.
40 x 1 = 40.
480 + 40 = 520.
so the money did she make from selling quilts = $520.

Question 17.
Be Precise Write two comparison statements about the fractions shown below.

Answer:
3/3 > 3/4.

Explanation:
In the above-given question,
given that,
the two fractions are 3/3 and 3/4.
3/3 = 1/3 + 1/3 + 1/3.
3/4 = 1/4 + 1/4 + 1/4.
so 3/3 > 3/4.

Question 18.
Higher Order Thinking John says that when you compare two fractions with the same numerator, you look at the denominators because the fraction with the greater denominator is greater. Is he correct? Explain, and give an example.

Answer:
Yes, he was correct.

Explanation:
In the above-given question,
given that,
John says that when you compare two fractions with the same numerator,
3/3 and 3/4.
3/3 = 1.
3/4 = 1/4 + 1/4 + 1/4.
1 > 1/4.
so he was correct.

Assessment Practice

Question 19.
These fractions refer to the same whole. Which of these comparisons are correct? Select all that apply.

Answer:
2/4 > 2/3, 1/2 > 1/4, 5/6 = 5/6, and 3/4 > 3/6.

Explanation:
In the above-given question,
given that,
the fractions are 2/4 and 2/3.
2/4 = 1/4 + 1/4.
2/3 = 1/3 + 1/3.
the fractions are 1/2 and 1/4.
1/4 x 1 = 1/4.
1/2 x 1 = 1/2.
the fractions are 3/4 and 3/6.
3/4 = 1/4 + 1/4 + 1/4.
3/6 = 1/6 + 1/6 + 1/6.
so the four fractions are correct.

Lesson 13.5 Compare Fractions: Use Benchmarks

Solve & Share
Mr. Evans wrote \(\frac{2}{8}, \frac{4}{8}, \frac{6}{8}, \frac{1}{8}, \frac{3}{8}, \frac{5}{8}\) on and \(\frac{7}{8}\) on the board. Then he circled the fractions that are closer to 0 than to 1. Which fractions did he circle? Which fractions did he not circle? Explain how you decided.
I can … use what I know about the size of benchmark numbers to compare fractions.

Look Back! Eric says that \(\frac{3}{8}\) is closer to 1 than to 0 because \(\frac{3}{8}\) is greater than \(\frac{1}{8}\). Is he correct? Use benchmark numbers to evaluate Eric’s reasoning and justify your answer.

Answer:
Yes, Eric was correct.

Explanation:
In the above-given question,
given that,
Eric says that 3/8 is closer to 1.
3/8 is greater than 1/8.
3/8 = 1/8 + 1/8 + 1/8.
so 3/8 > 1/8.
so Eric was correct.

Essential Question
How Can Benchmark Numbers Be Used to Compare Fractions?

Visual Learning Bridge
Keri wants to buy of a container of roasted peanuts. Alan wants to buy of a container of roasted peanuts. The containers are the same size. Who will buy more peanuts?

Compare each fraction to the benchmark number \(\frac{1}{2}\). Then see how they relate to each other in size.

So, \(\frac{2}{6}\) is less than \(\frac{2}{3}\).
\(\frac{2}{6}\) < \(\frac{2}{3}\)
Alan will buy more peanuts than Keri.

Convince Me! Make Sense and Persevere Candice buys \(\frac{2}{8}\) of a container of roasted peanuts. The container is the same size as those used by Keri and Alan. She says \(\frac{2}{8}\) is between \(\frac{1}{2}\) and 1, so she buys more peanuts than Alan. Is Candice correct? Explain.

Answer:
Candice, she was correct.

Explanation:
In the above-given question,
given that,
Candice buys \(\frac{2}{8}\) of a container of roasted peanuts.
The container is the same size as those used by Keri and Alan.
She says \(\frac{2}{8}\) is between \(\frac{1}{2}\) and 1.
2/8 = 1/8 + 1/8.
1/2 x 1 = 1/2.
so Candice was correct.

Guided Practice

Do You Understand?
Question 1.
Tina used benchmark numbers to decide that \(\frac{3}{8}\) is less than \(\frac{7}{8}\). Do you agree? Explain.

Answer:
Yes, 3/8 is less than 7/8.

Explanation:
In the above-given question,
given that,
Tina used benchmark numbers to decide that 3/8 is less than 7/8.
3/8 = 1/8 + 1/8 + 1/8.
7/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
so 3/8 is less than 7/8.

Question 2.
Write two fractions with a denominator of 6 that are closer to 0 than to 1.

Answer:
The two fractions are 3/6 and 4/6.

Explanation:
In the above-given question,
given that,
the two fractions are 3/6 and 4/6
3/6 = 1/6 + 1/6 + 1/6.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
so 3/6 and 4/6 equal to 0 and 1.

Question 3.
Write two fractions with a denominator of 8 that are closer to 1 than to 0.

Answer:
The two fractions are 2/8 and 7/8.

Explanation:
In the above-given question,
given that,
the two fractions with a denominator of 8 that are closer to 1 than to 0.
2/8 = 1/8 + 1/8.
7/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
so the two fractions are 2/8 and 7/8 is equal to 0 and 1.

Do You Know How?
In 4-6, choose from the fractions \(\frac{1}{8}, \frac{1}{4}, \frac{6}{8}\) and \(\frac{3}{4}\). Use fraction strips to help.
Question 4.
Which fractions are closer to 0 than to 1?

Answer:
The two fractions are 3/4 and 1/4.

Explanation:
In the above-given question,
given that,
the fractions are 1/8, 1/4, 6/8, and 3/4.
3/4 = 1/4 + 1/4 + 1/4.
1/4 x 1 = 1/4
so the two fractions are 3/4 and 1/4.

Question 5.
Which fractions are closer to 1 than to 0?

Answer:
The fractions are 6/8 and 3/4.

Explanation:
In the above-given question,
given that,
the fractions are 1/8, 1/4, 6/8, and 3/4.
6/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
3/4 = 1/4 + 1/4 + 1/4.
so the fractions closer to 1 than to 0 are 6/8 and 3/4.

Question 6.
Use the two fractions with a denominator of 8 to write a true statement: < .

Answer:
1/8 < 6/8.

Explanation:
In the above-given question,
given that,
the fractions are 1/8, 1/4, 6/8, and 3/4.
6/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
3/4 = 1/4 + 1/4 + 1/4.
the two fractions with a denominator of 8.
so 1/8 < 6/8.

Independent Practice

In 7 and 8, choose from the fractions, \(\frac{2}{3}, \frac{7}{8}, \frac{1}{4}\), and \(\frac{2}{6}\).
Question 7.
Which of the fractions are closer to 0 than to 1?

Answer:
The fractions are closer to 0 than to 1 are 2/3 and 1/4.

Explanation:
In the above-given question,
given that,
the fractions are 2/3, 7/8, 1/4, and 2/6.
2/3 = 1/3 + 1/3.
1/4 x 1 = 1/4.
so the fractions are closer to 0 than to 1 are 2/3 and 1/4.

Question 8.
Which of the fractions are closer to 1 than to 0?

Answer:
The fractions are closer to 1 than to 0 are 7/8 and 2/6.

Explanation:
In the above-given question,
given that,
the fractions are 2/3, 7/8, 1/4, and 2/6.
7/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
2/6 = 1/6 + 1/6.
so the fractions are closer to 1 than to 0 are 7/8 and 2/6.

In 9-14, use a strategy to compare. Write <, >, or =.

Question 9.
\(\frac{5}{8}\) \(\frac{7}{8}\)

Answer:
5/8 < 7/8.

Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 7/8.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
7/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
so 5/8 < 7/8.

Question 10.
\(\frac{5}{8}\) \(\frac{2}{8}\)

Answer:
5/8 > 2/8.

Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 2/8.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
2/8 = 1/8 + 1/8.
so 5/8 > 2/8.

Question 11.
\(\frac{3}{4}\) \(\frac{3}{6}\)

Answer:
3/4 > 3/6.

Explanation:
In the above-given question,
given that,
the two fractions are 3/4 and 3/6.
3/4 = 1/4 + 1/4 + 1/4.
3/6 = 1/6 + 1/6 + 1/6.
so 3/4 < 3/6.

Question 12.
\(\frac{4}{6}\) \(\frac{4}{8}\)

Answer:
4/6 < 4/8.

Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 4/8.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
so 4/6 < 4/8.

Question 13.
\(\frac{2}{6}\) \(\frac{2}{4}\)

Answer:
2/6 > 2/4.

Explanation:
In the above-given question,
given that,
the two fractions are 2/6 and 2/4.
2/6 = 1/6 + 1/6.
2/4 = 1/4 + 1/4.
so 2/6 > 2/4.

Question 14.
\(\frac{2}{3}\) \(\frac{1}{3}\)

Answer:
2/3 > 1/3.

Explanation:
In the above-given question,
given that,
the two fractions are 2/3 and 1/3.
2/3 = 1/3 + 1/3.
1/3 = 1/3 x 1.
so 2/3 > 1/3.

Problem Solving

In 15-17, use the table at the right.

Question 15.
Which people have walked closer to 1 mile than to 0 miles?

Answer:
Mr. Nunez and Miss Lee have walked closer to 1 mile than to 0 miles.

Explanation:
In the above-given question,
given that,
there are 5 people in the chart.
they are 1/6, 5/6, 1/3, 4/8, and 4/6.
the people closer to 1 mile than to 0 miles are Mr. Nunez and Miss.
the fractions closer to 1 mile is 5/6 and 4/6.

Question 16.
Which people have walked closer to 0 miles than to 1 mile?

Answer:
Mrs. Avery and Miss Chang have walked closer to 0 miles than to 1 mile.

Explanation:
In the above-given question,
given that,
there are 5 people in the chart.
they are 1/6, 5/6, 1/3, 4/8, and 4/6.
the people closer to 0 miles than to 1 mile are Mrs. Avery and Miss chang.
the fractions closer to 0 miles is 1/6 and 1/3.

Question 17.
Who has walked a fraction of a mile that is closer to neither 0 nor 1? Explain.

Answer:
Mr. O’Leary has walked closer to neither 0 nor 1.

Explanation:
In the above-given question,
given that,
there are 5 people in the chart.
they are 1/6, 5/6, 1/3, 4/8, and 4/6.
the people closer to neither 0 nor 1.
the fractions are 4/8.

Question 18.
Rahul compares two wholes that are the same size. He says that \(\frac{2}{6}\) < \(\frac{2}{3}\) because \(\frac{2}{6}\) is less than \(\frac{1}{2}\), and \(\frac{2}{3}\) is greater than \(\frac{1}{2}\). Is he correct? Explain.

Answer:
Yes, he was correct.

Explanation:
In the above-given question,
given that,
Rahul compares two wholes that are the same size.
He says that \(\frac{2}{6}\) < \(\frac{2}{3}\).
\(\frac{2}{6}\) is less than \(\frac{1}{2}\).
2/6 < 2/3.
2/6 < 1/2.
2/3 > 1/2.
so he was correct.

Question 19.
Make Sense and Persevere Manish drives 265 more miles than Janice. Manish drives 642 miles. How many miles does Janice drive?

Answer:
The number of miles does Janice drive =

Explanation:
In the above-given question,
given that,
Manish drives 265 more miles than Janice.
Manish drives 642 miles.
642 – 265 = 377.
so the number of miles does Janice drives = 377.

Question 20.
Algebra Nika has 90 pencils. Forty of them are yellow, 13 are green, 18 are red, and the rest are blue. How many blue pencils does Nika have?

Answer:
The number of blue pencils does Nika have = 47.

Explanation:
In the above-given that,
given that,
Algebra Nika has 90 pencils.
Forty of them are yellow, 13 are green, 18 are red, and the rest are blue.
13 + 18 = 43.
90 – 43 = 47.
so the number of blue pencils does Nika have = 47.

Question 21.
Higher Order Thinking Omar says that \(\frac{2}{6}\) < \(\frac{4}{6}\) because \(\frac{2}{6}\) is between 0 and \(\frac{1}{2}\), and \(\frac{4}{6}\) is between \(\frac{1}{2}\) and 1. Is he correct? Explain.

Answer:
Yes, he was correct.

Explanation:
In the above-given question,
given that,
2/6 < 4/6.
2/6 is between 0 and 1/2.
4/6 is between 1/2 and 1.
0, 2/6, and 1/2.
1/2, 4/6, and 1.
so Omar was correct.

Assessment Practice

Question 22.
Each of the fractions in the comparisons at the right refer to the same whole. Use benchmark fractions to reason about the size of each fraction. Select all the correct comparisons.

Answer:
2/3 < 2/4, 3/6 > 3/8, and 3/8 > 5/8.

Explanation:
In the above-given question,
given that,
the fractions are 2/3 < 2/4, 2/4 < 2/3, 3/8 > 5/8, 1/4 < 2/4, and 3/6 > 3/8.
so the 2/3 < 2/4.
2/3 < 1 and 1/2 > 1.
3/6 > 3/8.
3/8 > 5/8.
so the correct fractions are 2/3 < 2/4, 3/6 > 3/8, and 3/8 > 5/8.

Lesson 13.6 Compare Fractions: Use the Number Line

Solve & Share
Tanya, Riaz, and Ryan each used a bag of flour to make modeling clay. The bags were labeled lb, á lb, and Ź lb. Show these fractions on a number line. How can you use the number line to compare two of these fractions?
I can … compare two fractions by locating them on a number line.

Look Back! If the bags were labeled \(\frac{4}{8}\) lb, \(\frac{3}{8}\) lb, and \(\frac{6}{8}\) lb, how could a number line help you solve this problem?

Answer:
3/8 < 4/8 < 6/8.

Explanation:
In the above-given question,
given that,
if the bags were labeled 4/8 lb, 3/8 lb, and 6/8 lb.
so the fractions from least to greatest are 3/8, 4/8, and 6/8.
3/8 is near to 0.
4/8 is in between 0 and 1.
6/8 is near to 1.

Essentials Question
How Can You Compare Fractions Using the Number Line?

Visual Learning Bridge
Talia has two different lengths of blue and red ribbon. Does she have more blue ribbon or more red ribbon?

The fractions both refer to 1 yard of ribbon. This is the whole.
You can use a number line to compare \(\frac{1}{3}\) and \(\frac{2}{3}\).
The farther the distance of the fraction from zero on the number line, the greater the fraction.

On the number line, \(\frac{2}{3}\) is farther to the right than \(\frac{1}{3}\).
So, \(\frac{2}{3}\) > \(\frac{1}{3}\).
Talia has more blue ribbon than red ribbon.

Convince Me! Use Structure Talia has an additional length of green ribbon that measures \(\frac{2}{4}\) yard. How can you compare the length of the green ribbon to the lengths of the blue and red ribbons?

Guided Practice

Do You Understand?
Question 1.
When two fractions refer to the same whole, what do you notice when the denominators you are comparing are the same?

Answer:
The denominators are greater than the numerators.

Explanation:
In the above-given question,
given that,
if two fractions are the same.
the denominators are greater than the numerators.

Question 2.
Write a problem that compares two fractions with different numerators.

Answer:
1/3 > 2/3.

Explanation:
In the above-given question,
given that,
the two different fractions are 1/3 and 2/5.
1/3 x 1 = 1/3.
2/3 = 1/3 + 1/3.
so 1/3 > 2/3.

Do You Know How?
In 3-5, compare fractions using <, >, or =. Use the number lines to help.
Question 3.

Answer:
2/4 < 2/3.

Explanation:
In the above-given question,
given that,
the two fractions are 2/4 and 2/3.
2/4 = 1/4 + 1/4.
2/3 = 1/3 + 1/3.
2/4 is the half portion in the number line.
so 2/4 > 2/3.

Question 4.

Answer:
2/6 < 2/3.

Explanation:
In the above-given question,
given that,
the two fractions are 2/6 and 2/3.
2/6 = 1/6 + 1/6.
2/3 = 1/3 + 1/3.
2/6 is below the half portion in the number line.
so 2/6 < 2/3.

Question 5.

Answer:
5/8 > 3/8.

Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 3/8.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
3/8 = 1/8 + 1/8 + 1/8.
3/8 is the half portion in the number line.
so 5/8 > 3/8.

Independent Practice

In 6-9, use the number lines to compare the fractions. Write >, <, or =.
Question 6.

Answer:
1/4 > 3/4.

Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 3/4.
1/4 = 1/4 x 1.
3/4 = 1/4 + 1/4 + 1/4.
1/4 is nearest to 0.
so 1/4 > 3/4.

Question 7.

Answer:
4/6 < 3/6.

Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 3/6.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
3/6 = 1/6 + 1/6 + 1/6.
so 4/6 < 3/6.

Question 8.

Answer:
1/2 > 1/4.

Explanation:
In the above-given question,
given that,
the two fractions are 1/4 and 1/2.
1/2 = 1/2 x 1.
1/4 = 1/4 x 1
1/4 is nearest to 0.
so 1/2 > 1/4.

Question 9.

Answer:
1/3 > 1/8.

Explanation:
In the above-given question,
given that,
the two fractions are 1/3 and 1/8.
1/3 = 1/3 x 1.
1/8 = 1/8 x 1.
1/8 is nearest to 0.
so 1/3 > 1/8.

Problem Solving

Question 10.
Number Sense Randy wants to save $39. The table shows how much money he has saved. Explain how you can use estimation to decide if he has saved enough money.

Answer:
Yes, he has saved enough money.

Explanation:
In the above-given question,
given that,
Randy wants to save $39.
in march month he saved $14.
in April he saved $11.
in May he saved $22.
14 + 11 + 22 = 47.
so he has saved enough money.

Question 11.
Scott ate \(\frac{2}{8}\) of a fruit bar. Anne ate \(\frac{4}{8}\) of a same-sized fruit bar. Can you tell who ate more of a fruit bar, Scott or Anne? Explain.

Answer:
Anne ate more of a fruit bar.

Explanation:
In the above-given question,
given that,
Scott ate \(\frac{2}{8}\) of a fruit bar.
Anne ate \(\frac{4}{8}\) of a same-sized fruit bar.
2/8 = 1/8 + 1/8.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
4 > 2.
so the whole is 8.
so Anne ate more of a fruit bar.

Question 12.
Be Precise Matt and Adara have identical pieces of cardboard for an art project. Matt uses \(\frac{2}{3}\) of his piece. Adara uses \(\frac{2}{6}\) of her piece. Who uses more, Matt or Adara? Draw two number lines to help explain your answer.

Answer:
Matt uses more cardboard.

Explanation:
In the above-given question,
given that,
Matt and Adara have identical pieces of cardboard for an art project.
matt uses 2/3 of his piece.
Adara uses 2/6 of her piece.
2/3 = 1/3 + 1/3.
2/6 = 1/6 + 1/6.
in 1st 3 is the whole part.
2 is near to 3.
so matt uses more cardboard.

Question 13.
Higher Order Thinking Some friends shared a pizza. Nicole ate \(\frac{2}{8}\) of the pizza. Chris ate \(\frac{1}{8}\) more than Johan. Mike ate \(\frac{1}{8}\) of the pizza. Johan ate more than Mike. Who ate the most pizza?

Answer:
Chris ate more pizza.

Explanation:
In the above-given question,
given that,
Some friends shared a pizza.
Nicole ate \(\frac{2}{8}\) of the pizza.
Chris ate \(\frac{1}{8}\) more than Johan.
Mike ate \(\frac{1}{8}\) of the pizza.
1/8 + 1 = 2/8.
2/8 + 1 = 3/8.
so Chris ate more pizza.

Question 14.
Inez has 2 rows of plants. There are 8 plants in each row. Each plant has 3 flowers. How many flowers are there in all?

Answer:
The number of flowers is there = 48.

Explanation:
In the above-given question,
given that,
Inez has 2 rows of plants.
there are 8 plants in each row.
each plant has 3 flowers.
8 x 2 =16.
16 x 3 = 48.
so the number of flowers is there = 48.

Assessment Practice

Question 15.
Daniel walked \(\frac{3}{4}\) of a mile. Theo walked \(\frac{3}{8}\) of a mile. Use the number lines to show 0 the fraction of a mile Daniel and Theo each walked. Then select all the correct statements that describe the fractions.

☐ \(\frac{3}{4}\) is equivalent to \(\frac{3}{8}\) because the fractions mark the same point.
☐ \(\frac{3}{4}\) is greater than \(\frac{3}{8}\) because it is farther from zero.
☐ \(\frac{3}{4}\) is less than \(\frac{3}{8}\) because it is farther from zero.
☐ \(\frac{3}{8}\) is less than \(\frac{3}{4}\) because it is closer to zero.
☐ \(\frac{3}{8}\) is greater than \(\frac{3}{4}\) because it is closer to zero.

Answer:
Option B is the correct answer.

Explanation:
In the above-given question,
given that,
Daniel walked \(\frac{3}{4}\) of a mile.
Theo walked \(\frac{3}{8}\) of a mile.
in the 1st line, the 3 is farther from the 0.
so 3/4 > 3/8.
so option B is the correct answer.

Lesson 13.7 Whole Numbers and Fractions

Solve & Share
Jamie’s family ate 12 pieces of apple pie during the week. Each piece was \(\frac{1}{6}\) of a whole pie. How many whole pies did Jamie’s family eat? What fraction of a pie was left over? Explain how you decided.
I can … use representations to find fraction names for whole numbers.

Look Back! Jamie cuts another pie into smaller pieces. Each piece of pie is \(\frac{1}{8}\) of the whole. Jamie gives away 8 pieces. Does Jamie have any pie left over? Explain how you know.

Answer:
Jamie does not have left any pie.

Explanation:
In the above-given question,
given that,
Jamie cuts another pie into smaller pieces.
Each piece of pie is \(\frac{1}{8}\) of the whole.
Jamie gives away 8 pieces.
8 – 8 = 0.
so Jamie does not have left any pie.

Essential Question
How Can You Use Fraction Names to Represent Whole Numbers?

Visual Learning Bridge
What are some equivalent fraction names for 1, 2, and 3?
You can write a whole number as a fraction by writing the whole number as the numerator and

The number line shows 3 wholes. Each whole is divided into 1 equal part.
1 whole divided into 1 equal part can be written as \(\frac{1}{1}\).
2 wholes each divided into 1 equal part can be written as \(\frac{2}{1}\).
3 wholes each divided into 1 equal part can be written as \(\frac{1}{1}\)
1 = \(\frac{1}{2}\)
2 = \(\frac{2}{1}\)
3 = \(\frac{3}{1}\)

You can find other equivalent fraction names for whole numbers.

Convince Me! Reasoning What equivalent fraction names can you write for 4 using denominators of 1, 2, or 4?

Another Example!
You can use fractions to name whole numbers.

Twelve \(\frac{1}{3}\) fraction strips equal 4 whole fraction strips.
All whole numbers have fraction names. You can write 4 = \(\frac{12}{3}\).
You also know 4 = \(\frac{4}{1}\), so you can write 4 = \(\frac{4}{1}\) = \(\frac{12}{3}\).

Guided Practice

Do You Understand?
Question 1.
Explain how you know that \(\frac{4}{1}\) = 4.

Answer:
4/1 = 4.

Explanation:
In the above-given question,
given that,
12/3 = 4/1.
3 x 1 = 3.
3 x 4 = 12.
so 4/1 = 4.

Do You Know How?
Question 2.
Complete the number line.

Answer:
The missing numbers in upside are 1/3, 3/3, 4/3, and 6/3.
the missing numbers on the downside are 1/6, 2/6, 4/6, 5/6, 6/6, 7/6, 9/6, 10/6, 11/6, and 12/6.

Explanation:
In the above-given question,
given that,
the number line is 1/3, 2/3, 3/3, 4/3, 5/3, 6/3.
2/6 = 1/3.
1 x 2 = 2.
3 x 2 = 6.
6/6 = 1.
9/6 = 3/2.
3 x 3 = 9.
3 x 2 = 6.
so the missing numbers are 1/3, 3/3, 4/3, and 6/3.
1/6, 2/6, 4/6, 5/6, 6/6, 7/6, 9/6, 10/6, 11/6, and 12/6.

Question 3.
Look at the number line. Write two equivalent fractions for each whole number.

Answer:
1 = 3/3 = 6/6.
2 = 6/3 = 12/6.

Explanation:
In the above-given question,
given that,
the two numbers are 1 and 2.
1 = 3/3.
6 / 6 = 1.
6/3 = 2.
12 / 6 = 2.

Independent Practice

In 4-7, write two equivalent fractions for each whole number. You can draw number lines to help.
Question 4.

Answer:
4 = 8/2 = 4/1.

Explanation:
In the above-given question,
given that,
the number is 4.
8/2 = 4.
2 x 1 = 2.
2 x 4 = 8.
4 / 1 = 4.
so the missing numbers are 8 and 4.

Question 5.

Answer:
1 = 4/4 = 1/1.

Explanation:
In the above-given question,
given that,
the number is 1.
4/4 = 1.
4 x 1 = 4.
1 x 4 = 4.
1 / 1 = 1.
so the missing numbers are 4 and 1.

Question 6.

Answer:
2 = 6/3 = 2/1.

Explanation:
In the above-given question,
given that,
the number is 2.
6/3 = 2.
3 x 1 = 3.
3 x 2 = 6.
2 / 1 = 2.
so the missing numbers are 6 and 1.

Question 7.

Answer:
5 = 10/2 = 5/1.

Explanation:
In the above-given question,
given that,
the number is 5.
10/2 = 5.
2 x 1 = 2.
2 x 5 = 10.
5 / 1 = 5.
so the missing numbers are 10 and 5.

In 8-11, for each pair of fractions, write the equivalent whole number.
Question 8.
\(\frac{6}{2}\) = \(\frac{3}{1}\) =

Answer:
\(\frac{6}{2}\) = \(\frac{3}{1}\) = 3.

Explanation:
In the above-given question,
given that,
for each pair of fractions, write the equivalent whole number.
6/2 = 3.
3/1 = 3.
so \(\frac{6}{2}\) = \(\frac{3}{1}\) = 3.

Question 9.
\(\frac{3}{3}\) = \(\frac{6}{6}\) =

Answer:
\(\frac{3}{3}\) = \(\frac{6}{6}\) = 1.

Explanation:
In the above-given question,
given that,
for each pair of fractions, write the equivalent whole number.
3/3 = 1.
6/6 = 1.
so \(\frac{3}{3}\) = \(\frac{6}{6}\) = 1.

Question 10.
\(\frac{8}{4}\) = \(\frac{6}{3}\) =

Answer:
\(\frac{8}{4}\) = \(\frac{6}{3}\) = 2.

Explanation:
In the above-given question,
given that,
for each pair of fractions, write the equivalent whole number.
8/4 = 2.
6/3 = 2.
so \(\frac{8}{4}\) = \(\frac{6}{3}\) = 2.

Question 11.
\(\frac{9}{3}\) = \(\frac{12}{4}\) =

Answer:
\(\frac{9}{3}\) = \(\frac{12}{4}\) = 3.

Explanation:
In the above-given question,
given that,
for each pair of fractions, write the equivalent whole number.
9/3 = 3.
12/4 = 3.
so \(\frac{9}{3}\) = \(\frac{12}{4}\) = 3.

Problem Solving

Question 12.
Henry needs to fix or replace his refrigerator. It will cost $376 to fix it. How much more will it cost to buy a new refrigerator than to fix the current one?

Answer:
The more it costs to buy a new refrigerator = $593.

Explanation:
In the above-given question,
given that,
Henry needs to fix or replace his refrigerator.
It will cost $376 to fix.
the new refrigerator cost is $969.
969 – 376 = 593.
so more it costs to buy a new refrigerator = $593.

Question 13.
Declan says, “To write an equivalent fraction name for 5, I can write 5 as the denominator and 1 as the numerator.” Do you agree with Declan? Explain.

Answer:
No, Declan was wrong.

Explanation:
In the above-given question,
given that,
To write an equivalent fraction name for 5, I can write 5 as the denominator and 1 as the numerator.
5/1 = 5.
so Declan was wrong.

Question 14.
Look for Relationships Describe a pattern in fractions equivalent to 1 whole.

Answer:

Question 15.
enVision® STEM There are four stages in a butterfly’s life cycle: egg, caterpillar, chrysalis, and butterfly. Dan makes one whole poster for each stage. Use a fraction to show the number of whole posters Dan makes.

Answer:
Dan makes the fractions 1/4, 2/4, 3/4, and 4/4.

Explanation:
In the above-given question,
given that,
There are four stages in a butterfly’s life cycle: egg, caterpillar, chrysalis, and butterfly.
1st stage is egg = 1/4.
2nd stage is caterpillar = 2/4.
3rd stage is chrysalis = 3/4.
4th stage is butterfly = 4/4.
so the fractions are 1/4, 2/4, 3/4, and 4/4.

Question 16.
Karen bought 4 movie tickets for $9 each. She has $12 left over. How much money did Karen have to start? Explain.

Answer:
The money Karen has to start = $48.

Explanation:
In the above-given question,
given that,
Karen bought 4 movie tickets for $9 each. She has $12 left over
4 x 9 = 36.
36 + 12 = 48.
so the money Karen has to start = $48.

Question 17.
Higher Order Thinking Peggy has 4 whole sandwiches. She cuts each whole into halves. Then Peggy gives away 1 whole sandwich. Show the number of sandwiches Peggy has left as a fraction.

Each sandwich is cut into equal parts.

Answer:
The number of sandwiches Peggy has left as a fraction = 6/8.

Explanation:
In the above-given question,
given that,
Peggy has 4 whole sandwiches.
She cuts each whole into halves.
4 x 2 = 8.
Then Peggy gives away 1 whole sandwich.
8 – 2 = 6.
so the number of sandwiches Peggy has left as a fraction = 6/8.

Assessment Practice

Question 18.
Complete the equations. Match the fractions with their equivalent whole numbers.

Answer:
6/1 = 12/2 = 6.
6/3 = 4/2 = 2.
4/4 = 1/1 = 1.
8/2 = 16/4 = 4.

Explanation:
In the above-given question,
given that,
the numbers are 1, 2, 4, and 6.
6/1 = 12/2 = 6.
6/3 = 4/2 = 2.
4/4 = 1/1 = 1.
8/2 = 16/4 = 4.

Lesson 13.8 Problem Solving

Construct Arguments
Solve & Share
Lindsey and Matt are running in a 1-mile race. They have both run the same distance so far. Write a fraction that shows how far Lindsey could have run. Write a different fraction that shows how far Matt could have run. Construct a math argument to support your answer.
I can … construct math arguments using what I know about fractions.

Thinking Habits
Be a good thinker! These questions can help you.

• How can I use numbers, objects, drawings, or actions to justify my argument?
• Am I using numbers and symbols correctly?
• Is my explanation clear and complete?
  

Look Back! Construct Arguments Are the two fractions you wrote equivalent? Construct a math argument using pictures, words, and numbers to support your answer.

Essential Question
How Can You Construct Arguments?

Visual Learning Bridge
Clara and Ana are making rugs. The rugs will be the same size. Clara has finished of her rug. Ana has finished of her rug. Who has finished more of her rug? Conjecture: Clara has finished a greater portion of her rug than Ana.

A conjecture is a statement that you think is true. It needs to be proved.

How can I explain why my conjecture is correct?
I need to construct an argument to justify my conjecture.

How can I construct an argument?
I can

• use numbers, objects, drawings, or actions correctly to explain my thinking.
• make sure my explanation is simple, complete, and easy to understand.

Here’s my thinking…
I will use drawings and numbers to explain my thinking.
The number lines represent the same whole. One is divided into fourths. One is divided into eighths.

The number lines show that 3 of the fourths is greater than 3 of the eighths.
So, \(\frac{3}{4}\) > \(\frac{3}{8}\). The conjecture is correct.

Convince Me! Construct Arguments Use numbers to construct another math argument to justify the conjecture above. Think about how you can look at the numerator and the denominator.

Guided Practice

Construct Arguments Paul and Anna were eating burritos. The burritos were the same size. Paul ate \(\frac{2}{6}\) of a burrito. Anna ate \(\frac{2}{3}\) of a burrito. Conjecture: Paul and Anna ate the same amount.
Question 1.
Draw a diagram to help justify the conjecture.

Answer:
No, Paul and Anna were correct.

Explanation:
In the above-given question,
given that,
Paul and Anna were eating burritos.
The burritos were the same size.
Paul ate \(\frac{2}{6}\) of a burrito.
Anna ate \(\frac{2}{3}\) of a burrito.
paul ate 2 of the sixths is less than the 2 of the thirds.
2/6 = 1/6 + 1/6.
2/3 = 1/3 + 1/3.
yes, the conjecture is not correct.

Question 2.
Is the conjecture correct? Construct an argument to justify your answer.

Answer:
No, the conjecture was not correct.

Explanation:
In the above-given question,
given that,
Paul and Anna were eating burritos.
The burritos were the same size.
Paul ate \(\frac{2}{6}\) of a burrito.
Anna ate \(\frac{2}{3}\) of a burrito.
paul ate 2 of the sixths is less than the 2 of the thirds.
2/6 = 1/6 + 1/6.
2/3 = 1/3 + 1/3.
yes, the conjecture is not correct.

Independent Practice

Construct Arguments Reyna has a blue ribbon that is 1 yard long and a red ribbon that is 2 yards long. She uses \(\frac{2}{4}\) of the red ribbon and \(\frac{2}{4}\) of the blue ribbon.

Conjecture: Reyna uses the same amount of red and blue ribbon.
Question 3.
Draw a diagram to help justify the conjecture.

Answer:
Yes, the conjecture was correct.

Explanation:
In the above-given question,
given that,
Reyna has a blue ribbon that is 1 yard long and a red ribbon that is 2 yards long.
She uses \(\frac{2}{4}\) of the red ribbon and \(\frac{2}{4}\) of the blue ribbon.
2/4 = 1/4 + 1/4.
2/4 = 1/4 + 1/4.
yes, the conjecture is correct.

Question 4.
Is the conjecture correct? Construct an argument to justify your answer.

Answer:
Yes, the conjecture is correct.

Explanation:
In the above-given question,
given that,
Reyna has a blue ribbon that is 1 yard long and a red ribbon that is 2 yards long.
She uses \(\frac{2}{4}\) of the red ribbon and \(\frac{2}{4}\) of the blue ribbon.
2/4 = 1/4 + 1/4.
2/4 = 1/4 + 1/4.
yes, the conjecture is correct.

Question 5.
Explain another way you could justify the conjecture.
Answer:

Problem Solving

Performance Task School Fair Twenty-one students worked at the school fair. Mrs. Gold’s students worked at a class booth. The table shows the fraction of 1 hour that her students worked. Mrs. Gold wants to know the order of the work times for the students from least to greatest.

Question 6.
Make Sense and Persevere What comparisons do you need to make to find out who worked the least?

Answer:
The student who worked least is Pedro.

Explanation:
In the above-given question,
given that,
School Fair Twenty-one students worked at the school fair.
Gold’s students worked at a class booth.
The table shows the fraction of 1 hour that her students worked.
Tim worked 4 hours.
Cathy worked 2/4 hours.
Jose worked 2/6 hours.
Pedro worked 3/4 hours.
3/4 < 2/4 < 2/6.
so the student who worked least is Pedro.

Question 7.
Be Precise What is the whole for each student’s time? Do all the fractions refer to the same whole?

Answer:
The same whole is 4.

Explanation:
In the above-given question,
given that,
School Fair Twenty-one students worked at the school fair.
Gold’s students worked at a class booth.
The table shows the fraction of 1 hour that her students worked.
Tim worked 4 hours.
Cathy worked 2/4 hours.
Jose worked 2/6 hours.
Pedro worked 3/4 hours.
3/4 < 2/4 < 2/6.
so the students who worked least is Pedro.

Question 8.
Use Appropriate Tools What tool could you use to solve this problem? Explain how you would use this tool.

Answer:

Question 9.
Construct Arguments What is the order of the work times from least to greatest? Construct a math argument to justify your answer.

Answer:
The student who worked the least is Pedro.

Explanation:
In the above-given question,
given that,
School Fair Twenty-one students worked at the school fair.
Gold’s students worked at a class booth.
The table shows the fraction of 1 hour that her students worked.
Tim worked 4 hours.
Cathy worked 2/4 hours.
Jose worked 2/6 hours.
Pedro worked 3/4 hours.
3/4 < 2/4 < 2/6.
so the student who worked least is Pedro.

Topic 13 Fluency Practice Activity

Find a Match
Work with a partner. Point to a clue. Read the clue.
Look below the clues to find a match. Write the clue letter in the box next to the match.
Find a match for every clue.
I can … multiply and divide within 100.

Clues
A. ls equal to 3 × 3
B. is equal to 4 × 4
C. is equal to 9 × 4
D. is equal to 0 ÷ 10
E. is equal to 35 ÷ 5
F. is equal to 12 ÷ 4
G. is equal to 5 × 4
H. is equal to 3 × 8
I. Is equal to 2 × 5
J. Is equal to 3 × 10
K. is equal to 9 × 2
L. is equal to 2 × 4

Answer:
6 x 6 = 36, 40 / 4 = 10, 0 x 9 = 0, 3 x 6 = 18, 32 / 4 = 8, 10 x 2 = 20, 5 x 6 = 30, 7 / 21 = 3, 8 x 2 = 16, and 6 x 4 = 24.

Explanation:
In the above-given question,
given that,
A is not equal to 9.
B is equal to 16.
C is equal to 36.
D is equal to 0.
E is equal to 35 / 5 = 7.
F is equal to 3.
G is equal to 20.
H is equal to 24.
I is equal to 10.
J is equal to 30.
K is equal to 18.
L is equal to 8.

Topic 13 Vocabulary Review

Word List

• denominator
• equivalent fractions
• fraction
• number line
• numerator
• unit fraction

Understand Vocabulary

Write T for true or F for false.
Question 1.
______ \(\frac{1}{6}\) and \(\frac{2}{6}\) have the same numerator.

Answer:
True.

Explanation:
In the above-given question,
given that,
the fractions are 1/6 and 2/6.
2/6 = 1/3.
2 x 1 = 2.
2 x 3 = 6.
so both the fractions have the same numerator.

Question 2.
________ \(\frac{1}{2}\) and \(\frac{4}{8}\) are equivalent fractions.

Answer:
True.

Explanation:
In the above-given question,
given that,
the fractions are 1/2 and 4/8.
4/8 = 1/2.
4 x 1 = 4.
4 x 2 = 8.
so both the fractions are equivalent fractions.

Question 3.
_______ \(\frac{3}{8}\) is a unit fraction.

Answer:
True.

Explanation:
In the above-given question,
given that,
the fraction is 3/8.
3/8 = 1/8 + 1/8 + 1/8.
so 3/8 is a unit fraction.

Question 4.
_________ A whole number can be written as a fraction.

Answer:
True.

Explanation:
In the above-given question,
given that,
A whole number can be written as a fraction.
2 / 2 = 1.
so the whole number can be written as a fraction.

Question 5.
________ The denominators in \(\frac{1}{3}\) and \(\frac{2}{3}\) in are the same.

Answer:
True.

Explanation:
In the above-given question,
given that,
the fractions are 1/3 and 2/3.
2/3 = 1/3 + 1/3.
in both the fractions, the numerator, and denominator are the same.
so both the fractions have the same denominators.

Question 6.
_______ A number line always shows fractions.

Answer:
A unit fraction is a number line that always shows fractions.

Explanation:
In the above-given question,
given that,
3/8 is a unit fraction.
3 is the numerator and 8 is a denominator.
so the unit fraction is a number line that always shows fractions.

For each of these terms, give an example and a non-example.

Answer:
1/2 is a fraction.
3/8 is a unit fraction.
1/2 = 2/4 are equivalent fractions.

Explanation:
In the above-given question,
given that,
the terms are fraction, unit fraction, and equivalent fractions.
1/2 is a fraction.
3/8 is a unit fraction.
1/2 = 2/4 are equivalent fractions.

Use Vocabulary in Writing
Question 10.
Use at least 2 terms from the Word List to explain how to compare \(\frac{1}{2}\) and \(\frac{1}{3}\).

Answer:
The two terms have different denominators.

Explanation:
In the above-given question,
given that,
the two fractions are 1/2 and 1/3.
1/2 = 2/4.
1/3 = 2/6.
so both the fractions have different denominators.

Topic 13 Reteaching

Set A pages 485-488

Two fractions are equivalent if they name the same part of a whole.
What is one fraction that is equivalent to \(\frac{6}{8}\)?
You can use fraction strips to find equivalent fractions.

\(\frac{6}{8}\) = \(\frac{3}{4}\)
You also can use area models to see that a I are equivalent fractions. The shaded fractions both show the same part of the whole.

Remember to check that both sets of strips are the same length

In 1 and 2, find an equivalent fraction. Use fraction strips and models to help.
Question 1.

Answer:
4/6 = 2/3.

Explanation:
In the above-given question,
given that,
the fraction is 4/6.
4/6 = 2/3.
2 x 2 = 4.
2 x 3 = 6.
so the equivalent fraction is 2/3.

Question 2.

Answer:
2/6 = 1/3.

Explanation:
In the above-given question,
given that,
the fraction is 2/6.
2/6 = 1/3.
1 x 2 = 2.
2 x 3 = 6.
so the equivalent fraction is 1/3.

Set B pages 489-492

Riley says the library is \(\frac{2}{8}\) of a mile from their house. Sydney says it is \(\frac{1}{4}\) of a mile.
Use the number lines to find who is correct.

The fractions \(\frac{2}{8}\) and \(\frac{1}{4}\) are equivalent. They are the same distance from 0 on a number line. Riley and Sydney are both correct.

Remember that equivalent fractions have different names, but they represent the same point on a number line.

In 1 and 2, write two fractions that name the same location on the number line.
Question 1.

Answer:
The two fractions that name the same location on the number line = 1.

Explanation:
In the above-given question,
given that,
the fractions are 8/8 and 4/4.
8/8 = 1.
4/4 = 1.
so the two fractions that name the same location on the number line = 1.

Question 2.

Answer:
The two fractions that name the same location on the number line = 3/6 and 1/2.

Explanation:
In the above-given question,
given that,
the fractions are 3/6 and 1/2.
3/6 = 1/2.
3 x 1 = 3.
3 x 2 = 6.
so the two fractions that name the same location on the number line = 3/6 and 1/2.

Set C pages 493-496

You can use fraction strips to compare fractions with the same denominator.
Compare \(\frac{3}{4}\) to \(\frac{2}{4}\).

The denominator of each fraction is 4.
Three \(\frac{1}{4}\) fraction strips show \(\frac{3}{4}\).
Two \(\frac{1}{4}\) fraction strips show \(\frac{2}{4}\).
The fraction strips showing \(\frac{3}{4}\) have 1 more unit fraction than the strips showing \(\frac{2}{4}\).
So \(\frac{3}{4}\) > \(\frac{2}{4}\).

Remember that if fractions have the same denominator, the greater fraction has a greater numerator.

In 1-3, compare. Write <, >, or =. Use fraction strips to help.
Question 1.

Answer:
3/6 < 5/6.

Explanation:
In the above-given question,
given that,
the two fractions are 3/6 and 5/6.
3/6 = 1/6 + 1/6 + 1/6.
5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6.
3/6 < 5/6.

Question 2.
\(\frac{4}{6}\) \(\frac{5}{6}\)

Answer:
4/6 < 5/6.

Explanation:
In the above-given question,
given that,
the two fractions are 4/6 and 5/6.
4/6 = 1/6 + 1/6 + 1/6 + 1/6.
5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6.
4/6 < 5/6.

Question 3.
\(\frac{5}{8}\) \(\frac{3}{8}\)

Answer:
5/8 > 3/8.

Explanation:
In the above-given question,
given that,
the two fractions are 5/8 and 3/8.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
3/8 = 1/8 + 1/8 + 1/8.
5/8 > 3/8.

Set D pages 497-500

You can use fraction strips to compare fractions with the same numerator.
Compare \(\frac{1}{6}\) to \(\frac{1}{2}\).

The numerator of each fraction is 1.
The \(\frac{1}{6}\) fraction strip is less than the \(\frac{1}{2}\) strip.
So \(\frac{1}{6}\) < \(\frac{1}{2}\)
You can use reasoning to understand. Think about dividing a whole into 6 pieces and dividing it into 2 pieces. One of 6 pieces is less than 1 of 2 pieces.

Remember that if fractions have the same numerator, the greater fraction has a lesser denominator.

In 1-3, compare. Write <, >, or=. Use fraction strips to help.
Question 1.

Answer:
3/4 < 3/8.

Explanation:
In the above-given question,
given that,
the two fractions are 3/4 and 3/8.
3/4 = 1/4 + 1/4 + 1/4.
3/8 = 1/8 + 1/8 + 1/8.
3/4 < 3/8.

Question 2.
\(\frac{5}{6}\) \(\frac{5}{8}\)

Answer:
5/6 < 5/8.

Explanation:
In the above-given question,
given that,
the two fractions are 5/6 and 5/8.
5/6 = 1/6 + 1/6 + 1/6 + 1/6 + 1/6.
5/8 = 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
5/6 < 5/8.

Question 3.
\(\frac{1}{3}\) \(\frac{1}{2}\)

Answer:
1/3 > 1/2.

Explanation:
In the above-given question,
given that,
the two fractions are 1/3 and 1/2.
1/3 = 2/6.
2/6 = 1/6 + 1/6.
1/3 > 1/2.

Set E pages 501-504

You can compare fractions using benchmark numbers such as 0, \(\frac{1}{2}\), and 1.

Chris and Mary are painting pictures. The pictures are the same size. Chris painted \(\frac{3}{4}\) of his picture. Mary painted her picture. Who painted the greater amount?
\(\frac{3}{4}\) is greater than \(\frac{1}{2}\).
\(\frac{3}{8}\) is less than \(\frac{1}{2}\).
Chris painted the greater amount.

Remember that you can compare each fraction to a benchmark number to see how they relate to each other.

In 1 and 2, use benchmark numbers to help solve.
Question 1.
Mike had \(\frac{2}{6}\) of a candy bar. Sally had \(\frac{4}{6}\) of a candy bar. Whose fraction of a candy bar was closer to 1? Closer to 0?

Answer:
Sally was closer to 1.

Explanation:
In the above-given question,
given that,
Mike had \(\frac{2}{6}\) of a candy bar.
Sally had \(\frac{4}{6}\) of a candy bar.
2/6 = 1/3.
4/6 = 2/3.
2/3 is closer to 1.
so sally was closer to 1.

Question 2.
Paul compared two bags of rice. One weighs \(\frac{4}{6}\) pound, and the other weighs \(\frac{4}{8}\) pound. Which bag is heavier?

Answer:
The 4/6 pounds bag is heavier.

Explanation:
In the above-given question,
given that,
Paul compared two bags of rice.
One weighs 4/6 pound.
the other weighs 4/8 pound.
4/6 = 2/3.
4/8 = 2/4.
so the 4/6 pounds bag is heavier.

Set F pages 505-508

You can use a number line to compare fractions.
Which is greater, \(\frac{3}{6}\) or \(\frac{4}{6}\)?

\(\frac{4}{6}\) is farther from zero than \(\frac{3}{6}\), so \(\frac{4}{6}\) is greater.
You also can compare two fractions with the same numerator by drawing two number lines.

Which is greater, \(\frac{2}{4}\) or \(\frac{2}{3}\)?

\(\frac{2}{3}\) is farther from zero than \(\frac{2}{4}\), so \(\frac{2}{3}\) is greater.

Remember to draw two number lines that are equal in length when comparing fractions with different denominators.

In 1 and 2, compare. Write <, >, or=. Use number lines to help.
Question 1.

Answer:
2/6 < 3/6.

Explanation:
In the above-given question,
given that,
the two fractions are 2/6 and 3/6.
2/6 = 1/3.
2/6 = 1/6 + 1/6.
3/6 = 1/2.
3/6 = 1/6 + 1/6 + 1/6.
so 2/6 < 3/6.

Question 2.

Answer:
3/4 > 3/6.

Explanation:
In the above-given question,
given that,
the two fractions are 3/4 and 3/6.
3/4 = 1/4 + 1/4 + 1/4.
3/6 = 1/6 + 1/6 + 1/6.
3/6 = 1/2.
so 3/4 > 3/6.

Set G pages 509-512

How many thirds are in 2 wholes?
You can use a number line or fraction strips to find a fraction name for 2 using thirds.

2 = \(\frac{6}{3}\)
The whole number 2 can also be written as the fraction \(\frac{6}{3}\).

Remember that when you write whole numbers as fractions, the numerator can be greater than the denominator.

In 1-4, write an equivalent fraction for each whole number.
Question 1.
3

Answer:
The equivalent fraction is 12/4.

Explanation:
In the above-given question,
given that,
the whole number is 3.
12/4 = 3.
3 x 4 = 12.
3 x 1 = 3.
so the equivalent fraction is 12/4.

Question 2.
2

Answer:
The equivalent fraction is 4/2.

Explanation:
In the above-given question,
given that,
the whole number is 2.
4/2 = 2/1.
2 x 2 = 4.
2 x 1 = 2.
so the equivalent fraction is 4/2.

Question 3.
5

Answer:
The equivalent fraction is 15/3.

Explanation:
In the above-given question,
given that,
the whole number is 5.
15/3 = 5.
3 x 1 = 3.
3 x 5 = 15.
so the equivalent fraction is 15/3.

Question 4.
1

Answer:
The equivalent fraction is 3/3.

Explanation:
In the above-given question,
given that,
the whole number is 1.
3/3 = 1.
so the equivalent fraction is 3/3.

In 5-8, write the equivalent whole number for each fraction.
Question 5.
\(\frac{6}{3}\)

Answer:
The equivalent whole number is 2.

Explanation:
In the above-given question,
given that,
The fraction is 6/3.
6/3 = 2.
3 x 1 = 3.
3 x 2 = 6.
so the equivalent whole number is 2.

Question 6.
\(\frac{10}{2}\)

Answer:
The equivalent whole number is 5.

Explanation:
In the above-given question,
given that,
The fraction is 10/2.
10/2 = 5.
2 x 1 = 2.
2 x 5 = 10.
so the equivalent whole number is 5.

Question 7.
\(\frac{14}{2}\)

Answer:
The equivalent whole number is 7.

Explanation:
In the above-given question,
given that,
The fraction is 14/2.
14/2 = 7.
2 x 1 = 2.
7 x 2 = 14.
so the equivalent whole number is 7.

Question 8.
\(\frac{8}{8}\)

Answer:
The equivalent whole number is 1.

Explanation:
In the above-given question,
given that,
The fraction is 8/8.
8/8 = 1.
8 x 1 = 8.
1 x 8 = 8.
so the equivalent whole number is 1.

Set H pages 513-516

Think about these questions to help construct arguments.
Thinking Habits

• How can I use numbers, objects, drawings, or actions to justify my argument?
• Am I using numbers and symbols correctly?
• Is my explanation clear and complete?
  

Remember that when you construct an argument, you explain why your work is correct.

Odell and Tamra paint two walls with the same dimensions. Odell paints \(\frac{1}{6}\) of a wall. Tamra paints \(\frac{1}{3}\) of the other wall. Conjecture: Odell paints less than Tamra.
Question 1.
Draw a diagram to justify the conjecture.

Answer:
Yes, Odell paints less than Tamra.

Explanation:
In the above-given question,
given that,
Odell and Tamra paint two walls with the same dimensions.
Odell paints \(\frac{1}{6}\) of a wall.
Tamra paints \(\frac{1}{3}\) of the other wall.
1/6 < 1/3.
so Odell paints less than Tamra.

Question 2.
Use the diagram to justify the conjecture.
Answer:

Topic 13 Assessment Practice

Question 1.
Two friends are working on a project. So far, Cindy has done \(\frac{4}{8}\) of the project, and Kim has done \(\frac{3}{8}\) of the project. Who has done more of the project? Explain.

Answer:
Cindy has done more of the project.

Explanation:
In the above-given question,
given that,
Two friends are working on a project.
Cindy has done \(\frac{4}{8}\) of the project.
Kim has done \(\frac{3}{8}\) of the project.
4/8 = 1/8 + 1/8 + 1/8 + 1/8.
3/8 = 1/8 + 1/8 + 1/8.
so Cindy has done more of the project.

Question 2.
Serena can compare \(\frac{3}{4}\) and \(\frac{3}{6}\) without using fraction strips. She says that a whole divided into 4 equal parts will have larger parts than the same whole divided into 6 equal parts. Three larger parts must be more than three smaller parts, so \(\frac{3}{4}\) is greater than \(\frac{3}{6}\). Is Serena correct? If not, explain Serena’s error. Then, write the correct comparison using symbols.

Answer:
Yes, Serena is correct.

Explanation:
In the above-given question,
given that,
Serena can compare 3/4 and 3/6 without using fraction strips.
3/4 = 1/4 + 1/4 + 1/4.
3/6 = 1/2.
3 x 1 = 3.
3 x 2 = 6.
so Serena is correct.

Question 3.
Jill finished reading \(\frac{2}{3}\) of a book for a summer reading project. Owen read \(\frac{2}{8}\) of the same book. Use the number lines to compare how much Jill and Owen each read. Who reads more of the book?

Answer:
The missing fractions are 1/3 and 2/3.
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, and 7/8.

Explanation:
In the above-given question,
given that,
Jill finished reading \(\frac{2}{3}\) of a book for a summer reading project
Owen read \(\frac{2}{8}\) of the same book.
2/8 = 1/4.
2 x 1 = 2.
4 x 2 = 8.
so Jill read more of the book.

Question 4.
A small cake is cut into 4 equal pieces. What fraction represents the entire cake? Explain.

Answer:
The fraction 4/4 represents the entire cake.

Explanation:
In the above-given question,
given that,
A small cake is cut into 4 equal pieces.
4 / 4 = 1.
so the fraction 4/4 represents the entire cake.

Question 5.
Mark and Sidney each have a piece of wood that is the same size. Mark paints \(\frac{2}{8}\) of his piece of wood. Sidney paints \(\frac{5}{8}\) of her piece of wood. Who painted a fraction that is closer to 1 than to 0? Explain how you found your answer. Then tell who painted less of his or her piece of wood.

Answer:
Sidney is closer to 1 than to 0.

Explanation:
In the above-given question,
given that,
Mark and Sidney each have a piece of wood that is the same size.
Mark paints \(\frac{2}{8}\) of his piece of wood.
Sidney paints \(\frac{5}{8}\) of her piece of wood.
2/8 is near to 0.
5/8 is closer to 1.
so Sidney is closer to 1 than to 0.

Question 6.
Greg colored the fraction model below.
A. Which fractions name the purple part of the model? Select all that apply.

Answer:
The fraction 6/8 names the purple part of the model.

Explanation:
In the above-given question,
given that,
the fractions are 1/2, 3/4, 2/3, 4/6, 6/8.
6 boxes are filled with purple color.
so the fraction 6/8 names the purple part of the model.

B. Does \(\frac{1}{4}\) name the unshaded part of the model? Explain.

Answer:
Yes, the fraction 1/4 names the unshaded part of the model.

Explanation:
In the above-given question,
given that,
the fractions are 1/2, 3/4, 2/3, 4/6, 6/8.
2 boxes are not filled with purple color.
so the fraction 2/8 names the unshaded part of the model.

Question 7.
Carl, Fiona, and Jen each had a sandwich. The sandwiches were the same size and cut into eighths. Carl ate \(\frac{7}{8}\) of a sandwich, Fiona ate \(\frac{3}{8}\) of a sandwich, and Jen ate \(\frac{6}{8}\) of a sandwich. Who ate the most? Explain.

Answer:
Carl ate more sandwiches.

Explanation:
In the above-given question,
given that,
Carl, Fiona, and Jen each had a sandwich.
The sandwiches were the same size and cut into eighths.
Carl ate \(\frac{7}{8}\) of a sandwich.
Fiona ate \(\frac{3}{8}\) of a sandwich.
Jen ate \(\frac{6}{8}\) of a sandwich.
3/8, 6/8, 7/8.
so carl ate more sandwiches.

Question 8.
George wants to know if two pieces of wire are the same length. One wire is \(\frac{6}{8}\) foot. The other is \(\frac{3}{4}\) foot. Are they the same length? Fill in the fractions on the number line to compare the lengths of the pieces of wire. Then explain your answer.

Answer:
The missing fractions are 1/4, 2/4, and 3/4.
2/8, 4/8, and 6/8.

Explanation:
In the above-given question,
given that,
George wants to know if two pieces of wire are the same length.
One wire is \(\frac{6}{8}\) foot.
The other is \(\frac{3}{4}\) foot.
6/8 = 3/4.
2 x 3 = 6.
2 x 4 = 8.
so the missing fractions are 1/4, 2/4, and 3/4.

Question 9.
Lezlie hiked \(\frac{3}{8}\) mile on Monday. On Wednesday she hiked \(\frac{3}{6}\) mile. She hiked a mile on Friday. Use benchmark fractions to arrange the lengths of the hikes in order from shortest to longest hike.

Answer:
The lengths of hikes in order from shortest and longest = 3/4, 3/6, and 3/8.

Explanation:
In the above-given question,
given that,
Lezlie hiked \(\frac{3}{8}\) mile on Monday.
On Wednesday she hiked \(\frac{3}{6}\) mile.
She hiked a mile on Friday.
8 – 2 = 6, 6 – 2 = 4.
so the lengths of hikes in order from shortest and longest = 3/4, 3/6, and 3/8.

Question 10.
A mural is divided into 3 equal parts. What fraction represents the entire mural? Explain.

Answer:
The entire mural is 3/3.

Explanation:
In the above-given question,
given that,
A mural is divided into 3 equal parts.
3/3 = 1.
so the entire mural is divided into 3 parts.

Question 11.
Meagan ate \(\frac{3}{4}\) of a cookie. Write an equivalent fraction for the amount of cookie Meagan did NOT eat. Then write a fraction that is equivalent to the amount of the cookie that Meagan did eat, and explain why your answer is correct.

Answer:
Megan did not eat = 1/4.

Explanation:
In the above-given question,
given that,
Meagan ate \(\frac{3}{4}\) of a cookie.
3/4 + 1/4 = 1.
3/4 = 1/4 + 1/4 + 1/4.
so megan did not ate = 1/4.

Question 12.
Circle each fraction that is equivalent to 1. Explain your reasoning. Then give another fraction that is equal to 1.

Answer:
The fraction that is equivalent to 1 is 3/3 and 6/6.

Explanation:
In the above-given question,
given that,
the fractions are 2/4, 3/3, 3/6, 4/6, and 6/6.
circle each fraction that is equivalent to 1.
3/3 = 1, and 6/6 = 1.

Question 13.
Use the number line to help order the fractions from least to greatest. Then explain how you found your answer.

Answer:
The fractions from least to greatest = 0/4, 1/2, 1/4, 6/8, and 4/4.

Explanation:
In the above-given question,
given that,
The fractions are 6/8, 4/4, 1/4, 1/2, and 0/4.
6/8 = 3/4.
2 x 3 = 6.
2 x 4 = 8.
so the fractions from least to greatest = 0/4, 1/2, 1/4, 6/8, and 4/4.

Question 14.
Eva and Landon had the same math homework. Eva finished the homework. Landon finished of the homework. Conjecture: Eva and Landon finished the same amount of their homework.
A. Complete the number lines to help think about the conjecture.

Answer:
The fractions are 1/4, 2/4, 3/4, and 4/4.
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, and 8/8.

Explanation:
In the above-given question,
given that,
Eva and Landon had the same math homework.
Eva finished the homework.
2/4 = 1/2.
2 x 1 = 2.
2 x 2 = 4.
so the missing fractions are 1/4, 2/4, 3/4, and 4/4.

B. Use your diagram to decide if the conjecture is correct. Explain.
Answer:

Question 15.
For each pair of fractions, write the equivalent whole number in the box.

Answer:
16/4 = 8/2 = 4.
6/3 = 4/2 = 2.
8/8 = 6/6 = 1.

Explanation:
In the above-given question,
given that,
the pair of fractions are 16/4, 8/2, 6/3, 4/2, 8/8, and 6/6.
16/4 = 8/2 = 4.
6/3 = 4/2 = 2.
8/8 = 6/6 = 1.

Topic 13 Performance Task

Clothing Store Devin, Jenna, Eli, and Gabby work at a clothing store. On Saturday they each worked the same number of hours.

The Time Spent at Cash Register table shows the fraction of time each person spent checking out customers. The Time Spent on Customer Calls table shows the fraction of an hour Jenna spent answering phone calls for the store.

Use the Time Spent at Cash Register table to answer Questions 1-3.

Question 1.
Draw fraction strips to show the fraction of time each person worked at the cash register.

Answer:
The fraction of time each person worked at the cash register = 3/6, 2/6, 6/6, and 5/6.

Explanation:
In the above-given question,
given that,
Devin, Jenna, Eli, and Gabby work at a clothing store.
Devin worked 3/6 hours a day.
Jenna worked 2/6 hours a day.
Eli worked 6/6 hours a day.
Gabby worked 5/6 hours a day.
the fraction of hours is 3/6, 2/6, 6/6, and 5/6.
so the fraction of time each person worked at the cash register = 3/6, 2/6, 6/6, and 5/6.

Question 2.
Who spent the most time at the cash register?

Answer:
The most time spent at the cash register = Gabby.

Explanation:
In the above-given question,
given that,
Devin, Jenna, Eli, and Gabby work at a clothing store.
Devin worked 3/6 hours a day.
Jenna worked 2/6 hours a day.
Eli worked 6/6 hours a day.
Gabby worked 5/6 hours a day.
3/6 = 1/2.
3 x 1 = 3.
3 x 2 = 6.
2/6 = 1/3.
2 x 1 = 2.
2 x 3 = 6.
6 / 6 = 1.
so the number of hours Gabby worked = 5/6.

Question 3.
Write a comparison to show the time Gabby spent at the cash register compared to the time Devin spent. Use >, <, or =.

Answer:
Gabby worked more hours than Devin.

Explanation:
In the above-given question,
given that,
Devin, Jenna, Eli, and Gabby work at a clothing store.
Devin worked 3/6 hours a day.
Jenna worked 2/6 hours a day.
Eli worked 6/6 hours a day.
Gabby worked 5/6 hours a day.
5/6 is greater than 3/6.
so Gabby worked more hours than Devin.

Question 4.
Use the Time Spent on Customer Calls table to answer this question: On which day did Jenna spend closest to one hour on the phone? Explain how you know.

Answer:
Jenna spends the closest to one hour on Monday.

Explanation:
In the above-given question,
given that,
on Saturday he spends a 3/6 fraction of an hour.
on Sunday he spends 3/5 fraction of an hour.
on Monday he spends 3/4 fraction of an hour.
3/6 = 1/2.
3/4 is nearest to the 1.
so Jenna spends the closest to one hour on Monday.

The store sells different colors of men’s socks. The Socks table shows the fraction for each sock color in the store.

Use the Socks table to answer Questions 5 and 6.

Question 5.
Part A
Complete the fractions on the number line. Label the fraction that represents each sock color.

Answer:
The fraction that represents each sock color = 1/4, 2/4, 3/4, and 1.
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, and 1.

Explanation:
In the above-given question,
given that,
The store sells different colors of men’s socks.
the white color socks are 1/8.
the black color sock is 1/4.
the brown color socks are 3/8.
the gray color socks are 2/8.
so the fraction that represents each sock color = 1/4, 2/4, 3/4, and 1.
1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, and 1.

Part B
Does the store have more brown socks or more white socks?

Answer:
The store has more brown socks = 3/8.

Explanation:
In the above-given question,
given that,
The store sells different colors of men’s socks.
the white color socks are 1/8.
the black color sock is 1/4.
the brown color socks are 3/8.
the gray color socks are 2/8.
3/8 is greater than 1/8.
so brown color socks are more than white color socks.

Question 6.
Use the number line in Exercise 5 Part A to construct an argument to justify the following conjecture: The store has an equal number of gray socks and black socks.

Answer:
Yes, the store has an equal number of gray socks and white socks.

Explanation:
In the above-given question,
given that,
The store sells different colors of men’s socks.
the white color socks are 1/8.
the black color sock is 1/4.
the brown color socks are 3/8.
the gray color socks are 2/8.
2/8 = 1/4.
2 x 1 = 2.
4 x 2 = 8.
so the store has the equal number of gray socks and white socks.

Question 7.
Use the Miguel’s Socks table to answer the question.

Miguel bought some socks at the clothing store. After he washed them, he counted the number of individual socks he has. Each sock is \(\frac{1}{2}\) of a pair. How many pairs of black socks does he have? Write this number as a fraction.

Answer:
The number of pairs of black socks does he have = 3 pairs.

Explanation:
In the above-given question,
given that,
Miguel bought some socks at the clothing store.
the number of black color socks = 6.
the number of gray color socks = 8.
3/6 and 4/8.
3/6 = 1/2.
4/8 = 1/2.
so the number of pairs of black socks does he have = 3 pairs.