Go through the enVision Math Common Core Grade 6 Answer Key Topic 5 Understand And Use Ratio And Rate regularly and improve your accuracy in solving questions.
enVision Math Common Core 6th Grade Answers Key Topic 5 Understand And Use Ratio And
Rate
Topic 5 Essential Question
What are ratios and rates? How can you use ratios and rates to describe quantities and solve problems?
3-ACT MATH

Get in Line
It is hard to call it a freeway when you are stuck in the middle of a traffic jam. To keep vehicles moving on the freeway, some on-ramps have traffic signals. Controlling when cars enter the freeway is not only about reducing delays. It can decrease air pollution and collisions.
These ramp meters typically have alternating green and red lights. The time for one cycle depends on the time of day and the amount of traffic on the freeway. Think about this during the 3-Act Mathematical Modeling lesson.

Topic 5 enVision STEM Project

Your Task: Get into Gear
Cyclists strive to achieve efficiency during continuous riding. But, which pairing of gears is the best or most efficient? And does the answer change depending on the terrain? You and your classmates will explore gear ratios and how they can affect pedaling and riding speeds.

Topic 5 Get Ready!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
- common factor
- common multiple
- equivalent fractions
- fraction
Question 1.
Fractions that name the same amount are called ___________
Answer:
Fractions that name the same amount are called equivalent fractions.
Explanation:
In the above-given question,
given that,
fractions that name the same amount are called equivalent fractions.
for example:
1/2 = 2/4.
2 x 1 = 2.
2 x 2 = 4.

Question 2.
The number 3 is a ___________ of 9 and 12.
Answer:
The number 3 is a factor of 9 and 12.
Explanation:
In the above-given question,
given that,
the number 3 is a factor of 9 and 12.
for example:
G.C.F of 9 and 12 = 3.
H.C.F of 9 and 12 = 3.
Question 3.
A number that can be used to describe a part of a set or a part of a whole is a(n) ___________
Answer:
A number that can be used to describe a part of a set or a part of a whole is a(n) common factor.
Explanation:
In the above-given question,
given that,
A number that can be used to describe a part of a set or a part of a whole is a(n) common factor.
for example:
G.C.F of 9 and 12 = 3.
H.C.F of 9 and 12 = 3.
Equivalent Fractions
Write two fractions equivalent to the given fraction.
Question 4.
\(\frac{3}{4}\)
Answer:
The two fractions are equivalent to the 3/4 = 9/12 and 27/36.
Explanation:
In the above-given question,
given that,
the fraction is 3/4.
the two fractions are equivalent to 3/4 is:
27/36 = 3/4.
9/12 = 3/4.
Question 5.
\(\frac{7}{8}\)
Answer:
The two fractions are equivalent to the 7/8 = 14/16 and 21/24.
Explanation:
In the above-given question,
given that,
the fraction is 7/8.
the two fractions are equivalent to 7/8 is:
14/16 = 7/8.
21/24 = 7/8.
Question 6.
\(\frac{12}{5}\)
Answer:
The two fractions are equivalent to the 12/5 = 24/10 and 84/60.
Explanation:
In the above-given question,
given that,
the fraction is 12/5.
the two fractions are equivalent to 12/5 is:
24/10 = 12/5.
84/60 = 12/5.

Question 7.
\(\frac{1}{2}\)
Answer:
The two fractions are equivalent to the 1/2 = 2/4 and 3/6.
Explanation:
In the above-given question,
given that,
the fraction is 1/2.
the two fractions are equivalent to 1/2 is:
2/4 = 1/2.
3/6 = 1/2.
Question 8.
\(\frac{8}{9}\)
Answer:
The two fractions are equivalent to the 8/9 = 16/18 and 24/27.
Explanation:
In the above-given question,
given that,
the fraction is 8/9.
the two fractions are equivalent to 8/9 is:
16/18 = 8/9.
24/27 = 8/9.
Question 9.
\(\frac{2}{3}\)
Answer:
The two fractions are equivalent to the 2/3 = 4/6 and 12/9.
Explanation:
In the above-given question,
given that,
the fraction is 2/3.
the two fractions are equivalent to 2/3 is:
4/6 = 2/3.
12/9 = 2/3.
Equation
Write an equation that represents the pattern in each table.
Question 10.
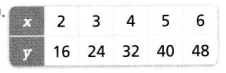
Answer:
The equation is y = 8x.
Explanation:
In the above-given question,
given that,
x contains numbers 2, 3, 4, 5, and 6.
y : 16, 24, 32, 40, and 48.
y = 8x.
16 = 8 x 2.
24 = 8 x 3.
32 = 8 x 4.
40 = 8 x 5.
48 = 8 x 6.
Question 11.

Answer:
The equation is y = 2x + 1.
Explanation:
In the above-given question,
given that,
x : 2, 4, 6, 8, and 10.
y : 5, 7, 9, 11, and 13.
y = 2x + 1.
5 = 2(2) + 1.
7 = 2(4) – 1.
9 = 2(6) – 3.

Units of Measure.
Choose the best unit of measure by writing inch, foot, yard, ounce, pound, ton, cup, quart, or gallon.
Question 12.
serving of trail mix
Answer:
The serving of a trail mix can be measured in cups.
Explanation:
In the above-given question,
given that,
Serving of a trail mix.
for example:
nutrition facts are also measured in cups.
Question 13.
height of a person
Answer:
The height of a person can be measured in feet.
Explanation:
In the above-given question,
given that,
the height of a person can be measured in feet.
for example:
the height of the short girl is 5 feet.
the height of the tall girl is 5.6 feet.
Question 14.
weight of a newborn kitten
Answer:
The weight of a newborn kitten can be measured in ounces.
Explanation:
In the above-given question,
given that,
the weight of a newborn kitten can be measured in ounces.
for example:
newborn kittens usually weigh about 3.5 ounces.
a healthy kitten should gain at least 10 grams per day.
Question 15.
gasoline
Answer:
Gasoline can be measured in cubic feet.
Explanation:
In the above-given question,
given that,
Gasoline can be measured in cubic feet.
for example:
gas is sometimes measured in cubic feet at a temperature of 60 degrees Fahrenheit and an atmospheric pressure of 14.7 pounds per square inch.
Measurement Conversions
Question 16.
Michael is 4 feet tall. Explain how Michael could find his height in inches. Then explain how he could find his height in yards.
Answer:
The height in inches = 48.
the height in yards = 12 yards.
Explanation:
In the above-given question,
given that,
Michael is 4 feet tall.
1 feet = 12 inches.
12 x 4 = 48 inches.
1 yard = 3 feets.
3 x 4 = 12 feets.
Language Development
A bag contains the following marbles:

Complete each math statement.
The following ratio statement reads, for every 1 red marble, there are ___2_____ yellow marbles.
A ratio that compares the yellow marbles to the green marbles is ___6_____ to ____4____.
3 : 4 is the ratio of red marbles to____green____ marbles.
The following ratio statement reads, for every 1 blue marble, there are 2 ___yellow_____ marbles.
\(\frac{3}{2}\) represents the ____ratio____ of red marbles to blue marbles.
4 to 15 is the ratio of green marbles to the ___total_____ number of marbles.
In the ratio of yellow marbles to blue marbles, 6:2, the quantities 6 and 2 are called __ratio______
A __ratio______ compares one ___quantity_____ to another ___quantity_____.
Pick A Project
PROJECT 5A
What animal would you most like to have as a pet?
PROJECT: COMPARE COSTS OF PET FOODS

Answer:
The animal I would most like to have as a pet is the dog.
Explanation:
In the above-given question,
given that,
the animal I would most like to have as a pet is the dog.
for example:
the cost of the lams is $1.07.
the cost of the Victor is $1.44.

PROJECT 5B
How fast do you think you can throw a baseball?
PROJECT: ANALYZE A SPORT STATISTIC

PROJECT 5C
What color would you want to paint a room?
PROJECT: EXPERIMENT WITH COMBINATIONS OF COLORS
Answer:
The color I would like to paint a room is cream color.
Explanation:
In the above-given question,
given that,
the color I would like to paint a room is cream color.
for example:
there are many different colors.
they are cream, red, pink, blue, and orange.
PROJECT 5D
If you could visit any U.S. National Park, which would it be?
PROJECT: PLAN A TOUR

Answer:
I could visit the Yellowstone National Park.
Explanation:
In the above-given question,
given that,
the Yellowstone national park wilderness and recreation area with active geysers like old faithful, plus canyons, rivers, and lakes.
so I could visit the Yellowstone national park.
the area of Yellowstone national park is 8,991 sq km.
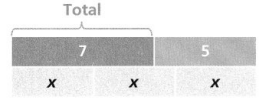
Lesson 5.1 Understand Ratios
Explore It!
A band just released an album that contains both pop songs and R&B (rhythm and blues) songs.
I can… use a ratio to describe the relationship between two quantities.

A. How can you describe the relationship between the number of pop songs and the number of R&B songs on the album?
Answer:
The relationship between the number of pop songs and the number of R&B songs is 3: 6.
Explanation:
In the above-given question,
given that,
there are 9 pop songs.
there are 6 R&B songs.
the relationship between the number of pop songs and the number of R&B songs is 9 and 6.
9 : 6 = 3 : 6.
3 x 3 = 9.
3 x 2 = 6.
so the relationship between the number of pop songs and the number of R&B songs is 3: 6.
B. How does the bar diagram represent the relationship between the number of pop songs and the number of R&B songs?

Answer:
The bar diagram represents the relationship between the number of pop songs and the number of R&B songs is 3: 6.
Explanation:
In the above-given question,
given that,
there are 9 pop songs.
there are 6 R&B songs.
the relationship between the number of pop songs and the number of R&B songs is 9 and 6.
9 : 6 = 3 : 6.
3 x 3 = 9.
3 x 2 = 6.
so the relationship between the number of pop songs and the number of R&B songs is 3: 6.
Focus on math practices
Reasoning Another album has 2 pop songs and 10 R&B songs. Draw a bar diagram that you could use to represent the relationship between the number of pop songs and the number of R&B songs.
Answer:
The relationship between the number of pop songs and the number of R&B songs = 1: 5.
Explanation:
In the above-given question,
given that,
Another album has 2 pop songs and 10 R&B songs.
2 : 10 = 1 : 5.
so the relationship between the number of pop songs and the number of R&B songs = 1: 5.

Essential Question
What is a mathematical way to compare quantities?
Try It!
What are three ways to write the ratio of the number of dogs to the total number of pets?
Answer:
The ratio of the number of dogs to the total number of pets = 3: 3.
Explanation:
In the above-given question,
given that,
the ratio of a number of dogs to the total number of pets is same.
for example:
3 : 3.
1: 1.
Convince Me! Is the ratio of dogs to cats the same as the ratio of cats to dogs? Explain.
Try It!
Chen’s friend Alisa can ride her bike 2 miles in 7 minutes. Use a bar diagram or a double number line diagram to find how long it would take Alisa to ride 10 miles if she rides at the same rate.
Answer:
The longer it would take Alisa to ride 10 miles = 70 minutes.
Explanation:
In the above-given question,
given that,
Chen’s friend Alisa can ride her bike for 2 miles in 7 minutes.
2 x 7 = 14 minutes.
10 x 7 = 70 minutes.
so the longer it would take Alisa to ride 10 miles = 70 minutes.
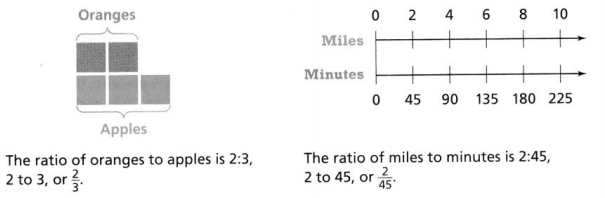
KEY CONCEPT
A ratio compares two quantities. A ratio can be written 3 ways: x to y, x:y, or Ratios can be represented using bar diagrams and double number line diagrams.
Do You Understand?
Question 1.
Essential Question What is a mathematical way to compare quantities?
Answer:
A ratio compares two quantities.
A ratio can be written in 3 ways: x to y, x: y, and x and y.
Explanation:
In the above-given question,
given that,
A ratio compares two quantities.
a ratio can be written in 3 ways are x to y.
x: y, and x/y.
so ratio compares two quantities.
Question 2.
Reasoning What are two different types of comparisons that a ratio can be used to make?
Answer:
The two different types of comparisons that a ratio can be used to make are x:y and x/y.
Explanation:
In the above-given question,
given that,
the ratio is x: y.
x to y.
x/y.
so the two different types of comparisons that a ratio can be used to make are x: y and x / y.
Question 3.
A science classroom has 5 turtles and 7 frogs. What is the ratio of frogs to total animals?

Answer:
The ratio of frogs to total animals is 7: 12.
Explanation:
In the above-given question,
given that,
A science classroom has 5 turtles and 7 frogs.
there are 7 frogs in the science classroom.
totally there are 12 animals.
frogs: animals.
7: 12.
so the ratio of frogs to total animals is 7: 12.

Question 4.
Tye is making trail mix with 3 cups of nuts for every 4 cups of granola. If Tye has 6 cups of nuts, how many cups of granola should he use?
Answer:
The number of cups of granola should use = 2: 3.
Explanation:
In the above-given question,
given that,
Tye is making trail mix with 3 cups of nuts for every 4 cups of granola.
6 : 3 = 2 : 3.
so the number of cups of granola should use = 2: 3.
Do You Know How?
In 5-7, use three different ways to write a ratio for each comparison.
A sixth-grade basketball team has 3 centers, 5 forwards, and 6 guards.
Question 5.
Forwards to guards
Answer:
Forwards to guards = 5: 6.
Explanation:
In the above-given question,
given that,
A sixth-grade basketball team has 3 centers, 5 forwards, and 6 guards.
Forwards to guards:
5: 6.
Question 6.
Centers to total players
Answer:
Centers to total players= 3: 14.
Explanation:
In the above-given question,
given that,
Centers to total players.
the total number of players = 14.
centers to total players = 3: 14.
Question 7.
Guards to centers
Answer:
Guards to centers = 6 : 3.
Explanation:
In the above-given question,
given that,
there are 6 Guards and 3 Guards.
6 : 3 = 2 : 3.
so Guards to centers = 6 : 3.
Question 8.
The ratio of blue cards to green cards is 2 to 5. There are 8 blue cards. Complete the diagram and explain how you can find the number of green cards.
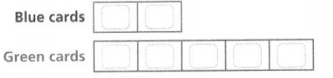
Answer:
The number of blue cards to the number of green cards = 8: 11.
Explanation:
In the above-given question,
given that,
The ratio of blue cards to green cards is 2 to 5.
There are 8 blue cards.
the number of green cards is 11.
so the number of blue cards to the number of green cards = 8: 11.
Practice & Problem Solving
In 9-14, use the data to write a ratio for each comparison in three different ways.
A person’s blood type is denoted with the letters A, B, and O, and the symbols + and -. The blood type A+ is read as A positive. The blood type B- is read as B negative.
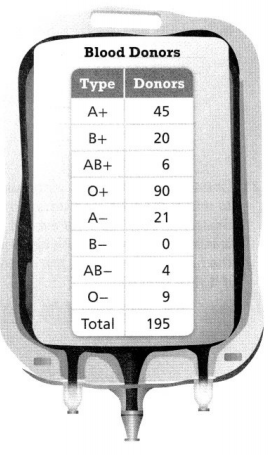
Question 9.
O+ donors to A+ donors
Answer:
O+ donors to A+ donors = 2 : 1.
Explanation:
In the above-given question,
given that,
A person’s blood type is denoted with the letters A, B, and O, and the symbols + and -.
O+ donors to A+ donors.
there are 90 O+ donors.
there are 45 A+ donors.
90 : 45 = 2 : 1.
Question 10.
AB-donors to AB+ donors
Answer:
AB- donors to AB+ donors = 2 : 3.
Explanation:
In the above-given question,
given that,
A person’s blood type is denoted with the letters A, B, and O, and the symbols+ and -.
AB- donors to AB+ donors.
there are 4 AB- donors.
there are 6 AB+ donors.
4 : 6 = 2 : 3.
so AB- donors to AB+ donors = 2 : 3.
Question 11.
B+ donors to total donors
Answer:
B+ donors to total donors = 20 : 195.
Explanation:
In the above-given question,
given that,
totally there are 195 donors.
B+ donors to total donors.
20: 195.
Question 12.
O- donors to A-donors
Answer:
O- donors to A- donors = 9 : 21.
Explanation:
In the above-given question,
given that,
O- donors to A- donors.
there are 9 O- donors.
there are 21 A- donors.
O- donors to A- donors = 9 : 21.
Question 13.
A+ and B+ donors to AB+ donors
Answer:
A+ and B+ donors to AB+ donors = 6 : 65.
Explanation:
In the above-given question,
given that,
A+ and B+ donors to AB+ donors.
there are A+ and B+ donors who are 65.
there are 6 AB+ donors.
A+ and B+ donors to AB+ donors = 6 : 65.
Question 14.
A- and B-donors to AB- donors
Answer:
A- and B- donors to AB- donors = 21: 4.
Explanation:
In the above-given question,
given that,
there are 21 A- donors.
there are 0 B- donors.
there are 4 AB- donors.
so A- and B- donors to AB- donors = 21: 4.
Question 15.
Which comparison does the ratio \(\frac{90}{9}\) represent?
Answer:
The ratio 90/9 represent = 10 : 1.
Explanation:
In the above-given question,
given that,
the ratio 90/9 represents.
90 : 9 = 10: 1.
so the ratio represent = 10 : 1.
Question 16.
Which comparison does the ratio 20:21 represent?
Answer:
The comparison does the ratio 20:21 represent = B+ and A-.
Explanation:
In the above-given question,
given that,
there are 20 B+ donors.
there are 21 A- donors.
so the ratio 20:21 represent = B+ and A+.
Question 17.
Sam is packing gift boxes with fruit. For each apple, he packs 3 plums and 5 oranges. If he puts 3 apples in a box, how many plums and oranges will Sam put in the box? Draw a diagram to solve the problem.

Answer:
The number of plums and oranges will Sam put in the box is 9:15.
Explanation:
In the above-given question,
given that,
Sam is packing gift boxes with fruit.
For each apple, he packs 3 plums and 5 oranges.
1:3, 2:6, and 3:9.
1:5, 2:10, and 3:15.
so the number of plums and oranges will Sam put in the box is 9:15.
Question 18.
Write a ratio that compares the number of teal squares to the total number of squares in the quilt.

Answer:
The ratio that compares the number of teal squares to the total number of squares in the quilt = 1:3.
Explanation:
In the above-given question,
given that,
there are 18 teal squares and 6 squares.
6 : 18 = 1:3.
so the ratio that compares the number of teal squares to the total number of squares in the quilt = 1:3.
Question 19.
Reasoning Rita’s class has 14 girls and 16 boys. How does the ratio 14:30 describe Rita’s class?
Answer:
The ratio 14:30 describes there are 7 girls and 15 boys.
Explanation:
In the above-given question,
given that,
Rita’s class has 14 girls and 16 boys.
there are 14 girls and 16 boys.
there are 14 girls and 30 boys.
14: 30 = 7:15.
so there are 7 girls and 15 boys.
Question 20.
A math class surveyed students about their musical preferences and recorded the results in the table. Use the data to write a ratio for each comparison in three different ways.

a. Students who prefer classical to students who prefer techno
Answer:
The students who prefer classical to students who prefer techno is 1:3.
Explanation:
In the above-given question,
given that,
there are 4 classical students.
there are 12 techno students.
4 : 12 = 1:3.
so the students who prefer classical to students who prefer techno is 1:3.
b. Students who prefer hip-hop to total number of students surveyed
Answer:
Students who prefer hip-hop to the total number of students surveyed = 15:53.
Explanation:
In the above-given question,
given that,
there are 15 hip-hop students.
the total number of students is 53.
so the ratio is 15:53.
Question 21.
Construct Arguments Justin used blocks to model the following situation: A car dealership sells 7 cars for every 4 minivans it sells. How can Justin use his model to find the number of minivans the dealership sells if it sells 35 cars?

Answer:
The number of minivans the dealership sells if it sells 35 cars = 20 minivans.
Explanation:
In the above-given question,
given that,
A car dealership sells 7 cars for every 4 minivans it sells.
35/7 = 5.
4 x 5 = 20.
so the number of minivans the sealership sells if it sells 35 cars = 20 minivans.
Question 22.
Make Sense and Persevere The ratio of adult dogs to puppies at a dog beach in Florida on Monday was 3:2. There were 12 puppies there that day. On Tuesday, 15 adult dogs were at the dog beach. What is the difference between the number of adult dogs at the dog beach on Monday and Tuesday?
Answer:
The difference between the number of adult dogs at the dog beach on Monday and Tuesday = 1:3.
Explanation:
In the above-given question,
given that,
The ratio of adult dogs to puppies at a dog beach in Florida on Monday was 3:2.
There were 12 puppies there that day.
On Tuesday, 15 adult dogs were at the dog beach.
12:15 = 4:5.
4:5 – 3:2 = 1:3.
so the difference between the number of adult dogs at the dog beach on Monday and Tuesday = 1:3.
Question 23.
Higher Order Thinking At 9:30 A.M., Sean started filling a swimming pool. At 11:30 A.M., he had filled 1,800 gallons. At what time will the pool be full?

Answer:
At 2:30 P.M the pool will fill completely.
Explanation:
In the above-given question,
given that,
At 9:30 A.M., Sean started filling a swimming pool.
At 11:30 A.M., he had filled 1,800 gallons.
for 2 hours it will fill 1800 gallons.
1800 + 1800 = 3600.
3600 + 900 = 4500.
so at 2:30 P.M the pool will fill completely.
Assessment Practice
Question 24.
The diagram below represents the relationship between the number of students taking Spanish and the number of students taking French in a foreign language class.
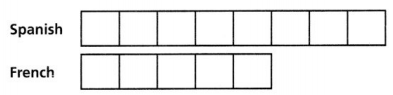
What is the ratio of the number of students taking Spanish to the number of students taking French?
A. 8 : 3
B. 8 : 5
C. 8 : 8
D. 8 : 13
Answer:
The ratio of the number of students taking Spinach to the number of students taking French = 8: 5.
Explanation:
In the above-given question,
given that,
the number of Spanish students is 8.
the number of French students is 5.
the ratio is 8:5.
so the ratio of a number of students taking spinach to the number of students taking french = 8:5.
Lesson 5.2 Generate Equivalent Ratios
Solve & Discuss It!
Sally used all of the paint shown below to make a certain tint of orange paint. How many pints of red paint should be mixed with 24 pints of yellow paint to make the same tint of orange?
I can… use multiplication and division to find equivalent ratios.

Look for Relationships
How can you use the relationship between the number of pints of yellow paint and the number of pints of red paint to answer the question?
Answer:
The ratio of yellow paint to the red paint is 4:3.
Explanation:
In the above-given question,
given that,
the number of yellow paint is 4.
the number of red paint is 3.
the relationship between the number of pints of yellow paint and the number of pints of red paint is 4:3.
Focus on math practices
Reasoning If Sally uses the same ratio of yellow paint to red paint, how many pints of yellow paint should she mix with 16 pints of red paint?
Essential Question
How can you find equivalent ratios?
Try It!
If you extend the table above, how would you find the next ratio of basketball players to soccer players?
Answer:
Convince Me! What is the relationship between the number of basketball players and the number of soccer players in each column in the table?
Try It!
Rashida uses 8 cups of tomatoes and 3 cups of onions to make salsa. How many cups of onions should Rashida use if she uses only 4 cups of tomatoes?
Answer:
Rashida use 1.5 cups of onions when she use 4 cups of tomatoes.
Explanation:
In the above-given question,
given that,
Rashida uses 8 cups of tomatoes and 3 cups of onions to make salsa.
for 1.5 cups of onions is used for 4 cups of tomatoes.
4 : 1.5.
so the ratio is 4:1.5.
Try It!
Which of the following ratios are equivalent to 16:20?
2:3, 4:5, 18:22, 20:25
Answer:
The ratio 4:5 equal to 16:20.
Explanation:
In the above-given question,
given that,
the ratios are 2:3, 4:5, 18:22, and 20:25.
16: 20 = 4:5.
so the ratio 4:5 equal to 16:20.
KEY CONCEPT
You can multiply or divide both terms of a ratio by the same nonzero number to find equivalent ratios.

Do You Understand?
Question 1.
Essential Question How can you find equivalent ratios?
Answer:
We can multiply or divide both terms of a ratio by the same nonzero number to find equivalent ratios.
Explanation:
In the above-given question,
given that,
multiply both terms by same non-zero number.
divide both terms by same non-zero number.
for example:
30 x 2 = 60.
40 x 2 = 80.
Question 2.
Critique Reasoning Deshawn says that the ratios 3:5 and 5:7 are equivalent ratios because by adding 2 to both terms of 3:5 you get 5:7. Is Deshawn correct? Explain.
Answer:
No, he was not correct.
Explanation:
In the above-given question,
given that,
Deshawn says that the ratios 3:5 and 5:7 are equivalent ratios because by adding 2 to both terms of 3:5 you get 5:7.
3:5 and 9:15.
so he was not correct.
Question 3.
What are two ways you can find an equivalent ratio for \(\frac{12}{16}\)?
Answer:
The equivalent ratio for 12/16 is 3:4.
Explanation:
In the above-given question,
given that,
the ratio is 12/16.
12: 16 = 3:4.
so the ratio is 3:4.
Question 4.
How can you show that the ratios 10:4 and 15:6 are equivalent?
Answer:
The ratios are not equal.
Explanation:
In the above-given question,
given that,
the ratios are 10:4 and 15:6.
10 : 4 = 15:6.
so the ratios are not equal.
Do You Know How?
Question 5.
Complete the table using multiplication to find ratios that are equivalent to 4:5.

Answer:
The ratios are 8:10, 12:15, and 16:20.
Explanation:
In the above-given question,
given that,
the ratio is 4:5.
8 : 10 = 4:5.
12:15 = 4:5.
16:20 = 4:5.
Question 6.
Complete the table using division to find ratios that are equivalent to 40:28.

Answer:
The ratios that are equivalent to 40:28 = 20:14 and 10:7.
Explanation:
In the above-given question,
given that,
the numbers are 40/28.
40/28 = 20/14.
40/28 = 10/7.
so the ratios that are equivalent to 40:28 = 20:14 and 10:7.
In 7-10, write an equivalent ratio for each given ratio.
Question 7.
\(\frac{12}{21}\)
Answer:
The equivalent ratio is
Explanation:
In the above-given question,
given that,
the ratio is 12/21.
Question 8.
1:3
Answer:
The equivalent ratio is 3:9.
Explanation:
In the above-given question,
given that,
the ratio is 1:3.
3:9 = 1:3.
3 x 1 = 3.
3 x 3 = 9.
so the equialent ratio is 3:9.
Question 9.
6 to 8
Answer:
The equivalent ratio is 3:4.
Explanation:
In the above-given question,
given that,
the ratio is 6 to 8.
6/8 = 3/4.
so the ratio is 3/4.
2 x 3 = 6.
2 x 4 = 8.
Question 10.
Pi (st) can be approximated using decimals as the ratio 3.14:1. Find 3 ratios equivalent to the ratio 3.14:1.
Answer:
The equivalent ratio is 22/7:1.
Explanation:
In the above-given question,
given that,
the ratio is 3.14:1.
22/7 = 3.14.
22/7:1 = 3.14:1.
Practice & Problem Solving
Question 11.
Eva is making French toast. How many ounces of milk should Eva use with 10 eggs?
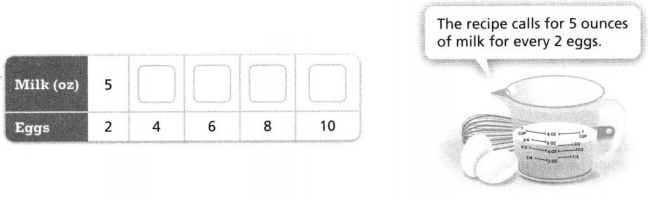
Answer:
The recipe uses 10, 15, 20, 25, and 30.
Explanation:
In the above-given question,
given that,
for 2 eggs the recipe uses 5 ounces of milk.
for 4 eggs the recipe uses 10 ounces of milk.
for 6 eggs the recipe uses 15 ounces of milk.
for 8 eggs the recipe uses 20 ounces of milk.
for 10 eggs the recipe uses 25 ounces of milk.
In 12-15, write three ratios that are equivalent to the given ratio.
Question 12.
\(\frac{6}{7}\)
Answer:
The three ratios are 3/14 and 18/21.
Explanation:
In the above-given question,
given that,
the ratio is 6/7.
3/14 = 6/7.
18/21 = 6/7.
so the three ratios are 3/14 and 18/21.
Question 13.
\(\frac{9}{5}\)
Answer:
The three ratios are 27/15 and 18/10.
Explanation:
In the above-given question,
given that,
the ratio is 9/5.
18/10 = 9/5.
27/15 = 9/5.
Question 14.
8:14
Answer:
The three ratios are 16/28 and 24/42.
Explanation:
In the above-given question,
given that,
the ratio is 8/14.
16/28 = 8/14.
24/42 = 8/14.
so the three ratios are 16/28 and 24/42.
Question 15.
7:9
Answer:
The three ratios are 6/28 and 21/27.
Explanation:
In the above-given question,
given that,
the ratio is 7/9.
6/28 = 7/9.
21/27 = 7/9.
Question 16.
A teacher kept track of what students consumed at a school picnic. For three grades, the ratios of the amount of water consumed to the amount of fruit juice consumed were equivalent. Complete the table.

Answer:
The juice contains 21 and 28 gallons.
Explanation:
In the above-given question,
given that,
A teacher kept track of what students consumed at a school picnic.
For three grades, the ratios of the amount of water consumed to the amount of fruit juice consumed were equivalent.
for 6th grade 24 gallons of water contains the juice 28 gallons.
for 7th grade 18 gallons of water contains the juice 21 gallons.
so the juice contains 21 and 28 gallons.
Question 17.
The attendant at a parking lot compared the number of hybrid vehicles to the total number of vehicles in the lot during a weekend. The ratios for the three days were equivalent. Complete the table.
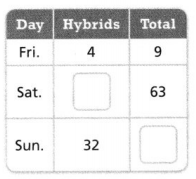
Answer:
The ratios for the three days were equivalent is 28 and 72.
Explanation:
In the above-given question,
given that,
The attendant at a parking lot compared the number of hybrid vehicles to the total number of vehicles in the lot during a weekend.
the ratios for the three days were equivalent.
28 and 72 are the equivalent ratio.
Question 18.
Shiloh is sharing jellybeans. The jar of jellybeans has the ratio shown. If Shiloh keeps the ratio the same and gives his friend 7 pink jellybeans, how many green jellybeans should he also share?
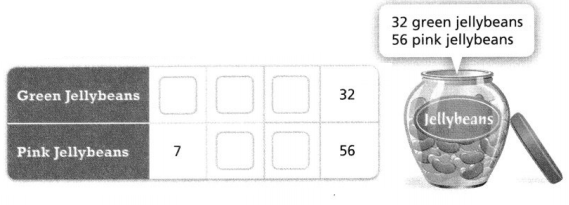
Answer:
The number of green jellybeans should he also share =
Explanation:
In the above-given question,
given that,
Shiloh is sharing jellybeans.
The jar of jellybeans has the ratio shown.
If Shiloh keeps the ratio the same and gives his friend 7 pink jellybeans.
Question 19.
Use Appropriate Tools Equivalent ratios can be found by extending pairs of rows or columns in a multiplication table. Write three ratios equivalent to \(\frac{2}{5}\) using the multiplication table.
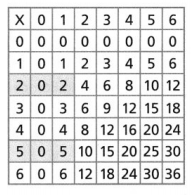
Answer:
The three ratios equivalent to 2/5 are 4/10 and 6/15.
Explanation:
In the above-given question,
given that,
the ratio is 2/5.
4/10 = 2/5.
6/15 = 2/5.
so the three ratios equivalent to 4/10 and 6/15.
Question 20.
If 5 mi ≈ 8 km, about how many miles would be equal to 50 km? Explain.

Answer:
The number of miles is equal to 31.069 miles.
Explanation:
In the above-given question,
given that,
5 miles ≈ 8 km.
50 km is equal to 31.069 miles.
so 31.069 miles is equal to 50 km.
Question 21.
Vocabulary How is the word term defined when used to describe a ratio relationship? How is the word term defined in the context of an expression?
Answer:
The term is one of the two numbers in the ratio a to b.
where a is the first term and b is the second term.
Explanation:
In the above-given question,
given that,
The term is one of the two numbers in the ratio a to b.
where a is the first term and b is the second term.
it is also used to indicate each one of the 4 numbers in a proportion.
if a = c.
then a,b,c, and d are the terms of the proportion.
Question 22.
Higher Order Thinking Three sisters are saving for a special vacation in Orlando, Florida. The ratio of Ada’s savings to Ellie’s savings is 7:3, and the ratio of Ellie’s savings to Jasmine’s savings is 3:4. Together all three girls have saved $56. How much has each girl saved? Complete the table. Explain how the table can be used to solve the problem.
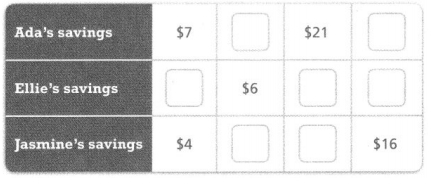
Answer:
The Ada’s savings are $14 and $28.
Ellie’s savings are $3, $9, and $12.
Jasmine’s savings are $8 and $12.
Explanation:
In the above-given question,
given that,
Three sisters are saving for a special vacation in Orlando, Florida.
The ratio of Ada’s savings to Ellie’s savings is 7:3, and the ratio of Ellie’s savings to Jasmine’s savings is 3:4.
Together all three girls have saved $56.
7 x 2 = 14, 7 x 4 = 28.
3 x 1 = 3, 3 x 3 = 9, and 3 x 4 = 12.
4 x 2 = 8, 4 x 3 = 12, and 4 x 4 = 16.
Assessment Practice
Question 23.
Corey is making key lime pies for the school fair. For every 3 egg yolks, he uses 2 tablespoons of key lime zest.
PART A
Complete the table to find equivalent ratios.
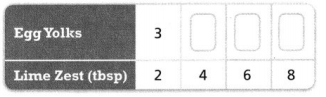
Answer:
The egg yolks are 6, 9, and 12.
Explanation:
In the above-given question,
given that,
Corey is making key lime pies for the school fair.
For every 3 egg yolks, he uses 2 tablespoons of key lime zest.
the equivalent ratios are 6, 9, and 12.
so the egg yolks are 6, 9, and 12.
PART B
How can you use the table to find how many egg yolks are needed for 8 tablespoons of lime zest?
Answer:
The number of egg yolks are 12 needed for 8 tablespoons of lime zest.
Explanation:
In the above-given question,
given that,
Corey is making key lime pies for the school fair.
For every 3 egg yolks, he uses 2 tablespoons of key lime zest.
3 x 1 = 3, 3 x 2 = 6, 3 x 3 = 9, and 3 x 4 =12.
so the number of egg yolks are 12 needed for 8 tablespoons of lime zest.
Question 24.
Which ratios can be represented by Pi (t)? Select all that apply.
☐ Diameter : Circumference
☐ Circumference : Diameter
☐ Circumference : Radius
☐ Radius : Circumference
☐ Circumference : Twice the radius
Answer:
Options A and B are correct.
Explanation:
In the above-given question,
given that,
diameter and circumference are represented.
so options A and B are correct.
Lesson 5.3 Compare Ratios
Solve & Discuss It!
Scott is making a snack mix using almonds and raisins. For every 2 cups of almonds in the snack mix, there are 3 cups of raisins. Ariel is making a snack mix that has 3 cups of almonds for every 5 cups of sunflower seeds. If Scott and Ariel each use 6 cups of almonds to make a batch of snack mix, who will make a larger batch?
I can… compare ratios to solve problems.

Model with Math
How can you use ratio tables to represent Scott’s and Ariel’s snack mixes?
Focus on math practices
Look for Relationships Scott and Ariel want to make as much snack mix as possible, but no more than 25 cups of mix. If they can use only full cups of ingredients, who can make more mix without going over?
Essential Question
How can you compare ratios to solve a problem?
Try It!
Marlon had 6 hits in 15 at bats. How does Marlon’s hits to at bats ratio compare to Adrian’s?
Answer:
The ratio is 2:5.
Explanation:
In the above-given question,
given that,
Marlon had 6 hits in 15 at bats.
6 : 15 = 2:5.
so the ratio is 2:5.
Convince Me! Based on their hits to at bats ratios, who would you expect to have more hits in a game, Marlon or Dustin? Explain.
Try It!
Tank 3 has a ratio of 3 guppies for every 4 angelfish. Complete the ratio table to find the number of angelfish in Tank 3 with 12 guppies.
Using the information in Example 2 and the table at the right, which tank with guppies has more fish?

Answer:
The number of Guppies is 6, 9, and 12.
the number of Angelfish is 8, 12, and 16.
Explanation:
In the above-given question,
given that,
Tank 3 has a ratio of 3 guppies for every 4 angelfish.
3 x 1 = 3.
3 x 2 = 6.
3 x 3 = 9.
3 x 4 = 12.
4 x 1 = 4.
4 x 2 = 8.
4 x 3 = 12.
4 x 4 = 16.
KEY CONCEPT
You can use ratio tables to compare ratios when one of the corresponding terms is the same.

Do You Understand?
Question 1.
Essential Question How can you compare ratios to solve a problem?
Answer:
We can use ratio tables to compare ratios when one of the corresponding terms is the same.
Explanation:
In the above-given question,
given that,
we can use ratio tables to compare ratios when one of the corresponding terms is the same.
for example:
5 x 2 = 10.
5 x 3 = 15.
5 x 4 = 20.
Question 2.
In Example 1, how many hits would Adrian have in 50 at bats? Explain.
Answer:
Question 3.
Reasoning During the first week of a summer camp, 2 out of 3 campers were boys. During the second week, 3 out of 5 campers were boys. There were 15 total campers each week. During which week were there more boy campers? Explain.
Answer:
In the second week, there are more boy campers.
Explanation:
In the above-given question,
given that,
During the first week of a summer camp, 2 out of 3 campers were boys.
During the second week, 3 out of 5 campers were boys.
There were 15 total campers each week.
so in the second week, there are more boy campers.
Do You Know How?
Question 4.
To make plaster, Kevin mixes 3 cups of water with 4 pounds of plaster powder. Complete the ratio table. How much water will Kevin mix with 20 pounds of powder?
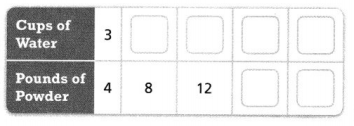
Answer:
The amount of Kevin mix with 20 pounds of powder = 15 cups of water.
Explanation:
In the above-given question,
given that,
To make plaster, Kevin mixes 3 cups of water with 4 pounds of plaster powder.
3 x 2 = 6.
3 x 3 = 9.
3 x 4 = 12.
3 x 5 = 15.
so the amount of Kevin mix with 20 pounds of powder = 15 cups of water.
Question 5.
Jenny makes plaster using a ratio of 4 cups of water to 5 pounds of plaster powder. Whose plaster recipe uses more water? Use the ratio table here and in Exercise 4 to compare.

Answer:
16 cups of water to 20 pounds of powder.
Explanation:
In the above-given question,
given that,
Jenny makes plaster using a ratio of 4 cups of water to 5 pounds of plaster powder.
8 cups of water to 10 pounds of powder.
12 cups of water to 15 pounds of powder.
16 cups of water to 20 pounds of powder.
Question 6.
Kevin and Jenny each use 12 cups of water to make plaster. Who will make more plaster? Explain.
Answer:
Kevin makes more plaster than Jenny.
Explanation:
In the above-given question,
given that,
Kevin and Jenny each use 12 cups of water to make plaster.
Kevin uses 12 cups of water to make 20 pounds of plaster.
Jenny uses 12 cups of water to make 15 pounds of plaster.
Practice & Problem Solving
In 7-10, use the ratio table at the right.

Question 7.
Local radio station WMTH schedules 2 minutes of news for every 20 minutes of music. Complete the ratios shown in the table at the right.
Answer:
The ratios are 30/3, 40/4, 50/5, and 60/6.
Explanation:
In the above-given question,
given that,
20 minutes of music is equal to 2 minutes of news.
20/2 = 10.
30/3 = 10.
40/4 = 10.
50/5 = 10.
60/6 = 10.
so the ratios are 30/3, 40/4, 50/5, and 60/6.
Question 8.
What is the ratio of minutes of music to minutes of news?
Answer:
The ratio of minutes of music to minutes of news = 10:1.
Explanation:
In the above-given question,
given that,
20 minutes of music is equal to 2 minutes of news.
20/2 = 10.
30/3 = 10.
40/4 = 10.
50/5 = 10.
60/6 = 10.
so the ratios are 30/3, 40/4, 50/5, and 60/6.
Question 9.
Radio station WILM broadcasts 4 minutes of news for every 25 minutes of music. Which radio station broadcasts more news each hour?
Answer:
The radio station broadcasts more news each hour =
Explanation:
In the above-given question,
given that,
Radio station WILM broadcasts 4 minutes of news for every 25 minutes of music.
Question 10.
Which station will have to be on the air longer to broadcast 4 minutes of news? Explain.
Answer:
The station will have to be on the air longer to broadcast 4 minutes of news = 40 minutes of music.
Explanation:
In the above-given question,
given that,
20 minutes of music is equal to 2 minutes of news.
20/2 = 10.
30/3 = 10.
40/4 = 10.
50/5 = 10.
60/6 = 10.
so the station will have to be on the air longer to broadcast 4 minutes of news = 40 minutes of music.
Question 11.
Reasoning The ratio tables at the right show the comparison of books to games for sale at Bert’s Store and at Gloria’s Store. Complete the ratio tables. Which store has the greater ratio of books to games? Explain.

Answer:
The ratio of Bert’s store is 5/7, 6/8, 7/9, and 8/10.
The ratio of Gloria’s store is 5/8, 6/9, 7/12, 8/15, and 9/18.
Explanation:
In the above-given question,
given that,
The ratio tables at the right show the comparison of books to games for sale at Bert’s Store and at Gloria’s Store.
the ratios of Bert’s store are 5/7, 6/8, 7/9, and 8/10.
the ratio of Gloria’s store is 5/8, 6/9, 7/12, 8/15, and 9/18.
Question 12.
The ratio of soy sauce to lime juice in a homemade salad dressing is 7:6. The ratio of soy sauce to lime juice in a store-bought dressing is 11:9. Which dressing has the greater ratio of soy sauce to lime juice?

Answer:
The ratio of Soy sauce to Lime juice is 7:6, 8:7, 9:8, 10:9, and 11:10.
the ratio of Soy sauce to lime juice is 11:9, 12:10, 13:11, 14:12, and 15:13.
Explanation:
In the above-given question,
given that,
The ratio of soy sauce to lime juice in a homemade salad dressing is 7:6.
The ratio of soy sauce to lime juice in a store-bought dressing is 11:9.
the ratio of soy sauce to the Lime juice is 7:6, 8:7, 9:8, 10:9, and 11:10.
the ratio of soy sauce to lime juice is 11:9, 12:10, 13:11, 14:12, and 15:13.
Question 13.
One bouquet of flowers has 3 milkweeds for every 5 tickseeds. Another bouquet has 4 tickseeds for every 5 canna lilies. If both bouquets have 20 tickseeds, which bouquet has more flowers?
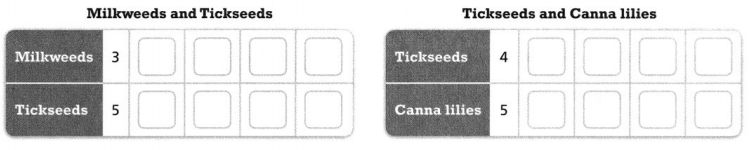
Answer:
Bouquet 4 has more flowers.
Explanation:
In the above-given question,
given that,
One bouquet of flowers has 3 milkweeds for every 5 tickseeds.
Another bouquet has 4 tickseeds for every 5 canna lilies.
3 x 5 =15.
4 x 6 = 24.
5 x 7 = 35.
6 x 8 = 48.
7 x 9 = 63.
4 x 5 = 20.
5 x 6 = 30.
6 x 7 = 42.
7 x 8 = 56.
8 x 9 = 72.
Question 14.
Higher Order Thinking Lauren can drive her car 320 miles on 10 gallons of gasoline. Melissa can drive her car 280 miles on 8 gallons of gasoline. Who can drive farther on 40 gallons of gasoline? Complete the ratio tables to justify your solution.
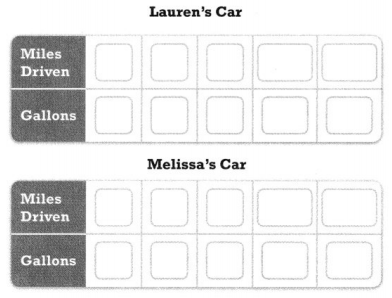
Answer:
Explanation:
In the above-given question,
given that,
Lauren can drive her car 320 miles on 10 gallons of gasoline.
Melissa can drive her car 280 miles on 8 gallons of gasoline.
320/10 and 280/8.
Assessment Practice
Question 15.
Fran buys Florida cone seashells in packages that contain 9 purple-dyed Florida cone seashells for every 3 pink-dyed Florida cone seashells. Mia buys Florida cone seashells in packages with a ratio of 2 pink-dyed Florida cone seashells to 4 purple-dyed Florida cone seashells.
PART A
Complete the tables using the ratios given.
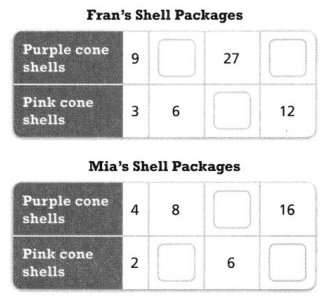
Answer:
The missing ratios of Fran’s shell packages are 18/6, 27/9, and 36/12.
the missing ratios of Mia’s shell packages are 8/4, 12/6, and 16/8.
Explanation:
In the above-given question,
given that,
Fran buys Florida cone seashells in packages that contain 9 purple-dyed Florida cone seashells for every 3 pink-dyed Florida cone seashells.
6 x 3 = 18, 3 x 3 = 9, 9 x 3 = 27, and 12 x 3 = 36.
2 x 2 = 4, 4 x 2 = 8, 6 x 2 = 12, and 8 x 2 = 16.
PART B
If the girls each buy packages that contain 6 pinkdyed Florida cone seashells, how many purple-dyed Florida cone seashells would each have? Explain.
Answer:
The number of purple-dyed Florida cone seashells would each have = 18.
Explanation:
In the above-given question,
given that,
If the girls each buy packages that contain 6 pink dyed Florida cone seashells.
6 x 3 = 18.
so the number of purple-dyed Florida cona seashells would each have = 18.
Lesson 5.4 Represent and Graph Ratios
Solve & Discuss It!
For every 4 adults at the beach one afternoon, there were 3 children. How many children were at the beach if there were 8, 12, 16, or 20 adults at the beach?
I can… solve ratio problems by using tables and graphs to show equivalent ratios.
Model with Math
How does the graph show the ratio?
Answer:
The graph shows the ratio y = x-1, y = x-2, y = x-4.
Explanation:
In the above-given question,
given that,
For every 4 adults at the beach one afternoon, there were 3 children.
if there were 8 adults there were 6 children.
if there were 12 adults there were 9 children.
4 x 1 = 4, 4 x 2 = 8, 4 x 3 = 12, and 4 x 4 = 16.
3 x 1 = 3, 3 x 2 = 6, 3 x 3 = 9, and 3 x 4 = 12.
Focus on math practices
Critique Reasoning There were 25 children and 15 adults at the beach. Emery said that there were 5 children for every 3 adults. Is he correct? Explain.
Answer:
Yes, Emery was correct.
Explanation:
In the above-given question,
given that,
There were 25 children and 15 adults at the beach.
Emery said that there were 5 children for every 3 adults.
3 x 5 = 15.
for 15 adults there were 25 children.
so Emery was correct.
Essential Question
How can you use tables and graphs to show equivalent ratios?
Try It!
What are the coordinates of the point that represents the number of balloons you can buy for $6?
Answer:
The coordinates of the point that represents the number of balloons we can but for $6 is (6,0) and (0,6).
Explanation:
In the above-given question,
given that,
for example:
for example:
the points are (6, 0) and (0,6).
Convince Me! How can you use the graph to find the cost of 15 balloons?
Try It!
Can you draw an object with a diameter of 10 inches and a circumference of 50 inches? Explain.
Answer:
Yes, we can draw a diameter of 10 inches and a circumference of 50 inches.
Explanation:
In the above-given question,
given that,
we can draw a diameter of 10 inches and a circumference of 50 inches.
the circumference is the center of the circle.
radius is half of the diameter.
diameter is 50/2 = 25.
so we can draw a diameter.
KEY CONCEPT
You can use ratio tables and graphs to show equivalent ratios. When ordered pairs representing equivalent ratios are graphed as points in the coordinate plane, they form a line.
Do You Understand?
Question 1.
Essential Question How can you use tables and graphs to show equivalent ratios?
Answer:
When ordered pairs representing equivalent ratios are graphed as points in the coordinate plane, they form a line.
Explanation:
In the above-given question,
given that,
for example:
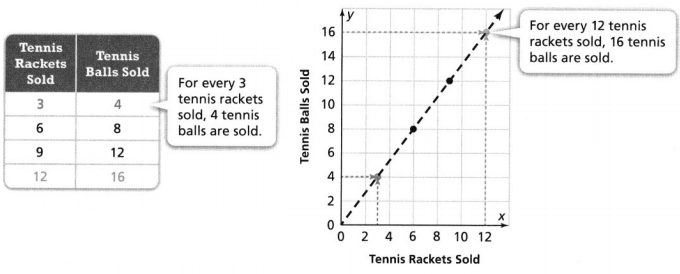
for every 3 tennis rackets sold, 4 tennis balls are sold.
for every 12 tennis rockets sold, 16 tennis balls are sold.
so when ordered pairs representing equivalent ratios are graphed as points in the coordinate plane, they form a line.
Question 2.
Look for Relationships In Example 2, how could you use the graph to find the number of apples needed for 30 celery sticks?
Answer:
The number of apples needed for 30 celery sticks = 40 apples.
Explanation:
In the above-given question,
given that,
if there are 30 celery sticks, there would be 40 apples.
3 x 10 = 30.
4 x 10 = 40.
so the number of apples needed for 30 celery sticks = 40 apples.
Question 3.
How could you use repeated addition to show ratios equivalent to 1:3 on a graph?
Answer:
The ratios forms a straight line.
Explanation:
In the above-given question,
given that,
for example:
for every 3 tennis rackets sold, 4 tennis balls are sold.
for every 12 tennis rockets sold, 16 tennis balls are sold.
so when ordered pairs representing equivalent ratios are graphed as points in the coordinate plane, they form a line.
Do You Know How?
Question 4.
Complete the table to show equivalent ratios representing a cost of $8 for every 3 boxes. Then write the pairs of values as points to be plotted on a coordinate plane.
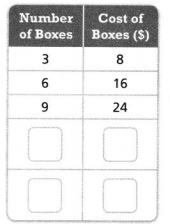
Answer:
The points are (12, 32) and (15, 40).
Explanation:
In the above-given question,
given that,
3 x 2 = 6, 3 x 3 = 9, 3 x 4 = 12, and 3 x 5 = 15.
8 x 2 = 16, 8 x 3 = 24, 8 x 4 = 32, and 8 x 5 = 40.
so the coordinate points are (12, 32) and (15, 40).
Question 5.
Model with Math Plot the equivalent ratios (3, 4), (6, 8), and (9, 12) on the graph. Use the graph to find the number of nonfiction books purchased if 10 fiction books are purchased.
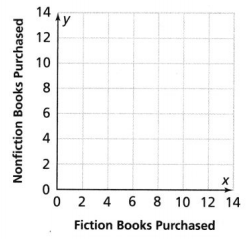
Answer:
The number of nonfiction books purchased if 10 fiction books are purchased = 14.
Explanation:
In the above-given question,
given that,
the equivalent ratios are (3, 4), (6, 8), (9, 12), and (10, 14).
the points form a straight line.
so the number of nonfiction books purchased if 10 fiction books are purchased = 14.
Practice & Problem Solving
Leveled Practice in 6 and 7, complete the table and graph the pairs of values.
Question 6.
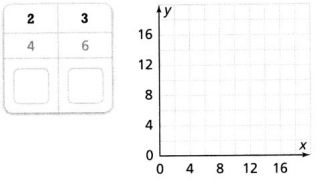
Answer:
The points are (6, 9).
Explanation:
In the above-given question,
given that,
The points are (2,3) and (4,6).
2 x 2 = 4, 2 x 3 = 6.
3 x 2 = 6, 3 x 3 = 9.
so the points are (6, 9).
Question 7.
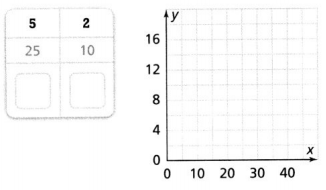
Answer:
The points are (50, 20).
Explanation:
In the above-given question,
given that,
the points are (5, 2) and (25, 10).
5 x 5 = 25, 5 x 10 = 50.
2 x 5 = 10, 2 x 10 = 20.
so the points are (50, 20).
Question 8.
A student runs 2 minutes for every 10 minutes she walks.
a. Complete the table. Graph the pairs of values.
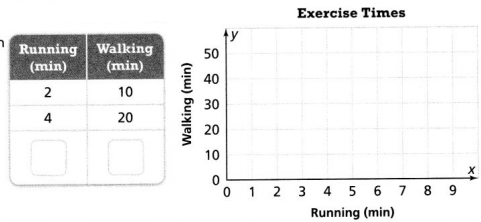
Answer:
The points are (6, 30).
Explanation:
In the above-given question,
given that,
the running minutes are 2, 4.
the walking minutes are 10, 20.
2 x 2 = 4.
2 x 3 = 6.
10 x 2 = 20.
10 x 3 = 30.
so the points are (6, 30).
b. For how long would the student walk if she runs for 7 minutes?
Answer:
The student walks if she runs for 7 minutes = 35.
Explanation:
In the above-given question,
given that,
the running minutes are 2, 4.
the walking minutes are 10, 20.
2 x 2 = 4.
2 x 3 = 6.
10 x 2 = 20.
10 x 3 = 30.
so the student walks if she runs for 7 minutes = 35.
Question 9.
A car magazine reports the number of miles driven for different amounts of gas for three cars. Which car travels the farthest on 1 gallon of gas? Explain.
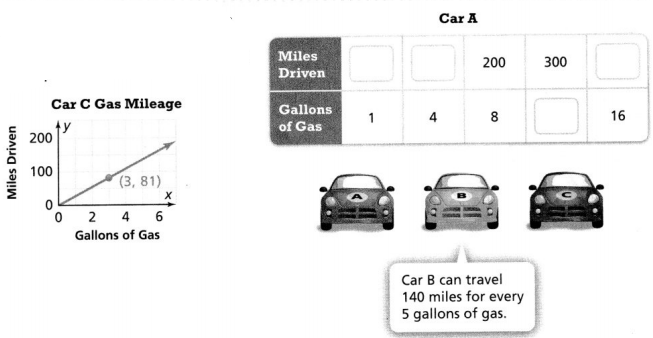
Answer:
Car A can travels the farthest on 1 gallon of gas.
Explanation:
In the above-given question,
given that,
Car A can travels for 1 gallon of gas the number of miles driven is 50.
Car B can travels for 1 gallon of gas the number of miles driven is 30.
Car C can travels for 1 gallon of gas the number of miles driven is 25.
So car A can travels the farthest on 1 gallon of gas.
Question 10.
Model with Math A bread recipe calls for 4 cups of white flour for every 5 cups of whole-wheat flour. Complete the table to show how many cups of whole-wheat flour are needed to mix with 16 cups of white flour. Then graph the pairs of values.
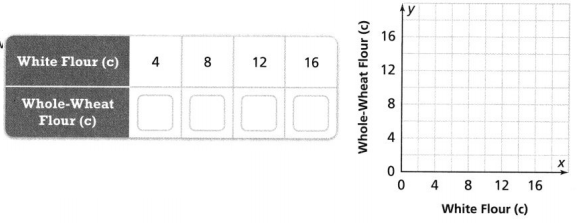
Answer:
The points of whole-wheat flour are 4, 8, 12, and 16.
Explanation:
In the above-given question,
given that,
A bread recipe calls for 4 cups of white flour for every 5 cups of whole-wheat flour.
4 x 1 = 4, 4 x 2 = 8, 4 x 3 = 12, and 4 x 4 = 16.
so the points of whole-wheat flour is 4, 8, 12, and 16.
Question 11.
The graph shows the relationship between the number of cups of sugar and the number of cups of flour in a key-lime bread recipe. What point on the graph represents the number of cups of sugar that would be used with 8 cups of flour?

Answer:
The number of cups of sugar that would be used with 8 cups of flour is 2.
Explanation:
In the above-given question,
given that,
the flour(c) is on the x-axis.
the sugar (c) is on the y-axis.
the points are (2, 0.5), (4, 1), (6, 1.5), (8, 2), (10, 2.5), (12, 3), and (14, 3.5).
so the number of cups of sugar that would be used with 8 cups of flour is 2.
Question 12.
Higher Order Thinking Ishwar can read 5 pages in 15 minutes. Anne can read 15 pages in 1 hour. Explain how you could use a table or graph to find how much longer it would take Anne to read a 300-page book than Ishwar.
Answer:
The much longer it would take Anne to read a 300-page book than Ishwar = 20 hours.
Explanation:
In the above-given question,
given that,
Ishwar can read 5 pages in 15 minutes.
Anne can read 15 pages in 1 hour.
30 pages in 2 hours.
60 in 4 hours.
90 in 6 hours.
90 + 90 = 180 pages in 12 hours.
8 hours is 120 pages.
12 + 8 = 20 hours.
Assessment Practice
Question 13.
The measurements of a circular object are given in the ratio table.
PART A
Find the missing dimensions of other circular objects by completing the ratio table.
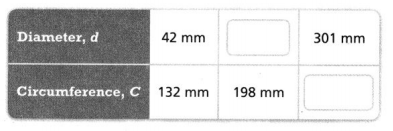
Answer:
The missing dimensions are 42 and 301.
Explanation:
In the above-given question,
given that,
The measurements of a circular object are given in the ratio table.
the missing dimensions are 42 and 301.
PART B
Graph the pairs of values.
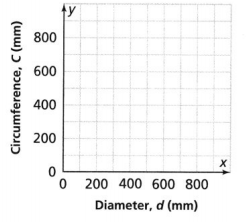
Answer:
The points are (200, 200), (400, 400), (600, 600), and (800, 800).
Explanation:
In the above-given question,
given that,
the diameter is shown on the x-axis.
the circumference is shown on y-axis.
so the points are (200, 200), (400, 400), (600, 600), and (800, 800).
Topic 5 Mid-Topic Checkpoint
Question 1.
Vocabulary How can a ratio be used to compare quantities? Lesson 5-1
Answer:
Question 2.
The circumference of the outside of a ring is 66 mm, and it has an outer diameter of 21 mm. If the circumference of the inside of the ring is 50 mm, what is the inner diameter of the ring? Lesson 5-4
Answer:
The inner diameter of the ring = 50 mm.
Explanation:
In the above-given question,
given that,
The circumference of the outside of a ring is 66 mm, and it has an outer diameter of 21 mm.
If the circumference of the inside of the ring is 50 mm.
the inner diameter of the ring = 50 mm.
Question 3.
During the breakfast service, the D-Town Diner sells 12 cups of coffee for every 10 glasses of orange juice. How many cups of coffee would the diner have sold if 40 glasses of orange juice had been sold? Complete the table with equivalent ratios. Lesson 5-2
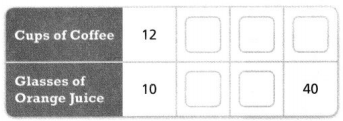
Answer:
The ratios are (24, 20), (36, 30), and (48,40).
Explanation:
In the above-given question,
given that,
During the breakfast service, the D-Town Diner sells 12 cups of coffee for every 10 glasses of orange juice.
2 x 5 = 10, and 2 x 6 = 12.
3 x 10 = 30, and 3 x 12 = 36.
4 x 10 = 40, and 4 x 12 = 48.
so the ratios are (24, 20), (36, 30), and (48, 40).
Question 4.
The ratio of cows to chickens at Old McDonald’s Farm is 2:7. Select all the farms that have a greater ratio of cows to chickens than Old McDonald’s Farm. Lessons 5-3
☐ Red’s Farm: 3 cows for every 5 chickens
☐ Pasture Farm: 2 cows for every 9 chickens
☐ Cluck & Moo Farm: 1 cow for every 5 chickens
☐ C & C Farm: 3 cows for every 8 chickens
☐ T Family Farm: 1 cow for every 3 chickens
Answer:
Question 5.
A package of 3 notebooks costs $5. Complete the ratio table and graph the pairs of values. How much will 18 notebooks cost? Lesson 5-4

Answer:
The cost of 18 notebooks is $30.
Explanation:
In the above-given question,
given that,
A package of 3 notebooks costs $5.
3 x 2 = 6, 3 x 3 = 9, 3 x 4 = 12, 3 x 5 =15, 3 x 6 = 18.
5 x 2 = 10, 5 x 3 = 15, 5 x 4 = 20, 5 x 5 = 25, 5 x 6 = 30.
so the cost of 18 notebook is $30.
Topic 5 Mid-Topic Performance Task
Hillsdale Orchard grows Fuji apples and Gala apples. There are 160 Fuji apple trees and 120 Gala apple trees in the orchard.
PART A
Hillsdale Orchard’s owners decide to plant 30 new Gala apple trees. Complete the ratio table to find the number of new Fuji apple trees the owners should plant if they want to maintain the same ratio of Fuji apple trees to Gala apple trees.
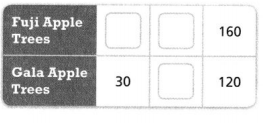
Answer:
The number of Fuji Apple trees to the Gala Apple trees is (40,30), (80, 60), and (160,120).
Explanation:
In the above-given question,
given that,
Hillsdale Orchard’s owners decide to plant 30 new Gala apple trees.
30 x 2 = 60.
60 x 2 = 120.
40 x 2 = 80.
80 x 2 = 160.
so the number of Fuji Apple trees to the Gala Apple trees is (40,30), (80, 60), and (160, 120).
PART B
Use the ratio table to complete a graph that shows the relationship between the number of Fuji apple trees and Gala apple trees at Hillsdale Orchard.
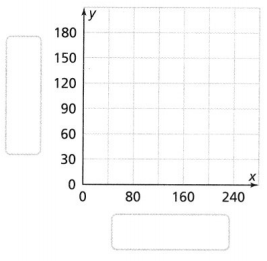
Answer:
Fuji Apple trees on the x-axis.
Gala Apple trees on the y-axis.
Explanation:
In the above-given question,
given that,
Fuji Apple trees on the x-axis.
Gala Apple trees on the y-axis.
the points are (80, 60), (160, 120), and (240, 180).
PART C
By the end of the next season, the owners of Hillsdale Orchard plan to have 240 Fuji apple trees. Explain how you could use the graph to find the total number of Fuji and Gala apple trees that Hillsdale Orchard will have if the owners achieve their goal.
Answer:
The total number of Fuji and Gala apple trees that Hillsdale Orchard is (240, 180).
Explanation:
In the above-given question,
given that,
the owners of Hillsdale Orchard plan to have 240 Fuji apple trees.
the points are (80, 60), (160, 120), and (240, 180).
so the total number of Fuji and Gala apple trees that Hillsdale Orchard is (240, 180).
Lesson 5.5 Understand Rates and Unit Rates
Solve & Discuss It!
What is the cost of 10 bottles of fruit juice?
I can… solve problems involving rates.

Make Sense and Persevere
How can you use tables or diagrams to make sense of the quantities in the problem?
Focus on math practices
Critique Reasoning Monica says, “If 4 bottles cost $10, then 2 bottles cost $5, and 8 bottles cost $20. So 10 bottles cost $5 + $20.” Is Monica correct? Explain.
Answer:
No Monica was not correct.
Explanation:
In the above-given question,
given that,
If 4 bottles cost $10, then 2 bottles cost $5, and 8 bottles cost $20.
4 bottles cost $10.
8 bottles cost $20.
10 bottles cost $30.
so Monica was not correct.
Essential Question
What are rates and unit rates?
Try It!
At the same rate, how long would it take the car to travel 60 kilometers?
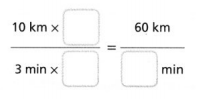
It will take the car _______ minutes to travel ________ kilometers.
Answer:
It will take the car 6 minutes to travel 60 kilometers.
Explanation:
In the above-given question,
given that,
10 x 6 = 60.
3 x 6 = 18.
it will take the car 6 minutes to travel 60 kilometers.
Convince Me! Sal draws the double number line diagram at the right. He says it shows that at this rate the race car will travel 35 kilometers in 10.5 minutes. Critique Sal’s reasoning. Is he correct? Explain.

Answer:
Yes, he was correct.
Explanation:
In the above-given question,
given that,
Sal draws the double number line diagram at the right.
He says it shows that at this rate the race car will travel 35 kilometers in 10.5 minutes.
the points are (3, 10), (6, 20), (9, 30), (10.5, 35), and (12, 40).
so he was correct.
Try It!
A recipe for scrambled eggs uses 2 tablespoons of milk for every 3 eggs. What are two unit rates that could represent the recipe?
Answer:
The two-unit rates that could represent the recipe = 2/3, 4/6, and 6/9.
Explanation:
In the above-given question,
given that,
A recipe for scrambled eggs uses 2 tablespoons of milk for every 3 eggs.
2 x 2 = 4, 2 x 3 = 6, 2 x 4 = 8.
3 x 2 = 6, 3 x 3 = 9, 3 x 4 = 12.
so the two-unit rates that could represent the recipe = 2/3, 4/6, and 6/9.
Try It!
A canoeing club travels 78 miles in 3 days. How far could they travel in 5 days if they maintain the same speed?
Answer:
They can travel 130 miles in 5 days.
Explanation:
In the above-given question,
given that,
A canoeing club travels 78 miles in 3 days.
78 miles in 3 days.
78/3 = 26.
26 + 26 = 52.
78 + 52 = 130.
so they can travel 130 miles in 5 days.
KEY CONCEPT
A rate compares quantities with unlike units of measure.
\(\frac{\$ 3.50}{7 \text { oranges }}\)
A unit rate compares a quantity to 1 unit of another quantity.
\(\frac{\$ 3.50}{7 \text { oranges }}=\frac{\$ 0.50}{1 \text { orange }}\)
Do You Understand?
Question 1.
Essential Question What are rates and unit rates?
Answer:
A rate compares quantities with unlike units of measure.
A unit rate compares a quantity to 1 unit of another quantity.
Explanation:
In the above-given question,
given that,
A rate compares quantities with unlike units of measure.
A unit rate compares a quantity to 1 unit of another quantity.
for example:
3.50/7 = 0.5.
Question 2.
Be Precise Use what you know about ratios to describe a rate.
Answer:
A rate compares quantities with unlike units of measure.
A unit rate compares a quantity to 1 unit of another quantity.
Explanation:
In the above-given question,
given that,
A rate compares quantities with unlike units of measure.
A unit rate compares a quantity to 1 unit of another quantity.
for example:
3.50/7 = 0.5.
Question 3.
Reasoning A bathroom shower streams 5 gallons of water in 2 minutes.
a. Find the unit rate for gallons per minute and describe it in words.
Answer:
The unit rate for gallons per minute is 2.5.
Explanation:
In the above-given question,
given that,
A bathroom shower streams 5 gallons of water in 2 minutes.
5/2 = 2.5.
so the unit rate for gallons per minute.
b. Find the unit rate for minutes per gallon and describe it in words.
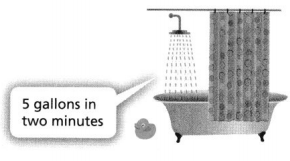
Answer:
The unit rate for minutes per gallon = 2.5.
Explanation:
In the above-given question,
given that,
A bathroom shower streams 5 gallons of water in 2 minutes.
5/2 = 2.5.
so the unit rate for gallons per minute.
Do You Know How?
In 4 and 5, find the value of n.
Question 4.

Answer:
The number of hours for n = 12.
Explanation:
In the above-given question,
given that,
the number of hours is 4 for the number of miles = 45.
45 + 45 + 45 = 135.
4 + 4 + 4 = 12.
so for the n hours the number of miles = 12.
Question 5.
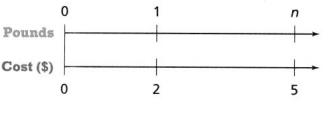
Answer:
The value of n is 4.
Explanation:
In the above-given question,
given that,
the cost in dollars are shown in the figure.
the pounds are also shown.
for 2 dollars the pounds count is 1.
for 3 dollars the pounds count is 2.
for 4 dollars the pounds count is 3.
for 5 dollars the pounds count is 4.
so the value of n is 4.
Question 6.
Jenny packaged 108 eggs in 9 cartons. Write this statement as a rate.
Answer:
Jenny packaged 108 eggs in 2 cartons.
Explanation:
In the above-given question,
given that,
Jenny packaged 18 eggs in 9 cartons.
18/9 = 2.
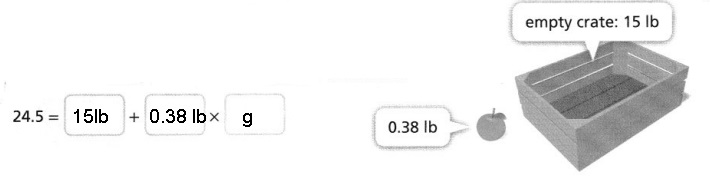
so the Jenny packaged 108 eggs in 9 cartons is 2.
Question 7.
Anna Maria read 40 pages in 60 minutes. What is her unit rate in pages per minute?
Answer:
The unit rate in pages per minute = 0.6.
Explanation:
In the above-given question,
given that,
Anna Maria read 40 pages in 60 minutes.
40/60 = 4/6.
2/3 = 0.6.
so the unit rate in pages per minute = 0.6.
In 8 and 9, use the unit rates that you found in Exercise 3.
Question 8.
How many gallons of water does the shower stream in 6 minutes?
Answer:
The number of gallons of water does the shower stream in 6 minutes = 6.6.
Explanation:
In the above-given question,
given that,
40/6 = 20/3.
20/3 = 6.6.
so the number of gallons of water does the shower stream in 6 minutes = 6.6.
Question 9.
How long can someone shower to use only 10 gallons of water?
Answer:
The shower to use only 10 gallons of water = 0.5.
Explanation:
In the above-given question,
given that,
the long can someone shower to use only 10 gallons of water.
10/20 = 1/2 = 0.5.
so the length can someone shower to use only 10 gallons of water = 0.5.
Practice & Problem Solving
In 10 and 11, write each statement as a rate.
Question 10.
Jan saw 9 full moons in 252 days.
Answer:
The rate is 0.03.
Explanation:
In the above-given question,
given that,
Jaw saw 9 full moons in 252 days.
9/252 = 0.03.
so the rate is 0.03.
Question 11.
It took Hannah 38 minutes to run 8 laps.

Answer:
The rate is 4.75.
Explanation:
In the above-given question,
given that,
It took Hannah 38 minutes to run 8 laps.
38/8 = 4.75.
so the rate is 4.75.
In 12 and 13, find the value of x.
Question 12.
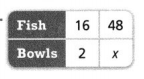
Answer:
The value of x is 8.
Explanation:
In the above-given question,
given that,
the number of bowls is 2.
the number of fish in 2 bowls is 16.
the number of bowls is 6.
the number of fish in 6 bowls is 48.
48/6 = 8.
so the value of x is 8.
Question 13.
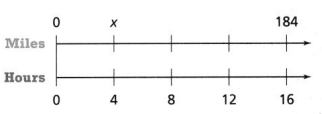
Answer:
The value of x is 46.
Explanation:
In the above-given question,
given that,
the number of miles and the number of hours are given.
the number of miles for 4 is 46.
the number of miles for 8 is 92.
the number of miles for 12 is 138.
the number of miles for 16 is 184.
In 14 and 15, find the unit rate.
Question 14.
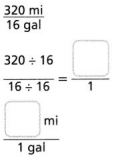
Answer:
The number of miles is 20.
Explanation:
In the above-given question,
given that,
320 mi/16 gal.
320/16 / 16/16.
20/1 = 20.
so the number of miles is 20.
Question 15.
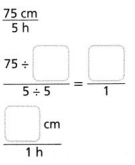
Answer:
The value of cm = 15.
Explanation:
In the above-given question,
given that,
75 cm to 5 h.
75/5 / 5/5.
15 / 1 = 15.
so the value of the cm = 15.
In 16-19, complete each table.
Question 16.
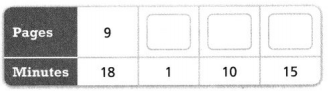
Answer:
The missing values are 2, 5, 5.
Explanation:
In the above-given question,
given that,
the minutes on the number of pages are given.
9 x 2 = 18.
1 x 2 = 2.
5 x 2 =10.
5 x 3 = 15.
Question 17.
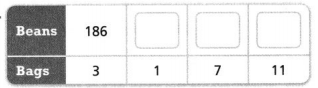
Answer:
The missing values are 62, 434, and 682.
Explanation:
In the above-given question,
given that,
186/3 = 62.
62/1 = 62.
434/7 = 62.
682/11 = 62.
so the missing values are 62, 434, and 682.
Question 18.

Answer:
The missing values are 12.3, 61.5, and 10.
Explanation:
In the above-given question,
given that,
12.3/1 = 12.3.
24.6/2 = 12.3.
61.5/5 =12.3.
123/10 = 12.3.
so the missing values are 12.3, 61.5, and 10.
Question 19.
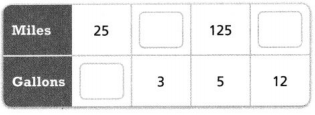
Answer:
The missing values are 1, 75, 300.
Explanation:
In the above-given question,
given that,
the number of gallons and miles are given.
125/5 = 25.
25/1 = 25.
75/3 = 25.
300/12 = 25.
so the missing values are 1, 75, and 300.
Question 20.
Which runner set the fastest pace? Explain.
Answer:
Allison runs at the fastest pace.
Explanation:
In the above-given question,
given that,
the runner Martha did 20 laps in 32 min.
the runner Allison did 16 laps in 25 min.
the runner Rachel did 17 laps in 27.2 min.
speed = distance/time.
Martha = 20/32.
Martha = 0.625.
Allison = 16/25.
Allison = 0.64.
Rachel = 17/27.2.
Rachel = 0.625.
Allison runs at the fastest pace.
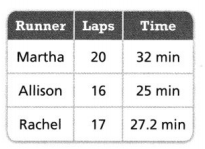
Question 21.
Model with Math Over the summer, Alexis read 15 books in 12 weeks. The diagram below can be used to track her progress. If Alexis read at the same rate each week, how many books had she read in 4 weeks? In 8 weeks? Complete the diagram.
Answer:
The missing books are 5 and 10.
Explanation:
In the above-given question,
given that,
Over the summer, Alexis read 15 books in 12 weeks.
Alexis read the 5 books in 4 weeks.
the number of books Alexis read in 8 weeks = 10.
5 x 1 = 5.
5 x 2 = 10.
5 x 3 = 15.
so the missing books are 5 and 10.
Question 22.
An elephant charges an object that is 0.35 kilometer away. How long will it take the elephant to reach the object?

Answer:
The distance will it take the elephant to reach the object = 0.5 km.
Explanation:
In the above-given question,
given that,
An elephant charges an object that is 0.35 kilometers away.
Elephants can charge at speeds of 0.7 km per minute.
0.35/0.7 = 0.5.
7 x 5 = 35.
so the distance will it take the elephant to reach the object = 0.5 km.
Question 23.
A machine takes 1 minute to fill 6 cartons of eggs. At this rate, how many minutes will it take to fill 420 cartons?
Answer:
The number of minutes will it take to fill 420 cartons = 70 min.
Explanation:
In the above-given question,
given that,
A machine takes 1 minute to fill 6 cartons of eggs.
70 x 6 = 420.
420/6 = 70.
so the number of minutes will it take to fill 420 cartons = 70 min.
Question 24.
Higher Order Thinking How are the ratios \(\frac{24 \text { laps }}{1 \text { hour }}\) and \(\frac{192 \text { laps }}{8 \text { hours }}\) alike? How are they different?
Answer:
They are same.
Explanation:
In the above-given question,
given that,
the ratios 24, 192, and 8 are alike.
8 x 1 = 8.
8 x 3 = 24.
24 x 8 = 192.
so they are same.
Assessment Practice
Question 25.
A bakery sells 12 gourmet orange-zest cupcakes for $36.00. Select all the statements that are true.
☐ \(\frac{\$ 3.00}{1 \text { cupcake }}\) is a unit rate for the cost per 1 cupcake cupcake.
☐ \(\frac{36}{12}\) represents the ratio of $36.00 for 12 cupcakes.
☐ Using the same rate, the bakery can sell 6 cupcakes for $20.00.
☐ Using the same rate, the bakery can sell 2 dozen cupcakes for $72.00.
☐ Using the same rate, it would cost $24.50 for 8 cupcakes.
Answer:
Option A is correct.
Explanation:
In the above-given question,
given that,
A bakery sells 12 gourmet orange-zest cupcakes for $36.00.
36/12 = 3.
12 x 3 = 36.
so option A is correct.
Lesson 5.6 Compare Unit Rates
Solve & Discuss It!
Rick and Nikki own remote-control cars. They use a stopwatch to record the speed of each car. Whose car is faster?
I can… compare unit rates to solve problems.

Be Precise
Use precise numbers and units to describe and compare rates.
Focus on math practices
Make Sense and Persevere If each car maintains its rate of speed, how long will it take Rick’s car to travel 300 feet? How long will it take Nikki’s car to travel the same distance? Explain.
Answer:
The long will it take Nikki’s car to travel the same distance = 60 sec.
Explanation:
In the above-given question,
given that,
Rick and Nikki own remote-control cars.
the distance in 30 sec is 150 feet.
the distance will it take 300 feet in 60 sec.
300/150 = 2.
30 x 2 = 60.
so the long will it take Nikki’s car to travel the same distance = 60 sec.
Essential Question
How can you use unit rates to make comparisons?
Try It!
Ashley is Austin’s older sister. She trains in the same pool and can swim 9 laps in 6 minutes. Is Ashley a faster swimmer than Austin?
Ashley swims 1.5 laps per minute. Because ________ 1.4, Ashley is a _______ swimmer than Austin.
Answer:
Ashley swims faster than Austin.
Explanation:
In the above-given question,
given that,
Ashley is Austin’s older sister.
She trains in the same pool and can swim 9 laps in 6 minutes.
Ashley swims 1.5 laps per minute.
9/1.5 = 6.
6/1.4 = 4.2.
so Ashley swims faster than Austin.
Convince Me! How can you use the unit rate in minutes per lap to compare Ashley’s speed to Austin’s speed?
Try It!
Explain how to decide which is the better value, 4 greeting cards for $10 or 6 greeting cards for $14.

Answer:
The better value is 4 greeting cards for $10.
Explanation:
In the above-given question,
given that,
4 greeting cards for $10.
6 greeting cards for $14.
10/4 = 2.5.
14/6 = 2.3.
so the better value is 4 greeting cards for $10.
KEY CONCEPT
You can use unit rates to make comparisons.
$8.50 per hour > $8.00 per hour
\(\frac{32 \mathrm{~cm}}{1 \mathrm{sec}}\) < \(\frac{45 \mathrm{~cm}}{1 \mathrm{sec}}\)
\(\frac{7 \text { laps }}{1 \mathrm{~min}}\) < \(\frac{9 \text { laps }}{1 \mathrm{~min}}\) 175 words per minute > 95 words per minute
Do You Understand?
Question 1.
Essential Question How can you use unit rates to make comparisons?
Answer:
We can use unit rates to make comparisons.
Explanation:
In the above-given question,
given that,
You can use unit rates to make comparisons.
$8.50 per hour > $8.00 per hour.
175 words per minute > 95 words per minute.
Question 2.
Critique Reasoning Paul says that a lower unit rate is a better value only if you can use all the items purchased to get the lower unit rate. Do you agree? Explain.
Answer:
Yes, i will agree.
Explanation:
In the above-given question,
given that,
Paul says that a lower unit rate is a better value only if you can use all the items purchased to get the lower unit rate.
so I will agree.
Question 3.
Reasoning Car A travels 115 miles on 5 gallons of gas. Car B travels 126 miles on 6 gallons of gas. How can you find which car gets better gas mileage?
Answer:
The Car A gets better gas mileage.
Explanation:
In the above-given question,
given that,
Car A travels 115 miles on 5 gallons of gas.
Car B travels 126 miles on 6 gallons of gas.
115/5 = 23.
126/6 = 21.
so car A gets better gas mileage.
Do You Know How?
Question 4.
Hakim’s car travels 600 feet in 20 seconds. Andre’s motorcycle travels 300 feet in 12 seconds. Which is faster, the car or the motorcycle? Explain.

a. Find the unit rates.
Answer:
The car is faster.
Explanation:
In the above-given question,
given that,
Hakim’s car travels 600 feet in 20 seconds.
Andre’s motorcycle travels 300 feet in 12 seconds.
300/12 = 25.
600/20 = 30.
so the car is faster.
b. Compare the unit rates.
Answer:
In 5 and 6, find each unit price.
Question 5.
7 movie tickets for $56
Answer:
Each ticket cost $8.
Explanation:
In the above-given question,
given that,
7 movie tickets for $56.
$56/7 = 8.
so each ticket cost $8.
Question 6.
12 fluid ounces of shampoo for $2.76
Answer:
12 fluid ounces of shampoo for $2.76.
Explanation:
In the above-given question,
given that,
12 fluid ounces of shampoo for $2.76.
12/2.76 = 4.34.
so 12 fluid ounces of shampoo for $2.76.
Question 7.
Which is the better value, 2 books for $15 or 6 books for $45? Explain.
Answer:
Both of them have better value.
Explanation:
In the above-given question,
given that,
2 books for $15.
6 books for $45.
15 + 15 + 15 = 45.
so both of them have the better value.
Practice & Problem Solving
Leveled Practice In 8 and 9, find each unit price.
Question 8.
9 pens for $3.60
\(\frac{\$ 3.60 \div 9}{9 \div 9}=\frac{ }{1}\)
Answer:
9 pens for $3.60 = $2.5.
Explanation:
In the above-given question,
given that,
9 pens for $3.60.
9/3.60 = 2.5.
so 9 pens for $3.60 = $2.5.
Question 9.
15 ounces of canned beans for $2.25
\(\frac{\$ 2.25 \div}{15 \div}=\frac{}{}\)
Answer:
15 ounces of canned beans for $2.25 = 6.6.
Explanation:
In the above-given question,
given that,
15 ounces of canned beans for $2.25.
15/2.25 = 6.6.
so 15 ounces of canned beans for $2.25 = 6.6.
In 10 and 11, determine which is the better value.
Question 10.
3 kilograms of charcoal for $7.95 or 5 kilograms of charcoal for $12.50
Answer:
7.95/3 = 2.65 and 12.50/5 = 2.5.
Explanation:
In the above-given question,
given that,
3 kilograms of charcoal for $7.95.
5 kilograms of charcoal for $12.50.
7.95/3 = 2.65.
12.50/5 = 2.5.
Question 11.
50 envelopes for $2.49 or 90 envelopes for $5.50
Answer:
50 envelopes for $2.49 or 90 envelopes for $5.50 is 16.36.
Explanation:
In the above-given question,
given that,
50 envelopes for $2.49 or 90 envelopes for $5.50.
50/2.49 = 20.08.
90/5.50 = 16.36.
In 12-15, compare the rates to find which is greater.
Question 12.
35 points in 20 minutes or 49 points in 35 minutes
Answer:
35 points in 20 minutes or 49 points in 35 minutes are 1.75 and 1.4.
Explanation:
In the above-given question,
given that,
35 points in 20 minutes or 49 points in 35 minutes.
35/20 = 1.75.
49/35 = 1.4.
Question 13.
12 laps in 8 minutes or 16 laps in 10 minutes
Answer:
16 laps in 10 minutes.
Explanation:
In the above-given question,
given that,
12 laps in 8 minutes or 16 laps in 10 minutes.
12/8 = 1.5.
16/10 = 1.6.
so 16 laps in 10 minutes.
Question 14.
45 strikeouts in 36 innings or 96 strikeouts in 80 innings
Answer:
45 strikeouts in 36 innings or 96 strikeouts in 80 innings = 1.2.
Explanation:
In the above-given question,
given that,
45 strikeouts in 36 innings or 96 strikeouts in 80 innings.
45/36 = 1.25.
96/80 = 1.2.
Question 15.
480 stickers on 6 sheets or 120 stickers on 2 sheets
Answer:
120 stickers on 2 sheets is 60.
Explanation:
In the above-given question,
given that,
480 stickers on 6 sheets or 120 stickers on 2 sheets.
480/6 = 80.
120/2 = 60.
so 120 stickers on 2 sheets is 60.
In 16-18, compare the rates to find which is the better value.

Question 16.
$27 for 4 large pizzas or $32 for 5 large pizzas
Answer:
The both values are same.
Explanation:
In the above-given question,
given that,
$27 for 4 large pizzas or $32 for 5 large pizzas.
$27/4 = $6.75.
$32/5 = $6.4.
so both values are same.
Question 17.
$30 for 100 flyers or $65 for 250 flyers
Answer:
$30 for 100 flyers = 3.3.
Explanation:
In the above-given question,
given that,
$30 for 100 flyers.
$65 for 250 flyers.
100/30 = 3.3.
250/100 = 2.5.
Question 18.
36 pictures for $8 or 24 pictures for $5
Answer:
24 pictures for $5 = 4.8.
Explanation:
In the above-given question,
given that,
36 pictures for $8 or 24 pictures for $5.
36/8 = 4.5.
24/5 = 4.8.
so 24 pictures for $5 = 4.8.
Question 19.
Model with Math Katrina and Becca exchanged 270 text messages in 45 minutes. An equal number of texts was sent each minute. The girls can send 90 more text messages before they are charged additional fees. Complete the double number line diagram. At this rate, for how many more minutes can the girls exchange texts before they are charged extra?
Answer:
The missing values are 90/6, 180/6, and 360/6.
Explanation:
In the above-given question,
given that,
Katrina and Becca exchanged 270 text messages in 45 minutes.
An equal number of texts was sent each minute.
The girls can send 90 more text messages before they are charged additional fees.
90/6 = 15.
180/6 = 30.
360/6 = 60.
so the missing values are 90/6, 180/6, and 360/6.
Question 20.
Reasoning Which container of milk would you buy? Explain.

Answer:
I will buy 1/2 gallon of milk for $2.29.
Explanation:
In the above-given question,
given that,
1/2 gallon of milk for $2.29.
1 gallon of milk for $3.99.
$2.29/0.5 = 4.58.
$3.99/1 = 3.99.
I will buy 1/2 gallon of milk for $2.29.
Question 21.
Higher Order Thinking Amil and Abe rode in a bike-a-thon. Abe rode for 77 minutes at a faster rate per mile than Amil. Find Amil’s unit rate. Then explain how you could use it to find a possible unit rate for Abe.

Answer:
Abe’s rate is 4.5.
Explanation:
In the above-given question,
given that,
Amil and Abe rode in a bike-a-thon.
Abe rode for 77 minutes at a faster rate per mile than Amil.
77/17 = 4.5.
so Abe’s rate was 4.5.
Assessment Practice
Question 22.
A food warehouse sells cans of soup in boxes. Bargain shoppers have four options.
PART A
Complete the table to find the unit price for each option.

Answer:
The unit price is 1.13, 1.17, 1.16, and 1.12.
Explanation:
In the above-given question,
given that,
A food warehouse sells cans of soup inboxes.
12 cans for $10.56 = 1.13.
16 cans for $13.60 = 1.17.
20 cans for $17.20 = 1.16.
24 cans for $21.36 = 1.12.
PART B
Compare the unit rates found in Part A and identify the best value.
Answer:
The best value is 1.17.
Explanation:
In the above-given question,
given that,
A food warehouse sells cans of soup inboxes.
12 cans for $10.56 = 1.13.
16 cans for $13.60 = 1.17.
20 cans for $17.20 = 1.16.
24 cans for $21.36 = 1.12.
Lesson 5.7 Solve Unit Rate Problems
Solve & Discuss It!
Suppose you are traveling by train to visit a friend who lives 275 miles away. How long will the trip take? Moving at a constant speed, how long would it take the train to travel 385 miles?
I can… use unit rates to solve problems.

Model with Math
How can you use what you know about unit rates to model and solve this problem?
Focus on math practices
Reasoning Suppose the train was traveling at a constant speed that is twice as fast as 55 miles per hour. How long would it take the train to go 275 miles? Explain.
Answer:
The long would it take the train to go 275 miles = 5.
Explanation:
In the above-given question,
given that,
Suppose you are traveling by train to visit a friend who lives 275 miles away.
the train travels at a constant speed of 55 miles per hour.
275/55 = 5.
so the long would it take the train to go 275 miles = 5.
Essential Question
How can you use unit rates to solve problems?
Try It!
At the same rate, how far would the jet fly in 75 minutes?
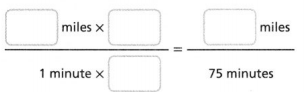
The jet would fly ________ miles.
Answer:
The jet would fly 1 mile.
Explanation:
In the above-given question,
given that,
15 x 5 = 75.
1 minute x 75 = 75.
75 miles/75 minutes = 1.
Convince Me! How could you use the table from Example 1 to find how far the jet would fly in 75 minutes? Explain.
Try It!
Jarod paid $13.80 for 5 tickets to the game. At the same rate, how much would 3 tickets cost?
Answer:
The 3 tickets cost is $8.28.
Explanation:
In the above-given question,
given that,
Jarod paid $13.80 for 5 tickets to the game.
$13.80/5 = $2.76.
$2.76 + $2.76 + $2.76 = $8.28.
so the 3 tickets cost is $8.28.
Try It!
A submarine travels 19 miles in \(\frac{1}{2}\) hour. Write an equation to find out how long it would take the submarine to travel 57 miles at the same rate. Then find the time.
Answer:
The submarine to travel 57 miles at the same rate = 3.
Explanation:
In the above-given question,
given that,
A submarine travels 19 miles in \(\frac{1}{2}\) hour.
19 miles in 0.5 hours.
19 x 3 = 57.
57/19 = 3.
so the submarine to travel 57 miles at the same rate = 3.
KEY CONCEPT
You can use ratio tables or unit rates to solve rate problems, including constant speed problems.

Do You Understand?
Question 1.
Essential Question How can you use unit rates to solve problems?
Answer:
We can use ratio tables to solve rate problems including constant speed problems.
Explanation:
In the above-given question,
given that,
we can use ratio tables to solve rate problems including constant speed problems.
Ant traveled 6 cm in 1.5 sec.
ant traveled 3 cm in 12 sec.
ant traveled 4.5 cm in 18 sec.
Question 2.
Construct Arguments An ostrich runs 6 miles in 12 minutes at a constant speed. Explain how you can use a unit rate to find how far the ostrich could run in 40 minutes.
Answer:
The far ostrich could run in 40 minutes = 8 miles.
Explanation:
In the above-given question,
given that,
An ostrich runs 6 miles in 12 minutes at a constant speed.
40/6 = 8.
so the far ostrich could run in 40 minutes = 8 miles.
Question 3.
Bananas sell for $0.58 per pound. How could you write an equation to show the relationship between the total cost, c, and the number of pounds of bananas, p?
Answer:
C = $0.58p.
Explanation:
In the above-given question,
given that,
Bananas sell for $0.58 per pound.
the total cost is written as c.
the number of pounds is written as p.
c = $0.58p.
Do You Know How?
In 4 and 5, use unit rates to solve.
Question 4.
A football player runs 80 yards in 25 seconds. If he maintains the same rate of speed, how far could he run in 60 seconds?
Answer:
The far could he run in 60 seconds = 1.3.
Explanation:
In the above-given question,
given that,
A football player runs 80 yards in 25 seconds.
80/25 = 3.2.
80/60 = 1.3.
so the far could he run in 60 seconds = 1.3.
Question 5.
On a family vacation, Amy’s dad drove the car at a constant speed and traveled 585 miles in 13 hours. At this rate, how long would it have taken the family to travel 810 miles? What was the car’s rate of speed?
Answer:
The rate of the car’s speed = 45 hours.
Explanation:
In the above-given question,
given that,
Amy’s dad drove the car at a constant speed and traveled 585 miles in 13 hours.
585/13 = 45.
45 x 13 = 585.
so the rate of the car’s speed = 45 hours.
Question 6.
Look at Exercise 5. Write an equation to find the total distance, d, that Amy’s family traveled after t hours.
Answer:
Practice & Problem Solving
Leveled Practice In 7-9, solve the rate problems.
Question 7.
A horse named Northern Dancer won the Kentucky Derby with a time of exactly 2 minutes. At this constant rate, how long would it take Northern Dancer to run the Belmont Stakes?
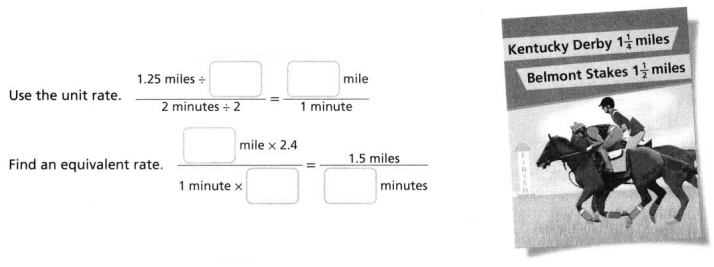
It would take Northern Dancer ______ minutes to run the Belmont Stakes.
Answer:
It would take Northern dancer 2 minutes to run the Belmont stakes.
Explanation:
In the above-given question,
given that,
A horse named Northern Dancer won the Kentucky Derby with a time of exactly 2 minutes.
1.25/ 1.25/1 = 1 mile/1 minute.
the equivalent rate is 1.5/2.
so it would take Northern dancer 2 minutes to run the Belmont stakes.
Question 8.
If a cyclist rides at a constant rate of 24 miles per hour, how long would it take the cyclist to ride 156 miles?
Answer:
The long would it take the cyclist to ride 156 miles = 6.5 hours.
Explanation:
In the above-given question,
given that,
If a cyclist rides at a constant rate of 24 miles per hour.
156/24 = 6.5.
so the long would it take the cyclist to ride 156 miles = 6.5 hours.
Question 9.
The price of an 8-minute phone call is $1.20. What is the price of a 17-minute phone call?
Answer:
The price of a 17-minute phone call = 0.07.
Explanation:
In the above-given question,
given that,
The price of an 8-minute phone call is $1.20.
$1.20/8 = 0.15.
$1.20/17 = 0.07.
so the price of a 17-minute phone call = 0.07.
In 10 and 11, use the map at the right.

The Garcia family is driving from Sacramento, California, to Key West, Florida. In 5 days, they have traveled 2,045 miles. At this rate, how long will it take them to travel from Sacramento to Key West?
Question 10.
How can you use rate reasoning to solve this problem? Explain.
Answer:
The rate will it take them to travel from Sacramento to Key West = 409.
Explanation:
In the above-given question,
given that,
The Garcia family is driving from Sacramento, California, to Key West, Florida.
In 5 days, they have traveled 2,045 miles.
2045/5 = 409.
so the rate will it take them to travel from Sacramento to Key West = 409.
Question 11.
Be Precise Show how to use numbers, units, and symbols precisely to solve the problem.
Answer:
Question 12.
Vik wrote the equation 470 • h = 3,008, where h is the number of hours it took a plane flying at a constant speed of 470 miles per hour to travel 3,008 miles. Solve for h.
Answer:
The number of miles per hour to travel 3008 miles = 6.4.
Explanation:
In the above-given question,
given that,
Vik wrote the equation 470 • h = 3,008,
470. h = 3008.
h = 3008/470.
h = 6.4.
so the number of miles per hour to travel 3008 miles = 6.4.
Question 13.
A nursery owner buys 7 panes of glass to fix some damage to his greenhouse. The 7 panes cost $15.05. Unfortunately, he breaks 2 more panes while repairing the damage. What is the cost of another 2 panes of glass?

Answer:
The cost of another 2 panes of glass = $7.5.
Explanation:
In the above-given question,
given that,
A nursery owner buys 7 panes of glass to fix some damage to his greenhouse.
the 7 panes cost $15.05.
$15.05 / 7 = $2.15.
$15.05 / 2 = 7.525.
so the cost of another 2 panes of glass = $7.5.
Question 14.
Cheyenne drew a circle with diameter 1 meter. She measured the circumference to estimate the value of Pi. Complete the table, and then write an equation to find the circumference, C, for a circle with diameter d.
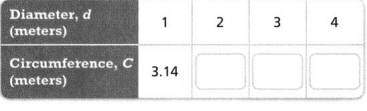
Answer:
The circumference, C, for a circle with diameter d is 6.28, 9.42, and 12.56.
Explanation:
In the above-given question,
given that,
Cheyenne drew a circle with a diameter of 1 meter.
She measured the circumference to estimate the value of Pi.
3.14 x 1 = 3.14.
3.14 x 2 = 6.28.
3.14 x 3 = 9.42.
3.14 x 4 = 12.56.
so the circumference, c, for a circle with diameter d is 6.28, 9.42, and 12.56.
Question 15.
Jayden bought 70 feet of speaker wire for $18.20. He needs 30 more feet. If the unit price is the same, how much will Jayden pay for the extra 30 feet of wire? Explain.
Answer:
The much will Jayden pay for the extra 30 feet of wire = 0.60.
Explanation:
In the above-given question,
given that,
Jayden bought 70 feet of speaker wire for $18.20.
He needs 30 more feet.
$18.20/70 = 0.26.
$18.20/30 = 0.60.
so the much will Jayden pay for the extra 30 feet of wire = 0.60.
Question 16.
Higher Order Thinking Sasha runs at a constant speed of 3.8 meters per second for \(\frac{1}{2}\) hour. Then she walks at a constant rate of 1.5 meters per second for \(\frac{1}{2}\) hour. How far did Sasha run and walk in 60 minutes?
Answer:
The far did Sasha run and walk in 60 minutes = 30.
Explanation:
In the above-given question,
given that,
Sasha runs at a constant speed of 3.8 meters per second for \(\frac{1}{2}\) hour.
Then she walks at a constant rate of 1.5 meters per second for \(\frac{1}{2}\) hour.
3.8/ 0.5 = 7.6.
1.5 / 0.5 = 30.
so the far did Sasha run and walk in 60 minutes = 30.
Assessment Practice
Question 17.
Suppose that a leatherback turtle swam 7.5 kilometers in 3 hours at a constant speed.
PART A
How many kilometers per hour did the turtle swim?
Answer:
The turtle swim per hour = 2.5 miles.
Explanation:
In the above-given question,
given that,
leatherback turtle swam 7.5 kilometers in 3 hours.
7.5/3 = 2.5.
so the turtle swim per hour = 2.5 miles.
PART B
At this rate, how long would it take the turtle to swim 10 kilometers?
Answer:
The long would it take the turtle to swim 10 kilometers = 0.75.
Explanation:
In the above-given question,
given that,
the long would it take the turtle to swim 10 kilometers.
7.5/10 = 0.75.
so the long would it take the turtle to swim 10 kilometers = 0.75.
3-ACT MATH
3-Act Mathematical Modeling: Get in Line

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.
Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
Question 5.
Plot your prediction on the same number line.
Answer:
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.

Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
Reflect
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?

Answer:
Question 14.
Generalize Will your model work on other lights? Explain your reasoning.
Answer:
SEQUEL
Question 15.
Use Structure Later that week, it took between 20 and 21 minutes to get through the same light. How many cars were in line?
Answer:
Lesson 5.8 Ratio Reasoning: Convert Customary Units
Solve & Discuss It!
If 6.5 feet of snow were to fall in a 24-hour period, would the 1921 record be broken? There are 12 inches in 1 foot.
I can… use ratio reasoning to convert customary measurements.

Reasoning
Use the relationship between inches and feet to solve the problem.
Focus on math practices
Make Sense and Persevere How many feet of snow would need to fall in Silver Lake, Colorado, to break the 1921 24-hour snowfall record from 1921?
Answer:
The record from 1921 is 3.15.
Explanation:
In the above-given question,
given that,
the number of feet of snow would need to fall in Silver Lake, Colorado, to break the 1921 24-hour snowfall record from 1921.
75.8 inches in 24 hours.
75.8/24 = 3.15.
so the record from 1921 is 3.15.
Essential Question
How can you use ratios to convert customary units of measure?
Try It!
According to city regulations, how many feet wide is the maximum sidewalk width? Explain.
Answer:
Convince Me! What conversion factor would you use when converting 66 inches to feet? Explain.
Try It!
Brandon is making bread. His recipe says to use 21 tablespoons of sugar. How many teaspoons of sugar should he use?
Answer:
The number of teaspoons of sugar should be used = 21 tablespoons.
Explanation:
In the above-given question,
given that,
Brandon is making bread.
His recipe says to use 21 tablespoons of sugar.
so the number of teaspoons of sugar should be used = 21 tablespoons.
Try It!
How many pounds does the elephant weigh?

Answer:
The elephant weigh about 3.3 tons.
Explanation:
In the above-given question,
given that,
stella weighs approximately 3.3 tons.
so the weight of the elephant is 3.3 tons.
KEY CONCEPT
You can convert customary measures by finding an equivalent rate or by using dimensional analysis.

Use an equivalent rate.
1 mi = 5,280 ft
\(\frac{5,280 \mathrm{ft} \times 4.25}{1 \mathrm{mi} \times 4.25}=\frac{22,440 \mathrm{ft}}{4.25 \mathrm{mi}}\)
Use dimensional analysis.
4.25 m1 × \(\frac{5,280 \mathrm{ft}}{1 \mathrm{~m}}\)
= 4.25 × 5,280 ft
= 22,440 ft
Do You Understand?
Question 1.
Essential Question How can you use ratios to convert customary units of measure?
Answer:
We can find an equivalent rate by using dimensional analysis.
Explanation:
In the above-given question,
given that,
You can convert customary measures by finding an equivalent rate or by using dimensional analysis.
1 feet = 12 inches.
1 yard = 36 inches.
1 yard = 3 feet.
1 mile = 5280 feet.
1 mile = 1760 yards.
5280 – 1760 = 3520.
so we can find an equivalent rate by using dimensional analysis.
Question 2.
What is a conversion factor that relates miles to yards?
Answer:
The conversion factor that relates miles to yards is 5280 feet.
Explanation:
In the above-given question,
given that,
for example:
1 mile = 5280 feet.
1 mile = 1760 yards.
5280 – 1760 = 3520.
so the conversion factor that relates miles to yards is 5280 feet.
Question 3.
Construct Arguments Jenna used the conversion factor \(\frac{1 \mathrm{~T}}{2,000 \mathrm{lb}}\) to convert 50 tons to pounds. Did she use the correct conversion factor? Explain.
Answer:
Yes, she uses the correct conversion factor.
Explanation:
In the above-given question,
given that,
Jenna used the conversion factor \(\frac{1 \mathrm{~T}}{2,000 \mathrm{lb}}\) to convert 50 tons to pounds.
2000/50 = 40.
so she use the correct conversion factor.
Question 4.
How can you use the conversion rates of fluid ounces to cups, and cups to pints, to find the number of fluid ounces in a pint?
Answer:
Do You Know How?
Question 5.
Convert 27 inches to yards by finding an equivalent rate.
Answer:
The equivalent rate is 0.729.
Explanation:
In the above-given question,
given that,
1 inch = 0.027 yards.
27 x 0.027 = 0.729.
the equivalent rate is 0.729.
Question 6.
Use dimensional analysis to convert 1.8 pounds to ounces.
Answer:
1.8 pounds to ounces = 28.8 ounces.
Explanation:
In the above-given question,
given that,
1 pound = 16 ounces.
1.8 x 16 = 28.8 ounces.
so 1.8 pounds to ounces = 28.8 ounces.
Question 7.
Critique Reasoning Sam is tripling a recipe for an organic cleaning solution. The new recipe calls for 15 tsp of orange oil. To find how many tbsp this is, Sam converted this way:
Conversion factor: \(\frac{3 \text { tsp }}{1 \text { tbsp }}\)
\(15 t s p \times \frac{3 t s p}{1 \text { tbsp }}=\frac{45}{1} \text { tbsp }=45 \text { tbsp }\)
What error did Sam make?
Answer:
Practice & Problem Solving
In 8-13, complete each conversion.
Question 8.
5 pt = _______c
Answer:
5 pt = 10 cups.
Explanation:
In the above-given question,
given that,
5 us liquid cups = 10 us cups.
5 pt = 10 us cups.
Question 9.
2\(\frac{1}{2}\)gal = _________ qt
Answer:
2\(\frac{1}{2}\)gal = 10 qt.
Explanation:
In the above-given question,
given that,
a half of a gallon equal to 2 quarts.
2 + 2 + 2 + 2 + 2 = 10.
2\(\frac{1}{2}\)gal = 10 qt.
Question 10.
2,640 yd = ________ mi
Answer:
2640 yd = 1.5 miles.
Explanation:
In the above-given question,
given that,
1 yard = 0.000568 miles.
2640 yards = 1.5 miles.
so 2640 yds = 1.5 miles.
Question 11.
Convert 16 yards to feet. Use the conversion rate 3 feet = 1 yard.
Answer:
16 yards = 48 feet.
Explanation:
In the above-given question,
given that,
3 feet = 1 yard.
16 yards = 48 feet.
16 x 3 = 48.
Question 12.
Convert 10 pints to quarts. Use the conversion rate 1 quart = 2 pints.
Answer:
10 pints = 5 quarts.
Explanation:
In the above-given question,
given that,
1 quart = 2 pints.
10 us liquid pints = 5 us liquid quarts.
10 pints = 5 quarts.
Question 13.
Convert 12 ounces to pounds. Use the conversion rate 16 ounces = 1 pound.
Answer:
12 ounces = 0.75 pounds.
Explanation:
In the above-given question,
given that,
16 ounces = 1 pound.
12 ounces = 0.75 pounds.
so 12 ounces = 0.75 pounds.
Question 14.
Two neighbors in a rural area want to know the distance between their homes in miles. What should the neighbors use as a conversion factor to convert this distance to miles?
Answer:
The distance to miles is 0.8 miles.
Explanation:
In the above-given question,
given that,
Two neighbors in a rural area want to know the distance between their homes in miles.
4224 x 2 = 0.8 miles.
1 feet = 12 inches.
so the distance to miles is 0.8 miles.
Question 15.
A school custodian discovered a leak in a water pipe. The custodian found that 1,920 fluid ounces of water had leaked out. How many gallons of water is this? Use the conversion factor \(\frac{1 \text { gallon }}{128 \text { fluid ounces }}\).
Answer:
The conversion factor is 15 gallons.
Explanation:
In the above-given question,
given that,
A school custodian discovered a leak in a water pipe.
The custodian found that 1,920 fluid ounces of water had leaked out.
1920/128 = 15.
1920 us fluid ounces = 15 us liquid gallons.
Question 16.
Critique Reasoning Two students, Stella and Vladimir, complete the conversion statement 12 feet 8 inches = __________ inches.
Stella stated that 12 feet 8 inches = 152 inches. Vladimir stated that 12 feet 8 inches = 9 inches.
Which student is incorrect? Explain.
Answer:
Vladimir is incorrect.
Explanation:
In the above-given question,
given that,
12 feet 8 inches = 152 inches.
Vladimir is incorrect.
Stella is correct.
Question 17.
The hole for a support post needs to be 6 feet deep. It is currently 1 foot 8 inches deep. How much deeper must the hole be? Use the conversion factor \(\)

Answer:
1 ft 8 in is 50.8 cm.
Explanation:
In the above-given question,
given that,
The hole for a support post needs to be 6 feet deep.
It is currently 1 foot 8 inches deep.
1 ft 8 in is 50.8 cm.
In 18 and 19, use the recipe card.

Question 18.
Look for Relationships Cheryl has measured 3 cups of water. Is this enough water for Cheryl to make a double recipe of green slime for a class project? Explain.
Answer:
Explanation:
In the above-given question,
given that,
Cheryl has measured 3 cups of water.
Question 19.
There are 16 tablespoons in 1 cup. How many tablespoons of cornstarch would Cheryl need to make the green slime recipe 15 times?
Answer:
The tablespoons of cornstarch would Cheryl need to make = 92 cups.
Explanation:
In the above-given question,
given that,
There are 16 tablespoons in 1 cup.
tablespoons = 1 cup.
so the tablespoons of cornstarch would Cheryl need to make = 92 cups.
Question 20.
Make Sense and Persevere Len plans to run at least 3 miles each day to get ready for a cross-country race. One lap of the school track is 440 yards. If Len runs 10 laps each day, will he cover at least 3 miles? Explain.
Answer:
The Len runs 10 laps each day, will he cover at least 3 miles = 146.6.
Explanation:
In the above-given question,
given that,
Len plans to run at least 3 miles each day to get ready for a cross-country race.
One lap of the school track is 440 yards.
440/3 = 146.6.
so len runs 10 laps each day, will he cover at least 3 miles = 146.6.
Question 21.
Higher Order Thinking Hunter is splitting a quart of ice cream with 7 members of his family. If the quart is split evenly, how many cups will each family member get? Explain.
Answer:
Explanation:
In the above-given question,
given that,
Hunter is splitting a quart of ice cream with 7 members of his family.
Question 22.
A fully loaded and fueled space shuttle can weigh close to 4.5 million pounds at liftoff. What is this weight expressed in tons?

Answer:
The weight expressed in tons = 2250 us tons.
Explanation:
In the above-given question,
given that,
A fully loaded and fueled space shuttle can weigh close to 4.5 million pounds at liftoff.
weighs almost 4.5 million pounds.
the weight expressed in tons = 2250 us tons.
Assessment Practice
Question 23.
Select all the conversions that are true.

☐ 18 ft = 6 yd
☐ 18 yd = 6 ft
☐ 0.5 mi = 10,560 ft
☐ 0.5 mi = 2,640 ft
☐ \(\frac{1}{2}\) mi = 880 yd
Answer:
18 ft = 6 yd.
Explanation:
In the above-given question,
given that,
1 ft = 12in.
1yd = 36 in.
6yd = 18 ft.
so 18 ft = 6 yd.
Lesson 5.9 Ratio Reasoning: Convert Metric Units
Solve & Discuss It!
Sam needs to fill a 5-liter water jug for his team. If Sam uses the water bottle to fill the jug, how many times does he
need to fill the water bottle to fill the jug?
I can… use unit rates to convert metric measurements.

Reasoning
How many milliliters are in 5 liters?
Metric Units of Capacity
1,000 milliliters (ml) = 1 liter (L)
100 centiliters (CL) = 1 liter
10 deciliters (dL) = 1 liter
1 dekaliter (dal) = 10 liters
1 hectoliter (hL) = 100 liters
1 kiloliter (KL) = 1,000 liters
Focus on math practices
Be Precise How many liters of water does Sam’s water bottle hold when full?
Essential Question
How can you use ratios to convert metric units of measure?
Try It!
The middle of the skate ramp is 2.5 meters wide. Emelia and her father want to use a board that is 23.5 decimeters long. Is this board wide enough for them to use? Convert the decimeters to meters to explain.
Answer:
Yes, it is board-wide enough for them to use.
Explanation:
In the above-given question,
given that,
The middle of the skate ramp is 2.5 meters wide.
Emelia and her father want to use a board that is 23.5 decimeters long.
23.5 = 2.35 meters.
so it is board-wide enough for them to use.
Convince Me! How can you convert 2.5 meters to decimeters to determine whether the board is wide enough?
Try It!
To make violet paint, Iris mixes 0.25 liter of red paint, 0.25 liter of blue paint, and 4.5 centiliters of white paint. How many centiliters of paint are in the mixture?
Answer:
The number of centiliters of paint are in the mixture = 0.545 liters.
Explanation:
In the above-given question,
given that,
Iris mixes 0.25 liter of red paint, 0.25 liter of blue paint, and 4.5 centiliters of white paint.
4.5 centiliters = 0.045 litre.
0.045 + 0.25 + 0.25 = 0.545.
so the number of centiliters of paint are in the mixture = 0.545 liters.
KEY CONCEPT
You can convert metric measures by finding an equivalent rate or by using dimensional analysis.
Use an equivalent rate.
1 kg = 1,000 g
\(\frac{1 \mathrm{~kg} \times 1.4}{1,000 \mathrm{~g} \times 1.4}=\frac{1.4 \mathrm{~kg}}{1,400 \mathrm{~g}}\)
Use dimensional analysis.
1.4 kg is equivalent to 1,400 g.
\(1.4 \mathrm{~kg} \times \frac{1,000 \mathrm{~g}}{1 \mathrm{~kg}}\)
= 1.4 × 1,000 g
= 1,400 g
Do You Understand?
Question 1.
Essential Question How can you use ratios to convert metric units of measure?
Answer:
We can convert metric measures by finding an equivalent rate or by using dimensional analysis.
Explanation:
In the above-given question,
given that,
1 kg = 1000 g.
1.4 kilogram is equivalent to 1400 g.
1.4 x 1000 = 1400 g.
Question 2.
Be Precise How are the metric units kilometer and kilogram the same? How are they different?
Answer:
The metrics units kilometers and kilogram are the same.
Explanation:
In the above-given question,
given that,
1 kg = 1000 g.
1.4 kilogram is equivalent to 1400 g.
1.4 x 1000 = 1400 g.
Question 3.
Reasoning Which is greater, 250 m or 0.25 km? Justify your reasoning.
Answer:
Both 250m or 0.25 km are the same.
Explanation:
In the above-given question,
given that,
250 meters = 0.25 kilometers.
divide the length value by 1000.
so both 250m or 0.25 km are the same.
Question 4.
How can you find the conversion rate for milliliters to kiloliters?
Answer:
The conversion rate for milliliters to kiloliters by 1000.
Explanation:
In the above-given question,
given that,
for example:
we can divide the length value by 1000.
1 ml = 1000 l.
Do You Know How?
Question 5.
What is the conversion factor when converting from liters to milliliters?
Answer:
Question 6.
Use an equivalent rate to convert 35 centimeters to meters.
Answer:
The equivalent rate to convert 35 centimeters to meters = 3500.
Explanation:
In the above-given question,
given that,
1 meter = 100 cm.
35 x 100 = 3500.
so the equivalent rate to convert 35 centimeters to meters = 3500.
Question 7.
Critique Reasoning Maddy wants to know how many centigrams are in 0.75 gram. She converted 0.75 gram to its equivalent in centigrams as shown. Is her work correct? Explain.
\(\frac{10 \mathrm{cg} \times 0.75}{1 \mathrm{~g} \times 0.75}=\frac{7.5 \mathrm{cg}}{0.75 \mathrm{~g}}\)
Answer:
Question 8.
Look at Exercise 7. Use dimensional analysis to convert 0.75 gram to centigrams.
Answer:
Practice & Problem Solving
Leveled Practice In 9 and 10, complete each conversion using an equivalent rate.
Question 9.
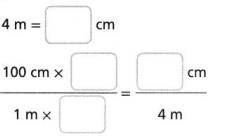
Answer:
4m = 400 cm.
Explanation:
In the above-given question,
given that,
4m = 400 cm.
100 cm x 4/1m x 4m.
400cm/4m.
Question 10.
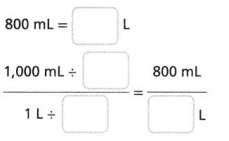
Answer:
800 ml = 0.8 l.
Explanation:
In the above-given question,
given that,
800 ml = 0.8 liter.
(1000 ml/ 8)/ (1l/ 1000).
800 ml/ 1000l.
0.8 l.
Leveled Practice In 11 and 12, complete each conversion using dimensional analysis.
Question 11.
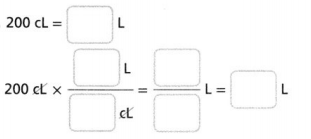
Answer:
200 cl = 2 liters.
Explanation:
In the above-given question,
given that,
200 cl = 2 liters.
200 cl x 20000/100cl.
200/100 l.
2 l.
Question 12.
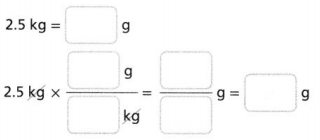
Answer:
2.5 kg = 2500 grams.
Explanation:
In the above-given question,
given that,
2.5 kg x 1000g/1 kg.
250000/100 = 2500.
2.5 kg = 2500 grams.
In 13 and 14, complete each conversion.
Question 13.
80 cm = _______ m
Answer:
80 cm = 0.8m.
Explanation:
In the above-given question,
given that,
1m = 100 cm.
0.8m = 80 cm.
8 = 800 cm.
Question 14.
2.1 g = ________ mg
Answer:
2.1 g = 2100 mg.
Explanation:
In the above-given question,
given that,
2.1 g = 2100 milligrams.
1 kg = 1000 g.
2.1 g = 2100 mg.
In 15-17, use the table showing the amount of liquid that Whitney drinks each day.

Question 15.
How many liters of water does Whitney drink each day?
Answer:
The number of liters of water does Whitney drinks each day = 1.5 l.
Explanation:
In the above-given question,
given that,
the amount of juice = 250 ml.
the amount of milk = 400 ml.
the amount of water = 1500 ml.
1 l = 1000 ml.
so the number of liters of water does Whitney drinks each day = 1.5 L.
Question 16.
What is the total amount of liquid, in liters, that Whitney drinks each day?
Answer:
The total amount of liquid in liters that Whitney drinks each day = 0.25 l.
Explanation:
In the above-given question,
given that,
the amount of juice = 250 ml.
the amount of milk = 400 ml.
the amount of water = 1500 ml.
1 l = 1000 ml.
so the total amount of liquid in liters that Whitney drinks each day = 0.25 L.
Question 17.
Troy drinks 1.8 L of water each day. How many more milliliters of water does Troy drink each day than Whitney?
Answer:
The more milliliters of water does Troy drink each day than Whitney = 300 ml.
Explanation:
In the above-given question,
given that,
Troy drinks 1.8 L of water each day.
1800 – 1500 = 300.
so the number of milliliters does Troy drink each day = 300 ml.
Question 18.
There are 10 millimeters in 1 centimeter, so about how many millimeters long is this dinosaur bone? Explain.

Answer:
The number of milliliters long is the dinosaur bone = 220 ml.
Explanation:
In the above-given question,
given that,
There are 10 millimeters in 1 centimeter.
22 x 10 = 220 ml.
so the number of milliliters long is the dinosaur bone = 220 ml.
Question 19.
Critique Reasoning Savannah says that 1 kilogram is equivalent to 1,000,000 milligrams. Is Savannah correct? Explain.
Answer:
Yes, Savannah was correct.
Explanation:
In the above-given question,
given that,
Savannah says that 1 kilogram is equivalent to 1,000,000 milligrams.
1 kg = 1000 g.
1 g = 1000 mg.
1000 x 1000 = 1000000 mg.
so Savannah was correct.
Question 20.
Model with Math Lucas hiked 14,300 meters through the Everglades in the morning. After lunch, he continued hiking. When he finished the hike, he had covered 31.5 kilometers in all. Write an equation that can be used to find how far Lucas hiked after lunch.
Answer:
Lucas hiked after lunch = 453.96.
Explanation:
In the above-given question,
given that,
Lucas hiked 14,300 meters through the Everglades in the morning.
After lunch, he continued hiking.
When he finished the hike, he had covered 31.5 kilometers in all.
14300/31.5 = 453.96.
so Lucas hiked after lunch = 453.96.
Question 21.
Tariq has a collection of 35 quarters that he wants to send to his cousin. What is the total weight of the quarters in kilograms?

Answer:
The total weight of the quarters in kilograms = 6.17.
Explanation:
In the above-given question,
given that,
Tariq has a collection of 35 quarters that he wants to send to his cousin.
One quarter weighs 5.67 grams.
35/5.67 = 6.17.
so the total weight of the quarters in kilograms = 6.17.
Question 22.
Higher Order Thinking Louis has a bag of 25 pen shells. Each pen shell is 18 centimeters long. What is the combined length of the pen shells in meters?
Answer:
The combined length of the pen shells in meters = 450.
Explanation:
In the above-given question,
given that,
Louis has a bag of 25 pen shells.
Each pen shell is 18 centimeters long.
25 x 18 = 450.
so the combined length of the pen shells in meters = 450.
Assessment Practice
Question 23.
Select all the conversions that are equivalent to the capacity of a 5.5-liter pitcher of lemonade.
☐ 0.0055 kL
☐ 55 mL
☐ 0.055 kL
☐ 550 mL
☐ 5,500 ml
Answer:
Option A is correct.
Explanation:
In the above-given question,
given that,
5.5 liter = 5.5 x 1000.
0.0055.
so option A is correct.
Question 24.
Select all the conversions that are equivalent to the mass of a 425-gram football.
☐ 42,000 mg
☐ 42,500 cg
☐ 450 dg
☐ 4.25 hg
☐ 00.425 kg
Answer:
Explanation:
In the above-given question,
given that,
425 grams.
Lesson 5.10 Relate Customary and Metric Units
Explain It!
Gianna and her friends are in a relay race. They have a pail that holds 1 liter of water. They need to fill the 1-liter pail, run 50 yards, and dump the water into the large bucket until it overflows. Gianna says that as long as they do not spill any of the water, they will need 7 trips with the 1-liter pail before the large bucket overflows.
I can… convert between customary and metric units.

A. Which conversion factor could you use to determine whether Gianna is correct? Explain.
Answer:
1 gal = 4 qt.
Explanation:
In the above-given question,
given that,
Gianna and her friends are in a relay race.
They have a pail that holds 1 liter of water.
1 gal is equal to 4 qt.
They need to fill the 1-liter pail, run 50 yards, and dump the water into the large bucket until it overflows.
1 gal = 4 qt.
B. Critique Reasoning Gianna’s friend Linus says that you cannot be certain how many trips it will take because the conversion is approximate. Is Linus’s reasoning appropriate? Explain.
Answer:
Yes, Gianna’s was correct.
Explanation:
In the above-given question,
given that,
Gianna and her friends are in a relay race.
They have a pail that holds 1 liter of water.
1 gal is equal to 4 qt.
They need to fill the 1-liter pail, run 50 yards, and dump the water into the large bucket until it overflows.
1 gal = 4 qt.
C. Construct Arguments Is Gianna correct that 7 trips are needed before the bucket overflows? If not, how many trips will it take? Use the table to justify your answer.
Answer:
Focus on math practices
Construct Arguments Morgan says that 4 liters is less than 1 gallon. Construct an argument to show that Morgan is incorrect.
Essential Question
How can you use ratios to convert customary and metric units of measure?
Try It!
Jacob is building a robot named T3-X that is 75 inches tall. To the nearest tenth, how many centimeters tall is T3-X?
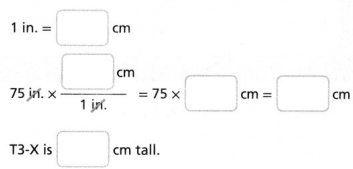
Answer:
T3-x is 75 cm tall.
Explanation:
In the above-given question,
given that,
Jacob is building a robot named T3-X that is 75 inches tall.
1 in = 12 cm.
75in ( 1 cm/1 in).
75 x 1 cm = 75 cm.
T3-x is 75 cm tall.
Convince Me! If you want to find the height of T3-X in meters, will you get the same answer if you convert inches to centimeters, and then centimeters to meters, as you would if you convert inches to feet, and then feet to meters? Explain.
Try It!
Find the length of a 100-yard football field in meters. Use 1 yard = 3 feet and 1 meter ≈ 3.28 feet. Round to the nearest tenth.
Answer:
1 yard = 3 feet.
1 meter = 3.28 feet.
Explanation:
In the above-given question,
given that,
the length of a 100-yard football field meters.
1 yard = 3 feet.
1 meter = 3.28 feet.
KEY CONCEPT
You can use what you know about converting within one measurement system to relate customary and metric units. You can convert measures with customary and metric units by finding an equivalent rate or using dimensional analysis.
Use an equivalent rate.
1 kg ≈ 2.20 lb
\(\frac{1 \mathrm{~kg} \times 5}{2.20 \mathrm{lb} \times 5}=\frac{5 \mathrm{~kg}}{11 \mathrm{lb}}\)
5 kg ≈ 11 lb
Use dimensional analysis.
\(5 \mathrm{~kg} \times \frac{2.20 \mathrm{lb}}{1 \mathrm{~kg}}\)
5 × 2.20 = 11 lb
5 kg ≈ 11 lb
Do You Understand?
Question 1.
Essential Question How can you use ratios to convert customary and metric units of measure?
Answer:
Question 2.
Reasoning When converting centimeters to inches, do you multiply or divide by 2.54? Explain.
Answer:
Question 3.
Use Structure How can you find the approximate number of liters in 1 pint?
Remember: 1 quart = 2 pints
Answer:
Question 4.
How is the conversion from inches to centimeters different from other conversions between customary and metric units?
Answer:
Do You Know How?
In 5-8, find the equivalent measure. Round to the nearest tenth.
Question 5.
5 in. = _______ cm
Answer:
5 in = 12.7 cm.
Explanation:
In the above-given question,
given that,
1 ft = 12 in.
5 in = 12.7 cm.
Question 6.
2 mi ≈ _______ km
Answer:
2 mi = 3.219 km.
Explanation:
In the above-given question,
given that,
2 mi is equal to 3.129 km.
1 mi = 1.5645 km.
so 2 miles = 3.219 km.
Question 7.
113 g ≈ _______ oz
Answer:
113 g = 4 oz.
Explanation:
In the above-given question,
given that,
113 g is equal to 3.986 ounces.
Question 8.
14 kg ≈ ______ lb
Answer:
14 kg = 30 lb.
Explanation:
In the above-given question,
given that,
14 kg = 30.865 pounds.
pounds is equal to lb.
so 14 kg = 30 lb.
Question 9.
Convert 30 gallons to liters by finding an equivalent rate.
Answer:
Question 10.
Approximately how many ounces are equivalent to 1 kilogram?
Answer:
Practice & Problem Solving
In 11-18, find the equivalent measure. Round to the nearest tenth.
Question 11.
9qt ≈ _______ L
Answer:
9 qt = 8.52 l.
Explanation:
In the above-given question,
given that,
1 l = 1.06 qt.
9 qt = 8.52 l.
Question 12.
2 gal ≈ _______ L
Answer:
2 gal = 7.571 liters.
Explanation:
In the above-given question,
given that,
1 l = 0.264 gal.
2 gal = 7.571 liters.
Question 13.
2 in. ≈ _______ cm
Answer:
2 in = 5.08 cm.
Explanation:
In the above-given question,
given that,
3 in = 7.62 cm.
2 in = 5.08 cm.
Question 14.
5 km ≈ _______ mi
Answer:
5 km = 3.1 miles.
Explanation:
In the above-given question,
given that,
2 miles = 3.129 km.
5 km = 3.1 miles.
Question 14.
5 km ≈ ______ mi
Answer:
5 km = 3.1 mi.
Explanation:
In the above-given question,
given that,
5 km = 3.1 mi.
Question 15.
10 L ≈ ______ qt
Answer:
10 L = 10.567 q.
Explanation:
In the above-given question,
given that,
10 L = 10.567 q.
10.567 q = 10 L.
Question 16.
5.5 t ≈ ______ T
Answer:
5.5 t = 5.401 T.
Explanation:
In the above-given question,
given that,
5.5 t = 5.401.
1 tone = 0.982.
5.5 t = 5.401 T.
Question 17.
50 lb ≈ ______ kg
Answer:
50 lb = 23 kg.
Explanation:
In the above-given question,
given that,
lb is equal to pounds.
50 pounds = 22.68 kg.
50 lb = 23 kg.
Question 18.
10 oz ≈ ______ g
Answer:
10 oz = 283.495.
Explanation:
In the above-given question,
given that,
10 oz = 283.495 g.
283.495 g = 10 oz.
Question 19.
A chef at a restaurant uses 12 pounds of butter each day. About how many grams of butter does the chef use each day? Use the conversion factors \(\frac{16 \text { ounces }}{1 \text { pound }}\) and \(\frac{28.35 \text { grams }}{1 \text { ounce }}\)
Answer:
Question 20.
Reasoning Simone wants to know whether a new chest of drawers will fit next to her bed. The chest she would like to buy is 73 centimeters wide. She knows that her room is 86 inches wide. The bed is 76 inches wide. Will the chest fit next to her bed? Explain.

Answer:
Yes, the chest fit next to her bed.
Explanation:
In the above-given question,
given that,
Simone wants to know whether a new chest of drawers will fit next to her bed.
The chest she would like to buy is 73 centimeters wide.
She knows that her room is 86 inches wide.
The bed is 76 inches wide.
so the chest fit next to her bed.
Question 21.
Be Precise Denali is the highest mountain in the United States. What is its height in meters? Round to the nearest whole number.
Answer:
Explanation:
In the above-given question,
given that,
Denali is the highest mountain in the United States.
Denali is approximately 20,320 ft high.
Question 22.
Construct Arguments Francesca wants to convert 1 foot to centimeters. Use what you know about customary units to explain how she can do this.
Answer:
Question 23.
Higher Order Thinking At the state fair, a person must be at least 138 centimeters tall to ride the roller coaster. Billy wants to ride the coaster. He is 4 feet 7 inches tall. Is Billy tall enough to ride the coaster? Explain.
Answer:
Question 24.
Paul’s car holds a maximum of 19 gallons of gas. About how many liters of gas does Paul need to fill his gas tank?

Answer:
The number of liters of gas does Paul need to fill his gas tank = 10 liters.
Explanation:
In the above-given question,
given that,
Paul’s car holds a maximum of 19 gallons of gas.
9 gallons is remaining as shown.
19 – 9 = 10.
so the number of liters of gas does paul need to fill his gas tank = 10 liters.
Assessment Practice
Question 25.
The posted speed limit is 65 miles per hour. Select all the metric measures that are faster than 65 miles per hour.
☐ 65 km per hour
☐ 97.5 km per hour
☐ 104 km per hour
☐ 105.7 km per hour
☐ 120.3 km per hour
Answer:
Option A is correct.
Explanation:
In the above-given question,
given that,
The posted speed limit is 65 miles per hour.
65 km per hour.
so option A is correct.
Question 26.
Boys competing in the long jump event must jump at least 15 feet to qualify for the state track and field meet. Select all the metric measures that are less than 15 feet.
☐ 6.5 m
☐ 5.0 m
☐ 4.5 m
☐ 3.92 m
☐ 3.5 m
Answer:
Topic 5 Review
Essential Question
What are ratios and rates? How can you use ratios and rates to describe quantities and solve problems?
Vocabulary Review
Complete each definition and then provide an example of each vocabulary word.
Use Vocabulary in Writing
Explain how you can convert 52 ounces to pounds. Use vocabulary words in your explanation.
Concepts and Skills Review
Lesson 5.1 Understand Ratios
Quick Review
A ratio is a relationship in which for every x units of one quantity there are y units of another quantity. A ratio can be written using the word “to,” a colon, or a fraction bar to separate the two terms.
Example
The ratio of men to women at a small wedding is 6:4. If there are 16 women at the wedding, how many men are at the wedding?
Draw a diagram to represent the ratio. Because 4 boxes represent 16 women, each box represents 4 women.

There are 24 men at the wedding.
Practice
A florist uses 5 red roses for every 2 white roses in her bouquets.
Question 1.
Write the ratio of white roses to red roses in three different ways.
Answer:
The ratio of white roses to red roses is 2:5.
Explanation:
In the above-given question,
given that,
A florist uses 5 red roses for every 2 white roses in her bouquets.
the ratio of white roses to red roses is 2:5.
so the ratio is 2:5.
Question 2.
Write the ratio of red roses to the total number of flowers in three different ways.
Answer:
The ratio of red roses to the total number of flowers is 5:7.
Explanation:
In the above-given question,
given that,
A florist uses 5 red roses for every 2 white roses in her bouquets.
the ratio of red roses to the total number of flowers is 5:7.
so the ratio is 5:7.
Question 3.
If the florist uses 10 red roses in a bouquet, how many white roses does she use?
Answer:
The ratio is 10:4.
Explanation:
In the above-given question,
given that,
A florist uses 5 red roses for every 2 white roses in her bouquets.
if the florist uses 10 red roses in a bouquet.
he can use 4 white roses.
10: 4.
5:2.
so the ratio is 10:4.
Question 4.
If the florist uses 10 white roses in an arrangement, how many red roses does she use?
Answer:
The ratio is 25:10
Explanation:
In the above-given question,
given that,
A florist uses 5 red roses for every 2 white roses in her bouquets.
if the florist uses 10 white roses in an arrangement.
he can use 25 red roses.
25:10.
5:2.
so the ratio is 25:10.
Lesson 5.2 Generate Equivalent Ratios
Quick Review
You can multiply or divide both terms of a ratio by the same nonzero number to find equivalent ratios.
Example
Find two ratios that are equivalent to \(\frac{21}{126}\)
One Way
Multiply.
\(\frac{21 \times 2}{126 \times 2}=\frac{42}{252}\)
Another Way
Divide.
\(\frac{21 \div 3}{126 \div 3}=\frac{7}{42}\)
Practice
In 1-4, find two ratios equivalent to the given ratio.
Question 1.
\(\frac{5}{12}\)
Answer:
The ratios are 10/24 and 1/2.4.
Explanation:
In the above-given question,
given that,
the ratio is 5/12.
5 x 2 = 10.
12 x 2 = 24.
the ratio is 10/24.
divide by 5.
5/5 = 1.
12/5 = 2.4.
so the ratio is 1/2.4
Question 2.
14:32
Answer:
The ratios are 7/16 and 5/12.
Explanation:
In the above-given question,
given that,
the ratio is 14/32.
7 x 2 = 14.
16 x 2 = 32.
the ratio is 7/16.
divide by 2.
10/2 = 5.
24/2 = 12.
so the ratio is 5/12.
Question 3.
3 to 4
Answer:
The ratios are 6/8 and 1/1.3.
Explanation:
In the above-given question,
given that,
the ratio is 3/4.
3 x 2 = 6.
4 x 2 = 8.
the ratio is 6/8.
divide by 3.
3/3 = 1.
4/3 = 1.3.
so the ratio is 1/1.3.
Question 4.
\(\frac{7}{8}\)
Answer:
The ratios are 14/16 and 1/1.14.
Explanation:
In the above-given question,
given that,
the ratio is 7/8.
7 x 2 = 14.
8 x 2 = 16.
the ratio is 14/16.
divide by 7.
7/7 = 1.
8/7 = 1.14.
so the ratio is 1/1.14.
Question 5.
For every 4 bagels sold at a bakery, 7 muffins are sold. How many muffins are sold when the bakery sells 24 bagels? Complete the table.
Answer:
The missing values are 14, 21, 28, 35, and 42.
Explanation:
In the above-given question,
given that,
For every 4 bagels sold at a bakery, 7 muffins are sold.
the ratio is 1:2.
4 x 1 = 4, 4 x 2 = 8, 4 x 3 = 12, 4 x 4 = 16, 4 x 5 = 20, and 4 x 6 = 24.
7 x 1 = 7, 7 x 2 = 14, 7 x 3 = 21, 7 x 4 = 28, 7 x 5 = 35, and 7 x 6 = 42.
so the missing values are 14, 21, 28, 35, and 42.
Lesson 5.3 Compare Ratios
Quick Review
To compare ratios, make a table to show each ratio and then find a value in which one of the terms is the same in both tables.
Example
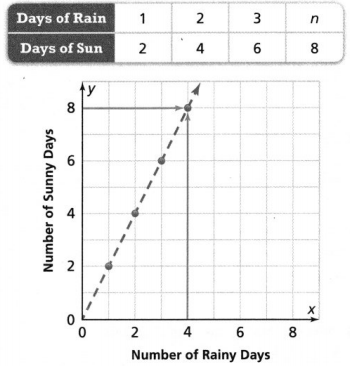
Erica can complete more facts than Klayton.
Answer:
The missing value is 4.
Explanation:
In the above-given question,
given that,
the number of days is 1, 2, 3, and 4.
the days of the sun are 2, 4, 6, and 8.
2 x 1 = 2.
2 x 2 = 4.
2 x 3 = 6.
2 x 4 = 8.
so the missing value is 4.
Practice
Question 1.
The school soccer team buys 3 soccer balls for every 2 players. The school volleyball team buys 7 volleyballs for every 5 players. Which team buys more balls per player?
Answer:
The team buys more balls per player = 6:35.
Explanation:
In the above-given question,
given that,
The school soccer team buys 3 soccer balls for every 2 players.
The school volleyball team buys 7 volleyballs for every 5 players.
3 x 2 = 6.
7 x 5 = 35.
so the team buys more balls per player = 6:35.
Question 2.
Jenna walks 12 miles in 5 days. Alex walks 7 miles in 3 days. Who walks more miles per day?
Answer:
The ratio is 60/21.
Explanation:
In the above-given question,
given that,
Jenna walks 12 miles in 5 days. Alex walks 7 miles in 3 days.
12 x 5 = 60.
7 x 3 = 21.
so the ratio is 60/21.
Lesson 5.4 Represent and Graph Ratios
Quick Review
You can solve some ratio problems by making a table of equivalent ratios and then graphing the pairs of values on a coordinate plane.
Example

There will be 4 rainy days if there are 8 sunny days.
Practice
Question 1.
In gym class, the sixth graders walk 2 laps for every 3 laps they run. If the students run 12 laps, how many laps will they walk? Complete the table. Then plot the pairs of values on the coordinate plane.
Answer:
The missing values are 4, 6, and 8.
Explanation:
In the above-given question,
given that,
In gym class, the sixth graders walk 2 laps for every 3 laps they run.
the run laps on the y-axis.
the walk laps on the x-axis.
3 x 2 = 6, 3 x 3 = 9, 3 x 4 = 12.
2 x 2 = 4, 2 x 3 = 6, 2 x 4 = 8.
Lesson 5.5 Understand Rates and Unit Rates
Quick Review
A rate is a ratio that relates two quantities with different units. A unit rate relates a quantity to 1 unit of another quantity. You can use what you know about dividing fractions to write a ratio of fractions as a unit rate.
Example
Write 20 meters in 4 minutes as a rate and as a unit rate.

Practice
Write each statement as a unit rate.
Question 1.
78 miles on 3 gallons
Answer:
The unit rate is 26/1.
Explanation:
In the above-given question,
given that,
78 miles on 3 gallons.
unit rate is 78/3.
3 x 1 = 3.
3 x 26 = 78.
so the unit rate is 26/1.
Question 2.
18 laps in 6 minutes
Answer:
The unit rate is 18.
Explanation:
In the above-given question,
given that,
18 laps in 6 minutes
unit rate is 18/6.
6 x 1 = 6.
3 x 6 = 18.
so the unit rate is 18/1.
Question 3.
48 sandwiches for 16 people
Answer:
The unit rate is 3.
Explanation:
In the above-given question,
given that,
48 sandwiches for 16 people.
unit rate is 48/16.
16 x 1 = 16.
3 x 16 = 48.
so the unit rate is 3.
Question 4.
49 houses in 7 blocks
Answer:
The unit rate is 7.
Explanation:
In the above-given question,
given that,
49 houses in 7 blocks.
unit rate is 49/7.
7 x 1 = 7.
7 x 7 = 49.
so the unit rate is 7.
Question 5.
6 desks in 2 rows
Answer:
The unit rate is 3.
Explanation:
In the above-given question,
given that,
6 desks in 2 rows.
unit rate is 6/2.
2 x 1 = 2.
3 x 2 = 6.
so the unit rate is 3.
Lesson 5.6 Compare Unit Rates
Quick Review
A unit rate compares a quantity to 1 unit of another quantity. To compare unit rates, compare the first terms.
Example
On Pet Day, Meg’s turtle crawled 30 feet in 6 minutes, and Pat’s turtle crawled 25 feet in 5 minutes. Whose turtle crawled at a faster rate?
Write each rate.

Both turtles crawled at the same rate.
Practice
Question 1.
Which is the better value? Circle it.
$5.00 for 4 mangoes
$6.00 for 5 mangoes
Answer:
Both have the same value.
Explanation:
In the above-given question,
given that,
$5.00 for 4 mangoes
$6.00 for 5 mangoes
$5/4 = 1.25.
$6/5 = 1.2.
so both of the values are the same.
Question 2.
Who earned more each month? Circle it.
Atif: $84 over 3 months
Jafar: $100 over 4 months
Answer:
Atif earned more than Jafar.
Explanation:
In the above-given question,
given that,
Atif: $84 over 3 months
Jafar: $100 over 4 months
84/3 = 28.
100/4 = 25.
so Atif earned more.
Question 3.
Which is a faster rate? Circle it.
3 laps in 5 minutes
4 laps in 7 minutes
Answer:
3 laps in 5 minutes is the faster rate.
Explanation:
In the above-given question,
given that,
3 laps in 5 minutes
4 laps in 7 minutes
3/5 = 0.6.
4/7 = 0.5.
option A is correct.
Question 4.
Which is the better value? Circle it.
3 sandwiches for $15.00
4 sandwiches for $21.00
Answer:
3 sandwiches for $15.00.
Explanation:
In the above-given question,
given that,
3 sandwiches for $15.00
4 sandwiches for $21.00
3/15 = 1/5.
1/5 = 0.2.
4/21 = 0.1.
Question 5.
Which is the greater rate? Circle it.
6 points in 3 attempts
15 points in 5 attempts
Answer:
15 points in 5 attempts.
Explanation:
In the above-given question,
given that,
6 points in 3 attempts
15 points in 5 attempts
6/3 = 2.
15/5 = 3.
15 points in 5 attempts.
Lesson 5.7 Solve Unit Rate Problems
Quick Review
You can use a ratio table or a unit rate to solve problems involving ratios or rates.
Example
A plane travels at a rate of 780 miles in 2 hours. At this rate, how far will it travel in 3.5 hours?
Find the unit rate
\(\frac{780 \text { miles } \div 2}{2 \text { hours } \div 2}=\frac{390 \text { miles }}{1 \text { hour }}\)
Find an equivalent rate.
\(\frac{390 \text { miles } \times 3.5}{1 \text { hour } \times 3.5}=\frac{1,365 \text { miles }}{3.5 \text { hours }}\)
The plane will travel 1,365 miles in 3.5 hours.
Practice
Question 1.
Doug has 5 hours to make an on-time delivery 273 miles away. Doug drives at a constant speed of 55 miles per hour. Will Doug make the delivery by the deadline? Explain.
Answer:
Yes, Doug makes the delivery by the deadline.
Explanation:
In the above-given question,
given that,
Doug has 5 hours to make an on-time delivery 273 miles away.
Doug drives at a constant speed of 55 miles per hour.
273/5 = 54.6.
54.6 x 55 = 3003.
Yes, Doug makes the delivery by the deadline.
Question 2.
Marie has 8 hours to write a 45-page chapter for her book. Marie writes at a constant speed of 4 pages per hour. Will Marie complete the chapter in time? Explain.
Answer:
Marie takes 90 hours to complete.
Explanation:
In the above-given question,
given that,
Marie has 8 hours to write a 45-page chapter for her book.
Marie writes at a constant speed of 4 pages per hour.
45 x 8 = 360.
360 /4 = 90.
Lesson 5.8 Ratio Reasoning: Convert Customary Units
Quick Review
You can convert customary measures by finding equivalent rates or by using dimensional analysis.
Example
How many pints are equivalent to 4 quarts?
Find an equivalent rate:
2 pints = 1 quart …….. Identify the conversion rate.

So, 8 pints are equivalent to 4 quarts.
Practice
In 1-4, complete each conversion.
Question 1.
2 mi = _______ ft
Answer:
2 miles = 10560 feet.
Explanation:
In the above-given question,
given that,
1 mile = 63360 in.
1 ft = 12 in.
2 mi = 63360 x 2.
126720/2 = 10560.
Question 2.
144 in. = _______ yd
Answer:
144 in = 4.0032 yd.
Explanation:
In the above-given question,
given that,
1 inch = 0.0278 yd.
144 x 0.0278.
4.0032.
144 in = 4.0032 yd.
Question 3.
4 oz = _______ lb
Answer:
4 oz = 0.0625 lb.
Explanation:
In the above-given question,
given that,
1 oz = 0.0625 lb.
4 oz = 4 x 0.0625.
0.25 lb.
Question 4.
3 gal = _______ qt
Answer:
3 gal = 12 qt.
Explanation:
In the above-given question,
given that,
1 gal = 4 us qt.
3 gal = 3 x 4.
3 gal = 12 qt.
Question 5.
The hippo at the zoo weighs 1.5 tons. How many pounds does the hippo weigh?
Answer:
The weight of the hippo is 3000 pounds.
Explanation:
In the above-given question,
given that,
The hippo at the zoo weighs 1.5 tons.
1 ton = 2000 pounds.
1.5 tons = 1.5 x 2000.
3000.
The weight of the hippo is 3000 pounds.
Lesson 5.9 Ratio Reasoning: Convert Metric Units
Quick Review
To convert metric units, use the same methods used for converting customary units. Either use the conversion rate to find an equivalent rate or use dimensional analysis.
Example
Tariq rode his bike 15,100 meters. How many kilometers did he ride his bike?
Find an equivalent rate:
1,000 meters = 1 kilometer
\(\frac{1,000 m \times 15.1}{1 \mathrm{~km} \times 15.1}=\frac{15,100 \mathrm{~m}}{15.1 \mathrm{~km}}\)
Use dimensional analysis:
\(15,100 \mathrm{~m} \times \frac{1 \mathrm{~km}}{1,000 \mathrm{~m} }=\frac{15,100}{1,000} \mathrm{~km}=15.1 \mathrm{~km}\)
Tariq rode 15.1 kilometers.
Practice
In 1-4, complete each conversion.
Question 1.
3 m = _______ mm
Answer:
3m = 3000 mm.
Explanation:
In the above-given question,
given that,
1 m = 1000 mm.
3 m = 3 x 1000.
3m = 3000 mm.
Question 2.
3,520 mm = _______ cm
Answer:
3520 mm = 352 cm.
Explanation:
In the above-given question,
given that,
1mm = 0.1 cm.
3520 mm = 352 cm.
Question 3.
4.2 kg = _______ g
Answer:
4.2 kg = 4200 g.
Explanation:
In the above-given question,
given that,
1 kg = 1000 g.
4.2 kg = 4.2 x 1000.
4.2 x 1000 = 4200 g.
4.2 kg = 4200 g.
Question 4.
300 mL = _______ L
Answer:
300 ml = 0.3 l.
Explanation:
In the above-given question,
given that,
1ml = 0.001 l.
300 ml = 300 x 0.001.
300 x 0.001 = 0.3 l.
300 ml = 0.3l.
Question 5.
Li needs to buy 2 kilograms of apples. If she buys 9 apples that each weigh approximately 150 grams, will she have enough? Explain.
Answer:
Yes, she has enough.
Explanation:
In the above-given question,
given that,
Li needs to buy 2 kilograms of apples.
If she buys 9 apples that each weigh approximately 150 grams.
150 x 9 = 1350 g.
2 kg = 2000 g.
so she has enough space.
Lesson 5.10 Relate Customary and Metric Units
Quick Review
To convert between metric and customary units, use the conversion rate and find an equivalent rate, or use dimensional analysis. Most conversions will be approximate because, except in the case of inches to centimeters, the conversion rates are approximate.
Example
Gwen has a cooler that holds 3 quarts. About how many liters does the cooler hold?
1 qt ≈ 0.95 L
3 qt × \(\frac{0.95 \mathrm{~L}}{1 \mathrm{~qt}}\) = (3 × 0.95) L = 2.85 L
Gwen’s cooler holds approximately 2.85 liters.
Practice
In 1-4, find the equivalent measure. Round to the nearest tenth.
Question 1.
100 g ≈ ________ oz
Answer:
100 g = 15372.2 oz.
Explanation:
In the above-given question,
given that,
1 gal = 153.722 oz.
100 g = 153.722 x 100.
15372.2.
Question 2.
6 ft ≈ _______ m
Answer:
6 ft = 1.83 m.
Explanation:
In the above-given question,
given that,
1 ft = 0.305 m.
6 ft = 6 x 0.305.
6 x 0.305 = 1.83.
6 ft = 1.83 m.
Question 3.
57 gal ≈ _______ L
Answer:
57 gal = 256.5 l.
Explanation:
In the above-given question,
given that,
1 gal = 4.5 l.
57 gal = 57 x 4.5.
57 x 4.5 = 256.5.
57 gal = 256.5 l.
Question 4.
27 km ≈ _______ mi
Answer:
27 km = 16.767 mi.
Explanation:
In the above-given question,
given that,
1 km = 0.621 mi.
27 km = 27 x 0.621.
27 x 0.621 = 16.767.
27 km = 16.767 mi.
Question 5.
The science class is raising monarch caterpillars. One of the caterpillars weighs 2.3 ounces. About how many grams does the caterpillar weigh? Round to the nearest tenth.
Answer:
The caterpillar weighs 65.2 grams.
Explanation:
In the above-given question,
given that,
The science class is raising monarch caterpillars.
One of the caterpillars weighs 2.3 ounces.
1 ounce = 28.35 grams.
2.3 x 28.35 = 65.205.
so the caterpillar weighs 65.2 grams.
Topic 5 Fluency Practice
Pathfinder
Shade a path from START to FINISH. Follow the sums and differences in which the digit in the ones place is greater than the digit in the tenths place. You can only move up, down, right, or left.
I can… add and subtract multidigit decimals.












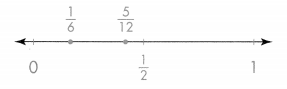








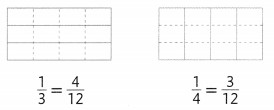
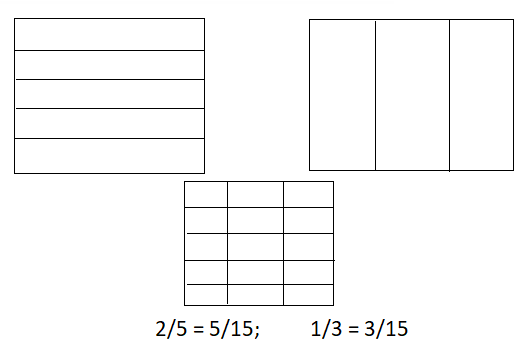

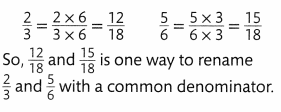

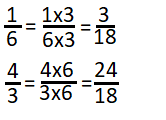




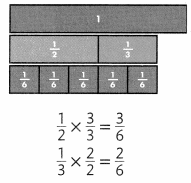
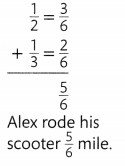
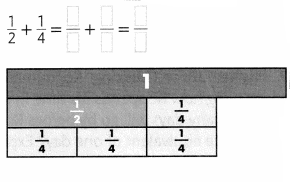
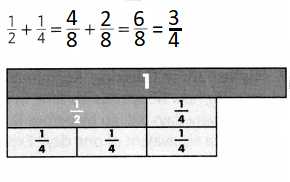

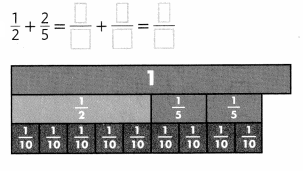
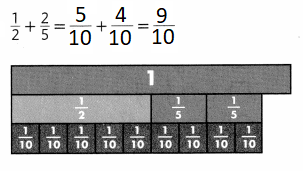
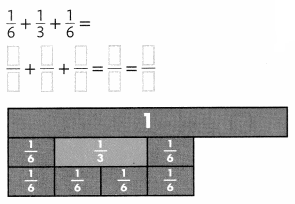
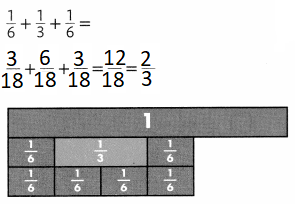
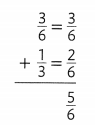


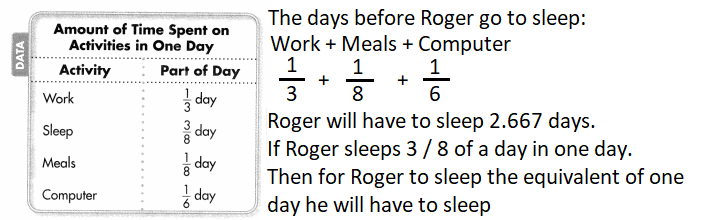

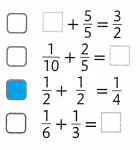
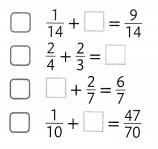

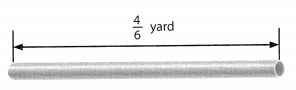

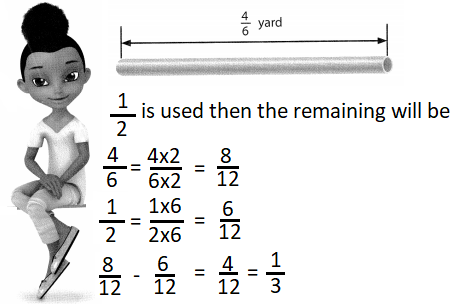


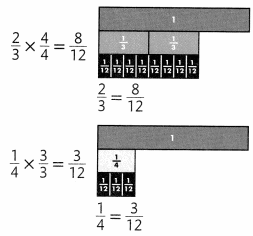
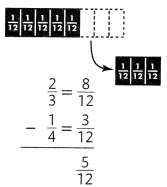
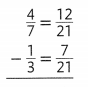
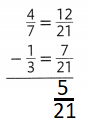
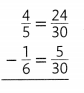
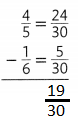
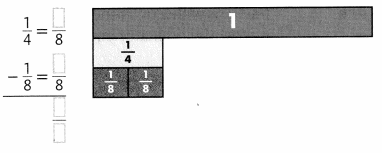
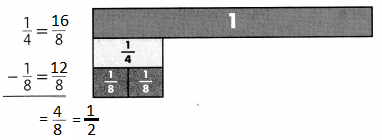

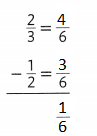
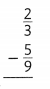
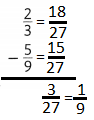
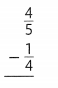
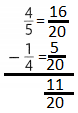
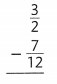
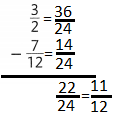
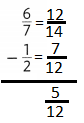

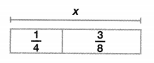

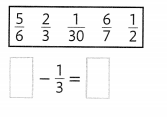


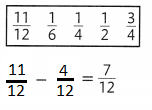





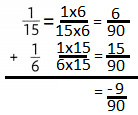
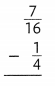

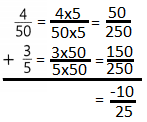
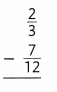

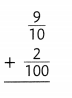
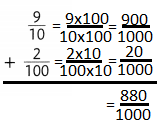




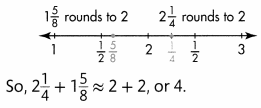

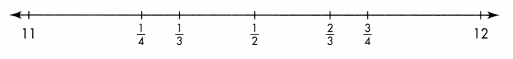

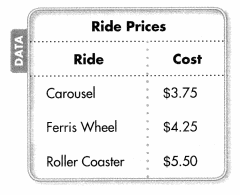

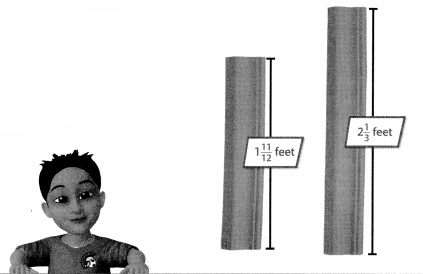
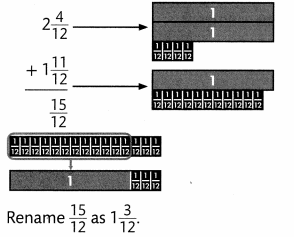

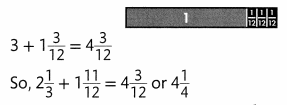





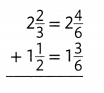
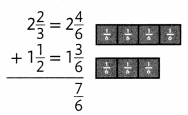
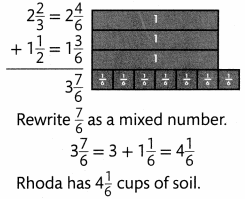
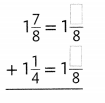
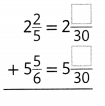

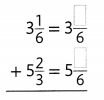

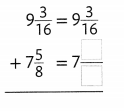

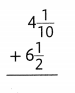
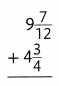
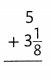





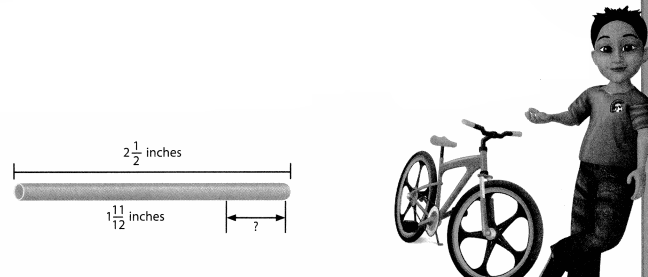






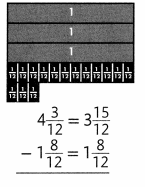

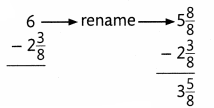
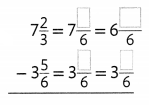
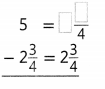

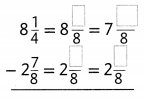
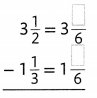

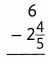
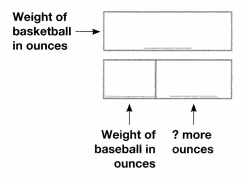
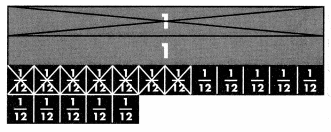

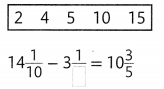
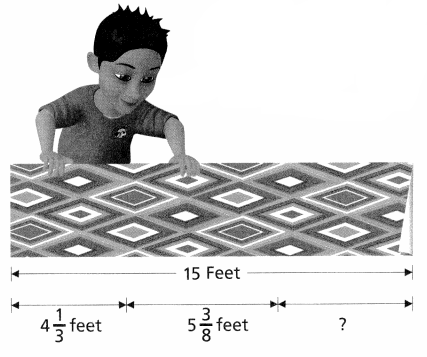

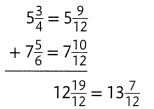

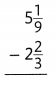
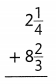
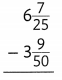
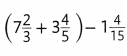
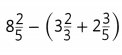
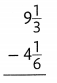
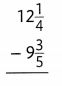
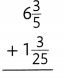
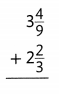
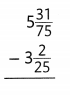

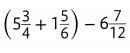
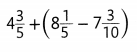

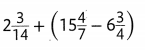
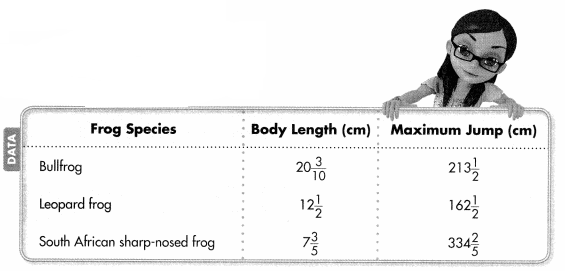
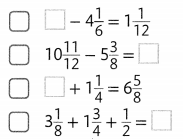
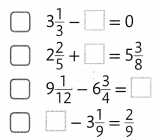
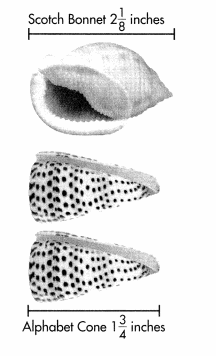



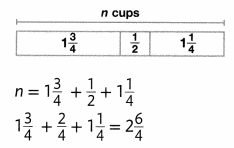







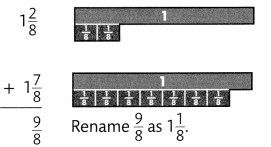

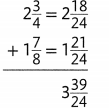
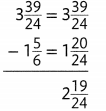
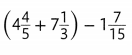



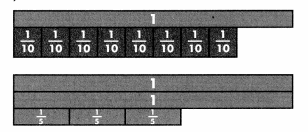









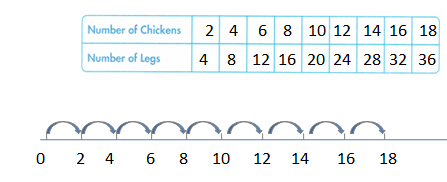

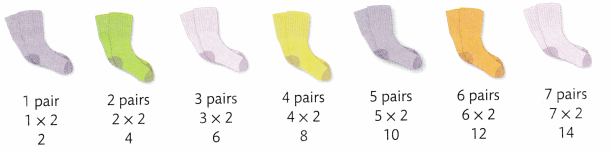





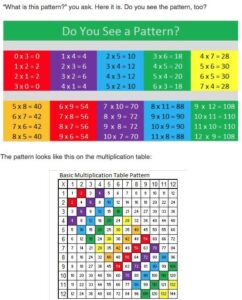
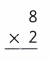

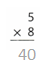



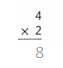

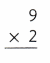

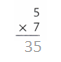







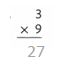
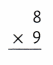

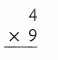
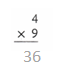
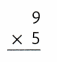
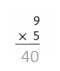
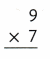
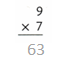
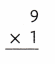
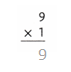










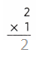

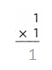










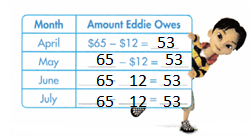



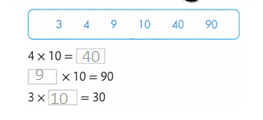


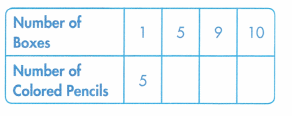


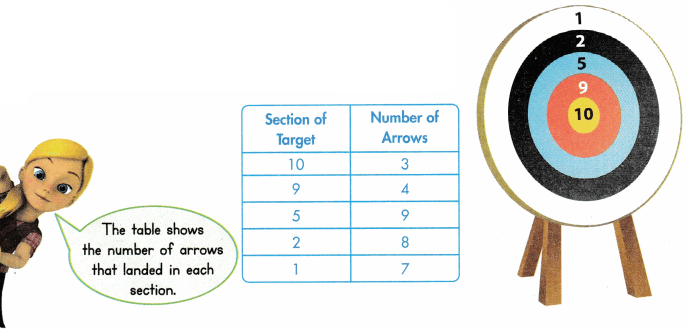
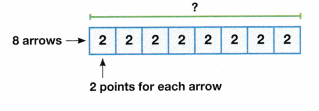
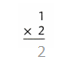
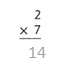

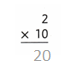
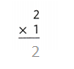
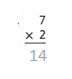
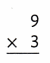
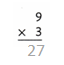
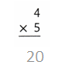










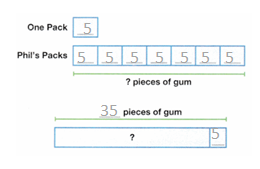

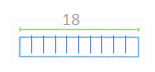





 .
.

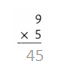




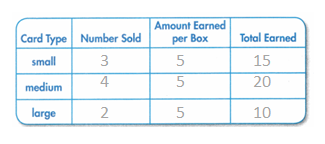



















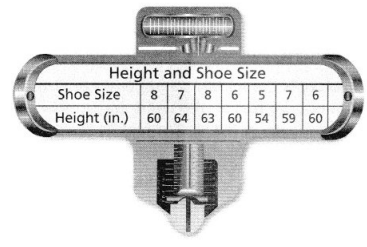
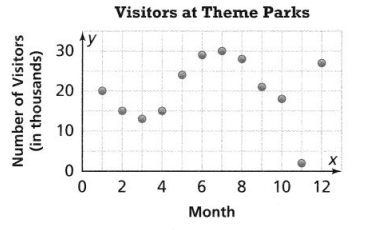

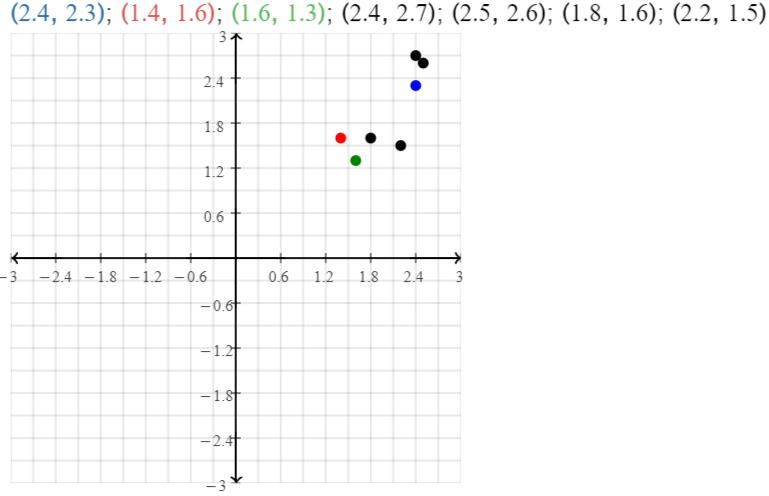
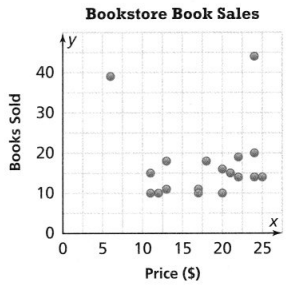

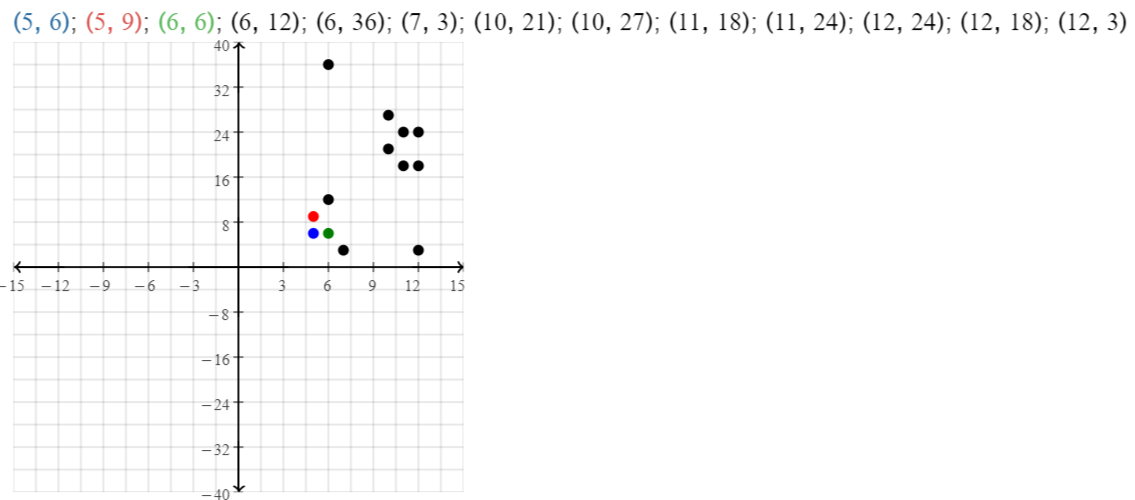











 x +
x + 

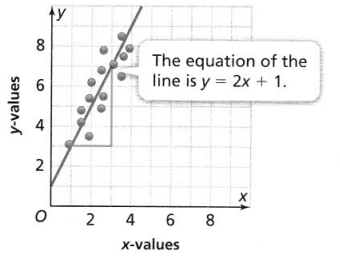






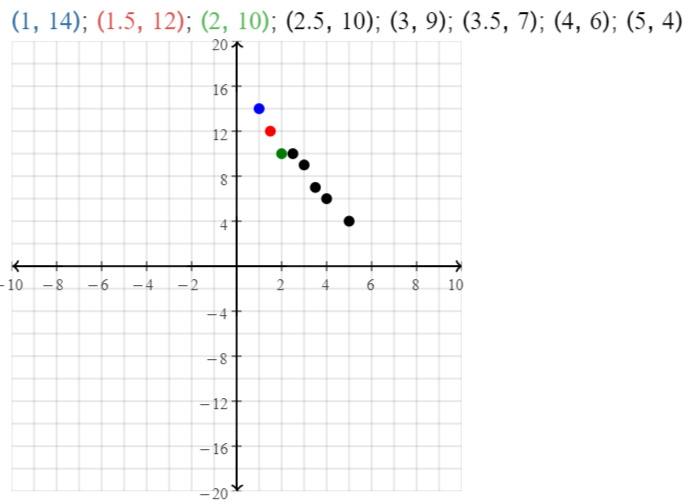


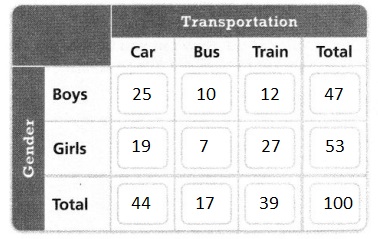



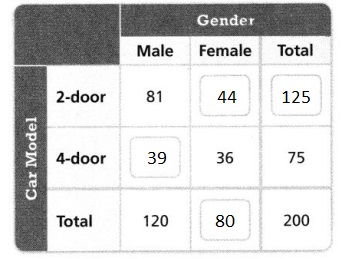

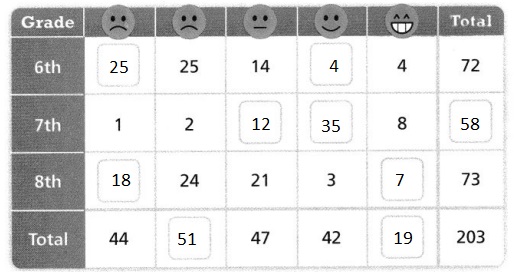
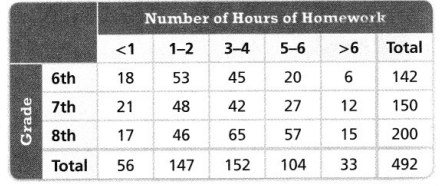

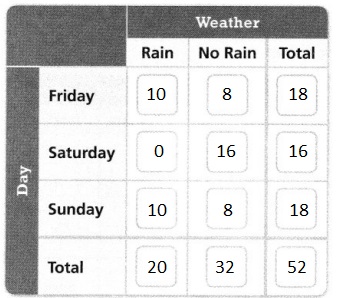
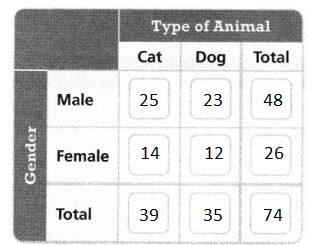
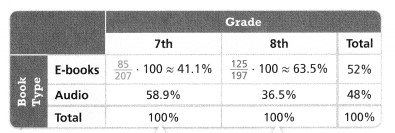

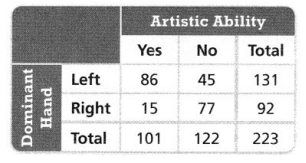
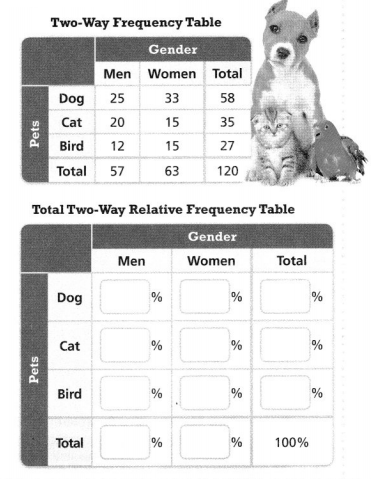
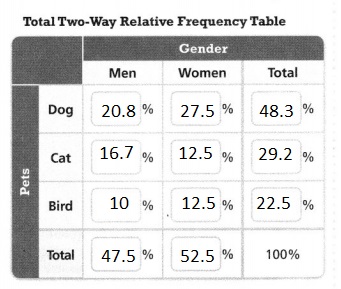
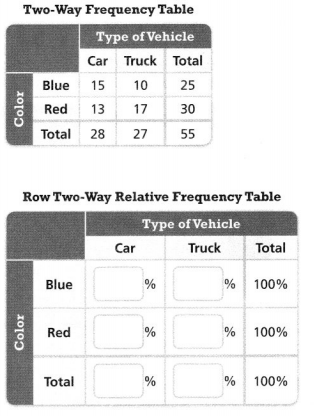
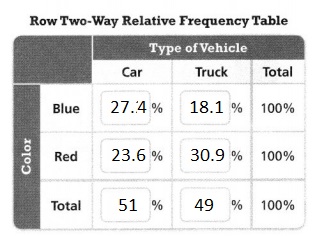


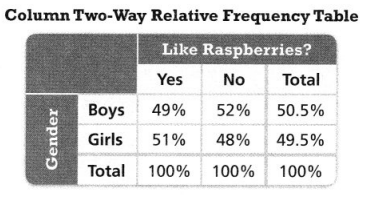
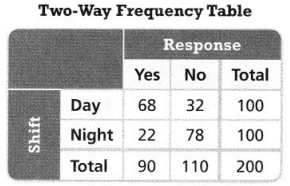










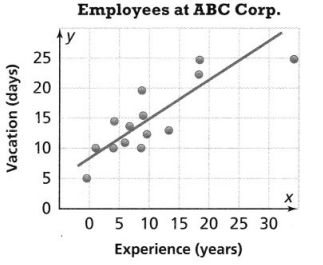

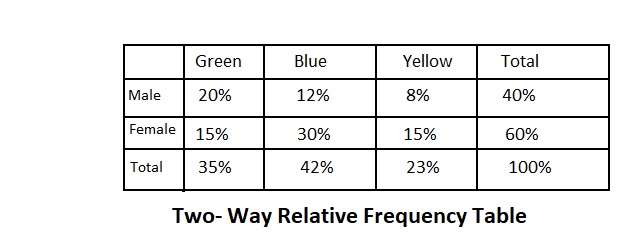























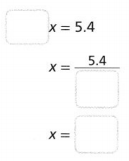








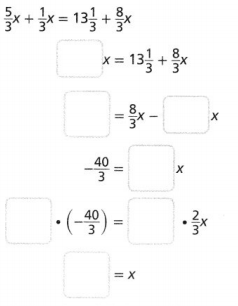


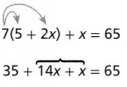
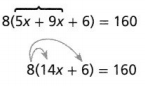











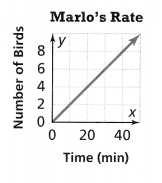



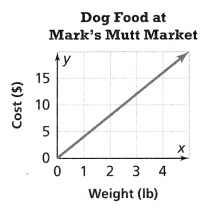
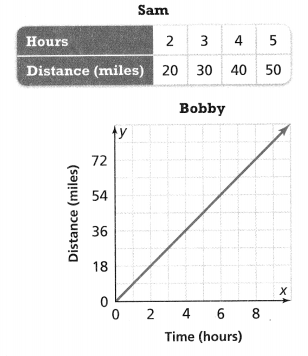



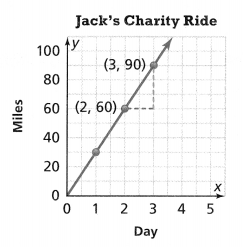

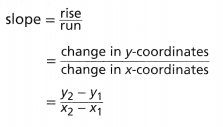
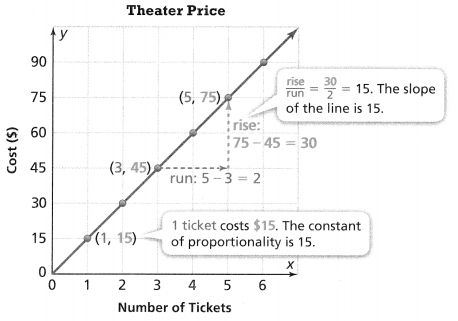
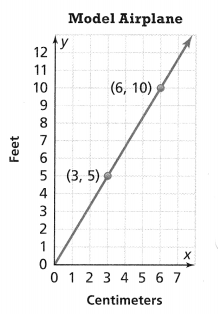
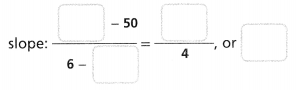
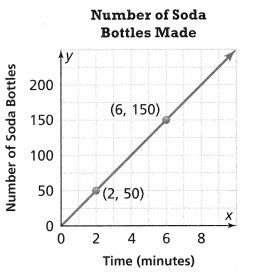




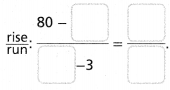 . The equation of the line is y =
. The equation of the line is y = 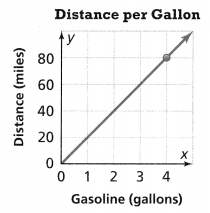

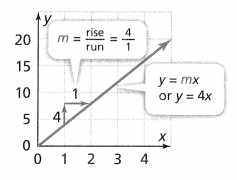
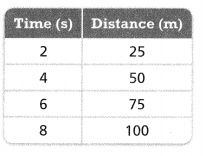
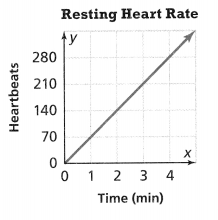
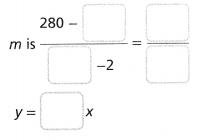


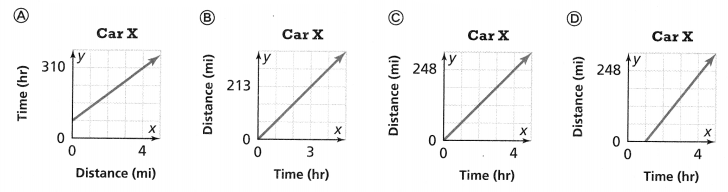








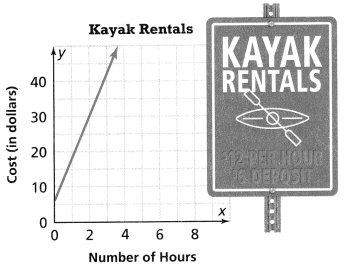

















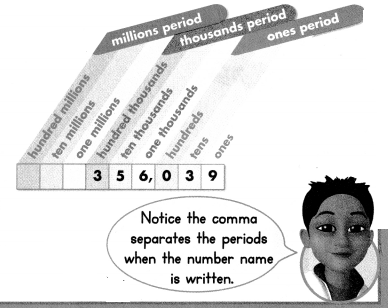
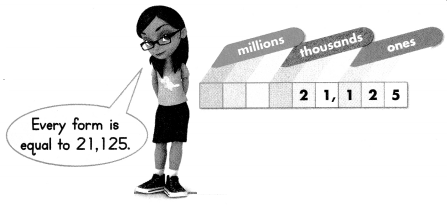

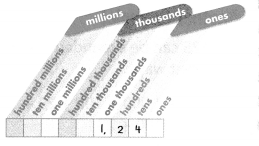
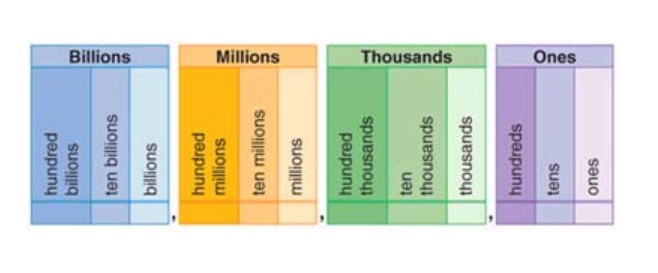
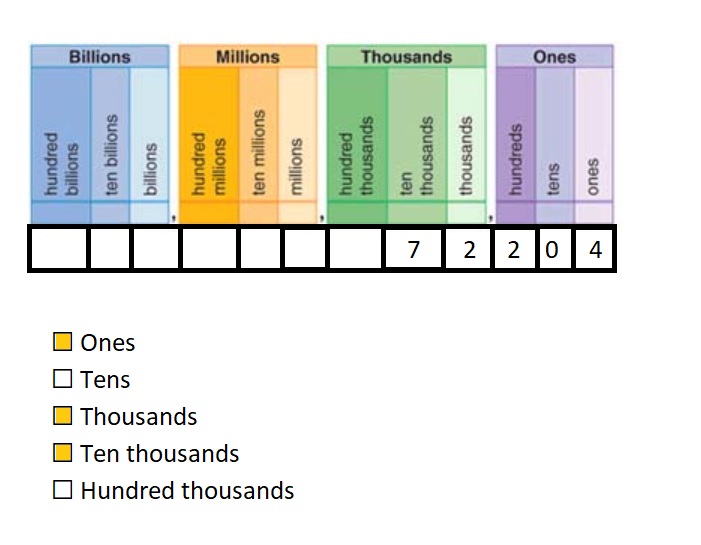





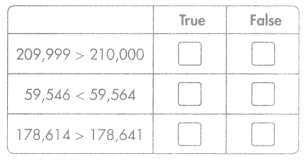
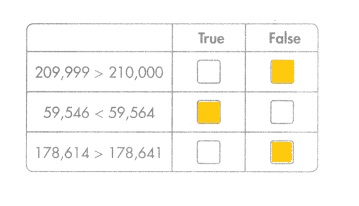






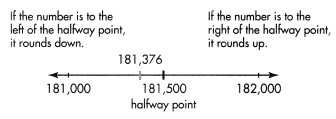


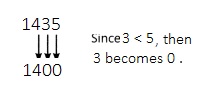






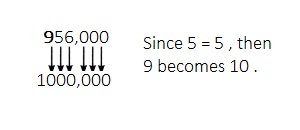
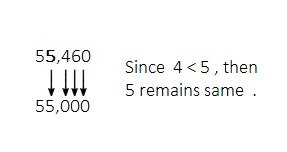
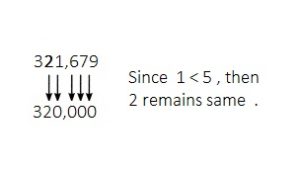

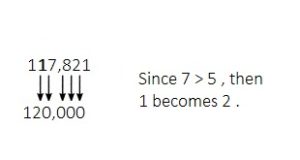
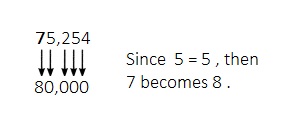

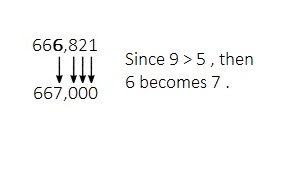


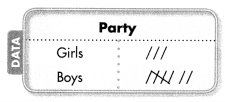

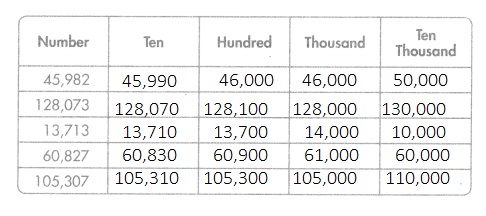





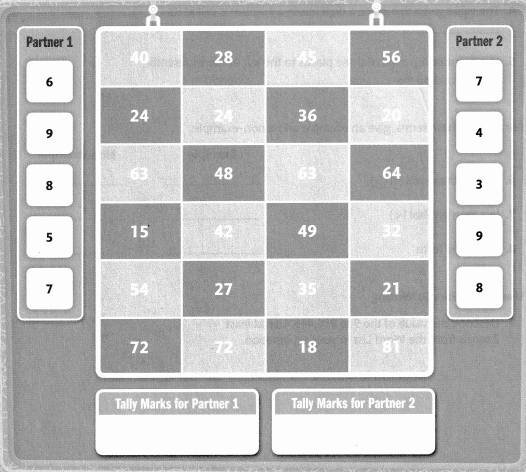
























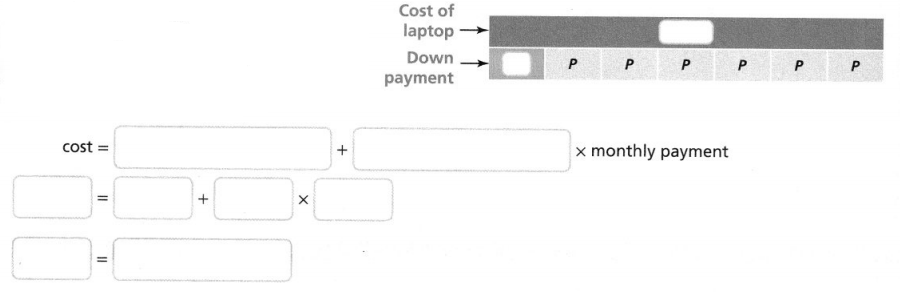 Answer:
Answer: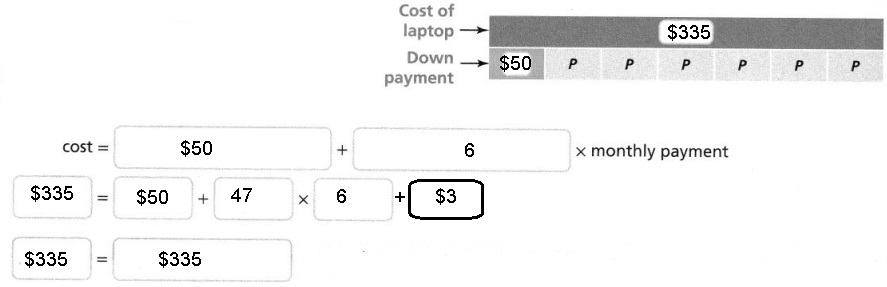

 Do You Understand?
Do You Understand?